单纯形法之单纯形表
单纯形法新版

1 2
2 1
1 0
10,A 中的2阶可逆子阵有
1
B 1
0
10,其相应的基向量为P3
,
P 4
,
基变量为x
3
,
x
,X
4
B1
x 3 ; x 4
1
B 2
2
2 1
,
其相应的基向量为P 1
,
P 2
,
基变量为x
1
,
x
2
,
X
B2
x 1 。 x 2
问题:本例旳A中一共有几种基? —— 6个。
一般地,m×n 阶矩阵A中基旳个数最多有多少个? — —C m 个。 n
p 1
7
(0 0
0) 4
7;
3
360 90
3
4
[ ] 中表达进基列与出基行旳交叉元,下一张表将实 施以它为主元旳初等行变换(称高斯消去)。措施是: 先将主元消成1,再用此1将其所在列旳其他元消成0。
C X B b1
B
B
0
x 3
360
0
x 4
200
0
x 5
300
0
x 3
240
0
x 4
50
(1)先将模型化为原则型
Maxz 7 x1 12x2
9x 1 4x 2 x 3
5x 2 10 x
2
x 4
200
x 300 5
x
1, x
2, x , x , x
3
4
5
0
(2) 拟定初始基可行解、检验
1
B 0
1
,
B
b1
第四节 单纯形法的计算步骤

上表中由于所有σ 上表中由于所有 j>0 ,表明已求得最优解 x1=4, x2=2, x3=0, x4=0, x5=0, x6=4, , , , , , , Z=14。 。 当确定x 为换入变量计算θ值时 值时, ◆当确定 6为换入变量计算 值时,有两个相 同的最小值: 同的最小值:2/0.5=4,8/2=4。任选其中一 , 。 个作为换出变量时, 个作为换出变量时,则下面表中另一基变 量的值将等于0,这种现象称为退化 退化。 量的值将等于 ,这种现象称为退化。含有 一个或多个基变量为0的基可行解称为 的基可行解称为退化 一个或多个基变量为 的基可行解称为退化 的基可行解。 的基可行解。
18
迭代
xB
次数
cB
x1
x2
x3
x4
x5 bi
θi
50
x1
100
0
0
0
50 0 100
1 0 0
0
0 0 1
0
1 -2 0
- 50
0 1 0
0
-1 1 1
- 50
50 50 250 -27500
2
x4 x2
σj
2010年8月
管理工程学院
18
《运筹学》 运筹学》
19
所有的检验数 σ j ≤ 0, 此基本可行解: 此基本可行解:
2010年8月
管理工程学院
5
《运筹学》 运筹学》
6
c1 … cl b b1´
⋮
c j→ cB c1
⋮
… cm … xm …0 …⋮ 0 …1 …
⋮
…cj …xj …a1j´ …⋮ a2j´ …⋮ amj´
… ck … cn … xk …xn …0 …⋮ 1 …0
运筹学单纯形法的计算步骤

b2
0… 0
a2,m+1
…
a2n
2
…
…
…
…
cm xm
bm
0… 1
am,m+1
…
amn
m
-z -z 值 0 … 0
m+1
…
n
XB 列——基变量, CB 列——基变量的价值系数(目标函数系数) cj 行——价值系数,b 列——方程组右侧常数 列——确定换入变量时的比率计算值
下面一行——检验数, 中间主要部分——约束方程系数
(4).根据max(j > 0) =k,拟定xk为换入变量,按 规则计算 =min{bi/aik\aik>0}
可拟定第l行旳基变量为换出变量。转入下一步。
(5).以 alk 为主元素进行迭代(即用高斯消去法或称为旋转变 换),把 xk 所对应的列向量变换为(0,0,…,1,…,0)T,将
XB 列中的第 l 个基变量换为 xk,得到新的单纯形表,返回(2)。
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 (2 ) 4
0 1 0 0 1/4 12
-z
-13
0
0 -2
0 1/4
X(2)=(2,3,0,8,0)T, z2 =13
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 4 0 x5 4 3 x2 2
量,给出第一阶段的数学模型为:
min = x6+x7
x1-2x2+x3+x4
单纯形表

xm非基1.变..量. XxNn
a1m1 ...a1n a 2 m 1N...a 2 n ......非基阵
a mm1 ...a mn cm1 N cn
b
b1
b2
bm 0
单纯形表
单纯形表结构
c j
C c12 c21 0
已知 C X
B
B
b
x1
x2
c1 x1 b '1
18
表格单纯形法求解步骤
第一步:将LP化为标准型,并加以整理。
引入适当的松驰变量、剩余变量和人工变量 ,使约束条件化为等式,并且约束方程组的系数 阵中有一个单位阵。
确定初始可行基,写出初始基本可行解
19
第二步:最优性检验
计算检验数,检查: 所有检验数是否≤ 0?
是——结束,写出最优解和目标函数最优值; 还有正检验数——检查相应系数列≤ 0?
是——结束,该LP无“有限最优解”! 不属于上述两种情况,转入下一步—基变换。
确定是停止迭代还是转入基变换?
20
第三步:基变换
选择(最大)正检验数对应的系数列 为主元列,主元列对应的非基变量为换 入变量;
最小比值对应的行为主元行,主元行 对应的基变量为换出变量。
确定进基变量和出基变量。
21
第四步 换基迭代(旋转运算、枢运算)
12 18
x1, x2 0
补充作业:请用单纯形表求解
minZ = x1-2x2+3x3+2x4
3x1-3x2-3x3+6x4=1
-x1+ x2+
x4 =1
xj>=0
min 单纯形表结构 i
单纯形法表的解题步骤
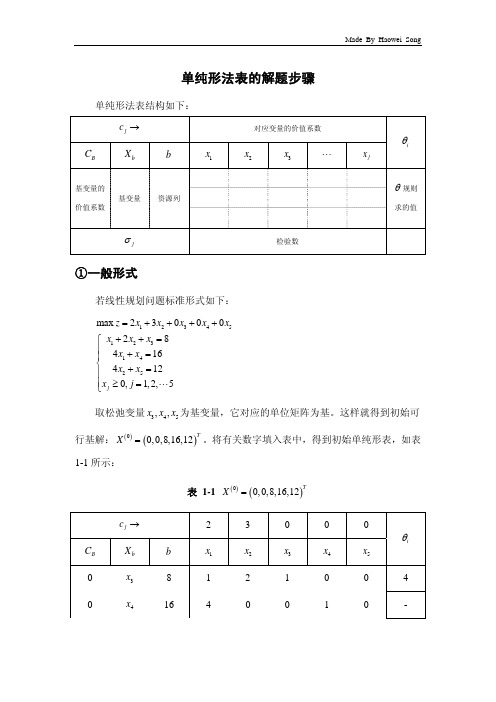
单纯形法表的解题步骤单纯形法表结构如下:j c →对应变量的价值系数i θB Cb Xb1x 2x 3x " j x基变量的价值系数基变量 资源列θ规则求的值j σ检验数①一般形式若线性规划问题标准形式如下:123451231425max 23000284164120,1,2,5j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨+=⎪⎪≥=⎩"取松弛变量345,,x x x 为基变量,它对应的单位矩阵为基。
这样就得到初始可行基解:()()00,0,8,16,12TX =。
将有关数字填入表中,得到初始单纯形表,如表1-1所示:表 1-1 ()()00,0,8,16,12TX =j c →2 3 0 0 0i θB C b X b1x 2x 3x 4x 5x0 3x 8 1 2 1 0 0 4 04x16 4 0 0 1 0 -5x12 0 [4] 0 0 1 3j σ2 3 0 0 0若检验数均未达到小于等于0,则对上表进行调整。
选择上表中检验数最大的列,该列对应的非变量为入基变量;再应用θ规则该列对应的各基变量对应的θ值,选出其中最小的一行,该行对应的基变量为出基变量。
修改单纯形表,对各行进行初等变换,确保基变量组成的矩阵为单为矩阵。
修改后的单纯形表如表1-2所示:表 1-2 ()()10,3,2,16,0TX =检验数12,0σσ>,则进行继续调整,调整后的单纯形法表如表1-3所示:表 1-3 ()()22,3,0,8,0TX =表1-3中, 50σ>,则继续进行调整,调整结果如表1-4所示:表 1-4 ()()34,2,0,0,4TX =检验数0j σ≤,这表示目标函数值已不可能再增大,于是得到最优解:()()3*4,2,0,0,4TX X ==*14z =②带人工变量现有线性规划问题:12312312313123min 321142321,,0z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解,在约束条件中加入松弛变量4x ,剩余变量5x ,人工变量6x ,7x 得到:1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨−++=⎪⎪≥=⎩"其中,M 是一个任意大的正数。
运筹学单纯形法

单纯形表
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
Cj CB XB b 0 0 Z X3 3 X4 1 0 1 2 0 0
标准化
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
X1 X2 X3 X4 1 0 1 1 1 2 1 0 0 0 1 0
Z=x1+2x2 x1+x2+ x3 =3 x2 +x4=1 单纯形表
Cj
1
2
0
0
单纯形法原理 单纯形表 CB XB b
z=x1+2x2 x3 =3-x1-x2 x4=1 -x2
x2进基,x4离基
X1 X2 X3 X4
3/1 11
0
1 0
1 1
1 1
2 2 0 1 0 2 0 1 0 0 1 0 -1 0
max z=x1+2x2 s.t. x1+x2+x3 =3 x2 +x4=1 x1, x2, x3, x40
x1=0
(x1,x2,x3,x4)= (0,1,2,0), z=2 C (x1,x2,x3,x4)= (2,1,0,0), z=4,最优解
B
x4=0 x3=0
(x1,x2,x3,x4)= (0,0,3,1), z=0
1 0
0 0
0 1
0
CB XB b 0 2 Z Cj CB XB b 1 2 Z X1 2 X2 1 4 X3 2 X2 1 2 1 1 0 0
X1 X2 X3 X4 1 0 1 1 0 0 0 -1 1 -1
单纯形法的表格解法

n
bi aij xj. i 1, 2,L , m
j m1
把以上的表达式带入目标函数,就有
m
n
z c1x1 c2 x2 L cn xn ci xi c j x j
i 1
j m 1
其中:
n
n
z0
c j z j x j z0 j x j
j m 1
j m 1
0 0 1 1 0 0 0 1 0 那么显然所求得的基本解一定是基本可行解,这个单位矩阵或由单位矩阵各列向 量组成的基一定是可行基。实际上这个基本可行解中的各个变量或等于某个bj或等 于零。
.
§1 单纯形法的基本思路和原理
在本例题中我们就找到了一个基是单位矩阵。
1 0 0
B2 0 1 0
0 0 1
m
z0 cibi , j c j z j ;
a1 j
i1 m
z j ciaij c1a1 j c2a2 j L
i 1
cmamj
c1, c2 ,L
, cm
a2
j
M
amj
c1, c2 ,L , cm p j .
§2 单纯形法的表格形式
上面假设x1,x2,…xm是基变量,即第i行约束方程的基变量正好是xi,而 经过迭代后,基将发生变化,计算zj的式子也会发生变化。如果迭代后的 第i行约束方程中的基变量为xBi,与xBi相应的目标函数系数为cBi,系数列
1. 最优性检验的依据——检验数σj 一般来说目标函数中既包括基变量,又包括非基变量。现在我们要求
只用非基变量来表示目标函数,这只要在约束等式中通过移项等处理就可 以用非基变量来表示基变量,然后用非基变量的表示式代替目标函数中基 变量,这样目标函数中只含有非基变量了,或者说目标函数中基变量的系 数都为零了。此时目标函数中所有变量的系数即为各变量的检验数,把变 量xi的检验数记为σi。显然所有基变量的检验数必为零。在本例题中目标 函数为50x1+100x2。由于初始可行解中x1,x2为非基变量,所以此目标函 数已经用非基变量表示了,不需要再代换出基变量了。这样我们可知 σ1=50,σ2=100,σ3=0,σ4=0,σ5=0。
单纯形法

•单纯形计算过程特别说明
1. 如何从单纯形表判断最优解
1)唯一最优解判别:最优表中所有非基变量的检验数大于零,则线性规划具有唯一最优解.
2)多重最优解判别:最优表中存在非基变量的检验数为零,则线性规划具有多重最优解(或无穷多最优解).
<0且a ik≤0(i=1,…,m)则线性规划具有无界解.
3)无界解判别:某个σ
k
4)无可行解的判别:当用大M单纯形法计算得到最优解并且存在Ri>0时,则表明原线性规划无可行解.
5)退化解的判别:
a)存在某个基变量为零的基本可行解;
[此时可能出现循环迭代而永远找不到最优解.该情况是由比值相同造成的.可以证明:当出现比值相同时,按下标最小的基变量作为换出变量可避免出现循环,具体可参阅有关文献];
b)人工变量在最优表的基中,但人工变量的取值为零.
[此种情况是由于存在多余约束(A不行满秩)造成的,可通过消去多余约束加以解决]
3. 计算过程需要特别注意的问题:
在确定了进基变量和出基变量,即确定主元后,单纯形变换的计算方法:
1)主元所在的行所有元素除以主元值,将主元变换成1;
2)用主元行的合适倍数加至其它各行(此时,改变的是其它各行,而主元行不发生变化!),以将主元列除主元外的其它元素变换成零。
注:采用以上变换方法(而不是任意初等变换)是为了保证:原来在基中并为发生改变的基变量,在变换计算后其对应的基向量不能发生改变。
也就是说:在任何时候,单纯形表中的所有基向量构成的矩阵均为单位矩阵!。
第三章3 单纯形法2

第二节 单纯形法
那么纯收入就为 140-240=- (相当于检验数小于零) 140 元, 纯收入就为 140-240=-100 相当于检验数小于零) 那么 , 说明炒股无利可图。 还有人们常说的炒股打了个平手 没有赚也没有 ( 说明炒股无利可图。 ,实际上已经亏了 亏) 实际上已经亏了 240 元。因为这笔钱不去炒股的话存在银行里 , 元的收入, 240=还可以有 240 元的收入,所以纯收入为 0-240=-240 元。 上面分析过,既然生产产品甲还有利可图, 上面分析过,既然生产产品甲还有利可图,那么就要把 x1 转化 为基变量, 将有一个被换出成为非基变量。 为基变量,原来是基变量的 x3、x4 将有一个被换出成为非基变量。 min{15/3,6/(3/5)}=5, 将被换出。 因为 min{15/3,6/(3/5)}=5,可知 x4 将被换出。通过行线性
第二节 单纯形法
这时的实际情况是没有生产任何产品,所以每一种产 这时的实际情况是没有生产任何产品, 品的机会费用都为零(关于机会费用的详细说明参考课 品的机会费用都为零( 本 23 页的内容) 检验数 Cj-Zj=利润-机会成本,它的值 的内容) ,检验数 , 利润-机会成本, 就是这种生产条件下生产第 j 种产品可能得到的纯利润, 种产品可能得到的纯利润, 从中可以看出,生产丙产品可能获得的最大的利润(因 从中可以看出,生产丙产品可能获得的最大的利润( 为 max{4,1,5}=5 ) 所以作为一个生产决策者首先应 max{4, ,所以作为一个生产决策者首先应 , 当想到生产丙产品。 当想到生产丙产品。
第二节 单纯形法
5 3 1 0 -1/3 0 1/3 -1/3 1 1 -1/5 2/5 1 x2 -1/3 1 11/3 -8/3 5 x3 0 1 5 0 0 x4 1/3 -1/5 1/3 -1/3 0 x5 -1/3 2/5 2/3 -2/3
第3章05-单纯形表法

第3章05单纯形表法同学们大家好,前面我们讲了单纯形法的原理,它的整个过程看似很复杂,但实际上,单纯形法的全部计算过程,可以简单地在一张类似增广矩阵的表格上进行,这种表格我们称为单纯形表,所以,今天我们就来学习线性规划模型的单纯形表法。
给定一个可行基,可以画出一张单纯形表。
单纯形表的行标是n个变量以及右端项b,列标是m个基变量以及检验数行σ。
所以,用矩阵的形式把它表示出来,就如下表所示我们注意到,像B,所以,是与原方程组等价的。
最后一行是检验数C-C B B-1A,右下角是-C B B-1b,它恰好是这个基B所对应的可行解的目标函数值的相反数。
用单纯形表法求解线性规划模型时,有下面的步骤:单纯形表法求解线性规划问题的步骤:Step1.转换一般的线形规划模型为标准型,并写出A,b,C。
Step2找初始基本可行解,写出B,B-1,X B,C B。
Step3计算单纯形表中的各矩阵B-1A,B-1b,C-C B B-1A,-C B B-1b,并构造初始单纯形表。
Step4判断基本最优解。
Step5换基迭代,返回Step4。
第一步是将一般的线性规划模型转化为标准形,并写出约束矩阵A,右端项b,以及价值向量C。
第二步,找初始的基本可行解。
根据上一讲单纯形法的原理,你要注意的是,我们总是从约束矩阵A里面选一个单位阵出来作为初始基,在右端项非负的条件下,这样选出来的单位阵一定是可行基,也就是找到了初始的基本可行解。
而如果约束矩阵A中没有单位阵,我们将会通过引入人工变量构造出一个单位阵,这种构造方法我们将在后面进行详细介绍。
初始基选出来之后,我们就能写出B,B-1,以及基变量X B和基变量所对应的价值向量C B。
第三步,计算B-1A,B-1b,C-C B B-1A,-C B B-1b,这样就可以把初始单纯形表写出来。
第四步,判断当前的基本可行解是不是最优解?按照我们上一讲介绍的单纯形法的原理,如果检验数行中所有的检验数都小于等于0,当前的基本解就是最优解;如果有一个非基变量的检验数是正的,而且它所对应A中的列的项都小于等于0,那么这个时候是无界解。
单纯形法解题步骤

三、单纯形法的解题步骤第一步:作单纯形表.)(1)把原线性规划问题化为标准形式;)(2)找出初始可行基,通常取约束方程组系数矩阵中的单位矩阵;)(3)目标函数非基化;)(4)作初始单纯形表.第二步:最优解的判定.(1) 若所有检验数都是非正数,即,则此时线性规划问题已取得最优解.(2) 若存在某个检验数是正数,即,而所对应的列向量无正分量,则线性规划问题无最优解.如果以上两条都不满足,则进行下一步.第三步:换基迭代.,并确定所在列的非基变量为进基变量.(1)找到最大正检验数,设为(2)对最大正检验数所在列实施最小比值法,确定出主元,并把主元加上小括号.主元是最大正检验数所在列,用常数项与进基变量所对应的列向量中正分量的比值最小者;替换出基变量,从而得到新的基变量.也就是主元所在(3)换基:用进基变量(4)利用矩阵的行初等变换,将主元变为1,其所在列其他元素都变为零,从此得到新的单纯形表;(5)回到第二步,继续判定最优解是否存在,然后进行新一轮换基迭代,直到问题得到解决为止.例3 求.解(1)化标准型:令,引进松弛变量,其标准型为求(2)作单纯形表:在约束方程组系数矩阵中的系数构成单位矩阵,故取为基变量,目标函数已非基化了,作初始单纯形表并“换基迭代”(见表6.8).表 6.8(3)最终结果:此时检验数均为非正数,线性规划问题取得最优解,最优解为标函数取得最优值.目性规划问题的最优解为:.原线目标函数的最优值为14,即.例4 用单纯形方法解线性规划问题.求.解此数学模型已是标准型了,其中约束方程含有一个二阶单位矩阵(1、2行,3、4列构成),取为基变量,而目标函数没有非基化.从约束方程找出,,代入目标函数, 经整理后,目标函数非基化了.作单纯形表,并进行换基迭代(见表6.9).最大检验数,由最小比值法知:为主元,对主元所在列施以行初等变换,基变量出基,非基变量进基.表 6.9目前最大检验数,其所在列没有正分量,所以该线性规划问题没有最优解.例5用单纯形方法解线性规划问题.求解此数学模型已是标准型了,其中约束方程含有一个二阶单位矩阵,取为基变量,而目标函数没有非基化.从约束方程找出,,代入目标函数,经整理得,目标函数已非基化.作单纯形表,并进行换基迭代(见表6.10).最大检验数,由最小比值法知:为主元,对主元所在列施以行初等变换,基变量出基,非基变量x2进基,先将主元化为1,然后再将主元所在列的其他元素化为零.表 6.10至此,检验数均为非正数,故得基础可行解.原问题的最优解为:.最优值为6,即.如果我们再迭代一次,将基变量出基,非基变量进基(见表6.11).表 6.11可得到另一个基础可行解,原问题的最优解为:,最优值仍为6,说明该线性规划问题有无穷多最优解,其最优解均为6.如何知道线性规划问题有无穷多最优解呢?这主要反映在单纯形表中.如果非基变量所对应的检验数为0,我们可对此列继续进行换基迭代,就可以得到另一个基础可行解.以此作下去,可得到许多基础可行解,即相对应的最优解有无穷多个.(4) 011 0。
单纯形法

单纯形法一、单纯形法的原理线性方程组的解:⎩⎨⎧=----=+-+-4322425432154321x x x x x x x x x x (1) 5个未知数,两个方程组。
方程的解多于1个。
两种初等变换:51)方程组的任一方程乘上一个不为零的数。
2)方程组的任一方程两边同乘上一个常数,分别加到另一个方程的两边。
式(1)做变换得到:(①×-1)⎩⎨⎧=-+-=+-+-2322242543254321x x x x x x x x x (2) 式(2)做变换得到:(②×2)⎩⎨⎧=-+-=---232642354325431x x x x x x x x (3)方程组(1)、(2)、(3)同解,可令0543===x x x 。
得到:61=x ,22=x 。
选择3x ,4x ,5x 不同的值,相应地有不同的1x 和2x 的值,因此方程组有多组解。
基本变量:如果变量i x 的系数在某一个方程为1,而在其它所有方程为0,则称i x 为该方程组中的基本变量。
非基本变量:凡不是基本变量的变量都叫做非基本变量。
1x ,2x 为基本变量;3x ,4x ,5x 为非基本变量。
旋转运算:运用初等变换,可使一给定变量化为基本变量,这一运算,成为旋转运算。
基本变量的个数,与方程的个数相同。
基本解:设非基本变量为0,求得相应的基本变量的值,得到一组解,这组解称为基本解。
基本可行解:基变量的值为非负时的基本解称为基本可行解。
单纯形法的思路;1)先不考虑目标函数,从满足约束条件开始,寻求一个初始基本可行解; 2)求具有较佳目标函数值的另一个基本可行解,以改进初始解;3)对目标函数做有限次的改善。
当某一个基本可行解不能再得到改善时,即求得最优解,单纯形法结束。
二、单纯形算法例:54321325max x x x x x Z +-++= 约束条件为:⎪⎩⎪⎨⎧≥≥≥≥≥=+++=+++0,0,0,0,0743********53214321x x x x x x x x x x x x x (5) 以上线性规划问题中,具有: 1)全部变量非负;2)全部约束条件都是等式;5 3)右端常数都是正的。
单纯形法

XB =B-1b-B-1NX N 代入目标函数,使目标函数用非基变量
表示,即:
Z=cT X=(cTB
cTN) XB XN =cTBXB +cTN XN =cTB (B-1b-B-1NXN )+cTN XN
=cTBB-1b+(cTN -cTBB-1N)XN cBT B-1b+σNXN cBT B-1b+(σm+1,σm+1,
Z=CTBB-1b+(σm+1 ,
σm+k ,
xm+1
σ
n
)
CTB B-1b+σ m+k
xn
因为 m+k 0, 故当λ→+∞时,Z→-∞。
18
表格单纯形法
B
N
b
CBT
CNT
I
B-1N
B-1b
0
CNT -CBT B-1N
19
可将这些重要结论的计算设计成如下一个简单的表格, 即单纯形表来完成:
min z=-6x1-4x2
x3 =100-2x1-3x2
+x4 =120-4x1-2x2
令 有 则有:
XN=(0,0)T XB=(100,120)T X(1)=(0,0,100,120)T为对应于基B1的基可行解。
问:
X(1)是否最优呢?——否
因为: x1和x2在目标函数中的系数为正,当x1↑,z ;x2↑,z 。
础上寻找一个新的基本可行解,并使目标函数值有所改善。
具体做法是:
先从检验数为负的非基变量中确定一个换入变量,使它从非基
纯形法之单纯形表

对于大规模问题,单纯形法可能需要较长时间才能得 到结果。
未来研究方向
改进算法效率
01
研究更高效的单纯形算法,以处理大规模问题。
扩展应用领域
02
将单纯形法应用于更多类型的优化问题,如非线性规划、整数
规划等。
与其他算法结合
03
探索单纯形法与其他优化算法的结合,以获得更好的优化效果。
感谢您的观看
金融投资优化
金融投资是企业实现资产增值的重要手段,通 过单纯形表的应用,可以优化投资组合,降低 投资风险和提高投资回报。
单纯形表可以帮助企业确定最佳的投资组合方 案,包括股票、债券、基金等金融产品的配置 比例和投资时机,以实现最优的投资收益。
单纯形表还可以考虑投资过程中的约束条件, 如投资金额、风险承受能力等,以实现更稳健 和理性的金融投资决策。
单纯形表的概念
单纯形表是线性规划问题的一种表格形式表示,包含了决策变量、约束条件和目标函数的系数、常数项等信息 。
单纯形表由标准形式和松弛形式两种类型组成,标准形式包含了所有非负约束的限制条件,而松弛形式则去掉 了这些限制条件。
单纯形表的应用场景
单纯形表广泛应用于生产计划、资源分配、运输优化等领域,通过求解线性规划 问题来找到最优解决方案。
单纯形表在数学建模中的应用
线性规划问题
线性规划是一种数学优化技术,旨在找到一组变量的最优解 ,使得一组线性不等式约束下的线性函数达到最大或最小值 。在解决线性规划问题时,单纯形表可以用来表示和解决线 性规划模型,通过迭代算法找到最优解。
线性规划问题在现实生活中应用广泛,如资源分配、生产计 划、运输问题等。单纯形表的应用使得线性规划问题的求解 更加简便和高效。
02
单纯形法

z z0 j x j
j m 1
n(1.2.21)称 j ( j m 1 ,, n ) 为检验数。
定理1.2.1 设(1.2.17)和(1.2.21)是最大
化线性规划问题关于当前基本可行解x*的两个典式。
若关于非基变量的所有检验数σ j≤0成立,则当前
基本可行解x*就是最优解。 将σ j≤0称为最大化问题的最优性准则。显然, 对于最小化问题最优性准则应是σ j≥0。
30x1 + x3 = 160 - 20x2 5x1 = 15 - x2 - x4 (1.2.6) x1 + x5 = 4 进一步分析,用消元法将(1.2.6)中x1的系数列向量 (30,5,1)T 化成(1.2.3)中x4的系数矩阵(0,1,0)T
的形式。得到:
x3 = 70 - 14x2 + 6x4 x1 = 3 - 1/5x2 - 1/5x4
(b'1, b'2, … , b'm ,0 , …, 0)T是当前基本可行解。若有一个非
基变量xm+t的检验数σ
m+t>0,且xm+t对应的系数列向量
P'm+t=(a'1,m+t,a'2,m+t,„,a'm,m+t)中,所有分量a'i,m+t≤0,则该 线性规划问题具有无界解(或称无最优解)。
1.2.2 单纯形表
x2= 5 - 1/14x3 + 3/7x4
x1 = 2 + 1/70x3 - 2/7x4
(1.2.11)
x5 = 2 - 1/70x3+ 2/7x4
将(1.2.11)代入目标函数式,得到用非基变 量x 3
1.4单纯形法的计算步骤

−z
x1
x2
L xm
xm+1
L xn L L a1n a2n M
0 1 0 L 0 a1,m+1 1 L 0 a2,m+1 0 0 M M M M 0 0 0 L 1 am,m+1 cm+1 1 c1 c2 L cm … -z+c1x1+c2x2+…+cmxm+cm+1xm+1+ +c
基变量 0
-z
3.确定主元素 3.确定主元素 确定 1.计算检验数, 1.计算检验数,由它 计算检验数 确定为换入变量
计算θ 2. 计算θ,由它确定为 换出变量
(2)以[4]为主元素进行旋转运算或迭代运算, [4]为主元素进行旋转运算或迭代运算, 为主元素进行旋转运算或迭代运算
c j→ CB 0 0 3 -z XB x3 x4 x2 b 2 16 3 -9 2 x1 1 4 0 2 3 x2 0 0 1 0 0 x3 1 0 0 0 0 x4 0 1 0 0 0 x5 -1/2 0 1/4 -3/4 θ 2 4 -
0 x4 0 1 0 0
0 x5 -1/2 2 1/4 1/4
0 X4 1/4 1/2 -1/8 -1/8 1 0 0
θ 4 12
c j→ CB 2 0 3 -z XB x1 x5 x2
0 x5 0 θ
表 1-5
-3/2
(4) 表1-6最后一行的所有检验数都已为负或零。 最后一行的所有检验数都已为负或零。 表示目标函数值已不可能再增大,于是得到最优解 表示目标函数值已不可能再增大,于是得到最优解
x1 x2
+ a1m+1xm+1 +L+ a1nxn = b1 + a2m+1xm+1 +L+ a2nxn = b2 O xm + amm+1xm+1 +L+ amnxn = bm
§2.2单纯形法

Maxz 7 x 12 x
1
Maxz 7 x1 12x2 0x3 0x4 0x5
3) 当模型中有某变量 xk 没有非负要求, 称为自由变量, 则可令 x x x ,x ,x 0
/ // / // k k k k k
化为标准型。 4) 若某个bi<0,两边乘(-1) 5) 对负变量 x j 0 ,换元设 xj x j 0
2. 最优性检验
问题:用什么检验? —— 目标。
1 1
X 而目标z CX (C C ) C (B b B N X ) C X X C B b (C C B N ) X
记 C C B N,则当 0 时,当前基可行解为最 优。
1
方法:计算每个变量 x 的检验数 c C B P ,
1
若 0, 则当前解为最优;否则 非最优。
问题:非最优的特征为何?
至少有某个检验数 0。
3. 寻找更好的基可行解(换基迭代) (基变换)
由于基可行解与基对应,即寻找一个新的基可行 解,相当于从上一个基B0变换为下一个新的基B1,因此, 本步骤也称为基变换。 进基
1 1 1 1
360 90 4
[ ] 中表示进基列与出基行的交叉元,下一张表将实行以它为主 元的初等行变换(称高斯消去)。方法是:先将主元消成1,再用此1将 其所在列的其余元消成0。
特点: (1) 目标函数求最大值 (2) 约束条件都为等式方程; (3) 非负约束:决策变量xj为非负; 右端常数项bi非负。
标准型的矩阵表示:
Maxz CX AX b s.t. X 0
其中,A 的秩为m(m n) , b 0。
