理论力学第四章-摩擦解析
合集下载
第四章 摩擦(赵) 理论力学课件

F max FN
2、FP = FPm,物体 处 于临界平衡状态。 Fmax ——极限摩擦力, 也称最大静摩擦力
(maximum static friction
force)。
Fmax ≈ fs ·FN ——库仑静摩擦定律 (Coulomb law of friction)
FN ——法向压力, f s——fric静tion摩fa擦cto因r)。数(static
FPmax
FN2 - FPmax sin - FQ cos = 0
补充 FL2 = f ·FN2
sinα+ f cosα
FPmax = cosα- f sinα
FQ
= FQ tan(α+φm )
2020/10/3
FQ FL1
FN1
∵ F Pmin = FQ tan(α-φm )
FQ FP
F Pmax = FQ tan(α+φm )
∴ 圆柱绕B点处于只滚不滑状态。
2020/10/3
例4 讨 论 条件:FP = 20 kN , fA = fB=0.3 ,FW = 10 kN ,
轮半径为R。求能使轮运动的拉力FR。
4m
FP
2m
O
R/2 R/2
A FW C
B
C
FR
2020/10/3
二、滚动摩擦
FQ
FT r mI
F FN
FN = -FQ, FT = -F
补充 FL1 = f ·FN1
sinα- f cosα
FPmin = cosα+f sinα FQ = FQ tan(α-φm )
2020/10/3
FQ FP
FPmin
FQ FL1
2、FP = FPm,物体 处 于临界平衡状态。 Fmax ——极限摩擦力, 也称最大静摩擦力
(maximum static friction
force)。
Fmax ≈ fs ·FN ——库仑静摩擦定律 (Coulomb law of friction)
FN ——法向压力, f s——fric静tion摩fa擦cto因r)。数(static
FPmax
FN2 - FPmax sin - FQ cos = 0
补充 FL2 = f ·FN2
sinα+ f cosα
FPmax = cosα- f sinα
FQ
= FQ tan(α+φm )
2020/10/3
FQ FL1
FN1
∵ F Pmin = FQ tan(α-φm )
FQ FP
F Pmax = FQ tan(α+φm )
∴ 圆柱绕B点处于只滚不滑状态。
2020/10/3
例4 讨 论 条件:FP = 20 kN , fA = fB=0.3 ,FW = 10 kN ,
轮半径为R。求能使轮运动的拉力FR。
4m
FP
2m
O
R/2 R/2
A FW C
B
C
FR
2020/10/3
二、滚动摩擦
FQ
FT r mI
F FN
FN = -FQ, FT = -F
补充 FL1 = f ·FN1
sinα- f cosα
FPmin = cosα+f sinα FQ = FQ tan(α-φm )
2020/10/3
FQ FP
FPmin
FQ FL1
理论力学第四章摩擦

P
2 22
2
F
F Nf 解得 : θ 2ctg-14 28.1
27
小物体A重G=10 N,放在粗糙的水平固定面上,它 与固定面之间的静摩擦因数fs=0.3。今在小物体A上施加 F=4 N的力,α =30°,试求作用在物体上的摩擦力。
F
α A
解:
1.取物块A为研究对
象,受力分析如图。
y
FG
αA x
b
B
M
e a
图示为凸轮
机构。已知推杆和滑
道间的摩擦因数为fs, 滑道宽度为b。设凸
轮与推杆接触处的摩
擦忽略不计。问a为
多大,推杆才不致被
32
卡住。
解: 取推杆为研究对象,受力分析如图。
列平衡方程
y
Fx 0, FNA FNB 0
Fy 0, FA FB F 0
A d FNA
M D F 0,
1
第四章 摩 擦
§4-1 摩擦的基本概念
一、摩擦的分类
干摩擦 按物体之间的润滑情况
湿摩擦
静摩擦 按物体之间是否有相对运动
动摩擦
滑动摩擦
按物体之间的相对运动形式
2
滚动摩擦
二、工程中的摩擦问题
3
4
5
6
7
8
二、摩擦产生的条件
1.条件:两个物体相互接触,并且有相对运动或相对 运动趋势。
2.概念:两个物体沿接触表面有相对滑动或相对滑动趋
G
x
Q
α
N
X 0 Q cos F G sin 0
Y 0 Qsin N G cos 0
得:
Q1 G(sin fs cos) (cos fs sin) Q2 G(sin fs cos) (cos fs sin)
理论力学教程(第四章)

静滑动摩擦力的特点
1 方向:沿接触处的公切线,
与相对滑动趋势反向;
2 大小:
3
(库仑摩擦定律)
④静摩擦系数的测定方法(倾斜法)
两种材料做成物体
和可动平面测沿下面滑
动时的 。
p
F=mgsin =fmgcos
2)、动滑动摩擦
tg f
两物体接触表面有相对运动时,沿接触面产生的切向 阻力称为动滑动摩擦力。
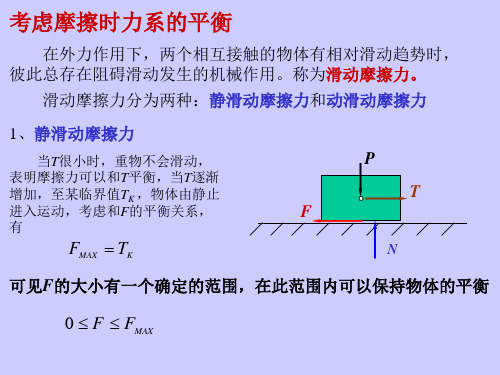
1)、静滑动摩擦
① 定义 两相接触物体虽有相对运动趋势,但仍保持相对静止F时,
给接触面产生的切向阻力,称为静滑动摩擦力或简称静摩 擦力。
满足
0 F Fmax (最大静摩擦力)
当 F Fmax时,则物体处于临界平衡状态
F
P Fmax f N (库仑静摩擦定律)
若物体静止,则 F P
摩擦的现象和概念
在大学物理已经讲到什么是摩擦:当物体与另一物体 沿接触面的切线方向运动或有相对运动的趋势时,在两物 体的接触面之间有阻碍它们相对运动的作用力,这种力叫 摩擦力。接触面之间的这种现象或特性叫“摩擦”。这里 来作更深入的研究,首先来看它的分类:滑动摩擦和滚动 摩擦。
滑动摩擦:相对运动为滑动或具有滑动趋势时的摩擦。
第四章 摩擦
欢迎加入湖 工大考试资
料群:
引言
前几章我们把接触表面都看成是绝对光滑的,忽略了物体 之间的摩擦,事实上完全光滑的表面是不存在的,一般情况下 都存在有摩擦。 [例]
平衡必计摩擦 3
摩擦
☆§4–1 滑动摩擦 ☆§4–2 摩擦角和自锁现象 ☆§4–3 考虑摩擦时物体的平衡问题 ☆§4–4 滚动摩阻的概念
性质:当物体静止在支承面时,支承面的总反力的偏角
理论力学第四章

同理求解得
F1min
G tan tanjf 1 tanjf tan
G tan(
jf
)
y
F1
x
Fmax
FN G
4、几何法求F1的最小值F1min,受力分析如图。
F1min
画力三角形如图。
由力三角形可得 F1min Gtan( jf )
物块平衡时,F1的大小应满足
FR2
-jf
jf
FR2
G
G F1min
对多数材料,通常情况下
f fs
理论力学
中南大学土木工程学院
3
第4页/共46页
§4-2 摩擦角与自锁现象
一、摩擦角 ①全约束力 即FR= FN + FS ,它与接触面的公法线成一偏 角j ,当物体处于临界平衡状态,即静摩擦力达到最大值 Fmax时,偏角j达到最大值jf,全约束力与法线夹角的最大 值jf叫做摩擦角。
fs2P 1 fs2
代入(3)
得
tan min
1 fs2 2 fs
1 tan2jf 2tanjf
cot 2jf
tan(
2
2jf
)
理论力学
中南大学土木工程学院
18
第19页/共46页
FNB
B
FSB Pmin A FSA
几何法求解
当梯子处于向下滑动的临界平衡状态
时,受力如图,显然 FRA FRB ,于是
G tan jf F1 G tan jf
理论力学
中南大学土木工程学院
17
第18页/共46页
[例] 梯子长AB=l,重为P,若梯子与墙和地面的静摩擦因数均为 f s=0.5,
求 多大时,梯子能处于平衡?
理论力学第4章 摩擦

所以增大摩擦力的途径为:①加大正压力N, ②加大摩擦系数f
4
3、 特征: 大小:0 F Fmax (平衡范围)满足 X 0
静摩擦力特征:方向:与物体相对滑动趋势方向相反
定律:Fmax f N ( f 只与材料和表面情况有 关,与接触面积大小无关。)
二、动滑动摩擦力:(与静滑动摩擦力不同的是产生了滑动)
所以物体运动:此时
F '动 N f '100.11N
(物体已运动)
25
[练习2] 已知A块重500N,轮B重1000N,D轮无摩擦,E 点的摩擦系数fE=0.2,A点的摩擦系数fA=0.5。
求:使物体平衡时块C的重量Q=? 解:① A不动(即i点不产
生 平移)求Q 由于
T 'F1 f AN1 0.5500250N
14
此力系向 A点简化
d'
滚阻力偶与主动力偶(Q,F)相平衡
①滚阻力偶M随主动力偶(Q , F)的增大而增大;
② 0 M Mmax
有个平衡范围;
滚动 摩擦 ③ M max 与滚子半径无关;
④滚动摩擦定律: M max d N,d 为滚动摩擦系数。
15
滚动摩擦系数 d 的说明:
①有长度量纲,单位一般用mm,cm; ②与滚子和支承面的材料的硬度和温度有关。
19
四、例题 [例1] 作出下列各物体
的受力图
20
[例2] 作出下列各物体的受力图
① P 最小维持平衡 ② P 最大维持平衡
状态受力图;
状态受力图
21
[例3] 构件1及2用楔块3联结,已知楔块与构件间的摩擦系数f=0.1,
求能自锁的倾斜角 。
解:研究楔块,受力如图
4
3、 特征: 大小:0 F Fmax (平衡范围)满足 X 0
静摩擦力特征:方向:与物体相对滑动趋势方向相反
定律:Fmax f N ( f 只与材料和表面情况有 关,与接触面积大小无关。)
二、动滑动摩擦力:(与静滑动摩擦力不同的是产生了滑动)
所以物体运动:此时
F '动 N f '100.11N
(物体已运动)
25
[练习2] 已知A块重500N,轮B重1000N,D轮无摩擦,E 点的摩擦系数fE=0.2,A点的摩擦系数fA=0.5。
求:使物体平衡时块C的重量Q=? 解:① A不动(即i点不产
生 平移)求Q 由于
T 'F1 f AN1 0.5500250N
14
此力系向 A点简化
d'
滚阻力偶与主动力偶(Q,F)相平衡
①滚阻力偶M随主动力偶(Q , F)的增大而增大;
② 0 M Mmax
有个平衡范围;
滚动 摩擦 ③ M max 与滚子半径无关;
④滚动摩擦定律: M max d N,d 为滚动摩擦系数。
15
滚动摩擦系数 d 的说明:
①有长度量纲,单位一般用mm,cm; ②与滚子和支承面的材料的硬度和温度有关。
19
四、例题 [例1] 作出下列各物体
的受力图
20
[例2] 作出下列各物体的受力图
① P 最小维持平衡 ② P 最大维持平衡
状态受力图;
状态受力图
21
[例3] 构件1及2用楔块3联结,已知楔块与构件间的摩擦系数f=0.1,
求能自锁的倾斜角 。
解:研究楔块,受力如图
理论力学教学PPT摩擦教学课件PPT

4
(2)临界平衡状态:
FS
Fmax
Fmax :最大静摩擦力
静摩 擦力有一个范围:0 Fs Fmax
Fmax
有限约束力
实验表明:Fm
的大小与接触面上法向反力
ax
FN
的大小成正比,方向与物体相对滑动趋势的方向相反.
P
Fmax
A
FN
Fmax = fs FN f s ----- 静摩擦系数
静滑动摩擦定律 T
49.61N m MC 70.39 N m
40
例5-14 已知: 力 P 角 ,不计自重的 A , B 块间的
静摩擦系数为 f s ,其它接触处光滑;
求:使系统保持平衡的力 F的值.
41
解: 取整体 Fy 0 FNA P 0 FNA P
设力 F小于 F1时,楔块 A 向右运动, 取楔块 A ,F1 FNA tan( ) P tan( )
解得 Fs 866 N FN 4500 N d 0.171m
而 Fmax fs FN 1800 N
因 Fs Fmax , 木箱不会滑动;
又 d 0 , 木箱无翻倒趋势.
木箱平衡
(2)设木箱将要滑动时拉力为 F1 Fx 0 Fs F1 cos 0 Fy 0 FN P F1 sin 0
画两杆受力图.
(a)
(b)
38
对图 (a) , M A 0 FN1 AB M A 0
对图 (b) , M C 0 M C1 FN1 l sin 60o Fs1 l cos 60o 0 又 Fs1 Fs1 fs FN1 fs FN1
解得 MC1 70.39N m
设 M C M C2 时,系统有顺时针方向转动趋势,
理论力学—摩擦

角jf之内,则无论这个力怎样大,
物块必保持静止。这种现象称为 自锁现象。因为在这种情况下, 主 动 力 的 合 力 FR 与 法 线 间 的 夹
角q < jf,因此, FR和全约束反
力FRA必能满足二力平衡条件,
且q j < jf 。
jf
jf
FR
q
A
j
FRA
jf
4.2.2 自锁现象
(2) 如果全部主动力的合力
线的方位也随之改变;在临界状态下,FR的作用线将 画出一个以接触点A为顶点的锥面,称为摩擦锥。设物 块与支承面间沿任何方向的摩擦系数都相同,即摩擦
角都相等,则摩擦锥将是一个顶角为2jf的圆锥。
4.2.2 自锁现象
物块平衡时,静摩擦力不一定达到最大值,可在
零与最大值Fmax之间变化,所以全约束反力与法线间
同而引起的切向力。
滑动摩擦——由于物体间相对滑动或有相 ② 对滑动趋势引起的摩擦。
滚动摩擦——由于物体间相对滚动或有相 对滚动趋势引起的摩擦。
三、摩擦有害的一面和有利的一面
⑴ 有害的一面:它是机械的多余阻力,使机械发热,引起 零部件的磨损,从而消耗能量,降低效率和使用寿命。
⑵ 有利的一面:可利用其进行传动、制动、调速、联接、 夹卡物体等。另外,人类的生活也时时离不开摩擦。
解2:(几何法)
jm B C
当梯子处于向下滑动的临界平衡 RB
状态时,受力如图,显然 RARB ,
E
于是
P
A amin
aj j j j m RA m i2 n m C A 2 m E A C 2 2 E m
故 a应满足的条件是:
2
a22jm
物块必保持静止。这种现象称为 自锁现象。因为在这种情况下, 主 动 力 的 合 力 FR 与 法 线 间 的 夹
角q < jf,因此, FR和全约束反
力FRA必能满足二力平衡条件,
且q j < jf 。
jf
jf
FR
q
A
j
FRA
jf
4.2.2 自锁现象
(2) 如果全部主动力的合力
线的方位也随之改变;在临界状态下,FR的作用线将 画出一个以接触点A为顶点的锥面,称为摩擦锥。设物 块与支承面间沿任何方向的摩擦系数都相同,即摩擦
角都相等,则摩擦锥将是一个顶角为2jf的圆锥。
4.2.2 自锁现象
物块平衡时,静摩擦力不一定达到最大值,可在
零与最大值Fmax之间变化,所以全约束反力与法线间
同而引起的切向力。
滑动摩擦——由于物体间相对滑动或有相 ② 对滑动趋势引起的摩擦。
滚动摩擦——由于物体间相对滚动或有相 对滚动趋势引起的摩擦。
三、摩擦有害的一面和有利的一面
⑴ 有害的一面:它是机械的多余阻力,使机械发热,引起 零部件的磨损,从而消耗能量,降低效率和使用寿命。
⑵ 有利的一面:可利用其进行传动、制动、调速、联接、 夹卡物体等。另外,人类的生活也时时离不开摩擦。
解2:(几何法)
jm B C
当梯子处于向下滑动的临界平衡 RB
状态时,受力如图,显然 RARB ,
E
于是
P
A amin
aj j j j m RA m i2 n m C A 2 m E A C 2 2 E m
故 a应满足的条件是:
2
a22jm
理论力学-摩擦

F
Fs
物块仍保持平衡,因为有
一个接触面障碍物块向右水平
P
ห้องสมุดไป่ตู้
运动的切向力——静摩擦力。
Fs = F
静摩擦力Fs的大小随着主动力F的增大而增大。
最大静滑动摩擦力
当 F 的大小达到某一数值时,物块处于平衡的
临界状态,这时的Fs 达到最大值—最大静摩擦力, 以 Fmax 表示。
0 ≤ Fs ≤ Fmax 由库仑定理
摩擦力的三要素:
1、作用于两物体的相互接触处 2、方向与相对滑动的趋势或相对滑动的
方向相反 3、大小由主动力决定(摩擦力为被动力)
滑动摩擦
根据研究物体的相对滑动趋势、平衡的临界状态和 滑动这三种情况,摩擦力可分为静滑动摩擦力、最 大静滑动摩擦力和动滑动摩擦力。
静滑动摩擦力
N
在物块上作用一个
大小可变的水平拉力F
N
F max = f s N
F
f s —— 静摩擦系数
Fs
f s需通过实验测定,影响其
P
的因素很复杂。
常用摩擦系数表
动滑动摩擦力
N
F Fs
P
当滑动摩擦力已经达到最大值,若再增大主动
力F,接触面之间将出现相对滑动。
动摩擦力
Fd = f N 一般情况下,
f 为动摩擦系数 f < fs
Thank you
第四章 摩擦
4-1 滑动摩擦 4-2 摩擦角和自锁现象 4-3 考虑摩擦时物体的平衡问题 4-4 滚动摩阻的概念
本章将讨论与研究物体的接触面不是光滑 的情况
按接触物间的相对运动情况:
滑动摩擦
按接触物间是否有润滑剂
干摩擦 湿摩擦
滚动摩擦
理论力学第七版第四章摩擦资料

F
施以水平阻力时,可能出现两种情况:
30
• 阻力较小,摩擦力阻止其向下运动 • 阻力较大,摩擦力阻止其向上运动
第一种情况
合力作用线
G
如右图,建立参考基,利用 静力平衡关系
y
Fm i n
Fm
x FN
n
Fix 0
i1
Fmin cos Fm Fg sin 0
m
(a)
n
Fiy 0
i1
第一类 问 题
F F max,,物体处于静止 状态,已知主动力求约束力, 与一般平衡问题无异。
第二类 问 题
平衡问题—临界运动趋势 不平衡问题—滑动或翻倒
F = F max
[ 确定平衡位置; 确定各主动力之间的关系。
考虑摩擦时 的平衡问题
例 题1
已知:三角块和矩 形块的质量分别为20 kg和10kg;各部分之 间的摩擦因数均为f s = 0.4 。
§5-3摩擦平衡问题
一、两种运动趋势与临界运动状态
1、滑动(slip)
WW W WW
FPFPFPFPFP
FmFamxFaxmFaxmFamx ax
FNFNFNFNFFNRFRFRFRFR
2、翻 倒(tip over)
FFFPPPFFP P
WWWWW
FFFFssss
FFFFFNNNNN
二、两类摩擦平衡问题
静止状态
运动状态
45° O
FP
F Fmax Fd
临界状态
静止状态
运动状态
O
FP
静止状态 — F=FP<F max
运动状 临态界状态
— F=Fd — F=F max = fs FN
一般静摩擦力的值: 0 ≤ F≤Fmax
理论力学摩擦.ppt
列平衡方程
F
C
G
A
FA
FB x
B
FNA
FNB
MB 0,
G
a 2
F
h
FNA
a
0
柜不绕 B 翻倒条件:
FNA≥0
a
解得
F ≤ Ga
2h
F
当h=b时,使柜翻倒的最小推力为
C b
G
h
F
Fmin2
Ga 2b
柜体保持滑动而不翻到时,应满足
Fmin2 F Fmin1
即
Ga 2b
F
Gfs
a
F
C b
G
h
在坑道施工中,广泛采用各种利用摩擦锁紧装置—楔联结。 坑道支柱中的联结结构装置如图所示。它包括顶梁I,楔块II,用 于调节高度的螺旋III及底座IV。螺旋杆给楔块以向上的推力FN1。 已知楔块与上下支柱间的静摩擦因数均为fs(或摩擦角φf )。求楔 块不致滑出所需顶角的大小。
Fx 0, FNC sin 60 FC cos 60 F FD 0 (c)
Fy 0, FNC cos 60 G FC sin 60 FND 0 (d)
MO F 0, FCr FDr 0
(e)
由式(e)可得 FD FC
将 FNC FNC 100 N, FD FC FC 40 N
B
FB
C r
F
O
G Aα
D
解: 此题在C,D两处都有摩擦,两个摩擦力之 中只要有一个达到最大值,系统即处于临 界状态。
B
FB
C r
F
O
G Aα
D
先假设C处的摩擦 达到最大值,当力F为 最小时,轮有沿水平 向右滚动的趋势。
华南理工大学理论力学第四章摩擦

19
②求保持木箱平衡的最大拉力。 设木箱临界滑动时拉力为F1。列平衡方程
F F
x y
0, 0,
Fs F1 cos 0 FN P F1 sin 0
(d) (e)
且 Fs Fmax f s FN
(f)
fs P 得 F1 1.876kN cos f s sin
• 摩擦角的正切等于静摩擦因数。
摩擦锥 -空间问题中,当滑动趋势方向改变时 时,全约束力作用线绕法线旋转一周, 构成的以接触点为顶点的锥面。
8
自锁现象
-当作用于物体的全部主动力的合力 FR 的作用线在摩擦
角之内,则无论该力多大,物体必保持静止的现象。
•自锁条件
0 f
f
f , 而 f
(2)能保持木箱平衡的最大拉力。
•分析:平衡满足两个条件 ①不发生滑动。
Fs Fmax f s FN
②不绕A点翻到。 法向约束力FN作用线在木箱内
18
•解:①研究木箱受力如图。列平衡方程
F F
x y
0, 0,
Fs F cos 0 FN P F sin 0
•当作用于物体的全部主动力的合力 FR 的作用线在摩擦
角之外,则无论该力多小,物体必滑动。
9
• 自锁应用举例
•摩擦系数的测定 -物块临界下滑 •螺纹自锁 -斜面的自锁条件
f s tg f tg
f
•千斤顶
f s 0.1
10
f 5 43
4 ~ 430
第4 章
(没动,F 等于外力) P 1N 时,由 Fx 0, F P 1N
②求保持木箱平衡的最大拉力。 设木箱临界滑动时拉力为F1。列平衡方程
F F
x y
0, 0,
Fs F1 cos 0 FN P F1 sin 0
(d) (e)
且 Fs Fmax f s FN
(f)
fs P 得 F1 1.876kN cos f s sin
• 摩擦角的正切等于静摩擦因数。
摩擦锥 -空间问题中,当滑动趋势方向改变时 时,全约束力作用线绕法线旋转一周, 构成的以接触点为顶点的锥面。
8
自锁现象
-当作用于物体的全部主动力的合力 FR 的作用线在摩擦
角之内,则无论该力多大,物体必保持静止的现象。
•自锁条件
0 f
f
f , 而 f
(2)能保持木箱平衡的最大拉力。
•分析:平衡满足两个条件 ①不发生滑动。
Fs Fmax f s FN
②不绕A点翻到。 法向约束力FN作用线在木箱内
18
•解:①研究木箱受力如图。列平衡方程
F F
x y
0, 0,
Fs F cos 0 FN P F sin 0
•当作用于物体的全部主动力的合力 FR 的作用线在摩擦
角之外,则无论该力多小,物体必滑动。
9
• 自锁应用举例
•摩擦系数的测定 -物块临界下滑 •螺纹自锁 -斜面的自锁条件
f s tg f tg
f
•千斤顶
f s 0.1
10
f 5 43
4 ~ 430
第4 章
(没动,F 等于外力) P 1N 时,由 Fx 0, F P 1N
理论力学-第四章 摩擦

设力 F 大于 F2 时, 楔块 A 向左运动 取楔块 A 分析,画受力图 分析,
F2 = FNA tan(θ + ϕ) = P tan(θ + ϕ)
P tan(θ − ϕ ) ≤ F ≤ P tan(θ + ϕ )
FR 2
ϕ
θ +ϕ
FNA
FR 2
FNA
斜面自锁条件
θ ≤ ϕf
§4-3 考虑滑动摩擦时物体的平衡问题
仍为平衡问题,平衡方程照用, 仍为平衡问题,平衡方程照用,求解步骤与前面基本 相同. 相同. 几个新特点 画受力图时,必须考虑摩擦力; 1 画受力图时,必须考虑摩擦力; 严格区分物体处于临界、非临界状态; 2 严格区分物体处于临界、非临界状态; 3 因 0 ≤ Fs ≤ Fmax ,问题的解有时在一个范围内. 问题的解有时在一个范围内.
动滑动摩擦力的特点 沿接触处的公切线,与相对滑动趋势反向; 方向:沿接触处的公切线,与相对滑动趋势反向; 大小: 大小:
Fd = f d FN
f d < f s (对多数材料,通常情况下) 对多数材料,通常情况下)
§4 - 2
摩擦角和自锁现象
一.摩擦角
r FR A ---全约束力
物体处于临界平衡状态时, 物体处于临界平衡状态时,全约束 力和法线间的夹角-----摩擦角 力和法线间的夹角---摩擦角
取整体分析, 解: 取整体分析,画受力图
P
FNB
F
ΣFy = 0 FNA − P = 0
FNA = P
设力 F 小于F1 时, 楔块 A 向右运动 取楔块 A 分析 ,画受力图
θ −ϕ
FNA
ϕ
FR1 F1
F1 = FNA tan(θ − ϕ ) = P tan
(完整版)理论力学---第四章摩擦

sin q cosq
fs cosq fs sinq
P
F
sin q cosq
fs cosq fs sinq
P
F1
22
第四章 摩擦
用几何法求解 解: 物块有向上滑动趋势时
F1max P tan(q )
23
第四章 摩擦
物块有向下滑动趋势时
F1min P tan(q )
P tan(q ) F P tan(q )
力偶矩的大小
A
M O
B
P
25
第四章 摩擦
已知:b , d , fs , 不计凸轮与挺杆处摩擦,不计挺杆质量;
求: 挺杆不被卡住之值. a
26
第四章 摩擦
解: 取挺杆,设挺杆处于刚好卡住位置.
Fx 0 FAN FBN 0
Fy 0 FA FB F 0 M A 0
FN
(a
d 2
)
FBd
利用三角公式与 tan fs ,
P sinq fs cosq F P sinq fs cosq
cosq fs sinq
cosq fs sinq
24
第四章 摩擦
无重杆OA AB.其中OA长度L与水平线的倾角
为q
AB 水平.将重为P的物块放在斜面上,斜面
倾角 大于接触面的摩擦角 f
问若想在OA 杆上加一主动力偶使物块静止 在斜面上,转向?
19
第四章 摩擦
已知: P ,q , fs .
求: 使物块静止,
水平推力
F的大小.
20
第四章 摩擦
解:
使物块有上滑趋势时,推力为
F1
画物块受力图
F 0, x
F1 cosq P sinq Fs1 0
理论力学第四章-摩擦(第七版)

解:
2a极限 tan 2a极限 fs
a极限 b 2 fs
b a 2 fs
§4-4滚动摩阻(擦)的概念 静滚动摩阻(擦)
Fx 0
MA 0
F Fs 0
M FR 0
0 Fs Fmax
0 M M max
Fmax fs FN
M max FN --最大滚动摩阻(擦)力偶
sin f s cos F1 P cos f s sin
sin f s cos sin f s cos PF P cos f s sin cos f s sin
例4-3 已知:b、d、fs, 不计凸轮与 挺杆处摩擦,不计挺杆质量; 求:挺杆不被卡住之 a 值. 解:取挺杆,设挺杆处于刚好卡住位置.
t anf
摩擦锥
全约束力和法线间的夹角的正切等于静滑动摩擦系数.
Fmax f s FN fs FN FN
0 f
二.自锁现象
3. 测定摩擦系数的一种简易方法,斜面与螺纹自锁条件
tan tanf f s
斜面自锁条件
f
螺纹自锁条件
f
§4-3考虑滑动摩擦时物体的平衡问题 仍为平衡问题,平衡方程照用,求解步骤与前面基本
Fx 0 F cos30 P sin 30 Fs 0
Fy 0 F sin 30 P cos30 FN 0
P
F
y
30°
Fs 403.6N
FN 1499N
(向上)
Fs x P FN
解:
取物块,画受力图,设物块平衡
Fx 0 Fy 0
fs 或
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FNB
下面判断系统是否处于静平衡
脚端A 与B 的最大静摩擦力分别为 :
y
C
FA fs A FNA 0.2 375 75 N
G
FB
f s B FNB
0.6 125
75 N
FSA A
FSA FSB 72.17 N
2d sin
Wr
f
cos
P
2d sin
Wr
f
cos
用摩擦角表示得:
Wr cos
d sin
P
Wr cos
d sin
[例]图示一折叠梯放在地面上,与地面的夹角 60o 。脚端A 与B和地面的摩擦因数分别为 fsA 0.2, fsB 0.6 。在折叠 梯的AC侧的中点处有一重为500N的重物。不计折叠梯的重量 ,问它是否平衡?如果平衡,计算两脚与地面的摩擦力。
y C G
A
B
x
(a)
处理此类问题时首先假定系
统为平衡。由于系统不一定处
于静摩擦的临界情况,可通过
平衡方程求得这些未知的静摩
擦力。所得的结果必须与最大
y
静摩擦力进行比较,以确认上
C
述系统平衡的假定是否成立。
G
A
B
x
(a)
以整体为对象,受力如图
MA 0
bFNB
bG 4
0
FNB 0.25G 125 N
无润滑
有润滑
0.15
0.1~0.12
0.3
0.15
0.1~0.15
0.18
0.3~0.5
0.15
0.4~0.6
0.1
动摩擦系数
无润滑
有润滑
0.09
0.05~0.1
0.18
0.05~0.15
0.15
0.1~0.15
0.15
0.07~0.12
0.3
0.15
0.8
0.5
0.2~0.5
0.07~0.15
§4-2 摩擦角和自锁现象
Fx 0
W
CD
FN1 cos FN 2 cos Fs1 sin Fs2 sin 0 FN1 FS1 FS2 FN2
Fy= 0 2FScos + 2FNsin = W
(2)
F S1= f FN1
(3)
F S2= f FN2
(4)
联立以上四式得: W
FN 2sin f cos
Wr
Pmax 2dsin f cos
2 fs 则抽屉不被卡住,e a .
2 fs
[例] 已知:B块重Q=2000N,与斜面的摩擦角 =15∘,A块与
水 平面的摩擦系数f=0.4,不计杆自重。图示位置AB杆水平, 求:使B块不下滑,物块A最小重量。
物体系统的的 临界平衡
P
FsA FN1
Q FsB FN2
P
FsA FN1
Q
FsB 解:①整体受力分析
第四章 摩擦
P2
以汽车后轮为例。 如果汽车发动机能 提供足够的动力使 汽车后轮转动,后 轮上与地面接触点 的摩擦力方向只能 向前,此力给予汽 车向前运动的外力, 称为驱动力。那么, 汽车驱动力克服了 地面作用在前轮上 的滑动摩擦阻力, 以及作用在车身上 的空气阻力就可向 前行驶。
§4-1 滑动摩擦
y
C G
Fy 0
FNA FNB G 0
FNA G FNB 375 N
FSA A
FNA
B FSB
x
FNB
(a)
Fx 0
FSA FSB
以杆 BC 为对象
F cx
Mc 0
FSB FNB tan 30 o 72.17 N
对于整体,
FSA FSB 72.17 N
F cy
FSB
0 FS Fmax
3、第三类问题:判断平衡状态的问题
[思考题] 已知:Q=50N, f = f 静 =0.2 求:P=200N; 300N, 400N 时的摩擦力
FS?
Q 200 FS 40
300 400 50 50
例
已知: 抽屉尺寸 a , b ,
f s(抽屉与两壁间),不计抽屉底部摩擦;
1 摩擦角
Fs
F RA F N F S
FRA全约束力
物体处于临界平衡状态时,
全约束力和法线间的夹角.
摩擦角
tan f
Fm ax FN
f s FN FN
fs
全约束力和法线间的夹角的
正切等于静滑动摩擦系数.Leabharlann 摩擦锥2 自锁现象
斜面自锁条件
斜面自锁条件 f
§4-3 考虑摩擦时物体的平衡问题
仍为平衡问题,平衡方程照用,求解步骤与前面 基本相同.
几个新特点 1 画受力图时,必须考虑摩擦力; 2 严格区分物体处于临界、非临界状态; 3 因 0 Fs Fmax ,问题的解有时在一个范围内.
常见的几类问题:
1、第一类问题:临界状态下的平衡问题
FS Fmax f s FN
2、第二类问题:普通状态下的平衡问题
例题. 在用铰链O固定的木板AO和BO间放一重 W,
半径为r的均质圆柱体, 并用大小等于P的两个水平力
维持平衡, 如图所示.设圆柱与木板间的摩擦系数为 f ,
不计铰链中的摩擦力以及木板的重量,求平衡时P的范
2d
围.
A
PP
B
第二类问题:转 化成临界平衡
W
CD
2
O
解:(1)求P的极小值
圆柱向下滑的临界状态,画受力图.
③ Fmax fs FN(库仑摩擦定律) f s 静摩擦系数
2.动滑动摩擦力 ①方向:与相对滑动的方向相反;
②大小: F f FN f 动摩擦系数
f f s (对多数材料,通常情况下)
常用材料的滑动摩擦系数
材料名称
钢—钢 钢—铸铁 钢—青铜 铸铁—铸铁 皮革—铸钢 橡皮—铸铁 木材—木材
静摩擦系数
FN2 Fx 0
FsA FsB sin 300 FN 2 cos 300 0 (1)
Fy 0
FN1 FN 2 sin 300 P Q 0 (2)
FAB
又 FsA fs FN1 FsB fs FN 2
(3)
②再取A滑块分析
Fy 0 FN1 P 0
(4)
联立以上各式可解得
Pmin 10000N 10KN
定义:相接触物体,产生相对滑动(趋势)时,其接触面 产生阻止物体运动的力叫滑动摩擦力。
摩擦
滑动摩擦
静滑动摩擦 动滑动摩擦
滚动摩擦
静滚动摩擦 动滚动摩擦
1.静滑动摩擦力 静滑动摩擦力的特点 ①方向:与相对滑动趋势相反;
② 大小: 0 Fs Fmax
(最大静滑动摩擦力) Fx 0 FT Fs 0 Fs FT
求: 拉抽屉不被卡住之e值。
单个物体的临 界平衡
解: 取抽屉分析,抽屉刚好被卡住的 临界状态
Fx 0 FNA FNC 0
Fy 0 FsA FsC F 0
M A 0 b
FsC b FNC a F( 2 e) 0
又 FsA fs FNA FsC fs FNC 联立解得 e a
下面判断系统是否处于静平衡
脚端A 与B 的最大静摩擦力分别为 :
y
C
FA fs A FNA 0.2 375 75 N
G
FB
f s B FNB
0.6 125
75 N
FSA A
FSA FSB 72.17 N
2d sin
Wr
f
cos
P
2d sin
Wr
f
cos
用摩擦角表示得:
Wr cos
d sin
P
Wr cos
d sin
[例]图示一折叠梯放在地面上,与地面的夹角 60o 。脚端A 与B和地面的摩擦因数分别为 fsA 0.2, fsB 0.6 。在折叠 梯的AC侧的中点处有一重为500N的重物。不计折叠梯的重量 ,问它是否平衡?如果平衡,计算两脚与地面的摩擦力。
y C G
A
B
x
(a)
处理此类问题时首先假定系
统为平衡。由于系统不一定处
于静摩擦的临界情况,可通过
平衡方程求得这些未知的静摩
擦力。所得的结果必须与最大
y
静摩擦力进行比较,以确认上
C
述系统平衡的假定是否成立。
G
A
B
x
(a)
以整体为对象,受力如图
MA 0
bFNB
bG 4
0
FNB 0.25G 125 N
无润滑
有润滑
0.15
0.1~0.12
0.3
0.15
0.1~0.15
0.18
0.3~0.5
0.15
0.4~0.6
0.1
动摩擦系数
无润滑
有润滑
0.09
0.05~0.1
0.18
0.05~0.15
0.15
0.1~0.15
0.15
0.07~0.12
0.3
0.15
0.8
0.5
0.2~0.5
0.07~0.15
§4-2 摩擦角和自锁现象
Fx 0
W
CD
FN1 cos FN 2 cos Fs1 sin Fs2 sin 0 FN1 FS1 FS2 FN2
Fy= 0 2FScos + 2FNsin = W
(2)
F S1= f FN1
(3)
F S2= f FN2
(4)
联立以上四式得: W
FN 2sin f cos
Wr
Pmax 2dsin f cos
2 fs 则抽屉不被卡住,e a .
2 fs
[例] 已知:B块重Q=2000N,与斜面的摩擦角 =15∘,A块与
水 平面的摩擦系数f=0.4,不计杆自重。图示位置AB杆水平, 求:使B块不下滑,物块A最小重量。
物体系统的的 临界平衡
P
FsA FN1
Q FsB FN2
P
FsA FN1
Q
FsB 解:①整体受力分析
第四章 摩擦
P2
以汽车后轮为例。 如果汽车发动机能 提供足够的动力使 汽车后轮转动,后 轮上与地面接触点 的摩擦力方向只能 向前,此力给予汽 车向前运动的外力, 称为驱动力。那么, 汽车驱动力克服了 地面作用在前轮上 的滑动摩擦阻力, 以及作用在车身上 的空气阻力就可向 前行驶。
§4-1 滑动摩擦
y
C G
Fy 0
FNA FNB G 0
FNA G FNB 375 N
FSA A
FNA
B FSB
x
FNB
(a)
Fx 0
FSA FSB
以杆 BC 为对象
F cx
Mc 0
FSB FNB tan 30 o 72.17 N
对于整体,
FSA FSB 72.17 N
F cy
FSB
0 FS Fmax
3、第三类问题:判断平衡状态的问题
[思考题] 已知:Q=50N, f = f 静 =0.2 求:P=200N; 300N, 400N 时的摩擦力
FS?
Q 200 FS 40
300 400 50 50
例
已知: 抽屉尺寸 a , b ,
f s(抽屉与两壁间),不计抽屉底部摩擦;
1 摩擦角
Fs
F RA F N F S
FRA全约束力
物体处于临界平衡状态时,
全约束力和法线间的夹角.
摩擦角
tan f
Fm ax FN
f s FN FN
fs
全约束力和法线间的夹角的
正切等于静滑动摩擦系数.Leabharlann 摩擦锥2 自锁现象
斜面自锁条件
斜面自锁条件 f
§4-3 考虑摩擦时物体的平衡问题
仍为平衡问题,平衡方程照用,求解步骤与前面 基本相同.
几个新特点 1 画受力图时,必须考虑摩擦力; 2 严格区分物体处于临界、非临界状态; 3 因 0 Fs Fmax ,问题的解有时在一个范围内.
常见的几类问题:
1、第一类问题:临界状态下的平衡问题
FS Fmax f s FN
2、第二类问题:普通状态下的平衡问题
例题. 在用铰链O固定的木板AO和BO间放一重 W,
半径为r的均质圆柱体, 并用大小等于P的两个水平力
维持平衡, 如图所示.设圆柱与木板间的摩擦系数为 f ,
不计铰链中的摩擦力以及木板的重量,求平衡时P的范
2d
围.
A
PP
B
第二类问题:转 化成临界平衡
W
CD
2
O
解:(1)求P的极小值
圆柱向下滑的临界状态,画受力图.
③ Fmax fs FN(库仑摩擦定律) f s 静摩擦系数
2.动滑动摩擦力 ①方向:与相对滑动的方向相反;
②大小: F f FN f 动摩擦系数
f f s (对多数材料,通常情况下)
常用材料的滑动摩擦系数
材料名称
钢—钢 钢—铸铁 钢—青铜 铸铁—铸铁 皮革—铸钢 橡皮—铸铁 木材—木材
静摩擦系数
FN2 Fx 0
FsA FsB sin 300 FN 2 cos 300 0 (1)
Fy 0
FN1 FN 2 sin 300 P Q 0 (2)
FAB
又 FsA fs FN1 FsB fs FN 2
(3)
②再取A滑块分析
Fy 0 FN1 P 0
(4)
联立以上各式可解得
Pmin 10000N 10KN
定义:相接触物体,产生相对滑动(趋势)时,其接触面 产生阻止物体运动的力叫滑动摩擦力。
摩擦
滑动摩擦
静滑动摩擦 动滑动摩擦
滚动摩擦
静滚动摩擦 动滚动摩擦
1.静滑动摩擦力 静滑动摩擦力的特点 ①方向:与相对滑动趋势相反;
② 大小: 0 Fs Fmax
(最大静滑动摩擦力) Fx 0 FT Fs 0 Fs FT
求: 拉抽屉不被卡住之e值。
单个物体的临 界平衡
解: 取抽屉分析,抽屉刚好被卡住的 临界状态
Fx 0 FNA FNC 0
Fy 0 FsA FsC F 0
M A 0 b
FsC b FNC a F( 2 e) 0
又 FsA fs FNA FsC fs FNC 联立解得 e a
