2019中考-“隐形圆”问题(共22张PPT)全面.ppt

合集下载

隐圆问题-利用圆的知识解决最值课件19张PPT

例1：如图，若AB＝OA＝OB＝OC，则∠ACB的大
小是_______
练习：如图，已知AB=AC=AD，∠CBD=2∠BDC， ∠BAC=44°，则∠CAD的度数为__________
县民政局依法行政工作计划总结 2 0 * * 年,在县委、县政府的正确领导下, 在县法制办的直接指导下, 我局认真贯彻落实党的十八大精神和国务院《全面推进依法行政实施纲要》, 坚持“ 以人为本, 为民解困、为民服务” 的工作理念, 认真履行“ 解决民生、落实民权、维护民利” 的工作职责, 以服务科学发展、创新体制机制、强化执法队伍建设, 全面推进依法行政工作, 推动民政工作制度化、规范化, 充分发挥在社会建设和管理中的职能作用, 积极实
施社会惠民保障工程。现将全年依法行政工作情况汇报如下: 一、齐抓共管, 加强对依法行政工作的组织领导
为使依法行政理念真正落到实处, 我局成立了“ 一把手” 局长、党组书记为组长, 分管副局长为副组长和各职能业务科室负责人为成员的依法行政工作领导小组, 并明确日常工作由办公室( 法制股) 组织实施。年初对全局的依法行政工作排出计划, 狠抓落实, 切实把本单位的依法行政工作列入重要议事日程。建立领导责任制, 做到有部署、有检查、有总结, 逐步形成法制工作“ 一把手” 局长亲自抓、分管领导分工抓、职能部门牵头抓、业务科室协同抓, 全局干部职工积极参与的工作格局, 并严格
例1：等腰直角△ABC中，∠C＝90°，AC＝BC＝ 4，D为线段AC上一动点，连接BD，过点C作 CH⊥BD于H，连接AH，则AH的最小值.
练习：1、如图，在正方形ABCD中，动点E、F分别从D、C两点同时出发，以相同的速度在边DC、 CB上移动，连接AE和DF交于点P，由于点E、F的移动，使得点P也随之运动.若，线段CP的最小值是_____________

2023年中考数学一轮复习专题利用隐形圆求圆的最值课件

8
方法总结：利用隐圆解决线圆最值问题时，第一：变化中寻找不变，找到隐圆；第二：“一线穿心”--过圆心向定线段作垂直找到圆上目标最值点，求得最值。
坚持用每一天的进步书写人生的辉煌
9
变式训练2：如图，在矩形ABCD中，AB＝3，BC＝4， O为矩形ABCD的中心，以D为圆心，1为半径作⊙D， P为⊙D上的一个动点，连接AP、OP、AO，则△AOP 面积的最大，延长AO至C点，过点D作 DF⊥AC于点F，延长FD交⊙D于点P′，连接AP′，OP′，要使△AOP面积最大，则只需AO边上的高最大，此时P′满足条件，即P′F为最大的高，
坚持用每一天的进步书写人生的辉煌
11
拓展：定弦定角型
如图1⊙O中，A、B为定点，则AB为定弦，点C为优弧上任一点，在C点运动过程中则∠ACB的度数不变⇒逆运用⇒ 如图2、点A、B为定点，点C为线段AB外一点，且 ∠ACB=θ（θ为固定值）⇒点C在以AB为弦的圆上运动（不与A、B重合）
是_______．
D
C
M A
AN
B
坚持用每一天的进步书写人生的辉煌
方法总结：利用隐圆解决点圆最值问题时，第一：变化中寻找不变，找到隐圆；第二：“一线穿心”--连接圆心和定点找到圆上目标最值点，求得最值。
坚持用每一天的进步书写人生的辉煌
6
变式训练1：如图，在Rt△ABC中，∠ABC＝90°， ∠C＝30°，AB＝1，点D在AC边上运动，点E为AC的中点，将△BCD沿BD翻折，点C的对应点为点F，则在点D从C到A的运动过程中，线段EF的最小值为___.
1
上的一点，且AM＝ AD，N是AB边上3 的一动点，将△AMN沿MN
所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值

中考数学“隐形圆模型”，“圆”来如此简单

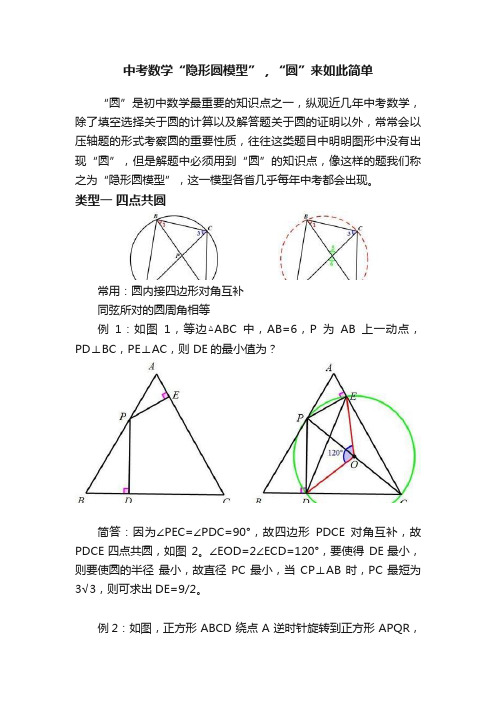
中考数学“隐形圆模型”，“圆”来如此简单“圆”是初中数学最重要的知识点之一，纵观近几年中考数学，除了填空选择关于圆的计算以及解答题关于圆的证明以外，常常会以压轴题的形式考察圆的重要性质，往往这类题目中明明图形中没有出现“圆”，但是解题中必须用到“圆”的知识点，像这样的题我们称之为“隐形圆模型”，这一模型各省几乎每年中考都会出现。

类型一四点共圆常用：圆内接四边形对角互补同弦所对的圆周角相等例1：如图1，等边△ABC中，AB=6，P为AB上一动点，PD⊥BC，PE⊥AC，则 DE的最小值为？简答：因为∠PEC=∠PDC=90°，故四边形PDCE对角互补，故PDCE四点共圆，如图2。

∠EOD=2∠ECD=120°，要使得DE最小，则要使圆的半径最小，故直径PC最小，当CP⊥AB时，PC最短为3√3，则可求出DE=9/2。

例2：如图，正方形 ABCD 绕点 A 逆时针旋转到正方形 APQR，连接 CQ，延长 BP 交于 CQ 于点 E，求证：E 是线段 CQ 的中点简答：因为 AC=AQ，AB=AP 且∠BAP=∠CAQ（旋转角相等）故△APB∽△AQC，故∠ABP=∠ACQ ，又因为∠1=∠2，故A、B、C、E 四点共圆（如图 2），因为∠ABC=90°，故 AC 是直径，故∠AEC=90°，又因为 AQ=AC，所以 AE 垂直且平分 QC（三线合一）类型二定义—动点到定点等于定长同一个端点处有多条相等线段时，要想到构造圆。

例:1：如图 1，四边形 ABCD 中，AB=AC=AD，若∠CAD=76°，则∠CBD= 度。

简答：如图 2，因为 AB=AC=AD，故 B、C、D 三点在以 A 为圆心的圆上，故∠CBD= 1/2∠CAD=38°例2：如图 1，长 2 米的梯子 AB 竖直放在墙角，在沿着墙角缓慢下滑直至水平地面过程中，梯子 AB 的中点 P 的移动轨迹长度为？.简答：由斜边上的中点等于斜边的一半可知，OP=1，动点P到定点O的距离始终等于1，满足圆的定义（到定点的距离等于定长的点的集合叫做圆），故P的运动轨迹是圆弧，圆心角为90°，轨迹长度为四分之一圆的长度。

中考数学专题：隐形圆解析

A
D
O
E
C
B
【分析】连接 CE ，由于 CD 为直径，故∠CED=90°，考虑到 CD 是动线段，故可以将此题看成定线段 CB 对直角∠CEB ．
A
D
E O
C
B
取 CB 中点 M，所以 E 点轨迹是以 M 为圆心、CB 为直径的圆弧．
A
D
E O
CM
B
连接 AM，与圆弧交点即为所求 E 点，此时 AE 值最小， AE AM EM 102 22 2 2 26 2 ．
【2017 四川德阳】如图，已知圆 C 的半径为 3，圆外一定点 O 满足 OC=5，点 P 为圆 C 上一动点，经过点 O 的直线 l 上有两点 A、B，且 OA=OB，∠APB=90°，l 不经过点 C，则 AB 的最小值为________．
C P
l AO B
【分析】连接 OP，根据△APB 为直角三角形且 O 是斜边 AB 中点，可得 OP 是 AB 的一半，若 AB 最小，则 OP 最小即可．
【2019 扬州中考】如图，已知等边△ABC 的边长为 8，点 P 是 AB 边上的一个动点（与点 A 、B 不重合）．直线 l 是经过点 P 的一条直线，把△ABC 沿直线 l 折叠，点 B 的对应点是点 B’．当 PB=6 时，在直线 l 变化过程中，求△ACB ’面积的最大值．
A P
B
A
P F
C
E
B
【分析】考虑到将△FCE 沿 EF 翻折得到△FPE，可得 P 点轨迹是以 F 点为圆心，FC 为半径的圆弧． A
P F
C
E
B
过 F 点作 FH ⊥AB，与圆的交点即为所求 P 点，此时点 P 到 AB 的距离最小．由相似先求 FH ，再减去 FP，即可得到 PH ．

“隐圆问题”

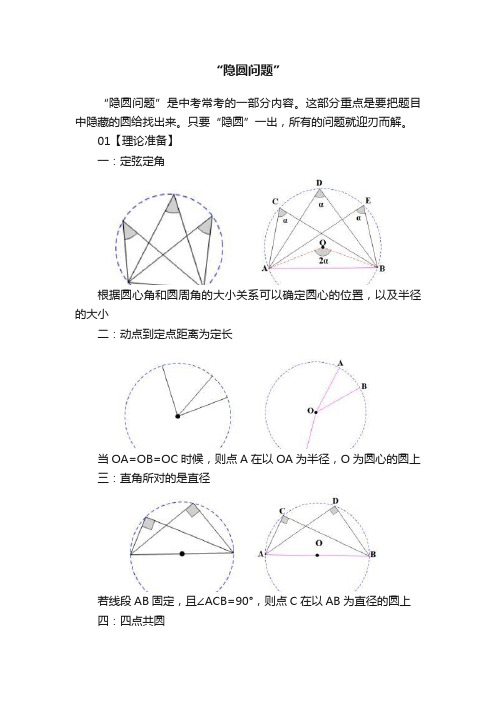
“隐圆问题”“隐圆问题”是中考常考的一部分内容。

这部分重点是要把题目中隐藏的圆给找出来。

只要“隐圆”一出，所有的问题就迎刃而解。

01【理论准备】一：定弦定角根据圆心角和圆周角的大小关系可以确定圆心的位置，以及半径的大小二：动点到定点距离为定长当OA=OB=OC时候，则点A在以OA为半径，O为圆心的圆上三：直角所对的是直径若线段AB固定，且∠ACB=90°，则点C在以AB为直径的圆上四：四点共圆可知：∠1=∠2，∠3=∠4，∠5=∠6，∠7=∠8。

△ABE∽△DCE,△ADE∽△BCE02【例题精讲】类型一：定弦定角1.如图，∠MON= 45°，线段AB=10，且A,B 分别在OM、ON 上移动，那么点O到AB的距离的最大值为__________．3.如图，△ABC为等边三角形，AB=2，若P为△ABC内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为__________类型二：动点到定点距离为定长1.如图，长2米的梯子AB竖直放在墙角，在沿着墙角缓慢下滑直至水平地面过程中，梯子AB的中点P的移动轨迹长度为？2.如图，在矩形ABCD中，AB=2，AD=3，点E，F分别为AD、DC边上的点，且EF=2，G为EF的中点，P为BC边上一动点，则PA+PG的最小值为？类型三：直角所对的是直径1.如图，E、F是正方形ABCD的边AD上两个动点，满足AE = DF，连接CF交BD于点G，连接BE交AG于点H，若正方形的边长为2，则线段DH长度的最小值是__________．2.如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且始终有AP⊥BP，则线段CP长的最小值为_________类型四：四点共圆1.如图，正方形ABCD中，∠EAF=45°，AF与BD交于N，AE与BD交于M，连接MF、NE，求证△ANE、△AMF是等腰直角三角形.2.如图，等边△ABC中，AB=6，P为AB上一动点，P D⊥BC，PE⊥AC，则DE的最小值为？03【总结】隐圆问题经常涉及和最值问题联系在一起。

2019高考数学二轮复习微专题6隐形圆问题课件ppt版本

的内部,则 1 m2 < 3 + 2 m2 .两边平方并化简,得 m2 - 5 < 3(2 m2) 恒成立.所
4
4
22
以只要m2≤2即可.故m的取值范围是[- 2 , 2 ].
【方法归纳】当直线与圆相交时,特征三角形(由弦心距、半弦长、半径构成)的应用是最普遍的,在特征三角形中应用边角关系求出动点的条件是解题的关键.
1-1 已知圆O:x2+y2=1,直线l:ax+y=3,若直线l上存在点P,过点P作圆O的两条
切线,切点为A,B,使得四边形OAPB为正方形,则实数a的取值范围是
.
答案
,
14 2

∪

14 2
,

解析由四边形OAPB为正方形,得∠APB=90°.所以∠APO=45°,PO= 2OA=
2-1 已知A,B是圆O:x2+y2=1上的动点,满足AB= 3,P是圆C:(x-3)2+(y-4)2=1上

的动点,则| PA+ PB |的取值范围是
.
答案 [7,13]
解析
设AB的中点为Q,则OQ= 1 ,点Q的轨迹方程是x2+y2= 1 .所以 PA

PB
=2
2
4
PQ
.又点P在圆C上,OC=5,所以 PQ
范围为
.
答案 [16,36]
解析函数f(x)的图象关于点C(3,4)对称,直线y=k(x-3)+4也经过点C(3,4),所以
A,B两点关于点C对称, PA

PB
=2 PC
=2, PC
=1,即点P的轨迹是以C为圆心、1

隐藏圆课件

提高教学效率
个性化教学
隐藏圆课件可以节省教师板书的时间，让他们有更多时间讲解重点和难点，从而提高教学效率。
隐藏圆课件可以根据不同学生的需求和水平，提供个性化的学习资源和教学方案。
缺点分析
技术依赖
隐藏圆课件依赖于一定的技术设备和软件，如果设备出现问题或软件崩溃，教学活动可能
会受到影响。
信息过载
引导与提示
隐藏圆可以作为引导用户注意的元素，如焦点指示、操作提示等，帮助用户更好地理解和使用界面。
04 隐藏圆的优缺点分析
CHAPTER
优点分析
提高课堂互动性
增强视觉效果
隐藏圆课件通过互动式设计，能够吸引学生的注意力，提高他们的学习兴趣和参与度。
通过动态演示和丰富的视觉元素，隐藏圆课件能够更直观地展示教学内容，帮助学生更好地理解和记忆。
使用Illustrator制作隐藏圆
在工具箱中选择椭圆工具，按住Shift键绘制一个圆形。
打开Illustrator软件，新建一个文档。
02
01
03
在图层面板中选中圆形图层，点击添加图层样式按钮，
选择“内阴影”。
在内阴影设置中，调整距离、大小和透明度等参数，使
圆形呈现隐藏效果。
04
05
点击确定，完成隐藏圆的制作。
根据设计需求选择合适的隐藏圆类型
01
02
03
基础型
适用于简单的遮挡和引导视线，使画面更加整洁。
提示型
用于提供交互提示或引导，增强用户体验。
装饰型
用于美化页面，提升视觉效果。
注意隐藏圆的适用场景和限制
适用场景
页面布局需要隐藏、遮挡部分内容；需要引导用户视线；交互设计需要提示或引导。

2019中考数学复习隐形圆问题大全(后有专题练习无答案)

2019中考数学复习隐形圆问题大全(后有专题练习无答案)2019中考数学复：隐形圆问题大全一定点+定长根据到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆的原理，可以应用到以下问题中：1.在四边形ABCD中，AB=AC=AD=2，BC=1，且AB∥CD，求BD的长度。

解析：因为AB=AC=AD=2，所以B、C、D在以A为圆心、2为半径的圆上。

又因为AB∥CD，所以DE=BC=1.根据勾股定理，易得BD=√15.2.在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是多少？解析：因为E是定点，EB′是定长，所以B′点路径为以E为圆心、EB′为半径的圆。

作穿心线DE可得B′D的最小值为2√10.3.在ΔABC中，AB=4，AC=2，以BC为边在ΔABC外作正方形BCDE，BD、CE交于点O，则线段AO的最大值为多少？解析：首先确定A、B点的位置，因为AC=2，所以C点在以A为圆心、2为半径的圆上。

因为点O是点C以点B为中心顺时针旋转45度并1：√2缩小而得，所以将圆A旋转45度再1：2缩小即可得到O点路径。

转化为求定点A到定圆F的最长路径，即AF+FO=3+2√2.二定线+定角根据与一条定线的两端夹角一定的动点路径是以定线为弦，定角为圆周角的弧的原理，可以应用到以下问题中：1.在矩形ABCD中，AB=10，AD=4，点P是CD上的动点，当∠APB=90°时求DP的长度。

解析：因为AB为定线，∠APB为定角（90°），所以P点路径为以AB为弦（直径）的弧。

根据勾股定理，可得DP为2或8.2.在等边三角形ABC中，∠XOY = 45°，点A、B分别在OX、OY上移动，且AB = 2，那么OC的最大值为多少？解析：因为AB为定线，∠XOY为定角，所以O点路径为以AB为弦所含圆周角为45°的弧。

中考数学专题《隐形圆解析》

A
D
E O
C
B
取 CB 中点 M，所以 E 点轨迹是以 M 为圆心、CB 为直径的圆弧．
A
D
E O
CM
B
连接 AM，与圆弧交点即为所求 E 点，此时 AE 值最小， AE AM EM 102 22 2 2 26 2 ．
A
E
C
M
B
【2019 园区一模】如图，正方形 ABCD 的边长为 4，动点 E、F 分别从点 A、C 同时出发，
C
M
E
A
O
B
【寻找定边与直角】如图，在 Rt△ABC 中，∠ACB =90°，BC=4，AC=10，点 D 是 AC 上的一个动点，以 CD 为直径作圆 O，连接 BD 交圆 O 于点 E，则 AE 的最小值为_________．
A
D
O
E
C
B
【分析】连接 CE ，由于 CD 为直径，故∠CED=90°，考虑到 CD 是动线段，故可以将此题看成定线段 CB 对直角∠CEB ．
A
D
O
P
F
B
E
C
连接 OC，与圆的交点即为 P 点，再通过勾股定理即可求出 PC 长度．思路概述：分析动点形成原理，通常“ 非直即圆” （不是直线就是圆），接下来可以寻找与动点相关有无定直线与定角．
【2013 武汉中考】如图，E 、F 是正方形 ABCD 的边 AD 上的两个动点，满足 AE =DF，连接 CF 交 BD 于点 G，连接 BE 交 AG 于点 H，若正方形边长为 2，则线段 DH 长度的最小值是________．
A
O
B
【辅助圆+相切】如图，在 Rt△ABC 中，∠ACB =90°，∠B=30°，AB =4，D 是 BC 上一动点， CE ⊥AD 于 E ，EF⊥AB 交 BC 于点 F，则 CF 的最大值是_________．

第2部分专题5 强基专题5 隐圆问题课件(共21张PPT)

d＝
k|82＋k| 1≤6，解得－3
7
7≤k≤3
7
7 .]
类型3 两定点A，B，动点P满足|PA|2＋|PB|2是定值，确定隐圆(距离平方圆)
【例3】如图，在平面直角坐标系xOy中，已知圆C：x2＋y2－ 4x＝0及点A(－1,0)，B(1,2)．
(1)在圆C上是否存在点P，使得PA2＋PB2＝12？若存在，求点P 的个数，若不存在，说明理由.
[跟进训练] 1．如果圆(x－2a)2＋(y－a－3)2＝4上总存在两个点到原点的距离为1，则实数a的取值范围是________．
－65，0 [由题意得圆(x－2a)2＋(y－a－3)2＝4与圆x2＋y2＝1相交，所以2－1< 2a2＋a＋32<1＋2,1<5a2＋6a＋9<9，
5a2＋6a＋8＞0， 5a2＋6a＜0，
第二部分核心专题师生共研
专题五解析几何强基专题5 隐圆问题
考查直线与圆、圆与圆的综合问题时题设条件中没有直接给出相关圆的信息，而是隐含在题目中，要通过分析和转化，发现圆(或圆的方程)，从而可以利用圆的相关知识来解决问题，这类问题称为“隐圆”问题．
类型1 利用圆的定义或垂直关系确定隐圆
(2)若圆C上存在唯一的点Q，使得Q→A·Q→B＋2＝λ，求λ的值．
[解] (1)圆C的标准方程为(x－2)2＋y2＝4，所以圆心C(2,0)，半径为2. 假设圆C上存在点P，
设P(x，y)，则(x－2)2＋y2＝4，PA2＋PB2＝(x＋1)2＋(y－0)2＋(x－1)2 ＋(y－2)2＝12，
≤y≤
27，所以点
M的纵坐标的取值范围是－
27，
27.]
【例1】 (1)已知圆C：(x－3)2＋(y－4)2＝1和两点A(－m,0)，

专题04 隐形圆-中考数学二次函数压轴题核心考点突破57页PPT

31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
专题04 隐形圆-中考数学二次函数压轴题核心考点突破
•
6、黄金时代是在我们的前面，而不在我们的后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性，但某些时候请收敛。
•
9、只为成功找方法，不为失败找借口 (蹩脚的工人总是说工具不好)。
•
10、只要下定决心克服恐惧，便几乎能克服任何恐惧。因为，请记住，除了在脑海中，恐惧无处藏身。-- 戴尔．卡耐基。

隐形圆

隐形圆问题
模型一定点定长作圆
一．模型分析
1.平面内，点A为定点，点B为动点，且AB长度固定，则点B的轨迹在以点A 为圆心，AB长为半径的圆上(如图). 依据的是圆的定义：圆是所有到定点的距离等于定长的点的集合．
2.推广：如图，点E为定点，点F为线段BD上的动点(不含点B)，将△BEF沿EF折叠得到△B′EF，则点B′的运动轨迹为以点E为圆心，以线段BE为半径的一段圆弧．
练习反馈
1. 如图，已知OC＝3，点A、B分别是平面内的动点，且OA＝2，BC＝4，请在平面内画出点A、B的运动轨迹．
解：如解图，点A的运动轨迹为圆O，点B的运动轨迹为圆C.。

人教版数学中考总复习——抓住题目中的隐形圆(共15张PPT)

过程中，BA′的长度始终保持不变；难点2:圆是到定点的距离等于定长的所有的
点的集合，想到点A′的运动轨迹是以点B为圆心、BA为半径的圆；难点3:圆外一点与圆上各点的连线中，哪条线段最短。
师生共同辨析
AP
D
A'
B
C
解：有题意可知：因为点A关于PB的对称点
是A′，所以BA=B A′，由此可见，在点P运动
。
A
D
P EG
B
C
再见
D。
2 52
问题情境再创设
问题2：如图，已知正方形ABCD的边长为4，
点M和点N分别从点B、C同时出发，以相同
的速度分别沿BC、CD方向向终点C和D运动，
连接AM和BN，交于点P，则PC长的最小值
为
。
A
D
N P
B
M
C
师生共同再辨析
分析：△ABM≌△BCN，
A
D
则∠BAM=∠CBN, 因为∠ABN+∠CBN=90º,则
2、对于基本图形的把握要到位，才能做到临题不乱。
3、知识的等价转化非常重要，这往往是我们深度理解知识的基础。
作业布置
题目4：如图，已知正方形ABCD的边长是4，
点E是AB边上的一动点，连接CE，过点B作
BG⊥CE于点G，点P是AB边上另一动点，则
PD+PG的最小值为
，此时PB的长
为
∠BAM+∠ABN=90º,ONPB NhomakorabeaM
C
于是在△ABP中，∠APB=90º
无论点M和点N如何运动，∠APB始终等于 90º,则在△ABP中，边AB和∠APB=90º是定值，则点P的轨迹就是以AB为直径的△APB的外

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

..
24
会出现。
..
3
..
4
..
5
..
6
对应练
1、如图,四边形ABCD中,AB=AC=AD,若 ∠CAD=76∘，则∠CBD=______度。
..
7
真题演练
1. 如图 1，四边形 ABCD 中，AB=AC=AD，若 ∠ CAD=76°，则∠ CBD= 度。
简答：如图 2，因为 AB=AC=AD，故 B、C、D 三点
..
23
班主任的专业发展一如治学之道，它不是遥不可及的事情，而是我们正在
谢谢！实践的工作；但也不是一蹴而就的，
而是一个不断发展，持续提高的过程。只要我们留守心中那盏信念的灯，拥有一颗热爱教育，热爱学生的心，再加上善于观察和反思教育生活的习惯，必然会收获内心的幸福，获得丰
满的教育人生。
..
17
真题演练
1.如图，长 2 米的梯子 AB 竖直放在墙角，在沿着墙角缓慢下滑
直至水平地面过程中，梯子 AB 的中点 P 的移动轨迹长度为（）
简答：由斜边上的中点等于斜边的一半可知，OP=1，动点P
到定点O的距离始终等于1，满足圆的定义（到定点的距离
等于定长的点的集合叫做圆），故P的运动轨迹是圆弧，圆
简答：如图 2，因为 AP⊥BP，
∠P=90°（定角），AB=6（定弦），
故 P 在以 AB 为直径的⊙H 上，当
H 、 P 、 C 三点共线时 CP 最
短，HB=3，BC=4 则 HC=5，故
CP=5-3=2 。
..
22
小结
以上例题说明，在求一类线段最值问题中，如果遇到
动点的运动路径是圆时，只需利用上面提到的方案1或方
心角为 90°，轨迹长度为四分之一圆的长度。
..
18
真题演练
2.如图 1，在 Rt△ABC 中，∠C=90°，AC=7， BC=8，点 F 在边 AC 上，并且 CF=2，点 E为边 BC 上的动点，将△CEF 沿直线 EF 翻折，点 C 落在点 P 处，则点 P 到边 AB 距离的最小值是（）。
福安市实验中学占文存
..
1
回顾 1、圆的定义 2、确定圆的条件
..
2
“圆”是初中数学重要的知识之一，纵观近几年中考数学，除了填空选择关于圆的计算以及解答题关于圆的证明以外，常常会以压轴题的形式考
察圆的重要性质，往往这类题目中明明图形中没有出现“圆”，但若能依据题目的特点把实际存在的圆找出来，再利用圆的有关性质来解决问题，像这样的题我们称之为“隐形圆模型”，这一模型几乎每年中考都
..
19
2.如图 1，在 Rt△ABC 中，∠C=90°， AC=6，BC=8，点 F 在边 AC 上，并且 CF=2，点 E为边 BC 上的动点，将△CEF 沿直线 EF 翻折，点 C 落在点 P 处，则点 P 到边 AB 距离的最小值是（）。
简答：E 是动点，导致 EF、EC、EP
都在变化，但是 FP=FC=2 不变，故 P
1
在以 A 为圆心的圆上，故∠CBD= 2∠CAD=38°
..
8
..
9
..
10
对应练
1、如图①,在Rt△ABC中,AB=4,BC=3,将△ABC绕点B顺时针旋转α(0<α<120∘)得△DBE，连接AD，EC，直线 AD、EC交于点M.在旋转的过程中，四边形ABCM的面积是否存在最大值?若存在，求出四边形ABCM面积的最大值；若不存在，请说明理由；
..
11
..
12
..
13
..
14
对应练
1、已知等腰直角三角形ABC中，∠ C=90°， AC=BC=4，D为线段AC上一动点，连接BD，过点 C作CH⊥BD于H，连接AH，则AH的最小值为
..
15
..
16
真题演练
1.如图，长 2 米的梯子 AB 竖直放在墙角，在沿着墙角缓慢下滑直至水平地面过程中，梯子 AB 的中点 P 的移动轨迹长度为（）
3. 如图 1，Rt△ABC 中，AB⊥BC，AB=6， BC=4，P 是△ABC 内部的一个动点，且始终有AP⊥BP，则线段 CP 长的最小值为（）。
..
21
3. 如图 1，Rt△ABC 中，AB⊥BC，AB=6， BC=4，P 是△ABC 内部的一个动点，且始终有AP⊥BP，则线段 CP 长的最小值为（）。
点到 F 点的距离永远等于 2，故 P 在
⊙F 上运动，如图。由垂线段最短可
知，FH⊥AB 时，FH 最短，当 F、P、
H 三点共线时，PH 最短，又因为
△AFH∽△ABC，所以
AF:FH:AH=5:4:3，又因为 AF=4，故
FH=3.2，又因为 FP=2，故 PH 最短为
1.2
பைடு நூலகம்..
20
真题演练
案3就可以解决。然而难点在于如何知道动点的运动路径
是圆，如何将这个隐身“圆”找出来？从以上例子得出以
下两种方法（1）观察到定点的距离，即圆是到定点距离
等于定长的点的集合；（2）“定弦对定角”如例中线段
是定值，当动点在运动过程中的大小不变等于90度（当
然不一定为直角），点的运动路径也是圆（或弧）。
牢记口诀：定点定长走圆周，定线定角跑双弧。直角必有外接圆，对角互补也共圆。