(完整word版)高中数学中的函数图象变换及练习题.doc
(word版)高中数学三角函数y=Asin(ωx+φ)图像变换练习题

三角函数y =Asin(ωx +φ)图像练习题一、单选题1. 函数f(x)=2sin(ωx +φ)(ω>0,−π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( )A. 2,−π3 B. 2,−π6 C. 4,−π6 D. 4,π32. 为了得到函数y =sin (2x +π3)的图象,只需要把函数y =sinx 的图象上( )A. 各点的横坐标缩短到原来的12,再向左平移π3个单位长度 B. 各点的横坐标缩短到原来的12,再向左平移π6个单位长度 C. 各点的横坐标伸长到原来的2倍,再向左平移π3个单位长度 D. 各点的横坐标伸长到原来的2倍,再向左平移π6个单位长度3. 要得到函数y =sinx +cosx 的图象,只需把函数y =√2sin (x −π12)的图象( )A. 向左平移π3个单位长度 B. 向右平移π3个单位长度 C. 向左平移13个单位长度D. 向右平移13个单位长度4. 要得到函数y =3sin (2x +π4)的图象,只需将y =3sin2x 的图象( )A. 向左平移π8个单位 B. 向右平移π8个单位 C. 向左平移π4个单位D. 向右平移π4个单位5. 已知函数f(x)=Msin(ωx +φ)(M >0,ω>0,|φ|<π2)在半个周期内的图象如图所示,则函数f(x)的解析式为( )A. f(x)=2sin(x +π6) B. f(x)=2sin(2x −π6)C. f(x)=2sin(x−π6)D. f(x)=2sin(2x+π6)6.为得到函数y=cos(x+π3)的图象,只需将函数y=sinx的图象()A. 向左平移π6个单位长度 B. 向右平移π6个单位长度C. 向左平移5π6个单位长度 D. 向右平移5π6个单位长度7.函数y=Asin(ωx+φ)在一个周期上的图象如图所示,则函数的解析式是()A. y=2sin(x2−23π)B. y=2sin(x2+43π)C. y=2sin(x2+23π)D. y=2sin(x2−π3)8.设ω>0,函数y=sin(ωx+π3)+2的图象向右平移4π3个单位长度后与原图象重合,则ω的最小值是().A. 23B. 43C. 32D. 39.如图所示,函数f(x)=Asin(2x+φ)(其中A>0,|φ|<π2)的图象过点(0,√3),则f(x)的图象的一个对称中心是()A. (−π3,0)B. (−π6,0)C. (π6,0)D. (π4,0)10.将函数y=sinωx(ω>0)的图象向左平移π6个单位长度,平移后的图象如图所示,则平移后的图象所对应的函数解析式为()A. y=sin(x+π6)B. y=sin(x−π6)C. y=sin(2x+π3)D. y=sin(2x−π3)11.将函数f(x)=sin(x+φ)图象上所有点的横坐标变为原来的1ω(ω>1)(纵坐标不变),得函数g(x)的图象.若g(π6)=1,g(2π3)=0,且函数g(x)在(π6,π2)上具有单调性,则ω的值为()A. 2B. 3C. 5D. 712.设函数的最小正周期为π,则下列说法正确的是()A. 函数f(x)的图象关于直线x=π3对称B. 函数f(x)的图象关于点(π12,0)对称C. 函数f(x)在(−5π12,π12)上单调递减D. 将函数f(x)的图象向右平移5π12个单位,得到的新函数是偶函数13.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π2),其图象相邻的最高点之间的距离为π,将函数y=f(x)的图象向左平移π12个单位长度后得到函数g(x)的图象,且g(x)为奇函数,则()A. f(x)的图象关于点(π6,0)对称 B. f(x)的图象关于点(−π6,0)对称C. f(x)在(−π6,π3)上单调递增 D. f(x)在(−2π3,−π6)上单调递增14.已知曲线C1:y=cosx,C2:y=sin(2x+2π3),则下面结论正确的是()A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C215.已知曲线y=sin(2x+π6)向左平移φ(φ>0)个单位,得到的曲线y=g(x)经过点(−π12,1),则()A. 函数y=g(x)的最小正周期T=π2B. 函数y=g(x)在[11π12,17π12]上单调递增C. 曲线y=g(x)关于直线x=π6对称D. 曲线y=g(x)关于点(2π3,0)对称16.若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π)的图象如图所示,则函数y=f(x)的解析式为()A. y=32sin(2x+π6)B. y=32sin(2x−π6)C. y=32sin(2x+π3)D. y=32sin(2x−π3)二、多选题17.已知函数f(x)=sin(2x+π3),将其图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若函数g(x)为奇函数,则φ的值可以为()A. π12B. π6C. π3D. 2π318.为了得到函数y=cos(2x+π4)的图象,只要把函数y=cosx图象上所有的点()A. 向左平移π4个单位长度,再将横坐标变为原来的2倍B. 向左平移π4个单位长度,再将横坐标变为原来的12倍C. 横坐标变为原来的12倍,再向左平移π8个单位长度 D. 横坐标变为原来的12倍,再向左平移π4个单位长度19. 已知函数f(x)=2cos 2ωx +√3sin2ωx −1(ω>0)的最小正周期为π,则下列说法正确的有( )A. ω=2B. 函数f(x)在[0,π6]上为增函数C. 直线x =π3是函数y =f(x)图象的一条对称轴 D. 点(512π,0)是函数y =f(x)图象的一个对称中心20. 将函数f(x)的图象向右平移π6个单位长度,再将所得函数图象上的所有点的横坐标缩短到原来的23,得到函数g(x)=Asin(ωx +φ)(A >0,ω>0,|φ|<π2)的图象.已知函数g(x)的部分图象如图所示,则下列关于函数f(x)的说法正确的是( )A. f(x)的最小正周期为π,最大值为2B. f(x)的图象关于点(π6,0)中心对称 C. f(x)的图象关于直线x =π6对称 D. f(x)在区间[π6,π3]上单调递减第II 卷(非选择题)三、解答题21. 已知函数f(x)=4cos xsin (x +π6)−1.(1)求f(x)的最小正周期;(2)求f(x)在区间[−π6,π4]上的最大值和最小值.22.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,−π2<φ<π2)的部分图象如图所示.(1)求函数f(x)的解析式;(2)若x∈[−53,53],求函数f(x)的值域.23.已知函数f(x)=2√3sinxcosx−cos(2x+π3)−cos(2x−π3).(Ⅰ)求f(π2)的值.(Ⅱ)求函数f(x)在区间[−π12,5π12]上的最大值和最小值.24.已知函数y=12sin (2x+π6),x∈R.(1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的简图;(3)该函数的图象可由y=sin x(x∈R)的图象经过怎样的平移和伸缩变换得到⋅25.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图像如图所示:(1)求函数f(x)的解析式;(2)将函数y=f(x)的图像上各点的横坐标缩短到原来的12,纵坐标不变,得到函数y=g(x)的图像,求函数y=g(x)在区间[0,π4]上的最大值及函数取最大值时相应的x 值.26.已知函数f(x)=cos2x+sin(2x−π6).(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)当x∈[0,π]时,求函数f(x)的单调递增区间.27.已知函数f(x)=2cos(x−π3)+2sin(3π2−x).(1)求函数f(x)的单调递减区间;(2)求函数f(x)的最大值,并求f(x)取得最大值时的x的取值集合;(3)若f(x)=65,求cos(2x−π3)的值.28.已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<π)的部分图像如图所示.(I)求f(x)的解析式;(II)在△ABC中,角A、B、C的对边分别为a,b,c,a=1,c=2,f(A)=1,求b的值.29.已知函数f(x)=√3sinxcosx+sin2x−12.(1)求f(x)的单调递增区间;(2)若A∈(π12,π3),f(A)=13,求cos(2A−5π6)的值.30.已知函数f(x)=4sinxcos(x+π3)+√3.(1)求函数f(x)的最小正周期及单调增区间;(2)求函数f(x)在区间[−π4,π6]上的值域和取得最大值时相应的x的值.答案和解析1.【答案】A本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,属于基础题.结合图象由周期求出ω,由特殊点的坐标求出φ的值.【解答】解:由题意可知T=2×(11π12−5π12)=π,∴ω=2,x=5π12时,函数取得最大值2,可得:2sin(2×5π12+φ)=2,,即,又∵−π2<φ<π2,所以φ=−π3.故选A.2.【答案】B本题考查了函数y=Asin(ωx+φ)的图象的伸缩平移,属于基础题.根据函数图象伸缩平移变换法则即可得到答案.【解答】解:y=sinx图象上各点的横坐标缩短到原来的12,得到y=sin2x的图象,再向左平移π6个单位长度得到y=sin[2(x+π6)]=sin(2x+π3)的图象,故选B.3.【答案】A【分析】本题主要考查函数y=Asin(ωx+φ)的图象的平移变换,辅助角公式,属于基础题.由辅助角公式,根据函数y=Asin(ωx+φ)的图象的平移变换可得答案.【解答】解:y =sinx +cosx,则要得到函数y =sinx +cosx 的图象,只需把函数y =√2sin (x −π12)的图象向左平移π3个单位长度. 故选A .4.【答案】A本题考查函数y =Asin(ωx +φ)的图象变换规律,属于基础题.由y =3sin (2x +π4)=3sin [2(x +π8)],根据左加右减的平移原理,即可得到结果. 【解答】解:y =3sin (2x +π4)=3sin [2(x +π8)],因此将函数y =3sin2x 的图象向左平移π8个单位,即可得到函数y =3sin (2x +π4)的图象. 故选A .5.【答案】A【分析】本题主要考查由函数y =Asin(ωx +φ)的部分图象求解析式,属于基础题. 由函数的最值求出A ,由周期求出ω,由五点法作图求出φ的值.【解答】解:由图象知M =2. 设函数f(x)的最小正周期为T , 则14T =π3−(−π6)=π2,可知T =2π,ω=2πT=1,将(π3,2)代入f(x)的解析式得sin(π3+φ)=1, 又|φ|<π2,可得φ=π6,故函数f(x)的解析式为f(x)=2sin(x +π6). 故选A .6.【答案】C本题考查了函数y =Asin(ωx +φ)的图象与性质、函数图象的变换的相关知识,属于基础题.根据函数y=Asin(ωx+φ)的图象变换的规则可得结论.【解答】解:故选C.7.【答案】C本题考查三角函数y=Asin(ωx+φ)的图象和性质,涉及诱导公式应用,属于基础题.依题意,根据图象求得A=2,ω=12,根据五点作图法得进而求得结果.【解答】解:由图知A=2,T2=8π3−2π3=2π=πω,ω=12,y=2sin(12x+φ),根据五点作图法知,代入得,,所以,k∈Z,故选C.8.【答案】C本题考查函数y=Asin(ωx+φ)的图象和性质,属于基础题.函数y=sin(ωx+π3)+2的图象向右平移4π3个单位长度后与原图象重合,可判断出4π3是此函数周期的整数倍,由此能求出ω的表达式,判断出它的最小值.【解答】解:由函数的图象向右平移4π3个单位长度后与原图象重合,得4π3是此函数周期的整数倍.又ω>0,∴2πω⋅k=4π3(k∈Z,且k>0),∴ω=3k2(k∈Z,且k>0),∴ωmin=32.故选C.9.【答案】B【解答】解:由函数图象可知A=2,由于图象过点(0,√3),可得2sinφ=√3,即sinφ=√32,由于|φ|<π2,解得φ=π3,即有f(x)=2sin(2x+π3).由2x+π3=kπ,k∈Z,解得x=kπ2−π6,k∈Z,故f(x)的图象的对称中心是(kπ2−π6,0),k∈Z,当k=0时,f(x)的图象的一个对称中心是(−π6,0).故选B.10.【答案】C本题考查三角函数图像的平移变换,函数的解析式,属于基础题.由三角函数图像的平移得为,代入点,得,得ω=2,从而得解析式.【解答】解:函数y=sinωx(ω>0)的图象向左平移π6个单位长度,则平移后的图象所对应的函数解析式为,代入点,得,,k∈Z,当k=0时,ω=2,即解析式为y=sin(2x+π3).故选C.11.【答案】B本题考查函数y=Asin(ωx+φ)的图象与性质,属于中档题.根据题意得出,得出ω=2n−1(n∈N∗),由函数g(x)在(π6,π2)上具有单调性,得出π2−π6⩽T2=πω,即可求出结果.【解答】解:由题意得,g(x)=sin(ωx+φ),最小正周期T=2πω,若g(π6)=1,g(2π3)=0,,∴ω=2n−1(n∈N∗),∵函数g(x)在(π6,π2)上具有单调性,∴π2−π6⩽T2=πω,解得ω⩽3,又ω>1,ω=2n−1(n∈N∗),∴ω=3.故选B.12.【答案】D本题考查函数y=Asin(ωx+φ)的图象与性质,正弦、余弦函数的图象与性质,属于中档题.先根据函数f(x)=12sin(ωx+π3)(ω>0)的最小正周期为π,求出ω=2,再根据选项逐一判断即可.【解答】解:∵函数f(x)=12sin(ωx+π3)(ω>0)的最小正周期为π,∴2πω=π,解得ω=2,则f(x)=12sin(2x+π3),对于A.当x=π3时,f(π3)=12sin(2×π3+π3)=0,∴函数f(x)的图象关于点(π3,0)对称,故A不正确;对于B.当x=π12时,f(π12)=12sin(2×π12+π3)=12,∴函数f(x)的图象关于直线x=π12对称,故B不正确;对于C.f(x)=12sin(2x+π3)的单调递减区间满足:2kπ+π2≤2x+π3≤2kπ+3π2,k∈Z,解得kπ+π12≤x≤kπ+7π12,k∈Z,k=−1时不符合,故C不正确;对于D.将函数f(x)的图象向右平移5π12个单位,得到新函数为g(x)=f(x−5π12)=1 2sin(2x−π2)=−12cos2x,是偶函数,故D正确.故选D.13.【答案】C本题考查三角函数的图象的性质,属一般题.根据题意求出函数解析式,然后验证对称性和单调性.【解答】解:f(x)=2sin(ωx +φ)(ω>0,|φ|<π2),其图象相邻最高点之间距离为,ω=2, 所以将函数y =f(x)的向左平移π12个单位长度后,,因为g(x)为奇函数, 所以,则,则,当,,当,,故A ,B 错误;当x ∈(−π6,π3)时,,所以f(x)在(−π6,π3)单调递增,故C 正确;当x ∈(−2π3,−π6)时,,所以f(x)在(−2π3,−π6)单调递减,故D 错误; 故选C .14.【答案】D本题考查三角函数的图象变换、诱导公式的应用. 利用三角函数的伸缩变换以及平移变换转化求解即可.【解答】解:把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变, 得到函数y =cos2x 图象,再把得到的曲线向左平移π12个单位长度, 得到函数y =cos2(x +π12)=cos(2x +π6) =sin(2x +2π3)的图象,即曲线C 2,故选D .15.【答案】D本题主要考查函数y =Asin(ωx +φ)的图象变换规律,三角函数的图象和性质,属于基础题.利用函数y =Asin(ωx +φ)的图象变换规律求得g(x)的解析式,再利用余弦函数的图象和性质,可得结论.【解答】解:把曲线y=sin(2x+π6)向左平移φ(φ>0)个单位,得到的曲线y=g(x)=sin(2x+2φ+π6),由于所得曲线经过点(−π12,1),∴sin(−π6+2φ+π6)=sin2φ=1,,,∵φ>0,,,,,故g(x)=cos(2x+π6)的最小正周期为2π2=π,故A错误;在[11π12,17π12]上,2x+π6∈[2π,3π],故函数y=g(x)在[11π12,17π12]上单调递减,故B错误;当x=π6时,g(x)=0,故g(x)的图象关于点(π6,0)对称,故C错误;当x=2π3时,g(x)=0,故g(x)的图象关于点(2π3,0)对称,故D正确,故选:D.16.【答案】D由图象求y=Asin(ωx+φ)(A>0,ω>0)解析式的方法;(1)A可由图象上最高点和最低点的纵坐标确定;(2)ω可由图象上最高点与最低点的横坐标确定,先求出最小正周期T,再由T=2πω求出ω;(3)φ可以由某一点处的函数值求得,要注意φ的范围.【解答】解:设f(x)的最小正周期为T,则12T=2π3−π6=π2,T=π,∴ω=2πT =2.又由图象可得A=32,∴f(x)=32sin(2x+φ).∵f(5π12)=32sin(2×5π12+φ)=32,∴5π6+φ=2kπ+π2,k∈Z,即φ=2kπ−π3,k∈Z,又|φ|≤π,∴φ=−π3,∴y=f(x)=32sin(2x−π3).故选D.17.【答案】BD【解析】【分析】本题考查了函数y=Asin(ωx+φ)的图象与性质的相关知识,试题难度较易由题意将函数f(x)图象向右平移φ(φ>0)个单位长度后,得到的图象对应的解析式g(x),又函数g(x)为奇函数,即可得出φ的值【解答】解:将函数f(x)图象向右平移φ(φ>0)个单位长度后,得到的图象对应的解析式为g(x)=sin[2(x−φ)+π3]=sin(2x−2φ+π3).由g(x)为奇函数可得−2φ+π3=kπ(k∈Z),故φ=π6−kπ2(k∈Z),又φ>0,结合选项,所以φ的值可以为π6,23π.故应选BD.18.【答案】BC【分析】本题考查函数y=Asin(ωx+φ)的图象与性质,函数图象的平移伸缩变换,属于基础题.依据函数y=Asin(ωx+φ)的图象平移伸缩变换的规则逐一判定即可.【解答】解:对于A,把函数y=cosx图象上所有的点向左平移π4个单位长度,可得函数,再将横坐标变为原来的2倍,可得函数,故A错误;对于B,把函数y=cosx图象上所有的点向左平移π4个单位长度,可得函数,再将横坐标变为原来的12倍,可得函数,故B正确;对于C,把函数y=cosx图象上所有的点横坐标变为原来的12倍,可得函数y=cos 2x,再向左平移π8个单位长度,可得函数,故C正确;对于D,把函数y=cosx图象上所有的点横坐标变为原来的12倍,可得函数y=cos 2x,再向左平移π4个单位长度,可得函数,故D错误.故选BC.19.【答案】BD本题考查三角函数的性质应用,考查两角和与差的三角函数公式,辅助角公式及二倍角公式应用,属基础题.依题意,根据两角和与差的三角公式及二倍角公式化简函数,再根据三角函数的性质求解即可.【解答】解:,因最小正周期为π得ω=1,故A错误,当时,,得函数f(x)在[0,π6]上为增函数,故B正确;当,,所以直线x=π3不是函数y=f(x)图象的一条对称轴,故C 错误;当,,得点(512π,0)是函数y=f(x)图象的一个对称中心,故D正确;故选BD.20.【答案】ACD本题考查三角函数的图象与性质,涉及正弦函数图象与性质的应用,属于中档题.先由函数图象得出g(x)的解析式,再由函数图象的变换得出f(x)的解析式,借助正弦函数的图象与性质得出答案即可.【解答】解:由图可知,A=2,T=4×(2π9−π18)=2π3,∴ω=2πT=3,又由g(2π9)=2,可得2π9×3+φ=π2+2kπ(k∈Z),且lφ|<π2,∴φ=−π6,∴g(x)=2sin(3x −π6),将函数g(x)的图象上所有点的横坐标伸长到原来的32,可得函数,再将函数图象向左平移π6个单位长度,得到函数,∴f(x)=2sin(2x +π6),∴f(x)的最小正周期为π,最大值为2,A 正确. 令2x +π6=kπ,k ∈Z ,得,∴函数f(x)图象的对称中心为(kπ2−π12,0)(k ∈Z), 由kπ2−π12=π6,得k =12,不符合k ∈Z ,B 错误; 对于选项C ,令2x +π6=π2+kπ(k ∈Z),得x =π6+kπ2(k ∈Z),∴函数f(x)图象的对称轴为直线x =π6+kπ2(k ∈Z),当k =0时,x =π6,故C 正确;当x ∈[π6,π3]时,2x +π6∈[π2,5π6],∴f(x)在区间[π6,π3]上单调递减,D 正确. 故选ACD .21.【答案】解:(1)因为f(x)=4cos xsin (x +π6)−1=4cos x (√32sin x +12cos x)−1=√3sin 2x +2cos 2x −1 =√3sin 2x +cos 2x=2sin (2x +π6), 所以f(x)的最小正周期为π; (2)因为−π6≤x ≤π4, 所以−π6≤2x +π6≤2π3.故当2x +π6=π2,即x =π6时,f(x)取得最大值2; 当2x +π6=−π6,即x =−π6时,f(x)取得最小值−1.【解析】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,属于中档题.(1)利用二倍角和两角和与差以及辅助角公式将函数化为y=Asin(ωx+φ)的形式,即可求出函数的最小正周期;(2)先根据x的取值范围求得2x+π6的范围,再由正弦函数的性质即可求出函数的最大值和最小值.22.【答案】解:(1)由图象知函数的最大值为1,即A=1,T2=3−(−1)=4,即周期T=8,即2πω=8,得ω=π4,则f(x)=sin(π4x+φ),由五点对应法得π4×1+φ=π2,得φ=π4,即f(x)=sin(π4x+π4).(2)若x∈[−53,53 ],则π4x+π4∈[−π6,2π3],∴当π4x+π4=−π6时,即x=−53时,f(x)最小,最小值为f(−53)=−12,当π4x+π4=π2时,即x=1时,f(x)最大,最大值为f(1)=1,∴f(x)的值域为[−12,1].【解析】本题主要考查三角函数的图象和性质,利用图象法求出函数的解析式以及结合三角函数的最值性质是解决本题的关键.难度不大.(1)根据函数图象先求出A和周期,结合周期公式求出ω,利用五点对应法求出φ即可求出函数的解析式.(2)求出角的范围,结合三角函数的最值关系进行求解即可.23.【答案】解:(Ⅰ;(Ⅱ)f(x)=2√3sinxcosx−cos(2x+π3)−cos(2x−π3)=√3sin2x−12cos2x+√32sin2x−12cos2x−√32sin2x=√3sin2x −cos2x =2sin(2x −π6),因为x ∈[−π12,5π12]∴−π3≤2x −π6≤2π3,∴2sin(2x −π6)∈[−√3,2]. 即函数f(x)在区间[−π12,5π12]上的最大值为2,最小值为−√3.【解析】本题考查三角函数的化简与求值,考查三角函数的性质,属基础题. (Ⅰ)将代入化简即可;(Ⅱ)利用辅助角公式化简得到f(x),由x 的取值范围得出2x −π6的范围,再由正弦函数的性质得出最值即可.24.【答案】解:(1)函数y =12sin (2x +π6)的振幅为12,周期为π,初相为π6.(2)列表:描点画图(如图所示):(3)函数y =sinx 的图象向左平移π6个单位长度,得到函数y =sin (x +π6)的图象, 再保持纵坐标不变,把横坐标缩短为原来的12倍,得到函数y =sin (2x +π6)的图象, 再保持横坐标不变,把纵坐标缩短为原来的12倍,得到函数y =12sin (2x +π6)的图象.【解析】本题主要考查了三角函数的图象和性质以及“五点法”作图和图象的平移和伸缩变换,属于基础题.(1)结合振幅、周期、初相的定义可得; (2)按照列表、描点、连线的步骤求解画图;(3)由y =sinx (x ∈R )的图象左移π6个单位得到数y =sin (x +π6),x ∈R 的图象,然后横坐标再伸缩得到y =sin (2x +π6),x ∈R 的图象,最后纵坐标再伸缩得到y =12sin (2x +π6),x ∈R 的图象.25.【答案】解:(1)如图可知,A =2,T =4×[π12−(−π6)]=π,∴ω=2πT=2.∵{2sin (2×π12+φ)=2|φ|<π2,∴φ=π3,即函数解析式为;(2)根据图象平移原则得g (x )=2sin (4x +π3), ∵x ∈[0,π4],∴4x +π3∈[π3,4π3],∴2sin (4x +π3)∈[−√3,2], 当,即x =π24时,函数g(x)在区间[0,π4]上的最大值为2.【解析】本题考查了三角函数的图象与性质的应用,求出函数f(x)的解析式是关键,属于中档题.(1)利用三角函数的图象,得出振幅A 与周期T ,代入特殊点求出φ,即可求出函数解析式;(2)根据图像平移,得到函数g(x)的解析式,最后利用正弦型函数的性质求出结果.26.【答案】解:(Ⅰ)函数f(x)=cos2x +sin(2x −π6)=cos2x +√32sin2x −12cos2x =sin(2x +π6),故它的最小正周期为2π2=π.(Ⅱ)令2kπ−π2≤2x +π6≤2kπ+π2,k ∈Z , 得kπ−π3≤x ≤2kπ+π6,k ∈Z ,∴函数的增区间为[kπ−π3,2kπ+π6],k∈Z,∵x∈[0,π],∴函数的增区间为[0,π6]、[2π3,π].【解析】本题主要考查两角和差的三角公式,正弦函数的周期性和单调性,属于基础题.(Ⅰ)由题意利用两角和差的三角公式化简函数f(x)的解析式,可得它的最小正周期.(Ⅱ)由题意利用正弦函数的单调性,求出函数f(x)的单调递增区间.27.【答案】解:f(x)=2cosxcosπ3+2sinxsinπ3−2cosx=cosx+√3sinx−2cosx=√3sinx−cosx=2sin(x−π6 ).(1)令2kπ+π2≤x−π6≤2kπ+32π(k∈Z),∴2kπ+2π3≤x≤2kπ+5π3(k∈Z),∴f(x)的单调递减区间为[2kπ+2π3,2kπ+5π3](k∈Z).(2)f(x)取最大值2时,x−π6=2kπ+π2(k∈Z),则x=2kπ+2π3(k∈Z).∴f(x)的最大值是2,取得最大值时的x的取值集合是{x|x=2kπ+2π3,k∈Z}.(3)∵f(x)=65,∴2sin(x−π6)=65,∴sin(x−π6)=35.∴cos(2x−π3)=1−2sin2(x−π6)=1−2×(35)2=725.【解析】本题考查了函数y=Asin(ωx+φ)的图象与性质,诱导公式,两角和与差的三角函数公式和二倍角公式,属于中档题.利用诱导公式和两角差的余弦函数公式得f(x)=√3sinx−cosx,即.(1)利用函数y=Asin(ωx+φ)的单调性,计算得结论;(2)利用函数y=Asin(ωx+φ)的最值,计算得结论;(3)利用题目条件得,再利用余弦的二倍角公式,计算得结论.28.【答案】解:(1)由最值可确定A=2,周期T=2×(π3+π6)=π⇒ω=2,又f(π3)=2,即,,即,∵|φ|<π,∴φ=−π6,所以f(x)=2sin (2x−π6);(2)f(A)=2sin (2A−π6)=1⇒sin (2A−π6)=12⇒2A−π6=π6或5π6,故A=π6或π2,当A=π2时,三角形为直角三角形,此时a>c,这与题目条件a=1,c=2矛盾,所以舍掉;当A=π6时,由余弦定理得:a2=b2+c2−2bccos A⇒b2−2√3b+3=0,解得b=√3.【解析】本题考查函数y=Asin(ωx+φ)的图象与性质,余弦定理,考查运算化简的能力,属于中档题.(1)由图可得A=2,,可得ω=2,再由f(π3)=2,结合|φ|<π可得φ,从而可得f(x)的解析式;(2)由(1)及f(A)=1,求得A=π6或π2,按A讨论结合余弦定理可得.29.【答案】解:(1)f(x)=√3sinxcosx+sin2x−12=√32sin2x+1−cos2x2−12=sin(2x−π6 ),令−π2+2kπ≤2x−π6≤π2+2kπ,k∈Z.解得,k∈Z.所以f(x)的单调增区间为[−π6+kπ,π3+kπ](k∈Z).(2)由(1)得f(x)=sin(2x−π6),所以f(A)=sin(2A−π6)=13,令θ=2A−π6,则0<θ<π2,所以sinθ=13,cosθ=2√23,则cos(2A−56π)=cos(θ−23π)=cosθcos23π+sinθsin23π=2√23×(−12)+13×√32=√3−2√26.【解析】本题考查了函数y=Asin(ωx+φ)的图象与性质和三角恒等变换,是中档题。
函数图像变换练习题

函数图像变换练习题函数图像变换练习题函数图像变换是数学中的重要概念,它帮助我们理解函数的性质和变化规律。
通过对函数图像进行变换,我们可以观察到函数在平移、伸缩和翻转等操作后的形态变化。
在这篇文章中,我们将通过一些练习题来加深对函数图像变换的理解。
1. 平移变换平移变换是指将函数图像沿着坐标轴的方向进行平移。
具体而言,平移变换可以分为水平平移和垂直平移两种情况。
练习题1:考虑函数f(x) = x^2,将其沿x轴方向平移3个单位,请画出平移后的函数图像。
解答:对于函数f(x) = x^2,进行水平平移3个单位后的函数可以表示为f(x-3) = (x-3)^2。
通过计算可知,平移后的函数图像与原函数相比,在x轴上整体向右平移了3个单位。
2. 伸缩变换伸缩变换是指将函数图像沿着坐标轴的方向进行拉伸或压缩。
具体而言,伸缩变换可以分为水平伸缩和垂直伸缩两种情况。
练习题2:考虑函数f(x) = x^2,将其在x轴方向进行压缩,使得函数图像变为原来的一半宽度,请画出压缩后的函数图像。
解答:对于函数f(x) = x^2,进行在x轴方向的压缩后的函数可以表示为f(2x) = (2x)^2。
通过计算可知,压缩后的函数图像与原函数相比,在x轴上整体变窄了一半。
3. 翻转变换翻转变换是指将函数图像沿着坐标轴进行翻转。
具体而言,翻转变换可以分为水平翻转和垂直翻转两种情况。
练习题3:考虑函数f(x) = x^2,将其进行水平翻转,请画出翻转后的函数图像。
解答:对于函数f(x) = x^2,进行水平翻转后的函数可以表示为f(-x) = (-x)^2。
通过计算可知,翻转后的函数图像与原函数相比,在y轴上对称翻转。
通过以上练习题,我们可以看到函数图像在不同的变换下发生了形态上的变化。
这些变换可以帮助我们更好地理解函数的性质和变化规律。
在实际应用中,函数图像变换也被广泛应用于物理、工程和经济等领域。
除了上述的平移、伸缩和翻转变换,函数图像还可以进行其他的变换,如旋转和剪切等。
专题 函数的图像变换结论总结(练习及答案)高三数学总复习

第88讲 函数的图像变换结论总结一、点的变换设(),P x y ,则它1.关于x 轴对称的点为(),x y -.2.关于y 轴对称的点为(),x y -.3.关于原点对称的点为(),x y --.4.关于直线y x =对称的点为(),y x .5.关于直线y x =-对称的点为(),y x --.6.关于直线y b =对称的点为(),2x b y -.7.关于直线x a =对称的点为()2,a x y -.8.关于直线y x a =+对称的点为(),y a x a -+.9.关于直线y x a =-+对称的点为(),a y a x --.10.关于点(),a b 对称的点为()2,2a x b y --.11.按向量(),a b 平移得到的点为(),x a y b ++.二、曲线的变换曲线(),0F x y =按下列变换后所得的方程:1.按向量(),a b 平移,得到(),0F x a y b --=.2.关于x 轴对称,得到(),0F x y -=.3.关于y 轴对称,得到(),0F x y -=.4.关于原点对称,得到(),0F x y --=.5.关于直线x a =对称,得到()2,0P a x y -=.6.关于直线y b =对称,得到(),20F x b y -=.7.关于点(),a b 对称,得到()2,20F a x b y --=.8.关于直线y x =对称,得到(),0F y x =.9.关于直线y x a =+对称,得到(),0F y a x a -+=.10.关于直线y x a =-+对称,得到(),0F a y a x --=.11.纵坐标不变,横坐标变为原来的a 倍,得到方程,0x F y a ⎛⎫= ⎪⎝⎭. 12.横坐标不变,纵坐标变原来的b 倍,得到方程,0y F x b ⎛⎫= ⎪⎝⎭. 三、两个函数的图像性质1.左右平移:()()0y f x a a =±>的图像可由()y f x =的图像向左()+或向右()-平移a 个单位得到.2.()()0,0y f mx a m a =±>>的图像可由()y f mx =的图像向左()+或向右()-平和多a m个单位而得到. 3.上下平移:()()0y f x b b =±>的图像可由()y f x =的图像向上()+或向下()-平移b 个单位而得到.4.()y f x =-的图像与()y f x =的图像关于y 轴对称,换句话说:()y f x =与()y g x =若满足()()f x g x =-,则它们关于0x =对称.5.()y f x =-的图像与()y f x =的图像关于x 轴对称,换句话说:()y f x =与()y g x =若满足()()f x g x =-,则它们关于0y =对称.6.()y f x =--的图像与()y f x =的图像关于原点对称.7.()y f x =的图像可如此得到()y f x =的图像在x 轴下方的部分以x 轴为对称轴翻折到x 轴的上方,其余不变.(下翻上)8.()y f x =的图像:保留()y f x =的图像在y 轴右侧的部分,并沿y 轴翻折到y 轴左边部分代替原y 轴左边部分.(去左翻右) 9.()y f x a =+与()y f b x =-关于直线2b a x -=对称.10.()y f a x =-与()y f x b =-关于直线2a b x +=对称. 11.()y f x =与()2y a f x =-关于直线y a =对称,换种说法:()y f x =与()y g x =若满足()()2f x g x a +=,则它们关于点(),a b 对称.12.()y f x =与()22y b f a x =--关于点(),a b 对称,换种说法:()y f x =与()y g x =,若满足()()22f x g a x b +-=,则它们关于点(),a b 对称.13.()1y f x -=与()y f x =关于直线y x =对称.14.()1y f x -=--的图像与()y f x =的图像关于直线y x =-对称.15.函数()y f a mx =+的图像与()y f b mx =-的图像关于直线2b a x m -=对称. 16.函数()y f x =与()a x f a y -=-的图像关于直线x y a +=成轴对称.17.伸缩变换:()()0y Af x A =>的图像,可将()y f x =的图像上每一个点的横坐标不变,纵坐标变为原来的A 倍而得到.18.()()0y f kx k =>的图像,可将()y f x =的图像上每一个点的纵坐标不变,横坐标变为原来的1k而得到. 四、单个函数的图像性质1.对任意x ,()()f x f a x =-⇔()y f x =的图像关于直线2a x =对称. 2.对任意x ,()f x a +是偶函数⇔()y f x =关于x a =对称.3.对任意x ,()()f x a f b x +=-()y f x ⇔=的图像关于直线2a b x +=对称. 4.若函数()y f x =对定义域中的任意x 的值,都满足()()f a mx f b mx +=-,则函数()y f x =的图像关于直线2a b x +=对称. 5.若函数()y f x =对定义域中的任意x ,都满足()()f a mx f b mx +=-,则函数()y f mx =的图像关于直线2a b x m+=对称.6.对任意x ,()()0f x f a x +-=⇔()y f x =的图像关于点,02a ⎛⎫ ⎪⎝⎭对称. 7.对任意x ,()f x a +是奇函数⇔()y f x =关于(),0a 对称.8.对任意x ,()()0f x a f b x ++-=()y f x ⇔=的图像关于点,02a b +⎛⎫ ⎪⎝⎭对称. 9.若函数()y f x =对定义域中的任意x 的值,都满足()()0f a x f b x ++-=,则函数()y f x =的图像关于点,02a b +⎛⎫ ⎪⎝⎭对称. 10.若函数()y f x =对定义域中的任意x ,都满足()()0f a mx f b mx ++-=,则函数()y f mx =的图像关于点,02a b m +⎛⎫ ⎪⎝⎭对称. 11.()y f x =的图像关于点(),a b 对称⇔对任意的x ,()()2f a x f a x b ++-=;更一般地:若()()f a x f b x c ++-=,则()y f x =的图像关于点,22a b c +⎛⎫ ⎪⎝⎭对称. 12.若()f x 有两条对称轴x a =和x b =,则函数()y f x =是周期函数,且2b a -是一个周期.13.若()f x 有两个对称中心(),0a 和(),0b ,则函数()y f x =是周期函数,且2b a -是一个周期.14.若()f x 以x a =为对称轴,且以(),0b 为对称中心,则函数()y f x =是周期函数,则4b a -是函数()f x 的一个周期.15.若()()f x A f x B +=+,则()f x 是周期函数,B A -是它的一个周期.16.对于非零数学A ,若函数()y f x =满足()()f x A f x +=-,则函数()y f x =必有一个周期为2A .17.若函数()y f x =对任意实数x ,都有()()f x A f x B M +++=,则函数()y f x =必有一个周期为2B A -.18.对于非零常数A ,函数()y f x =满足()()1f x A f x +=,则函数()y f x =的一个周期为2A .19.对于非零常数A ,函数()y f x =满足()()1f x A f x +=-,则函数()y f x =的一个周期为2A .20.对于非零常数A ,函数()y f x =满足()()()11f x f x A f x -+=+,则函数()y f x =的一个周期为2A .21.对于非零常数A ,函数()y f x =满足()()()11f x f x A f x ++=-,则函数()y f x =的一个周期为4A .22.对于非零常数A ,函数()y f x =满足()()()2f x A f x f x A +=++,则函数()y f x =的一个周期为6A .五、直线一般式的对称问题对称轴方程为0Ax By C ++=,则1.点(),A x y 与(),B x y ''关于直线0Ax By C ++=对称,则()()222222A Ax By C x x A B B Ax By C y y A B ++⎧'=-⎪⎪+⎨++⎪'=-⎪⎩+. 2.函数()y f x =与()()222222B Ax By C A Ax By C y f x A B A B ++++⎛⎫-=- ⎪++⎝⎭关于直线0Ax By C ++=成轴对称.3.(),0F x y =与()()222222,0A Ax By C B Ax By C F x y A B A B ++++⎛⎫--= ⎪++⎝⎭关于直线0Ax By C ++=成轴对称.。
高中数学《三角函数的图像和变换》以及经典习题

函数sin()y A x ωϕ=+的图象与变换【知识网络】1.函数sin()y A x ωϕ=+的实际意义;2.函数sin()y A x ωϕ=+图象的变换(平移平换与伸缩变换) 【典型例题】 [例1](1)函数3sin()226x y π=+的振幅是 ;周期是 ;频率是 ;相位是 ;初相是 .(2)函数2sin(2)3y x π=-的对称中心是 ;对称轴方程是;单调增区间是 .(3) 将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=-⎪⎝⎭平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )A .sin()6y x π=+ B .sin()6y x π=- C .sin(2)3y x π=+ D .sin(2)3y x π=-(4) 为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数R x x y ∈=,sin 2的图像上所有的点 ( ) (A )向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) (B )向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) (C )向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) (D )向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)(5)将函数x x f y sin )(= 的图象向右平移4π个单位后再作关于x 轴对称的曲线,得到函数x y 2sin 21-=的图象,则)(x f 的表达式是 ( )(A )x cos (B )x cos 2 (C )x sin (D )x sin 2[例2]已知函数2()2cos 2,(01)f x x x ωωω=<<其中,若直线3x π=为其一条对称轴。
(1)试求ω的值 (2)作出函数()f x 在区间[,]ππ-上的图象.[例3]已知函数2()sin ()(0,0,0)2f x A x A πωϕωϕ=+>><<,且()y f x =的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2). (I )求ϕ;(II )计算(1)(2)(2008)f f f +++.[例4]设函数2()sin cos f x x x x a ωωω=++(其中0,a R ω>∈)。
高一数学(必修1)专题复习二函数的图像变换

高一数学(必修1)专题复习二函数的图象变换一.平移变换:(1)函数)(h x f y )0(h 的图象是把)(x f y 的图象向左平移h 个单位得到的;(2)函数)(h x f y )0(h 的图象是把)(x f y 的图象向右平移h 个单位得到的;(3)函数k x f y )()0(k 的图象是把)(x f y 的图象向上平移k 个单位得到的;(4)函数k x f y)()0(k的图象是把)(x f y的图象向下平移k 个单位得到的.练习:1.将下列变换的结果填在横线上:(1)将函数xy 3的图象向右平移2个单位,得到函数的图象;(2)将函数)13(log 2x y的图象向左平移2个单位,得到函数的图象.2.函数)32(x f 的图象,可由)32(xf 的图象经过下述变换得到()A .向左平移6个单位B .向右平移6个单位C .向左平移3个单位D .向右平移3个单位3.讨论函数xx y3132的图像是由哪个反比例函数的图像通过哪些变换而得到?二.对称变换1.同一函数的对称性(自对称)若函数)(x f y对定义域内一切x(1))(x f =)(x f 函数)(x f y图象关于y 轴对称;(2)函数)(x f y的不可能关于x 轴对称(除0)(x f 外);(3))(x f =-)(x f 函数)(x f y 图象关于原点对称;(4))()(1x f x f函数)(x f y 图象关于直线x y对称;(5))()(x f x f 函数)(x f y图象关于直线y 轴对称;(6))()2(x f x af 函数)(x f y 图象关于直线a x对称;(7))()(x a f x a f 函数)(x f y 图象关于直线a x 对称;(8))()(x a f a x f 函数)(x f y 图象关于y 轴对称;(9))()(x b f x af 函数()yf x 的图象关于直线2a b x对称;(10))(2)2(x f bx a f 即bx f x af 2)()2(函数)(x f y 图象关于点),(b a 成中心对称.2.不同函数对称性(互对称)给出函数)(x f y (1)函数)(x f y 与)(x f y 的图象关于y 轴对称;(2)函数)(x f y 与)(x f y 的图象关于x 轴对称;(3)函数)(x f y 与)(x f y 的图象关于原点对称;(4)函数)(1x fy 与)(x f y的图象关于直线x y 对称;(5)函数)(x f y的图象可以看作)(x f y的图象去掉y 轴左边部分,保留y 轴右边部分,并在y 轴左方作右方关于y 轴对称的图象(注意)(x f y为偶函数);(6)函数)2(x a f y 与)(x f y 的图象关于直线a x对称;(7)函数)(x a f y 与)(x a f y 的图象关于y 轴对称;(8)函数)(a x f y 与)(x a f y 图象关于直线a x 对称;(9)函数)(x af y与)(x bf y的图象关于直线2ab x 对称;(10)函数)(x f y 与)2(2x a f b y (即)2(2x af yb)的图像关于点),(b a 成中心对称.三.训练题目1.已知函数)(x f y 的定义域为R ,则下列命题中:①若)2(x f 是偶函数,则函数)(x f 的图象关于直线2x对称;②若)2()2(xf x f ,则函数)(x f 的图象关于原点对称;③函数)2(x f y 与函数)2(x f y 的图象关于直线2x ④函数)2(xf y与函数)2(x f y的图象关于直线2x其中正确的命题序号是.2.已知函数x f 是定义域为R 的偶函数,且x f x f 2.若x f 在0,1上是减函数,则x f 在3,2上是()A .增函数B .减函数C .先增后减的函数D .先减后增的函数3.设实数集R 上定义的函数)(x f ,对任何R x 都有)(x f +)(x f =1,则这个函数的图象()A .关于原点对称B .关于y 轴对称C .关于点)21,0(对称D .关于点)1,0(对称4.函数)1(x f y 与)1(1x fy 的图像关于()对称A .直线x y B .直线1xy C .直线1x yD .直线xy5.设定义域为R 的函数)(x f y 、)(x g y 都有反函数,并且)1(x f 和)2(1x g 的函数图像关于直线x y 对称,若2002)5(g ,那么)4(f ()A .2002 B .2003C .2004D .20056.已知函数1)22(x f y 是定义在R 上的奇函数,函数)(x g y 的图象与函数)(x f y的图象关于直线0yx对称,若221x x ,则)()(21x g x g ()A .2B .2C .4D .47.已知函数)(x f y 满足:①是偶函数)1(x f y;②在,1上为增函数.若0,021x x ,且221x x ,则)(1x f 与)(2x f 的大小关系是()A .)()(21x f x fB .)()(21x f x f C .)()(21x f x f D .不能确定8.函数11xy 的图象与x 轴围成封闭区域的面积是.9.函数(21)yf x 是偶函数,则函数(2)y f x 的对称轴是.10.设)(x f 是定义在R 上的偶函数,且)1()1(x f x f ,当01x 时,x x f 21)(,则)6.8(f __.11.设)(x f 是定义在R 上的奇函数,且图象关于直线21x ,则)5()4()3()2()1(f f f f f __ ___.12.函数)(x f y 对一切实数x 都满足)21()21(x f x f 并且方程0)(x f 有三个实根,这三个实根的和.13.定义在R 上的函数)(x f 满足)()(x a f x f ,(a 是大于1的整数),若方程0)(x f 有n 个实根,它们的和为2001,N n,则a ,n 的值可能有___种.14.若函数)(x f y 的图象关于直线2x 对称,当2x 时,21)(x x f ,则当2x 时,则)(x f .15.已知曲线C 与抛物线142x xy 关于点(2,-1)对称,函数)(x f y的图象与曲线C 关于x 轴对称,则)(x f y的函数关系式为.16.定义在R 上的函数)(x f 满足)1(1)1(1)1(x f x f x f ,则)2000()3()2()1(f f f f 的值为_ _.。
函数的图像变换和例题

难点10 函数图象与图象变换函数的图象与性质是高考考查的重点内容之一,它是研究和记忆函数性质的直观工具,利用它的直观性解题,可以起到化繁为简、化难为易的作用.因此,考生要掌握绘制函数图象的一般方法,掌握函数图象变化的一般规律,能利用函数的图象研究函数的性质.●难点磁场(★★★★★)已知函数f (x )=ax 3+bx 2+cx +d 的图象如图,求b 的范围.●案例探究[例1]对函数y =f (x )定义域中任一个x 的值均有f (x +a )=f (a -x ),(1)求证y =f (x )的图象关于直线x =a 对称;(2)若函数f (x )对一切实数x 都有f (x +2)=f (2-x ),且方程f (x )=0恰好有四个不同实根,求这些实根之和.命题意图:本题考查函数概念、图象对称问题以及求根问题.属★★★★★级题目. 知识依托:把证明图象对称问题转化到点的对称问题.错解分析:找不到问题的突破口,对条件不能进行等价转化. 技巧与方法:数形结合、等价转化.(1)证明:设(x 0,y 0)是函数y =f (x )图象上任一点,则y 0=f (x 0),又f (a +x )=f (a -x ),∴f (2a -x 0)= f [a +(a -x 0)]=f [a -(a -x 0)]=f (x 0)=y 0,∴(2a -x 0,y 0)也在函数的图象上,而2)2(00x x a +-=a ,∴点(x 0,y 0)与(2a -x 0,y 0)关于直线x =a 对称,故y =f (x )的图象关于直线x =a 对称.(2)解:由f (2+x )=f (2-x )得y =f (x )的图象关于直线x =2对称,若x 0是f (x )=0的根,则4-x 0也是f (x )=0的根,由对称性,f (x )=0的四根之和为8.[例2]如图,点A 、B 、C 都在函数y =x 的图象上,它们的横坐标分别是a 、a +1、a +2.又A 、B 、C 在x 轴上的射影分别是A ′、B ′、C ′,记△AB ′C 的面积为f (a ),△A ′BC ′的面积为g (a ).(1)求函数f (a )和g (a )的表达式;(2)比较f (a )与g (a )的大小,并证明你的结论.命题意图:本题考查函数的解析式、函数图象、识图能力、图形的组合等.属★★★★★级题目. 知识依托:充分借助图象信息,利用面积问题的拆拼以及等价变形找到问题的突破口. 错解分析:图形面积不会拆拼.技巧与方法:数形结合、等价转化.解:(1)连结AA ′、BB ′、CC ′,则f (a )=S △AB ′C =S 梯形AA ′C ′C -S △AA ′B ′-S △CC ′B =21(A ′A +C ′C )=21(2++a a ),g (a )=S △A ′BC ′=21A ′C ′·B ′B =B ′B =1+a .)11121(21)]1()12[(21)122(21)()()2(<++-+++=-+-+-+=+-++=-aa a a a a a a a a a a g a f∴f (a )<g (a ). ●锦囊妙计1.熟记基本函数的大致图象,掌握函数作图的基本方法:(1)描点法:列表、描点、连线;(2)图象变换法:平移变换、对称变换、伸缩变换等.2.高考中总是以几类基本初等函数的图象为基础来考查函数图象的.题型多以选择与填空为主,属于必考内容之一,但近年来,在大题中也有出现,须引起重视.●歼灭难点训练一、选择题1.(★★★★)当a ≠0时,y =ax +b 和y =b ax 的图象只可能是( )2.(★★★★)某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了,再走余下的路,下图中y 轴表示离学校的距离,x 轴表示出发后的时间,则适合题意的图形是( )二、填空题3.(★★★★★)已知函数f (x )=log 2(x +1),将y =f (x )的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数y =g (x )的图象,则函数F (x )=f (x )-g (x )的最大值为_________.三、解答题 4.(★★★★)如图,在函数y =lg x 的图象上有A 、B 、C 三点,它们的横坐标分别为m ,m +2,m +4(m >1).(1)若△ABC 面积为S ,求S =f (m ); (2)判断S =f (m )的增减性.5.(★★★★)如图,函数y =23|x |在x ∈[-1,1]的图象上有两点A 、B ,AB ∥Ox 轴,点M (1,m )(m ∈R 且m >23)是△ABC 的BC 边的中点.(1)写出用B 点横坐标t 表示△ABC 面积S 的函数解析式S =f (t ); (2)求函数S =f (t )的最大值,并求出相应的C 点坐标. 6.(★★★★★)已知函数f (x )是y =1102+x-1(x ∈R )的反函数,函数g (x )的图象与函数y =-21-x 的图象关于y 轴对称,设F (x )=f (x )+g (x ).(1)求函数F (x )的解析式及定义域;(2)试问在函数F (x )的图象上是否存在两个不同的点A 、B ,使直线AB 恰好与y 轴垂直?若存在,求出A 、B 的坐标;若不存在,说明理由.7.(★★★★★)已知函数f 1(x )=21x -,f 2(x )=x +2, (1)设y =f (x )=⎩⎨⎧∈--∈]1,0[ ),(3)0,1[ ),(21x x f x x f ,试画出y =f (x )的图象并求y =f (x )的曲线绕x 轴旋转一周所得几何体的表面积;(2)若方程f 1(x +a )=f 2(x )有两个不等的实根,求实数a 的范围.(3)若f 1(x )>f 2(x -b )的解集为[-1,21],求b 的值.8.(★★★★★)设函数f (x )=x +x1的图象为C 1,C 1关于点A (2,1)对称的图象为C 2,C 2对应的函数为g (x ).(1)求g (x )的解析表达式;(2)若直线y =b 与C 2只有一个交点,求b 的值,并求出交点坐标; (3)解不等式log a g (x )<log a29 (0<a <1).参考答案难点磁场解法一:观察f (x )的图象,可知函数f (x )的图象过原点,即f (0)=0,得d =0,又f (x )的图象过(1,0),∴f (x )=a +b +c ①,又有f (-1)<0,即-a +b -c <0②,①+②得b <0,故b 的范围是(-∞,0)解法二:如图f (0)=0有三根,∴f (x )=ax 3+bx 2+cx +d =ax (x -1)(x -2)=ax 3-3ax 2+2ax ,∴b = -3a ,∵a >0,∴b <0.歼灭难点训练一、1.解析:∵y =b ax =(b a )x ,∴这是以b a 为底的指数函数.仔细观察题目中的直线方程可知:在选择支B 中a >0,b >1,∴b a>1,C 中a <0,b >1,∴0<b a<1,D 中a <0,0<b <1,∴b a>1.故选择支B 、C 、D 均与指数函数y =(b a )x 的图象不符合.答案:A2.解析:由题意可知,当x =0时,y 最大,所以排除A 、C.又一开始跑步,所以直线随着x 的增大而急剧下降.答案:D二、3.解析:g (x )=2log 2(x +2)(x >-2) F (x )=f (x )-g (x )=log 2(x +1)-2log 2(x +2) =log 21441log441log)2(122222+++=+++=++x x x x x x x x)1(21111log2->++++=x x x ∵x +1>0,∴F (x )≤41log211)1(21log 22=++⋅+x x =-2当且仅当x +1=11+x ,即x =0时取等号.∴F (x )max =F (0)=-2. 答案:-2三、4.解:(1)S △ABC =S 梯形AA ′B ′B +S 梯形BB ′C ′C -S 梯形AA ′C ′C . (2)S =f (m )为减函数. 5.解:(1)依题意,设B (t ,23 t ),A (-t ,23t )(t >0),C (x 0,y 0).∵M 是BC 的中点.∴2x t +=1,2230y t + =m .∴x 0=2-t ,y 0=2m -23t .在△ABC 中,|AB |=2t ,AB 边上的高h AB =y 0-23t =2m -3t .∴S =21|AB |·h AB =21·2t ·(2m -3t ),即f (t )=-3t 2+2mt ,t ∈(0,1).(2)∵S =-3t 2+2mt =-3(t -3m )2+32m ,t ∈(0,1],若⎪⎪⎩⎪⎪⎨⎧>≤<23130m m ,即23<m ≤3,当t =3m 时,S max =32m ,相应的C 点坐标是(2-3m ,23m ),若3m >1,即m >3.S =f (t ) 在区间(0,1]上是增函数,∴S max =f (1)=2m -3,相应的C 点坐标是(1,2m -3).6.解:(1)y =1102+x-1的反函数为f (x )=lg xx +-11(-1<x <1).由已知得g (x )=21+x ,∴F (x )=lgxx +-11+21+x ,定义域为(-1,1).(2)用定义可证明函数u =xx +-11=-1+12+x 是(-1,1)上的减函数,且y =lg u 是增函数.∴f (x )是(-1,1)上的减函数,故不存在符合条件的点A 、B .7.解:(1)y =f (x )=⎪⎩⎪⎨⎧∈+--∈-]1,0[,1)0,1[,12x x x x .图略.y =f (x )的曲线绕x 轴旋转一周所得几何体的表面积为(2+2)π. (2)当f 1(x +a )=f 2(x )有两个不等实根时,a 的取值范围为2-2<a ≤1. (3)若f 1(x )>f 2(x -b )的解集为[-1,21],则可解得b =235-.8.(1)g (x )=x -2+41-x .(2)b =4时,交点为(5,4);b =0时,交点为(3,0).(3)不等式的解集为{x |4<x <29或x >6}.。
(完整版)(完整版)高一函数经典图像题
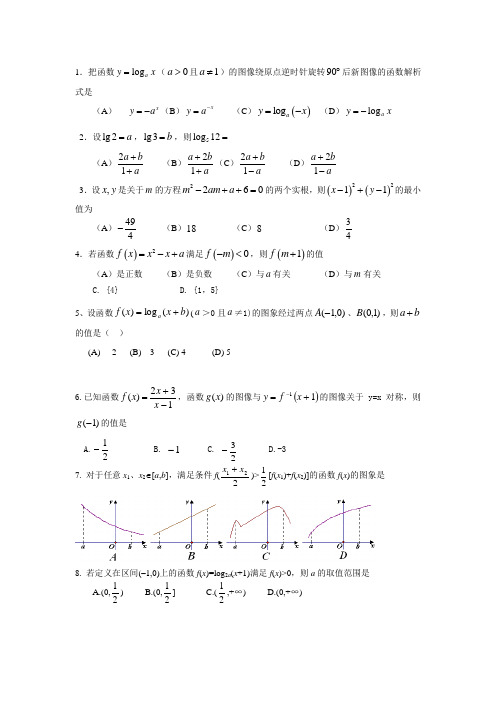
1.把函数log a y x =(0a >且1a ≠)的图像绕原点逆时针旋转90︒后新图像的函数解析式是(A )x y a =-(B )x y a -=(C )()log a y x =- (D )log a y x =-2.设lg 2a =,lg3b =,则5log 12=(A )21a ba++ (B )21a b a ++(C )21a ba+- (D )21a ba+- 3.设,x y 是关于m 的方程2260m am a -++=的两个实根,则()()2211x y -+-的最小值为(A )494-(B )18(C )8(D )344.若函数()2f x x x a =-+满足()0f m -<,则()1f m +的值(A )是正数(B )是负数(C )与a 有关(D )与m 有关C. {4}D. {1,5}5、设函数)(log )(b x x f a +=(a >0且a ≠1)的图象经过两点)0,1(-A 、)1,0(B ,则b a +的值是( ) (A) 2 (B) 3 (C) 4 (D) 56.已知函数132)(-+=x x x f ,函数)(x g 的图像与()11+=-x f y 的图像关于y=x 对称,则)1(-g 的值是A.21-B. 1-C. 23- D.-3 7. 对于任意x 1、x 2∈[a ,b ],满足条件f (221x x +)>21[f (x 1)+f (x 2)]的函数f (x )的图象是8. 若定义在区间(–1,0)上的函数f (x )=log 2a (x +1)满足f (x )>0,则a 的取值范围是A.(0,21) B.(0,21] C.(21,+∞) D.(0,+∞)9.若函数()f x 的图象是连续不断的,且(0)0>f ,(1)0>f ,(2)0<f ,则加上下列哪个条件可确定()f x 有唯一零点A. (3)0<fB. (1)0->fC. 函数在定义域内为增函数D. 函数在定义域内为减函数10、将函数x y 2sin =的图象的各点向左平移2π、向上平移1个长度单位后,的到的图象对应的函数解析式是( )A.12cos +=x yB. 12cos +-=x yC. 12sin +=x yD. 12sin +-=x y 11、函数)62sin(2π+=x y 的单调增区间为( )A.)](65,3[Z k k k ∈++ππππ B. )](32,6[Z k k k ∈++ππππC. )](6,3[Z k k k ∈+-ππππD. )](,65[Z k k k ∈++ππππ12. 已知函数 f (n )= ⎩⎨⎧<+≥-)10)](5([)10(3n n f f n n ,其中n ∈N ,则f (8)等于 ( )A. 2B. 4C. 6D. 713. 下列关系式中正确的是( )A 313232215121⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛ B 323231512121⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛C 323132212151⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛ D 313232212151⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛14.已知0lg lg =+b a ,则函数xa x f =)(与函数x x gb log )(-=的图象可能是 ( )15.已知函数2()22(4)1f x mx m x =--+,()g x mx =,若对于任一实数x ,()f x 与()g x 至少有一个为正数,则实数m 的取值范围是 ( ) A . (0,8) B .(0,2) C .(2,8) D . (,0)-∞ 16.( 本小题满分6分)化简、求值:0.2563238log 2log (log 27)+⨯ 17、(江苏省启东中学高三综合测试四)已知函数错误!未找到引用源。
函数的图象Word版含答案

函数的图象【课前回顾】1.描点法作函数图象其基本步骤是列表、描点、连线,具体为:(1)①确定函数的定义域;②化简函数的解析式;③讨论函数的性质(奇偶性、单调性、周期性).(2)列表(注意特殊点、零点、最大值点、最小值点以及坐标轴的交点). (3)描点、连线. 2.函数图象的变换 (1)平移变换①y =f (x )的图象―――――――→a >0,右移a 个单位a <0,左移|a |个单位y =f (x -a )的图象; ②y =f (x )的图象――――――――→b >0,上移b 个单位b <0,下移|b |个单位y =f (x )+b 的图象. (2)对称变换①y =f (x )的图象―――――→关于x 轴对称 y =-f (x )的图象; ②y =f (x )的图象―――――――→关于y 轴对称 y =f (-x )的图象; ③y =f (x )的图象――――――→关于原点对称y =-f (-x )的图象; ④y =a x (a >0且a ≠1)的图象――――――→关于直线y =x 对称y =log a x (a >0且a ≠1)的图象. (3)伸缩变换①y =f (x )的图象y =f (ax )的图象;②y =f (x )的图象――――――――――――――――――――→a >1,纵坐标伸长为原来的a 倍,横坐标不变0<a <1,纵坐标缩短为原来的a 倍,横坐标不变y =af (x )的图象. (4)翻转变换①y =f (x )的图象―――――――――→x 轴下方部分翻折到上方x 轴及上方部分不变y =|f (x )|的图象; ②y =f (x )的图象―――――――――――→y 轴右侧部分翻折到左侧原y 轴左侧部分去掉,右侧不变y =f (|x |)的图象.【课前快练】1.下列图象是函数y =⎩⎪⎨⎪⎧x 2,x <0,x -1,x ≥0的图象的是( )答案:C2.函数f (x )的图象向右平移1个单位长度,所得图象与曲线y =e x 关于y 轴对称,则f (x )=( )A .e x +1B .e x -1C .e-x +1D .e-x -1解析:选D 与曲线y =e x 关于y 轴对称的图象对应的解析式为y =e -x ,将函数y =e -x的图象向左平移1个单位长度即得y =f (x )的图象,∴f (x )=e -(x +1)=e -x -1,故选D.3.已知函数f (x )的图象如图所示,则函数g (x )=log2f (x )的定义域是________.解析:当f (x )>0时,函数g (x )=log2f (x )有意义,由函数f (x )的图象知满足f (x )>0时,x ∈(2,8].答案:(2,8]4.若关于x 的方程|x |=a -x 只有一个解,则实数a 的取值范围是________.解析:由题意得a =|x |+x ,令y =|x |+x =⎩⎪⎨⎪⎧2x ,x ≥0,0,x <0,其图象如图所示,故要使a =|x |+x 只有一个解,则a >0.答案:(0,+∞)考点一 函数图象的识辨1.学会寻找函数图象与解析式之间的5种对应关系(1)从函数的定义域,判断图象的左右位置,从函数的值域(或有界性),判断图象的上下位置;(2)从函数的单调性,判断图象的升降变化趋势;(3)从函数的奇偶性,判断图象的对称性:奇函数的图象关于原点对称,在对称的区间上单调性一致,偶函数的图象关于y 轴对称,在对称的区间上单调性相反;(4)从函数的周期性,判断图象是否具有循环往复特点;(5)从特殊点出发,排除不符合要求的选项,如f (0)的值,当x >0时f (x )的正负等. 2.函数图象变换问题的3个注意(1)函数图象中左、右平移变换可记口诀为“左加右减”,但要注意加、减指的是自变量.(2)注意含绝对值符号的函数的对称性,如y =f (|x |)与y =|f (x )|的图象是不同的. (3)分清条件“f (x +1)=f (x -1)”与“f (x +1)=f (1-x )”的区别,前者告诉函数的周期为2,后者告诉函数的图象关于直线x =1对称.【典型例题】考法(一) 根据函数解析式或图象识辨函数图象1.函数f (x )=1+log 2x 与g (x )=⎝⎛⎭⎫12x在同一直角坐标系下的图象大致是( )解析:选B 因为函数g (x )=⎝⎛⎭⎫12x 为减函数,且其图象必过点(0,1),故排除A 、D.因为f (x )=1+log 2x 的图象是由y =log 2x 的图象上移1个单位长度得到的,所以f (x )为增函数,且图象必过点(1,1),故可排除C ,选B.2.(2017·全国卷Ⅰ)函数y =sin 2x1-cos x的部分图象大致为( )解析:选C 令函数f (x )=sin 2x1-cos x ,其定义域为{x |x ≠2k π,k ∈Z},又f (-x )=sin (-2x )1-cos (-x )=-sin 2x1-cos x =-f (x ),所以f (x )=sin 2x1-cos x 为奇函数,其图象关于原点对称,故排除B ;因为f (1)=sin 21-cos 1>0,f (π)=sin 2π1-cos π=0,故排除A 、D ,选C.3.已知定义在区间[0,4]上的函数y =f (x )的图象如图所示,则y =-f (2-x )的图象为( )解析:选D 法一:先作出函数y =f (x )的图象关于y 轴的对称图象,得到y =f (-x )的图象;然后将y =f (-x )的图象向右平移2个单位,得到y =f (2-x )的图象;再作y =f (2-x )的图象关于x 轴的对称图象,得到y =-f (2-x )的图象.故选D. 法二:先作出函数y =f (x )的图象关于原点的对称图象,得到y =-f (-x )的图象;然后将y =-f (-x )的图象向右平移2个单位,得到y =-f (2-x )的图象.故选D.[题型技法]1.知式选图的2种常用方法找出所给函数对应的基本初等函数并作出该函数的图象,然后利用平移变换、伸缩变换、对称变换、翻折变换规则得出函数图象.考法(二) 根据实际背景、图形判断函数图象4.如图,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记∠BOP =x .将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( )解析:选B 当x ∈⎣⎡⎦⎤0,π4时,f (x )=tan x +4+tan 2x ,图象不会是直线段,从而排除A 、C.当x ∈⎣⎡⎦⎤π4,3π4时,f ⎝⎛⎭⎫π4=f ⎝⎛⎭⎫3π4=1+5,f ⎝⎛⎭⎫π2=2 2.∵22<1+5,∴f ⎝⎛⎭⎫π2<f ⎝⎛⎭⎫π4=f ⎝⎛⎭⎫3π4,从而排除D ,故选B.5.如图,不规则四边形ABCD 中,AB 和CD 是线段,AD 和BC 是圆弧,直线l ⊥AB 交AB 于E ,当l 从左至右移动(与线段AB 有公共点)时,把四边形ABCD 分成两部分,设AE =x ,左侧部分的面积为y ,则y 关于x 的图象大致是( )解析:选C 当l 从左至右移动时,一开始面积的增加速度越来越快,过了D 点后面积保持匀速增加,图象呈直线变化,过了C 点后面积的增加速度又逐渐减慢.故选C.[题型技法]根据实际背景、图形判断函数图象的方法(1)根据题目所给条件确定函数解析式,从而判断函数图象(定量分析);(2)根据自变量取不同值时函数值的变化、增减速度等判断函数图象(定性分析).考点二 函数图象的应用求解函数图象的应用问题,其实质是利用数形结合思想解题,其思维流程一般是:角度(一) 研究函数的性质1.已知函数f (x )=x |x |-2x ,则下列结论正确的是( ) A .f (x )是偶函数,递增区间是(0,+∞) B .f (x )是偶函数,递减区间是(-∞,1) C .f (x )是奇函数,递减区间是(-1,1) D .f (x )是奇函数,递增区间是(-∞,0)解析:选C 将函数f (x )=x |x |-2x 去掉绝对值得f (x )=⎩⎪⎨⎪⎧x 2-2x ,x ≥0,-x 2-2x ,x <0,画出函数f (x )的图象,如图,观察图象可知,函数f (x )的图象关于原点对称,故函数f (x )为奇函数,且在(-1,1)上单调递减.[题型技法] 利用函数的图象研究函数的性质对于已知或解析式易画出其在给定区间上图象的函数,其性质常借助图象研究: ①从图象的最高点、最低点,分析函数的最值、极值; ②从图象的对称性,分析函数的奇偶性;③从图象的走向趋势,分析函数的单调性、周期性. 角度(二) 研究不等式2.设奇函数f (x )在(0,+∞)上为增函数,且f (1)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1)解析:选D 因为f (x )为奇函数,所以不等式f (x )-f (-x )x <0可化为f (x )x <0,即xf (x )<0,f (x )的大致图象如图所示.所以xf (x )<0的解集为(-1,0)∪(0,1).3.若不等式(x -1)2<log a x (a >0,且a ≠1)在x ∈(1,2)内恒成立,则实数a 的取值范围为( )A .(1,2] B.⎝⎛⎭⎫22,1 C .(1,2) D .(2,2)解析:选A 要使当x ∈(1,2)时,不等式(x -1)2<log a x 恒成立,只需函数y =(x -1)2在(1,2)上的图象在y =log a x 的图象的下方即可.当0<a <1时,显然不成立;当a >1时,如图,要使x ∈(1,2)时,y=(x -1)2的图象在y =log a x 的图象的下方,只需(2-1)2≤log a 2,即log a 2≥1,解得1<a ≤2,故实数a 的取值范围是(1,2].故选A.[题型技法] 利用函数的图象研究不等式思路当不等式问题不能用代数法求解,但其与函数有关时,常将不等式问题转化为两函数图象的上下关系问题,从而利用数形结合求解.【针对训练】1.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x ≤0,ln (x +1),x >0.若|f (x )|≥ax ,则a 的取值范围是( )A .(-∞,0]B .(-∞,1]C .[-2,1]D .[-2,0]解析:选D 由y =|f (x )|的图象(如图所示)知,①当x >0时,只有a ≤0时才能满足|f (x )|≥ax ,可排除B 、C.②当x ≤0时,y =|f (x )|=|-x 2+2x |=x 2-2x .故由|f (x )|≥ax 得x 2-2x ≥ax .当x =0时,不等式为0≥0成立; 当x <0时,不等式等价为x -2≤a .∵x -2<-2,∴a ≥-2.综上可知,a ∈[-2,0].2.设函数f (x )是定义在R 上的偶函数,且对任意的x ∈R 恒有f (x +1)=f (x -1),已知当x ∈[0,1]时,f (x )=⎝⎛⎭⎫121-x,则:①2是函数f (x )的周期;②函数f (x )在(1,2)上递减,在(2,3)上递增;③函数f (x )的最大值是1,最小值是0;④当x ∈(3,4)时,f (x )=⎝⎛⎭⎫12x -3.其中所有正确命题的序号是________.解析:由已知条件得f (x +2)=f (x ),则y =f (x )是以2为周期的周期函数,①正确; 当-1≤x ≤0时,0≤-x ≤1,f (x )=f (-x )=⎝⎛⎭⎫121+x, 函数y =f (x )的部分图象如图所示:由图象知②正确,③不正确;当3<x <4时,-1<x -4<0,f (x )=f (x -4)=⎝⎛⎭⎫12x -3,因此④正确.故正确命题的序号为①②④.答案:①②④【课后演练】1.图中阴影部分的面积S 是关于h 的函数(0≤h ≤H ),则该函数的大致图象是( )解析:选B 由题图知,随着h 的增大,阴影部分的面积S 逐渐减小,且减小的越来越慢,结合选项可知选B.2.为了得到函数y =2x -3-1的图象,只需把函数y =2x 的图象上所有的点( )A .向右平移3个单位长度,再向下平移1个单位长度B .向左平移3个单位长度,再向下平移1个单位长度C .向右平移3个单位长度,再向上平移1个单位长度D .向左平移3个单位长度,再向上平移1个单位长度解析:选A y =2x ――――→向右平移3个单位长度y =2x -3―――――→向下平移1个单位长度y =2x -3-1. 3.若函数f (x )=⎩⎪⎨⎪⎧ax +b ,x <-1,ln (x +a ),x ≥-1的图象如图所示,则f (-3)等于( )A .-12B .-54C .-1D .-2解析:选C 由图象可得-a +b =3,ln(-1+a )=0,得a =2,b =5,∴f (x )=⎩⎪⎨⎪⎧2x +5,x <-1,ln (x +2),x ≥-1,故f (-3)=2×(-3)+5=-1,故选C. 4.下列函数y =f (x )图象中,满足f ⎝⎛⎭⎫14>f (3)>f (2)的只可能是( )解析:选D 因为f ⎝⎛⎭⎫14>f (3)>f (2),所以函数f (x )有增有减,排除A 、B.在C 中,f ⎝⎛⎭⎫14<f (0)=1,f (3)>f (0),即f ⎝⎛⎭⎫14<f (3),排除C ,选D.5.已知函数f (x )=(x -a )(x -b )(其中a >b )的图象如图所示,则函数g (x )=a x +b 的图象是( )解析:选A由f(x)的图象与x轴的交点位置知:0<a<1,b<-1.由0<a<1可排除C、D,又由g(0)=1+b<0可排除B,故选A.6.函数f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=x-1,则不等式xf(x)>0在(-1,3)上的解集为()A.(1,3)B.(-1,1)C.(-1,0)∪(1,3) D.(-1,0)∪(0,1)解析:选C作出函数f(x)的图象如图所示.当x∈(-1,0)时,由xf(x)>0得x∈(-1,0);当x∈(0,1)时,由xf(x)>0得x∈∅;当x∈(1,3)时,由xf(x)>0得x∈(1,3).故x∈(-1,0)∪(1,3).7.已知函数y=f(x+1)的图象过点(3,2),则函数y=f(x)的图象一定过点________.解析:因为函数y=f(x+1)的图象过点(3,2),所以函数y=f(x)的图象一定过点(4,2).答案:(4,2)8.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集为________.解析:令y =log 2(x +1),作出函数y =log 2(x +1)图象如图.由⎩⎪⎨⎪⎧ x +y =2,y =log 2(x +1),得⎩⎪⎨⎪⎧x =1,y =1.∴结合图象知不等式f (x )≥log 2(x +1)的解集为{x |-1<x ≤1}.答案:{x |-1<x ≤1}9.如图,定义在[-1,+∞)上的函数f (x )的图象由一条线段及抛物线的一部分组成,则f (x )的解析式为________.解析:当-1≤x ≤0时,设解析式为f (x )=kx +b (k ≠0), 则⎩⎪⎨⎪⎧ -k +b =0,b =1,得⎩⎪⎨⎪⎧k =1,b =1.∴当-1≤x ≤0时,f (x )=x +1.当x >0时,设解析式为f (x )=a (x -2)2-1(a ≠0),∵图象过点(4,0),∴0=a (4-2)2-1,∴a =14. 故函数f (x )的解析式为 f (x )=⎩⎪⎨⎪⎧ x +1,-1≤x ≤0,14(x -2)2-1,x >0.答案:f (x )=⎩⎪⎨⎪⎧x +1,-1≤x ≤0,14(x -2)2-1,x >0 10.设函数f (x )=|x +a |,g (x )=x -1,对于任意的x ∈R ,不等式f (x )≥g (x )恒成立,则实数a 的取值范围是________.解析:如图,作出函数f (x )=|x +a |与g (x )=x -1的图象,观察图象可知:当且仅当-a ≤1,即a ≥-1时,不等式f (x )≥g (x )恒成立,因此a 的取值范围是[-1,+∞).答案:[-1,+∞)11.(2018·惠州三调)函数f (x )=⎝⎛⎭⎫x -1x cos x (-π≤x ≤π且x ≠0)的图象可能为( )解析:选D 函数f (x )=⎝⎛⎭⎫x -1x cos x (-π≤x ≤π且x ≠0)为奇函数,排除选项A 、B ;当x =π时,f (x )=⎝⎛⎭⎫π-1πcos π=1π-π<0,排除选项C ,故选D. 12.若函数y =f (x )的图象如图所示,则函数y =-f (x +1)的图象大致为( )解析:选C 要想由y =f (x )的图象得到y =-f (x +1)的图象,需要先将y =f (x )的图象关于x 轴对称得到y =-f (x )的图象,然后再向左平移一个单位得到y =-f (x +1)的图象,根据上述步骤可知C 正确.13.已知函数f (x )=⎩⎪⎨⎪⎧3x -1,x >0,x 2+1,x ≤0,若存在x 1∈(0,+∞),x 2∈(-∞,0],使得f (x 1)=f (x 2),则x 1的最小值为( )A .log 23B .log 32C .1D .2解析:选B 作出函数f (x )的图象如图所示,由图可知,当x 1取得最小值时,3x 1-1=1,x 1=log 32,即x 1的最小值为log 32.14.若函数f (x )=ax -2x -1的图象关于点(1,1)对称,则实数a =________. 解析:函数f (x )=ax -2x -1=a +a -2x -1(x ≠1),当a =2时,f (x )=2,函数f (x )的图象不关于点(1,1)对称,故a ≠2,其图象的对称中心为(1,a ),即a =1.答案:115.若直线y =1与曲线y =x 2-|x |+a 有四个交点,则a 的取值范围是________.解析:y =x 2-|x |+a =⎩⎪⎨⎪⎧x 2-x +a ,x ≥0,x 2+x +a ,x <0, 作出函数图象如图所示.此曲线与y 轴交于点(0,a ),最小值为a -14,要使y =1与其有四个交点,只需a -14<1<a ,∴1<a <54. 答案:⎝⎛⎭⎫1,54 16.已知函数f (x )=|x |(x -a ),a >0.(1)作出函数f (x )的图象;(2)写出函数f (x )的单调区间;(3)当x ∈[0,1]时,由图象写出f (x )的最小值. 解:(1)f (x )=⎩⎪⎨⎪⎧ x (x -a ),x ≥0-x (x -a ),x <0,其图象如图所示.(2)由图知,f (x )的单调递增区间是(-∞,0),⎝⎛⎭⎫a 2,+∞;单调递减区间是⎝⎛⎭⎫0,a 2. (3)由图象知,当a 2>1,即a >2时,f (x )min =f (1)=1-a ; 当0<a 2≤1,即0<a ≤2时,f (x )min =f ⎝⎛⎭⎫a 2=-a 24. 综上,f (x )min =⎩⎪⎨⎪⎧-a 24,0<a ≤2,1-a ,a >2.17.已知函数f (x )的图象与函数h (x )=x +1x +2的图象关于点A (0,1)对称.(1)求f (x )的解析式;(2)若g (x )=f (x )+a x,且g (x )在区间(0,2]上为减函数,求实数a 的取值范围. 解:(1)设f (x )图象上任一点P (x ,y ),则点P 关于(0,1)点的对称点P ′(-x,2-y )在h (x )的图象上,即2-y =-x -1x +2,∴y =f (x )=x +1x (x ≠0).(2)g (x )=f (x )+a x =x +a +1x ,∴g ′(x )=1-a +1x 2. ∵g (x )在(0,2]上为减函数,∴1-a +1x 2≤0在(0,2]上恒成立,即a +1≥x 2在(0,2]上恒成立, ∴a +1≥4,即a ≥3,故实数a 的取值范围是[3,+∞).。
高二数学三角函数图象变换试题答案及解析

高二数学三角函数图象变换试题答案及解析1.函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是()A.B.C.D.【答案】D【解析】将函数的图象向左平移个单位, 得到再向上平移1个单位,得到,所得图象的函数解析式是,故选D.【考点】三角恒等变换.2.将函数的图像向左平移个单位,再向上平移1个单位,所得图像的函数解析式是()A.B.C.D.【答案】B【解析】函数y=sin2x的图象向左平移个单位得y=sin(2x+),再向上平移1个单位得y=sin(2x+)+1=1+cos2x=2cos2x,故答案为:y=2cos2x.【考点】函数y=Asin(ωx+φ)的图象变换.3.为了得到函数的图象,可以将函数的图象( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】B【解析】,所以为了得到函数的图象,可以将函数的图象向右平移个单位长度,故选B.【考点】函数y=Asin(ωx+φ)的图象变换.4.为了得到函数的图像,只需把函数的图像()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【答案】D【解析】三角函数的左右平移就是x的值的变化,相应y值的变化.所以要将函数中的x变为,就可得函数,所以图像是向右平移了个单位.即选D.【考点】三角函数图像的平移.5.已知为锐角,且,则=_________.【答案】【解析】因为,为锐角,且,所以,。
=。
【考点】三角函数诱导公式,两角和的三角函数,特殊角的三角函数值。
点评:简单题,利用三角函数公式,转化成特殊角的三角函数值。
关键是注意变角。
6.如图是函数在区间上的图像,为了得到这个函数的图象,只要将的图象上所有的点A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变【答案】A【解析】观察函数的图象可知,A=1,T=π,即,将(,0)代入得,,取,,故只要将的图象上所有的点向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变。
2021高中数学-函数的图像及其图像变换(精选试题)

高中数学-函数的图像及其图像变换1、设曲线C的方程是y=x3-x,将C沿x轴、y轴正向分别平行移动t,s单位长度后得曲线C1.(1)写出曲线C1的方程;(2)证明曲线C与C1关于点At2s2对称;(3)如果曲线C与C1有且仅有一个公共点,证明s=t34-t且t≠0.2、给出下列说法:①从匀速传递的产品生产线上每隔20分钟抽取一件产品进行某种检测,这样的抽样为系统抽样;②若随机变量若ξ-N(1,4),Pξ≤0=m,则P(0ξ1)=12-m;③在回归直线ŷ=0.2x+2中,当变量x每增加1个单位时,ŷ平均增加2个单位;④在2×2列联表中,K2=13.079,则有99.9%的把握认为两个变量有关系.附表:其中正确说法的序号为____________(把所有正确说法的序号都写上)3、若fx是R上的减函数,且fx的图像经过点A(0,3)和B(3,-1),则不等式丨fx+1-1丨2的解集是_______________.4、为备战2021年伦敦奥运会,国家篮球队分轮次进行分项冬训,训练分为甲、乙两组,根据经验,在冬训期间甲、乙两组完成各项训练任务的概率分别为23和p(p>0),假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响,若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为``友好组”.(1)若p=12,求甲、乙两组在完成一轮冬训中成为``友好组’’的概率;(2)设在6轮冬训中,甲、乙两组成为``友好组’’的次数为ξ,当Eξ≤2时,求p的取值范围.5、姚明比赛时罚球命中率为90%,则他在3次罚球中罚失1次的概率是________.6、设随机变量ξ~B(2,p),若P(ξ≥1)=59,则p=_____.7、设随机变量ξ∼N(0,1),若pξ≥1=p,则P(−1ξ0)=()A.1-pB.pC.12+pD.12-P8、已知随机变量ξ服从二项分布ξ∼B(6,12),则E2ξ+4=()A.10B.4C.3D.99、下列随机变量ξ服从二项分布的是()①随机变量ξ表示重复抛掷一枚骰子n次中出现点数是3的倍数的次数;②某射手击中目标的概率为0.9,从开始射击到击中目标所需的射击次数ξ;③有一批产品共有N件,其中M件为次品,采用有放回抽取方法,ξ表示n次抽取中出现次品的件数(MN);④有一批产品共有N件,其中M件为次品,采用不放回抽取方法,ξ表示n次抽取中出现次品的件数(MN).A.②③B.①④C.③④D.①③10、如图,李先生家住H小区,他工作在C科技园,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为12;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为34、35.(1)若走L1路线,求最多遇到1次红灯的概率;(2)若走L2路线,求遇到红灯次数X的数学期望;(3)按照:``平均遇到红灯次数最少’’的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.11、若随机变量X服从两点分布,且成功概率为0.7;随机变量Y服从二项分布,且Y~B(10,0.8),则EX,DX,EY,DY分别是________,________,________,________.12、已知函数fx和gx的图象关于原点对称,且fx=x2+2x.(Ⅰ)解关于x的不等式gx≥fx-|x-1|;(Ⅱ)如果对∀x∈R,不等式gx+c≤fx-|x-1|恒成立,求实数c的取值范围.13、某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间统计结果如下:从第一个顾客开始办理业务时计时.(1)估计第三个顾客恰好等待4分钟开始办理业务的频率;(2)X表示至第2分钟末已办理完业务的顾客人数,求X的分布列及数学期望.14、某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为23,得到乙、丙公司面试的概率均为P,且三个公司是否让其面试是相互独立的.记X 为该毕业生得到面试的公司个数.若PX=0=112,则随机变量X的数学期望EX=__________.15、若不等式4-x2≤kx+1的解集为区间ab,且b-a=1,则k=________________.16、下列说法正确的个数是()(1)线性回归方程y=bx+a必过(x̄,ȳ)(2)在一个2×2列联表中,由计算得K2=4.235,则有95%的把握确认这两个变量间没有关系(3)复数i2+i3+i41-i=12-12i(4)若随机变量ξ∼N(2,1),且p(ξ4)=p,则p(0ξ2)=2p−1.A.1B.2C.3D.417、已知随机变量X~N(2,σ2)(σ>0),若X在(0,2)内取值的概率为0.3,则X在(4,+∞)内的概率为______.18、某批量较大的产品的次品率为10%,从中任意连续取出4件,则其中恰好含有3件次品的概率是()A.0.001B.0.0036C.0.0486D.0.291619、设随机变量ξ∼N(μ,σ2),对非负数常数k,则P(|ξ−μ|≤k σ)的值是()A.只与k有关B.只与μ有关C.只与σ有关D.只与μ和σ有关20、某城市从南郊某地乘坐公共汽车前往北区火车站有两条路线可走,第一条路线穿过市区,路线较短,但交通拥挤,所需时间(单位:分)服从正态分布N(50,102);第二条路线沿环城公路走,路线较长,但交通阻塞少,所需时间服从正态分布N(60,42).(Ⅰ)若只有70分钟可用,问应走哪一条路线?(Ⅱ)若只有65分钟可用,问应走哪一条路线?(已知Φ(3.9)=1.000,Φ(2)=0.9772,Φ(2.5)=0.9938,Φ(1.5)=0.9332,Φ(1.25)=0.8944)21、某学校的场室统一使用“佛山照明”的一种灯管,已知这种灯管使用寿命ξ(单位:月)服从正态分布N(μ,σ2),且使用寿命不少于12个月的概率为0.8,使用寿命不少于24个月的概率为0.2. (1)求这种灯管的平均使用寿命;(2)假设一间功能室一次性换上4支这种新灯管,使用12个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.22、某品牌的摄像头的使用寿命ξ(单位:年)服从正态分布,且使用寿命不少于2年的概率为0.8,使用寿命不少于6年的概率为0.2.某校在大门口同时安装了两个该品种的摄像头,则在4年内这两个摄像头都能正常工作的概率为_________.23、某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为__________.24、设随机变量ξ服从正态分布N(2,9),若P(ξ>c+1)=P(ξc-1),则c=()A.1B.2C.3D.425、已知随机变量ξ服从正态分布N(2,a2),且P(ξ4)=0.8,则P(0ξ2)=()A.0.6B.0.4C.0.3D.0.226、设随机变量X~N(3,1),若P(X>4)=p,则P(2X4)=()A.12+pB.1-pC.1-2pD.12−p27、设两个正态分布N(μ1,σ12)(σ1>0)和N(μ2,σ22)(σ2>0)曲线如图所示,则有()A.μ1μ2,σ1>σ2B.μ1μ2,σ1σ2C.μ1>μ2,σ1>σ2D.μ1>μ2,σ1σ228、设随机变量ξ服从标准正态分布N(0,1).已知φ(−1.96)=0.025,则P|ξ|1.96)=()A.0.025B.0.050C.0.950D.0.97529、下列函数中,以π为最小正周期的偶函数,且在(0,π2)内递增的是()A.y=sin|x|B.y=cos2xC.y=sin2xD.y=|sinx|30、函数fx=2x−2,x⩽1 x2−4x+3,x>1的图象和函数gx=lnx-1的图象的交点个数是_____________.fx=|x|,如果方程fx=a有且只有一个实根,那么实数a应满足()A.a0B.0a1C.a=0D.a>132、已知函数fx=x-x,其中x表示不超过x的最大整数,例如[-1,1]=-2,[1,2]=1,2=2,若方程fx=bx+b(b>0)有3个相异的实根.则实数b的取值范围是()A.[15,14)B.(14,13]C.[14,13)D.[14,13]33、方程x2-y2=0表示的图形是()A.两条相交直线B.两条平行直线C.两条重合直线D.一个点34、已知左图对应的函数为y=fx,则右图对应的函数为()A.y=f|x|B.y=-f|x|C.y=|fx|D.y=f-|x|35、设函数hx=f(x),当f(x)≤g(x)时g(x),当f(x)>g(x)时其中fx=|x|,gx=-x-12+3,则hx+1的最大值为()A.0B.1C.2D.336、若函数y=fx(x∈R)满足fx+2=fx,且x∈[-1,1]时,fx=|x|,函数y=gx是偶函数,且x∈(0,+∞)时,gx=|log3x|.则函数y=fx的图象与函数y=gx图象的交点个数为____________.37、已知函数fx=|x2-4x-3|,则函数的单调增区间________________.38、设随机变量X∼Nμσ2,且PX≤c=P(X>c),则c的值()A.0B.1C.μD.μ239、某幼儿园举行讲故事、唱歌、跳舞、写字比赛,凡有一项优胜,则奖励一朵小红花.李云水同学跳舞一定优胜;讲故事、写字有一半的把握优胜;唱歌有七成把握优胜.则李云水能获得不少于三朵小红花的概率是()A.0.175B.0.250C.0.425D.0.60040、作出下列函数的图象.(1)y=sinx|sinx|;(2)y=|tan|x||.41、对于二次函数y=-4x2+8x-3(Ⅰ)指出图象的开口方向、对称轴方程、顶点坐标;(Ⅱ)说明它的图象由y=-4x2经过怎样平移得来;(Ⅲ)写出其单调区间.42、已知二次函数fx的图象过A(-1,0),B(3,0),C(1,-8). (1)求fx的解析式;(2)求不等式fx≥0的解集.(3)将fx的图象向右平移2个单位,求所得图象的函数解析式gx.43、某工厂从2000年开始,近八年以来生产某种产品的情况是:前四年年产量的增长速度越来越慢,后四年年产量的增长速度保持不变,则该厂这种产品的产量y与时间t的函数图象可能是()A.B.C.D.44、如图,已知正四棱锥S-ABCD所有棱长都为1,点E是侧棱SC上一动点,过点E垂直于SC的截面将正四棱锥分成上、下两部分.记SE=x(0x1),截面下面部分的体积为Vx,则函数y=Vx的图象大致为()A.B.C.D.45、如图,半径为2的⊙O切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交⊙O于点Q,设∠POQ为x,弓形PMQ的面积为S=fx,那么fx的图像大致是()A.@B.C.@D.46、设函数y=fx定义在实数集上,则函数y=fx-1与y=f1-x的图象关于()A.直线y=0对称B.直线x=0对称C.直线y=1对称D.直线x=1对称47、已知A,B两地之间有6条网线并联,这6条网线能通过的信息量分别为1,1,2,2,3,3.现从中任取3条网线,设可通过的信息量为X,当X≥6时,可保证线路信息畅通(通过的信息量X为三条网线上信息量之和),则线路信息畅通的概率为_______.48、在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数y=fx的图象恰好经过k个格点,则称函数y=fx为k阶格点函数.已知下列函数:①f(x)=2(x2−1);②f(x)=ex+1;③f(x)=12log2x;④f(x)=2cos(x−π3).则其中为一阶格点函数的序号为________.(写出所有正确命题的序号)49、设随机变量ξ的概率分布列为P(ξ=k)=c2k,k=1,2,3,…,6,其中c为常数,则Pξ≤2的值为____.50、已知随机变量ξ∼N(0,σ2),若P(-1ξ0)=0.3,则P(ξ1)=____________.51、某市10000名考生参加某次模拟考试,他们的数学成绩近似地服从正态分布N85102,则数学成绩在65—75分之间的考生人数约为(参考数据为:P(|x−u|σ)=0.6826,P(|x−u|2σ)=0.9544,其中u为均值,σ为标准差)()A.1259B.1359C.1459D.155952、已知随机变量x服从正态分布N(3,14),且p(x>72)=0.1587,则p(52≤x≤72)=()A.0.6588B.0.6883C.0.6826D.0.658653、函数y=x2cosx(−π2≤x≤π2)的图象是()A.@B.C.@D.54、设a为常数,函数fx=x2-4x+3,若fx+a在[0,+∞)上是增函数,则a的取值范围是________.55、函数y=1+1x-1的图象是()A.@B.C.@D.56、有甲、乙、丙三位同学,投篮命中的概率如下表:现请三位同学各投篮一次,设ξ表示命中的次数,若Eξ=76,则a=___________.57、抛掷两个骰子,至少有一个4点或5点出现时,就说这些实验成功,则在10次试验中,成功次数ξ的期望是()A.103B.559C.809D.50958、已知fx=x-ax-b+1,并且α,β是方程fx=0的两根,则实数α,β,a,b的大小可能是()A.αaβbB.aαbβC.aαβbD.αabβ59、设H(x)=0,当x≤01,当x>0画出函数y=Hx-1的图象.60、若随机变量X服从两点分布,且成功概率为0.7;随机变量Y服从二项分布,且Y∼B(10,0.8),EX,DX,EY,DY分别是__________,__________,__________,__________.η∼B(2,p),且Dη=49,则P0≤η≤1=()A.59B.49C.59或49D.59或8962、设随机变量ξ∼N(0,1),若P(ξ⩾1)=p,则P(-1ξ0)=()A.1-pB.pC.12+pD.12−p63、小王通过某种英语测试的概率是13,如果他连续测试3次,那么其中恰有1次通过的概率是()A.227B.29C.427D.4964、已知图甲中的图象对应的函数y=fx,则图乙中的图象对应的函数在下列给出的四式中只可能是()A.y=f|x|B.y=|fx|C.y=f-|x|D.y=-f|x|65、已知函数y=fx的周期为2,当x∈[-1,1]时fx=x2,那么函数y=fx的图象与函数y=|lgx|的图象的交点共有()A.10个B.9个C.8个D.1个66、有一个样本容量为66的样本,数据的分组及各组的频数如下:11.515.52 15.519.54 19.52 3.59 23.527.51827.531.511 31.535.512 35.539.5739.543.53根据样本的频率分布估计,大于或等于31.5的数据约占()A.211B.13C.12D.2367、某市高三调研考试中,对数学在90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为90,那么90~100分数段的人数为()A.630B.720C.810D.90068、如果随机变量ξ∼N-1ξ2,且P(−3⩽ξ⩽−1)=0.4,则P(ξ⩾1)=___________.69、若随机变量ξ∼N21,且P(ξ>3)=0.1587,求P(ξ>1).70、设fx是一个三次函数,f’x为其导函数,如图所示的是y=x⋅f’x 的图象的一部分,则fx的极大值与极小值分别是()A.f1与f-1B.f-1与f1C.f-2与f2D.f2与f-271、设函数fx=|x2-2x-1|,若a>b>1,且fa=fb,则ab-a-b的取值范围()A.(-2,3)B.(-2,2)C.(1,2)D.(-1,1)72、已知ab,函数fx=x-ax-b的图象如图所示,则函数gx=logbx+a 的图象可能为()A.B.C.D.73、若函数fx=2∣x-3∣-logax+1无零点,则a的取值范围为_________.74、设10≤x1x2x3x4≤104,x3=103,随机变量ξ1,取值x1,x2,x3,x4,x5的概率均为0.2,随机变量ξ2取值x1+x22,x2+x32,x3+x42,x4+x52,x5+x12的概率均也为0.2,若记Dξ1,Dξ2分别为ξ1,ξ2的方差,则()A.Dξ1>Dξ2B.Dξ1=Dξ2C.Dξ1Dξ2D.Dξ1与Dξ2的大小关系与x1,x2,x3,x4的取值有关75、一牧场有10头牛,因误食含有病毒的饲料而被感染,已知该病的发病率为0.02.设发病的牛的头数为ξ,则Dξ等于()A.0.2B.0.8C.0.196D.0.80476、某单位为绿化环境,移栽了甲、乙两种大树各2株,设甲、乙两种大树移栽的成活率分别23和12,且各株大树是否成活互不影响,求移栽的4株大树中:(1)求甲种树成活的株数η的方差;(2)两种大树各成活1株的概率;(3)成活的株数ξ的分布列与期望.77、已知定义域为R的函数fx在(-5,+∞)上为减函数,且函数y=fx-5为偶函数,设a=f-6,b=f-3,则a,b的大小关系为________________.78、在密码理论中,``一次一密’’的密码体系是理论上安全性最高的.某部队执行特殊任务使用四个不同的口令a,b,c,d,每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用a口令,那么第5次也使用a口令的概率是()A.727B.61243C.1108D.124379、设fx=-2x,x≤0fx-1,x>0,若fx=x+a有且仅有三个解,则实数a 的取值范围()A.[1,2]B.(-∞,2)C.[1,+∞)D.(-∞,1)80、若定义在R上的函数y=fx满足f(x+1)=1f(x),且当x∈(0,1]时,fx=x,函数gx=l og3x(x>0)2x+1x≤0,则函数hx=fx-gx在区间[-4,4]内的零点个数为()A.9B.7C.5D.481、已知fx是定义在R上的函数,且对任意实数x有fx+4=-fx+22,若函数y=fx-1的图象关于直线x=1对称,则f2021=()A.-2+22B.2+22C.22D.282、如果函数y=|x|-2的图象与图象与曲线C:x2+y2=λ恰好有两个不同的公共点,则实数λ的取值范围是()A.{2}∪(4,+∞)B.(2,+∞)C.{2,4}D.(4,+∞)83、某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为45,第二、第三种产品受欢迎的概率分别为m,n,且不同产品是否受欢迎相互独立.记ξ为公司向市场投放三种新型产品受欢迎的数量,其分布列为则m+n=_.84、如图,李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为12;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为34、35.(1)若走L1路线,求最多遇到1次红灯的概率;(2)若走L2路线,求遇到红灯次数X的数学期望;(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.85、一位国王的铸币大臣在每箱100枚的硬币中各掺入一枚劣币,国王怀疑大臣作弊,他用两种方法来检测.方法一:在10箱中各任意抽查一枚;方法二:在5箱中各任意抽查两枚.国王用方法一、二能发现至少一枚劣币的概率分别记为P1和P2.则()A.P1=P2B.P1P2C.P1>P2D.以上三种情况都有可能86、设随机变量X服从二项分布X~B(5,12),则函数fx=x2+4x+X存在零点的概率是()A.56B.45C.3132D.1287、从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:(1)求这500件产品质量指标值的样本平均数x¯和样本方差s2(同一组中数据用该组区间的中点值作代表);(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布Nμσ2,其中μ近似为样本平均数x¯,σ2近似为样本方差s2.①利用该正态分布,P(187.8Z212.2);②某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间187.8212.2的产品件数,利用①的结果,求EX. 附:150≈12.2若Z-Nμσ2则P(μ-σZμ+σ)=0.6826,P(μ-2σZμ+2σ)=0.954488、下列四个命题中①∫01exdx=e②设回归直线方程为ŷ=2-2.5x,当变量x增加一个单位时y大约减少2.5个单位;③已知ξ服从正态分布N(0,σ2)且P-2≤ξ≤0=0.4则P(ξ>2)=0.1④对于命题P:xx−1≥0则¬p:xx−10.其中错误的命题个数是()A.0B.1C.2D.389、若随机变量x-N14,Px≤0=m,则P(0x2)=()A.1-2mB.1−π2C.1−2m2D.1-m90、下列四个命题中①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均增加3个单位;②命题P:“∃x0∈R,x02-x0-1>0”的否定¬P:“∀x∈R,x2-x-1≤0”;③设随机变量X服从正态分布N01,若P(X>1)=p,则P(-1X0)=12−p;④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.其中正确的命题的个数有()附:本题可以参考独立性检验临界值表A.1个B.2个C.3个D.4个y=fx的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是()A.B.C.D.92、小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是()A.B.C.D.93、如图所示,函数y=fx的图像由两条射线和三条线段组成,若∀x ∈R,fx>fx-1,则正实数a的取值范围为__________.94、已知函数fx=x3+ax2+bx+c有两个极值点x1,x2,若fx1=x1x2,则关于x的方程3fx2+2afx+b=0的不同实根个数为()A.3B.4C.5D.695、设函数fx在R上可导,其导函数为f’x,且函数fx在x=-2处取得极小值,则函数y=xf’x的图象可能是()A.B.C.D.96、已知函数fx=1lnx+1-x;则y=fx的图象大致为()A.B.C.D.97、某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N1000502,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为________.98、已知函数fx=|x2+5x+4|,x≤02|x-2|,x>0,若函数y=fx-a|x|恰有4个零点,则实数a的取值范围为___________.99、已知函数fx=1x+1-3,x∈-10x,x∈01,且gx=fx-mx-m在-11内有且仅有两个不同的零点,则实数m的取值范围是()A.-94-2∪012B.-114-2∪012C.-94-2∪023D.-114-2∪023100、记函数y=fx的反函数为y=f-1x.如果函数y=fx的图象过点(1,0),那么函数y=f-1x+1的图象过点()A.(0,0)B.(0,2)C.(1,1)D.(2,0)101、已知函数fx=-x2+2x,x≤0lnx+1,x>0,若|fx|≥ax,则a的取值范围是()A.(-∞,0]B.(-∞,1]C.[-2,1]D.[-2,0]102、函数y=cos6x2x-2-x的图象大致为()A.B.C.D.103、电视传媒公司为了了解某地区电视观众对某体育节目的收视情况,随机抽取了100名观众进行调查,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.(1)根据已知条件完成下面2×2列联表,并据此资料你是否认为“体育迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望EX和方差DX.104、对于实数a和b,定义运算“*”:a∗b=a2−ab,a⩽bb2−ab,a>b,设fx=2x-1*x-1,且关于x的方程为fx=mm∈R恰有三个互不相等的实数根x1,x2,x3,则x1x2x3的取值范围是_____________.105、某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为______.106、已知函数fx=1lnx+1-x;则y=fx的图象大致为()A.B.C.D.107、从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:(1)求这500件产品质量指标值的样本平均数x¯和样本方差s2(同一组中数据用该组区间的中点值作代表);(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数x¯,σ2近似为样本方差s2. (ⅰ)利用该正态分布,求P(187.8Z212.2);(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100产品中质量指标值位于区间(187.8,212.2)的产品件数,利用(ⅰ)的结果,求EX.附:150≈12.2.若Z-N(μ,σ2),则P(μ−σZμ+σ)=0.6826,P(μ−2σZμ+2σ)=0.9544.108、假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p0.(I)求p0的值;(参考数据:若X~N(μ,σ2),有P(μ−σX≤μ+σ)=0.6826,P(μ−2σX≤μ+2σ)=0.9544,P(μ−3σX≤μ+3σ)=0.9974.)(II)某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次,A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的运营成本分别为1600元/辆和2400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A 型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆?109、如图,|OA|=2(单位:m),OB=1(单位:m),OA与OB的夹角为π6,以A为圆心,AB为半径作圆弧BDC⌢与线段OA延长线交与点C.甲、乙两质点同时从点O出发,甲先以速度1(单位:m/s)沿线段OB行至点B,再以速度3(单位:m/s)沿圆弧BDC⌢行至点C 后停止;乙以速率2(单位:m/s)沿线段OA行至A点后停止.设t 时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为StS0=0,则函数y=St的图象大致是()A.@B.C.@D.110、某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和系统B在任意时刻发生故障的概率分别为110和p.1若在任意时刻至少有一个系统不发生故障的概率为4950,求p的值;2求系统A在3次相互独立的检测中不发生故障的次数大于发生故障的次数的概率.111、已知函数y=|x2-1|x-1的图象与函数y=kx的图象恰有两个交点,则实数k的取值范围是_________.112、现在4个人去参加娱乐活动,该活动有甲、乙两个游戏可提供参加者选择.为增加趣味性,约定:每个人通过一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.(1)求这4个人中恰有2人去参加甲游戏的概率;(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率:(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望Eξ.113、已知函数y=|x2-1|x-1的图象与函数y=kx-2的图象恰有两个交点,则实数k的取值范围是______.114、计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的频率,假设各年的年入流量相互独立.(Ⅰ)求未来4年中,至多有1年的年入流量超过120的概率;(Ⅱ)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?115、函数y=cos6x2x-2-x的图象大致为()A.B.。
函数图象的变换测试题(含解析)

函函函函函函函函函函一、单选题(本大题共11小题,共55分)1. 为了得到函数y =sin(2x −π3)+1的图象,可将函数y =sin2x 的图象( ) A. 向右平移π6个单位长度,再向上平移1个单位长度 B. 向右平移π3个单位长度,再向下平移1个单位长度 C. 向左平移π6个单位长度,再向下平移1个单位长度 D. 向左平移π3个单位长度,再向上平移1个单位长度2. 若函数y =sin(ωx +π3)的图象向右平移π6个单位长度后与函数y =cosωx 的图象重合,则ω的值可能为( )A. −1B. −2C. 1D. 23. 为了得到函数y =sin(3x −π6)的图象,需将函数y =sin(x −π6)的图象上所有点的( ) A. 纵坐标变为原来的3倍,横坐标不变 B. 横坐标变为原来的3倍,纵坐标不变 C. 横坐标变为原来的13,纵坐标不变D. 纵坐标变为原来的13,横坐标不变4. 函数y =sin2x 的图象可由函数y =cos(2x +π6)的图象( ) A. 向左平移π12个单位长度得到 B. 向右平移π6个单位长度得到 C. 向左平移π4个单位长度得到D. 向右平移π3个单位长度得到5. 将函数y =sin(4x −π3)图象上的横坐标进行怎样的变换,得到y =sin(2x −π3)的图象( ) A. 伸长了2倍B. 伸长了12倍C. 缩短了12倍D. 缩短了2倍6. 把函数y =sin(2x −π4)的图象向左平移π8个单位长度,所得到的图象对应的函数是( ) A. 奇函数B. 偶函数C. 既是奇函数也是偶函数D. 非奇非偶函数7. 已知函数f(x)=sin(x +π3).给出下列结论:①f(x)的最小正周期为2π; ②f(π2)是f(x)的最大值;③把函数y =sinx 的图象上的所有点向左平移π3个单位长度,可得到函数y =f(x)的图象. 其中所有正确结论的序号是( )A. ①B. ①③C. ②③D. ①②③8. 把函数y =f(x)图像上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得曲线向右平移π3个单位长度,得到函数y =sin(x −π4)的图像,则f(x)=( )A. sin(x 2−7π12)B. sin(x 2+π12)C. sin(2x −7π12)D. sin(2x +π12)9. 为了得到函数y =sin (2x −π3)的图象,只需把函数y =sin (2x +π6)的图象( ) A. 向左平移π4个单位长度 B. 向右平移π4个单位长度 C. 向左平移π2个单位长度D. 向右平移π2个单位长度10. 先把函数f(x)=sin (x −π6)的图象上各点的横坐标变为原来的12(纵坐标不变),再把新得到的图象向右平移π3个单位,得到y =g(x)的图象,当x ∈(π4,3π4)时,函数g(x)的值域为( )A. (−√32,1]B. (−12,1]C. (−√32,√32)D. [−1,0)11. 要得到函数y =2cos(x2+π6)sin(π3−x2)−1的图象,需将y =12sinx +√32cosx 的图象( ) A. 向左平移π4个单位长度 B. 向右平移π4个单位长度 C. 向左平移π2个单位长度D. 向右平移π2个单位长度二、多选题(本大题共2小题,共10分)12. (多选)下列四种变换方式,其中能将y =sinx 的图象变为y =sin(2x +π4)的图象的是( ) A. 向左平移π4个单位长度,再将横坐标缩短为原来的12 B. 横坐标缩短为原来的12,再向左平移π8个单位长度 C. 横坐标缩短为原来的12,再向左平移π4个单位长度 D. 向左平移π8个单位长度,再将横坐标缩短为原来的1213. 将函数y =cos (2x +π3)的图象向左平移π4个单位长度得到函数f(x)图象,则( )A. y =sin (2x +π3)是函数f(x)的一个解析式 B. 直线x =7π12是函数f(x)图象的一条对称轴 C. 函数f(x)是周期为π的奇函数D. 函数f(x)的递减区间为[kπ−5π12,kπ+π12](k ∈Z)三、填空题(本大题共4小题,共20分)14. 函数y =sin(2x −π4)图象上所有点的横坐标保持不变,将纵坐标 (填“伸长”或“缩短”)为原来的 倍,将会得到函数y =3sin(2x −π4)的图象.15. 函数y =sin(2x +π3)的图象可由y =cos(2x +π4)的图象 得到.16. 函数y =cos(2x +φ)(−π≤φ<π)的图象向右平移π2个单位后,与函数y =sin(2x +π3)的图象重合,则φ= .17. 若函数f(x)=32sin2x −3√32cos2x 的图象为C ,则下列结论中正确的序号是 .①图象C 关于直线x =11π12对称; ②图象C 关于点(2π3,0)对称;③函数f(x)在区间(−π12,5π12)内不是单调的函数;④由y =3sin2x 的图象向右平移π3个单位长度可以得到图象C . 四、解答题(本大题共1小题,共12分)18. (本小题12分)把函数y =f(x)的图象上的各点向右平移π6个单位长度,然后把横坐标伸长到原来的2倍,再把纵坐标缩短到原来的23,所得图象的解析式是y = 2sin(12x +π3),求f(x)的解析式.答案和解析1.解:∵y =sin(2x −π3)+1=sin2(x −π6)+1,∴把y =sin2x 的图象上所有的点向右平移π6个单位长度,再向上平移1个单位长度 即可得到函数y =sin(2x −π3)+1的图象.故选A .2.解:函数y =sin(ωx +π3)的图象向右平移π6个单位后,可得函数y =sin [ω(x −π6)+π3]的图象,再根据所得函数的图象与函数y =cosωx 的图象重合,∴π3−ω⋅π6=2kπ+π2,k ∈Z , ∴当k =0时,ω=−1.故选A .3.解:将函数y =sin(x −π6)的图象横坐标变为原来的13,纵坐标不变即可得到函数y =sin(3x −π6)的图象.故选C .4.解:由sin2x =cos(2x −π2)=cos[2(x −π3)+π6],所以函数y =sin2x 的图象可由函数y =cos(2x +π6)的图象向右平移π3个长度单位,故选D . 5.解:将函数y =sin(4x −π3)图象上的横坐标伸长为原来的2倍即可得到y =sin(2x −π3)的图象.故选A .6.解:把函数y =sin(2x −π4)的图象向左平移π8个单位长度,得到y =sin[2(x +π8)−π4]=sin2x 为奇函数,故选A .7.解:因为f(x)=sin(x +π3),①由周期公式可得,f(x)的最小正周期T =2π,故①正确; ②f(π2)=sin(π2+π3)=sin 5π6=12,不是f(x)的最大值,故②错误;③根据函数图象的平移法则可得,函数y =sinx 的图象上的所有点向左平移π3个单位长度,可得到函数y =f(x)的图象,故③正确.故选:B .8.解:∵把函数y =f(x)图像上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得曲线向右平移π3个单位长度,得到函数y =sin(x −π4)的图像,∴把函数y =sin(x −π4)的图像,向左平移π3个单位长度,得到y =sin(x +π3−π4)=sin(x +π12)的图像;再把图像上所有点的横坐标变为原来的2倍,纵坐标不变,可得f(x)=sin(12x +π12)的图像.故选:B .9.解:y =sin (2x +π6)=sin 2(x +π12),y =sin (2x −π3)=sin 2(x −π6),所以将y =sin (2x +π6)的图象向右平移π4个单位长度得到y =sin (2x −π3)的图象.故选B . 10.解:把函数f(x)=sin(x −π6)的图象上各点的横坐标变为原来的12倍(纵坐标不变),可得函数y =sin(2x −π6)的图象;再把新得到的图象向右平移π3个单位,得到y =g(x)=sin[2(x −π3)−π6]=sin(2x −5π6)的图象.当x ∈(π4,3π4)时,2x −5π6∈(−π3,2π3), 故当2x −5π6趋于−π3时,g(x)的最小值趋于−√32,当2x −5π6=π2时,g(x)取得最大值为1,故选:A .11.解:y =2cos(x 2+π6)sin(π3−x 2)−1=2cos(x 2+π6)sin[π2−(π6+x 2)]−1=2cos(x 2+π6)cos(π6+x2)−1=cos(x +π3),又y =12sinx +√32cosx = sin(x +π3)向左平移π2个单位长度y =sin(x +π3+π2)=cos(x +π3),故选C .12.解:将y =sinx 的图象先向左平移π4个单位长度,再将横坐标缩短为原来的12或先横坐标缩短为原来的12,再向左平移π8个单位长度都可以得到y =sin(2x +π4)的图象.故选AB13.解:由题意,函数y =cos (2x +π3)的图象向左平移π4个单位长度得到函数f(x)=cos[2(x +π4)+π3]=cos(2x +5π6),于是下面对各选项进行分析: 对A ,因为y =cos(2x +5π6)=−sin(2x +π3),x ∈R ,故A 不正确;对B ,因为f(x)=cos(2x +5π6),根据余弦函数图像性质可知,其对称轴为2x +5π6=kπ,k ∈Z ,即x =kπ2−5π12,k ∈Z ,取k =2,可知x =7π12是函数f (x )图象的一条对称轴,故B 正确;对C ,因为f(x)=cos(2x +5π6),其最小正周期为T =2π2=π,又f(0)=cos(5π6)=−√32≠0,可知C 不正确;对D ,因为f(x)=cos(2x +5π6),根据余弦函数图像性质可知,令2kπ⩽2x +5π6⩽2kπ+π, k ∈Z ,即得单调递减区间为x ∈[kπ−5π12,kπ+π12](k ∈Z),故D 正确.故选BD .14. 解:A =3>1,故函数y = sin(2x −π4)图象上所有点的横坐标保持不变,将纵坐标伸长为原来的3倍即可得到函数y =3sin(2x −π4)的图象.15.解:y =cos(2x +π4)=sin(2x +π4+π2)=sin(2x +3π4), 将函数y =sin(2x +3π4)的图象向右平移5π24个单位长度可得函数y =sin(2x +π3)的图象.16.解:将y =cos (2x +φ)的图象向右平移π2个单位长度后,得到y =cos [2(x −π2)+φ]的图象,化简得y =−cos (2x +φ),又可变形为y =sin (2x +φ−π2).由题意可知φ−π2=π3+2kπ(k ∈Z ),所以φ=5π6+2kπ(k ∈Z ),结合−π≤φ<π,知φ=5π6.故答案为5π6.17.解:f(x)=32sin2x −3√32cos2x =3sin(2x −π3),因为当x =11π12时,f(x)=3sin(2×11π12−π3)=3sin3π2=−3,所以直线x =11π12是图象C 的对称轴,故①正确;因为当x =2π3时,f(x)=3sin(2×2π3−π3)=0,所以函数图象C 关于点(2π3,0)对称,故②正确;令−π2≤2x −π3≤π2,解得x ∈[−π12,5π12],所以函数的一个增区间是[−π12,5π12],因此f(x)在区间(−π12,5π12)上是增函数,故③不正确; 由y =3sin2x 的图象向右平移π3个单位,得到的图象对应的函数表达式为 y =3sin2(x −π3)=3sin(2x −2π3),故④不正确.故答案为:①②. 18.解:y =2sin(12x +π3)的图象的纵坐标伸长为原来的32,得到y = 3sin(12x +π3);再将其横坐标缩短到原来的12,得到y =3sin(x +π3);再将其图象上的各点向左平移π6个单位长度,得到y =3sin(x +π2)=3cosx ,故f(x)=3cosx.。
数学课程函数图像变换练习题及答案

数学课程函数图像变换练习题及答案
1. 问题描述:
下列函数的图像经过怎样的变换可以得到另一个函数的图像?请写出变换的类型和具体变换的过程。
(1) 函数f(x) = x^2
(2) 函数g(x) = |x|
(3) 函数h(x) = 1/x
(4) 函数k(x) = sin(x)
2. 答案及解析:
(1) 函数f(x) = x^2
变换类型:平移和缩放
具体变换过程:将函数图像沿x轴向左平移2个单位,然后沿y轴向上平移3个单位,最后沿y轴方向缩放2倍。
(2) 函数g(x) = |x|
变换类型:翻折
具体变换过程:将函数图像绕x轴翻折。
(3) 函数h(x) = 1/x
变换类型:反比例函数的变换
具体变换过程:无需进行图像变换,因为反比例函数的图像已经是h(x)的图像。
(4) 函数k(x) = sin(x)
变换类型:平移
具体变换过程:将函数图像沿x轴向右平移π/2个单位。
以上答案给出了每个函数的图像变换类型和具体的变换过程。
通过对函数图像的变换练习,可以帮助学生更好地理解函数的特点和图像的变化规律,提升数学学习的效果。
注意:在解答图像变换过程时,可以使用几何变换的专业术语,如平移、翻折、缩放等,以确保解答的准确性和规范性。
在写出具体的变换过程时,要注明是在x轴还是y轴方向进行变换,并注明平移或缩放的单位或比例。
高中数学函数图象及其变换专题.doc

专题函数图象及其变换考点精要1.理解指数函数的概念、图彖及性质.2•理解对数函数的概念图象和性质.1 13•理解幕函数y三X, y=x2, y三?,尸一,y = x2的图象及其性质.x4.掌握一次函数、正比例函数、二次函数、反比例函数的图象及其性质. 5•理解图象的平移变换、伸缩变换、对称变换.热点分析函数的图象是函数的一种重要表示方法,利用函数的图像可以帮助我们更好地理解函数的重要性质.基本初等函数的图像及其变换,是考查的热点;利用变换作图,也是考查的重点,利用形数结合的数学思想解题,看图想性质,数形转化灵活解题.知识梳理函数的图象及其变换基础矢口识・1.图W:就是用函数图象表示两个变量之间的关系优点:能直观形象地表示出函数的变化情况.体现:映射与反演、形数结合的数学思想.2.基本初等函数图象y=x n y=a^ y=\og(l x y=siru: y=cos^ }?=taiLv 初等函数图像:y=kx y=kx+b y=aX1-^-bx+c y = - y = ax+ -x x3.作图基本方法(1)利用描点法作图:①确定函数的定义域:图象沿兀轴展布范围及渐近线;②化简函数解析式:等价变形;③讨论函数的性质:奇偶性:关于图象对称性单调性:关于图象升降性周期性:关于图象重要性极值、最值:关于图象最高点、最低点截距:与x轴、y轴交点坐标④画出函数的图象(2)利用基本初等函数的图象的变换作图:①平移变换y=f(^ >y=f(皿尸/⑴忌■驟〉y=f M②伸(放)缩变换:③ 对称变换:y=f (x) ——―> y= -f (x) y-f (x)―> y-f (-x) 冃(x) 冃(x)y=f (兀) y=f (^)待三角函数的复习屮再集屮进行研究. 例题精讲:例I 作出函数尸欝的图像,并指出函数的单调区间,图象的对称中心.例2作岀函数的图像:(7) y = 2X+2例4、若不等式x 2-lo g</x<0对施(0丄)恒成立,则实数Q 的取值范围是沿兀轴: 沿y 轴:y = /(x)0«o<l-伸K 到丄倍y = f(cox) (69>0)0<4<1.» 短?M 倍尸/⑴小伸2钿/厂心(兀)3>0)> W (M ) y=f (x)上方图紀上掉用卜•方■片把卜方图娥对納fesu> y=\f (x)④几种基本变换的合成.y=f (x ) -------------- > y = A /(ex + 0) + k (1) y= x 2 -2x-3(3) y =—X(4)(]屮T (2) y=丄(2丿(5) y = |log 2x-1(6) y= lgx已知函数/(x )和g (兀) 的图像关于原点对称、且/ (x ) =F+2X .(1)求函数g (x )的解析式;(2)解不等式g(x)>f(x)-\x-l\.l ,L -Vr=<j > y=f (2a-x)> y= -f (-x)侧血轴右型图紀恸粕 右边用線.井把仃边图後対称到左边x + 2A 、0<tz< 1B 、—<a<lC 、0<6i<—D 、a > 1 16 16例6、若直线y = x-m 与曲线『=Jl-x?有两个不同的交点,则实数加的取值范IH 是 ___________ o针对训练1. 函数f(x) = --x 的图像关于XA. y 轴对称C.坐标原点对称2. 函数y=l+cosx 的图像A.关于兀轴对称B. 直线y=-兀对称 D.直线〉=兀对称B. 关于y 轴对称D.关于直线•怕对在区间(—,0)上单调递减C. 是奇函数,在区间(0, + oo)上单调递增7. 函数y = l-—的图像是x-1在区间(0,4-oo)上单调递减 C.关于原点对称3. 称设 函数 y 二(x-a) 2 (x-b)的图像可能是4. 5.与曲线y =—・关于原点对称的曲线为 x-1A. y = —!—• 1 +兀 函数 y=lg|x| A ・是偶函数,yA / 0/9cC. y 1~l-xy/V()/-1在区间(YO ,0)上单调递增B. 是偶函数,D. 是奇函数,-VD.D15.函数f(x)=-4x-4 X 2-4X + 3Bx<\的图像和函数g (X )=10g2兀的图彖的交点个数是8.是函数f (x) =\x-a\在区间[1, + x)上为增函数的A ・充分不必要条件 B.必要不充分条件C ・充要条件D.既不充分也不必要条件9. 已知定义域为R 的函数/(%)在区间(& + oo)上为减函数,且函数y=f (x+8) 为偶函数,则A- f (6) >f (7) B. f (6) >f (9) C. f (7) >f (9) D./(7)>f(10) 10. 函数/ (兀)的图象如右图,其中G, b 为常数,则下列结论正确的是B. a>\, b>0 D. 0<a<\, b<0 11. 若0SV1, bv-1,则函数y 寸(Q =/+b 的图彖不经过A.第一彖限B.第二彖限 C ・第三象限 D.第四彖限 12. 函数y=f (x)的图像与函数g (x) =log 2x (x>0)的图象关于原点对称,则 f (x)的表达式为 A ・ /O)= —(兀 >0) B. /(x) = log 2(-x) (x<0) log 2xI Iy1 1 111 1O 'vA. a>\, b<0C. 0<6/<1, b>0C ・ /(x) = -log 2x(x>0)13・向高为力的水瓶注水,注满为止, 示,那么水瓶的形状是D ・ f(x) = -log 2(-x) (x < 0)若注水量v 与水深h 的函数关系如右图所ACD14.函数尸严环-1|的图像大致是hD.X答案:针对训练1. C2. B 3・ C 4. A 5・ B 6. A 7・ B 8. A 9・ D 10. D 11. A12. D 13. B 14. D 15. 3高考链接1(06北京理)在下列四个函数屮,满足性质:“对于区间(1,2)上的任意兀],兀2(兀I 工兀2),l/(-r i)_/(X2)l<l X2_X l IB成立”的只有(A) /(x)=-(B)/(x) =|x|(C) f(x) = 2X(D) /(x) = x22(全国)若0<a<\,/?<-1,则函数y寸(x)的图象不经过A.第一象限B.第二象限C・第三象限 D.第四象限3(08北京)如图,函数/(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4(全国)函数y=\g\x\A・是偶函数,在区间(—,0)上单调递增 B.是偶函数,在区间(-8, 0)上单调递减C・是奇函数,在区间(0, + oo)上单调递增 D.是奇函数,在区间(0, + oo)上单调递减5(08山东)函数f (x) =a x^的图象如右图,其中d, b为常数,则下列结论正确的是A. d>\, b<0C.0<a<\, b>0答案:1A 2 A 3 2_ 4B 5 D B. a>\ b>0 D> 0<a<l, b<0。
(完整word版)三角函数图像变换练习题(有答案)

三角函数图像变换练习题一、选择题(本大题共13小题,共65.0分)1. 为得到函数y =6sin (2x +π3)的图象,只需要将函数y =6cos2x 的图象( )A. 向右平行移动π6个单位 B. 向左平行移动π6个单位 C. 向右平行移动π12个单位D. 向左平行移动π12个单位2. 已知函数f(x)=sin(x +π3)sinx +cos 2x 的图象向右平移π6单位,再把横坐标缩小到原来的一半,得到函数g(x),则关于函数g(x)的结论正确的是 ( )A. 最小正周期为πB. 关于x =π6对称 C. 最大值为1D. 关于(π24,0)对称3. 函数的图象y =3cos2x 可以看作把函数y =3sin2x 的图象向( )而得到的A. 左平移π2个单位 B. 左平移π4个单位 C. 右平移π2个单位D. 右平移π4个单位4. 将函数y =sin(4x −π6)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得图象向左平移π6个单位长度,得到函数f(x)的图象,则函数f(x)的解析式为( )A. f(x)=sin(2x +π6) B. f(x)=sin(2x −π3) C. f(x)=sin(8x +π6)D. f(x)=sin(8x −π3)5. 要得到函数f(x)=cos(2x −π6)的图象,只需将函数g(x)=sin2x 的图象A. 向左平移π6个单位 B. 向右平移π6个单位 C. 向左平移π3个单位D. 向右平移π3个单位6. 将函数f(x)=√3sin2x −cos2x 的图象向右平移π3个单位得到函数g(x)的图象,若有g(θ)=2cos π6,则θ的可能取值为A. 3π4B. 5π6C. π6D. π47. 将函数的图象上的所有点向右平移π12个单位得到函数g(x)的图象,则g(x)的函数解析式为( )A.B.C.D.8. 如果两个函数的图象经过平移后能够重合,那么这两个函数称为“和谐”函数.下列函数中与g(x)=√2sin(x +π4)能构成“和谐”函数的是( )A. f(x)=sin(x +π4) B. f(x)=2sin(x −π4) C. f(x)=√2sin(x2+π4)D. f(x)=√2sin(x +π4)+29. 若将函数f (x )=√2sin(2x +π4)的图像向右平移φ(φ>0)个单位,所得图像关于原点对称,则φ的最小值为( )A. π8B. π4C. 3π8D. 3π410. 函数y =sin (2x +π3)的图象可由函数y =cosx 的图象( )A. 先把各点的横坐标缩短到原来的12,再向左平移π6个单位 B. 先把各点的横坐标缩短到原来的12,再向右平移π12个单位 C. 先把各点的横坐标伸长到原来的2倍,再向左平移π6个单位 D. 先把各点的横坐标伸长到原来的2倍,再向右平移π12个单位11. 若将函数y =2sin 2x 的图象向左平移π12个单位长度,则平移后的图象的对称轴为( )A. x =kπ2−π6(k ∈Z)B. x =kπ2+π6(k ∈Z)C. x =kπ2−π12(k ∈Z) D. x =kπ2+π12(k ∈Z)12. 将函数的图象向左平移π6个单位长度得到函数g(x)的图象,则下列说法正确的是( )A. 函数g(x)的周期是π2B. 函数g(x)的图象关于直线x =−π12对称C. 函数g(x)在(π6,π2)上单调递减D. 函数g(x)在(0,π6)上最大值是113.已知将函数的图象向左平移φ个单位长度后,得到函数g(x)的图象,若g(x)的图象关于原点对称,则f(π3)=()A. −√32B. √32C. −12D. 12二、填空题(本大题共1小题,共5.0分)14.将函数y=sin(−2x)的图象向左平移π4个单位,所得图象的解析式为_______________.三、解答题(本大题共4小题,共48.0分)15.若函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π2)的图象经过点(0,√3),且相邻的两个零点差的绝对值为6.(1)求函数f(x)的解析式;(2)若将函数f(x)的图象向右平移3个单位后得到函数g(x)的图象,当x∈[−1,5]时,求g(x)的值域.16.设函数,其中0<ω<3.已知f(π6)=0.(1)求ω;(2)将函数f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移π4个单位,得到函数g(x)的图象,求g(x)在[−π4,3π4]上的最小值及相应x的值.17.已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,0<φ<π,函数f(x)图像上相邻的两个对称中心之间的距离为π4,且在x=π3处取到最小值−2.(1)求函数f(x)的解析式;(2)若将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将向左平移π6个单位,得到函数g(x)图象,求函数g(x)的单调递增区间。
函数(8)函数的图象及其变换 Word版含答案

函数的图象及其变换1、在同一直角坐标系中,函数()()0af x xx =>,()log a g x x =的图象可能是( )A. B.C. D.2、某人骑自行车沿直线匀速行驶,先前进了km a ,休息了一段时间,又沿原路返回km()b a b >,再前进km c ,则此人离起点的距离s 与时间t 的关系示意图是( )A. B.C. D.3、函数f (x )=()2x xe ef x x --=的图象大致为( )A. B.C. D.4、函数2()2x f x x =-的图象大致是( )A. B.C. D.5、如图可能是下列哪个函数的图象( )A. 221x y x =-- B. 2sin 41x x xy =+C. ()22x y x x e =-D. ln xy x=6、函数ln(2)y x =-的大致图象为图中的( )A. B.C. D.7、函数(01)x y a a a =>≠且与函数()y f x =的图象关于直线y x =对称,则函数()y f x =与二次函数2(1)y a x x =--在同一坐标系内的图象可能是图中的( )A. B.C. D.8、如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的高度,则H 与下落时间t(分)的函数关系表示的图象只可能是( )A. B.C. D.9、函数3222x xxy-=+在[]6,6-的图象大致为( )A.B.C .D .10、定义运算()()a ab a b b a b ≤⎧⎪⊗=⎨>⎪⎩,则函数()12x f x =⊗的图象大致为( ) A. B.C. D.11、已知函数()y f x =的图象经过点(1)2,,则函数()1y f x =+的图象经过点________. 12、已知()f x 是定义在[)(]2,00,2-U 上的奇函数,当0x >,()f x 的图象如图所示,那么()f x 的值域是__________.13、如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量y 与净化时间t (月)的近似函数关系:(0,01)t y a t a a =≥>≠且的图象.有以下叙述:①第4个月时,剩留量就会低于15;②每月减少的有害物质量都相等;③若剩留量为111,,248时,所经过的时间分别是123,,t t t ,则123t t t +=.其中所有正确叙述的序号是__________. 14、已知函数211x y x -=-的图象与函数2y kx =-的图象恰有两个交点,则实数k 的取值范围是____________.15、已知函数()f x 是定义在R 上的偶函数,当0x ≤时,2()=2f x x x =.现已画出函数()f x 在y 轴左侧的图象,如图所示.(1)画出函数()f x 在y 轴右侧的图象,并写出函数()f x 在R 上的单调区间; (2)求函数()f x 在R 上的解析式.-=答案=-以及解析1-=答案=-及解析: -=答案=-:D解析:根据对数函数性质知,0a >,所以幂函数是增函数,A 错误(利用点()1,1也可以排除);选项B 中,从对数函数图象看1a <,与幂函数图象矛盾;选项C 中,从对数函数图象看1a >,与幂函数图象矛盾;选项D 中图象正确. 故选D.2-=答案=-及解析: -=答案=-:C解析:因为他休息了一段时间,所以在这段时间内,时间在增长,路程没有变化,排除A ;沿原路返回km b ,说明随着时间的增长,他离起点近了,排除D ;虽然离出发地近了,但时间没有增长,排除B. 故选C.3-=答案=-及解析: -=答案=-:B解析:函数22()()()x x x xe e e ef x f x x x-----==-=--,函数()f x 为奇函数,图象关于原点对称,排除A ;当1x =时,1(1)0f e e=->,排除D ;当x →∞+时,()f x →∞+,排除C. 故选B.4-=答案=-及解析: -=答案=-:B解析:∵函数2()2xf x x =-,∴()39810f =-=>,故排除C ,D ;∵()12101,20.21425f f ⎛⎫ ⎪=-=⎝⎭=- A.故选B.5-=答案=-及解析: -=答案=-:C解析:曲线经过原点,因此该图象不可能是函数ln xy x=的图象; 当0x <时,0y >,因此该图象不可能是函数2sin 41x x xy =+的图象;对于221x y x =--,当1x =-时,0y <,因此该图象不可能是函数221x y x =--的图象.故选C.6-=答案=-及解析: -=答案=-:A解析:∵20x ->,解得22x -<<,∴函数ln(2)y x =-的定义域为(2,2)-,关于原点对称. ∵()ln(2)ln(2)()f x x x f x -=--=-=,∴函数ln(2)y x =-在定义域上为偶函数,排除C 和D. 当32x =时,1ln 02y =<,排除B.故选A.7-=答案=-及解析: -=答案=-:A解析:∵函数(01)x y a a a =>≠且与函数()y f x =的图象关于直线y x =对称, ∴()log a f x x =.当1a >时,对数函数在(0,)+∞上是增函数,且二次函数图象的对称轴在y 轴右侧,二次函数的图象开口向上,过坐标原点;当01a <<时,对数函数在(0,)+∞上是减函数,且二次函数图象的对称轴在y 轴左侧,二次函数的图象开口向下,过坐标原点.综上,图象可能是A.故选A.8-=答案=-及解析: -=答案=-:B解析:由于所给的圆锥形漏斗上口大于下口,当时间取12t 时,漏斗中液面下落的高度不会达到漏斗高度的12,对比四个选项的图象可得结果.故选B.9-=答案=-及解析: -=答案=-:B解析:设32()22x x x y f x -==+,则332()2()()2222x xx x x x f x f x ----==-=-++,所以()f x 是奇函数,图象关于原点成中心对称,排除选项C .又34424(4)022f -⨯=>+,排除选项D ;36626(6)722f -⨯=≈+,排除选项A.故选B .10-=答案=-及解析: -=答案=-:A解析:∵,*,a a ba b b a b ≤⎧=⎨>⎩,若0x >可得,21x >,∴()1*21x f x ==;若0x ≤可得,21x ≤,∴()1*22x xg x ==,∴当0x ≤时,21x ≤.故选A.11-=答案=-及解析: -=答案=-:()0,2解析:由题意知, ()12f =,则对()1y f x =+,可令11x +=,得0x =, 此时()12y f ==,故函数()1y f x =+的图象经过点()0,2.12-=答案=-及解析: -=答案=-:(][)2,33,2--U解析:∵f(x)是定义在[)(]2,00,2-U上的奇函数,∴图象关于原点对称,作出其在y轴左侧的图象,如图.由图可知:f(x)的值域是(2,3]∪[−3,−2).故-=答案=-为(][)2,33,2--U.13-=答案=-及解析:-=答案=-:①③解析:根据题意,函数的图象经过点42,9⎛⎫⎪⎝⎭,故函数为23ty⎛⎫= ⎪⎝⎭,令4t=时,161815y=<,故①正确;当1t=时,23y=,减少13,当2t=时,49y=,减少29,每月减少有害物质质量不相等,故②不正确;分别令111,,248y=,解得1231log2t=,2231log4t=,3231log8t=,123t t t+=.故③正确.14-=答案=-及解析:-=答案=-:()()0,11,4⋃解析:据已知得()()()1,1111,11x xx xf xx xx+>-+⎧⎪==⎨-+<-⎪⎩,如图,若使其图象与直线2y kx=-恰有个交点,由于直线过定点()0,2D-,只需直线介于DB与DE之间或介于直线DE与DA之间即可,故01k<<或14k<<.15-=答案=-及解析: -=答案=-:(1)如图所示:()f x 的单调递减区间为()(),1,0,1-∞-,单调递增区间为()()1,0,1,-+∞. (2)令0x >则0x -<,所以()()()2222f x x x x x -=-+-=-, 又函数 ()f x 为偶函数,即()()f x f x =-, 所以当0x >时2()2f x x x =-, 所以222,0()2,0x x x f x x x x ⎧+≤=⎨->⎩.。
高中数学中的函数图象变换及练习题

高中数学中的函数图象变换及练习题①平移变换:Ⅰ、水平平移:函数yf ( x a) 的图像能够把函数yf ( x) 的图像沿 x 轴方向向左(a 0) 或向右 (a0) 平移 | a | 个单位即可获得;左移 h右移 h1) y =f ( x )y =f ( x +h) ; 2)y =f ( x )y =f ( x h) ;x 轴方向向上Ⅱ、竖直平移:函数yf ( x) a 的图像能够把函数 yf ( x) 的图像沿 (a 0) 或向下 (a0) 平移 | a |个单位即可获得;上移 h下移 h1) y =f ( x ) y =f ( x )+h ; 2) y =f ( x )y =f ( x ) h 。
②对称变换:Ⅰ、函数 y f ( x) 的图像能够将函数 yf ( x) 的图像对于 y 轴对称即可获得;y 轴y =f ( x )y =f ( x )f ( x) 的图像对于 x 轴对称即可获得; Ⅱ、函数 yf ( x) 的图像能够将函数 yy =f ( x )x 轴y = f ( x )Ⅲ、函数 yf ( x) 的图像能够将函数 yf ( x) 的图像对于原点对称即可获得;原点y =f ( x )y = f ( x )Ⅳ、函数 xf ( y) 的图像能够将函数 yf ( x) 的图像对于直线 y x 对称获得。
直线 y xy =f ( x )x =f ( y )Ⅴ、函数 y f ( 2a x) 的图像能够将函数 yf (x) 的图像对于直线 x a 对称即可获得③翻折变换:f ( x) 的图像的 x 轴下方部分沿 x 轴翻折到 x 轴上Ⅰ、函数 y | f (x) |的图像能够将函数 y 方,去掉原 x 轴下方部分,并保存 yf ( x) 的 x 轴上方部分即可获得;Ⅱ、函数 y f (| x |) 的图像能够将函数 y f ( x) 的图像右侧缘 y 轴翻折到 y 轴左侧代替原y 轴左侧部分并保存 yf ( x) 在 y 轴右侧部分即可获得④伸缩变换:Ⅰ、函数 y af ( x) ( a 0) 的图像能够将函数 y f (x) 的图像中的每一点横坐标不变纵坐(a 1)0 a 1 )为本来的 a 倍获得;= ( x )y a标伸长或压缩( y =af ( x )y fⅡ、函数 y f (ax) (a0) 的图像能够将函数 yf (x) 的图像中的每一点纵坐标不变横坐标伸长 (a 1) 或压缩( 0a 1)为本来的1倍获得。
高考图像函数转换练习题

高考图像函数转换练习题高考数学中,图像函数转换是一个重要的考点,涉及到平移、翻折、旋转等多种转换方式。
掌握图像函数转换的方法,不仅可以帮助我们更好地理解数学概念,还可以提高解题的效率和准确性。
下面,我们来通过一些练习题,来进一步巩固和应用这些知识。
1. 平移平移是图像函数转换中最基本的操作之一。
在平面直角坐标系中,图像函数y=f(x)平移h个单位长度向右,我们可以通过将x的值减h来实现。
类似地,向左平移h个单位长度,可以通过将x的值加上h来实现。
例如,设函数y=x^2的图像经过平移后得到函数y=f(x+2),求f(x)的表达式。
我们可以通过令x+2=u,然后代入y=u^2得出f(x)=f(u-2)=(u-2)^2=(x+2-2)^2=x^2。
2. 翻折翻折是图像函数转换中另一个基本的操作。
在平面直角坐标系中,图像函数y=f(x)关于y轴翻折,我们可以通过将x的值变为-x来实现。
类似地,关于x轴翻折,可以通过将y的值变为-y来实现。
例如,设函数y=x^3的图像经过翻折后得到函数y=f(-x),求f(x)的表达式。
我们可以通过令-x=u,然后代入y=u^3得出f(x)=f(-u)=(-u)^3=(-x)^3=-x^3。
3. 旋转旋转是图像函数转换中较为复杂的操作。
在平面直角坐标系中,图像函数y=f(x)绕原点逆时针旋转α角度,我们可以通过沿着原点将坐标轴旋转α角度来实现。
例如,设函数y=x的图像经过逆时针旋转45°后得到函数y=f(x'),求f(x)的表达式。
我们可以通过坐标轴旋转45°后,将y轴上的点(x,y)变为x'轴上的点(x',y),其中x'=x*cos45°-y*sin45°,然后代入y=x得出f(x)=f(x'=x*cos45°-x*sin45°)。
总结起来,图像函数转换是高考数学中一个重要的考点,涉及到平移、翻折、旋转等多种转换方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学中的函数图象变换及练习题
①平移变换:
Ⅰ、水平平移:函数
y
f ( x a) 的图像可以把函数
y
f ( x) 的图像沿 x 轴方向向左
(a 0) 或向右 (a
0) 平移 | a | 个单位即可得到;
左移 h
右移 h
1) y =f ( x )
y =f ( x +h) ; 2)y =f ( x )
y =f ( x h) ;
x 轴方向向上
Ⅱ、竖直平移:函数
y
f ( x) a 的图像可以把函数 y
f ( x) 的图像沿 (a 0) 或向下 (a
0) 平移 | a |个单位即可得到;
上移 h
下移 h
1) y =f ( x ) y =f ( x )+h ; 2) y =f ( x )
y =f ( x ) h 。
②对称变换:
Ⅰ、函数 y f ( x) 的图像可以将函数 y
f ( x) 的图像关于 y 轴对称即可得到;
y 轴
y =f ( x )
y =f ( x )
f ( x) 的图像关于 x 轴对称即可得到; Ⅱ、函数 y
f ( x) 的图像可以将函数 y
y =f ( x )
x 轴
y = f ( x )
Ⅲ、函数 y
f ( x) 的图像可以将函数 y
f ( x) 的图像关于原点对称即可得到;
原点
y =f ( x )
y = f ( x )
Ⅳ、函数 x
f ( y) 的图像可以将函数 y
f ( x) 的图像关于直线 y x 对称得到。
直线 y x
y =f ( x )
x =f ( y )
Ⅴ、函数 y f ( 2a x) 的图像可以将函数 y
f (x) 的图像关于直线 x a 对称即可得到
③翻折变换:
f ( x) 的图像的 x 轴下方部分沿 x 轴翻折到 x 轴上
Ⅰ、函数 y | f (x) |的图像可以将函数 y 方,去掉原 x 轴下方部分,并保留 y
f ( x) 的 x 轴上方部分即可得到;
Ⅱ、函数 y f (| x |) 的图像可以将函数 y f ( x) 的图像右边沿 y 轴翻折到 y 轴左边替代原
y 轴左边部分并保留 y
f ( x) 在 y 轴右边部分即可得到
④伸缩变换:
Ⅰ、函数 y af ( x) ( a 0) 的图像可以将函数 y f (x) 的图像中的每一点横坐标不变纵坐
(a 1)
0 a 1 )为原来的 a 倍得到;
= ( x )
y a
标伸长
或压缩( y =af ( x )
y f
Ⅱ、函数 y f (ax) (a
0) 的图像可以将函数 y
f (x) 的图像中的每一点纵坐标不变横坐
标伸长 (a 1) 或压缩( 0
a 1)为原来的
1
倍得到。
f ( x ) y =f ( x )
x a
y =f ( ax )
a
1. 画出下列函数的图像
(1) y log 1
( x)
( 2) y(
1
) x (3) y log 2 x
(4) y x 2
1
2
2
(5)要得到 y
lg( 3 x) 的图像,只需作 y lg x 关于 _____轴对称的图像,再向 ____平移
3 个单位而得到。
( 6 ) 当 a 1 时 , 在 同 一 坐 标 系 中 函 数 y
a x 与 y
log a x 的
图 像 (
)
2 、已知函数 f ( x) 的图像关于直线x 1 对称,且当 x 0, 时,有
f ( x)
1
,则当
x
x , 2 时, f (x)的解析式是()
( A)1
( B)( C)
1
( D)
1 x x
2 2 x
3 、将函数y sin 2x 按向量 a ,1 平移后的函数解析式是
6
( A)y sin( 2x ) 1 ( B)y sin(2x ) 1
3 3
( C)y sin(2x ) 1 (D)y sin( 2x ) 1
6 6
y
【典型例题】
例 1(1) 已知函数f (x) ax3 bx 2 cx d 的图象如右图所示, 则
A)b ( ,0) B)b (0,1) O
1 2 x
C )b (1,2)
D )b (2, )
(2) 将函数y b a 的图象向右平移 2 个单位后又向下平移 2 个单位 , 所得图象如果与
x a
原图象关于直线y=x 对称 , 那么( )
( A)a 1,b 0 (B)a 1, b R
(C )a 1,b 0 ( D )a 0,b R
(3)已知函数 y=f(x) 和函数 y=g(x) 的图象如下 : 则函数 y=f(x)g(x) 的图象可能是
例 2. 作出下列函数的图象
(1) y x 2 ( x 1)(2) y lg x 1 (3)
2 x y
1
x
例 3 方程kx 1 ( x 2) 2有两个不相等的实根, 求实数 k 的取值范围
【课后作业】
1、 f(x)是定义在区间c, c 上的奇函数,其图象如图所示, 令 g(x)=af(x)+b则下列关于函
数 g(x) 的叙述正确的是
(A)若 a 0,则函数g(x)的图象关于原点对称
(B) 若a1, 2 b 0 ,则方程g(x)=0有大于2的实根
(C)若 a 0,b 2 ,则方程g(x)=0有两个实根
(D)若 a 1, b 2 ,则方程g(x)=0有三个实根
2、(福建卷)函数 f ( x) a x b的图象如图,其中a、 b 为常数,则下列结论正确的是
()
A.a 1,b 0 B.a 1, b 0
C.0 a 1,b 0 D.0 a 1, b 0
3、(湖北卷)函数y e|ln x| | x 1 |的图象大致是()
4、(福建卷)已知函数y=log 2x 的反函数是y=f -1 (x) ,则函数y= f -1 (1-x)的图象是()
5、已知 f ( x) 是偶函数,则 f ( x2) 的图像关于__________对称。
6、将函数y log 1 x 的图像沿x轴向右平移 1 个单位,得到图像C,图像 C1与 C关于原点
2
对称,图像C2与 C1关于直线 y=x 对称,求C2对应的函数。
7、试讨论方程 1 x kx 的实数根的个数。
8.( 1)方程lg x+x=3的解所在区间为()
A.(0,1) B.(1,2) C.(2,3) D .(3, +∞) ( 2)设 a 为常数,试讨论方程lg( x 1) lg( 3 x) lg( a x) 的实根的个数。
9.(上海,文、理8)在下列图象中,二次函数y=ax2+bx 与指数函数y=(b
)x的图象只可a
能是()。
