光学习题课
B8_光学习题课

x x r2 D
o
λ
S1 d S2 n, l
r1
r2 r1 = d sin θ x 或 r2 r1 = d D
(2) 插玻璃片 插玻璃片后条纹怎样移动? 插玻璃片后条纹怎样移动
A.向上 向上 B.向下 向
k 级条纹原位置
插玻璃片后光程差 k 级条纹新位置
Dλ x r2 r1 = d = kλ x = k D d
4 , 4 , 4 , 4 , 4 , , 4 4
λ
R
e
x
A e′ B
(2)明暗条纹距中轴线的距离 x 明暗条纹距中轴线的距离 两反射光的光程差
δ = 2e + λ
2
d0 e
λ
o R
明纹: 明纹: 由图 得
2
δ = kλ
2
x
A e′ B
′ ) 2 ≈ 2 Re′,e′ =d0 e) x = R (R e (
5. 如图白光照射,30°方向观察,肥皂膜呈黄色 如图白光照射 白光照射, °方向观察, (λ=5500),n = 1.32,观察反射光 , ,观察反射光 1 2 膜的最小厚度; 求:(1)膜的最小厚度 膜的最小厚度 i i (2)与法线成 °方向,膜的颜色;n′ 与法线成60° 与法线成 方向,膜的颜色; e n > n′ r (3)垂直照射,膜的颜色? 垂直照射, 垂直照射 膜的颜色? n′ 解:(1) 膜最小厚度: 膜最小厚度:
12
4nemin 得 λ= 2k 1
取 k =1
e
λ=6494 黄色
6. 如图,A---平玻璃片;B---平凹柱面透镜 如图, 平玻璃片; 平玻璃片 平凹柱面透镜 空气膜最大厚度为d 已知, 空气膜最大厚度为 0,λ , R已知, 已知 o 观察反射光 反射光干涉条纹 观察反射光干涉条纹 条纹形状及分布; 求:(1)条纹形状及分布; 条纹形状及分布 (2)明,暗纹的 x 值 明 条纹形状: 解:(1)条纹形状: 条纹形状 直条纹 如d0=(7/4)λ,画出明条纹 d0 λ 画出明条纹 分布:内稀外密(7条 分布:内稀外密 条) 对应的空气膜的厚度e分别 对应的空气膜的厚度 分别 明纹 自左至右) 为(自左至右 自左至右 λ 3λ 5λ 7λ 5λ 3λ λ
仪器分析习题课(光学分析部分)

(3)待测元素吸收线和试样中共存元素的吸收线重叠,可选择待测 元素的其它吸收灵敏线作分析线,若其它吸收灵敏线的测定灵敏度过低, 可采取分离干扰元素的方法解决。
C(Mg)=5.62 ng·mL-1
第六章:原子吸收分光光度分析
1.简述原子吸收分光光度分析的基本原理,并从原理上 比较发射光谱法和原子吸收分光光度法的区别?
答:原子吸收分光光度分析中,被测试样在原子化中经 雾化、蒸发、干燥、离解、原子化过程后,被测元素被转化 为基态原子,由锐线光源辐射的锐线为被测元素所吸收而减 弱,透过光线经单色器分光后而为检测器所接收,被测元素 的吸光度与试样中的浓度成正比,此既为原子吸收分光光度 分析的基本原理。
优点:分析速度快,灵敏度高,选择性好,检测限低, AAS较AES受原子化温度影响小,设备也较便宜,AES适合 于多元素同时分析。
2.何谓锐线光源,AAS为何使用锐线光源? 答:锐线光源是指能辐射出半宽度很窄的发射线的光源。 原子吸收光谱由于受谱线变宽的影响,谱线具有一定的 轮廓,而试样中被测元素的基态原子总数是与积分吸收成正 比的,但是由于原子吸收谱线的半宽度太小,其积分吸收是 不能直接测定的。但若使用锐线光源,由于其发射线宽度远 小于吸收线宽度,而两者的中心频率是重合的,而峰值吸收 与积分吸收成正比,因此,可利用测量峰值吸收来代替积分 吸收,此时峰值吸收与被测元素浓度成正比。
3.在原子吸收分光光度计中,为什么不采用连续光源(例如钨丝 灯或氘灯),而在分光光度计中则需要采用连续光源?
答:原子吸收光谱为线状光谱,其半宽度很小,仅10-2—10-3nm,如 要测量其积分吸收,则要求入射光的通带宽度应远小于原子吸收线的半 宽度,若采用连续光源,则要求单色器的分辨率很高,至少应在五十万分 之一,这在当前技术条件下难以作到。一般分光光度计的通带宽度均大 于0.1nm,若直接测量原子吸收,则由于其通带宽度远大于原子吸收线的 半宽度,由待测元素原子产生的吸收占通带内的入射光的比例很小(约 1%以内),导致测量的误差太大,因此原子吸收分光光度法中,不采用 连续光源,而采用空心阴极灯等锐线光源作光源,测量原子的峰值吸收。
大学物理重点知识习题课解答-光学

300
600
S .. .. . . .. .. ..
I0
P2
I21
解:
P1 P3P1
P1
入射光通过偏振片I和II后,透射光强为
I1
1 2
I0
cos2
600
插入偏振片III后,其透射光强为
I2
1 2
I0
cos2
300
cos
2
300
I2 2.25I1
27
选择题1. 等倾干涉光程差公式 2d
为了12满I足0 线I偏0 振co部s2分振, 动方4向5在0 出射后“转
过”900,
只要第一个偏振片偏振化方向与入射光中线偏振
光的光振动方向夹角为450,第二个偏振片的偏振
化方向与第一偏振片偏振化方向夹角为450就行.
E
所以,只要两个偏振片就行.
P1
450
P127
I0
.
450 .
E
I0
P1
450
将有关数据代入可得
1
o
d 5 /n2 n1 8.0m
d
4
3。在折射率n3=1.52的照相机镜头表面涂有一层折射率
n2=1.38的MgF2增透膜,若此膜仅适用于波长 =550nm的
光,则此膜的最小厚度为多少?
n1 1
解:因为 光相干相
n2 1.38 d
综合效应。其中明条纹的位置由光栅方程决定,但各 明纹的强度受单缝衍射效应的调制,透射光能量的大 部分将分布在原单缝衍射中央明纹范围(中央包线) 内的各明纹上。
23
17、光栅明纹位置由d sin k 决定。单缝衍射极
小位置由 b sin k决定,当 时 ,光栅明纹
哈尔滨工业学 光学习题课 4衍射光学.

9
2 A2 2
第二个半波带未被遮挡部分的复振幅:
2 A2 ~ U ' '2 exp[ i (1 / 4)] 2
结论:环形遮挡后复振幅的位相和振幅都发生了变化。
2)求如图(b)形式遮挡的衍射光强
(1)解题思路:将衍射波前分割成一个个半波带。求出每个半波带中未被遮挡
部分的振幅矢量 Ai ,求出总的振幅矢量以及总光强。
1 A' 2 A2 2
而未被遮挡部分的光程变化仍然是
/2
位相变化仍然是
第二个半波带未被遮挡部分的复振幅:
A2 ~ U '2 exp( i(1 )) 2
结论:扇形遮挡后,只改变复振幅中的振幅,不改变其位相。
(3)若遮挡是如图的环形遮挡 假设露出的仅仅是第二个半波带的 后半部分,则由于露出部分的前边 缘到后边缘的位相变化变为 /2 如图, A 的矢量方向相对 A 右旋 2 2 了450,振幅也变为: A' ' 2
相同点是主要的
不同点:
1)、干涉是几个离散相干点源发出的光波相遇时的相干迭加,衍射则是无数个 连续分布的次波点源发出的次波相遇时的相干迭加。
2)、求合光强的问题虽然都归结为先求出复振幅的和,然后取其共轭,但一 个是通过Σ 求和求得复振幅的和,一个是通过积分求得复振幅的和。
3)、离散相干点源是真实光源,其光线遵循几何光学传播规律,次波源是人 2 为假设的相干点源,其光线一般不服从几何光学耳衍射:光源和接收屏幕距离衍射屏幕有限远。 菲涅耳圆孔衍射: 自由传播时:
1 A( P0 ) [ A1 (1) ( n 1) An ] 2 1 A( P0 ) A1 ( P0 ) 2
光的干涉、衍射(习题课)

x
(二)、起偏和检偏
起偏:使自然光(或非偏振光)变成线偏振光的过程。 检偏:检查入射光的偏振性。
(三)、 马吕斯定律 如果入射线偏振光的光强为I1,透过检偏器后, 透射光的光强 I 为 I I cos 2
2 1
消光——透射光强 I 为零的情况
(四)、布儒斯特定律
入射角等于某一特定值i0且满足:
解(1)
xk D k级 明 纹 位 置 : xk k , 又 tan d D D 相邻两 条 纹 的间距: Δx λ d
相 邻 两 条 纹 的 角 间 距 : 同理:
x
D
d
x
D
d
而: (1 0.1)
( 1 0.1 ) 648.2 ( nm )
D
在恰能分辨时,两个点光源在透镜 前所张的角度,称为最小分辨角。
最小分辨角的倒数
(四)、光栅衍射
1
R
称为光学仪器的分辨率
1、光栅衍射是单缝衍射与多缝干涉的综合效应,即:它
是一种被单缝衍射调制的多缝干涉条纹。
2、屏幕上主极大位置由光栅公式决定
(a+b)sin =k
k=0,±1, ±2, ±3 · · ·
(2) 放入水中后, 钠黄光的波长变为
此 时 相 邻 两 条 纹 的 角 距 间变为: 1 0.20 o 0.15 nd d n n 1.33
n
1
o
2、 在空气中垂直入射的白光从肥皂膜 上反射(假定膜的厚度是均匀的) ,在可见光谱 中630nm处有一干涉极大,而在525nm处 有一干涉极小,在这极大与极小之间没有另 外的极大和极小。求这膜的厚度。 (肥皂水的折射率看作与水相同,为1.33。)
波动光学 光学习题课2(课后问题)

观察它是否移动,向哪个方向移动。(2)条纹间距是否
变化。
x 0 2n2
劈尖上表面向上平移,角不变,所以干涉条纹间距不变
(3)寻常光和非常光 一束光线进入各向异性的晶体后分解为两束折射光的现象 叫做双折射。遵循折射定律的叫做寻常光或o光不遵循折 射定律的叫做非常光或e光。寻常光在晶体内各方向上的 传播速度相同;而非常光的传播速度随传播方向的变化而 变化。
(4)光轴 在双折射晶体内有一确定方向,光沿这一方向传播时, 寻常光和非常光的传播速度(或折射率)相同,不产生 双折射现象,这个方向叫做光轴。
答:光照射到薄肥皂膜泡上,会发生反射和折射,各
条反射光或各条折射光互为相干光,又由于白光是复
色光,它含有各个波长的光,各条光线发生干涉,干
涉图样是彩色的,所以我们看到膜泡出现颜色。
当膜即将破裂时,膜的厚度约等于波长的1/4,即使发 生干涉的透射光的光程差为/2,发生干涉相消,所以 从透射方向看膜上出现黑色。当膜厚度远小于波长时, 反射光的光程差约等于/2,所以从反射方向看薄膜程 黑色。
但等厚度的位置向左移动,因此干涉条纹向左移动。如果
玻璃片向上移动太多,使劈尖厚度增大太多,则相干光的
条件得不到满足,干涉条纹消失。
劈尖上表面向右平移, 角不变,条纹间距不变,等厚度
位置向右移动,所以条纹向右移动。
当增大时,条纹间距减小;等厚度的位置向左移动,所 以干涉条纹向左方密集。
x 0 2n2
17-2、如本题图所示,由相干光源 S1和S2发出波长为 的单色光,分别通过两种介质(折射率分别为n1和 n2,且n1>n2),射到这两种介质分界面上一点P。已 知两光源到P的距离均为r。问这两条光的几何路程是
光学习题课(大学物理A2)

(三)光的偏振性 马吕斯定律
1.自然光和偏振光 包含了各个方向的光振动,没有哪一个方向的光 振动会占优势,这样的光叫自然光。 自然光经过某些物质的反射、折射或吸收后,可 能保留某一方向的光振动,称为线偏振光或者完全 偏振光。若一个方向光振动较与之相垂直方向上的 光振动占优势,则称为部分偏振光。
2.马吕斯定律 光强为 I 0 的线偏振光,当其偏振方向与检偏器 偏振化方向的夹角为 时,则透射过检偏器后的 透 I I 0 cos2 射光强为 该式称为马吕斯定律
8.折射率为1.60的两块标准平面玻璃板之间形成一个劈形膜 (劈尖角 很小)。用波长 600 nm 的单色光垂直入射,产 生等候干涉条纹。加入在劈形膜内充满 n 1.40 液体时的相邻 明纹间距比劈形膜内是空报时的间距缩小 l 0.5mm ,那么劈 尖角 应是多少?
【分析】利用劈尖干涉中相邻条纹的间距l 2n和题给出条件可求出 解 劈形膜内为空气时 劈形膜内为液体时 则由 得
光学习题课
干涉、衍射、偏振、双折射
一、内容小结
(一)光的干涉
1.相干光 (1)相干条件:同频率、同振动方向、相位差恒 定; (2)获得相干光方法:分波阵面、分振幅 2.光程与光程差 光程:=nr ;光程差:=n2r2-n1r1 3.半波损失 光从光疏介质向光密介质入射,反射光有的相位 突变,相当光程增加或减少/2,称半波损失。
4.杨氏双缝干涉 劳埃德镜 光程差:r =r2-r1dsin dsin=k, k=0,1,2…… 明条纹 dsin=(2k+1)/2, 暗条纹 条纹特点: 均匀明暗相间,白光照射为彩色条纹,但 中央条纹仍为白色。
r1
几何关系:D d
d
D
x r2
大学物理光学习题课

(1)子波,(2)子波干涉. 所缺级次为 k=k'(a+b)/a. 2.单缝衍射由半波带法得出 4.园孔衍射爱里斑的角半径: 中央明纹: =0.61/a=1.22/d 坐标 =0, x=0; 光学仪器的最小分辩角 宽度 02/(na), =0.61/a=1.22/d x2f/(na) 分辩率 R=1/=d/(1.22) 其他条纹: 5.x射线的衍射: 暗纹 asin=k/n 布喇格公式 2dsin=k 明纹 asin(2k+1)/(2n) (d为晶格常数,为掠射角) 条纹宽度/(na), 三光的偏振 xf/(na) 1.自然光,偏光,部分偏光; 3.光栅:单缝衍射与多光束干 偏振片,偏化方向,起偏, 涉乘积效果,明纹明亮,细锐. 检偏. 光栅方程式 2.马吕期定律 I=I0cos2. (a+b)sin=k 3.反射光与折射光的偏振 缺级 衍射角同时满足 一般:反射折射光为部分偏光 (a+b)sin=k 反射光垂直振动占优势; asin=k ' 折射光平行振动占优势.
n3
4. 在如图28.4所示的单缝夫琅和 费衍射实验装置中,s为单缝,L 为透镜,C为放在L的焦面处的屏 幕,当把单缝s沿垂直于透镜光轴 的方向稍微向上平移时,屏幕上 的衍射图样( C ) (A) 向上平移. (B) 向下平移. (C) 不动. (D) 条纹间距变大.
3. 如下图所示,平行单色光垂 直照射到薄膜上,经上下两表面 反射的两束光发生干涉,若薄膜 的厚度为e,并且n1<n2>n3,1 为入射光在折射率为n1 的媒质中 的波长,则两束反射光在相遇点 的位相差为( C ) (A) 2 n2 e / (n1 1 ). (B) 4 n1 e / (n2 1 ) +. (C) 4 n2 e / (n1 1 ) +. (D) 4 n2 e / (n1 1 ). n1 n2 λ e
几何光学习题课

f
n nL n n nL r r2 1
1 1.5 1 20 1 1.5 15
120
1 s
1 s
1 f
s 40
1
1 s
s s
1 40
1 120
3 2
s 60 虚像
60 40
2 s
代入上式得: u 23.5cm / s 符号说明向凹面镜顶点靠近 直接利用公式结果一样
u f
2 2
( a f )
u
1-11题,如图,证明:
pp (1
1 n
)d
i1
o
i2
p
Q
··
l
p′
l
i1′
sin( i1 i2 ) cos i2
d
证明:设两条 光线平移的距离为l ,由折射定律:
2 15
1 3
s 10
实像
2
10 30
第三面成像 (折射成像) (光线自右向左传播)
s 10
r 20
1 s 1.5 10 1 1.5 20
s 8
实像
3
ns ns
1.5 8 1 ( 10)
1.2
1 2 3
n 1
n 1.5
r 20
ns ns
1.5 s
1 40
1.5 1 20
s 30
虚像
1
30 1.5 40
1 2
第二面成像 (反射成像)
1 s 1 s 2 r
光学习题课——精选推荐

光学习题课光学习题课Ⅰ教学基本要求波动光学1.理解获得相⼲光的⽅法。
掌握光程的概念以及光程差和相位差的关系。
能分析、确定杨⽒双缝⼲涉条⽂及薄膜等厚⼲涉条纹的位置,了解麦克尔孙⼲涉仪的⼯作原理。
2.了解惠更斯—⾮涅⽿原理。
理解分析单缝夫琅⽲费衍射暗纹分布规律的⽅法。
会分析缝宽及波长对衍射条纹分布的影响。
3.理解光栅衍射公式。
会确定光栅衍射谱线的位置。
会分析光栅常量及波长对光栅衍射谱线分布的影响。
4.理解⾃然光和线偏振光。
理解布儒斯特定律及马吕斯定律。
了解双折射现象。
了解线偏振光的获得⽅法和检验⽅法。
Ⅱ内容提要⼀、光的⼲涉1.相⼲条件:与波的相⼲条件相同(略).2.光程=nl,光程差δ=n2l2-n1l1;理想透镜不产⽣附加光程差;半波损失:光从疏媒质向密媒质⼊射时,在反射光中产⽣半波损失;折射光不产⽣半波损失;半波损失实质是位相突变π.3.明纹、暗纹的条件:明纹δ=±2kλ/2,k=0,1,2,…;暗纹δ=±(2k-1)λ/2,k=0,1,2,….4.分波阵⾯法(以杨⽒双缝⼲涉为代表):光程差δ=nxd/D明纹坐标x=±2k(D/d)λ/(2n)暗纹坐标x=±(2k-1)(D/d)λ/(2n)条纹宽度?x=(D/d)(λ/n)5.分振幅法(薄膜⼲涉,以n1n3为例)(1)光程差:反射光δr=2n2e cos r+λ/2=2e(n22-n12sin2i)1/2+λ/2透射光δt=2n2e cos r=2e(n22-n32sin2r’)1/2(2)等厚⼲涉(光垂直⼊射,观察反射光):相邻条纹(或⼀个整条纹)所对应薄膜厚度差?e=λ/(2n)劈尖⼲涉条纹宽度?l=λ/(2nθ)⽜顿环的条纹半径明纹r=[(k-1/2)Rλ/n]1/2(k=1,2,3,…)暗纹r=(kRλ/n)1/2(k=0,1,2,3,…)(3)等倾⼲涉(略).(4)迈克⽿逊⼲涉仪:M1与M'2平⾏为等倾条纹,此时如动镜移动λ/2,则中⼼涨出或陷⼊⼀个条纹;M1与M'2不严格平⾏为等厚条纹,此时如动镜移动λ/2,则条纹平⾏移动⼀个条纹的距离.⼆、光的衍射1.惠更斯—费涅⽿原理(1)⼦波(2)⼦波⼲涉.2.单缝衍射半波带法中央明纹:坐标θ=0,x=0;宽度?θ 0≈2λ/a,?x≈2λf/a其他条纹:暗纹⾓坐标θ满⾜a sinθ=±kλ明纹⾓坐标θ近似满⾜a sinθ≈±(2k+1)λ条纹宽度?θ≈λ/a?x≈λf/a3.光栅(多光束⼲涉受单缝衍射调制)明纹明亮、细锐光栅⽅程式(a+b)sinθ=±kλ缺级衍射⾓θ同时满⾜(a+b)sinθ=±kλa sinθ=±k'λ时,出现缺级,所缺级次为k=k' (a+b)/a.4.圆孔衍射爱⾥斑⾓半径θ=0.61λ/a=1.22λ/d光学仪器的最⼩分辩⾓δθ=0.61λ/a=1.22λ/d5.x射线的衍射布喇格公式2d sinθ=kλ三、光的偏振1.⾃然光、偏振光、部分偏振光;偏振⽚,偏振化⽅向,起偏、检偏.2.马吕期定律I=I0cos2α.3.反射光与折射光的偏振⼀般情况:反射光为垂直⼊射⾯振动⼤于平⾏⼊射⾯振动部分偏振光,折射光为垂直⼊射⾯振动⼩于平⾏⼊射⾯振动部分偏振光.布儒斯特定律:当⼊射⾓满⾜tg i0=n2/n1,即反射光与折射光相互垂直时,反射光为垂直⼊射⾯振动的完全偏振光,折射光仍为部分偏振光.4、双折射:寻常光线(o光)满⾜普通折射定律,为垂直⾃⼰主平⾯的偏振光;⾮常光线(e光)不满⾜普通的折射定律,为平⾏⾃⼰主平⾯的偏振光.双折射晶体的光轴,主截⾯、主平⾯.5、旋光现象:偏振⾯旋转的⾓度旋光溶液中?θ=αCl旋光晶体中?θ=αl(α为旋光系数,C为浓度).Ⅲ。
大学物理-游璞-于国萍-光学-课后习题-答案

第一章 习题
1.2 解:从图中可以看出: i2=i1+q
激光器
i2+q=i1+a
∴a=2q
又
tana = 5
50
a=5.71o ∴ q=2.86o
i2 q
q
i1 i1
i2
O
a
50cm
A 5cm
B
用途:平面镜微小的角度改变,转化为屏幕上可测量的长度改 变。力学中钢丝杨氏模量的测量、液体表面张力的测量等。
)2
=
( n1 n1
− +
n2 n2
)2
=
0.04
Rp
=
rp 2
=
( n1 cos i1 n1 cos i1
− n2 + n2
cos i2 cos i2
)2
=
( n2 n2
− n1 )2 + n1
=
0.03
3.4 解:(1)不加树脂胶时,两个透镜之间有空气,所以当自然光正入射
时,在第一个透镜与空气的分界面I上,
R2 + f 2 = nz + x2 + y2 + ( f − z)2 (n2 −1)z2 − z(n R2 + f 2 − f )z − (x2 + y2 ) = −R2
1.11 证明 n' − n = n' − n p' p r
1 +1 =2 p' p r
f = f= r 2
1.13 解:
f '=
Ey
=
A cos[ (t
−
z) c
几何光学习题课
射率 和
nL
=
1.52,
.曲率半r径1分0别.4为59m
r2 0.236m
求 它在水中的焦距. (水的折射率 n1.33)
r1
r2
解 透镜焦距
f f
(nL
1 1)(1 1)
n
r1 r2
ff(1.5 21) (1 1
1
m 3.4m 0 )
1.33 0.450 9 .236
例 如图所示用放大镜观察一个微小的物体,
透镜的焦距 f = 0.0849 m , 物体置于离透镜
0.0760 m 处,
求透镜的横向放大率.
F
P’ F
p
f
解 薄透镜成像公式
1 1 1 p p f
横向放大率
V p 9.54
1 11 1.38m1 p p f
p
p0.72m 5
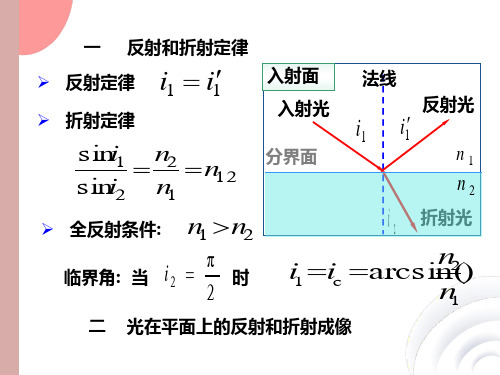
一 反射和折射定律
➢ 反射定律 i1 i1
➢ 折射定律
s ini1 s ini2
n2 n1
n1 2
入射面 入射光
分界面
法线
反射光
i1 i1
n1 n2
➢ 全反射条件: n1 n2
i 2 折射光
临界角: 当Biblioteka i2π 2时
i1
ic
arcs inn2() n1
二 光在平面上的反射和折射成像
三 光在球面上的反射和折射成像
➢
球面折射成像公式 (近轴光线)
n n nn p p r
➢ 横向放大率 Vhi ho
V n p V 0 像正立 V
n p
0 像倒立
f f 1 p p
1 放大 1 缩小
➢ 球面特殊 光线作图法
2023年大学_《光学》(赵凯华钟锡华著)课后习题答案下载

2023年《光学》(赵凯华钟锡华著)课后习题答案
下载
《光学》(赵凯华钟锡华著)内容简介
绪论
第一章几何光学
第二章波动光学基本原理
第三章干涉装置光场的时空相干性
第四章衍射光栅
第五章傅里叶变换光学
第六章全息照相
第七章光在晶体中的传播
第八章光的吸收、色散和散射
第九章光的量子性激光
《光学》(赵凯华钟锡华著)目录
《光学(上下)》分上、下两册。
上册主要内容:几何光学、波动光学基本原理、干涉装置和光场的`时空相干性。
下册主要内容:衍射光栅、傅里叶变换光学、全息照相、光在晶体中的传播、光的吸收、色散和散射、光的量子性和激光。
光学光干涉习题

习题课-光的干涉
例1 在杨氏双缝实验中,双缝间距d=0.20mm,缝屏间距D=1.0m,
试求:(1) 若第二级明条纹离屏中心的距离为6.0mm,计算此单
色光的波长; (2)相邻两明条纹间的距离.
解: 其任意点P的光程差为:
y
r2 r1 k
由几何关系:r2
r1
d
y D
由明纹干涉条件可得:
2ne
2
k
(2k
1)
明纹
暗纹
2
其中:e r 2 / 2R
对明纹来说:
当n=1时,
38R (1.40102 )2
r2 (2k 1)R / 2n
当n=?时,
38R / n (1.27102 )2
即第10级亮环直径为
d120 38R / n
n 1.402 /1.272 1.22
习题课-光的干涉
s1
d
s2
r1
P
r2
O
D
(1)明条纹离屏中心的距离y k D
d
(2)相邻明条纹间距离 y D
d
yd kD
600.0nm
y 3.0mm
习题课-光的干涉
例2 在双缝装置中,用一很薄的云母片(n=1.58)覆盖其中的一条 缝,结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明 纹的位置.若入射光的波长为550.0nm,求此云母片的厚度.
则用1时第3条暗环的半径为:
r kR1 1.85mm
e r2 / 2R
R
re
2e
2
k
(2k
1)
明纹
暗纹
2
习题课-光的干涉
例7 当牛顿环状之中的透镜与玻璃之间的空间充以液体时,第 10级亮环的直径由d1=1.40×10-2m变为d2=1.27×10-2m ,求液体 的折射率。
光学习题课1

几何光学习题课1基本知识在经典物理的范畴内,光是电磁播,其传播规律由麦克斯韦方程组来描述,但由于光的波长很短,在研究的问题中涉及到的尺度远大于光波波长时,光的波动性可以忽略,用光线来取代波线,由此建立起来的光传播理论就是所谓的几何光学。
几何光学在方法上是几何的,在物理上不涉及光的本质。
1. 折射率 几何光学的三个定律 全反射 折射率的定义:vc n =,c 是光在真空中的速度,v 是光在该种媒质中的传播速度;相对折射率的定义:1212n n n =。
光的直线传播定律:在均匀媒质中光沿直线传播。
光的反射和折射定律:(1)反射线和折射线都在入射面内,并分居在法线的两侧;(2)反射角等于入射角;(3)折射角与入射角的正弦比与入射角无关,是一个与媒质和光的波长有关的常数(相对折射率)。
(斯涅耳定律)全反射:当光线从光密媒质(2n )射向光疏媒质(21n n <)时,当入射角等于或大于某一角度时(临界角121/sin n n i C -=),折射光线消失,光线全部反射的现象。
2.棱镜与色散 偏向角:'11i i +=δ,1i :入射角,'1i :出射角;最小偏向角产生的充要条件:'11i i =或'22i i =作用:用来测透明介质的折射率:)2sin(/)2sin(minαδα+=n 。
色散产生的原因:介质的折射率n 是光束波长的函数,)(λn n =棱镜可以用做光谱仪,进行光谱分离。
3.光程 费马原理 光程:⎰=PQndlQP)(,光程可以理解为在相同的时间内光线在真空中传播的距离。
注意,光程是一个非常重要的一个概念,在后面的课程中研究光的干涉、衍射、位相延迟时要经常用到。
费马原理:QP 两点间光线的实际路径是光程)(QP为平稳的路径。
数学表达式为:0=⎰PQndl δ注意:费马原理的实质是揭示光线在媒质中沿什么路径传播。
4.光的可逆性原理当光线的方向反转时,光线将沿着同一路径传播。
工程光学-5-习题课-1

5-2
一个焦距为100mm的透镜与一个在其后方相隔20mm的光孔组成的系统对无限远物体成像。
设透镜的口径为15mm,光孔的口径为10mm。
(1)分别计算系统的入瞳和出瞳的位置和大小?
(2)分别计算光线从左到右与从右到左入射时的系统相对孔径?
解 (2)光线从左到右入射时,
光孔的共轭像是入瞳,故有相对孔径
眼通过放大镜所看到的最大物面范围。
解 (1)求系统的孔径光阑、入瞳和出瞳 放大镜的共轭像就是其本身,
求瞳孔的物空间共轭像,将系统翻转180, 经透镜成像
1 1 1 l ' 10 25
l ' 16.67mm
D1 D2
D2'
l ' 16.67 1.667
l 10
D2 ' D2 3.334mm
解 (2)解析法 A
F1
L1
L2
F2
L2' F1' F2'
透镜L1的共轭像就是其本身;求透镜L2的物空间共轭像,将系统翻转180,经透镜成像
1 1 1 l ' 50 100
l ' 100mm
从物点A作L1和L2'的边缘光线,
l ' 100 2
l 50
D2=1)及系统有一半渐晕(K=0.5)时的视场角各为多少?
解 (1)作经过透镜和圆孔边缘的光线,并延伸与光轴相交 D1
D2
l 50 15 l 20
l 200mm
可得,当物体处于无穷远至-200mm范围内,光孔是孔径光阑;当物体 处于-200mm至0范围内,透镜是孔径光阑。
-l
(2)物体在无穷远,系统无渐晕,对应光路如右图,有
光学部分课后习题

q1'=asin(n/2/n)=30 度 所以光线FG平行于AB,垂直于CD
C
q3=45 度 所以GH垂直于AB q2‘=30 度 所以q2=asin(n/2) 又因为AC垂直于AE 所以入射光与出射光垂直。
G q3 q1' D E q2‘ B
F q1 A
H
q2
3.8. 某观察者通过一块薄玻璃板去看凸面镜中他自己的 像.他移动着玻璃板,使得在玻璃板中与在凸面镜中所 看到的他眼睛的像重合在一起,若凸面镜的焦距为 10cm ,眼睛距凸面镜顶点的距离为40cm,问玻璃板观察 者眼睛的距离为多少? 高斯公式: 1/s'+1/s=1/f' 假设人眼在左,凸面镜在右,玻璃板居中。 对于凸面镜,f'=10 cm, s=-40 cm 可得 s'= 8 cm 因此玻璃板的位置是 (s+s')/2 = - 16 cm 距离眼睛为-16+40 = 24 cm
4.10.有一光阑直径为5cm,放置在薄透镜后3cm 处。透镜的焦距为5cm,孔径为6cm。现有一高 为3cm的物PQ置于透镜前12cm处。要求:⑴计 算对主轴上P点的入射光瞳和出射光瞳的大小和 位置; ⑵找到象的位置; ⑶作光路图。
光学习题课

光学习题课
光学小结
一、光的干涉
Ⅰ 基本概念
1 光的相干条件:
振动频率相同 振动方向相同
位相相同或位相差恒定
只能利用同一原子的同一波列
2、相干光的获得:
把由光源上同一点发出的光设法分成两部分,再迭
加起来。
分波阵面法
分振幅法
2020/3/2
2
长江大学物理教程
3、光程与光程差
相邻明纹的间距:
x xk1 xk D / d
2020/3/2
19
长江大学物理教程
3.已知:S2 缝上覆盖的介质
厚度为 h ,折射率为 n ,设 入射光的波长为.
S1
r1
问:原来的零级条纹移至何处?S2
r2
若移至原来的第 k 级明条纹处, h
其厚度 h 为多少?
原来 k 级明条纹位置满足:
s
(o') (R2' r2' ) (R1' r1' ) 0
R1' s1
R1 R2
R2'
s2
r1 r2
X
o
r1'
r2'
o'
R2' R1'
r2' r1'
(o) (R1' r1) (R2' nt t r2 )
零级明纹下移,则整个条纹下移. (R1' R2' ) (r1 r2 ) (n 1)t 0
解:从S1和S2发出的相干 光所对应的光程差
r2 r1 k
设有介质时零级明条纹移到原
(r2 h nh) r1 来第 k 级处,它必须同时满足:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
暗条纹条件: a sin k k 1, 2, 3,
七、小孔衍射
1. 爱里斑的半角宽度 1.22
D
2. 光学仪器最小分辨角
min
1.22
D
八、光栅衍射
1. 平行光照射光栅时,在黑暗背景上呈现出窄细 明亮的谱线。
2. 光栅方程: (1) 垂直入射时,有:
(a b)sin k,
折射率为 n1 和 n2 的透明介质膜覆盖(n1 ﹥ n2), 波长λ的平行光斜入射到双缝上,入射角为θ,双缝
间距为 d,在屏幕中央 O 处 S1O S2O ?
解:加介质片后 O 点的光程差
d sin (n1 n2 )e
2
S1 n1
d
n2
O
2
十、五种偏振状态:
自然光、线偏振光、部份偏振光、圆偏振光、 椭圆偏振光
十一、马吕斯定律
I2 I1 cos 2
强度为I0 的自然光入射于理想偏振片产
生线偏振光的强度为:
1
I1 2 I0
十二、布儒斯特定律 十三、双折射现象
tgi0
n2 n1
n21
O光 e光
一、填空题
1. 如图所示,双缝干涉实验中用两个厚度均为 e,
屏幕上第一级光谱的宽度。
解:由光栅方程: d sin
[d
sin
(n1
n2
)e]
S2 e
若 n1 n2 则也可写成: d sin (n2 n1 )e
2. 在双缝干涉实验中,所用光的波长 5.461104 mm
双缝与屏的距离为 D = 300 mm 双缝间距 d = 0.134
mm,则中央明纹两侧的两个第三级明纹之间的距离
产生的干涉条纹相邻两明纹的角距离(相邻两明纹对双 缝中心处的张角)为 0.20 度。(1) 对什么波长光,此装 置所得相邻两明纹角距离比钠光大10%。(2) 假如浸入 水中(n = 1.33),相邻两明纹角距离为多大?
解:(1)
x D
nd
角距离: x
D nd
2 2 / nd 0.22 1 1 / nd 0.2
装置,若将一折射率为 n 劈尖角为 A 的透明劈尖插入
光线 2 中,则当劈尖缓慢地向上移动时(只遮住 S2), 屏上的干涉条纹:
A. 间隔变大,向下移动
S1
C
B. 间隔变小,向上移动
C. 间隔不变,向下移动
1
d
O
2
D. 间隔不变,向上移动
S2
9. 在迈克尔逊干涉仪的一支光路中,放入一片折射率
为 n 的透明介质薄膜后,测出两束光的光程差的改变
D
2
暗纹位置:
x
D
(2k 1)
nd
2
k = 0,1,2,...
四. 薄膜干涉
1. 等厚干涉:同一级干涉条纹对应的薄膜厚度相等。 等厚条纹的形态与薄膜等厚线的走向一致。
2. 劈尖干涉:等间距直干涉条纹。
中心位置: l
明条纹:
2ne
2n sin
k 暗条纹:
2
2ne
2 1.11 6482.3 A
(2) 假如浸入水中,则有:
1 0.2 0.15
nd n 1.33
3. 折射率为 1.60 的两块标准玻璃板之间形成一个劈尖( 很小), = 600 nm(1nm = 10-9 m) ,产生等厚干涉条
纹,在劈尖内充满 n=1.40 的液体时相邻明纹间距比劈
面反射的两束光发生干涉,若薄膜厚度为 e,并且
n1< n2 > n3,1 为入射光在折射率为 n1 的媒质的波长,
则两束光在相遇点的相位差为______。
A.
B. C. D.
2n2e /(n11 )
4n1e /(n21 ) 4n2e /(n11 ) 4n2e /(n11 )
k 0, 1, 2,
(2) 斜入射时,有:
(a b)(sin sin ) k, k 0, 1, 2,
3. 谱线强度受单缝衍射的调制,出现缺级时满足:
ab
k
k'
a
ab
4. 最高级次满足:
kmax
九、X射线的衍射: 2d sin k, k 1, 2, 3,
2
(2n2e 2
4n2e n11
)
n1 n2 e n3
5. 一束光是自然光和线偏振光的混和,让它垂直通过
一偏振片。若以此入射光束为轴旋转偏振片,测得透
射光强最大值是最小值的 5 倍,那么入射光中自然光
与线偏振光的比值是__. A. 1/2 B. 1/5 C. 1/3 D. 2/3
尖内是空气时的间距小 △l = 0.5mm ,求 = ?
解:由题意知:
l e e sin 2n
因而:
l
l0
l
2
2n
(1 1 ) 2 n
(1 1 )
2l n
600 109
1
2
0.5 103
(1
)rad 1.40
( I0 I)/ I0 5
2
2
I0 1 I 2
6. 一束波长为 的单色光由空气入射到折射率为 n 的
透明介质上,要使反射光得到干涉加强,则膜的最小厚
度为:
( A) / 4
(B) /(4n)
2ne k
2
1 23
(C ) / 2 (D) /(2n) k 0, e e n
量为一个波长λ,则薄膜C. / n D. /[2(n 1)] 2ne 2e 2(n 1)e
三、计算题
1. 在双缝干涉实验中,波长 = 5500A°的单色平行光
垂直照射到缝间距为 a = 2×10-4 m 的双缝上,屏到双
( 2k
1)
2
亮 暗
k4
2n2e
9 2
e 9
4n2
n1 n2
n3
4. 光强均为 I0 的两束相干光发生干涉时在相遇的区
域可能出现的最大光强是 4 I0 。
I A2 (2 A0 )2 4 A02 4I0
5. 迈克耳逊干涉仪的可动反射镜 M 移动了 0.620mm 的过程,观察到条纹移动了 2300 条,则所用光的波
2
(2k
1)
2
3. 牛顿环:
明环半径: rk
(2k 1)R
2n
kR 暗环半径: rk n
4. 等倾干涉:薄膜厚度均匀。同一级条纹对应入 射线倾角相同。同心圆环状干涉条纹。
五、迈克尔逊干涉仪: 六、单缝衍射
nd N 2
半波带法 明条纹条件:
a sin (2k 1)
明介质中,从 A 沿某一路径传播到 B 点,路径的长度
为 l 。A,B 两点的光振动相位差记为 △ 。 则:
A. l 3 / 2, 3
1. 若l 3 ,则
2
B. l 3 / 2n, 3n
C. l 3 / 2n, 3
D. l 3n / 2, 3n
A. 向上平移动。 B. 向下平移动。
C. 不动。
D. 条纹间距变大。
2. 单缝的夫琅和费衍射实验中,若减小缝宽,其他条
件不变则中央明纹
A. 宽度变小。
B. 宽度变大 。
C. 宽度不变,且中心强度不变。
D. 宽度不变,但中心强度变小。
中央明纹宽度
f
x1 2 a
3. 真空中波长为 的单色光,在折射率为 n 的均匀透
11. 一自然光通过两个偏振片,若两片的偏振化方向 间夹角由 A 转到 B,则转前和转后透射光强之比为
_c_o_s_2_A_/_c_o_s_2_B_。
I0 2
cos 2
A/
I0 2
cos 2
B
cos 2 cos 2
A B
二、选择题
1. 如图所示的单缝的夫琅和费衍射实验中,把单缝 垂直透镜光轴稍微向上平移时,屏上的衍射图样将
nl 3n ,
2
2 3n
2. 若l 3 , 则 nl 3 , 2 2 3 3
2n
2
2
3. 若l 3n ,
则
nl
3n2 ,
2
2
3n2
3n2
2
2
2
4. 如图所示平行单色光垂直照射到薄膜上,经上下表
缝的距离 D = 2m。求:(1) 中央明纹两侧两条 10 级明
纹中心的距离; (2) 以厚度为 e = 6.6×10-5 m,折射率
为 n = 1.58 的玻璃片覆盖后,零级明纹将移到原来的第
几故解级::的x1位(01)置双x。缝10 干 涉2 的120明4纹条20件 550x0k 10nDd10k0.11m
1 3
5
2 4
13
2
2
2
P
f
8. 在单缝的夫琅和费衍射实验中,波长为 的单色光
垂直入射到缝宽为 a = 的单缝上,对应于衍射角为
30 度方向,单缝处的波面可分成的半波带的数目为
_1_个_。 a sin sin30
