减速路障间距设计 ;经典数学建模题目分析

合集下载

减速带间距设定(建模优秀论文)

2012工程数学建模选拔赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：本科组B题我们的参赛报名号为（如果赛区设置报名号的话）：gc12003所属学校（请填写完整的全名）：湖北工业大学工程技术学院参赛队员(打印并签名) ：1. 10机制五班26 冯白桦2. 10机制八班08 曹艺3. 10机制八班34 徐淼指导教师或指导教师组负责人(打印并签名)：日期： 2012年 05 月 27 日2012工程数学建模选拔赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国评阅编号（由全国组委会评阅前进行编号）：道路减速器摘要经过分析我们建立了模型，模型一我们考虑了汽车通过减速带时上下振动的时间与通过减速带的速度的关系，得出最小临界速度min ν的公式：228a b r a =+；min ν=MATLAB 作图求出上下振动时间和速度的最优组合。

模型二我们考虑了在设置减速带前后，单位时间内某段路程通过的车辆数的变化情况，并建立两者的函数关系，以此来衡量减速带所起的效果。

最终通过作图比较得出最优解模型二我们引进了车密度的概念，考虑了在设置减速带前后，减速带间公路段的车密度，并建立两者的函数关系，以此来衡量减速带所起的效果。

最终通过作图与分析得出最优解。

模型三我们考虑对时间的优化，建立了减速带间距离与车辆经过减速区域时间的函数关系，并继续用减速系数为η来衡量减速效果。

《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛B题是一道涉及复杂系统建模与优化的题目，要求参赛者针对实际问题进行数学建模、求解及分析。

本文将详细介绍该题目的背景、意义、解题思路及总结，以期为其他参赛者提供参考。

二、题目背景与意义本题以城市交通拥堵问题为背景，要求参赛者建立数学模型，对城市交通流量进行预测及优化。

该问题具有较高的现实意义，因为随着城市化进程的加速，交通拥堵已成为各大城市面临的重要问题。

通过数学建模，我们可以更好地理解交通拥堵的成因，为解决交通拥堵问题提供理论依据。

三、解题思路1. 问题分析首先，我们需要对题目进行深入分析，明确问题的背景、目标及约束条件。

本题主要涉及城市交通流量的预测及优化，需要考虑到交通网络的复杂性、交通流量的时变性、道路资源的有限性等因素。

2. 数学建模根据问题分析，我们可以建立相应的数学模型。

本题中，我们采用交通流理论及运筹学原理，建立了一个多因素影响的城市交通流量预测模型。

模型中考虑了道路类型、交通状况、天气等因素对交通流量的影响。

同时，为了优化交通流量，我们还建立了一个基于遗传算法的交通信号灯配时优化模型。

3. 模型求解在建立数学模型后，我们需要进行模型求解。

本题中，我们采用MATLAB软件进行模型求解。

首先，我们利用历史数据对预测模型进行训练，得到各因素对交通流量的影响程度。

然后，我们根据实时交通数据及天气数据，利用预测模型对未来一段时间内的交通流量进行预测。

最后，我们利用遗传算法对交通信号灯配时进行优化，以达到缓解交通拥堵的目的。

四、解题方法与技巧在解题过程中，我们需要掌握一些方法和技巧。

首先，我们要对题目进行深入分析，明确问题的本质及需求。

其次，我们要建立合理的数学模型，考虑到各种因素的影响。

在求解过程中，我们需要选择合适的算法及软件工具，以提高求解效率及准确性。

此外，我们还需要注重模型的验证与优化，确保模型的可靠性和实用性。

数学建模减速带

四、
4.1 减速带类型的选取
建模准备
汽车减速带是为保障行人安全设置的一种交通设施，在遏制交通事故的发生中发挥了重要的作用。目前减速带的类型有道钉减速带、圆弧式（驼峰式）减速带、水泥台减速带、热塑振动减速带、路面凹槽减速带、沥青混合料减速带、防滑减速带、卵石减速带等，不同减速带的使用条件不同[2]。由新疆博乐市辖区对四台大坡的交通安全的评价得到：在所有限速控制设施中， 87% [3] 的驾驶员认为驼峰式减速带的减速效果最好。驼峰式减速带是为了适应严峻的道路交通安全形势而产生的，其应用的基本原理是在道路上设置凸起设施，当车辆经过时会产生碰撞和颠簸，使得驾驶员和车上的人产生不舒服的感觉，通过这种方式迫使驾驶员放慢速度，达到道路限速的目的。国内驼峰式减速带主要有：水泥台减速带和橡胶减速带，水泥台减速带是在道路表面用水泥浇筑的凸出地面 20cm ~ 40cm 的圆拱。由于水泥台的刚性太强，对车辆造成的顺坏大而且安装和拆卸时易对地面造成损坏，所以大多数情况下，都是以橡胶减速带为主。橡胶减速带由橡胶、添加物经模板压制而成，表面具有花纹或凸点，颜色一般为黑黄相间，高 8cm ~ 15cm ，通行长度为 30cm ~ 90cm ，纵切面为圆弧状。根据长安大学的研究表明，橡胶减速带的减速效果要优于水泥台减速带[4]，因此针对此题，本文只对橡胶驼峰式减速带进行研究。 4.2 减速带横断面轮廓形状的选取目前具体的减速带横断面轮廓曲线并没有统一的标准，较常见的道路减速带的横断 [5] 面轮廓有梯形、圆弧形和抛物线形等，如图 1 所示。
图 3 圆弧形减速带与汽车轮胎接触状态的几何模型
其中， r 为减速带圆弧半径， R 为汽车轮胎外胎半径， h 为圆弧减速带横截面的高度，b 为圆弧形减速带横截面的宽度， c 的计算式为 c r h 。由图 3 减速带与汽车轮胎接触状态的几何分析可知： b ( r h) 2 ( ) 2 r 2 2 化简后得

初等方法建模4交通事故调查--数学建模案例分析

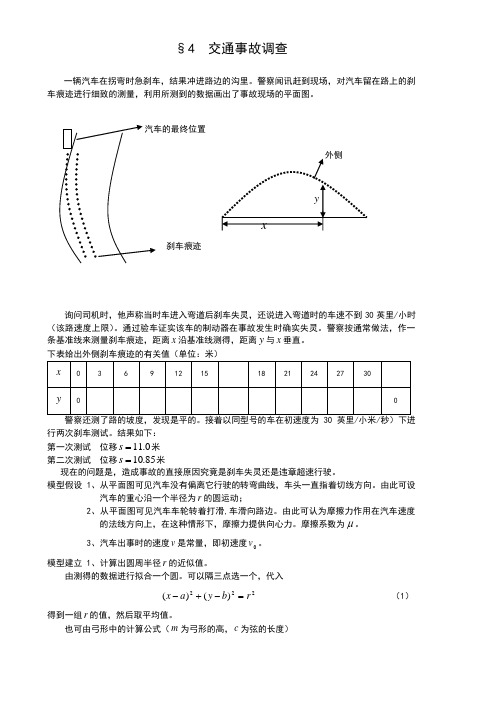
§4 交通事故调查一辆汽车在拐弯时急刹车，结果冲进路边的沟里。

警察闻讯赶到现场，对汽车留在路上的刹车痕迹进行细致的测量，利用所测到的数据画出了事故现场的平面图。

询问司机时，他声称当时车进入弯道后刹车失灵，还说进入弯道时的车速不到30英里/小时（该路速度上限）。

通过验车证实该车的制动器在事故发生时确实失灵。

警察按通常做法，作一条基准线来测量刹车痕迹，距离x 沿基准线测得，距离y 与x 垂直。

警察还测了路的坡度，发现是平的。

接着以同型号的车在初速度为30英里/小米/秒）下进行两次刹车测试。

结果如下：第一次测试位移0.11=s 米第二次测试位移85.10=s 米现在的问题是，造成事故的直接原因究竟是刹车失灵还是违章超速行驶。

模型假设 1、从平面图可见汽车没有偏离它行驶的转弯曲线，车头一直指着切线方向。

由此可设汽车的重心沿一个半径为r 的圆运动；2、从平面图可见汽车车轮转着打滑,车滑向路边。

由此可认为摩擦力作用在汽车速度的法线方向上，在这种情形下，摩擦力提供向心力。

摩擦系数为μ。

3、汽车出事时的速度v 是常量，即初速度0v 。

模型建立 1、计算出圆周半径r 的近似值。

由测得的数据进行拟合一个圆。

可以隔三点选一个，代入222)()(r b y a x =-+- （1）得到一组r 的值，然后取平均值。

也可由弓形中的计算公式（m 为弓形的高，c 为弦的长度）刹车痕迹222)2()(c m r r +-= （2）得到r 的近似值。

2、计算地面的刹车系数a （减速度a ）由 as v v 2202-=及0=v ，得sv s v v a 2220220=-= （3）3、导出计算初速度0v 的公式由假设2，rv m mg 20=μ，即 μrg v =20，又由牛顿第二定律mg ma μ=有 g a μ= 从而a r v =20 （4）模型求解 1、通过表中数据拟合，得到r 的以下各值 , ,取平均值就得到67.40=r 米或将55.3,27.33==m c 代入（2），得到75.40=r 米。

减速路障间距设计;数学建模题目分析

减速路障间距设计;数学建模题目分析文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]组号：702 田宇；孙蕙雯；樊博校园减速路障间距设计摘要：减速路障的间距设计合理对于减速带作用的发挥具有重要的意义。

本文利用查阅的相关资料，采用Lingo回归分析和最小二乘法，对汽车的加速时加速度和加速时的加速度进行了参数估计。

根据题意进行数学建模，建立了汽车在一条具有多个减速带的公路上加速后减速匀速通过减速带的一维直线运动的模型。

通过牛顿运动学公式进行了模型求解，最后得出了相邻减速带间的最佳距离。

关键词：减速带间距；一维直线运动模型；最小二乘法一、问题的提出问题的背景校园、居民小区的道路中间，常常设置用于限制汽车速度的减速带（路障）。

减速带使路面稍微拱起以达到车辆减速目的，设置在需要车辆减速慢行的路段和容易引发交通事故的路段，是用于减速机动车、非机动车行使速度的新型交通专用安全设置。

减速带很大程度减少了各交通要道口的事故发生，是交通安全的新型专用设施。

汽车在行驶中既安全又起到缓冲减速目的，提高交通道口的安全。

随着校园车辆的逐渐增多，在校园中合理的设置减速带又成为一个很重要的实际问题。

减速带的使用效果在很大程度上取决于车辆的运行速度和减速带的放置间距间距。

因此，为确保限速安全和驾驶人的舒适，合理设定道路的限速具有很重要的意义。

问题重述校园道路需要设置路障以限制车速，如果车速不超过40km/h，应该相距多远二、问题的分析模型预备知识道路减速带的减速原理：道路减速带的减速是通过影响驾驶员的驾驶心理实现的。

当车辆以较高速度进入道路减速带时,剧烈的振动会从轮胎经车身及座椅传递给驾驶员,使驾驶员产生强烈的生理刺激(包括振动刺激和视觉刺激)和心理刺激,从而促使驾驶员主动减速,使车辆以较低的速度通过道路减速带。

2.2问题的分析1、汽车通过减速带时速度近于零，过减速带后加速。

2、车速达到40km/h时因为前面有下一个减速带而减速，至减速带处车速又近于零。

道路减速带减速模型分析

道路减速带减速模型分析摘要：摘要减速带作为一种强化型的道路安全交通设施，在遏制交通事故的发生中发挥了重要的作用，它是在行车道上设置的某种突起设施，当汽车以较高车速通过时会产生激烈的机械振动，这种振动从轮胎输入经由车身及座椅传递给汽车驾驶员，使其产生不舒服的感觉，从而提示并促使车辆驾驶员自觉、主动地降低车速，但不合理的设置，则会使其成为路障，给行人和车辆带来不便，甚至产生安全隐患。

问题一中，减速带应既能起到强制控速的作用,也要使振动对车辆的破坏度及对乘客的舒适度影响适中。

视轮胎为刚体建立车辆与减速带碰撞数学模型,对车辆通过减速带产生的振动进行分析，得出车辆驾驶员通过减速带时的期望速度。

利用MATLAB 软件对所建立的模型进行仿真,最终获得效果较好的减速带数学模型：g x b r r r r v a y ≤--++-=2/3212212212])2()[()(，由此求的司机的期望速度v 。

问题二，在第一问模型的基础上，我们建立了车辆通过整个区域的运动学模型，设置合理的参数，计算出车辆在该区域内达到的最大速度，及所用总时间。

并通过该模型，建立三道减速带设置的最优化模型，从中求得最优解为。

最后根据现实中存在的问题结合所建模型，对减速带设置提出最总方案，并对模型进行稳定性分析。

关键词：舒适度碰撞模型期望速度模型仿真运动学一．问题的重述减速带作为一种强化型的道路安全交通设施，在遏制交通事故的发生中发挥了重要的作用。

某单位的办公场所地处一主干道边上，主干道上车流量较大，车速达到平均每小时60公里，对人员的进出造成了一定的威胁。

如何在该路段路面合理设置减速带，达到既可以使来往车辆减速的目的，又可最大限度的降低减速带对主干道上车流量的影响。

提出以下三个问题：（1）建立道路减速带减速的数学模型；（2）利用所建的数学模型分析在等距连续设置三道减速带的减速效果；（3）利用所建的数学模型给出减速效果最优的三道减速带的设置方案；通过对模型的分析与求解，对交警部门如何设置减速带提出合理的建议。

道路减速带的减速模型的研究 (数学建模)

道路减速带的减速模型的研究一．摘要本文将轮胎视为刚体建立车辆经过减速带时的减速模型——圆弧形数学模型和相切抛物形数学模型，对车辆经过减速带时进行动力学分析，并建立适当的平面直角坐标系进行相应的几何分析得到车辆速度和加速度的表达式，利用MATLAB 和Lingo 等计算软件进行求解，进而对减速带的减速效果进行分析。

对于问题一，模型一得出汽车轮轴在经过减速带时的轨迹方程，分别对时间求一阶导数和二阶导数得到相应的速度和加速度的表达式。

考虑到车辆通过减速带的安全性和平稳性，运用物理知识对汽车通过减速带时进行力学分析，得到临界速度e v =加汽车通过减速带的安全性，经MATLAB 对该数学模型仿真发现相切抛物线作为过渡曲线为最佳减速带形状，用类似于模型一的方法得到临界速度12e v =。

通过查阅文献得知六种减速带的尺寸参数，分别代入上述表达式便求得相应的临界速度。

对于问题二，模型一定义减速效果为在车辆通过减速区域的时间内车辆以初速度做匀速直线运动通过的距离与在相同时间内同过减速区域的距离之差再与做匀速直线运动通过的距离之商。

相应的距离通过相关的动力学分析和计算便可得到，最后将所对应的六种减速带的尺寸规格与减速带之间的距离的关系用MATLAB 画出它们的关系图。

模型二则是通过对车辆通过减速带前后的动力学分析，求得车辆通过减速带的总时间以及在减速区域内的最大速度来说明减速带的减速效果，总时间为12.79s ，减速区域中的最大速度为13.1m/s 。

对于问题三，定义减速效果最优为在不超过限制速度的前提下，人体的舒适度最大，并且保证不堵车的情况下的通过减速带的时间最短。

模型一对能达到最优减速效果的车辆速度每隔10km/h 设定了限速区间，在不同的限速区间内减速带的最优设置不同，对0~60/km h 范围内的速度进行分析，最终得到每一个限速区间所对应的减速带的最优设置尺寸和通过相应减速带的最短时间。

模型二在其对问题二分析的基础上，对减速带之间的距离进行限制，使得车辆在第二次减速之前的速度还未加速到初始速度，再在最优减速效果的基础上求使经过减速区域的总时间最小的三条减速带两两之间的距离，结果为当11882m S =或时，即第一二两条减速带之间距离为18或82米，二三两条减速带之间为82或18米时，最短时间为11.9659t s =。

减速路障的设计

目录摘要 (1)一、问题的提出 (2)二、模型的假设 (3)三、符号说明及有关概念的定义 (3)四、模型的建立及求解 (4)汽车在两条减速带间达到原来速度的临界情况 (9)第一条减速带到第二条减速带之间的距离为： (12)减速区域内驾驶员的感受 % (12)建议信 (15)六、参考文献 (17)摘要卧龙路是我市出入城区的主干道之一。

车流量大，同时有两大高校，人口活动密集，车辆速度又过快，存在严重事故隐患。

所以需要设置一定的减速设施，如减速垄，而减速垄的设计正是我们研究课题的一方面。

但是车辆与减速垄反复碰撞易造成周边环境振动、噪音污染、车辆损坏和减速垄损坏等问题。

另一方面我们提出将垄单元横向布设的方法以解决上述问题．列出不等式组保证车辆通过垄单元时不发生倾斜，我们根据控速路段的限速要求和通行车辆车轴两侧轮间距选定设计参数，最后求解不等式组得到适合于具体路段的垄单元横向宽和通道宽。

该方法使强制减速措施人性化，赋予其可设计性，且具有造价低、布设简便、美观大方等优点，因而具有较大应用推广价值。

关键词：减速路障；减速垄；减速带；交通安全一、问题的提出1.1问题背景近年来，随着我国社会经济的发展，公路等级不断提升，城市私家车数量猛增，城市道路上的交通事故也日益突出。

在我国许多城市道路上，主要由于机动车、非机动车、行人混行严重，加之行人和驾驶员的安全意识较差，致使支路和社区、学校周边存在严重的交通安全隐患。

像我们学校师院附近就经常发生这样的事故，严重危害学生的身体健康。

为了降低学校道路及其周边道路的机动车车速，我国越来越多的地方采用了类似西方国家的交通平静化措施。

减速垄作为限制机动车垂直行驶速度的措施之一，对遏制交通事故的发生发挥了重要的作用，近年来在国内业内也取得了很大的认同。

但是由于减速垄缺乏人性化设计与论证，在安全、舒适、方便等方面尚未达到较高水平。

与此同时，道路使用者对减速垄的要求不再局限于“安全”这一最低层面上，而是越来越关注使用减速垄的舒适性。

2021数学建模b题解析

2021数学建模b题解析一、题目背景及分析2021年数学建模B题是一道具有实际背景的应用题，涉及到了交通流量优化、城市规划等热门话题。

题目要求我们分析城市道路网络中的交通拥堵问题，并提出相应的解决方案。

题目背景中给出了道路网络的简化图，以及各个路段的流量需求和容量。

我们需要利用数学建模的方法，合理分配交通流量，使得整个城市道路网络的拥堵程度最小。

二、解题思路和方法为了解决这个问题，我们可以将道路网络建模为一个有向图，其中每个节点代表一个路段，每条边代表两个节点之间的道路。

然后，我们可以利用图论中的最短路径算法，求解从起点到终点的最短路径，从而得到交通流量的分配方案。

三、具体步骤和计算过程1.构建道路网络图：根据题目给出的道路网络简化图，构建一个有向图，其中节点表示路段，边表示道路。

2.计算最短路径：利用Dijkstra算法或Floyd算法，求解从起点到终点的最短路径。

3.分配交通流量：根据最短路径的结果，合理分配各个路段的交通流量。

需要注意的是，要确保每个路段的流量需求不超过其容量。

4.计算拥堵程度：根据分配后的交通流量，计算整个道路网络的拥堵程度。

拥堵程度可以用道路拥堵指数（CI）来衡量，公式为：CI = ∑(Qi / Qi)，其中Qi表示第i个路段的实际流量，Qi表示第i个路段的容量。

5.优化模型：根据计算结果，分析道路网络的拥堵情况，并对模型进行优化。

例如，可以调整道路的网络结构，增加道路容量，或者采用动态交通定价策略等。

四、模型检验和优化为了检验模型的有效性，我们可以采用多种方法进行检验，如：敏感性分析、实例验证等。

同时，根据检验结果，对模型进行优化，以提高其在实际应用中的准确性和实用性。

五、结论和启示通过以上分析，我们可以得出以下结论：利用图论中的最短路径算法，可以有效地解决城市道路网络的交通拥堵问题。

此外，本题还为我们提供了一个将数学知识应用于实际问题的机会，使我们认识到数学建模在解决实际问题中的重要性。

路障间距的设计数学建模

路障间距的设计数学建模随着交通工具的普及和城市化进程的加快，道路交通问题已经成为城市发展的瓶颈之一。

为了保障道路交通的安全和畅通，路障设计成为了非常重要的一环。

在路障设计中，道路障碍物的间距是一个非常关键的参数，因为它直接影响到车辆的行驶速度和安全。

在本文中，我们将探讨如何利用数学建模的方法来设计道路障碍物的间距。

首先，我们需要明确障碍物的种类和形状。

常见的道路障碍物包括路障、护栏、花坛、绿化带等，它们的形状也千差万别。

在设计路障间距时，我们需要考虑到这些障碍物的形状和大小，以及车辆的行驶速度和安全性。

接下来，我们需要确定一个合适的数学模型来描述车辆行驶过程中的障碍物间距。

最简单的模型是线性模型，即假设车辆以匀速行驶，并且障碍物之间的间距为恒定值。

但是，在实际情况下，车辆的行驶速度和加速度往往是不稳定的，障碍物的形状和大小也不一定相同，这使得线性模型的适用性受到了很大的限制。

因此，我们需要使用更复杂的模型来描述车辆行驶过程中的障碍物间距。

一种常用的模型是基于车辆的动力学模型，即考虑车辆的加速度、制动力和转向力等因素。

在这种模型中，障碍物之间的间距不再是固定值，而是根据车辆的行驶速度和加速度等因素动态调整。

另一种常用的模型是基于道路交通流的模型，即考虑车辆行驶的流量和密度等因素。

在这种模型中，障碍物之间的间距也是动态调整的，但是调整的依据是道路交通流的变化情况。

无论是哪种模型，我们需要利用数学方法来求解最优的障碍物间距。

最常用的方法是优化算法，即通过最小化目标函数来求解最优解。

目标函数可以根据不同的模型和需求进行设计，比较常见的目标函数包括车辆行驶时间、交通流量、安全性等。

除了数学建模和优化算法，我们还需要考虑到实际应用中的一些限制因素，比如障碍物的数量、形状和大小等。

这些限制因素可以通过引入约束条件来加以考虑。

综上所述，道路障碍物的间距设计是一个复杂的问题，需要综合考虑到车辆行驶动力学、道路交通流和实际应用中的限制因素等多个因素。

道路减速带的设置

道路减速带的设置摘要本文解决的是减速带减速的数学模型，我们通过分析减速原理，建立相切抛物线模型,讨论了不同减速带间隔S 和不同初始速度0v 对减速效果的影响，利用Matlab 求出最佳减速带的最佳设计方案，属于多目标规划的最优解问题。

对于问题一：我们分析了减速带的减速原理，建立了圆弧数学模型和相切抛物线模型。

考虑到驾驶员的舒适性、行驶安全性和对地面的损坏度，比较两模型中驾驶员通过减速带时在竖直方向的加速度a 的大小，在相同情况下，a 越小则综合效益最好，最后选择相切抛物线模型作为减速带减速的数学模型。

对于问题二：分析驾驶员在通过第一个减速带到通过第二个减速带之间的运动情况，将其分步求解，分别求出驾驶员在通过第一个减速带后加速行驶的路程1S ，反应时间内匀速行驶的路程2S 和发现减速带后减速行驶的路程3S ，比较不同减速带间隔321S S S S ++=和不同初始速度0v 时，等距连续设置的三道减速带的减速情况，得到减速带的间隔对减速效果影响较大，通过减速带之前的初始速度对减速效果有影响，但影响较小。

对于问题三：在问题二的基础上，考虑到满足最佳减速效果的同时，还要考虑在减速带之间行驶的时间最短，以保证车流量较小，最佳的设置方案是T 最小的同时，S 最大时的减速带设置方案。

然后我们将多目标改进为单目标S T min,利用Matlab 求出等距的三道减速带的最佳设置方案如下：对于问题四：根据三峡大学的实际情况，建立了上下坡模型和平坦路面模型，对于三峡大学的具体情况，我们选取期望车速为h km v q /30=，给出了设置方案如下：关键词：减速带圆弧模型相切抛物线模型多目标规划最优化1. 问题重述三峡大学校内大学路车流量比较大，在未设置减速带之前车速平均为V公里/小时，对学生、教工的安全造成了一定的威胁。

学校于前几年在该路段路面设置了减速带，达到了使来往车辆减速的目的，学校希望使来往车辆的速度减到v公里/小时以内。

减速路障的放置解读

A．道路减速带*某单位的办公场所地处一主干道边上，主干道上车流量较大，车速达到平均每小时60公里，对人员的进出造成了一定的威胁。

交警部门打算在该路段路面设置减速带，达到使来往车辆减速的目的。

（1）建立道路减速带减速的数学模型；（2）利用所建的数学模型分析在等距连续设置三道减速带的减速效果；（3）利用所建的数学模型给出减速效果最优的三道减速带的设置方案；（4）给交警部门写一封建议信。

*减速带（如图1）是一种设置在在道路路面上凸起的障碍条，其目的是迫使高速行驶的车辆减速，从而保障行人安全，减少交通事故。

图1 道路减速带B. 快递公司送货策略目前，快递行业正蓬勃发展，为我们的生活带来更多方便。

一般地，所有快件到达某地后，先集中存放在总部，然后由业务员分别进行派送；对于快递公司，为了保证快件能够在指定的时间内送达目的地，必须有足够的业务员进行送货，但是，太多的业务员意味着更多的派送费用。

假定所有快件在早上7点钟到达，早上9点钟开始派送，要求于当天17点之前必须派送完毕，每个业务员每天平均工作时间不超过6小时，在每个送货点停留的时间为10分钟，途中速度为25km/h，每次出发最多能带25千克的重量。

为了计算方便，我们将快件一律用重量来衡量，平均每天收到总重量为184.5千克，公司总部位于坐标原点处（如图2），每个送货点的位置和快件重量见下表，并且假设送货运行路线均为平行于坐标轴的折线。

（1）请你运用有关数学建模的知识，给该公司提供一个合理的送货策略（即需要多少业务员，每个业务员的运行线路，以及总的运行公里数）；（2）如果业务员携带快件时的速度是20km/h，获得酬金3元/km kg；而不携带快件时的速度是30km/h，酬金2元/km，请为公司设计一个费用最省的策略；（3）如果可以延长业务员的工作时间到8小时，公司的送货策略将有何变化？图2 送货点分布图。

数学建模：道路优化问题)

目录一、问题的提出——————————————————————2二、问题分析——————————————————————--2三、基本假设——————————————————————--3四、符号说明——————————————————————--3五、模型的建立与求解——————————————————--4六、模型的评价——————————————————————8七、参考文献———————————————————————9摘要本题利用方程（组）模型，求两只路灯连线的路面上的最暗点。

通过查阅资料可知光照强度公式为r2Psin kI α=，由原题坐标图，通过实际情况假设部分数据，列出方程，利用MATLAB 软件进行求解，求出最小光照强度点X 的位置，并计算出如何通过调整路灯高度来极大化X 点的光照强度，并制定出合理的优化方案。

关键字：路灯照明方程（组） MATLAB 程序最值一、问题的提出1.1 引言随着城市化水平的不断提高，城市街道越来越多，街道上的路灯数量也会大量增加，如何合理安放路灯便成为一个重要问题。

在能源日益紧张的今天，更需要一种能够尽可能节约能源的路灯安置方案。

1.2 问题的提出为了更好地优化路灯的照明能力，本文依次提出以下问题： ⑴. 建立数学模型找出具有最小照明强度的点X （即最暗点）； ⑵. 通过改变第二盏灯的高度以极大化X 点的照明强度； ⑶. 如何调整两盏灯的高度来优化道路照明。

1.3 问题研究的意义：通过对路灯问题的研究，找到一种安置方案，优化现有路灯布局，使路灯能耗降低，以节省经济投入。

二、问题分析问题一：问题要求找出两路灯之间具有最小照度的点X ，但题中没有具体说明如路灯瓦数、路灯高度和路灯光照范围等数据，因此需要我们自己根据资料自己假设，算出合理的X 点的位置。

问题二：问题要求我们通过改变一端路灯的高度来尽量增强由问题一求出的最小光照强度的点（即最暗点）的光照强度，虽然题目同样没有进行数据的限制，但是作为一个实际问题，我们应该通过查找资料来确定一个符合实际情况的路灯高度的大致范围，再通过MATLAB 程序算出数据，然后根据范围选出路灯高度。

道路减速带的减速模型的研究 (数学建模)

对于问题一，模型一得出汽车轮轴在经过减速带时的轨迹方程，分别对时间求一阶导数和二阶导数得到相应的速度和加速度的表达式。

通过查阅文献得知六种减速带的尺寸参数，分别代入上述表达式便求得相应的临界速度。

相应的距离通过相关的动力学分析和计算便可得到，最后将所对应的六种减速带的尺寸规格与减速带之间的距离的关系用MATLAB 画出它们的关系图。

对于问题三，定义减速效果最优为在不超过限制速度的前提下，人体的舒适度最大，并且保证不堵车的情况下的通过减速带的时间最短。

停车距离问题——数学建模案例

停车距离问题——数学建模案例摘要：汽车在行驶中，为规避险情，常常需要急刹车。

怎样实施刹车操作，最大限度地规避险情，保障司乘人员、车辆、障碍物的安全呢？在交通事故发生后，交管部门对事故现场的勘探，也常常需要还原驾驶人员刹车的操作是否规范？车辆是否在事故发生时超速行驶？以便公正、公平地进行事故责任认定。

所以，研究汽车刹车问题就具有现实意义。

本文旨在通过对行驶中的汽车刹车距离问题的探索，用数学模型刻画影响汽车刹车距离的关键因素，及各因素之间的数量关系。

为驾驶人的安全驾驶及交管部门的事故责任认定，提供有价值的参考。

关键词：距离、速度、参数、假设、检验、线性回归、数学建模。

一、符号说明驾驶人在实施刹车前，要根据险情判断何时开始刹车及刹车力度。

从做出判断到实施刹车这段时间，我们定义为反应时间，记作，这段时间汽车滑行的速度记作，滑行的距离定义为反应距离，记作；从汽车刹车到汽车停车滑行的这段时间，定义为制动时间，记作，这段时间汽车滑行距离定义为制动距离，记作；从做出需要刹车得判断到汽车停止滑行的这段时间定义为停车时间，记作，这段时间汽车滑行的距离定义为停车距离，记作；汽车刹车时，车辆轮胎与路面的滚动摩擦力记作；汽车的质量记作；刹车时汽车滑行的加速度记作。

二、基本假设2.1.在反应时间段内，驾驶人在判断需要刹车时，一般都会松开油门踏板。

此时，汽车滑行仅受轮胎与地面滚动摩擦力的较小影响，我们假设这期间汽车保持油门踏板松开的那一时刻的瞬时速度匀速行驶。

由于在现实生活中，因人而异，很难确定的具体数值，因此，最终只能确定与成正比。

2.2.在制动时间段内，驾驶人在实际操作中，刹车受力大小一般是由小逐渐快速增大的，增大的速度也并不均匀，在汽车停止滑动的瞬间，受力又突然变为零。

车辆的防抱死系统也是为了避免急刹车时，因驾驶人瞬间踩死刹车，使车辆仅受轮胎与路面的巨大滑动摩擦力控制，造成更大的危险（如爆胎、侧翻、方向盘失灵等）。

这里，我们仅研究假设这期间刹车受力F的大小为定值，其近似等于车辆轮胎与路面的滚动摩擦力。

减速带间距设定研究(建模优秀论文)

道路减速带控制车速原理及评价参数选择道路减速带的控制车速原理：车辆的行驶速度很大程度上取决于驾驶员的期望车速，而驾驶员的期望速度又是根据其行驶安全感和乘坐舒适性决定的。

如果驾驶员的安全感高、乘坐舒适性好，则他的期望车速比较高;反之，驾驶员的期望车速就比较低。

道路减速带的减速是通过影响驾驶员的驾驶心理实现的。

当车辆以较高车速通过道路减速带时，剧烈的振动会从轮胎经由车身及座椅传递给驾驶员，产生强烈的生理刺激(包括振动刺激和视觉刺激)和心理刺激。

生理刺激使驾驶员产生很强烈的不舒服感，心理刺激会加深驾驶员的不安全疑虑，进一步降低了驾驶员对道路环境的安全感。

一般情况下，驾驶员认为不舒服感越强，车辆行驶安全性也越小，即安全感越小。

由此可知，道路减速带的设置会大大降低驾驶员行车安全感和乘坐舒适性的期望值，促使驾驶员选择较低的期望车速。

在期望车速的指导下，驾驶员将在没有外界压力的情况下，主动使车辆以较低的行车速度接近道路减速带。

欧美各国相关研究结果表明，如果设计正确，布置合理，道路减速带可使85%的车辆车速降低10至20 km/ h，事故率降低约60%，事故伤亡人数降低50%-70%。

对云南、陕西高等级公路道路减速带使用效果调研发现，道路减速带可大幅降低车辆行驶速度、事故发生率和事故严重程度。

理想道路减速带的设计所谓的理想道路减速带就是我们希望得到的减速带，它安装在道路上时表现出最接近我们希望得到的对车辆的响应。

理想道路减速带必须保证车辆在通过时不会发生失控，以及重要安全部件受到冲击时不会产生断裂等危险状况，即应该拥有较高的行驶和结构安全性。

车辆的行驶安全性绝不允许一直随着车速的增加而降低，而是应在降低到一定程度后保持在一个稳定水平，甚至随着车速的升高行驶安全性还有所提高。

由道路减速带控制车速原理可知，车辆高速通过时，驾驶员所产生的不舒服感是道路减速带能够有效控制车速的关键原因，不舒服感越强，驾驶员的减速愿望也越强。