第13章全等三角形专题训练三全等三角形的基本模型练习
初中数学《全等三角形》基本模型训练含解析

全等三角形基本模型专项训练一、单选题1如图,在Rt△ABC中,AB=AC,∠BAC=90°,点D,E分别在边BC及其延长线上,BD2+CE2=DE2,F为△ABC外一点,且FB⊥BC,FA⊥AE,则结论:①FA=AE;②∠DAE=45°;③S△ADE=14AD⋅EF;④CE2+BE2=2AE2,其中正确的是()A.①②③④B.①②④C.①③④D.①②【答案】A【分析】根据全等三角形的性质,证明△ABF和△ACE全等,即可得到FA=AE;连接DF如图见解析,证明△ADE和△ADF全等,即可得到∠DAE=45°;延长AD交EF于H如图见解析,利用等腰直角△AFE三线合一的性质,∠FAE=90°,∠DAE=45°∠DAE=45°,可知AH⊥EF,S△ADE=12AD⋅EH,HE=HF=12EF,即可判断③;在Rt△EBF和Rt△EAF中,利用勾股定理以及等式的性质,即可判断④.【详解】解:∵AB=AC,∠BAC=90°∴∠ABC=∠ACB=45°∴∠ACE=180°-∠ACB=135°∵FB⊥BC∴∠FBE=90°∴∠ABF=∠ABC+∠FBE=135°∴∠ABF=∠ACE∵FA⊥AE∴∠FAE=90°=∠BAC∴∠FAE-∠FAC=∠BAC-∠FAC即∠CAE=∠BAF在△ABF和△ACE中,∠ACE=∠ABF AC=AB∠CAE=∠BAF∴△ACE≌△ABF ASA∴FA=EA,故①正确;连接DF,如图:∵△ACE≌△ABF∴BF=CE在Rt△BDF中,BD2+BF2=DF2∴BD2+CE2=DF2∵BD2+CE2=DE2∴DE=DF∵AE=AF,AD=AD∴△ADE≌△ADF SSS∴∠DAE=∠DAF∴∠DAE=12∠EAF=45°,故②正确;延长AD交EF于H,如图:∵AE=AF,∠EAD=∠FAD∴AH⊥EF,HE=HF=12EF∴S△ADE=12AD⋅EH=12AD⋅12EF=14AD⋅EF,故③正确;在Rt△EBF中,BE2+BF2=EF2∵CE=BF∴BE2+CE2=EF2∵AE=AF,∠FAE=90°∴EF2=AE2+AF2=2AE2∴BE2+CE2=2AE2,故④正确,综上所述,正确的有①②③④,故选:A.【点睛】本题考查了全等三角形的判定与性质、勾股定理、等腰直角三角形性质等知识,解题的关键是灵活运用所学知识.2如图所示,△ABC中,AC=BC,M、N分别为BC、AC上动点,且BM=CN,连AM、CN,当AM +BN最小时,CMCN=( ).A.2B.32C.54D.1【答案】D 【分析】过B 点在BC 下方作BH ∥AC ,且BH =AC ,链接BH ,AH ,先证明△BCN ≌△HBM ,即有BN =HM ,则AM +BN =AM +MH ,当A 、M 、H 三点共线时,AM +MH 值最小,再证明△ACM ≌△HBM ,问题随之得解.【详解】如图,过B 点在BC 下方作BH ∥AC ,且BH =AC ,链接BH ,AH ,∵BH ∥AC ,∴∠C =∠CBH ,∵BH =AC ,BM =CN ,∴△BCN ≌△HBM ,∴BN =HM ,∴AM +BN =AM +MH ,当A 、M 、H 三点共线时,AM +MH 值最小,如图,此时∵BH ∥AC ,∴∠C =∠CBH ,∠CAM =∠BHM ,∵AC =BC ,∴△ACM ≌△HBM ,∴CM =BM ,∵BM =CN ,∴CM CN=CM BM =1,故选:D .【点睛】本题主要考查了全等三角形的判定与性质,作出辅助线,构造全等三角形是解答本题的关键.3如图,正五边形ABCDE 中,点F 是边CD 的中点,AF ,BC 的延长线交于点N ,点P 是AN 上一个动点,点M 是BN 上一个动点,当PB +PM 的值最小时,∠BPN =()A.72°B.90°C.108°D.120°【答案】C【分析】本题考查了正多边形的定义,全等三角形的判定与性质等知识.连接BF ,EF ,PE ,EM ,根据全等三角形的判定与性质可得EP =BP ,则当E 、P 、M 三点共线,且EM ⊥BC 时,PB +PM 的值最小,过点E 作EH ⊥BC 于H ,交AF 于P ,分别求出∠BAP 和∠ABP 的度数,然后利用三角形外角的性质求解即可.【详解】解:连接BF ,EF ,PE ,EM ,∵正五边形ABCDE ,∴AE =AB =BC =ED ,∠BAE =∠AED =∠BCD =∠EDC =5-2 ×180°5=108°,∵点F 是边CD 的中点,∴CF =DF ,∴△BCF ≌△EDF SAS ,∴BF =EF ,又AE =AB ,AF =AF ,∴△AEF ≌△ABF SSS ,∴∠EAF =∠BAF =12∠BAE =54°,∴△AEP ≌△ABP SAS∴EP =BP ,∴PB +PM =EP +PM ≥EM ,∴当E 、P 、M 三点共线,且EM ⊥BC 时,PB +PM 的值最小,过点E 作EH ⊥BC 于H ,交AF 于P ,同理可求∠ABP =∠AEP =12∠AED =54°,∴∠BP N =∠BAP +∠ABP =108°,即当PB +PM 的值最小时,∠BPN =108°.故选:C .4如图,在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形ABEF ,正方形BCGH 和正方形ACMN ,给出下列结论:①AB =MG ;②S △ABC =S △AFN ;③过点B 作BI ⊥EH 于点I ,延长B 交AC 于点J ,则AJ =CJ .④若AB =1,则EH 2+FN 2=5.其中正确的结论个数是()A.1个B.2个C.3个D.4个【答案】D 【分析】本题考查勾股定理,全等三角形的性质和判定,解题的关键是正确作出辅助线.首先根据题意证明出△ACB ≌△MCG SAS ,进而得到AB =MG ,即可判断①;过点F 作FO ⊥NA 交NA 延长线于点O ,证明出△AFO ≌△ABC AAS ,得到OF =BC ,然后利用三角形面积公式即可得到S △ABC =S △AFN ,即可判断②;过点A 作AP ⊥BJ 交BJ 的延长线于点P ,过点C 作CQ ⊥BJ ,证明出△ABP ≌△BEI AAS ,得到AP =BI ,同理得到CQ =BI ,得到CQ =AP ,然后证明出△AJP ≌△CJQ AAS ,得到AJ =CJ ,即可判断③;根据全等三角形的性质得到EH =2BJ ,然后利用勾股定理证明出EH 2=AC 2+4BC 2,同理得到NF 2=4AC 2+BC 2,然后得到EH 2+NF 2=5AB 2=5,即可判断④.【详解】∵在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形ABEF ,正方形BCGH 和正方形ACMN ,∴AC =MC ,BC =GC ,∠MCA =∠GCB =90°∵∠ACB =90°∴∠MCG =∠ACB =90°∴△ACB ≌△MCG SAS∴AB =MG ,故①正确;如图所示,过点F 作FO ⊥NA 交NA 延长线于点O ,∵∠FAO +∠BAO =∠CAB +∠BAO =90°∴∠FAO =∠CAB又∵∠O =∠ACB =90°,AF =AB∴△AFO ≌△ABC AAS∴OF =BC∵AN =AC∵S △ANB =12AN ⋅OF ,S △ACB =12AC ⋅BC ∴S △ABC =S △AFN ,故②正确;如图所示,过点A 作AP ⊥BJ 交BJ 的延长线于点P ,过点C 作CQ ⊥BJ∵∠ABP +∠BEI =90°,∠EBI +∠BEI =90°∴∠ABP =∠BEI又∵∠P =∠BIE =90°,AB =BE∴△ABP ≌△BEI AAS∴AP =BI同理可证,△BCQ ≌△HBI AAS ∴CQ =BI∴CQ =AP∵∠P=∠CQJ=90°,∠AJP=∠CJQ∴△AJP≌△CJQ AAS∴AJ=CJ,故③正确;∵△ABP≌△BEI AAS∴BP=EI∵△BCQ≌△HBI AAS∴BQ=HI∵△AJP≌△CJQ AAS∴PJ=QJ∵EH=EI+HI=PB+BQ=PJ+QJ+BQ+BQ=2BJ ∵AJ=CJ∴BJ2=CJ2+BC2=14AC2+BC2∴EH2=2BJ2=4BJ2=414AC2+BC2=AC2+4BC2同理可证,NF2=4AC2+BC2∴EH2+NF2=AC2+4BC2+4AC2+BC2=5AC2+BC2=5AB2=5×12=5,故④正确.综上所述,正确的结论个数是4.故选:D.5如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠E=∠F=90 °,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE= CF;④△ACN≅△ABM.其中正确的结论是()A.①③④B.①②③④C.①②③D.①②④【答案】A【分析】本题考查了两个全等三角形的判定及性质,根据已知条件判定两个三角形全等,可得到对应边及对应角相等,据此可判断①③,再结合条件证明两个三角形全等,可得到④,即可求得结果,灵活运用两个全等三角形的条件及性质是解题的关键.【详解】解:∵∠EAC=∠FAB,∴∠EAB=∠FAC,在△EAB 和△FAC 中,∠E =∠F =90 °AE =AF ∠EAB =∠FAC,∴△EAB ≌△FAC ASA ,∴∠B =∠C ,BE =CF ,AB =AC ,∴①③都正确,在△ACN 和△ABM 中,∠B =∠CAB =AC ∠CAN =∠BAM,∴△ACN ≌△ABM ASA ,故④正确,根据已知条件无法证明②是否正确,故①③④正确,故选:A .二、填空题6如图,在△ABC 中,AH 是高,AE ⎳BC ,AB =AE ,在AB 边上取点D ,连接DE ,DE =AC ,若S △ABC =5S △ADE ,BH =1,则BC =.【答案】2.5【分析】过点E 作EF ⊥AB ,交BA 的延长线于点F ,先分别证明△ABH ≌△EAF ,Rt △ACH ≌Rt △EDF ,由此可得S △ABH =S △EAF ,S △ACH =S △EDF =S △EAF +S △ADE ,再结合S △ABC =S △ABH +S △ACH =5S △ADE 可得S △ACH S △ABH =32,由此可得CH BH=32,进而即可求得答案.【详解】解:如图,过点E 作EF ⊥AB ,交BA 的延长线于点F ,∵EF ⊥AB ,AH ⊥BC ,∴∠EFA =∠AHB =∠AHC =90°,∵AE⎳BC ,∴∠EAF =∠B ,在△ABH 与△EAF 中,∠AHB =∠EFA∠B =∠EAFAB =EA∴△ABH ≌△EAF (AAS ),∴AH =EF ,S △ABH =S △EAF ,在Rt△ACH与Rt△EDF中,AH=EF AC=DE∴Rt△ACH≌Rt△EDF(HL),∴S△ACH=S△EDF=S△EAF+S△ADE,∵S△ABC=S△ABH+S△ACH=5S△ADE,∴S△ABH+S△EAF+S△ADE=5S△ADE,∴2S△ABH+S△ADE=5S△ADE,解得:S△ABH=2S△ADE,∴S△ACH=5S△ADE-S△ABH=3S△ADE,∴S△ACHS△ABH=3S△ADE2S△ADE=32,∴12CH⋅AH12BH⋅AH=32,即CHBH=32,又∵BH=1,∴CH=1.5,∴BC=BH+CH=2.5,故答案为:2.5.【点睛】本题考查了全等三角形的判定与性质以及三角形的面积公式,作出正确的辅助线并能灵活运用全等三角形的判定与性质是解决本题的关键.7如图,在△ADE和△ABC中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE,垂足为F,DE交CB的延长线于点G,连接AG.四边形DGBA的面积为12,AF=4,则FG的长是.【答案】3【分析】过点A作AH⊥BC于H,证△ABC≌△AED,得AF=AH,再证Rt△AFG≌Rt△AHG,同理Rt△ADF≌Rt△ABH,得S四边形DGBA=6,进而得到FG的长.【详解】解:过点A作AH⊥BC于H,如图所示:在△ABC 和△ADE 中,BC =DE∠C =∠E CA =EA,∴△ABC ≌△AED SAS∴AD =AB ,S △ABC =S △AED ,又∵AF ⊥DE ,∴12×DE ×AF =12×BC ×AH ,∴AF =AH ,∵AF ⊥DE ,AH ⊥BC ,∴∠AFG =∠AHG =90°,在Rt △AFG 和Rt △AHG 中,AG =AG AF =AH ,∴Rt △AFG ≌Rt △AHG HL ,同理:Rt △ADF ≌Rt △ABH HL ,∴S 四边形DGBA =S 四边形AFGH =12,∵Rt △AFG ≌Rt △AHG ,∴S Rt △AFG =6,∵AF =4,∴12×FG ×4=6,解得:FG =3;故答案为:3.【点睛】本题考查了全等三角形的判定与性质以及三角形面积等知识,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.8如图,动点C 与线段AB 构成△ABC ,其边长满足AB =9,CA=2a +2,CB =2a -3.点D 在∠ACB 的平分线上,且∠ADC =90°,则a 的取值范围是,△ABD 的面积的最大值为.【答案】a >52454【分析】在△ABC 中,由三角形三边关系“在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边”可知AC +BC >AB ,代入数值即可确定a 的取值范围;延长AD 、CB交于点E ,首先利用“ASA ”证明△ACD ≌△ECD ,由全等三角形的性质可得AC =EC =2a +2,AD =ED ,进而可求得BE =5,结合三角形中线的性质易知S △ABD :S △ABE =1:2,确定△ABE 面积的最大值,即可获得答案.【详解】解:∵在△ABC 中,AC +BC >AB ,∴2a +2+2a -3>9,解得a >52;如下图,延长AD 、CB 交于点E ,∵CD 为∠ACB 的平分线,∴∠ACD =∠ECD ,在△ACD 和△ECD 中,∠ACD =∠ECDCD =CD ∠ADC =∠EDC =90°,∴△ACD ≌△ECD (ASA ),∴AC =EC =2a +2,AD =ED ,∵CB =2a -3,∴BE =2a +2-(2a -3)=5,∵AD =ED ,∴S △ABD :S △ABE =1:2,当BE ⊥AB 时,△ABE 的面积取最大值,即S △ABE max =12×9×5=452,∴S △ABD max =454.故答案为:a >52,454.【点睛】本题主要考查了三角形三边关系、解一元一次不等式、角平分线、全等三角形的判定与性质、三角形中线的性质等知识,熟练掌握相关知识,正确作出辅助线是解题关键.9如图,AB =AC ,AD=AE ,∠BAC =∠DAE =40°,BD 与CE 交于点F ,连接AF ,则∠AFB 的度数为.【答案】70°/70度【分析】本题考查了全等三角形的判定与性质,三角形内角和定理,构造全等三角形是解答本题的关键.过点A作AM⊥BD于点M,AN⊥CE于点N,根据手拉手模型证明△BAD≌△CAE,得到∠ADM=∠AEN,然后证明△AMD≌△ANE,得到∠DAM=∠EAN,AM=AN,进一步推得∠MAN=∠DAE= 40°,再证明△AMF≌△ANF,可得∠FAM=20°,最后根据三角形内角和定理即得答案.【详解】过点A作AM⊥BD于点M,AN⊥CE于点N,∵∠BAC=∠DAE=40°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE SAS,∴∠ADM=∠AEN,∵∠AMD=∠ANE=90°,AD=AE,∴△AMD≌△ANE AAS,∴∠DAM=∠EAN,AM=AN,∴∠DAM+∠DAN=∠EAN+∠DAN,即∠MAN=∠DAE=40°,∵∠AMF=∠ANF=90°,AM=AN,AF=AF,∴△AMF≌△ANF HL,∴∠FAM=∠FAN=1∠MAN=20°,2∴∠AFB=180°-90°-∠FAM=70°.故答案为:70°.10如图所示,已知△ABC,∠BAC=90°,AB=AC,点D和点E分别是AB和AC边上的动点,满足AD=CE,连接DE,点F是DE的中点,则CDAF的最大值为.【答案】5+1/1+5【分析】作EM⊥ED,且EM=ED,连DM,MC,取ME中点N,连ND、NC、NF,可根据“SAS”证明△ADE≌△CEM,可得∠ECM=90°,再设AF=1,并表示DE,EM,及CN,然后根据勾股定理求出DN,最后根据三角形的三边关系ND+NC≥DC,求出CD最大值,可得答案.【详解】解:过E作EM⊥ED,且EM=ED,连DM,MC.取ME中点N,连ND、NC、NF.∵∠ADE+∠AED=90°,∠AED+∠MEC=90°,∴∠ADE=∠MEC.∵AD=CE,DE=EM,∴△ADE≌△CEM,∴∠ECM=∠DAE=90°.设AF=1,∵F为DE中点,∴DE=2AF=2,∴EM=2.∵N为EM中点,∴CN=EN=1.∴DN=DE2+EN2= 5.∵ND+NC≥DC,∴CD最大值5+1,=5+1.∴CDAF故答案为:5+1.【点睛】本题主要考查了全等三角形的性质和判定,勾股定理,根据三角形的三边关系求最大值,作出辅助线是解题的关键.三、解答题11数学兴趣小组在活动时,老师提出了这样,一个问题:如图1:在△ABC中,AB=3,AC=5,D是BC的中点,求BC边上的中线AD的取值范围.【问题初探】:第一小组经过合作交流,得到如下解决方法:如图2延长AD至E.使得DE=AD,连接BE.利用三角形全等将线段AC转移到线段BE,这样就把线段AB,AC,2AD集中到△ABE中.利用三角形三边的关系即可得到中线AD的取值范围,第二小组经过合作交流,得到另一种解决方法:如图3过点B作AC的平行线交AD的延长线于点F,利用三角形全等将线段AC转移到BF,同样就把线段AB,AC,2AD集中到△ABF中,利用三角形三边的关系即可得到中线AD的取值范围.(1)请你选择一个小组的解题思路.写出证明过程【方法感悟】当条件中出现“中点”“中线”等条件时,可考虑将中线延长一倍或者作一条边的平行线.构造出“平行八字型”全等三角形;这样就把分散的已知条件和所证的结论集中到一个三角形中,顺利解决问题【类比分析】(2)如图4:在△ABC中,∠B=90°,AB=6,AD是△ABC的中线,CE⊥BC,CE=10且∠ADE=90°.求AE的长度.【思维拓展】(3)如图5:在△ABC中,AF⊥BC于点F在AB右侧作AD⊥AB,且AD=AB,在AC的左侧作AE⊥AC,且AE=AC,连接DE,延长AF交DE于点O,证明O为DE中点.【答案】(1)见解析(2)16(3)见解析【分析】(1)选择第一个小组的解题思路:延长AD到点E,使DE=AD,证明△ADC≌△EDB(SAS),得到BE=AC=10,再根据在△ABE中,5-3<AE<5+3,即2<2AD<8,求解即可;选择第二个小组的解题思路:过点B作AC的平行线交AD的延长线于点F,先证明△BDF≌△CDA (AAS),得到DF=AD,BF=AC=5,则2AD=AF,再根据在△ABF中,5-3<AF<5+3,即2<2AD<8,求解即可;(2)延长AD到点F,使DF=AD,连接CF,先证明△ABD≌△FCD SAS,得到∠FCD=∠ABD=90°,CF=AB=6,再证明E、C、F三点共线,得到EF=EC+CF=10+6=16,然后证明△ADE≌△FDE SAS,得到AE=EF=16解决问题;(3)过点E作EM∥AD交AD延长线于M,先证明△AEM≌△CAB AAS,得到EM=AB,再证明△AOD≌△MOE AAS,得到OD=OE,即可得出结论.【详解】解:(1)选择第一个小组的解题思路:如图2,延长AD到点E,使DE=AD,∵D是BC的中点,∴BD=CD,∵∠ADC=∠EDB,∴△ADC≌△EDB(SAS),∴BE=AC=10,△ABE中,5-3<AE<5+3,∴2<2AD<8,∴1<AD<4;选择第二个小组的解题思路:如图3,过点B作AC的平行线交AD的延长线于点F,∵D是BC的中点,∴BD=CD,∵BF∥AC,∴∠FBD=∠C,∠F=∠CAD,∴△BDF≌△CDA(AAS),∴DF=AD,BF=AC=5,∴2AD=AF,在△ABF中,5-3<AF<5+3,∴2<2AD<8,(2)延长AD到点F,使DF=AD,连接CF,如图4,∵D是BC的中点,∴BD=CD,∵∠ADB=∠FDC,DF=AD,∴△ABD≌△FCD SAS,∴∠FCD=∠ABD=90°,CF=AB=6,∵CE⊥BC,∴∠BCD=90°,∴∠FCD+∠ECD=180°,∴E、C、F三点共线,∴EF=EC+CF=10+6=16,∵∠ADE=90°,∴∠FDE=∠ADE=90°,∵DE=DE,AD=DF,∴△ADE≌△FDE SAS,∴AE=EF=16;(3)证明:过点E作EM∥AD交AD延长线于M,如图4,∵AD⊥AB,AE⊥AC,∴∠3+∠2+∠CAD=∠3+∠2+∠BAE=90°,∴∠CAD=∠BAE,又∵AF⊥BC,∴∠3+∠2+∠CAD=∠3+∠BAE+∠B=90°,∴∠2=∠B,∵EM∥AD,∴∠2=∠M,∴∠B=∠M,∵AE⊥AC,AF⊥BC,∴∠3+∠CAM=∠C+∠CAM=90°,∴∠3=∠C,∵AE=AC,∴△AEM≌△CAB AAS,∵AB =AD ,∴EM =AD ,∵∠2=∠M ,∠AOD =∠EOM ,∴△AOD ≌△MOE AAS ,∴OD =OE ,∴O 为DE 中点.【点睛】本题考查三角形三边的关系,全等三角形的判定与性质,余角的性质,平行线的性质,熟练掌握倍长中线,构造出“平行八字型”全等三角形是解题的关键.12已知,在等腰直角三角形ABC 中,AB =AC ,∠BAC =90°,∠ABC =∠ACB =45°,点D 是线段BC 上一点,点D 不与点B ,点C 重合,连接AD ,以AD 为一边作△ADE ,AD =AE ,∠DAE =90°,且点E 与点D 在直线AC 两侧,DE 与AC 交于点H ,连接CE .(1)如图1,求证:△ABD ≌△ACE .(2)如图2,在CE 的延长线上取一点F ,当∠AEF =∠AFE 时,求证:CD =CF .(3)过点A 作直线CE 的垂线,垂足为G ,当CD =6EG 时,直接写出△CDH 与△CEH 的面积比.【答案】(1)见详解(2)见详解(3)32或34【分析】本题主要考查了全等三角形的判定与性质,涉及SAS 、AAS 以及HL 等判定方法,(1)利用“SAS ”证明△ABD ≌△ACE 即可作答;(2)结合(1)的结论,再利用“AAS ”证明△ACD ≌△ACF 即可作答;(3)分类讨论,第一种情况:点G 在点E 的下方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,先证明△AOC ≌△AGC ,即有AO =AG ,CO =CG ,同理可证明:MH =NH ,再证明Rt △AOD ≌Rt △AGE HL ,可得OD =GE ,问题即可作答;第二种情况:点G 在点E 的上方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,按照第一种情况作答即可.【详解】(1)∵∠DAE =90°,∠BAC =90°,∴∠DAE -∠DAH =∠BAC -∠DAH ,∴∠CAE =∠BAD ,又∵AB =AC ,AD =AE ,∴△ABD ≌△ACE SAS ;(2)∵△ABD ≌△ACE SAS ,∴∠ADB =∠AEC ,∠ABD =∠ACE =45°,∴180°-∠ADB =180°-∠AEC ,∠ACB =∠ACE =45°,∴∠ADC =∠AEF ,∵∠AEF =∠AFE ,∴∠ADC =∠AFE ,在△ACD 和△ACF 中,∴∠ACD =∠ACF∠ADC =∠AFC AC =AC,∴△ACD ≌△ACF AAS ,∴CD =CF ;(3)分类讨论:第一种情况:点G 在点E 的下方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,如图,∵AO ⊥BC ,AG ⊥CE∴∠AOC =∠AGC =90°,又∵∠ACB =∠ACE =45°,AC =AC ,∴△AOC ≌△AGC ,∴AO =AG ,CO =CG ,同理可证明:MH =NH ,又∵AD =AE ,∴Rt △AOD ≌Rt △AGE HL ,∴OD =GE ,∵CD =6EG ,∴CO =CD -OD =5EG ,∴CG =CO =5EG ,∴CE =CG -EG =4EG ,∵S △CHD =12×CD ×MH ,S△CHE =12×CE ×NH ,MH =NH ,∴S △CHD S △CHE =12×CD ×MH 12×CE ×NH =CD ×MH CE ×NH ,∵CD =6EG ,CE =4EG ,MH =NH ,∴S △CHD S △CHE =CD ×MH CE ×NH=32;第二种情况:点G 在点E 的上方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,如图,同理可得:OD =GE ,OC =CG ,MH =NH ,∵CD =6EG ,∴CO =CD +OD =7EG ,∴CG =CO =7EG ,∴CE =CG +EG =8EG ,∴S △CHD S △CHE =CD ×MH CE ×NH=34;综上:△CDH 与△CEH 的面积比为32或者34.13如图,在平面直角坐标系中,O 为坐标原点,△ABC 的边BC 在x 轴上,A 、C 两点的坐标分别为A (0,m ),C (n ,0),B (-5,0),且m ,n 满足方程组m +2n =103m -n =9 ,点P 从点B 出发,以每秒2个单位长度的速度沿射线BO 匀速运动,设点P 运动时间为t 秒.(1)求A 、C 两点的坐标;(2)连接P A ,用含t 的代数式表示△AOP 的面积,并直接写出t 的取值范围;(3)当点P 在线段BO 上运动时,在y 轴上是否存在点Q ,使△POQ 与△AOC 全等?若存在,请求出t 的值并直接写出Q 点标;若不存在,请说明理由.【答案】(1)A (0,4),C (3,0);(2)0≤t <52,S △AOP =10-4t ;t >52,S △AOP =4t -10.(3)存在,Q (0,3)或(0,-3)或Q (0,4)或(0,-4).【分析】本题考查了全等三角形的性质和判定,二元一次方程组的解法,坐标与图形性质等知识点的综合运用,关键是利用分类讨论求出符合条件的所有情况.(1)解二元一次方程组求出m ,n 的值即可;(2)分为两种情况:当0≤t <52时,P 在线段OB 上,②当t >52时,P 在射线OC 上,求出OP 和OA ,根据三角形的面积公式求出即可;(3)分为四种情况:①当BP =1,OQ =3时,②当BP =2,OQ =4时,③④利用图形的对称性直接写出其余的点的坐标即可.【详解】(1)解方程组m +2n =103m -n =9 得m =4n =3 ,∴ A 的坐标是0,4 ,C 的坐标是3,0 ;(2)由已知,BP =2t ,OB =5.①0≤t <52,P 在线段OB 上.OP =OB -BP =5-2tS △AOP =12×OP ×OA 2=12×(5-2t )×4=10-4t .②t >52,P 在射线OC 上,OP =BP -OP =2t -5S △AOP =12×OA ×OP =12×4×(2t -5)=4t -10(3)在y 轴上存在点Q ,使△AOC 与△POQ 全等.①△POQ ≌△AOC 时,OQ =OC =3.OP =OA =4.t =5-42=12,Q (0,3)或Q (0,-3)②△POQ ≌△COA 时,OQ =OA =4,OP =OC =3.t =5-32=1 Q (0,4)或(0,-4)t =12,Q (0,3)或(0,-3);t =1,Q (0,4)或(0,-4);综上所述,t =12,Q (0,3)或(0,-3);t =1,Q (0,4)或(0,-4).14某校课后延时兴趣小组尝试用尺规来“作一条线段的三等分点”,请认真阅读下面的操作过程并完成相应的学习任务.如图1,①分别以点A ,B 为圆心,大于12AB 的长为半径在AB 两侧画弧,四段弧分别交于点C ,点D ;②连接AC ,BC ,AD ,作射线BD ;③以D 为圆心,BD 的长为半径画弧,交射线BD 于点E ;④连接CE ,交于AB 点F .点F 即为AB 的一个三等分点(即AF =13AB ).学习任务:(1)填空:四边形ADBC的形状是,你的依据是;(2)证明:AF=13AB;(3)如图2,若CE交AD于点H,∠CAD=60°,AC=6,将CH绕着点C旋转,当点H的对应点H 落在直线FD上时,求DH 的长.【答案】(1)菱形;四条边相等的四边形为菱形(2)见解析(3)DH′的长为33+32或33-32【分析】本题考查了菱形的判定与性质、相似三角形的判定与性质、等边三角形的判定与性质、全等三角形的判定与性质、勾股定理,善于利用特殊叫以及直角三角形中的关系是解题的关键.(1)根据菱形的性质判定即可.(2)证明△AFC∽△BFE,得出AFFB =ACBE,再根据线段关系即可求出.(3)利用菱形及已知条件推出相关信息,证明△ACD为等边三角形,再根据AAS证明△AHC≌△DHE,求得CH ;然后证明△AKF∽△BDF,根据相似三角形的性质得出AK、CK;最后用勾股定理解三角形即可.CH绕着点C旋转,点H的对应点H 需要分情况讨论.【详解】(1)解:由图的作法可知:AC=AD=BC=BD,∴四边形ADBC的形状是菱形,依据是:四条边相等的四边形为菱形.故答案为:菱形;四条边相等的四边形为菱形;(2)证明:∵四边形ADBC的形状是菱形,∴AC∥BE,∴△AFC∽△BFE,∴AF FB =ACBE.∵AC=BD,BD=DE,∴BE=2AC,∴AF FB =12,∴FB=2AF,∴AB=3AF.∴AF=13AB.(3)解:①当点H 在线段FD上时,连接CD,如图,∵AC=AD,∠CAD=60°,∴△ACD为等边三角形,∴CD=AD=6,∠ADC=60°.∵AC∥BE∴∠ACF =∠DEC .在△AHC 和△DHE 中,∠AHC =∠DHE∠ACE =∠DEC AC =DE,∴△AHC ≌△DHE AAS ,∴AH =HD =3,∵△ACD 为等边三角形,∴CH ⊥AD ,∠ACH =∠DCH =30°,∴CH =33.∴CH =CH =33.设FD 与AC 交于点K ,∵AC ∥BE ,∴△AKF ∽△BDF ,∴AK BD =AF FB=12.同理:CK ED =AF FB=12,∴AK BD =CK ED.∵BD =ED ,∴AK =CK =3,∴HK ⊥AC ,∠CDK =12∠ADC =30°.∴H K =CH 2-CK 2=32,DK =33.∴DH =DK -H K =33-32.②当点H 在射线FD 上时,连接CD ,如图,由①知CH =CH =33,HK ⊥AC ,AK =KC =3,∴DK =AD 2-AK 2=33,∴H K =CH 2-CK 2=32.∴DH =H K +DK =33+32.综上,DH 的长为33+32或33-32.15(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC 中,∠BAC =90°,AB =AC ,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D 、E .证明:DE =BD +CE .(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线l 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.【答案】(1)见解析;(2)DE =BD +CE ,见解析;(3)见解析【分析】本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD =AE 、CE =AD 是解题的关键.(1)由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°-α,且∠DBA +∠BAD =180°-α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点.【详解】解:(1)如图1,∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD ,在△ABD 和△CAE 中,∠ABD =∠CAE∠BDA =∠CEA AB =AC,∴△ABD ≌△CAE AAS ,∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(2)成立,理由如下:如图,证明如下:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α,∴∠DBA =∠CAE ,在△ABD 和△CAE 中.∠BDA =∠AEC∠DBA =∠CAE AB =AC.∴△ABD ≌△CAE AAS∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(3)如图3,过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N .∴∠EMI =∠EMA =∠GNA =90°,∠BAE =90°,∴∠EAM +BAH =90°,∵AH 是BC 边上的高,∴∠AHB =90°,∴∠BAH +∠ABH =90°,∴∠ABH =EAM ,∵AE =AB ,∴△ABH ≌△EAM ,∴EM =AH ,同理△ACH ≌△GAN ,∴AH =GN ,∴EM =GN ,在△EMI 和△GNI 中,∠EIM =∠GIN∠EMI =∠GNI EM =GN,∴△EMI ≌△GNI AAS ,∴EI =GI ,∴I 是EG 的中点.16如图,在△ABC 中,BC =5,高AD 、BE 相交于点O ,BD =2,且AE =BE.(1)请说明△AOE ≌△BCE 的理由;(2)动点P 从点O 出发,沿线段OA 以每秒1个单位长度的速度向终点A 运动,动点Q 从点B 出发沿射线BC 以每秒4个单位长度的速度运动,P 、Q 两点同时出发,当点P 到达A 点时,P 、Q 两点同时停止运动.设点P 的运动时间为t 秒,求当t 为何值时,△AOQ 的面积为3.(3)在(2)的条件下,点F 是直线AC 上的一点且CF =BO .当t 为何值时,以点B 、O 、P 为顶点的三角形与以点F 、C 、Q 为顶点的三角形全等?(请直接写出符合条件的t 值).【答案】(1)见解析(2)当t 为15或45时,△AOQ 的面积为3(3)t =1或53s 时,△BOP 与△FCQ 全等【分析】本题考查三角形综合题、全等三角形的判定和性质、三角形的面积等知识,(1)首先推导出∠EAO =∠EBC ,通过ASA 即可证明△AOE ≌△BCE ;(2)分两种情形讨论求解即可①当点Q 在线段BD 上时,QD =2-4t ,②当点Q 在射线DC 上时,DQ =4t -2时;依据三角形面积计算公式解答即可;(3)分两种情形求解即可①如图2中,当OP =CQ 时,BOP ≌△FCQ .②如图3中,当OP =CQ 时,△BOP ≌△FCQ .【详解】(1)如图1中,∵AD 是高,∴∠ADC =90°,∵BE 是高,∴∠AEB =∠BEC =90°,∴∠EAO +∠ACD =90°,∠EBC +∠ECB =90°,∴∠EAO =∠EBC ,在△AOE 和△BCE 中,∠EAO =∠EBCAE =BE ∠AEO=∠BEC,∴△AOE ≌△BCE ASA ,(2)解:由(1)知△AOE ≌△BCE ,∴OA =BC =5,∵BD =2,∴CD =3,由题意OP =t ,BQ =4t ,①当点Q 在线段BD 上时,QD =2-4t ,∴S △AOQ =12OA ⋅QD =12×5×2-4t =3,解得:t =15;②当点Q 在BD 延长线上时,DQ =4t -2,∴S △AOQ =12OA ⋅DQ =12×5×4t -2 =3,解得:t =45,综上,当t 为15或45时,△AOQ 的面积为3;(3)存在.①如图2中,当OP =CQ 时,∵OB =CF ,∠POB =∠FCQ ,∴△BOP ≌△FCQ .∴CQ =OP ,∴5-4t =t ,解得t =1,②如图3中,当OP =CQ 时,∵OB =CF ,∠POB =∠FCQ ,∴△BOP ≌△FCQ .∴CQ =OP ,∴4t -5=t ,解得t =53.综上所述,t =1或53s 时,△BOP 与△FCQ 全等.17如图1,在△ABC 中,BD 为AC 边上的高,BF 是∠ABD 的角平分线,点E 为AF 上一点,连接AE ,∠AEF =45°.(1)求证:AE平分∠BAF(2)如图2,连接CE交BD于点G,若△BAE与△CAE的面积相等,求证:BG=CF【答案】(1)见解析;(2)见解析【分析】本题主要考查了全等三角形的证明以及性质运用,角平分线的判定以及基本性质,熟练掌握全等三角形的几种判定方法以及角平分线的判定是解答该题的关键.(1)根据BF是∠ABD的角平分线和,BD为AC边上的高,可得12∠BAD=45°-12∠ABD,由∠AEF=45°得∠BAE=45°-∠ABE=45°-12∠ABD,即可证明∠BAE=12∠BAD;(2)过点E作EM⊥AB于点M,EN⊥AC于点N,由角平分线性质可以得EM=EN,由△BAE与△CAE的面积相等可得AB=AC,证明△ABE≌△ACE(SAS),得出∠AEB=∠CEB=135°,BE=EC,即可得出∠BEG=∠CEF=360°-∠AEB-∠AEC=90°,再根据垂直模型证明△BEG≌△CEF(ASA),即可得出结论.【详解】(1)证明:∵BD为AC边上的高,即∠ADB=90°,∴∠ABD+∠BAD=90°,∴12(∠ABD+∠BAD)=45°,∴1 2∠BAD=45°-12∠ABD∵∠AEF=∠ABF+∠BAE=45°,∴∠BAE=45°-∠ABF,∵∠ABF=12∠ABD,∴∠BAE=45°-12∠ABD,∴∠BAE=12∠BAF,即:AE平分∠BAF.(2)过点E作EM⊥AB于点M,EN⊥AC于点N,∵AE平分∠BAC,且EM⊥AB,EN⊥AC,∴EM=EN.∵S△ABE=S△ACE,∴AB=AC,∵AE平分∠BAC,∴∠BAE=∠CAE,在△ABE和△ACE中,AB=BC∠BAE=∠CAE AE=AE∴△ABE≌△ACE(SAS),∴∠AEB=∠CEB,BE=EC,∵∠AEF=45°,∴∠AEB=∠AEC=135°,∴∠BEG=∠CEF=360°-∠AEB-∠AEC=90°,∵BD为AC边上的高,∴∠ADB=90°,∴∠FBD+∠BFC=∠BFC+∠FCE,∴∠EBG=∠ECF.在△BEG和△CEF中,∠BEG=∠CEF BE=CE∠EBG=∠ECF∴△BEG≌△CEF(ASA).∴BG=CF .18如图,已知A a,0,B0,b,AB=AC且AB⊥AC,AC交y轴于E点.(1)如图1,若a2+b2-4a-8b+20=0,求C点坐标;(2)如图2,A,B两点分别在x轴,y轴正半轴上,E为AC的中点,BC交x轴于G点,连EG,若a=3,求G点的坐标;(3)如图3,A在x轴的负半轴上,以BC为边在BC的右侧作等边△BCD,连OD,当∠BOD=60°时,请探究线段OA、OB、OD之间的数量关系,并证明.【答案】(1)(-2,-2)(2)(-2,0)(3)OD=OB+2OA【分析】(1)利用完全平方公式将等式变形为两个数平方和的形式,即可求出a=2,b=4,如图1中,过点C作CH ⊥x轴于点H,证明△AHC≌△BOA,可得CH=OA=2,AH=OB=4,即可得到点C坐标.(2)根据(1)可得CH=OA=a,AH=OB=b,再由a=3,E为AC的中点,可得点C(-3,-3),AH=OB=6,再利用面积法求出AG =5,即可解题;(3)过点C 作CH ⊥x 轴于点H ,在OD 上取一点M ,使得OM =OB ,证明△OBM 是等边三角形,进而证明△MBD ≌△OBC ,得∠BMD =∠BOC =120°,MD =OC ,再证明∠COH =30°,得OC =2CH =2OA ,即可得出OD =OB +2OA .【详解】(1)解:∵a 2+b 2-4a -8b +20=0,∴(a 2-4a +4)+(b 2-8b +16)=0,即(a -2)2+(b -4)2=0,∴a =2,b =4,∴A 2,0 ,B 0,4如图1中,过点C 作CH ⊥x 轴于点H ,∵∠AHC =∠BOA =∠BAC =90°,∴∠CAH +∠BAO =90°,∠BAO +∠ABO =90°,∴∠CAH =∠ABO ,在△AHC 和△BOA 中,∠AHC =∠BOA∠CAH =∠ABO AC =BA,∴△AHC ≌△BOA (AAS ),∴CH =OA =2,AH =OB =4,∴OH =AH -OA =4-2=2∴点C 坐标为(-2,-2);(2)如图2,同理(1)可证明:CH =OA =a ,AH =OB =b ,∵a =3,E 为AC 的中点,OE 平行于CH ,∴OA =OH =3,CH =3,∴点C (-3,-3),AH =OB =6,AB =AC =OA 2+OB 2=62+32=35,∵S △ABC =S △AGC +S △AGB ,即12×35×35=12×3⋅AG +12×6⋅AG ,∴AG =5,∴GO =AG -OA =5-3=2,∴点G 坐标为(-2,0);(3)结论:OD =OB +2OA ,如图3,过点C 作CH⊥x轴于点H ,同理可得:CH =OA ,AH =OB ,在OD 上取一点M ,使得OM =OB ,∵OM =OB ,∠BOD =60°,∴△OBM 是等边三角形,∴BO =BM ,∠OMB =60°,∴∠BMD =120°,∵△BCD 是等边三角形,∴BC =BD ,∠CBD =∠OBM =60°,∴∠DBM =∠CBO ,在△MBD 和△OBC 中,BM =OB∠DBM =∠CBO BD =BC,∴△MBD ≌△OBC (SAS ),∴∠BMD =∠BOC =120°,MD =OC ,∴∠COH =120°-90°=30°,∵CH ⊥x 轴,∴OC =2CH =2OA ,∵OD =OM +MD ,∴OD =OB +OC =OB +2OA【点睛】本题考查了等腰直角三角形的性质,等边三角形的判定和性质,全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.19已知△ABC 为等边三角形,D 是边AC 上的一点,连接BD ,E 为BD 上的一点,连接CE.(1)如图1,延长CE 交AB 于点G .若∠DCG =15°,BG =2,求BC 的长;(2)如图2,将△BEC 绕点B 逆时针旋转60°至△BFA ,延长CB 至点M ,使得BM =DC ,连接AM 交BF 于点N ,探究线段FN ,DE ,BE 之间的数量关系,并说明理由;(3)如图3,在(2)问的条件下,过点A 作AH ⊥BC 于点H ,过点B 作BK ∥AH 且BK =AH ,连接HK ,NK ,NH ,NC .若BC =4,当12BD +NK 的值最小时,请直接写出CD NH的值.【答案】(1)1+3(2)2FN +DE =BE .理由见解析(3)277【分析】(1)作CF⊥BC,解直角三角形BFG求得BF和FG,进而解直角三角形CFG求得CF,从而得出结果;(2)延长BF至G,使FG=DE,连接AG,作BH∥AF,交BF于H,证明△ABG≌△CBD,进而证明△ANG≌ΔMNB,△AFN≌△MHN,△BMH≌△DCE,进一步得出结论;BD+NK最小,此时BG⊥AG,即BD⊥AC,进一步得出(3)可得出当K、N、G共线且与AG垂直时,12结果.【详解】(1)解:如图1,作CF⊥BC于F,∴∠CFG=∠BFG=90°,∵△ABC是等边三角形,∴∠ACB=∠ABC=60°,在Rt△BFG中,BG=2,∠ABC=60°,=1,∴BF=2cos60°=2×12=3,FG=2⋅sin60°=2×32在Rt△CFG中,FG=3,∠FCG=∠ACB-∠ACG=60°-15°=45°,∴CF=FG=3,tan∠FCG∴BC=BF+FC=1+3;(2)证明:如图2,延长BF至G,使FG=DE,连接AG,作BH∥AF,交BF于H,∴∠MHN=∠AFN,∠NMH=∠FAN,∴∠MHB=∠AFG∵△BEC绕点B逆时针旋转60°至△BFA,∴BF=BE,∠ABF=∠CBE,AB=BC,∴BG=BD,∴△ABG≌△CBD,∴AG=CD=BM,∠G=∠BDC=180°-∠CBE-∠ACB=120°-∠CBE,∵∠MBN=180°-∠ABC-∠ABF=120°-∠CBE,∴∠G=∠MBN,∴△ANG≌△MNB,∴AN=MN,∴△AFN≌△MHN,∴FN=NH,∵△ANG ≌△MNB ,∴NG =BN ,∵FN =NH ,∴BH =FG ,∵FG =DE∴BH =DE ,∵旋转,∴CE =AF ,∵△AFN ≌△MHN ,∴AF =MH ,∴MH =CE ,∵CD =BM ,∴△BMH ≌△DCE ,∴BH =DE ,∵FN +NH +BH =BF ,∴2FN +DE =BE ;(3)解:如图3,由(2)知:BD =BG =2BN ,∴12BD +NK =GN +NK ,∴当K 、N 、G 共线且与AG 垂直时,12BD +NK 最小,此时BG ⊥AG ,即BD ⊥AC ,如图4,连接NH ,∵AC =BC =4,∴CD =BH =2,BD =32BC =23,BN =GN =12BG =12BD =3,∵NH =BH 2+BN 2=2+(3)2=7,∴CD NH=277.【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,解直角三角形等知识,解决问题的关键是作辅助线,构造全等三角形.。
三角形全等几何模型(一线三等角)(精选精练)(专项练习)(教师版) 24-2025学年八年级数学上册

专题12.12三角形全等几何模型(一线三等角)(精选精练)(专项练习)一、单选题(本大题共10小题,每小题3分,共30分)1.(22-23七年级下·辽宁朝阳·期末)王强同学用10块高度都是2cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC BC =,90ACB ∠=︒),点C 在DE 上,点A 和B 分别与木墙的顶端重合.则两堵木墙之间的距离DE 是()A .10cmB .15cmC .20cmD .25cm2.如图所示,,,B C E 三点在同一条直线上,AC CD =,90B E ∠=∠=︒,AC CD ⊥,则下列结论错误的是()A .A ∠与D ∠互余B .2A ∠=∠C .ABC CED △≌△D .12∠=∠3.如下图所示,在△ABC 中,∠ACB=90°,AC=BC ,BE ⊥CE 于点E ,AD ⊥CE 于点D .DE=6cm ,AD=9cm ,则BE 的长是()A .6cmB .1.5cmC .3cmD .4.5cm4.(23-24八年级上·重庆开州·阶段练习)如图,在平面直角坐标系中,ABC 为等腰直角三角形,90,ACB AC BC ∠=︒=.点()0,1B -,点()1,1C .则点A 坐标为()A .()1,3-B .()3,1-C .()2,1-D .()1,2-5.(22-23七年级下·广东深圳·期末)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A 处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m 高的B 处接住她后用力一推,爸爸在C 处接住她.若妈妈与爸爸到OA 的水平距离BD 、CE 分别为1.4m 和1.8m ,90BOC ∠=︒.爸爸在C 处接住小丽时,小丽距离地面的高度是()A .1mB .1.6mC .1.8mD .1.4m6.(22-23八年级上·山东青岛·单元测试)2002年8月在北京召开的第24届国际数学家大会,会标中的图案如图,其中的四边形ABCD 和EFGH 都是正方形,则ABF DAE ≌的理由是().A .SSSB .AASC .SASD .HL7.(23-24八年级上·河北唐山·期中)如图,在ABC 和CDE 中,点B ,C ,E 在同一条直线上,B E ACD ∠∠∠==,AC CD =,若2AB =,6BE =,则DE 的长为()A .8B .6C .4D .28.(2024·山西吕梁·一模)如图,在平面直角坐标系中,点()0,2A 处有一激光发射器,激光照射到点()1,0B 处倾斜的平面镜上发生反射,使得反射光线照射到点C 处的接收器上,若入射角45α=︒,AB BC =,则点C 处的接收器到y 轴的距离为()A .1B .2C .3D .49.(17-18八年级上·河南郑州·期中)如图中,AE ⊥AB 且AE =AB ,BC ⊥CD 且BC =CD ,若点E 、B 、D 到直线AC 的距离分别为6、3、2,则图中实线所围成的阴影部分面积S 是()A .50B .44C .38D .3210.(22-23八年级下·新疆乌鲁木齐·期末)如图,AB CD ⊥,且AB CD =,E ,F 是AD 上两点,CE AD ⊥,BF AD ⊥.若4CE =,3BF =,2EF =,则AD 的长为()A .3B .5C .6D .7二、填空题(本大题共8小题,每小题4分,共32分)11.(21-22八年级上·山西吕梁·期中)如图,一个等腰直角三角形ABC 物件斜靠在墙角处(∠O =90°),若OA =50cm ,OB =28cm ,则点C 离地面的距离是cm .12.(20-21八年级上·黑龙江·期中)如图,在平面直角坐标系内,OA ⊥OC ,OA=OC ,若点A 的坐标为(4,1),则点C 的坐标为13.(2022·四川成都·二模)如图所示,ABC 中,,90AB AC BAC =∠=︒.直线l 经过点A ,过点B 作BE l ⊥于点E ,过点C 作CF l ⊥于点F .若2,5==BE CF ,则EF =.14.(19-20八年级上·江苏苏州·期中)如图,△ABC 中,∠C =90°,点D 为AC 上一点,∠ABD =2∠BAC =45°,若AD =12,则△ABD 的面积为.15.(23-24八年级上·江苏无锡·期中)如图,两根旗杆间相距12米,某人从点B 沿BA 走向点A ,一段时间后他到达点M ,此时他仰望旗杆的顶点C 和D ,两次视线的夹角为90︒,且CM DM =.已知旗杆BD 的高为9米,该人的运动速度为1米/秒,则这个人运动到点M 所用时间是秒.16.(23-24八年级上·辽宁大连·期末)如图,在ABC 中,90ACB ∠= ,CD 为AB 边上的高,3BC =,6AC =,点E 从点B 出发,在直线BC 上以每秒2cm 的速度移动,过点E 作BC 的垂线交直线CD 于点F ,当点E 运动s 时,AB CF =.17.(19-20八年级上·江苏连云港·阶段练习)如图,线段AB =8cm ,射线AN ⊥AB ,垂足为点A ,点C 是射线上一动点,分别以AC ,BC 为直角边作等腰直角三角形,得△ACD 与△BCE ,连接DE 交射线AN 于点M ,则CM 的长为.18.(22-23七年级下·四川成都·期末)在ABC 中,AB AC =,90BAC ∠<︒,点D 在边BC 上,2CD BD =,点E ,F 在线段AD 上,BED CFD BAC ∠=∠=∠.若ABC 的面积为9,则ABE CDF S S += .三、解答题(本大题共6小题,共58分)19.(8分)如图,在ABC 中,90ACB ∠=︒,AC BC =,BE CE ⊥,于点E AD CE ⊥,于点D .BEC 与CDA 全等吗?请说明理由.20.(8分)如图,90ABC ∠=︒,FA AB ⊥于点A ,D 是线段AB 上的点,AD BC =,AF BD =.(1)判断DF 与DC 的数量关系为,位置关系为.(2)如图2,若点D 在线段AB 的延长线上,点F 在点A 的左侧,其他条件不变,试说明(1)中结论是否成立,并说明理由.21.(10分)如图,在ABC 中,AB BC =.(1)如图1,直线NM 过点B ,AM MN ⊥于点M ,⊥CN MN 于点N ,且90ABC ∠=︒,求证:MN AM CN =+.(2)如图2,直线NM 过点B ,AM 交NM 于点M ,CN 交NM 于点N ,且AMB ABC BNC ∠=∠=∠,则MN AM CN =+是否成立?请说明理由!22.(10分)如图,在ABC 中,2AB AC ==,40B C ∠=∠=︒,点D 在线段BC 上运动(D 不与B 、C 重合),连接AD ,作40ADE ∠=︒,DE 交线段AC 于E .(1)当115BDA ∠=︒时,EDC ∠=°,DEC ∠=°;点D 从B 向C 运动时,BDA ∠逐渐变(填“大”或“小”);(2)当DC 等于多少时,ABD DCE △△≌,请说明理由;(3)在点D 的运动过程中,ADE V 的形状可以是等腰三角形吗?若可以,请直接写出BDA ∠的度数.若不可以,请说明理由.23.(10分)(23-24八年级上·重庆江津·期末)通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图,90ACE ∠=︒,AC CE =,过点A 作AB BC ⊥于点B ,过点E 作ED BC ⊥交BC 的延长线于点D .由90ACB DCE DCE E ∠+∠=∠+∠=︒,得CAB E ∠=∠.又90ABC CDE ∠=∠=︒,AC CE =,可以推理得到ABC CDE △△≌,进而得到AB =______,BC =______.(请完成填空)我们把这个数学模型称为“K 字”模型或“一线三等角”模型.【模型应用】(2)①如图,90ACE BCD ∠=∠=︒,AC CE =,BC CD =,连接AB 、DE ,且DE CG ⊥于点G ,AB 与直线CG 交于点F ,求证:点F 是AB 的中点;②如图,若点M 为x 轴上一动点,点N 为y 轴上一动点,点P 的坐标为()51,,是否存在以M 、N 、P 为顶点且以PM 为斜边的三角形为等腰直角三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.24.(12分)(22-23八年级上·江苏南京·阶段练习)已知,在ABC 中,AB AC =,D A E ,,三点都在直线m 上,且9DE cm BDA AEC BAC =∠=∠=∠,.(1)如图①,若AB AC ⊥,则BD 与AE 的数量关系为___________,CE 与AD 的数量关系为___________;(2)如图②,判断并说明线段BD ,CE 与DE 的数量关系;(3)如图③,若只保持7BDA AEC BD EF cm ∠=∠==,,点A 在线段DE 上以2cm/s 的速度由点D 向点E 运动,同时,点C 在线段EF 上以cm /s x 的速度由点E 向点F 运动,它们运动的时间为s t ().是否存在x ,使得ABD △与EAC 全等?若存在,求出相应的t 的值;若不存在,请说明理由.参考答案:1.C【分析】由题意易得90ADC CEB ∠=∠=︒,则有BCE DAC ∠=∠,进而可证ADC CEB ∆∆≌,然后根据全等三角形的性质求解即可.【详解】解:∵AC BC =,90ACB ∠=︒,AD DE ⊥,BE DE ⊥,∴90ADC CEB ∠=∠=︒,∴90ACD BCE ∠+∠=︒,90ACD DAC ∠+∠=︒,∴BCE DAC ∠=∠,∵在ADC ∆和CEB ∆中,ADC CEB DAC BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADC CEB ∆∆≌;∴6cm EC AD ==,14cm DC BE ==,∴20(cm)DE DC CE =+=,故选C .【点拨】本题主要考查全等三角形的性质与判定,熟练掌握三角形全等的判定条件是解题的关键.2.D【分析】利用同角的余角相等求出2A ∠=∠,再利用“角角边”证明ABC 和CED 全等,根据全等三角形对应边相等,对应角相等,即可解答.【详解】∵90B E ∠=∠=︒,∴190A ∠+∠=︒,290D ∠+∠=︒,∵AC CD ⊥,∴1290∠+∠=︒,故D 错误;∴2A ∠=∠,故B 正确;∴90A D ∠+∠=︒,故A 正确;在ABC 和CED 中,2A B E AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABC CED ≅ ,故C 正确;故选: D .【点拨】本题考查了全等三角形的判定与性质,等角的余角相等的性质,熟练掌握三角形全等的判定方法并确定出全等的条件2A ∠=∠是解题的关键.3.C【分析】本题可通过全等三角形来求BE 的长.△BEC 和△CDA 中,已知了一组直角,∠CBE 和∠ACD 同为∠BCE 的余角,AC=BC ,可据此判定两三角形全等;那么可得出的条件为CE=AD ,BE=CD ,因此只需求出CD 的长即可.而CD 的长可根据CE 即AD 的长和DE 的长得出,由此可得解.【详解】解:∵∠ACB=90°,BE ⊥CE ,∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°;∴∠ACD=∠CBE ,又AC=BC ,∴△ACD ≌△CBE ;∴EC=AD ,BE=DC ;∵DE=6cm ,AD=9cm ,则BE 的长是3cm .故选C .【点拨】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.4.D【分析】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.过C 作直线l y ∥轴,过B 作BE l ⊥于E ,过A 作AD l ⊥于D ,于是得到90ADC ACB BEC ∠=∠=∠=︒,得到CAD BCE ∠=∠,根据全等三角形的性质得到,AD CE CD BE ==,根据点()0,1B -,点()1,1C ,得到1,112BE CD AD CE ====+=,于是得到结论.【详解】解:过C 作直线l y ∥轴,过B 作BE l ⊥于E ,过A 作AD l ⊥于D ,∴90ADC ACB BEC ∠=∠=∠=︒,∴90DAC ACD ACD BCE ∠+∠=∠+∠=︒,∴CAD BCE ∠=∠,在ACD 与CBE △中,CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ACD CBE ≌,∴,AD CE CD BE ==,∵点()0,1B -,点()1,1C ,∴1,112BE CD AD CE ====+=,∴()1,2A -.故选:D .5.D【分析】利用全等三角形判定()AAS ,证得OBD 与COE 全等,根据全等三角形性质可求出OE 和OD 的值,进而求出OA 的值,最后根据OA OE AE -=,即可求出问题答案.【详解】解:90BOC ∠=︒ ,90BOD COE ∴∠+∠=︒,90BDO ∠=︒ ,90CEO ∠=︒,90BOD OBD ∴∠+∠=︒,90COE OCE ∠+∠=︒,COE OBD ∴∠=∠,BOD OCE ∠=∠,又OB CO = ,()OBD COE AAS ∴≅ ,1.4m OE BD ∴==, 1.8m OD CE ==,1.8m 1m 1.4m 1.4m AE OA OE OD DA OE ∴=-=+-=+-=.故选:D .【点拨】本题考查了利用三角形全等测距离的问题,理解题意及熟知三角形的性质与判定是解题关键.6.B【分析】由正方形的性质知,AB DA =,由同角的余角相等知,BAF ADE ∠=∠,又有90AFB DEA ∠=∠=︒,故根据AAS 证得ABF DAE ≌.【详解】证明:∵四边形ABCD是正方形,∴90AB DA BAF DAE =∠+∠=︒,,∵90ADE DAE ∠+∠=︒,∵BAF ADE ∠=∠,在ABF △与DAE 中,BAF ADE AFB AED AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABF DAE ≌△△.故选:B .【点拨】本题利用了正方形的性质,同角的余角相等,全等三角形的判定,学生要以常用的几种判定方法掌握并灵活运用.7.C【分析】本题考查了三角形全等的判定与性质,根据三角形内角和定理,证明()AAS ABC CED ≌ ,由DE BC BE AB ==-即可求出结果.【详解】解:180B ACB BAC ∠+∠+∠=︒ ,B E ACD ∠∠∠==,180ACD ACB BAC ∴∠+∠+∠=︒,180ACD ACB DCE ∠+∠+∠=︒,BAC DCE ∴∠=∠,在ABC 和CED △中,BAC DCE B E AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABC CED ≌ ,,BC DE AB CE ∴==,2AB =,6BE =,∴624DE BC BE CE BE AB ==-=-=-=,故选:C .8.C【分析】本题主要考查坐标与图形,全等三角形的判定与性质,过点C 作CM x ⊥轴于点M ,证明ABO BCM ≌V V 得出2BM OA ==,进一步得出3OM =即可【详解】解:过点C 作CM x ⊥轴于点M ,如图,则90,CBM BCM ∠+∠=︒根据题意得90,ABC ∠=︒∴90,ABO CBM ∠+∠=︒∴,ABO BCM ∠=∠又,90,AB BC AOB BMC =∠=∠=︒∴,AOB BMC ≌V V ∴2,BVM AB ==∴123,OM OB BM =+=+=即点C 处的接收器到y 轴的距离为3,故选:C9.D【分析】由已知和图形根据“K ”字形全等,用AAS 可证△FEA ≌△MAB ,△DHC ≌△CMB ,推出AM =EF =6,AF =BM =3,CM =DH =2,BM =CH =3,从而得出FH =14,根据阴影部分的面积=S 梯形EFHD -S △EF A -S △ABC -S △DHC 和面积公式代入求出即可.【详解】∵AE ⊥AB ,EF ⊥AF ,BM ⊥AM,∴∠F =∠AMB =∠EAB =90°,∴∠FEA +∠EAF =90°,∠EAF +∠BAM =90°,∴∠FEA =∠BAM ,在△FEA 和△MAB 中F BMA FEA BAM AE AB ∠∠⎧⎪∠∠⎨⎪⎩===,∴△FEA ≌△MAB (AAS ),∴AM =EF =6,AF =BM =3,同理CM =DH =2,BM =CH =3,∴FH =3+6+2+3=14,∴梯形EFHD 的面积=12EF DH FH + ()=126241⨯+⨯()=56,∴阴影部分的面积=S 梯形EFHD -S △EF A -S △ABC -S △DHC =11566322183322-⨯⨯-⨯⨯-⨯⨯=32.故选D .【点拨】本题考查了三角形的面积,梯形的面积,全等三角形的性质和判定等知识点,关键是把不规则图形的面积转化成规则图形的面积.10.B【分析】本题考查全等三角形的判定和性质.正确掌握相关性质内容是解题的关键.由AB CD ⊥可得90A D ∠+∠=︒,由CE AD ⊥,BF AD ⊥可得90CED AFB ∠=∠=︒,A B ∠∠=︒+90,从而B D ∠=∠,进而证得()AAS ABF CDE ≌,可得4AF CE ==,3BF DE ==,推出()AD AF DF AF DE EF =+=+-,代入数据即可解答.【详解】∵AB CD ⊥,∴90A D ∠+∠=︒,∵CE AD ⊥,BF AD ⊥,∴90CED AFB ∠=∠=︒,∴1801809090A B AFB ∠+∠=︒-∠=︒-︒=︒,∴B D ∠=∠,∵AB CD =,∴()AAS ABF CDE ≌,∴4AF CE ==,3BF DE ==,∴()()4325AD AF DF AF DE EF =+=+-=+-=.故选:B11.28【分析】作CD ⊥OB 于点D ,依据AAS 证明D AOB B C ∆≅∆,GMF ,再根据全等三角形的性质即可得到结论.【详解】解:过点C 作CD ⊥OB 于点D,如图,∴90CDB AOB ∠=∠=︒∵ABC ∆是等腰直角三角形∴AB =CB ,90ABC ∠=︒∴90ABO CBD ∠+∠=︒又90CBD BCD ∠+∠=︒∴ABO BCD∠=∠在ABO ∆和BCD ∆中,AOB BDC ABO BCD AB CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABO BCD AAS ∆≅∆∴28cmCD BO ==故答案为:28.【点拨】本题主要考查了等腰直角三角形的性质、三角形全等的判定与性质,正确作出辅助线构造全等三角形是解答本题的关键.12.(-1,4)【分析】过点A 和点C 作x 轴的垂线,垂足为D ,E ,证明△COE ≌△OAD ,得到OE=AD ,CE=OD ,再根据点A 的坐标可得结果.【详解】解:过点A 和点C 作x 轴的垂线,垂足为D ,E ,∵∠AOC=90°,∴∠COE+∠AOD=90°,又∠CEO=90°,则∠COE+∠OCE=90°,∴∠OCE=∠AOD ,在△COE 与△OAD 中,OCE AOD CEO ODA OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△COE ≌△OAD (AAS ),∴OE=AD ,CE=OD ,∵点A 的坐标为(4,1),∴OD=4,AD=1,∴CE=OD=4,OE=AD=1,∴点C 的坐标为(-1,4),故答案为:(-1,4).【点拨】本题考查了全等三角形的判定和性质,坐标与图形,解题的关键是利用已知条件,作出辅助线,证明全等.13.7【分析】根据全等三角形来实现相等线段之间的关系,从而进行计算,即可得到答案;【详解】解:∵BE ⊥l ,CF ⊥l ,∴∠AEB =∠CFA =90°.∴∠EAB +∠EBA =90°.又∵∠BAC =90°,∴∠EAB +∠CAF =90°.∴∠EBA =∠CAF .在△AEB 和△CFA 中∵∠AEB =∠CFA ,∠EBA =∠CAF ,AB =AC ,∴△AEB ≌△CFA .∴AE =CF ,BE =AF .∴AE +AF =BE +CF .∴EF =BE +CF .∵2,5==BE CF ,∴257EF =+=;故答案为:7.【点拨】本题考查了全等三角形的判定和性质,余角的性质,解题的关键是熟练掌握所学的知识,正确的证明三角形全等.14.36.【分析】作DE ⊥DB 交AB 于E ,EF 垂直AC 于F ,则∠DEB =90°-∠ABD =45°,证出AE =DE =DB ,通过证明△AEF ≌△BCD ,得出BC ==AF=12AD=6,由三角形面积公式即可得出答案.【详解】作DE ⊥DB 交AB 于E ,EF 垂直AC 于F ,如图所示:则∠DEB =90°-∠ABD =45°,∴△BDE 是等腰直角三角形,∴DB =DE ,∵∠ABD =2∠BAC =45°,∴∠BAC =22.5°,∴∠ADE =∠DEB -∠BAC =22.5°=∠BAC ,∴AE =DE =DB ,∵∠AFE=90°,∴F 是AD 中点,AF=FD ,又∵∠C=90°,∴∠CBD=90°-45°-22.5°=22.5°,在Rt △AEF 和Rt △BCD 中A CBD AFE BCD AE BD =⎧⎪=⎨⎪=⎩∠∠∠∠∴Rt △AEF ≌Rt △BCD (AAS ),∴AF=BC=12AD=6,∴△ABD 的面积S=12AD ×BC =12×12×6=36;故答案为:36.【点拨】本题考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,三角形面积公式的的计算,熟记特殊三角形的判定和性质定理是解题关键.15.3【分析】本题考查了全等三角形的应用;解答本题的关键是利用互余关系找三角形全等的条件,对应角相等,并巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.本题的关键是求得ACM BMD ≌.【详解】解:∵90CMD ∠=︒,∴90CMA DMB +=︒∠∠,又∵90CAM ∠=︒,∴90CMA C ︒∠+∠=,∴C DMB ∠=∠,在ACM 和BMD 中,A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ACM BMD ≌,∴9BD AM ==米,1293BM =-=(米),∵该人的运动速度1米/秒,他到达点M 时,运动时间为313÷=(秒).故答案为:3.16.1.5或4.5【分析】本题考查了全等三角形的判定和性质,直角三角形的性质,分①当点E 在射线BC 上移动时,639BE CE BC ''=+=+=,②当点E 在射线CB 上移动时,()633cm BE AC BC =-=-=,熟练正确全等三角形的判定和性质是解题的关键.【详解】解:∵EF BC ⊥,∴90CEF ACB ∠=︒=∠,在CEF △和ACB △中,ECF A CEF ACB CF AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS CEF ACB ≌,∴6CE AC ==,如图,①当点E 在射线BC 上移动时,639BE CE BC ''=+=+=,∵点E 从点B 出发,在直线BC 上以2cm 的速度移动,∴E 移动了:()92 4.5s ÷=;②当点E 在射线CB 上移动时,()633cm BE AC BC =-=-=,∵点E 从点B 出发,在直线BC 上以2cm 的速度移动,∴E 移动了:()32 1.5s ÷=;综上所述,当点E 在射线CB 上移动4.5s 或1.5s 时,CF AB =,故答案为:1.5或4.5.17.4cm.【分析】过点E 作EF ⊥AN 于F ,先利用AAS 证出△ABC ≌△FCE ,从而得出AB=FC=8cm ,AC=FE ,然后利用AAS 证出△DCM ≌△EFM,从而求出CM 的长.【详解】解:过点E 作EF ⊥AN 于F ,如图所示∵AN ⊥AB ,△BCE 和△ACD 为等腰直角三角形,∴∠BAC=∠BCE=∠ACD=∠CFE =90°,BC=CE ,AC=CD∴∠ABC+∠ACB=90°,∠FCE+∠ACB =90°,∴∠ABC =∠FCE ,在△ABC 和△FCE 中BAC CFE ABC FCE BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△FCE∴AB=FC=8cm ,AC=FE∴CD=FE在△DCM 和△EFM 中90DMC EMF DCM EFM CD FE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△DCM ≌△EFM∴CM=FM=12FC=4cm.故答案为:4cm.【点拨】此题考查的是全等三角形的判定及性质,掌握用AAS 证两个三角形全等是解决此题的关键.18.6【分析】本题属于全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定方法.证明ABE ≌CAF V ,推出ABE 与CAF V 面积相等,可得结论.【详解】解:在等腰三角形ABC 中,AB AC =,2CD BD =,ABD ∴ 与ADC △等高,底边比值为1:2,ABD ∴ 与ADC △的面积比为1:2.ABC 的面积为9,ABD ∴ 与ADC △的面积分别为3和6,BED CFD ∠=∠ ,AEB AFC ∴∠=∠.BED ABE BAE ∠=∠+∠ ,BAE CAF BAC ∠+∠=∠,BED BAC ∠=∠,BAC ABE BAE ∴∠=∠+∠,CAF ABE ∴∠=∠.在ABE 和CAF V 中,AEB AFC ABE CAF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS ABE CAF ∴ ≌,ABE ∴ 与CAF V 面积相等,ABE ∴ 与CDF 的面积之和为ADC △的面积,ABE ∴ 与CDF 的面积之和为6.故答案为:6.19.全等,理由见解析【分析】首先证明CAD BCE ∠=∠,即可证明CDA BEC ≌V V ,即可解题.【详解】全等,理由如下:BE CE ⊥,E AD CE ⊥,,90ACB ∠=︒∴90BCE DCA ∠+∠=︒,90DAC DCA ∠+∠=︒.∴CAD BCE ∠=∠;在BEC 和DAC △中,90BCE DAC BEC CDA BC AC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()AAS BEC DAC ≌V V .【点拨】此题是三角形综合题,主要考查了全等三角形的判定,掌握证明全等三角形的方法是解题的关键.20.(1)CD DF =,CD DF⊥(2)成立,见解析【分析】(1)根据题意可直接证明AFD BDC ≌ ,即可得出结论;(2)仿照(1)的证明过程推出ADF BCD ≌ ,即可得出结论.【详解】(1)解:由题意,90A B ∠=∠=︒,在AFD △与BDC 中,AF BD A B AD BC =⎧⎪∠=∠⎨⎪=⎩∴()SAS AFD BDC ≌ ,∴DF DC =,ADF BCD ∠=∠,在Rt BDC 中,90BDC BCD ∠+∠=︒,∴90BDC ADF ∠+∠=︒,∴90FDC ∠=︒,∴CD DF ⊥,综上可知CD DF =,CD DF ⊥;(2)解:成立,理由如下:AF AB ⊥,∴90DAF ∠=︒,在ADF △和BCD △中,AF DB DAF CBD AD BC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADF BCD ≌ ,∴DF DC =,ADF BCD ∠=∠,90BCD CDB ∠+∠=︒,∴90ADF CDB ∠+∠=︒,即90CDF ∠=︒,∴CD DF ⊥;∴(1)中结论仍然成立.【点拨】本题考查全等三角形的判定与性质,以及直角三角形两锐角互余等,熟练掌握全等三角形的判定定理是解题关键.21.(1)见解析(2)成立,理由见解析【分析】(1)本题主要考查全等三角形的判定和性质综合,利用题目中的已知条件导角,可推导CBN BAM ∠=∠,最后证明(AAS)≌AMB BNC ,直接可证.(2)利用AMB ABC ∠=∠及ABN ∠是ABM 的外角,可以推出MAB CBN ∠=∠,再利用AAS 可以判定(AAS)≌AMB BNC ,再利用全等的性质导边即可证明.【详解】(1)证明:∵AM MN ⊥于点M ,⊥CN MN 于点N ;∴90AMB BNC ∠=∠=︒;∴90MAB ABM ∠+∠=︒;∵90ABC ∠=︒,∴90ABM NBC ∠+∠=︒;∴MAB NBC ∠=∠;在ABM 和BCN △中,AMB BNC MAB NBC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABM BCN ≌;∴AM BN =,BM CN =;∴MN BN BM AM CN =+=+.(2)MN AM CN =+成立.理由如下:设AMB ABC BNC α∠=∠=∠=;∴180ABM BAM ABM CBN α∠+∠=∠+∠=︒-;∴BAM CBN ∠=∠;在ABM 和BCN △中;BAM CBN AMB BNC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABM BCN ≌;∴AM BN =,BM CN =;∴MN BN BM AM CN =+=+;故MN AM CN =+成立.22.(1)25;115;小(2)当2DC =时,ABD DCE≌△△(3)可以;BDA ∠的度数为110︒或80︒【分析】(1)由已知平角的性质可得180EDC ADB ADE ∠=︒-∠-∠,再利用三角形内角和定理进而求得DEC ∠,即可判断点D 从B 向C 运动过程中,BDA ∠逐渐变小;(2)当2DC =时,由已知和三角形内角和定理可得140DEC EDC ∠+∠=︒,140ADB EDC ∠+∠=︒,等量代换得ADB DEC ∠=∠,又由2AB AC ==,可得()AAS ABD DCE ≌△△;(3)根据等腰三角形的判定定理,利用三角形内角和定理求解即可.【详解】(1)解:1801801154025EDC ADB ADE ∠=︒-∠-∠=︒-︒-︒=︒,1801802540115DEC EDC C ∠=︒-∠-∠=︒-︒-︒=︒,点D 从B 向C 运动时,BDA ∠逐渐变小,故答案为:25;115;小.(2)解:当2DC =时,ABD DCE ≌△△,理由:40C ∠=︒ ,140DEC EDC ∴∠+∠=︒,又40ADE ∠=︒ ,∴140ADB EDC ∠+∠=︒,ADB DEC ∴∠=∠,又 B C ∠=∠,2AB DC ==,∴()AAS ABD DCE ≌△△;(3)解:当BDA ∠的度数为110︒或80︒时,ADE V 的形状是等腰三角形;理由:110BDA ∠=︒ 时,70704030ADC EDC ∴∠=︒∠=︒-︒=︒,,40C ∠=︒ ,70DAC ∴∠=︒,304070AED C EDC ∠=∠+∠=︒+︒=︒,DAC AED ∴∠=∠,∴ADE V 是等腰三角形;80BDA ∠=︒ 时,100ADC ∴∠=︒,40C ∠=︒ ,40DAC ∴∠=︒,DAC ADE ∴∠=∠,∴ADE V 的形状是等腰三角形.【点拨】本题考查了等腰三角形的判定和性质,全等三角形的判定,熟练掌握知识点是解题的关键.23.(1)CD ,DE ;(2)见解析;(3)存在,()4,0-或()6,0-【分析】本题是三角形综合题目,考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、坐标与图形性质、直角三角形的性质等知识;(1)由全等三角形的性质可得出答案;(2)过点A 作AM FG ⊥交FG 于点M ,过点B 作BN FG ⊥交FG 于点N ,证明(AAS)ACM CEG ≌,得出AM CG =;同理可得:BCN CDG ≌.得出BN CG =,证明(AAS)AMF BNF ≌,由全等三角形的性质可得出AF BF =;(3)分两种情况,由全等三角形的性质可得出答案.【详解】(1)解:由题意可知ABC CDE △≌△,AB CD ∴=,BC DE =,故答案为:CD ,DE ;(2)证明:如图1,过点A 作AM FG ⊥交FG 于点M ,过点B 作BN FG ⊥交FG 于点N,ED CG ⊥ ,90ACE ∠=︒,90ACF ECG ECG E ∴∠+∠=∠+∠=︒,ACF E ∴∠=∠,在ACM △和CEG 中,ACM E AMC CGE AC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)ACM CEG ∴ ≌,AM CG ∴=;同理可得:BCN CDG ≌.BN CG ∴=,AM BN ∴=,在AMF 和BNF 中,AFM BFN AMF BNF AM BN ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)AMF BNF ∴ ≌,AF BF ∴=,∴点F 是AB 的中点.(3)解:如图,当点N 在x 轴正半轴上时,由【模型呈现】可知MEN NDP ≌,5EM DN ∴==,DP EN =,514DP ∴=-=,4EN ∴=,(4,0)M ∴-;当点N 在x 轴负半轴上时,同理可得(6,0)M -.综上所述,点M 的坐标为(4,0)-或(6,0)-.24.(1)BD AE CE AD==,(2)DE BD CE=+(3)12t x ==,或928,49t x ==【分析】(1)利用平角的定义和三角形内角和定理得CAE ABD ∠=∠,再利用AAS 证明ABD CAE ≌, 得BD AE CE AD =,=;(2)由(1)同理可得ABD CAE △△≌,得BD AE CE AD ==,,可得答案;(3)分DAB ECA ≌ 或DAB EAC ≌△△两种情形,分别根据全等三角形的性质可解决问题.【详解】(1)解:∵BDA AEC BAC ∠=∠=∠,∴BAD CAE BAD ABD ∠+∠=∠+∠,∴CAE ABD ∠=∠,∵BDA AEC BA CA ∠=∠=,,∴ABD CAE AAS ≌() ,∴BD AE CE AD ==,,故答案为:BD AE CE AD ==,;(2)DE BD CE =+,由(1)同理可得ABD CAE AAS ≌() ,∴BD AE CE AD ==,,∴DE BD CE =+;(3)存在,当DAB ECA ≌ 时,∴2,7AD CE cm BD AE cm ====,∴1t =,此时2x =;当DAB EAC ≌△△时,∴ 4.5,7,AD AE cm DB EC cm ====∴924AD t ==,928749x =÷=,综上:12t x ==,或928,49t x ==.【点拨】本题是三角形综合题,主要考查了全等三角形的判定与性质,熟练掌握一线三等角基本模型是解题的关键,同时渗透了分类讨论的数学思想.。
初中数学《全等三角形的常见基本模型》专题训练
专题训练:全等三角形的常见模型【回归概念】两个全等三角形一般用边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)、和直角三角形的斜边,直角边(HL)来判定。
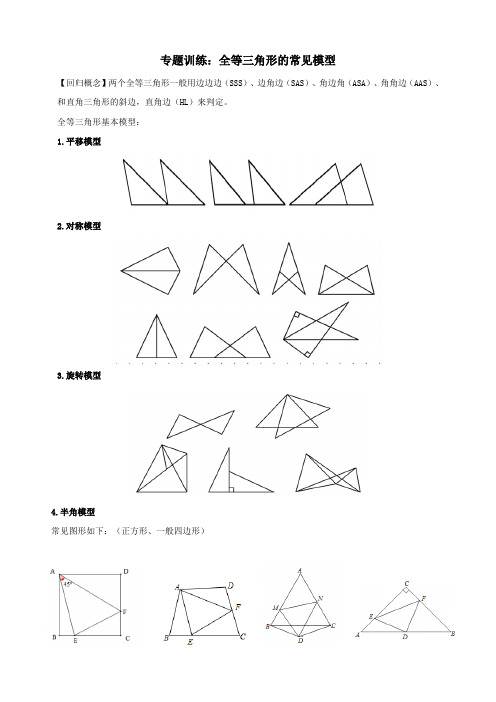
全等三角形基本模型:1.平移模型2.对称模型3.旋转模型4.半角模型常见图形如下:(正方形、一般四边形)5.一线三等角全等模型6. 手拉手模型 顶角相等的两任意等腰三角形:手拉手模型 两个等边三角形:手拉手模型 两个等腰直角三角形:CDEAB图①CDE AB图②CDE AB图③PCABDECE FAB【例题一】在△ABC 中,∠ACB= 900,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E 。
(1)当直线MN 绕点C 旋转到图1的位置时,△ADC ≌△CEB ,且 DE=AD+BE 。
你能说出其中的道理吗?(2)当直线MN 绕点C 旋转到图2的位置时, DE =AD-BE 。
说说你的理由。
(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系。
【例题二】如图,过ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.【例题三】如图,已知△ABD 和△BCE 为等边三角形,连接AE 交BD 于点G ,连接CD 交BE 于点F ,AE 与CD 交点为M ,A 、B 、C 三点共线。
则有哪些结论:CDEFG AB51234宜宾市2014-2019年期末试题1.(2014年八上24题10分)如图,等边△ABC 中,AO 是∠BAC 的角平分线,D 为AO 上一点,以CD 为一边且在CD 下方作等边△CDE ,连接BE . (1)求证:△ACD ≌△BCE ;(2)延长BE 至Q ,P 为BQ 上一点,连接CP 、CQ 使CP=CQ=5,若BC=8时,求△BPC 的面积.2.(2015年八上24.12分)如图:在△ABC 中,AB =AC ,D 、A 、E 在直线m 上,∠ADB =∠AEC =∠BAC . (1) 求证:DE =DB +EC(2) 若∠BAC =120°,AF 平分∠BAC ,且AF =AB ,连结FD 、FE .请判断△DEF 的形状, 并写出证明过程.3.(2016年八上24.本题满分12分)如图,△OAB 与△OCD 都是等边三角形,连接AC 、BD 相交于点E .(1)求证:①△OAC ≌△OBD , ②∠AEB =60; (2)连结OE ,OE 是否平分∠AED ?请说明理由.4.(2017年八上14.) 如图,90ACB ∠=,AC BC =,BE CE ⊥,AD CE ⊥,垂足分别为E ,D ,13AC =,5BE =,则DE = .5.(2018年八上24.本题满分12分)如图,在△ABC 中,2==AC AB ,32=BC , 且︒=∠120BAC ,点D 是线段BC 上的一动点(不与点B 、C 重合),连接AD ,作︒=∠30ADE , DE 交AC 于点E . ⑴求证:EDC BAD ∠=∠;⑵当BD= 时,△ABD ≌△EDC ,并说明理由. ⑶当△ADE 是直角三角形时,求AD 的长? 6. (2019年八上18.)如图,已知AB AF =, 60=∠FAB ,AC AE =, 60=∠EAC ,CF 和BE 交于O 点,则下列结论:①BE CF =;② 120=∠COB ;③OA 平分FOE ∠;④OB OA OF +=.其中正确的有 .第24题图C BFDEAm第24题图OBACDE ABCDE第24题图。
八年级数学上册第13章全等三角形集训课堂练素养手拉手(共顶点)模型的等腰三角形新版华东师大版7

集训课堂 1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月22日星期二下午3时49分40秒15:49:4022.3.22
BC=AC, 在△BCE 和△ACD 中,∠BCE=∠ACD,
EC=DC, ∴△BCE≌△ACD(S.A.S.). ∴∠CBE=∠CAD=20°. ∴∠BEC=180°-20°-15°=145°.
3 如图,△ABC与△EDC都是等边三角形,当点B,C, D在一条直线上时,连结AD,BE交于点M,连结CM, 试探究线段BM与线段AM,CM之间的数量关系,并 说明理由.
2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那 些善于独立思考的人,给那些具有锲而不舍的人。2022年3月下午3时49分22.3.2215:49March 22, 2022
3、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。 2022年3月22日星期二3时49分40秒15:49:4022 March 2022
第13章
全等三角形
集课训题课2堂 练 素 养
“手拉手”(共顶点)模型的等腰三角形
习题链接
温馨提示:点击 进入讲评
1 2 3 4
1 【中考·哈尔滨】已知△ACB和△DCE都是等腰直角三 角形,∠ACB=∠DCE=90°,连结AE,BD交于点O, AE与DC交于点M,BD与AC交于点N. (1)如图①,求证:AE=BD;
冀教版八年级上册数学第13章 全等三角形 提分专项(五) 全等三角形常用模型

因为 A∠OA=ODOB=,∠OBC, 所以△AOODD≌=△OBBCC,(SAS).
(2)若∠ADO=35°,求∠DOC的度数.
解:因为△AOD≌△OBC, 所以∠ADO=∠OCB=35°. 因为OD∥BC, 所以∠DOC=∠OCB=35°.
冀教版八年级上
第13章 全等三角形
提分专项(五) 全等三角形常用模型
1 见习题 2 见习题 3 见习题 4 见习题 5 见习题
提示:点击 进入习题
6 见习题 7 见习题 8 见习题 9 见习题
答案显示
1.【2019·四川南充】如图,点O是线段AB的中点,OD∥BC且OD=BC. (1)求证:△AOD≌△OBC;
9.【2020·广西河池】(1)如图①,已知CE与AB交于点E,AC=BC,∠1 =∠2.求证:△ACห้องสมุดไป่ตู้≌△BCE.
证明:在△ACE和△BCE中,
AC=BC, ∴∵△A∠CE1≌=△B∠CE2(,SAS).
CE=CE,
(2)如图②,已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与 BE的数量关系,并说明理由.
(1)△ABE≌△CBD;
证明:(1)∵∠1=∠2, ∴∠1+∠CBE=∠2+∠CBE,即∠ABE= ∠CBD, 在△ABE和△CBD中.
A∠BA=BEC=B,∠CBD, BE=BD,
∴△ABE≌△CBD(SAS).
(2)∠1=∠3.
证明:∵△ABE≌△CBD, ∴∠A=∠C, 又∵∠AFB=∠CFE, ∴∠1=∠3.
证明:如图,连接AC,AD.
全等三角形模型总结及经典练习题

全等三角形模型及习题练习第一部分全等模型图一、平移模型特征:可看成是三角形在一边所在直线上移动构成的,故在同一直线上的对应边的相等关系一般可由加(减)公共边证得,对应角的相等关系可由平行线的性质证得。
二、平行模型(X型)特征:平行线所形成的同位角、内错角相等三、折叠轴对称模型(翻转型,部分X型)特征:图形关于某一条直线对称,则这条直线两边的部分能完全重合,重合的顶点就是全等三角形的对应点。
图①中有公共角∠A;图②中对顶角相等(∠AOC=∠BOD);图③④中分别有公共边AB,BD四、旋转模型特征:可看成是以三角形某一个顶点为中心旋转构成的,故一般有一对相等的角隐含在对顶角、某些角的和或差中五、角平分线模型旋转有重叠特征:角平分线形成的两个角相等,若把角平分线看成一条公共边,在角的两边再截取相等的线段,就可根据SAS得到全等三角形(如图①,ΔA1BD1≌ΔC1BD1),或者利用角平分线上的点到角两边的距离相等找到一组相等的边,就可根据HL得到全等三角形(如图②,ΔA2BD2≌ΔC2BD2)六、双直角三角形模型特征:证明多数可以用到同(等)角的余角相等这个定理,相等的角就是对应角七、一线三等角模型(K型)特征:如图①,,三个等角指的是α(图②中,α=90°),利用外角定理可证得∠1=∠2或∠3=∠4第二部分精选例题例1.如图,已知AB∥CD,AD∥BC,F在DC的延长线上,AM=CF,FM 交DA的延长线上于E.交BC于N,求证:AE=CN.思路分析:欲证AE=CN.看它们在哪两个三角形中,设法证这两个三角形全等即可.结合图形可发现△AME≌△FCN可证.题设告知AM=CF,AD∥BC,AB∥CD.由两平行条件,可找两对角相等.∵∠1=∠2(对顶角相等)∴∠2=∠E(等量代换)∴AE=CN (全等三角形的对应边相等)例2.△ABC中,∠ACB=90°,AC=BC,过C的一条直线CE⊥AE于E,BD⊥CE的延长线于D,求证:AE=BD+DE.思路分析:从本例的结论知是求线段和的问题,由此入手,很难找到突破口.此时可迅速调整思维角度,可仔细观察图形,正确的图形是证题的“向导”,由此可发现△ACE与△CBD好像(猜测)全等.那么AE=CD=CE+DE.又BD=CE.那么,此时已水落石出.AC=BC(已知)∠1=∠3 (已证)∠AEC=∠CDB(已证)∴△ACE≌△CBD(AAS)∴BD=CE,AE=CD(全等三角形的对应边相等)∵AE=CE=CE+DE∴AE=BD+DE(等量代换)例3.如图,AD是△ABC的中线,DE,DF分别平分∠ADB和∠ADC,连接EF,求证:EF<BE+CF. 定对象:△ABC定角度:三角形全等分析:由结论EF<BE+CF很容易与定理“三角形两边之和大于第三边”联系在一块,观察图形,BE,CF,EF 条件分散,不在一个三角形中,必须设法(平移,旋转,翻转等)把三者集中在一个三角形中,是打开本例思路的关键.由角的平分线这一线索,可将△BDE沿角平分线翻转180°,即B点落在AD的点B'上(如图)(也就是在DA上截取DB'=BD),连结EB',B'F,此时△BDE与△B'DE完全重合,所以△BDE≌△B'DE(两个三角形能够完全重合就是全等三角形,所以BE=B'E(全等三角形的对应边相等).在△EFB'中,EF<B'E+B'F(三角形的两边之和大于第三边).∴EF<BE+CF(等量代换).例4 如图,已知CD⊥AB于D,BE⊥AC于E,△ABE≌△ACD,∠C= 20°,AB=10,AD= 4, G为AB延长线上一点.求∠EBG的度数和CE的长.定对象:如图定角度:三角形全等分析:(1)图中可分解出四组基本图形:有公共角的Rt△ACD 和Rt△ABE;△ABE≌△ACD,△ABE的外角∠EBG或∠ABE的邻补角∠EBG.例5已知:如图,△ABC≌△ADE,BC的延长线交DA于F,交 DE于G,∠ACB=105°,∠CAD=10°,∠D=25°.求∠EAC,∠DFB,∠DGB的度数.例6.在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=20 cm,则△DBE的周长等于多少?分析:对象:△DBE的周长角度:(1)BD,DE,BE的长解:因为DE⊥AB,所以AED ACD∠=∠因为AD是∠BAC的平分线,所以EAD CAD≅则AE=AC ∠=∠又因为AD为公共边所以AED ACD DE=DC所以△DBE的周长=BE+DE+BD=AB-AE+BC=20例7如图13—3—8所示,已知在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.求证:EF⊥AD.分析:对象:△ABC 角度:(1)AD是∠BAC的平分线,(2)DE⊥AB于E,DF⊥AC于F证明:因为DE⊥AB于E,DF⊥AC于F,所以0∠=∠=又因AED AFD90为AD是∠BAC的平分线,所以EAD FAD∠=∠由于AD是公共边所以AED AFD≅则AE=AF 因为AD是∠BAC的平分线所以EF⊥AD。
专题13 全等三角形重难点模型(五大模型)(原卷版)

专题13全等三角形重难点模型(五大模型)模型一:一线三等角型模型二:手拉手模型模型三:半角模型模型四:对角互补模型模型五:平行+线段中点构造全等模型【典例分析】【模型一:一线三等角型】如图一,∠D=∠BCA=∠E=90°,BC=AC。
结论:Rt△BDC≌Rt△CEA模型二一线三等角全等模型如图二,∠D=∠BCA=∠E,BC=AC。
结论:△BEC≌△CDA图一图二应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).(1)当a=2时,则C点的坐标为;(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.【变式1】点A的坐标为(4,0),点B为y轴负半轴上的一个动点,分别以OB、AB为直角边在第三象限和第四象限作等腰Rt△OBC和等腰Rt△ABD.(1)如图一,若点B坐标为(0,﹣3),连接AC、OD.①求证:AC=OD;②求D点坐标.(2)如图二,连接CD,与y轴交于点E,试求BE长度.【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.【变式2】已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE =9cm,∠BDA=∠AEC=∠BAC(1)如图①,若AB⊥AC,则BD与AE的数量关系为,CE与AD 的数量关系为;(2)如图②,判断并说明线段BD,CE与DE的数量关系;(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.【模型二:手拉手模型】应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;②作辅助线构造手拉手模型,难度比较大。
华师版八年级数学上册作业课件(HS)第十三章 全等三角形 专题练习(五) 全等三角形的基本模型

(2)由(1)知AE=AF. ∵∠EAF = 90° , AH⊥EF , 易 证 △ AHE≌△AHF , 而 ∠ AEF + ∠AFE=90°,∴∠AEF=∠AFE=45°. ∴∠AHF=∠AHE=90°=∠CFH. ∴∠EAH=90°-∠AEF=45°=∠AEF,过点H作AE的垂线可证AH =EH. ∵D 为 AC 中 点 , ∴ AD = CD.∵∠ADH = ∠ CDF , ∴△ADH≌△CDF(AAS).∴AH=CF. ∴EH=CF
A.5.5 B.4 C.4.5 D.3
2.如图,在正三角形 ABC中,点D在边AB上,点E在边AC上,将 △ ADE 折 叠 , 使 点 A 落 在 BC 边 上 的 点 F 处 , 则 ∠ BDF + ∠ CEF = ____1_2_0_°____.
3.已知点A,D,C,F在一条直线上,BC与DE交于点G,AD=CF, BC∥EF且BC=EF,求证:△ABC≌△DEF.
5.如图,在Rt△ABC中,∠CAB=90°,AB=AC,D为AC的中点, 过点C作CF⊥BD,交BD的延长线于点F,过点A作AE⊥AF交BD于点E.
(1)求证:△ABE≌△ACF; (2)过点A作AH⊥BF于点H,求证:CF=EH. 证明:(1)∵AE⊥AF,∴∠EAF=∠CAB=90°. ∴∠EAF-∠EAC=∠CAB-∠EAC,即∠CAF=∠BAE.∵CF⊥BD, ∴∠BFC=90°=∠CAB. ∴∠ADB+∠ABD=∠DCF+∠FDC=90°. ∵∠ADB=∠FDC,∴∠ABD=∠DCF. ∵AB=AC,∴△ABE≌△ACF(ASA)
类型之三 三垂直型
解题模型:利用“同(等)角的余角相等”寻找角相等,已知一组直角三 角形的等角,再寻找一组对应边相等,即可证明全等.
2021——2022冀教版初二上学期第十三章 三角形全等几何模型-斜边上的中线(专项练习)

专题13.5 三角形全等几何模型-斜边上的中线(专项练习)通过斜边上的中线达到线段、角、面积等等的变换,此模型在几何证明中占据相当重要的地位,在压轴题里常常有此类题的身影,因为通过此模型的学习,对初学三角形全等的学生来讲,是十分必要的,对提升学生几何综合能力是相当重要。
本专题汇编了一些斜边上中线的常考题,供师生选择使用。
知识储备:0=∆∠∆∆如图一,在ABC 中,C 90,则边AB 叫ABC 的斜边,AC 、BC 是ABC 的直角边。
图一0=∆∠∆如图二,在ABC 中,C 90,CO 为ABC 斜边上的中线,则 OA=OB=OC 或AB=2OC ,即直角三角形斜边上的中线等于斜边一半。
图二一、填空题1.一副三角板如图摆放,点F 是45角三角板ABC 的斜边的中点,4AC =.当30角三角DEF 的直角顶点绕着点F 旋转时,直角边DF EF ,分别与,AC BC 相交于点.M N ,则CMFN 的面积为____________.二、解答题2.如图,在等腰直角三角形ABC 中,90C ∠=︒,AC a =,点E 为边AC 上任意一点,点D 为AB 的中点,过点D 作DF DE ⊥交BC 于点F .求证:CE CF +为定值.3.已知:在ABC 中,AC=BC ,∠ACB=90°,点D 是AB 的中点,点E 是AB 边上一点.(1)直线BF 垂直于CE 于点F ,交CD 于点G (如图1),求证:AE=CG ;(2)直线AH 垂直于CE ,垂足为H ,交CD 的延长线于点M (如图2),求证:BCE CAM ≌.4.如图在Rt ABC △中,AB AC =,90BAC ∠=︒,O 为BC 的中点.(1)写出点O 到ABC 的三个顶点A 、B 、C 的距离的大小关系.(2)如果点M 、N 分别在线段AB 、AC 上移动,移动中保持AN BM =,请判断OMN 的形状,并证明你的结论.(3)当点M 、N 分别在AB 、AC 上运动时,四边形AMON 的面积是否发生变化?说明理由.5.已知:三角形ABC 中,∠A =90°,AB =AC ,D 为BC 边的中点,(1)如图∠,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:∠DEF 为等腰直角三角形.(2)如图∠,若E ,F 分别为AB ,CA 延长线上的点,仍有BE =AF ,其他条件不变,那么,∠DEF 是否仍为等腰直角三角形?证明你的结论.6.已知:如图,等腰直角三角形ABC 中,90A ∠=︒,D 为BC 中点,E 、F 分别为AB 、AC 上的点,且满足EA CF =.连接AD .求证:DE DF =.7.如图,在Rt ABC 中,90ACB ∠=︒,6AC BC ==,点D 为斜边AB 的中点,90EDF ∠=︒,DEF 的顶点E ,F 分别在边AC ,BC 上,求EC CF +的长.8.如图,在ABC 中,,90CA CB ACB =∠=︒,O 为AB 的中点,D ,E 分别在,AC BC上,且OD OE ⊥.求证:CE CD AC +=.9.如图,在ABC 中,90,,ACB AC BC D ︒∠==是AB 的中点,点E 在AC 上,点F 在BC 上,且AE CF =.求证:,DE DF DE DF =⊥.10.∠ABC 中,AC=BC ,∠ACB=90°,CD=BD ,∠1=∠2,求证:CM∠AD 。
第十三章 全等三角形 5.专项二 全等三角形的常见模型强化练

专项二 全等三角形的常见模型强化练
4. 新定义型阅读理解题 阅读材料,回答下列问题.筝形的定义:两组邻边 分别相等的四边形叫做筝形,几何图形的定义通常可作为图形的性质也可以作 为图形的判定方法.也就是说,如图,若四边形 ABCD 是一个筝形,则 DA=DC ,BA=BC;若 DA=DC,BA=BC,则四边形 ABCD 是筝形.如图,四边形 ABCD 是 一个筝形,其中 DA=DC,BA=BC.对角线 AC,BD 相交于点 O,过点 O 作 OE⊥AB,OF⊥BC,垂足分别为 E,F,求证:四边形 BEOF 是筝形.
专项二 全等三角形的常见模型强化练
解:(1)证明:∵AB⊥DC,∴∠ABC=∠DBE=90°,在△ABC 和△DBE 中, AB=DB,∠ABC=∠DBE,BC=BE,∴△ABC≌△DBE(SAS),∴DE=AC;
(2)题图 2:由平移变换知 EF⊥BC,EF=BC,DF=AB. ∴∠ABC=∠DFE=90°.在△DFE 和△ABC 中,EF=CB,∠DFE=∠ABC,DF=AB, ∴△DFE≌△ABC(SAS),∴DE=AC.故在题图 2 中的结论仍然成立.题图3,4 中 可类似地推证出(1)的结论也成立.
专项二 全等三角形的常见模型强化练
解决图形变换问题需要抓住的三个特点:(1)变化前后的结论及说理过程对 变化前后的结论起到重要的作用;(2)在图形变化前后,明确哪些关系发生变化 ,哪些关系没有发生变化,变化前的等角、等线段在变化后是否还存在;(3)几 种变化图形之间,说理思路存在内在联系,变化后的说理思路可模仿与借鉴变化 前的结论与过程.变化后的结论有时发生变化,有时不发生变化.
ቤተ መጻሕፍቲ ባይዱ 专项二 全等三角形的常见模型强化练
解:(2)AF∥CD,理由如下:如图,作 AG⊥BF 于点 G,AH⊥CE 于点 H,由(1)知△ABD≌△ACE,∴ 易知 AG=AH.∵∠AGF=∠AHF=90°,AF=AF, 又易知∠HAF=∠AFD,∴△AGF≌△FHA;∴AG=HF,∴AH=HF,∴ 易知 ∠HFA=45°,∴∠AFD=45°,∵∠BDC=135°,∴∠FDC=45°,∴∠AFD=∠FDC, ∴AF∥CD.
【差】全等三角形简单模型(解析版)

全等三角形简单模型【模型讲解】模型1、平移全等模型,如下图:【巩固训练】1.如图,AB DE =,A D ∠=∠,要说明ABC DEF △≌△,需添加的条件不能是()A .//AB DE B .//AC DF C .AC DE ⊥D .AC DF =【答案】C 【分析】直接根据三角形证明全等的条件进行判断即可;【详解】A 、∵AB ∥DE ,∴∠ABC=∠DEC ,∴根据ASA 即可判定三角形全等,故此选项不符合题意;B 、∵AC ∥DF ,∴∠DFE=∠ACB ,∴根据AAS 即可判定三角形全等,故此选项不符合题意;C 、AC ⊥DE ,不符合三角形全等的证明条件,故此选项符合题意;D 、∵AC=DF ,∴根据SAS 即可判定三角形全等,故此选项不符合题意;故选:C .【点睛】本题考查了三角形证明全等所需添加的条件,正确掌握知识点是解题的关键;2.如图:已知AD BE =,BC EF =且//BC EF ,求证:ABC DEF ≌△△.【答案】见解析【分析】由AD=BE 可求得AB=DE ,再结合条件可证明△ABC ≌△DEF .【详解】证明:∵AD BE =∴AD BD BE BD +=+∴AB DE=又∵//BC EF ∴ABC DEF∠=∠在ABC 和DEF 中AB DE ABC DEF BC EF =⎧⎪∠=∠⎨⎪=⎩∴ABC DEF △≌△(SAS )【点睛】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,即SSS 、SAS 、ASA 、AAS 和HL .3.如图,在△ABC 和△DEF 中,B ,E ,C ,F 在同一条直线上,AB //DE ,AB =DE ,∠A =∠D .(1)求证:ABC DEF ≌;(2)若BF =11,EC =5,求BE的长.【答案】(1)见解析;(2)BE =3.【分析】(1)根据平行线的性质由AB ∥DE 得到∠ABC =∠DEF ,然后根据“ASA”可判断△ABC ≌△DEF ;(2)根据三角形全等的性质可得BC =EF ,由此可求出BE =CF ,则利用线段的和差关系求出BE .【详解】(1)证明:∵AB ∥DE ,∴∠ABC =∠DEF ,在△ABC 和△DEF 中A D AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF (ASA );(2)解:∵△ABC ≌△DEF ,∴BC =EF ,∴BC -EC =EF -EC ,即BE =CF ,∵BF =11,EC =5,∴BF -EC =6.∴BE +CF =6.∴BE =3.【点睛】本题考查了全等三角形的判定与性质,掌握全等三角形的判定与性质是解答此题的关键.4.如图,已知点C 是AB 的中点,CD ∥BE ,且CD BE =.(1)求证:△ACD ≌△CBE .(2)若87,32A D ∠=︒∠=︒,求∠B的度数.【答案】(1)见解析;(2)61【分析】(1)根据SAS 证明△ACD ≌△CBE ;(2)根据三角形内角和定理求得∠ACD ,再根据三角形全等的性质得到∠B=∠ACD .【详解】(1)∵C 是AB 的中点,∴AC =CB ,∵CD//BE ,∴ACD CBE ∠=∠,在△ACD 和△CBE 中,AC CB ACD CBE CD BE =⎧⎪∠=∠⎨⎪=⎩,∴ACD CBE ∆≅∆;(2)∵8732A D ︒︒∠=∠=,,∴180180873261ACD A D ︒︒︒︒︒∠=-∠-∠=--=,又∵ACD CBE ∆≅∆,∴61B ACD ︒∠=∠=.【点睛】考查了全等三角形的判定和性质,解题关键是根据SAS 证明△ACD ≌△CBE .5.如图,AB//CD ,AB=CD 点E 、F 在BC 上,且BF=CE .(1)求证:△ABE ≌△DCF (2)求证:AE//DF .【答案】(1)见详解;(2)见详解【分析】(1)由题意易得B C ∠=∠,BE CF =,然后问题可得证;(2)由(1)可得DFC AEB ∠=∠,则有EFD AEF ∠=∠,然后问题可得证.【详解】证明:(1)∵AB ∥CD ,∴B C ∠=∠,∵BF =CE ,∴CF EF BE EF +=+,∴BE CF =,∵AB =CD ,∴ABE DCF △≌△(SAS );(2)由(1)可得:ABE DCF △≌△,∴DFC AEB ∠=∠,∵180,180DFC EFD AEF AEB ∠+∠=︒∠+∠=︒,∴EFD AEF ∠=∠,∴//AE DF .【点睛】本题主要考查三角形全等的判定及性质,熟练掌握全等三角形的判定定理是解题的关键.6.如图1,A ,B ,C ,D 在同一直线上,AB =CD ,DE ∥AF ,且DE =AF ,求证:△AFC ≌△DEB .如果将BD 沿着AD 边的方向平行移动,如图2,3时,其余条件不变,结论是否成立?如果成立,请予以证明;如果不成立,请说明理由.【思路】可以根据已知利用SAS 判定△AFC ≌△DEB .如果将BD 沿着AD 边的方向平行移动,如图(2)、(3)时,其余条件不变,结论仍然成立.可以利用全等三角形的常用的判定方法进行验证.【解答过程】解:∵AB =CD ,∴AB +BC =CD +BC ,即AC =BD .∵DE ∥AF ,∴∠A =∠D .在△AFC 和△DEB 中,AF DE∠A ∠D AC DB,∴△AFC ≌△DEB (SAS ).在(2),(3)中结论依然成立.如在(3)中,∵AB =CD ,∴AB ﹣BC =CD ﹣BC ,即AC =BD ,∵AF ∥DE ,∴∠A =∠D .在△ACF 和△DEB 中,AF DE∠A ∠D AC DB,∴△ACF ≌△DEB (SAS ).模型2.对称(翻折)全等模型,如下图:【巩固训练】1.如图,四边形ABCD 的对角线AC ,BD 相交于点O ,ABO ADO △≌△,下列结论:①AC BD ⊥;②CB CD =;③ABC ADC △≌△;④DA DC =,其中正确结论的序号是__________.【答案】①②③【分析】根据全等三角形的性质得出AB=AD ,∠BAO =∠DAO ,∠AOB =∠AOD =90°,OB=OD ,再根据全等三角形的判定定理得出△ABC ≌△ADC ,进而得出其它结论.【详解】由△ABO ≌△ADO 得:AB=AD ,∠AOB =∠AOD =90°,∴AC ⊥BD ∠BAC =∠DAC ,又AC =AC ,所以,有△ABC ≌△ADC ,∴CB=CD ,所以,①②③正确.由已知条件得不到DA=DC ,故④不正确.故答案为:①②【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定方法:SSS ,SAS ,ASA ,AAS ,以及HL ,是解题的关键.2.如图,已知ACB DBC ∠=∠,若要使得ABC DCB ∆≅∆,则添加的一个条件不能是()A .A D∠=∠B .ABC DCB ∠∠=C .AB =DC D .AC =DB【答案】C 【分析】根据全等三角形的判定方法对各选项进行判断,即可得出结论.【详解】解:∵ACB DBC ∠=∠,BC =CB ,A 、当添加∠A =∠D 时,可利用“AAS”判断△ABC ≌△DCB ,故此选项不符合题意;B 、当添加ABC DCB ∠=∠时,可利用“ASA”判断△ABC ≌△DCB ,故此选项不符合题意;C 、当添加AB=DC 时,利用“SSA”不能判断△ABC ≌△DCB ,故此选项符合题意;D 、当添加AC=DB 时,可利用“SAS”判断△ABC ≌△DCB ,故此选项不符合题意.故选:C .【点睛】本题考查了全等三角形的判定:全等三角形的判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.3.如图,12∠=∠,BC EC =,请补充一个条件:______,能使用“ASA ”方法判定ABC DEC ≌△△.【答案】∠B =∠E【分析】已知∠1=∠2,就是已知∠ACB =∠DCE ,则根据三角形的判定定理“ASA ”即可证【详解】可以添加∠B =∠E .理由是:∵∠1=∠2,∴∠1+∠BCE =∠2+∠BCE ,∴∠ACB =∠DCE ,∴在△ABC 和△DEC 中,ACB DCE BC EC B E ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△DEC (ASA ).故答案是:∠B=∠E【点睛】本题考查了三角形全等的判定,熟练掌握“两角及夹边对应相等的两个三角形全等”是解题关键.4.在数学课上,林老师在黑板上画出如图所示的图形(其中点B 、F 、C 、E 在同一直线上),并写出四个条件:①AB =DE ,②BF =EC ,③∠B =∠E ,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:;结论:.(均填写序号)证明:【答案】①②③;④;证明过程见解析;【分析】根据三个不同的情况进行讨论分析即可;【详解】情况一:题设①②③,结论④;∵BF=EC ,∴BF CF EC CF +=+,即BC EF =,在△ABC 和△DEF 中,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩,∴ABC DEF ≅ ,∴12∠=∠;情况二:题设①③④,结论③;在△ABC 和△DEF 中,12B E AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ABC DEF ≅ ,∴BC EF =,∴BC FC EF FC -=-,即BF EC =;情况三:题设②③④,结论①;∵BFEC =,∴BF CF EC CF +=+,即BC EF =,在△ABC 和△DEF 中,12BC EF B E ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ABC DEF ≅ ,∴AB DE =;故答案为:①②③;④.【点睛】本题主要考查了全等三角形的判定与性质,准确分析证明是解题的关键.5.如图,在ABC 中,点D ,E 分别是AB 、AC 边上的点,BD CE =,ABE ACD ∠=∠,BE 与CD 相交于点F ,求证:AB AC =.【答案】见详解;【分析】依题意,BD =CE ,∠ABE =∠ACD ,∠BFD =∠CFE ,可得△BDF ≌△CEF ,可得DF =EF ,BF =CF ;可得CD =BE ,可得△ABE ≌△ACD ,即可;【详解】由题知:BD =CE ,∠ABE =∠ACD ,又∠BFD 和∠CFE 为对顶角,∴∠BFD =∠CFE ;在△BDF 和△CEF 中ABE ACD BFD CFE BD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDF ≌△CEF (AAS );∴DF =EF ,BF =CF ;又CD =DF +CF ,BE =BF +EF ;∴CD =BE ;在△ABE 和△ACD 中A A ABE ACD BE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ACD (AAS );∴AB =AC ;【点睛】本题主要考查对顶角相等、用AAS 证明全等及其性质,熟练构造出全等的三角形是关键;6.如图,已知∠C =∠F =90°,AC =DF ,AE =DB ,BC 与EF 交于点O ,(1)求证:Rt△ABC≌Rt△DEF;(2)若∠A=51°,求∠BOF的度数.【答案】(1)见解析;(2)78°【分析】(1)由AE=DB得出AE+EB=DB+EB,即AB=DE,利用HL即可证明Rt△ABC ≌Rt△DEF;(2)根据直角三角形的两锐角互余得∠ABC=39°,根据全等三角形的性质得∠ABC=∠DEF=39°,由三角形外角的性质即可求解.【详解】(1)证明:∵AE=DB,∴AE+EB=DB+EB,即AB=DE.又∵∠C=∠F=90°,AC=DF,∴Rt△ABC≌Rt△DEF.(2)∵∠C=90°,∠A=51°,∴∠ABC=∠C-∠A=90°-51°=39°.由(1)知Rt△ABC≌Rt△DEF,∴∠ABC=∠DEF.∴∠DEF=39°.∴∠BOF=∠ABC+∠BEF=39°+39°=78°.【点睛】本题主要考查直角三角形的两锐角互余,三角形外角的性质,全等三角形的判定与性质,证明三角形全等是解题的关键.模型3.旋转全等模型,如下图:【巩固训练】1.如图,△ABC和△AED共顶点A,AD=AC,∠1=∠2,∠B=∠E.BC交AD于M,DE交AC于N,甲说:“一定有△ABC≌△AED.”乙说:“△ABM≌△AEN.”那么()A .甲、乙都对B .甲、乙都不对C .甲对、乙不对D .甲不对、乙对【答案】A 【分析】利用AAS 判定△ABC ≌△AED ,则可得到AB=AE ,再利用ASA 判定△ABM ≌△AEN .【详解】∵∠1=∠2,∴∠1+∠MAC =∠2+∠MAC ,∴∠BAC =∠EAD,在△BAC 和△EAD 中,B E BAC EAD AC AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BAC ≌△EAD ,∴甲说的正确;∵△BAC ≌△EAD (AAS ),∴AB=AE ,在△BAM 和△EAN 中,12B E AB AE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BAM ≌△EAN (ASA ),∴乙说的正确;故选A .【点睛】本题考查了三角形全等的判定方法,根据题目的特点,补充适当条件,活用判定定理是解题的关键.2.如图,已知AB AD =,BC DE =,且10CAD ∠=︒,25B D ∠=∠=︒,120EAB ∠=︒,则EGF ∠的度数为()A .120︒B .135︒C .115︒D .125︒【答案】C【分析】由已知得△ABC ≌△ADE ,故有∠BAC =∠DAE ,由∠EAB =120°及∠CAD =10°可求得∠AFB 的度数,进而得∠GFD 的度数,在△FGD 中,由三角形的外角等于不相邻的两个内角的和即可求得∠EGF 的度数.【详解】在△ABC 和△ADE 中AB AD B D BC DE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴∠BAC =∠DAE∵∠EAB =∠BAC +∠DAE +∠CAD =120°∴∠BAC =∠DAE ()112010552=⨯︒-︒=︒∴∠BAF =∠BAC +∠CAD =65°∴在△AFB 中,∠AFB =180°-∠B -∠BAF =90°∴∠GFD =90°在△FGD 中,∠EGF =∠D +∠GFD =115°故选:C【点睛】本题考查了三角形全等的判定和性质、三角形内角和定理,关键求得∠BAC 的度数.3.已知:如图,C 为线段BE 上一点,AB//DC ,AB=EC ,BC=CD .求证:∠A=∠E.【答案】见详解【分析】直接利用全等三角形的判定方法得出△ABC ≌△ECD ,即可得出答案.【详解】证明:∵AB ∥DC ,∴∠B =∠ECD ,在△ABC 和△ECD 中,AB EC B ECD BC CD ⎧⎪∠∠⎨⎪⎩===,∴△ABC ≌△ECD (SAS ),∴∠A =∠E (全等三角形的对应角相等).【点睛】此题主要考查了全等三角形的判定与性质,正确掌握全等三角形的判定方法是解题关键.4.如图,,,,AC BC DC EC AC BC DC EC ⊥⊥==,求证:(1)ACE BCD ∆≅∆;(2)AE BD ⊥.【答案】(1)见解析;(2)见解析【分析】(1)根据垂直得到90ACB DCE ∠=∠=︒,求出DCB ECA ∠=∠,即可得到结果;(2)设AC 交BD 于N ,AE 交BD 于O ,根据全等三角形的性质得到A B ∠=∠,再根据已知条件转换即可;【详解】证明:()1AC BC ⊥Q ,DC EC ⊥,90ACB DCE ∴∠=∠=︒,ACB ACD DCE ACD ∴∠+∠=∠+∠,∴∠=∠DCB ECA ,在DCB ∆和ECA ∆中,AC BC DCB ECA CD CE =⎧⎪∠=∠⎨⎪=⎩,()DCB ECA SAS ∴∆≅∆;()2如图,设AC 交BD 于N ,AE 交BD 于O ,∆≅∆ DCB ECA ,A B ∴∠=∠,∠=∠ AND BNC ,90∠+∠=︒B BNC ,90∴∠+∠=︒A AND ,90∴∠=︒AON ,AE BD ∴⊥.【点睛】本题主要考查了全等三角形的判定与性质,准确证明是解题的关键.。
全等三角形模型总结及经典练习题

全等三角形模型总结及经典练习题从全等三角形的角度入手,找到可以构成全等三角形的条件。
观察图形可知,△ACE和△BCD是直角三角形,且AC=BC,因此可以得到∠XXX∠CBD和△ACE≌△BCD。
接下来,需要证明AE=BD+DE,可以将BD+DE表示为BC-CE+DE,再利用全等三角形的性质证明△ACE≌△XXX,从而得到AE=BD+DE。
具体证明过程如下:ACE≌△BCDCAE=∠CBDCAE+∠EAD=∠CBD+∠XXXCAE+∠XXX∠CBD+∠EDCCAD=∠XXXXXX≌△CDEAE=CD=BD+DE(因为BD=BC-CD,CE=AE-AC,所以BD+DE=BC-CE)。
因此,得证AE=BD+DE。
角度:观察图形,可以猜测△ACE与△CBD全等。
由此可以得出XXX,以及BD=CE。
因此,可以得出AC=BC(已知),∠1=∠3(已证),∠XXX∠CDB(已证)。
根据AAS准则,可以得出△ACE≌△CBD。
因此,BD=CE,AE=CD(全等三角形的对应边相等)。
又因为AE=CE=CE+DE,所以可以进行等量代换,得出AE=BD+DE。
例3:定对象为△ABC,定角度为三角形全等。
观察图形,可以发现BE、CF、EF条件分散,不在一个三角形中。
因此,需要将三者集中在一个三角形中,可以利用角的平分线这一线索,将△BDE沿角平分线翻转180°,使B点落在AD的点B'上,连结EB'和B'F。
此时,△BDE与△B'DE完全重合,因此可以得出BE=B'E(全等三角形的对应边相等)。
在△EFB'中,可以得出EF<B'E+B'F,进行等量代换,得出EF<BE+CF。
例4:定对象为如图所示,定角度为三角形全等。
可以分解出四组基本图形:有公共角的Rt△ACD和Rt△ABE,△ABE≌△ACD,可以得出△XXX的外角∠XXX或△ABE的邻补角∠XXX。
2024八年级数学上册第十三章全等三角形练素养3.全等三角形的常见模型习题课件新版冀教版

1
2
3
4
5
6
7
模型4 不共顶点旋转模型
4. 如图, A , F , C , D 四个点在同一条直线上, AB ⊥
BC , DE ⊥ EF , AC = DF , AB = DE .
求证: BF ∥ CE .
【证明】在 Rt△ ABC 与Rt△ DEF 中,
=,
ቊ
=,
1
2
3
4
5
6
7
∵∠ EAF = ∠ BAD ,∴∠ GAF =∠ DAG +
∠ DAF =∠ BAE +∠ DAF =∠ BAD -∠ EAF =
∠ BAD ,∴∠ EAF =∠ GAF .
=,
在△ AEF 和△ AGF 中,ቐ∠=∠,
=,
∴△ AEF ≌△ AGF (SAS),∴ EF = FG .
∠ BAD =120°,∠ B =∠ ADC =90°, E , F 分别是
BC , CD 上的点,且∠ EAF =60°,试探究图中线段
BE , EF , FD 之间的数量关系.
(1)小王同学探究此问题的方法是延长 FD
到点 G ,使 DG = BE ,连接 AG ,先证
明△ ABE ≌△ ADG ,再证明△ AEF ≌
直线 AE 同侧时, BD = DE - CE . 当点 B , C 在直线
AE 异侧时,若 BD > CE ,则 BD = DE + CE ;若 BD
< CE ,则 BD = CE - DE .
1
2
3
4
5
6
7
模型6 手拉手模型
6. 如图,∠ BAE =∠ CAF =90°, EC , BF 相交于点 M ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(三) 全等三角形的基本模型
►模型一平移模型
常见的平移模型:
1.如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E.
2.如图,点A,B,C,D在同一条直线上,AB=CD,AE∥BF,CE∥DF.求证:AE=BF.
►模型二轴对称模型
常见的轴对称模型:
3.如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
4.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
5.如图,A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.求证:DE=CF.
6.如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.
常见的旋转模型:
7.如图,已知AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:AD=AE.
►模型四一线三等角模型
8.如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE;
(2)若∠A=40°,求∠BCD的度数.
平移+对称模型:平移+旋转模型:
9.如图,点B,F,C,E在同一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
10.如图,AB=BC,BD=CE,AB⊥BC,CE⊥BC.求证:AD⊥BE.
详解详析1.证明:∵BC∥DE,
∴∠ABC=∠D.
在△ABC和△EDB中,
∵AB=DE,∠ABC=∠D,BC=DB,
∴△ABC≌△EDB(S.A.S.),
∴∠A=∠E.
2.证明:∵AE∥BF,∴∠A=∠FBD.
∵CE∥DF,∴∠D=∠ACE.
∵AB=CD,∴AB+BC=CD+BC,
即AC=BD.
在△ACE和△BDF中,
∵∠A=∠FBD,AC=BD,∠D=∠ACE,
∴△ACE≌△ABDF(A.S.A.),
∴AE=BF.
3.解:答案不唯一,如添加∠BAC=∠DAC. 理由:在△ABC和△ADC,
∵∠B=∠D,∠BAC=∠DAC,AC=AC,
∴△ABC≌△ADC(A.A.S.).
4.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ADB和△AEC中,
∵∠ADB=∠AEC,AD=AE,∠A=∠A,
∴AB=AC.
又AD=AE,
∴AB-AE=AC-AD,
即BE=CD.
5.证明:∵AC=BD,
∴AC+CD=BD+CD,
即AD=BC.
在△AED和△BFC中,
∵∠A=∠B,
AD=BC,
∠ADE=∠BCF,
∴△AED≌△BFC(A.S.A.),
∴DE=CF.
6.证明:∵BE⊥AC,CD⊥AB,
∴∠BEA=∠CDA=90°.
又∵∠A=∠A,BE=CD,
∴△ABE≌△ACD,
∴AB=AC.
7.证明:∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
∵∠BAD=∠CAE,AB=AC,∠ABD=∠ACE,
8.解:(1)证明:∵AC∥DE,
∴∠ACB=∠E,∠ACD=∠D.
∵∠ACD=∠B,
∴∠D=∠B.
在△ABC和△CDE中,
∵∠ACB=∠E,∠B=∠D,AC=CE,
∴△ABC≌△CDE(A.A.S.),
∴BC=DE.
(2)∵△ABC≌△CDE,
∴∠A=∠DCE=40°,
∴∠BCD=180°-40°=140°.
9.证明:∵FB=CE,
∴FB+FC=CE+FC,∴BC=EF.
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE.
在△ABC和△DEF中,
∵∠B=∠E,BC=EF,∠ACB=∠DFE,
∴△ABC≌△DEF(A.S.A.),
∴AC=DF.
10.证明:设AD,BE交于点F.
∵AB⊥BC,CE⊥BC,∴∠ABD=∠C=90°. 在△ABD和△BCE中,
∵AB=BC,∠ABD=∠C,BD=CE,
∴△ABD≌△BCE,
∴∠A=∠CBE.
∵∠CBE+∠ABE=90°,∴∠A+∠ABE=90°,则∠AFB=90°,
∴AD⊥BE.。
