12.3角平分线的性质课件
合集下载
12.3 第2课时 角平分线的判定 初中数学人教版八年级上册课件
图形
C P
已知 条件
结论
OP 平分∠AOB PD⊥OA 于 D PE⊥OB 于 E
PD = PE
C P
PD⊥OA 于 D PE⊥OB 于 E PD = PE OP 平分∠AOB
当堂小结
内容
角平分线 的判定定
理
作用
相关 结论
角的内部到角两边距离相等 的点在这个角的_平__分__线__上
判断一个点是否在角的平分线上
位置关系
数量关系
应用格式:
∵ PD⊥OA,PE⊥OB,PD = PE, ∴ 点 P 在∠AOB 的平分线上.
O
A
D C
P EB
回顾导入
如图,要在 S 区建一个风筝主题公园,使它到公路 和铁路的距离相等,并且离公路与铁路交叉处距离为
500 m,这个风筝主题公园应建在何处? O
解:作夹角的角平分线 OC,
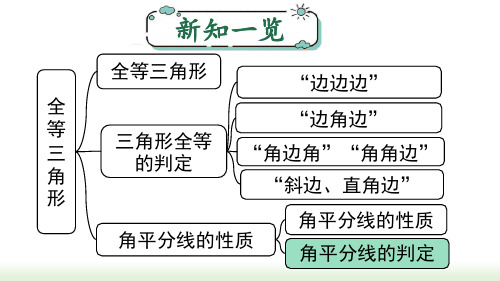
新知一览
全等三角形
“边边边”
全 等 三 角 形
三角形全等 的判定
“边角边” “角边角”“角角边”
“斜边、直角边”
角平分线的性质
角平分线的性质
角平分线的判定
第十二章 全等三角形
12.3 角的平分线的性质
第 2 课时 角平分线的判定
人教版八年级(上)
新课导入 如图,要在 S 区建一个风筝主题公园,使它到公路
B
A P2
P1 C
P3
典例精析 例1 如图,∠ABC 的平分线与∠ACB 的外角平分线相交 于点 D,连接 AD. 求证:AD 是∠BAC 的外角平分线.
分析:
求证:AD 是∠BAC 的外角平分线.
求证:D 到 BA,AC 的距离相等.
人教版数学八年级上册 第十二章 12.3 角的平分线的性质 第一课时 课件(共33张PPT)

PD⊥OA,PE⊥OB,且
O
P
PD=PE
E B ∴OP是∠AOB的平分线
动脑想一想
• 我们之间就学习了三角形的角分线,之前 谈到过,三条角分线一定交于一点,不过 当时我们没有给出证明,而只是通过画图 的方法给出了印证。
• 现在我们学习了角分线的性质和判定定理, 怎样证明这个结论呢?我们先看下面的例 题。
DC=BC(已知) ∴ △ADC≌△ABC (SSS) ∴∠DAC=∠BAC(对应角相等) 即 AE平分∠BAD
动脑想一想
• 通过刚才的启发,你能想到怎样画出下面 的角的平分线吗?
A
仅用尺规作图,
已知∠AOB,
求作∠AOB的
平分线
O
B
尺规法画角平分线
A M
O
NB
以点O为圆心,任意适当长度为半径画弧,
• 对折之后的折痕和 这个角有什么关系?
• 如果是木板不能对 折,该怎么平分?
动脑想一想
• 如图是一个平分角的仪器, 其中AB=AD,BC=DC,将 点A放在角的顶点,AB和 AD沿着角的两边放下,则 AC所在直线就是这个角的 平分线。
• 你能说明这是为什么吗?
动脑想一想
证明: 在△ADC和△ABC 中 AB=AD(已知) AC=AC(公共边相等)
角分线上的点到角两边的距离相等
A D
∵OC平分∠AOB,
O
P C PD⊥OA,PE⊥OB
∴PD=PE
EB
动脑想一想
• 如图,要在S区建一个 集贸中心,使它到铁路、 公路的距离相等,并且 离公路与铁路的交叉处 500m,这个集贸中心应 建在哪里?
动脑想一想
• 角分线上的点到角两边的距离相等。 • 到角的两边的距离相等的点是否也在角的
12.3 角的平分线的性质 课件 2024—2025学年人教版数学八年级上册

∴∠AOC=∠BOC
求证:PE=PF
在△EOP和△FOP中
EA
∠AOC=∠BOC ∠OEP=∠OFP
PC
OP=OP
O
∴ △EOP≌△FOP(AAS)
∴ PE=PF
FB
角平分线的性质 角平分线 上的点 到角两边的距离 相等
几何语言
∵ OP是∠AOB的角平分线
PE⊥OA PF⊥OB
O
∴ PE=PF
EA P
∴ △OEC≌△OFC(SSS) ∴ ∠AOC=∠BOC 即 OC平分∠AOB
E
F
为什么?
新知学习二
猜想:角平分线上的点到角两边的距离相等
同学能用学过的知识证明它吗?
命题证明:角平分线上的点到角两边的距离相等
已知:OC是∠AOB的角平分线,
点P在OC上,
证明:∵ OC是∠AOB的角平分线
PF⊥OB PE⊥OA
E
∴ PD=PE=PF
即点P到三边AB,BC,CA的距离相等.
课堂小结
内容:1. 角平分线上的点到角两边的距离相等 2. 证明几何命题的步骤
应用角平分线性质的条件:1. 存在角平分线 2.涉及距离问题
布置作业
课本P51:第1、2题
配套练习前8题
感谢您的观看
人教版数学八年级上册
12.3第一课时
角平分线的性质
教材分析
情景导入
新知学习一
A
已知:∠AOB
求作∠AOB的平分线
O
B
③ ① ② 作以分射点别线以O为点O圆CM心、,N为适圆当心长,为大半于径画M弧N,为交半O径A于画点弧M,,两O弧B交于于点点NC
证明:在△OEC和△OFC中, OE=OF EC=FC OC=OC
八年级数学12.3《角平分线的性质》(共23张PPT)优秀课件

二、重点难点
学生学好数学的信心. 到角两边的距离的正确理解;
2、掌握角平分线性质定理的运用 。
关键:通过情景问题的设计,引导
活动1 给出一个纸片做的角,不利用工具,能不能找出
这个角的角平分线呢? 〔对折〕
再翻开纸片 ,看看折痕与这个角有何关系?
活动 2
如果前面活动中的纸片换成木板、 A 钢板等没法折的角,又该怎么办呢?
C
∴∠CAD=∠CAB〔全等三角形的 E 对应边相等〕
∴AC平分∠DAB〔角平分线的定义〕
B C
根据角平分仪的制作原 理怎样作一个角∠EAF 的平分线?〔不用角平
分仪或量角器〕
A
D
E
B
作法:1.以A为圆心,适当长为半径作弧, AE于点B,交AF于点D;
2.分别以B、D为圆心,大于线段BD 一 半 的 长 为 半 径 作 弧 , 两 弧 在 ∠ EAF 的内部交于点C;
1、如图,是一个角平分仪,其中 AB=AD,BC=DC。将点A放在角的顶 D 点,AB和AD沿着角的两边放下, 过点A、C画一条射线AE,AE就是 角平分线,你能说明它的道理吗?
B C E
A
2、证明:
在△ACD和△ACB中
AD=AB〔〕
D
B
DC=BC〔〕
CA=CA〔公共边〕
∴ △ACD≌ △ACB〔SSS〕
3.作射线AC。
A
DF
二 角平分线的性质
实验:OC是∠AOB的平分线,点P是角平分线OC上 的任意一点
1.操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA , PE⊥OB,点D、E为垂足,测量PD、PE的长。将三次数据填入下表:
A
D
CD PE
角平分线的性质(课件)人教版数学八年级上册

拓展训练 2.如图,△ABC 中,∠C = 90°,AD 是△ABC 的角
平分线,DE⊥AB 于 E,F 在 AC 上 BD=DF.求证:CF=EB.
证明:∵AD 平分∠CAB,DE⊥AB,∠C= 90°(已知), ∴CD=DE (角的平分线的性质). 在Rt △CDF 和 Rt△EDB 中, CD=DE (已证),DF=DB(已知), ∴ Rt△CDF ≌ Rt△EDB(HL). ∴ CF=EB (全等三角形对应边相等).
互动新授 思考
如图,要在S区建一个集贸市场,使它到公路、铁路的距 离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建 于何处(在图上标出它的位置,比例尺为1:20000)?
S
互动新授
解:在Rt△ABC与Rt△ABD中:
AB=AB
BC=BD
∴ Rt△ABC ≌ Rt△ABD(HL).
∴∠CAB=∠DAB
M
即点B在∠CAD的角平分线上
你能得出什 A么结论呢?
C
D
B S
N
角的平分线的判定: 角的内部到角的两边的距离相等的点在 角的平分线上.
典例精析
例:如图,△ABC的角平分线BM,CN相交于点P.求证:点P 到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB交于点D,PE⊥BC交于点E,
PF⊥AC交于点F.
AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE.
∵AC=BC,
∴AE=BC,
∴△DEB的周长为8cm.
课堂小结
三角形的角 平分线
角的平分线上的点到角的两边的距离相等.
角的内部到角的两边的距离相等的点在 角的平分线上.
人教版数学八年级上册12.3.1 角平分线的性质课件(共22张PPT)

P
E,交 OB 于F;
(2) 分别以 E,F 为圆心,大于 EF 的长为半径
作弧,两弧在∠AOB内部交于点 C;
(3) 作射线 OC. 则射线 OC 与直线MN相交与点P,
点P即为所求.
M
O
E
C
F
B
N
12.3.1 角平分线的性质
二 角平分线的性质
利用尺规我们可以作一个角的平分线,那么角的平分线有什么性质呢?
12.3.1 角平分线的性质
使用定理时这样书写:
∵ OC 平分∠AOB,
PD⊥OA,PE⊥OB,
∴PD = PE.
推理的条件有三个,必须
写全,不能少.
12.3.1 角平分线的性质
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤
进行,即
1. 明确命题中的已知和求证;
2. 根据题意,画出图形,并用符号表示已知和求证;
12.3.1 角平分线的性质
12.3.1 角平分线的性质
学习目标
1. 会用尺规作图:作一个角的平分线. 重点
2. 探索并证明角平分线的性质定理:角平分线上的点到角两边的距离
相等. 难点
3. 会用角平分线的性质解决实际问题. 难点
12.3.1 角平分线的性质
新课引入
思考
如图是一个平分角的仪器,其中 AB = AD,
DE = 2,AB = 4,则 AC 的长是 ( D )
A. 6
B. 5
C. 4
D. 3
分析:过点 D 作 DF⊥AC 于 F,
∵ AD 是△ABC 的角平分线,DE⊥AB.
∴ DF = DE = 2.
1
1
S△ABC 4 2 AC 2 7, 解得 AC=3.
12.3《角平分线的性质》说课课件

角的平分线的性质
说课内容
地位作用
一.说 教 材
本节课主要学习了角平分线的作 法,角平分线的性质及其应用,是在学 生学习了角平分线的概念和三角形全 等的基础上引入的.
学情分析
八年级学生已经具备了初步归纳 的能力,但是他们全面深入探究问题 能力较弱,他们对问题的认识主要依 赖于感性认识.
重点难点 教学目标
且EM=3cm,求点E到OA的距离.
A
A
E
E
F
∟
O
MB
B
D
C
(1题图)
(2题图)
2.已知:如图,在△ABC中,AD是它的角平分线,且 BD=CD,
DE⊥AB,DF⊥AC垂足分别是E,F.
求证:EB=FC.
四.说教学过程
复
创
习
设
提
情
问
景
导
探
入
究
新
新
课
知
例
合
课
题
作
堂
讲
交
小
解
流
结
形
巩
布
成
固
置
技
提
作
能
高
业
A
D
OE于点N,交OF于点M.
E
2.分别以M,N为圆心,大于MN一半的
N
C
长为半径作弧,两弧在∠EOF的内
部交于点C.
3.作射线OC.
O
F
M
将∠AOB对折,在折痕上任取一点P,过P点再折出一个 直角三角形(使第一条折痕为斜边),然后展开,观察两次折 叠形成的三条折痕,你能得出什么结论?
A
D C
P
结论:PO为∠AOB的角平分线,PD⊥OA, PE⊥OB,且PD=PE.
说课内容
地位作用
一.说 教 材
本节课主要学习了角平分线的作 法,角平分线的性质及其应用,是在学 生学习了角平分线的概念和三角形全 等的基础上引入的.
学情分析
八年级学生已经具备了初步归纳 的能力,但是他们全面深入探究问题 能力较弱,他们对问题的认识主要依 赖于感性认识.
重点难点 教学目标
且EM=3cm,求点E到OA的距离.
A
A
E
E
F
∟
O
MB
B
D
C
(1题图)
(2题图)
2.已知:如图,在△ABC中,AD是它的角平分线,且 BD=CD,
DE⊥AB,DF⊥AC垂足分别是E,F.
求证:EB=FC.
四.说教学过程
复
创
习
设
提
情
问
景
导
探
入
究
新
新
课
知
例
合
课
题
作
堂
讲
交
小
解
流
结
形
巩
布
成
固
置
技
提
作
能
高
业
A
D
OE于点N,交OF于点M.
E
2.分别以M,N为圆心,大于MN一半的
N
C
长为半径作弧,两弧在∠EOF的内
部交于点C.
3.作射线OC.
O
F
M
将∠AOB对折,在折痕上任取一点P,过P点再折出一个 直角三角形(使第一条折痕为斜边),然后展开,观察两次折 叠形成的三条折痕,你能得出什么结论?
A
D C
P
结论:PO为∠AOB的角平分线,PD⊥OA, PE⊥OB,且PD=PE.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角平分线的定义:
从一个角的顶点出发,把这个角分成 相等的两个角的射线叫做这个角的角
平分线。
B
C
O
A
B
C
O
A
∠AOC =∠BOC ∠AOB =2∠AOC =2∠BOC
= =
在△ADC和 △ABC中, AD= AB DC=BC AC=AC
∴△ADC ≌ △ABC (SSS) ∴ ∠DAE=∠DAE
4 PE=__________cm.
A
C
P
D B
E
O
例1:如图,在△ABC中,∠C=900,AD平分 ∠BAC交BC于点D,若BC=8,BD=5,则点 D到AB的距离为?
A E 线BM、CN相交 于点P。求证:点P到三角形三边的距离均相等。
A
F N
G
M
P
B
E
C
尺规作图
用尺规作角的平分线. 已知:∠AOB,如图. 求作:射线OC,使∠AOC=∠BOC.
A
D
C
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE. 2.分别以点D和E为圆心,以大于DE/2长 O 为半径作弧,两弧在 ∠AOB内交于点C..
EB
3.作射线OC.
则射线OC就是∠AOB的平分线.
例3:在△OAB中,OE是∠ AOB的角平分线, 且EA=EB,EC、ED分别垂直OA,OB,垂足 为C,D,求证:AC=BD。
O
C
D
A
E
B
1、如图,OC平分∠AOB, PM⊥OB于点M, PN⊥OA于点N, △POM的面积为6,OM=6, 则PN=___2____。
N
A
C
0
P
MB
2、如图:△ABC中, ∠C=900,AD是 ∠BAC的平分线,DE⊥AB于E,F在AC上, BD=DF,求证:CF=EB
如图,为了促进当地旅游发展,某地要在三条公 路围成的一块平地上修建一个度假村.要使这个度 假村到三条公路的距离相等,应在何处修建?
练习1:如图,△ABC的∠B的外角的平
分线BD与∠C的外角的平分线CE相交于
点P.求证:点P到三边AB,BC,CA
所在直线的距离相等.
HD
C
F PE
A
BG
练习2: 如图,求作一点P,使PC=PD,
A
F
E
C
D
B
3、如图,△ABC中,∠C=90°,AC=CB, AD为∠BAC的平分线,DE⊥AB于点E。 求证:△DBE的周长等于AB。
C
D
A
EB
思考:
如图所示OC是∠AOB 的平分线,P 是OC上任意 一点,问PE=PD?为什么? O
EA PC
D
B
PD,PE没有垂直OA,OB,它们不是角 平分线上任一点这个角两边的距离, 所以不一定相等.
OP=OP ∴ △PDO≌△PEO(AAS)
EB
∴ PD=PE
角平分线性质: 角的平分线上的点到角的两边的距离相等。
几何语言:
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB
O
∴PD=PE
(角的平分线上的点到角的两边距离相等)
A D
C P
E B
1 、 如 图 ,OC 是 ∠ AOB 的 平 分 线 , 点 P 在 OC 上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则
并且点P到∠AOB的两边的距离相等.
B
P
D●
C●
O
A
知识拓展
如图,在△ABC中,
A
AC=BC,∠C=90°,
AD是△ABC的角平分线,
DE⊥AB,垂足为E。
(1)已知CD=4cm,求 AC的长;
E
(2)求证:AB=AC+CD C
D
B
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
老师提示:
作角平分线是最基本的尺规作图,这种方法 要确实掌握.
角平分线有什么性质呢?
OC是∠AOB的平分线,点P是射线OC上的任意一点,
1. 操 作 测 量 : 取 点 P 的 三 个 不 同 的 位 置 , 分 别 过 点 P 作
PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的
长.将三次数据填入下表:
A
PD PE
D
C 第一次
p
第二次
第三次
O
E
B
2. 观察测量结果,猜想线段PD与PE的大小关系,
写出结论:___P_D_=_P__E____
结论:
角平分线的性质:角的平分线上的点
到角的两边的距离相等
题设:一个点在一个角的平分线上 结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,
PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
A
求证:PD=PE.
D
C
P
O
B
E
已知:∠AOC= ∠BOC ,点P在OC上,PD⊥OA于D, PE⊥OB于E
求证: PD=PE
证明: ∵ PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO= 90°
在△POD和△PEO中
A
D
C
P
∠ PDO=∠PEO O ∠ AOC=∠BOC
从一个角的顶点出发,把这个角分成 相等的两个角的射线叫做这个角的角
平分线。
B
C
O
A
B
C
O
A
∠AOC =∠BOC ∠AOB =2∠AOC =2∠BOC
= =
在△ADC和 △ABC中, AD= AB DC=BC AC=AC
∴△ADC ≌ △ABC (SSS) ∴ ∠DAE=∠DAE
4 PE=__________cm.
A
C
P
D B
E
O
例1:如图,在△ABC中,∠C=900,AD平分 ∠BAC交BC于点D,若BC=8,BD=5,则点 D到AB的距离为?
A E 线BM、CN相交 于点P。求证:点P到三角形三边的距离均相等。
A
F N
G
M
P
B
E
C
尺规作图
用尺规作角的平分线. 已知:∠AOB,如图. 求作:射线OC,使∠AOC=∠BOC.
A
D
C
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE. 2.分别以点D和E为圆心,以大于DE/2长 O 为半径作弧,两弧在 ∠AOB内交于点C..
EB
3.作射线OC.
则射线OC就是∠AOB的平分线.
例3:在△OAB中,OE是∠ AOB的角平分线, 且EA=EB,EC、ED分别垂直OA,OB,垂足 为C,D,求证:AC=BD。
O
C
D
A
E
B
1、如图,OC平分∠AOB, PM⊥OB于点M, PN⊥OA于点N, △POM的面积为6,OM=6, 则PN=___2____。
N
A
C
0
P
MB
2、如图:△ABC中, ∠C=900,AD是 ∠BAC的平分线,DE⊥AB于E,F在AC上, BD=DF,求证:CF=EB
如图,为了促进当地旅游发展,某地要在三条公 路围成的一块平地上修建一个度假村.要使这个度 假村到三条公路的距离相等,应在何处修建?
练习1:如图,△ABC的∠B的外角的平
分线BD与∠C的外角的平分线CE相交于
点P.求证:点P到三边AB,BC,CA
所在直线的距离相等.
HD
C
F PE
A
BG
练习2: 如图,求作一点P,使PC=PD,
A
F
E
C
D
B
3、如图,△ABC中,∠C=90°,AC=CB, AD为∠BAC的平分线,DE⊥AB于点E。 求证:△DBE的周长等于AB。
C
D
A
EB
思考:
如图所示OC是∠AOB 的平分线,P 是OC上任意 一点,问PE=PD?为什么? O
EA PC
D
B
PD,PE没有垂直OA,OB,它们不是角 平分线上任一点这个角两边的距离, 所以不一定相等.
OP=OP ∴ △PDO≌△PEO(AAS)
EB
∴ PD=PE
角平分线性质: 角的平分线上的点到角的两边的距离相等。
几何语言:
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB
O
∴PD=PE
(角的平分线上的点到角的两边距离相等)
A D
C P
E B
1 、 如 图 ,OC 是 ∠ AOB 的 平 分 线 , 点 P 在 OC 上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则
并且点P到∠AOB的两边的距离相等.
B
P
D●
C●
O
A
知识拓展
如图,在△ABC中,
A
AC=BC,∠C=90°,
AD是△ABC的角平分线,
DE⊥AB,垂足为E。
(1)已知CD=4cm,求 AC的长;
E
(2)求证:AB=AC+CD C
D
B
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
老师提示:
作角平分线是最基本的尺规作图,这种方法 要确实掌握.
角平分线有什么性质呢?
OC是∠AOB的平分线,点P是射线OC上的任意一点,
1. 操 作 测 量 : 取 点 P 的 三 个 不 同 的 位 置 , 分 别 过 点 P 作
PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的
长.将三次数据填入下表:
A
PD PE
D
C 第一次
p
第二次
第三次
O
E
B
2. 观察测量结果,猜想线段PD与PE的大小关系,
写出结论:___P_D_=_P__E____
结论:
角平分线的性质:角的平分线上的点
到角的两边的距离相等
题设:一个点在一个角的平分线上 结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,
PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
A
求证:PD=PE.
D
C
P
O
B
E
已知:∠AOC= ∠BOC ,点P在OC上,PD⊥OA于D, PE⊥OB于E
求证: PD=PE
证明: ∵ PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO= 90°
在△POD和△PEO中
A
D
C
P
∠ PDO=∠PEO O ∠ AOC=∠BOC
