初二升初三数学试题及答案
初二升初三初中数学试卷

姓名:__________________ 班级:_______ 学号:_______ 日期:_______一、选择题(每题3分,共30分)1. 下列数中,是整数的是()A. √4B. -√9C. 3.14D. √252. 下列图形中,具有对称轴的是()A. 等腰三角形B. 正方形C. 长方形D. 等边三角形3. 下列代数式中,正确的是()A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 - b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^24. 下列方程中,有唯一解的是()A. 2x + 5 = 3x - 1B. 3x + 4 = 2x + 7C. 4x - 2 = 2x + 6D. 5x - 3 = 2x + 95. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x^2D. y = 3x6. 在直角坐标系中,点A(-2,3)关于原点对称的点是()A.(2,-3)B.(-2,-3)C.(3,2)D.(-3,2)7. 下列图形中,面积最大的是()A. 正方形B. 长方形C. 平行四边形D. 梯形8. 下列式子中,计算错误的是()A. (a + b)(a - b) = a^2 - b^2B. (a + b)^2 = a^2 + 2ab + b^2C. (a - b)^2 = a^2 - 2ab + b^2D. a^2 - b^2 = (a + b)(a - b)9. 下列等式中,正确的是()A. a^2 = b^2 → a = bB. a^2 = b^2 → a = b 或 a = -bC. a^2 + b^2 = c^2 → a, b, c 构成直角三角形D. a^2 + b^2 = c^2 → a, b, c 构成等腰三角形10. 下列函数中,是奇函数的是()A. y = x^2B. y = 2xC. y = -x^3D. y = |x|二、填空题(每题5分,共20分)11. 计算:3^2 + 2^3 - 4^2 = _______12. 等腰三角形的底边长为6cm,腰长为8cm,求三角形的面积。
初二升初三暑假数学试卷

一、选择题(每题5分,共50分)1. 下列各数中,有理数是()A. √9B. √-16C. πD. 2√22. 下列各式中,正确的是()A. 2x + 3 = 2(x + 3)B. 3x - 2 = 3(x - 2)C. 4x + 5 = 4(x + 5)D. 5x - 6 = 5(x - 6)3. 若x² - 4x + 3 = 0,则x的值为()A. 1B. 2C. 3D. 44. 已知等差数列的前三项分别为a、b、c,且a + b + c = 12,a + c = 8,则该等差数列的公差为()A. 2B. 3C. 4D. 55. 在直角坐标系中,点P(2, 3)关于x轴的对称点为()A. (2, -3)B. (-2, 3)C. (-2, -3)D. (2, 6)6. 下列函数中,y是x的一次函数的是()A. y = 2x² + 3x + 1B. y = 3x³ - 2x + 1C. y = -4x + 5D. y = √x + 27. 已知正方形的对角线长为10,则该正方形的面积为()A. 50B. 100C. 200D. 2508. 若等腰三角形的底边长为6,腰长为8,则该三角形的面积为()A. 18B. 24C. 30D. 369. 下列各式中,正确的是()A. (a + b)² = a² + b²B. (a - b)² = a² - b²C. (a + b)² = a² + 2ab + b²D. (a - b)² = a² - 2ab + b²10. 下列各式中,正确的是()A. a² + b² = (a + b)²B. a² + b² = (a - b)²C. a² - b² = (a + b)²D. a² - b² = (a - b)²二、填空题(每题5分,共50分)11. 若x² - 3x + 2 = 0,则x的值为______。
初二升初三数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,正整数是()A. -2B. 0C. 3.5D. -1/22. 下列各数中,无理数是()A. √4B. √9C. √25D. √-13. 下列各数中,平方根为正数的是()A. 4B. -4C. 0D. -94. 下列各数中,立方根为负数的是()A. -8B. -27C. 0D. 645. 下列各数中,能被2整除的是()A. 5B. 10C. 15D. 206. 下列各数中,能被3整除的是()A. 4B. 6C. 8D. 107. 下列各数中,能被5整除的是()A. 3B. 10C. 15D. 208. 下列各数中,能被7整除的是()A. 4B. 14C. 21D. 289. 下列各数中,能被11整除的是()A. 12B. 22C. 32D. 4210. 下列各数中,能被13整除的是()A. 14B. 23C. 34D. 43二、填空题(每题5分,共25分)11. 3的平方根是________,9的立方根是________。
12. 下列各数中,-3的平方是________,-2的立方是________。
13. 下列各数中,能被4整除的是________,能被6整除的是________。
14. 下列各数中,能被8整除的是________,能被9整除的是________。
15. 下列各数中,能被10整除的是________,能被12整除的是________。
三、解答题(每题10分,共30分)16. 简化下列各数:(1)√36 + √64 - √81(2)-√25 + √49 - √10017. 求下列各数的平方根和立方根:(1)√-16(2)√-2718. 求下列各数的倒数:(1)1/2(2)-1/3四、应用题(每题15分,共30分)19. 某市一居民小区共有居民150户,其中50户安装了太阳能热水器,30户安装了空气能热水器,安装了太阳能热水器或空气能热水器的居民共有多少户?20. 某商店销售一批商品,原价为每件200元,打八折后每件商品售价为160元。
升初三数学试题及答案

升初三数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数不是实数?A. πB. -3C. √2D. i2. 如果一个二次方程的判别式为负数,那么该方程:A. 有一个实数解B. 有两个实数解C. 没有实数解D. 有无穷多个解3. 一个圆的半径为5,那么它的面积是:A. 25πB. 50πC. 75πD. 100π4. 函数y = 3x + 2的斜率是:A. 2B. 3C. -3D. -25. 下列哪个是等差数列?A. 2, 4, 6, 8B. 1, 3, 5, 7C. 1, 1, 1, 1D. 3, 6, 9, 126. 一个三角形的内角和为:A. 90°B. 180°C. 270°D. 360°7. 如果一个数的绝对值是5,那么这个数可以是:A. 5B. -5C. 5或-5D. 都不是8. 一个直角三角形的两条直角边分别是3和4,那么斜边的长度是:A. 5B. 6C. 7D. 89. 将一个圆分成四个相等的扇形,每个扇形的圆心角是:A. 90°B. 180°C. 360°D. 45°10. 下列哪个是奇函数?A. y = x^2B. y = |x|C. y = sin(x)D. y = x^3二、填空题(每题2分,共20分)11. 一个数的平方根是它本身的数是______。
12. 一个数的立方根是它本身的数有______。
13. 一个数的倒数是它本身的数是______。
14. 一个数的相反数是它本身的数是______。
15. 一个数的绝对值是它本身的数是______。
16. 一个数的平方是25,这个数是______。
17. 一个数的立方是27,这个数是______。
18. 一个数的平方根是2,这个数是______。
19. 一个数的立方根是3,这个数是______。
20. 一个数的倒数是2,这个数是______。
初二升初三试卷数学及答案

一、选择题(每题3分,共30分)1. 下列数中,有理数是()A. √-1B. √2C. πD. 0.1010010001…2. 已知a > 0,b < 0,则下列不等式中正确的是()A. a > bB. a < bC. -a > -bD. -a < -b3. 下列函数中,自变量的取值范围是全体实数的是()A. y = √(x - 1)B. y = x² - 1C. y = log₂xD. y = √(2 - x)4. 若m² + 4 = 0,则m的值为()A. 2B. -2C. 2 或 -2D. 无解5. 下列图形中,属于相似图形的是()A. 等腰三角形B. 正方形C. 等边三角形D. 长方形6. 已知等腰三角形底边长为8cm,腰长为10cm,则该三角形的周长为()A. 26cmB. 24cmC. 22cmD. 18cm7. 下列方程中,无解的是()A. 2x + 3 = 5B. 2x - 3 = 5C. 2x + 3 = -5D. 2x - 3 = -58. 下列命题中,正确的是()A. 若a > b,则a² > b²B. 若a > b,则a - b > 0C. 若a > b,则a + b > 0D. 若a > b,则a - b < 09. 下列函数中,单调递增的是()A. y = 2x + 3B. y = -2x + 3C. y = 2x - 3D. y = -2x - 310. 下列数中,绝对值最小的是()A. -1B. 0C. 1D. -3二、填空题(每题3分,共30分)11. 已知x² - 5x + 6 = 0,则x的值为______。
12. 若a² + b² = 1,则ab的最大值为______。
13. 下列函数中,自变量的取值范围是全体实数的是______。
初二升初三数学试卷及答案

一、选择题 本大题共 10 小题,每题 3 分,共 30 分.在每题给出的四个选项中.只有一项为哪一项切合题目要求的,请将选择题的答案写在答题纸相应的地点上.1.若二次根式 2 x 存心义,则 x 的取值范围是A . x<2B . x ≠2C . x ≤ 2D .x ≥ 2 2.正三角形、正方形、等腰直角三角形、平行四边形中,既是轴对称图形又是中心对称图形的是A .正三角形B .正方形C .等腰直角三角形D .平行四边形 3.对于函数 y = 6 ,以下说法错误的选项是xA .它的图像散布在第一、三象限B .它的图像与直线 y =- x 无交点C .当 x>0 时, y 的值随 x 的增大而增大D .当 x<0 时, y 的值随 x 的增大而减小4.以下运算正确的选项是x y x yB . a 2 b 2 a b x 1 1 a 2 b 2 a b A . a b 2 a bC . x 1D . a b x y x y 1 x 2 a b 2 5.以下各 根式中与是同类二次根式的是A . 9B . 1C . 18D . 3036.对于频次与概率有以下几种说法:①“明日下雨的概率是90%”表示明日 下雨的可能性很大;②“抛一枚硬币正面向上的概 率为 1 ”表示每抛两次就有一次正面向上;③“某彩票中奖的概率是 1%”表示买 10 张该种2彩票不行能中奖;④“抛一枚硬币正面向上的概率为 1 ”表示跟着投掷次数的增添,“抛 2出正面向上”这一事件发生的频次稳固在 1 邻近,正确的说法是2A .①④B .②③C .②④D .①③ 7.如图,点 F 是□ABCD 的边 CD 上一点,直线 BF 交 AD 的延伸线于点E ,则以下结论错误的 是A .EDDF B . DE EF EA AB BC FB C .BC BFD .BFBC DE BE BE AE 8.如图,矩形 AOBC 中,极点 C 的坐标 (4 ,2) ,又反比率函数 y = k 的图像经过矩形的对角x线的交点 P ,则该反比率函数关系式是A . y = 8 (x>0)B . y = 2 (x>0) x xC . y = 4(x>0) D . y = 1 (x>0) x x9.计算 1142 642 502 的值为A . 0B . 25C . 50D . 8010.如图,在△ ABC 中,∠ C = 90°, BC =6, D , E 分别在 AB , AC 上, 将△ ADE 沿 DE 翻折后,点 A 落在点 A' 处,若 A' 为 CE 的中点,则 折痕 DE 的长为A . 1B . 2C . 4D . 6二、填空题 本大题共 8 小题.每题 3 分,共 24 分.把答案直接填在答题纸相对应的位 置上.11.若分式 2 存心义,则 a 的取值范围是▲ .a112.袋中共有 2 个红球, 2 个黄球, 4 个紫球, 从中任取—个球是白球, 这个事件是 ▲ 事 件.13.化简 1 = ▲ .2 114.小丽同学想利用树影丈量校园内的树高,她在某一时辰测得小树高为 1.5m 时,其影长 为 1.2 m ,此时她丈量教课楼旁的一棵大树影长为 5m ,那么这棵大树高约 ▲ m .15.如图,在△ ABC 中,∠ ACB = 90°,∠A = 35°,若以点 C 为旋转中心,将△ ABC 旋转 θ°到△ DEC 的地点,使点 B 恰巧落在边 DE 上,则 θ 值等于 ▲ .16.如图,等 腰梯形 ABCD 中, AD ∥BC , AD = 2, BC = 4,高 DF = 2.腰 DC 的长等于 ▲ .17.如图,点 A 、B 在反比率函数 y = k (k>0 ,x>0) 的图象 上,过点 A 、B 作 x 轴的垂线,垂x足分别为 M 、N ,延伸线段 AB 交 x 轴于点 C ,若 OM =MN = NC ,S △BNC = 2,则 k 的值为 ▲. 18.已知 n 是正整数, 189n 是整数,则 n 的最小值是 ▲ .三、解答题 本大题 共 11 小题,共 76 分.把解答过程写在答题纸相对应的地点上.解答时 应写出必需的计算过程、推演步骤或文字说明.作图时用 2B 铅笔或黑色墨水署名笔.19.(此题满分 8 分,每题 4 分)计算:(1) x 2 6 x 9 12 4x (2) 1 a 2 a 2 41 4x 4x2 2x 1 a a 2 2a20.(此题满分 8 分,每题 4 分)计算 :(1)53 15212(2) 8x 2x 2x 1 8x2 4 xx 02 221.(此题满分 5 分)解方程:4x 5 2x .x 1 x 122.(此题满分 5 分)如图, E、 F 分别是□ABCD的边 BC、 AD上的点,且BE= DF(1)求证:四边形 AECF是平行四边形;(2)若 BC=10,∠ BAC= 90°,且四边形 AECF是菱形,求 BE的长.23.(此题满分 5 分)如图,“精选 1 号”水稻的实验田是边长为 a m(a>1) 的正方形去掉一个边长为1m的正方形蓄水池后余下的部分;“精选2号”水稻的实验田是边长为(a - 1)m 的正方形,两块试验田的水稻都收了600 kg .(1)精选▲ 号水稻的单位面积产量高;(2) “精选 2 号”水稻的单位面积产量是“精选 1 号”水稻的单位面积产量的多少倍?24.(此题满分 6 分)如图,在□ ABCD中,点 E 在 BC上,∠ CDE=∠ DAE.(1)求证:△ ADE∽△ DEC;( 2) 若 AD= 6, DE=4,求 BE的长.25.(此题满分 6 分)“初中生骑电动车上学”的现象愈来愈遇到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的见解,统计整理制作了的统计图,请回答以下问题:(1)此次抽查的家长总人数是多少?(2)请补全条形统计图和扇形统计图;(3)从此次接受检查的学生中,随机抽查一个学生,则抽到持哪一类态度学生的可能性大?26.(此题满分8 分)已知m 3 2 n 0(1)求1 6的值;m n(2)将如图等腰三角形纸片沿底边 BC上的高 AD剪成两个三角形,此中 AB= AC= m, BC= n.用这两个三角形你能拼成多少种平行四边形?分别求出它们对角线的长(画出所拼成平行四边形的表示图)27.(此题满分8 分)如图,在平面直角坐标系中,双曲线经过点O按顺时针方向旋转90°并延伸至A,使 OA= 2OB,且点 A 的坐标为B,连结 OB.将(4 ,2) .OB绕点(1)求过点 B 的双曲线的函数关系式;(2) 依据反比率函数的图像,指出当x<- 1 时, y 的取值范围;(3)连结 AB,在该双曲线上能否存在一点P,使得 S△ABP=S△ABO,若存在,求出点P 坐标;若不存在,请说明原因.28.(此题满分8 分)喝绿茶前需要烧水和沏茶两个工序,即需要将电热水壶中的水烧到100℃,而后停止烧水,等水温降低到合适的温度时再沏茶,烧水时水温y( ℃ ) 与时间 x(min)成一次函数关系;停止加热过了 1 分钟后,水壶中水的温度y (℃ )与时间x(min)近似于反比率函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.(1)分别求出图中所对应的函数关系式,而且写出自变量x的取值范围;(2)从水壶中的水烧开 (100 ℃ ) 降到 80℃就能够进行泡制绿茶,问从水烧开到沏茶需要等候多长时间?29.(此题满分9 分)如图①,两个菱形ABCD和 EFGH是以坐标原点形,对角线均在座标轴上,已知菱形EFGH与菱形 ABCD的相像比为此中 AD= 4.(1)点 D坐标为▲,点E坐标为▲;(2)固定图①中的菱形ABCD,将菱形 EFCH绕 O点顺时针方向旋转并延伸 OE交 AD于 P,延伸 OH交 CD于 Q,如图②所示,①当α= 30°时,求点P 的坐标;②尝试究:在旋转的过程中能否存在某一角度α,使得四边形存在,请推测出α 的值;若不存在,说明原因;O为位似中心的位似图1:2 ,∠ BAD= 120°,α度角 (0 ° <α <90° ) ,AFEP是平行四边形?若。
初二升初三数学试卷答案

一、选择题(每题5分,共25分)1. 下列各数中,有理数是()A. √2B. πC. 0.1010010001…(无限循环小数)D. -1/3答案:D解析:有理数是可以表示为两个整数比的数,即分数形式。
选项A和B是无理数,选项C是无限循环小数,只有选项D是分数形式,所以选D。
2. 下列各数中,绝对值最小的是()A. -2B. -1C. 0D. 1答案:C解析:绝对值表示数与0的距离,显然0的绝对值最小,所以选C。
3. 下列各式中,正确的是()A. (-3)² = -9B. (3/4)³ = 27/64C. (-2)×(-3) = 6D. (5/2)÷(3/4) = 10/3答案:B解析:选项A中,(-3)²等于9,而不是-9;选项C中,(-2)×(-3)等于6,而不是-6;选项D中,(5/2)÷(3/4)等于10/3,而不是10/6;只有选项B正确。
4. 下列各式中,a² + b² = c²不成立的是()A. a = 3, b = 4, c = 5B. a = 5, b = 12, c = 13C. a = 7, b = 24, c = 25D. a = 8, b = 15, c = 17答案:A解析:勾股定理表明,在直角三角形中,两直角边的平方和等于斜边的平方。
选项A中的a² + b² = 3² + 4² = 9 + 16 = 25,而c² = 5² = 25,所以选项A成立。
其他选项均满足勾股定理。
5. 下列各函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x²D. y = x³答案:B解析:反比例函数的形式是y = k/x,其中k是常数。
选项B符合这个形式,所以选B。
二、填空题(每题5分,共25分)6. 3/4的倒数是__________。
初二初三数学试卷含答案

一、选择题(每题5分,共30分)1. 下列各数中,有理数是()A. √2B. πC. √9D. 无理数答案:C2. 下列代数式中,同类项是()A. x^2yB. 2xyC. x^2D. 3y答案:B3. 如果a > b,那么下列不等式中正确的是()A. a + 1 > b + 1B. a - 1 > b - 1C. a + 2 < b + 2D. a - 2 < b - 2答案:A4. 已知等腰三角形底边长为6cm,腰长为8cm,则该三角形的周长为()A. 16cmB. 18cmC. 20cmD. 22cm答案:C5. 下列函数中,定义域为全体实数的是()A. y = √xB. y = x^2C. y = 1/xD. y = |x|答案:B二、填空题(每题5分,共25分)6. 若a = 3,b = -2,则a^2 + b^2 = ________。
答案:137. 若x - 3 = 0,则x = ________。
答案:38. 若等边三角形边长为a,则其周长为 ________。
答案:3a9. 若一个数的平方等于4,则这个数是 ________。
答案:±210. 若一个数的倒数等于1/3,则这个数是 ________。
答案:3三、解答题(每题15分,共60分)11. (15分)计算下列各式的值:(1)(2a - 3b) + (5a + 2b)(2)(x + 2)(x - 1)(3)(3x^2 - 2x + 1) ÷ (x - 1)答案:(1)7a - b(2)x^2 + x - 2(3)3x + 112. (15分)已知等腰三角形底边长为10cm,腰长为13cm,求该三角形的面积。
答案:面积 = (底边长× 高) / 2 = (10 × 12) / 2 = 60cm²13. (15分)解下列方程:(1)2x + 3 = 11(2)5(x - 2) = 3x + 10答案:(1)x = 4(2)x = 1014. (15分)已知函数y = 2x - 3,求x = 5时的函数值。
初二升初三数学试题及答案

D CBA 、B 、C 、D 、初二升初三数学测试题一、选择题(每小题有且只有一个答案正确,每小题4分,共40分) 1、如图,两直线a ∥b ,与∠1相等的角的个数为( ) A 、1个 B 、2个 C 、3个 D 、4个2、不等式组x>3x<4⎧⎨⎩的解集是( )A 、3<x<4B 、x<4C 、x>3D 、无解 3、如果a>b ,那么下列各式中正确的是( ) A 、a 3<b 3-- B 、a b<33C 、a>b --D 、2a<2b -- 4、如图所示,由∠D=∠C,∠BAD=∠ABC 推得△ABD ≌△BAC ,所用的的判定定理的简称是( ) A 、AAS B 、ASA C 、SAS D 、SSS5、已知一组数据1,7,10,8,x ,6,0,3,若x =5,则x 应等于( ) A 、6 B 、5 C 、4 D 、26、下列说法错误的是( )A 、长方体、正方体都是棱柱;B 、三棱住的侧面是三角形;C 、六棱住有六个侧面、侧面为长方形;D 、球体的三种视图均为同样大小的图形; 7、△ABC 的三边为a 、b 、c ,且2(a+b)(a-b)=c ,则( ) A 、△ABC 是锐角三角形; B 、c 边的对角是直角; C 、△ABC 是钝角三角形; D 、a 边的对角是直角;8、为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是( )A 、中位数;B 、平均数;C 、众数;D 、加权平均数;9、如右图,有三个大小一样的正方体,每个正方体的六个面上都按照相同的顺序,依次标有1,2,3,4,5,6这六个数字,并且把标有“6”的面都放在左边,那么它们底面所标的3个数字之和等于( )A 、8B 、9C 、10D 、1110、为鼓励居民节约用水,北京市出台了新的居民用水收费标准:(1)若每月每户居民用水不超过4立方米,则按每立方米2米计算;(2)若每月每户居民用水超过4立方米,则超过部分按每立方米4.5米计算(不超过部分仍按每立方米2元计算)。
中考数学初二升初三试卷

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -3B. 2C. -1D. 02. 若a、b是方程x²-5x+6=0的两根,则a+b的值为()A. 2B. 5C. 6D. 103. 在直角坐标系中,点A(-2,3)关于x轴的对称点坐标是()A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,3)4. 若a²+b²=1,则(a+b)²的值为()A. 1B. 2C. 3D. 45. 在△ABC中,∠A=45°,∠B=60°,则∠C的度数为()A. 75°B. 80°C. 85°D. 90°6. 下列函数中,y是x的线性函数的是()A. y=x²B. y=2x+3C. y=x³D. y=√x7. 若a、b、c是等差数列的连续三项,且a+b+c=18,则a²+b²+c²的值为()A. 54B. 63C. 72D. 818. 下列各式中,正确的是()A. 2√3 > 3√2B. 2√3 < 3√2C. 2√3 = 3√2D. 2√3 ≠ 3√29. 若a=√2+1,b=√2-1,则a²-b²的值为()A. 4B. 2C. 0D. -210. 在等腰三角形ABC中,底边BC=6cm,腰AB=AC=8cm,则底角∠B的度数为()A. 30°B. 45°C. 60°D. 90°二、填空题(每题4分,共20分)11. 若x=√5,则x²-5的值为______。
12. 若a、b是方程x²-6x+9=0的两根,则a²+b²的值为______。
13. 在直角坐标系中,点P(-3,2)到原点O的距离为______。
14. 若sinθ=0.6,则cosθ的值为______。
初二升初三入学数学试卷

一、选择题(每题5分,共50分)1. 若a、b、c是等差数列,且a+b+c=12,b+c-a=6,则该数列的公差是()A. 1B. 2C. 3D. 42. 若x^2+2x+1=0,则x的值为()A. -1B. 1C. 2D. -23. 在直角坐标系中,点A(1,2)关于y轴的对称点是()A.(1,-2)B.(-1,2)C.(-1,-2)D.(1,-2)4. 若a、b、c是等比数列,且a+b+c=12,b+c-a=6,则该数列的公比是()A. 1B. 2C. 3D. 45. 已知函数f(x)=2x+1,若f(x+y)=f(x)f(y),则x+y的值为()A. 0B. 1C. 2D. 36. 若a、b、c是等差数列,且a^2+b^2+c^2=24,则abc的值为()A. 1B. 2C. 3D. 47. 在直角坐标系中,点P(3,4)到直线x+y=7的距离是()A. 1B. 2C. 3D. 48. 若x^2+2x+1=0,则x的值为()A. -1B. 1C. 2D. -29. 在直角坐标系中,点A(1,2)关于x轴的对称点是()A.(1,-2)B.(-1,2)C.(-1,-2)D.(1,-2)10. 若a、b、c是等比数列,且a+b+c=12,b+c-a=6,则该数列的公比是()A. 1B. 2C. 3D. 4二、填空题(每题5分,共50分)11. 已知等差数列{an}中,a1=3,公差d=2,则第10项an=______。
12. 若x^2-3x+2=0,则x的值为______。
13. 在直角坐标系中,点P(3,4)到直线2x+3y-6=0的距离是______。
14. 已知函数f(x)=x^2+2x+1,若f(x+y)=f(x)f(y),则x+y的值为______。
15. 若a、b、c是等差数列,且a^2+b^2+c^2=24,则abc的值为______。
16. 已知等比数列{an}中,a1=2,公比q=3,则第5项an=______。
升初三数学试题及答案

升初三数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是无理数?A. 3.14159B. √2C. 0.333...D. 1.52. 如果一个正数的平方根等于它本身,那么这个数是:A. 0B. 1C. -1D. 23. 一个数的绝对值是其本身,这个数可能是:A. 正数B. 负数C. 0D. 正数或04. 以下哪个不是二次根式?A. √3B. -√2C. √(-1)D. √(2x)5. 一个三角形的内角和等于:A. 90°B. 180°C. 360°D. 270°6. 一个数的立方等于它自身,这个数是:A. 0B. 1C. -1D. 27. 以下哪个是整式?A. 3x² + 2x + 1B. √xC. 3x²/2D. 3x² + √x8. 一个数的倒数是它自身,这个数是:A. 0B. 1C. -1D. 29. 下列哪个是一元一次方程?A. x² + 2x = 5B. x + 2 = 3xC. 2x - 3 = 0D. 3x + 2y = 510. 以下哪个是二次方程?A. x² + 2x + 1 = 0B. x + 2 = 3C. 2x - 3 = 0D. 3x + 2y = 5二、填空题(每题2分,共20分)11. 一个数的平方根是4,这个数是______。
12. 一个数的绝对值是5,这个数可能是______。
13. 一个三角形的外角和等于______。
14. 如果一个数的立方等于8,那么这个数是______。
15. 一个数的倒数是1/2,这个数是______。
16. 一个一元一次方程的一般形式是______。
17. 一个二次方程的一般形式是______。
18. 一个正数的平方根是2,这个数是______。
19. 一个数的立方根是3,这个数是______。
20. 一个数的绝对值是它自身,这个数是______。
初二升初三数学习题
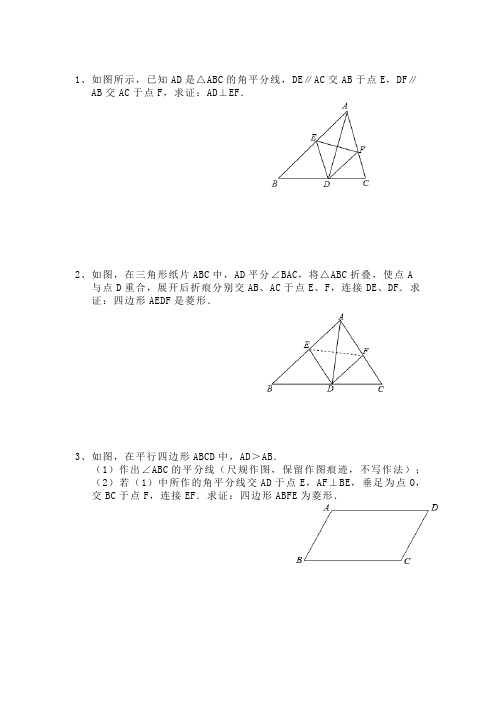
1、如图所示,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,求证:AD⊥EF.2、如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.3、如图,在平行四边形ABCD中,AD>AB.(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.4、如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.(1)求证:四边形BMDN是菱形;(2)若AB=4,AD=8,求MD的长.5、如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB与点E,且CF=AE,(1)求证:四边形BECF是菱形;(2)若四边形BECF为正方形,求∠A的度数.6、菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.7、正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM;(2)当AE=1时,求EF的长.8、如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.(1)求证:①△ABG≌△AFG;②BG=CG;(2)求△FGC的面积9、在平面直角坐标系xOy中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.(1)当∠BAO=45°时,求点P的坐标;(2)求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由.10、如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.(1)求证:OE=OF;DN12、已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.13、已知:如图,正方形ABCD中,E、F分别为AB、BC的中点,CE、DF交于M.(1)试判断CE和DF的关系,并证明;(2)求证:AM=AD.14、如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).(1)当α=60°时,求CE的长;(2)当60°<α<90°时,是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.15、【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)证明:AM=AD+MC;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.16、如图,△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,连AD,BE,F为线段AD的中点,连CF.(1)如图1,当D点在BC上时,试探索出BE与CF的数量关系,并说明理由;(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变,问(1)中的关系是否仍然成立?如果成立请证明.如果不成立,请写出相应的正确的结论并加以证明.17、邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.(1)判断与推理:①邻边长分别为2和3的平行四边形是阶准菱形;②小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.(2)操作、探究与计算:①已知▱ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出▱ABCD及裁剪线的示意图,并在图形下方写出a的值;②已知▱ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出▱ABCD是几阶准菱形.18、一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD 为2阶奇异矩形.(1)判断与操作:如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.(2)探究与计算:已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.(3)归纳与拓展:已知矩形ABCD两邻边的长分别为b,c(b<c),且它是4阶奇异矩形,则b:c= (写出所有值).19、如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.(1)试用含t的式子表示AE、AD的长;(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;(3)连接DE,当t为何值时,△DEF为直角三角形?(4)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形 AEA′D为菱形?并判断此时点A是否在BC上?请说明理由.20、如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O 时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).(1)∠PBD的度数为,点D的坐标为(用t表示);(2)当t为何值时,△PBE为等腰三角形?(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.21、如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:(1)当t=2时,判断△BPQ的形状,并说明理由;(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?22、如图所示,在直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14cm,A点坐标为(16,0),C点坐标为(0,2).点P、Q分别从C、A同时出发,点P以2cm/s的速度由C向B运动,点Q以4cm/s的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为ts(0≤t≤4).(1)求当t为多少时,四边形PQAB为平行四边形.(2)求当t为多少时,PQ所在直线将梯形OABC分成左右两部分的面积比为1:2,求出此时直线PQ的函数关系式.23、如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A 落在BC边上的G处,E、F分别在AD、AB上,且F点的坐标是(2,4).(1)求G点坐标;(2)求直线EF解析式;(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G 为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.24、如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30度,(1)求B、C两点的坐标;(2)把矩形沿直线DE对折使点C落在点A处,DE与AC相交于点F,求直线DE的解析式;(3)若点M在直线DE上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.直平分线CD分别与AB、x轴、y轴交于点C、G、D.(1)求点G的坐标;(2)求直线CD的解析式;(3)在直线CD上和平面内是否分别存在点Q、P,使得以O、D、P、Q 为顶点的四边形是菱形?若存在,求出点Q得坐标;若不存在,请说明理由.。
初二升初三数学试卷答案

一、选择题(每题3分,共30分)1. 下列数中,哪个是质数?A. 18B. 19C. 28D. 30答案:B2. 下列方程中,哪个方程的解是x=2?A. 2x + 3 = 9B. 3x - 1 = 5C. 4x + 2 = 8D. 5x - 3 = 7答案:A3. 下列图形中,哪个是轴对称图形?A. 正方形B. 长方形C. 等腰三角形D. 等边三角形答案:D4. 下列分数中,哪个是最简分数?A. $\frac{12}{18}$B. $\frac{15}{25}$C. $\frac{18}{27}$D. $\frac{20}{30}$答案:B5. 下列数中,哪个是偶数?A. 13B. 14C. 15D. 16答案:B6. 下列函数中,哪个是反比例函数?A. y = 2x + 3B. y = 3x - 2C. y = $\frac{3}{x}$D. y = 2x^2 + 1答案:C7. 下列几何图形中,哪个图形的面积是πr^2?A. 圆柱B. 圆锥C. 球D. 立方体答案:C8. 下列方程中,哪个方程的解是x=0?A. 2x + 4 = 8B. 3x - 6 = 0C. 4x + 8 = 16D. 5x - 10 = 20答案:B9. 下列数中,哪个是立方数?A. 8B. 27C. 64D. 81答案:B10. 下列图形中,哪个是中心对称图形?A. 正方形B. 长方形C. 等腰三角形D. 等边三角形答案:A二、填空题(每题5分,共50分)11. 如果a=3,那么a^2 + a + 1的值是______。
答案:1312. 分数$\frac{4}{5}$与$\frac{8}{10}$是______。
答案:同分母分数13. 圆的直径是10cm,那么圆的半径是______cm。
答案:514. 一个等腰三角形的底边长是6cm,腰长是8cm,那么这个三角形的周长是______cm。
答案:2215. 下列数列中,下一个数是______。
初二升初三测试卷数学

一、选择题(每题5分,共25分)1. 下列选项中,不是二次方程的是()A. x^2 - 3x + 2 = 0B. x^2 + 2x - 3 = 0C. x^2 - 4 = 0D. 2x^2 + 3x - 1 = 02. 下列选项中,不是一元二次方程的是()A. x^2 - 2x + 1 = 0B. x^2 - 3x + 4 = 0C. x^2 + 2x - 3 = 0D. 2x^2 + 3x - 1 = 03. 下列选项中,不是一元一次方程的是()A. 2x + 3 = 0B. 3x - 4 = 0C. 2x^2 + 3x - 1 = 0D. 5x - 7 = 04. 下列选项中,不是方程的是()A. 2x + 3 = 0B. 3x - 4 = 0C. 2x^2 + 3x - 1 = 0D. 5x - 7 = 05. 下列选项中,不是一元一次方程的解集是()A. x = 2C. x = -1D. x = 3二、填空题(每题5分,共25分)6. 一元二次方程x^2 - 3x + 2 = 0的解为:x1 = __,x2 = __。
7. 一元一次方程2x - 5 = 0的解为:x = __。
8. 若a > 0,则不等式ax > 0的解集为:x > __。
9. 若a < 0,则不等式ax > 0的解集为:x < __。
10. 若a > 0,则不等式ax < 0的解集为:x < __。
三、解答题(每题10分,共30分)11. (10分)解下列方程:(1)2x^2 - 5x + 2 = 0;(2)3x^2 - 2x - 1 = 0。
12. (10分)已知一元二次方程x^2 - 4x + 3 = 0,求:(1)该方程的解;(2)该方程的判别式。
13. (10分)已知一元一次方程2x - 5 = 0,求:(1)该方程的解;(2)该方程的系数。
四、应用题(每题10分,共20分)14. (10分)某工厂生产一批产品,计划每天生产50个,实际每天生产60个。
初二升初三数学入学测试卷(含答案)
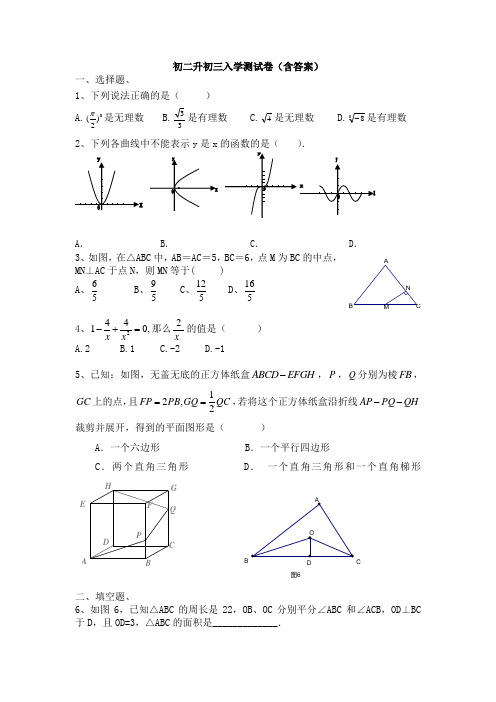
初二升初三入学测试卷(含答案)一、选择题、1、下列说法正确的是( ) A.0)2(π是无理数B.33是有理数 C.4是无理数 D.38-是有理数2、下列各曲线中不能表示y 是x 的函数的是( ).A .B .C .D . 3、如图,在△ABC 中,AB =AC =5,BC =6,点M 为BC 的中点,MN ⊥AC 于点N ,则MN 等于( )A 、65B 、95C 、125D 、1654、,04412=+-x x 那么x2的值是( )A.2B.1C.-2D.-15、已知:如图,无盖无底的正方体纸盒ABCD EFGH -,P ,Q 分别为棱FB ,GC 上的点,且12,2FP PB GQ QC ==,若将这个正方体纸盒沿折线AP PQ QH --裁剪并展开,得到的平面图形是( )A .一个六边形B .一个平行四边形C .两个直角三角形D . 一个直角三角形和一个直角梯形QPHGFED C BA二、填空题、6、如图6,已知△ABC 的周长是22,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD=3,△ABC 的面积是_____________.N MB C A 图6DBC7、.当=m 时,关于x 的方程313292-=++-x x x m 有增根. 8、如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =3.其中正确个数是 。
三、解答题、9、计算:36 -(-2)2 +(214)2+|3.14-π|10、如图,在梯形ABCD 中,DC ‖AB ,AD=BC , BD 平分,60.ABC A ∠∠=o过点D 作DE AB ⊥,过点C 作CF BD ⊥,垂足分别为E 、F ,连接EF ,求证:DEF △为等边三角形.10题图11、如图,直线6y kx =+与x 轴y 轴分别交于点E 、F ,点E 的坐标为(-8,0), 点A 的坐标为(-6,0).(1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 与x 的函数关系式,并写出自变量x 的取值范围;(3)探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由.12、以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH .(1)如图1,当四边形ABCD 为正方形时,我们发现四边形EFGH 是正方形;如图2,当四边形ABCD 为矩形时,请判断:四边形EFGH 的形状(不要求证明); (2)如图3,当四边形ABCD 为一般平行四边形时,设∠ADC =α(0°<α<90°), ① 试用含α的代数式表示∠HAE ; ② 求证:HE =HG ;③ 四边形EFGH 是什么四边形?并说明理由.A BCDHEFG(第12题图2)E BFGD HAC(第12题图3)(第12题图1)A BCDH EFG初二升初三数学答案 1~5DBCBB 6、33 7、6或12 8、3个9、解:3.11+π10、证明:因为DC ‖AB ,,60AD BC A =∠=o ,所以60ABC A ∠=∠=o .又因为BD 平分ABC ∠,所以130.2ABD CBD ABC ∠=∠=∠=o因为DC ‖AB ,所以30BDC ABD ∠=∠=o,所以,CBD CDB ∠=∠所以.CB CD =因为CF BD ⊥,所以F 为BD 中点, 又因为DE AB ⊥,所以.DF BF EF == 由30ABD ∠=o,得60BDE ∠=o, 所以DEF △为等边三角形.11、解:(1)把点E 的坐标为(-8,0)代入6y kx =+,得0=-8k+634k =;(2)∵点A 的坐标为(-6,0), ∴OA=6.∵点P (x ,y )是第二象限内的直线上的一个动点,E (-8,0);∴-8<x <0, >0. ∴△OPA 的面积 ∴(3)把S=278代入9184S x =+,得364y x =+364y x =+119366182244S OA y x x ⎛⎫=⨯=⨯⨯+=+ ⎪⎝⎭918(80)4S x x =+-<<132x =-. 再把132x =-代入 ,得98y =∴当P 点的坐标为139,28⎛⎫- ⎪⎝⎭时,△OPA 的面积为278.12、(1)四边形EFGH 是正方形. (2) ①∠HAE=90°+a .在□ABCD 中,AB ∥CD ,∴∠BAD=180°-∠ADC=180°-a ; ∵△HAD 和△EAB 都是等腰直角三角形,∴∠HAD=∠EAB=45°,∴∠HAE=360°-∠HAD -∠EAB -∠BAD =360°-45°-45°-(180°-a )=90°+a .②∵△AEB 和△DGC 都是等腰直角三角形,∴AE=2AB ,DG=2CD ,在□ABCD 中,AB=CD ,∴AE=DG ,∵△HAD 和△GDC 都是等腰直角三角形, ∴∠DHA=∠CDG= 45°,∴∠HDG=∠HAD +∠ADC +∠CDG =90°+a =∠HAE . ∵△HAD 是等腰直角三角形,∴HA=HD ,∴△HAE ≌△HDG ,∴HE=HG . ③四边形EFGH 是正方形.由②同理可得:GH=GF ,FG=FE ,∵HE=HG (已证),∴GH=GF=FG=FE , ∴四边形EFGH 是菱形;∵△HAE ≌△HDG (已证),∴∠DHG=∠AHE , 又∵∠AHD=∠AHG +∠DHG=90°,∴∠EHG=∠AHG +∠AHE =90°, ∴四边形EFGH 是正方形.364y x =+。
初二初三数学试卷含答案

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -2B. 1C. 0D. -12. 若a=2,b=-3,则a²+b²的值为()A. 1B. 5C. 13D. 173. 下列图形中,是轴对称图形的是()A. 正方形B. 等边三角形C. 平行四边形D. 长方形4. 已知一元二次方程x²-5x+6=0,则方程的解为()A. x=2, x=3B. x=1, x=6C. x=2, x=4D. x=3, x=55. 下列函数中,是反比例函数的是()A. y=x²B. y=x+1C. y=1/xD. y=2x6. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数为()A. 75°B. 105°C. 120°D. 135°7. 若等差数列的前三项分别为1,4,7,则该数列的公差为()A. 2B. 3C. 4D. 58. 已知二次函数y=ax²+bx+c(a≠0)的图象开口向上,且顶点坐标为(2,-3),则a的值为()A. 1B. 2C. 3D. 49. 下列不等式中,正确的是()A. 2x > 4B. 2x < 4C. 2x ≥ 4D. 2x ≤ 410. 若x=3,则代数式2x²-5x+2的值为()A. 1B. 4C. 7D. 10二、填空题(每题5分,共25分)11. 若m=5,n=-3,则m²-n²的值为______。
12. 在△ABC中,若AB=AC,则∠B与∠C的关系是______。
13. 等差数列{an}的前10项和为100,公差为2,则第5项an的值为______。
14. 已知二次函数y=ax²+bx+c(a≠0)的图象与x轴的交点坐标为(-1,0)和(3,0),则该函数的表达式为______。
15. 若不等式2x-3>5,则x的取值范围为______。
升初三综合数学试卷及答案

一、选择题(每题3分,共30分)1. 下列各数中,无理数是()A. √4B. √9C. √16D. √252. 若x=2是方程2x+1=5的解,则方程x-3=?的解是()A. 5B. 6C. 7D. 83. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数是()A. 75°B. 90°C. 105°D. 120°4. 下列函数中,自变量x的取值范围正确的是()A. y=√(x-3)B. y=√(3-x)C. y=√(x+3)D. y=√(x-3)5. 已知函数y=2x-3,当x=4时,y的值是()A. 5B. 7C. 9D. 116. 若a、b、c是等差数列,且a+b+c=12,a+c=8,则b的值是()A. 2B. 4C. 6D. 87. 下列命题中,正确的是()A. 等腰三角形的底角相等B. 直角三角形的斜边最长C. 平行四边形的对角线互相平分D. 矩形的对角线相等8. 下列数中,是偶数的是()A. 1/2B. √4C. √9D. √169. 若a、b、c、d是等比数列,且a+b+c+d=20,a+d=4,则b+c的值是()A. 6B. 8C. 10D. 1210. 下列各数中,是实数的是()A. √(-1)B. √4C. √9D. √16二、填空题(每题5分,共20分)11. 若x=3是方程3x-2=7的解,则x的值是______。
12. 在△ABC中,若∠A=90°,∠B=30°,则∠C的度数是______。
13. 函数y=2x+1中,当x=0时,y的值是______。
14. 若a、b、c是等差数列,且a+b+c=12,a+c=8,则公差d的值是______。
15. 下列函数中,自变量x的取值范围正确的是______。
三、解答题(每题10分,共30分)16. 解方程:2x+3=5x-1。
17. 已知函数y=√(x-2),求函数的定义域。
初二升初三数学试卷及解析

一、选择题(每题5分,共50分)1. 已知等腰三角形ABC中,AB=AC,∠B=40°,则∠C的度数是()A. 40°B. 50°C. 60°D. 70°2. 下列各数中,有理数是()A. √2B. πC. -√2D. -π3. 若x=2,则x²-3x+2的值为()A. 1B. 2C. 3D. 44. 已知一次函数y=kx+b(k≠0)的图象经过点(1,2),则下列选项中正确的是()A. k=2,b=1B. k=1,b=2C. k=2,b=2D. k=1,b=15. 已知正方形的边长为4,则其对角线的长度为()A. 2B. 4C. 6D. 86. 下列各式中,正确的是()A. a²+b²=c²(a,b,c为任意实数)B. (a+b)²=a²+2ab+b²(a,b为任意实数)C. (a-b)²=a²-2ab+b²(a,b为任意实数)D. (a+b)²=a²-b²(a,b为任意实数)7. 已知一元二次方程x²-5x+6=0,则其解为()A. x=2,x=3B. x=1,x=6C. x=2,x=4D. x=3,x=58. 下列图形中,是轴对称图形的是()A. 等边三角形B. 等腰三角形C. 正方形D. 长方形9. 已知平行四边形ABCD中,AB=6,AD=8,则对角线BD的长度为()A. 10B. 12C. 14D. 1610. 下列函数中,是奇函数的是()A. y=x²B. y=x³C. y=x²+1D. y=x³+1二、填空题(每题5分,共50分)11. 若x=3,则x²-4x+3的值为________。
12. 已知等腰三角形ABC中,AB=AC,∠B=50°,则∠A的度数是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D C
B
A 、
B 、
C 、
D 、
初二升初三数学测试题
一、选择题(每小题有且只有一个答案正确,每小题4分,共40分) 1、如图,两直线a ∥b ,与∠1相等的角的个数为( ) A 、1个 B 、2个 C 、3个 D 、4个
2、不等式组x>3
x<4
⎧⎨⎩的解集是( )
A 、3<x<4
B 、x<4
C 、x>3
D 、无解 3、如果a>b ,那么下列各式中正确的是( ) A 、a 3<b 3-- B 、
a b
<33
C 、a>b --
D 、2a<2b -- 4、如图所示,由∠D=∠C,∠BAD=∠ABC 推得△ABD ≌△BAC ,所用的的判定定理的简称是( ) A 、AAS B 、ASA C 、SAS D 、SSS
5、已知一组数据1,7,10,8,x ,6,0,3,若x =5,则x 应等于( ) A 、6 B 、5 C 、4 D 、2
6、下列说法错误的是( )
A 、长方体、正方体都是棱柱;
B 、三棱住的侧面是三角形;
C 、六棱住有六个侧面、侧面为长方形;
D 、球体的三种视图均为同样大小的图形; 7、△ABC 的三边为a 、b 、c ,且2
(a+b)(a-b)=c ,则( ) A 、△ABC 是锐角三角形; B 、c 边的对角是直角; C 、△ABC 是钝角三角形; D 、a 边的对角是直角;
8、为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是( )
A 、中位数;
B 、平均数;
C 、众数;
D 、加权平均数;
9、如右图,有三个大小一样的正方体,每个正方体的六个面上都按照相同的顺序,依次标有1,
2,3,4,5,6这六个数字,并且把标有“6”的面都放在左边,那么它们底面所标的3个数字之和等于( )
A 、8
B 、9
C 、10
D 、11
10、为鼓励居民节约用水,北京市出台了新的居民用水收费标准:(1)若每月每户居民用水不超过4立方米,则按每立方米2米计算;(2)若每月每户居民用水超过4立方米,则超过部分按每立方米4.5米计算(不超过部分仍按每立方米2元计算)。
现假设该市某户居民某月用水x 立方米,水费为y 元,则y 与x 的函数关系用图象表示正确的是( )
1
a b
A B
C
D E
F
A B
O C
D
二、填空题(每小题4分,共32分)
11、不等式2x-1>3的解集是__________________;
12、已知点A 在第四象限,且到x 轴,y 轴的距离分别为3,5,则A 点的坐标为_________;
13、为了了解某校初三年级400名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指________;
14、某班一次体育测试中得100分的有4人,90分的有11人,80分的有11人,70分的有8人,60分的有5人,剩下的8人一共得了300分,则中位数是_____________。
15、如图,已知∠B=∠DEF ,AB=DE ,请添加一个条件使△ABC ≌△DEF ,则需添加的条件是__________; 16、如图,AD 和BC 相交于点O ,OA=OD ,OB=OC ,若∠B=40°,∠AOB=110°,则∠D=________度; 17、弹簧的长度y(cm)与所挂物体的质量x (kg)的关系是一次函数, 图象如右图所示,则弹簧不挂物体时的长度是___________cm ;
第15题图 第16题图 第17题图 18、如下图所示,图中是一个立体图形的三视图,请你根据视图,说出立体图形的名称:
对应的立体图形是________________的三视图。
三、解答题(共78分) 19、(8分)解不等式x+1
(x 1)12
--≤,并把解集在数轴上表示出来。
20、(8分)填空(补全下列证明及括号内的推理依据): 如图:已知:AD ⊥BC 于D ,EF ⊥BC 于F ,∠1=∠3, 求证:AD 平分∠BAC 。
主视图
左视图
俯视图
2 1
3 A B
C
D
E
F
答案:
一、选择题
1 C
2 A
3 D
4 A
5 B
6 B
7 D
8 C
9 A 10 C
二、填空题
11、X>2 12、(5,-3) 13、某校初三年级400名学生体重情况的全体 14、80分 15、BC=EF
16、80 17、9 18、四菱形或五面体
三、解答题
19、解:x+1
(x1)1 2
--≥
x+12(x1)2
--≥)
x12x22
+-+≥
x1
-≥-
x1
≤
20、证明:∵AD⊥BC,EF⊥BC于F(已知)
∴AD∥EF(同位角相等,两直线平等或在同一平面内,垂直于同一条干线的两条直线平行) ∴∠1=∠E(两条直线平行,同位角相等)
∠2=∠3(两条直线平行,内错角相等)
又∵∠3=∠1(已知)
∴∠1=∠2(等量代换)
∴AD平分∠BAC(AD平分∠BAC∵∠1=∠2,AD为∠BAC平分线)。
