水力学2.4静止流体对平面的作用力
合集下载
水力学25静止流体对曲面的作用力资料
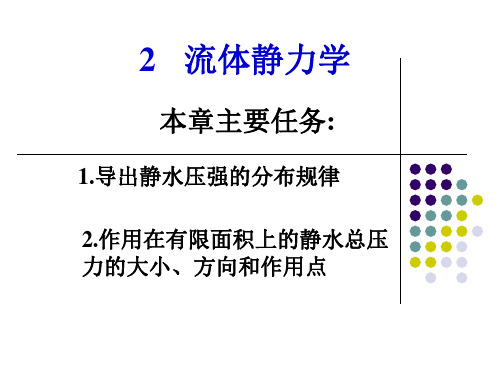
dPx dP cos hdAcos hdAx dPz dPsin hdAsin hdAz
(2.22)(2.23)
2.5.1 总压力的大小、方向和作用点
Px dPx Ax hdAx Ax hdAx (2.24)
Pz dPz Az hdAz
Ax hdAx
曲面EF在铅直面上的投影面对水平轴的
Az hdAz
整个曲面AB上的液体重,即柱状体 ABDCC'D'B'A'内的液体重。
2.5.1 总压力的大小、方向和作用点
于是铅直分量: Pz V
PZ的方向如何?
(2.26)
2.5.2 压力体
ABDCC'D'B'A'—称为压力体,即作用在 曲面AB上的液体体积,该体积计为V。
压力体的组成:
1.曲面; 2.液面或液面的延伸面; 3.通过曲面四周边缘的
铅直平面。
5.2 压力体
实压力体: 液体与压力体在曲面的同侧.PZ向下 虚压力体: 液体与压力体在曲面的两侧.PZ向上
对于规则曲面可求其总压力: P Px2 Pz2
P与水平线的夹角: arctan Pz
Px
2.5.2 压力体
复杂曲面的压力体:图2.27
2.5.3 浮力
阿基米德定律:物体在液体中所受的浮力的 大小等于它所排开同体积的水所受的重力
2 流体静力学
本章主要任务:
1.导出静水压强的分布规律
2.作用在有限面积上的静水总压 力的大小、方向和作用点
2.5 静止流体对曲面的作用力
根据静水压强分布 规律,作用于曲面 上任意点的静水压 强,沿着作用面的 法线方向并指向作 用面,且其大小与 该点所在的水下深 度成线性关系。
水力学 第二章 流体静力学

解: 在作用下小活塞上产生流体静压
强为
p
1
P1
按帕斯卡定律, p1 将不变地传递到ω 2 上,所以
2 P2 p 2 P1 1
§2一2 流体平衡微分方程——欧拉平衡微分方程 13
§2一3 流体静力学基本方程
2-3-1 重力作用下的流体平衡方程
静止重力流体:所受的质量力只有重力的静止流体。
单位质量流体上的质量力在各坐标轴方向的分量 。
f x 0, f y 0, f z g
代入
dp ( f x dx f y dy f z dz )
得:
dp gdz
对于不可压缩均质流体,ρ=常数,积分得 : p z C p gz C1 g
§2一3 流体静力学基本方程
FP x 0, FP y 0, FP z 0,
现以x轴方向为例:
FPx FPn cos( n, x ) Fx 0
1 FPx p x dydz 2 1 FPn cos( n, x ) pn dAn cos( n, x ) pn dAn cos(n, x) pn dydz 2
§2一3 流体静力学基本方程
15
p1 /
h
(2) (1)
p2 /
Z1
Z2
o
o
2-3-1 重力作用下的流体平衡方程
自由表面上为大气压强 p0 的液体,水静力学基本方程为 说明: 1)静止流体中某一点的静水压强随深度按线性规律增加。 2)静止流体中某一点的静水压强等于表面压强加上流体 的容 重与该点淹没深度的乘积。后一部分即为单位面积上淹没深度液柱 的重量 。
pv pa p'
hv
流体静力学

yD
y2dA
Ix
yC A yC A
❖平行移轴公式
Ix yC2 A+IC
yD
Ix yC A
yC2 A+IC yC A
yD
yC
IC yC A
流体与平面间作用力
常见图形的惯性矩
y y
y
流体与平面间作用力
如图所示为一矩形平面挡水闸板,长l=2.5m,宽b=1.5m,A 点到水面高度h=3m。求水闸关闭时,在B点处必须施加的作 用力F。
CD
2
1000 9.8 (3 2.5 1)1.5 2.5
Fp
22
133218.75 (N )
流体与平面间作用力
如图所示为一矩形平面挡水闸板,长l=2.5m,宽b=1.5m,A 点到水面高度h=3m。求水闸关闭时,在B点处必须施加的作 用力F。
yD
yc
Ic yc A
Ic
P yD y dP
P pC A yC sin A
dP y sindA
yC sin A yD y2 sindA
压力中心D 的y坐标为:
yD
y2dA
Ix
yC A yC A
p0=0
o pα
P
x
CA D y
作用在平面上的总压力
流体与平面间作用力
根据力矩平衡
F AB Fp AD
D
Fp =?
Fp
AD=?
流体与平面间作用力
如图例所题示为一矩形平面挡水闸板,长l=2.5m,宽b=1.5m,A
点到水面高度h=3m。求水闸关闭时,在B点处必须施加的作 用力F。
第05讲流体静力学1

ds
V
n
S
y
∫∫
S
p nds =
∫∫∫
V
∇ p dV
则力平衡方程转化为:
x
∫∫∫ ( ρ f − ∇p )dV = 0
V
由于所取流体团是任意的,上式恒成立的充要条件是被积函数为零:
f =
1
ρ
∇p
这就是静止流体的平衡微分方程,它表明作用在单位质量静止流体上的质 量力与压力的合力相互平衡。
平衡微分方程在直角坐标系中的表达式为:
斜管压力计
斜管压力计是一种结构简单、使用方便、能够测量较小压力差的压力 计。其结构如图。 压力计存在如下的几何关系:
p
P0
h2
F
l
⎫ ⎬ h1 = l sin α ⎭
据静力学方程有: 将 K = 1+
Fh2 = lf
α
f
h1
进行压力测量时,液面产生高度差。图中斜管液面上升表示p<p0。根
f 定义为斜管压力计的校准系数,此时待测压力: F sin α
上述合力及合力矩公式是计算理想流体作用于任意曲面上的压力合力 和合力矩的通用积分式,对静止流体和运动流体都适用。 静止流体的压力分布规律由静力学基本方程导出。运动流体的压力分 布规律在第4章讨论
静止流体对平板的作用力
平板与坐标系:平板放在水下一定深度,平板与水平面夹角设为α; 平板表面与 xoy 坐标面重合,如图所示。 问题分析:压力垂直于平板表 面,是平行力系,合力与压力方向 相同;将分布的压力沿板面积分即 可求得合力。 合力的大小:
Px f = ∫∫ xpds ⎫ ⎪ S ⎬ Py f = ∫∫ ypds⎪ S ⎭
将压力 p
= γy sin α
流体力学 第二章 水静力学(1)

M
z
b’ dy dx c’
c
y o x
泰勒级数前两项
a
a’
作用在六面体左右两端面上的表面力为
1 p PM p dxdydz 2 x 1 p PM p dxdydz 2 x
p 1 p dx 2 x
d
M′
b
p x, y , z
的夹角
即:质量力作功等于它在各轴向分力作功之和。 又,在平衡液体等压面上
即质量力与ds正交。式中,ds是等压面上的任意两邻点的线矢。
① 等压面就是等势面。 ② 作用在静止液体中任一点的质量力必然垂直于通过该点的等压面。
③ 等压面不能相交
相交 → 一点有2个压强值:错误
④ 绝对静止液体的等压面是水平面
1 p 0 x 1 p Y 0 y 1 p Z 0 z X
1 p X x 1 p Y y 1 p Z z
a
a’Leabharlann p1 p dx 2 x
d
M′
b
p x, y , z
的力势函数W0和静水压强p0,则由上式可得
p p0 W W0
(Ⅲ )
这就是不可压缩均质液体平衡微分方程积分后的普遍关系式。
通常在实际问题中,力的势函数W的一般表达式并非直接给出,因此实
际计算液体静水压强分布时,采用式(Ⅱ)进行计算较式(Ⅲ)更为方便。
dp Xdx Ydy Zdz
坐
标
压 强 (平均静水压强)
pM p pM p pM 1 p dx 2 x 1 p p dx 2 x
1 p p dx 2 x
流体静力学

工程大气压的倍数
p pa
78.4 98
0.8[ pa]
标准大气压
的倍数
p patm
78.4 101 .3
0.744[ patm ]
[例题2.4]一封闭水箱如图示2.11,箱内水面到 N-N面的距离,N-N面到点的距离,求点绝对压强 和相对压强。箱内液面为多少?箱内液面处若有真 空求出其真空值。
表面力
Px
px d
Ax
1 2
px dydz
Py
py d
Ay
1 2
py dxdz
Pz
pz d
Az
1 2
pz dxdy
Pn pn d An
。
Pn 在三个坐标方向的投影分别
Pn cos(n, x)、Pn cos(n, y)、
Pn co(s n,z)
质量力 F, 分量为Fx、Fy、Fz
单位质量的质量力: X、Y、Z
压力表测出的压强 是相对压强,又称表压强。
习惯上称只测正压的表 叫压力表。
金属真空计
指针的指示值 为真空值。常称 这种只测负压的表
为真空表。
[例题2.5] 图2.17为一倒U形差压计(又称空气比压 计),管顶部留有空气。利用阀C可进气或放气,以调节 管中液面的高差。a为两测点的位置高度差,h为两测压管
真空度约为(0.6~0.7) 。
一个标准大气压( patm )
101 .3kN / m2 (kPa)
一个工程大气压为
98kN / m2 (kPa)
压强的单位有下列三种表示形式:
(1)用单位面积上的力表示。在SI制中,压强的单位为N/kN。 (2)用液柱高度表示。常用水柱和水银柱高度表示压强的大小。 (3)以大气压表示。
流体静力学

Pz dPz dP sin g hdA sin g hdAz
A A A A
式中Az为面积A在自由液面xoy平面或其延伸面上的投影 面积。 hdAz 为以曲面ab为底,投影面积Az为顶以及曲 A 面周边各点向上投影的所有垂直母线所包围的一个空 间体积称为压力体积,以V表示。 则
Px dPx dP cos g hdA cos g hdAx
A A A A
式中:Ax为面积A在yoz平面的投影, hdAx 为面积Ax对 A oy轴的静面矩,所以 hdAx=hc Ax
A
则
Px ghc Ax
(8 )
2019/2/9
18
(8)式即为流体作用在曲面壁上的总压力水平分 力公式。此式说明水平分力等于液体作用在曲面投影 面积Ax上的总压力。 二、总压力的垂直分力Pz
2019/2/9 23
中点。相对于此运动坐标系来说,单位质量液体所受的 质量力有两个:一是垂直向下的单位质量重力 g ,另一 是与加速度反向的单位质量惯性力 a 。单位质量力的 三个坐标方向上的分量
这就是流体平衡压强分布规律的基本微分关系式。由 (3)式可以看出静止流体的一些特性: 等压面也是等势面。 等压面与质量力正交。
2019/2/9 6
§2.3 流体静力学基本方程
一、质量力只有重力时静力学基本方程 在实际应用中,作用在平衡流体上的质量力常常只 有重力,以下就讨论重力场中静止流体的压强分布规律。 对静止流体,因: 由(3)式有
总压力的方向
Pz arctan 17 Px
2019/2/9 22
2
2
§2.5 液体的相对平衡
下面以流体平衡微分方程式为基础,讨论质量力除 重力外,还有牵连惯性力同时作用的液体平衡规律。 在这种情况下,液体相对于地球虽然是运动的,但液 体质点之间、质点与器壁之间都没有相对运动,所以 这种运动称为相对平衡。现讨论以下两种相对平衡。 一、直线等加速器皿中液体的相对平衡 如后图,盛有液体的容器在与水平面成α角的斜 面由上向下作匀加速直线运动,加速度为a。当α为零 时,显然液面为水平面。设加速度为a时液面与水平面 成β角倾斜。设定xoz坐标,坐标原点取在自由液面的
水力学2.4静止流体对平面的作用力
2 流体静力学
本章主要任务:
1.导出静水压强的分布规律 2.作用在有限面积上的静水总压 力的大小、方向和作用点
2.4 静止流体对平面的作用力
本节主要任务:
2.4.1 静水压强分布图 2.4.2 图解法 2.4.3 解析法
2.4.1 静水压强分布图
用一定比例尺的线段,按静水压强分布规律 表示的静水压强的大小和方向的图形。 因为建筑物一般都在大气中,各方向大气压 抵消,所以压强分布图只需画出相对压强。 压强分布图常有: 空间压强分布图 平面压强分布图 一般画的都是平面压强分布图
2.4.3 解析法
所以,总压力
P sin yc A hc A pc A
(2.18)
即任意平面上的静水总压力的大小等于该平 面的面积与其形心处的压强的乘积。 形心处的压强 pc相当于该平面上的平均压强。 总压力的作用点: 根据合力矩定理求得
2.4.3 解析法
总压力的作用点: yD, xD 对ox轴取力矩得
PyD A dPy A hdAy A y sin d A sin A y dA
2 2
A
y dA为EF对ox轴的惯性矩Iox
2
PyD sin I ox
根据平行移轴定理
I ox I c y A
2 c
PyD sin ( I c yc2 A)
3 h1 h2
总压力的方向与作用面的内法线方向一致
2.4.2 图解法
图2.22
2.4.2 图解法
表2.1
2.4.3 解析法
根据理论力学和数学分析的方法来求总压力
2.4.3 解析法
如图2.19,EF为任意形状的平面,面积为A,其形 心为C,形心处的水深为hc,自由液面上的压强为 大气压,平面的延伸面与自由液面的交角为θ,设 总压力的作用点为D。ox轴为平面的延伸面与自由 液面的交线,oy轴为过平面内的任意点E且与ox轴 垂直的直线.
本章主要任务:
1.导出静水压强的分布规律 2.作用在有限面积上的静水总压 力的大小、方向和作用点
2.4 静止流体对平面的作用力
本节主要任务:
2.4.1 静水压强分布图 2.4.2 图解法 2.4.3 解析法
2.4.1 静水压强分布图
用一定比例尺的线段,按静水压强分布规律 表示的静水压强的大小和方向的图形。 因为建筑物一般都在大气中,各方向大气压 抵消,所以压强分布图只需画出相对压强。 压强分布图常有: 空间压强分布图 平面压强分布图 一般画的都是平面压强分布图
2.4.3 解析法
所以,总压力
P sin yc A hc A pc A
(2.18)
即任意平面上的静水总压力的大小等于该平 面的面积与其形心处的压强的乘积。 形心处的压强 pc相当于该平面上的平均压强。 总压力的作用点: 根据合力矩定理求得
2.4.3 解析法
总压力的作用点: yD, xD 对ox轴取力矩得
PyD A dPy A hdAy A y sin d A sin A y dA
2 2
A
y dA为EF对ox轴的惯性矩Iox
2
PyD sin I ox
根据平行移轴定理
I ox I c y A
2 c
PyD sin ( I c yc2 A)
3 h1 h2
总压力的方向与作用面的内法线方向一致
2.4.2 图解法
图2.22
2.4.2 图解法
表2.1
2.4.3 解析法
根据理论力学和数学分析的方法来求总压力
2.4.3 解析法
如图2.19,EF为任意形状的平面,面积为A,其形 心为C,形心处的水深为hc,自由液面上的压强为 大气压,平面的延伸面与自由液面的交角为θ,设 总压力的作用点为D。ox轴为平面的延伸面与自由 液面的交线,oy轴为过平面内的任意点E且与ox轴 垂直的直线.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 流体静力学
本章主要任务:
1.导出静水压强的分布规律 2.作用在有限面积上的静水总压 力的大小、方向和作用点
2.4 静止流体对平面的作用力
本节主要任务:
2.4.1 静水压强分布图 2.4.2 图解法 2.4.3 解析法
2.4.1 静水压强分布图
用一定比例尺的线段,按静水压强分布规律 表示的静水压强的大小和方向的图形。 因为建筑物一般都在大气中,各方向大气压 抵消,所以压强分布图只需画出相对压强。 压强分布图常有: 空间压强分布图 平面压强分布图 一般画的都是平面压强分布图
P dP pd A b 压强分布体的体积
压强分布体的体积=压强分布图的面积A×宽度b
2.4.2 图解法
作用在此受压面上的静水总压力的大小, 在数值上就是压强分布体的体积。 总压力的作用点:是分布体的体积的重心, 若为对称图形,即为其形心。 对于梯形,其形心为 e l 2h1 h2
图2.23
图2.19
2.4.3 解析法
图2.19
2.4.3 解析法
在平面任意点M处取一微面积dA, dA上的压力为dP=pdA=γhdA, h=ysinθ所以 总压力为
P
dP
A
A
pdA
A
hd A
A
y sin dA sin
ydA
A
ydA 是EF对ox轴的静矩 A ydA yc A
2.4.3 解析法
yD
sin ( I c yc2 A)
P
Ic yc A
sin ( I c yc2 A) Ic yc (2.19) yc sin A yc A
因为yc与 总是同号,所以|yD|>|yC|,即 总压力作用点D总是在作用面的形心之下 只有当受压面水平时,总压力作用点才与形 心重合。 I cxy 同理,对oy轴取矩,可得 xD xc y A
3 h1 h2
总压力的方向与作用面的内法线方向一致
2.4.2 图解法
图2.22
2.4.2 图解法
表2.1
2.4.3 解析法
根据理论力学和数学分析的方法来求总压力
2.4.3 解析法
如图2.19,EF为任意形状的平面,面积为A,其形 心为C,形心处的水深为hc,自由液面上的压强为 大气压,平面的延伸面与自由液面的交角为θ,设 总压力的作用点为D。ox轴为平面的延伸面与自由 液面的交线,oy轴为过平面内的任意点E且与ox轴 垂直的直线.
2.4.3 解析法
所以,总压力
P sin yc A hc A pc A
(2.18)
即任意平面上的静水总压力的大小等于该平 面的面积与其形心处的压强的乘积。 形心处的压强 pc相当于该平面上的平均压强。 总压力的作用点: 根据合力矩定理求得
2.4.3 解析法
总压力的作用点: y图
图2.20
2.4.1 静水压强分布图
2.4.2 图解法
利用压强分布图求矩形平面上的静水总压力 实际上就是求平行力系的合力问题
2.4.2 图解法
如图所示,取微面积dω,其上的压强p, 因为dω很小,可认为p在其上均匀分布, 于是, 微面积上的力dP=pdω=微小柱体的体积 总压力
c
其中,Icxy是平面MN对过形心并与ox,oy轴 平行的轴的惯性积.
2.4.3 解析法
其中,Icxy是平面MN对过形心并与ox,oy轴 平行的轴的惯性积
由于Icxy可正可负,因此xD可能大于或小于xC
注意:当液体表面的压强不是大气压时, 上述结果不能用。
2.4.3 解析法
例2.7 一铅直矩形板ABFE如图2.23,板宽 b=1.5m,板高h=2.0m,板顶的水深h1=1m, 求总压力的大小和作用点。
PyD A dPy A hdAy A y sin d A sin A y dA
2 2
A
y dA为EF对ox轴的惯性矩Iox
2
PyD sin I ox
根据平行移轴定理
I ox I c y A
2 c
PyD sin ( I c yc2 A)
本章主要任务:
1.导出静水压强的分布规律 2.作用在有限面积上的静水总压 力的大小、方向和作用点
2.4 静止流体对平面的作用力
本节主要任务:
2.4.1 静水压强分布图 2.4.2 图解法 2.4.3 解析法
2.4.1 静水压强分布图
用一定比例尺的线段,按静水压强分布规律 表示的静水压强的大小和方向的图形。 因为建筑物一般都在大气中,各方向大气压 抵消,所以压强分布图只需画出相对压强。 压强分布图常有: 空间压强分布图 平面压强分布图 一般画的都是平面压强分布图
P dP pd A b 压强分布体的体积
压强分布体的体积=压强分布图的面积A×宽度b
2.4.2 图解法
作用在此受压面上的静水总压力的大小, 在数值上就是压强分布体的体积。 总压力的作用点:是分布体的体积的重心, 若为对称图形,即为其形心。 对于梯形,其形心为 e l 2h1 h2
图2.23
图2.19
2.4.3 解析法
图2.19
2.4.3 解析法
在平面任意点M处取一微面积dA, dA上的压力为dP=pdA=γhdA, h=ysinθ所以 总压力为
P
dP
A
A
pdA
A
hd A
A
y sin dA sin
ydA
A
ydA 是EF对ox轴的静矩 A ydA yc A
2.4.3 解析法
yD
sin ( I c yc2 A)
P
Ic yc A
sin ( I c yc2 A) Ic yc (2.19) yc sin A yc A
因为yc与 总是同号,所以|yD|>|yC|,即 总压力作用点D总是在作用面的形心之下 只有当受压面水平时,总压力作用点才与形 心重合。 I cxy 同理,对oy轴取矩,可得 xD xc y A
3 h1 h2
总压力的方向与作用面的内法线方向一致
2.4.2 图解法
图2.22
2.4.2 图解法
表2.1
2.4.3 解析法
根据理论力学和数学分析的方法来求总压力
2.4.3 解析法
如图2.19,EF为任意形状的平面,面积为A,其形 心为C,形心处的水深为hc,自由液面上的压强为 大气压,平面的延伸面与自由液面的交角为θ,设 总压力的作用点为D。ox轴为平面的延伸面与自由 液面的交线,oy轴为过平面内的任意点E且与ox轴 垂直的直线.
2.4.3 解析法
所以,总压力
P sin yc A hc A pc A
(2.18)
即任意平面上的静水总压力的大小等于该平 面的面积与其形心处的压强的乘积。 形心处的压强 pc相当于该平面上的平均压强。 总压力的作用点: 根据合力矩定理求得
2.4.3 解析法
总压力的作用点: y图
图2.20
2.4.1 静水压强分布图
2.4.2 图解法
利用压强分布图求矩形平面上的静水总压力 实际上就是求平行力系的合力问题
2.4.2 图解法
如图所示,取微面积dω,其上的压强p, 因为dω很小,可认为p在其上均匀分布, 于是, 微面积上的力dP=pdω=微小柱体的体积 总压力
c
其中,Icxy是平面MN对过形心并与ox,oy轴 平行的轴的惯性积.
2.4.3 解析法
其中,Icxy是平面MN对过形心并与ox,oy轴 平行的轴的惯性积
由于Icxy可正可负,因此xD可能大于或小于xC
注意:当液体表面的压强不是大气压时, 上述结果不能用。
2.4.3 解析法
例2.7 一铅直矩形板ABFE如图2.23,板宽 b=1.5m,板高h=2.0m,板顶的水深h1=1m, 求总压力的大小和作用点。
PyD A dPy A hdAy A y sin d A sin A y dA
2 2
A
y dA为EF对ox轴的惯性矩Iox
2
PyD sin I ox
根据平行移轴定理
I ox I c y A
2 c
PyD sin ( I c yc2 A)
