小学升初中数学应用题专题带答案偏难
小升初数学应用题大全100例附答案(完整版)

小升初数学应用题大全100例附答案(完整版)1. 一桶水可灌3/4 壶水,1 壶水可以冲2 杯水,1 桶水可以冲几杯水?答案:1 桶水可灌3/4 壶水,1 壶水冲2 杯水,所以1 桶水可以冲3/4 ×2 = 3/2 = 1.5 杯水。
2. 小明看一本120 页的故事书,已经看了全书的5/6,还剩多少页没看?答案:全书120 页,已经看了全书的5/6,即看了120×5/6 = 100 页,还剩120 - 100 = 20 页。
3. 一个长方形的长是8 厘米,宽是长的1/4,这个长方形的面积是多少?答案:宽是长的1/4,所以宽为8×1/4 = 2 厘米,面积= 长×宽= 8×2 = 16 平方厘米。
4. 一辆汽车从甲地开往乙地,每小时行60 千米,5 小时到达。
若要4 小时到达,则每小时需要多行多少千米?答案:甲乙两地的距离为60×5 = 300 千米。
若4 小时到达,速度应为300÷4 = 75 千米/小时,每小时需要多行75 - 60 = 15 千米。
5. 某工厂有男职工120 人,女职工人数是男职工人数的4/5,这个工厂共有职工多少人?答案:女职工人数为120×4/5 = 96 人,全厂职工人数为120 + 96 = 216 人。
6. 学校买来180 本图书,按4:5 分给五年级和六年级,五年级分得多少本?答案:一共分成4 + 5 = 9 份,每份180÷9 = 20 本,五年级分得4 份,即20×4 = 80 本。
7. 果园里有苹果树240 棵,梨树的棵数比苹果树少1/4,梨树有多少棵?答案:梨树比苹果树少1/4,所以梨树的棵数为240×(1 - 1/4) = 180 棵。
8. 修一条路,已经修了全长的3/7 ,还剩360 米没修,这条路全长多少米?答案:没修的占全长的1 - 3/7 = 4/7 ,全长为360÷4/7 = 630 米。
小学升初中数学应用题150道及答案

小学升初中数学应用题150道及答案1. 小明有10 个苹果,小红的苹果数比小明多5 个,小红有多少个苹果?-解题提示:用小明的苹果数加上5 就是小红的苹果数。
-答案:10 + 5 = 15(个)2. 商店里有30 支铅笔,卖出12 支,还剩多少支?-解题提示:用原有的铅笔数减去卖出的就是剩余的。
-答案:30 - 12 = 18(支)3. 一本书有80 页,小明第一天看了25 页,第二天看了30 页,还剩多少页没看?-解题提示:用总页数依次减去前两天看的页数。
-答案:80 - 25 - 30 = 25(页)4. 一个长方形的长是12 厘米,宽比长短3 厘米,这个长方形的周长是多少厘米?-解题提示:先求出宽,再根据长方形周长= (长+ 宽)×2 计算。
-答案:宽为12 - 3 = 9 厘米,周长= (12 + 9)×2 = 42 厘米5. 同学们排队做操,每行站15 人,正好站8 行。
如果每行站20 人,可以站多少行?-解题提示:先算出总人数,再除以每行站的人数。
-答案:总人数为15×8 = 120 人,120÷20 = 6 行6. 一辆汽车3 小时行驶180 千米,照这样的速度,5 小时行驶多少千米?-解题提示:先求出速度,再用速度乘以时间。
-答案:速度为180÷3 = 60 千米/小时,5 小时行驶60×5 = 300 千米7. 果园里有苹果树250 棵,梨树比苹果树少50 棵,梨树有多少棵?-解题提示:用苹果树的数量减去50 。
-答案:250 - 50 = 200(棵)8. 学校买了5 个篮球,每个80 元,又买了2 个足球,一共花了500 元,一个足球多少钱?-解题提示:先算出买篮球花的钱,用总钱数减去买篮球的钱就是买足球的钱,再除以足球个数。
-答案:买篮球花5×80 = 400 元,买足球花500 - 400 = 100 元,一个足球100÷2 = 50 元9. 一条路长600 米,已经修了240 米,剩下的要6 天修完,平均每天修多少米?-解题提示:先算出剩下的长度,再除以天数。
小升初较难必考数学题

小升初较难必考数学题一、工程问题1. 一项工程,甲队单独做需要10天完成,乙队单独做需要15天完成。
两队合作3天后,剩下的工程由乙队单独完成,还需要多少天?解析:- 把这项工程的工作量看作单位“1”。
- 根据工作效率 = 工作量÷工作时间,甲队的工作效率为1÷10=(1)/(10),乙队的工作效率为1÷15=(1)/(15)。
- 两队合作3天的工作量为((1)/(10)+(1)/(15))×3。
- 先计算括号内的值:(1)/(10)+(1)/(15)=(3 + 2)/(30)=(1)/(6)。
- 再乘以3得到(1)/(6)×3=(1)/(2)。
- 剩下的工作量为1-(1)/(2)=(1)/(2)。
- 乙队单独完成剩下工程需要的时间为(1)/(2)÷(1)/(15)=(1)/(2)×15 = 7.5(天)2. 修一条路,甲、乙两队合作8天完成。
如果甲队单独修12天可以完成。
实际上先由乙队修了若干天后,再由甲队继续修,全部完成时共用了15天。
求甲、乙两队各修了多少天?解析:- 设乙队的工作效率为x。
- 因为甲、乙两队合作的工作效率为(1)/(8),甲队单独的工作效率为(1)/(12),则x=(1)/(8)-(1)/(12)=(3 - 2)/(24)=(1)/(24)。
- 设甲队修了y天,则乙队修了(15 - y)天。
- 根据工作量 = 工作效率×工作时间,可得到方程(1)/(12)y+(1)/(24)(15 - y)=1。
- 去括号得(1)/(12)y+(15)/(24)-(1)/(24)y = 1。
- 移项合并同类项得((1)/(12)-(1)/(24))y=1-(15)/(24)。
- 即(1)/(24)y=(9)/(24),解得y = 9。
- 所以甲队修了9天,乙队修了15 - 9=6天。
二、行程问题1. 甲、乙两车分别从A、B两地同时相向而行,速度比是5:3。
小升初考试数学难题及答案

2024年小升初考试数学难题及答案2024年小升初考试数学难题及答案问题一:一个长方形的周长是24厘米,长和宽的比是2:1。
求这个长方形的面积是多少平方厘米?答案:这是一个长方形周长和长宽比例的问题。
根据周长公式,我们可以列出方程:2(l + w) = 24,其中l为长,w为宽。
根据题目中的长宽比例,我们可以列出另一个方程:l/w = 2/1。
解这个方程组,可以得到长为8厘米,宽为4厘米。
因此,这个长方形的面积为32平方厘米。
问题二:一个圆柱体的体积是314立方厘米,底面半径为5厘米。
求这个圆柱体的高是多少厘米?答案:这是一个圆柱体体积和底面半径的问题。
根据体积公式,我们可以列出方程:πr²h = 314,其中r为底面半径,h为高。
根据题目中的条件,已知圆柱体的体积和底面半径,代入公式中,得到高为8厘米。
因此,这个圆柱体的高是8厘米。
问题三:一个等腰三角形的顶角是70度,底角是45度。
求这个等腰三角形的底边是多少厘米?答案:这是一个等腰三角形角度的问题。
根据角度和三角形边长的关系,我们可以列出方程:底边/斜边 = 余弦(底角),其中底角为45度,斜边为1(假设斜边长度为1)。
根据余弦公式和题目中的角度,代入公式中,得到底边为0.7071厘米。
因此,这个等腰三角形的底边是0.7071厘米。
小升初数学应用题易错题难题集锦通用版小升初数学应用题是考试的重点和难点,对于即将参加小升初考试的学生来说,了解和应用解决这类问题的策略至关重要。
本文将列举一些常见的小升初数学应用题易错题和难题,并给出解析和例题演练,帮助读者更好地掌握解决这类问题的技巧和方法。
一、行程问题1、甲、乙两车同时从A、B两地相对开出,经过6小时相遇。
已知甲车每小时行驶60千米,乙车每小时行驶70千米。
求A、B两地的距离。
解析:此题为相对速度问题,可采用相对速度的公式来求解。
2、小明从家到学校需要步行30分钟,如果他以每分钟60米的速度行走,那么他家到学校的距离是多少?解析:此题为简单的速度、时间、距离问题,可使用速度公式来求解。
小升初数学解决问题解答应用题练习题30篇带答案解析1
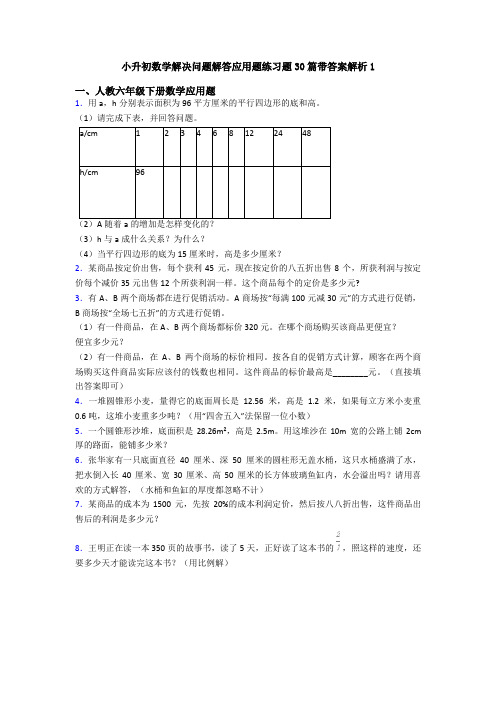
小升初数学解决问题解答应用题练习题30篇带答案解析1一、人教六年级下册数学应用题1.用a,h分别表示面积为96平方厘米的平行四边形的底和高。
(1)请完成下表,并回答问题。
a/cm123468122448h/cm96(2)A随着a的增加是怎样变化的?(3)h与a成什么关系?为什么?(4)当平行四边形的底为15厘米时,高是多少厘米?2.某商品按定价出售,每个获利45元,现在按定价的八五折出售8个,所获利润与按定价每个减价35元出售12个所获利润一样。
这个商品每个的定价是多少元?3.有A、B两个商场都在进行促销活动。
A商场按“每满100元减30元”的方式进行促销,B商场按“全场七五折”的方式进行促销。
(1)有一件商品,在A、B两个商场都标价320元。
在哪个商场购买该商品更便宜?便宜多少元?(2)有一件商品,在A、B两个商场的标价相同。
按各自的促销方式计算,顾客在两个商场购买这件商品实际应该付的钱数也相同。
这件商品的标价最高是________元。
(直接填出答案即可)4.一堆圆锥形小麦,量得它的底面周长是12.56米,高是1.2米,如果每立方米小麦重0.6吨,这堆小麦重多少吨?(用“四舍五入”法保留一位小数)5.一个圆锥形沙堆,底面积是28.26m²,高是2.5m。
用这堆沙在10m宽的公路上铺2cm 厚的路面,能铺多少米?6.张华家有一只底面直径40厘米、深50厘米的圆柱形无盖水桶,这只水桶盛满了水,把水倒入长40厘米、宽30厘米、高50厘米的长方体玻璃鱼缸内,水会溢出吗?请用喜欢的方式解答,(水桶和鱼缸的厚度都忽略不计)7.某商品的成本为1500元,先按20%的成本利润定价,然后按八八折出售,这件商品出售后的利润是多少元?8.王明正在读一本350页的故事书,读了5天,正好读了这本书的,照这样的速度,还要多少天才能读完这本书?(用比例解)9.(1)请你在如图的圆中画一小圆,使得大圆和小圆的面积比是4:1.(2)如果这个大圆的比例尺是1:200,请测量出所需数据并计算大圆的实际周长.(测量时保留整厘米数)10.小明调制了两杯蜂蜜水。
(完整版)小升初数学应用题50道附参考答案【完整版】

(完整版)小升初数学应用题50道一.解答题(共50题,共286分)1.新华书店打折出售图书,张老师用340元买了一套《中国四大名著》,而原价是400元。
这套《中国四大名著》打了几折?2.一个圆柱体的蓄水池,从里面量底面周长31.4米,深2米,在它的内壁与底面抹上水泥。
(1)抹水泥的面积是多少平方米?(2)蓄水池能蓄多少吨水?(每立方米水约重1.1吨)3.下表是部分城市同一天的气温情况。
(1)哪个城市的气温最高?哪个城市的气温最低?(2)把各个城市的最低气温从低到高排列出来。
(3)把各个城市的最高温从高到低排列出来。
4.一个装满玉米的圆柱形粮囤,底面周长6.28米,高2米。
如果将这些玉米堆成一个高1米的圆锥形的玉米堆,圆锥底面积是多少平方米?5.张经理的公司今年盈利500万元,按国家规定应缴纳20%的税款,张经理最后应得利益是多少万元?6.出租车司机小王某天下午营运是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,这天下午他的行程(单位:千米)如下:+5 -2 +8 -10 -3 -4 +7 +2 -9 +6小王最后是否能回到出发点?7.某水果店新进一批水果,其中苹果占新进水果总量的30%,香蕉占40%,已知这两种水果共70kg,这批水果的总量是多少?8.用96厘米长的铁丝围成一个直角三角形,这个直角三角形三条边的长度比是3∶4∶5,这个三角形的面积是多少?9.广州的气温的15℃,上海的气温是0℃,北京的气温是-9℃,请问气温最高的地方比气温最低的地方温度高多少度?10.修一段路,第一天修了全长的15%,第二天修了960米,还余全长的65%未修,这段路全长多少米?11.一个无盖的圆柱形铁皮水桶,底面直径是0.4米,高是0.8米,要在水桶里、外两面都漆防锈漆,油漆的面积大约是多少平方米?(得数保留一位小数)12.学校购进图书2000本,其中文学类图书占80%,将这些文学书按2:3全部分给中、高年级,高年级可以分得多少本?13.王林参加射击比赛,打了20组子弹,每组10发。
小升初数学应用题40道附参考答案(完整版)

小升初数学应用题40道一.解答题(共40题,共222分)1.一个圆柱形铁皮水桶(无盖),高10dm,底面直径是6dm,做这个水桶大约要用多少铁皮?2.六年级有200名同学,本学期的体育成绩如下图。
(1)不合格的人数占全年级总人数的百分之几?(2)各个等级的人数分别是多少?3.学校购进图书2000本,其中文学类图书占80%,将这些文学书按2:3全部分给中、高年级,高年级可以分得多少本?4.幼儿园买回240个苹果,按照大、中、小三个幼儿班的人数分配给各个班。
大班有28人,中班有25人,小班有27人。
三个班各应分多少个苹果?5.用96厘米长的铁丝围成一个直角三角形,这个直角三角形三条边的长度比是3∶4∶5,这个三角形的面积是多少?6.某服装店卖一种裙子,原来每条售价为120元,是进价的150%。
现在店主计划打折促销,但要保证每条裙子赚的钱不少于10元。
问:折扣不能低于几折?7.一个圆柱和一个圆锥底面积比为2:3,体积比为5:6,求高的比。
8.一辆客车从甲地开往乙地,去时速度是40千米/小时,返回时速度是60千米/小时,返回时的速度比去时的速度提高了百分之几?9.庄稼如果重量增加500克,记作+500,那么如果增加2千克,那么应该记作?10.甲、乙两种商品,成本共2200元,甲商品按20%的利润定价,乙商品按15%的利润定价。
后来都按定价的九折打折出售,结果仍获利131元。
甲商品的成本是多少元?11.某商场在五月份进了甲、乙两种商品共100件,甲商品进货价每件40元,乙商品进货价每件60元。
如果两种商品都按20%的利润来定零售价.这样当两种商品全部销售完后,共获利润940元。
(利润是指“销价与进货价的差”。
)(1)甲、乙两种商品每件可获利润各是多少元?(2)其中甲种商品进了多少件?12.王林参加射击比赛,打了20组子弹,每组10发。
有10发子弹没有打中目标,请你算一算,王林射击的命中率是多少?13.买来一批煤,计划每天烧吨,可烧20天;实际每天比原来节约20%,这样可以烧多少天?(用比例解答)14.有一个圆锥形沙堆,底面半径是10米,高是4.8米,把这些沙子均匀地铺在一条宽20米,厚40厘米的通道上,可以铺多长?15.一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米。
小升初数学高难度应用试题及答案

小升初数学高难度应用试题及答案如下:以题中的等量为等量关系建立方程例题:有两桶油,甲桶油重量是乙桶油的2倍,现在从甲桶中取出25.8千克,从乙桶中取出剩下的两桶油重量相等,两桶油原来各有多少千克?解设:乙桶油为X千克,那么甲桶油为2X千克甲桶剩下的油=乙桶剩下的油2X一25.8=X一5.22X一X=25.8一5.2X=20.62X=20.6×2=41.2答:甲桶油重4102千克,乙桶油重20.6千克,练一练:① 甲厂有钢材148吨,乙厂有112吨,如果甲厂每天用18吨,乙厂每天用12吨,多少天后两厂剩下的钢材相等?② 一个两层的书架,上层放的书是下层的3倍,如果把上层的书放90本到下层,则两层的书相等,原来上下层各有书多少本?③ 甲车间有54人,乙车间有48人,在式作时,为了使两车间人数相等,甲车间应调多少人去乙车间?④ 超市存有大米的袋数是面粉的3倍,大米买掉180袋,面粉买掉50袋后,大米、面粉剩下的袋数相等,大米、面粉原各多少袋?⑤ 某校有苦于人住校。
若每一间宿舍住6人,则多出34人;若每一间宿舍住7人,则多出4间宿舍。
问有多少人住校?有几间宿舍?⑥ 甲仓所存的面粉是乙仓的3倍,如果从甲仓运走900千克,从乙仓运出80千克,则两仓所存的面粉相等,两仓原有面粉各多少千克?⑦ 有箱桔子,甲箱的重量是乙箱的1.8倍,如果从甲箱中取出1.2千克放篱乙箱,那么两箱的重量相等了,原来甲乙两箱各多少千克?⑧ 一个通讯员骑自行车要在规定的时间内把信件送到某地,他每小时15千米查以早到24分钟,每小时骑12千米要迟到15分钟,规定时间是多少?他去某地的路程有多远?⑨ 一列火车从甲地开往乙地每小时 50千米,一小时后另一列火车也从甲地开往乙地每小时行60千米,结果两列火车同时到达乙3地,甲、乙两地相距多少千米?⑩甲级糖每千克16.60元,乙级糖每千克8.80元。
商店用80千克甲级糖和若干乙级糖混合后平均每千克售价14.00元,乙级糖要多少千克?以较大的量或几倍数为等量关系建立方程例题:两筐苹果,每筐的个数相等,从甲筐卖出150个,从乙筐卖出194个后,剩下的苹果甲筐是乙筐的3倍,原来每筐有多少个?解设:原来每筐X个甲筐剩下的=乙筐剩下的3倍X一150=X一194×3X一150=3X一5822X=432X=216答:原来甲筐有苹果216。
(完整版)小升初数学应用题100道及完整答案(历年真题)

(完整版)小升初数学应用题100道一.解答题(共100题,共581分)1.某商场冰箱五月份销售量是80台,后来举行了促销活动,六月份的销售量是110台。
六月份比五月份增长了百分之几?2.一个圆柱体的蓄水池,从里面量底面周长31.4米,深2米,在它的内壁与底面抹上水泥。
(1)抹水泥的面积是多少平方米?(2)蓄水池能蓄多少吨水?(每立方米水约重1.1吨)3.一个圆柱体水桶,从里面量,底面直径是32厘米,高是50厘米,这个水桶大约能盛水多少千克?(1dm3的水重1千克)4.一个圆柱和一个圆锥底面积比为2:3,体积比为5:6,求高的比。
5.一个圆锥体钢制零件,底面半径是3cm,高是2m,这个零件的体积是多少立方厘米?6.某电视机厂去年电视机生产情况统计图(单位:台; 2011年1月)看图列式计算:(1)全年共生产电视机多少台?(2)平均每月生产电视机多少台?(3)第四季度比第一季度增产百分之几?7.下表是银行定期存款利率。
8.某服装店凭优惠卡可打七折,妈妈用优惠卡买了一件衣服,省了60元。
这件衣服原价多少钱?9.我们把李明从家出发,向西走了500米记作走了-500米,那么李明又接着走了+800米是什么意思?这时李明离家的距离有多远?10.如图是一种钢制的配件(图中数据单位:cm),请计算它的表面积和体积。
( π 取3.14)11.一个圆柱形的粮仓,从里面量得底面直径是3米,装有2.5米高的小麦.如果每立方米小麦重0.7吨,这个粮仓装有多少吨的小麦?12.求圆柱体的表面积和体积。
13.把一个底面半径是4厘米,高是6分米的铁制圆锥体放入盛满水的桶里,将有多少立方厘米的水溢出?14.一块长方形土地的周长是162米,长与宽的比是5∶4,这块土地的面积是多少平方米?15.几种食物中蛋白质含量如下表:利用上表数据,请你计算出600克牛奶中和800克瘦猪肉中各含有多少克蛋白质。
16.-1与0之间还有负数吗?-与0之间呢?-和0之间呢?如果有,请你举出例子来。
小学升初中数学专题训练卷系列应用题(含答案)(范文大全)

小学升初中数学专题训练卷系列应用题(含答案)(范文大全)第一篇:小学升初中数学专题训练卷系列应用题(含答案)小学升初中数学专题训练卷系列应用题(有答案)训练A卷班级______ 姓名______ 得分______(1)小阳期终考试时语文和数学的平均分数是96分,数学比语文多8分。
语文是()分,数学是()分。
(2)甲、乙两个仓库共存大米42吨,如果从甲仓库调3吨大米到乙仓库,那么两个仓库所存的大米就正好同样多。
原来甲仓库存大米()吨,乙仓库存大米()吨。
(5)参加少年宫科技小组的同学,今年比去年的3倍少35人,去年比今年少41人,今年参加科技小组的同学有()人。
(6)父亲今年47岁,儿子今年19岁,()年前父亲的年龄是儿子的5倍。
2.甲、乙、丙三数之和是1160,甲是乙的一半,乙是丙的2倍。
三个数各是多少?3.某招待所开会,每个房间住3人,则36人没床位;每个房间住4人,则还有13人没床位,如果每个房间住5人,那么情况又怎么样?4.小明读一本书,第一天读83页,第二天读74页,第三天读71页,第四天读64页,第五天读的页数比这五天中平均读的页数要多3.2页。
小明第五天读了多少页?5.在桥上测量桥高,把绳子对折后垂到水面时绳子还剩下8米;把绳子三折后,垂到水面时绳子还剩下2米,求桥高和绳长各是多少米。
6.44名学生去划船,一共乘坐10只船,其中每只大船坐6人,每只小船坐4人。
大船和小船各有多少只?7.实验小学四年级举行数学竞赛,一共出了10道题,答对一题得10分,答错一题倒扣5分。
张华把10道题全部做完,结果得了70分。
他答对了几道题?8.买4支铅笔和5块橡皮,共付6元;买同样的6支铅笔和2块橡皮,共付4.60元。
每支铅笔和每块橡皮各多少钱?9.修一条路,第一天修了全长的一半多6米,第二天修了余下的一半少20米,第三天修了30米,最后还剩14米没修。
这条路长多少米?10.张强用270元买了一件外衣,一顶帽子和一双鞋子,外衣比鞋贵140元,买外衣和鞋比帽子多花210元,张强买这双鞋花了多少钱?11.红光厂计划每天生产电冰箱40台,经过技术革新后,每天比原计划多生产5台,这样提前2天完成了这批生产任务,并且比原计划还多生产了35台。
小升初数学20种必考应用题(含例题及答案解析),收藏练习!

小升初数学20种必考应用题(含例题及答案解析),收藏练习!以下20个题目是小升初考试中经常会遇到的题型,希望你的孩子能够全部吃透,并熟练运用其中的知识点。
转给孩子,快来复习吧!解题思路:由已知条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的(10-1)倍,由此可求得一把椅子的价钱。
再根据椅子的价钱,就可求得一张桌子的价钱。
解:一把椅子的价钱:288÷(10-1)=32(元)一张桌子的价钱:32×10=320(元)答:一张桌子320元,一把椅子32元。
解题思路:根据在距离中点4千米处相遇和甲比乙速度快,可知甲比乙多走4×2千米,又知经过4小时相遇。
即可求甲比乙每小时快多少千米。
解:4×2÷4=8÷4=2(千米)答:甲每小时比乙快2千米。
解题思路:根据两人付同样多的钱买同一种铅笔和李军要了13支,张强要了7支,可知每人应该得(13+7)÷2支,而李军要了13支比应得的多了3支,因此又给张强0.6元钱,即可求每支铅笔的价钱。
解:0.6÷[13-(13+7)÷2]=0.6÷[13—20÷2]=0.6÷3=0.2(元)答:每支铅笔0.2元。
解题思路:根据已知两车上午8时从两站出发,下午2点返回原车站,可求出两车所行驶的时间。
根据两车的速度和行驶的时间可求两车行驶的总路程。
解:下午2点是14时。
往返用的时间:14-8=6(时)两地间路程:(40+45)×6÷2=85×6÷2=255(千米)答:两地相距255千米。
解题思路:第一小组停下来参观果园时间,第二小组多行了[3.5-(4.5-3.5)]?千米,也就是第一组要追赶的路程。
又知第一组每小时比第二组快(?4.5-3.5)千米,由此便可求出追赶的时间。
解:第一组追赶第二组的路程:3.5-(4.5-?3.5)=3.5-1=2.5(千米)第一组追赶第二组所用时间:2.5÷(4.5-3.5)=2.5÷1=2.5(小时)答:第一组2.5小时能追上第二小组。
小学数学小升初应用题150道及答案

小学数学小升初应用题150道及答案1. 学校图书馆有科技书320 本,比故事书少80 本,两种书一共有多少本?答案:故事书有320 + 80 = 400 本,两种书一共320 + 400 = 720 本。
2. 果园里有苹果树180 棵,梨树比苹果树多20 棵,桃树的棵数是苹果树和梨树总棵数的2 倍,桃树有多少棵?答案:梨树有180 + 20 = 200 棵,苹果树和梨树总棵数为180 + 200 = 380 棵,桃树有380×2 = 760 棵。
3. 小明家离学校1200 米,他每天步行上学,往返一次需要20 分钟,小明平均每分钟走多少米?答案:往返一次走的路程是1200×2 = 2400 米,速度= 路程÷时间,即2400÷20 = 120 米/分钟。
4. 一辆汽车4 小时行驶320 千米,照这样计算,7 小时行驶多少千米?答案:汽车的速度为320÷4 = 80 千米/小时,7 小时行驶80×7 = 560 千米。
5. 工厂要生产800 个零件,已经生产了300 个,剩下的要在5 天内完成,平均每天生产多少个?答案:还剩下800 - 300 = 500 个,平均每天生产500÷5 = 100 个。
6. 学校买了6 个篮球和8 个排球,一共用了500 元,篮球每个40 元,排球每个多少元?答案:篮球花费6×40 = 240 元,排球花费500 - 240 = 260 元,每个排球260÷8 = 32.5 元。
7. 一块长方形菜地,长30 米,宽20 米,如果每平方米种8 棵白菜,这块地一共可以种多少棵白菜?答案:面积为30×20 = 600 平方米,一共可以种600×8 = 4800 棵白菜。
8. 小明有20 元钱,买了一支钢笔用去8 元,剩下的钱买每本2 元的笔记本,可以买几本?答案:剩下20 - 8 = 12 元,能买笔记本12÷2 = 6 本。
小升初小学数学应用题100例附答案(完整版)

小升初小学数学应用题100例附答案(完整版)1. 一桶水,用去它的3/4,还剩8 千克,这桶水原来重多少千克?解:8÷(1 - 3/4) = 32(千克)答:这桶水原来重32 千克。
2. 一个长方形的周长是24 厘米,长与宽的比是2:1,这个长方形的面积是多少平方厘米?解:长和宽的和为24÷2 = 12(厘米)长:12×2/3 = 8(厘米)宽:12×1/3 = 4(厘米)面积:8×4 = 32(平方厘米)答:这个长方形的面积是32 平方厘米。
3. 学校把植树任务按5:3 分给六年级和五年级。
六年级实际栽了108 棵,超过原分配任务的20%。
原计划五年级植树多少棵?解:六年级原计划栽树:108÷(1 + 20%) = 90(棵)五年级原计划栽树:90÷5×3 = 54(棵)答:原计划五年级植树54 棵。
4. 商店运来一些水果,梨的筐数是苹果筐数的3/4,苹果的筐数是橘子筐数的4/5,运来梨15 筐,运来橘子多少筐?解:苹果筐数:15÷3/4 = 20(筐)橘子筐数:20÷4/5 = 25(筐)答:运来橘子25 筐。
5. 某班男生人数是女生人数的5/6,女生的平均身高比男生高10%,全班的平均身高是116 厘米,求男、女生的平均身高各是多少?解:设女生有6 人,男生有 5 人。
全班总身高:116×(6 + 5) = 1276(厘米)设男生平均身高为x 厘米,则女生平均身高为1.1x 厘米。
5x + 6×1.1x = 12765x + 6.6x = 127611.6x = 1276x = 110女生平均身高:1.1×110 = 121(厘米)答:男生平均身高110 厘米,女生平均身高121 厘米。
6. 一项工程,甲单独做20 天完成,乙单独做30 天完成。
甲乙合做了几天后,乙因事请假,甲继续做,从开工到完成任务共用了16 天。
小升初数学题难题大全

小升初数学题难题大全
1. 已知正方形ABCD的面积是16平方厘米,求边长。
2. 某车站离一个城市16千米,小明骑自行车从车站出发,行
进了12千米后回头,问他共骑行了多少千米?
3. 甲乙两车同时从A、B两地出发,相向而行,甲车每小时行80千米,乙车每小时行60千米,如果相继行驶3个小时后相遇,求AB两地的距离。
4. 甲、乙、丙三个人共有168元,甲给乙5元,乙给丙3元,
丙还给甲1元,问三个人原本各有多少钱?
5. 小明爸爸今年35岁,小明今年10岁,问过几年后,小明的年龄是他爸爸的一半?
6. 小燕买了一些书,每本书35元,花了120元后还剩下4本,问小燕买了几本书?
7. 甲、乙、丙三个人摘苹果,甲每天摘50个,乙每天摘45个,丙每天摘30个,如果他们连续摘了7天,共摘了多少个苹果?
8. 某数的百位是9,十位比个位大2,个位比百位小2,这个
三位数是多少?
9. 一个数加上它的三分之一等于20,这个数是多少?
10. 一个四位数的千位是奇数,千位比百位小2,百位比十位
小2,十位比个位大2,这个四位数是多少?。
小学升初中数学应用题专题(带答案偏难)

小学升初中数学应用题专题(带答案偏难)第一篇:小学升初中数学应用题专题(带答案偏难)一:应用题专题一、和差倍问题(一)和差问题:已知两个数的和及两个数的差,求这两个数。
方法①:(和-差)÷2=较小数,和-较小数=较大数方法②:(和+差)÷2=较大数,和-较大数=较小数例如:两个数的和是15,差是5,求这两个数。
方法:(15-5)÷2=5,(15+5)÷2=10.(二)和倍问题:已知两个数的和及这两个数的倍数关系,求这两个数。
方法:和÷(倍数+1)=1倍数(较小数)1倍数(较小数)⨯倍数=几倍数(较大数)或和-1倍数(较小数)=几倍数(较大数)例如:两个数的和为50,大数是小数的4倍,求这两个数。
方法:50÷(4+1)=10 10⨯4=40(三)差倍问题:已知两个数的差及两个数的倍数关系,求这两个数。
方法:差÷(倍数-1)=1倍数(较小数)1倍数(较小数)⨯倍数=几倍数(较大数)或和-1倍数(较小数)=几倍数(较大数)例如:两个数的差为80,大数是小数的5倍,求这两个数。
方法:80÷(5-1)=20 20⨯5=100二、年龄问题年龄问题的三大规律:1.两人的年龄差是不变的;2.两人年龄的倍数关系是变化的量;3.随着时间的推移,两人的年龄都是增加相等的量.解答年龄问题的一般方法是:几年后年龄=大小年龄差÷倍数差-小年龄,几年前年龄=小年龄-大小年龄差÷倍数差.三、植树问题(一)不封闭型(直线)植树问题直线两端植树:棵数=段数+1=全长÷株距+1;全长=株距⨯(棵数-1);株距=全长÷(棵数-1);直线一端植树:全长=株距⨯棵数;棵数=全长÷株距;株距=全长÷棵数;直线两端都不植树:棵数=段数-1=全长÷株距-1;株距=全长÷(棵数+1);(二)封闭型(圆、三角形、多边形等)植树问题棵数=总距离÷棵距;总距离=棵数⨯棵距;棵距=总距离÷棵数.四、方阵问题在方阵问题中,横的排叫做行,竖的排叫做列,如果行数和列数都相等,则正好排成一个正方形,就是所谓的“方阵”。
较难小升初数学试题及答案

较难小升初数学试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 一个长方体的长、宽、高分别是12厘米、8厘米和10厘米,其体积是多少立方厘米?A. 960B. 192C. 1152D. 384答案:A3. 一个数除以3的余数是2,除以5的余数是1,那么这个数除以15的余数是多少?A. 3B. 4C. 5D. 6答案:B4. 一辆汽车以每小时60公里的速度行驶,2小时后它行驶了多少公里?A. 120B. 100C. 80D. 90答案:A5. 一个班级有48名学生,其中2/3是男生,女生有多少人?A. 16B. 32C. 24D. 20答案:A二、填空题(每题3分,共15分)6. 一个数的1/4加上它的1/2等于这个数的_________。
答案:3/47. 一本书的价格是35元,如果打8折,那么现价是_________元。
答案:288. 一个正方形的周长是32厘米,它的边长是_________厘米。
答案:89. 一辆自行车车轮的直径是70厘米,要经过一个长9.42米的圆弧形障碍物,自行车需要滚动_________圈。
答案:3010. 甲、乙两地相距360千米,一辆汽车以每小时60公里的速度从甲地开往乙地,需要_________小时。
答案:6三、解答题(共25分)11. 一块梯形的苗圃,上底长8米,下底长16米,高为10米。
这块苗圃的面积是多少平方米?答案:梯形的面积公式为 \( A = \frac{(a + b) \times h}{2} \),其中 \( a \) 是上底, \( b \) 是下底, \( h \) 是高。
代入数值得到 \( A = \frac{(8 + 16) \times 10}{2} = 140 \) 平方米。
12. 小明和小红合伙买了一些文具,小明出了总钱数的2/5,小红出了总钱数的3/5。
已知小红比小明多出了24元,请问他们一共出了多少钱?答案:设总钱数为 \( x \) 元,根据题意可得方程\( \frac{3}{5}x - \frac{2}{5}x = 24 \)。
小学数学小升初列方程解应用题专项练习(有难度附参考答案)

小升初数学列方程解应用题练习班级考号姓名总分1、甲有书的本数是乙有书的本数的3倍,甲、乙两人平均每人有82本书,求甲、乙两人各有书多少本。
2、一只两层书架,上层放的书是下层的3倍,如果把上层的书搬60本到下层,那么两层的书一样多,求上、下层原来各有书多少本.3、有甲、乙两缸金鱼,甲缸的金鱼条数是乙缸的一半,如从乙缸里取出9条金鱼放人甲缸,这样两缸鱼的条数相等,求甲缸原有金鱼多少条.4、汽车从甲地到乙地,去时每小时行60千米,比计划时间早到1小时;返回时,每小时行40千米,比计划时间迟到1小时.求甲乙两地的距离.5、新河口小学的同学去种向日葵,五年级种的棵数比四年级种的3倍少10棵,五年级比四年级多种62棵,两个年级各种多少棵?6、熊猫电视机厂生产一批电视机,如果每天生产40台,要比原计划多生产6天,如果每天生产60台,可以比原计划提前4天完成,求原计划生产时间和这批电视机的总台数.7、甲仓存粮32吨,乙仓存粮57吨,以后甲仓每天存人4吨,乙仓每天存人9吨.几天后,乙仓存粮是甲仓的2倍?8、一把直尺和一把小刀共1.9元,4把直尺和6把小刀共9元,每把直尺和每把小刀各多少元?9、甲、乙两个粮仓存粮数相等,从甲仓运出130吨、从乙仓运出230吨后,甲粮仓剩粮是乙粮仓剩粮的3倍,原来每个粮仓各存粮多少吨?10、师徒俩要加工同样多的零件,师傅每小时加工50个,比徒弟每小时多加工10个.工作中师傅停工5小时,因此徒弟比师傅提前1小时完成任务.求两人各加工多少个零件.11、买2.5千克苹果和2千克橘子共用去13.6元,已知每千克苹果比每千克橘子贵2.2元,这两种水果的单价各是每千克多少元?12、买4支钢笔和9支圆珠笔共付24元,已知买2支钢笔的钱可买3支圆珠笔,两种笔的价钱各是多少元?13、一个两位数,个位上的数字是十位上数字的2倍,如果把十位上的数字与个位上的数字对调,那么得到的新两位数比原两位数大36.求原两位数.14、一个两位数,十位上的数字比个位上的数字小1,十位上的数字与个位上的数字的和是这个两位数的0.2倍.求这个两位数.15、有四只盒子,共装了45个小球.如变动一下,第一盒减少2个;第二盒增加2个;第三盒增加一倍;第四盒减少一半,那么这四只盒子里的球就一样多了.原来每只盒子中各有几个球?16、25除以一个数的2倍,商是3余1,求这个数.17、甲、乙分别从相距18千米的A、B两地同时同向而行,乙在前甲在后.当甲追上乙时行了1.5小时.乙车每小时行48千米,求甲车速度.18、甲、乙两车同时由A地到B地,甲车每小时行30千米,乙车每小时行45千米,甲车先出发2小时后乙车才出发,两车同时到达B地.求A、B两地的距离.19、师徒俩加工同一种零件,徒弟每小时加工12个,工作了3小时后,师傅开始工作,6小时后,两人加工的零件同样多,师傅每小时加工多少个零件.20、有甲、乙两桶油,甲桶油再注入15升后,两桶油质量相等;如乙桶油再注人145升,则乙桶油的质量是甲桶油的3倍,求原来两桶油各有多少升?21、一个工程队由6个粗木工和1个细木工组成.完成某项任务后,粗木工每人得200元,细木工每人工资比全队的平均工资多30元.求细木工每人得多少元.附:参考答案1、甲有书的本数是乙有书的本数的3倍,甲、乙两人平均每人有82本书,求甲、乙两人各有书多少本。
小升初中数学超难试卷答案

一、选择题(每题5分,共50分)1. 下列哪个数是质数?()A. 15B. 16C. 17D. 18答案:C2. 一个长方形的长是8cm,宽是5cm,那么这个长方形的周长是多少cm?()A. 10B. 15C. 16D. 20答案:C3. 一个圆的半径是3cm,那么这个圆的面积是多少cm²?()A. 9B. 12C. 15D. 18答案:A4. 下列哪个数是偶数?()A. 3B. 4C. 5D. 6答案:B5. 一个正方形的边长是4cm,那么这个正方形的周长是多少cm?()A. 8B. 12C. 16D. 20答案:C二、填空题(每题5分,共50分)6. 一个数加上它的倒数等于2,那么这个数是()。
答案:17. 一个梯形的上底是4cm,下底是6cm,高是3cm,那么这个梯形的面积是()cm²。
答案:158. 一个圆柱的底面半径是2cm,高是5cm,那么这个圆柱的体积是()cm³。
答案:20π9. 一个三角形的底是6cm,高是4cm,那么这个三角形的面积是()cm²。
答案:1210. 一个长方体的长是10cm,宽是5cm,高是3cm,那么这个长方体的体积是()cm³。
答案:150三、解答题(每题20分,共80分)11. 一辆汽车从A地出发,以每小时60km的速度行驶,行驶了3小时后到达B地。
如果汽车以每小时80km的速度行驶,需要多少小时才能到达B地?答案:2小时12. 一个长方形的长是10cm,宽是5cm,将这个长方形分割成4个相同的小长方形,每个小长方形的面积是多少cm²?答案:12.5cm²13. 一个圆的半径增加了2cm,那么这个圆的面积增加了多少cm²?答案:16πcm²四、附加题(30分)14. 一个等边三角形的边长是10cm,那么这个三角形的面积是多少cm²?答案:25√3cm²15. 一个长方体的长、宽、高分别是3cm、4cm、5cm,那么这个长方体的体积是多少cm³?答案:60cm³16. 一个正方体的边长是2cm,那么这个正方体的表面积是多少cm²?答案:24cm²以上是小升初数学超难试卷的答案,希望能对同学们有所帮助。
小升初数学难题应用题100例附答案(完整版)

小升初数学难题应用题100例附答案(完整版)1. 小明家养了5只鸡和3只鸭,鸡比鸭多多少?答案:鸡比鸭多2只。
2. 一个长方形的长是12厘米,宽是8厘米,求它的面积。
答案:96平方厘米。
3. 一辆汽车从甲地开往乙地,每小时行驶60千米,用了4小时到达。
如果速度提高到每小时80千米,需要多少小时才能到达?答案:3小时。
4. 小红有20个苹果,小明给她一半,小红又给了小华3个,最后小红还剩多少个苹果?答案:14个。
5. 一个正方形的边长增加了10%,新的面积比原来增加了多少?答案:21%。
6. 小华买了一本书,书原价100元,书店打八折出售,小华实际支付了多少元?答案:80元。
7. 一个圆形的半径增加了50%,新的周长比原来增加了多少?答案:75%。
8. 一辆火车从A站出发,以每小时80千米的速度行驶,经过3小时到达B站。
如果火车速度提高到每小时100千米,还需要多少小时到达B站?答案:2小时。
9. 小明和小华一起买了一个篮球,小明付了60元,小华付了40元,后来小华又给小明10元,现在每人各付了多少元?答案:小明70元,小华30元。
10. 一个班级有男生25人,女生30人,全班共有多少人?答案:55人。
11. 一个长方形的长是15厘米,宽是10厘米,求它的周长。
答案:50厘米。
12. 一辆自行车以每小时15千米的速度行驶,行驶了6小时后,距离起点多少千米?答案:90千米。
13. 小明有一盒铅笔,他每天用掉3支,10天后他还剩多少支?答案:7支。
14. 一个圆的直径是14厘米,求它的面积。
答案:153.86平方厘米。
15. 一辆汽车从城市A出发,以每小时60千米的速度行驶,行驶了5小时后到达城市B。
如果汽车速度提高到每小时80千米,还需要多少小时到达城市B?答案:3.75小时。
16. 小华有50元,她买了5个苹果,每个苹果5元,她还剩多少元?答案:15元。
17. 一个长方形的长是20厘米,宽是15厘米,求它的对角线长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一:应用题专题一、和差倍问题(一)和差问题:已知两个数的和及两个数的差,求这两个数。
方法①:(和-差)2÷=较小数,和-较小数=较大数方法②:(和+差)2÷=较大数,和-较大数=较小数例如:两个数的和是15,差是5,求这两个数。
方法:(155)25-÷=,(155)210+÷=.(二)和倍问题:已知两个数的和及这两个数的倍数关系,求这两个数。
方法:和÷(倍数1+)1=倍数(较小数)1倍数(较小数)⨯倍数=几倍数(较大数)或和1-倍数(较小数)=几倍数(较大数)例如:两个数的和为50,大数是小数的4倍,求这两个数。
方法:50(41)10⨯=÷+=10440(三)差倍问题:已知两个数的差及两个数的倍数关系,求这两个数。
方法:差÷(倍数1-)1=倍数(较小数)1倍数(较小数)⨯倍数=几倍数(较大数)或和1-倍数(较小数)=几倍数(较大数)例如:两个数的差为80,大数是小数的5倍,求这两个数。
方法:80(51)20⨯=÷-=205100二、年龄问题年龄问题的三大规律:1.两人的年龄差是不变的;2.两人年龄的倍数关系是变化的量;3.随着时间的推移,两人的年龄都是增加相等的量.解答年龄问题的一般方法是:几年后年龄=大小年龄差÷倍数差-小年龄,几年前年龄=小年龄-大小年龄差÷倍数差.三、植树问题(一)不封闭型(直线)植树问题1直线两端植树:棵数=段数1+=全长÷株距1+;全长=株距⨯(棵数1-);株距=全长÷(棵数1-);2直线一端植树:全长=株距⨯棵数;棵数=全长÷株距;株距=全长÷棵数;3直线两端都不植树:棵数=段数1-=全长÷株距1-;株距=全长÷(棵数1+);(二)封闭型(圆、三角形、多边形等)植树问题棵数=总距离÷棵距;总距离=棵数⨯棵距;棵距=总距离÷棵数.四、方阵问题在方阵问题中,横的排叫做行,竖的排叫做列,如果行数和列数都相等,则正好排成一个正方形,就是所谓的“方阵”。
方阵的基本特点是:①方阵不论在哪一层,每边上的人(或物)数量都相同.每向里一层,每边上的人数就少2,每层总数就少8.②每边人(或物)数和每层总数的关系:每层总数[=每边人(或物)数1]4⨯;每边人(或物)数=每层总数41÷+.③实心方阵:总人(或物)数=每边人(或物)数×每边人(或物)数.五、还原问题已知一个数,经过某些运算之后,得到了一个新数,求原来的数是多少的应用问题,它的解法常常是以新数为基础,按运算顺序倒推回去,解出原数,这种方法叫做逆推法或还原法,这种问题就是还原问题.还原问题又叫做逆推运算问题.解这类问题利用加减互为逆运算和乘除互为逆运算的道理,根据题意的叙述顺序由后向前逆推计算.在计算过程中采用相反的运算,逐步逆推.在解题过程中注意两个相反:一是运算次序与原来相反;二是运算方法与原来相反.六、盈亏问题按不同的方法分配物品时,经常发生不能均分的情况.如果有物品剩余就叫盈,如果物品不够就叫亏,这就是盈亏问题的含义.一般地,一批物品分给一定数量的人,第一种分配方法有多余的物品(盈),第二种分配方法则不足(亏),当两种分配方法相差n个物品时,那就有:盈数+亏数=人数n⨯,这是关于盈亏问题很重要的一个关系式.解盈亏问题的窍门可以用下面的公式来概括:(盈+亏)÷两次分得之差=人数或单位数,(盈-盈)÷两次分得之差=人数或单位数,(亏-亏)÷两次分得之差=人数或单位数.解盈亏问题的关键是要找到:什么情况下会盈,盈多少?什么情况下“亏”,“亏”多少?找到盈亏的根源和几次盈亏结果不同的原因.另外在解题后,应进行验算.七、假设问题鸡兔同笼,这是一个古老的数学问题,在现实生活中也是普遍存在的.重点掌握鸡兔同笼问题的解法——假设法,并会将这种方法应用到一些实际问题中.解鸡兔同笼问题的基本关系式是:鸡数=(每只兔子脚数×鸡兔总数-实际脚数)÷(每只兔子脚数-每只鸡的脚数)兔数=鸡兔总数-鸡数当然,也可以先假设全是鸡,那么就有:兔数=(实际脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡的脚数)八、牛吃草问题(一)牛吃草的由来在英国伟大的科学家牛顿所著的《普通算术》一书中有一道非常有名的关于牛在牧场上吃草的题目:“12格尔(格尔:牧场面积单位),同样的牧草,21头牛9周吃10格尔.问24格尔牧草,多少头牛4周吃牧草133头牛吃18周吃完?”后来人们就把这类题目称为“牛顿问题”,也称为“牛吃草”问题.(二)牛吃草的解题步骤同一片牧场中的“牛吃草”问题,一般的解法可总结为:⑴设定1头牛1天吃草量为“1”;⑵草的生长速度=(对应牛的头数⨯较多天数-对应牛的头数⨯较少天数)÷(较多天数-较少天数);⑶原来的草量=对应牛的头数⨯吃的天数-草的生长速度⨯吃的天数;⑷吃的天数=原来的草量÷(牛的头数-草的生长速度);⑸牛的头数=原来的草量÷吃的天数+草的生长速度.(三)牛吃草的变式题“牛吃草”问题有很多的变例,像抽水问题、检票口检票问题等等,只有理解了“牛吃草”问题的本质和解题思路,才能以不变应万变,轻松解决此类问题.(四)多块草地的牛吃草问题多块草地的“牛吃草”问题,一般要将草地面积变得统一,一般情况下可以找多块草地面积的最小公倍数,这样可以避开小数分数运算,但如果数据较大时我们一般把面积统一为“1”相对会简单些。
九、工程问题工程问题,究其本质是运用分数应用题的量率对应关系,即用对应分率表示工作总量与工作效率,这种方法可以称作是一种“工程习惯”,这一类问题称之为“工程问题”。
1.解题关键是把“一项工程”看成一个单位,运用公式:工作效率×工作时间=工作总量,表示出各个工程队(人员)或其组合在统一标准和单位下的工作效率。
2.利用常见的数学思想方法,如代换法、比例法、列表法、方程法等。
抛开“工作总量”,和“时间”,抓住题目给出的工作效率之间的数量关系,转化出与所求相关的工作效率,最后利用先前的假设“把整个工程看成一个单位”,求得问题答案,一般情况下,工程问题求的是时间。
有的情况下,工程问题并不表现为两个工程队在“修路筑桥、开挖河渠”,甚至会表现为“行程问题”、“经济价格问题”等等,工程问题不仅指一种题型,更是一种解题方法。
十、浓度问题将糖溶于水就得到了糖水,糖水甜的程度是由糖与糖水二者重量的比值决定的.糖与糖水重量的比值叫糖水的浓度,这个比值一般我们将它写成百分数.其中糖叫溶质,水叫溶剂,糖水叫溶液.不光是糖水中存在着浓度,我们日常生活中的盐水、酒精等溶液只能够都存在着浓度的问题.=+溶液溶质溶剂;100%100%⨯=⨯+=溶质溶剂溶质溶质浓度溶液. ⑵常用方法:①抓不变量:一般情况下在经济问题中成本是不变量,浓度问题中溶剂是不变量,我们可以用画图来分析; ②方程法:对于经济浓度问题,采用方程来求解是简便、有效的方法; ③十字交叉法:(甲溶液浓度大于乙溶液浓度);形象表达:④浓度三角:浓度三角在解决浓度问题时非常有用.十一、利润问题商店出售商品时,为了获得最大的利润,商家总是“低进高出”,只有这样才能赚取差价,这个差价就会产生利润.实际上,在商品贸易上的许多数学问题都会涉及到三个量:成本、利润及定价.成本——购进商品所需的本钱,又叫进价或成本价;定价——商品出售的价格,又叫售价或卖卖价;利润——产品定价中高于成本以上的那一部分.为了衡量获得利润的大小,通常采用:“利润百分数”或“利润率”这个量:100%100%1100%-=+=⨯=⨯=⎛⎫-⨯ ⎪⎝⎭售价成本售价成本利润,利润率利润售价成本成本成本由上面的公式还可以引申出下面两个公式: 1⨯售价=成本(+利润率),=售价成本1+利润率.二:习题1. 商店进了300支钢笔,每售出1支,可获40%的利润当这批钢笔售出芸时,共获得利润750元,求每支钢笔的进货价.2. 商场以每个3.2元的价格购进了一批文具盒,每个售价5元,还剩下80个没售出时,除了成本已经获利500元.问这批文具盒一共有多少个?3. 人民商厦运来一批彩电,按定价出售可以获利2.8万元,如果按定价的九五折出售,则仍可获利2000元.问彩电的成本价共是多少元?4.红星商场进了一批玩具,六月一日这天以定价的八折出售,当天售出的玩具仍可获得10%的利润,问这批玩具定价时的利润是百分之几?5.一批商品,按照能获得50%的利润定价,结果只销掉了70%的商品.为尽快将剩下的商品销售出去,商店决定打折出售,这样所获得的全部利润是原来能获利润的82%.问剩下的商品打了多少折出售?6.有300克浓度为10%的盐水.现在要将这盐水的浓度变为8%,问应加入多少克水?7.要从含糖16%的20千克糖水中蒸去水分,制出含糖20%的糖水,问应当蒸去多少千克水分?8.要配制浓度为20%的硫酸溶液1000克,需要用浓度为18%和23%的硫酸溶液各多少克?9.大瓶酒精溶液是小瓶酒精溶液的2倍,大瓶酒精溶液的浓度为20%,小瓶酒精溶液的浓度为35%.将两瓶酒精溶液混合后,酒精溶液的浓度是多少?10.在甲、乙、丙三缸酒精溶液中,纯酒精的含量分别占48%、62.5%和23.已知三缸酒精溶液总量是100千克,其中甲缸酒精溶液的量等于乙、丙两缸酒精溶液的总量.三缸溶液混合后,听含纯酒精的百分数将达56%,那么,丙缸中纯酒精的量是多少千克?(1997年小学数学奥林匹克预赛C卷第12题)11.甲瓶中有纯酒精11升,乙瓶中有水15升,第一次将甲瓶中的一部分酒精倒入乙瓶中,使酒精和水混合.第二次将乙瓶中的一部分混合液倒入甲瓶中.这样,甲瓶中的纯酒精含量为62.5%,乙瓶中的纯酒精含量为25%.问第二次从乙瓶倒人甲瓶的混合液是多少升?12. 李明和王林在周长为400米的环形跑道上练习跑步,李明每分钟跑200米,是王林每分钟跑的98,如果两人从同一地点出发,沿同一方向前进,问至少要经过几分钟两人才能相遇?13. 从360米长的环形跑道上的同一地点向相同方向跑步,甲每分钟跑305米,乙每分钟跑275米,两人起跑后,问第一次相遇在离起点多少米处?14. 绕湖一周是21.1千米,小明和小华从湖边同一地点同时相背而行小明以每小时4.6千米的速度每走1小时后就休息5分钟,小华以每小时5.4千米的速度每走50分钟后就休息10分钟,问两人出发后多少小时相遇?15. 12点整时,钟面上的时针、分针和秒针刚好重合.那么,再过多长时间,钟面上的时针和分针再次重合?重合时,时针、分针分别走了几圈几格?(钟面一圈分成60格)16. 有一个台式钟,在3月29日零时比标准时间慢4分半,它一直走到4月5日上午7时,比标准时间快3分钟,那么这个台钟所指时间是正确的时刻在几月几日几时?17. 小红和妈妈的年龄加在一起是40岁,妈妈年龄是小红年龄的4倍,小红有________岁,妈妈有 __岁.18. 甲、乙、丙、丁四个人一共做了370个零件,如果把甲做的个数加2,乙做的个数减3,丙做的个数乘2,丁做的个数除以2,四个人做的零件个数正好相等,问四个人各做多少个零件?19.叔叔比小华大20岁,明年叔叔的年龄是小华的3倍,小华今年_______岁.20.女儿今年(1994年)12岁,妈妈对女儿说:“当你有我这么大岁数时,我已经60岁喽!”问:妈妈12岁时,是哪一年?21.五位老人的年龄互不相同,其中年龄最大的比年龄最小的大6岁,已知他们的平均年龄为85岁,其中年龄最大的一位老人为________.22.今年父亲的年龄为儿子的年龄的4倍,20年后父亲的年龄为儿子的年龄的2倍,儿子今年_______岁。
