基于频域的校正方法及实验设计
基于频域的串联校正控制器设计

姓名: 指导老师: 成绩: 学院:电气工程学院 专业:自动化 班级: 实验内容:基于频域的串联校正控制器设计 【实验时间】 【实验地点】 【实验目的】1. 学会采用MATLAB 进行串联超前、滞后和滞后—超前校正控制器的设计;2. 掌握采用有源放大器模拟电路实现串联超前、滞后和滞后—超前校正的方法;3. 练习控制性能比较与评估的方法。
【实验设备与软件】bACT 试验台与虚拟示波器2.MATLAB 软件3.Multisim 软件 【实验原理】1、被模拟对象模型描述控制函数: ;式中)/(d t e t k k Rb k K +=为传动系数,)/(em t e k k Rb JR T +=为机电时间常数。
2、基于串联超前或串联滞后或滞后—超前校正的闭环控制系统的串联校正方法主要是通过在前向通路上增加校正装置实现保证系统稳定基础上提高系统的暂态性能。
从频率的角度,就是通过校正装置改变原系统的频率特性,包过幅频特性和相频特性,从而达到所要求的性能指标。
串联校正闭环控制框图如下。
串联校正装置有无源和有源之分,均可设计成串联超前或串联滞后或滞后—超前校正方法式。
矫正的基本形式是式中,K 和a 、b 是两类可变参数。
b=1,a>1表示相位超前;a=1,b>1表示相位滞后。
K 用于系统校正后的静态增益,以满足稳态性能指标和扰动抑制性能。
K 的选择取决于抚恤的稳态误差,减小稳态误差就必须增大比列系数,但并不是比例系数越大越好。
【实验内容、方法、过程与分析】 1、实验内容过程与分析)1()(+=s T s K s G em d−−→−)s (R 11s ++=s b s a KC ττ)(用有有缘放大模拟电路模拟永磁他励电枢控制式直流电机机对象,采用基于Bode 图的频率设计方法对以下三种参数的性能指标设计串联校正控制器。
标称参数取J=0.001Kgm2,b=0.01Nm,Kt=Ke=0.1Nm/A,R=1Ω。
实验五 控制系统的频域法校正设计
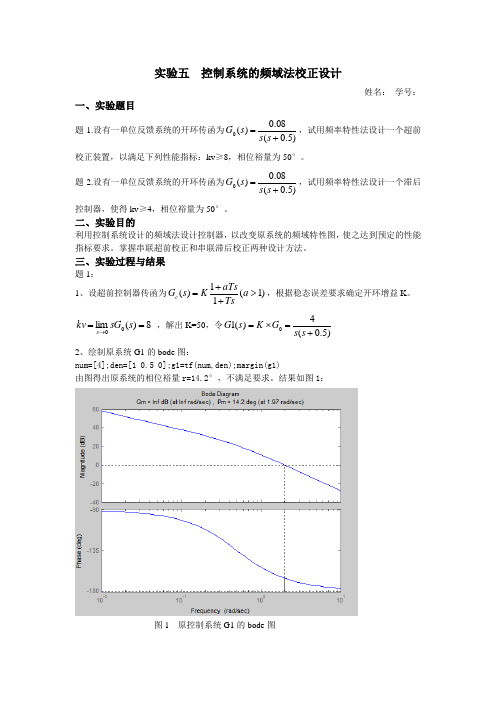
实验五 控制系统的频域法校正设计姓名: 学号:一、实验题目题1.设有一单位反馈系统的开环传函为)5.0(08.0)(0+=s s s G ,试用频率特性法设计一个超前校正装置,以满足下列性能指标:kv ≥8,相位裕量为50°。
题2.设有一单位反馈系统的开环传函为)5.0(08.0)(0+=s s s G ,试用频率特性法设计一个滞后控制器,使得kv ≥4,相位裕量为50°。
二、实验目的利用控制系统设计的频域法设计控制器,以改变原系统的频域特性图,使之达到预定的性能指标要求。
掌握串联超前校正和串联滞后校正两种设计方法。
三、实验过程与结果题1:1、设超前控制器传函为)1(11)(>++=a TsaTs K s G c ,根据稳态误差要求确定开环增益K 。
8)(lim 00==→s sG kv s ,解出K=50,令)5.0(4)(10+=⨯=s s G K s G 2、绘制原系统G1的bode 图:num=[4];den=[1 0.5 0];g1=tf(num,den);margin(g1)由图得出原系统的相位裕量r=14.2°,不满足要求。
结果如图1:图1 原控制系统G1的bode 图3、求所需超前角fai :fai=50°-14.2°+5°=40.8°4、计算a:fai=40.8*pi/180;a=(1+sin(fai))/(1-sin(fai))得出a = 4.77075、求m ω:a=4.7707;10*log10(a)=6.7858在0db 线下10lga=6.7858处作水平线,与原系统G1的bode 图幅频特性曲线的交点对应的w 值即为m ω,由图知m ω=2.93,结果如图2:图2 作图解m ω6、求T :wm=2.93;T=1/(wm*sqrt(a))运行得到T=0.1563,因此超前控制器为ss s G c 156.01744.0150)(++⨯= 7、校验性能指标:num=[4];den=[1 0.5 0];g1=tf(num,den);nc=[0.744 1];dc=[0.156 1];gc=tf(nc,dc);g=g1*gc;bode(g1);hold on;bode(gc);hold on;bode(g);legend('g1','gc','g')原系统g1的bode 图,超前控制器gc 的bode 图,校正后系统g 的bode 图如图3:图3 校验校正后系统性能指标由图知相位裕量为50.5°,满足要求。
精编完整版 基于频率法的超前校正设计毕业论文

学号:课程设计题目基于频率法的超前校正设计学院专业班级姓名指导教师课程设计任务书学生姓名:陈洁专业班级:自动化1101 班指导教师:谭思云工作单位:自动化学院题目 : 基于频率法的超前校正设计初始条件:已知系统的传递函数模型为:要求完成的主要任务 : (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)掌握采用频率法设计超前校正装置的具体步骤;设计超前校正环节,使其校正后系统的静态速度误差系数,相角裕度为;1.采用 Matlab 工具进行分析设计,并绘制校正前后系统的单位阶跃响应曲线,开环 Bode 图和 Nyquist 图;2.分析比较采用校正前后的 Bode图和 Nyquist 图,说明其对系统的各项性能指标的影响。
总结频率法校的优缺点及其适应条件;3.对上述任务写出完整的课程设计说明书,说明书中必须写清楚分析计算的过程,并包含 Matlab 源程序或 Simulink 仿真模型,说明书的格式按照教务处标准书写。
时间安排:( 1)课程设计任务书的布置,讲解(一天)(2)根据任务书的要求进行设计构思。
(一天)(3)熟悉 MATLAB中的相关工具(一天)(4)系统设计与仿真分析。
(四天)(5)撰写说明书。
(两天)(6)课程设计答辩(一天)指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (1)Abstract (1)1控制系统超前校正的任务 (2)2控制系统校正前分析 (3)2.1用 MATLAB做出校正前系统的伯德图、奈奎斯特图和阶跃响应曲线 (3)2.1.1系统的开环传递函数 (3)2.1.2校正前系统的波德图 (3)2.1.3校正前系统的奈奎斯特图 (4)2.1.4校正前系统的单位阶跃响应曲线 (5)3控制系统超前校正分析设计 (6)3.1串联超前校正原理分析 (6)3.2采用 MATLAB工具进行串联超前校正设计 (7)3.2.1利用 MATLAB进行超前校正设计的程序 (7)3.2.2开环频率特性系数扩大即K 值的确定 (9)3.2.3利用 MATLAB工具设计超前校正结果 (11)3.3理论计算 (13)4控制系统校正前后的对比 (15)4.1控制系统校正前后的伯德图、奈奎斯特图和阶跃响应曲线对比 (15)4.1.1系统校正前后伯德图与奈奎斯特图对比 (15)4.1.2系统校正前后单位阶跃曲线对比及分析 (17)5频率法校正优缺点及适用条件 (18)5.1频率法超前校正的优缺点及适用条件 (18)5.1.1频率法超前校正的优缺点: (18)5.1.2频率法超前校正的适用条件: (18)5.2频率法校正的其他情况 (18)5.3频率法校正的优缺点及适用条件 (19)6心得体会 (20)7参考文献 (21)摘要自动控制理论是研究自动控制共同规律的技术科学。
基于频域的校正方法及实验设计

2016届毕业(设计)论文题目基于频域的校正方法及实验设计专业班级过程自动化学号 1204160134学生姓名于春明第一指导教师陈杰指导教师职称学院名称电气信息院完成日期: 2016年 5月 20日基于频域的校正方法及实验设计Correction Method and Experimental Design based on Frequency Domain学生姓名于春明第一指导教师陈杰摘要在经典控制理论中,系统校正设计,就是在给定的性能指标下,对于给定的对象模型,确定一个能够完成系统满足的静态与动态性能指标要求的控制器,即确定校正器的结构与参数。
串联校正控制器的频域设计方法中,使用的校正器有超前校正器、滞后校正器、滞后-超前校正器等。
超前校正设计方法的特点是校正后系统的截止频率比校正前的大,系统的快速性能得到提高,这种校正设计方法对于要求稳定性好、超调量小以及动态过程响应快的系统被经常采用。
滞后校正设计方法的特点是校正后系统的截止频率比校正前的小,系统的快速性能变差,但系统的稳定性能却得到提高,因此,在系统快速性要求不是很高,而稳定性与稳态精度要求很高的场合,滞后校正设计方法比较适合。
滞后-超前校正设计是指既有滞后校正作用又有超前校正作用的校正器设计。
它既具有了滞后校正高稳定性能、高精确度的好处,又具有超前校正响应快、超调小的优点,这种设计方法在要求较高的场合经常被采用。
关键词:ABSTRACTIn classical control theory, system design correction, that is, given the performance for a given object model to determine a controller to complete the system meets the static and dynamic performance requirements, namely to determine the structure and corrector parameter. Frequency Domain controller series corrected using correction has lead corrector corrector lag lag - lead Corrector like. Features advanced design correction method is to correct the system cut-off frequency than the fast performance is improved before the correction is large, the system, this correction method for design requires good stability, small overshoot and dynamic process of rapid response systems are often use. Lag compensation design approach is characterized by system after correcting the cutoff frequency than the fast performance before correction is small, the system is deteriorated but stable performance of the system has improved, therefore, the system speed requirements are not high, and the stability and steady-state high precision of the occasion, lag compensation design method is more suitable. Lag - lead Corrector design means there are both lagging corrective action ahead of corrective action calibration designs. It has a lag correction high stability, high accuracy advantages, but also has the leading correction fast response, small overshoot of the advantages of this design approach in demanding situations are often used.Keywords:第1章绪论1.1 题目背景、研究意义自动控制系统的计算机仿真是一门综合性较强的学科,它涉及到计算机技术,系统科学,控制工程。
实验报告7--频域法串联超前校正南昌大学

② 量程选择开关 S2 置下档,调节“设定电位器 1” ,使之矩形波宽度≥3 秒(D1 单元左显示) 。 ③ 调节 B5 单元的“矩形波调幅”电位器使矩形波输出电压= 2.5V(D1 单元右显示) 。 (1) 构造模拟电路:按图 3-3-2 安置短路套及测孔联线,表如下。 (a)安置短路套 (b)测孔联线 1 2 3 4 5 模块号 1 A1 跨接座号 S4,S8 信号输入 r(t) 运放级联 运放级联 负反馈 运放级联 B5(OUT)→A1(H1) A1(OUT)→A5(H1) A5A(OUTA) →A6 (H1) A6(OUT)→A1(H2) A6(OUT)→A3(H1)
运行、观察、记录: 运行程序同《未校正系统的频域特性的测试》 。 在串联超前校正后的相频特性曲线上可测得串联超前校正后系统的频域特性: 穿越频率ωc= 14.45 rad/s, 相位裕度γ= 54.5° 测试结果表明符合设计要求。 5。串联超前校正系统的时域特性的测试 串联超前校正后系统时域特性测试的模拟电路图见图 4。
图1
未校正系统模拟电路图
6 0.2S(1 0.3S)
未校正系统的开环传递函数为: G( S )
模拟电路的各环节参数:积分环节(A5 单元)的积分时间常数 Ti=R1*C1=0.2S, 惯性环节(A6 单元)的惯性时间常数 T=R2*C2=0.3S, 开环增益 K=R2/R3=6。 实验步骤: 注: ‘S ST’ 用“短路套”短接! (1)将函数发生器(B5)单元的矩形波输出作为系统输入 R。 (连续的正输出宽度足够大的阶跃信 号) ① 在显示与功能选择(D1)单元中,通过波形选择按键选中‘矩形波’ (矩形波指示灯亮) 。
南昌大学实验报告
学生姓名: 学 号: 专业班级: 电力 111 班 实验日期: 实验成绩: 实验类型: □验证 ■综合 □ 设计 □ 创新
频率法校正

《自动控制原理》仿真实验报告学年学期: 2014-2015学年第1学期实验内容:频率法校正姓名:王建宙班级: 12电4 指导教师:田晴分数:一.实验目的:1. 学习结构图编程,掌握结构图simulink 文件的设计方法;2. 对给定的控制系统,设计满足频域性能指标的校正环节,并通过仿真结果验证设计的准确性。
二.实验内容内容1:已知单位反馈系统,开环传递函数 10(s)(0.2s 1)(0.5s 1)o G s =++ 1. 对给定系统,建立m 文件,确定其伯德图以及相位裕量、穿越频率,闭环系统单位阶跃响应。
2. 要求串联校正后,相位裕量()45c γω>o ,增益裕量6dB GM ≥,设计串联校正环节(分别采用超前、滞后两种方法)3. 在上述m 文件,编写控制器程序。
将控制器、校正后系统伯德图与原系统伯德图绘制在同一figure 中。
校正后系统与原系统阶跃响应绘制在同一figure 中。
4. 在SIMULINK 环境下,搭建系统的结构框图,进行原系统与校正后系统的阶跃响应仿真1)问题分析:本设计中选取滞后校正方法,其原理是观察原系统在穿越频率附近相位迅速衰减,适合采取滞后校正的方法。
所谓滞后校正,就是通过采取适当的滞后校正装置,降低穿越频率w ,使相位裕量提高。
不过降低穿越频率会造成暂态响应时间增大。
2)问题解决:问题一:用MATLAB 建立校正前系统的开环传递函数,确定其相位裕量、穿越频率,伯德图,和闭环系统单位阶跃响应。
程序及说明如下:num=10; %系统K 取10den=conv([0.5 1],conv([0.2 1],[1 0]));G=tf(num,den);[gm,pm,wcg,wcp]=margin(G);disp(['相位裕量=',num2str(pm)]) %校正前系统相位裕量disp(['穿越频率=',num2str(wcp)]) %校正前系统穿越频率disp(['增益裕量=',num2str(gm)]) %校正前系统增益裕量sys=feedback(G,1); % 校正前系统闭环传函margin(G) %校正前系统bode 图step(sys) %校正前系统阶跃响应图grid on运行结果:相位裕量=-8.8865穿越频率=3.7565增益裕量=0.7可见原系统相位裕量小于零,是不稳定的,且增益裕量=0.7。
频域法校正

目录1.任务书......................................................... (2)2.设计思想及内容 (3)2.1设计思想 (3)2.2内容 (3)3.编制的程序................................................... (3)3.1运用MATLAB编程 (3)4.结论 (10)5.设计总结 (10)参考文献 (10)《自动控制理论Ⅱ》课程设计任务书2. 设计内容及思想 :2.1 内容:已知过程控制系统的被控广义对象的传递函数)110)(12)(15(1+++=S S S G ,用Bode图超前校正方法进行校正设计,使校正后系统满足阶跃响应超调量及调节时间满足要求: 即超调量%σ ≤ 30%,调节时间 s t s 5.14=≤15s 。
2.2 思想:在控制系统中,校正方式有多种,恩提要求用超前校正,并不代表只能用该方法,在设计中,遵循校正方法,利用MATLAB 编写程序即可完成校正。
3. 编制的程序:3.1 运用MATLAB 编程:频域法校正:编制程序绘制校正前的Bode 图和阶跃响应曲线:K=1;n1=1;d1=conv(conv([5 1],[2 1]),[10 1]); %对传递函数输入描述 s1=tf(K*n1,d1);figure(1);margin(s1);hold on %绘制得到Bode 图 figure(2);sys=feedback(s1,1);step(sys) %绘制得到阶跃响应曲线得如下阶跃响应曲线图2-1和Bode 图2-2.Step ResponseTime (sec)A m p l i t u d e051015202530354045500.10.20.30.40.50.60.7图2-1阶跃响应曲线M a g n i t u d e (d B )10-310-210-110101102P h a s e (d e g )Bode DiagramGm = 22 dB (at 0.412 rad/sec) , P m = -180 deg (at 0 rad/sec)Frequency (rad/sec)图2-2 Bode 图由Bode 图和阶跃响应曲线知:超调量=%σ7%,峰值时间s tp2.23=,调节时间(5%误差带) s t s 7.28=。
频域校正方法

4 写出 Gc s Ts 1 5 检验(画Bd图)
Ts 1
6 不满足时,可增大 m 或 的余量,重新 设计
注意:超前串联校正不能用与不稳定系统 以及 c 附近相位迅速衰减系统。
解:首先确定开环增益K
K v lim sG ( s) K 30
s 0
图6-18 控制系统
未校正系统开环传递函数应取 30 G( s) s(0.1s 1)(0.2s 1) 画出未校正系统的对数幅频渐近特性曲线,请看下页!
由图可得
100 50 0 -50 -100 -2 10 -50 -100 -150 -200 -250 -300 -2 10
1 1 , T T
附近。(可取
1 0.1 c T
)
例6-2 设控制系统如图6-18所示。若要求校正后的静态速 度误差系数等于30/s,相角裕度40度,幅值裕度不小于 10dB,截止频率不小于2.3rad/s,试设计串联校正装置。
R(s)
K s(0.1s 1)(0.2s 1)
C(s)
为了补偿因超前校正网络的引入而造成系统开环增益的衰减, 必须使附加放大器的放大倍数为a=4.2
s 4.4 1 0.227 s aGc ( s ) 4.2 s 18.4 1 0.0542 s
40 20 0 -20 -40 -60 0 10
10
1
10
2
50 0 -50 -100 -150 -200 0 10
G (s)
40 20 0 -20 -40 -60 0 10
4K s( s 2)
设计超前校正装置
频域法串联校正

d ( s)
Gc (s )
找出Ф d和Gc的简单近似关系
1) Gc ( j )Gg 2 ( j ) 2) Gc ( j )Gg 2 ( j ) 1 1 d ( j ) 1 Gc ( j )Gg 2 ( j ) Gc ( j ) 1 d ( j ) Gg 2 ( j ) 1 Gc ( j )Gg 2 ( j ) Gg 2 ( j ) Gg 2 ( j )
频域法串联校正
• 比例微分校正(PD)
Gc ( s ) K c (Tc s 1) K c (T1s 1) Gc ( s ) (T2 s 1) T1大于T2几倍到几十倍
Gc(s) G(s)
1/T1
1/T2
• 比例积分校正(PI) Kc (T2 s 1) Gc ( s) ;T1大于T2 (T1s 1) • 比例积分微分校正(PID)
例:
Gg 1 ( s )
Gg 2 ( s )
Gg 1 ( s )
d ( s)
Gc (s )
c2 1 2 s , t s 0.25s, p 30% 2! 250 K g1 K g1 Gg 1 ( s ) = , T f s 1 0.007 s 1 K v 1000 s 1 , Gg 2 ( s ) Kg2 s (Tm s 1) Kg2 s (0.9 s 1)
L0 A Lx -40 高频 干扰区
i LM
Lm
k
当 G0 ( j ) 1时,临界角频率
k
k
em
,
2 k em c 为电机极限角加速度
过ω k做-40db/十倍频,即得高频限制线。
如果功率限制区与精度限制区矛盾,则要重选电机。
实验二.三系统的频域分析法及校正

第二节 控制系统的设计方法
•
控制系统的设计,就是在系统 中引入适当的环节,用以对原有系 统的某些性能进行校正,使之达到 理想的效果,故又称为系统的校正, 下面介绍几种常用的系统校正方法 的计算机辅助设计实现。
性能如何描述? 控制器的设计:传递函数的结构 与参数 选择
或
num( s) 1 K 0 den( s)
利用rlocus( )函数可绘制出当开环增益K由0至∝变 化时,闭环系统的特征根在s平面变化的轨迹,函 数的调用格式为:
rlocus(GH); rlocus(GH,k); [r,K]=rlocus(num,den) [r,K]=rlocus(a,b,c,d)
练习 已知系统的开环传递函数
50 G( s) H ( s) ( s 5)( s 2)
绘制系统nyquist曲线。
解 MATLAB编程如下: » k=50; » z=[]; » p=[-5 2]; » [num,den]=zp2tf(z,p,k); »nyquist(num,den)
10 G( s) 2 s 1.2s 10
的nyquist图和bode图。
解 MATLAB编程如下: » num=[10]; » den=[1,1.2,10]; » w=logspace(-2,2,1000); »nyquist(num,den,w) » grid » bode(num,den,w) » grid
其中:返回值r为系统的闭环极点, K为相应的增益。
+ -
G(s) H(s) 图7-12
例
R(s)
-
s 1 1 K 3 0 2 s 5s 6s
基于频域的串联校正控制器设计

广西大学实验报告纸姓名:刘志浩指导老师:胡立坤成绩:学院:电气工程学院专业:自动化班级:132实验内容:基于频域的串联校正控制器设计2015年6月15日其他组员:鲁巍和刘志浩设计了MATLAB仿真并一起调试了动手实验夏超设计了电路图并在multism中做了仿真刘志浩通过和鲁巍,夏超讨论对实验结果进行了分析,撰写了实验报告【实验时间】2015年6月15日【实验地点】广西大学综合楼8081.学会采用MATLAB进行串联超前、滞后和滞后、超前校正控制器的设计2.掌握采用有缘放大器模拟电路实现串联超前、滞后和滞后、超前校正的方法3.联系控制性能比较和评估的方法【实验设备与软件】bACT试验台和虚拟示波器2.MATLAB软件3.Multisim软件【实验原理】1、被模拟对象模型的描述控制函数:;为传动系数,为机电时间常数。
2、基于串联超前或串联滞后或滞后—超前校正的闭环控制系统的串联校正方法主要是通过在前向通路上增加校正装置实现保证系统稳定基础上提高系统的暂态性能。
从频率的角度,就是通过校正装置改变原系统的频率特性,包过幅频特性和相频特性,从而达到所要求的性能指标。
串联校正闭环控制框图如下。
串联校正装置有无源和有源之分,均可设计成串联超前或串联滞后或者滞后—超前校正方式。
校正的基本形式是式中,K和a、b是两类可变参数。
b=1,a>1表示相位超前;a=1,b>1表示相位滞后。
K用于系统校正后的静态增益,以满足稳态性能指标和扰动抑制性能。
K的选择取决于抚恤的稳态误差,减小稳态误差就必须增大比列系数,但并不是比例系数越大越好。
【实验内容、方法、过程与分析】动手实验与分析:用有源放大模拟电路模拟永磁他励电枢控制式直流电机机对象,采用基于Bode 图的频率设计方法对以下三种参数的性能指标设计串联校正控制器。
(一) 1.超前校正题目:标称参数取J=0.001Kgm2,b=0.01Nm,Kt=Ke=0.1Nm/A,R=1Ω。
频域法校正

目录1.任务书......................................................... (2)2.设计思想及内容 (3)2.1设计思想 (3)2.2内容 (3)3.编制的程序................................................... (3)3.1运用MATLAB编程 (3)4.结论 (10)5.设计总结 (10)参考文献 (10)《自动控制理论Ⅱ》课程设计任务书题目频域法校正学生姓名学号专业班级设计内容与要求一.设计内容:已知过程控制系统的被控广义对象的传递函数)110)(12)(15(1+++=SSSG,用Bode图超前校正方法进行校正设计,使校正后系统满足阶跃响应超调量及调节时间满足要求:即超调量%σ≤30%,调节时间st s5.14=≤15s。
二.设计要求:(1)绘制原系统的Bode图,并计算出原系统的幅值裕量及相角裕量;(2)选择校正方式,进行校正装置的设计,得到相应的校正装置参数;(3)编程绘制校正后系统的Bode图,并计算出校正后系统的幅值裕量和相角裕量;(4)整理设计结果,提交设计报告;起止时间2011 年12 月26 日至2011 年12月31日指导教师签名年月日系(教研室)主任签名年月日学生签名年月日2. 设计内容及思想 :2.1 内容:已知过程控制系统的被控广义对象的传递函数)110)(12)(15(1+++=S S S G ,用Bode图超前校正方法进行校正设计,使校正后系统满足阶跃响应超调量及调节时间满足要求: 即超调量%σ ≤ 30%,调节时间 s t s 5.14=≤15s 。
2.2 思想:在控制系统中,校正方式有多种,恩提要求用超前校正,并不代表只能用该方法,在设计中,遵循校正方法,利用MATLAB 编写程序即可完成校正。
3. 编制的程序:3.1 运用MATLAB 编程:频域法校正:编制程序绘制校正前的Bode 图和阶跃响应曲线:K=1;n1=1;d1=conv(conv([5 1],[2 1]),[10 1]); %对传递函数输入描述 s1=tf(K*n1,d1);figure(1);margin(s1);hold on %绘制得到Bode 图 figure(2);sys=feedback(s1,1);step(sys) %绘制得到阶跃响应曲线得如下阶跃响应曲线图2-1和Bode 图2-2.Step ResponseTime (sec)A m p l i t u d e051015202530354045500.10.20.30.40.50.60.7System: sys Time (sec): 28.7Amplitude: 0.525图2-1阶跃响应曲线-150-100-50M a g n i t u d e (d B )10-310-210-110101102-270-180-90P h a s e (d e g )Bode DiagramGm = 22 dB (at 0.412 rad/sec) , P m = -180 deg (at 0 rad/sec)Frequency (rad/sec)图2-2 Bode 图由Bode 图和阶跃响应曲线知:超调量=%σ7%,峰值时间s tp2.23=,调节时间(5%误差带) s t s 7.28=。
频域校正方法

c 12rad / s
c 12rad / s
27
10
-1
10
0
10
1
10
2
27
10
10
10
1
10
2
*也可算出 (g ) 180 g 7.07rad / s , c 12rad / s
180 90 arctgc 0.1 arctgc 0.2
再利用
1 0.1 c bT
1 T 41.1s 0.1cb
bT=3.7s,则滞后网络的传递函数
Gc ( s )
1 bTs 1 3.7 s 1 Ts 1 41s
c 2.7rad / s
100 50
(c) 90 arctg(0.1c) arctg(0.2c)
50
21dB
0 -50 -100 -2 10 0
46.5
G0 Gc
10
-1
10
0
10
1
GcG0
10
2
-100
-200
-300 -2 10
10
-1
10
0
10
1
10
2
验算指标(相位裕度和幅值裕度)
41.3 40
h(dB ) 20 lg Gc ( j )Go ( j ) 10.5dB 10 dB g g
180
-200 0 10
17
10
1
10
2
计算超前校正网络的转折频率
m
1 T a
1
m
9 4.4 a 4.2
自动控制原理实验七 基于MATLAB控制系统频域法串联校正设计

实验七基于MATLAB控制系统频域法串联校正设计一、实验目的(1)对给定系统设计满足频域或时域指标的串联校正装置;(2)掌握频域法设计串联校正的方法;(3)掌握串联校正环节对系统稳定性及过渡过程的影响。
二、实验原理及内容利用MATLAB可以方便的画出Bode图并求出幅值裕量和相角裕量。
将MATLAB应用到经典理论的校正方法中,可以方便的校验系统校正前后的性能指标。
通过反复试探不同校正参数对应的不同性能指标,能够设计出最佳的校正装置。
1、串联超前校正用频域法对系统进行超前校正的基本原理,是利用超前校正网络的相位超前特性来增大系统的相位裕量,以达到改善系统瞬态响应的目标。
为此,要求校正网络最大的相位超前角出现在系统的截止频率(剪切频率)处。
串联超前校正的特点:主要对未校正系统中频段进行校正,使校正后中频段幅值的斜率为-20dB/dec,且有足够大的相位裕度;超前校正会使系统瞬态响应的速度变快,校正后系统的截止频率增大。
这表明校正后,系统的频带变宽,瞬态响应速度变快,相当于微分效应;但系统抗高频噪声的能力变差。
用频率法对系统进行串联超前校正的一般步骤为:1)根据稳态误差的要求,确定开环增益K。
2)根据所确定的开环增益K,画出未校正系统的波特图,计算未校正系统的相位裕度。
3)计算超前网络参数a和T。
4)确定校正网络的转折频率。
5)画出校正后系统的波特图,验证已校正系统的相位裕度。
【7-1】给定系统如图7-1所示,试设计一个串联校正装置,使系统满足幅值裕量大于10分贝,相位裕量≥45o为了满足上述要求,试探地采用超前校正装置G c(s),使系统变为图7-2的结构。
图7-1 校正前系统用下面地MATLAB语句得出原系统的幅值裕量与相位裕量。
>> G=tf(100, [0.04, 1, 0]);[Gw, Pw, Wcg, Wcp]=margin(G);Gw =InfPw =28.0243Wcg=InfWcp=46.9701可以看出,这个系统有无穷大的幅值裕量,并且其相位裕量γ=28o,幅值穿越频率Wcp=47rad/sec。
频域校正法

《自动控制原理》课程设计任务书一 课程设计题目1题目 频域法第一题某单位负反馈系统前向通道的传递函数为G(s)=)2(9+s s ,设计校正装置使系统的相角裕量γ≥45°,截止频率ωc 不小于4rad/s 。
2要求(1) 程绘制原系统的Bode 图,并计算出原系统的幅值裕量及相角裕量; (2)选择较正方式,进行校正装置设计,得出相应的校正装置的参数; (3)编程绘制校正后的系统Bode 图,并计算出校正装置的幅值裕量及相角裕量;(4)整理设计结果,提交设计报告。
二 设计思想及内容1 设计思想当系统的性能指标已幅值裕量、相位裕量和误差系数等频域指标出现时,运用频域法分析设计是很方便的。
运用频域法进行校正,其目的是改变系统频域特性,是校正后系统的频域特性拥有合适的低中频和高频特性,及足够的稳定裕量,从而满足设计性能指标。
控制系统中常用的串联校正装置是带有单零、极点的滤波器。
若其零点比极点更靠近原点,则称为PD 校正,反之,则是PI 校正,另外还有PID 校正。
2设计内容本题为设计超前校正,其目的是产生超前相角,用于补偿系统固有部附近的相角滞后,以提高相角稳定裕量,改善系统动态性能,达分在ωc不小于4rad/s。
到设计要求:相角裕量γ≥45°,截止频率ωc三设计步骤1)做原系统的Bode图做原系统的Bode图,检查是否满足题目要求性能指标与要求。
在程序文件方式下执行如下MATLAB程sh1.m%sh1.mcleark=9;n1=1;d1=conv([1,0],[1,2]);s1=tf(k*n1,d1); %原系统传递函数figure(1);margin(s1) %输出原系统Bode图程序运行后,得到图5-1所示未校正系统的Bode图,及其性能指标值Bode DiagramGm = Inf dB (at Inf rad/sec) , Pm = 36.7 deg (at 2.69 rad/sec)Frequency (rad/sec)-80-60-40-2002040M a g n i t u d e (d B )10-110101102-180-135-90P h a s e (d e g )图 5-1原系统Bode 图 由图5-1可得原系统频域性能指标:幅值稳定裕度:h=∞dB -π穿越频率:ωg =∞ rad/s ,相角稳定裕度:γ=36.7° 剪切频率:ωc =2.69rad/s可知系统校正前,相角稳定裕度:γ=36.7<45°,剪切频率:ωc =2.69rad/s <4 rad/s ,都未满足要求,原系统需要校正。
频域法校正——精选推荐

频域法校正摘要:根据被控对象及给定的技术指标要求,设计自动控制系统,既要保证所设计的系统有良好的性能,满足给定技术指标的要求,还要考虑给定方案的可靠性和经济性。
本设计给出了在指定的技术指标下,对控制系统的设计。
在对系统进行校正的时,采用了波特图的串联滞后—超前校正,对系统校正前后的性能作了分析和比较,并用MATLAB进行了绘图和仿真。
对已校正系统的高频特性有要求时,采用频域法校正较其它方法更为方便。
关键词:控制系统;校正;Bode图;MATLAB;前言如果系统设计要求满足的性能指标属频域特征量,则通常采用频域校正方法。
在开环系统对数频率特性基础上,以满足稳态误差、开环系统截止频率和相角裕度等要求为出发点,进行串联校正的方法。
在伯德图上虽然不能严格定量地给出系统的动态性能,但却能方便地根据频域指标确定校正装置的形式和参数,特别是对已校正系统的高频特性有要求时,采用频域法校正较其它方法更方便。
串联滞后—超前校正兼有滞后校正和超前校正的优点,当待校正系统不稳定,且要求校正后系统的响应速度、相角裕度和稳态精度要求较高时,应采用串联滞后—超前校正。
其基本原理是利用滞后—超前网络的超前部分来增大系统的相角裕度,同时利用滞后部分来改善系统的稳态性能。
1 设计目的(1)掌握控制系统设计与校正的步骤和方法。
(2)掌握对控制系统相角裕度、幅值裕量度的求取方法。
(3)掌握利用Bode图对控制系统分析的技能。
(4)提高控制系统设计和分析能力。
2 设计任务书2.1设计任务单位负反馈系统的开环传递函数为:()()()200.00110.51G s s s s =++ ,设计系统使相角裕量65r ≥ ,幅值裕量34h dB =。
2.2设计要求(1) 编程绘制原系统的Bode 图,并计算出原系统的幅值裕量及相角裕量; (2)选择校正方式,进行校正装置的设计,得出相应的校正装置的参数; (3)编程绘制校正装置的Bode 图,并计算出校正后系统的幅值裕量及相角裕量;(4)整理设计结果,提交设计报告。
频域法校正的设计

⑵对校正装置进行设计。
二、设计要求:
(1)编程绘制原系统的Bode图,并计算出原系统的幅值裕量及相角裕量;
(2)选择校正方式,进行校正装置的设计,得出相应的校正装置的参数;
(3)编程绘制校正后系统的Bode图,并计算出校正后系统的幅值裕量及相角裕量;
相角稳定裕度:γ=45.4°剪切频率: =1.09rad/s
校正前系统不稳定,各参数不符合要求,校正后各参数系统稳定,并且各参数符合题目要求。校正后系统稳定性提高
5.设计总结:
本次课程设计虽然花的时间较多,但是我也学了不少东西,遇到了很多困难,主要是因为对串联校正所掌握的知识不够。在通过与同学的讨论和自己翻阅资料查询计算最终完成课程设计。在采用串联滞后校正法时,因计算的方法不合适本题而导致反复计算几次后才转换思路,找到了正确的方法。此外由于对MATLAB绘图和SIMULINK仿真比较陌生,所以在这个上面画得时间也较多。通过做课程设计,体会到了MATLAB这一工具的方便所在,同时也使我更深入了解了系统校正的过程。
clear
K=360*35/60/3;%确定开环增益K
n1=1;
d1=conv(conv([1 0],[0.5 1]),[0.166 1]);
s1=tf(K*n1,d1);%待校正系统传递函数
figure(1);
margin(s1);
hold on%画出原系统的幅值相角频域Bode图
figure(2);sys=feedback(s1,1);step(sys)%画出原系统开环传函的单位阶跃响应
2)求校正装置的传函:
待校正系统传递函数
Transfer function:
频域校正

目录1 任务书.................................................................22 设计思想及内容........................................................33 编制的程序............................................................33.1运用MATLAB编程..................................................33.2在SIMULINK中绘制状态图......................................... 114 结论..................................................................135 设计总结..............................................................13参考文献............................................................14《自动控制理论Ⅱ》课程设计任务书题目频域法校正学生姓名学号专业班级设计内容与要求一.设计内容:已知单位反馈系统传递函数)15.0)(1()(++=sssksG设计一串联校正网路,使校正后开环增益k=5,相位裕量大于400,幅值裕量大于10dB:二.设计要求(1)编程绘制原系统的Bode图,并计算出原系统的幅值裕量及相角裕量;(2)选择校正方式,进行校正装置的设计,得出相应的校正装置的参数;(3)编程绘制校正后系统的Bode图,并计算出校正后系统的幅值裕量及相角裕量;(4)整理设计结果,提交设计报告起止时间 2012年12月18日至 2012年12月25日指导教师签名年月日系(教研室)主任签名年月日学生签名 2012 年 12月 25日2设计内容及思想 : 1) 设计内容:已知单位反馈系统传递函数)15.0)(1()(++=s s s ks G设计一串联校正网路,使校正后开环增益k=5,相位裕量大于40,幅值裕量大于10dB2) 设计思想:MATLAB 软件控制领域最流行的设计和计算工具,使用该软件可以很方便进行控制系统的建模,能方便画系统的根轨迹,奈氏曲线和bode 图,能进行各种计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016届毕业(设计)论文题目基于频域的校正方法及实验设计专业班级过程自动化学号 1204160134学生姓名于春明第一指导教师陈杰指导教师职称学院名称电气信息院完成日期: 2016年 5月 20日基于频域的校正方法及实验设计Correction Method and Experimental Design based on Frequency Domain学生姓名于春明第一指导教师陈杰摘要在经典控制理论中,系统校正设计,就是在给定的性能指标下,对于给定的对象模型,确定一个能够完成系统满足的静态与动态性能指标要求的控制器,即确定校正器的结构与参数。
串联校正控制器的频域设计方法中,使用的校正器有超前校正器、滞后校正器、滞后-超前校正器等。
超前校正设计方法的特点是校正后系统的截止频率比校正前的大,系统的快速性能得到提高,这种校正设计方法对于要求稳定性好、超调量小以及动态过程响应快的系统被经常采用。
滞后校正设计方法的特点是校正后系统的截止频率比校正前的小,系统的快速性能变差,但系统的稳定性能却得到提高,因此,在系统快速性要求不是很高,而稳定性与稳态精度要求很高的场合,滞后校正设计方法比较适合。
滞后-超前校正设计是指既有滞后校正作用又有超前校正作用的校正器设计。
它既具有了滞后校正高稳定性能、高精确度的好处,又具有超前校正响应快、超调小的优点,这种设计方法在要求较高的场合经常被采用。
关键词:ABSTRACTIn classical control theory, system design correction, that is, given the performance for a given object model to determine a controller to complete the system meets the static and dynamic performance requirements, namely to determine the structure and corrector parameter. Frequency Domain controller series corrected using correction has lead corrector corrector lag lag - lead Corrector like. Features advanced design correction method is to correct the system cut-off frequency than the fast performance is improved before the correction is large, the system, this correction method for design requires good stability, small overshoot and dynamic process of rapid response systems are often use. Lag compensation design approach is characterized by system after correcting the cutoff frequency than the fast performance before correction is small, the system is deteriorated but stable performance of the system has improved, therefore, the system speed requirements are not high, and the stability and steady-state high precision of the occasion, lag compensation design method is more suitable. Lag - lead Corrector design means there are both lagging corrective action ahead of corrective action calibration designs. It has a lag correction high stability, high accuracy advantages, but also has the leading correction fast response, small overshoot of the advantages of this design approach in demanding situations are often used.Keywords:第1章绪论1.1 题目背景、研究意义自动控制系统的计算机仿真是一门综合性较强的学科,它涉及到计算机技术,系统科学,控制工程。
控制系统仿真本身是以计算机为工具以数学模型验证控制系统,与实际的控制系统无关,这是一种测试和研究的实用方法如果系统被设计成通过利用矫正方法,以满足频域,频域的量的性能指标的要求。
开环系统的基础上,对数频率特性,以达到起点,串联的校正方法的稳态误差,开环系统的截止频率和相位裕要求。
动态性能,虽然没有严格的定量给定的系统,但它可以容易地确定根据在Bode图的频率域的形式和校正装置的参数,尤其是对于需要高频特性的校正系统中,使用频域校正方法比其它方法更方便。
串联滞后超前校正网络,当确定系统不稳定,需要校正以提高响应速度以及相位裕度,稳定性,校正优点滞后系列应使用 - 超前校正。
其基本原理是利用滞后 - 铅网络的引线部分,以提高系统的相位余量,同时服用的滞后部分的优点,提高了系统的稳定状态的性能。
在当今世界上,最流行的计算机辅助控制系统的设计语言是MATLAB语言,实践证明了MATLAB语言是计算机辅助控制系统分析与设计的最佳伙伴。
MATLAB应用的进一步推广有一大部分原因是图形模型输入交互式计算机仿真环境simulink的加入。
现在,MATLAB语言已经风靡全球,它已成为控制系统cad的最热门的领域,是最流行的软件环境。
随着时代的发展,并在航空航天,机器人控制,导弹制导和核能高科技领域的计算机技术,自动控制理论及应用技术等也越来越深入和广泛。
在21世纪,不管是生物,医学,环境还是经济管理社会生活,许多领域都是自动控制技术大施拳脚的地方,已经是现代社会必要组成部分。
时代在发展,人民生活水平不断提高,人类探索未来,认识和改造自然,建设一个高度文明发达的社会等活动的展开,自动控制理论和技术将进一步发挥更重要的作用。
作为一个工程技术人员了解和掌握自动控制的知识是必要的。
现在几乎全部工厂都使用了自动控制技术,生产效率大大调高,工人的劳动强度大大减轻。
自动控制,这一高精确度的工作,还大大提高了武器效能和作战效率,如火炮自动跟踪系统使用自动控制打下了认为控制和电脑控制的高速飞行的飞机。
有些场合人不直接参与甚至自动控制技术,更离不开一些危险工作工作,如原子能生产,大炮或导弹制导等。
MATLAB软件仿真工具SIMULINK可以为自动控制系统建立数学模型,分析系统并仿真结果,能够随时更改结构与参数,可以快速直观的实现系统的设计并进一步优化。
1.2 自动控制理论发展概述1868年,麦克斯韦用研究数学的方法来研究控制系统的方式,奠定了时域分析方法的基础。
到现在为止,已经出现了经典控制理论和现代控制理论两大基础理论。
自动控制理论随着科学技术的发展,被控对象越来越多,要求的性能要求也越来越高,这之间伴随着自动控制理论的不断发展和完善。
经典控制理论是基于反馈为基础,为系统的数学模型研究了单输入传递函数 - 单输出线性时不变系统的分析和设计,主要用于工业控制和二战期间的军事装备。
1932年,以美国为首的物理学家终于建立了成熟的标准,奠定了频域分析法的基础,随着bode的进一步发展,以频域分析为基础的经典控制理论最终形成。
20世纪60年代,随着现代应用数学成果的应用和引进计算机技术,为了适用航空航天技术的发展,形成了以现代控制理论为基础的状态空间描述,以提高主要的性能,提高精度的最优控制线性可变多参数系统。
现代控制理论不仅在理论上有着理想的结果,在我们国防技术工业控制上也有着不可替代的地位。
但现代科学技术不断发展,人们的要求越来越高,现代工业控制系统也水涨船高,现行反馈控制已经不能够适用于现代社会实际需要。
我们接触到的大多是控制系统都是非线性的即便将其近似线性模型化也难以表现出非线性部分的特点,只能减小难度,控制器的设计也不足以满足要求。
线性系统不能解释众多的实际非线性工作。
在没有非线性系统的理论支持下,只能用线性系统对付分段线性的非线性特性,再用线性控制理论的分析和设计。
在20世纪90年代,由于以微分几何为主的现代数学理论的完善,突破性的解决了复杂控制系统的分析和设计及其优化。
自动控制理论与人类的发展而发展,并随着技术的进步,提高生产率和持续改进。
1.2.1 自动控制理论历史自动控制的开端:自动控制技术始于18世纪,由于第一次工业革命的发展,人们的生产力极大提高,如何在提高生产效率的同时保证生产稳定并且减小人力资源的浪费成为了人们关注的焦点特点:简单单一对象控制。
经典控制理论时期(1940-1960)最开始引起关注的是单一变量系统,比如电动机的调速,汽车速度的控制。
1942年哈里斯最先将传递函数应用于自动控制;1948年伊万恩提出了根轨迹法;1945年Bode出版的《Network Analysis and Amplifier》,是自动控制理论的基础。
1949年vina关于经典控制的著述。
特点:在这时,传函是最基本的研究手段,频域法进入人们的视线,只能够设计单变量线性定常系统,不能解决非线性系统。
现代控制理论时期(20世纪50年代末-60年代初)随着数学的发展,开始研究多变量问题,航天科技的发展以及高科技武器比如导弹,潜艇的火控问题使得人们对于高性能自动控制系统无比渴切。
最优滤波理论;极大值原理等一些重要规律被总结出来。
特点:采用时域法研究时变系统、非线性系统等高性能要求的自动控制系统。
大系统控制时期(1970s-)随着计算机技术的极大发展,各个不同领域互相交织,被计算机系统高效的利用起来。
但是要需要解决的问题也越来越复杂,研究对象复杂无比,多输入多输出非线性成为常态。
智能控制时期近几年来,计算机的简单思想已经不足以解决问题,这时人们提出了人工智能技术,用人的思想指导机器,以人的技巧解决复杂的问题。
