一元一次不等式组—含参问题
专题03 解一元一次不等式(组)及参数问题八种模型(学生版)

专题03解一元一次不等式(组)及参数问题八种模型【类型一解一元一次不等式模型】例题:(2022·陕西·模拟预测)解不等式3136x x-<-,并在如图所示的数轴上表示出该不等式的解集.【变式训练1】(2022·陕西·西安市西光中学二模)解不等式7132184x x->--,并把它的解集在如图所示的数轴上表示出来.【变式训练2】(2021·上海徐汇·期中)解不等式38236x x---≤,把解集在数轴上表示出来,并求出最小整数解.【变式训练3】(2022·福建·三明一中八年级阶段练习)解不等式:(1)2(41)58x x -≥-(2)261136x x +-≤【变式训练4】(2022·河南驻马店·八年级阶段练习)解下列一元一次不等式,并把它们的解集表示在数轴上:(1)2﹣5x <8﹣6x ;(2)53-x +1≤32x .【类型二解一元一次不等式组模型】例题:(2022·福建·三明一中八年级阶段练习)解不等式组52331132x xx x -≤⎧⎪-+⎨<-⎪⎩,并把不等式组的解集在数轴上表示出来:【变式训练1】(2022·广东·汕头市龙湖实验中学九年级阶段练习)解不等式组:1011122x x -≥⎧⎪⎨--<⎪⎩,并写出它的所有整数解.【变式训练2】(浙江省温州市2020-2021学年八年级上学期3月月考数学试题)解一元一次不等式组523(1)131722x x x x ->+⎧⎪⎨-≤-⎪⎩,并把解集在数轴上表示出来.【变式训练3】(2022·广东揭阳·八年级阶段练习)解不等式组:12(1)2235xx x x ⎧+<-⎪⎪⎨+⎪>⎪⎩,并把它的解集在数轴上表示出来.【变式训练4】(2022·湖南岳阳·八年级期末)(1)解不等式121132x x+++≥;(2)解不等式组:3242(1)31x x x -<⎧⎨-≤+⎩,并把它的解集在数轴上表示出来.【类型三一元一次不等式的定义时含参数问题】例题:(2021·全国·七年级课时练习)已知不等式||1(2)20n n x --->是一元一次不等式,则n =____.【变式训练1】(2022·山东·枣庄市第十五中学八年级阶段练习)已知()3426m m x --+>是关于x 的一元一次不等式,则m 的值为______.【变式训练2】(2021·黑龙江·肇源县超等蒙古族乡学校八年级期中)若21(2)15m m x --->是关于x 的一元一次不等式,则m 的值为______________.【类型四一元一次不等式整数解中含参数问题】例题:(2022·上海·七年级期中)如果不等式2x ﹣3≤m 的正整数解有4个,则m 的取值范围是_____.【变式训练1】(2020·全国·八年级单元测试)已知不等式30x m -≤有5个正整数解,则m 的取值范围是________.【类型五一元一次方程组与不等式间含参数问题】例题:(2022·全国·八年级)关于x 的方程42158x m x -+=-的解是负数,则满足条件的m 的最小整数值是_____.【变式训练1】(2021·四川成都·八年级期末)已知关于x 的方程35x a x +=-的解是正数,则实数a 的取值范围是______.【变式训练2】(2021·全国·七年级课时练习)如果关于x 的方程2435x a x a++=的解不是负数,那么a 的取值范围是________.【变式训练3】(2021·全国·七年级课时练习)当m________时,关于x的方程222x m xx---=的解为非负数.【类型六二元一次方程组与不等式间含参数问题】例题:(2021·内蒙古呼和浩特·七年级期末)已知关于x、y的二元一次方程组231231x y kx y k+=+⎧⎨+=-⎩的解满足x+y<4,则满足条件的k的最大整数为____.【变式训练1】(2021·四川绵阳·x,y的二元一次方程组221x yx y k+=⎧⎨+=+⎩的解为正数,则k的取值范围为__.【变式训练2】(2021·江苏江苏·七年级期末)已知关于x,y的二元一次方程组231323x y mx y m+=+⎧⎨-=+⎩,且x,y满足x+y>3.则m的取值范围是___.【变式训练3】(2021·四川南充·七年级期末)已知关于x,y的方程组24223x y kx y k+=⎧⎨+=-+⎩,的解满足x﹣y>0,则k的最大整数值是______________.【变式训练4】(2021·甘肃·九年级专题练习)若关于x,y的二元一次方程组3331x yx y a+=⎧⎨+=+⎩的解满足x+y<2,则a的取值范围为_______.【类型七解一元一次不等式组中有无解集求参数问题】例题:(2021·内蒙古·包头市青山区教育教学研究中心八年级期中)关于x的不等式组352x ax a->⎧⎨-<⎩无解,则a的取值范围是_____.【变式训练1】(2022·广西贵港·八年级期末)若关于x的不等式组33235x xx m-<⎧⎨->⎩有解,则m的取值范围是______.【变式训练2】(2021·四川凉山·七年级期末)已知关于x的不等式组5122x ax x->⎧⎨->-⎩无解,则a的取值范围是_________.【变式训练3】(2021·河南南阳·三模)已知关于x的不等式组3xx m>⎧⎨≤⎩有实数解,则m的取值范围是____.【变式训练4】(2022·江苏南通·九年级阶段练习)如果关于x的不等式组232x ax a>+⎧⎨<-⎩无解,则常数a的取值范围是______________.【类型八解一元一次不等式组中有整数解求参数问题】例题:(2021·宁夏中卫·八年级期末)不等式组,3x ax>⎧⎨<⎩的整数解有三个,则a的取值范围是_________.【变式训练1】(2021·安徽·马鞍山二中实验学校七年级期中)已知不等式组211x x a-<⎧⎨-≤⎩,只有三个整数解,则a 的取值范围是_________.【变式训练2】(2021·黑龙江佳木斯·模拟预测)不等式组2312x ax -⎧⎨-≤⎩<有3个整数解,则a 的取值范围是_____.【变式训练3】(2020·内蒙古·北京八中乌兰察布分校一模)关于x 的不等式组3x ax <⎧⎨≥⎩只有两个整数解,则a 的取值范围是_____.【变式训练4】(2022·湖南湘潭·八年级期末)已知关于x 的不等式组3010x a x -≤⎧⎨-≤⎩①②,有且只有3个整数解,则a 的取值范围是______________。
人教版初中数学七年级下册第九章一元一次不等式(组)含参专题——有、无解问题课件(共12张PPT)

问题反转,运用自如
问题3:如果不等式组
x x
2m 0 ① 有解,怎样确定
m 3②
m
的取值范围?
解不等式①得x≤2m 解不等式②得x≥3-m
自主操作:在数轴上画出有解的情况.
图⑧
自主分析:3-m和2m的大小关 系是?“=”能取?为什么.
2m 3-m 图⑨
3-m ≤ 2m
∴m的取值范围是:m ≥ 1
x x
2m 0 m3
你能确定不等式组的解集吗?请结合数轴分析.
析:由例题知两个不等式的解集分别为x<2m和x>3-m, 那么这两个解集在数轴上会有几种情况?
3-m
2m
图①
2m
3-m
图③
3-m 2m 图②
思考1:图①②③对应解集情况?
问题2:如果这个不等式组
x 2m 0 x m 3
无解,你能确定m
教学重点、难点
重点:
含参一元一次不等式组的分类解法.
难点:
1.一元一次不等式中字母参数的讨论, 2.一元一次不等式中运用数轴分析参数的范围.
温故知新,问题设疑
例1:解下列关于x两个不等式 (1)x-2m<0 (2)x+m>3
解:(1)得x<2m (2) 得x>3-m
问题引导,合作交流
问题1:如果将上述两个不等式联立成不等式组
x x
2m 0① m 3②
时,
不等式组无解,m的取值又会有改变吗?
解不等式①得x≤2m 解不等式②得x≥3-m
思考4:你能在数轴上画出无解的情况?
图⑥
2m 3-m 图⑦
同学们有没有画出图⑦这种情 况的?你认为不等式组无解, 会不会出现像图⑦3-m和2m两 个点重合的情况?
一元一次不等式组有解、无解、整数解求参问题
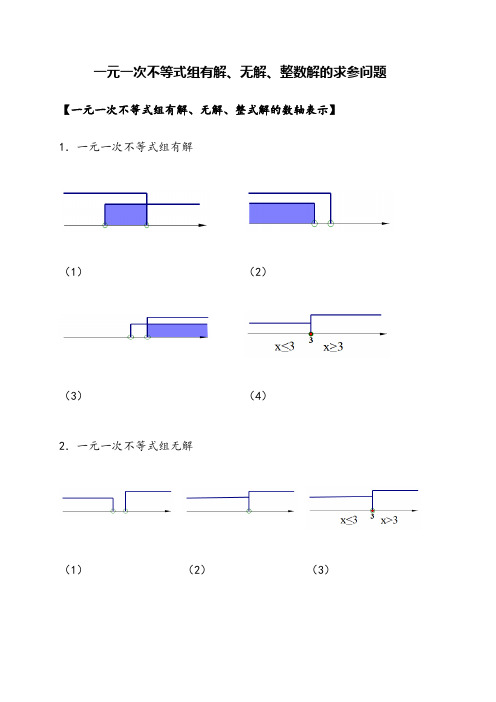
一元一次不等式组有解、无解、整数解的求参问题【一元一次不等式组有解、无解、整式解的数轴表示】1.一元一次不等式组有解(1)(2)(3)(4)2.一元一次不等式组无解(1)(2)(3)3.一元一次不等式组整数解4.验证端点的取舍【总结】①解一元一次不等式②数形结合,画数轴分析③验证端点的取舍例1-a.一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为()A.x<﹣3B.x≥2C.﹣3<x≤2D.无解例2-a.如图表示的是某个关于x的一元一次不等式组解集,则此不等式组的解集是()A.x≥﹣3B.﹣3≤x<1C.x<1D.无解例3-b.若关于x的一元一次不等式组无解,则m的取值范围为()A.m>﹣B.m≤C.m<﹣D.m≥﹣例4-b.一元一次不等式组的解集是x>1,则m的取值范围是()A.m≥0B.m≤0 C.m>0D.m<0例5-b.一元一次不等式组的整数解的个数是.例6-b.若关于x的一元一次不等式组有解,则m的取值范围是.例7-b .一元一次不等式组有5个整数解,则a 的取值范围是 .例8-a .关于x 的一元一次不等式组⎩⎨⎧><mx x 3有解,求m 的取值范围.例9-c .关于x 的一元一次不等式组⎩⎨⎧-≥-≥-1230x a x ,(1)有解,求a 的取值范围. 变式:(2)有五个整数解,求a 的取值范围.例10-b .关于x 的一元一次不等式组⎩⎨⎧>-≥+mx x x 148无解,求m 的取值范围.例11-b .关于x 的一元一次不等式组⎩⎨⎧->+<121m x m x 无解,求m 的取值范围.例12-b .关于x 的一元一次不等式组⎪⎩⎪⎨⎧>+<--x x a x x 422)2(3有解,求a 的取值范围.例13-b .现场学习:我们学习了由两个一元一次不等式组成的不等式组的解法,知道可以借助数轴准确找到不等式组的解集,即两个不等式的解集的公共部分.解决问题:解不等式组并利用数轴确定它的解集;拓展探究:由三个一元一次不等式组成的不等式组的解集是这三个不等式解集的公共部分.(1)直接写出的解集为;(2)已知关于x的不等式组无解,则a的取值范围是.。
不等式含参题型及解题方法初一下册

不等式含参题型及解题方法初一下册初一下册学习数学时,不等式含参题型是一个重要的知识点。
学生需要掌握不等式的性质和解题方法,以便能够熟练地解决各种不等式问题。
本文将深入探讨不等式含参题型及解题方法,希望能够帮助学生更好地理解和掌握这一知识点。
一、不等式含参题型的基本概念不等式含参题型是指在不等式中含有未知数的题型。
通常情况下,不等式含参题型可以用代数的方法解决。
学生在解题时需要根据不等式的性质和解题方法进行分析和推演,最终得出解的过程。
不等式含参题型有以下几种常见形式:1.一元一次不等式:形如ax+b>c或ax+b≤c的不等式,其中a、b、c为常数,x为未知数。
2.一元二次不等式:形如ax^2+bx+c>0或ax^2+bx+c≥0的不等式,其中a、b、c为常数,x为未知数。
3.绝对值不等式:形如|ax+b|<c或|ax+b|≥c的不等式,其中a、b、c为常数,x为未知数。
二、不等式含参题型的解题方法解不等式的关键在于将不等式化为可以比较大小的形式,并找出未知数的取值范围。
下面将分别介绍解一元一次不等式、一元二次不等式和绝对值不等式的方法。
1.解一元一次不等式解一元一次不等式的方法主要有两种:用图形法和用代数法。
(1)图形法:将不等式对应的不等式式画出来,从图像上找出解集。
(2)代数法:通过代数运算和不等式的性质将不等式化为常见的形式,找出解的范围。
2.解一元二次不等式解一元二次不等式的方法通常采用代数法。
(1)先将不等式移项,将不等式转化为二次函数的问题。
(2)通过判别式求解二次不等式的解集,得出解的范围。
3.解绝对值不等式解绝对值不等式的方法也通常采用代数法。
(1)将绝对值不等式根据不同情况进行讨论:当ax+b≥0时,|ax+b|=ax+b;当ax+b<0时,|ax+b|=-(ax+b)。
(2)进一步化简绝对值不等式,得出解的情况。
三、不等式含参题型的解题技巧在解不等式含参题型时,学生可以借助一些解题技巧来提高解题效率和准确性。
专题8.5 不等式中含参问题【十大题型】(举一反三)(华东师大版)(解析版)

专题8.5不等式中含参问题【十大题型】【华东师大版】【题型1根据一元一次不等式的解(集)求参数】 (1)【题型2根据一元一次不等式组的解集求参数】 (3)【题型3根据一元一次不等式有最值解求参数】 (5)【题型4根据一元一次不等式(组)的整数解的个数求参数】 (8)【题型5根据一元一次不等式组有解或无解求参数】 (10)【题型6根据一元一次不等式组的整数解的和求参数】 (12)【题型7根据一元一次不等式组无整数解求参数】 (14)【题型8一元一次方程与不等式(组)综合求参数】 (16)【题型9二元一次方程组与不等式(组)综合求参数】 (19)【题型10新定义问题与不等式综合求参数】 (22)【题型1根据一元一次不等式的解(集)求参数】【例1】(2023春·江苏·七年级统考期末)已知关于的不等式B+>0的解集为<12,则不等式−3+ <0的解集是.【答案】<5.【分析】不等式B+>0的解集是<12,判断出a<0且−=12则可以得到>0,得到=−2再解出不等式−3+<0的解集即可.【详解】解:∵不等式B+>0的解集是<12根据不等式的性质可知,当>0时,不等式的解集为>−不符合题意∴可以判断出<0,即不等式的解集为<−∴−=12,即>0且=−2−3+<0即−3<−,则<3−=3+2=5∴不等式的解集为<5故答案为:<5.【点睛】本题考查了不等式的解集,熟悉不等式的性质是解题的关键.【变式1-1】(2023春·四川南充·七年级统考期末)已知关于x的不等式ax+b>0的解集为<13,则不等式bx+a<0的解集是.【答案】<3【分析】根据已知不等式的解集确定出a与b的关系,用b表示出a,代入所求不等式求出解集即可.【详解】解:∵关于x的不等式ax+b>0的解集为x<13,∴−=13且a<0,整理得:a=−3b,b>0,代入所求不等式得:bx−3b<0,解得:x<3.故答案为:x<3.【点睛】此题考查了解一元一次不等式,熟练掌握不等式的基本性质是解本题的关键.【变式1-2】(2023春·江苏镇江·七年级统考期末)若实数3是不等式3+2<−3的一个解,则可取的最大整数是()A.−1B.2C.−3D.3【答案】C【分析】解不等式可得<−6−9,结合题意“实数3是不等式3+2<−3的一个解”,可得−6−9>3,解该不等式即可获得答案.【详解】解:由不等式3+2<−3,得<−6−9,∵实数3是不等式3+2<−3的一个解,∴−6−9>3,解得<−2,∴可取的最大整数为−3.故本题选:C.【点睛】本题主要考查了一元一次不等式的应用以及解一元一次不等式,结合题意得到不等式−6−9>3是解题关键.【变式1-3】(2023春·全国·七年级期末)已知关于x的一元一次不等式K22+2<2r33与2﹣x<0的解集相同,则m=.【答案】23【分析】首先计算出两个不等式的解集,再根据题意可得-6m+6=2,再解即可.【详解】解:∵2﹣x<0∴x>2−22+2<2+333−2+12<22+33x-6m+12<4x+6,解得:x>-6m+6,∵关于x的一元一次不等式K22+2<2r33与2﹣x<0的解集相同∴-6m+6=2,解得:=23故答案为:23【点睛】此题主要考查了不等式的解集,关键是正确确定两个不等式的解集.【题型2根据一元一次不等式组的解集求参数】【例2】(2023春·广西贺州·七年级校考期中)已知不等式组+2>+−1<−1的解集为−1<<2,则+ 2023=.【答案】1【分析】先求出两个不等式的解集,再根据不等式组的解集列出关于、的方程,然后求出、的值,最后代入代数式进行计算即可得解.【详解】解:+2>+s−1<−1②,解不等式①得,>+−2,解不等式②得,<,所以不等式组的解集是+−2<<,∵不等式组的解集为−1<<2,∴+−2=−1=2,解得=2=−1,∴+2023=(2−1)2023=1.故答案为:1.【点睛】本题主要考查了一元一次不等式组解集的求法、解二元一次方程以及代数式求值,根据不等式组的解集列出关于、的方程是解题的关键.【变式2-1】(2023春·河南南阳·七年级统考期末)已知是使不等式组<+1>2−1无解的最小整数,请你解关于,的方程组8−3=−−7−3=3+7.【答案】=−1=−2【分析】先根据不等式组无解得出2−1≥+1,解之得≥2,再结合是使不等式组无解的最小整数知=2,从而还原方程组,利用加减消元法求解即可.【详解】解:由题意得2−1≥+1,解得≥2,所以最小整数=2,代入原方程组,得8−3=−2 ①−7−3=13 ②由①−②,得15=−15,解得=−1.把=−1代入①,得=−2.所以原方程组的解为=−1=−2.【点睛】本题主要考查一元一次不等式组的整数解,解题的关键是根据不等式组无解得出的值,并熟练掌握解一元一次不等式组和二元一次方程组的能力.【变式2-2】(2023春·浙江宁波·七年级浙江省余姚市实验学校校考期末)试求出所有的实数对a、b,使得关于x的不等式组B+3>2+43B−4<−5+1的解集为2<<5.【答案】 =52=−43【分析】先解不等式组,再由不等式组B+3>2+43B−4<−5+1的解集为2<<5,转化成关于a,b的方程组来解即可.【详解】解:不等式组B+3>2+4①3B−4<−5+1②由①得−2>1,由②得,3+5<5,∵不等式组B+3>2+43B−4<−5+1的解集为2<<5∴−2≠0,3+5≠0∴当>2,>−53时,有>1K2,<53r5,当<2,<−5时,有<1K2,>53r5,2 3r5=55 3r5=2,∴解得 =52=−43或 =115=−56(<2,<−53,不符合舍去)∴实数对a、b为 =52=−43.【点睛】此题考查不等式组和二元一次方程组的解法,解题关键在于要灵活运用运算法则.【变式2-3】(2023春·河南南阳·七年级统考期末)已知不等式组2+1≥−1−+2≥2(−1),要使它的解集中的任意x的值都能使不等式3≥+3成立,则m的取值范围是.【答案】≤−9【分析】解不等式组得到解集,结合3≥+3成立列式求解即可得到答案;【详解】解:分别解不等式得,≥−2,≤43,∴−2≤≤43,∴−6≤3≤4,∵3≥+3,∴+3≤−6,解得:≤−9,故答案为:≤−9;【点睛】本题考查解不等式组及根据解集求参数,解题的关键是正确的求出不等式组的解集.【题型3根据一元一次不等式有最值解求参数】【例3】(2023春·江苏·七年级阶段练习)若不等式2<1−3的解集中所含的最大整数为4,则a的范围为.【答案】-3≤a<-73.【分析】先求出不等式的解集,根据解集中所含的最大整数为4,求出a的取值范围即可.【详解】2x<1-3a,x<1−32,∵解集中所含的最大整数为4,∴4<1−32≤5,解得:-3≤a<-73,故答案为-3≤a<-73.【点睛】本题考查了解一元一次不等式,解一元一次不等式组,一元一次不等式的整数解的应用,解此题的关键是能求出关于a的不等式组,难度适中.【变式3-1】(2023春·安徽六安·七年级校联考期中)关于x的不等式3−+2>0的最小整数解为2,则实数m的取值范围是()A.5≤<8B.5<<8C.5≤≤8D.5<≤8【答案】A【分析】解出不等式,然后根据不等式的最小整数解为2,即可列出关于m的不等式,从而求出m的取值范围.【详解】解:解不等式3−+2>0,得>K23,∵不等式的最小整数解为2,∴1≤K23<2,解得5≤<8,故A正确.故选:A.【点睛】此题主要考查的是含参数的一元一次不等式,掌握根据不等式的最小整数解求参数的取值范围是解决此题的关键.【变式3-2】(2023春·全国·七年级专题练习)若关于x的不等式2x﹣3a+2≥0的最小整数解为5,则实数a 的值为【答案】103<a≤4【分析】先将a看作常数解不等式,根据最小整数解为5,得4<3K22≤5,解出即可.【详解】解不等式2x-3a+2≥0得x≥3K22,∵不等式的最小整数解为5,∴4<3K22≤5,∴103<a≤4,故答案为103<a≤4.【点睛】本题考查了一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.【变式3-3】(2023春·湖北武汉·七年级校考期末)已知关于x的不等式x﹣a<0的最大整数解为3a+6,则a=.【答案】−103【分析】求出不等式的解集,根据已知得出3+6<≤3+7,求出−3.5≤<−3,设=3+6,则= 13−2,得出不等式组−3.5≤13−2<−3,求出即可.【详解】解:解不等式−<0得:<,∵关于的不等式−<0的最大整数解为3+6,∴3+6<≤3+7,解得:−3.5≤<−3,∵3+6为整数,设=3+6,则=13−2,即−3.5≤13−2<−3,解得:−4.5≤<−3,∵为整数,∴=−4,即=13×(−4)−2=−103,故答案为:−103.【点睛】本题考查了一元一次不等式的整数解,解此题的关键是得出关于的不等式组.【题型4根据一元一次不等式(组)的整数解的个数求参数】【例4】(2023春·辽宁沈阳·七年级统考期中)已知关于的不等式组K2≥2−4≤3−2的最小整数解是2,则实数的取值范围是()A.−3≤<−2B.−3<≤−2C.−3<<−2D.−3≤≤−2【答案】B【分析】分别求出每一个不等式的解集,根据口诀:同大取大及不等式组的最小整数解求解即可.【详解】解:解不等式K2≥2,得:x≥4+m,解不等式x−4≤3(x−2),得:x≥1,∵不等式组的最小整数解是2,∴1<4+m≤2,解得−3<m≤−2,故选:B.【点睛】本题考查的是一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.【变式4-1】(2023春·江西赣州·七年级统考期末)若关于x的不等式x﹣a>0恰好有两个负整数解,则a 的范围为.【答案】﹣3≤a<﹣2.【分析】首先解不等式,然后根据条件即可确定a的值.【详解】解:∵x−a>0,∴x>a,∵不等式x−a>0恰有两个负整数解,则其负整数解为-1、-2且-3不是负整数解∴a的取值范围为:−3≤a<−2故答案为:−3≤a<−2.【点睛】本题主要考查含参的一元一次不等式的解法,含参的不等式指的是不等式未知数的系数或常数项用字母表示的不等式,利用分类讨论及数形结合思想,可结合数轴,解决含参不等式.【变式4-2】(2023春·云南曲靖·七年级统考期末)若关于的不等式2−≥0的负整数解为−1,−2,−3,则的取值范围是.【答案】−8<≤−6【分析】首先解不等式求得解集,然后根据不等式只有负整数解为-1,-2,-3,得到关于m的不等式,求得m的范围.【详解】解:∵2x-m≥0,∴2x≥m,∴x≥2.则-4<2≤-3,解得:-8<m≤-6.故答案为:-8<m≤-6.【点睛】此题考查了根据不等式解集的情况求参数的取值范围,根据x的取值范围正确确定2的范围是解题的关键.【变式4-3】(2023春·四川宜宾·七年级统考期末)若关于x的一元一次不等式组+1≥03−<0,有3个非负整数解,则m的取值范围是()A.6<≤9B.6≤<9C.2<≤3D.2≤<3【答案】A【分析】表示出不等式组的解集,根据解集中有3个非负整数解,确定出m的范围即可.【详解】解:不等式组整理,得:≥−1<3,解得:−1≤<3,∵不等式组有3个非负整数解,即非负整数解为0,1,2,∴2<3≤3,解得:6<≤9.故选:A.【点睛】此题考查了一元一次不等式组的整数解,熟练掌握不等式组的解法是解本题的关键.【题型5根据一元一次不等式组有解或无解求参数】【例5】(2023春·吉林松原·七年级校联考期中)若不等式组1<≤2>无解,则的取值范围是()A.≥2B.<1C.≤2D.1≤<2【答案】A【分析】由已知不等式组无解,确定出k的范围即可.【详解】解:∵不等式组1<≤2>无解,∴k的范围为k≥2,故选:A.【点睛】此题考查了不等式组的解集,熟练掌握确定每个不等式的解集是解本题的关键.【变式5-1】(2023春·重庆渝中·七年级重庆市求精中学校校考期中)不等式组2(+1)<3−6<4无解,则的取值范围是.【答案】≤2【分析】根据不等式组无解的条件确定出m的范围即可.【详解】不等式组整理得:>8<4,由不等式组无解,得到4≤8,解得:≤2,则的取值范围是≤2.故答案为:≤2.【点睛】本题考查了不等式的解集,弄清不等式组无解的条件是解本题的关键.【变式5-2】(2023春·广西梧州·七年级统考期末)关于的不等式组−>32+8>4有解且每一个的值均不在−2≤≤6的范围中,则的取值范围是()A.<1B.≤1C.1≤≤5D.≥5【答案】A【分析】求出不等式组−>32+8>4的解集,根据不等式组解集所处条件范围,列出关于a的不等式,解不等式可得答案.【详解】解:−>3①2+8>4t,解不等式①得:<−3,解不等式②得:>2−4,∴原不等式组的解集为:2−4<<−3,∵不等式组有解且每一个的值均不在−2≤≤6的范围中,∴2−4≥6或−3≤−2,解得:≥5或≤1,∵不等式组有解集,∴−3>2−4,解得:<1,综上,的取值范围是<1.故选:A.【点睛】本题主要考查了不等式组的解集,解一元一次不等式,掌握不等式的性质,逆向应用是本题的特点.【变式5-3】(2023春·安徽滁州·七年级校考期中)若关于>0>−1无解,且方程2−+1=−32−的解是非负数,则满足条件的整数的值有()个.A.1B.2C.3D.4【答案】C【分析】先分别求出不等式组中每一个不等式的解集,继而根据不等式组无解确定出a的范围,再解一元一次方程求出用含a的式子表示的x的值,进而根据方程解为非负数得到关于a的不等式,解不等式求出a的取值范围,进而即可确定出符合所有条件的整数a的值.>0①>−1②,由①得:x>a,由②得:x<1,由于不等式组无解,所以a≥1;解方程2−+1=−32−得x=7−22,由方程2−+1=−32−的解是非负数,则有7−22≥0,解得:a≤72,所以a的取值范围为1≤a≤72,所以满足条件的整数a为1、2、3,共3个,故选C.【点睛】本题考查了一元一次方程的解、不等式组无解问题,熟练掌握相关解法是解题的关键.【题型6根据一元一次不等式组的整数解的和求参数】【例6】(2023春·全国·七年级专题练习)已知关于x的不等式组{3x+<0>−5的所有整数解的和为-9,则m 的取值范围()A.3≤m<6B.4≤m<8C.3≤m<6或-6≤m<-3D.3≤m<6或-8≤m<-4【答案】C【分析】先求解不等式组,再根据条件判断出含参代数式的范围,从而求得参数的范围即可.【详解】解原不等式得:{<−3>−5,即−5≤<−3,由所有整数解的和为-9,可知原不等式包含的整数为-4,-3,-2或-4,-3,-2,-1,0,1,当整数为-4,-3,-2时,则−2<−3≤−1,解得:3≤<6,当整数为-4,-3,-2,-1,0,1时,则1<−3≤2,解得:−6≤<−3,故选:C.【点睛】本题考查含参不等式组求解问题,熟练掌握对含参代数式范围的确定是解题关键.【变式6-1】(2023春·湖南长沙·七年级统考期末)若关于的不等式组3−2<5+4≤−1的所有整数解的和为0,则的值不可能是()A.3B.3.2C.3.7D.4【答案】D【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后根据整数解的和为0,确定整数解,即可求得的取值范围.【详解】解:3−2<5+4①≤−1②,解①得>−3,解②得≤−1,∵所有整数解的和为0,∴整数解是−2,−1,0,1,2,∴2≤−1<3,解得:3≤<4,∴的值不可能是4,故选:D.【点睛】本题考查了一元一次不等式组的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.【变式6-2】(2023春·安徽亳州·七年级校考阶段练习)已知不等式组r1310 +5r43>+1+的正整数解为=1和2,求的取值范围.【答案】1<≤32【分析】先求解一元一次不等式组,再根据题意建立关于参数的不等式即可求解.【详解】解:r13+12>0①+5r43>43+1+t解①得:>−52解②得:<2∵不等式组的正整数解为=1和2∴2<2≤3∴1<≤32【点睛】本题考查根据一元一次不等式组的解集情况确定参数的取值范围.注意计算的准确性.【变式6-3】(2023春·四川绵阳·七年级统考期末)若关于x≤−1−15s2>−12的最大整数解与最小整数解的和为−2,则满足条件的整数m的和为.【答案】27【分析】依据题意,解出不等式组的解集,然后再由最大整数解与最小整数解的和为−2,进而计算可以得解.≤−1−15s2>−12t,∴由①得,≤52;由②得,>2−12.∴原不等式组的解集为2−12<≤52.∴这个不等式组的最大整数解为2.又最大整数解与最小整数解的和为−2,∴这个不等式组的最小整数解为−4.∴−5≤2−12<−4.∴12<≤14.∴满足题意的整数有13,14.∴满足题意的整数的和为27.故答案为:27.【点睛】本题主要考查了一元一次不等式组的整数解,解题时要熟练掌握并理解是关键.【题型7根据一元一次不等式组无整数解求参数】【例7】(2023春·安徽安庆·七年级校考期中)已知关于的不等式组5−2>1>无整数解,则的取值范围是()A.≥1B.>1C.1<≤2D.>2【答案】A【分析】先求出不等式①的解集,根据不等式组无整数解即可得到答案.【详解】5−2>1①>t,解不等式①得x<2,∵不等式②知x>a,不等式组5−2>1>无整数解,∴≥1.故选:.【点睛】此题考查解一元一次不等式组,根据不等式组的解的情况求未知数的取值范围.【变式7-1】(2023春·上海·六年级校考阶段练习)关于的不等式组2−5<0−>0无整数解,则的取值范围为.【答案】≥2【分析】先分别求出两个不等式的解集为<52和>,再分两种情况:①≥52和②<52进行讨论即可得.【详解】解:由2−5<0−>0得:<52>,①当≥52时,原不等式组无解,符合题意;②如图,当<52时,要使原不等式组无整数解,则≥2,所以此时2≤<52;综上,≥2,故答案为:≥2.【点睛】本题考查了一元一次不等式组的解,熟练掌握不等式组的解法,正确分两种情况讨论是解题关键.【变式7-2】(2023春·安徽安庆·七年级统考期末)若不等式组2>3−33−<−6无正整数解,则a的取值范围为()A.a≤15B.a<9C.a<15D.a≤9【答案】D【分析】解一元一次不等式组【详解】2x>3x-3,3x-a>﹣6即x<3,x>(a−6)3因为不等式组无正整数解,所以不等式解集为x<1则(a−6)3≤1a-6≤3a≤9【点睛】掌握解一元一次不等式组的步骤:(1)求出这个不等式组中各个不等式的解集.(2)利用数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集.【变式7-3】(2023春·七年级单元测试)关于x的不等式组2+1><−3有解但是无整数解,则m的取值范围为.【答案】-7≤m<-5【详解】解:2+1>s<−3②.∵解不等式①得:x>K12.又∵关于x的不等式组2+1><−3有解但是无整数解,∴﹣4≤K12<﹣3,解得:﹣7≤m<﹣5.故答案为﹣7≤m<﹣5.点睛:本题考查了解一元一次不等式组,不等式组的整数解的应用,能求出关于m的不等式组﹣4≤K12<﹣3是解答此题的关键.【题型8一元一次方程与不等式(组)综合求参数】【例8】(2023春·全国·七年级期末)若关于的方程−2=3−2的解为非负数,且关于的不等式组−2−1≤32r3≥有解,则符合条件的整数值的和为()A.2B.3C.5D.6【答案】C【分析】根据关于的方程−2=3−2的解为非负整数,且关于的不等式组−2−1≤32r3≥有解,可以求得的取值范围,从而可以求得符合条件的整数的值的和,本题得以解决.【详解】解:由方程−2=3−2,得=3−,∵关于的方程−2=3−2的解为非负整数,∴3−≥0,得≤3,−2−1≤3①2r3≥②,由①,得≥−1,由②,得≤,∵关于的不等式组−2−1≤32r3≥有解,∴−1≤,得≥−1,由上可得,−1≤≤3,∴符合条件的整数的值为:−1,0,1,2,3,∴符合条件的整数的值的和为:−1+0−1+1+2+3=5.故选:C.【点睛】本题考查解一元一次方程、解一元一次不等式组、一元一次不等式组的整数解,解答本题的关键是明确解方程和不等式的方法.【变式8-1】(2023春·陕西安康·七年级统考期末)关于x的方程2−3=2+8的解是负数,求m的取值范围.【答案】<−112【分析】先解方程,用含m的代数式表示出x,根据解是负数得到关于m的不等式,解不等式即可.【详解】解:解方程2−3=2+8,得=+112,∵关于x的方程2−3=2+8的解是负数,∴=+112<0,∴<−112.【点睛】本题考查解一元一次方程和解一元一次不等式,解题的关键是用含m的代数式表示出x.【变式8-2】(2023春·甘肃兰州·七年级校考期中)若关于x的一元一次不等式组−2r34<22+7<4(+1)的解集为K32,且关于y的方程3−2=2K(5−3p2的解为非负整数,则符合条件的所有整数m的积为().A.2B.7C.11D.10【答案】D【分析】不等式组整理后,根据已知解集确定出m的范围,由方程有非负整数解,确定出m的值,求出之积即可.【详解】解:−2r34<2s2+7<4(+1)②,由①得:K310,由②得K32,由解集为K32,得到310≤32,即≤5,方程去分母得:6−4=2−5+3,即=2K13,由为非负整数,结合≤5且为整数,∴=5或=2,∴符合条件的所有整数m的积为2×5=10,故选D.【点睛】本题考查了解一元一次方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.【变式8-3】(2023春·河南洛阳·七年级统考期中)已知关于x的方程:K22−1=43+.(1)若方程的解是=3.那么=?(2)若该方程的解是负数,并且m是负整数,请你试求该方程的解.【答案】(1)=−412(2)=−65【分析】(1)把=3代入方程得到一个关于m的方程,求得常数即可;(2)求出关于x的方程,进一步探讨得出答案即可.【详解】(1)把=3代入K22−1=43+,得:12−1=4+,解得:=−412.(2)K22−1=43+去分母得,3−6−6=8+6,解得:=−12−65,∵<0,∴−12−65<0,∴>−2.∵m是负整数,∴=−1,∴=−65.【点睛】此题考查了方程解的定义和解方程的步骤与方法,注意审清题意,正确理解方程的解.【题型9二元一次方程组与不等式(组)综合求参数】【例9】(2023春·重庆·七年级统考期末)若关于x的不等式组K24<K134−≤4−恰有2个整数解,且关于x,y的方程组B+=43−=0也有整数解,则所有符合条件的整数m的和为()A.−2B.−3C.−6D.−7【答案】D【分析】表示出不等式组的解集,根据解集中恰有2个整数解,确定出m的范围,再由方程组有整数解,确定出满足题意的整数m的值,求出之和即可.【详解】解:不等式组整理得:>−2≤r45,解得:-2<x≤r45,∵不等式组恰有2个整数解,即-1,0,∴0≤r45<1,解得:-4≤m<1,即整数m=-4,-3,-2,-1,0,解方程组B+=43−=0得:=4r3=12r3,∵x,y为整数,∴m+3=±1或±2或±4,解得:m=-4或-2或-1,则m值的和为-4-2-1=-7.故选:D.【点睛】此题考查了一元一次不等式的整数解,以及二元一次方程组的解,熟练掌握各自的解法是解本题的关键.【变式9-1】(2023春·四川宜宾·七年级统考期末)若关于、的二元一次方程组+2=42+=3−(1)用含的代数式表示+.(2)若方程组的解满足−>−4,求的取值范围.(3)在(2)的条件下,若为正整数,求关于的方程B−1−2=5的解.【答案】(1)+=7−3(2)<3(3)=113或=115.【分析】(1)把两个方程相加,再利用等式基本性质,两边同时除以3即可;(2)解含有字母参数m的方程组,求出a,b,代入不等式进行解答即可;(3)根据已知条件,求出m,把m值代入方程,进行解答.【详解】(1)解:+2=4①2+=3−t,由①+②得:3+3=7−,∴+=7−3;(2)解:+2=4①2+=3−t,由②−①得:−=−1−,∵又−>−4,∴−1−>−4,解得:<3,∴的取值范围是<3;(3)解:由(2)得的取值范围是<3,为正整数,则为1或2,当=1时,关于的方程化为−1−2=5,解得:=113;当=2时,关于的方程化为2−1−2=5,解得:=115.【点睛】本题主要考查了二元一次方程组、一元一次不等式组及一元一次方程的解法,解题关键是熟练掌握解二元一次方程组、一元一次不等式组及一元一次方程.【变式9-2】(2023春·福建福州·七年级福建省福州屏东中学校考期末)已知关于x,y的方程组−3=4−+=3,其中−3≤≤1,若=−,则M的最小值为()A.−2B.−1C.2D.3【答案】B【分析】由①+②得x-y=2+t,将=−代入得t=M-2,再根据−3≤≤1可得−1≤≤3即可得出答案.【详解】解:−3=4−s+=3t①+②得2x-2y=4+2t即x-y=2+t,∵=−,∴M=2+t,∴t=M-2∵−3≤≤1,∴−3≤−2≤1即−1≤≤3∴M的最小值为-1故选:B.【点睛】本题考查含参二元一次方程组参数满足的条件求字母的最小值问题,用整体思想直接找到两个参数之间的关系是解题的关键.【变式9-3】(2023春·四川南充·七年级统考期末)关于,的方程组−=1+=6−7的解,都是非负数,如果2+=1,=+,那么的取值范围是.【答案】≤−13【分析】根据二元一次方程组的解法求出−=1+=6−7的解,再根据解的情况得到≥43,从而由2+= 1,=+得到=+=+1−2=1−,即可得到的取值范围.【详解】解:−=1①+=6−7②,①+②得:2=6−6,解得:=3−3,②−①得:2=6−8,解得:=3−4,∵关于,的方程组−=1+=6−7的解,都是非负数,∴3−3≥03−4≥0,解得:≥43,∴−≤−43,∵2+=1,即=1−2,∴=+=+1−2=1−,则的范围是≤1+−=−13,故答案为:≤−13.【点睛】本题考查解二元一次方程组、根据二元一次方程组解的情况求参数范围,熟练掌握二元一次方程组的解法、二元一次不等式组的解法、不等式的性质是解决问题的关键.【题型10新定义问题与不等式综合求参数】【例10】(2023春·江西景德镇·七年级统考期中)定义一种新运算max,规定:当>时,max s=;当=时,max s==;当<时,max s=.(1)max3,−1=______,max6,9=______;(2)若关于的方程,满足max3+2=r12,求的取值范围;(3)若关于的方程组max1,2+1=2+1,max s+3=2+s无解,求的取值范围.【答案】(1)3;9(2)≥9(3)<2【分析】(1)根据新定义求值即可;(2)根据新定义列不等式计算即可;(3)先根据新定义求出含参数的x的取值范围,再由无解求的取值范围.(1)∵3>-1,∴max3,−1=3∵9>6,∴max6,9=9(2)∵max3+2=r12∴r12≥3+2解得≥9(3)由max−1,2+1=2+1可得:2+1≥−1解得≥−2由max s+3=2+可得:2+≥+3解得:≤2−6∵关于的方程组B1,2+1=2+1,B+s+3=2+s无解,即≥−2≤2−6无解∴2−6<−2解得:<2【点睛】本题考查一元一次不等式应用,理解新定义,能将所求知识根据新定义转化为一元一次不等式求解是解题的关键.【变式10-1】(2023春·甘肃兰州·七年级校考期中)我们定义;如果两个一元一次不等式有公共解,那么称这两个不等式互为“云不等式”,其中一个不等式是另一个不等式的“云不等式”(1)不等式≥2≤2的“云不等式”:(填“是”或“不是”).(2)若关于的不等式+2≥0不是2−3<+1“云不等式”,求的取值范围.(3)若≠−1,关于的不等式+3>与不等式B−1≤−互为“云不等式”,求的取值范围.【答案】(1)是(2)<−32(3)<−1或−1<<4【分析】(1)根据云不等式的定义即可求解;(2)解不等式+2≥0可得≥−2,解不等式2−3<+1得<4,再根据云不等式的定义可得−2>3,解不等式即可求解;(3)分两种情况讨论,根据云不等式的定义得到含的不等式,解得即可.【详解】(1)解:∵不等式≥2和不等式≤2有公共整数解2,∴不等式≥2是≤2的“云不等式”,故答案为:是;(2)解:解不等式+2≥0可得≥−2,解不等式2−3<+1得<4,∵关于的不等式+2≥0不是2−3<+1的“云不等式”,∴−2>3,解得<−32.故的取值范围是<−32;(3)解:∵B−1≤−,∴B+≤+1,∴+1≤+1,①当+1>0时,即>−1时,+1≤+1的解集是≤1,∵+3>,∴>−3,由题可得−3<1,即<4,故−1<<4;②当+1<0时,即<−1时,+1≤+1的解集是≥1,此时始终符合题意,故<−1,综上所述:的取值范围为<−1或−1<<4.【点睛】本题主要考查了新定义运算,以及解一元一次不等式组,熟练掌握解一元一次不等式组解集的确定方法是解题的关键.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.【变式10-2】(2023春·湖北武汉·七年级统考期末)定义运算:s=B+B,已知2,3=7,3,4=10.(1)直接写出:=______,=______;(2)若关于的不等式组+1,2−≥02s−<0无解,求的取值范围;(3)若B+3s2−B≥3+4的解集为≤13,求不等式B−s3−B≥+的解集.【答案】(1)2;1(2)≤−20(3)≤139【分析】(1)根据定义的新运算,列出二元一次方程组,解方程组可求出,的值;(2)根据(1)求出的,的值和新运算列出一元一次不等式组,解不等式组并根据不等式组解集的情况可求出的取值范围;(3)根据(1)求出的,的值和新运算列出一元一次不等式,根据解集为≤13可得出与的数量关系;再根据,的值和新运算列出一元一次不等式求解即可.【详解】(1)解:由题意得:2+3=73+4=10,解得:=2=1,故答案为:2;1;(2)把=2,=1代入s=B+B得s=2+,∴不等式组+1,2−≥02s−<0可转化为2+1+2−≥02×2+−<0,解得:≥−4<5,∵关于的不等式组+1,2−≥02s−<0无解,∴5≤−4,解得:≤−20,∴的取值范围是≤−20;(3)不等式B+3s2−B≥3+4转化为2B+3+2−B≥3+4,整理,得:2−≥−2,∵B+3s2−B≥3+4的解集为≤13,∴2−<0,解得:≤K22K,∴K22K=13,∴=5,∴2×5−<0,解得:<0,不等式B−s3−B≥+转化为2B−+3−B≥+,整理,得:2−≥3−2,。
人教版初中数学七年级下册第9章一元一次不等式(组)含参专题——有、无解问题(专题课)教案

人教版初中数学七年级下册第九章一元一次不等式(组)含参专题——有、无解问题(专题课)教案核心素养:1.使学生加深对一元一次不等式组和它的解集的理解,会用数轴确定含参数的一元一次不等式组的参数范围;2.培养学生探究、独立思考的学习习惯,感受数形结合的作用,熟悉并掌握数形结合的思想方法,提高分析问题和解决的能力;3.提升学生之间合作与交流以及对问题的探讨能力,从中发现数学的乐趣.【教学重难点】重点:含参一元一次不等式组的分类解法难点:1.一元一次不等式中字母参数的讨论2.一元一次不等式中运用数轴分析参数的范围【教学过程】1.问题引导 合作交流出示问题:请同学们解下列两个不等式(1)x-2m<0,(2)x+m >3并思考m 的取值范围. 同学们不难得出不等式(1)的解为x <2m ;(2)的解为x >3-m.引导分析m 的取值范围. 师引导,生回答:任意实数.[问题1]如果将上述两个不等式联立成不等式组⎩⎨⎧>+<-302m x m x ,你能确定不等式组的解集吗? 师提示学生画数轴 ,问:能画几种情况[问题2]如果这个不等式组无解,你能确定m 的取值范围吗?(学生分组讨论)(借助数轴)师生一起分析:如果不等式组无解,则2m <3-m ,解得m <1。
确定一下“<”要不要添加“=”(这是参数取值问题中的难点)学生借助数轴讨论.师生总结:2m 和3-m 在两个不等式的解中都不包含,所以2m 可以等于3-m ,即m ≤1.2.变式拓展 强化理解变式1:若不等式组⎩⎨⎧⋅⋅⋅⋅⋅>+⋅⋅⋅≤-②①302m x m x 无解,这时m 的取值会有变化吗?解不等式①得x ≤2m 解不等式②得x >3-m(学生分组探究)引导:虽然第一个不等式“<”改成“≤”通过数轴可以看到由于和第二个不等式的解集不包含3-m ,所以2m ≤3-m ,m 的取值范围仍然是m ≤1.变式2:如果不等式组变化为⎩⎨⎧⋅⋅⋅⋅⋅≥+⋅⋅⋅≤-②①302m x m x ,这时m 的取值又会有改变吗?(学生分组探究)由于两个不等式都含有等号,这时2m 和3-m 可能是公共点,而要想使不等式组无解,2m 和3-m 不能重合,只能2m <3-m ,所以m 不能等于1,即m <1.3.问题反转[问题3]如果不等式组⎩⎨⎧⋅⋅⋅⋅⋅≥+⋅⋅⋅≤-②①302m x m x 有解,怎样确定 m 的取值范围?把两个不等式的解集在数轴上表示出,同学们观察数轴 ,不难得出要想使不等式组有解,只要2m ≥3-m ,即m ≥1这样两个不等式的解集有公共部分,不等式组有解,所以m 的取值范围m ≥14.方法小结 归纳步骤解含参一元一次不等式(组)有、无解问题时注意掌握四个步骤:一解 .解不等式组,用参数分别表示出两个不等式的解集;二画.借助数轴进行视觉观察,画出有无解的情况;三验:验证端点取舍判断等号是否可取;四:列出不等式,确定取值范围5,拓展演练 题型再变[问题4]下面这种类型的一元一次不等式组如何确定字母参数取值范围?例:已知不等式组⎩⎨⎧⋅⋅⋅-<⋅⋅⋅⋅⋅⋅⋅⋅≥-②①22-10x x a x 的解集是x >1,求a 的取值范围?学生分组解出每个不等式的解集:解①得:x ≥a 解②得:x >1因为不等式的解集是x >1,(学生分组探讨):a 的位置在数轴上应该在哪个位置? 分析得出:a 在数轴上的位置应该在1的左侧.把不等式组的解集在数轴上表示出来:即a <1,[思考3]a 可不可以等于1?因为a=1时不等式组的解集仍然是x >1.所以a 可以等于1,即a 的取值范围a ≤15.基础过关1.若不等式组⎩⎨⎧≤≥-m x x 062 无解,求m 的取值范围? 2.若不等式组⎩⎨⎧>+<--xx a x x 422)2(3有解,求a 的取值范围?3.若不等式组⎩⎨⎧+>+<+1137m x x x 的解集是x >3,求m 的取值范围?。
专题11 一元一次不等式(组)中的参数问题(原卷版)

七年级数学下册解法技巧思维培优专题11 一元一次不等式(组)中的参数问题题型一 解集求参数的值【典例1】〔2021•綦江区期末〕假设不等式组{x +2a >32x −b <1解集为1<x <2,那么〔a +2〕〔b ﹣1〕值为 .【点拨】首先解不等式组求得不等式组的解集,然后根据不等式组的解集即可求得a 、b 的值,然后代入代数式求值即可.【典例2】〔2021•巴南区期中〕如果关于x 的不等式组{x−m2>0x−23−x <−2的解集为x >2,且式子√3−|m|的值是整数,那么符合条件的所有整数m 的个数是〔 〕 A .5B .4C .3D .2【点拨】先解不等式组,得出m ≤2,再由式子√3−|m|的值是整数,得出|m |=3或2,于是m =﹣3,+3,﹣2,2,由m ≤2,得m =﹣3,﹣2,2.题型二 解集的情况求参数的取值范围【典例3】〔2021•鄂州一模〕假设关于x 的不等式组{2x >3x −33x −a >5有实数解,那么a 的取值范围是〔 〕A .a <4B .a ≤4C .a >4D .a ≥4【点拨】分别求出各不等式的解集,再根据不等式组有实数解即可得到关于a 的不等式,求出a 的取值范围即可.【典例4】〔2021•滨湖区校级期末〕设关于x 的不等式组{2x −m >23x −2m <−1无解,求m 的取值范围.【点拨】先解每个不等式,再根据不等式组{2x −m >23x −2m <−1无解,推出m 的值.题型三 整数解的情况求参数的值或取值范围【典例5】〔2021•万州区期末〕使得关于x 的不等式组{−x2≤−m2+1−2x +1≥4m −1有解,且使得关于y 的方程1+〔m﹣y 〕=2〔y ﹣2〕有非负整数解的所有的整数m 的个数是〔 〕 A .0个B .1个C .2个D .3个【点拨】根据关于x 的不等式组{−x2≤−m2+1−2x +1≥4m −1有解,可以求得m 的取值范围,再根据关于y 的方程1+〔m ﹣y 〕=2〔y ﹣2〕有非负整数解可以求得m 的值,从而可以解答此题.【典例6】〔2021•西城区校级期中〕如果关于x 的不等式组{2x+23<x +a x+52>x −3只有3个整数解,求a 的取值范围. 【点拨】首先利用不等式的根本性质解不等式组,再从不等式的解集中找出适合条件的整数解,在确定字母的取值范围即可.【典例7】〔2021•东营模拟〕关于x 的不等式组{4(x −1)+2>3x x −1<6x+a 7,有且只有三个整数解,求a 的取值范围.【点拨】先解两个不等式得到x >2和x <a +7,由于不等式组有解,那么2<x <a +7,由不等式组有且只有三个整数解,所以5<a +7≤6,然后在解此不等式组即可.【典例8】〔2021•大石桥市校级月考〕假设关于x 的不等式组{x+152>x −32x−23>x +a 的正整数解只有2个,求a 的取值范围.【点拨】首先解两个不等式,根据不等式有两个正整数解即可得到一个关于a 的不等式组,从而求得a 的范围.稳固练习1.〔2021•百色〕不等式组{12−2x <203x −6≤0的解集是〔 〕A .﹣4<x ≤6B .x ≤﹣4或x >2C .﹣4<x ≤2D .2≤x <4 2.〔2021•济南二模〕假设关于x 的不等式组{2x +7>4x +1x −k <2的解集为x <3,那么k 的取值范围为〔 〕A .k >1B .k <1C .k ≥1D .k ≤13.〔2021•沙坪坝区校级期末〕如果关于x 的不等式组{x−m2≥2x −4≤3(x −2)的解集为x ≥1,且关于x 的方程m3−1−x 3=x ﹣2有正整数解,那么所有符合条件的整数m 的值之和是〔 〕A .﹣3B .﹣4C .﹣8D .﹣94.〔2021•道外区期末〕不等式组{5−2x ≥1−2x <4的解集是 .5.〔2021•成都校级月考〕求不等式组{1−(x −2)>05x+12+1≥2x−13的正整数解.6.〔2021•松桃县期末〕求不等式组{2x −6<6−2x 2x +1>3+x 2的整数解.7.〔2021•邻水县期末〕是否存在整数k ,使方程组{2x +y =kx −y =1的解中,x 大于1,y 不大于1,假设存在,求出k 的值,假设不存在,说明理由.。
一元一次不等式组中的参数问题(学生版)

一元一次不等式组中的参数问题1.已知关于x的不等式组220x ab x->⎧⎨->⎩的解集为11x-<<,则a b+为.2.已知不等式组122x ax b+>⎧⎨-<⎩的解集为23x-<<,则2023()a b-的值为.3.不等式组6321x xx m+<+⎧⎨+>⎩的解集是2x>,则m的取值范围是.4.若关于x的不等式组313232()x xa x x a-⎧-⎪⎨⎪+-<-⎩,的解集为3x,则a的取值范围是.5.若不等式组123x ax a->⎧⎨->⎩的解集是1x a>+,则a的取值范围是.6.不等式组5335x xx a-<+⎧⎨<⎩的解集为4x<,则a满足的条件是.7.若数m使关于x的不等式组5()02132x mx x-⎧⎪+⎨->⎪⎩的解集为2x<-,且使关于y的方程36422mm y-=+的解为负整数,则符合条件的所有整数m的和为8.若不等式组11233x xx m+⎧<+⎪⎨⎪>⎩有解,则m的取值范围为.9.关于x的一元一次不等式组35128xx a-⎧⎨+<⎩有解,则a的取值范围是.10.若关于x的一元一次不等式组2012x mx-<⎧⎨+⎩无解,则m的取值范围为.11.若关于x的不等式组122x ax x-⎧⎨--⎩无解,则a的取值范围是.12.关于x的不等式组3284a xx a->⎧⎨+>⎩有解且每一个x的值均不在26x-的范围中,则a的取值范围是.13.已知关于x的不等式组12xx m+⎧⎨-<⎩有3个整数解,则m的取值范围是.14.关于x 的不等式组35241x m x x >+⎧⎨-<+⎩的整数解仅有4个,则m 的取值范围是 . 15.若关于x 的不等式组2()213x x a x x <-⎧⎪⎨-⎪⎩恰有3个整数解,则a 的取值范围是 . 16.不等式组633()31722x x a x x +>+⎧⎪⎨--⎪⎩的所有整数解的和为9,则整数a 的值有 . 17.若关于x 的一元一次不等式组22232()0x x x m +⎧-⎪⎨⎪-<⎩的所有整数解的和是9-,则m 的取值范围是 . 18.已知关于x 的不等式组53(1)217x a x x --⎧⎨-⎩的所有整数解的和为7,则a 的取值范围为 . 19.已知不等式组1x x a ⎧⎨<⎩至少有两个整数解,则a 的取值范围是 . 20.已知关于x 的不等式组()5131138222x x x x a +>-⎧⎪⎨-+⎪⎩①②至少有三个整数解,则整数a 的最小值是 . 21.若关于x 的不等式组2(2)2122x x k x x ---<⎧⎪⎨--+⎪⎩最多有2个整数解,且关于y 的一元一次方程3(1)2()7y y k ---=的解为非正数,则符合条件的所有整数k 的和为 .22.若关于x 的不等式组101155112x x x m -⎧--⎪⎪⎨⎪->-⎪⎩的最大整数解与最小整数解的和为2-,则满足条件的整数m 的和为 .23.若整数a 使关于x 的不等式组12539123x x x a x a ++⎧⎪⎪⎨--+⎪>⎪⎩至少有3个整数解,且使关于y ,z 的方程组2424ay z y z +=-⎧⎨+=⎩的解为非负整数,那么满足条件的所有整数a 的和是 . 24.如果关于x 的不等式组312364x x x a +⎧-⎪⎨⎪+>+⎩有且只有5个整数解,且关于y 的方程3622y a y +=-的解为非负整数,则符合条件的所有整数a 的和为 .。
一元一次不等式组含参问题

一元一次不等式组含参问题一元一次不等式组含参问题是指在一元一次不等式组中引入一个或多个参数,求解参数使得不等式组成立或不成立的问题。
解决这类问题的一般方法是通过对参数的取值范围进行讨论,将不等式系统转化为关于参数的方程或不等式,然后解方程或不等式来确定参数的取值范围。
下面通过几个例子来说明如何解决一元一次不等式组含参问题。
【例1】求参数m的取值范围,使得不等式组 3x - 2 < mx + 1和 2x + 3 < 4m + 1 同时成立。
解:首先,我们可以通过将不等式组化简来得到关于参数m的方程组,然后解方程来确定参数的范围。
将不等式组化简得到:3x - mx < 3 + 2 和 2x - 4m < -2。
化简后的不等式组可以写成关于参数m的方程组:3 - m > 0和 -4m - 2 < 2x。
解这个方程组可以得到参数m的取值范围。
对不等式3 - m > 0,我们可以将m移到左边得到m < 3。
因此,参数m的取值范围是m < 3。
这是因为当m小于3时,不等式3 - m > 0成立。
对于不等式-4m - 2 < 2x,我们可以将m移到右边得到2x > -4m - 2,再除以2得到x > -2m - 1。
这说明在参数m小于3时,也必须满足x > -2m - 1,才能使得不等式组成立。
综上所述,参数m的取值范围是m < 3,并且在这个范围内,x > -2m - 1。
【例2】求参数a的取值范围,使得不等式组 2x + a - 1 < 3 和5 - 3x < 2a 同时成立。
解:首先,我们可以通过将不等式组化简来得到关于参数a的方程组,然后解方程来确定参数的范围。
化简不等式组得到:a + 2x < 4 和 3x + 5 < 2a。
化简后的不等式组可以写成关于参数a的方程组:a - 4 < -2x和 2a - 3x > 5。
一元一次不等式(组)含参问题探究

一元一次不等式(组)含参问题类型一、已知解集求参数1.若不等式组⎩⎨⎧->+<-3212b x a x 的解集是225<<-x ,求代数式)1)(1(+-ab a b 的值.2.若关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧-<+-<+x x m x 23212的解集是1-<x ,且关于y 的方程m m y 31)(2=-+的解为正整数,求m 的值.类型二、已知解集的情况求参数的取值范围3.若关于x 不等式组⎪⎪⎩⎪⎪⎨⎧≥-+>+-2312121x x m x 无解,求m 的取值范围.4.若关于x 不等式组⎪⎪⎩⎪⎪⎨⎧>+--<++`2122121m x x m x 有解,且23关于y 的不等式122332--≥-y m y 的解,求m 的取值范围.类型三、已知整数解的情况求参数的值或取值范围5.若关于x 不等式组⎩⎨⎧-<++->-1237)1(2m x x x 无正整数解,求m 的取值范围.6.若关于x 不等式组⎪⎪⎩⎪⎪⎨⎧+≥--+<+121312x x a x x 有且只有4个整数解,求a 的取值范围.7.若关于x 不等式组⎪⎪⎩⎪⎪⎨⎧+>+-≥-21231202x x x m 至少有3个整数解,求m 的取值范围.类型四、已知范围满足解集的情况求参数的范围8.若31<<x 满足关于x 的不等式组⎪⎩⎪⎨⎧--<-+≥+122112x m x x m x ,求m 的取值范围.跟踪训练:1.4≤x 是不等式13≤-a x 的解集,求a .2.关于x 的方程k k x -=-233的解不小于2,求k 的取值范围.3.已知关于y x ,的方程组⎩⎨⎧+=++=-9335a y x a y x 的解满足y x ≥+2,求a 的取值范围.4.关于x 的不等式4<x 是不等式2522<-a x 的解集,求a 的值.5.若不等式组⎩⎨⎧-≤-≥322m x m x 无解,求m 的取值范围.6.若不等式组⎩⎨⎧+<->52n x m x 的解集为31<<x ,求n m +的值.7.若1)1(+>+k x k 的解集为1<x ,求k 的取值范围.。
一元一次不等式含多个参数问题

一元一次不等式含多个参数问题引言一元一次不等式含多个参数是数学中常见的问题。
通过对不等式中的参数进行约束,我们可以确定不等式的范围,从而解决实际问题。
本文将介绍一元一次不等式含多个参数的基本概念和求解方法。
基本概念一元一次不等式含多个参数通常具有以下形式:$a_1x + a_2y + a_3z + ... \le b$,其中 $a_1, a_2, a_3, ...$ 是参数,$x, y, z, ...$ 是变量,$b$ 是常数。
求解方法要求解一元一次不等式含多个参数,我们可以采用以下步骤:1. 确定参数的取值范围:根据实际问题,确定参数的取值范围。
这可以根据物理意义、限制条件或经验得出。
2. 构造不等式:根据所给的条件和问题要求,将问题抽象化为一元一次不等式含多个参数的形式。
3. 解不等式:根据不等式的符号和参数的取值范围,可以通过简单的代数运算或图形法求解不等式。
4. 验证解的合理性:得到不等式的解后,需要将解带回原始问题进行验证,确保解在问题的范围内且符合实际意义。
实例分析以下是一个实例分析,展示如何求解一元一次不等式含多个参数的问题。
问题:某公司生产两种产品A和B,产品A需要5个资源X和3个资源Y,产品B需要2个资源X和4个资源Y。
资源X的总数为20,资源Y的总数为15。
假设该公司每天的生产量不能超过100个产品,问该公司最多能生产多少个产品A和B的组合?解答:根据所给条件,我们可以得到以下一元一次不等式含多个参数:$5A + 2B \le 20$(资源X的限制条件)$3A + 4B \le 15$(资源Y的限制条件)$A + B \le 100$(生产量限制条件)根据这些不等式,我们可以得到参数的取值范围:$0 \le A \le 20$$0 \le B \le 50$接下来,我们可以通过代数运算或图形法求解这组不等式,得到参数的解(A和B的取值)。
然后,将解带回原问题进行验证,确保解在问题的范围内且符合实际意义。
一元一次不等式(组)提升专题(含参不等式组)

一元一次不等式(组)提升专题(含参不等式组)一元一次不等式(组)提升专题【问题归纳】1、知含参不等式组的解集,求参数的取值范围;2、知含参不等式组有解、无解,求参数的取值范围;3、知含参不等式组整数解的情况;求参数的取值范围;4、不等式与方程综合,求多元代数式的取值范围;5、与不等式相关的新定义(高斯函数,“四舍五入”).【典例讲练】【例1】若关于x 的不等式组<++>+01456m x x x 的解集为x <4,则m 的取值范围是__________.【练】关于x 的不等式组1235a x a x -<<+??<【例2】(1)如果关于x 的不等式(m -n )x +m -7n >0的解集为x <1,那么关于x 的不等式nx ≥m 的解集为__________.【练】若不等式(2a -b )x +3a -4b <0的解集是x >94,求不等式(a -4b )x +2a -3b >0的解集.【例3】(1)若关于x 的不等式组++>-++>-x m m x m x x m 122)15(253有解,求m 的取值范围.【练】若关于x 的一元一次不等式组0230x a x a +>??-+?≤有解,则a 的取值范围为____________.【变1】若关于x 的不等式组121x m x m <+??>-?无解,则m 的取值范围是____________.【变2】若关于x 的不等式组204(1)20x a x a +>??-+>?无解,则a 的取值范围是____________.【例4】若关于x 的不等式组0721x m x -【练】若关于x 的不等式组?>-≥-0240x a x 的整数解共有5个,求a 的取值范围.【变1】若关于x 的不等式组423()23(2)5x x a x x +>+>-+??仅有三个整数解,则a 的取值范围是__________.【变2】若关于x 的不等式组5060x m x n -【拓1】若关于x 的不等式组3190x x a +【拓2】关于x 的不等式组2132x x x m+?>-【拓3】(1)已知关于x 、y 的方程组2525x y x y a -=??+=?的解满足不等式x +y <b ,且满足条件的正整数a 仅有2个,则b 的范围是________.(2)已知关于x ,y 的方程组3434x y a x y a -=+??+=+?的解满足不等式x -2y ≥b ,且满足条件的正整数a 仅有4个,则b 的范围是________.【例6】已知x 、y 为非负数,且满足x +2y -3=0,求m =2x +y 的最大值.【变】若a ,b 满足3a +5|b |=7,且S =2a -3|b |,求S 的取值范围.【拓1】已知4325x y -+≤≤,13x y -≤≤,则2x y +的最大值为__________,最小值为__________.【拓2】已知实数a 、b 满足14a b +≤≤,01a b -≤≤,且2a b -有最大值,求82018a b +的值.【拓3】已知三个非负数a 、b 、c 满足3a +2b +c =5和2a +b -3c =1,若m =3a +b -7c ,求m 的最大值和最小值.【拓4】已知非负数a ,b ,c 满足条件a +b =7,c ﹣a =5,设S =a +b +c 的最大值为m ,最小值为n ,则m ﹣n 的值为__________.【拓5】已知非负实数x 、y 、z 满足123234x y z ---==,记345W x y z =++,求W 的最大值、最小值.【例7】对非负实数x “四舍五入”到个位的值记为<x >,即:当n 为非负整数时,如果n -21≤x <n +21,则<x >=n .如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…①填空:<π>=_________(π为圆周率);②如果<2x ﹣1>=3,求实数x 的取值范围.【变】已知[x ]表示不超过x 的最大整数,如[﹣1]=﹣1,[﹣1.5]=﹣2,[3.5]=3,则满足方程x ﹣2[x ]﹣103=0的解的个数为__________.【拓】设[x ]表示不超过x 的最大整数(例如:[2]=2,[1.25]=1),则方程3x -2[x ]+4=0的解为 _______________.【思考题】1、已知有理数x 满足31752233x x x -+-≥-,若32x x --+的最小值为a ,最大值为b ,求ab .2、若a +b =﹣2,且a ≥2b ,则()A .a b 有最小值21 B .b a 有最大值1 C .b a 有最大值2 D .b a 有最小值98-3、已知a +b +c =0,a >b >c ,则ac 的取值范围是_______________.4、求满足下列条件的最小正整数n ,对于n 存在正整数k 使871513nn k <<+成立.5、已知a 、b 、c 、d 是正整数,且a +b =20,a +c =24,a +d =22,设a +b +c +d 的最大值为M ,最小值为N ,则M -N =______________.6、已知关于x 的不等式组122x a x a<+??->?的解集中的整数恰好有2个,求实数a 的取值范围.(34a <<或45a <或a =6)【补充练习】1、已知关于x 的不等式(4a -3b )x >2b -a 的解集是x <94,求ax >b 的解.2、(1)若不等式12634x x a -(2)关于x 的不等式12634x x a -≤仅有两个负整数解,求a 的取值范围.(3)如果关于x 的不等式2≤3x +b <8的整数解之和为7,求b 的取值范围是.(4)若不等式组9080x a x b -??-(5)已知关于x ,y 的方程组922x y x y a -=??+=?的解满足不等式x +y ≤b ,且满足条件的正整数a 仅有3个,则b 的范围是________.(6)已知关于x 、y 的方程组521365x y a x y a -=+??-=+?的解满足不等式2x -y >b ,且满足条件的非正整数a 仅有4个,则b 的范围是________.3、(1)m 为何值时,方程组713x y m x y m+=-??-=+?的解满足2x +3y >0.(2)已知方程组5331x y x y m+=??+=?的解为非负数,求m 的整数解.(3)求同时满足a +b +c =6,2a -b +c =3和b ≥c ≥0的a 的最大值及最小值.(4)已知13a b -<+<,24a b <-<,求23a b +的取值范围.(5)当x 、y 、z 为非负数时,且3x +3y +z =4,x -3y -2z =-3,求t =3x -2y +z 的最大值和最小值.4、(1)定义取整函数[]x 为不超过x 的最大整数,例如[]4.54=,[]55=,若整数x 、y 满足2133x +??=, 342y +??=,则有序数对(x ,y )共有__________对.(2)对非负实数x ,“四舍五入”到个位的值记为<x >,即:当n 为非负整数时,如果n -21≤x < n +21,则<x >=n .如:<0.48>=0,<3.5>=4;如果<2x -1>=3,则实数x 的取值范围为__________;如果<x >=34x ,则x =__________.。
一元一次不等式组含参问题

一元一次不等式组含参问题一、概述在初中数学的学习中,我们接触到了一元一次不等式组含参问题。
这样的问题往往涉及到多个未知数和多个方程,需要我们采用适当的方法进行求解。
下面,本文将对一元一次不等式组含参问题进行详细的讲解,希望能够帮助同学们更好地掌握这个难点。
二、问题类型一元一次不等式组含参问题的形式多种多样,以下是几种常见的类型:1、求参数的取值范围此类问题给定一组不等式组,其中包含一个或多个未知参数,要求我们求出这个参数的取值范围,使得所有方程都成立。
2、最小(大)值问题此类问题给出一组不等式组,其中包含一个或多个未知参数,要求我们求出这个参数使得某个式子取得最小(大)值。
3、问题的实际应用此类问题往往会给出一些实际情况,要求我们运用一元一次不等式组基本原理来解决实际问题。
三、方法掌握要解决一元一次不等式组含参问题,我们需要掌握以下方法:1、列出方程组首先需要将问题中所有信息转化为方程式,然后再结合问题,列出一元一次不等式组含参的求解式。
2、解析式求解对于参数范围问题,我们要在联立的不等式组中找出一个代表所有不等式的式子,然后将未知数与参数隔离,使其成为一项含参的式子,最后解决参数的范围。
对于最值问题,我们要将式子进行变形,使其成为一个用参数表示的函数,然后再利用数学方法求解。
3、实践运用在处理实际问题时,我们要结合实际情况进行分析,将其中的条件转化为不等式,然后列方程组求解。
四、应用案例下面,我们通过具体的应用案例来加深对一元一次不等式组含参问题的理解。
例1、现有12个黄色球,红色球的数量不确定,小明从中随机抽出4个球,要使得其中至少有3个为黄色球,求红色球的最少数量。
解:用x表示红色球的数量,则不等式组为:x+12≥4,3x+12<4,其中x为未知的参数。
化简后得到:x≥-8,x<-\frac{8}{3}最终,根据实际情况得到,红球至少有 3 颗。
例2、某社区小学针对学生荣誉评定制定了一种评定方案:评定范围为高度荣誉,理论荣誉和优秀荣誉三级,其中高度荣誉取得条件为文化课成绩在前10%且思品课成绩在前20%,理论荣誉要求文化课成绩在前20%或思品课成绩在前30%,优秀荣誉要求满足以上条件之一。
数学人教版七年级下册一元一次不等式的含参问题

学习目标
解决一元一次不等式(组)中 含有字母参数的问题。
知识回顾
1.解一元一次不等式的基本依据是什么? 2.解一元一次不等式的主要步骤是什么? 3.解一元一次不等式组的主要步骤是什么?
(1)分别解不等式组中的各个不等式; (2)在数轴上表示各个不等式的解集; (3)求出这几个不等式解集的公共部分.
x m 2、若不等式组 有解,那么 m 的取值范围是_________。 x 2
x 2 3、已知关于 x 的不等式组 x 1 无解,则 a 的取值范围是_________ x a
【考点2:与二元一次方程结合的待 定系数类】
3x y k 1 1、若方程组 x 3 y 3
x> 3 x a
A a 3 B a> 3
C
a 3 D a 3
变式训练2
已知关于x的不等式组
x a b 2x a < 2b 1
的值
的解集为3≤x<5,求
b a
练一练
x a 2 1、若不等式组 的解集是-1<x<1,则(a+b)=______. b 2 x 0
1 A.-1<k<2 1 B.0<k< 2
C.0<k<1
1 D. <k<1 2
小结
达标检测
x a 1、若关于x的不等式组 x 3 0 只有三个整数解,求a的取值范围
1 x 2 2、若关于x的不等式组 x m 有解,求m的取值范围。
x m 1 3、若关于x的不等式组 x 2 m 1
例1.关于x的不等式3m-x<5的解集 x>2,求m的值。
一元一次不等式组—含参问题

C. m ? 8
D. m ? 8
大家好
5
探究1
例1、如果不等式组
?x
? ?
x
? ?
m ? 1 无解,
2m? 1
则m的取值范围是 m ? 2 。
2m? 1? m? 1
大家好
6
练习
1、不等式组
?x? 2 ? ??3x ? (x
3a ? 1)
?
a
?
(3 ?
的解集
x)
为 x ? 3a ? 2 则a的取值范围是 a≥-3 。
注 意!
最后一定要检验能不能取等号!
大家好
9
探究2
例2、已知 3x ? a ? 0 的正整数解有
4个,求a的取值范围。
4? a ?5 3
12 ? a ? 15
大家好
10
练习2
(1) 已知不等式4x-a<0的正整数解是 1、2,求a的取值范围。
8 < a≤ 12
(2)
已知不等式组
? ? ?
x x
? ?
? x? y ? 1? a
? ?
x
?
y
?
3a
?
5
的解,x是非正数, y是负数,求 a 的取
值范围。 3 ? a ? 2 2、当m取什么2 值时,关于 x的方程
3x ? m ? 2(m ? 2) ? 3m ? x
的解在-5和5之间(包括-5和5)。
? 3 ? m ? 3 大家好
13
2
2
作业 1、若不等式
最后一定要检验能不能取等号!
大家好
3
2、如果不等式组
? ? ?
x x
? ?
人教版初中数学中考复习 一轮复习 —一元一次不等式(组)解法及含字母(参数)问题

8
4
.
解:(2)去分母,得:8﹣(7x﹣1)>2(3x﹣2),
去括号,得:8﹣7x+1>6x﹣4,
移项,得:﹣7x﹣6x>﹣4﹣1﹣8,
合并同类项,得:﹣13x>﹣13,
系数化1,得:x<1.
考点二:解不等式(组)并在数轴上表示解(集)
5.(2021•武汉)解不等式组
2x x 1 ① 4x 10 x 1 ②
考点一:不等式的性质
C 1.(2021•常德)若a>b,下列不等式不一定成立的是( )
A.a﹣5>b﹣5
B.﹣5a<﹣5b
C. a b
cc
D.a+c>b+c
考点一:不等式的性质
2.(2021•临沂)已知a>b,下列结论:①a2>ab;②a2>b2;③若b<0,
A 则a+b<2b;④若b>0,则 1 1 ,其中正确的个数是( ) ab
性质3:不等式两边同时乘或除同一个负数,不等号的。方向改变
知识点梳理:
二、一元一次不等式(组)及其解法
一元一次不等 含有一个未知数,未知数的次数是
1
式定义
的不等式
解一元一次不 等式的步骤
去分母→去括号→移项→合并同类项→系数化为1
一元一次 一般地,关于同一个未知数的几个一元一次不等式合在一起,
不等式组 就组成一个一元一次不等式组
3.(2021•南京)解不等式1+2(x﹣1)≤3,并在数轴上表示解集. 解: 1+2(x﹣1)≤3, 去括号,得1+2x﹣2≤3. 移项、合并同类项,得2x≤4. 化系数为1,得x≤2.
表示在数轴上为:
考点二:解不等式(组)并在数轴上表示解(集)
Hale Waihona Puke 4.(2021•泰安)(2)解不等式: 1- 7x 1 3x 2
一元一次不等式含参问题

一元一次不等式含参问题一元一次不等式含参问题类型一:根据不等式组的整数解情况确定字母的取值范围。
例1:已知不等式组begin{cases}4x+2>3(x+a)\\2x>3(x-2)+5\\5x+2>3(x-1)end{cases}有3个整数解,则$m$的取值范围是什么?变式练1:已知不等式组,如果有3个整数解,则$m$的取值范围是什么?变式练2:已知关于$x$的不等式组,如果解集为$x>3$,则$a$的取值范围是什么?变式练3:已知关于$x$的不等式组begin{cases}4x+2>3(x+a)\\2x>3(x-2)+5\\5x+2>3(x-1)end{cases}如果只有4个整数解,则实数$a$的取值范围是什么?变式练4:已知关于$x$的不等式组begin{cases}3x\leq 8-x+2a\\22a\leq xend{cases}如果仅有4个整数解,则实数$a$的取值范围是什么?类型二:根据不等式组的解集确定字母的取值范围。
例2:已知关于$x$的不等式组无解,则$a$的取值范围是什么?变式练1:若关于$x$的不等式组有解,则实数$a$的取值范围是什么?变式练2:若不等式组的解集为$x>3$,则$a$的取值范围是什么?变式练3:若关于$x$的不等式组的解集为$x<2$,则$a$的取值范围是什么?变式练4:已知不等式组无解,则$a$的取值范围是什么?类型三:根据未知数解集或者未知数间的关系确定字母的取值范围。
例3:已知方程组begin{cases}2x+y=1+3m\\x+2y=1-mend{cases}满足$x+y<2$,求$m$的取值范围。
变式练1:若关于$x,y$的二元一次方程组begin{cases}x+2y=4k\\2x+y=2k+1end{cases}的解满足$x+y<1$,则$a$的取值范围是什么?变式练2:已知关于$x$的不等式$1-a)x>3$的解集为$x<2$,则$a$的值为多少?变式练3:若不等式$3m-2x3$,则实数$m$的值为多少?变式练4:若不等式组的解集为$3\leq x\leq 4$,则不等式$ax+b<0$的解集为什么?综合练:1.关于$x$的一元一次不等式$7x-14\leq 0$的解集是什么?A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2m 1m 1
大家好
6
练习
1、不等式组 3xx2(x 3a1)a(3x)的解集
为 x3a2则a的取值范围是 a≥-3 。
2
、若不等式组
Байду номын сангаас
2
x
x3 m
0无解,则m的
取值范围是
m3 2
。
大家好
7
3、若不等式
2x a 1
x
2b
3
的解集
为 1x2,求 (a1)(b1)的值。
大家好
8
1.用参数把各不等式的解集表示出来. 2.根据条件列出关于参数的不等式(等式)
x x
2 m
的解集为 xm,
则m的取值范围是( D )
A. m2
B. m2
C. m2
D. m2
大家好
4
x 8
3、如果不等式组
x
m
有解,则m的
取值范围是( C )
A . m8
B. m8
C. m8
D. m8
大家好
5
探究1
例1、如果不等式组
x x
m 1 无解,
2m 1
则m的取值范围是 m2 。
大家好
11
探究3
例3、已知关于x、y的方程组
x y a 3 2x y 5a
的解是正数,求a的取值范围。
分 析
x 2a 1
y
a
2
2a 1 0 a 2 0
a2
大家好
12
练习 1、当关于x、y的方程组
x y 1a x y 3a5
的解,x是非正数,y是负数,求a的取
值范围。 3 a 2 2、当m取什么2值时,关于x的方程
注 意!
最后一定要检验能不能取等号!
大家好
9
探究2 例2、已知 3xa0的正整数解有
4个,求a的取值范围。
4 a 5 3
12a15
大家好
10
练习2
(1) 已知不等式4x-a<0的正整数解是 1、2,求a的取值范围。
8 < a≤ 12
(2)
已知不等式组
x x
a 3
有三个整 0
数解,求a的取值范围。 0 ≤a <1
3 x m 2 (m 2 ) 3 m x
的解在-5和5之间(包括-5和5)。
3
3
2 m大家好 2
13
作业 1、若不等式
x
4
2x
1 2
的解集
x m
2、若为不x 等 4式12 组,求xmx的2ab取b值a 范的围解。集是
2 x 7 ,求a、b的值。
2
3、已知 2xm0的非负整数解
一元一次不等式组 ——含参问题
大家好
1
※ 如果a< 2,那么不等式组 解集是什么?
x x
a 2
的
x2
※ 如果a≥2,那么不等式组 解集是什么?
x x
a的
2
xa
大家好
2
练习:
1、若不等式组
x x
m 3
1
的解集为
x 3,求m的取值范围.m2
注 意!
最后一定要检验能不能取等号!
大家好
3
2、如果不等式组
是0、1、2、3,求m的取值范围。
大家好
14
结束
大家好
15
