高一下册期中考试数学试题及答案(人教版)【最新】
(最新)高一下册期中考试数学试题及答案(人教版)

高一下学期期中质量调查数学试题 第Ⅰ卷(选择题 共24分)一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列命题正确的是A.若0a b <<,则 ac bc <B. 若,a b c d >>,则 ac bd >C.若a b >,则1a b <D.若22,0a bc c c>≠,则a b > 2.在数列{}n a 中,111,3n n a a a +=-=-,则4a = A. 10- B. 7- C. 5- D. 113.若13,24a b <<<<,则ab的范围是A. 1,12⎛⎫ ⎪⎝⎭B. 3,42⎛⎫ ⎪⎝⎭C. 13,42⎛⎫⎪⎝⎭D.()1,44.在ABC V中,已知,24c A a π===,则角C =A.3π B. 23π C. 3π或23π D.12π或512π5.已知数列{}n a 为等比数列,有51374a a a -=,{}n b 是等差数列,且77a b =,则59b b +=A. 4B. 8C. 16D. 0或86.在ABC V 中,已知sin 2cos sin A B C =,则ABC V 的形状时 A. 直角三角形 B. 等腰三角形 C.等腰直角三角形 D.不确定7.设n S 是等差数列{}n a 的前n 项和,若3613S S =,则612SS = A. 13 B. 18 C. 19 D.3108.已知数列{}n a 前n 项和21nn S =-,则此数列奇数项和前n 项和是A. ()21213n -B. ()11213n +-C. ()21223n -D. ()11223n +-第Ⅱ卷(非选择题 共76分)二、填空题:本大题共6小题,每小题4分,共24分.9.在数列{}n a 中,223n a n =-,则125是这个数列的第 项.10.在ABC V 中,三边,,a b c 成等比数列,222,,a b c 成等差数列,则三边,,a b c 的关系为 .11.对于任意实数x ,不等式23204mx mx +-<恒成立,则实数m 的取值范围是 . 12.在等差数列{}n a 中,已知11a =,前5项和535,S =则8a 的值是 .13.在ABC V 中,若120,5,7,A AB BC ===o,则ABC V 的面积S = .14.已知数列{}n a 满足,11232,2nn n a a a +=+⋅=,则数列{}n a 的通项公式是 .三、解答题:本大题共6小题,共52分,解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分8分)已知不等式2320ax x -+>的解集为{}|x 1x b x <>或.(1)求,a b 的值;(2)解关于x 的不等式()2220ax b a x b ---<.16.(本小题满分8分)已知等比数列{}n a 中,11a =,公比为q ,且()1.n n n b a a n N *+=-∈ (1)判断数列{}n b 是否为等比数列?请说明理由. (2)求数列{}n b 的通项公式.17.(本小题满分8分)已知数列{}n a 的前项和22 4.n n S +=-(1)求数列{}n a 的通项公式;(2)设等差数列{}n b 满足,73154,b a b a ==,求数列{}n b 的前项和.n T18.(本小题满分12分)若等比数列{}n a 的前n 项和1.2n n n S a =- (1)求实数a 的值;(2)求数列{}n na 的前n 项和.n T19.(本小题满分10分)在ABC V 中,角,,A B C 的对边分别为,,a b c ,已知45,cos .5b c A == (1)求sin C 的值;(2)若ABC V 的面积为3sin sin ,2ABC S B C =V 求a 的值.20.(本小题满分10分)已知数列{}n a 的前n 项和为n S ,满足11110,2,.n n n n n n n n a a S a S a a n N -*+++≠-=∈ (1)求证:12;n n n S a -=(2)设1nn n a b a +=,求数列{}n b 的前n 项和.n T。
北京市人大附中2022-2023学年高一下学期期中模拟数学试题(含答案解析)

北京市人大附中2022-2023学年高一下学期期中模拟数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题A .12B .16.若arctan(3)-=()A .2π3B .-7.已知tan 2θ=,则2sin θ+A .45B .-8.要得到函数πsin 23y x ⎛⎫=- ⎪⎝⎭的图象,只需将函数A .向左平移π6个单位长度A .()f α的定义域是{|αB .()f α的图象的对称中心是C .()f α的单调递增区间是D .()f α对定义域内的α10.已知单位向量a 、b 、c ,满足123a b c λλλ++的最大值为(A .3B .二、双空题11.已知(1,2),(3,4)a b == ,则三、填空题12.已知向量(1,2)a = ,与向量四、双空题13.已知扇形的半径为6cm 扇形的面积为cm 五、填空题六、双空题七、解答题17.已知函数()sin(ω=f x x π2π,63⎛⎫⎪⎝⎭上单调.(1)从条件①、条件②、条件③中选一个作为已知,使得析式;条件①:函数()f x 的图象经过点(Ⅰ)用,OA OB 表示CB;(Ⅱ)点P 在线段AB 上,且八、单选题19.函数4()cos 3f x x =--A ..C ...已知集合()2{|,,M a a x y ==N 且}1y ≥,O 为坐标原点,当)()11222,,,y M OB x y M ∈∈=()1212,A B x x y y =-+-)332,y M ∈,则“存在0λ>是“()()(,,+=d A B d B C d A .充分不必要条件.必要不充分条件C .充要条件D .既不充分也不必要条件九、双空题①1秒钟后,点P 的横坐标为②t 秒钟后,点P 到直线l 的距离用十、填空题24.若关于x 的方程cos x ⎛+ ⎝则321x x x ++=.25.定义一种向量运算“⊗”:十一、解答题26.给定正整数2n ≥,设集合12{|(,,,),{0,1},1,2,,}n k M t t t t k n ==∈=L L αα.对于集合M 中的任意元素12(,,,)n x x x =L β和12(,,,)n y y y =L γ,记1122n n x y x y x y ⋅=+++L βγ.设A M ⊆,且集合12{|(,,,),1,2,,}i i i i in A t t t i n ===L L αα,对于A 中任意元素,i j αα,若,,1,,i j p i j i j αα=⎧⋅=⎨≠⎩则称A 具有性质(,)T n p .(1)判断集合{(1,1,0),(1,0,1),(0,1,1)}A =是否具有性质(3,2)T ?说明理由;(2)判断是否存在具有性质(4,)T p 的集合A ,并加以证明;(3)若集合A 具有性质(,)T n p ,证明:12(1,2,,)j j nj t t t p j n +++==L L .参考答案:17.(1)π()sin 26f x x ⎛=+ ⎝(2)ππ,66⎡⎤-⎢⎥⎣⎦【分析】(1)根据题意得到三个方程,分析方程组即可求解;(2)先求出π26x +所在的范围,正弦函数的性质得到【详解】(1)因为()f x 在区间因为2T ωπ=,且0ω>,解得又因为π6x =是函数()f x 的对称轴,所以若选条件①:因为函数f 因为||2ϕπ<,所以π6ϕ=当0k =时,2ω=,满足题意,故若选条件②:因为π,03⎛⎫⎪⎝⎭因为1BO AD == ,2CD BO = 所以()()()2,0,0,1,3,2A B C .所以()1,2AC = ,()2,1AB =-.因为点P 在线段AB 上,且AB 所以121,333AP AB ⎛⎫==- ⎪⎝⎭ 所以55,33CP AP AC ⎛⎫=-=--⎪⎝⎭因为()3,1CB =--,所以cos 53CP CB PCB CP CB ⋅∠==⋅ 【点睛】本题考查了向量的线性运算,向量夹角的计算,属于中档题.19.A【分析】利用函数的奇偶性和代入特殊值即可求解【详解】由已知条件得函数(f x【详解】建立如图所示的平面直角坐标系,则3π=可知,ABC 三点在一个定圆上,g x的图象如图所示,所以函数()由函数()g x 的图象得到()g x 不是周期函数,故选项①不正确;所以函数()g x 的值域是{}0,1,2,故选项②正确;由ππ244g f ⎡⎤⎛⎫⎛⎫⎡⎤-=-== ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦所以函数()g x 的图象不关于x =对于方程()π2g x x ⋅=,当()0g x =时,0x =,方程有一个实数根;当()1g x =时,π2x =,此时π2g ⎛ ⎝当()2g x =时,πx =,此时(π)g 故方程()π2g x x ⋅=只有一个实数根,故选项④正确故选:B.23.3-32sin π⎛- ⎝【分析】设1秒钟后点P 运动到此确定1P 的坐标,设t 秒钟后点不妨设t 秒钟后,点P 的横坐标为由已知函数()f t 为周期函数,周期为最小值为2-,最大值为2,故可设()(sin x A t A ωϕ=+>所以2A =,2π2ω=,所以ω由已知点0P 逆时针旋转5π6后,点所以56t =秒时,点P 的横坐标为所以5π2sin 26ϕ⎛⎫+=- ⎪⎝⎭,所以所以2π2π3k ϕ=+,所以2π2sin π2π+3x t k ⎛⎫=+= ⎪⎝⎭所以t 秒钟后,点P 到直线l 故答案为:3-;32sin π⎛- ⎝24.4π【分析】设()πcos 6g x x ⎛⎫=+ ⎪⎝⎭结合条件证明1322x x x +=,(2)假设集合A 具有性质(4,)T p ,分别考虑1,2,3,4p =时,集合A 中的元素,即可根据(,)T n p 的定义求解.(3)根据假设存在j 使得1j c p +≥,考虑当1c n =时以及11p c n +<≤时,分量为1的个数即可讨论求解.【详解】(1)因为(1,1,0)(1,1,0)1111002⋅=⨯+⨯+⨯=,同理(1,0,1)(1,0,1)(0,1,1)(0,1,1)2⋅=⋅=.又(1,1,0)(1,0,1)1110011⋅=⨯+⨯+⨯=,同理(1,1,0)(0,1,1)(1,0,1)(0,1,1)1⋅=⋅=.所以集合{(1,1,0),(1,0,1),(0,1,1)}A =具有性质(3,2)T .(2)当4n =时,集合A 中的元素个数为4.由题设{0,1,2,3,4}p ∈.假设集合A 具有性质(4,)T p ,则①当0p =时,{(0,0,0,0)}A =,矛盾.②当1p =时,{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}A =,不具有性质(4,1)T ,矛盾.③当2p =时,{(1,1,0,0),(1,0,1,0),(1,0,0,1),(0,1,1,0),(0,1,0,1),(0,0,1,1)}A ⊆.因为(1,1,0,0)和(0,0,1,1)至多一个在A 中;(1,0,1,0)和(0,1,0,1)至多一个在A 中;(1,0,0,1)和(0,1,1,0)至多一个在A 中,故集合A 中的元素个数小于4,矛盾.④当3p =时,{(1,1,1,0),(1,1,0,1),(1,0,1,1),(0,1,1,1)}A =,不具有性质()4,3T ,矛盾.⑤当4p =时,{(1,1,1,1)}A =,矛盾.综上,不存在具有性质(4,)T p 的集合A .(3)记12(1,2,,)j j j nj c t t t j n =+++=L L ,则12n c c c np +++=L .若0p =,则{(0,0,,0)}A =L ,矛盾.若1p =,则{(1,0,0,,0)}A =L ,矛盾.故2p ≥.假设存在j 使得1j c p +≥,不妨设1j =,即11c p +≥.当1c n =时,有j c =0或1j c =(2,3,,)j n =L 成立.所以12,,,n αααL 中分量为1的个数至多有(1)212≤n n n n np +-=-<.当11p c n +<≤时,不妨设11211,111,0p n t t t t +=====L .因为n n p αα⋅=,所以n α的各分量有p 个1,不妨设23,11n n n p t t t +====L .由i j ≠时,1i j αα⋅=可知,{2,3,,1}q p ∀∈+L ,121,,,,q q p q t t t +L 中至多有1个1,即121,,,p +αααL 的前1p +个分量中,至多含有121p p p ++=+个1.又1i n αα⋅=(1,2,,1)i p =+L ,则121,,,p +αααL 的前1p +个分量中,含有(1)(1)22p p p +++=+个1,矛盾.所以(1,2,,)j c p j n =L ≤.因为12n c c c np +++=L ,所以j c p =(1,2,,)j n =L .所以12(1,2,,)j j nj t t t p j n +++==L L .【点睛】求解新定义运算有关的题目,关键是理解和运用新定义的概念以及元算,利用化归和转化的数学思想方法,将不熟悉的数学问题,转化成熟悉的问题进行求解.对于新型集合,首先要了解集合的特性,抽象特性和计算特性,抽象特性是将集合可近似的当作数列或者函数分析.计算特性,将复杂的关系通过找规律即可利用已学相关知识求解.。
2023学年一年级下册数学期中考试单元素养测评卷(一)(人教版)(含解析)

保密★启用前2023-2023学年一年级下册数学期中考试1-4单元素养测评卷(一)考试分数:100分;考试时间:60分钟注意事项:1.答题前,填写好自己的姓名、班级、考号等信息,请将答案写在规定的位置上。
2.选择题、判断题必须使用2B铅笔填涂答案,非选择、判断题必须使用黑色墨迹签字笔或钢笔答题,请将答案填写在规定的位置上。
3.考试结束后将试卷交回。
一、反复比较,谨慎选择。
(每题2分,共16分)1.水果店有7个西瓜,15个哈密瓜,哈密瓜卖掉()个后就和西瓜一样多。
A.4 B.8 C.152.下面物体中,()是不同类的一项。
A.B.C.3.下面每组图形中,能拼成正方形的是()。A.B.C.4.一副七巧板是由()种图形组成的。
A.3 B.4 C.75.下图中,不同类的是()。
A.B.C.6.“39”在数线上的位置()最合适。
A.A B.B C.C7.5个十和1个一组成的数是()。
A.51 B.15 C.608.12个小朋友玩“老鹰抓小鸡”的游戏,从前往后数,小飞是第5只鸡,小飞后面还有几只鸡?()A.5 B.6 C.7二、仔细思考,准确判断。
(每题2分,共8分)9.小狗比小猫多8只,则小猫比小狗少8只。
()10.分类的标准不同,分类的结果就不同。
()11.用4个同样的正方形可以拼成长方形或者正方形。
()12.79和89之间有10个数。
()三、用心思考,正确填空。
(每题2分,共16分)13.可以剪成()个相同的。
14.明明有12支笔,红红有8支笔,明明给红红()支笔后,两人的笔就同样多了。
15.计算14-6=□可以这样想();也可以这样想()。
16.按不同标准分一分。
方法一:();方法二:()。
17.十位上的数字比个位上的数字大2的两位数有()个,其中最小的是()。
18.用2、5、0组成的两位数中,最大的是(),最小的是()。
19.有65块糖,每10块糖装一袋,可以装满()袋,还剩()块。
20.下图是由4个相同的()形拼成的一个()形。
人教版高一数学上学期期中考试试题及详细答案解析全文

人教版高一数学上学期期中考试数学试题(满分150分时间120分钟)一、单选题(12小题,每题5分)。
1.已知集合(){}{}0222>==-==x ,y x B ,x x lg y x A x,是实数集,则()A.B.C.D.以上都不对2.下列函数中,是偶函数且在上为减函数的是()A.2xy = B.xy -=2C.2-=x y D.3xy -=3.下列各组函数中,表示同一函数的是()A.2xy =和()2x y =B.()12-=x lg y 和()()11-++=x lg x lg y C.2x log y a =和xlog y a 2= D.x y =和xa alog y =4.已知3110220230...c ,b ,.log a ===,则c ,b ,a 的大小关系是()A.cb a << B.b ac << C.bc a << D.ac b <<5.在同一直角坐标系中,函数()()()x log x g ,x x x f a a=≥=0的图像可能是()A. B. C. D.6.若132=log x ,则x x 93+的值为()A.3B.C.6D.7.函数()x x x f 31+-=的单调递增区间是()A.B.C.D.8.某同学求函数()62-+=x x ln x f 零点时,用计算器算得部分函数值如下表所示:则方程062=-+x x ln 的近似解(精确度0.1)可取为()A.2.52B.2.625C.2.66D.2.759.函数()xx lg x f 1-=的零点所在的区间是()A.(0,1)B.(1,10)C.(10,100)D.(100,+∞)10.已知函数()2211xxx f -+=,则有()A.()x f 是奇函数,且()x f x f -=⎪⎭⎫⎝⎛1 B.()x f 是奇函数,且()x f x f =⎪⎭⎫⎝⎛1C.()x f 是偶函数,且()x f x f -=⎪⎭⎫⎝⎛1 D.()x f 是偶函数,且()x f x f =⎪⎭⎫⎝⎛111.如图,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h 与注水时间t 之间的函数关系,大致是()A. B. C. D.12.已知函数()⎪⎩⎪⎨⎧>+-≤<=0621100x ,x x x ,x lg x f ,若a ,b ,c 均不相等,且()()()c f b f a f ==,则abc的取值范围是A.(1,10)B.(5,6)C.(10,12)D.(20,24)二、填空题(4小题,每题5分)13.若对数函数()x f 与幂函数()x g 的图象相交于一点(2,4),则()()=+44g f ________.14.对于函数f (x )的定义域中任意的x 1,x 2(x 1≠x 2),有如下结论:①f (x 1+x 2)=f (x 1)f (x 2);②f (x 1x 2)=f (x 1)+f (x 2);③()()02121>--x x x f x f .当f (x )=e x 时,上述结论中正确结论的序号是______.15.已知3102==b,lg a ,用a,b 表示=306log _____________.16.设全集{}654321,,,,,U =,用U 的子集可表示由10,组成的6位字符串,如:{}42表示的是第2个字符为1,第4个字符为1,其余均为0的6位字符串010100,并规定空集表示的字符串为000000.(1)若,则M C U 表示6位字符串为_____________.(2)若,集合表示的字符串为101001,则满足条件的集合的个数为____个.三、解答题。
2021人教版一年级下册数学《期中考试试题》及答案
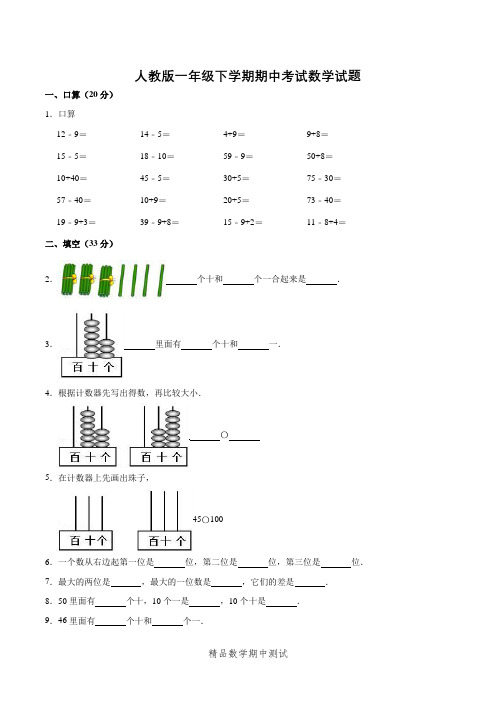
人教版一年级下学期期中考试数学试题一、口算(20分)1.口算12﹣9=14﹣5=4+9=9+8=15﹣5=18﹣10=59﹣9=50+8=10+40=45﹣5=30+5=75﹣30=57﹣40=10+9=20+5=73﹣40=19﹣9+3=39﹣9+8=15﹣9+2=11﹣8+4=二、填空(33分)2.个十和个一合起来是.3.里面有个十和一.4.根据计数器先写出得数,再比较大小.〇5.在计数器上先画出珠子,45〇1006.一个数从右边起第一位是位,第二位是位,第三位是位.7.最大的两位是,最大的一位数是,它们的差是.8.50里面有个十,10个一是,10个十是.9.46里面有个十和个一.10.个位上是2,十位上是8的数是.11.与70相邻的两个数是和.12.比91小,比88大的数是和.13.一个两位数的个位上是9,十位上是5,这个数写作是,读作是.14.选择合适的数填在圈里.48,76,45,64,49,83三、在正确答案下面画“√”(4分)15.在正确答案下面画“√”的价钱比30元少一些.多少元?10元27元32元16.在正确答案下面画“√”用同样长的小棒摆出1个长方形,最少要用多少根小棒?8根6根4根四、数图形.(8分)17.数图形.这辆小火车里有□,有△,有个〇,有个.五、看图列式.(16分)18.看图列式.(1)(2)(3)(4)六、解决问题(19分).19.我养了8条小金鱼,我养的和你同样多.他们一共养了多少条小金鱼?20.一共要种86棵树,还剩6棵没有种,已经种了多少棵树?21.小伟有30本,小红有35本,小红比小伟多多少本?22.学校乒乓球队有16人,足球队有13人,篮球队有10人.(1)乒乓球队和篮球队一共有多少人?(2)请你再提出一个问题,并解答.答案与解析一、口算1.【分析】根据整数加减法的计算方法计算即可.整数加法计算法则:相同数位对齐,从低位加起,哪一位上的数相加满十,就向前一位进一;整数减法计算法则:相同数位对齐,从低位减起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减.整数四则混合运算的顺序:同级运算时,从左到右依次计算;含有两级运算时,先算乘除,后算加减;有括号时,先算括号里面的,再算括号外面的.【解答】解:12﹣9=314﹣5=94+9=139+8=1715﹣5=1018﹣10=859﹣9=5050+8=5810+40=5045﹣5=4030+5=3575﹣30=4557﹣40=1710+9=1920+5=2573﹣40=3319﹣9+3=1339﹣9+8=3815﹣9+2=811﹣8+4=7【点评】此题考查了整数加减法的计算方法,属于基本的计算,要注意运算符号和数据,然后再进一步计算.在平时注意积累经验,逐步提高运算的速度和准确性.二、填空(33分)2.【分析】1捆小棒是10,3捆即3个十,然后与4个一合起来,就是34.【解答】解:3个十和4个一合起来是34.故答案为:3,4,34.【点评】本题是考查整数的组成,关键是掌握数位顺序表.3.【分析】计数器标的是63,是由6个十和3个一组成.【解答】解:63里面有6个十和3个一;故答案为:6,3.【点评】此题考查的是数的组成,能够根据计数器说出各数,并能明确该数的组成.4.【分析】左图:十位上是6个珠子,个位上是3个珠子,按从高位到低位顺序即可写出这个数;右图:十位上是3个珠子,个位上是6个珠子,按从高位到低位顺序即可写出这个数.比较两个整数的大小,首先看这两个整数的位数是否相同,如果位数不同,位数多的大于位数少的,如果位数相同,从高位比较,高位上的数大则这个数大,高位上的数相同,就比较下一位.【解答】解:十位上是6个珠子,个位上是3个珠子,这个数是63;十位上是3个珠子,个位上是6个珠子,这个数是36.63>36.故答案为:63,>,36.【点评】此题考查了学生对计数器的认识,以及用计数器表示数的能力.5.【分析】45的十位上的数是4,所以十位上拨4个珠子,个位上的数是5,所以个位上拨5个珠子;100的百位上的数是1,所以百位上拨1个珠子,十位数和个位数都是0,不用拨珠子.再根据三位数大于两位数即可比较大小.【解答】解:故答案为:45<100.【点评】此题考查了学生对计数器的认识,以及用计数器表示数的能力.6.【分析】根据整数数位顺序表进行解答即可.【解答】解:一个数从右边起第一位是个位,第二位是十位,第三位是百位;故答案为:个,十,百.【点评】解答此题的关键是熟练掌握整数数位顺序表.7.【分析】最大的两位是99,最大的一位数是9,进而根据题意,用“99﹣9”解答即可.【解答】解:最大的两位是99,最大的一位数是9,它们的差:99﹣9=90;故答案为:99,9,90.【点评】解答此题的关键:应明确最大的两位数和最大的一位数分别是多少,进而根据题意进行解答即可.8.【分析】根据十进制计数法,两个相邻单位间的进率都是十,据此即可解答.【解答】解:50里面有5个十,10个一是10,10个十是100.故答案为:5,10,100.【点评】本题考查了十进制计数法,每相邻的两个计数单位之间的进率都为十,注意相邻二字.9.【分析】根据数位顺序表中数位和它们对应的计数单位以及十进制的定义可以解决问题.【解答】解:4在十位上,表示4个十;6在个位上,表示6个一.故答案为:4;6.【点评】此题考查了数的组成.10.【分析】个位上是2,十位上是8,按从高位到低位顺序即可写出这个数.【解答】解:个位上是2,十位上是8的数是82.故答案为:82.【点评】本题是考查整数的读法和写法.整数的读、写都是从高位到低位.11.【分析】根据自然数的排列规律:相邻的自然数相差1,与70相邻的两个数分别是70﹣1、70+1.据此解答.【解答】解:70﹣1=6970+1=71答:与70相邻的两个数是69和71.故答案为:69,71.【点评】此题考查的目的是理解自然数的意义,掌握自然数的排列规律.12.【分析】根据相邻的两个自然数相差1进行数数即可得出结果.【解答】解:从88开始一个一个的数,数到91,即88、89、90、91.所以比91小,比88大的数是90、89.故答案为:90、89.【点评】本题主要考查了整数的读写,熟知相邻的两个自然数相差1是解答本题的关键.13.【分析】一个两位数的个位上是9、十位上是5,按从高位到低位顺序即可写出这个数;读这个数时按照从高位到低位的顺序读出即可.【解答】解:一个两位数的个位上是9,十位上是5,这个数写作是59,读作是五十九.故答案为:59、五十九.【点评】本题是考查整数的读法和写法.整数的读、写都是从高位到低位.14.【分析】找到十位是4的数填写即可;找到比50大的数填写即可.【解答】解:【点评】考查了整数的认识和整数大小的比较,解题的关键是看清题目的要求.三、在正确答案下面画“√”15.【分析】根据整数大小比较的分,当几个数的位数相同时,从最高位开始比较,最高位上大的数就大,如果最高相同,再比较次高位,依此类推.【解答】解:因为32大于30,所以排除32 元;又因为30比10大很多,所以排除10元,因为30比27大一些,所以书包的价格是27元.故答案为:10元27元32元√【点评】此题考查的目的是理解掌握整数大小比较的方法及应用.16.【分析】用同样长的小棒摆出1个长方形,最少是长2宽1,即需要(2+1)×2=6根小棒.【解答】解:(2+1)×2=6(根)8根6根4根√【点评】解答此题的关键是明确长方形的特征.四、数图形.17.【分析】正方形、长方形都是由四条线段围成的图形,所以都是四边形,圆是由曲线围成的封闭图形;由3条首尾相连的线段围成的图形叫做三角形,据此即可解答.【解答】解:根据分析可得,这辆小火车里有6□,有5△,有6个〇,有5个.故答案为:6、5、6、5.【点评】本题主要考查平面图形的分类及识别,熟练掌握正方形、长方形、三角形与圆的特征是解答本题的关键.五、看图列式.18.【分析】(1)根据图文中的信息,用8+5计算,即可得到一共有多少只大雁;(2)根据图文中的信息,用12﹣3计算,即可得到盒子中的苹果数量;(3)根据图文中的信息,用15﹣3﹣4计算,即可得到盒子中的苹果数量;(4)根据图文中的信息,用40+5计算,即可得到一共有多少根铅笔.【解答】解:(1)8+5=13(只)答:一共有13只大雁;(2)12﹣3=9(个)答:盒子中有9个苹果;(3)15﹣3﹣4=12﹣4=8(个)答:袋子中有8个苹果;(4)40+5=45(根)答:一共有45根铅笔.【点评】本题是一道图文应用题,明确题意,从图文中获取解答问题的信息是解答本题的关键.六、解决问题(19分).19.【分析】我养了8条小金鱼,我养的和你同样多,所以你养了8条小金鱼.求一共养了多少条小金鱼,用加法计算即可.【解答】解:8+8=16(条)答:他们一共养了16条小金鱼.【点评】此题考查了整数加法的应用,要根据题意准确找出两个加数.20.【分析】一共要种86棵树,还剩6棵没有种,求已经种了多少棵树,用减法计算,是86﹣6=80(棵).【解答】解:86﹣6=80(棵)答:已经种了80棵树.【点评】此题考查了整数减法的应用,要根据题意准确找出被减数和减数.21.【分析】用小红的本数减去小伟的本数,列式计算可求小红比小伟多多少本.【解答】解:35﹣30=5(本)答:小红比小伟多5本.【点评】考查了整数的减法,关键是根据题意正确列出算式进行计算求解.22.【分析】(1)把乒乓球队和篮球队的人数相加即可求解;(2)问题:足球队比篮球队多多少人?把足球队和篮球队的人数相减即可求解.【解答】解:(1)16+10=26(人)答:乒乓球队和篮球队一共有26人.(2)足球队比篮球队多多少人?13﹣10=3(人)答:足球队比篮球队多3人.【点评】考查了整数的加法和减法,关键是根据题意正确列出算式进行计算求解.。
2024年最新人教版初三数学(下册)期中考卷及答案(各版本)

2024年最新人教版初三数学(下册)期中考卷一、选择题(每题3分,共30分)1. 若一个数的立方根是3,则这个数是()A. 9B. 27C. 9D. 272. 下列各式中,正确的是()A. $ \sqrt{9} = 3 $B. $ \sqrt[3]{8} = 2 $C. $ \sqrt{16} = 4 $D. $ \sqrt[3]{27} = 3 $3. 下列各式中,错误的是()A. $ 3^2 = 9 $B. $ (3)^2 = 9 $C. $ 3^3 = 27 $D.$ (3)^3 = 27 $4. 下列各式中,正确的是()A. $ 2^4 = 16 $B. $ 2^5 = 32 $C. $ 2^6 = 64 $D. $ 2^7 = 128 $5. 下列各式中,错误的是()A. $ 5^2 = 25 $B. $ 5^3 = 125 $C. $ 5^4 = 625 $D.$ 5^5 = 3125 $6. 下列各式中,正确的是()A. $ 10^2 = 100 $B. $ 10^3 = 1000 $C. $ 10^4 = 10000 $D. $ 10^5 = 100000 $7. 下列各式中,错误的是()A. $ 2^0 = 1 $B. $ 3^0 = 1 $C. $ 4^0 = 1 $D. $ 5^0 = 1 $8. 下列各式中,正确的是()A. $ 0^2 = 0 $B. $ 0^3 = 0 $C. $ 0^4 = 0 $D. $ 0^5 = 0 $9. 下列各式中,正确的是()A. $ (1)^2 = 1 $B. $ (1)^3 = 1 $C. $ (1)^4 = 1 $D. $ (1)^5 = 1 $10. 下列各式中,错误的是()A. $ (2)^2 = 4 $B. $ (2)^3 = 8 $C. $ (2)^4 = 16 $D. $ (2)^5 = 32 $二、填空题(每题3分,共30分)11. 若一个数的平方根是5,则这个数是__________。
高一数学期中考试试题及答案

1.已知全集 U={0, 1 , 2, 3, 4},2.设集合M x 0 x 2 , N高一数学期中考试试题第I 卷选择题(共60 分)、选择题:(本大题共12小题,每小题5分,共60分•在每小题给出的四个选项中,只有一项是符合 题目要求的) M={0 , 1, 2} , N={2 , 3},则(C u M )n N =A • 2,3,4B • 2C • 3D •0,1,2,3,4y 0 y 2 ,给出如下四个图形,其中能表示从集合 M 到集合N 的A.[ 4, )B. [0,5]C. [ 4,5] 25. 3log342733lg0.01 lneA. 14B. 0C. 1 6.在映射f : AB 中,A B{(x,y)|x, y 在集合B 中的像为A. ( 1, 3)B. (1,3)C. (3,1)D. [ 4,0]D. 6R},且 f : (x, y) (x y, x y),则 A 中的元素(1,2)D. ( 3,1)7.三个数a 0.312, b log 20.31 , c 2。
31之间的大小关系为函数关系的是3.设 f x 3x 3x 8,用二分法求方程 3x 3x 8 1,2内近似解的过程中得 f 1 0, f 1.5 0, f 1.25 0 ,则方程的根落在区间 A. (1,1.25) B. (1.25,1.5) C.(1.5,2) D. 不能确定 4.二次函数f (x ) x 24x (x [0,5])的值域为12.若函数f (x)为定义在R 上的奇函数,且在(0,)内是增函数,又f(2) 0,则不等式xf(x) 0的解集为-A . ( 2,0) U(2,)B. ( , 2)U(0,2) 一已知函数y f (x)在R 上为奇 函数,且当 x 0时, f(x) x 22x ,贝析式为A . f(x) x(x 2)B .f(x) x(x 2) C. f(x) x(x 2)D.f(x)x(x 2)函数y a x 与ylog a x(a 0,且a 1)在同一坐标系中的图像只可能是8. x 0时,函数f(x)的解10.设 log a 2 2 0,则9. A. 0 B. D.11.函数 f(x) 4x 5在区间[0, m ]上的最大值为5, 最小值为1,则实数m 的取值范围是A.[2,B.[2,4] C. [0,4] D.(2,4] C. ( , 2)U(2,) D. ( 2,0) (0,2)13.函数 f(X )2x 3 (x Xz2(x 2),则f [f( 3)]的值为2)x 0在区间 a, b 上高一数学期中考试答题卷、选择题:(本大题小共12题,每小题5分,共60分•在每小题给出的四 第II 卷非选择题(共90分)、填空题:(本大题共4小题,每小题4分,共16 分)14.计算: log 4 3 log 9 815. 二次函数y kx 24x 8在区间[5,20]上是减少的,则实数 k 的取值范围为 _____________________ 16. 给出下列四个命题:① 函数y |x|与函数y c x)2表示同一个函数;② 奇函数的图像一定通过直角坐标系的原点;2 2③ 函数y 3(x 1)的图像可由y 3x 的图像向右平移1个单位得到; ④若函数f (x)的定义域为[0,2],则函数f(2x)的定义域为[0,4]; ⑤设函数f x 是在区间a,b 上图像连续的函数,且 f a f b 0 ,则方程 至少有一实根;个选项中,只有一项是符合题目要求的)其中正确命题的序号是________________ •(填上所有正确命题的序号)已知函数f(x) 2x1 2x 1 .三、解答题:(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)17. (本题满分12分)已知全集U R,集合A XX 4,或x 1,B x 3 x 1 2,(1)求AB、(C U A) (QB);(2)若集合M x2k 1 x 2k 1是集合A的子集,求实数k的取值范围.18. (本题满分12分)⑴判断函数f(x)的奇偶性,并证明;⑵利用函数单调性的定义证明: f (x)是其定义域上的增函数19. (本题满分12分)已知二次函数f(x) x2 2ax 1 a在区间0,1上有最大值2,求实数a的值20. (本题满分12分)函数f (x) log a(3 ax)(a 0,a 1)(1)当a 2时,求函数f (x)的定义域;(2)是否存在实数a,使函数f (x)在[1,2]递减,并且最大值为1,若存在,求出a的值;若不存在,请说明理由21. (本题满分13分)广州亚运会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向广州亚组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售 400枚,而每增加一元则减少销售 100 枚,现设每枚纪念章的销售价格为X元.(1) 写出该专营店一年内销售这种纪念章所获利润y(元)与每枚纪念章的销售价格x(元)的函数关系式(并写出这个函数的定义域);(2) 当每枚纪念章销售价格x为多少元时,该特许专营店一年内利润y(元)最大,并求出最大值.22. (本题满分13分)设f(X)是定义在R上的奇函数,且对任意 a、b R,当a b 0时,都有丄® 理0. a b(1)若a b,试比较f (a)与f (b)的大小关系;(2)若f(9X2 3X) f (2 9X k) 0对任意x [0,)恒成立,求实数k的取值范围题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CDBCBDCAABBD• 2分 • 4分6分 10分12分 • 1分x 1 x 22x1参考答案131 13.15・(,0)(0, ] 16.8 410三、解答题: 17.(1)B x 3 x 1 2 x 2 x 3ABx1x 3 ,(C U A) (C U B) xx1,或x 3(2)由题意:2k 11 或 2k 14 ,5解得:k 1或k 5.218.(1) f (x)为奇函数.2x2, 2x1 2x20,又 2x11 0,2x210,又 f( x)2 %1 1 2x2X1 f (x)2 x 1 1 2x2X 1f (x)为奇 :函数(2) f(x) 1 22x 1任取 x 1、 x 2 R , 设x 1 X 2 ,2x 1 0, f (x)的定义域为R , 2f(xj f(X 2)(1 J J(1 X 21)2(11)2(2x1 2x2) 0 1)(2x21)f(xj f(X 2)0, f(xjf(X 2).f (x)在其定义域R 上是增函数12分、选择题: 、填空题:③⑤19.函数f (x)的对称轴为:x a ,当a 0时,f(x)在[0,1]上递减, f (0) 2,即1 a 2, a 1 ;当0 a 1时,f(x)在[0,a ]递增,在[a,1]上递减, 与0 a 1矛盾;综上:a 1或a 2 20. ( 1 )由题意:f(x) log 2(3 2x), 3 2x f (a)2,即 a 2a 12,解得:a12分0,即 卩 x所以函数f(x)的定义域为( (2)令 u 3 ax ,则 u 3 ax 在[1,2]上恒正, a 0, a 3 a 2 0,即卩 a (0,1) (%)又函数f(x)在[1,2]递减, u 3 ax 在[1,2]上单调递减, 1,即 又 函数f (x)在[1,2]的最大值为 1, f(1) 即 f (1) log a (3 a 1) 1,3 ax 在[1,2]上单调递减,a d,|)11分 3 3 a 2与a (1,2)矛盾,12分依题意y[2000 400(20 x)](x 7), 7 x 20, x N [2000 100(x 20)](x 7), 20 x 40, x N400[(x 2佝281],7 x20, x Ny47 21089100[(x 2)4 ], 20 x 40, x N定义域为x N 7 x 40400[(x 16)2 81], 7 x 20, x Na 不存在. ⑵•- y 2 100[(x 21. (1) •••当 0 当20 综上:当x 16时, x 20时,则x ^089], 20 x 40,x N ' 4 16 , Y max 32400 (元)47 2 , Y max该特许专营店获得的利润最大为 x 40时,则x 27225 (元) 32400 元. 10分13分22. (1)因为a b ,所以a b 0 ,由题意得: ―0,所以 f(a) f( b) 0 , a b又f (x)是定义在R 上的奇函数,f (9x 2 3x ) f (2 9x k) 0对任意x[0, )恒成立,f (9x 2 3x )f (2 9x k) ,即 f(9x 2 3x)f(k 2 9x ),.....9分9x 2 3xk 2 9x,k x3 92 3 x对任意 x [0,)恒成立,即k 小于函数u 3 9X2 3X,x [0,)的最小值...... 11分xxx21 2 1令 t 3x,则 t [1,) u 3 9x 2 3x 3t 22t 3(t- 1, 3 3k 1..... 13 分。
高一数学必修一期中考试试题及答案

考试时间:100分钟,满分100分.一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.下列关系正确的是:A .Q ∈2B .}2{}2|{2==x x x C .},{},{a b b a = D .)}2,1{(∈∅2.已知集合}6,5,4,3,2,1{=U ,}5,4,2{=A ,}5,4,3,1{=B ,则)()(B C A C U U ⋃A .}6,3,2,1{B .}5,4{C .}6,5,4,3,2,1{D .}6,1{ 3.下列函数中,图象过定点)0,1(的是A .x y 2=B .x y 2log =C .21x y = D .2x y =4.若b a ==5log ,3log 22,则59log 2的值是: A .b a -2B .b a -2C .b a 2D .ba25.函数3log )(3-+=x x x f 的零点所在的区间是A .(0,1)B .(1,2)C .(2,3)D .(3,+∞) 6.已知函数ax x x f +=2)(是偶函数,则当]2,1[-∈x 时,)(x f 的值域是: A .]4,1[ B .]4,0[ C .]4,4[- D .]2,0[8.某林场计划第一年造林10 000亩,以后每年比前一年多造林20%,则第四年造林 A .14400亩 B .172800亩 C .17280亩 D .20736亩9.设c b a ,,均为正数,且a a21log 2=,b b 21log 21=⎪⎭⎫ ⎝⎛,c c2log 21=⎪⎭⎫ ⎝⎛.则A .c b a <<B .a b c <<C .b a c <<D .c a b <<10.已知函数()log a f x x =(0,1a a >≠),对于任意的正实数,x y 下列等式成立的是A .()()()f x y f x f y +=B .()()()f x y f x f y +=+C .()()()f xy f x f y =D . ()()()f xy f x f y =+二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卷中的横线上.11.若幂函数()f x 的图象过点2,2⎛ ⎝⎭,则()9f = _________12.函数()f x =的定义域是13. 用二分法求函数)(x f y =在区间]4,2[上零点的近似解,经验证有0)4()2(<⋅f f 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一下学期期中质量调查数学试题 第Ⅰ卷(选择题 共24分)
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目
要求的.
1.下列命题正确的是
A.若0a b <<,则 ac bc <
B. 若,a b c d >>,则 ac bd >
C.若a b >,则1a b <
D.若22,0a b
c c c
>≠,则a b > 2.在数列{}n a 中,111,3n n a a a +=-=-,则4a = A. 10- B. 7- C. 5- D. 11
3.若13,24a b <<<<,则a
b
的范围是
A. 1,12⎛⎫ ⎪⎝⎭
B. 3,42⎛⎫ ⎪⎝⎭
C. 13,42⎛⎫
⎪⎝⎭
D.()1,4
4.在ABC V
中,已知,24
c A a π
==
=,则角C =
A.
3π B. 23π C. 3π或23π D.12π或512
π
5.已知数列{}n a 为等比数列,有51374a a a -=,{}n b 是等差数列,且77a b =,则59b b +=
A. 4
B. 8
C. 16
D. 0或8
6.在ABC V 中,已知sin 2cos sin A B C =,则ABC V 的形状时 A. 直角三角形 B. 等腰三角形 C.等腰直角三角形 D.不确定
7.设n S 是等差数列{}n a 的前n 项和,若3613S S =,则612
S
S = A. 13 B. 18 C. 19 D.310
8.已知数列{}n a 前n 项和21n
n S =-,则此数列奇数项和前n 项和是
A. ()21213n -
B. ()11213n +-
C. ()21223n -
D. ()11
223
n +-
第Ⅱ卷(非选择题 共76分)
二、填空题:本大题共6小题,每小题4分,共24分.
9.在数列{}n a 中,2
23n a n =-,则125是这个数列的第 项.
10.在ABC V 中,三边,,a b c 成等比数列,222
,,a b c 成等差数列,则三边,,a b c 的关系为 .
11.对于任意实数x ,不等式2
3
204
mx mx +-
<恒成立,则实数m 的取值范围是 . 12.在等差数列{}n a 中,已知11a =,前5项和535,S =则8a 的值是 .
13.在ABC V 中,若120,5,7,A AB BC ===o
,则ABC V 的面积S = .
14.已知数列{}n a 满足,11232,2n
n n a a a +=+⋅=,则数列{}n a 的通项公式是 .
三、解答题:本大题共6小题,共52分,解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分8分)
已知不等式2
320ax x -+>的解集为{}
|x 1x b x <>或.
(1)求,a b 的值;
(2)解关于x 的不等式()2220ax b a x b ---<.
16.(本小题满分8分)
已知等比数列{}n a 中,11a =,公比为q ,且()
1.n n n b a a n N *+=-∈ (1)判断数列{}n b 是否为等比数列?请说明理由. (2)求数列{}n b 的通项公式.
17.(本小题满分8分)
已知数列{}n a 的前项和2
2 4.n n S +=-
(1)求数列{}n a 的通项公式;
(2)设等差数列{}n b 满足,73154,b a b a ==,求数列{}n b 的前项和.n T
18.(本小题满分12分)
若等比数列{}n a 的前n 项和1.2
n n n S a =- (1)求实数a 的值;
(2)求数列{}n na 的前n 项和.n T
19.(本小题满分10分)
在ABC V 中,角,,A B C 的对边分别为,,a b c ,已知45,cos .5
b c A == (1)求sin C 的值;
(2)若ABC V 的面积为3
sin sin ,2
ABC S B C =V 求a 的值.
20.(本小题满分10分)
已知数列{}n a 的前n 项和为n S ,满足11110,2,.n n n n n n n n a a S a S a a n N -*
+++≠-=∈ (1)求证:1
2;n n n S a -=
(2)设1
n
n n a b a +=,求数列{}n b 的前n 项和.n T。
