计算传热学 第3讲 数学模型与求解区域的离散化 习题课 Patanker 3.1
传热学-第三章

同样可得:
t tm,n1 2tm,n tm,n1 o(y 2 ) y 2 m,n y 2
2
未明确写出的级数余项 中的Δ X的最低阶数为2
对于二维稳态导热问题,在直角坐标中,其导热 微分方程为:
2t 2t v 0 2 2 x y
其节点方程为:
温度ti-1,j
tm1,n
t 2t x 2 3t x3 t m ,n x 2 3 x m,n x m,n 2! x m,n 3!
若取上面式右边的前三项,并将式①和式③相加 移项整理即得二阶导数的中心差分:
2t x 2
m ,n
tm1,n 2tm,n tm1,n o(x 2 ) x 2
Φ 内热源: v Φ V Φ xy
Φ上 Φ下 Φ左+Φ右 Φv 0
tm1,n tm ,n tm1,n tm ,n tm ,n1 tm ,n tm ,n1 tm ,n y y x x x x y y Φxy 0
例如:根据第 k 次迭代的数值 可以求得节点温度:
(k) (k) (k) t1 、t2 ....tn
( ( ( ( ( t1 k 1) a11t1 k ) a12t2k ) ...... a1ntnk ) b1 k )
在计算后面的节点温度时应按下式(采用最新值)
( ( ( ( ( t 2k 1) a21t1 k 1) a22t 2k ) ...... a2 n t nk ) b2k ) ( ( ( ( ( t3k 1) a31t1 k 1) a32t 2k 1) ...... a3n t nk ) b3k )
h1t f
x
传热学课件第3章

3-2 集总参数法的简化分析
4 Biv Fov 的物理意义
l 物体内部导热热阻 Bi = 1 h 物体表面对流换热热阻 hl
换热时间 Fo 2 l a 边界热扰动扩散到 l 2 面积上所需的时间
无量纲 热阻
Fo越大,热扰动就能越深入地传播 到物体内部,因而,物体各点的温度 就越接近周围介质的温度。
无量纲 时间
3-2 集总参数法的简化分析
5 集总参数法的适用范围
Biv
或
是与物体几何形状 有关的无量纲常数
h( V A )
Bi
hl
0.1M
采用此判据时,物体中各点 过余温度的差别小于5%。
V A A A V R 2 R A 2R 2 4 3 R V R 3 2 A 4R 3 Biv Bi Biv Bi 2
第三章 非稳态导热
本章重点内容
重点内容: ① 非稳态导热的基本概念及特点; ② 集总参数法的基本原理及应用; ③ 一维非稳态导热问题。 掌握内容: ① 确定瞬时温度场的方法; ② 确定在一时间间隔内物体所传导热量的 计算方法。 了解内容: 无限大物体非稳态导热的基本特点。
作业
3-7,3-9 3-12,3-17
3-2 集总参数法的简化分析
3 瞬态热流量:Φ ( ) hA(t ( ) t ) hA
hA 0 e
hA Vc
W
hA Vc
导热体在时间 0~ 内传给流体的总热量:
Q 0 Φ ( )d Vc 0 (1 e
) J
当物体被加热时(t0<t),计算式相同(为什么?)
方程中指数的量纲:
传热学传热学--第三章 第三节 一维非稳态导热问题

传热学--第三章第三节一维非稳态导热问题§3 — 3 一维非稳态导热的分析解本节介绍第三类边界条件下:无限大平板、无限长圆柱、球的分析解及应用。
如何理解无限大物体,如:当一块平板的长度、宽度>> 厚度时,平板的长度和宽度的边缘向四周的散热对平板内的温度分布影响很少,以至于可以把平板内各点的温度看作仅是厚度的函数时,该平板就是一块“无限大”平板。
若平板的长度、宽度、厚度相差较小,但平板四周绝热良好,则热量交换仅发生在平板两侧面,从传热的角度分析,可简化成一维导热问题。
一、无限大平板的分析解已知:厚度的无限大平板,初温t0,初始瞬间将其放于温度为的流体中,而且>t0,流体与板面间的表面传热系数为一常数。
试确定在非稳态过程中板内的温度分布。
解:如图3-5 所示,平板两面对称受热,所以其内温度分布以其中心截面为对称面。
对于x 0 的半块平板,其导热微分方程:(0<x< , )定解条件:t(x,0)= t0(0 x )(边界条件)(边界条件)引入过余温度:则(0<x< , )(3-9)(x,0)= (0 x ) (初始条件)(边界条件)(边界条件)对偏微分方程分离变量求解得:(3-10 )其中离散值是下列超越方程的根,称为特征值。
其中Bi 是以特征长度为的毕渥数。
由此可见:平板中的无量纲过余温度与三个无量纲数有关:以平板厚度一半为特征长度的傅立叶数、毕渥数及即:(3-12)二、非稳态导热的正规状况阶段1 、平板中任一点的过余温度与平板中心的过余温度的关系前述得到的分析解是一个无穷级数,计算工作量大,但对比计算表明,当Fo>0.2 时,采用该级数的第一项与采用完整的级数计算平板中心温度的误差小于1% ,因此,当Fo>0.2时,采用以下简化结果:(3-13 )其中特征值之值与Bi 有关。
由上式(3-13 )可知:Fo>0.2 以后平板中任一点的过余温度(x ,τ) 与平板中心的过余温度(0 ,τ)=(τ )之比为:(3-14 )此式反映了非稳态导热过程中一种很重要的物理现象:即当Fo>0.2 以后,虽然(x ,τ) 与(τ )各自均与τ 有关,但其比值则与τ 无关,而仅取决于几何位置(x/ )及边界条件(Bi )。
传热学第三章答案(精品资料).doc

【最新整理,下载后即可编辑】第三章思考题1. 试说明集中参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。
而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数,数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。
2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数hA cvc ρτ=,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。
3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。
如薄板两侧均匀加热或冷却、炉墙或冷库的保温层导热等情况可以按无限大平板处理。
4.什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍随时间变化,但过余温度的比值已与时间无关,只是几何位置(δ/x)和边界条件(Bi数)的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。
这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。
5.有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是:这个图表明,物体中各点的过余温度的比值与几何位置及Bi有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。
你是否同意这种看法,说明你的理由。
答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变但各点温度的绝对值在无限接近。
这与物体中各点温度趋近流体温度的事实并不矛盾。
传热学 第3章

1) 数学模型
2 τ = 0, Θ = Θ 0 = 1 δ Fo是无量纲特征数 Fo是无量纲特征数, 是无量纲特征数, Θ X = 0, =0 称为傅里叶数 称为傅里叶数 x hδ Θ hδ 称为毕渥数 称为毕渥数 4 X = 1, = Θ Bi = λ X λ
2Θ = ( Fo) X 2 τ = 0, Θ = Θ 0 = 1 Θ X = 0, =0 X Θ X = 1, = Bi Θ X
2 1
上面两式之比
x f Bi , δ 可见, 非稳态导热进入正规状况阶段以后, 可见,当Fo ≥ 0.2,非稳态导热进入正规状况阶段以后, 都随时间变化,但它们的比值与时间无关, 虽然θ与θm都随时间变化,但它们的比值与时间无关, 只取决于毕渥数Bi与几何位置 与几何位置x/ 只取决于毕渥数Bi与几何位置x/δ 。 认识正规状况阶段的温度变化规律具有重要的实 际意义, 际意义,因为工程技术中的非稳态导热过程绝大部分 时间都处于正规状况阶段 。 10
第三章
主要内容: 主要内容:
非稳态导热
非稳态导热过程中温度场的变化规律及换热量的分 析求解方法。包括: 析求解方法。包括: 1. 一维非稳态导热的分析解法; 一维非稳态导热的分析解法; 2. 非稳态导热的集总参数分析法; 非稳态导热的集总参数分析法; 3. 半无限大固体的非稳态导热 ;
3-1 非稳态导热的基本概念
14
( 2)
θ θ0 θ x = = cos 1 = θm θm θ0 δ
x f Bi , δ
15
2 Q 2sin 1 1 Fo ( 3) = 1 2 e = f ( Bi , Fo ) 1 + 1 sin 1 cos 1 Q0
2
16
几点说明:
传热学第3章

u
温度尚未变化,仍为t0,x也称为 穿透深度。
tw
(2)当 x2/16a 时,深度x
处的温度保持不变,时间
称为深度x 处的惰性时间。
t0
1 2 3
x1 x2 x3 x
根据傅里叶定律,半无限大物体内任意一点在 时刻的热流 密度为
qx x ttw π at0exp 4 x a 2
控制方程 初始条件
方程式改写为:
d
hVAcd
第三章 非稳态导热
25
d hAd Vc
积分
0dhVAc0d
ln hA
tt ehVAc
0
Vc
0 t0t
其中的指数: hAhV A2 cV AV2c
过余温度比
h(V A) a
(V
A)2
BviFov
B v i h ( V A ) F v o ( V a A ) 2
Fo越大,热扰动就能越深入地传播到物体内 部,因而,物体各点地温度就越接近周围介 质的温度。
无量纲 时间
第三章 非稳态导热
32
5 集总参数法的应用条件 采用此判据时,物体中各点过余温度的差别小于5%
h(VA)
Biv 0.1M
是与物体几何形状
有关的无量纲常数
对厚为2δ的
无限大平板
对半径为R的 无限长圆柱
上式说明,当Fo 0.2,进入正规状况阶段后,所有各点的冷却率都相
同,且不随时间而变化,其大小取决于物体的物性、几何形状与尺寸及 表面传热系数。
4. 毕渥数
本章以第三类边界条件为重点。
(1) 问题的分析
如图所示,存在两个换热环节:
tf
h
a 流体与物体表面的对流换热环节
计算传热学第3讲数学模型与求解区域的离散化

求解区域的离散化:网格参数
一维为例
(x)w
(x)+w
(x)e (x)-e
W
w
P
(x)-w
x
图 1 一维问题空间区域的离散化
e
E
(x)+e
网格参数:名称与定义
(x)w=(x)+w+(x)-w 节点W-P之间的距离 (x)e=(x)+e+(x)-e 节点P-E之间的距离 (x)+w 控制界面w-节点P之间的距离 (x)-e 节点P-控制界面e之间的距离 x = (x)+w +(x)-e 控制容积
(13) [E P ( )P (x)e ](x)2w[(x)e (x)w ]
1 2
2 x2
(x)
2 e
(x)2w[(x)e
(x)w
]
P
1 3
3! x3
(x)
2 w
(x)e2[(x)e2
(x)2w
]
P
1 4
4! x4
(x)
2 e
(x)2w[(x)3e
(x)3w
]
.......
P
非均匀步长:二阶导数(2阶精度)
区域的大小对计算结果没有明显的影响。 例子:
求解区域的界定:例子
流动问题的出口界面:
求解区域的界定:例子
无穷大区域的“无穷远界面”
半无限大介质中的稳态导热 Tf, h
Tf, h Tw
求解区域的界定:例子
无穷大区域的“无穷远界面”
无限大介质中的非稳态导热
y
x
求解区域的界定
对称区域:对称问题的求解区域
(W
P )]
O[(x)
w
传热学讲义——第三章
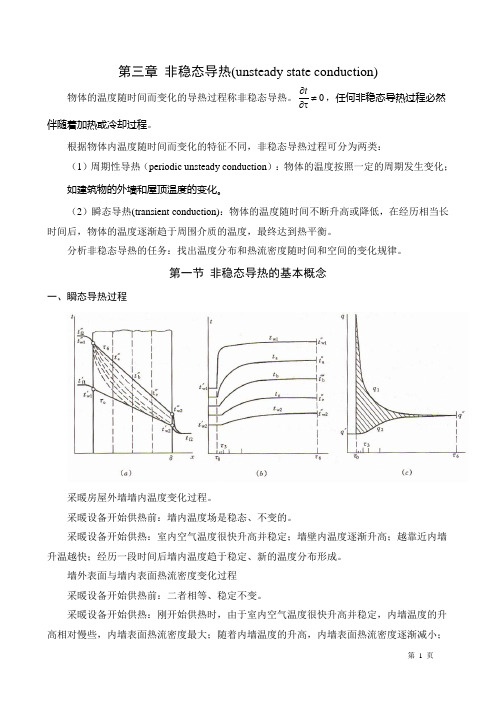
第三章 非稳态导热(unsteady state conduction)物体的温度随时间而变化的导热过程称非稳态导热。
0≠τ∂∂t,任何非稳态导热过程必然伴随着加热或冷却过程。
根据物体内温度随时间而变化的特征不同,非稳态导热过程可分为两类:(1)周期性导热(periodic unsteady conduction ):物体的温度按照一定的周期发生变化; 如建筑物的外墙和屋顶温度的变化。
(2)瞬态导热(transient conduction):物体的温度随时间不断升高或降低,在经历相当长时间后,物体的温度逐渐趋于周围介质的温度,最终达到热平衡。
分析非稳态导热的任务:找出温度分布和热流密度随时间和空间的变化规律。
第一节 非稳态导热的基本概念一、瞬态导热过程采暖房屋外墙墙内温度变化过程。
采暖设备开始供热前:墙内温度场是稳态、不变的。
采暖设备开始供热:室内空气温度很快升高并稳定;墙壁内温度逐渐升高;越靠近内墙升温越快;经历一段时间后墙内温度趋于稳定、新的温度分布形成。
墙外表面与墙内表面热流密度变化过程 采暖设备开始供热前:二者相等、稳定不变。
采暖设备开始供热:刚开始供热时,由于室内空气温度很快升高并稳定,内墙温度的升高相对慢些,内墙表面热流密度最大;随着内墙温度的升高,内墙表面热流密度逐渐减小;随着外墙表面的缓慢升高,外墙表面热流密度逐渐增大;最终二者相等。
上述非稳态导热过程,存在着右侧面参与换热与不参与换热的两个不同阶段。
(1)第一阶段(右侧面不参与换热)是过程开始的一段时间,特点是:物体中的一部分温度已经发生变化,而另一部分仍维持初始状态时的温度分布(未受到界面温度变化的影响),温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布,物体内各处温度随时间的变化率是不一样的,即:在此阶段物体温度分布受t分布的影响较大,此阶段称非正规状况阶段或初始阶段(initialregime)。
(2)第二阶段(右侧面参与换热)当右侧面参与换热以后,物体中的温度分布不受t影响,主要取决于边界条件及物性。
计算传热学

(xo,yo) t, x
iii. 双曲型方程
前一时刻 t t+Δt
推进
也是步进问题。但依赖区域仅在两条特征区域之间。 例如:无粘性流体的非稳态问题;无粘性流体的稳态超音速流动。
2. 流动类型
(xo,yo) t, x
偏微分方程组或积分方程组及边界条件。必须选择应用的目标: • 不可压缩ÅÆ可压缩 • 非粘性的ÅÆ粘性 • 湍流ÅÆ层流 • 2 维或 3 维 • 单相ÅÆ多相 • 。。。 由此可以选择不同的简化守恒方程。
1.2.9 流动基本方程式
1. 流动守恒定理(Conservation Laws)
i. 连续性方程(质量守恒方程, continuity equation)
错误!未定义书签。
∂ρ ∂t
=
−(∇ ⋅
ρu ) +
Ms
( 0-2 )
单位体积的质量流束的散度净量为内部密度的增加速度。用全导数表
示:
Dρ Dt
的守恒,也要保证总体的守恒。使用有限体积法或基于严格的守恒形式进行的离 散,则可保证每个控制体的守恒。其它离散方法则要充分注意守恒问题。
守恒问题在求解方法中是非常重要的特性。非守恒方法会导致人工源(阱) 的产生。但非守恒方法有时(如采用极小的网格)能保证相容性和稳定性,而产 生正确的解。但一般因采用粗的网格,故建议使用守恒形式。
ii. 有限体积法(finite volume method FVM) 积分方程
使用控制体积,选择表面和体积积分的近似方法。 • 将区域离散成有限个控制体积,适用任何形状的网格; • 选择未知函数对时间和空间的局部分布曲线(线性或曲线分布); • 对每个 CV 进行空间(表面、体积)和时间的积分; • 整理出关于节点上未知数的代数方程式。 特点:适用任何形状的网格,可用复杂几何形状 与坐标类型无关 提示:网格、积分方程、分布曲线、表面和体积分、代数方程
传热学第三章

unsteady state heat conduction
3-1 非稳态导热过程的特点
一、定义 导热体的温度随时间而变化的导热过程称为非稳态导热
∂t t = f ( x, y , z , τ ) , ≠0 ∂τ
工程中的许多过程都是非稳态导热: 冶金、热处理和热加工;工件被加热和冷却; 锅炉、内燃机、燃气轮机等装置启动、停机、变工况; 自然环境温度,供暖和停暖过程中墙内与室内空气温度。
四、导温系数(热扩散系数)
∂t ∂ t ρcp =λ 2 ∂τ ∂x
2
λ a = ρc p
∂t ∂ 2t =a 2 ∂τ ∂x
反映了物体的导热能力和储热能力之比,它可以用来衡量 物体在加热或冷却时内部温度变化传播速度。 λ越大,说明在相同的温度梯度下可以传递更多的热量;ρ c p 越小,单位体积的物体温度升高1℃所需要的热量越小,可以 剩下更多的热量继续向物体内部传递,使得物体内部各点温度 趋于一致的能力提高。
五、毕渥准则对温度分布的影响 αδ 毕 渥 准 则 — 无 量 纲 数 δ —平板厚度之半 Bi = λ αδ δ / λ 物体内部导热热阻 Bi = = λ 1/α 物体表面对流换热热阻
t0
τ
t0
τ
t0
τ
tf
tf
tf
tf
tf
tf
1 / α << δ / λ
Bi→∞
1 / α >> δ / λ
毕渥数Bi对平板温度场变化的影响
例题3-1 一直径为50mm的钢球,初始温度为450℃,突然 被置于温度为30℃的空气中。设钢球表面与周围空气的对流 换热系数为24W/(m2·K),试计算钢球冷却到300℃时所需要 的时间。已知钢球的 c p = 480 J /(kg ⋅ K ), ρ = 7753kg / m3 , λ = 33W /(m ⋅ K ). 解: 首先检验是否可以采用集总参数法。
传热学第三讲优秀课件

§2 导热微分方程
导入微元体的总热流量+微元体内热源的生成热
=导出微元体的总热流量+微元体热力学能(即内能)的增量
一、直角坐标系导热微分方程的形式
1.导入微元体的总热流量
x
t x
dydz
y
t y
dxdz
z
t z
dxdz
2.导出微元体的总热流量
xdx
x
x
dx
x
x
t x
dydz dx
、 及c 各为微元体的密度、时间及比热容
c t
x
t x
y
t y
z
t z
•
三维直角坐标系非稳态有内热源的导热微分方程
※ 为常数时
•
t
a
2t x 2
2t y 2
2t z 2
c
热扩散率(导温系数) ,m2 / s c
※ 为常数且无内热源时 ※ 为常数且稳态时
t
a
2 x
t
2
2t y 2
2t z 2
•
2t x2
2t y 2
2t z 2
0
※ 为常数、无内热源、稳态时 2t 2t 2t 0
x2 y 2 z 2
二、圆柱坐标系导热微分方程的形式
x r cos; y r sin ; z z
圆柱坐标系
(r, , z)
qr
t r
q
1 r
t
qz
t z
c t
1 r
r
r
t r
2
t
•
四、定解条件
1.初始条件 0时 t f (x, y, z) 2.边界条件
第三章 区域离散化

与式(2-6b)比较:
in1 in
t
u
n in 1 i 1
2x
n n in 2 1 i i 1
x
2
S
n i
(2—6b)
计算传热学
第 3 章 区域离散化及获得离散方程的方法
关于型线假设的进一步讨论
型线的选取:控制容积界面上被求函数的插值方式.
1、在有限容积法中,选取型线的目的是:导出离散方程。
2、考虑实施的方便及所形成的离散方程具有满 意的数值特性, 不必追求一致性(p42)。 如:上述推导中:
计算传热学
第 3 章 区域离散化及获得离散方程的方法
t t e
源项:
S d d t S t
t w
t
从而可得离散方程(常物性、均分网格)
t t t p p
t
(u ) (u ) 2x
t E t W
t t t E 2 p W
x
两种方法的比较: (1)边界节点所代表的控制容 积不同,如图2—3所示 ; (2)当网格不均分时,节点位 置不同,如图2—4所示;
计算传热学
两种方法的比较:
第 3 章 区域离散化及获得离散方程的方法
(3)当网格不均分时,界面位置不同,如图2—5所示 ;
计算传热学
第 3 章 区域离散化及获得离散方程的方法
(4)
计算传热学
第 3 章 区域离散化及获得离散方程的方法
2y 2y Ti ,1 4Ti , 2 Ti , 3 Tf 3 k k
(4)、(5)式均为边界节点方程
(5 )
3.2.3 控制容积平衡法:
第四版传热学第三章习题解答

第四版传热学第三章习题解答第三章思考题1. 试说明集总参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。
而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数,数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。
2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数hA cvc ρτ=,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。
3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。
如薄板两侧均匀加热或冷却、炉墙或冷库的保温层导热等情况可以按无限大平板处理。
4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍随时间变化,但过余温度的比值已与时间无关,只是几何位置(δ/x )和边界条件(Bi 数) 的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。
这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。
5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是:这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。
你是否同意这种看法,说明你的理由。
答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变但各点温度的绝对值在无限接近。
这与物体中各点温度趋近流体温度的事实并不矛盾。
计算传热学 对流扩散方程的离散格式PPT资料(正式版)

6.1 同位网格上的SIMPLE算法
同位网格
Ø交错网格数据存储不方便 Ø同位网格变量均存储在节点上 Ø如何解决前面所述的两个问题?
6.1 同位网格上的SIMPLE算法
同位网格动量方程的离散形式6. 同位网格上的SIMPLE算法
同位网格 在这里引入了1-deta压差
以上方程可以求解,但是比较复杂
计算传热学 对流扩散方程的离 散格式
主要内容
原始变量法 两个问题 交错网格 交错网格的压力修正方法 同位网格的压力修正方法
6.1 原始变量法
原始变量—非原始变量 基于密度—基于压力 耦合求解—分层求解
6.1 原始变量法
6.1 两个问题
压差
如何求解压力
6.1 两个问题
压差
6.1 两个问题
1 同位网格上的界SIM面PLE上算法的速度如何处理呢?
同位网格的压力修正方法 交错网格的压力修正方法
在这里引入了1-deta压差
6.1 同位网格上的SIMPLE算法
同位网格
Ø同位网格的SIMPLE算法思想与交错网格相同 Øu’,v‘,p’的关系类似于交错网格 Øue,uw等的表达式中的系数需要插值
6.1 压力修正方法
压力修正法的基本思想
u假定压力场,P* u利用压力场求解动量离散方程,得出u*,v* u利用连续方程构造相应的方法,改进压力场,要求改进的 压力场能够满足连续性方程,修正值 p’,u’,v’ uu*+u’,v*+v’,p*+p’作为新的解,开始下一层次的计算 ü如何获得p’? ü如何在p‘的基础上获得u‘,v’
6.1 压力修正方法
压力修正法的基本思想
ü如何获得p’? ü如何在p‘的基础上获得u‘,v’ 只有一个连续方程,因此,只能求解一个变量,需要把u’, v’转换成p‘的形式
传热学课件-第3章-非稳态导热分析解法精选全文

是与物体几何形状 有关的无量纲常数
对厚为2δ的 无限大平板
M 1
对半径为R的无 限长圆柱
M
1 2
对半径为R的 球
M 1 3
V A
AA
V R2 R
A 2R 2
V A
4 R3
3
4R 2
R 3
Biv Bi
Biv
Bi 2
Biv
Bi 3
对于一个复杂形体的形状修正系数时,可以将
修正系数M取为1/3,即 BiV 0.0333
由此可见,上述两个热阻的 相对大小对于物体中非稳态导热 的温度场的变化具有重要影响。 为此,我们引入表征这两个热阻 比值的无量纲数毕渥数。
Bi h 1h
1)毕渥数的定义:
Bi h 1h
毕渥数属特征数(准则数)。
2)Bi 物理意义: 固体内部单位导热面积上的导 热热阻与单位表面积上的换热热阻之比。Bi的大小
0
1
τ/τs
工程上认为= 4τc时导热体已达到热平衡状态
3 Bi F物o 理意义
hl l
Bi =
物体内部导热热阻
1 h 物体表面对流换热热阻
换热时间
Fo l2 a 边界热扰动扩散到l2面积上所需的时间
无量纲 热阻
无量纲 时间
Fo越大,热扰动就能越深入地传播到物体内部物体, 各点地温度就越接近周围介质的温度。
t(x, ) t — 过余温度
2
a
x2
0, t -t
0
0
x 0, 0
x , - x h x
采用分离变量法求解:
(, 0
)
n 1
Cn
exp(n2Fo) cos(n)
传热学-第三章

无量纲数
当Bi→∞时,⇒rλ>>rh ;因此,可以忽略对流换热热阻 当Bi→0 时,⇒rλ<<rh;因此,可以忽略导热热阻
(4) 无量纲数的简要介绍 基本思想:当所研究的问题非常复杂,涉及到的参数很 多,为了减少问题所涉及的参数,将一些参数组合起来, 使之能表征一类物理现象,或物理过程的主要特征,并且 没有量纲。 因此,这样的无量纲数又被称为特征数,或者准则 数,比如,毕渥数又称毕渥准则。以后会陆续遇到许多类 似的准则数。特征数涉及到的几何尺度称为特征长度,一 般用符号 l 表示。 对于一个特征数,应该掌握其定义式+物理意义,以 及定义式中各个参数的含义。
着重讨论瞬态非稳态导热
3. 温度分布:
4. 两个不同的阶段
非正规状况阶段 (不规则情况阶段) 正规状况阶段 (正常情况阶段) 温度分布主要受初始温度 分布控制 温度分布主要取决于边界 条件及物性
非稳态导热过程总会经历:非稳态导热非正规状况阶段 (起始阶段)、正规状况阶段、新的稳态
5. 热量变化
可以采用集总参数法。时间常数为
13110 × 0.138 × 1000 × 0.953 × 10 −3 = = 148 τc = hA 11.63
ρcV
s
⎛ hA ⎞ 11.63 × 5 × 60 θ ⎛ ⎞ = exp⎜ − ⎟ ⎜ ρcV ⋅ τ ⎟ = exp⎜ − ⎟ −3 θ0 ⎝ 13110 × 0.138 × 1000 × 0.953 × 10 ⎠ ⎝ ⎠ = exp(− 2.02 ) = 0.133
5. 集总参数法的应用条件
对于平板、圆柱及圆球,如果Bi满足如下条件,则 物体中各点过余温度的差别小于5%
Bi v =
对厚为2δ的 无限大平板 对半径为R的 无限长圆柱 对半径为R的 球
