2010清华大学自主招生数学试题
2010复旦交大清华北大自主招生数学试题

O x O xO x则该多面体的体积为______________A. 32个;B. 30个;C.28个;D.26个7、给定平面向量(1,1),那么,平面向量(231-,231+)是将向量(1,1)经过________. A .顺时针旋转60°所得;B .顺时针旋转120°所得;C .逆时针旋转60°所得;D .逆时针旋转120°所得;8、在直角坐标系Oxy 中已知点A 1(1,0),A 2(1/2,3/2),A 4(−1,0),A 5(−1/2,−3/2)和A6(1/2, −3/2).问在向量−−→−ji A A (i,j=1,2,3,4,5,6,i≠j)中,不同向量的个数有_____.A.9个;B.15个;C.18个;D.30个 9、对函数f:[0,1]→[0,1],定义f 1(x)=f(x),……,f n (x) =f(f n−1(x)),n=1,2,3,…….满足f n (x)=x的点x ∈[0,1]称为f 的一个n−周期点.现设⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤=121,22,210,2)(x x x x x f 问f 的n−周期点的个数是___________.A.2n 个;B.2n 2个;C.2n 个;D.2(2n −1)个.10、已知复数z 1=1+3i ,z 2=−3+3i ,则复数z 1z 2的幅角__________. A.13π/12;B.11π/12;C.−π/4;D.−7π/12.11、设复数βαβαcos sin ,sin cos i w i z +=+=满足z w =3/2,则sin(β−α)=______. A.±3/2;B.3/2,−1/2;C. ±1/2;D.1/2,−3/2.12、已知常数k 1,k 2满足0<k 1<k 2,k 1k 2=1.设C 1和C 2分别是以y=±k 1(x−1)+1和y=±k 2(x−1)+1为渐近线且通过原点的双曲线.则C 1和C 2的离心率之比e 1/e ·等于_______.A.222111k k ++; B.212211k k ++ C.1 D.k 1/k 213、参数方程0,)cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 所表示的函数y=f(x)是____________.A .图像关于原点对称;B .图像关于直线x=π对称;C .周期为2aπ的周期函数D .周期为2π的周期函数.14、将同时满足不等式x−ky−2≤0,2x+3y−6≥0,x+6y−10≤0 (k>0)的点(x,y)组成集合D 称为可行域,将函数(y+1)/x 称为目标函数,所谓规划问题就是求解可行域中的点(x,y)使目标函数达到在可行域上的最小值.如果这个规划问题有无穷多个解(x,y),则k 的取值为_____.A.k≥1;B.k≤2C.k=2;D.k=1.15、某校有一个班级,设变量x 是该班同学的姓名,变量y 是该班同学的学号,变量z 是该班同学的身高,变量w 是该班同学某一门课程的考试成绩.则下列选项中正确的是________.A. y 是x 的函数;B. z 是y 的函数;C. w 是z 的函数;D. w 是x 的函数.16、对于原命题“单调函数不是周期函数”,下列陈述正确的是________. A. 逆命题为“周期函数不是单调函数”; B. 否命题为“单调函数是周期函数”; C. 逆否命题为“周期函数是单调函数”; D. 以上三者都不正确17、设集合A={(x,y)|log a x+log a y>0},B={(x,y)|y+x<a}.如果A∩B=∅,则a 的取值范围是_______A .∅;B .a>0,a≠1;C .0<a≤2, a≠1D .1<a≤218、设计和X 是实数集R 的子集,如果点x 0∈R 满足:对任意a>0,都存在x ∈X 使得0<|x−x 0|<a ,则称x 0为集合X 的聚点.用Z 表示整数集,则在下列集合(1){n/(n+1)|n ∈Z, n≥0}, (2) R\{0}, (3){1/n|n ∈Z, n≠0}, (4)整数集Z 中,以0为聚点的集合有_____.A .(2), (3);B .(1), (4);C .(1), (3);D .(1), (2), (4)19、已知点A(−2,0),B(1,0),C(0,1),如果直线kx y =将三角形△ABC 分割为两个部分,则当k=______时,这两个部分得面积之积最大?A .23-B .43-C .34-D .32- 20、已知x x x x f 2cos 3cos sin )(+=,定义域⎥⎦⎤⎢⎣⎡=ππ127,121)(f D ,则=-)(1x f_____A .π12123arccos 21+⎪⎪⎭⎫ ⎝⎛-xB .π6123arccos 21-⎪⎪⎭⎫ ⎝⎛-x C .π12123arcsin 21+⎪⎪⎭⎫ ⎝⎛--x D .π6123arcsin 21-⎪⎪⎭⎫ ⎝⎛-x 21、设1l ,2l 是两条异面直线,则直线l 和1l ,2l 都垂直的必要不充分条件是______ A .l 是过点11l P ∈和点22l P ∈的直线,这里21P P 等于直线1l 和2l 间的距离 B .l 上的每一点到1l 和2l 的距离都相等 C .垂直于l 的平面平行于1l 和2l D .存在与1l 和2l 都相交的直线与l 平行22、设ABC−A’B’C’是正三棱柱,底面边长和高都为1,P 是侧面ABB ’A’的中心,则P到侧面ACC’A’的对角线的距离是_____A .21 B .43 C .814 D .82323、在一个球面上画一组三个互不相交的圆,成为球面上的一个三圆组.如果可以在球面上通过移动和缩放将一个三圆组移动到另外一个三圆组,并且在移动过程中三个圆保持互不相交,则称这两个三圆组有相同的位置关系,否则就称有不同的位置关系.那么,球面上具有不同的位置关系的三圆组有______A .2种B .3种C .4种D .5种24、设非零向量()()()321321321,,,,,,,,c c c c b b b b a a a a ===为共面向量,),,(31x x x x x = 是未知向量,则满足0,0,0=⋅=⋅=⋅x c x b x a的向量x 的个数为_____A .1个B .无穷多个C .0个D .不能确定 25、在Oxy 坐标平面上给定点)1,2(),3,2(),2,1(C B A ,矩阵⎪⎪⎭⎫⎝⎛-112k 将向量,,分别变换成向量',',',如果它们的终点',','C B A 连线构成直角三角形,斜边为''C B ,则k 的取值为______A .2±B .2C .0D .0,−2 26、设集合A,B,C,D 是全集X 的子集,A∩B≠∅,A∩C≠∅.则下列选项中正确的是______. A.如果B D ⊂或C D ⊂,则D∩A≠∅;B.如果A D ⊂,则C x D∩B≠∅,C x D∩C≠∅;C.如果A D ⊃,则C x D∩B=∅,C x D∩C=∅;D.上述各项都不正确.27、已知数列{}n a 满足21=a 且n a n ⎧⎫⎨⎬⎩⎭是公比为2的等比数列,则∑==nk k a 1______A .221-+n n B .22)1(1+-+n n C .)1(22-+n n n D .n n n 22)1(+-28、复平面上圆周2211=+--iz z 的圆心是_______ A .3+i B .3−i C .1+i D .1−i29.已知C 是以O 为圆心、r 为半径的圆周,两点P 、P *在以O 为起点的射线上,且满足|OP|∙|OP *|=r 2,则称P 、P *关于圆周C 对称.那么,双曲线22x y -=1上的点P(x,y)关于单位圆周C':x 2+y 2=1的对称点P *所满足的方程是(A)2244x y x y -=+ (B)()22222x y x y -=+ (C)()22442x y x y -=+(D)()222222x y x y-=+30、经过坐标变换⎩⎨⎧+-=+=θθθθcos sin 'sin cos 'y x y y x x 将二次曲线06532322=-+-y xy x 转化为形如1''2222=±by a x 的标准方程,求θ的取值并判断二次曲线的类型_______A .)(6Z k k ∈+=ππθ,为椭圆 B .)(62Z k k ∈+=ππθ,为椭圆C .)(6Z k k ∈-=ππθ,为双曲线D .)(62Z k k ∈-=ππθ,为双曲线31、设k, m, n 是整数,不定方程mx+ny=k 有整数解的必要条件是____________ A. m,n 都整除k ; B. m,n 的最大公因子整除k ; C. m,n,k 两两互素; D. m,n,k 除1外没有其它共因子2010年五校合作自主选拔通用基础测试 数学试题 适用高校:清华大学、上海交通大学等五校 一、选择题1.设复数2()1a i w i+=+,其中a 为实数,若w 的实部为2,则w 的虚部为( ) (A)32- (B)12- (C)12 (D)322.设向量,a b ,满足||||1,==⋅=a b a b m ,则||+a tb ()t R ∈的最小值为( ) (A)2(C)13. 无试题4. 无试题5.在ABC ∆中,三边长,,a b c ,满足3a c b +=,则tan tan 22A C的值为( ) (A)15 (B)14 (C)12 (D)236.如图,ABC ∆的两条高线,AD BE 交于H ,其外接圆圆心为O ,过O 作OF 垂直BC 于F ,OH 与AF 相交于G ,则OFG ∆与GAH ∆面积之比为( )(A)1:4 (B)1:3 (C)2:5 (D)1:2O H G FEDCBA7.设()e (0)axf x a =>.过点(,0)P a 且平行于y 轴的直线与曲线:()C y f x =的交点为Q ,曲线C 过点Q 的切线交x 轴于点R ,则PQR ∆的面积的最小值是( )(A)1 (C)e2(D)2e 48.设双曲线2212:(2,0)4x y C k a k a -=>>,椭圆2222:14x y C a +=.若2C 的短轴长与1C 的实轴长的比值等于2C 的离心率,则1C 在2C 的一条准线上截得线段的长为( )(A) (B)2 (C) (D)49.欲将正六边形的各边和各条对角线都染为n 种颜色之一,使得以正六边形的任何3个顶点作为顶点的三角形有3种不同颜色的边,并且不同的三角形使用不同的3色组合,则n 的最小值为( )(A)6 (B)7 (C)8 (D)910.设定点A B C D 、、、是以O 点为中心的正四面体的顶点,用σ表示空间以直线OA 为轴满足条件()B C σ=的旋转,用τ表示空间关于OCD 所在平面的镜面反射,设l 为过AB 中点与CD 中点的直线,用ω表示空间以l 为轴的180°旋转.设στ表示变换的复合,先作τ,再作σ.则ω可以表示为( )(A)στστσ (B)στστστ (C)τστστ (D)στσστσ 二、解答题11.在ABC ∆中,已知22sin cos 212A BC ++=,外接圆半径2R =. (Ⅰ)求角C 的大小;(Ⅱ)求ABC ∆面积的最大值.12.设A B C D 、、、为抛物线24x y =上不同的四点,,A D 关于该抛物线的对称轴对称,BC 平行于该抛物线在点D 处的切线l .设D 到直线AB ,直线AC 的距离分别为12,d d ,已知12d d +=.(Ⅰ)判断ABC ∆是锐角三角形、直角三角形、钝角三角形中的哪一种三角形,并说明理由;(Ⅱ)若ABC ∆的面积为240,求点A 的坐标及直线BC 的方程.O(Ⅱ)一般地,设正n 棱锥的体积V 为定值,试给出不依赖于n 的一个充分必要条件,使得正n 棱锥的表面积取得最小值.14.假定亲本总体中三种基因型式:,,AA Aa aa 的比例为:2:u v w (0,0,0,21)u v w u v w >>>++=且数量充分多,参与交配的亲本是该总体中随机的两个.(Ⅰ)求子一代中,三种基因型式的比例;(Ⅱ)子二代的三种基因型式的比例与子一代的三种基因型式的比例相同吗?并说明理由.15.设函数()1x m f x x +=+,且存在函数()1(,0)2s t at b t a ϕ==+>≠,满足2121()t s f t s-+=. (Ⅰ)证明:存在函数()(0),t s cs d s ψ==+>满足2121()s t f s t +-=; (Ⅱ)设113,(),1,2,.n n x x f x n +===证明:1123n n x --≤.2010年名牌大学自主招生考试试题(3)适用高校:清华大学、上海交通大学等五校(样题)一、选择题(每题5分,共25分)1.函数y=32cos sin cos x x x +-的最大值为 (A)2827 (B)3227 (C)43 (D)40272.已知a 、b 、c 、d 是实数,az bcz dω+=+, 且当Imz>0时,In ω>0.则 (A)ad+bc>0; (B)ad+bc <0; (C)ad−bc >0; (D)ad−bc<0.3.甲、乙、丙、丁等七人排成一排,若要求甲在中间,乙丙相邻,且丁不在两端,则不同的排法共有( )(A)24种; (B)48种; (C)96种; (D)120种4.己知F 为抛物线y 2=2px 的焦点,过点F 的直线l 与该抛物线交于A 、B 两点,l 1、l 2分别是该抛物线在A 、B 两点处的切线,l 1、l 2相交于点C ,设|AF|=a ,|BF|=b ,则|CF|=(C)2a b+;5.设θ是三次多项式f(x)=x 3−3x +10的一个根,且α=222θθ+-,若h(x)是一个有理系数的二次多项式,满足条件()h αθ=.则h(0)= (A)−2; (B)2; (C)12-; (D)12二、解答题(本大题共55分)1.(本题15分)己知f(x)是定义在R 上的奇函数,且当x <0时,f(x)单调递增,f(−1)=0.设函数()2sin cos 2x x m x m ϕ=+-,集合M=()|0,,02m x x πϕ⎧⎫⎡⎤∈<⎨⎬⎢⎥⎣⎦⎩⎭对任意的,N=()|0,,[]02m x f x πϕ⎧⎫⎡⎤∈<⎨⎬⎢⎥⎣⎦⎩⎭对任意的,求MN.2.(本题20分)甲、乙、丙、丁等4人相互传球,第一次由甲将球传出,每次传球时,传球者将球等可能地传给另外3人中的任何1人.(l)经过2次传球后,球在甲乙两人手中的概率各是多少?(2)经过n 次传球后,球在甲手中的概率记为p n (n=1,2,…) ,试求1n P +与n P 的关系式,并求n P 的表达式及lim n n P →∞3.(本题20分)设p 、q 是一元二次方程x 2+2ax−1=0(a>0)的两个根.其中p >0,令y 1=p−q,yn+1=2n y −2,n=1,2,…,证明:11212111lim ......n n y y y y y y →∞⎛⎫+++⎪⎝⎭=p. 2010年北京大学、香港大学、北京航空航天大学三校联合自主招生考试试题(数学部分)1.(仅文科做)02απ<<,求证:sin tan ααα<<.(25分) 2.AB 为边长为1的正五边形边上的点.证明:AB(25分)3.AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值.(25分)4.向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ 在0t 时取得最小值,问当0105t <<时,夹角的取值范围.(25分)5.(仅理科做)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.(25分)。
近十年清华北大自主招生试题汇总

1.(2007清华)对于集合2M R ⊆(表示二维点集),称M 为开集,当且仅当0,0P M r ∀∈∃>,使得{}2P R PP r M ∈<⊆⎰。
判断集合{}(,)4250x y x y +->⎰与集合{}(,)0,0x y x y ≥>⎰是否为开集,并证明你的结论。
2,(2009北大)已知,cos cos 21x R a x b x ∀∈+≥-恒成立,求max ()a b +3,(2009清华)已知,,0x y z >,a 、b 、c 是x 、y 、z 的一个排列。
求证:3a b c x y z ++≥。
4,(2006清华)已知a ,b 为非负数,44M a b =+,a+b=1,求M 的最值。
5,(2008北大)实数(1,2,i i a i b i ==满足123a a a b b b ++=++,122313122313a a a a a a bb b b bb ++=++,123123min(,,)min(,,)a a a b b b ≤。
求证:12312m a x (,,)m a x (,,)a a a b b b ≤。
6,(2009清华)试求出一个整系数多项式110()n n n n f x a x a x a --=+++…,使得()0f x =有一根为7,(2009清华)x>0,y>0,x+y=1,n 为正整数,求证:222112n n n xy -+≥8,(2007北大) 已知22()5319653196f x x x x x =-++-+,求f(1)+f(2)+…+f(50)。
9,(2006清华)设正三角形1T 的边长为a ,1n T +是n T 的中点三角形,n A 为n T 除去1n T +后剩下三个三角形内切圆面积之和,求1lim n k n k A →∞=∑。
10,(2008北大)数列{}1n n a ∞=定义如下:1234561,2,3,a a a a a a ======……(1) 给定自然数n ,求使l a n =的L 的范围;(2) 令221m m l l b a ==∑,求3limm m b m →∞。
华约自主招生2010数学

2010年清华大学等五校合作自主选拔通用基础测试数学一、选择题(本大题共10小题,每小题3分) 1、设复数其中为实数,若的实部为,则的虚部为( )A .B .C .D .【分析】复数的基本概念和运算.基础题.【解析】 A .∴的实部为虚部为.2、设向量满足则的最小值为( )A .2BC .D【分析】向量的模长与数量积.基础题.【解析】 D .,∴,当时取到等号.3、如果平面直线点满足:且与所成的角为与所成的角为那么与所成角的大小为( )A .B .C .D .【分析】异面直线所成角.本题用常规的作平行线的方法的话不容易求,由已知条件作出与所成的角后,注意到与垂直,转化为求与所成的角,问题会比较简单. 【解析】 B .如图,设在内的射影为,则.作于,则. 由三垂线定理,.2i 1i a w +æö=ç÷+èø,a w 2w 32-12-1232()()()()22i 1i 11i 44a a a w +-++-éùéùëûëû==w()()221124a a a +--==()()221113422a a a +--==-,ab !!1a b a b m ==×=!!!!,,()a tb t +ÎR !!1()222222221211a tb a tb ta b t mt t m m m +=++×=++=++--!!!!!!≥a tb +!!≥t m =-a b ,,m n ,,A B ,m n A m B n a b a b ÌÌÎÎ∥,,,,,ABa π4n AB m ⊥,,AB π3,m n π3π4π6π8AB a BAH Ðn AH AH m B a H π4BAH Ð=BC m ^C π3BAC Ð=AC CH ^设,则,. 又,所以面,所以. 于是与所成的角为.4、在四棱锥中,分别为侧棱的中点,则四面体的体积与四棱锥的体积之比为( ) A . B . C .D .【分析】割补法求体积. 【解析】 C .设四棱锥的体积为,则,,,∴.5、在中,三边长满足则的值为( )A .B .C .D .【分析】正弦定理与三角恒等变换.先将已知条件的边的关系转化为角的等式,再利用三角公式把所有的角都转成,最后化简就可以得出结果. 【解析】 C .H Cβαnm BA1AB =12AC =AH =π4CAH Ð=n AB n BH ^^,n ^ABH n AH ^m n π4P ABCD -11B D ,PB PD ,11AB CD P ABCD -1:61:51:41:3B 1D 1DCBAPP ABCD -V 112B ABC P ABC V V --=112D ACD P ACD V V --=1114P B D C C PBD V V --=1114P B D A A PBD V V --=11111244A B D C V V V V V -=--=ABC △a b c ,,3a c b +=,tan tan 22A C1514122322A C,3a c b +=sin sin 3sin A C B Þ+=2sincos 6sin cos 2222A C A CB B+-Þ=.【总结】和差化积公式作为三角恒等变换的重要公式,需要熟记.和差化积公式:6、如图的两条高线交于其外接圆圆心为过作垂直于与相交于则与面积之比为( )A .B .C .D .【分析】相似三角形的面积比.如果学过平面几何的竞赛知识的话,知道是的欧拉线,马上可以得出是的重心,,结论也就很显然了.如果没学过欧拉线的相关知识的话,纯粹的平面几何方法相对难想,可以考虑用三角结合平面几何求解与的比例关系. 【解析】 A由,可得,又是的欧拉线,所以 另解:中,由正弦定理,有(为的半径),所以.又,所以,于是所求比值为.7、设过点且平行于轴的直线与曲线的交点为曲线过点的切线交轴于点则的面积的最小值是( ) A .1BC .D .【分析】用导数求最值.cos3sin 22A C B -Þ=cos 3cos 22A C A C-+Þ=cos cos sin sin 3cos cos 3sin sin 22222222A C A C A C A C Þ+=-4sin sin 2cos cos 2222A C A C Þ=1tan tan 222A C Þ=sin sin 2sin cos22a ba ba b +-+=sin sin 2cossin22a ba ba b +--=cos cos 2cos cos22a b a ba b +-+=cos cos 2sin sin22a b a ba b +--=-ABC △AD BE ,H ,O ,O OF BC F ,OH AF G ,OFG △GAH △FD BCO GH EA1:41:32:51:2OGH ABC △G ABC △12OG GH =AH OF OF AH ∥OGF HGA △△∽OGH ABC △12OG GH =ABH △2sin sin sin AH AB ABR ABH AHB C===ÐÐR ABC △2sin 2cos AH R ABH R A =Ð=cos OF R A =2AH OF =1:4()()e 0ax f x a =>,()0P a ,y ():C y f x =Q ,C Q x R ,PQR △e 22e 4【解析】 B由已知得,,切线方程为,令,解得.所以,于是.令,则,可得处取得最小值.因此.8、设双曲线椭圆,若的短轴长与的实轴长的比值等于的离心率,则在的一条准线上截得线段的长为( ) A .B .C .D .4【分析】圆锥曲线的参数.本题唯一的难点是准线的概念,其它的按常规来算就可以了.【解析】D. 将的一条准线(其中,解出,所以截线段长为.【总结】椭圆()的准线方程有两条,为左准线,为右准线,其中.由椭圆的第二定义,椭圆上的点到左焦点的距离与到左准线的距离比为常数,等于椭圆的离心率.9、欲将正六边形的各边和各条对角线都染为种颜色之一,使得以正六边形的任何3个顶点作为顶点的三角形有3种不同颜色的边,并且不同的三角形使用不同的3色组合,则的最小值为( ) A .6B .7C .8D .9【分析】组合最值.典型的竞赛题,因为三角形的个数为,如果不同的三角形使用不同的3色组合,则,即.如果刚好是的话,则种颜色应该是平等的,它们染的线段的条数应该一样,但顶点的连线数不是的倍数,这说明6种不行.然后尝试举出7种可行的例子.【解析】 B如果是种颜色的话,因为种颜色的色组合有种,而正六边形的顶点所形成的三角形共个,由题设,这些三角形的色组合都不同,所以种颜色所有的色组合都恰好出现一次.另一方面,个顶点的连线共条,因此存在一种颜色只有条,含有这种颜色的三角形只有个,但含有此种颜色的色组合却有种,这与色组合都出现一次矛盾,故种颜色不行.2(,e )a Q a ()e ax f x a ¢=22e e ()a a y a x a -=-0y =1x a a=-1,0R a a æö-ç÷èø2111||||e 22a PQR S PR PQ a =×=××△2e ()a g a a =221()2e a g a a æö¢=-ç÷èø()g a ()min12PQR S g ==△()2212:204x y C k a k a -=>>,,2222:14x y C a +=2C 1C 2C 1C 2C 2244a k =Þ=+2C 2a x c =c ==2224a y k c -=2y =±422221x y a b +=0a b >>2a x c =-2a x c=c =n n 36C 336C C n !6n ≥6626C 15=666336C 36C 363626C 15=2248´=325C 10=36染种颜色时,如图,各条线上的数字代表染的颜色,有种,剩下的条对角线染第种颜色,则满足要求.10、设定点是以点为中心的正四面体的顶点,用表示空间以直线为轴满足条件的旋转,用表示空间关于所在平面的镜面反射,设为过中点与中点的直线,用表示空间以为轴的旋转,设表示变换的复合,先作,再作,则可以表示为( ) A . B . C . D .【分析】空间想象力与代数变换.【解析】 D记四面体为,则,即、分别互换.而故可以表示为,选D .二、解答题:解答应写出文字说明,证明过程或演算步骤. 11、 (本题满分14分)在中,已知,外接圆半径.⑴ 求角的大小;⑵ 求面积的最大值. 【分析】解三角形与均值不等式.基础题. 【解析】 ⑴ 解得或(舍去),于是.⑵ 由正弦定理,又,得.从而仅当时取到.∴面积的最大7637123456654321A B C D 、、、O s OA ()B C s =t OCD l AB CD w l 180°s t !t s w s t s t s !!!!s t s t s t !!!!!t s t s t !!!!s t s s t s !!!!!(),,,A B C D ()(),,,,,,A B C D B A D C w =,A B ,C D (),,,A B C D s t s s t s !!!!!()()(),,,,,,,,,A C D B B C D A C D B A s t s s t s t s s s t s ===!!!!!!!!!()()(),,,,,,,,,D B C A D A C B B A D C s t s ===!w s t s s t s !!!!!ABC △22sin cos 212A BC +-=2R =C ABC △22sin cos 212A BC +-=()()21cos 2cos 11A B C Û-+--=22cos cos 10C C Û--=1cos 2C =-cos 1C =2π3C =2sin c R C ==2222cos 22cos 3c a b ab C ab ab C ab =+--=≥243c ab =!1sin 2sin 2ABC S ab C C ==△≤2a b ==ABC △12、(本题满分14分)设为抛物线上不同的四点,关于该抛物线的对称轴对称,平行于该抛物线在点处的切线.设到直线直线的距离分别为已知.⑴ 判断是锐角三角形、直角三角形、钝角三角形中的哪一种三角形,并说明理由; ⑵ 若的面积为240,求点的坐标及直线的方程.【分析】圆锥曲线问题.第一问是探索性问题,由已知的等式强算的话,是不可行的.需要有一定的联想和猜测能力,由结论反推,很多条件就会豁然开朗,解答也就顺理成章了.如果第一问解决了,第二问会比较简单.【解析】 ⑴ 设、、、,则切线方程为,∴切线斜率为,于是.,于是、因此,.从而.又,∴,∴为直角三角形. ⑵ 由⑴,,.∴,解得,于是点的坐标为,进而容易算得对应的方程为.【总结】对于隐藏一些中间结论,需要一定的观察和联想力的解析几何题,除了平时的扎实基础外,丰富的经验也是不可或缺的.看看下面这道题:已知抛物线上的三个点,抛物线在三点上的切线两两相交,交点分别为,求证:.13、 (本小题满分14分)⑴ 正三棱锥的体积求正三棱锥的表面积的最小值; ⑵正四棱锥的体积求正四棱锥的表面积的最小值; A B CD ,,,24x y =A D ,BC D l D AB ,AC 12d d ,,12d d AD +=ABC △ABC △A BC ()00,A x y -()00,D x y ()11,B x y ()22,C x y ()002x x y y =+02x 02BCxk=2020204AC y y x x k x x --==+104AB x x k -=234BC x x k +=230204AC AB x x x k k +-+==AC AB k k =-12d d =12d d +=45BAD CAD Ð=Ð=°ABC △1AC k =1AB k =-204x x -=104x x -=-))()()201000142422ABC S AC AB x x x x x x =×=++=+-+△240=08x =±A ()8,16±BC 412y x =±-24x y =A B C ,,A B C ,,D E F ,,2ABC DEF S S =△△V =V =⑶ 一般地,设正棱锥的体积为定值,试给出不依赖于的一个充分必要条件,使得正棱锥的表面积取得最小值.【分析】立体几何最值.设出参数,表面积的表达式都很好表达,就是计算有点复杂,由求导求最小值,也可以用均值不等式,但不太好凑.【解析】 设底面中心到底面的边的距离为,底面积为,正棱锥的高为,体积为,表面积为,则. 对于底面的正边形,有,可得.于是,由,可得. 设,则 ,令,求导,得. 令,解得.当时,;当时,,所以()在时取到最小值,最小值是,故时,侧面与底面所成的角的大小为而且. 对于第⑴问,,,所以正四棱锥表面积的最小值为. 对于第⑵问,,所以正四棱锥表面积的最小值为.对于第⑶问,当正棱锥的体积为定值时,正棱锥的表面积取得最小值的一个充要条件是棱锥侧面与底面的夹角大小为14、(本小题满分14分)假定亲本总体中三种基因型式:的比例为 且数量充分多,参与交配的亲本是该总体中随机的两个.⑴ 求子一代中,三种基因型式的比例;n V n n d d S h V S d VS h3=n πtan d d d n S n 1æö2×=ç÷2èøπtan d S d n n 2=πtan dd d d S S S d n S S n d æ2æö=2×=+=1+çç÷çèøèπtan d V S d n h n 23==223223ππtan 9tan d V d S d n V n h n n h æöæöæö==ç÷ç÷ç÷èøèøèø2d x h æö=ç÷èøππtan tan d d S S V n V n x n h n 33323322ææææö=1+=91+=9×1+çççç÷çççèøèèè()32π9tan 1f x V n x n æ=×+ççè())2π9tan 21f x V n x n ¢=-()0f x ¢=18x =108x <<()0f x ¢<18x >()0f x ¢>()f x 3S 18x =2π72tan V n n S 18x =hd=arctan 4d S S =3V n ===4V n ==4=4n n arctan AA Aa aa ,,:2:(0002u v w u v w u v >>>+,,,1)w +=⑵ 子二代的三种基因型式的比例与子一代的三种基因型式的比例相同吗?并说明理由.【分析】统计问题. 【解析】 ⑴ 列表如下:∴⑵ 记,,则.⑴中比例为.因此子二代的比例为.于是子二代与子一代的比例相同.15、(本小题满分14分) 设函数且存在函数满足. ⑴ 证明:存在函数满足; ⑵ 设证明:. 【分析】函数、数列与不等式综合.对于数列的分式型递推,通常用不动点法求通项公式. 【解析】 ⑴ , ∴ 即. 上式对一切恒成立,对比系数必有,, ∴,. 又,. 由 对比系数,有,,∴存在函数. ⑵ 用不动点法,求得,∴ AA AA +AA Aa +AA aa +Aa AA +Aa Aa +Aa aa +aa AA +aa Aa +aa aa +AA 2u uv 0uv 2v 0000Aa 0uv uw uv 22v vw wu wv 0aa 00002v vw 0wv 2w ()()()22222::2:2222:2AA Aa aa u uv v uv uw vw v v w vw =+++++++()()()()22:2:u v u v v w v w =++++u v x +=v w y +=1x y +=22:2:x xy y ()()()()222222:2:xxy x xy xy y xy y ++++22:2:x xy y =()1x m f x x +=+,()102s t at b t a f æö==+>¹ç÷èø,,2121t s f t s -+æö=ç÷èø()()0t s cs d s f ==+>,2121s t f s t +-æö=ç÷èø()11312n n x x f x n +===!,,,,,1123n n x --!()212121212121311t mm t t t mt t f t t t t t t-++---+æö===ç÷--+-èø+()2121221at b s at b s at b at b +++++==++()2122131m t at b t at b+-++=-+()()()()2131221m t at b t at b Þ+-+=-++éùëû()()()()2222663221m at bm b a t b at b a t b +++--=++--+12t >4m =3a =1b =-()41x f x x +=+()31s t t j ==-12421161213121s s s f f s s s s++++æöæö=+==ç÷ç÷+èøèø++()2121cs d t t cs d +--=+221cs d cs d +-=+()()22612216666322131s cs d cs d c s d cs d c s d s cs d++-=Þ+++=+-++-++3c =1d =()31s s y =+()12531n n n x x -+=×--()114123531n n n x ---=×--!(∵当为奇数时,当为偶数时,)【总结】对于型如的递推数列,求通项公式的方法:令,解得的两个根,这两个根叫做数列的不动点. 当时,是等比数列;当时,由,两边取倒数,令,可得到关于的一阶递推式,求出的通项公式就可得到的通项公式.1n -()11153115343n n n ---×--=+×>×1n -()11153153143n n n ---×--=×-×≥1n n n ax bx cx d++=+ax bx cx d+=+x a b ,a b ¹n n x x a b ìü-íý-îþa b =1n n n ax b x cx d a a ++-=-+1n n y x a =-n y n y n x。
2010 年五校合作自主选拔高校特色测试数学试题(清华大学)

2010年五校合作自主选拔高校特色测试(清华大学)试题高级综合(理科)注意事项1. 本试卷包括四个部分,第1-4题为第一部分,第5-8题为第二部分,第9题为第三部分,第10题为第四部分。
四个部分的原始分均为100分。
2. 本试卷题目数量较多,难度较大。
考生可以根据自己的特点选择其中部分题目做答,其中第一、第二部分至多选择6题。
3. 考生应当在答题卡上做答,在试卷制作答无效。
回答第一、第二部分试题是应当用2B 铅笔将选答题目的题号填涂在答题卡相应位置;未填涂题号的答案不能评阅,题号填涂错误的不给分。
第三、第四部分试题直接在答题卡指定位置做答。
4. 四个部分的成绩将分别评阅并折算为标准分。
最终成绩将根据四个部分的标准分情况决定。
某一个或者几个部分成绩特别突出,或者整体表现较为突出的,成绩可评定为A 。
第一部分1.(25分)计算?70sin 50sin 10sin 444=︒+︒+︒2.(25分)现有一段长度为n 的木棍,希望将其锯成尽可能多的小段,要求每一小段的长度都是整数,并且任何一个时刻,当前最长的一段的长度都要严格小于当前最短的一段的长度的两倍。
例如:当n =6时最多只能锯成两段:6=3+3,但n =7时最多可以锯成3段:7=3+4,然后4可以在锯成2+2。
问:n =30时最多能够锯成多少段?3.(25分)请设计一种方案,对1维实数轴上的每一个点进行染色,使得任意距离为1、2或者5的两个点都不同色,要求所使用的颜色数目尽可能少。
4.(25分)12个人围坐在一个圆桌旁参加一个游戏,主持人给每个人发一顶帽子,帽子的颜色包括红、黄、蓝、紫。
每一个人都可以看到所有其他11个人头上帽子的颜色,这12个人可以事先约定好一种策略,但是当游戏开始后就不能再进行交流。
他们的目标是使12个人同时回答正确的机会最大。
假定主持人给每个人发的帽子的颜色是完全随机的,试给出一种策略,并分析再次策略下所有人都猜对的概率。
第二部分5.(35分)一个质量为m 的质点,初始时刻静止,从光滑的半球面顶点开始下滑,半球固定,其半径为R .求:(1)小球到达地面时距离初始位置的水平距离;(2)对地面的冲量.(假设小球落地时没有弹起来)6.(20分)直立的汽缸被活塞封闭有1mol 气体,活塞上装有中物,活塞及重物的总质量为m ,活塞面积A ,重力加速度g ,活塞与汽缸间摩擦可忽略,但活塞可以传导热量.初始时活塞位置固定,气体温度与环境平衡,气体体积为V o .活塞被放松后将振动起来,最后活塞静止于具有较大体积的新的平衡位置.假设环境压强P o ,环境温度为T o .试问:(1)若气体是理想气体,活塞从运动达到平衡过程,气体向环境吸热多少?(2)实际气体中分子间平均是吸引力,若气缸内气体是实际气体,其它量都与理想气体时相同,则上述过程气体向环境吸热比理想气体情形多还是少?7.(30分)有个半球壳均匀带电Q ,球壳在空间直角坐标系o-xyz 中方程为: []0,,2222R x R z y x -∈=++.求:(1)半球中心O (0,0,0)点的电势;(2)半球直径面上S (0,y ,0)点的电势(y >R );(3)半球对称轴上P ’(x ,0,0)点的电势.假设另一对称点P (-x ,0,0)点电势U p 为已知(x >R ).8.(15分)有一圆柱形玻璃柱,一光束从圆柱底面入射.为了简单我们只考虑圆柱轴线在入射面(光线与入射点发现构成的平面)上的情形.无论入射角多大,光束进入玻璃柱后都不能从侧面射出.求玻璃的折射率应满足什么条件?这其实就是光纤通讯的基本原理.现在我们减小圆柱形玻璃柱的直径是其小于1微米,以上讨论还有效吗?为什么?请给予简短讨论.第三部分9.太湖是中国第三大淡水湖,是苏锡常地区重要的饮用水水源地。
2008-2010年清华大学自主招生试卷

2008年清华大学考题1.求()x e f x x=的单调区间及极值.2.设正三角形1T 边长为a ,1n T +是n T 的中点三角形,n A 为n T 除去1n T +后剩下三个三角形内切圆面积之和.求1lim nk n k A →∞=∑.3.已知某音响设备由五个部件组成,A 电视机,B 影碟机,C 线路,D 左声道和E 右声道,其中每个部件工作的概率如下图所示.能听到声音,当且仅当A 与B 中有一工作,C 工作,D 与E 中有一工作;且若D 和E 同时工作则有立体声效果.求:(1)能听到立体声效果的概率;(2)听不到声音的概率.4.(1)求三直线60x y+=,1 2y x=,0y=所围成三角形上的整点个数;(2)求方程组21260y xy xx y<⎧⎪⎪>⎨⎪+=⎪⎩的整数解个数.5.已知(1,1)A--,△ABC是正三角形,且B、C在双曲线1(0)xy x=>一支上.(1)求证B 、C 关于直线y x =对称;(2)求△ABC 的周长.6.对于集合2M R ⊆,称M 为开集,当且仅当0P M ∀∈,0r ∃>,使得20{}P R PP r M ∈<⊆.判断集合{(,)4250}x y x y +->与{(,)0,0}x y x y ≥>是否为开集,并证明你的结论.2009年清华大学自主招生数学试题第一天(共11题,艺术生做1-7,10-11,其他考生1-9题)1.求公差是8、由三个质数组成的数列。
2.证明:一个2n+1项的整数数列,它们全部相等的充分必要条件是满足条件p ,条件p 为任意取出2n 个数,都存在一种划分方法,使得两堆数每堆含有n 个数,并且这两堆数的和相等。
3.四面体ABCD,AB=CD,AC=BD,AD=BC 。
(1)求证:这个四面体的四个面都是锐角三角形。
(2)设底面为BCD ,设另外三个面与面BCD 所形成的二面角为α,β,γ。
2010年北大清华浙大复旦等校自主招生试题

选择出维吾尔族的特征:题干部分涉及藏族建筑(碉房),维吾尔族的地方舞蹈(十二木卡姆),维吾尔族的日常饮食(馕)和维吾尔族的历史(回鹘)等。
作文题调考察权利和义务的均等精神,题目是给出著名学者梁漱溟的一段话:“西方人讲自由、平等、权利,动不动就是有我的自由权,个人的权利放在第一位,借此分庭对抗。但中国不是这样,注重的是义务,而不是权利……”要求考生根据这个观点撰写短文。
请联系社会实际,选择一个角度进行探讨,发表你的见解。写一篇不少于800字的论述文。
文科综合特色测试
有关国庆阅兵的军事知识,还考了经济学、心理学知识、蝴蝶效应、东盟自由贸易区、有关澳门回归的《七子之歌》等,此外,还有《哈姆雷特》、《双城记》等英文原著的经典语句以及国际组织的英文缩写等。其中写作题还出自一位境外学者之手,要求考生以梁漱溟的一段话,结合自己的实际生活,撰写短文阐述中国人是权利本位还是责任本位。
理科综合特色测试
2007年夏初太湖发生严重的水华事件,导致无锡市供水危机,引起世人关注。据此引出数学、物理、化学三门科目的5道计算题。其中一道数学题是:根据给出的太湖水位、水面面积、平均水深等数据,在假定太湖水体是一个规则的球缺的前提下,计算湖水最深处是多少米、总蓄水量多少;另一道化学题是:水体富营养化的主要营养元素是氮、磷,要求写出元素在水体中可能参与的生物化学反应过程。
2.物体做斜抛运动(1),抛出速度V与水平面夹角为θ,求落回抛出平面时与抛出点的距离。(2)若人以Vo抛出一个球,落回抛出平面时与抛出点的距离为L,求抛出速度的最小值,以及此时的θ。
3.
4.理想气体,从A状态到B状态到C状态后回到A状态,AB为等温变化(P减小V增大),BC等压变化(V减小),CA为等积变化(P减小)
清华大学自主招生试题 数学 Word版含解析

一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=( ) (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x yf xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有( )(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有( ) (A)b=2a (B)△ABC 的周长为3 (C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-,则( )(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值 (C)若方程()f x =b 恰有一个实根,则b>36e(D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则( )(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为( ) (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n ,总存在正整数m ,使得n S =m a ,则( )(A ){n a }可能为等差数列 (B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ,总存在正整数m ,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( ) (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为( )(A)13 (B)23(C)22 (D)6313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ,其面积为S ,则( )(A)若S=4,则k 的值唯一 (B)若S=12,则k 的值有2个(C)若D 为三角形,则0<k ≤23(D)若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅=( ) (A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立,且P(B)=0.5,P(A −B)=0.2,则( )(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的( ) (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有( )(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于( ) (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|,则( ) (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数,a =(mcosα,msinα),b =(ncosβ,nsinβ),其中α,β∈[0,2π)α,β∈[0,2π).定义向量12a =(2m α2m α),12b =(2n β2n β),记θ=α−β,则( )(A)12a ·12a =a (B)1122a b ⋅=2mn θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则( ) (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有( ) (A )ρ=1cos sin θθ+ (B )ρ=12sin θ+ (C )ρ=12cos θ- (D )ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则( )(A )()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ,若△ABC 为锐角三角形,则( ) (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1),若(0)f =(0)f '=1,则存在实数δ∈(0,1),使得( ) (A)()f x >0,x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1,x ∈(0,δ) (D)()f x >1,x ∈(−δ,0)26.在直角坐标系中,已知A(−1,0),B(1,0).若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n),总存在两个不同的点i P ,j P ,使得|sin ∠A i P B −sin ∠A j P B|≤13,则n 的最小值为( )(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1,则22x y + )(A)最小值为45 (B)最小值为25(C)最大值为1 (D)最大值为12328.对于50个黑球和49个白球的任意排列(从左到右排成一行),则( )(A)存在一个黑球,它右侧的白球和黑球一样多 (B)存在一个白球,它右侧的白球和黑球一样多(C)存在一个黑球,它右侧的白球比黑球少一个 (D)存在一个白球,它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有( ) (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则( ) (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()333(cossin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]663i ππ-+- 31sin )6623i i ππ+=1,选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ,与公差d 的符号有关,选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅2211221111(1)(1)x x x x ++2121111x x +++11122||||x x +⋅=2,正确;答案(B),|OA|+|OB|≥2||||OA OB ⋅22,正确;答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程,错误;答案(D),原点到直线AB :(111x x -)x-y+1=0的距离2111()1x x -+1,正确。
清华大学等五校2010年自主招生联考试题251

2010清华大学自主招生考试试题第一二部分(略)第三部分如下白骨一堆粉丝李国文中国文学,一直有大众化和小众化的分野。
唐代的白居易,则是最能代表中国文学大众化的典型诗人。
白居易,生于公元772年(唐代宗大历七年),终于公元846年(唐武宗会昌六年),活了74岁。
经历顺宗、宪宗、穆宗、敬宗、文宗、武宗六朝。
无论当时,无论后世,谈及这位诗人,离不开以下三点:一,他在诗坛领袖群伦,推动潮流的地位;二,他在朝野引起轰动,遐迩知名的程度;三,作为诗人,他在当时中国人之大多数心目中的无与伦比的尊崇,非同凡响的声望,他的粉丝,可以说是举国上下,遍地皆是,大江南北,无处不在,这也许是最值得大书而特书的中国文学的“白居易现象”。
他的朋友元稹为他的诗集《白氏长庆集》序中,这样写道:“二十年间,禁省、观寺、邮候、墙壁之上无不书,王公、妾妇、马走之口无不道。
缮写模勒,炫卖于市井中,或持之以交酒茗者,处处皆是。
”明人胡震享的《唐音癸签》一书中引《丰年录》:“开成中,物价至贱,村路卖鱼肉者,俗人买以胡绡半尺,士大夫买以乐天诗。
”白居易的一首诗,竟可以换来一条胖头鱼,一方五花肉,我估计当代诗人的作品,怕难以卖出这样的高价来。
所以,我一直认为,白居易大众化的文学追求,和白居易诗歌的大众化现象,是特别应该加以研究的对象。
因为与之相对的文学小众化,文人的小圈子化,贵族化,雅痞化,老爷化,使得文学脱节于现实,疏隔于生活,陌生于人民,淡漠于民众,再这样下去,不但换不来鱼,换不来肉,被人唾弃,视作敝屣的日子,也就不远了。
为什么要研究,因为在唐朝,中国文人的作品,其传播的范围,速度,方法,手段,都是极其有限的。
然而,白居易能够在这有限的空间里,创造出来无限的局面,在中国文学史上,是少有的被他同时代广大公众所追捧,千载以来被更广大公众所认可的成功者。
“自长安抵江西三四千里,凡乡校、佛寺、通旅、行舟之中,往往有题仆诗者;士庶、僧徒、孀妇、处女之口,每每有咏仆诗者。
2010清华大学自主招生试题数学试题

父本、母本的基因型 相应情况 子一代基因 子一代基因 子一代基因
式
出现的概率 为 的概率 为 的概率 为 的概率
父母
父母
父母
父母
父母
父母
第 7页(共 13页)
父母 父母 父母
子一代的基因型式为 的概率为
……………3 分 由对称性知子一代的基因型式为 的概率为 . ……………………6 分 子一代的基因型式为 的概率为
把
代入,整理得
所以 因为
都不平行于 轴,
所以直线
斜率之和为
可知直线
的倾角互补,而 平行于 轴,
所以 平分
作
为垂足
则
可得
由已知
,
可得
,所以
所以
为直角三角形
(Ⅱ)如图,根据的结果,可以设直线的方程分别为
第 5页(共 13页)
把
分别代入,得
所以
由已知可知
,
所以
所以
或
解得
,
当取
时,求得
,又 斜率
,
所以直线 方程为
.
………
若记
,
, 的比例为
……………………9 分
,则
,
,
,子一代三种基因型式: ,
. …………10 分
(Ⅱ)由(Ⅰ)可知子二代的基因型式为 , , 的比例为
,
.
由
,可得
,
.
………… ,其中
故子二代三种基因型式 , , 的比例为
例相 同.
……………………14 分
第 8页(共 13页)
,与子一代基因型式的比
正棱锥的表面积
由(Ⅰ)知,当时,正棱锥的表面积取得最小值。由于正棱锥的表面积与底面机之比为
清华大学自主招生试题含答案
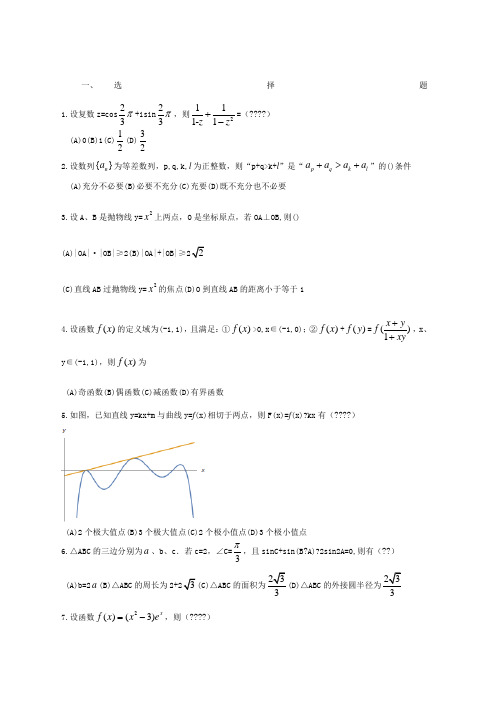
一、 选择题1.设复数z=cos23π+isin 23π,则2111-1z z +-=() (A)0(B)1(C)12(D)322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的()条件 (A)充分不必要(B)必要不充分(C)充要(D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则()(A)|OA|·|OB|≥2(B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点(D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x yf xy++,x 、y ∈(-1,1),则()f x 为(A)奇函数(B)偶函数(C)减函数(D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)?kx 有()(A)2个极大值点(B)3个极大值点(C)2个极小值点(D)3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B?A)?2sin2A=0,则有(??) (A)b=2a (B)△ABC 的周长为3(C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-,则()(A)()f x 有极小值,但无最小值(B)()f x 有极大值,但无最大值 (C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则()(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ,12y y +=b(D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为() (A)1(B)2 (C)3(D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n ,总存在正整数m ,使得n S =m a ,则() (A ){n a }可能为等差数列(B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ,总存在正整数m ,使得n a =m S 11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是()(A)甲(B)乙(C)丙(D)丁12.长方体ABCD?1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为(??)(A)13(B)23(C)2(D)313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ,其面积为S ,则()(A)若S=4,则k 的值唯一(B)若S=12,则k 的值有2个 (C)若D 为三角形,则0<k ≤23(D)若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅=() (A)0(B)?15 (C)?212(D)?29215.设随机事件A 与B 互相独立,且P(B)=0.5,P(A?B)=0.2,则()(A)P(A)=0.4(B)P(B?A)=0.3 (C)P(AB)=0.2(D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的() (A)最小值为34(B)最小值为45(C)最大值为43(D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有() (A)105种(B)225种(C)315种(D)420种18.已知存在实数r ,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于() (A)4(B)6 (C)8(D)1219.设复数z 满足2|z|≤|z?1|,则() (A)|z|的最大值为1(B)|z|的最小值为13(C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数,a =(mcosα,msinα),b =(ncosβ,nsinβ),其中α,β∈[0,2π)α,β∈[0,2π).定义向量12a =(2α,2α),12b =(2β2β),记θ=α?β,则()(A)12a ·12a =a (B)1122ab ⋅=2θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则() (A)?n ∈N?,n a <3(1)n +(B)?n ∈N?,n a ≠2015(C)?n ∈N?,n a 为完全平方数(D)?n ∈N?,n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有()(A )ρ=1cos sin θθ+(B )ρ=12sin θ+(C )ρ=12cos θ-(D )ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则()(A )()f x ≤43(B)|()f x |≤5|x|(C)曲线y=()f x 存在对称轴(D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ,若△ABC 为锐角三角形,则()(A)sinA>cosB(B)tanA>cotB(C)222a b c +>(D)333a b c +>25.设函数()f x 的定义域是(?1,1),若(0)f =(0)f '=1,则存在实数δ∈(0,1),使得(?)(A)()f x >0,x ∈(?δ,δ)(B)()f x 在(?δ,δ)上单调递增 (C)()f x >1,x ∈(0,δ)(D)()f x >1,x ∈(?δ,0)26.在直角坐标系中,已知A(?1,0),B(1,0).若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n),总存在两个不同的点i P ,j P ,使得|sin ∠A i P B?sin ∠A j P B|≤13,则n 的最小值为(?) (A)3(B)4 (C)5(D)627.设非负实数x,y 满足2x+y=1,则的(??)(A)最小值为45(B)最小值为25(C)最大值为1(D)最大值为13+28.对于50个黑球和49个白球的任意排列(从左到右排成一行),则()(A)存在一个黑球,它右侧的白球和黑球一样多(B)存在一个白球,它右侧的白球和黑球一样多 (C)存在一个黑球,它右侧的白球比黑球少一个(D)存在一个白球,它右侧的白球比黑球少一个 29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有()(A)300个(B)450个(C)900个(D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则() (A)L 是轴对称图形(B)L 是中心对称图形 (C)L?{(x,y)∣22x y +≤1}(D)L?{(x,y)∣?12≤y ≤12} ##Answer##1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+-- =212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )662i i ππ+-=1,选B2.【简解】()p q k l a a a a +-+=[(p+q)-(k+l)]d ,与公差d 的符号有关,选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅==2,正确;答案(B),|OA|+|OB|≥2≥2,正确;答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x -方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程,错误;答案(D),原点到直线AB :(111x x -)x-y+1=0的距离≤1,正确。
清华大学等五校2010年自主招生试题

清华大学等五校2010年自主招生试题语文:语文题量很大,包括两篇现代文阅读、古诗词鉴赏、古文翻译、古文断句等。
两篇现代文阅读,一篇为“科学与人文”摘自杨叔子《融则利而育全人》一书,所选段落涉及DNA知识、《红楼梦》、《老子》、《大学》等诸多内容。
另一篇是俄国作家蒲宁的文章《山口》。
此外有一篇古代诗文阅读《寻陆鸿渐不遇》。
两篇文言文阅读,断句,以及将《论语·泰伯》、《世说新语·汰侈》部分段落译为现代汉语。
作文是材料作文,有五十分,题目为“网瘾”。
卫生部日前发出通知称:“电击治疗网瘾”技术的安全性尚不确切,暂不宜应用于临床。
《中国青年报》:在过去三年里,已有近3000名网瘾少年在某网瘾戒治中心接受过电击治疗。
《亚太经济时报》:从电击疗法寿终正寝推及其他对青少年的教育方法,问题的根本在于教育已到了革故鼎新的时刻。
《东方早报》:当孩子网络成瘾后,学校除了把孩子当作“差生”、“问题生”推给家长之外,并没有针对这些孩子开展相应的教育。
《新民晚报》:治疗网瘾已成为迫切需要解决的时代课题,有效的治疗手段,一定会带来巨大的利润。
新浪网:一旦网瘾确实能被电击治愈,那么如烟瘾、酒瘾等好多棘手问题都将成为科学实验室的目标。
请联系社会实际,选择一个角度进行探讨,发表你的见解。
写一篇不少于800字的论述文。
文科综合特色测试有关国庆阅兵的军事知识,还考了经济学、心理学知识、蝴蝶效应、东盟自由贸易区、有关澳门回归的《七子之歌》等,此外,还有《哈姆雷特》、《双城记》等英文原著的经典语句以及国际组织的英文缩写等。
其中写作题还出自一位境外学者之手,要求考生以梁漱溟的一段话,结合自己的实际生活,撰写短文阐述中国人是权利本位还是责任本位。
另外考察了“猪肉价格下降的原因”、“三农问题含义”等与农村考生联系密切的知识点。
选择出维吾尔族的特征:题干部分涉及藏族建筑(碉房),维吾尔族的地方舞蹈(十二木卡姆),维吾尔族的日常饮食(馕)和维吾尔族的历史(回鹘)等。
2010清华大学自主招生数学试题

2010 年清华大学自主招生数学试题一、选择题:本大题共 10小题,每题3 分,在每题给出的四个选项中,只有一项为哪一项切合题目要求的.a i21.,此中 a 为实数 .若 w 的实部为 2,则 w 的虚部为()设复数 wi1A 、3B 、1C、1D、322222.设向量 a, b 知足 a b 1, a b m ,则a tb (t R )的最小值为()A 、2B 、 1 m2C、1D、 1 m23. 假如平面,,直线 m, n,点 A, B 知足:, m, n, A, B,且 AB与所成的角为4, m AB ,n与AB所成的角为,那么 m 与 n 所成角的大小为()3A 、B 、C、D、34684.在四棱锥 V-ABCD 中, B1, D1分别为侧棱 VB,VD 的中点,则四周体 AB1CD1的体积与四棱锥 V-ABCD的体积之比为()A 、1:6B、1:5C、1: 4D、1:35.在△ABC 中,三边长a,b,c知足 a c3b ,则tan AtanC的值为()22A 、1B 、1C、1D、2 54236.如图,△ ABC 的两条高线AD,BE交于H,其外接圆圆心为O,A过 O 作 OF 垂直 BC 于 F,OH 与 AF 订交于 G.则△OFG与△GAH面积之比为()EA、1:4B、1:3C、2:5D、1:2OH GB D F C7. 设 f x e ax(a0 ).过点P a,0且平行于 y 轴的直线与曲线C: y f x 的交点为 Q,曲线 C 过点Q 的切线交 x 轴于点 R,则△PQR 的面积的最小值是()A 、1B 、2e C、eD、 e22242 22 28.设双曲线 C 1 :x2y k ( a2 , k0 ),椭圆 C 2 :x2y 1 .若 C 2 的短轴长与 C 1 的实轴长的比a4a4值等于 C 2 的离心率,则 C 1 在 C 2 的一条准线上截得线段的长为()A 、 2 2 kB 、 2C 、 4 4 kD 、 49.欲将正六边形的各边和各条对角线都染为n 种颜色之一,使得以正六边形的任何 3 个极点作为极点的 三角形有 3 种不一样颜色的边,而且不一样的三角形使用不一样的 3 色组合,则 n 的最小值为( )A 、6B 、 7C 、8D 、 910. 设定点 A 、B 、C 、D 是以 O 点为中心的正四周体的极点, 用 表示空间以直线 OA 为轴知足条件(B) C的旋转,用 表示空间对于 OCD 所在平面的镜面反射,设 l 为过 AB 中点与 CD 中点的直线,用表示空间以 l 为轴的 180°旋转.设表示变换的复合,先作,再作 .则能够表示为()A 、B 、C 、D 、二、解答题:解答应写出文字说明,证明过程或演算步骤.11. (此题满分 14 分)在 △ABC 中,已知2A Bcos2C 1 ,外接圆半径 R 2 .2sin2( 1)求角 C 的大小;( 2)求 △ ABC 面积的最大值.12. (本小题满分 14 分)设 A , B ,C , D 为抛物线 x 24 y 上不一样的四点, A , D 对于该抛物线的对称轴对称,BC 平行于该抛 物线在点 D 处的切线 l .设 D 到直线 AB ,直线 AC 的距离分别为 d 1 , d 2 ,已知 d 1d 22 AD .( 1)判断 △ABC 是锐角三角形、直角三角形、钝角三角形中的哪一种三角形,并说明原因: ( 2)若 △ ABC 的面积为 240,求点 A 的坐标及直线 BC 的方程.13. (本小题满分 14 分)( 1)正四棱锥的体积 V2,求正四棱锥的表面积的最小值;3( 2)一般地,设正 n 棱锥的体积 V 为定值,试给出不依靠于 n 的一个充足必需条件,使得正n 棱锥的表面积获得最小值.14. (本小题满分 14 分)假订婚本整体中三种基因型式:AA ,Aa ,aa 的比率为 u : 2v : w ( u 0 , v 0, w 0 , u 2v w 1)且数目充足多,参加交配的亲本是该整体中随机的两个.( 1)求子一代中,三种基因型式的比率;( 2)子二代的三种基因型式的比率与子一代的三种基因型式的比率同样吗?并说明原因.15. (本小题满分 14 分)函数f( )x m ,且存在函数s ( t)at b (1, a0),足2t12s 1xx1 f ().2t s ( 1)明:存在函数t( s) cs d (s0 ),足 f (2s1)2t 1 ;s t( 2) x1 3 , x n 1 f ( x n ) , n1,2, ⋯ .明: x n21.n 13。
[高考]2009、2010清华北大自主招生试题
![[高考]2009、2010清华北大自主招生试题](https://img.taocdn.com/s3/m/bb933beeba4cf7ec4afe04a1b0717fd5360cb29a.png)
2009北京大学自主招生语数外物化试题(理科)时间:2009-11-06 作者:来源:网络资源一数学1 圆内接四边形ABCD,AB=1,BC=2,CD=3,DA=4。
求圆半径。
2 已知一无穷等差数列中有3项:13,25,41。
求证:2009为数列中一项。
3 是否存在实数x使tanx+(根3)与cotx+(根3)为有理数?4 已知对任意x均有acosx+bcos2x>=-1恒成立,求a+b的最大值5 某次考试共有333名学生做对了1000道题。
做对3道及以下为不及格,6道及以上为优秀。
问不及格和优秀的人数哪个多?二英语1 单选20道,四级难度,20分。
2 阅读两篇,四级难度,10道,40分。
第一篇是关于“ideal body”的,第二篇是关于“materialism”的。
3 英译汉3句,比较简单,20分4 汉译英4句,仍然简单,20分三. 语文1 基础(1)写两个成语,然后曲解,6分。
(2)改病句:1我们都有一个家,名字叫中国。
2素胚勾勒出青花笔锋浓转淡。
6分(3)对联:博雅塔前人博雅(博雅塔为北大一风景),8分2 翻译古文一篇300字左右的文不加点的文言文,要求翻译全文(20分)书杜袭喻繁钦语后[1]·(清)林纾吴人之归,有绮其衣者[2],衣数十袭[3],届时而易之。
而特居于盗乡,盗涎而妇弗觉[4],犹日炫其华绣于丛莽之下[5],盗遂杀而取之。
盗不足论,而吾甚怪此妇知绮其衣,而不知所以置其身。
夫使托身于荐绅之家[6],健者门焉,严扃深居,盗乌得取?唯其濒盗居而复炫其装[7],此其所以死耳。
天下有才之士,不犹吴妇之绮其衣乎?托非其人,则与盗邻,盗贪利而耆杀[8],故炫能于乱邦,匪有全者。
杜袭喻繁钦曰:“子若见能不已[9],非吾徒也。
”钦卒用其言,以免于刘表之祸[10]。
呜呼!袭可谓善藏矣,钦亦可谓善听矣。
不尔,吾未见其不为吴妇也。
3 大阅读,20分阅读理解是一篇选自鲁迅《野草》的文章,要求指出很多意像的象征意义求乞者我顺着剥落的高墙走路,踏着松的灰土。
2010年北京海淀区清华大学自主招生数学试卷-学生用卷

2010年北京海淀区清华大学自主招生数学试卷-学生用卷一、解答题(本大题共5小题)1、【来源】 2010年北京海淀区清华大学自主招生第1题高三上学期单元测试《三角函数与恒等变换》自招第5题高一上学期单元测试《三角函数进阶》第13题求的值.2、【来源】 2010年北京海淀区清华大学自主招生第2题在蒲丰投针试验中,平行线间距为,针长为,试求针与线相交概率与、的关系,并求在什么情况下概率是.3、【来源】 2010年北京海淀区清华大学自主招生第3题设计一种为一维数轴的全体实数染色的方案,使得数轴上任意两个相距为,,的点都不同色,要求使用的颜色最少.4、【来源】 2010年北京海淀区清华大学自主招生第4题高二下学期单元测试《组合问题》自招第4题长为的木棒(为整数)可以锯成长为整数的两段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的两倍.例如长为的木棒可以锯成的两段,而长为的木棒第一次可以锯成的两段,第二次可以锯成的两段,此时第三段无法再锯.问:长为的木棒至多可以锯成多少段?5、【来源】 2010年北京海淀区清华大学自主招生第5题个人玩一个游戏,游戏开始后每个人被随机戴上红、黄、蓝,绿四种颜色之一的帽子,每个人可以看到其余个人的帽子的颜色,但不能看到自己帽子的颜色,游戏开始后人不能再交流,并被要求猜出自己头上帽子的颜色.请为这个人在游戏前商定一个方案,使得他们同时猜对自己头上帽子颜色的概率尽可能地大,并求出这种方案下同时猜对的概率.1 、【答案】.;2 、【答案】当时,概率是.;3 、【答案】第一步先对数集染色,只需要为偶数时染黑色,为奇数时染白色就可以了.第二步然后对其他实数染色.如果某个实数来被染色,即,那么写出集合,按第一步中的方法染色.同时已染色集合扩充到了.重复第二步,就可以完成对任意实数的染色.之所以能够成功地用两种颜色染色,实质上就是:①把实数集写成了无数个形如的集合的并集,且这些集合是互不相交的;②这些集合中任意两个不同的集合和中的元素,(设,)的距离;③每个集合都可以用两种颜色染色.;4 、【答案】段.;5 、【答案】.;。
2010年北大清华等名校自主招生面试试题总汇

2010年北大清华等名校自主招生面试试题总汇近日,北京大学举行了自主招生考生的面试,其中备受关注的首批90名中学校长实名推荐的学生也参加了北大2010年自主招生面试,为了让考生提前了解名校自主招生的出题方向和考察重点,特别整理2010年自主招生部分面试试题,希望对考生的备考有所帮助。
北京大学1,哥本哈根会议是不是一场政治博弈?2,人的生命是否属于自己?3,优质学生享受优质教育是天经地义吗?4,如果你是联合国秘书长,如何解决索马里海盗问题?5,何为碳汇,谈谈对碳排放交易权的看法。
6,南方人性格柔弱,北方人性格粗犷,你如何评价?7,农村的孩子会种地,城里的孩子会画画,前者是否也是一种素质?8,蔬菜价格上涨超过肉类,怎么看这个现象?9,怎么看逆向思维?10,英国一思想家说,”国家的首要荣誉应该属于立法者和国家缔造者。
”怎么看这句话?11,中国目前是否有信仰,与道德、伦理和法制是否冲突?12,水蒸气也是温室气体,为什么只治理二氧化碳?13,怎样看教育多元化和教育公平的关系?14,谈谈雷锋精神的内涵理解,现在社会该不该提倡雷锋精神?15,现代社会需要包公吗?16,”狗咬人不是新闻,人咬狗才是新闻”,你怎么看?17,何为软实力,如何构建国家软实力?18,”我是一个克隆人,我有血和骨,把我的Y基因换成X基因,我的小克隆人长大后就成了异性。
”怎么看这首诗。
清华大学现场面试题目:1,如何看待高考加分政策?2,《阿凡达》很火,欧美大片、日本动漫也很受欢迎。
如何在这种环境下发展中国文化?3,用一个成语形容你眼中的哥本哈根气候会议。
4,用关键词概括2009年中国现状。
5,中国是否已步入高房价时代,你的观点是?6,一根火柴在不能折断的前提下,如何摆成一个三角形?7,就张磊向耶鲁大学捐款8888888美元发表观点。
8,第一次和第二次世界大战期间,有什么重大的化学发明?9,为什么要把清华大学作为第一志愿填报?远程面试题目:1,谈古论今:任选中国古代和当代人物各一位作对比阐释。
清华大学自主招生试题含答案
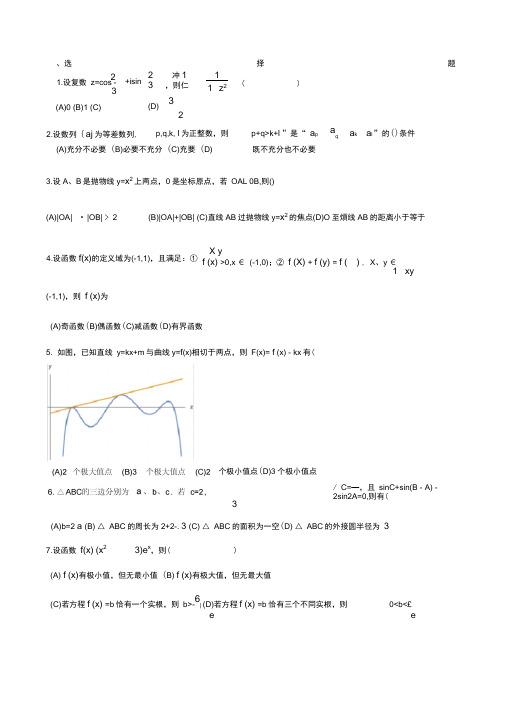
、选择题2( )(A)充分不必要(B)必要不充分(C)充要(D)3.设A、B是抛物线y=x2上两点,0是坐标原点,若OAL 0B,则()(A)|OA| •|OB| > 2 (B)|OA|+|OB| (C)直线AB过抛物线y=x2的焦点(D)O至煩线AB的距离小于等于X yf (x) >0,x € (-1,0);② f (X) + f (y) = f ( ) , X、y €1 xy(-1,1),则f (x)为(A)奇函数(B)偶函数(C)减函数(D)有界函数5. 如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)= f (x) - kx有(/ C=—,且sinC+sin(B - A) -2sin2A=0,则有(3(A)b=2 a (B) △ ABC的周长为2+2-. 3 (C) △ ABC的面积为一空(D) △ ABC的外接圆半径为37.设函数f(x) (x23)e x,则( )(A) f (x)有极小值,但无最小值(B) f (x)有极大值,但无最大值(C)若方程f (x) =b恰有一个实根,则b>-6| (D)若方程f (x) =b恰有三个不同实根,则0<b<£e e1.设复数z=cos -3+isin (A)0 (B)1 (C) 2 冲13 ,则仁(D)3211 z22.设数列{aj为等差数列, p,q,k, l为正整数,则p+q>k+l ”是“ a p aqa k a l ”的()条件既不充分也不必要4.设函数f(x)的定义域为(-1,1),且满足:①个极小值点(D)3个极小值点8.已知 A={(x,y) 1 x 22 2y r },B={(x,y)1 (x2 2 2a) (y b) r ,已知 A n B={(x 1,yJ ,( X 2,y 2)},则()(A)0< a 2 b 2 <2r 2(B)aXX 2) b(y1 y 2) 0(C)X 1 X 2 = a , y 1y 2=b (D)2a b 2 = 2ax 1 2by 19.已知非负实数x,y,z满足4x 24y 22z +2z=3, 则5x+4y+3z 的最小值为()(A)1 (B)2 (C)3 (D)410.设数列{ a n }的前n 项和为S n ,若对任意正整数n ,总存在正整数 m,使得S n =a m ,则( )(A ){ a n }可能为等差数列(B ){ a n }可能为等比数列(c ){a n }的任意一项均可写成{a n }的两项之差(D)对任意正整数n ,总存在正整数 m 使得a n = S m 11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测: 3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名•比赛后发现没有并列名次,且甲、乙、丙、丁中只有 1人猜对比赛结果,此人是( )(A)甲(B)乙(C)丙(D) 丁1(A)若S=4,则k 的值唯一(B) 若S=^,贝U k 的值有2个22(C)若D 为三角形,则0<k <(D)若D 为五边形,则312.长方体 ABCDAEGD 中,AB=2, AD=A A 1=1,贝U A 到平面 A BD 的距离为((A) - (B)3(D)13.设不等式组|x| |y| 2 y 2 k(x 1)所表示的区域为 D,其面积为S,U(k>414. △ ABC 勺三边长是 2,3,4,其外心为 0,则 uuu uuu OA AB uuu uuu uuur uuu OB BC 0C CA =((A)0 (B)-15 (C) -21(D)229 215. 设随机事件 A 与B 互相独立,且 P(B)=0.5(A)P(A)=0.4 (B)P(B -A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916. 过厶ABC 的重心作直线将厶 3(A)最小值为一(B)最小值为417. 从正15边形的顶点中选出,P(A- B)=0.2,则(ABC 分成两部分,则这两部分的面积之比的(4 4(C)最大值为一533个构成钝角三角形,5(D 最大值为一4则不同的选法有((A)105 种(B)225 种(C)315 种(D)420 种18. 已知存在实数r,使得圆周x2y2 r2上恰好有n个整点,则n可以等于(22.在极坐标系中,下列方程表示的图形是椭圆的有(4 2 1 V2(A)最小值为一(B)最小值为一 (C)最大值为1 (D)最大值为--------------------5 5 3(A)4 (B)6 (C)8 (D)1219. 设复数z 满足2|z| w |z-1|,则(1(A)|z|的最大值为1 (B)|z| 的最小值为—(C)z321的虚部的最大值为2(D)z 的实部的最大值为13320.设 m,n 是大于零的实数, a =(mcos a ,msin a ),b =(ncos 3 ,nsin 3 ),其中 a , B€ [0,2 n ) a , B€r 1, _[0,2 n ) •定义向量 a 2 =( 、、. m cos — ,、. m sin 一 ), b 2=(、. n 2cos — 2 ,、齐 sin —),记 9 = a - 3,贝U2r [ r 1 r r 1 r 1 ___ (A) a 2 • a 2 = a (B) a 2 b 2=、.mn cos — (C) 2r] r] … |a 2 b 2|4、一 mn sin 2 —4r 1 r] 2 _ 2 (D) |a 2 b 2 |24, mncos 2 —421.设数列{ a n }满足:a 1=6, an 1,则((A) ? n € N?, a n <(n 1)3 (B) ? n € N?, a n 丰 2015 (C) ? n € N?, a n 为完全平方数(D)? n € N?, a n 为完全立方数1 (A )p=cos sin23. 设函数 f(x)s in x,则( x x 14(A ) f(x) w (B)| f (x) | w 5|x| (C)曲线 y= f (x)存在对称轴324. △ ABC 的三边分别为a ,b,c ,若△ ABC 为锐角三角形,则((B )p=—1(C ) 2 sin1p= —2 cos(D )(D) 1 1 2si n曲线y= f (x)存在对称中心(A)si nA>cosB (B)ta nA>cotB (C) a 2 b 2 c 2 (D) a 3 b 3 c 325.设函数f (x)的定义域是(-1,1), 若f(0) = f (0) =1,则存在实数 s€ (0,1),使得()(A) f (x) >0, x € (- S , S) (B)f (x)在(-S , S )上单调递增 (C) f (x) >1, x € (0, S) (D)f (x)>1 , x € (- S ,0)26.在直角坐标系中,已知A(-1,0),B(1,0) •若对于y 轴上的任意n 个不同的点 P k (k=1,2,…,n),总存在两个不同的点R ,P j ,1使得 |sin / A P j B-sin / A P j B| w —,贝V n 的最小值为( 3(A)3 (B)4(C)5 (D)627.设非负实数x,y 满足2x+y=1,则 x+ x 2 y 2 的()128.对于50个黑球和49个白球的任意排列(从左到右排成一行),则((A)存在一个黑球,它右侧的白球和黑球一样多(B)存在一个白球,它右侧的白球和黑球一样多(C)存在一个黑球,它右侧的白球比黑球少一个 (D)存在一个白球,它右侧的白球比黑球少一个 29.从1,2,3,4,5 中挑出三个不同数字组成五位数, 同的五位数有( (A)300 个(B)450其中有两个数字各用两次,例如 12231,则能得到的不 30.设曲线L 的方程为 (A)L 是轴对称图形 (C)L ? {(x,y) I ##A nswer##1.【解析】 丄1-z) 个(C)900 y 4 (2x 2(B)L 个(D)1800 个 2 4 2 2)y (x 2x ) =0,则(是中心对称图形 1 (D)L ? {(x,y)zz 1 zz_______ 1 - 2. 21-cos i sin332 cos 3..2 i sin ___ 3 2 2i sin32sin 2 i 2sin cos —3 3 3 cos0 isinO 2sin — [cos( —) i sin(-)i sin(3、、3(cos —2-洽 2os(cos( i sin ) 27) i sin(67)]丄(cos — isi n —.3 6 6△ )=1,选 B22.【简解】 a p (a k Q )=[(p+q)-(k+l)]d ,与公差 d 的符号有关,选 3.【解析】设A( 2X 1,X 1 ),B( 2 uuu uuu X 2,X 2 ), OA OB =X 1X 2(1 X 1X 2) =0 X 2 X1 答案(A), |0A| l OBI ^x^(1 好)4(1 —1^) = j1 X2 1 2 X 11 > /2 2|X 1 | 丄=2,正确; |X 1 | 答案(B),|OA|+|OB| > 2..|OA 「|OB| > 2 .2,正确;答案(C),直线 AB 的斜率为 2 22^=X 2 x 2 x 1X1程为 y- xj =( x 1 1)(x-x 1),焦点(0, 1)不满足方程,错误;答案(D),原点到直线AB :(4X11)x-y+ 仁X 1的距离d=w 1,正确。
2010年清华大学自主招生试题

语文第一题:科技说明文杨叔子《融则利而育全人》一书中的选段。
第二题:现代文阅读没时间了,就没怎么看。
山口蒲宁 <俄>夜幕已垂下很久,可我仍举步维艰地在崇岭中朝山口走去,朔风扑面而来,四周寒雾弥漫,我对于能否走至山口已失却信心,可我牵在身后的那匹浑身湿淋淋的、疲惫的马,却驯顺地跟随着我亦步亦趋,空荡荡的马蹬叮叮当当地碰响着。
在迷蒙的夜色中,我走到了松林脚下,过了松林便是这条通往山巅的光秃秃的荒凉的山路了。
我在松林外歇息了一会儿,眺望着山下宽阔的谷地,心中漾起一阵奇异的自豪感和力量感,这样的感觉,人们在居高临下时往往都会有的。
我遥遥望见山下很远的地方,那渐渐昏暗下去的谷地紧傍着狭窄的海湾,岸边点点灯火犹依稀可辨。
那条海湾越往东去就越开阔,最终形成一堵烟霞空蒙的暗蓝色障壁,围住了半壁天空。
但在深山中已是黑夜了。
夜色迅速地浓重起来,我向前走去,离松林越来越近。
只觉得山岭变得越来越阴郁,越来越森严,由高空呼啸而下的寒风,驱赶着浓雾,将其撕扯成一条条长长的斜云,使之穿过山峰间的空隙,迅疾地排空而去。
高处的台地上缭绕着大团大团松软的雾。
半山腰中的雾就是由那儿刮下来的。
雾的坠落使得群山间的万仍深渊看上去更显阴郁,更显幽深。
雾使松林仿佛冒起了白烟,并随同喑哑、深沉、凄冷的松涛声向我袭来。
周遭弥漫着冬天清新的气息,寒风卷来了雪珠……夜已经很深了,我低下头避着烈风,久久地在山林构成的黑咕隆咚的拱道中冒着浓雾向前行去,耳际回响着隆隆的松涛声。
“马上就可以到山口了,”我宽慰自己说。
“马上就可以翻过山岭到没有风雪而有人烟的明亮的屋子里去休息了……”但是半个小时过去了,一个小时过去了……每分钟我都以为再走两步就可到达山口,可是那光秃秃的石头坡道却怎么也走不到尽头。
松林早已落在半山腰,低矮的歪脖子灌木丛也早已走过,我开始觉得累了,直打寒颤。
我记起了离山口不远的松树间有好几座孤坟,那里埋葬着被冬天的暴风雪刮下山的樵夫。
2010年清华自主招生试题

2010年清华自主招生试题(理科)1. 求值:(sin10)^4 + (sin40)^4 + (sin70)^42.长为L(L为整数)的木棒可以锯成长为整数的两段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的2倍。
例如长为4的木棒可以锯成2+2两段,而长为7的木棒第一次可以锯成3+4,第二次可以再将长为4的木棒锯成2+2,这时2+2+3三段不能再锯。
问:长为30的木棒至多可以锯成多少段?3. 将数轴上的每个点用N种颜色之一染色,要求任意距离为1、根号2 或根号5的两点不同色。
求N的最小值。
4. 12个人玩一个游戏,游戏开始后每个人被随机的戴上红、黄、蓝、绿四种颜色之一的帽子,每个人可以看到其余11个人帽子的颜色,但不能看到自己帽子的颜色,游戏开始后12个人不能再交流,并被要求猜出自己帽子的颜色。
请为这12个人在游戏前商定一个方案,使得他们同时猜对自己头上帽子颜色的概率尽可能大。
2010清华特色测试数学试题与解答第一部分1. 求值:(sin10)^4 + (sin40)^4 + (sin70)^4答案:9/8.(解答过程略,条条大路通罗马)2.长为L(L为整数)的木棒可以锯成长为整数的两段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的2倍。
例如长为4的木棒可以锯成2+2两段,而长为7的木棒第一次可以锯成3+4,第二次可以再将长为4的木棒锯成2+2,这时2+2+3三段不能再锯。
问:长为30的木棒至多可以锯成多少段?解:至多可以锯成6段。
锯成6段的方案:30=12+18, 18=8+10, 12=6+6, 10=5+5, 8=4+4.引理1:每次只能锯当前最长的一段。
引理2:如果当前最长的不少于两段,则无法再锯下去。
利用这两个引理(证略),对各种锯木棒的方案分类讨论。
此处略。
3. 将数轴上的每个点用N种颜色之一染色,要求任意距离为1、根号2 或根号5的两点不同色。
求N的最小值。
解:N的最小值为2。
自主招生数学试题

【题文】在欧非杯排球赛中,欧洲的参赛队伍比非洲的参赛队伍多9支.每两支球队赛一场,胜者得1分,败者得0分.若欧洲球队所得总分为非洲所得总分的9倍,则非洲球队的各支球队中得分的最大可能值是()A.8;B.9;C.10;D.11.【题文】已知有位乒乓球选手,它们互相进行了若干场乒乓球双打比赛,并且发现任意两名选手作为队友恰好只参加过一次比赛,试求的所有可能值.【题文】在中取一组数,使得其中任意两数之和不能被其差整除,最多能取多少个数?【题文】【题文】(2010年清华大学特色测试)设计一种为一维数轴的全体实数染色的方案,使得数轴上任意相距为的点都不同色,要求使用颜色最少【题文】(2010年五校联考)对正六边形的边和所有对角线染色,任意三角形三边染色不同,任意两组三角形染色方式不同,求至少要染色多少种颜色.(注:原题为选择题)【题文】(中国科技大学)2008个白球和2009个黑球任意排成一列.求证:无论如何排列,都至少存在一个黑球,其左侧(不包括自己)的黑球和白球个数相等(可以为0).【题文】(上海交大)这是一个由9个小的九宫格组成的的方格,请逐步确定每个空格中的数字,使其符合两个条件:(1)每一行每一列中的9个数必须为不重复的1到9;(2)每一个小九宫格中的9个数字必须是不重复的1到9,你填写的每一个数字必须是经由推理唯一确定的.【题文】已知平面上有n(n>3)个点,其中无三点共线,也无四点共圆,是否存在通过其中三个点的圆,它的内部不含任何一个已知点()A.一定存在B.一定不存在 C.不一定存在D,结论随n的大小而不同【题文】目前有n(n≥2 )位乒乓球选手,他们互相进行了若干场乒乓球双打比赛,并且发现任意两名选手作为队友恰好值参加一次比赛,请问n的所有可能值。
【题文】(2001年上海交大联读班)若一个圆盘被条相等间隔的半径与一条割线所分割,则这个圆盘能够被分成的不交迭区域的最大个数是()A. B. C. D.【题文】(五校2010选拔)欲将正六边形的各边和各条对角线都染为n种颜色之一,使得以正六边形的任何3个顶点作为顶点的三角形有3种不同颜色的边,并且不同的三角形使用不同的3色组合,则n的最小值为()A.6B.7C.8D.9【题文】(2011年清华)请设计一种方案,对1维实数轴上的每一个点进行染色,使得距离为1,或的两个点不同色,要求所使用的颜色数目尽可能少.【题文】(2010 清华)现有一段长度为的木棍,希望将其锯成尽可能多的小段,要求每一小段的长度都是整数,并且任何一个时刻,当前最长的一段都严格小于当前最短的一段的长度的2 倍. 例如:当=6时最多只能锯成两段:,当= 7时最多可锯成:.问:=30时最多能锯成多少段?【题文】(2009年清华)现有一游戏:图上有若干个点和若干条线,甲提供若干个硬币,乙可以任意将这些硬币全部摆放在点上,并且指定一个目标定点.现定义操作:从一个至少有2个硬币的点取走2个硬币,在它一个相邻的点上放回1个硬币. 在指定的图下,甲最少提供多少个硬币,可以保证经过若干次操作,一定能使目标顶点至少有1枚硬币?(1)图是一个包含5 个点的线段;(2)图是一个包含7 个点的圈.【题文】(2008年上海交大冬令营)世界杯预选赛中,中国、澳大利亚、卡塔尔和伊拉克被分在A组,进行主客场比赛. 规定每场比赛胜者得3分,平局各得1分,败者不得分. 比赛结束后前两名可以晋级.(1)由于4支队伍均为强队,每支队伍至少得3分. 于是甲专家预测:中国队至少得10分才能确保出线;乙专家预测:中国队至少得11分才能确保出线. 问:甲、乙专家哪个说的对?为什么?(2)若不考虑(1)中条件,中国队至少得多少分才能确保出线?【题文】(2002年上海交大联读班、保送生)有一个环形地带上顺次有五所学校A、B、C、D、E,它们各有15、7、11、3、14台机器,现要使机器平均分配,规定机器的运输必须在相邻学校间进行,为使总的运输台数最少,则A应给B_____台,B应给C_____台,A应给E_____台,总共运输______台.【题文】(2008年上海交大冬令营)30个人排成矩形,身高各不相同. 把每列最矮的人选出,这些人中最高的设为;把每行最高的人选出,这些人中最矮的设为.(1)是否有可能比高?(2)和是否可能相等?【题文】将一个正11边形对角线划分为9个三角形,这些对角线在正11边形内两两不相交,则()A.存在某种分法,所分出的三角形都不是锐角三角形B.存在某种分法,所分出的三角形恰有两个锐角三角形C.存在某种分法,所分出的三角形至少有3个锐角三角形D.任何一种分法所分出的三角形恰有1个锐角三角形【题文】【题文】(交大2002保送)某市环形马路上顺次有第一小学至第五小学等5所小学,各小学分别有电脑15,7,11,3,14的电脑数相等,各向相邻小学移交若干台,且要使移交的电脑的总台数量最小,因此,从第一小学向第二小学移交了______台。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年清华大学自主招生数学试题
一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设复数2
1a i w i +⎛⎫= ⎪+⎝⎭
,其中a 为实数.若w 的实部为2,则w 的虚部为( )
A 、3
2-
B 、12
-
C 、
12
D 、
32
2. 设向量a ,b 满足1a b ==,a b m ⋅=,则a tb +(R t ∈)的最小值为( )
A 、2
B
C 、1
D
3. 如果平面α,β,直线m ,n ,点A ,B 满足:αβP ,m α⊂,n β⊂,A α∈,B β∈,且AB 与α
所成的角为4π,m AB ⊥,n 与AB 所成的角为3
π
,那么m 与n 所成角的大小为( ) A 、3π B 、4π C 、6π D 、8
π
4. 在四棱锥V -ABCD 中,1B ,1D 分别为侧棱VB ,VD 的中点,则四面体11AB CD 的体积与四棱锥V -ABCD
的体积之比为( ) A 、1:6 B 、1:5 C 、1:4 D 、1:3
5. 在ABC △中,三边长a ,b ,c 满足3a c b +=,则tan
tan 22
A C
的值为( ) A 、1
5
B 、14
C 、12
D 、
23
6. 如图,ABC △的两条高线AD ,BE 交于H ,其外接圆圆心为O ,
过O 作OF 垂直BC 于F ,OH 与AF 相交于G .则OFG △与GAH △面积之比为( ) A 、1:4 B 、1:3 C 、2:5 D 、1:2
7. 设()ax f x e =(0a >).过点(),0P a 且平行于y 轴的直线与曲线C :()y f x =的交点为Q ,曲线C 过点
Q 的切线交x 轴于点R ,则PQR △的面积的最小值是( ) A 、1
B
C 、2
e
D 、2
4
e
A
E C
O
G
H B
D
F
8. 设双曲线1C :22
24x y k a -=(2a >,0k >)
,椭圆2C :22214
x y a +=.若2C 的短轴长与1C 的实轴长的比值等于2C 的离心率,则1C 在2C 的一条准线上截得线段的长为( )
A 、
B 、2
C 、
D 、4
9. 欲将正六边形的各边和各条对角线都染为n 种颜色之一,使得以正六边形的任何3个顶点作为顶点的
三角形有3种不同颜色的边,并且不同的三角形使用不同的3色组合,则n 的最小值为( ) A 、6 B 、7 C 、8 D 、9
10. 设定点A 、B 、C 、D 是以O 点为中心的正四面体的顶点,用σ表示空间以直线OA 为轴满足条件()B C σ=的旋转,用τ表示空间关于OCD 所在平面的镜面反射,设l 为过AB 中点与CD 中点的直线,用ω表
示空间以l 为轴的180°旋转.设στo 表示变换的复合,先作τ,再作σ.则ω可以表示为( ) A 、στστσo o o o B 、στστστo o o o o C 、τστστo o o o D 、στσστσo o o o o
二、解答题:解答应写出文字说明,证明过程或演算步骤. 11. (本题满分14分)
在ABC △中,已知2
2sin cos212
A B
C +==,外接圆半径2R =. (1)求角C 的大小;
(2)求ABC △面积的最大值.
12. (本小题满分14分)
设A ,B ,C ,D 为抛物线24x y =上不同的四点,A ,D 关于该抛物线的对称轴对称,BC 平行于该抛
物线在点D 处的切线l .设D 到直线AB ,直线AC 的距离分别为1d ,2d ,已知12d d +=. (1)判断ABC △是锐角三角形、直角三角形、钝角三角形中的哪一种三角形,并说明理由: (2)若ABC △的面积为240,求点A 的坐标及直线BC 的方程.
13. (本小题满分14分)
(1)正四棱锥的体积V =
(2)一般地,设正n 棱锥的体积V 为定值,试给出不依赖于n 的一个充分必要条件,使得正n 棱锥的表面积取得最小值.
14. (本小题满分14分)
假定亲本总体中三种基因型式:AA ,Aa ,aa 的比例为:2:u v w (0u >,0v >,0w >,21u v w ++=)且数量充分多,参与交配的亲本是该总体中随机的两个. (1)求子一代中,三种基因型式的比例;
(2)子二代的三种基因型式的比例与子一代的三种基因型式的比例相同吗?并说明理由.
15. (本小题满分14分)
设函数()1x m f x x +=
+,且存在函数()s t at b φ==+(12t >,0a ≠),满足2121
()t s f t s
-+=. (1)证明:存在函数()t s cs d ψ==+(0s >),满足2121
()s t f s t +-=
; (2)设13x =,1()n n x f x +=,1,2,n =….证明:1
123n n x --≤.。
