2019年北京清华大学自主招生数学理科试题Word版

合集下载

2019清华大学自主招生试题(含答案)

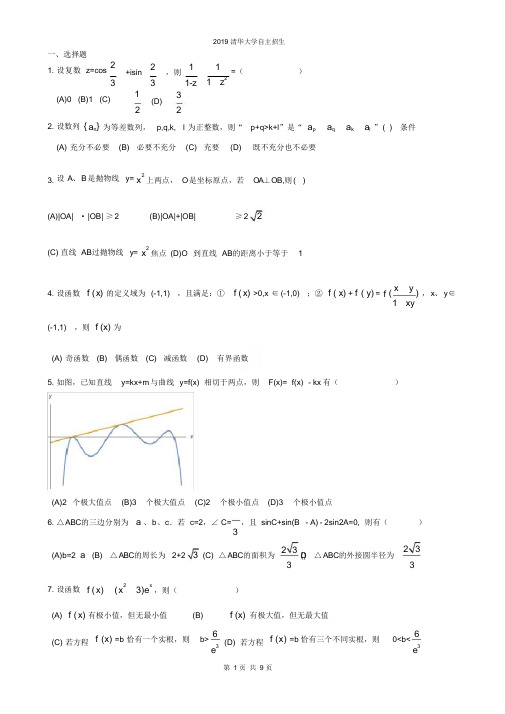
一、选择题1. 设复数 z=cos 22 1 1 +isin ，则=（）3 (A)0 (B)1 (C) 12 3 (D) 321-z1 z 22. 设数列 { a n } 为等差数列， p,q,k, l 为正整数，则“ p+q>k+l ”是“ a pa q a k a l ” ( ) 条件(A) 充分不必要 (B) 必要不充分 (C) 充要 (D) 既不充分也不必要3. 设 A 、B 是抛物线 y= x 2上两点， O 是坐标原点，若 OA ⊥ OB,则( )(A)|OA| · |OB| ≥ 2(B)|OA|+|OB|≥ 2 2(C) 直线 AB 过抛物线 y= x 2焦点 (D)O 到直线 AB 的距离小于等于 14. 设函数 f ( x) 的定义域为 (-1,1) ，且满足：① f ( x) >0,x ∈ (-1,0) ；② f ( x) + f ( y) = f ( x y )， x 、 y ∈1 xy(-1,1) ，则 f (x) 为(A) 奇函数 (B) 偶函数 (C) 减函数 (D) 有界函数5. 如图，已知直线 y=kx+m 与曲线 y=f(x) 相切于两点，则 F(x)= f(x) - kx 有（）(A)2 个极大值点 (B)3 个极大值点 (C)2 个极小值点 (D)3 个极小值点6. △ ABC 的三边分别为 a 、b 、c ．若 c=2，∠ C= ，且 sinC+sin(B - A) - 2sin2A=0, 则有（）3(A)b=2 a (B) △ ABC 的周长为 2+2 3 (C) △ ABC 的面积为 2 33 (D ) △ ABC 的外接圆半径为 2 3 37. 设函数 f ( x) ( x23)e x，则（）(A) f ( x) 有极小值，但无最小值(B)f (x) 有极大值，但无最大值(C) 若方程 f (x) =b 恰有一个实根，则 b> 6 e 3 (D) 若方程 f (x) =b 恰有三个不同实根，则 0<b< 6e312 1 2 1 18. 已知 A={(x,y) ∣ x222 2yr } ， B={(x,y) ∣ ( x a)2( y b)2r ，已知 A ∩ B={( x 1 , y 1 ),( x 2 , y 2 )} ，则（）(A ) 0< a2b 2<2 r2(B )a(x x ) b(yy ) 012 12(C ) (C)x x = a ， y y =b (D) a2b 2= 2ax 2by9. 已知非负实数 x,y,z 满足 4 x24 y2z 2+2z=3，则 5x+4y+3z 最小值为（）(A)1 (B)2 (C)3 (D)410. 设数列 { a n } 前 n 项和为 S n ，若对任意正整数 n ，总存在正整数 m ，使得 S n =a m ，则（）（ A ） { a n } 可能为等差数列（ B ） { a n } 可能为等比数列（ C ） { a n } 的任意一项均可写成 { a n } 的两项之差 (D) 对任意正整数 n ，总存在正整数 m ，使得 a n = S m11. 运动会上，有 6 名选手参加 100 米比赛，观众甲猜测： 4 道或 5 道的选手得第一名；观众乙猜测： 3 道的选手不可能得第一名；观众丙猜测： 1,2,6 道选手中的一位获得第一名；观众丁猜测： 4,5,6 道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1 人猜对比赛结果，此人是（）(A) 甲 (B) 乙 (C)丙 (D)丁12. 长方体 ABCD - A 1B 1C 1 D 1 中， AB=2， AD=A A 1=1，则 A 到平面 A 1 BD 的距离为（）(A) 1 3(B)2 3(C) 22 (D)6313. 设不等式组| x | | y | 2所表示的区域为 D ，其面积为 S ，则（）y 2 k( x 1)(A) 若 S=4，则 k 的值唯一(B)若 S= 12，则 k 的值有 2 个(C) 若 D 为三角形，则 0<k ≤ 23(D) 若 D 为五边形，则 k>4u u u r u uu r u uu r uu u r uu u r u u u r14. △ ABC 的三边长是 2,3,4 ，其外心为 O ，则 OA AB OB BC OC CA =（）21 (A)0 (B)- 15 (C) -229 (D) -215. 设随机事件 A 与 B 互相独立，且 P(B)=0.5 ，P(A- B )=0.2 ，则（）(A)P(A)=0.4 (B)P(B- A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916. 过△ ABC 的重心作直线将△ ABC 分成两部分，则这两部分的面积之比的（）(A) 最小值为3 (B) 最小值为44 4 (C) 最大值为535 (D 最大值为417. 从正 15 边形的顶点中选出 3 个构成钝角三角形，则不同的选法有（）(A)105 种 (B)225 种 (C)315 种 (D)420 种2019 清华大学自主招生18. 已知存在实数r ，使得圆周x2y2 r 2 上恰好有n 个整点，则n 可以等于（）| (A)4 (B)6 (C)8 (D)1219. 设复数 z 满足 2|z| ≤ |z - 1| ，则（）(A)|z| 的最大值为 1 (B)|z| 的最小值为 1 3 r (C) z 的虚部的最大值为 2 3 r(D) z 的实部的最大值为 1320. 设 m,n 是大于零的实数， a =(mcos α,msin α) ， b =(ncos β,nsin β) ，其中 α, β∈ [0,2 π) α, β∈[0,2 π) ．定义向量（）r 1a 2=( m cos , 2 m sin ), 2 r1 b 2=( n cos , 2n sin) ，记 θ=α- β，则 2r 1 r 1 r r 1 r 1 r 1 r 1 r 1 r 1 (A) a 2 · a 2 = a (B) a 2 b 2 = mn cos 2 (C) | a 2 b 2 2 24 mn sin 4(D) | a 2b 2| 24 mn cos421. 设数列 { a n } 满足： a 1 =6， a n 1n 3n ，则（）n(A) ? n ∈ N?, a n < (n 1)3(B) ? n ∈ N?, a n ≠ 2015(C) ? n ∈ N?, a n 为完全平方数(D)? n ∈ N?,a n 为完全立方数22. 在极坐标系中，下列方程表示的图形是椭圆的有（）1（ A ）ρ=1（ B ）ρ=1（ C ）ρ=1（ D ）ρ=cossin 2 sin2 cos 1 2sin23. 设函数 f (x)sin x 2 x x ，则（）1（ A ） f ( x) ≤ 4 3(B)| f (x) | ≤ 5|x| (C) 曲线 y= f ( x) 存在对称轴 (D) 曲线 y= f ( x) 存在对称中心24. △ ABC 的三边分别为 a ,b,c ，若△ ABC 为锐角三角形，则（）(A) s inA>cosB (B)tanA>cotB (C)a2b2c 2 (D) a3b3c325. 设函数 f (x) 的定义域是 ( - 1,1) ，若 f (0) = f (0) =1，则存在实数 δ∈ (0,1) ，使得（）(A) f ( x) >0， x ∈ ( - δ, δ) (B)f (x) 在( - δ, δ) 上单调递增(C) f ( x) >1， x ∈(0, δ) (D)f (x) >1， x ∈ ( - δ,0)26. 在直角坐标系中，已知A( - 1,0) ， B(1,0) ．若对于 y 轴上的任意 n 个不同的点 P k (k=1,2,,n) ，总存在两个不同的点 P , P ，使得 |sin ∠A P B- sin ∠ A P B| ≤ 1，则 n 的最小值为（）ijij3(A)3 (B)4 (C)5 (D)627. 设非负实数 x,y 满足 2x+y=1，则 x+x2y 2的（）(A) 最小值为 4 5 (B) 最小值为 25(C) 最大值为 1 (D) 最大值为 1 2 3 a 2128. 对于 50 个黑球和 49 个白球的任意排列（从左到右排成一行），则（）(A) 存在一个黑球，它右侧的白球和黑球一样多(B) 存在一个白球，它右侧的白球和黑球一样多(C) 存在一个黑球，它右侧的白球比黑球少一个(D) 存在一个白球，它右侧的白球比黑球少一个29. 从 1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（）(A)300 个 (B)450个 (C)900 个 (D)1800 个30. 设曲线 L 的方程为 y2(2 x22) y42( x2 x ) =0，则（）(A) L 是轴对称图形 (B)L是中心对称图形(C)L ? {(x,y) ∣ x 2##Answer##y 2≤ 1} (D)L? {(x,y) ∣ - 1 2≤y ≤ 1} 2cos 2i sin 21. 【解析】1 1 = 1 zz = 1 z = 1 33 1-z 1 z 2 1-z zz z 2 1-z z z2 2 2 1-cosi sin2i sincos(2 ) i sin(2 )333=1-332sin 23 i 2sin cos 3 3 3(cos 2i sin )2 =cos0 i sin 0-1[cos( 7 ) i sin( 7)]2sin [cos( ) i sin( )]3 6 63 6 6=1(cos i sin3 1i )=1，选 B36 6 2 22. 【简解】 a p a q (a ka l ) =[(p+q)-(k+l)]d，与公差 d 的符号有关，选 D3. 【解析】设 A( x 1, x1 ),B(x 2 , x2 u u u r u uu r),OA OB = x 1x 2 (11 x 1 x2 ) =0x 2x 1答案 (A), | OA | | O B | =x 2 (1 x 2)1 (11 ) = 1 x 21 1 ≥2 2 | x | 1 =2，正确；答案11x2x2 1x2 | x |1111x 2 x 2 1(B) ,|OA|+|OB| ≥ 2| OA| | OB | ≥ 2 2 , 正确；答案 (C), 直线 AB 的斜率为 21= x x = x 方 x 2 x 1 2 1 1x 1程为 y- 2x 1 =( x 11 )(x- x 1x ), 焦点 (0, 1) 不满足方程，错误；答案 (D) ，原点到直线 AB ：( x41 )x-y+1=0x 1的距离 d=(x 11 1 )2x 1≤ 1，正确。

2019年北京卷理科数学高考真题及答案解析(word精编)

2019年普通高等学校招生全国统一考试数学（理）（北京卷）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

(1)（A（B（C ）3（D ）5 （2）执行如图所示的程序框图，输出的s 值为（A ）1（B ）2（C ）3（D ）4（3）已知直线l 的参数方程为x =1+3t y =2+4tìíî （t 为参数），则点（1，0）到直线l 的距离是（A ）15（B）2 5（C）4 5（D）6 5（4）已知椭圆2x2a +2y2b=1（a>b>0）的离心率为12，则（A）a2=2b2.（B）3a2=4b2.（C）a=2b（D）3a=4b（5）若x,y满足的最大值为（A）-7 （B）1（C）5 （D）7（6）在天文学中，天体的明暗程度可以用星等或亮度来描述。

两颗星的星等与亮度满足m2-m1=52lgE1E2，其中星等为m k的星的亮度为E k（k=1,2）。

已知太阳的星等为-26.7，天狼星的星等为-1.45，则太阳与天狼星的亮度的比值为（A）1010.1（B）10.1（C）lg10.1（D）10-10.1（7）设点A,B,C不共线，则“与的夹角是锐角”是“的（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件（8）数学中有许多形状优美、寓意美好的曲线，曲线C:x2+y2=1+x y就是其中之一（如图）。

给出下列三个结论：①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C上任意一点到原点的距离都不超过2;③曲线C所围城的“心形”区域的面积小于3.其中，所有正确结论的序号是（A）①（B）②（C）①②（D）①②③第二部分(非选择题共10分)二、填空题共6小题,每小题5分，共30分。

(9) 函数f(x)=sin22x的最小正周期是________。

清华大学2019年自主招生试题及答案

2019清华自主招生试题与答案(2018清华自主招生)1、如图的电路，闭合开关S ，当滑动变阻器滑片P 向右移动时，下列说法正确是 CA．电流表读数变小，电压表读数变大B．小电泡L 变暗C．电容器C 上电荷量减小D．电源的总功率变小(2018清华自主招生)2、如图，固定的倾斜光滑杆上套有一个质量为m的圆环，圆环与竖直放置的轻质弹簧一端相连，弹簧的另一端固定在地面上的A点，弹簧处于原长h。

让圆环沿杆滑下，滑到杆的底端时速度为零．则在圆环下滑过程中 CA．圆环机械能守恒B．弹簧的弹性势能先增大后减小C．弹簧的弹性势能变化了mgh D．弹簧的弹性势能最大时圆环的动能最大3、(2018清华自主招生)4、如图所示，有三个斜面a，b，c，底边的长分别为L、L 、2L高度分别为2h、h、h ，某物体与三个斜面间的动摩擦因数都相同，这个物体分别沿三个斜面从顶端由静止下滑到底端，忽略空气阻力，三种情况相比较，下列说法正确的是BDA．物体克服摩擦力做的功W c= 2W b= 4W aB．物体克服摩擦力做的功W c= 2W b= 2W aC．物体到达底端的动能E ka= 2E kb= 2E kcD ．物体到达底端的动能E ka >2E kb >2E kc解：克服摩擦力做的功 cos W mg x mgx =μθ=μ斜底则有 ::W 2:1:1c b a W W =动能定理 k mgx mgx E -μ=高底则有 E ka >2E kb >2E kc(2018清华自主招生)10、2013 年 12 月 6 日，“嫦娥三号”携带月球车“玉兔号”运动到地月转移轨道的P 点时做近月制动后被月球俘获，成功进入环月圆形轨道Ⅰ上运行，如图所示。

在“嫦娥三号”沿轨道Ⅰ经过 P 点时，通过调整速度使其进入椭圆轨道Ⅱ，在沿轨道Ⅱ经过Q 点时，再次调整速度后又经过一系列辅助动作，成功实现了其在月球上的“软着陆”。

对于“嫦娥三号”沿轨道Ⅰ和轨道Ⅱ运动的过程，若以月球为参考系，且只考虑月球对它的引力作用，下列说法中正确的是 ACA ．沿轨道Ⅱ经过 P 点时的速度小于经过Q 点时的速度B ．沿轨道Ⅱ经过 P 点时的机械能小于经过Q 点时的机械能C ．沿轨道Ⅰ经过 P 点时的速度大于沿轨道Ⅱ经过 P 点时的速度D ．沿轨道Ⅰ经过 P 点时的加速度大于沿轨道Ⅱ经过 P 点时的加速度1发射m 1前后动量守恒 0111()m m m m υυυ=+-由角动量守恒定律和机械能守恒守恒定律11()()m m m R m m R υυ-=-′(2018清华自主招生)11．下列说法中正确是 BEA ．一弹簧连接一物体沿水平方向做简谐运动，则该物体做的是匀变速直线运动B ．若单摆的摆长不变，摆球的质量增加为原来的4倍，摆球经过平衡位置时速度减为原来的1/2，则单摆振动的频率将不变，振幅变小C ．做简谐运动的物体，当它每次经过同一位置时，速度一定相同D ．单摆在周期性的外力作用下做简谐运动，则外力的频率越大，单摆的振幅越大E ．机械波在介质中传播时，各质点将不会随波的传播而迁移，只在平衡位置附近振动(2018清华自主招生)15．两电荷量分别为q 1 和q 2 的点电荷放在 x 轴上的O 、M 两点，两电荷连线上各点电势φ 随x 变化的关系如图所示，其中A 、N 两点的电势为零， ND 段中C 点电势最高，则ADA ． C 点的电场强度大小为零B ． A 点的电场强度大小为零C ． NC 间场强方向向 x 轴正方向D ．将一负点电荷从 N 点移到 D 点，电场力先做正功后做负功拓展：（20届复赛）六、(23分)两个点电荷位于x轴上，在它们形成的电场中，若取无限远处的电势为零，则在正x 轴上各点的电势如图中曲线所示，当0x →时，电势U →∞：当x →∞时，电势0U →；电势为零的点的坐标0x , 电势为极小值0U -的点的坐标为 0ax （a ＞2）。

(精校版)2019年北京卷理数高考试题文档版(有答案)

绝密★本科目考试启用前2019年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知复数z =2+i ，则z z ⋅=（A （B （C ）3 （D ）5（2）执行如图所示的程序框图，输出的s 值为（A ）1 （B ）2 （C ）3 （D ）4（3）已知直线l 的参数方程为13,24x t y t=+=+⎧⎨⎩（t 为参数），则点（1，0）到直线l 的距离是（A ）15 （B ）25 （C ）45 （D ）65（4）已知椭圆2222 1x y a b+=（a ＞b ＞0）的离心率为12，则（A ）a 2=2b 2 （B ）3a 2=4b 2 （C ）a =2b （D ）3a =4b（5）若x ，y 满足|1|x y ≤-，且y ≥−1，则3x+y 的最大值为（A ）−7 （B ）1 （C ）5 （D ）7（6）在天文学中，天体的明暗程度可以用星等或亮度来描述．两颗星的星等与亮度满足m 2−m 1=52lg 21E E ，其中星等为m k 的星的亮度为E k （k =1，2）．已知太阳的星等是−26.7，天狼星的星等是−1.45，则太阳与天狼星的亮度的比值为（A ）1010.1 （B ）10.1 （C ）lg10.1 （D ）10−10.1（7）设点A ，B ，C 不共线，则“AB u u u r 与AC uuu r 的夹角为锐角”是“||||AB AC BC +>u u u r u u u r u u u r ”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（8）数学中有许多形状优美、寓意美好的曲线，曲线C ：221||x y x y +=+就是其中之一（如图）．给出下列三个结论：①曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C ；③曲线C 所围成的“心形”区域的面积小于3．其中，所有正确结论的序号是（A ）① （B ）② （C ）①② （D ）①②③第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

自主招生数学试题及答案-word文档

自主招生数学试题及答案同学们都在忙碌地复习自己的功课，为了帮助大家能够在考前对自己多学的知识点有所巩固，下文整理了这篇数学试题及答案，希望可以帮助到大家!2019年清华等五校自主招生英语试题及答案1.以和为两根的有理系数多项式的次数最小是多少?A.2B.3C.5D.6解析：显然为满足要求的多项式，其次数为5.若存在次有理系数多项式以和为两根，则必含有因式，即最小次数为5.故选C.2.在的棋盘中停放着3个红色車和3个黑色車，每一行、每一列都只有一个車，共有多少种停放方法?A.720B.20C.518400D.14400解析：先排3个红色車，从6行中任取3行，有种取法;在选定的3行中第一行有6种停法，第一行选定后第二行有5种停法，第二行选定后第三行有4种停法;红車放定后，黑車只有6种停法.故停放方法共种.故选D.3.已知，求的值.解析：∵又由，有或当时，有当时，4.如图，△ABC中，AD为BC边上的中线，DM、DN分别为ADB、ADC的角平分线，试比较BM+CN与MN的大小关系，并说明理由.解析：延长ND至E，使ND=ED，连结BE、ME，则△BED≌△CND，△MED≌△MND，ME=MN，由BM+BEEM，得BM+CNMN.5.设数列满足，前项和为，求解析：∵由，有时，，于是特征方程有重根2，可设将代入上式，得于是6.模长为1的复数满足，求解析：取，便能得到=1.下面给出证明，=1.7.最多有多少个两两不等的正整数，满足其中任意三数之和都为素数.解析：设满足条件的正整数为个.考虑模3的同余类，共三类，记为则这个正整数需同时满足①不能三类都有;②同一类中不能有3个和超过3个.否则都会出现三数之和为3的倍数.故当时，取1，3，7，9，其任意三数之和为11，13，17，19均为素数，满足题意，所以满足要求的正整数最多有4个.8.已知为2019个实数，满足，且，求证解析：设若，则于是，进而若这2019个数去掉绝对值号后只能取和两值，又即这2019个数去掉绝对值号后取和两值的个数相同，这不可能.9.对于任意的，求的值.解析：各式相加，得10.已知有个实数，排列成阶数阵，记作使得数阵的每一行从左到右都是递增的，即对任意的，当时，有;现将的每一列原有的各数按照从上到下递增的顺序排列，形成一个新的阶数阵，记作，即对任意的，当时，有，试判断中每一行的各数的大小关系，并加以证明.解析：数阵中的中每一行的各数仍是递增的.下面用反证法给出证明. 若在第行存在，令，其中，则当时，即在第列中至少有个数小于，也就是在数阵中的第列中至少排在第行，这与排在第行矛盾.所以数阵中的中每一行的各数仍是递增的.这篇数学试题及答案就为大家分享到这里了。

清华大学自主招生试题数学 Word版含解析

一、选择题1.设复数z=cos 23π+isin 23π，则2111-1z z +-=（） (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列，p,q,k,l 为正整数，则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点，O 是坐标原点，若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1)，且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x yf xy++，x 、y ∈(-1,1)，则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)−kx 有（）(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c ．若c=2，∠C=3π，且sinC+sin(B −A)−2sin2A=0,则有（） (A)b=2a (B)△ABC 的周长为3 (C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-，则（）(A)()f x 有极小值，但无最小值 (B) ()f x 有极大值，但无最大值 (C)若方程()f x =b 恰有一个实根，则b>36e(D)若方程()f x =b 恰有三个不同实根，则0<b<36e 8.已知A={(x,y)∣222x y r +=}，B={(x,y)∣222()()x a y b r -+-=，已知A∩B={(11,x y ),(22,x y )}，则（）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ，12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3，则5x+4y+3z 的最小值为（） (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ，若对任意正整数n ，总存在正整数m ，使得n S =m a ，则（）（A ）{n a }可能为等差数列（B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ，总存在正整数m ，使得n a =m S11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（） (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中，AB=2，AD=A 1A =1，则A 到平面1A BD 的距离为（）(A)13 (B)23(C)22 (D)6313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ，其面积为S ，则（）(A)若S=4，则k 的值唯一 (B)若S=12，则k 的值有2个(C)若D 为三角形，则0<k ≤23(D)若D 为五边形，则k>4 14.△ABC 的三边长是2,3,4，其外心为O ，则OA AB OB BC OC CA ⋅+⋅+⋅=（） (A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立，且P(B)=0.5，P(A −B)=0.2，则（）(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分，则这两部分的面积之比的（） (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形，则不同的选法有（）(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ，使得圆周222x y r +=上恰好有n 个整点，则n 可以等于（） (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|，则（） (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数，a =(mcosα,msinα)，b =(ncosβ,nsinβ)，其中α,β∈[0,2π)α,β∈[0,2π)．定义向量12a =(2m α2m α),12b =(2n β2n β)，记θ=α−β，则（）(A)12a ·12a =a (B)1122a b ⋅=2mn θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足：1a =6，13n n n a a n++=，则（） (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中，下列方程表示的图形是椭圆的有（）（A ）ρ=1cos sin θθ+ （B ）ρ=12sin θ+ （C ）ρ=12cos θ- （D ）ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+，则（）（A ）()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ，若△ABC 为锐角三角形，则（） (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1)，若(0)f =(0)f '=1，则存在实数δ∈(0,1)，使得（） (A)()f x >0，x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1，x ∈(0,δ) (D)()f x >1，x ∈(−δ,0)26.在直角坐标系中，已知A(−1,0)，B(1,0)．若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n)，总存在两个不同的点i P ,j P ，使得|sin ∠A i P B −sin ∠A j P B|≤13，则n 的最小值为（）(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1，则22x y + ）(A)最小值为45 (B)最小值为25(C)最大值为1 (D)最大值为12328.对于50个黑球和49个白球的任意排列（从左到右排成一行），则（）(A)存在一个黑球，它右侧的白球和黑球一样多 (B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（） (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0，则（） (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()333(cossin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]663i ππ-+- 31sin )6623i i ππ+=1，选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ，与公差d 的符号有关，选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅2211221111(1)(1)x x x x ++2121111x x +++11122||||x x +⋅=2，正确；答案(B),|OA|+|OB|≥2||||OA OB ⋅22,正确；答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程，错误；答案(D)，原点到直线AB ：(111x x -)x-y+1=0的距离2111()1x x -+1，正确。

2019年清华大学自主招生暨领军计划数学试题(解析版)

清华大学自主招生暨领军计划数学试题（解析版）1．已知函数x e a x x f )()(2+=有最小值，则函数a x x x g ++=2)(2的零点个数为（）A ．0B ．1C ．2D ．取决于a 的值【答案】C【解析】注意)()(/x g e x f x =，答案C ．2．已知ABC ∆的三个内角C B A ,,所对的边为c b a ,,．下列条件中，能使得ABC ∆的形状唯一确定的有（）A ．Z c b a ∈==,2,1B ．B bC a C c A a A sin sin 2sin sin ,1500=+= C ．060,0sin cos )cos(cos sin cos ==++C C B C B C B AD ．060,1,3===A b a【答案】AD ．3．已知函数x x g x x f ln )(,1)(2=-=，下列说法中正确的有（） A ．)(),(x g x f 在点)0,1(处有公切线B ．存在)(x f 的某条切线与)(x g 的某条切线平行C ．)(),(x g x f 有且只有一个交点D ．)(),(x g x f 有且只有两个交点【答案】BD【解析】注意到1-=x y 为函数)(x g 在)0,1(处的切线，如图，因此答案BD ．4．过抛物线x y 42=的焦点F 作直线交抛物线于B A ,两点，M 为线段AB 的中点．下列说法中正确的有（）A ．以线段AB 为直径的圆与直线23-=x 一定相离B ．||AB 的最小值为4C ．||AB 的最小值为2D ．以线段BM 为直径的圆与y 轴一定相切【答案】AB【解析】对于选项A ，点M 到准线1-=x 的距离为||21|)||(|21AB BF AF =+，于是以线段AB 为直径的圆与直线1-=x 一定相切，进而与直线23-=x 一定相离；对于选项B ，C ，设)4,4(2a a A ，则)1,41(2a a B -，于是2414||22++=a a AB ，最小值为4．也可将||AB 转化为AB 中点到准线的距离的2倍去得到最小值；对于选项D ，显然BD 中点的横坐标与||21BM 不一定相等，因此命题错误．5．已知21,F F 是椭圆)0(1:2222>>=+b a b y a x C 的左、右焦点，P 是椭圆C 上一点．下列说法中正确的有（）A ．b a 2=时，满足02190=∠PF F 的点P 有两个B ．b a 2>时，满足02190=∠PF F 的点P 有四个C ．21F PF ∆的周长小于a 4D ．21F PF ∆的面积小于等于22a【答案】ABCD ．【解析】对于选项A ，B ，椭圆中使得21PF F ∠最大的点P 位于短轴的两个端点；对于选项C ，21PF F ∆的周长为a c a 422<+；选项D ，21PF F ∆的面积为22212121212||||21sin ||||21a PF PF PF F PF PF =⎪⎭⎫ ⎝⎛+≤∠⋅．6．甲、乙、丙、丁四个人参加比赛，有两花获奖．比赛结果揭晓之前，四个人作了如下猜测：甲：两名获奖者在乙、丙、丁中；乙：我没有获奖，丙获奖了；丙：甲、丁中有且只有一个获奖；丁：乙说得对．已知四个人中有且只有两个人的猜测是正确的，那么两个获奖者是（） A ．甲B ．乙C ．丙D ．丁【答案】BD【解析】乙和丁同时正确或者同时错误，分类即可，答案：BD ．7．已知AB 为圆O 的一条弦（非直径），AB OC ⊥于C ，P 为圆O 上任意一点，直线PA 与直线OC 相交于点M ，直线PB 与直线OC 相交于点N ．以下说法正确的有（） A ．P B M O ,,,四点共圆 B ．N B M A ,,,四点共圆 C ．N P O A ,,,四点共圆D ．以上三个说法均不对【答案】AC【解析】对于选项A ，OPM OAM OBM ∠=∠=∠即得；对于选项B ，若命题成立，则MN 为直径，必然有MAN ∠为直角，不符合题意；对于选项C ，MAN MOP MBN ∠=∠=∠即得．答案：AC ．8．C B A C B A cos cos cos sin sin sin ++>++是ABC ∆为锐角三角形的（） A ．充分非必要条件 B ．必要非充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】必要性：由于1cos sin )2sin(sin sin sin >+=-+>+B B B B C B π，类似地，有1sin sin ,1sin sin >+>+A B A C ，于是C B A C B A cos cos cos sin sin sin ++>++．不充分性：当4,2ππ===C B A 时，不等式成立，但ABC ∆不是锐角三角形．9．已知z y x ,,为正整数，且z y x ≤≤，那么方程21111=++z y x 的解的组数为（）A ．8B ．10C ．11D ．12【答案】B【解析】由于x z y x 311121≤++=，故63≤≤x ．若3=x ，则36)6)(6(=--z y ，可得)12,12(),15,10(),18,9(),24,8(),42,7(),(=z y ；若4=x ，则16)4)(4(=--z y ，可得)8,8(),12,6(),20,5(),(=z y ；若5=x ，则6,5,320,211103=≤≤+=y y y z y ，进而解得)10,5,5(),,(=z y x ；若6=x ，则9)3)(3(=--z y ，可得))6,6(),(=z y ．答案：B ． 10．集合},,,{21n a a a A =，任取Aa a A a a A a a n k j i i k k j j i ∈+∈+∈+≤<<≤,,,1这三个式子中至少有一个成立，则n 的最大值为（） A ．6B ．7C ．8D ．9【答案】B11．已知000121,61,1===γβα，则下列各式中成立的有（）A ．3tan tan tan tan tan tan =++αγγββαB ．3tan tan tan tan tan tan -=++αγγββαC ． 3tan tan tan tan tan tan =++γβαγβα D ． 3tan tan tan tan tan tan -=++γβαγβα【答案】BD【解析】令γβαtan ,tan ,tan ===z y x ，则3111=+-=+-=+-zx zx yz y z xy x y ，所以)1(3),1(3),1(3zx z x yz y z xy z y +=-+=-+=-，以上三式相加，即有3-=++zx yz xy ．类似地，有)11(311),11(311),11(311+=-+=-+=-zx x z yz z y xy y x ，以上三式相加，即有3111-=++=++xyz zy x zx yz xy ．答案BD ．12．已知实数c b a ,,满足1=++c b a ，则141414+++++c b a 的最大值也最小值乘积属于区间（）A ．)12,11(B ．)13,12(C ．)14,13(D ．)15,14(【答案】B【解析】设函数14)(+=x x f ，则其导函数142)(/+=x x f ，作出)(x f 的图象，函数)(x f 的图象在31=x 处的切线321)31(7212+-=x y ，以及函数)(x f 的图象过点)0,41(-和)7,23(的割线7174+=x y ，如图，于是可得321)31(7212147174+-≤+≤+x x x ，左侧等号当41-=x 或23=x 时取得；右侧等号当31=x 时取得．因此原式的最大值为21，当31===c b a 时取得；最小值为7，当23,41=-==c b a 时取得，从而原式的最大值与最小值的乘积为)169,144(37∈．答案B ．13．已知1,1,,,222=++=++∈z y x z y x R z y x ，则下列结论正确的有（） A ．xyz 的最大值为0B ．xyz 的最大值为274-C ．z 的最大值为32D ．z 的最小值为31-【答案】ABD14．数列}{n a 满足)(6,2,1*1221N n a a a a a n n n ∈-===++，对任意正整数n ，以下说法中正确的有（） A ．nn n a a a 221++-为定值 B ．)9(mod 1≡n a 或)9(mod 2≡n aC ．741-+n n a a 为完全平方数 D ．781-+n n a a 为完全平方数【答案】ACD 【解析】因为2112221122213226)6(++++++++++++-=--=-n n n n n n n n n n n a a a a a a a a a a a nn n n n n n a a a a a a a 22121122)6(++++++-=+-=，选项A 正确；由于113=a ，故76)6(2121121221-=+-=--=-++++++n n n n n n n n n n n a a a a a a a a a a a ，又对任意正整数恒成立，所以211211)(78,)(74n n n n n n n n a a a a a a a a +=--=-++++，故选项C 、D 正确．计算前几个数可判断选项B 错误．说明：若数列}{n a 满足nn n a pa a -=++12，则nn n a a a 221++-为定值．15．若复数z 满足11=+z z ，则z 可以取到的值有（）A ．21B ．21-C ．215-D ． 215+【答案】CD【解析】因为11||1||=+≤-z z z z ，故215||215+≤≤-z ，等号分别当i z 215+=和i z 215-=时取得．答案CD ．16．从正2016边形的顶点中任取若干个，顺次相连构成多边形，若正多边形的个数为（）A ．6552B ．4536C ．3528D ．2016 【答案】C【解析】从2016的约数中去掉1，2，其余的约数均可作为正多边形的边数．设从2016个顶点中选出k 个构成正多边形，这样的正多边形有k 2016个，因此所求的正多边形的个数就是2016的所有约数之和减去2016和1008．考虑到732201625⨯⨯=，因此所求正多边形的个数为352810082016)71)(931)(32168421(=--++++++++．答案C ．17．已知椭圆)0(12222>>=+b a b y a x 与直线x y l x y l 21:,21:21-==，过椭圆上一点P 作21,l l 的平行线，分别交21,l l 于N M ,两点．若||MN 为定值，则=b a（）A ．2B ．3C ．2D ．5【答案】C【解析】设点),(00y x P ，可得)2141,21(),2141,21(00000000y x y x N y x y x M +--++，故意2020441||y x MN +=为定值，所以2,1641422===b ab a ，答案：C ．说明：（1）若将两条直线的方程改为kx y ±=，则k b a 1=；（2）两条相交直线上各取一点N M ,，使得||MN 为定值，则线段MN 中点Q 的轨迹为圆或椭圆．18．关于y x ,的不定方程yx 21652=+的正整数解的组数为（）A ．0B ．1C ．2D ．3【答案】B19．因为实数的乘法满足交换律与结合律，所以若干个实数相乘的时候，可以有不同的次序．例如，三个实数c b a ,,相乘的时候，可以有 ),(),(,)(,)(ca b ab c c ba c ab 等等不同的次序．记n 个实数相乘时不同的次序有nI 种，则（）A ．22=IB ．123=IC ．964=ID ．1205=I【答案】B【解析】根据卡特兰数的定义，可得1121221)!1(!1------=⋅==n n n n n n n n C n n C n A C I ．答案：AB ．关于卡特兰数的相关知识见《卡特兰数——计数映射方法的伟大胜利》．20．甲乙丙丁4个人进行网球淘汰赛，规定首先甲乙一组、丙丁一组进行比赛，两组的胜者争夺冠军．4个人相互比赛的胜率如表所示：表中的每个数字表示其所在的选手击败其所在列的选手的概率，例如甲击败乙的概率是0.3，乙击败丁的概率是0.4．那么甲刻冠军的概率是．【答案】0.165【解析】根据概率的乘法公式，所示概率为165.0)8.05.03.05.0(3.0=⨯+⨯． 21．在正三棱锥ABC P -中，ABC ∆的边长为1．设点P 到平面ABC 的距离为x ，异面直线CP AB ,的距离为y ．则=∞→y x lim ．【答案】23【解析】当∞→x 时，CP 趋于与平面ABC 垂直，所求极限为ABC ∆中AB 边上的高，为23．22．如图，正方体1111D C B A ABCD -的棱长为1，中心为A A E A BC BF O 1141,21,==，则四面体OEBF 的体积为．【答案】196【解析】如图，EBF G EBF O OEBF V V V --==21961161212111=⋅==--B BCC E GBF E V V ．23．=+-⎰-dx x x n n )sin 1()(22012ππ ．【答案】0【解析】根据题意，有)sin 1()sin 1()(21222012=+=+-⎰⎰---dx x x dx x x n n n n ππππ．24．实数y x ,满足223224)(y x y x =+，则22y x +的最大值为．【答案】1【解析】根据题意，有22222322)(4)(y x y x y x +≤=+，于是122≤+y x ，等号当2122==y x 时取得，因此所求最大值为1．25．z y x ,,均为非负实数，满足427)23()1()21(222=+++++z t x ，则z y x ++的最大值与最小值分别为．【答案】2322-【解析】由柯西不等式可知，当且仅当)0,21,1(),,(=z y x 时，z y x ++取到最大值23．根据题意，有41332222=+++++z y x z y x ，于是,)(3)(4132y z y x z y x +++++≤解得2322-≥++z y x ．于是z y x ++的最小值当)2322,0,0(),(-=yz x 时取得，为2322-． 26．若O 为ABC ∆内一点，满足2:3:4::=∆∆∆COA BOC AOB S S S ，设AC AB AO μλ+=，则=+μλ ．【答案】23【解析】根据奔驰定理，有329492=+=+μλ．27．已知复数32sin 32cos ππi z +=，则=+++2223z z z z ．【答案】12i - 【解析】根据题意，有i z z z z z z 35sin 35cos 122223+=-=+=+++ππ28．已知z 为非零复数，z z 40,10的实部与虚部均为不小于1的正数，则在复平面中，z 所对应的向量OP 的端点P 运动所形成的图形的面积为 .【答案】2003003π+-【解析】设),(R y x yi x z ∈+=，由于2||4040z z z =，于是⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥,140,140,110,1102222y x y y x x y x 如图，弓形面积为1003100)6sin 6(20212-=-⋅⋅πππ，四边形ABCD 的面积为100310010)10310(212-=⋅-⋅. 于是所示求面积为30031003200)1003100()1003100(2-+=-+-ππ.29．若334tan =x ，则=+++x x x x x x x x x x x cos sin cos 2cos sin 2cos 4cos 2sin 4cos 8cos 4sin ．【解析】根据题意，有x x x x x x x x x x x cos sin cos 2cos sin 2cos 4cos 2sin 4cos 8cos 4sin +++38tan tan )tan 2(tan )2tan 4(tan )4tan 8(tan ==+-+-+-=x x x x x x x x ．30．将16个数：4个1，4个2，4个3，4个4填入一个44⨯的数表中，要求每行、每列都恰好有两个偶数，共有种填法．【答案】44100031．设A 是集合}14,,3,2,1{ 的子集，从A 中任取3个元素，由小到大排列之后都不能构成等差数列，则A 中元素个数的最大值为．【答案】8【解析】一方面，设},,,{21k a a a A =，其中141,*≤≤∈k N k ．不妨假设k a a a <<< 21．若9≥k ，由题意，7,33513≥-≥-a a a a ，且1335a a a a -≠-，故715≥-a a ．同理759≥-a a ．又因为1559a a a a -≠-，所以1519≥-a a ，矛盾！故8≤k ．另一方面，取}14,13,11,10,5,4,2,1{=A ，满足题意．综上所述，A 中元素个数的最大值为8．。

2019北京大自主招生考试数学(网传试题与解析)

综上可知 x 2ab ab
法二：
2
2
考虑到
x2
2ax a2
x2
2bx b2 =
x
2 2
a

a2
2
x
2 2
b

b2 可视为 2
点
P

x,
0
到点
A

2 a, 2
2 2
a

与点
B

2 b, 2
2 2
b ຫໍສະໝຸດ 的距离之和.显然 OA a, OB b ， AB a2 b2
A
显然有 PA PB AB ，结合题意，故 PA PB = AB
即 P 在 AB 上。
2a 2b
2a
由 kPA kPB 可得
2 2 a
2 2b
2 2 ax
22
2
O
P‘
P
B
求得 x 2ab ab
2. 复数 z1, z2 满足 z1 3i 2, z2 8 1 ，则由复数 z1 z2 所确定区域的面积是
解析：考虑到 z1 3i z2 8 z1 z2 3i 8 z1 3i z2 8
即1 z1 z2 3i 8 3
5+
2
5 + 5
5 2 62 3 1 2sin2 sin
2 5+ 5 5 5
5
1 5
故 IP 1 5 sin
8.已知数列an 满足： ak1 ak 4k 3k 1, 2, ，求 a2 a2020
解析：
a2 a1 a3 a2 a4 a3 a2019 a2018 a2020 a2019 a1 a2020 41009+4 2019+3=4043

清华大学2019年自主招生数学试题(含详细解析)

1清华大学自主招生数学试题2019.061.一个四面体棱长分别为6，6，6，6，6，9，求外接球的半径.2.求值：1221(1sin )x x dx --⎰.3.已知P 为单位圆上一动点，(0,2)A ，(0,1)B -，求2||||AP BP ⨯的最大值.4.AB 为圆O 的直径，CO AB ⊥，M 为AC 中点，CH MB ⊥，则下列选项正确的是（）A.2AM OH =B.2AH OH =C.△BOH ∽△BMAD.忘记5.{1,2,3,,15}A =⋅⋅⋅，{1,2,3,4,5}B =，f 是A 到B 的映射，若满足()()f x f y =，则称有序对(,)x y 为“好对”，求“好对”的个数最小值.6.若对c ∀∈R ，,a b ∃，使得()()()f a f b f c a b -=-成立，则称函数()f x 满足性质T ，下列函数不满足性质T 的是（）A.32()33f x x x x =-+ B.21()1f x x =+ C.1()x f x e += D.()sin(21)f x x =+7.已知||||1a b == ，12a b ⋅= ，()()0c a c b --= ，若||1d c -= ，求||d 的最大值.8.椭圆22162x y +=，过(2,0)F 的直线交椭圆于A 、B 两点，点C 在直线3x =上，若△ABC 为正三角形，求△ABC 的面积.9.圆224x y +=上一点00(,)x y 处的切线交抛物线28y x =于A 、B 两点，且满足90AOB ∠=︒，其中O 为坐标原点，求0x .10.设a 为44444444各位数字和，b 是a 的各位数字之和，c 为b 的各位数字之和，求c 的值.11.实数x 、y 满足22(2)1x y +-≤的最大值和最小值.初高中数学学习资料的店。

2019年北京大学、清华大学、浙江大学、中国科技大学自主招生数学试题及参考答案

2019年北京大学自主招生数学试题2019年清华大学自主招生数学试题2019年中国科学技术大学自主招生数学试题4．记3cos(),4cos()36x t y t =+-=++，则22x y +的最大值为__________。

5．设点0(1,0)P ，i OP (i =1,2,3…)绕原点按顺时针旋转θ得到向量i OQ ， i Q 关于y 轴对称点记为1 i P +，则2019P 的坐标为__________。

．，且．已知，且9．将△D 1D 2D 3的各中点连线，折成四面体ABCD ，已知12233112,10,8D D D D D D ===，求四面体ABCD 的体积。

10．求证：对于任意的在R 上有仅有一个解0x =11．已知(1)求证：存在多项式()p x ，满足cos (cos )n p θθ=；(2)将()p x 在R [x ]上完全分解。

2019年中国科学技术大学自主招生数学试题参考答案2.B红色曲线为y =sin 2x ,蓝色曲线为y =-cos 3x综上，知：00100110cos sin cos sin 01sin cos sin cos x x x y y y θθθθθθθθ---⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭那么222(,)P x y 满足：200020002cos sin 10sin cos 01x x x x y y y y θθθθ--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭这也就说明了20,P P 重合。

故2019P 坐标为(cos ,sin )θθ--6.首先将递推公式两侧取倒数，则：112(1)11112(1)n n n n nn x n x x x x ++++=⇔-=+累加，即：21122(1)n n n k k x x n n =-=⇒=+∑裂项求和，则：2019112019*********k k x ==-=∑7.如图所示，我们定义a ~b 表示复数a 和b之间的边11z z -+是纯虚数，表明0~(z-1)与0~(z+1)垂直，进而说明|z~(z-1)|=|0~z|=|z~(z+1)|=1故||1z =，进一步，我们设cos sin z i θθ=+则222222222|3|(cos 2cos 3)(sin 2sin )cos 2cos 96cos 6cos 22cos cos 2sin 2sin 2sin 2sin 116cos 2812cos 8cos 53z z cos θθθθθθθθθθθθθθθθθθ++=++++=++++++++=++=++≥等号成立条件为1cos 3θ=-8.9.简解：由题意，易知四面体ABCD为等腰四面体，将其嵌入长方体后割补法即可图示蓝色边框为等腰四面体，黑色为被嵌入的长方体答案：410.首先，我们定义()()n f x 代表函数()f x 的n 阶导数令0()!kn x k x f x e k ==-∑注意到()()1n x f x e =-在R 上单调递增，故其在R 上仅有一根x =0，从而(1)()1n x f x e x -=--在R 上有最小值，即(1)(1)()(0)0n n f x f --≥=进而2(2)()12n x x f x e x -=---在R 上单调递增以此类推，可知：(2)()n k f x -在R 上单调递增，仅有一根x =0(21)()n k f x --在R 先减后增，且恒为非负实数，且仅有一根x =0综上，不论n 取何值，0()!knx k x f x e k ==-∑在R 上仅有一根x =011.本题考察内容十分清晰，旨在考察Chebyshev 多项式（1）采取归纳法证明，若对于不同的n ，存在满足题设的多项式，则记其为()n p x 首先，当1n =时，存在多项式1()p x x=其次，当2n =时，存在多项式22()21p x x =-我们假定命题在2,1n n --的情形下成立，下面考察n 的情形cos cos[(1)]cos(1)cos sin(1)sin 1cos(1)cos [cos cos(2)]2n n n n n n n θθθθθθθθθθθ=-+=-⋅--⋅=-⋅+--进而有cos 2cos cos(1)cos(2)n n n θθθθ=---即12()2()()n n n p x xp x p x --=-因为12(),()n n p x p x --都是多项式，所以()n p x 也是多项式。

清华大学自主招生试题含答案

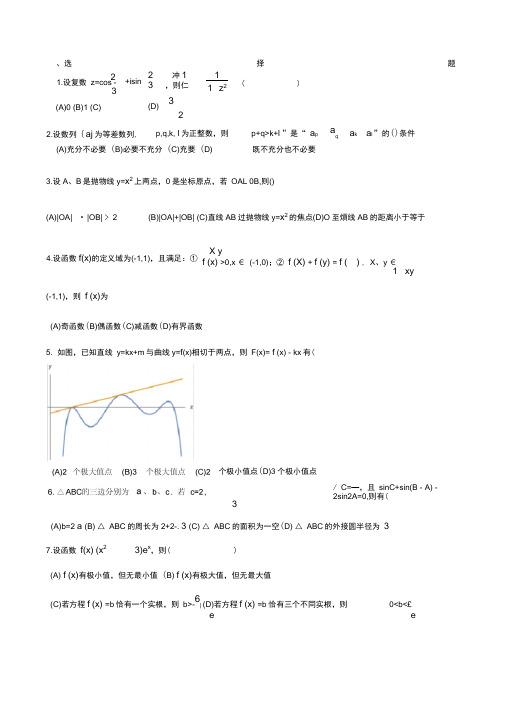
、选择题2( )(A)充分不必要(B)必要不充分(C)充要(D)3.设A、B是抛物线y=x2上两点，0是坐标原点，若OAL 0B,则()(A)|OA| •|OB| > 2 (B)|OA|+|OB| (C)直线AB过抛物线y=x2的焦点(D)O至煩线AB的距离小于等于X yf (x) >0,x € (-1,0)；② f (X) + f (y) = f ( ) , X、y €1 xy(-1,1)，则f (x)为(A)奇函数(B)偶函数(C)减函数(D)有界函数5. 如图，已知直线y=kx+m与曲线y=f(x)相切于两点，则F(x)= f (x) - kx有(/ C=—，且sinC+sin(B - A) -2sin2A=0,则有(3(A)b=2 a (B) △ ABC的周长为2+2-. 3 (C) △ ABC的面积为一空(D) △ ABC的外接圆半径为37.设函数f(x) (x23)e x，则( )(A) f (x)有极小值，但无最小值(B) f (x)有极大值，但无最大值(C)若方程f (x) =b恰有一个实根，则b>-6| (D)若方程f (x) =b恰有三个不同实根，则0<b<£e e1.设复数z=cos -3+isin (A)0 (B)1 (C) 2 冲13 ，则仁(D)3211 z22.设数列｛aj为等差数列, p,q,k, l为正整数，则p+q>k+l ”是“ a p aqa k a l ”的()条件既不充分也不必要4.设函数f(x)的定义域为(-1,1)，且满足：①个极小值点(D)3个极小值点8.已知 A={(x,y) 1 x 22 2y r },B={(x,y)1 (x2 2 2a) (y b) r ,已知 A n B={(x 1,yJ ,( X 2,y 2)},则()(A)0< a 2 b 2 <2r 2(B)aXX 2) b(y1 y 2) 0(C)X 1 X 2 = a , y 1y 2=b (D)2a b 2 = 2ax 1 2by 19.已知非负实数x,y,z满足4x 24y 22z +2z=3, 则5x+4y+3z 的最小值为()(A)1 (B)2 (C)3 (D)410.设数列｛ a n ｝的前n 项和为S n ，若对任意正整数n ,总存在正整数 m,使得S n =a m ，则( )(A )｛ a n ｝可能为等差数列(B )｛ a n ｝可能为等比数列(c )｛a n ｝的任意一项均可写成｛a n ｝的两项之差(D)对任意正整数n ，总存在正整数 m 使得a n = S m 11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测： 3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名•比赛后发现没有并列名次，且甲、乙、丙、丁中只有 1人猜对比赛结果，此人是( )(A)甲(B)乙(C)丙(D) 丁1(A)若S=4,则k 的值唯一(B) 若S=^，贝U k 的值有2个22(C)若D 为三角形，则0<k <(D)若D 为五边形，则312.长方体 ABCDAEGD 中,AB=2, AD=A A 1=1，贝U A 到平面 A BD 的距离为((A) - (B)3(D)13.设不等式组|x| |y| 2 y 2 k(x 1)所表示的区域为 D,其面积为S,U(k>414. △ ABC 勺三边长是 2,3,4，其外心为 0,则 uuu uuu OA AB uuu uuu uuur uuu OB BC 0C CA =((A)0 (B)-15 (C) -21(D)229 215. 设随机事件 A 与B 互相独立，且 P(B)=0.5(A)P(A)=0.4 (B)P(B -A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916. 过厶ABC 的重心作直线将厶 3(A)最小值为一(B)最小值为417. 从正15边形的顶点中选出,P(A- B)=0.2，则(ABC 分成两部分，则这两部分的面积之比的(4 4(C)最大值为一533个构成钝角三角形，5(D 最大值为一4则不同的选法有((A)105 种(B)225 种(C)315 种(D)420 种18. 已知存在实数r，使得圆周x2y2 r2上恰好有n个整点，则n可以等于(22.在极坐标系中，下列方程表示的图形是椭圆的有(4 2 1 V2(A)最小值为一(B)最小值为一 (C)最大值为1 (D)最大值为--------------------5 5 3(A)4 (B)6 (C)8 (D)1219. 设复数z 满足2|z| w |z-1|，则(1(A)|z|的最大值为1 (B)|z| 的最小值为—(C)z321的虚部的最大值为2(D)z 的实部的最大值为13320.设 m,n 是大于零的实数， a =(mcos a ,msin a ),b =(ncos 3 ,nsin 3 )，其中 a , B€ [0,2 n ) a , B€r 1, _[0,2 n ) •定义向量 a 2 =( 、、. m cos — ,、. m sin 一 ), b 2=(、. n 2cos — 2 ，、齐 sin —)，记 9 = a - 3,贝U2r [ r 1 r r 1 r 1 ___ (A) a 2 • a 2 = a (B) a 2 b 2=、.mn cos — (C) 2r] r] … |a 2 b 2|4、一 mn sin 2 —4r 1 r] 2 _ 2 (D) |a 2 b 2 |24, mncos 2 —421.设数列｛ a n ｝满足：a 1=6, an 1，则((A) ? n € N?, a n <(n 1)3 (B) ? n € N?, a n 丰 2015 (C) ? n € N?, a n 为完全平方数(D)? n € N?, a n 为完全立方数1 (A )p=cos sin23. 设函数 f(x)s in x，则( x x 14(A ) f(x) w (B)| f (x) | w 5|x| (C)曲线 y= f (x)存在对称轴324. △ ABC 的三边分别为a ,b,c ，若△ ABC 为锐角三角形，则((B )p=—1(C ) 2 sin1p= —2 cos(D )(D) 1 1 2si n曲线y= f (x)存在对称中心(A)si nA>cosB (B)ta nA>cotB (C) a 2 b 2 c 2 (D) a 3 b 3 c 325.设函数f (x)的定义域是(-1,1), 若f(0) = f (0) =1,则存在实数 s€ (0,1)，使得()(A) f (x) >0, x € (- S , S) (B)f (x)在(-S , S )上单调递增 (C) f (x) >1, x € (0, S) (D)f (x)>1 , x € (- S ,0)26.在直角坐标系中，已知A(-1,0),B(1,0) •若对于y 轴上的任意n 个不同的点 P k (k=1,2，…,n)，总存在两个不同的点R ,P j ,1使得 |sin / A P j B-sin / A P j B| w —,贝V n 的最小值为( 3(A)3 (B)4(C)5 (D)627.设非负实数x,y 满足2x+y=1，则 x+ x 2 y 2 的()128.对于50个黑球和49个白球的任意排列(从左到右排成一行)，则((A)存在一个黑球，它右侧的白球和黑球一样多(B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个 29.从1,2,3,4,5 中挑出三个不同数字组成五位数, 同的五位数有( (A)300 个(B)450其中有两个数字各用两次，例如 12231,则能得到的不 30.设曲线L 的方程为 (A)L 是轴对称图形 (C)L ? {(x,y) I ##A nswer##1.【解析】丄1-z) 个(C)900 y 4 (2x 2(B)L 个(D)1800 个 2 4 2 2)y (x 2x ) =0,则(是中心对称图形 1 (D)L ? {(x,y)zz 1 zz_______ 1 - 2. 21-cos i sin332 cos 3..2 i sin ___ 3 2 2i sin32sin 2 i 2sin cos —3 3 3 cos0 isinO 2sin — [cos( —) i sin(-)i sin(3、、3(cos —2-洽 2os(cos( i sin ) 27) i sin(67)]丄(cos — isi n —.3 6 6△ )=1,选 B22.【简解】 a p (a k Q )=[(p+q)-(k+l)]d ，与公差 d 的符号有关，选 3.【解析】设A( 2X 1,X 1 ),B( 2 uuu uuu X 2,X 2 ), OA OB =X 1X 2(1 X 1X 2) =0 X 2 X1 答案(A), |0A| l OBI ^x^(1 好)4(1 —1^) = j1 X2 1 2 X 11 > /2 2|X 1 | 丄=2,正确; |X 1 | 答案(B),|OA|+|OB| > 2..|OA 「|OB| > 2 .2,正确；答案(C),直线 AB 的斜率为 2 22^=X 2 x 2 x 1X1程为 y- xj =( x 1 1)(x-x 1),焦点(0, 1)不满足方程，错误；答案(D)，原点到直线AB ：(4X11)x-y+ 仁X 1的距离d=w 1,正确。