正态分布、T分布、F分布表
6.2数理统计中几种常用的分布.

性质3. 设T~t(n),则:T ~F(1,n) .
2
证明:
由t分布定义 T
2
X Y /n
其中X∼N(0,1),Y~χ (n),且X与Y相互独立. 2 2 (1) / 1 X /1 2 F T 2 Y /n ( n) / n
且 2 (1)与 2 ( n)相互独立.
由F分布定义, ∴ F = T2~F(1,n) .
2
条件: 的点χ
P ( n)
2 2
2
( n )
f ( x)dx
2
(n)为χ 2(n)分布的上分位点.
χ (n)分布 的上分位点 图形如右图.
χ2(n)分布的上分位点可以查 附表5.
2Hale Waihona Puke 13例1:求2 2 0 ( 10 ) , )。 .05 0.1 (20
1.) 因为
P X z0.05 1 P X z0.05 1 0.05 0.95.
P X 1.64 0.9495.
P X 1.65 0.9505.
z0.05 1.64 1.65 1.645. 2
4
2.)
P X z0.005 1 PX z0.005 1 0.005 0.995.
i 1 n i 1
n
EX i2 n.
2 DX i
D D(
2n.
10
4.应用中心极限定理可得,若 若 X ~ 2 (n) ,则当n充分大时, X n 2n 的分布近似正态分布N(0,1).
11
2 (n)
分布的密度函 数的图形如右 图.
t分布表_精品文档

t分布表1. 什么是t分布表t分布表(t-distribution table)是统计学中常用的一种参考表格,用于计算学生t分布的临界值。
t分布是由William Gosset于1908年引入的,也被称为学生分布。
与正态分布不同的是,t分布的形状取决于自由度。
自由度(degrees of freedom,缩写为df)是t分布中的一个参数,表示数据集中的可用信息的数量。
t 分布在小样本情况下(自由度较低)更适用,而正态分布在大样本情况下更为适用。
t分布表通过提供t分布的不同自由度和置信水平下的临界值,帮助研究人员进行统计推断。
2. t分布表的用途t分布表的主要用途是计算t检验的临界值。
t检验是一种用于比较两个样本均值之间差异的统计方法。
通过比较计算出的t值与t分布表中的临界值,可以确定样本均值差异的显著性。
在进行t检验时,需要指定置信水平和自由度,然后参考t分布表找到对应的临界值。
此外,t分布表还可用于计算统计推断中的置信区间。
置信区间是对参数的估计范围,用于描述样本估计值与真实值之间的不确定性。
通过查找t分布表,可以确定在给定的置信水平和样本大小下,t分布的临界值,从而得到参数的置信区间。
3. t分布表的构造t分布表按照不同的自由度和置信水平划分为不同的表格,每个表格中包含了对应自由度和置信水平的t值。
以表格的行表示自由度,表格的列表示置信水平。
例如,当样本自由度为9,置信水平为95%时,在t分布表中可以找到一个特定的值,即为t(0.025, 9)。
这个值是指在自由度为9的条件下,95%置信水平对应的t临界值。
在进行t检验或计算置信区间时,可以通过查找t分布表得到相应的临界值。
需要注意的是,由于t分布的对称性质,t分布表中只提供了t值的正侧临界值。
要获得t值的负侧临界值,可以通过对应正侧临界值取反得到。
4. 实际使用示例假设现有一组实验数据,样本容量为15。
我们想要计算该样本的平均值的置信区间。
标准正态分布对照表

标准正态分布对照表摘要:一、标准正态分布的定义与性质1.标准正态分布的定义2.标准正态分布的概率密度函数3.标准正态分布的累积分布函数二、标准正态分布对照表的应用1.对照表的构成与意义2.对照表的使用方法3.对照表在实际问题中的应用举例三、标准正态分布与其他分布的关系1.标准正态分布与正态分布的关系2.标准正态分布与t 分布的关系3.标准正态分布与卡方分布的关系四、标准正态分布在统计学中的重要性1.描述性统计分析中的应用2.推断性统计分析中的应用3.概率论与数理统计的基础知识正文:标准正态分布,又称为高斯分布(Gaussian distribution),是一种连续型概率分布。
它具有对称的钟形曲线,其分布的均值(μ)为0,标准差(σ)为1。
标准正态分布广泛应用于统计学、概率论、工程学等领域,其对照表是研究和解决实际问题的关键工具。
一、标准正态分布的定义与性质标准正态分布的定义可以追溯到19 世纪初,德国数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss)对这一分布的深入研究。
标准正态分布的概率密度函数为:f(x) = (1 / (√(2π))) * e^(-(x^2) / 2)其累积分布函数为:F(x) = 1 / (√(2π)) * ∫[e^(-(t^2) / 2), t ≤ x] dt二、标准正态分布对照表的应用标准正态分布对照表是一个重要的工具,它可以帮助我们快速查找标准正态分布在一定置信水平下的临界值。
对照表通常包括正态分布的累积分布函数值、z 分数(Z-score)以及对应的概率。
使用对照表时,我们可以根据实际问题中所给的置信水平,找到对应的z 分数,从而求解问题。
例如,在产品质量控制中,我们希望确定一个产品的合格率。
已知过去经验表明,合格率约为95%。
我们可以使用对照表查找标准正态分布在95% 置信水平下的z 分数,得到±1.96。
然后,将这个z 分数代入到正态分布的累积分布函数中,得到产品的合格率。
统计学附录_F分布,t分布临界值表_全
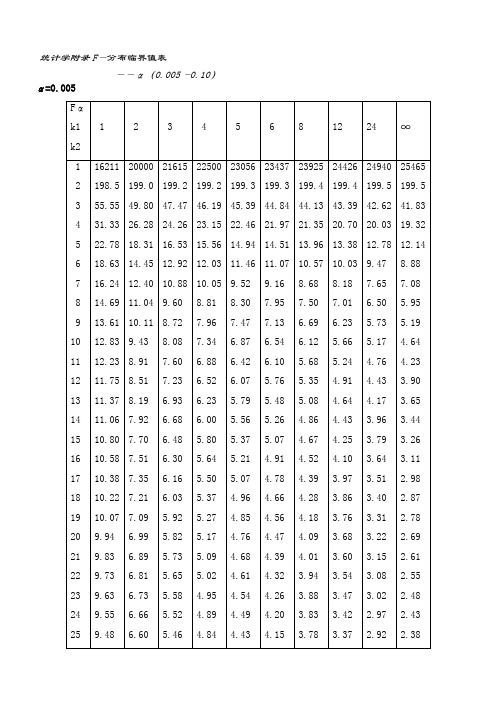
14.88
9.36
7.15
5.99
5.29
4.82
4.48
4.24
4.04
3.89
3.77
3.66
3.58
3.50
3.44
3.38
3.33
3.29
3.25
3.22
3.18
3.15
3.13
3.10
3.08
3.06
3.04
3.03
2.90
2.79
2.67
2.57
937.1
39.33
14.73
9.20
7.23
6.93
6.68
6.48
6.30
6.16
6.03
5.92
5.82
5.73
5.65
5.58
5.52
5.46
5.41
5.36
5.32
5.28
5.24
4.98
4.73
4.50
22500
199.2
46.19
23.15
15.56
12.03
10.05
8.81
7.96
7.34
6.88
6.52
6.23
6.00
3.28
3.25
3.21
3.18
2.95
2.74
2.54
24940
199.5
42.62
20.03
12.78
9.47
7.65
6.50
5.73
5.17
4.76
4.43
4.17
3.96
3.79
3.64
t分布表精确完整图

t分布在概率论和统计学中,t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。
如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
t分布曲线形态与n(确切地说与自由度df)大小有关。
与标准正态分布曲线相比,自由度df越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度df 愈大,t分布曲线愈接近正态分布曲线,当自由度df=∞时,t分布曲线为标准正态分布曲线。
设随机变量T ∼ t n, 则其密度函数为:t n(x)=Γ(n+12)Γ(n2)√nπ(1+x2)−n+12,−∞<x<∞该密度函数的图形如下:t分布表如下:n | α0.250.10 0.050.0250.010.005 1 1.0000 3.0777 6.3138 12.7062 31.8205 63.6567 20.8165 1.8856 2.9200 4.3027 6.9646 9.9248 30.7649 1.6377 2.3534 3.1824 4.5407 5.8409 40.7407 1.5332 2.1318 2.7764 3.7469 4.6041 50.7267 1.4759 2.0150 2.5706 3.3649 4.0321 60.7176 1.4398 1.9432 2.4469 3.1427 3.7074 70.7111 1.4149 1.8946 2.3646 2.9980 3.4995 80.7064 1.3968 1.8595 2.3060 2.8965 3.3554 90.7027 1.3830 1.8331 2.2622 2.8214 3.2498 100.6998 1.3722 1.8125 2.2281 2.7638 3.1693 110.6974 1.3634 1.7959 2.2010 2.7181 3.1058 120.6955 1.3562 1.7823 2.1788 2.6810 3.0545 130.6938 1.3502 1.7709 2.1604 2.6503 3.0123 140.6924 1.3450 1.7613 2.1448 2.6245 2.9768 150.6912 1.3406 1.7531 2.1314 2.6025 2.9467160.6901 1.3368 1.7459 2.1199 2.5835 2.9208 170.6892 1.3334 1.7396 2.1098 2.5669 2.8982 180.6884 1.3304 1.7341 2.1009 2.5524 2.8784 190.6876 1.3277 1.7291 2.0930 2.5395 2.8609 200.6870 1.3253 1.7247 2.0860 2.5280 2.8453 210.6864 1.3232 1.7207 2.0796 2.5176 2.8314 220.6858 1.3212 1.7171 2.0739 2.5083 2.8188 230.6853 1.3195 1.7139 2.0687 2.4999 2.8073 240.6848 1.3178 1.7109 2.0639 2.4922 2.7969 250.6844 1.3163 1.7081 2.0595 2.4851 2.7874 260.6840 1.3150 1.7056 2.0555 2.4786 2.7787 270.6837 1.3137 1.7033 2.0518 2.4727 2.7707 280.6834 1.3125 1.7011 2.0484 2.4671 2.7633 290.6830 1.3114 1.6991 2.0452 2.4620 2.7564 300.6828 1.3104 1.6973 2.0423 2.4573 2.7500 310.6825 1.3095 1.6955 2.0395 2.4528 2.7440 320.6822 1.3086 1.6939 2.0369 2.4487 2.7385 330.6820 1.3077 1.6924 2.0345 2.4448 2.7333 340.6818 1.3070 1.6909 2.0322 2.4411 2.7284 350.6816 1.3062 1.6896 2.0301 2.4377 2.7238 360.6814 1.3055 1.6883 2.0281 2.4345 2.7195 370.6812 1.3049 1.6871 2.0262 2.4314 2.7154 380.6810 1.3042 1.6860 2.0244 2.4286 2.7116 390.6808 1.3036 1.6849 2.0227 2.4258 2.7079 400.6807 1.3031 1.6839 2.0211 2.4233 2.7045 410.6805 1.3025 1.6829 2.0195 2.4208 2.7012 420.6804 1.3020 1.6820 2.0181 2.4185 2.6981 430.6802 1.3016 1.6811 2.0167 2.4163 2.6951 440.6801 1.3011 1.6802 2.0154 2.4141 2.6923 450.6800 1.3006 1.6794 2.0141 2.4121 2.6896 460.6799 1.3002 1.6787 2.0129 2.4102 2.6870 470.6797 1.2998 1.6779 2.0117 2.4083 2.6846 480.6796 1.2994 1.6772 2.0106 2.4066 2.6822 490.6795 1.2991 1.6766 2.0096 2.4049 2.6800 500.6794 1.2987 1.6759 2.0086 2.4033 2.6778 510.6793 1.2984 1.6753 2.0076 2.4017 2.6757 520.6792 1.2980 1.6747 2.0066 2.4002 2.6737 530.6791 1.2977 1.6741 2.0057 2.3988 2.6718 540.6791 1.2974 1.6736 2.0049 2.3974 2.6700 550.6790 1.2971 1.6730 2.0040 2.3961 2.6682 560.6789 1.2969 1.6725 2.0032 2.3948 2.6665 570.6788 1.2966 1.6720 2.0025 2.3936 2.6649 580.6787 1.2963 1.6716 2.0017 2.3924 2.6633 590.6787 1.2961 1.6711 2.0010 2.3912 2.6618600.6786 1.2958 1.6706 2.0003 2.3901 2.6603 610.6785 1.2956 1.6702 1.9996 2.3890 2.6589 620.6785 1.2954 1.6698 1.9990 2.3880 2.6575 630.6784 1.2951 1.6694 1.9983 2.3870 2.6561 640.6783 1.2949 1.6690 1.9977 2.3860 2.6549 650.6783 1.2947 1.6686 1.9971 2.3851 2.6536 660.6782 1.2945 1.6683 1.9966 2.3842 2.6524 670.6782 1.2943 1.6679 1.9960 2.3833 2.6512 680.6781 1.2941 1.6676 1.9955 2.3824 2.6501 690.6781 1.2939 1.6672 1.9949 2.3816 2.6490 700.6780 1.2938 1.6669 1.9944 2.3808 2.6479 710.6780 1.2936 1.6666 1.9939 2.3800 2.6469 720.6779 1.2934 1.6663 1.9935 2.3793 2.6459 730.6779 1.2933 1.6660 1.9930 2.3785 2.6449 740.6778 1.2931 1.6657 1.9925 2.3778 2.6439 750.6778 1.2929 1.6654 1.9921 2.3771 2.6430 760.6777 1.2928 1.6652 1.9917 2.3764 2.6421 770.6777 1.2926 1.6649 1.9913 2.3758 2.6412 780.6776 1.2925 1.6646 1.9908 2.3751 2.6403 790.6776 1.2924 1.6644 1.9905 2.3745 2.6395 800.6776 1.2922 1.6641 1.9901 2.3739 2.6387 810.6775 1.2921 1.6639 1.9897 2.3733 2.6379 820.6775 1.2920 1.6636 1.9893 2.3727 2.6371 830.6775 1.2918 1.6634 1.9890 2.3721 2.6364 840.6774 1.2917 1.6632 1.9886 2.3716 2.6356 850.6774 1.2916 1.6630 1.9883 2.3710 2.6349 860.6774 1.2915 1.6628 1.9879 2.3705 2.6342 870.6773 1.2914 1.6626 1.9876 2.3700 2.6335 880.6773 1.2912 1.6624 1.9873 2.3695 2.6329 890.6773 1.2911 1.6622 1.9870 2.3690 2.6322 900.6772 1.2910 1.6620 1.9867 2.3685 2.6316 910.6772 1.2909 1.6618 1.9864 2.3680 2.6309 920.6772 1.2908 1.6616 1.9861 2.3676 2.6303 930.6771 1.2907 1.6614 1.9858 2.3671 2.6297 940.6771 1.2906 1.6612 1.9855 2.3667 2.6291 950.6771 1.2905 1.6611 1.9853 2.3662 2.6286 960.6771 1.2904 1.6609 1.9850 2.3658 2.6280 970.6770 1.2903 1.6607 1.9847 2.3654 2.6275 980.6770 1.2902 1.6606 1.9845 2.3650 2.6269 990.6770 1.2902 1.6604 1.9842 2.3646 2.6264 1000.6770 1.2901 1.6602 1.9840 2.3642 2.6259 1010.6769 1.2900 1.6601 1.9837 2.3638 2.6254 1020.6769 1.2899 1.6599 1.9835 2.3635 2.6249 1030.6769 1.2898 1.6598 1.9833 2.3631 2.62441040.6769 1.2897 1.6596 1.9830 2.3627 2.6239 1050.6768 1.2897 1.6595 1.9828 2.3624 2.6235 1060.6768 1.2896 1.6594 1.9826 2.3620 2.6230 1070.6768 1.2895 1.6592 1.9824 2.3617 2.6226 1080.6768 1.2894 1.6591 1.9822 2.3614 2.6221 1090.6767 1.2894 1.6590 1.9820 2.3610 2.6217 1100.6767 1.2893 1.6588 1.9818 2.3607 2.6213 1110.6767 1.2892 1.6587 1.9816 2.3604 2.6208 1120.6767 1.2892 1.6586 1.9814 2.3601 2.6204 1130.6767 1.2891 1.6585 1.9812 2.3598 2.6200 1140.6766 1.2890 1.6583 1.9810 2.3595 2.6196 1150.6766 1.2890 1.6582 1.9808 2.3592 2.6193 1160.6766 1.2889 1.6581 1.9806 2.3589 2.6189 1170.6766 1.2888 1.6580 1.9804 2.3586 2.6185 1180.6766 1.2888 1.6579 1.9803 2.3584 2.6181 1190.6766 1.2887 1.6578 1.9801 2.3581 2.6178 1200.6765 1.2886 1.6577 1.9799 2.3578 2.6174 1210.6765 1.2886 1.6575 1.9798 2.3576 2.6171 1220.6765 1.2885 1.6574 1.9796 2.3573 2.6167 1230.6765 1.2885 1.6573 1.9794 2.3570 2.6164 1240.6765 1.2884 1.6572 1.9793 2.3568 2.6161 1250.6765 1.2884 1.6571 1.9791 2.3565 2.6157 1260.6764 1.2883 1.6570 1.9790 2.3563 2.6154 1270.6764 1.2883 1.6569 1.9788 2.3561 2.6151 1280.6764 1.2882 1.6568 1.9787 2.3558 2.6148 1290.6764 1.2881 1.6568 1.9785 2.3556 2.6145 1300.6764 1.2881 1.6567 1.9784 2.3554 2.6142 1310.6764 1.2880 1.6566 1.9782 2.3552 2.6139 1320.6764 1.2880 1.6565 1.9781 2.3549 2.6136 1330.6763 1.2879 1.6564 1.9780 2.3547 2.6133 1340.6763 1.2879 1.6563 1.9778 2.3545 2.6130 1350.6763 1.2879 1.6562 1.9777 2.3543 2.6127 1360.6763 1.2878 1.6561 1.9776 2.3541 2.6125 1370.6763 1.2878 1.6561 1.9774 2.3539 2.6122 1380.6763 1.2877 1.6560 1.9773 2.3537 2.6119 1390.6763 1.2877 1.6559 1.9772 2.3535 2.6117 1400.6762 1.2876 1.6558 1.9771 2.3533 2.6114 1410.6762 1.2876 1.6557 1.9769 2.3531 2.6111 1420.6762 1.2875 1.6557 1.9768 2.3529 2.6109 1430.6762 1.2875 1.6556 1.9767 2.3527 2.6106 1440.6762 1.2875 1.6555 1.9766 2.3525 2.6104 1450.6762 1.2874 1.6554 1.9765 2.3523 2.6102 1460.6762 1.2874 1.6554 1.9763 2.3522 2.6099 1470.6762 1.2873 1.6553 1.9762 2.3520 2.60971480.6762 1.2873 1.6552 1.9761 2.3518 2.6095 1490.6761 1.2873 1.6551 1.9760 2.3516 2.6092 1500.6761 1.2872 1.6551 1.9759 2.3515 2.6090 1510.6761 1.2872 1.6550 1.9758 2.3513 2.6088 1520.6761 1.2871 1.6549 1.9757 2.3511 2.6086 1530.6761 1.2871 1.6549 1.9756 2.3510 2.6083 1540.6761 1.2871 1.6548 1.9755 2.3508 2.6081 1550.6761 1.2870 1.6547 1.9754 2.3506 2.6079 1560.6761 1.2870 1.6547 1.9753 2.3505 2.6077 1570.6761 1.2870 1.6546 1.9752 2.3503 2.6075 1580.6760 1.2869 1.6546 1.9751 2.3502 2.6073 1590.6760 1.2869 1.6545 1.9750 2.3500 2.6071 1600.6760 1.2869 1.6544 1.9749 2.3499 2.6069 1610.6760 1.2868 1.6544 1.9748 2.3497 2.6067 1620.6760 1.2868 1.6543 1.9747 2.3496 2.6065 1630.6760 1.2868 1.6543 1.9746 2.3494 2.6063 1640.6760 1.2867 1.6542 1.9745 2.3493 2.6061 1650.6760 1.2867 1.6541 1.9744 2.3492 2.6060 1660.6760 1.2867 1.6541 1.9744 2.3490 2.6058 1670.6760 1.2866 1.6540 1.9743 2.3489 2.6056 1680.6760 1.2866 1.6540 1.9742 2.3487 2.6054 1690.6759 1.2866 1.6539 1.9741 2.3486 2.6052 1700.6759 1.2866 1.6539 1.9740 2.3485 2.6051 1710.6759 1.2865 1.6538 1.9739 2.3484 2.6049 1720.6759 1.2865 1.6538 1.9739 2.3482 2.6047 1730.6759 1.2865 1.6537 1.9738 2.3481 2.6045 1740.6759 1.2864 1.6537 1.9737 2.3480 2.6044 1750.6759 1.2864 1.6536 1.9736 2.3478 2.6042 1760.6759 1.2864 1.6536 1.9735 2.3477 2.6041 1770.6759 1.2864 1.6535 1.9735 2.3476 2.6039 1780.6759 1.2863 1.6535 1.9734 2.3475 2.6037 1790.6759 1.2863 1.6534 1.9733 2.3474 2.6036 1800.6759 1.2863 1.6534 1.9732 2.3472 2.6034 1810.6758 1.2862 1.6533 1.9732 2.3471 2.6033 1820.6758 1.2862 1.6533 1.9731 2.3470 2.6031 1830.6758 1.2862 1.6532 1.9730 2.3469 2.6030 1840.6758 1.2862 1.6532 1.9729 2.3468 2.6028 1850.6758 1.2861 1.6531 1.9729 2.3467 2.6027 1860.6758 1.2861 1.6531 1.9728 2.3466 2.6025 1870.6758 1.2861 1.6530 1.9727 2.3465 2.6024 1880.6758 1.2861 1.6530 1.9727 2.3463 2.6022 1890.6758 1.2860 1.6530 1.9726 2.3462 2.6021 1900.6758 1.2860 1.6529 1.9725 2.3461 2.6020 1910.6758 1.2860 1.6529 1.9725 2.3460 2.60181920.6758 1.2860 1.6528 1.9724 2.3459 2.6017 1930.6758 1.2860 1.6528 1.9723 2.3458 2.6015 1940.6758 1.2859 1.6527 1.9723 2.3457 2.6014 1950.6757 1.2859 1.6527 1.9722 2.3456 2.6013 1960.6757 1.2859 1.6527 1.9721 2.3455 2.6011 1970.6757 1.2859 1.6526 1.9721 2.3454 2.6010 1980.6757 1.2858 1.6526 1.9720 2.3453 2.6009 1990.6757 1.2858 1.6525 1.9720 2.3452 2.6008 2000.6757 1.2858 1.6525 1.9719 2.3451 2.6006 2010.6757 1.2858 1.6525 1.9718 2.3450 2.6005 2020.6757 1.2858 1.6524 1.9718 2.3449 2.6004 2030.6757 1.2857 1.6524 1.9717 2.3449 2.6003 2040.6757 1.2857 1.6524 1.9717 2.3448 2.6001 2050.6757 1.2857 1.6523 1.9716 2.3447 2.6000 2060.6757 1.2857 1.6523 1.9715 2.3446 2.5999 2070.6757 1.2857 1.6522 1.9715 2.3445 2.5998 2080.6757 1.2856 1.6522 1.9714 2.3444 2.5997 2090.6757 1.2856 1.6522 1.9714 2.3443 2.5996 2100.6757 1.2856 1.6521 1.9713 2.3442 2.5994 2110.6757 1.2856 1.6521 1.9713 2.3442 2.5993 2120.6756 1.2856 1.6521 1.9712 2.3441 2.5992 2130.6756 1.2855 1.6520 1.9712 2.3440 2.5991 2140.6756 1.2855 1.6520 1.9711 2.3439 2.5990 2150.6756 1.2855 1.6520 1.9711 2.3438 2.5989 2160.6756 1.2855 1.6519 1.9710 2.3437 2.5988 2170.6756 1.2855 1.6519 1.9710 2.3437 2.5987 2180.6756 1.2854 1.6519 1.9709 2.3436 2.5986 2190.6756 1.2854 1.6518 1.9709 2.3435 2.5985 2200.6756 1.2854 1.6518 1.9708 2.3434 2.5984 2210.6756 1.2854 1.6518 1.9708 2.3433 2.5983 2220.6756 1.2854 1.6517 1.9707 2.3433 2.5982 2230.6756 1.2854 1.6517 1.9707 2.3432 2.5981 2240.6756 1.2853 1.6517 1.9706 2.3431 2.5980 2250.6756 1.2853 1.6517 1.9706 2.3430 2.5979 2260.6756 1.2853 1.6516 1.9705 2.3430 2.5978 2270.6756 1.2853 1.6516 1.9705 2.3429 2.5977 2280.6756 1.2853 1.6516 1.9704 2.3428 2.5976 2290.6756 1.2853 1.6515 1.9704 2.3427 2.5975 2300.6756 1.2852 1.6515 1.9703 2.3427 2.5974 2310.6756 1.2852 1.6515 1.9703 2.3426 2.5973 2320.6755 1.2852 1.6514 1.9702 2.3425 2.5972 2330.6755 1.2852 1.6514 1.9702 2.3425 2.5971 2340.6755 1.2852 1.6514 1.9702 2.3424 2.5970 2350.6755 1.2852 1.6514 1.9701 2.3423 2.59692360.6755 1.2851 1.6513 1.9701 2.3423 2.5968 2370.6755 1.2851 1.6513 1.9700 2.3422 2.5967 2380.6755 1.2851 1.6513 1.9700 2.3421 2.5966 2390.6755 1.2851 1.6513 1.9699 2.3421 2.5966 2400.6755 1.2851 1.6512 1.9699 2.3420 2.5965 2410.6755 1.2851 1.6512 1.9699 2.3419 2.5964 2420.6755 1.2851 1.6512 1.9698 2.3419 2.5963 2430.6755 1.2850 1.6511 1.9698 2.3418 2.5962 2440.6755 1.2850 1.6511 1.9697 2.3417 2.5961 2450.6755 1.2850 1.6511 1.9697 2.3417 2.5960 2460.6755 1.2850 1.6511 1.9697 2.3416 2.5960 2470.6755 1.2850 1.6510 1.9696 2.3415 2.5959 2480.6755 1.2850 1.6510 1.9696 2.3415 2.5958 2490.6755 1.2850 1.6510 1.9695 2.3414 2.5957 2500.6755 1.2849 1.6510 1.9695 2.3414 2.5956 2510.6755 1.2849 1.6509 1.9695 2.3413 2.5956 2520.6755 1.2849 1.6509 1.9694 2.3412 2.5955 2530.6755 1.2849 1.6509 1.9694 2.3412 2.5954 2540.6755 1.2849 1.6509 1.9693 2.3411 2.5953 2550.6755 1.2849 1.6509 1.9693 2.3411 2.5952 2560.6754 1.2849 1.6508 1.9693 2.3410 2.5952 2570.6754 1.2849 1.6508 1.9692 2.3409 2.5951 2580.6754 1.2848 1.6508 1.9692 2.3409 2.5950 2590.6754 1.2848 1.6508 1.9692 2.3408 2.5949 2600.6754 1.2848 1.6507 1.9691 2.3408 2.5949 2610.6754 1.2848 1.6507 1.9691 2.3407 2.5948 2620.6754 1.2848 1.6507 1.9691 2.3407 2.5947 2630.6754 1.2848 1.6507 1.9690 2.3406 2.5947 2640.6754 1.2848 1.6506 1.9690 2.3406 2.5946 2650.6754 1.2848 1.6506 1.9690 2.3405 2.5945 2660.6754 1.2847 1.6506 1.9689 2.3404 2.5944 2670.6754 1.2847 1.6506 1.9689 2.3404 2.5944 2680.6754 1.2847 1.6506 1.9689 2.3403 2.5943 2690.6754 1.2847 1.6505 1.9688 2.3403 2.5942 2700.6754 1.2847 1.6505 1.9688 2.3402 2.5942 2710.6754 1.2847 1.6505 1.9688 2.3402 2.5941 2720.6754 1.2847 1.6505 1.9687 2.3401 2.5940 2730.6754 1.2847 1.6505 1.9687 2.3401 2.5940 2740.6754 1.2846 1.6504 1.9687 2.3400 2.5939 2750.6754 1.2846 1.6504 1.9686 2.3400 2.5938 2760.6754 1.2846 1.6504 1.9686 2.3399 2.5938 2770.6754 1.2846 1.6504 1.9686 2.3399 2.5937 2780.6754 1.2846 1.6504 1.9685 2.3398 2.5936 2790.6754 1.2846 1.6503 1.9685 2.3398 2.59362800.6754 1.2846 1.6503 1.9685 2.3397 2.5935 2810.6754 1.2846 1.6503 1.9684 2.3397 2.5934 2820.6754 1.2846 1.6503 1.9684 2.3396 2.5934 2830.6754 1.2846 1.6503 1.9684 2.3396 2.5933 2840.6754 1.2845 1.6502 1.9684 2.3395 2.5933 2850.6754 1.2845 1.6502 1.9683 2.3395 2.5932 2860.6753 1.2845 1.6502 1.9683 2.3395 2.5931 2870.6753 1.2845 1.6502 1.9683 2.3394 2.5931 2880.6753 1.2845 1.6502 1.9682 2.3394 2.5930 2890.6753 1.2845 1.6501 1.9682 2.3393 2.5929 2900.6753 1.2845 1.6501 1.9682 2.3393 2.5929 2910.6753 1.2845 1.6501 1.9681 2.3392 2.5928 2920.6753 1.2845 1.6501 1.9681 2.3392 2.5928 2930.6753 1.2844 1.6501 1.9681 2.3391 2.5927 2940.6753 1.2844 1.6501 1.9681 2.3391 2.5927 2950.6753 1.2844 1.6500 1.9680 2.3391 2.5926 2960.6753 1.2844 1.6500 1.9680 2.3390 2.5925 2970.6753 1.2844 1.6500 1.9680 2.3390 2.5925 2980.6753 1.2844 1.6500 1.9680 2.3389 2.5924 2990.6753 1.2844 1.6500 1.9679 2.3389 2.5924 3000.6753 1.2844 1.6499 1.9679 2.3388 2.5923 3010.6753 1.2844 1.6499 1.9679 2.3388 2.5923 3020.6753 1.2844 1.6499 1.9679 2.3388 2.5922 3030.6753 1.2844 1.6499 1.9678 2.3387 2.5922 3040.6753 1.2843 1.6499 1.9678 2.3387 2.5921 3050.6753 1.2843 1.6499 1.9678 2.3386 2.5920 3060.6753 1.2843 1.6498 1.9677 2.3386 2.5920 3070.6753 1.2843 1.6498 1.9677 2.3386 2.5919 3080.6753 1.2843 1.6498 1.9677 2.3385 2.5919 3090.6753 1.2843 1.6498 1.9677 2.3385 2.5918 3100.6753 1.2843 1.6498 1.9676 2.3384 2.5918 3110.6753 1.2843 1.6498 1.9676 2.3384 2.5917 3120.6753 1.2843 1.6498 1.9676 2.3384 2.5917 3130.6753 1.2843 1.6497 1.9676 2.3383 2.5916 3140.6753 1.2843 1.6497 1.9675 2.3383 2.5916 3150.6753 1.2842 1.6497 1.9675 2.3382 2.5915 3160.6753 1.2842 1.6497 1.9675 2.3382 2.5915 3170.6753 1.2842 1.6497 1.9675 2.3382 2.5914 3180.6753 1.2842 1.6497 1.9675 2.3381 2.5914 3190.6753 1.2842 1.6496 1.9674 2.3381 2.5913 3200.6753 1.2842 1.6496 1.9674 2.3381 2.5913 3210.6753 1.2842 1.6496 1.9674 2.3380 2.5912 3220.6753 1.2842 1.6496 1.9674 2.3380 2.5912 3230.6753 1.2842 1.6496 1.9673 2.3379 2.59113240.6752 1.2842 1.6496 1.9673 2.3379 2.5911 3250.6752 1.2842 1.6496 1.9673 2.3379 2.5910 3260.6752 1.2842 1.6495 1.9673 2.3378 2.5910 3270.6752 1.2841 1.6495 1.9672 2.3378 2.5909 3280.6752 1.2841 1.6495 1.9672 2.3378 2.5909 3290.6752 1.2841 1.6495 1.9672 2.3377 2.5909 3300.6752 1.2841 1.6495 1.9672 2.3377 2.5908 3310.6752 1.2841 1.6495 1.9672 2.3377 2.5908 3320.6752 1.2841 1.6495 1.9671 2.3376 2.5907 3330.6752 1.2841 1.6494 1.9671 2.3376 2.5907 3340.6752 1.2841 1.6494 1.9671 2.3376 2.5906 3350.6752 1.2841 1.6494 1.9671 2.3375 2.5906 3360.6752 1.2841 1.6494 1.9670 2.3375 2.5905 3370.6752 1.2841 1.6494 1.9670 2.3375 2.5905 3380.6752 1.2841 1.6494 1.9670 2.3374 2.5905 3390.6752 1.2841 1.6494 1.9670 2.3374 2.5904 3400.6752 1.2840 1.6493 1.9670 2.3374 2.5904 3410.6752 1.2840 1.6493 1.9669 2.3373 2.5903 3420.6752 1.2840 1.6493 1.9669 2.3373 2.5903 3430.6752 1.2840 1.6493 1.9669 2.3373 2.5902 3440.6752 1.2840 1.6493 1.9669 2.3372 2.5902 3450.6752 1.2840 1.6493 1.9669 2.3372 2.5902 3460.6752 1.2840 1.6493 1.9668 2.3372 2.5901 3470.6752 1.2840 1.6493 1.9668 2.3371 2.5901 3480.6752 1.2840 1.6492 1.9668 2.3371 2.5900 3490.6752 1.2840 1.6492 1.9668 2.3371 2.5900 3500.6752 1.2840 1.6492 1.9668 2.3370 2.5899 3510.6752 1.2840 1.6492 1.9667 2.3370 2.5899 3520.6752 1.2840 1.6492 1.9667 2.3370 2.5899 3530.6752 1.2840 1.6492 1.9667 2.3370 2.5898 3540.6752 1.2839 1.6492 1.9667 2.3369 2.5898 3550.6752 1.2839 1.6492 1.9667 2.3369 2.5897 3560.6752 1.2839 1.6491 1.9666 2.3369 2.5897 3570.6752 1.2839 1.6491 1.9666 2.3368 2.5897 3580.6752 1.2839 1.6491 1.9666 2.3368 2.5896 3590.6752 1.2839 1.6491 1.9666 2.3368 2.5896 3600.6752 1.2839 1.6491 1.9666 2.3368 2.5896 3610.6752 1.2839 1.6491 1.9666 2.3367 2.5895 3620.6752 1.2839 1.6491 1.9665 2.3367 2.5895 3630.6752 1.2839 1.6491 1.9665 2.3367 2.5894 3640.6752 1.2839 1.6491 1.9665 2.3366 2.5894 3650.6752 1.2839 1.6490 1.9665 2.3366 2.5894 3660.6752 1.2839 1.6490 1.9665 2.3366 2.5893 3670.6752 1.2839 1.6490 1.9664 2.3366 2.58933680.6752 1.2839 1.6490 1.9664 2.3365 2.5893 3690.6752 1.2839 1.6490 1.9664 2.3365 2.5892 3700.6752 1.2838 1.6490 1.9664 2.3365 2.5892 3710.6752 1.2838 1.6490 1.9664 2.3364 2.5891 3720.6751 1.2838 1.6490 1.9664 2.3364 2.5891 3730.6751 1.2838 1.6489 1.9663 2.3364 2.5891 3740.6751 1.2838 1.6489 1.9663 2.3364 2.5890 3750.6751 1.2838 1.6489 1.9663 2.3363 2.5890 3760.6751 1.2838 1.6489 1.9663 2.3363 2.5890 3770.6751 1.2838 1.6489 1.9663 2.3363 2.5889 3780.6751 1.2838 1.6489 1.9663 2.3363 2.5889 3790.6751 1.2838 1.6489 1.9662 2.3362 2.5889 3800.6751 1.2838 1.6489 1.9662 2.3362 2.5888 3810.6751 1.2838 1.6489 1.9662 2.3362 2.5888 3820.6751 1.2838 1.6489 1.9662 2.3361 2.5888 3830.6751 1.2838 1.6488 1.9662 2.3361 2.5887 3840.6751 1.2838 1.6488 1.9662 2.3361 2.5887 3850.6751 1.2838 1.6488 1.9661 2.3361 2.5887 3860.6751 1.2837 1.6488 1.9661 2.3360 2.5886 3870.6751 1.2837 1.6488 1.9661 2.3360 2.5886 3880.6751 1.2837 1.6488 1.9661 2.3360 2.5886 3890.6751 1.2837 1.6488 1.9661 2.3360 2.5885 3900.6751 1.2837 1.6488 1.9661 2.3359 2.5885 3910.6751 1.2837 1.6488 1.9660 2.3359 2.5885 3920.6751 1.2837 1.6488 1.9660 2.3359 2.5884 3930.6751 1.2837 1.6487 1.9660 2.3359 2.5884 3940.6751 1.2837 1.6487 1.9660 2.3358 2.5884 3950.6751 1.2837 1.6487 1.9660 2.3358 2.5883 3960.6751 1.2837 1.6487 1.9660 2.3358 2.5883 3970.6751 1.2837 1.6487 1.9660 2.3358 2.5883 3980.6751 1.2837 1.6487 1.9659 2.3358 2.5882 3990.6751 1.2837 1.6487 1.9659 2.3357 2.5882 4000.6751 1.2837 1.6487 1.9659 2.3357 2.5882 4010.6751 1.2837 1.6487 1.9659 2.3357 2.5881 4020.6751 1.2837 1.6487 1.9659 2.3357 2.5881 4030.6751 1.2837 1.6486 1.9659 2.3356 2.5881 4040.6751 1.2837 1.6486 1.9659 2.3356 2.5881 4050.6751 1.2836 1.6486 1.9658 2.3356 2.5880 4060.6751 1.2836 1.6486 1.9658 2.3356 2.5880 4070.6751 1.2836 1.6486 1.9658 2.3355 2.5880 4080.6751 1.2836 1.6486 1.9658 2.3355 2.5879 4090.6751 1.2836 1.6486 1.9658 2.3355 2.5879 4100.6751 1.2836 1.6486 1.9658 2.3355 2.5879 4110.6751 1.2836 1.6486 1.9658 2.3355 2.58784130.6751 1.2836 1.6486 1.9657 2.3354 2.5878 4140.6751 1.2836 1.6485 1.9657 2.3354 2.5878 4150.6751 1.2836 1.6485 1.9657 2.3354 2.5877 4160.6751 1.2836 1.6485 1.9657 2.3353 2.5877 4170.6751 1.2836 1.6485 1.9657 2.3353 2.5877 4180.6751 1.2836 1.6485 1.9657 2.3353 2.5876 4190.6751 1.2836 1.6485 1.9656 2.3353 2.5876 4200.6751 1.2836 1.6485 1.9656 2.3353 2.5876 4210.6751 1.2836 1.6485 1.9656 2.3352 2.5876 4220.6751 1.2836 1.6485 1.9656 2.3352 2.5875 4230.6751 1.2836 1.6485 1.9656 2.3352 2.5875 4240.6751 1.2836 1.6485 1.9656 2.3352 2.5875 4250.6751 1.2835 1.6484 1.9656 2.3352 2.5874 4260.6751 1.2835 1.6484 1.9655 2.3351 2.5874 4270.6751 1.2835 1.6484 1.9655 2.3351 2.5874 4280.6751 1.2835 1.6484 1.9655 2.3351 2.5874 4290.6751 1.2835 1.6484 1.9655 2.3351 2.5873 4300.6751 1.2835 1.6484 1.9655 2.3351 2.5873 4310.6751 1.2835 1.6484 1.9655 2.3350 2.5873 4320.6751 1.2835 1.6484 1.9655 2.3350 2.5873 4330.6751 1.2835 1.6484 1.9655 2.3350 2.5872 4340.6751 1.2835 1.6484 1.9654 2.3350 2.5872 4350.6751 1.2835 1.6484 1.9654 2.3350 2.5872 4360.6751 1.2835 1.6484 1.9654 2.3349 2.5872 4370.6751 1.2835 1.6483 1.9654 2.3349 2.5871 4380.6751 1.2835 1.6483 1.9654 2.3349 2.5871 4390.6750 1.2835 1.6483 1.9654 2.3349 2.5871 4400.6750 1.2835 1.6483 1.9654 2.3349 2.5870 4410.6750 1.2835 1.6483 1.9654 2.3348 2.5870 4420.6750 1.2835 1.6483 1.9653 2.3348 2.5870 4430.6750 1.2835 1.6483 1.9653 2.3348 2.5870 4440.6750 1.2835 1.6483 1.9653 2.3348 2.5869 4450.6750 1.2835 1.6483 1.9653 2.3348 2.5869 4460.6750 1.2835 1.6483 1.9653 2.3347 2.5869 4470.6750 1.2834 1.6483 1.9653 2.3347 2.5869 4480.6750 1.2834 1.6483 1.9653 2.3347 2.5868 4490.6750 1.2834 1.6483 1.9653 2.3347 2.5868 4500.6750 1.2834 1.6482 1.9652 2.3347 2.5868 4510.6750 1.2834 1.6482 1.9652 2.3346 2.5868 4520.6750 1.2834 1.6482 1.9652 2.3346 2.5867 4530.6750 1.2834 1.6482 1.9652 2.3346 2.5867 4540.6750 1.2834 1.6482 1.9652 2.3346 2.5867 4550.6750 1.2834 1.6482 1.9652 2.3346 2.58674570.6750 1.2834 1.6482 1.9652 2.3345 2.5866 4580.6750 1.2834 1.6482 1.9652 2.3345 2.5866 4590.6750 1.2834 1.6482 1.9651 2.3345 2.5866 4600.6750 1.2834 1.6482 1.9651 2.3345 2.5866 4610.6750 1.2834 1.6482 1.9651 2.3345 2.5865 4620.6750 1.2834 1.6482 1.9651 2.3344 2.5865 4630.6750 1.2834 1.6482 1.9651 2.3344 2.5865 4640.6750 1.2834 1.6481 1.9651 2.3344 2.5865 4650.6750 1.2834 1.6481 1.9651 2.3344 2.5864 4660.6750 1.2834 1.6481 1.9651 2.3344 2.5864 4670.6750 1.2834 1.6481 1.9651 2.3344 2.5864 4680.6750 1.2834 1.6481 1.9650 2.3343 2.5864 4690.6750 1.2834 1.6481 1.9650 2.3343 2.5864 4700.6750 1.2834 1.6481 1.9650 2.3343 2.5863 4710.6750 1.2834 1.6481 1.9650 2.3343 2.5863 4720.6750 1.2833 1.6481 1.9650 2.3343 2.5863 4730.6750 1.2833 1.6481 1.9650 2.3343 2.5863 4740.6750 1.2833 1.6481 1.9650 2.3342 2.5862 4750.6750 1.2833 1.6481 1.9650 2.3342 2.5862 4760.6750 1.2833 1.6481 1.9650 2.3342 2.5862 4770.6750 1.2833 1.6481 1.9649 2.3342 2.5862 4780.6750 1.2833 1.6480 1.9649 2.3342 2.5862 4790.6750 1.2833 1.6480 1.9649 2.3342 2.5861 4800.6750 1.2833 1.6480 1.9649 2.3341 2.5861 4810.6750 1.2833 1.6480 1.9649 2.3341 2.5861 4820.6750 1.2833 1.6480 1.9649 2.3341 2.5861 4830.6750 1.2833 1.6480 1.9649 2.3341 2.5860 4840.6750 1.2833 1.6480 1.9649 2.3341 2.5860 4850.6750 1.2833 1.6480 1.9649 2.3341 2.5860 4860.6750 1.2833 1.6480 1.9649 2.3340 2.5860 4870.6750 1.2833 1.6480 1.9648 2.3340 2.5860 4880.6750 1.2833 1.6480 1.9648 2.3340 2.5859 4890.6750 1.2833 1.6480 1.9648 2.3340 2.5859 4900.6750 1.2833 1.6480 1.9648 2.3340 2.5859 4910.6750 1.2833 1.6480 1.9648 2.3340 2.5859 4920.6750 1.2833 1.6480 1.9648 2.3340 2.5859 4930.6750 1.2833 1.6480 1.9648 2.3339 2.5858 4940.6750 1.2833 1.6479 1.9648 2.3339 2.5858 4950.6750 1.2833 1.6479 1.9648 2.3339 2.5858 4960.6750 1.2833 1.6479 1.9648 2.3339 2.5858 4970.6750 1.2833 1.6479 1.9647 2.3339 2.5858 4980.6750 1.2833 1.6479 1.9647 2.3339 2.5857 4990.6750 1.2833 1.6479 1.9647 2.3338 2.58575000.6750 1.2832 1.6479 1.9647 2.3338 2.5857。
t分布的概念及表和查表方法

t分布介绍在概率论和统计学中,学生t-分布(t-distribution),可简称为t分布,用于根据小样本来估计呈正态分布且方差未知的总体的均值。
如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
t分布曲线形态与n(确切地说与自由度df)大小有关。
与标准正态分布曲线相比,自由度df越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度df愈大,t分布曲线愈接近正态分布曲线,当自由度df=∞时,t分布曲线为标准正态分布曲线。
目录1历史2定义3扩展4特征5置信区间6计算历史在概率论和统计学中,学生t-分布(Student's t-distribution)经常应用在对呈正态分布的总体的均值进行估计。
它是对两个样本均值差异进行显著性测试的学生t测定的基础。
t检定改进了Z检定(en:Z-test),不论样本数量大或小皆可应用。
在样本数量大(超过120等)时,可以应用Z检定,但Z检定用在小的样本会产生很大的误差,因此样本很小的情况下得改用学生t检定。
在数据有三组以上时,因为误差无法压低,此时可以用变异数分析代替学生t检定。
当母群体的标准差是未知的但却又需要估计时,我们可以运用学生t-分布。
学生t-分布可简称为t分布。
其推导由威廉·戈塞于1908年首先发表,当时他还在都柏林的健力士酿酒厂工作。
因为不能以他本人的名义发表,所以论文使用了学生(Student)这一笔名。
之后t检验以及相关理论经由罗纳德·费雪的工作发扬光大,而正是他将此分布称为学生分布。
定义由于在实际工作中,往往σ是未知的,常用s作为σ的估计值,为了与u变换区别,称为t变换,统计量t 值的分布称为t分布。
假设X服从标准正态分布N(0,1),Y服从分布,那么的分布称为自由度为n 的t分布,记为。
分布密度函数,其中,Gam(x)为伽马函数。
扩展正态分布(normal distribution)是数理统计中的一种重要的理论分布,是许多统计方法的理论基础。
标准正态分布分位数表

分位数定义:对于任意给定的实数P,(0<P<1),如果存在X_xp,则让随机变量X的分布函数为f(X)。
β7{px6}p=px6?6个?7)=P,然后x_PXP?6个?7是概率分布的p分位数。
例如:在此处插入图像说明如上图所示,图像是一个标准正态分布的X_PXP?概率密度函数。
6个?7是p分位数。
高分位数定义:对于一个随机变量x和一个给定的α(0<alphaα<1),如果xαα存在呢?6等于7,那么P{x?GEQ≥Xαα?6个?7} =?αα,所谓的Xα?6个?7是X的上分位数。
此处插入图片说明如上图所示,X\Alpha?7是上层吗?标准正态分布的α分位数。
在数理统计过程中,标准正态分布的高分位数记录为:U_ualphauα6-7 Python实现首先,让我们介绍一些常见的分配函数进口scipy.stats公司作为st标准规范()正态分布St.t()訛t分布St.f()ා f分布圣基2()Chi^2χ2分布然后介绍基本操作:概率密度函数CDF分布函数PPF分布函数的反函数SF损伤函数(1-cdf)逆破坏函数这是代码实现在此处插入图像说明当你看到结果时,你可能会问为什么它与数理统计书附录中的t分位数表不同,因为这本书需要一个高位表。
画最后一幅画在此处插入图像说明把它扔掉展开文本如何查看正态分布表读数:49,2019年8月6日也就是说,首先将其转换为标准正态分布,然后通过查找表获得。
当标准正态分布变为Z时,垂直值+水平值是Z值对应的分布函数的概率。
也就是说,首先将其转换为标准正态分布,然后通过查找表获得。
当标准正态分布变为Z时,垂直值+水平值是Z值对应的分布函数的概率。
抽样分布公式t分布卡方分布F分布

抽样分布公式t分布卡方分布F分布抽样分布公式:t分布、卡方分布、F分布抽样分布是统计学中的重要概念,用于推断总体参数以及进行假设检验。
本文将重点介绍三种常见的抽样分布公式:t分布、卡方分布和F分布。
一、t分布公式t分布是用于小样本情况下进行参数估计和假设检验的重要分布。
它的定义如下:假设有一个总体,样本容量为n,总体的均值和标准差未知。
如果从该总体中随机抽取一个样本,计算样本均值与总体均值的差异,用t 值来衡量。
那么,t值的概率分布就是t分布。
t分布的公式如下:t = (x - μ) / (s / √n)其中,x为样本均值,μ为总体均值,s为样本标准差,n为样本容量。
t分布的自由度为n-1。
在实际应用中,可以利用t分布表或统计软件来查找不同自由度下的t值对应的概率。
二、卡方分布公式卡方分布是应用于统计推断的重要分布,主要用于分析分类资料或定类变量的相关性。
它的定义如下:假设有一个总体,样本容量为n,比较观察值与理论值之间的差异。
我们将差异的平方进行求和,并除以理论值,得到统计量,称为卡方统计量。
卡方分布的公式如下:χ^2 = Σ((O - E)^2 / E)其中,O为观察值,E为理论值。
卡方分布的自由度取决于总体参数的个数减去估计的参数个数。
在实际应用中,同样可以利用卡方分布表或统计软件来查找不同自由度下的卡方值对应的概率。
三、F分布公式F分布是应用于统计推断的另一重要分布,主要用于比较两个或多个总体方差是否相等。
它的定义如下:假设有两个总体A、B,分别进行抽样,计算两个样本方差的比值,得到F统计量。
F分布的公式如下:F = (s1^2 / σ1^2) / (s2^2 / σ2^2)其中,s1^2和s2^2分别为样本A和样本B的方差,σ1^2和σ2^2分别为总体A和总体B的方差。
F分布的自由度取决于样本容量和总体个数。
在实际应用中,同样可以利用F分布表或统计软件来查找不同自由度下的F值对应的概率。
附表二标准正态分布表

附 录附表一:随机数表_________________________________________________________________________2 附表二:标准正态分布表___________________________________________________________________3 附表三:t 分布临界值表____________________________________________________________________4附表四:分布临界值表__________________________________________________________________5 2χ附表五:F 分布临界值表(α=0.05)_________________________________________________________7 附表六:单样本K-S 检验统计量表____________________________________________________________9 附表七:符号检验界域表__________________________________________________________________10 附表八:游程检验临界值表_________________________________________________________________11 附表九:相关系数临界值表________________________________________________________________12 附表十:Spearman 等级相关系数临界值表___________________________________________________13 附表十一:Kendall τ等级相关系数临界值表__________________________________________________14 附表十二:控制图系数表__________________________________________________________________15 附表十三 威尔克逊秩和检验临界表(01.0=α)____________________________________________16 附表十四 威尔克逊秩和检验临界表(025.0=α)___________________________________________17 附表十五 威尔克逊秩和检验临界表(05.0=α)____________________________________________18 附表十六 威尔克逊符号秩和检验临界表____________________________________________________19 附表十七 Durbin Watson 序列相关检验表(05.0=α)_________________________________________20附表一:随机数表(查表时注意:v是指自由度,并分单侧和双侧两种类型)(左侧的示意图是单侧检验的情形)附表四:分布临界值表 2χ附表五:F分布临界值表(α=0.05)F分布临界值表(α=0.01)附表六:单样本K-S 检验统计量表[])(1)()(sup 0d D P x F x F D n n x n ≤−=−=α附表七:符号检验界域表附表十:Spearman等级相关系数临界值表附表十一:Kendallτ等级相关系数临界值表附表十二:控制图系数表附表十三威尔克逊秩和检验临界表(01.0α)=附表十四威尔克逊秩和检验临界表(025α)=.0附表十五威尔克逊秩和检验临界表(05.0α)=附表十六威尔克逊符号秩和检验临界表m α=0.05α=0.025α=0.01α=0.0055 0 156 2 19 0 217 3 25 2 26 0 288 5 31 3 33 1 35 0 369 8 37 5 40 3 42 1 4410 10 45 8 47 5 50 3 5211 13 53 10 56 7 59 5 6112 17 61 13 65 9 69 7 7113 21 70 17 74 12 79 9 8214 25 80 21 84 15 90 12 9315 30 90 25 95 19 101 15 10516 35 101 29 107 23 113 19 11717 41 112 34 119 28 125 23 13018 47 124 40 131 32 139 27 14419 53 137 46 144 37 153 32 15820 60 150 52 158 43 167 37 17321 67 164 58 173 49 182 42 18922 75 178 66 187 55 198 48 20523 83 193 73 203 62 214 54 22224 91 209 81 219 69 231 61 23925 100 225 89 236 76 249 68 257附表十七 Durbin Watson 序列相关检验表(05.0=α)检验正序列相关:如果,拒绝 如果,接受 如果L d d <0H U d d >0H U L d d d <<,没有结论 检验序列相关时,把上述的改为d d U − P=2P=3P=4P=5P=6n L d U d L d U d L d U d L d U d L dU d 15 1.08 1.36 0.95 1.54 0.82 1.75 0.69 1.97 0.56 2.21 16 1.10 1.37 0.98 1.54 0.86 1.73 0.74 1.93 0.62 2.15 17 1.13 1.38 1.02 1.54 0.90 1.71 0.78 1.90 0.67 2.10 18 1.16 1.39 1.05 1.53 0.93 1.69 0.82 1.87 0.71 2.06 19 1.18 1.40 1.08 1.53 0.97 1.68 0.86 1.85 0.75 2.0220 1.20 1.41 1.10 1.54 1.00 1.68 0.90 1.83 0.79 1.99 21 1.22 1.42 1.13 1.54 1.03 1.67 0.93 1 81 0.83 1.96 22 1.24 1.43 1.15 1.54 1.05 1.66 0.96 1.80 0.86 1.94 23 1.26 1.44 1.17 1.54 1.08 1.66 0.99 1.79 0.90 1.92 24 1.27 1.45 1.19 1.55 1.10 1.66 1.01 1.78 0.93 1.9025 1.29 1.45 1.21 1.55 1.12 1.66 1.04 1.77 0.95 1.89 26 1.30 1.46 1.22 1.55 1.14 1.65 1.06 1.76 0.98 1.88 27 1.32 1.47 1.24 1.56 1.16 1.65 1.08 1.76 1.01 1.86 28 1.33 1.48 1.26 1.56 1.18 1.65 1.10 1.75 1.03 1.85 29 1.34 1.48 1.27 1.56 1.20 1.65 1.12 1.74 1.05 1.8430 1.35 1.49 1.28 1.57 1.21 1.65 1.14 1.74 1 07 1.83 31 1.36 1.50 1.30 1.57 1.23 1.65 1.16 1.74 1.09 1.83 32 1.37 1.50 1.31 1.57 1.24 1.65 1.18 1.73 1.11 1.82 33 1.38 1.51 1.32 1.58 1.26 1.65 1.19 1 73 1.13 1.81 34 1.39 1.51 1.33 1.58 1.27 1.65 1.21 1.73 1.15 1.8135 1.40 1.52 1.34 1.58 1.28 1.65 1.22 1 73 1.16 1.80 36 1.41 1.52 1.35 1.59 1.29 1.65 1.24 1.73 1.18 1.80 37 1.42 1.53 1.36 1.59 1.31 1.66 1.25 1.72 1.19 1.80 38 1.43 1.54 1.37 1.59 1.32 1.66 1.26 1.72 1.21 1.7940 1.44 1.54 1.39 1.60 1.34 1.66 1.29 1.72 1.23 1.79 45 1.48 1.57 1.43 1.62 1.38 1.67 1.34 1.72 1.29 1.78 50 1.50 1.59 1.46 1.63 1.42 1.67 1.38 1.72 1.34 1.77 55 1.53 1.60 1.49 1.64 1.45 1.68 0.07 1.72 1.38 1.77 60 1.55 1.62 1.51 1.65 1.48 1.69 1.44 1.73 1.41 1.7765 1.57 1.63 1.54 1.66 1.50 1.70 1.47 1.73 1.44 1.77 70 1.58 1.64 1.55 1.67 1.52 1.70 1.49 1.74 1.46 1.77 75 1.60 1.64 1.57 1.68 1.54 1.71 1.51 1.74 149 1.77 80 1.61 1.66 1.59 1.69 1.56 1.72 1.53 1.74 1.51 1.77 85 1.62 1.67 1.60 1.70 1.57 1.72 1.55 1.75 1.52 1.7790 1.63 1.68 1.61 1.70 1.59 1.73 1.57 1.75 1.54 1.78 95 1.64 1.69 1.62 1.71 1.60 1.73 1.58 1.75 1.56 1.78 100 1.65 1.69 1.63 1.72 1.61 1.74 1.59 1.76 1.57 1.78。
数理统计查表方法

数理统计查表方法
数理统计中常用的查表方法有两种:查正态分布表和查t分布表。
1. 查正态分布表:正态分布表是用来计算正态分布的累积概率(即给定值以下的概率)和临界值(即给定累积概率对应的值)。
一般的正态分布表会给出标准正态分布(均值为0,标准差为1)的值。
如果需要计算其他均值和标准差的正态分布,可以通过标准化处理后再查询表格。
在查表时,一般需要根据给定的概率或值,在表格中找到对应的行和列,得到对应的数值。
2. 查t分布表:t分布表是用来计算t分布的累积概率和临界值的。
t分布主要应用于样本较小或总体方差未知的情况下。
和正态分布表类似,t分布表也提供了不同自由度下的t分布的临界值和累积概率。
在查表时,需要根据给定的自由度和概率或值,在表格中找到相应的数值。
需要注意的是,表格只提供了一部分数值,如果要查询的数值不在表中,通常需要进行插值来估算。
此外,现代计算机软件和统计学软件通常都提供了更精确和快捷的计算方法,可以避免手动查表的过程。
概率论常用统计分布

又因为 Xi ~ N (0, 1),
由定义
X
2 i
~
2 (1),
即
X
2 i
~
1 2
,
1 2
,
i 1, 2, L , n.
因为X1, X2, , Xn相互独立,
所以
X12 ,
X
2 2
,
,
X n2也相互独立,
根据 分布的可加性知
2 n
n i 1
Xi2
~
n 2
,
1 2
.
(3) 2 分布的性质
,
(n2 4)
3) 设F ~ F (n1, n2 ),则当n2 4时,对任意x有
lim P{F E(F ) x} x
1
e
t2 2
dt
n1
D(F )
2π
这说明F分布极限分布也是正态分布.
例4 已知 T ~ t(n),试证 T 2 ~ F (1,n).
证 因为 T ~ t(n), 由定义5.7有 T X Yn
可直接查表5 ~ 8.
F0.05(14,30) 2.31 .
F0.025(7,8) 4.90,
此外,还可利用关系
F1
( n1 ,
n2 )
F
1 (n2 ,
. n1 )
由F求得F1 .
如:
F0.95 (12,9)
1 F0.05(9, 12)
1 2.8
0.357 .
F1
( n1 ,
n2 )
F
1 (n2 ,
h(t)
n
2
πn
1 n
1
t2 n
n1
2
,
常见概率分布间的关系

两个中心分布
(1)正态分布 (2)指数分布 指数分布通过它在连续分布中唯一具有无记忆性的特征正好和几何分布 在离散型分布中唯一具有该特性联系在了一起,这一特性是…………的桥
梁。 卷积原理(埃尔兰分布),两者联合,构造卡方分布,T分布,F分布等。
祝各位老师身体健康, 工作顺利!
均匀分布于其他分布的联系
概率分布间的关系的应用
分布的特殊情形的应用
用简便的方法计算巴斯卡分布的期望,方差和特征函数. ……………………
分布的变换的应用 指数分布参数 的区间估计.
……………………
分布的极限的应用
如何获得的N ( , 2 ) 的随机数. ……………………
均匀分布的应用
构造参数的置信限.
概率分布间的关系图表示
两条主线
(1)伯努利试验过程 在伯努利实验中,成功次数服从二项分布。为等待第一次成功,等待时 间服从几何分布,为等待第r次成功,等待时间服从巴斯卡分布。 (2)泊松过程 在泊松过程中,来到数服从泊松分布。为等待第一次来到,等待时间服 从指数分布,为等待第r次来到,等待时间服从埃尔兰分布。
常见概率分布概率分布概率分布函数概率分布类型正态分布概率联合概率分布f分布概率密度函数正态分布概率公式常用概率分布连续概率分布
常见概率分布间的关系 及其应用
1.用简便的方法计算巴斯卡分 布的期望,方差和特征函数? 巴斯卡分布 几何分布 你想过 2.指数分布参数 的区间估计? 下面的问题吗? 指数分布 卡方分布 3.如何获得的N (, 2 ) 的随机数? 均匀分布 正态分布 4.如何构造未知参数的置信限? 均匀分布与其它分布间的联系
3章几种常见的分布

在Gamma分布中:k=n(正整数)时的gamma分布可以看作n个独立的k=1的 gamma分布(即指数分布)之和,按照中心极限定理,独立同分布随机变量 之和趋于正态分布。
几种常见的分布
2019/5/27
1
分类
连续型随机分布
◆ 正态分布、均匀分布、指数分布、对数正态分布、柯西分布、 Gamma分布、瑞利分布、韦伯分布、三角形分布
离散型随机分布
◆ 二项分布、几何分布、超几何分布、泊松分布
三大抽样分布
◆ 卡方分布、F分布、t分布
分布之间的关系
2019/5/27
应用:在自然情况下,均匀分布极为罕见。在实际问题中,当我们无法区分在 区间内取值的随机变量取不同值的可能性有何不同时,我们就可以假定随机变 量服从区间上的均匀分布。
2019/5/27
4
三、指数分布(Exponential distribution)
应用:主要用于描述独立事件发生的时间间隔。自然界中有很多种“寿命”可 以用指数分布来描述,如电子元件的寿命、动物的寿命、电话的通话时间、服 务系统的服务时间等。
定义:已知一个事件在伯努利试验中每次的出现概率是p,在一连串伯努利 试验中,一件事件刚好在第r + k次试验出现第r次的概率。
2019/5/27
取r = 1,负二项分布等于几 何分布。其概率质量函数 为
13
十二、几何分布
定义:在第 n 次伯努利实验,才得到第一次成功的机率。更详细的说是:n 次伯努利试验,前 n-1 次皆失败,第 n 次才成功的概率。
应用:泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。如某 一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台 的候客人数,机器出现的故障数,自然灾害发生的次数,一块产品上的缺陷 陷数,显微镜下单位分区内的细菌分布方分布
正态分布卡方分布t分布f分布的特点

正态分布卡方分布t分布f分布的特点正态分布(Normal Distribution)是统计学中最重要的概率分布之一,也是最常见的概率分布之一。
它的形状类似于一个钟形曲线,两头低,中间高,呈对称分布。
正态分布具有许多独特的特点,其中一些特点包括对称性、峰度和偏度的性质、标准正态分布等。
首先,正态分布的最重要特点之一是它的对称性。
这意味着分布的左侧和右侧是镜像对称的。
换句话说,正态分布的均值(mean)、中位数(median)和众数(mode)是相等的,这是它对称性的一个基本特征。
这也意味着在正态分布中,随机变量的概率密度在均值处达到最大值,并且向两侧逐渐减小,形成了典型的钟形曲线。
其次,正态分布具有一个重要的特点是其峰度(kurtosis)和偏度(skewness)的性质。
峰度描述了分布曲线的尖锐程度,它是描述分布形态的重要指标之一。
正态分布的峰度为3,这意味着它的尖峰程度与标准正态分布相当。
偏度则描述了分布曲线的偏斜程度,正态分布的偏度为0,这意味着它是对称的。
这些特点使得正态分布在统计学中有着广泛的应用,特别是在假设检验和统计推断中被广泛使用。
另外,正态分布还有一个重要的特点是标准正态分布。
标准正态分布是均值为0,标准差为1的正态分布。
它是统计学中非常重要的一种分布,因为许多统计量都服从于标准正态分布,比如t值、z值等。
正态分布的重要性在于中心极限定理,它指出了当随机变量的数量足够大时,它们的总和或者平均值会接近于正态分布,这使得正态分布在实际问题中有着广泛的应用。
除了正态分布外,卡方分布(Chi-square Distribution)也是统计学中重要的概率分布之一。
卡方分布是以卡方统计量为基础的分布,它在统计学中有着重要的应用。
卡方分布的特点包括其形状、参数和性质等。
首先,卡方分布的形状是非对称的。
它是一个正偏分布,即分布的右侧长尾较长,左侧短尾较短。
这与正态分布的对称性形成了鲜明的对比。
如何快速识别“F分布”与“t分布”

如何快速识别“F分布”与“t分布”F分布和t分布是统计学中常用的分布,用于进行假设检验和计算置信区间。
本文将介绍如何快速识别这两种分布,并说明它们的特点和应用场景。
1. F分布(F-distribution)F分布是一种概率分布,通常用于比较两个或更多组数据集的方差是否显著不同。
F分布有两个自由度参数,分别称为分子自由度(numerator degree of freedom)和分母自由度(denominator degree of freedom)。
在F分布曲线上,分子自由度决定曲线的横向位置,分母自由度决定曲线的形状。
2. t分布(t-distribution)t分布是一种概率分布,通常用于从样本中推断总体参数的分布。
与F分布不同,t分布只有一个自由度参数,称为样本自由度(sample degree of freedom)。
t分布曲线的形状取决于样本自由度,当样本自由度增加时,t分布逐渐收敛于标准正态分布。
3. 区别与应用F分布和t分布之间的主要区别在于其应用场景和使用方法。
F 分布用于比较组间方差的差异,常用于方差分析和回归分析等多组数据的比较。
t分布用于从小样本中推断总体参数的分布,常用于小样本的假设检验和计算置信区间。
4. 快速识别方法快速识别F分布和t分布的方法是通过查看自由度的个数。
如果分布有两个自由度参数,那么它是F分布;如果只有一个自由度参数,那么它是t分布。
总结:- F分布比较组间方差的差异,有两个自由度参数。
- t分布推断总体参数的分布,有一个自由度参数。
- 通过自由度参数个数可以快速识别F分布和t分布。
