2008-2009-01时间序列分析06级期末A卷答案
时间序列分析考试卷及答案

时间序列分析考试卷及答案考核方式 闭卷 考核时间 120 分钟注:B 为延迟算子;使得1-=t t Y BY ;∇为差分算子;1--=∇t t t Y Y Y 。
一、单项选择题(每小题3 分;共24 分。
)1. 若零均值平稳序列{}t X ;其样本ACF 和样本PACF 都呈现拖尾性;则对{}t X 可能建立( B )模型。
A. MA(2)B.ARMA(1,1)C.AR(2)D.MA(1)2.下图是某时间序列的样本偏自相关函数图;则恰当的模型是( B )。
A. )1(MAB.)1(ARC.)1,1(ARMAD.)2(MA3. 考虑MA(2)模型212.09.0--+-=t t t t e e e Y ;则其MA 特征方程的根是( C )。
(A )5.0,4.021==λλ (B )5.0,4.021-=-=λλ (C )5.2221==λλ, (D ) 5.2221=-=λλ,4. 设有模型112111)1(----=++-t t t t t e e X X X θφφ;其中11<φ;则该模型属于( B )。
A.ARMA(2,1) B.ARIMA(1,1,1) C.ARIMA(0,1,1) D.ARIMA(1,2,1)5. AR(2)模型t t t t e Y Y Y +-=--215.04.0;其中64.0)(=t e Var ;则=)(t t e Y E ( B )。
A.0 B.64.0 C. 16.0 D. 2.06.对于一阶滑动平均模型MA(1): 15.0--=t t t e e Y ;则其一阶自相关函数为( C )。
A.5.0- B. 25.0 C. 4.0- D. 8.07. 若零均值平稳序列{}t X ∇;其样本ACF 呈现二阶截尾性;其样本PACF 呈现拖尾性;则可初步认为对{}t X 应该建立( B )模型。
A. MA(2)B.)2,1(IMAC.)1,2(ARID.ARIMA(2,1,2)8. 记∇为差分算子;则下列不正确的是( C )。
期末考试试题06级A卷(参考答案)

第 1 页(共 4 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
n
∂ϕ 2 Q ds = S 2 ∂R ε0
④ (4 分)
dn p n (cosθ ) R n+1
第 3 页(共 4 页)
由③得
⎧ p f cos θ n + ∑ a n R1 p n (cos θ ) = ϕ 0 ⎪ 2 n ⎪ 4πε 0 R1 ⎨ dn ⎪ p f cos θ + p (cosθ ) = ϕ 0 ∑ n+1 n ⎪ 4πε R 2 n R 0 2 ⎩
评阅人
四、计算题(共 40 分,每题 20 分,要求具有逻辑推理,必 要的文字说明和步骤)
v 1. 空心导体球壳的内外半径为R1和R2 ,球中心放置一偶极子 Pf ,球壳上带电Q ,求空间各
点电势和电荷分布。
Q ϕ1 Pf
ϕ0
ϕ2
R1 标系。取原点在球心的球坐标,z轴沿Pf 方向。 方程。 (4 分) 3 空间各点的电势是偶极子产生的电势ϕd =Pf ⋅R /4πε0R 与球壳上自由电荷产生的电势ϕ′ 之和。因为壳内、外没有自由电荷分布,故壳内外的电势ϕ1′和ϕ2′满足拉普拉斯方程: ∇2ϕ′=0 (4 分) (三) 对称性与通解的形式。本题有轴对称性,故通解为 b ' 壳内: ϕ 1 = ϕ d + ϕ 1 = ϕ d + ∑ (a n R n + nn+ 1 ) p n (cos θ ) R n b ' 壳外: ϕ 2 = ϕ d + ϕ 2 = ϕ d + ∑ (a n R n + nn+1 ) p n (cos θ ) R n (四) 边界条件和边值关系。 (4 分) (1) 电荷分布在有限区域: ϕ 2 | R→∞ = 0 ①
时间序列期末考试A卷答案

第(-)学期考试试卷课程代码6024000课程名称时间序列分析B(A卷)考试时间____________(注:匕}为均值为零的白噪声序列)一、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其字母代号写在该题【1 内。
答案错选或未选者,该题不得分。
每小题4分,共20分。
)1.X,的k阶差分是【C】(A) Px严Xt—X.k(B) 丁X严P-'X厂p-'Xj(c) =v A-,x/-v A-'x/_1(D)v*x r=V A-,X,_1-V A-,X/_22.MA⑵模型X f=^-1.1£-Z_I+0.24^_2,则移动平均部分的特征根是【A】(A)人=0.8, /U=0.3 (B) =-0.8, /U=0.3(C)人=-0.8, = -0.3 (D) & =一0.8,入=0.23•关于差分X,—1.3Xi+0.4X一2=0,其通解是【D】(A) q(08+0.3‘)(B) q(o.&+o.5『)(C) qO.S+C/O.M (D) Cfi.S1+C20S4.AR(2)模型X, =£—l.lXj+0.24X_2,其中£>£=0.04,则EX 禺=[B 】(A) 0 (B) 0.04(C) 0.14 (D) 0.25.ARMA(2,l)tMgy X, -X,., -0.24X z_2 =^; -0.8^,.,,其延迟表达式为【A 】(A) (l-B-0.24B2)X, =(l-0.8BX (B) (B2-B-0.24)%, =(B-0.8X(C) (B2-B-0.24)X f =0.8V^ (D) (1 -B-0.24/?2)X f = Vf r二、简答题(10分)对于均值为零的平稳序列,其自相关系数存在两个估计量,请写出两个估计量,并说出它们各自优缺点。
三、(15 分)已知 MA (2)模型为 X r =^-0.6^_,+0.5^_2,其中 Ds, = 0.04 ,(1)计算前3个逆函数,/…; = 1,2,3; -------------------------- (8分) (2)计算Var{X t );------------------------------------ (7 分)解答:(1) X 」勺逆转形式为:或J 壬 --------------------------------------------------------- (1分) /■]J-0将其代入原模型得:X, = (1 -0.6B + 0.5B 2)(1 -I.B- I 2B 2 • • •)%, -------- (1 分) 比较B 的同次幕系数得:B:-Z 1-0.6 = 0=>/l =-0.6 ---------------- (2 分) B 2:-Z 2 + 0.6/, + 0.5 = 0 Z 2 = 0.14 ---------------- (2 分)肝:一人+0・6厶+0・5人=0=>厶=0.384 ------ (2分)(2) EX t = E (s j -0.6^ + 0.5^_2) = 0 ---------- (1 分)EX ; = E[(£ _0・6吕-]+0・5名-2)(吕 _0・6吕-]+0・5爲_2)](2分)所以:Var (X z ) = EX ; = (1 + 0.62 + 0.52)x0.04 = 0.0644 -- (2 分) 四、(15 分)已知 AR (2)模型为(1—0・53)(1-0・33)/=爲 Ds. =a ;= 0.5(1)计算偏相关系数%伙=123); -------------------------------- (8分)(2) W/r (XJ ; ----------------------------------------- (7 分) 解答(1) (l-0・5B )(l-0・3B )X 『 =X 『—O ・8X"i+O ・15X_=£,所以:% =0.=-0」5对于A&2)模型其系数满足2阶Yule-Walker 方程:姑金“69565 和/金+ *“40652,产生偏相关系数的相关序列为,相应Yule-Wolker 方程为:‘1 p\/ 、 '1 P\ V 0.8、(PC<P1 16l.Pi 1315丿4所以:(2分)当£ = 2时, P\ P\Po >2ij =rpi~他」一1因为0, m b ; = 0.04, t= s将其代入原模型得:(1-加-02肝)丘手一广吕一(1分)7-0比较B 的同次幕系数得:G° = lB :G\- %G ()= 0 => G] = (p 、= £ -------- ( 2 分)3’ : G, — %G] +(P 、G Q = 0 => G? = --------- ( 2 分) 225 553G 3 —(pfi 2 一(p 2G } =0=>G 3= 〜0」6385 -------- (2 分)^7P\=(P\\P Q 即 ®I =ZV 所以(Pw= P\ 0.69565% =[。
应用时间序列A卷答案

优质文本一、填空题(24分,每题3分) 1.对任意的T t t n ∈,...1和任意的h 使得n i T h t i ,...,2,1,=∈+有()()()()h t X h t X h t X n +++,...,,21与()()()()n t X t X t X ,...,,21相同的联合分布;2.()()⎪⎩⎪⎨⎧=•<∀-+++=--0,,0...211t s t tp t p t t X E t s WN X X X εσεεφφ; 3. 231,231-+; 4. 拖尾; 5 连续型时间序列分析和离散型时间序列分析;6.频域分析和时域分析;7. 矩估计、极大似然估计和最小二乘估计 8 AIC 和SBC;二、简答题(共20分,每题10分)1.(本题10分)解:(1)时间序列分析方法强调变量值序列顺序的重要性;2分 (2)时间序列各观察值之间存在一定的依存关系; 2分(3)时间序列分析根据自身的变化规律来预测未来; 2分 (4)时间序列是一组随机变量的一次样本实现; 2分 (5)时间序列分析和回归分析的建模思路不同。
2分2.(本题10分)解:(1)模型识别:即确定自回归模型阶数p 和移动平均模型阶数q 。
2 分 (2)参数估计:即给出均值、自回归参数和移动平均参数,以与白噪音方差2σ的估计值。
3分 (3)模型的检验和模型选择:对所选择的不同阶数p 和q 的值,重复估计步骤,直至选出最优模型为止。
3 分(4)应用信息准则法进行模型优化选择。
2 分三.证明题(共12分)证明:()t f 是具有周期T 的函数,因而是有界函数,ε是区间(0,T)上均匀分布的随机变量,因而()()()()011=+•+=•+=⎰⎰t d Tt f d Tt f X E TTεεεε 5分为常数,()()()()()()()()()[]()()[]()()⎩⎨⎧≠-=-=•=-•-=nTs t nTs t t X s X t X E s X E s X t X E t X E s t ,0,var ,γ 5分 因而()t X 的二阶矩都存在,均值函数为常数,协方差函数只与t-s 有关,因而为宽平稳过程。
时间序列分析06a
山东财政学院2006—2007学年第一学期期末考试《时间序列分析》试卷A(考试时间为120分钟)学院__________ 班级__________ 学号__________姓名__________一、判断题(填√或╳, 10分,每空2分)1、 ( )2、对平稳时间序列有: )1(ˆ+k X t 与)(ˆ1k X t +都是对1++kt x 的预测( );且前者比后者的预测精度高( )3、是季节乘积模型,其季节周期步长为4。
( )4.MA(2)与AR(1)分别是对同一序列拟合的模型,且模型和参数均通过显著性检验,AR(1)优于MA(2) ( )。
二、填空(15分,每空3分)1、 用后移算子B 可表示为2、 AR(p)模型平稳的充要条件是3、可逆概念的重要性在于:4、过差分的后果是5、平稳AR(P)模型的自相关系的数递推公式是:三、画图(10分)请画出ARIMA 模型建模的流程图11)(--±=±t t t t y x y x B tt B B x B B ε4428132.044746.011)1)(1(+-=--k t t t k x x x --=∇四、分析题(10分)检验下列模型的平稳性与可逆性 1、t t t t a X X X +-=--213.01.1 2、214.03.1---+=t t t t t a a a X五、应用分析(15分)一非平稳序列经一阶差分后的自相关和偏自相关图如下1以下(a )和(b )分别是对其进行的两种识别和估计 (a):(b)1、写出(a )所确定的模型口径,并说明模型的有效性和参数的显著性.2、写出(b )所确定的模型口径, 并说明模型的有效性和参数的显著性。
3、应选择那个模型?依据是什么?六、计算题(10分) 求ARMA(1,1): 模型系数的矩估计七、应用题(15分)八、证明题(15分)若序列{}t X 适合MA 模型则{}t X 的自相关函数截尾1111---+=t t t t x x εθεφ共 4 页第4 页。
时间序列练习题答案

时间序列练习题答案一、选择题1. 时间序列分析中的自回归模型(AR)是指:A. 模型中的误差项B. 模型预测值依赖于自身过去的值C. 模型预测值依赖于其他变量的值D. 模型预测值依赖于未来的值2. 移动平均模型(MA)的主要特征是:A. 预测值依赖于过去的误差项B. 预测值依赖于过去的观测值C. 预测值依赖于未来的误差项D. 预测值依赖于未来的观测值3. 以下哪个不是时间序列分析中的平稳性检验方法?A. 单位根检验B. 协整检验C. KPSS检验D. 方差比检验4. 时间序列的差分操作通常用于:A. 消除季节性效应B. 消除趋势C. 消除周期性变化D. 消除随机波动5. 季节性调整的目的是:A. 消除随机波动B. 消除季节性效应C. 消除长期趋势D. 消除周期性变化二、简答题1. 简述自回归积分滑动平均模型(ARIMA)的基本组成部分。
2. 解释什么是时间序列的平稳性,并说明为什么在时间序列分析中需要考虑平稳性。
3. 描述季节性时间序列的特点,并说明如何识别和处理季节性效应。
三、计算题1. 给定以下时间序列数据:\[ y_t = \{10, 15, 20, 25, 30, 35, 40, 45, 50, 55\} \] 假设这是一个一阶自回归模型AR(1),其中自回归系数φ=0.8。
请计算下一个时间点的预测值。
2. 假设一个时间序列模型的ACF(自相关函数)在滞后1时显著不为0,而在滞后2及以后时显著为0。
根据这个信息,推测该时间序列可能属于哪种类型的模型?四、案例分析题1. 某公司销售数据呈现明显的季节性变化,如何在时间序列分析中对数据进行季节性调整?2. 一个时间序列模型的ADF(Augmented Dickey-Fuller)检验结果表明存在单位根,这意味着什么?如何对数据进行处理以消除单位根?五、论述题1. 论述时间序列分析在金融领域中的应用,并举例说明。
2. 讨论时间序列分析中的因果关系检验方法,并说明在实际应用中如何选择合适的方法。
edA考试卷(带答案)

2008~2009学年第一学期EDA技术A卷适用:06级电子信息工程专业EDA技术A一、填空题:(共20分,每空1分)1、在VHDL程序设计中,常用的库有(IEEE库)(STD )(WORK )库等。
2、Max_plusII为原理图输入设计配备了各种需要的元件库,它们分别是(基本逻辑元件库)(宏功能元件库)(宏功能块LPM库)。
3、采用原理图输入设计的文件后缀为(.gdf ),采用波形图输入设计的文件后缀为(.wdf )4、在VHDL中的数值类属性测试函数主要有(left)(right)(high )和LOW。
5、FPGA/CPLD的设计流程为(设计输入)、(综合)(适配)(时序仿真与功能仿真)(编程下载)(硬件测试)。
6、若D<= “11” & ‘00’ & “01”,则D的值为(“110001”)。
7、若定义W : BUFFER STD_LOGIC_VECTOR(0 TO 5),程序中有W<=“100111”;则W(2)的值为(0 )。
8、定义signal f,g:std_logic_vector(5 downto 0); 若f的值为“101011”,若执行g<=(5=>f(1),4=>’1’, others=>f(4)); 则g的值是(110000 )。
二、简答题:(共10分)1、VHDL程序一般包括几个组成部分,每部分的作用是什么?答:VHDL程序一般包括3个组成部分,它们是(1)实体,它描述的是电路器件的端口构成和信号属性;(2)结构体,描述设计实体的内部结构和外部设计实体端口间的逻辑关系;(3)库及程序包的声明,在设计实体中的语句可以使用库中相应程序包的数据和文件。
2、什么叫顺序语句,它的适用范围是什么?VHDL有那几种基本的顺序语句?答:执行顺序与它们的书写顺序基本一致的语句叫顺序语句,顺序语句只能出现在进程和子程序中,子程序包括函数和过程。
2008-2009学年 第2学期 期末考试 A卷 试卷及解答
中国海洋大学2008-2009学年第2学期期末考试试卷数学科学学院《线性代数》课程试题(A卷) 共4 页第2 页中国海洋大学 2008-2009学年 第2学期 期末考试试卷数学科学 学院 《线性代数》 课程试题(A 卷) 共 4 页 第 3 页解: 1X A B -=,根据初等行变换求解可得 ()()213132132323102211022110221311133,201570015702,521891014510012110021010351,100121rr r r r r r r r r r r ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-------+---+-⎪ ⎪ ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭--⎛⎫ ⎪-⨯-⨯-⎪ ⎪---⎝⎭uuuuuuuuuuuuu r uuuuu r uuuuuuuuuuuuu r uuuuu r 100210103500121--⎛⎫ ⎪--⎪ ⎪⎝⎭uuuuuuuuuuu因此213521X --⎛⎫ ⎪=-- ⎪ ⎪⎝⎭4. 已知3R 的两组基为()()()1231,0,0,1,1,0,1,1,1TTTααα==-=与()()()1231,2,1,2,3,3,3,7,1T T Tβββ===,求:(1)基{}123,,ααα到基{}123,,βββ的过渡矩阵; (2)向量()5,2,1Tα=在基{}123,,ααα下的坐标。
解:(1)设基{}123,,ααα到基{}123,,βββ的过渡矩阵为C ,则()()123123,,,,C βββααα=,即123111237011131001C ⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因此1111123011237001131C -⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭,利用初等变换法求解得()2313122111123110012100118011237,010106,1010106001131001131001131r r r r r r r --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪----+⨯--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭uuuuuuuuuuu r uuuuuuuuuuuuur12,,,,n αααβL 线性无关;(2)若1β可由12,,,n αααL 表出,而2β不能由12,,,n αααL 表出, 则1212,,,,n αααββ+L 线性无关。
(整理)《时间序列分析》试卷a答案.

2010—2011学年第一学期2007应用数学《时间序列分析》试卷A 答案一 (18分,每空1分)1 112211t t t t t X X X a a ϕϕθ-----=-2 偏自相关函数;自相关函数3 矩估计法、最小二乘估计法、极大似然估计法4 B5 1ϕ;06 1,1,2,i i n λ<=7 m8利用序列图进行判断;利用样本自相关函数ˆk ρ进行平稳性检验;利用单位根检验进行判断9 12222011ˆ 1.96()t l a l X G G G σ+-±+++ 10 存在11 使得预测误差的均方値达到最小10 (1)S DB -二 (8分,每小题1分)1 错;2错;3对;4对;5 错;6 错;7 错;8对三 (12分,每小题2分)1 (1)2(10.80.5)t t X B B a =-+;(2) 21(10.5)(1 1.20.4)t t B X B B a --=-+2 (1) 稳定;(2)稳定3 (1)120.5,0.25G G ==; (2) 120.5,0G G =-=四 (4分)AR{1}五 (12分)(1)34321324321ˆ(1)(,,)([100.60.3],,)100.697.20.39696.12X E X X X X E X X a X X X ==+++=+⨯+⨯=;(2分)35321435321ˆ(2)(,,)([100.60.3],,)100.697.120.397.297.432X E X X X X E X X a X X X ==+++=+⨯+⨯=;(2分) 36321546321ˆ(3)(,,)([100.60.3],,)100.697.4320.397.1297.5952X E X X X X E X X a X X X ==+++=+⨯+⨯= (2分)(2)010110.6G G G ϕ===221/21/2011.96() 1.966 1.3613.7144G G σ+=⨯⨯=五月份销售额的 95%的置信区间为(83.7176,111.1464) (2分)六 (50分)1 (1)AR(1)模型:10.667831t t t X X a -=+ (5分)疏系数的ARMA(1,6)模型:160.5578970.47526t t t t X X a a --=++ (5分)(2)上边AR(1)模型的AIC 值为-0.804969,第二个模型的AIC 值为-0.876542,根据AIC 准则可知,第二个模型拟合效果更好。
时间序列分析习题答案

时间序列分析习题答案时间序列分析习题答案时间序列分析是一种广泛应用于统计学和经济学领域的方法,用于研究随时间变化的数据。
通过对时间序列数据的建模和分析,我们可以揭示数据背后的规律和趋势,从而进行预测和决策。
下面我将给出一些时间序列分析习题的答案,希望能对大家的学习和理解有所帮助。
1. 什么是时间序列?时间序列是按照时间顺序排列的一系列数据观测值。
它可以是连续的,比如每天的股票价格,也可以是离散的,比如每个月的销售额。
时间序列分析的目标是通过对这些数据的分析和建模,揭示数据背后的规律和趋势。
2. 时间序列分析的步骤是什么?时间序列分析一般包括以下几个步骤:- 数据收集:收集并整理时间序列数据,确保数据的准确性和完整性。
- 数据可视化:通过绘制时间序列图,观察数据的趋势、季节性和周期性等特征。
- 数据平稳性检验:通过统计检验方法,判断时间序列数据是否平稳。
如果不平稳,需要进行差分处理。
- 模型选择:根据数据的特征和目标,选择适合的时间序列模型,比如ARIMA模型、季节性ARIMA模型等。
- 模型拟合:利用选定的模型,对时间序列数据进行拟合和参数估计。
- 模型诊断:对拟合的模型进行诊断,检验模型的残差序列是否符合模型假设。
- 模型预测:利用已拟合的模型,对未来的数据进行预测。
3. 如何判断时间序列数据的平稳性?平稳性是时间序列分析的基本假设之一,它要求时间序列的均值、方差和自相关函数在时间上都是常数。
常用的平稳性检验方法有:- 绘制时间序列图:观察数据是否具有明显的趋势、季节性和周期性。
- 平稳性统计检验:常用的统计检验方法有ADF检验、KPSS检验等。
这些检验方法的原理是基于单位根检验,判断序列是否存在单位根,从而判断序列的平稳性。
4. 如何选择适合的时间序列模型?选择适合的时间序列模型需要考虑数据的特征和目标。
常用的时间序列模型有:- AR模型:自回归模型,利用过去的观测值对当前值进行预测。
- MA模型:移动平均模型,利用过去的白噪声误差对当前值进行预测。
(精校版)时间序列分析试卷及答案

(完整word版)时间序列分析试卷及答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)时间序列分析试卷及答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)时间序列分析试卷及答案的全部内容。
时间序列分析试卷1一、 填空题(每小题2分,共计20分)1. ARMA (p , q)模型_________________________________,其中模型参数为____________________.2. 设时间序列{}t X ,则其一阶差分为_________________________。
3. 设ARMA (2, 1):1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________.4. 对于一阶自回归模型AR(1): 110t t t X X φε-=++,其特征根为_________,平稳域是_______________________.5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-,当a 满足_________时,模型平稳.6. 对于一阶自回归模型MA (1): 10.3t t t X εε-=-,其自相关函数为______________________.7. 对于二阶自回归模型AR (2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。
8. 设时间序列{}t X 为来自ARMA (p,q )模型:1111t t p t p t t q t q X X X φφεθεθε----=++++++则预测方差为___________________.9. 对于时间序列{}t X ,如果___________________,则()~t X I d .10. 设时间序列{}t X 为来自GARCH (p ,q )模型,则其模型结构可写为_____________。
华东师范大学期末试卷08-09(A)参考答案

华东师范大学期末试卷(A )参考答案2008——2009学年第一学期1.填空题(20分)1) 描述地理数据一般水平的指标有 平均值 、 中位数 、 众数 ;描述地理数据分布的离散程度的指标有 极差 、 离差 、 离差平方和 、 方差与标准差 、 变异系数 ;描述地理数据分布特征的参数有 偏度系数 、峰度系数 ;揭示地理数据分布均衡度的指数有 基尼系数 、 锡尔系数 。
(每空0.5分)2) 秩相关系数与简单相关系数的区别在于: 秩相关系数是以两要素样本值的大小排列位次来代替实际数据而求得的一种统计量 。
(1分)3) 多元线性回归模型中常数0b 及偏回归系数i b 的求解公式b = A -1B=(X T X )-1X TY (请用矩阵形式表达),其中各矩阵的具体表达式为:、 、 ; 其显著性检验中,回归平方和U 的自由度为 自变量的个数k ,剩余平方和Q 的自由度为n-k-1,n 为样本个数 。
(每空0.5分)4) 主成分分析的主要计算步骤: ①计算相关系数矩阵 , ②计算特征值与特征向量 , ③计算主成分贡献率及累计贡献率 , ④计算主成分载荷 。
(每空0.5分) 5) 全局空间自相关的度量指标有 Moran 指数 、 Geary 系数 ;局部空间自相关分析方法包括: LISA(空间联系的局部指标) 、 G 统计量 、 Moran 散点图 。
(每空0.5分) 6) 请写出线形规划问题: Min Z=2X 1+5X 2+X 3 满足 X 1+2X 2+X 3≥63X 1-X 2+2X 3≥6X 1,X 2,X 3≥0 的对偶问题max Z=6Y 1+6Y 2 Y 1+3Y 2≤22Y 1-Y 2≤5 Y 1+2Y 2≤1 Y 1,Y 2≥0_______________________________。
(1.5分)7) 在目标规划模型中,除了决策变量外,还需引入正、负偏差变量,其中,正偏差变量表示 决策值超过目标值的部分 ,负偏差变量表示 决策值未达到目标值的部分 。
时间序列分析期末题库试题及答案

时间序列分析期末题库试题及答案(以下是一个范例,您可以根据需要进行修改和调整)时间序列分析期末题库试题及答案时间序列分析是一门研究随时间变化的数据模式和规律的统计学方法,广泛应用于物理学、经济学、环境科学等领域。
在进行时间序列分析时,掌握相关的试题及其答案是提高分析能力和应对考试的重要途径。
本文将为您提供一份时间序列分析期末题库试题及答案,希望能帮助您更好地掌握这门学科。
一、简答题1. 请解释什么是时间序列分析。
答:时间序列分析是一种统计学方法,用于研究随时间变化的数据。
它可以揭示出数据内在的趋势、季节性和周期性等模式,帮助我们进行预测和决策。
2. 时间序列分析的主要步骤有哪些?答:时间序列分析的主要步骤包括:数据收集和整理、数据可视化、确定模型、模型识别和拟合、模型检验和评估、模型预测和应用。
3. 请解释平稳时间序列的概念。
答:平稳时间序列是指其数学期望、方差和自协方差不随时间的变化而发生显著变化的时间序列。
平稳时间序列的均值和方差不依赖于时间,具有稳定的趋势和季节性。
4. 如何进行时间序列的平稳性检验?答:常见的平稳性检验方法包括ADF检验、KPSS检验和单位根检验。
这些方法可以通过检验时间序列数据的单位根是否存在来判断其是否平稳。
5. 时间序列分析中的自相关和偏自相关函数有什么作用?答:自相关函数(ACF)和偏自相关函数(PACF)用于分析时间序列数据的相关性。
ACF可以帮助确定数据的季节性和周期性,而PACF可以帮助确定数据的自回归阶数。
二、计算题请根据以下时间序列数据,回答下面的问题:年份 | 销售额(万元)-----------------------2015 | 2002016 | 2302017 | 2502018 | 2802019 | 3002020 | 3201. 请绘制销售额的时间序列图。
答:(在此插入相应的时间序列图)2. 根据观察的时间序列图,总结该时间序列的趋势和季节性。
时间序列分析试题-时间序列分析试卷及答案

第九章 时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。
这种模型将时间序列按构成分解为 ( ) 等四种成分,各种成分之间 ( ) ,要测定某种成分的变动,只须从原时间序列中 ( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他 影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其 他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他 影响成分的变动D. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其 他影响成分的变动答案: C2、加法模型是分析时间序列的一种理论模型。
这种模型将时间序列按构成分解为 ( ) 等四种成分,各种成分之间 ( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其 他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去 其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其 他影响成分的变动D. . 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去 其他影响成分的变动答案: B3、利用最小二乘法求解趋势方程最基本的数学要求是( )。
A.(Y Y ?t )2 任意值 B. (Y Y ?t ) 2 min C. (Y Y ?t )2 max D. (Y Y ?t )2 0答案: B4、从下列趋势方程 Y ?t 125 0.86t 可以得出( )。
Y 增加 0.86 个单位Y 减少 0.86 个单位Y 平均增加 0.86 个单位Y 平均减少 0.86 个单位 答案: D. )。
B. 只能是相对数 D. 上述三种指标均可以 答案: D.6、下列时间序列中,属于时点序列的有( )。
(完整word版)06级本科--软件工程期末考卷A卷参考答案

一、 单项选择题(30%, 每小题2分):DDAAC DADCD DDAAD二、 简答题(25%, 每小题5分):1.请简要说明需求分析的三个层次包括那些主要内容。
1个2分,2个4分,3个5分软件需求包括三个不同的层次—业务需求、用户需求和功能需求—也包括非功能需求。
业务需求反映了组织机构或客户对系统、产品高层次的目标要求。
用户需求文档描述了用户使用产品必须要完成的任务。
功能需求定义了开发人员必须实现的软件功能,使得用户能完成他们的任务,从而满足了业务需求。
2.为什么要设计独立性强的模块以及如何判断模块的独立性? 第一3分,耦合1分,内聚1分模块独立性强,则:(1)系统容易开发(2)系统可靠性高(3)系统容易维护判断模块独立性的基本原则:“耦合小,内聚大”3.若现有类已经进行了彻底的测试,为什么必须对从现有类中实例化的子类进行重新测试?使用的场景:3分. 2分因为父类和子类的运行环境是不同的。
另外,如果是多重继承会显著地增加派生类的复杂程度,导致一些难以厦门大学《 软件工程 》课程试卷软件 学院____系 2006 年级 软件工程 专业主考教师:林坤辉 试卷类型:(A 卷)发现的隐含错误。
4.要开发质量“非常好”的软件,请从软件工程的角度分析其利与弊。
利:3分;弊:2分利:容易维护,用户比较满意弊:成本高,周期长5、采用面向对象方法设计软件系统时,子系统的划分常采用水平划分或垂直划分的方式,请说明这两种划分所得子系统的特点。
c/s:3分,p2p:2分水平划分系统的p2p:每个字系统可以调用任意其他子系统,比c/s复杂,可能死锁。
垂直划分c/s:客户端调用服务器端,服务器提供服务,并返回结果。
客户端需要知道服务器的接口,而服务器不必知道客户端接口。
三、应用题(45%,1-3每小题10分,4小题15分)1.公司计划采用新技术开发一款新的手机软件产品,希望尽快占领市场,假设你是项目经理,你会选择哪种软件过程模型?为什么?选模型:5分;原因:5分选用模型:可采用增量模型/增量+ 原形/螺旋模型等等。
世界文明史试卷(期末)a

06级思政教育专业《世界文明史》
题号
一
二
三
总分
分值
10
24
66
100
得分
评卷人
得分
一、列举题(每小题5分,共10分)
1、“文艺复兴艺术三杰”(5分)
2、伊斯兰教的“五功”(5分)
得分
二、简答题(每小题12分,共24分)
1、简述十字军东征对西欧社会的影响。(12分)
2、什么是浪漫主义?并列举三位浪漫主义的代表人物及其作品。(12分)
1、阐述原始宗教观念的主要表现及其文化内涵。(22分)
2、简述佛教的基本教义,并谈谈你对这些教义的认识。(22分)
3、你怎么认识苏格拉底的名言“认识你自己”?(22分)
计量经济学第二套试题及参考答案

1、对联立方程模型参数的单方程估计法包括(
)
A、工具变量法
B、间接最小二乘法 C、完全信息极大似然估计法
D、二阶段最小二乘法 E、三阶段最小二乘法
2、希斯特(Shisko)研究了什么因素影响兼职工作者的兼职收入,模型及其估计结果为:
wˆ m 37.07 0.403w0 90.06race 113.64reg 2.26age (0.062) (24.47) (27.62) (0.94)
R2 (n k) B、 (1 R2 ) (k 1)
ESS (k 1) C、 RSS (n k)
ESS D、 RSS (n k )
5、根据样本资料估计得出人均消费支出 Y 对人均收入 X 的回归模型为 LnYˆi 2.0 0.56 X i ,
这表明人均收入每增加 0.01 个单位,则人均消费支出将增加( )
满足库伊克变换的假定,则长期影响乘数为( )
A、不能确定
B、 k 0
C、 1 k 1 0
D、 0 1
19、关于自适应预期模型和局部调整模型,下列说法错误的有( )
A、它们由某种期望模型演变形成的
B、它们最终都可以转换成自回归模型
C、它们都满足古典线性回归模型的所有假设,从而可直接 OLS 方法进行估计
R 2 0.74
df 311
其中:wm 为兼职工薪(美元/小时);w0 为主业工薪(美元/小时);race 为虚拟变量,若 是白人取值为 0,非白人取值为 1;reg 为虚拟变量,当被访者是非西部人时,reg 取值为 0 为当被访者是西部地区人时,人 reg 取值为 1;age 为年龄;关于这个估计结果,下列说法
西南财经大学2008 - 2009 学年第 一 学期 经济类其他 专业 本 科 2006 级( 三 年级 一 学期)
2008-2009-01时间序列分析06级期末A卷答案

北京师范大学珠海分校2008-2009学年第一学期期末考试(A 卷)答案开课单位: 应用数学系 课程名称:时间序列分析任课教师: 吴春松 考试类型: 闭卷 考试时间: 120 分钟试卷说明:(本试卷共4页,满分100分)--------------------------------------------------------------------------------------------一、填空题(每空3分,共30分);1. 所谓时间序列是指:按照时间的顺序把随机事件变化发展的过程等时间距离的记录下来,就是一个时间序列。
2. 平稳时间序列的两个统计性质是:(1)常数均值:t EX μ=;(2)自协方差函数和自相关系数只依赖于时间的平移长度而与时间的起止点无关:γγ(t,s)=(k,k+s-t)。
3. 白噪声序列满足:(1)任取t∈T ,有EX t =µ,;(2) 任取t,s∈T ,有⎩⎨⎧≠==st st s t ,0,),(2σγ, 称序列}{t X 为纯随机序列(又称白噪声序列)。
4. 已知AR (1)模型为:),0(~x 7.0x 2t t 1-t t εσεεWN ,+=,则)(t x E =___0____, 偏自相关系数11φ=______0.7_______,kkφ=______0_______(k>1);5. 设{}x t 为一时间序列,且)(,t t 21-t t t x x x x x ∇∇=∇-=∇=2t 1t t x x 2x --+-;6. 假设线性非平稳序列{}x t 形如:t t a t 21x ++=,,0a E t =)(其中 ,)(2t a Var σ= 1t 0a a Cov 1-t t ≥∀=,),(,问应该对其进行__一__阶差分后化成平稳序列分析;7. 模型ARIMA (0,1,0)称为_随机游走_模型, 其序列的方差=)(t x V ar 2εσt ;8. 如果序列1阶差分后平稳,并且该差分序列的自相关图1阶截尾,偏相关图拖尾, 则选用什么ARIMA 模型来拟合: ARIMA(0,1,1) ;9. 条件异方差模型中,形如⎪⎪⎪⎩⎪⎪⎪⎨⎧++==+=∑∑=-=---3122121),,,(j j t j i i t i t t t t tt t t h h e h x x t f x εληωεεΛ式中,),,,(21Λ--t t x x t f 为{t x }的回归函数,N(0,1)~i.i.dt e ,该模型简记为GARCH (2,3)模型;10. Cox 和Jenkins 在1976年研究多元时间序列分析时要求输入序列与响应序列均要_ 平稳 _,Engle 和Granger 在1987年提出了__协整 _关系,即当输入序列与响应序列之间具有非常稳定的线性相关关系(回归残差序列平稳)。
时间序列分析习题及答案
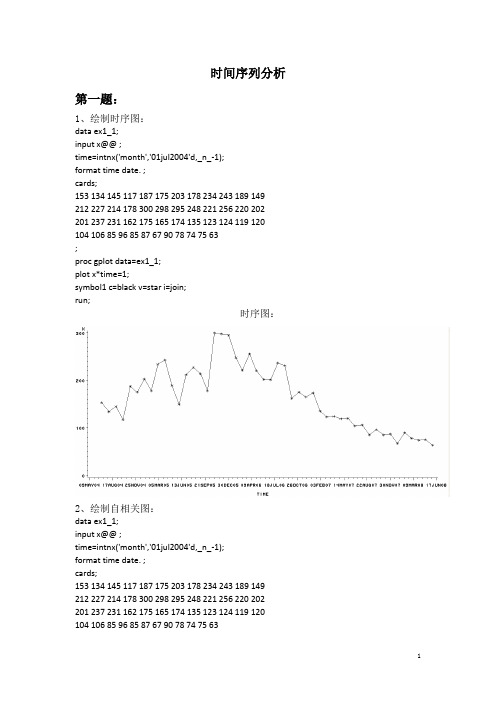
时间序列分析第一题:1、绘制时序图:data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc gplot data=ex1_1;plot x*time=1;symbol1 c=black v=star i=join;run;时序图:2、绘制自相关图:data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc arima data=ex1_1;identify var=x;run;样本自相关图:白噪声检验输出结果:因为P值小于α,所以该序列为非白噪声序列,根据时序图看出数据并不在一个常数值附近随机波动,后期有递减的趋势,所以不是平稳序列。
第二题:1、选择拟合模型方法一:首先绘制该序列的时序图,直观检验序列平稳性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008-2009-1-17190170-95004-11 时间序列分析A 卷
北京师范大学珠海分校
2008-2009学年第一学期期末考试(A 卷)答案
开课单位: 应用数学系 课程名称:时间序列分析
任课教师: 吴春松 考试类型: 闭卷 考试时间: 120 分钟
试卷说明:(本试卷共4页,满分100分)
--------------------------------------------------------------------------------------------
一、填空题(每空3分,共30分);
1. 所谓时间序列是指:按照时间的顺序把随机事件变化发展的过程等时间距离的记录下来,就是一个时间序列。
2. 平稳时间序列的两个统计性质是:(1)常数均值:t EX μ=;
(2)自协方差函数和自相关系数只依赖于时间的平移长度而与时间的起止点无关:
γγ(t,s)=(k,k+s-t)。
3. 白噪声序列满足:(1)任取t∈T ,有EX t =µ,;(2) 任取t,s∈T ,有
⎩⎨
⎧≠==s
t s t s t ,
,),(2
σγ, 称序列}{t X 为纯随机序列(又称白噪声序列)。
4. 已知AR (1)模型为:),0(~x 7.0x 2t t 1-t t εσεεWN ,+=,则)(t x E =___0____,
偏自相关系数11φ=______0.7_______,kk
φ=______0_______(k>1);
5. 设{}x t 为一时间序列,且)(,t t 21-t t t x x x x x ∇∇=∇-=∇=2
t 1t t x x 2x --+-;
6. 假设线性非平稳序列{}x t 形如:t t a t 21x ++=,,0a E t =)(其中 ,)(2t a Var σ=
1t 0a a Cov 1-t t ≥∀=,),(,问应该对其进行__一__阶差分后化成平稳序列分析;
7. 模型ARIMA (0,1,0)称为_随机游走_模型, 其序列的方差=
)(t x Var 2
ε
σt ;
8. 如果序列1阶差分后平稳,并且该差分序列的自相关图1阶截尾,偏相关图拖尾, 则选用什么ARIMA 模型来拟合: ARIMA(0,1,1) ;
9. 条件异方差模型中,形如⎪⎪⎪⎩
⎪
⎪⎪⎨⎧
++==+=∑∑=-=---3
122121),,,(j j t j i i t i t
t t t t
t t t h h e h x x t f x εληωεε
式中,),,,(21 --t t x x t f 为{t x }的回归函数,N(0,1)~i.i.d
t e ,该模型简记为GARCH (2,3)模型;
10. Cox 和Jenkins 在1976年研究多元时间序列分析时要求输入序列与响应序列均要
_ 平稳 _,Engle 和Granger 在1987年提出了__协整 _关系,即当输入序列与响
应序列之间具有非常稳定的线性相关关系(回归残差序列平稳)。
二、(10分)试用特征根判别法或平稳域判别法检验下列四个AR 模型的平稳性。
(1)t 1-t t x 8.0x ε+-= (2)t
1-t t x 3.1x ε+=
(3)t
2-t 1-t t x 6
1x 61x ε++
=
(4)t
2-t 1-t t x 2x x ε++=
解:
AR (p )模型平稳性的特征根判别法要求所有特征根绝对值小于1;
AR (1)模型平稳性的平稳域判别法要求1||1<φ,
AR (2)模型平稳性的平稳域判别法要求:1,1||122<±<φφφ。
(1) 8.01-=λ 特征根判别法:平稳;18.0||1<=φ,平稳域判别法:平稳;
(2) 3.11=λ 特征根判别法:非平稳;13.1||1>=φ,平稳域判别法:非平稳;
(3) 特征方程为: 2
1,31
,0)13)(12(016212=
-==+-=--λλλλλλ即
由特征根判别法:平稳;
10,
13
1,
161||12122<=-<=
+<=
φφφφφ,平稳域判别法:平稳;
(4) 特征方程为: 2,1,0)2)(1(02212=-==-+=--λλλλλλ即 由特征根判别法:非平稳;
11,13,12||12122不小于=->=+>=φφφφφ,平稳域判别法:非平稳。
三、 (10分=4+3+3分)非平稳序列的确定性分析
1. 某一观察值序列最后4期的观察值为:=-3T x 5,=-2T x 5.4,=-1T x 5.8,=T x 6.2,
使用4期移动平均法预测2ˆ+T x。
解:使用4期移动平均法预测
()()75
.54
6
.52.68.54.5ˆ4
1ˆ6.542
.68.54.5541ˆ112
21231=+++=+++==+++=+++=+--+---+T T T T T T T T T T x
x x x x
x x x x x
2. 对某一观察值序列{}t x 使用指数平滑法1~)1(~--+=t t t x x x αα,已知6=T x , 4.6~1=-T x ,平滑系数25.0=α,求二期预测值2ˆ+T x。
解:使用指数平滑法1~)1(~
--+=t t t x x x αα 3.6ˆˆ)1(ˆˆ3.64.675.0625.0~75.025.0~ˆ111211==-+===⨯+⨯=+==++++-+T T T T T T T T x x x x
x x x x αα
3. 下表是某序列季节指数计算表,请在空白处填上准确结果。
四、 (10分)试推导一般ARMA (1,1)模型1
-t 1t 1-t 1t
x x εθεφ-=-的传递形
式和逆转形式;并进而给出ARMA (1,1)模型为:1-t t 1-t t 8.0x 5.0x εε-=-的传
递形式与逆转形式。
解:(1)ARMA (1,1)模型1-t 1t 1-t 1t x x εθεφ-=-的传递形式: t 1t 1B 1x B 1εθφ)()(-=-
t
2
2
111t 11t B B 1B 1B 1B 1x εφφθεφθ))(()
()( +++-=--=
t
k 11
k 1k
1312
13
12112
111t ])B )B )B )B 1[x εθφφθφφθφφθφ +-++-+-+-+=-((((
代入 8.0,5.011==θφ,得
t
k
1
k 322t ]B
5
.03.0B 5.03.0B 15.0B 3.01[x ε +⋅--⋅---=-
(2)ARMA (1,1)模型1
-t 1t 1-t 1t x x εθεφ-=-的逆转形式:
t 1t 1B 1x B 1εθφ)()(-=- t
2
2111t 11t x B B 1B 1x B 1B 1))(()
()( +++-=--=
θθφθφε
t
k
11
k 1k
1312
13
12112
111t ]x )B )B )B )B 1[ +-++-+-+-+=-φθθφθθφθθφθε((((
代入 8.0,5.011==θφ,得t k 1k 322t ]x B 8.03.0B 8.03.0B 24.0B 3.01[ +⋅++⋅+++=-ε
五、 (10分)给出ARIMA 模型的建模流程:
模型建模步骤如下
Y
六、 (30分)实践题(另交3-10页的题目、程序和答案纸)
要求:总结各章上机指导的相关内容,从问题出发,提供不超过三个可以独立运行的SAS 程序,
解决时间序列分析有关具体问题,包括数据的输入、输出,时序图、自相关图、偏相关图,ARIMA 过程的较完整运用,以及其它自己熟悉的时间序列分析程序过程(如自回归、X11等)的运用。
