电磁场与电磁波期末试题2010A
电磁场与电磁波期末试题

电磁场与电磁波期末试题一、选择题(10×2=20分)1.产生电场的源为( C )A 位移电流和传导电流;B 电荷和传导电流;C 电荷和变化的磁场;D 位移电流和变化的磁场。
2.在有源区,静电场电位函数满足的方程是( A )A 泊松方程;B 亥姆霍兹方程;C 高斯方程;D 拉普拉斯方程。
3. 如果真空中有一个点电荷q 放在直角坐标系的原点,则坐标),,(z y x 处的电位=Φ( D )A 22241z y xq++πε; B 222041z y x q++πε; C 22241zy x q ++πε; D 22241zy x q ++πε。
4. 某金属在频率为1MHz 时的穿透深度为60m μ,当频率提高到4 MHz 时,其穿透深度为( B )A 15m μ;B 30m μ;C 120m μ;D 240m μ。
5. 在正弦电磁场中,位移电流应与该处电场的方向一致,其相位( C ) A 与电场相同; B 与电场相反; C 超前电场90°; D 滞后电场90°。
6. 一个半径为a 的导体球,球外为非均匀电介质,介电常数为a r 0εε=,设导体球的球心与坐标原点重合,则导体球与无穷远点的电容为( B )A a 04πε; B a 08πε; C a 012πε; D a 02πε。
7.对于非磁性介质,平行极化的均匀平面斜入射到介质分界面上,发生全透射的条件为( B )A 反射波平行极化;B 入射角等于布儒斯特角;C 入射角等于临界角;D 入射波为左旋园极化。
8.麦克思韦提出的( D )的概念,使在任何状态下的全电流都可保持连续A 传导电流;B 时变电流;C 运流电流;D 位移电流。
9. 如图所示的一个电量为q 的点电荷放在060导体内坐标),(d a 处,为求解导体包围空间的电位,需要( C )个镜像电荷A 1个;B 3个;C 5个;D 8个。
10. 已知良导体的电导率磁导率和介电常数分别为σμ和ε,则频率为ω的平面电磁波入射到该导体上时的集肤深度为( A ) Aωμσ2; B 2ωμσ; Cωμσ21;D σωμ2。
电磁场与电磁波期末试题2010A

北京工业大学电控学院2009――2010学年第 2 学期《电磁场与电磁波》 课程试卷A适用专业: 电子工程、通信工程 考试方式:闭卷 考试时间 :2009年6 月 29 日班级学号 姓名: 成绩 得分登记(由阅卷教师填写)考生须知:答卷前务必首先写清班级学号和姓名,否则无成绩;一、简答题(30分)1.写出静电场的电位泊松方程,并给出其两种理想介质分界面的边界条件。
2ρϕε∇=-; 在两种完纯介质分界面上电位满足的边界条件:12ϕϕ= 1212snnϕϕεερ∂∂-=-∂∂2.讨论均匀平面波在无界空间传播时本征阻抗与波阻抗的区别。
3.写出均匀平面波在无界良导体中传播时相速的表达式。
4.写出时谐电磁场条件下亥姆霍兹方程。
5.写出传输线输入阻抗公式。
6.证明电场矢量和磁场矢量垂直。
证明:任意的时变场(静态场是时变场的特例)在一定条件下都可以通过Fourier展开为不同频率正弦场的叠加。
垂直。
也与垂直与垂直。
与乘定义,可知根据E H H X∴=⨯-=⨯-∂∂-=⨯∇B B E B E k B j E k j tBE ωω7.写出线性各向同性的电介质、磁介质和导电介质的本构关系式。
EJ H B EDσμε=== 8.写出均匀平面波在两介质分界面的发射系数和投射系数表达式。
9.写出对称天线的归一化方向函数。
10.解释TEM 、TE 、TM 波的含义。
二、计算题1. (10分)已知矢量222()()(2)x y z x axz xy by z z czx xyz =++++-+-E e e e ,试确定常数a 、b 、c 使E 为无源场。
解 由(2)(2)(122)0x az xy b z cx xy ∇=++++-+-= E ,得2,1,2a b c ==-=-2.已知标量函数22223326u x y z x y z =+++--。
(1)求u ∇;(2)在哪些点上u ∇等于零。
解 (1)(23)(42)(66)xyzx y z u u u u x y z xyz∂∂∂∇=++=++-+-∂∂∂e e e e e e ;(2)由(23)(42)(66)0x y z u x y z ∇=++-+-=e e e ,得 32,12,1x y z =-==3. 两块很大的平行导体板,板间距离为d ,且d 比极板的长和宽都小得多。
电磁场与电磁波期末试题(通信2010)

2、 (13 分)两块无限大的理想导体平板分别置于 z 0 和 z d 处,如 图所示。若平板之间的电场强度为 z E (x, z , t) e y E0 s i n ( ) ct o sk (x x V ) m / d 式中 E0 、 kx 皆为常数。试求: (1)与 E 相伴的磁场强度 H(x, z, t) ;
线
明:当 q 与 Q 同号,且 力。
Q RD3 R 成立时, F 表现为吸引 2 2 2 q (D R ) D
课 程 名 称
专
业
xx 大 学
试 卷
第 4 页 共 5 页
4、 (12 分)两块无限大导体平板分别置于 x 0 和 x d 处,板间充满 x 电荷,其体电荷密度为 0 ,极板的电位分别设为 0 和 U 0 ,如图 d 所示,求两导体板之间的电位和电场强度。
5、 (15 分)如图的导体槽在 z 方向无限长,底面保持为电位y=0 V0, 其余两面电位为零,利用分离变量法,求槽内电位分布 ( x, y ) 。
xx 大
学 试
卷
第 5 页 共 5 页
考 试 日 期
姓 名
密
学 号
附录:
真空介电常数 0
1 10 9 F / m, 磁导率 0 4 10 7 H / m 36
H (z ,) t
x
e0 . 1 5 c o s ( 9.8 3 6t 10
y3 . 1 A2 m )
/
(2)一大功率电容器在填充的油中产生的电场强度
E (z, t) ex 0.9cos(3.77 102 t 2.81106 z)
设油的相对介电常数 r 5 。
MV / m
电磁场与波期末考试试题A卷含答案

莆田学院期末考试试卷 (A )卷2011 — 2012 学年第 一 学期课程名称: 电磁场与波 适用年级/专业: 09/电信 试卷类别 开卷( ) 闭卷(√) 学历层次 本科 考试用时 120分钟《.考生..注意:答案要全部抄到答题纸上,做在试卷上不给分.......................》.一、填空题(每空2分,共30分)1.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ① ,矢量B A ⋅= ② 。
2.高斯散度定理的积分式为 ① ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
3.已知任意一个矢量场A ,则其旋度的散度为 ① 。
4.介质中恒定磁场的基本方程的积分式为 ① , ② , ③ 。
5.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ① ,位置位于 ② ;当点电荷q 向无限远处运动时,其镜像电荷向 ③ 运动。
6.标量场2),,(x xyz z y x +=ψ通过点P(1,1,2)的梯度为① 。
7.引入位移电流的概念后,麦克斯韦对安培环路定律做了修正,其修正后的微分式是 ① ,其物理含义是: ② 。
8.自由空间传播的电磁波,其磁场强度)sin(z t H a H m y βω-=,则此电磁波的传播方向是 ① ,磁场强度复数形式为 ② 。
二、单项选择题(每小题2分,共20分)1.自由空间中的平行双线传输线,导线半径为a ,线间距为D ,则传输线单位长度的电容为 。
A .)ln(1aaD C -=πε B. )ln(201aa D C -=πε C. )ln(2101a a D C -=πε2.如果某一点的电场强度为零,则该点的电位为 。
A.一定为零 B.不一定为零 C.为无穷大3.真空中一个电流元在某点产生的磁感应强度dB 随该点到电流元距离变化的规律为 。
电磁场与电磁波期末复习题

电磁场与电磁波模拟题一、选择题1. 已知:e e e e e e z y x z y x B A 432;543++=++=;计算:A⃗×B ⃗⃗= ( A ) A. e x ⃗⃗⃗⃗+2e y ⃗⃗⃗⃗⃗(10−12)+e z ⃗⃗⃗⃗ B. 4e x ⃗⃗⃗⃗⃗⃗⃗+2e y ⃗⃗⃗⃗⃗⃗⃗+e z ⃗⃗⃗⃗ C. 6e x ⃗⃗⃗⃗−12e y ⃗⃗⃗⃗⃗+20e z ⃗⃗⃗⃗D. 6e x ⃗⃗⃗⃗+12e y ⃗⃗⃗⃗⃗(A y B z −A z B y )+20e z ⃗⃗⃗⃗2. E ⃗⃗=e x ⃗⃗⃗⃗(x 2+bxz )+e y ⃗⃗⃗⃗⃗(xy 2+ay )+e z ⃗⃗⃗⃗(z −z 2+czx −2xyz )为无源场,求a ,b ,c 的值分别为:( B )A. a=3,b=3,c=1B. a=-1,b=2,c=-2C. a= -2 b=2 ,c=1D. a=1 ,b=2 ,c=-2 3. 自由空间中毕澳-萨伐卡定律表述正确的是:( A ) A. B ⃗⃗=μ04π∫J ⃗×R ⃗⃗R 3dV V B. B ⃗⃗=μ04π∮Idl ⃗×R ⃗⃗R 3 S C. B ⃗⃗=μ02π∮Idl ⃗×R ⃗⃗R 2 CD. B ⃗⃗=μ02π∫J S ⃗⃗⃗⃗⃗×R ⃗⃗R 3dS S4.对于线性及各向同性的媒质,电磁场的电场强度、电位移矢量、磁场强度、磁感应强度本构关系不正确的是( D )A. D⃗⃗=εE ⃗⃗ B. B ⃗⃗=μH ⃗⃗ C. J ⃗=σE ⃗⃗ D. H ⃗⃗=μB ⃗⃗ 5.静电场中电场能量存在于整个电场空间中,和电场强度及电位移矢量相关,下面正确的是:(A )A. W e =12∮φD ⃗⃗∙dS ⃗S +12∫E ⃗⃗∙D ⃗⃗dV V B. W e =12∮φD ⃗⃗∙dl ⃗C +12∫E ⃗⃗∙D ⃗⃗dV VC. W e =12∮φD ⃗⃗∙dS ⃗ S +12∮E ⃗⃗∙D ⃗⃗dlCD. W e =12∮φD ⃗⃗∙dl ⃗C +12∮E ⃗⃗∙D ⃗⃗dl C6. 恒定磁场中磁场能量存在于整个磁场空间中,下面正确的是:(A )A. W m =12∫J ⃗∙A ⃗dVV =12∫H ⃗⃗∙B ⃗⃗dV VB. W e =12∫H ⃗⃗∙B ⃗⃗dVVC. W e =12∫J ⃗∙A ⃗dVV =12∫H ⃗⃗∙B ⃗⃗dV V D. W m =12∫J ⃗∙A ⃗dV V +12∫H ⃗⃗∙B ⃗⃗dV V7. 设点电荷2q 在球坐标系中(d ,0,0)处,接地导体球半径为a,的球心在z=0处,两者组成系统中,在r>a处的电位函数为:()A. φ=q4πε[√22d√r2+(a2d)2−2r a2dcosθ]B. φ=q2πε[d√r2+(2d)2−2r2dcosθ]C. φ=q4πε[d√r2+(d)2−2rdcosθ]D. φ=q2πε[√d√r2+(2d)2−2r2dcosθ]8.无界空间中,媒质为线性及各向同性材料,电磁波传播满足的波动方程为:()A. ∇2E⃗⃗−μεð2E⃗⃗ðt2=μðJ⃗ðt+∇∙ρε;∇2H⃗⃗−μεð2H⃗⃗ðt2=∇×J⃗B. ∇2E⃗⃗+μεð2E⃗⃗ðt2=μðJ⃗ðt+∇∙ρε;∇2H⃗⃗+μεð2H⃗⃗ðt2=∇×J⃗C. ∇2E⃗⃗−μεð2E⃗⃗ðt2=μðJ⃗ðt−∇∙ρε;∇2H⃗⃗−μεð2H⃗⃗ðt2=∇∙J⃗D. ∇2E⃗⃗+μεð2E⃗⃗ðt2=μðJ⃗ðt−∇∙ρε;∇2H⃗⃗+μεð2H⃗⃗ðt2=∇∙J⃗9.空间区域中电磁能守恒的坡印廷定理为:()A. −ddt ∫wdVV=∫J⃗∙VE⃗⃗dV+∮S⃗∙dS S⃗⃗⃗⃗S SB. ddt ∫wdVV=∫J⃗∙VE⃗⃗dV−∮S⃗∙dS S⃗⃗⃗⃗S SC. ddt ∫wdVV=∫J⃗∙VE⃗⃗dV+∮S⃗∙dS S⃗⃗⃗⃗S SD. −ddt ∫wdVV=∫J⃗∙VE⃗⃗dV−∮S⃗∙dS S⃗⃗⃗⃗S S10.均匀平面波在两种媒质都为理想介质中传播时,其反射系数和透射系数为:()A. Γ=E rmE im =η2−η1η2+η1;τ=E tmE im=1+Γ=2η2η2+η1B. Γ=E rmE im =η2+η1η2−η1;τ=E tmE im=1+Γ=2η2η2+η1C. Γ=E rmE im =η2−η1η2+η1;τ=E tmE im=1+Γ=2η2η2−η1D. Γ=E rmE im =η2+η1η2−η1;τ=E tmE im=1+Γ=2η2η2−η111.计算:e n⃗⃗⃗⃗⃗(A⃗⃗∙B⃗⃗)+ A⃗×B⃗⃗=( )A. e n⃗⃗⃗⃗⃗A⃗B⃗⃗(cosθ−sinθ)B. e n⃗⃗⃗⃗⃗A⃗B⃗⃗(cosθ+sinθ)C. e n⃗⃗⃗⃗⃗AB(cosθ+sinθ)D. e n⃗⃗⃗⃗⃗AB(cos θ−sin θ) 12. 计算:∫∇∙F ⃗dV V +∫∇×F ⃗∙dS ⃗S = (A ) A .∮F ⃗∙dS ⃗+∮F ⃗∙dl ⃗C S B .∮F ⃗×dS ⃗+∮F ⃗×dl ⃗C S C .∮∇×F ⃗∙dS ⃗S D .∮∇×F ⃗∙dl ⃗c13.真空中库伦定律的公式,正确的是:( B )A.E r ⃗⃗⃗⃗⃗=12πε0∫ρS R ⃗⃗⃗R 3dS S B.E r ⃗⃗⃗⃗⃗=14πε0∫ρl R⃗⃗⃗R 3dl l C.E r ⃗⃗⃗⃗⃗=14πε0∫ρR ⃗⃗⃗R 2dV V D. E r ⃗⃗⃗⃗⃗=12πε0∫ρR⃗⃗⃗R 3dV V 14.从宏观效应来分析,在电磁场的作用下,媒质会发生极化、磁化和传导三种现象,对应媒质的三种特性的参数分别是: ( A ) A.介电系数ε、磁导率μ、电导率σ B.介电系数σ、磁导率ε、电导率μ C.介电系数μ、磁导率σ、电导率ε D.介电系数μ、磁导率ε、电导率σ15.静电场中,对于点电荷、线电荷、面电荷、体电荷,电位函数与求解公式正确的是:( A )A. φ=14πε∑qiR in i=1+cB. φ=14πε∫ρl dl R 2l +cC. φ=14πε∫ρS dS R 2S+cD. φ=14πε∫ρ dV R 2V+c16.由电流元Idl ⃗产生的恒定磁场,其矢量磁位的公式正确的是:( B ) A. A ⃗=μ4π∫Idl ⃗R 2l +C ⃗ B. A ⃗=μ4π∫Idl ⃗Rl +C ⃗; C.A⃗=μ2π∫Idl⃗R 2 l +C ⃗D. A⃗=μ2π∫Idl⃗Rl +C⃗; 17. 设点电荷2q 在直角坐标系中(0,0,h )处,在z=0处有无限大接地导体,两者组成系统中,在z >0处的电位函数为:( ) A.φ=q2πε[√x 2+y 2+(z−h)2−√x 2+y 2+(z+h)2] B.φ=q 4πε[222−222] C.φ=q2πε[222−222] D.φ=q4πε[222−222]18.无界空间里为线性及各向同性材料,电磁波传播满足的波动方程为:( )A. ∇2E⃗⃗−μεð2E⃗⃗ðt2=μðJ⃗ðt+1ε∇ρ∇2H⃗⃗−μεð2H⃗⃗ðt2=∇×j⃗B.∇2E⃗⃗+μεð2E⃗⃗ðt2=μðJ⃗ðt+1ε∇ρ∇2H⃗⃗+μεð2H⃗⃗ðt2=∇×j⃗C.∇2E⃗⃗−μεð2E⃗⃗ðt2=μðJ⃗ðt−1ε∇ρ∇2H⃗⃗−μεð2H⃗⃗ðt2=∇×j⃗D.∇2E⃗⃗+μεð2E⃗⃗ðt2=μðJ⃗ðt−1ε∇ρ∇2H⃗⃗+μεð2H⃗⃗ðt2=∇×j⃗19.无界空间里媒质为线性及各向同性材料,电磁波传播满足的达朗贝尔方程为:( A)A. ∇2A⃗−μεð2A⃗ðt2=−μJ⃗ ; ∇2φ−μεð2φðt2=−ρεB.∇2A⃗−μεð2A⃗ðt2=μJ⃗ ; ∇2φ−μεð2φðt2=ρεC.∇2A⃗+μεð2A⃗ðt2=−μJ⃗ ; ∇2φ+μεð2φðt2=−ρεD. ∇2A⃗+μεð2A⃗ðt2=μJ⃗ ; ∇2φ+μεð2φðt2=ρε20. E⃗⃗⃗=e x⃗⃗⃗⃗⃗E xm cos(ωt−kz+ϕx)+e y⃗⃗⃗⃗⃗E ym sin(ωt−kz+ϕy)复矢量:(A)A. E m=e x⃗⃗⃗⃗⃗E xm e j(−kz+ϕz)+e y⃗⃗⃗⃗⃗E ym e j(−kz+ϕy−π2)B. E m=e x⃗⃗⃗⃗⃗E xm e j(−kz+ϕz)+e y⃗⃗⃗⃗⃗E ym e j(−kz+ϕy+π2)C. E m=e x⃗⃗⃗⃗⃗E xm e j(−kz−ϕz)+e y⃗⃗⃗⃗⃗E ym e j(−kz−ϕy)D. E m=e x⃗⃗⃗⃗⃗E xm e j(−kz−ϕz)+e y⃗⃗⃗⃗⃗E ym e j(−kz−ϕy)二、填空题1.矢量函数A⃗⃗通量的密度称为散变 ,即div A⃗⃗= ;2.自由电荷在其周边空间中形成的电场称为电磁场,为无旋场;恒定电流在其周边空间形成的磁场称为恒定磁场,为无散场。
电磁波与电磁场期末复习题(试题+答案)

电磁波与电磁场期末试题一、填空题(20分)1.旋度矢量的散度恒等与零,梯度矢量的旋度恒等与零。
2.在理想导体与介质分界面上,法线矢量n 由理想导体2指向介质1,则磁场满足的边界条件:01=⋅B n ,s J H n =⨯1 。
3.在静电场中,导体表面的电荷密度σ与导体外的电位函数ϕ满足的关系式n ∂∂=ϕεσ-。
4.极化介质体积内的束缚电荷密度σ与极化强度P 之间的关系式为P ⋅-∇=σ。
5.在解析法求解静态场的边值问题中,分离变量法是求解拉普拉斯方程的最基本方法;在某些特定情况下,还可用镜像法求拉普拉斯方程的特解。
6.若密绕的线圈匝数为N ,则产生的磁通为单匝时的N 倍,其自感为单匝的2N 倍。
7.麦克斯韦关于位移电流的假说反映出变化的电场要产生磁场。
8.表征时变场中电磁能量的守恒关系是坡印廷定理。
9.如果将导波装置的两端短路,使电磁波在两端来回反射以产生振荡的装置称为谐振腔。
10.写出下列两种情况下,介电常数为ε的均匀无界媒质中电场强度的量值随距离r 的变化规律:带电金属球(带电荷量为Q)E =24rQπε;无限长线电荷(电荷线密度为λ)E =rπελ2。
11.电介质的极性分子在无外电场作用下,所有正、负电荷的作用中心不相重合,而形成电偶极子,但由于电偶极矩方向不规则,电偶极矩的矢量和为零。
在外电场作用下,极性分子的电矩发生转向,使电偶极矩的矢量和不再为零,而产生极化。
12.根据场的唯一性定理在静态场的边值问题中,只要满足给定的边界条件,则泊松方程或拉普拉斯方程的解是唯一的。
二、判断题(每空2分,共10分)1.应用分离变量法求解电、磁场问题时,要求整个场域内媒质必须是均匀、线性的。
(×)2.一个点电荷Q 放在球形高斯面中心处。
如果此电荷被移开原来的球心,但仍在球内,则通过这个球面的电通量将会改变。
(×)3.在线性磁介质中,由IL ψ= 的关系可知,电感系数不仅与导线的几何尺寸、材料特性有关,还与通过线圈的电流有关。
电磁场与电磁波-试卷A

分
六、如图2所示,同轴线的内导体半径为a,外导体的内半径为b,其间填充均应的理想介质。设内外导体间外加缓变电压为 ,导体中流过缓变电流为 。(1)在导体为理想导体的情况下,计算同轴线中传输的平均功率;(2)当导体的电导率 为有限值时,定性分析对传输线功率的影响。(15分)
得
分
四、空气中传播的均匀平面波的电场强度 。求
(1)电磁波的传播方向;
(2)此平面波的波长 和频率 ;
(3)电磁波的磁场强度 ;
(4)当此电磁波入射到Z=0处的无限大理想导体平面时,求导体表面上的电流密度 。(15分)
得
分
五、已知无源的自由空间中,电磁场的电场强度复矢量为 ,其中k和E0为常数。求:(1)磁场强度复矢量 ;(2)瞬时坡印廷矢量 ;(3)平均坡印廷矢量 。(15分)
课程考试试题纸
课程名称:
电磁场与电磁波
(A卷)
考试方式:
闭卷
学院:
物理系与电子技术学院
任课教师:
周海
专业年级:
2010级电子科学与技术、微电子、通信工程、电子信息专业
题
号
一
二
三
四
五
六
七
八
总分
阅卷
教师
得
分
……………………………………………………………………………………………………
得
分
一、填空题(每小题4分,共20分)
1.已知三角形的三个顶点分别为P1(0, 2,2)、P2(0, 4,2)和P3(0, 2,8),其三角形的面积为。
2.已知标量函数u=xyz,则u在点p(1,3,1)处的梯度为,u在p处沿着方向 的方向导数为。
3.已知磁感应强度 ,则m的值为。
《电磁场与电磁波》期末考试参考题

1、一半径为a 的均匀带电圆环,电荷总量为q ,求圆环轴线上离环中心o 点为z 处的电场强度E。
解:设圆环电荷线密度为λ,再在圆环上任取微元dl ,则dl dq λ=∴圆环上点电荷元dq 在p 处产生的电场强度为204RdqE d πε=根据对称性原理可,整个圆环在p 点产生的场强为沿轴线方向分量之和,即()232202044cos za dl z RzR dq E d E d z +===πελπεθ∴ ()⎰+=lz dl za z E 232204πελ又a dl lπ2=⎰ λπa q 2=∴ ()232204za zq E z +=πε2、在介电常数为ε的无限大约均匀介质中,有一半径为a 的带电q 的导体球,求储存在介质中的静电能量。
解:导体在空间各点产生的电场为)(4)0(02a r r q E a r E r w >=<<=πε故静电能量为a q dr r r q dV E dV E D W V V πεππεεε844212121202222=⎪⎭⎫ ⎝⎛==•=⎰⎰⎰∞ 3、一电荷面密度为σ的“无限大”平面,在距离平面a 的一点的场强大小的一半是由平面上的一个半径为R 的圆面积范围内的电荷所产生。
圆半径的大小。
解:电荷面密度为σ的“无限大”平面,在其周围任意点的场强为:2εσ=E 以图中O 点为圆心,取半径为r 的环形圆,其电量为:rdr dq πσ2=它在距离平面为a 的一点处产生的场强为:()2/32202ra ardrdE +=εσ则半径为R 的圆面积内的电荷在该点的场强为:()⎪⎪⎭⎫⎝⎛+-=+=⎰22002/322122R a a r ardra E Rεσεσ 0220412εσεσ=⎪⎪⎭⎫ ⎝⎛+-R a a∴ a R 3=4、已知两半径分别为a 和)(a b b >的同轴圆柱构成的电容器,其电位差为V 。
试证:将半径分别为a 和b ,介电常数为ε的介质管拉进电容器时,拉力为abV F ln )(20εεπ-=证明:内外导体间的电场为ab r V E r ln=插入介质管后的能量变化为a b zV dz dr r a b r B dV E W z b a v ln )(ln 2)(21)(21200222020εεππεεεε-=⎪⎭⎫ ⎝⎛-=-=⎰⎰⎰ 式中z 为介质管拉进电容器内的长度。
2010期末考试标准试卷A卷标准答案和评分标准-推荐下载
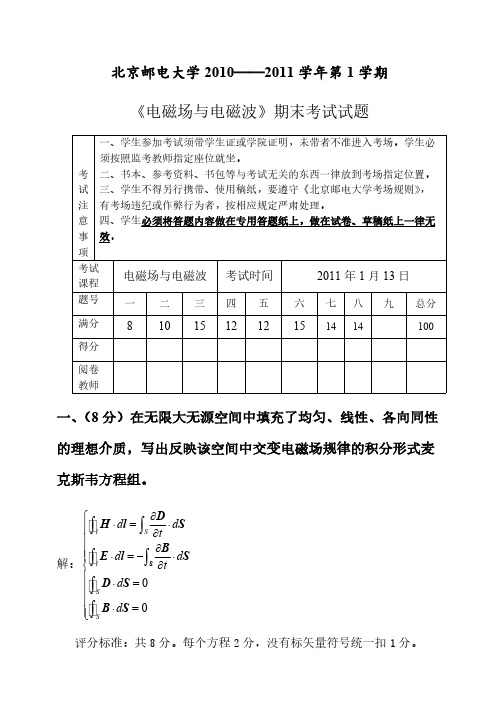
注 有考场违纪或作弊行为者,按相应规定严肃处理。
意 四、学生必须将答题内容做在专用答题纸上,做在试卷、草稿纸上一律无
事 效。
项
考试
电磁场与电磁波 考试时间
课程
题号 一 二 三 四 五 六 七 八 九 总分
满分 8 10 15 12 12 15 14 14
得分
阅卷 教师
一、(8 分)在无限大无源空间中填充了均匀、线性、各向同性
? 100 ,此频率下铝可视作良导体。
1
厨房中常用的薄膜铝皮厚度完全可以。 评分标准:共 10 分。判断为良导体,3 分;计算出趋肤深度,3 分;
所需铝皮厚度,2 分;最后结论,2 分。
三、(15 分)已知某理想介质( 0 )中均匀平面波电场为
E 3102 ex 2ey Ez0ez cos 30 108 t 4 3x 2 y z V/m,
评分标准:共 5 分。公式 3 分,答案 2 分。 5.
H
1
= 120 1.5
24 14
ek
E
103 (12ex
1 14
(3ex
22ey
2ey
2
4ez
2.25
ez
评分标准:共 5 分。公式 2 分,答案 2 分,单位 1 分。
)
3 102
)cos 30
3.
H
H
H
H
(
z,
2
H
t
ez
ez
)
E0
+
2
(完整word版)电磁场与电磁波期末复习题库

物理与电信工程学院《电磁场与电磁波》 期末复习题库一,单项选择题1.电磁波的极化特色由__ B ___决定。
A. 磁场强度B.电场强度C. 电场强度和磁场强度D. 矢量磁位2.下述对于介质中静电场的基本方程不正确的选项是__ D ___E dlE dS qDE 0SA.B.C.?CD.?r3. 一半径为 a 的圆环(环面法向矢量 ne z)经过电流 I ,则圆环中心处的磁感觉强度 B 为__ D ___0 Ie rB. 0 IeC. 0 Ie zD.0 Ie zA.2a 2a 2a 2 a 4. 以下对于电力线的描绘正确的选项是__ D ___A. 是表示电子在电场中运动的轨迹B. 只好表示 E 的方向,不可以表示 E 的大小C. 曲线上各点 E 的量值是恒定的D.既能表示 E 的方向,又能表示 E 的大小5.B 0 说明 __ A ___A. 磁场是无旋场B. 磁场是无散场C. 空间不存在电流D.以上都不是6.以下对于交变电磁场描绘正确的选项是__ C ___A. 电场和磁场振幅同样,方向不同样样B.电场和磁场振幅不同样样,方向同样 C. 电场和磁场各处正交D.电场和磁场振幅同样,方向也同样7.对于时变电磁场的表达中,不正确的选项是:( D )A. 电场是有旋场B. 电场和磁场互相激发C. 电荷可以激发电场D.磁场是有源场8. 以下对于在导电媒质中流传的电磁波的表达中,正确的选项是__B ___A. 不再是平面波B. 电场和磁场不同样样相C.振幅不变D.以TE波形式流传9.两个载流线圈之间存在互感,对互感没有影响的是_C ____A. 线圈的尺寸B.两个线圈的相对地点C.线圈上的电流D.空间介质10.用镜像法求解静电场边值问题时,判断镜像电荷的采纳能否正确的依据__C___A.镜像电荷能否对称B. 电位所知足的方程能否改变C.界限条件能否保持不变D.同时选择B和C11.地区V所有所适用非导电媒质填补,当此地区中的电磁场能量减少时,必定是_ A___A.能量流出了地区B. 能量在地区中被耗资C.电磁场做了功D.同时选择A和C12.磁感觉强度为rr(32)r r, 试确立常数 a 的值。
电磁场与电磁波期末试卷A卷答案

电磁场与电磁波期末试卷A卷答案淮海工学院10 - 11 学年第 2 学期电磁场与电磁波期末试卷(A 闭卷)答案及评分标准题号一二三四五1 五2 五3 五4 总分核分人分值 10 30 10 10 10 10 10 10 100得分1.任一矢量A r的旋度的散度一定等于零。
(√ )2.任一无旋场一定可以表示为一个标量场的梯度。
(√ )3.在两种介质形成的边界上,磁通密度的法向分量是不连续的。
(× )4.恒定电流场是一个无散场。
(√ )5.电磁波的波长描述相位随空间的变化特性。
(√ ) 6.在两介质边界上,若不存在自由电荷,电通密度的法向分量总是连续的。
(√) 7.对任意频率的电磁波,海水均可视为良导体。
(× ) 8.全天候雷达使用的是线极化电磁波。
(× )9.均匀平面波在导电媒质中传播时,电磁场的振幅将随着传播距离的增加而按指数规律衰减。
(√ )10.不仅电流可以产生磁场,变化的电场也可以产生磁场。
(√ )二、单项选择题(本大题共10小题,每题3分,共30分) 1.设点电荷位于金属直角劈上方,如图所示,则镜像电荷和其所在的位置为[ A ]。
A 、-q(-1,2,0);q(-1,-2,0) ;-q(1,-2,0)B 、q(-1,2,0);q(-1,-2,0); q(1,-2,0)C 、q(-1,2,0);-q(-1,-2,0); q(1,-2,0);D 、-q(-1,2,0);q(-1,-2,0); q(1,-2,0)。
2.用镜像法求解静电场边值问题时,判断镜像电荷设置是否正确的依据是[ C ]。
A 、镜像电荷的位置是否与原电荷对称;B 、镜像电荷是否与原电荷等值异号;C 、待求区域内的电位函数所满足的方程与边界条件是否保持不变;D 、镜像电荷的数量是否等于原电荷的数量。
3.已知真空中均匀平面波的电场强度复矢量为2π()120 (V/m)j z E z e e π-=x r r则其磁场强度的复矢量为[ A ]A 、2π=(/)j z y H e e A m -r r ;B 、2π=(/)j z y H e e A m r r; C 、2π=(/)j z x H e e A m -r r ; D 、2π=-(/)j z y H e eA m -r r 4.空气(介电常数为10εε=)与电介质(介电常数为204εε=)的分界面是0z =的平面。
《电磁场与电磁波》2010试题+部分答案

《电磁场与电磁波》试题1填空题(每小题1分,共10分)1.在均匀各向同性线性媒质中,设媒质的导磁率为μ,则磁感应强度B 和磁场H 满足的方程为: B=uH 。
2.设线性各向同性的均匀媒质中,02=∇φ称为 拉普拉斯 方程。
3.时变电磁场中,数学表达式H E S ⨯=称为 坡印廷矢量(电磁能流密度矢量) 。
4.在理想导体的表面,电场的切向分量等于零。
5.矢量场)(r A 穿过闭合曲面S 的通量的表达式为: ()S d r A S ⋅⎰ 。
6.电磁波从一种媒质入射到理想 导体 表面时,电磁波将发生全反射。
7.静电场是无旋场,故电场强度沿任一条闭合路径的积分等于 0 。
8.如果两个不等于零的矢量的 点乘 等于零,则此两个矢量必然相互垂直。
9.对平面电磁波而言,其电场、磁场和波的传播方向三者符合 右手螺旋 关系。
10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是无散场,因此,它可用 磁矢位 A函数的旋度来表示。
二、简述题 (每小题5分,共20分)11.已知麦克斯韦第二方程为t B E ∂∂-=⨯∇ ,试说明其物理意义,并写出方程的积分形式。
12.试简述唯一性定理,并说明其意义。
答:在静电场中,在给定的边界条件下,拉普拉斯方程或泊松方程的解是唯一的,这一定理称为唯一性定理。
它的意义:给出了定解的充要条件:既满足方程又满足边界条件的解是正确的14.写出位移电流的表达式,它的提出有何意义? .答:位移电流:tD J d ∂∂= 位移电流产生磁效应代表了变化的电场能够产生磁场,使麦克斯韦能够预言电磁场以波的形式传播,为现代通信打下理论基础。
三、计算题 (每小题10分,共30分)15.按要求完成下列题目(1)判断矢量函数y x e xz e y B ˆˆ2+-= 是否是某区域的磁通量密度?(2)如果是,求相应的电流分布。
17.在无源的自由空间中,电场强度复矢量的表达式为()jkz y x e E e E e E --=004ˆ3ˆ(1) 试写出其时间表达式;(2) 说明电磁波的传播方向;四、应用题 (每小题10分,共30分)18.均匀带电导体球,半径为a ,带电量为Q 。
《电磁场与电磁波》2010期末考试试卷一

长沙理工大学考试试卷一………………………………………………………………………………………………………课程名称(含档次) 《电磁场与电磁波A 》 课程代号 002587专业 电信、光电 层次(本部、城南) 本部 考试方式(开、闭卷) 闭卷一、选择题(5小题,共15分)(3分)[1] 比较位移电流与传导电流,下列陈述中,不正确的是: A. 位移电流与传导电流一样,也是电荷的定向运动 B. 位移电流与传导电流一样,也能产生涡旋磁场C. 位移电流与传导电不同,它不产生焦耳热损耗(3分)[2] 恒定电流场中,不同导电媒质交界面上自由电荷面密度0σ=的条件是 A 、1122γεγε>B 、1122γεγε=C 、1122γεγε<(3分)[3] 已知电磁波的电场强度为)sin()cos(),(z t e z t e t z E y x βωβω---=,则该电磁波为A 、左旋圆极化波B 、右旋圆极化波C 、椭圆极化波(3分)[4] xOz 平面为两种媒质的分界面,已知分界面处z y x e e e H26101++=,z y e e H242+=,则分界面上有电流线密度为:A 、z S e J 10=B 、z x S e e J 410+=C 、z S e J 10-=(3分)[5] 若介质1为理想介质,其介电常数102εε=,磁导率10μμ=,电导率10γ=;介质2为空气。
平面电磁波由介质1向分界平面上斜入射,入射波电场强度与入射面平行,若入射角/4θπ=,则介质2 ( 空气) 中折射波的折射角'θ为 A 、/4π B 、/2π C 、/3π二、填空题(5小题,共20分)(4分)[1] 恒定磁场中不同媒质分界面处, H 与B 满足的边界条件是:( ), ( ) 或( ),( )。
(4分)[2] 静电比拟是指( ), 静电场和恒定电流场进行静电比拟时,其对应物理量间的比似关系是( )。
电磁场与电磁波 复习 试卷(A)参考答案

《电磁场与电磁波》试卷(A)
常熟理工学院
试题参考答案及评分标准
一、填充题: (共 16 分)
1、 A ⋅ B = 5,
A × B = −11ex − ey + 7 ez ;[2 分]
2、库仑定律,毕—萨定律,电磁感应定律;[各 1 分 共 3 分] 3、 n × ( H 2 − H 1 ) = J , n ⋅ ( B2 − B1 ) = 0 4、相等, ±π 2 5、 z , 15 × 108 Hz , 0.2m , y 线极化 [1 分,2 分,1 分,1 分。共 5 分] 6、 r [1 分,2 分]
µ0 a 4
r
(
4
+
2a 2 )eϕ 3
[2 分] [共 12 分]
3、[解] 根据镜像法原理,在下半空间对称的位置 −h 放一点电荷 −Q ,取图示坐标系。这样满足 无限大的 xy 平面上的点位都等于零。根据叠加原理: (1)
ϕ ( x, y, z) =
Q 1 1 − 2 2 2 4πε 0 x + y + ( z − h)2 x2 + 2 试题参考答案及评分标准 y + ( z + h)
µε 。[2 分]
二、选择题(每题 2 分,共 12 分)
1、C; 2、A; 3、D; 4、D; 5、C; 6、B。
三、问答题: (每题 5 分,共 10 分)
1、[答] 如区域 V 内给定自由电荷分布 ρ ,在 V 的边界上给定电势或电势的法向导数,则 V 内的电 场唯一确定。 分]唯一性定理提出了定解的充分必要条件, [2 求解时可首先判断问题的边界条件是否足 够,[1 分]当满足必要的边界条件时,则可断定解必定是唯一的。用不同的方法得到的形式上不同的解 必定等价的。[1 分]还启示我们只要能找出一个满足边界条件的位函数,则就是我们所要求的解。[1 分] 2、[答] 位移电流 J D = ∂ D 是由电场的变化而产生,是麦克斯韦为了对环路定律的推广而进行的假 ∂t 设,它于同样的规律产生磁场,但不会产生热效应。[2 分]传导电流由电荷运动产生,在导电媒介中存
电磁场与波期末考试试题3套含答案(大学期末复习资料)

莆田学院期末考试试卷 (A )卷2011 — 2012 学年第 一 学期课程名称: 电磁场与波 适用年级/专业: 09/电信 试卷类别 开卷( ) 闭卷(√) 学历层次 本科 考试用时 120分钟《.考生注意:答案要全部抄到答题纸上,做在试卷上不给分.........................》.一、填空题(每空2分,共30分)1.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ① ,矢量B A ⋅= ② 。
2.高斯散度定理的积分式为 ① ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
3.已知任意一个矢量场A ,则其旋度的散度为 ① 。
4.介质中恒定磁场的基本方程的积分式为 ① , ② , ③ 。
5.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ① ,位置位于 ② ;当点电荷q 向无限远处运动时,其镜像电荷向 ③ 运动。
6.标量场2),,(x xyz z y x +=ψ通过点P(1,1,2)的梯度为① 。
7.引入位移电流的概念后,麦克斯韦对安培环路定律做了修正,其修正后的微分式是 ① ,其物理含义是: ② 。
8.自由空间传播的电磁波,其磁场强度)sin(z t H a H m y βω-=,则此电磁波的传播方向是 ① ,磁场强度复数形式为 ② 。
二、单项选择题(每小题2分,共20分)1.自由空间中的平行双线传输线,导线半径为a ,线间距为D ,则传输线单位长度的电容为 。
A .)ln(1aaD C -=πε B. )ln(201aa D C -=πε C. )ln(2101a a D C -=πε2.如果某一点的电场强度为零,则该点的电位为 。
A.一定为零 B.不一定为零 C.为无穷大3.真空中一个电流元在某点产生的磁感应强度dB 随该点到电流元距离变化的规律为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、简答题(30分)1.写出静电场的电位泊松方程,并给出其两种理想介质分界面的边界条件。
2ρϕε∇=-;在两种完纯介质分界面上电位满足的边界条件:12ϕϕ=1212sn nϕϕεερ∂∂-=-∂∂ 2.讨论均匀平面波在无界空间传播时本征阻抗与波阻抗的区别。
3.写出均匀平面波在无界良导体中传播时相速的表达式。
4.写出时谐电磁场条件下亥姆霍兹方程。
5.写出传输线输入阻抗公式。
6.证明电场矢量和磁场矢量垂直。
证明:任意的时变场(静态场是时变场的特例)在一定条件下都可以通过Fourier展开为不同频率正弦场的叠加。
垂直。
也与垂直与垂直。
与乘定义,可知根据E H H X∴=⨯-=⨯-∂∂-=⨯∇B B E BE k B j E k j tB E ωω7.写出线性各向同性的电介质、磁介质和导电介质的本构关系式。
EJ HB ED σμε=== 8.写出均匀平面波在两介质分界面的发射系数和投射系数表达式。
9.写出对称天线的归一化方向函数。
10.解释TEM 、TE 、TM 波的含义。
二、计算题1. (10分)已知矢量222()()(2)x y z x axz xy by z z czx xyz =++++-+-E e e e ,试确21212212rm im tm im E E E E ηηηηητηη-Γ==+==+定常数a 、b 、c 使E 为无源场。
解 由(2)(2)(122)0x az xy b z cx xy ∇=++++-+-= E ,得2,1,2a b c ==-=-2.已知标量函数22223326u x y z x y z =+++--。
(1)求u ∇;(2)在哪些点上u ∇等于零。
解 (1)(23)(42)(66)xy z x y z u u uu x y z x y z∂∂∂∇=++=++-+-∂∂∂e e e e e e ; (2)由(23)(42)(66)0x y z u x y z ∇=++-+-=e e e ,得32,12,1x y z =-==3. 两块很大的平行导体板,板间距离为d ,且d 比极板的长和宽都小得多。
两板接上直流电压为U 的电源充电后又断开电源,然后在板间放入一块均匀介质板,它的相对介电常数为9r ε= ,厚度比d 略小一点,留下一小空气隙,如图所示。
试求放入介质板前后,平行导体板间各处的电场强度。
并由此讨论电介质的作用。
(20分)解:(1)建立坐标系如图。
加入介质板前,因两极板已充电,板间电压为U ,间距d 远小于平板尺寸,可以认为极板间电场均匀,方向与极板垂直。
所以板间电场为0zU d=-E e 设两极板上所带自由电荷面密度分别为s ρ和s ρ-,根据高斯定理sss d d Q S ερ===∆⎰⎰D S E S即000s D E S S ερ=∆=∆得0000s UD E dερε=== r ε=d Uz(2)加入介质板后,因充电后电源断开,所以极板上的自由电荷面密度保持不变。
应用高斯定理,可求得极板间任一点的电位移矢量z z s z U D dρε=-=-=-D e e e 根据ε=D E 的关系得空气隙中的电场强度为10zU dε==-DE e 电介质中的电场强度2019zz r DU dεεε==-=-⋅DE e e 可见空气隙中的电场强度与未加介质板前相同,而介质板中的电场强度却只有未加介质板前场强的1/9。
4 .求下列情况下的位移电流密度的大小:某移动天线发射的电磁波的磁场强度()80.15cos 9.3610 3.12A/m x t y =⨯-H e ;由t∂∇⨯=∂D H 得 ()()88200.15cos 9.3610 3.120.468sin 9.3610 3.12A/m xy zx d z x zz H t xy z y H t y y t y ∂∂∂∂∂==∇⨯==-=∂∂∂∂∂∂⎡⎤-⨯-=⎣⎦∂-⨯-e e e D J H e e e故20.468A/m d =J5. 无限长线电荷通过点(6,8,0)且平行于z 轴,线电荷密度为l ρ;试求点P (x ,y ,z )处的电场强度E 。
解 线电荷沿z 方向为无限长,故电场分布与z 无关。
设点P 位于z =0平面上,如题2.9图所示,线电荷与点P 的距离矢量为()()()()()()()()222268686868x y x y R x y x y x y x y =-+-=-+--+-==-+-R e e R e e R e R根据高斯定律得点P 处的电场强度为()()()()220006822268x y l l l R x y x y ρρρπεπεπε-+-==⋅=⋅-+-e e RE e R R R6.如图所示的平行双线传输线,导线的半径为a ,两导线的轴线相距为D ,且D >>a 。
试求传输线单位长度的电容。
由于D>>a ,近似认为电荷均匀分布在导体表面,且可将导线看成线电荷,则利用高斯定理得x 轴上的电场分布7.求半径为a 的金属导体球形接地器的接地电阻。
土壤的电导率为σ。
yρlxPx Da-ρl()0112l x x x D x ρπε⎛⎫=+ ⎪-⎝⎭E e ()0011ln 2D a D a l l x a a D a U x dx dx x D x a ρρπεπε---⎛⎫==+= ⎪-⎝⎭⎰⎰E e 两导线间的电位差为00ln ln l l C D a D Ua aρπεπε==≈-两导线间单位长度 的电容为解:导体深埋,不考虑地表对接地电阻的影响8.自由空间中的电磁场为0(,)100cos()V m x z t t kz ω=-E e (,) 2.65cos()A m y z t t kz ω=-H e式中000.42rad m k ωμε==。
求:(1)瞬时坡印廷矢量; (2)平均坡印廷矢量;解 (1)瞬时坡印廷矢量22650cos ()z t kz ω=⨯=-S E H e 2W m(2)平均坡印廷矢量2202650cos ()d 13252av z z t kz t πωωωπ=-=⎰S e e 2W m 9.在半径为a 、电导率为σ的无限长直圆柱导线中,沿轴向通以均匀分布的恒定电流I ,且导线表面上有均匀分布的电荷面密度S ρ。
求导线表面外侧的坡印廷矢量S 。
解:当导线的电导率σ为有限值时,导线内部存在沿电流方向的电场IaσJ 22444r r aI I IU d r r aππσπσ∞⇒⇒====⎰J e E e E r 144U R G a I aπσπσ=⇒⇒==i E 2zIa σπσ==Je 根据边界条件,在导线表面上电场的切向分量连续,即iz E oz E =。
因此,在导线表面外侧的电场的切向分量为2ozaIE a ρπσ==又利用高斯定理,容易求得导线表面外侧的电场的法向分量为So aE ρρρε==故导线表面外侧的电场为20S oz aI a ρρρεπσ==+E e e 利用安培环路定理,可求得导线表面外侧的磁场为2oaI aφρπ==H e故导线表面外侧的坡印廷矢量为2230()22S oo o z aaI I a aρρρρπσπε===⨯=-+S E H e e 2W m10.已知土壤相对介电常数εr =10,电导率σ =10-2S/m ,磁导率μ =μ0=4π×10-7H/m 。
f =100MHz 的均匀平面波在其中传播时,如其电场为E (z,t )=ex 0.2e -αz cos(ωt- βz ) (V/m),试计算传播常数、相速、本征阻抗和平均功率密度。
11.已知平面波的电场jkz m y jkzm x e E e j eE e z E --+= )(,说明它的极化形式。
12.已知平面波的电场jkzmy jkz m x e E e e E e z E --+= )(,试将其分解为两个振幅相228110.592,11 6.65220.592 6.65,0.9410,117.510.49p ccj j v j μεσμεσαωβωωεωεωμγαβηβε⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥⎢⎥=+-==++= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦=+=+==⨯==+()()22220.592 1.1841Re cos 220.2cos 5.11692118z xm z czzz z E z z e e e αϕη*--⨯-⎡⎤=⨯==⎣⎦==⨯S E H e e e等,旋向相反的圆极化波。
13.一圆极化波自空气中垂直入射于一介质板上,介质板的本征阻抗为η2.入射波电场为 z j m y zj m x e E e j e E e z E ββ--+= )( 。
求反射波与透射波的电场,它们的极化情况如何?20ηηηη-Γ+= τ()j z m m x y E E e e j e β-=Γ+反射波的电场两个分量的振幅相等,相位与入射波相比无变化,故为右旋极化波透射波沿+z 方向传播的左旋圆极化波 14设矩形波导中传输TE10波,求填充介质(介电常数为ε)时的截止频率及波导波长。
解:截止频率:22210g 22221211TE 1,02222112(c cc c m n f a b m n f a a f f ffπππμεππμεμεππλλβωμεπλωμε⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭⎛⎫==∴== ⎪⎝⎭===--=对于波波导波长为无界空间介质中的波长)15.平行双线传输线的线间距D=8cm ,导线的直径d=1cm,周围是空气,试计算分布电感和分布电容;11()2lxe x D x ρπε=+- x E11()ln 2D aD allaa D a U E d l dx x D x a ρρπεπε---=∙=+=-⎰⎰1/ln[()/]ln(/)ln(2/)lC F mU D a a D a D d ρπεπεπε≈=-==C =2D ln16ln dεπεπ==16.横截面为矩形的无限长接地金属导体槽,上部有电位为U0的金属盖板;导体槽的侧壁与盖板间有非常小的间隙以保证相互绝缘,求此导体槽内的电位分布222200(0,)0(0)(,)0(0)(,0)0(0)(,)(0)xy y y b a y y b x x a x b U x a ϕϕϕϕϕϕ∂∂+=∂∂=≤<⎧⎪=≤<⎪⎨=≤≤⎪⎪=≤≤⎩2212222()sin()(0)sin(0)0()sin()0,,1,2,3.()()sin(),0x x x x xx n n n x y y xf x A k x f A k f a A k a n k x n k n an k a n f x A x A a k k k k ππππ∞===========+=⇒=-∑满足边界条件本征值为待定的常数12211001()sinh()cosh()0,(0)00()sinh()(x,y)=sin()sinh(),(x,b)=U U sin()sinh()x x x nn n n g y B k y B k y y g B g y B k y n n C x y a a y b n n C x b a a ππϕϕππ∞=∞==+===⇒===∑∑只能有通解形式:0001sin()U sinh()sin()sin()aa n n m n m n x dx Cb x x dx a a a a ππππ∞==∑⎰⎰00001()()sin()sin()(cos()cos()212(1cos()21()()(cos()cos()2a a a am n m n m n x x dx x x dx a a a a n x dx m n a m n m n x x dx m n a a πππππππ-+=-⎧-=⎪⎪=⎨-+⎪-≠⎪⎩⎰⎰⎰⎰0()()cos()sin()0()1sin()sin()20aaa m n a m n x dx x a m n a a m n m n x x dx a a m nπππππ--==-⎧=⎪=⎨⎪≠⎩⎰⎰()()()20000000020sin()sinh()sin ()sin()cos 11sinh()sin ()sinh 24 1.3.5aa n aanan n n n n n U x dx C b x dxa a aaU U a n n U x dx x a n a n C n n n b C b x dx a a a a U C n ππππππππππ==-=--⎛⎫⎪⎝⎭⇒==⋅⋅⋅⋅⋅⎰⎰⎰⎰=3.(15分)如图。
