第7章方差分析课件说课材料
6 第七章 方差分析(单元)

对数代换实例
剂 X1 量 A1 0.1 A2 4.3
X2 (标准药物)
R 0.12 3.7
lgx1 -1 0.633
lgx2 -0.658 0.903
R 0.342 0.27
0.22 8
A3 7.2
13.8
6.6
0.857
1.14
0.283
data aa; do trt=1 to 3; input x1 x2@@;y1=log10(x1);y2=log10(x2); output; end; cards; 0.1 0.22 4.3 8 7.2 13.8 ; proc print;run;
处理间 k-1 SSt 试验误差 (r-1)(k-1) SSe 总变异 rk-1 SST
MSt MSt/MSe MSe
2 e
2 e
ss总 ss处理间 ss误差
若F显著,则进行多重比较。 依题意写统计结论。例
P90例7.1 有4个水稻的大田比较试验,于成熟期作随机 取样,每品种取6个点,结果如表所列。试比较这4个水 稻品种的产量差异显著性。 水稻品种比较试验产量表 品种 A B C D 各小区产量(斤/区) 64 78 75 55 72 91 93 66 68 97 78 49 77 82 71 64 56 85 63 70 95 77 76 68
7.7 正交设计试验资料
7.1 方差分析概论
Analysis of Variance简称AOV
方差分析是一种最常用的强有力的统计分析 方法,最初是由.A.Fisher(1923)提出。 1.方差分析的功用 解决多个处理的比较问题,充分利用资料 的全部信息,提高分析的精确度。
2、方差分析的条件
方差分析法PPT课件

计算各样本平均数 y 如i 下:
表 6-2
型号
ABCDE F
yi
9.4 5.5 7.9 5.4 7.5 8.8
•5
引言 方差分析的基本概念和原理
两个总体平均值比较的检验法 把样本平均数两两组成对:
y 1与 y ,2 与y 1 ,…y 3 与 y ,1 与y 6 ,…y ,2 与y 3 ,共有y (5
6.3 显著性检验
利用(6-17)式来检验原假设H0是否成立.对于给定的显著水
平,可以从F分布表查出临界值
A的值.
F(k1,k(再m根1)据),样本观测值算出F
当 FAF(k1,时k(m ,拒1绝))H0,
当 FAF(k1,,时k(m ,接1 受))H0。
即:如果H0成立,F应等于1;相反应大于1,而且因素的影响越大, F值也越大
m
km
T Tj Yij
•38
j1
作统计假设:6种型号的生产线平均维修时数无显 著差异,即
H0: i=0(i=1,2,…,6),H1:i不全为零
•37
6.3 显著性检验
计算SA及SE
k
SA
k
m
i1
(Yi
Y)2
Ti2
i1
m
T2 km
k
km
km
Ti2
SE i1
(Yij Yi)2
j1
i1
j1Yij2i1m
m
Ti Yij
j 1
相当于检验假设
H0 : i 0 (i=1,2,…,k) , H1 : αi不全为零
•29
6.3 显著性检验
可以证明当H0为真时,
ST
2
~2(k
第七章 方差分析法 PPT课件

i= 1 j= 1
邋 邋 ? k
k
n
kn
= n (xi.- x..)2 + 2 [(xi.- x..) (xij - xi.)] +
(xij - xi.)2
i= 1
i= 1
j= 1
i= 1 j= 1
2020/7/1
版权所有 BY 统计学课程组
35
离差平方和的自由度与均方
三个平方和的自由度分别是 SST 的自由度为nk-1,nk为全部观察值的个数 SSA的自由度为k-1,其中k为因素水平的个数 SSE 的自由度为nk-k
第七章
方差分析
Analysis of Variance (ANOVA )
2020/7/1
版权所有 BY 统计学课程组
1
学习目标
掌握方差分析中的基本概念; 掌握方差分析的基本思想和原理; 掌握单因素方差分析的方法及应用; 初步了解多重比较方法的应用; 了解双因素方差分析的方法及应用。
2020/7/1
为因素的水平。
2020/7/1
版权所有 BY 统计学课程组
13
7.1.1 方差分析中的几个基本概念
方差分析主要用来研究一个定量因变量与一个 或多个定性自变量的关系
只有一个自变量的方差分析称为单因素方差分 析。
研究多个因素对因变量的影响的方差分析称为 多因素方差分析,其中最简单的情况是双因素 方差分析。
由于方差分析法是通过比较有关方差的大小而 得到结论的,所以在统计中,常常把运用方差 分析法的活动称为方差分析。
方差分析的内容很广泛,既涉及到实验设计的 模式,又关乎数据分析模型中因素效应的性质。 本章在完全随机试验设计下,讨论固定效应模 型方差分析的基本原理与方法,重点介绍单因 素方差分析及两因素方差分析的内容。
方差分析(共66张PPT)

18~岁 21.65 20.66
… … 18.82 16 22.07 8.97
30~岁 27.15 28.58
… … 23.93 16 25.94 8.11
45~60岁 20.28 22.88 … … 26.49 16 25.49 7.19
基本步骤
(1)建立假设,确定检验水准
H0:三个总体均数相等,即三组工作人员的 体重指数总体均数相等
单因素方差分析
例1 在肾缺血再灌注过程的研究中,将36只雄性大鼠随机等分成三组, 分别为正常对照组、肾缺血60分组和肾缺血60分再灌注组,测得 各个体的NO数据见数据文件,试问各组的NO平均水平是否相同?
单因素方差分析
分析:
对于单因素方差分析,其资料在SPSS中的数据结构应当由两 列数据构成,其中一列是观察指标的变量值,另一列是用以表 示分组变量。实际上,几乎所有的统计分析软件,包括SAS, STATA等,都要求方差分析采用这种数据输入形式,这一点也暗 示了方差分析与线性模型间千丝万缕的联系。
H1:三个总体均数不等或不全相等
(2)计算检验统计量F值
变异来源
SS 自由度(df)
MS
F
组间 组内 总变异
143.406 363.86 507.36
2
71.703
8.87
45
8.09
47
(3)确定p值,作出统计推断
,本次F值处于F界值之外,说明组间均方组内 均方比值属于小概率事件,因此拒绝H0,接受 H1,三个总体均数不等或不全相等
分凝血活酶时间有无不同?
方差分析步骤 :
(1)提出检验假设,确定检验水准
H0:μ1=μ2=μ3 H1:μ1,μ2,μ3不全相同 a=
生物统计单因素方差分析PPT课件

i1
i1
j1
i1 j1
2020/4/18
.
16
7.2.2 平方和与自由度的分解
n
其中: (xij xi. ) 0 j 1
所以: k n
k
kn
(x ij x .) .2 n(x i. x .) .2 (x ij x i.)2
i 1j 1
i 1
i 1j 1
上式右边第一项为各处理平均数与总平均数的 离均差平方和与重复数n的乘积 ,反映了重复 n 次的处理间变异 ,称为处理间平方和,记为 SSA,即
若接受H0则不存在处理效应,每个观测值都
是由总平均数加上随机误差构成。若拒绝H0则 存在处理效应,每个观测值是由总平均数、处 理效应及误差三部分构成。
2020/4/18
.
15
7.2.2 平方和与自由度的分解
方差分析的基本思想就是将总的变差分解为构成 总变差的各个部分。对单因素实验,可以将总 平方和(total sum of spuares)做如下分解:
2020/4/18
.
8
7.1.1 方差分析的一般概念
例如,我们打算用一对一对比较的方法检验5 个平均数之间的相等性,共需检验C52=10对。假 设每一对检验接受零假设的概率都是1-a=0.95, 而且这些检验都是独立的,那么10对都接受的概 率是(?)犯Ⅰ型错误的概率(?)。用方差分析 的方法做检验可以防止上述问题的出现。方差分析 的内容很广泛,上面讲到的那种情况是方差分析中 最简单的情况,称为单因素方差分析(one- factor analysis of variance)或者称为一种方式 分组的方差分析(one way classification analysis of variance)。
第7章---方差分析PPT课件
方差分析的基本思想和原理 (两类误差)
1. 随机误差
▪ 因素的同一水平(总体)下,样本各观察值之间
的差异
• 比如,同一行业下不同企业被投诉次数之间的差异
▪ 这பைடு நூலகம்差异可以看成是随机因素的影响,称为
随机误差
2. 系统误差
▪ 因素的不同水平(不同总体)之间观察值的差异
• 比如,不同行业之间的被投诉次数之间的差异
犯第一类错误的概率为,连续作6次检验犯第Ⅰ
类 错 误 的 概 率 增 加 到 1-(1-)6=0.265 , 大 于
0.05。相应的置信水平会降低到0.956=0.735
2. 一般来说,随着增加个体显著性检验的次数,偶然 因素导致差别的可能性也会增加,(并非均值真的 存在差别)
3. 方差分析方法则是同时考虑所有的样本,因此排除 了错误累积的概率,从而避免拒绝一个真实的原假 设
第5页/共90页
由于各种因素的影响,研究所得的数 据呈现波动状。造成波动原因可分成两类:
一类是不可控的随机因素, 另一类是研究中施加的对结果形成影 响的可控因素
第6页/共90页
学习内容
7.1 方差分析引论 7.2 单因素方差分析 7.3 双因素方差分析
第7页/共90页
学习目标
1. 解释方差分析的概念 2. 解释方差分析的基本思想和原理 3. 掌握单因素方差分析的方法及应用 4. 理解多重比较的意义 5. 掌握双因素方差分析的方法及应用 6. 掌握试验设计的基本原理和方法
构造检验的统计量
(计算组间平方和 SSA)
1. 各组平均值 xi (i 1,2,与, 总k ) 平均值 的离x 差
平方和
2. 反映各总体的样本均值之间的差异程度
方差分析课件-PPT

增重表就是选用S-N-K法作均数多重两两比较得结果:
本例按a=0、05水准,将无显著性差异得数归为一类 (Subset for alpha=0、05)。可见
品种5、2、3得样本均数位于同一个子集( Subset )内,说 明品种5、品种2、品种3得样本均数两两之间无显著差异; 品种3、4、1位于同一个Subset内,她们之间无显著差异;而 品种5、2与品种4、1得样本均数有显著差异。
即三组均数间差异极显著,即不同时期切痂对大鼠肝脏 ATP含量有影响。
LSD法多重比较:
“*”显著性标注 两组均数得差
•S-N-K法:本例按0、5水平,将无显著差异得均数归为一类。
•第一组与第三组为一类,无显著差异,它们与第二组之间均数差 异显著。
•LSD与S-N-K法,不同得两两比较法会有不同。
如欲了解就是否达到极显著差异,需要将显著水平框中得 值输入0、01。
例、 为了研究烫伤后不同时间切痂对大鼠肝脏 ATP得影响,现将30只雄性大鼠随机分成3组,每组 10只:A组为烫伤对照组,B组为烫伤后24小时切痂 组,C组为烫伤后96小时切痂组。全部大鼠在烫伤 168小时候处死并测量器肝脏ATP含量,结果如下。 问试验3组大鼠肝脏ATP总数均数就是否相同。
该12个观察值得总得均值为91、5,标准差为34、 48。
上图为品系、剂量间均值得方差分析(F检验)结果
由表中可知,品系得F=23、771,P=0、001<0、01,差异极显著;
剂量得F=33、537,P=0、001<0、01,差异极显著。说明不同品系与 不同雌激素剂量对大鼠子宫得发育均有极显著影响,故有必要进一步对 品系、雌激素剂量两因素不同水平得均值进行多重比较。
第七章方差分析(AnalysisofVariance,ANOVA)

第七章方差分析(Analysis of Variance, ANOVA)7.1 方差分析概述7.2 单因素方差分析7.3 无重复双因素方差分析7.4 可重复双因素方差分析7.5 案例研究7.6 试验设计初步7-17.1 方差分析概述⒈方差分析的概念⒉方差分析中的基本术语⒊ANOVA:对比多个总体的均值⒋方差分析中的基本假定7-27-3方差分析的概念方差分析:通过检验多个总体均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
解决:①A 、B 、C 是否Y 的重要影响因素;②如果为重要影响因素,最优水平?研究系统A B C分类型自变量Y数值型因变量A (a 1,a 2,a 3,…)B (b 1,b 2,b 3,…)C (c 1,c 2,c 3,…)7-4方差分析中的基本术语第1周第9周第14周第2周第7周第16周第4周第12周第17周第5周第10周第13周第3周第8周第18周第6周第11周第15周AB品牌底部中部顶部货架位置因素因素水平实验单元:“一周”响应变量:“每周销售量”处理:品牌—货架位置组合随机安排试验例:一项市场营销研究。
考察品牌和货架位置对咖啡周销售量的影响。
试验单元(experiment unit )、响应变量(responsevariable )、因素(factor )、因素水平(factor level )、处理(treatment )。
ANOVA:对比多个总体的均值佣金固定薪金佣金加固定薪金165120140981151561309022021012611219510713418715523524080总平均样本均值175.00113.29166.17151.48三类报酬构成的推销人员的月销售额(千美元)问题:(1)三种报酬类型销售人员的销售业绩是否存在显著差异?(2)如果存在差异,哪类销售人员的业绩最佳?三个总体的均值是否相等?7-57-6散点图佣金固定薪金佣金+固定薪金50100150200250300分类型自变量销售业绩均值差异分析:(1)同一总体内部的差异(随机差异)?(2)不同总体之间的差异(随机差异+系统差异)?(3)两类差异大小分析?7-71x 2x 3x ()f x x31x 2x 3x ()f x x2 1 H 0为真时,样本均值的抽样分布H 0为假时,样本均值的抽样分布方差分析中的基本假定•基本假定:•(1)每个总体均服从正态分布;•(2)每个总体的方差相等;•(3)来自每一总体的样本都是独立随机样本三个总体均值是否相等?012311::H H 23,,不全相等7.2 单因素方差分析(One-way Analysis of Variance)⒈基本概念与数据结构表⒉ANOVA:k个总体均值的检验⒊ANOVA表:单因素方差分析⒋最佳方案的选择7-87-9基本概念与数据结构研究一个分类型自变量对一个数值型因变量的影响。
方差分析课件PPT精

Source
DF Squares Square F Value Pr > F
GROUP
2 0.4281 0.2141 0.20 0.8198
Error
21 22.4065 1.0670
Corrected Total 23 22.8346
完全随机设计
四.多个样本均数间的两两比较(又称多重比较)
1.多个样本均数间每两个均数的比较 适用于:在研究设计阶段未预先考虑或未预料到,经
某湖水中不同季节氯化物含量测定值(mg/L)
春
夏
秋
冬
22.6
19.1
18.9
19.0
22.8
22.8
13.6
16.9
21.0
24.5
17.2
17.6
16.9
18.0
15.1
14.8
20.0
15.2
16.6
13.1
21.9
18.4
14.2
16.9
21.5
20.1
16.7
16.2
21.2
21.2
19.6
方差分析采用F检验统计量,也称F检验。
2.基本思想
关于记号—— xij表示第 I 组第 j 个样本观察值,
x 表示第i组的均数(= i.
1
x ij
ni j
),
x ( x..)
表示总平均=
x 1
N ij ij
例1 某克山病区测得11例克山病患者与13名健 康人的血磷值(mmol/L)如下,问该地急性 克山病患者与健康人的血磷值是否不同?
i
j
xij
SS总=SS处理+SS区组+SS误差
农学课件方差分析

试验模型属固定模型或随机模型的区别仅在于F 测验和统计推断上,而与自由度、平方和的分解无关。
二、 方差分析的期望均方线性可加模型将每一观察值看作是几个分量的总和。
最简单的情况是平均数μ加随机误差ε。
但平均数μ又可以是另一些分量的总和,对于完全随机设计,各处理观察值数目相等资料而言,即有ij i ij x ετμ++= (k i ,,2,1 =;n j ,,2,1 =)对于ij ε部分的假定已于上节说明,即它是彼此独立的,以零为平均数的正态分布,且不同处理内具有同质的方差。
本节要说明的是关于i τ部分的假定。
固定模型(模型Ⅰ)和随机模型(模型Ⅱ)是由于对效应τ有不同的解释而产生的。
从理论上讲,固定模型是指各个处理的平均效应)(μμτ-=i i 是固定的一个常量,且满足0=∑i τ (或0=i i n τ∑)。
随机模型是指各个处理效应i τ不是一个常量,而是从平均数为零、方差为2τσ的正态总体中得到的一个随机样本的结果。
在实际工作中,我们可以这样理解这两种模型的区别。
例如在田间试验中,若我们的目的仅在于了解某几个特定处理的效应,如要了解水稻新品种的产量或几种密度、几种肥料、几种农药的效应等,则处理效应i τ为固定的处理效应。
换言之,固定模型仅在于了解供试处理范围内处理间的不同效应,其结论是不能推广应用于范围以外的其他处理的。
如果我们的目的不是研究选出供试的那几个处理的效应,而是要对这些处理所属的总体作出推断,例如,为研究东北地区大豆地方品种的生态类型和特性,我们从大量地方品种中随机抽取一部分品种作为代表进行试验,以便通过这部分供试品种的试验结果推论整个东北地区大豆地方品种的情况,这种处理效应便是随机模型的处理效应。
在随机模型中,因为各处理仅是所属总体的随机样本,故总体方差2τσ是重要的研究对象。
由上可知,固定模型和随机模型,在设计思想和统计推断上是明显不同的。
对于固定模型,如进行重复试验,则一定包括同样组别的τ在新试验里,我们的注意力是集中于研究这些τ(效应)的大小上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
什么是方差分析(一个例子)
➢ 某水产研究所为了比较四种不同配合饲料对鱼 的饲喂效果,选取了条件基本相同的鱼20尾, 随机分成四组,投喂不同饲料,经一个月试验 以后,各组鱼的增重结果列于下表。
▪ 四种饲料对鱼的增重效果是否相同
饲料
A1 A2 A3 A4 合计
31.9 24.8 22.1 27.0
鱼的增重 x i j
方差分析的基本思想
➢ 将所有测量值间的总变异按照其变异的来源分 解为多个部份,然后进行比较,评价由某种因 素所引起的变异是否具有统计学意义。
离均差平方和的分解
总变异
组间变异 组内变异
离均差平方和的分解(例子分析)
➢ 共有三种不同的变异
▪ 总变异(Total variation):全部测量值 x i j与总
kn
k
SSe (xij xi)2 (n1)si2
i 1j 1
i 1
e k(n1)
三种“变异”之间的关系
➢ 平方和分解 SST SSt SSe
➢ 自由度分解
T t e
➢ 导Hale Waihona Puke 组内数据不一致的原因 ▪ 随机误差
➢ 导致组间数据不一致的原因 ▪ 处理因素 ▪ 随机误差
One-Factor ANOVA Partitions of Total Variation
Total Variation SST
= Variation Due to Treatment SSB
+
➢ Commonly referred to as:
Sum of Squares Among, or
Sum of Squares Between, or
Sum of Squares Model, or
SSt
k Ti2
i1 n
C
1(155.92 131.42 123.72 139.82)C 5
15283.315169.03114.27
➢ 处理内平方和
SSeSSTSSt 199.67114.2785.40
平方和、自由度计算实例(续2)
➢ 总变异自由度
T nk 1
54119 ➢ 处理间变异自由度
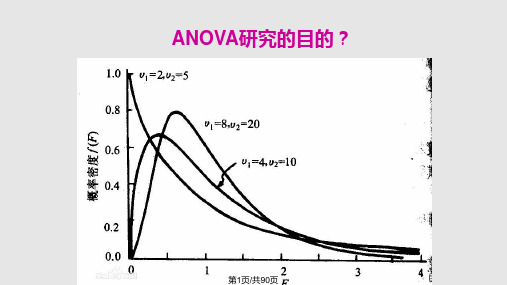
曲线图下,Fa (1 , 2 ) 右方的面积为 a ,则称 Fa (1 , 2 )
为第1自由度为 1 、第2自由度为 2 的F分
Among Groups Variation
Variation Due to Random Sampling SSW
➢ Commonly referred to as: Sum of Squares Within, or Sum of Squares Error, or Within Groups Variation
总变异:所有测量值之间总的变异程度
➢ 计算公式
SST
kn
xij x
2
kn
xi2j
C
i1 j1
i1 j1
nk
xi2j C=(nk1)sT2
i, j
T nk 1
kn
➢ 矫正系数
( xij )2
C i1 j1
T2
nk
nk
组间变异:各组均数与总均数的 离均差平方和
➢ 计算公式
SSt i k1n(xi x)2 i k1Tn i2C
➢ 组间均方和组内均方的计算公式为:
M St
SSt
t
M Se
SSe
e
F 值与F分布
➢ 如果各组样本的总体均数相等( H 0:12 ...k ),
即各处理组的样本来自相同总体,无处理因素的作用, 则组间变异同组内变异一样,只反映随机误差作用的 大小。
➢ 组间均方与组内均方的比值称为F统计量
FMSt MSe
t k 1
SSt反映了各组均数 x i 的变异程度
组间变异=①随机误差+②处理因素效应
组内变异
➢ 在同一处理组内,虽然每个受试对象接受的处 理相同,但测量值仍各不相同,这种变异称为
组内变异,也称SSe。
➢ 用各组内各测量值 x i j 与其所在组的均数差
值的平方和来表示,反映随机误差的影响。
➢ 计算公式
第7章 方差分析 Analysis of Variance
(ANOVA)
Section 7.1
Principle of ANOVA 方差分析的基本原理
什么是方差分析
➢ ANOVA 由英国统计 学家R.A.Fisher首 创,为纪念Fisher 以F命名,故方差 分析又称 F 检验 (F test)。用于 推断多个总体均数 有无差异
均数 x27.54间的差异 ▪ 组间变异( between group variation ):各组
的均数 x i 与总均数 x27.54 间的差异
▪ 组内变异(within group variation ):每组的每
x 个测量值 x i j 与该组均数 i 的差异
➢ 用离均差平方和(sum of squares of deviations from mean,SS)反映变异的大小
平方和、自由度计算实例
➢ 矫正系数
C T25 5 0 .8 2/(54 )1 5 1 6 9 .0 3 n k
➢ 总平方和
nk
SST xi2j C
i, j
31.92 27.92 L 28.52 C 15368.7 15169.03 199.67
平方和、自由度计算实例(续1)
➢ 处理间平方和
1t
2 e
➢ F值接近于l,就没有理由拒绝H0;反之,F值越大,拒 绝H0的理由越充分。数理统计的理论证明,当H0成立时, F统计量服从F分布。
1.4 f( F)
1.2
1.0
11,2 5
0.8 0.6
15,2 5
0.4
110,210
0.2
0.0
0
1
2F
3
4
F 分布曲线
单侧临界值
➢ 在第1自由度为 1 、第2自由度为 2 的F分布
t k 1
4 1 3
➢ 处理内变异自由度
e T t
19 3 16
均方差,均方(mean square,MS)
➢ 变异程度除与离均差平方和的大小有关外,还 与其自由度有关,由于各部分自由度不相等, 因此各部分离均差平方和不能直接比较,须将 各部分离均差平方和除以相应自由度,其比值 称为均方差,简称均方(mean square,MS)。
27.9 31.8 28.4 25.7 26.8 27.9 23.6 27.3 24.9 30.8 29.0 24.5
合计T i 平均 x i
35.9 155.9 31.18 26.2 131.4 26.28 25.8 123.7 24.74 28.5 139.8 27.96
T=550.8 x27.54
