双变量回归模型分析案例及模型形式的探讨(精)
计量经济学第三章 双变量线性回归模型

双变量线性回归模型的统计假设
(1). E(ut) = 0, t= 1, 2, ...,n 即各期扰动项的均值(期望值)为0.
(5) (6)
其中:Y Yt , X X t
n
n
xt X t X ,
yt Yt Y
样本均值 离差
(5)式和(6)式给出了OLS法计算ˆ 和 ˆ 的 公式,ˆ 和 ˆ称为线性回归模型 Yt = + Xt + ut
的参数 和 的普通最小二乘估计量 (OLS estimators)。
一. 双变量线性回归模型的概念
设 Y = 消费, X = 收入, 我们根据数据画出散点图
Y
*
*
*
*
*
图1
这意味着
Y = + X
(1)
写出计量经济模型
Y = + X + u
(2)
其中 u = 扰动项或 误差项
Y为因变量或被解释变量
X
X为自变量或解释变量
和 为未知参数
设我们有Y和X的n对观测值数据,则根据(2)式, 变量Y的每个观测值应由下式决定:
=β
——假设(4) ——假设(1)
这表明,ˆ 是β的无偏估计量。
在证明 ˆ 无偏性的过程中, 我们仅用到(1)和(4)两
条假设条件。
由 ˆ Y ˆ X ,我们有:
E(ˆ ) E(Y ˆ X ) E( X u ˆ X ) X E(u) X E(ˆ)
第二章2双变量回归分析

线性
解释变量是线性:被解释变量是解释变量的 线性函数 参数线性的:被解释变量的条件均值是估计 参数的线性函数
PRF的随机设定(统计误差)
每个观测值可能高于或低于条件均值(回归 值) 设:ui = Yi - E(Y|Xi) Yi = E(Y|Xi) + ui ui 随机误差项 随机总体回归方程:Yi =B1 + B2 Xi +ui
经典线性回归模型的基本假定
1、线性模型:参数线性 2、解释变量是固定的 3、干扰项的均值为0,即: E(ui) = 0 4、同方差:var(ui) = 2 5、干扰项之间无自相关Cov (ui, uj) = 0 , i not equal to j 6、Xi和ui的协方差为0,即:Cov(Xi*ui) = 0 7、观测次数大于待估参数 8、X值有变异 9、模型设定正确 10、解释变量之间无完全多重共线性(无完全的线性关系)
在满足基本假设条件下,对一元线性回归模型
Yi 0 1 X i i
:
随机抽取n组样本观测值(Xi, Yi) (i=1,2,…n)。 假如模型的参数估计量已经求得,为
那么Yi服从如下的正态分布: 于是,Y的概率分布函数为
2 ˆ Y i ~ N ( 0 ˆ 1 X i , )
第二章2 双变量回 归分析
一些基本概念
一个实例
计量经济学中回归研究内容:具有因果关系的 经济变量之间的统计依赖关系 假想社会中:消费与收入之间的关系 假想社区中:某产品销量与价格的关系
回归的含义
回归分析:研究一个经济变量与另一个或多个经济变 量之间具体统计依赖关系的计算方法的理论 被解释变量:随机变量;解释变量:确定值 回归结果:给定解释变量的条件下,被解释变量所 有可能对应值的平均值。 例:商品价格对其需求量在统计上有什么影响关系? 进一步:商品价格对需求量有多大程度的影响? 回归分析: 给定价格水平,需求量的总体平均值!!
双变量线性回归分析结果的报告以及案例

数据清洗
处理缺失值、异常值和重复数据,确保数据质 量。
数据探索
初步分析数据,了解变量之间的关系和分布情况。
模型建立
确定变量
选择与响应变量相关的预测变量,并考虑变量的 多重共线性。
建立模型
使用最小二乘法或其他优化算法拟合线性回归模 型。
模型诊断
检查模型的残差图、散点图等,确保模型满足线 性回归的前提假设。
卧室数量与房价之间存 在正相关关系,但影响 较小。
地理位置对房价有显著 影响,靠近市中心的房 屋价格更高。
周边设施对房价有积极 影响,特别是学校和公 园等设施。
05 双变量线性回归分析的未 来研究方向
深度学习与线性回归的结合
01
深度学习技术可以用于特征提 取,将原始数据转化为更高级 别的特征表示,然后利用线性 回归模型进行预测。
双变量线性回归分析结果的报告以 及案例
目录
• 双变量线性回归分析概述 • 线性回归分析的步骤 • 双变量线性回归分析的案例 • 线性回归分析的局限性 • 双变量线性回归分析的未来研究方向
01 双变量线性回归分析概述
定义与原理
双变量线性回归分析是一种统计学方法,用于研究两个变量之间的线性关系。通 过最小二乘法等数学手段,找到一条最佳拟合直线,使得因变量能够根据自变量 进行预测。
线性回归分析假设因变量和自变 量之间存在线性关系,但在实际 应用中,非线性关系可能更为常 见。
独立性假设
自变量之间应相互独立,但在实 际数据中,自变量之间可能存在 多重共线性,影响回归结果的准 确性。
无异常值和缺失值
假设
数据集中不应含有异常值和缺失 值,否则会影响回归模型的稳定 性和准确性。
模型泛化能力
双变量回归模型分析案例及模型形式的探讨

双变量回归模型分析案例及模型形式的探讨首先,我们来讨论一个实际案例,即研究收入和教育水平之间的关系。
假设我们收集了一组数据,包括每位受访者的收入和教育水平。
我们想要探究这两个变量之间的关系,即教育水平对收入的影响。
这时候,我们可以使用双变量回归模型进行分析。
在进行回归分析之前,我们首先需要确定要使用的模型形式。
常见的双变量回归模型包括线性回归模型、非线性回归模型和多项式回归模型等。
在这个案例中,我们可以使用线性回归模型来建立收入和教育水平之间的关系。
假设教育水平为自变量X,收入为因变量Y,那么线性回归模型可以写为:Y=β0+β1*X+ε其中,Y表示因变量(收入),X表示自变量(教育水平),β0表示截距项,β1表示自变量的系数,ε表示误差项。
在进行实际分析时,我们需要采集一定数量的数据,并使用统计软件进行回归分析。
通过拟合数据,我们可以得到回归方程的系数估计值,并根据显著性检验来判断自变量的影响是否具有统计学意义。
在本案例中,我们可以通过拟合数据得到回归方程的系数估计值,比如β0=3000,β1=1000。
这个结果可以被解释为,每增加一个教育水平单位,平均收入会增加1000元。
同时,我们还可以通过t检验或F检验来评估系数的显著性。
除了线性回归模型外,我们还可以使用非线性回归模型或多项式回归模型来分析双变量关系。
非线性回归模型可以用于探究非线性关系,例如指数关系或对数关系。
多项式回归模型可以用于探究曲线关系,例如二次曲线关系或三次曲线关系。
总之,双变量回归模型是一种常见的统计分析方法,在实际研究中具有广泛应用。
通过建立适当的模型形式,我们可以研究两个变量之间的关系,并通过回归分析得到相关参数的估计值。
这些参数可以帮助我们了解变量之间的关系,并为实际问题的解决提供参考依据。
双变量回归模型(一元线性回归模型)

* * * * * * * * * *
* * * * * * * * * *
* * ** * * *
* * * * * * * * * *
总体回归曲线
E (Y X i ) f ( X i )
E (Y X i ) 1 2 X i
150 175 200 225 250 275 300 325 350 375 每周个人可支配收入( X)
每周个人可支配收入( X)
总体回归模型的随机形式
Yi 1 2 X i ui
随机总体回归函数
Yi可表示成两部分之和 系统成分(确定性成分):1 2 X i 非系统成分(随机成分):ui
引入随机干扰项的意义
1、理论的不完全性
与因变量相关的因素很多,随机干扰项替代了 未纳入模型的全部变量。
X
Xi
总体回归函数
E (Y X i ) 1 2 X i
1、 2为“未知但固定”的参数, 称为“回归系数” 。 1称为截距( Intercept ), 2 称为斜率( Slope)
斜率度量了解释变量X每变动一个单位, 因变量Y的条件均值变化多少个单位。 截距项度量了解释变量为零时因变量 的条件均值。一般来说,不解释其经 济意义。 该形式的总体回归函数称为
双变量回归模型
(一元线性回归模型)
双变量回归模型
(最简单的回归模型)
模型特点 因变量(Y)仅依赖于唯一的一个解释变量(X)。 回归分析的内容与目的 1、通过样本数据去估计出因变量与解释变量的统 计依赖关系式(总体回归函数); 2、给定解释变量的取值,去估计因变量的均值; 3、假设检验; 4、根据样本外解释变量的取值,预测因变量的均 值。
bivariate logistic models双变量逻辑模型

bivariate logistic models双变量逻辑模型一、什么是双变量逻辑模型(bivariate logistic models)双变量逻辑模型是一种统计学方法,用于分析两个分类变量之间的关系。
这种模型通常用于预测一个事件发生的概率,特别是在医疗、社会科学、市场营销等领域。
通过建立两个分类变量之间的概率依赖关系,我们可以更好地理解这些变量之间的相互作用。
二、为什么要使用双变量逻辑模型1.分析两个分类变量之间的关联性:双变量逻辑模型可以帮助我们确定两个分类变量之间是否存在显著关联,以及关联的程度。
2.预测概率:借助双变量逻辑模型,我们可以预测一个事件发生的概率,从而为决策提供依据。
3.发现关联规律:通过分析变量间的概率关系,我们可以发现潜在的关联规律,为后续研究提供方向。
三、如何构建双变量逻辑模型1.数据准备:收集与两个分类变量相关的数据,确保数据具有完整性、准确性和一致性。
2.模型设定:确定自变量和因变量,建立双变量逻辑回归模型。
3.模型训练:使用统计软件(如SPSS、R、Python等)对模型进行训练,确定模型参数。
4.模型评估:通过模型预测准确率、校准曲线、信息矩阵等指标评估模型性能。
5.结果解释:根据模型参数,解释自变量对因变量概率的影响程度。
四、双变量逻辑模型的应用领域1.医学:预测疾病风险、评估治疗效果等。
2.社会科学:分析教育、收入、性别等因素对某个结果的影响。
3.市场营销:分析消费者行为、评估广告效果等。
五、优缺点分析优点:1.易于理解和解释模型结果。
2.可以分析两个分类变量之间的关联性。
3.预测精度较高。
缺点:1.依赖大样本数据。
2.模型稳定性受样本量和变量选择影响。
3.无法处理多个变量之间的关系。
六、实际案例分享某医疗机构希望通过分析患者病史、生活习惯等因素,预测患某种疾病的概率。
在这种情况下,可以使用双变量逻辑模型来分析各个因素与疾病之间的关系,并为患者提供个性化的预防建议。
双变量回归模型估计问题课件

在应用双变量回归模型进行预测之前,需要对模型进行假设检验,以确保模型的有效性和可靠性。
03
CHAPTER
双变量回归模型大样本可以提供更稳定和准确的估计。
异常值可能对估计稳定性产生负面影响。在回归分析中,需要谨慎处理异常值,以避免对估计稳定性的不良影响。
总结词
在气候变化对农业产量影响的案例中,可以选择一些与农业产量密切相关的气候因素作为自变量,如温度、降雨量、光照等。通过双变量回归模型,可以建立这些气候因素与农业产量之间的线性关系,并利用历史数据来估计模型的参数。通过预测未来气候因素的变动,可以进一步预测未来农业产量的变化趋势,为农业生产和资源管理提供决策依据。
详细描述
06
CHAPTER
结论与展望
01
总结了双变量回归模型估计问题的基本概念、方法和应用场景。
02
分析了双变量回归模型估计问题中存在的挑战和问题,如多重共线性、异方差性等。
03
介绍了解决这些问题的常用方法和技巧,如主成分分析、岭回归等。
04
强调了双变量回归模型估计问题在实践中的重要性和应用价值。
最小二乘法具有很多优点,例如它对数据的要求较低、计算相对简单等,因此在回归分析中得到了广泛应用。
模型的假设主要包括线性假设、误差项独立同分布假设、误差项无偏性假设等。
对假设的检验可以通过一些统计方法进行,例如残差分析、Jarque-Bera检验等。如果模型的假设不满足,则需要对模型进行调整或重新设定。
双变量回归模型估计问题课件
目录
引言双变量回归模型基础双变量回归模型的估计问题解决双变量回归模型估计问题的方法实际案例分析结论与展望
01
CHAPTER
引言
03
估计问题是指在使用回归模型时,如何准确地估计未知的参数值。
双变量回归模型分析案例及模型形式的探讨

双变量回归模型分析案例及模型形式的探讨双变量回归模型是一种用于分析两个变量之间关系的统计模型。
它可以用来预测一个变量(因变量)受另一个变量(自变量)的影响程度,或者研究两个变量之间的相关性。
本文将探讨一个双变量回归模型的分析案例,并探讨该模型的形式。
假设我们想要分析一个人的身高和体重之间的关系。
我们收集了一组数据,包括100个人的身高和体重数据。
我们想要建立一个双变量回归模型,来预测一个人的体重受其身高的影响程度。
首先,我们需要将收集到的数据进行整理和描述性统计分析。
我们可以计算身高和体重的平均值、方差和相关系数等指标。
这些指标可以提供有关数据的整体特征和两个变量之间的关系强度的信息。
接下来,我们可以使用散点图来可视化身高和体重之间的关系。
散点图可以显示每个人的身高和体重,并观察它们之间的模式和趋势。
基于散点图的观察,我们可以大致判断两个变量之间是否存在线性关系。
然后,我们可以使用最小二乘法来估计回归方程的系数。
回归方程的形式可以表示为:Y=β0+β1X,其中Y代表体重,X代表身高,β0和β1分别是回归方程的截距和斜率。
最小二乘法的目标是最小化实际观测值和回归方程预测值之间的误差平方和。
在估计回归系数之后,我们可以对回归方程进行模型拟合和评估。
拟合优度指标,如R平方和调整后的R平方,可以用来评估模型的拟合程度。
R平方的取值范围在0到1之间,越接近1说明模型对数据的解释能力越强。
最后,我们可以使用回归模型进行预测和推断。
通过将新的身高值代入回归方程,我们可以预测对应的体重。
此外,我们还可以进行假设检验和置信区间估计,以评估回归系数的显著性和区间估计。
总之,双变量回归模型可以用于分析两个变量之间的关系,并进行预测和推断。
在实际应用中,我们需要注意模型的前提假设、数据的合理性和模型的解释力。
另外,还可以通过添加交互项、多项式项或考虑其他模型形式来扩展双变量回归模型。
线性回归分析——双变量模型

线性回归分析——双变量模型在进行线性回归分析之前,我们首先需要明确我们要解决的问题,确定自变量和因变量。
比如,我们可以研究体重和身高之间的关系,其中体重是因变量,身高是自变量。
收集到数据后,我们可以进行描述性统计分析来对数据进行初步的了解。
我们可以计算出体重和身高的平均值、方差、最大值和最小值等统计指标。
此外,我们还可以绘制散点图来观察变量之间的关系。
在进行线性回归分析之前,我们需要满足一些假设条件。
首先,我们假设自变量和因变量之间存在线性关系。
其次,我们假设观测误差服从正态分布。
最后,我们假设观测误差的方差是常数。
接下来,我们可以通过最小二乘法来估计线性回归模型的参数。
最小二乘法的目标是最小化观测值与预测值之间的残差的平方和。
我们可以使用统计软件或者编程语言来进行计算。
线性回归模型可以表示为:Y=β0+β1X+ε其中,Y表示因变量,X表示自变量,β0表示截距,β1表示斜率,ε表示观测误差。
在进行参数估计后,我们可以对模型进行拟合优度的评估。
拟合优度指标可以帮助我们判断模型的拟合程度。
常见的拟合优度指标有R方值、调整R方值和残差分析。
R方值表示因变量的变异程度可以由自变量解释的比例。
R方值的取值范围是0到1,越接近1表示模型的拟合效果越好。
调整R方值是在R方值的基础上考虑模型中自变量的个数进行修正。
残差分析可以用来评估模型中未解释的部分。
在进行结果解释时,我们需要注意解释截距和斜率的意义。
截距表示当自变量为0时,因变量的值。
斜率表示自变量的单位变化对因变量的影响。
最后,我们还可以对模型的统计显著性进行检验。
常见的方法有t检验和F检验。
t检验可以用来判断截距和斜率的显著性,F检验可以用来判断模型整体的显著性。
总结:线性回归分析是一种常用的数据分析方法,可以用于研究两个变量之间的线性关系。
通过收集数据,建立模型,估计参数和进行拟合优度评估,我们可以获得对变量之间关系的深入认识。
同时,我们还可以通过检验模型的显著性来判断模型的可靠性。
3.6 双变量线性回归分析结果的报告以及案例

一、双变量线性回归分析结果的报告
ˆ ˆ X ˆ Y i 1 2 i
r2
df n 2
F1,n2
ˆ ˆ X ˆ Y i 1 2 i
df n 2
r2
二、双变量线性回归分析结果的评价 回归系数的估计值的符号是否与理论或事先 预期相一致?
案例2: 教材P81 习题3.23
回归系数是不是统计上显著的?
回归模型在多大程度上解释了因变量Y的变 异?
补充:正态性检验
残差直方图 正态概率图 雅克-贝拉(JB)检验
S 2 ( K 3) 2 JB n[ ] 6 24
案例分析
案例1:
伊春林区位于黑龙江省东北部,森林覆盖率 为62.5%,是我国主要的木材工业基地之一。 1999年伊春林区木材采伐量为532万m3。按 此速度44年之后,1999年的蓄积量将被采伐 一空。所以目前亟待调整木材采伐规划与方 式,保护森林生态环境。为缓解森林资源危 机,并解决部分职工就业问题,除了做好木 材的深加工外,还要充分利用木材剩余物生 产林业产品,如纸浆、纸袋、纸板等。因此 预测林区的年木材剩余物是安排木材剩余物 加工生产的一个关键环节。
计量经济学方法论
陈述经济学理论或感兴趣的经济现象; 设定数理经济学模型; 设定相应的计量经济学模型; 采集数据; 估计计量经济模型的参数; 基于所估计பைடு நூலகம்模型进行假设检验; 模型的应用。
建立工作文件,完成数据输入 散点图 OLS估计 模型的统计检验 1)拟合优度检验 2)变量的显著性检验 3)区间估计 4)正态性检验 报告估计结果 预测
双变量模型实验报告(3篇)

第1篇一、实验背景与目的随着社会经济的发展和科学技术的进步,双变量模型在统计学、经济学、生态学等领域得到了广泛应用。
本实验旨在通过构建和验证双变量模型,探讨两个变量之间的关系,并进一步分析其影响机制。
二、实验方法与步骤1. 数据收集与整理:首先,从相关数据库或公开数据源收集所需数据。
本实验以某地区居民收入和消费支出为例,收集了500个样本数据。
2. 模型构建:根据数据特点,选择合适的双变量模型。
本实验采用线性回归模型,即y = β0 + β1x1 + β2x2 + ε,其中y为因变量,x1和x2为自变量,β0为截距,β1和β2为系数,ε为误差项。
3. 模型估计:利用统计软件(如SPSS、R等)对模型进行估计,得到系数估计值、标准误、t值和p值等。
4. 模型检验:对估计的模型进行假设检验,包括t检验、F检验和R²检验等,以验证模型的有效性和可靠性。
5. 结果分析:根据模型估计结果和检验结果,分析两个变量之间的关系,并探讨其影响机制。
三、实验结果与分析1. 模型估计结果:通过线性回归分析,得到以下结果:- y = 1000 + 0.8x1 + 0.5x2 + ε- β0 = 1000,β1 = 0.8,β2 = 0.5其中,x1和x2的系数分别为0.8和0.5,说明居民收入和消费支出对居民消费水平有显著的正向影响。
2. 模型检验结果:- t检验:x1和x2的t值分别为2.31和1.94,p值分别为0.023和0.053,均小于0.05,说明x1和x2对y的影响显著。
- F检验:F值为5.68,p值为0.021,小于0.05,说明模型整体显著。
- R²检验:R²为0.65,说明模型解释了65%的因变量变异。
3. 结果分析:- 居民收入和消费支出对居民消费水平有显著的正向影响。
随着居民收入的增加,消费支出也随之增加,反之亦然。
- 模型解释了65%的因变量变异,说明模型具有一定的解释力。
双变量回归模型
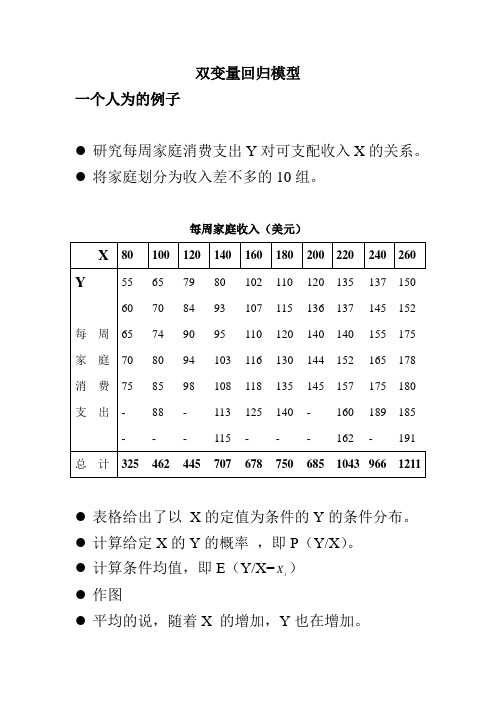
双变量回归模型一个人为的例子●研究每周家庭消费支出Y对可支配收入X的关系。
●将家庭划分为收入差不多的10组。
每周家庭收入(美元)●表格给出了以X的定值为条件的Y的条件分布。
●计算给定X的Y的概率,即P(Y/X)。
●计算条件均值,即E(Y/X=X)i●作图●平均的说,随着X 的增加,Y也在增加。
● 条件均值落在一根有正斜率的直线上,总体回归线(population regression line ), Y 对X 的回归。
● 对每一个iX 都有Y 值的一个总体和相应的均值,回归线是穿过了这些条件均值的线。
总体回归函数(PRF )的概念● 图中看到,每一条件均值E (Y/iX )都是iX 的一个函数,并且是线性函数。
i i i X X f X Y E 21)()/(ββ+==● 1β和2β是未知但固定的参数,被分别称为截距和斜率参数。
“线性”一词的含义● 对变量为线性非线性的例子:221)/(i i X X Y E ββ+=● 对参数为线性非线性的例子:i i X X Y E 21)/(ββ+= ● 本课程中,只对参数是线性的。
PRF 的随机设定● 随着家庭收入的增加,家庭消费平均的说也增加。
● 但某一个别家庭的消费支出却不一定。
● 个别家庭的消费支出聚集在收入为Xi的所有家庭的平均消费支出的周围。
ii i u X Y E Y +=)/(● E(Y/X i )代表相同收入水平的所有家庭的平均消费支出,称为系统性(systematic )成分,ui称为随机或非系统性(non-systematic)成分。
● 假定E(Y/X i )是对Xi为线性的,则i i i i i u X u X Y E Y ++=+=21)/(ββ● 0)/(=i i X u E随机干扰项的意义1.理论的含糊性 2.数据的欠缺 3.核心变量与周边变量 4.人类行为的内在随机性 5.糟糕的替代变量 6.节省原则7.错误的函数形式样本回归函数●以上讨论局限在与X值相对应的Y值总体●现在我们考虑抽样问题样本:YX7080651009012095140110160115180120200140220155240150260●我们能从样本预测整个总体中对应于选定X的平均每周消费支出Y吗?●从N个不同的样本会得到N个不同的SRF,并且这些SRF不大会是一样的。
2--双变量回归:模型估计

实际值的分解
(1)式可以分解为两个部分之和:① EY X i 代表相同收入水平的所有家庭的平均消费 支出,这一成分被称为系统性或确定性成 分;②ui为随机或非系统性成分,并假定它 是所有可能影响Y的,但又未能包括到回归 模型中的被忽略变量的替代变量。
24
对(1)式两边取期望,得到
4
父亲们的身高与儿子们的身高之间 关系的研究
1889年F.Gallton(1822-1911)和他的 学生K.Pearson(1856-1936)收集了上 千个家庭的身高等数据的记录企图寻找 出儿子们身高与父亲们身高之间关系的 具体表现形式。 下图是根据1078个家庭的调查所作的散 点图(略图)
25
一. 随机扰动项
为什么要引入随机扰动项 模型中引入反映不确定因素影响的随 机扰动项e的目的在于使模型更符合客观 经济活动实际。
26
1.简单线性需求函数——不可能 包罗万象地引入全部影响变量
我们以最简单的线性需求函数为例进行分析。 Qd=b0+b1X1 理论分析和实践经验表明,某种商品需求量不仅 趋近于价格,而且趋近于替代商品的价格X2,消费者 收入X3和消费者偏好X4等等。将所有对需求量有影响的 个变量引入方程: Qd=b0+b1X1+b2X2+b3X3+b4X4++bnXn 即使如此也还可能有其他次要因素影响需求量, 譬如社会风尚,心理变化甚至天气等等。总之,不可 能巨细无遗的全部都引入。
y a bx u ˆ 33.73 0.516x y
结论:父母平均身高每增加一个单位,其成年儿子 的身高也平均增加0.516个单位,但父辈身高增加一 个单位,儿子身高仅增加半个单位左右。儿子们的 身高回复于全体男子的平均身高,即“回归”。 后人将此种方法普遍用于寻找变量之间的规律 7
chapter02经典线性回归模型:双变量线性回归模型

每 月 家 庭 消 费 支 出 Y
1489 1538
1600 1702
1712 1778
1841 1886
2078 2179
2298 2316
2289 2313
2398 2423
2487 2513
2538 2567
2853 2934
3110
3142 3274
1900
2012
2387
2498 2589
例:100个家庭构成的总体
(单位:元)
每 月 家 庭 可 支 配 收 入 X
1000 820 888 932 960 1500 962 1024 1121 1210 1259 1324 2000 1108 1201 1264 1310 1340 1400 1448 2500 1329 1365 1410 1432 1520 1615 1650 3000 1632 1726 1786 1835 1885 1943 2037 3500 1842 1874 1906 1068 2066 2185 2210 4000 2037 2110 2225 2319 2321 2365 2398 4500 2275 2388 2426 2488 2587 2650 2789 5000 2464 2589 2790 2856 2900 3021 3064 5500 2824 3038 3150 3201 3288 3399
E(Y X i ) = f ( X i )
这个函数称为总体回归函数(PRF)
例:100个家庭构成的总体
(单位:元)
每 月 家 庭 可 支 配 收 入 X
1000 820 888 932 960 1500 962 1024 1121 1210 1259 1324 2000 1108 1201 1264 1310 1340 1400 1448 2500 1329 1365 1410 1432 1520 1615 1650 3000 1632 1726 1786 1835 1885 1943 2037 3500 1842 1874 1906 1068 2066 2185 2210 4000 2037 2110 2225 2319 2321 2365 2398 4500 2275 2388 2426 2488 2587 2650 2789 5000 2464 2589 2790 2856 2900 3021 3064 5500 2824 3038 3150 3201 3288 3399
第二章双变量线性回归分析

[计量经济学] 第二章:双变量线性回归分析§1 经典正态线性回归模型(CNLRM)一、一些基本概念1、一个例子条件分布:以X取定值为条件的Y的条件分布条件概率:给定X的Y的概率,记为P(Y|X)。
例如,P(Y=55|X=80)=1/5;P(Y=150|X=260)=1/7。
条件期望(conditional Expectation):给定X的Y的期望值,记为E(Y|X)。
例如,E(Y|X=80)=55×1/5+60×1/5+65×1/5+70×1/5+75×1/5=65总体回归曲线(Popular Regression Curve)(总体回归曲线的几何意义):当解释变量给定值时因变量的条件期望值的轨迹。
2、总体回归函数(PRF)E(Y|X i)=f(X i)当PRF的函数形式为线性函数,则有,E(Y|X i)=β1+β2X i其中β1和β2为未知而固定的参数,称为回归系数。
β1和β2也分别称为截距和斜率系数。
上述方程也称为线性总体回归函数。
3、PRF的随机设定将个别的Y I围绕其期望值的离差(Deviation)表述如下:u i=Y i-E(Y|X i)或Y i=E(Y|X i)+u i其中u i是一个不可观测的可正可负的随机变量,称为随机扰动项或随机误差项。
4、“线性”的含义“线性”可作两种解释:对变量为线性,对参数为线性。
本课“线性”回归一词总是指对参数β为线性的一种回归(即参数只以它的1次方出现)。
模型对参数为线性?模型对变量为线性?是不是是LRM LRM不是NLRM NLRM注:LRM=线性回归模型;NLRM=非线性回归模型。
5、随机干扰项的意义随机扰动项是从模型中省略下来的而又集体地影响着Y 的全部变量的替代物。
显然的问题是:为什么不把这些变量明显地引进到模型中来?换句话说,为什么不构造一个含有尽可能多个变量的复回归模型呢?理由是多方面的: (1)理论的含糊性 (2)数据的欠缺(3)核心变量与周边变量 (4)内在随机性 (5)替代变量 (6)省略原则(7)错误的函数形式6、样本回归函数(SRF ) (1)样本回归函数iY ˆ=1ˆβ+2ˆβi X 其中Y ˆ=E(Y|X i )的估计量;1ˆβ=1β的估计量;2ˆβ=2β的估计量。
计量经济学-双变量回归模型估计问题PPT课件

01
03
随着大数据和人工智能技术的不断发展,未来的研究 可以结合这些技术,对双变量回归模型进行改进和优
化,提高模型的预测能力和适应性。
04
在实际应用中,需要考虑更多的因素,如时间序列数 据、异方差性、自相关性等问题,需要进一步完善和 改进双变量回归模型。
06 参考文献
参考文献
[1] 李子奈,潘文卿. 计量经济学 (第四版)[M]. 北京:高等教育出版
03
探讨模型结果的经济学意义和实际应用价 值。
04
提出可能的改进方向和未来研究展望。
05 结论与展望
研究结论
双变量回归模型在计量经济学中具有 重要应用,能够有效地分析两个变量 之间的线性关系。
在实际应用中,需要考虑变量的选择、 数据的收集和处理、模型的适用性和 检验等问题,以确保模型的准确性和 可靠性。
变量,另一个变量是自变量。
假设条件
双变量回归模型假设因变量和自 变量之间存在稳定的线性关系, 且误差项是独立的、同分布的。
应用场景
双变量回归模型适用于分析两个 变量之间的因果关系,例如分析 收入与教育程度之间的关系、消
费与收入之间的关系等。
02 双变量回归模型的理论基 础
线性回归模型的定义
01
线性回归模型是一种预测模型, 用于描述因变量与一个或多个自 变量之间的线性关系。
计量经济学的重要性
01
02
03
实证分析
计量经济学提供了一种实 证分析的方法,通过数据 和模型来检验经济理论。
政策制定
计量经济学可以帮助政策 制定者评估政策效果,制 定更加科学合理的政策。
预测
计量经济学可以通过建立 预测模型,对未来经济趋 势进行预测。
《双变量回归模型》课件

通过对双变量回归模型的深入研究,可以更好地理解数据之间的关系和规律,为相关领域的决策提供 科学依据。同时,本研究也有助于推动双变量回归模型的发展和完善,为未来的研究提供更多的思路 和方法。
02
双变量回归模型的理论 基础
线性回归模型的定义
线性回归模型是一种预测模型,用于描述因变量与一个或多个自变量之间的线性关系。在双变量回归模型中,因变量与两个 自变量之间存在线性关系。
在许多领域,如经济学、金融学、生 物统计学等,双变量回归模型都发挥 着重要的作用。通过对两个变量之间 关系的建模和分析,可以更好地理解 数据背后的规律和机制。
研究目的和意义
研究目的
双变量回归模型虽然被广泛应用,但仍然存在一些问题和挑战。本研究旨在深入探讨双变量回归模型 的原理、方法和应用,以期为相关领域的
数据预处理
在建立双变量回归模型之前,需要对数据进 行清洗和整理,包括缺失值处理、异常值剔
除、数据类型转换等。
模型的建立和检验
01
模型选择
根据研究目的和数据特征,选择 线性回归模型作为本案例的模型 。
模型建立
02
03
模型检验
利用SPSS软件,通过输入自变量 和因变量,设置回归选项,运行 模型。
对回归结果进行统计检验,包括 拟合优度检验、显著性检验等, 以确保模型的可靠性和有效性。
双变量线性回归模型的假设
线性关系假设
自变量与因变量之间存在线性关系,即因变量的 变化可以用自变量的线性组合来解释。
无异方差性假设
误差项的方差应该相等且恒定,即误差项的方差 不随自变量或因变量的值的变化而变化。
ABCD
无多重共线性假设
自变量之间不存在多重共线性,即自变量之间没 有高度的相关性,各自独立地影响因变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半对数模型
对数-线性模型 线性-对数模型
对数-线性模型:
ln Yi 0 1 X i ui
(5-2)
可用于测度增长率 X 每增加一个单位, 解释: Y 以1001 %的 速度增长
复利公式
Yt Yt 1 t
菲利普曲线
货 币 工 资 变 化 率
自然失业率
0
1
UN
失业率
对数倒数模型 (5-5) Y 首先以递增的速度增加,然后以递减的 速度增加。 注重对变化趋势的描述
1 ln Yi 0 1 ui Xi
生产函数
如果劳动和资本是一个生产函数的投 入,保持资本投入不变但增加劳动投入,那 么产出与劳动之间的短期关系类似下图。
R-squared 0.996950 Adjusted R-squared S.E. of regression Sum squared resid Log likelihood F-statistic 2614.830 Prob(F-statistic)
0.996569 67.63763 36598.79 -55.21531
Yi 159.8788 0.7616 X i
se : (52.9184) t : (3.0212)
(0.0149) (51.1354)
p值: (0.0165)
(0.0000)
R 2 0.9970
解释:家庭月可支配收入增加1000元,家庭月 消费支出约提高761.6元。
5、假设检验
Yi 0 1 X i ui
根据经济理论,预期 1 0
4、收集并整理数据
X
Y
1000 1500 2000 2500 3000 3500 4000 4500 5000 5500
900 1320 1620 2140 2480 2740 3300 3520 4020 4310
5、参数估计
Y
X
双对数模型
怎样测度弹性
ln Yi 0 1 ln X i ui
(5-1) 双对数模型的一个诱人并且是使它获得普遍 应用的特点,是斜率系数1 测度了Y 对 X 的弹性。 Y 则提高约 1 % 。 解释:若X 提高 1% ,
耐用消费品支出与个人总消费支出的关系
ln 耐用品支出t 9.6971 1.905ln 总支出t
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion Hannan-Quinn criter. Durbin-Watson stat
0.000000
Y = 159.878787879 + 0.761575757576*X
Dependent Variable: Y Method: Least Squares Date: 09/20/10 Time: 21:02 Sample: 1 10 Included observations: 10 Variable C X Coefficient 159.8788 0.761576 Std. Error 52.91844 0.014893 t-Statistic 3.021230 51.13541 Prob. 0.0165 0.0000 2635.000 1154.655 11.44306 11.50358 11.37668 3.391406
回归系数大于0,符合经济理论预期;通过 t 检验知回归系数高度显著,表明可支配收入 确实能够影响消费支出。 正态性检验:残差直方图
雅克-贝拉检验(JB检验)
6、预测 区间预测 点预测
Y11 4729.333
Y12 5110.121
5.2 计量模型的形式探讨
双对数模型 半对数模型 倒数模型 对数倒数模型
r
ln Yt ln Y0 t ln 1 r
ln Yt 0 1t
其中 0 ln Y0
1 ln 1 r
例:劳务支出的增长模型
ln 劳务支出t 7.7890 0.00743t
在2000年第一季度到第四季度期间,劳务支出以每季度 0.743% 的速度增长。
线性-对数模型
(5-3) X 每提高一个百分点( 解释: 1% ), Y 平均 1 增加约 100 单位。
Yi 0 1 ln X i ui
恩格尔支出
用于食物的总支出以算术级数增加,而总支 出以几何级数增加。
食物支出i 1283.912 257.2700ln 总支出i
当总支出每提高1%,导致样本中家庭的食物 支出平均增加约 2.57 美元。
倒数模型
(5-4) 1 1 X 项趋于零, 特点:随着 X 无限的增大, 1 而 趋于极限或渐近值 。 Y Y 1 ui Xi
第五讲
双变量回归模型分析案例及模 型形式探讨
主要内容:
双变量回归案例分析 计量模型的形式探讨
5.1 双变量回归案例分析
消费函数是宏观经济学中最重要的范畴 之一,这一概念是凯恩斯提出来的,它 反映的是消费支出水平与个人可支配收 入水平之间的关系。 其假设的前提是,消费和收入之间 存在着一种以经验为依据的稳定关系。
现在,我们想去验证这一假设的合理性, 是否消费水平与可支配收入之间存在着 这样的稳定关系?如果存在,二者在数 量上的变动关系如何?如何利用该数量 关系去进行预测?
计量经济模型建模步骤: 1、对经济理论的阐述或对经济行为的 理论分析 根据凯恩斯的理论,消费支出主要 受到可支配收入的影响;消费支出随着 可支配收入的增加而增加,二者具有正 向的变动趋势。
2、数理模型的建立 由上述对经济理论的阐述,我们确立的被解 释变量是“居民月消费支出”,解释变量是“居 民月 可支配收入”,这两个变量的数据容易收集,因 此,利用这两个变量,我们建立数理模型为:
y f x
y 居民年消费支出
x 居民年可支配收入
3、计量经济模型的建立 实际中,消费支出除了受到可支配收入的影 响,还受到其他随机因素的影响,但根据经济理 论的分析,我们主要关注可支配收入因素,将其 他随机因素均归入随机误差项 u i 中,并假定二者 具有如下关系:
