电介质物理缩印本
静电场中的电介质大学物理学第六章...

由于极化通过闭合的S面移出S的总电荷: d S
q dq'
qint P
S
S E
由电荷守恒:
q' intFra bibliotekP dS
S
上式是利用非极性分子电介质所推出,但对极
性分子电介质第亦六章成静立电场中的导体和电介质
14
大学 物理学
§6.3 静电场中的电介质
(3)电介质表面极化电荷面密度
dq P dS
27
大学
§6.3 静电场中的电介质
物理学
1
2 r 1r
0
0
2
2
1r
0
0
E1
E2
2 0
0 1 r
2
1r
E0
D1 1
1 s
2
+ + + + + + + + + + ++
D2 2
U
-
-D1-
εr
- E-1 -
D2 E2
----
d
-
1
2
第六章 静电场中的导体和电介质
28
大学 物理学
§6.3 静电场中的电介质
P dS
S
qi'nt
S
E dS
1
0
S
q0i
1
0
P dS
S
即 (0E P) dS q0int
S
i
定义电位移矢量: D 0E P
D dS qi 0int -- 电介质存在时的高斯定理
S
第六章 静电场中的导体和电介质
19
大学 物理学
10-7静电场中的电介质
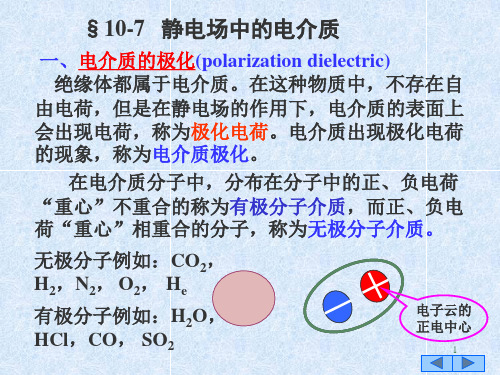
一、电介质的极化(polarization dielectric) 绝缘体都属于电介质。在这种物质中,不存在自
由电荷,但是在静电场的作用下,电介质的表面上 会出现电荷,称为极化电荷。电介质出现极化电荷 的现象,称为电介质极化。
在电介质分子中,分布在分子中的正、负电荷
“重心”不重合的称为有极分子介质,而正、负电 荷“重心”相重合的分子,称为无极分子介质。
对于各向同性的电介质 D 0 r E E
物理意义
D dS 0d i q0i
S
自由电荷
Hale Waihona Puke 对于任一闭合曲面的电位移通量,等于该闭
合曲面所包围的自由电荷的代数和。
高斯定理的微分形式: D 0
10
六、边界条件
在两种不同的电介质分界面两侧, D和E一般要发生突变,但必须遵循
D1 1
r1
一定的边界条件。
式中 0 r 是电介质的绝对电容率,也称电介质
的电容率。由于电场强度的减小,电容器极板间的
电 势 差 U12 也 相 应 减 小 了 , 并 为 电 介 质 不 存 在 时 的
1/r ,即
U 12
Ed
E0
r
d
1
r
U 012
式中U012是电介质不存在时电容器极板间的
电势差,d是两极板之间的距离。
7
在保持电容器极板所带电量不变的情况下,
特殊的名称,叫做退极化场(epolarization field) 。
5
以平行板电容器为例 , 如果极板电容器上
所带自由电荷面密度分别为 和,则两 +0
板之间的电场强度的大小为E0=σ/ε0 在电容
电介质物理学

电介质物理学绪论电介质(dielectric)是在电场作用下具有极化能力并能在其中长期存在电场的一种物质。
电介质具有极化能力和其中能够长期存在电场这种性质是电介质的基本属性.也是电介质多种实际应用(如储存静电能)的基础。
静电场中电介质内部能够存在电场这一事实,已在静电学中应用高斯定理得到了证明,电介质的这一特性有别于金属导体材料,因为在静电平衡态导体内部的电场是等于零的。
如果运用现代固体物理的能带理论来定义电介质,则可将电介质定义为这样一种物质:它的能级图中基态被占满.基态与第一激发态之间被比较宽的禁带隔开,以致电子从正常态激发到相对于导带所必须的能量,大到可使电介质变到破坏。
电介质的能带结构可以用图一示意,为了便于将电介质的能带结构和半导体、导体的能带结构相比较,图中分别画出了它们的能带结构示意图.电介质对电场的响应特性不同于金属导体。
金属的特点是电子的共有化,体内有自由载流子,从而决定了金属具有良好的导电件,它们以传导方式来传递电的作用和影响。
然而,在电介质体内,一股情况下只具有被束缚着的电荷。
在电场的作用下,将不能以传导方式而只能以感应的方式,即以正、负电荷受电场驱使形成正、负电荷中心不相重合的电极化方式来传递和记录电的影响。
尽管对不同种类的电介质,电极化的机制各不相同,然而,以电极化方式响应电场的作用,却是共同的。
正因为如此研究电介质在电场作用下发生极化的物理过程并导出相应的规律,是电介质物理的一个重要课题。
由上所述,电介质体内一般没有自由电荷,具有良好的绝缘性能。
在工程应用上,常在需要将电路中具有不同电势的导体彼此隔开的地方使用电介质材料,就是利用介质的绝缘特性,从这个意义上讲,电介质又可称为绝缘材料(Insulating material)或绝缘体(insulator)。
与理想电介质不同,工程上实际电介质在电场作用下存在泄漏电流相电能的耗散以及在强电场下还可能导致电介质的破坏。
因此,如果将电介质物理看成是一种技术物理,那么除要研究极化外,还要研究有关电介质的电导、损耗以及击穿特性,这些就是电介质物理需要研究的主要问题。
静电场中的电介质

SD dS Q0
选半径为r,长度为L的高斯圆柱 面
r
R2 R1
SD dS l
D2 π rl l D
2πr
E D
ε0εr 2 π ε0εrr
(R1 r R2 )
P
0 E
( r
1) 0 E
r 1 2 πrr
r
R2 R1
(2) E
2π
0
r
r
E1 2 π 0 r R1 (r R1)
q0 有关.
s内
特例: 真空——特别介质
特例: 真空——特别介质
q' 0 , P 0 , D 0E P 0E
回到:
1
E
s
dS
0
(
q0
S内 )
3. 如何求解介质中电场?
本课程只要 求特殊情况
各向同性电介质 q0 ,q' 分布具有某些对称性
(1)各向同性电介质:
P
0E
为常数
D 0E P 0E 0E 0(1 )E
模型 “电子气”
与电场的 相互作用
静电感应
电偶极子
无极分子电介质: 位移极化 有极分子电介质: 转向极化
宏观 效果
静电平衡
导体内 E 导体表面
0, 0 E表面
内部:分子偶极矩矢量
和不为零
pi 0
i
感应电荷 0E 出现束缚电荷(极化电荷)
4.极化现象的描述
1) 从分子偶极矩角度
单位体积内分子偶极矩矢量和——极化强度.
R2的薄导体圆筒组成,其间充
以相对电容率为r的电介质. 设
直导体和圆筒单位长度上的电
荷分别为+和- . 求(1)电介 质中的电场强度、电位移矢量
高电压 缩印版

1.夹层极化的产生原因、过程、后果、特点。
答;过程:如图(1-1-3)所示双层介质极化模型,各层介质的电容分别为C1和C2,各层介质的电导分别为G1和G2,直流电源电压为U,设C1=1,C2=2,G1=2,G2=1,U=3,当U加在AB两端的初瞬,整个介质的等值电容为Ceq=Q/U=2/3,到达稳态时,整个介质的电容为Ceq=Q/U=4/3,C1与C2分界面上堆积的电荷量Q=+4-1=+3。
原因:夹层极化是最明显的空间电荷极化。
它是带电质点(电子或正负离子)的移动形成的。
在大多数绝缘结构中,电介质往往呈层式结构,电介质中也可能存在某些晶格缺陷。
在电场的作用下,带电质点在电介质中移动时、可能被晶格缺陷捕获或在两层结止的界面上堆积,造成电荷在介质空间中新的分布,从而产生电矩。
这种极化称为空间电荷极化后果:夹层的存在将会造成电荷在夹层界面上的堆积和等值电容的增大,这是夹层极化效应。
特点:1,极化所需时间长,故夹层极化只有在低频时才有意义。
具有夹层绝缘的设备断开电源后,应短接进行彻底放电以免危及人身安全,大容量电容器不加电压时也应短接;2,极化涉及电荷的移动和积聚,所以必然伴随能量损耗。
2.某些电容量较大的设备经直流高电压试验后,其接地放电时间要求长达5~10min,为什么?电介质的等效电路如图(1-4-2)所示第9页,容型设备的存储电荷是较多的,放电实质是-RC电路,公式为U(1-e的T次方),其中时间常数为T=?,电容越大、放电的时间越长。
R1K —泄漏电阻 I1K—泄漏电流 Cg—介质真空和无损耗极化所形成的电容 Ig—流过Cg的电流 Rp—有损耗极化所形成的等效电阻 Cp—有损耗极化所形成的电容Ip—流过Rp- Cp支路的电流。
3.长气隙火花放电与短气隙火花放电的本质区别在哪里?形成先导过程的条件是什么?为什么长气隙击穿的平均场强远小于短气隙的?答:①是否有先导过程,长气隙有先导过程,而短气隙火花放电没有先导过程。
电介质物理 孙目珍 华南理工(缩印版)

电介质的极化:在外电场的作用下,电介质内部沿电场方向产生感应偶极矩,在电介质表面出现极化电荷的现象称为电介质的极化。
电介质的损耗:电介质在外电场的作用下,将一部分电能转变为热能的物理过程,称为电介质的损耗。
电介质电击穿:在电场直接作用下发生的电介质被破坏的现象称为电介质点击穿。
极化强度P:一种为了衡量电介质极化的强弱,用单位体积中电介质感应偶极矩的矢量和所表示的物理量。
单位是C/m2。
退极化电场:电介质极化以后,电介质表面的极化电荷将削弱极板上的自由电荷所形成的电场,所以由极化电荷所产生的场强被称为自发极化:在没有外电场的作用下,晶体的正、负电荷重心不重合而呈现电偶极矩的现象称为电介质的自发极化。
电介质热击穿:由于电介质内部热的不稳定过程所造成的击穿现象。
迁移率:单位电场作用下的载流子沿电场方向的平均漂移速度称为载流子的迁移率。
自持放电:在电场强度临界值E m点之后,即使将外界电离因素去掉,放电仍将继续维持的,称为自持放电。
居里温度:由顺电相向铁电相转变的温度。
以针-板电场(针极分别为正极和负极)为例分析不均匀电场中气体放电的极性效应答:当针尖为正时,正的空间电荷削弱了针尖附近的电场,加强了正空间电荷到极板之间的弱电场。
这种情况相当于高电场区从针尖移向板极,像是正电极向负电极延伸了一段距离,因此击穿电压比针尖为负时低。
当针尖为负时,正空间电荷包围了针电极,加强了针尖附近的电场,而削弱了正空间电荷到极板之间的电场,使极板附近原来就比较弱的电场更加减弱了,像是增加了针尖的曲率半径,电极间的距离虽然缩短了一些,但电场却均匀了,因此负针-板电极的击穿电压高于正针-板电极的击穿电压。
简述钛酸钡铁电晶体180°畴和90°畴极化反转特点答:180°畴特点:①畴壁生长速度约是声速1/10~1/5。
②侧向移动速度约是10-6~10-2cm/s。
③空间电荷对于畴壁移动的影响,阻碍电畴的反转。
电介质物理_李翰如

李波
电子科技大学 微电子与固体电子学院
第一章 电介质的极化
1.1 静电学基本定律 1.2 介电常数与介质极化 1.3 有效内电场(Ei) 1.3 克劳修斯-莫索缔方程 1.4 翁萨格有效电场 1.5 电子位移极化 1.6 离子位移极化 1.7 转向极化 1.8 热离子极化 1.9 空间电荷极化 1.10 离子晶体电介质
−
1 R2
⎟⎟⎠⎞
C
=
Q V
=
4πε0ε r
R1R2 R2 − R1
15
(2)电容器的电容计算
③ 柱形电容器
设单位长度带电量为 q = Q L
在两极板之间 R1 < r < R2
-Q +Q
L
R1
E= q 2πε0ε rr
R2
∫ ∫ V = R2 Edr = R2 q dr = q ln R2
R1
R1 2πε0ε r r
+
-
+
-
+
-
+
-
+
-
C0
=
Q0 V
=
σ0S V
+
⊕Θ
-
⊕Θ
+
-
⊕
+
Θ
εr
⊕
Θ
-
⊕
+
Θ
⊕ Θ-
+⊕ Θ
⊕ Θ-
Q = Q0 + Q′ σ =σ0 +σ′
C = Q = Q0 + Q′ VV
C = (σ 0 + σ ′)S
V
(σ 0 + σ ′)S
ε=C = C0
电介质物理基础知识

电介质物理基础知识电介质物理啊,这可是个很有趣的领域呢。
咱们就从最基本的说起吧。
电介质啊,就好比是一群很守规矩的小居民。
在普通的物质里,它们可不像那些调皮捣蛋的自由电子到处乱跑。
电介质里的电子啊,就像是被家长管得很严的小孩子,只能在自己的小范围内活动。
你想啊,要是把物质比作一个大社区,导体里的电子就像是那些满大街乱窜的小毛孩,而电介质里的电子呢,就乖乖地待在自己的小院子里。
那电介质的极化又是怎么回事呢?这就像是一群本来站得比较松散的小居民,突然来了一个指挥官(外电场)。
这个指挥官一出现,小居民们就开始按照一定的方向排队了。
有的电介质呢,是那种比较听话的,电子云中心和原子核中心稍微错开一点,就像是队伍稍微歪了一点点,这就是电子位移极化。
还有一种呢,就像是一些小家庭(分子)整个地转了个方向,这就是取向极化啦。
你看,这多像我们生活中的场景啊,一群人在某种指挥下改变自己的状态。
介电常数这个概念也很重要哦。
它就像是电介质的一个性格标签。
这个数值越大,就说明这个电介质在电场里的表现越特别。
比如说,空气的介电常数比较小,就像一个比较普通的人,没什么特别的反应。
而水的介电常数比较大,就像是一个特别敏感的人,电场一来,它的反应就比较强烈。
电介质在电容器里可有着大作用呢。
电容器就像是一个小仓库,用来储存电荷。
电介质在这个小仓库里啊,就像是仓库里的隔板。
有了这个隔板啊,电容器就能储存更多的电荷了。
如果没有电介质,就好比这个仓库没有隔板,电荷就会乱跑,能储存的电量就少多了。
再说说电介质的损耗吧。
这就像是电介质在电场里干活,干着干着就有点累了,然后就会消耗一些能量。
有些电介质损耗小,就像那些精力旺盛的小伙子,能长时间在电场里好好工作。
而有些电介质损耗大呢,就像是体弱多病的人,干不了多久就不行了。
电介质的击穿现象可就有点吓人了。
这就好比是电介质在电场的压力下突然崩溃了。
本来好好的,但是电场太强了,就像洪水冲破了堤坝一样,电介质的绝缘性就没了。
电介质物理缩印本

1、电极矩:一点电荷q 与到某一参考点的径向量r 的乘积。
对总电荷量为零的电荷系统,电极矩同参考点的位置无关。
2、电偶极矩:由于正电荷等于负电荷量,故其电极矩称为电偶极矩。
3、由等量的正负电荷不对称分布而形成的电偶极矩的分子为电偶极子。
4、点偶极子的电场:53013[]4p r Er r rµµπε=−r r r r r ,①px 5013=4xzE r µπε;②50134py yzE r µπε=;③2250134pz z r E r µπε−=5、电介质的分类:非极性电介质,极性电介质,离子性电介质;①非极性电介质:在无外电场作用时,分子的正负电荷重心重合,故分子的电偶极矩等于零,这类分子称为非极性分子。
由非极性分子组成的电介质称为非极性电介质(或中性电介质)②极性电介质:在无电场作用时,分子的正负电荷重心不重合,故分子具有固有偶极矩,这类分子称为极性分子。
由极性分子组成的电介质称为极性电介质。
根据固有偶极矩的大小又可分为:弱极性电介质,强极性电介质和中性电介质。
③离子性电介质:由正负离子所组成,不存在单个分子,包括离子型晶体玻璃,陶瓷以及其他一些无机电介质。
6、(1)非极性电介质的极化<1>无外场是,E=0,分子的固有偶极矩为零,μ0=0;<2>加上外场,E≠0,分子形成电偶极矩,μ≠0,电介质内部形成沿外场方向的宏观偶极矩,电介质表面出现束缚电荷;(2)极性电介质的极化<1>无外场作用时,E=0,分子的固有偶极矩μ≠0,但由于热运动,宏观上的偶极矩为0;<2>加上外电场,E≠0,分子固有偶极矩μ受电场力矩的作用,趋于转向外电场方向,从而沿外电场方向的宏观偶极矩不为零,在电介质表面出现束缚电荷。
电介质的极化:在外电场的作用下,电介质内部沿电场方向出现宏观偶极矩,在电介质表面出现束缚电荷,这就是电介质的极化7、极化强度P :表征电介质在外电场作用下极化程度的向量,其定义为单位体检电介质内部沿外电场方向的电偶极矩的总和,即:i P Vµ=∆∑r r (无限大,均匀,线性,各项同性电介质)8、克劳修斯方程根据电介质极化的极化强度P 的定义,当电介质中每个分子在电场方向的感应偶极矩为μ时,且单位体检分子数位N,则P=Nμ,如果每个分子的感应偶极矩μ认为与作用在其上面的电场强度Ei 成正比,即μ=αEi,则有00(1)i r P N E E αεε==−r r r,整理可得01i rN E Eαεε−=rr ,如果此处不带有矢量符号,说明有效场与外电场方向一致。
电介质物理学-8页文档资料

电介质物理学照片电介质的特征是以正、负电荷重心不重合的电极化方式传递或记录(存储)电的作用和影响;在其中起主要作用的是束缚电荷。
电介质物理主要是研究介质内部束缚电荷在电或和光的作用下的电极化过程,阐明其电极化规律与介质结构的关系,揭示介质宏观介电性质的微观机制,进而发展电介质的效用。
电介质物理也研究电介质绝缘材料的电击穿过程及其原理,以利于发展电绝缘材料。
目录定义基本概念电介质一般性质固体电介质的击穿电介质特殊效应展开定义基本概念电介质一般性质固体电介质的击穿电介质特殊效应展开编辑本段定义电介质物理学dielectric physics实际上金属也具有介电性质;但金属的介电性是来源于电子气在运动过程中感生出虚空穴(正电荷)所引起的动态屏蔽效应。
因其基本上不涉及束缚电荷,故不把金属的介电性列入电介质物理研究的范畴。
电介质有气体的、液体的和固体的,分布极广。
编辑本段基本概念电极化过程电极化的基本过程有三:①原子核外电子云的畸变极化;②分子中正、负离子的(相对)位移极化;③分子固有电矩的转向极化。
在外界电场作用下,介质的介电常数ε是综合地反映这三种微观过程的宏观物理量;它是频率ω的函数ε(ω)。
只当频率为零或频率很低(例如1千赫)时,三种微观过程都参与作用,这时的介电常数ε(0)对于一定的电介质而言是个常数,通称为介电常数,这也就是静电介电常数εs或低频介电常数。
随着频率的增加,分子固有电矩的转向极化逐渐落后于外场的变化,这时,介电常数取复数形式ε(ω)=ε′(ω)-jε″(ω),其中虚部ε″(ω)代表介质损耗;它是由于电极化过程追随不上外场的变化而引起的。
实部随着频率的增加而显著下降,虚部出现峰值,如图1所示。
频率再增加,实部ε′(ω)降至新值,虚部ε″(ω)变为零,这表示分子固有电矩的转向极化已不能响应了。
当频率进入到红外区,分子中正、负离子电矩的振动频率与外场发生共振时,实部ε′(ω)先突然增加,随即陡然下降,ε″(ω)又出现峰值;过此以后,正、负离子的位移极化亦不起作用了。
电介质,电容

介质中的高斯定理: 在静电场中,通过任意封闭曲面的电 位移通量等于该曲面所包围的自由电荷的代数和。
SDdSqi
在各向同性的电介质中:
D0rE
真空中:
D0E0
有电介质时场强的计算
1. 根据电介质中的高斯定理计算出电位移矢量。
SDdSqi
2. 根据电场强度与电位移矢量的关系计算场强。
§8-6 静电场中的电介质 一、电介质的极化
电介质:不导电的绝缘介质 两大类电介质分子结构:
1. 无极分子: 分子的正、负电荷中心在无外场时重合, 不存在固有分子电偶极矩。
=
CH4
2. 有极分子: 分子的正、负电荷中心在无外场时不重合, 分子存在固有电偶极矩。
O
O
=
H
H
q2 q2
400R 80R
H
H2O
O
电偶极子
H
无极分子的位移极化
在外电场的作用下,介质表面产生电荷的现象称为电 介质的极化。
EEEE
q/
q/
由于极化,在介质表面产生的电荷称为极化电荷或称 束缚电荷。
有极分子的取向极化
- +
E0
有极分子在外场中发生偏转而产生的极化称为取向极化。
极化电荷产生的电场:E
Q
40r
1rR124Q0
1 R2
当r> R2时
U 2rEdrrE 2dr4Q 0r
§8-7 电容 电容器
一、孤立导体的电容
1、电容
C q U
单位:法拉
反映的是孤立导体储存电能的本领,称之为电容
高二物理竞赛静电场中的电介质课件

两板间电介质内的电场强度E ,电极化强
度P ,板和电介质
的电荷面密度,
电介质内的电位
+++++++++++
移D.
U εr
d
-----------
10
解
E0
U d
103
kV m1
E E0 r 3.33102 kV m1
P ( r 1)0E 5.89 10 6 C m-2
r =3,
d=1 mm,
d
-----------
12
例2 图中是由半径为R1的 长直圆柱导体和同轴的半径为
R2的薄导体圆筒组成,其间充
以相对电容率为r的电介质. 设
直导体和圆筒单位长度上的电
荷分别为+和- . 求(1)电介 质中的电场强度、电位移和极
化强度; (2)电介质内外表面 的极化电荷面密度.
R2 R1
13
解 (1) SD dS l
r ' -+- -+- -+- - +- - +- -
故
εE
S
dS
Q0
8
εE S
dS
Q0
电位移矢量
电位移通量
D 0 r E E
SD dS
有介质时的高斯定理
n
D dS S
Q0i
i 1
9
例1 把一块相对电容率r =3的电介质,
放在相距d=1 mm的两平行带电平板之间.
放入之前,两板的电势差是1 000 V . 试求
2'
( r
1) 0E2
( r 1) 2 π r R2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
1 3ε 0
r P ; 2、洛伦兹有效场
r r 1r r Ei =E + 3ε0 P + E2 。
莫索缔有效场:对非极性或弱极性液体介质,分子相互间作用较弱,
球内分子在球心被研究分子处产生处产生的电场很弱,可近似认为等
于零,E2=0;考虑到
r P
=
ε0
(ε
r
r -1)E
,则
r Ei
=
ε
r +2 3
寇克伍德修正
1、昂扎杰理论的优点:用极性分子的反作用电场对其本身的作用来考 虑极性分子间的相互作用,比洛伦兹模型有所改进;2、昂扎杰理论的 缺点:在昂扎杰模型中,把每个极性分子周围都看成连续均匀的介质,
这实际上忽略了近邻分子的相互作用;3、用昂扎杰理论计算的 ε r 值
比实测值低得多;
※非极性和弱极性液体电介质
αe
=
3ε 0 N
n2 −1 n2 + 2
代入,整理得,
r µ
=
(n2 + 2)(2εr +1) 3(2εr + n2 )
r µ0
+
ε r (n2 −1) 2εr + n2
3ε 0 N
r E
=
r µ1
r + α1E
,μ1
是极性分子总偶极矩μ在μ0 方向的分量,由于反作用电场 R 的作用, μ1 比单个极性分子的固有偶极矩μ0 大。它可看作当介质宏观平均电 场 E 为零时液体分子的偶极矩。 α1 是极性分子在外场方向的等效极化率,α1>αe,这说明由于考虑 了极性分子间的相互作用,使得在外场方向的位移极化加强了。
µe = αeEi ,αe = 4πε0a3 结论:1、αe 数量级约为 10-40F·m2,随原子半径的增大而增大;2、
电子极化率与温度基本无关;3、计算所用的原子结构模型比较粗糙, 采用的电子云的概念与量子力学不符,所的电子极化率比实际小。 离子位移极化:在外电场作用下,构成分子的异性离子之间发生相对 弹性位移而产生感应偶极矩的现象。它仅存在与离子晶体中,建立或 消除的时间很短,与离子的晶格震动周期有相同的数量级,约 为
r rr r 研究分子上的有效电场为 Ei = E + E1 + E2 ;
其中, E----电介质内部的宏观平均电场强度; E1-----球外分子作用产生的电场强度; E2------球内分子作用产生的电场畸变 洛伦兹有效场:1、球外分子作用产生的电场可由其极化后在球表面产
r 生的束缚电荷来计算, E 1
r D = Dmei(wt−δ )
,
复
介
电
常
数
ε*=
Dm
ε '' (cosδ − i sin δ ) = ε '− iε '' , tan δ =
ε 0 Em
ε'
2、物理意义:复介电常数的实部与介质中的无功电流 Iq 相对应,与
介质的实介电常数具有相同意义,复介电常数的虚部与介质中的有功
电流相对应,表示介质中由于松弛极化引起的能量损耗。
rr
r
即 μ=αEi,则有 P= NαEi =ε0(εr −1)E0,整理可得
r
εr −1 =
N α rE i ,如果此处不带有矢量符号,说明有效场与外电 ε 0E
场方向一致。一般说来,作用于分子上的有效场或内电场 Ei 并不等于
介质中的宏观平均电场强度。
9、电介质的介电常数:是描述电介质极化的宏观参数,在静电场中,
10-12~10-13.
表达式:
αa
=
4πε 0 a3 n −1
结论:1、离子极化率的数量级为 10-40F·m2,与电子极化率具有相同的 数量级;2、离子位移极化只能在离子晶体中,而不可能存在于气体, 液体介质中;3、对离子间距不随温度而变化的离子晶体,离子极化率 与温度无关。 偶极子转向极化:极性电介质的分子本身就具有偶极矩,但由于分子 无规则的热运动偶极矩在各方向分布几率相等,因此无宏观偶极矩。 在外电场作用下,固有偶极矩由于受到外电场例句的作用,趋于转向 电场方向,从而在介质内部产生沿电场方向的宏观偶极矩,这种极化
的松弛时间较长,室温下约 1.6×10-2s
分子极化率:电介质分子极化率应等于各种极化率之和:
α =αe + αa + αd + αT ,但对于具体某种介质,往往有一种或两种
极化占主导地位,而其他次要的极化形式则可以忽略。 11、有效场理论 洛伦兹有效场模型:1、无限大平板电容器间充以均匀连续各向同性电 介质;2、被研究分子处于半径 r 的圆球中心,a<<r<<l;3、作用在被
①有效电场:
r Ei
=
εr
+ 3
2
r E
(莫索缔内电场)
②极化形式:α=αe
③极化方程: ε r −1 = Nα (克莫方程) ε r + 2 3ε0
极性固体介质 I)极低温度时,主要是电子位移极化和弹性偶极子极化,介电常数很 小; II)温度升高时,由于极性基团旋转定向,而发生松弛极化,介电常数 增大; III)温度高于波化温度时,温度偶极子高弹态极化,介电常数进一步 增大; IIII)温度进一步升高,由于分子热运动的无序化作用,使介电常数开 始减小。 ※极化的建立过程和吸收电流 1、根据极化建立所需的时间,可以将极化分为:瞬时位移极化和松弛
晶体玻璃,陶瓷以及其他一些无机电介质。
6、(1)非极性电介质的极化
<1>无外场是,E=0,分子的固有偶极矩为零,μ0=0;
<2>加上外场,E≠0,分子形成电偶极矩,μ≠0,电介质内部形成沿
外场方向的宏观偶极矩,电介质表面出现束缚电荷;
(2)极性电介质的极化
<1>无外场作用时,E=0,分子的固有偶极矩μ≠0,但由于热运动,宏
3、德
拜
方
程
:
①
ε
'
=
ε∞
+
εs 1+
−ε∞ w2τ 2
;②
ε
''
=(ε s
wτ − ε∞ ) 1+ w2τ
2
;③ tan δ
=ε
'' ε
'
=
(εs − ε∞ )wτ ε s + ε∞w2τ 2
柯尔--柯尔图
德拜方程是在单一松弛时间的情况下的得到的,但实际中的松弛时间 并不是单一的,这就造成了大多数电介质的实验频率特性曲线与德拜 方程不一致,往往是一段圆弧。这是由于电介质具有一组不同的弛豫 时间,而实际介质的松弛时间是围绕其最大几率的一个分布,而实验
体或固体介质中均会发生,但由于偶极分子间的长程作用,定量即使
比较困难。
热离子等效极化:在含有弱联系离子或缺陷离子的固体介质中,由于
热振动能超过近邻分子对其的束缚势垒而脱离原来的平衡位置,在外
电场作用下,这些弱联系离子发生定向迁移,从而使正负离子分布不
均,在电介质内部形成宏观偶极矩,这种由于热运动而导致的极化现
象称为热离子等效极化。
结论:1、热离子极化是由热运动所引起的,电场作用只是是已脱离平
衡位置的弱联系离子作定向迁移,造成介质内部电荷分布不均,形成
偶极矩。2、当电场不太强时,决定极化建立速度的松弛时间τ 只与温
度有关,而与电场强度无关。3、极化强度随电场强度的增加而线性的
增加,这是由于电场是定向迁移离子数随场强而线性增加;4、热离子
※电介质的损耗
1、损耗的定义:电介质在单位时间内所消耗的能量,称为损耗。来源:
电导,松弛极化,结构损耗。
2、介质损耗的表征
在恒定外场作用下,电介质的损耗仅由电导所引起,用体积电导
率就可以描述在交变电场作用下,除电导外,还有周期性的松弛极化
所引起的损耗。 ta n δ = 有 功 / 无 功
3、损耗角正切的 tan δ
r− ] r3
,
①
1 3xz
1 3yz
Epx = 4πε0 r5 µ ; ② Epy = 4πε0 r5 µ ; ③
1 3z2 − r2 Epz = 4πε0 r5 µ
5、电介质的分类:非极性电介质,极性电介质,离子性电介质;
①非极性电介质:在无外电场作用时,分子的正负电荷重心重合,故
分子的电偶极矩等于零,这类分子称为非极性分子。由非极性分子组
观上的偶极矩为 0;
<2>加上外电场,E≠0,分子固有偶极矩μ受电场力矩的作用,趋于转
向外电场方向,从而沿外电场方向的宏观偶极矩不为零,在电介质表
面出现束缚电荷。
电介质的极化:在外电场的作用下,电介质内部沿电场方向出现宏观
偶极矩,在电介质表面出现束缚电荷,这就是电介质的极化
7、极化强度 P:表征电介质在外电场作用下极化程度的向量,其定义为
rr r 极化。故电介质的极化强度 P 一般可写成: P = P∞ + Pr ;
※吸收电流 在极化建立过程中,电介质中的总电流可看作两部分之和:
i总 =IR + ID ,IR:电导电流,ID:位移电流, i总 =IR + I∞ + ia , I∞ :
瞬时充电电流, ia : 吸收电流
可见,在实际的电容器中,缓慢的松弛极化形成了滞后于电压并随时 间而衰减的吸收电流,这就是介质的松弛现象,需指出,吸收电流只 有在交变电场时才存在,它是介质在交变电场作用下引起介质损耗的 重要来源。
4 πa3N 3
r =1,µ
=
r µ0
r + αeEi
;2、作用
rrr
于极性液体分子的有效场 Ei 由两部分所组成, Ei =G + R ,式中,G:
