实验四-离散傅里叶变换
数字信号处理 实验4_离散信号的频域分析

实验四离散信号的频域分析1. 计算序列的DTFT和DFT,观察栅栏效应设)()(4nRnx=,要求用MATLAB实现:(1)计算)(nx的傅里叶变换)(ωj eX,并绘出其幅度谱;(2)分别计算)(nx的4点DFT和8点DFT,绘出其幅度谱。
并说明它们和)(ωj eX的关系。
(提示:DFT变换可用MA TLAB提供的函数fft实现,也可以自己用C语言或matlab 编写)源程序:n1=4;n2=8;n=0:n1-1;k1=0:n1-1;k2=0:n2-1;w=2*pi*(0:2047)/2048;Xw=(1-exp(-j*4*w))./(1-exp(-j*w))xn=[(n>=0)&(n<4)];X1k=fft(xn,n1);X2k=fft(xn,n2);subplot(3,1,1)plot(w/pi,abs(Xw));title('x(n)的傅里叶变换的幅度谱')subplot(3,1,2)stem(k1,abs(X1k))title('4点的DFT[x(n)]=X1(k)的幅度谱')subplot(3,1,3)stem(k2,abs(X2k))title('8点的DFT[x(n)]=X1(k)的幅度谱')实验结果图:由实验结果图可知,X(k)是)(ωj e X 的等间隔采样,采样间隔是2π/N 。
2.计算序列的FFT ,观察频谱泄漏已知周期为16的信号)1612cos()1610cos()(n n n x ππ+=。
(1) 截取一个周期长度M=16点,计算其16点FFT 其频谱,并绘出其幅度谱;(2) 截取序列长度M=10点,计算其16点FFT 其频谱,绘出其幅度谱,并与(1)的结果进行比较,观察频谱泄漏现象,说明产生频谱泄漏的原因。
(1)源程序:T=16;fs=1/T;n=0:15;xn=cos(10*pi/16*n*T)+cos(12*pi/16*n*T);Xk=fft(xn,16)stem(n,abs(Xk))实验结果图:(2)源程序:T=16;fs=1/T;n=0:9;xn=cos(10*pi/16*n*T)+cos(12*pi/16*n*T); Xk1=fft(xn,16)stem(0:15,abs(Xk1))实验结果图:如图,可得出,当截取有限长信号时,频谱不再是单一的频谱,它的能量散布到整个频谱的各处。
实验四离散傅立叶变换DFT

实验四离散傅立叶变换DFT实验四离散傅里叶变换(DFT )一实验目的(1)理解信号变换的基本概念(2)理解离散傅立叶变换的基本概念二实验原理及实例分析 1、离散傅里叶变换傅里叶变换是信号分析和处理的重要工具。
有限长序列作为离散信号的一种,在数字信号处理中占有着极其重要的位置。
对于有限长序列,离散傅立叶变换不仅在理论上有着重要的意义,而且有快速计算的方法-快速傅立叶变换FFT 。
所以在各种数字信号处理的运算方法中,越来越起到核心的作用。
1.1 傅里叶变换的几种形式1、非周期连续时间信号的傅里叶变换非周期连续时间信号)(t x 的傅立叶变换)(ωj X 可以表示为)(ωj X =dt e t x tj ?∞∞--ω)(逆变换为ωωπωd j x t x tj ?∞∞-=)(21)(在这里,ω是模拟角频率。
可以看到,时域的连续函数造成频域的非周期谱,时域的非周期性造成频域的连续谱。
结论:非周期连续时间函数对应于一非周期连续频域变换函数。
2、周期连续时间信号的傅里叶变换周期为T 的周期性连续时间信号)(t x 傅立叶变换是离散频域函数,可表示为-=22)(1)(T T tjm d e t x Tjm X ωωω 逆变换为ωωωd ejm X t x tjm m ∑∞-∞==)()(这就是经常称之为傅里叶级数的变换形式。
在这里,ω也是模拟角频率。
可以看到,时域的连续函数造成频率域的非周期谱,频域函数的离散造成时域函数的周期性。
结论:周期连续时间函数对应于一离散非周期频域变换函数。
3、非周期离散时间信号)(n x 的傅立叶变换)(ωj e X 可以表示为∑∞-∞=-=nnj j e n x e X ωω)()(逆变换为ωπωππωd e e X n x n j j ?-=)(21)( 在这里,ω是数字频率,它和模拟角频率的关系为T Ω=ω。
可以看到,时域的取样对应于频域的周期延拓,而时域函数的非周期性造成频域的连续谱。
实验四离散信号频谱分析
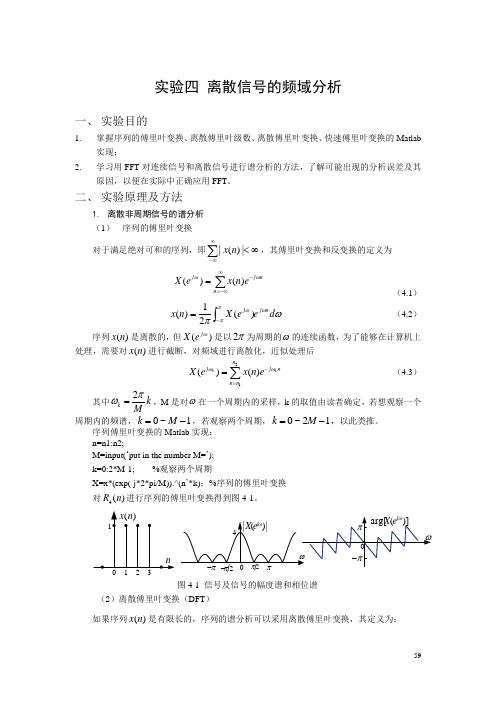
实验四 离散信号的频域分析一、 实验目的1. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab 实现;2.学习用FFT 对连续信号和离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
二、 实验原理及方法1. 离散非周期信号的谱分析 (1) 序列的傅里叶变换对于满足绝对可和的序列,即∞<∑∞∞-|)(|n x ,其傅里叶变换和反变换的定义为∑∞-∞=-=n nj j en x e X ωω)()( (4.1)ωπωππωd eeX n x nj j ⎰-=)(21)( (4.2)序列)(n x 是离散的,但)(ωj e X 是以π2为周期的ω的连续函数,为了能够在计算机上处理,需要对)(n x 进行截断,对频域进行离散化,近似处理后21()()kk n j j nn n X ex n eωω-==∑(4.3)其中2k k Mπω=,M 是对ω在一个周期内的采样,k 的取值由读者确定,若想观察一个周期内的频谱,0~1k M =-,若观察两个周期,0~21k M =-,以此类推。
序列傅里叶变换的Matlab 实现: n=n1:n2;M=input(…put in the number M=‟); k=0:2*M-1; %观察两个周期X=x*(exp(-j*2*pi/M)).^(n ‟*k);%序列的傅里叶变换 对4()R n 进行序列的傅里叶变换得到图4-1。
图4-1 信号及信号的幅度谱和相位谱(2)离散傅里叶变换(DFT )如果序列)(n x 是有限长的,序列的谱分析可以采用离散傅里叶变换,其定义为:10,)()]([)(10-≤≤==∑-=N k W n x n x DFT k X N n knN(4.4)10,)(1)]([)(1-≤≤==∑-=-N n Wk X Nk X IDFT n x N k kn N(4.5)因为)(n x 与)(k X 都是离散的,所以可以利用计算机进行数值计算。
实验四 信号的分解与合成

实验四信号的分解与合成实验目的:1.了解信号的分解与合成原理;2.掌握连续时间信号的傅里叶级数分解公式及其应用;3.掌握离散时间信号的傅里叶变换公式及其应用。
实验原理:1.信号的分解任何信号都可以分解成若干谐波的叠加。
这是因为任何周期信号都可以表示为若干谐波的叠加。
傅里叶级数分解公式:$$x(t)=\sum_{n=-\infty}^{+\infty} C_ne^{jn\omega_0t}$$其中,$C_n$为信号的各级谐波系数,$\omega_0$为信号的基波频率。
当信号为实信号时,其傅里叶级数中只有实系数,且对称性可利用,因此实际计算中可以只计算正频率系数,即$$x(t)=\sum_{n=0}^{+\infty} A_n\cos(n\omega_0t+\phi_n)$$其中,$A_n$为信号各级谐波幅度,$\phi_n$为各级谐波相位。
若信号不是周期信号,则可以采用傅里叶变换进行分解。
2.信号的合成对于任意信号$y(t)$,都可以表示为其傅里叶系数与基波频率$\omega_0$的乘积的叠加,即$$y(t)=\sum_{n=-\infty}^{+\infty}C_ne^{jn\omega_0t}$$若$y(t)$为实信号,则其傅里叶系数中只有正频率系数,即$$y(t)=\sum_{n=0}^{+\infty}A_n\cos(n\omega_0t+\phi_n)$$实验步骤:一、连续时间信号的傅里叶级数分解1.打开Matlab软件,使用line或scatter等函数绘制出函数$f(x)=x(0<x<2\pi)$的图像。
2.使用Matlab的fft函数对f(x)进行逆傅里叶变换得到其傅里叶级数分解。
3.将得到的傅里叶级数分解与原函数的图像进行比较,分析级数中谐波幅度的变化规律。
二、离散时间信号的傅里叶变换1.使用Matlab生成一个为$sin(\pi k/4),0\le k\le 15$的离散时间信号。
实验四 离散时间信号的傅里叶变换

实验四离散时间信号的傅里叶变换1.实验目的(1)理解离散序列傅里叶变换的原理和方法。
(2)掌握快速傅里叶变换的原理和方法。
2.实验原理(1)离散傅里叶变换(DFT)和快速傅里叶变换(FFT)在MATLAB中,离散傅里叶正变换采用fft( )函数,离散傅里叶逆变换采用ifft( )函数。
调用格式为:Xk=fft(x) 表示计算信号x的快速傅里叶变换Xk。
Xk=fft(x,N) 表示计算信号x的N点快速傅里叶变换。
xn=ifft(Xk)表示计算Xk的快速傅里叶逆变换xn。
Xn=ifft(Xk,N) 表示计算Xk的N点快速傅里叶逆变换xn。
另外,MATLAB中使用fftshift()函数来移动零频点到频谱中间,重新排列fft( )的输出结果,便于观察傅里叶变换。
其调用格式为:X=fftshift(Xk)(2)离散时间系统的频率特性在用MATLAB计算系统的频率响应时,可调用freqz( )函数进行求解,其调用格式为:H=freqz(b,a,w)其中b为系统函数中分子多项式的系数向量,a为分母多项式的系数向量,w为角频率向量,向量H则返回在w所定义的频率点上系统函数的值。
该函数还有其他调用形式[h,w]=freqz(b,a,n)该形式计算默认范围内n个频率点的系统函数的值(n的默认值为512)。
freqz(b,a)该形式并不返回系统函数的值,而是以对数坐标的方式绘出系统频率响应曲线。
3.实验内容(1)求有限长序列x[n]=(0.7e^(jpi/4))^n,0<=n<=16的傅里叶变换。
N=17;n=0:N-1;x=(0.7*(exp(j*pi/4))).^n;X=fft(x,N);stem(n,fftshift(X));grid on;0246810121416(2)已知无限长序列x[n]=a^n*u[n](a=0.7),用fft( )计算其频谱。
a=0.7;N=51;n=0:N-1;x=(a.^n).*heaviside(n);X=fft(x,N);stem(n,fftshift(X));grid on;05101520253035404550(3)对于矩阵脉冲波序列x[n]=1(-M<=n<=M),0(n为其他值),自取M值用freqs( )函数求幅度频谱。
数字信号处理实验离散傅里叶变换及其特性验证

数字信号处理实验离散傅⾥叶变换及其特性验证数字信号处理实验报告实验名称:离散傅⾥叶变换及其特性验证学号:姓名:评语:成绩:⼀、实验⽬的1、掌握离散时间傅⽴叶变换(DTFT )的计算⽅法和编程技术。
2、掌握离散傅⽴叶变换(DFT )的计算⽅法和编程技术。
3、理解离散傅⽴叶变换(DFT )的性质并⽤MA TLAB 进⾏验证。
⼆、实验原理与计算⽅法1、离散时间傅⽴叶变换如果序列x (n )满⾜绝对可和的条件,即∞<∑∞-∞=n n x |)(|,则其离散时间傅⽴叶变换定义为: ∑∞-∞=-==n nj j en x n x F e X ωω)()]([)( (1)如果x (n )是⽆限长的,则不能直接⽤MATLAB 由x (n )计算X (e j ω),但可以⽤它来估计X (e j ω)表达式在[0,π]频率区间的值并绘制它的幅频和相频(或实部和虚部)曲线。
如果x (n )是有限长的,则可以⽤MATLAB 对任意频率ω处的X (e j ω)进⾏数值计算。
如果要在[0,π]间按等间隔频点估计X (e j ω),则(1)式可以⽤矩阵-向量相乘的运算来实现。
假设序列x (n )在N n n n ≤≤1(即不⼀定在[0, N -1])有N 个样本,要估计下列各点上的X (e j ω):M k k Mk ...,2,1,0==, πω它们是[0,π]之间的(M +1)个等间隔频点,则(1)式可写成: M k n x ee X Nl l kn Mjj l...,2,1,0)()(1==∑=-, πω(2)将{x (n l )}和{X (e j ωk)}分别排列成向量x 和X ,则有:X=Wx (3)其中W 是⼀个(M +1)×N 维矩阵:=≤≤=-M k n n n e N kn M j ...,2,1,0;1, πW将{k }和{n }排成列向量,则????????? ?-=n k W T M j πexp 在MA TLAB 中,把序列和下标排成⾏向量,对(3)式取转置得:?-=k n x X T T T M j πexp其中n T k 是⼀个N ×(M +1)维矩阵。
第四章离散傅里叶变换

• 设 ~x(n)为周 期 为 N 的 周 期 序 列 , 则 其 离
散 傅 里 叶 级 数 (DFS) 变 换 对 为 :
• 正变换
X~(k)
DFS[~x(n)]
N
1
~x (n)e
j
2 N
nk
N1 ~x (n)WNnk
• 反变换
n0
n0
•
~x (n)
其中:
IDFS [ X~ (k )]
1 N
x%2 m … 5 4 3 2 1 0 5 4 3 2 1 0 … 10 x%2 1 m … 0 5 4 3 2 1 0 5 4 3 2 1 … 8 x%2 2 m … 1 0 5 4 3 2 1 0 5 4 3 2 … 6 x%2 3 m … 2 1 0 5 4 3 2 1 0 5 4 3 … 10 x%2 4 m … 3 2 1 0 5 4 3 2 1 0 5 4 … 14 x%2 5 m … 4 3 2 1 0 5 4 3 2 1 0 5 … 12
解: y%(n) x%1(m)x%2 (n m)
m0
5
x%1(m)x%2 (n m)
m0
n m …-4 -3 -2 -1 0 1 2 3 4 5 6 7 …
x%1 n / m … 1 1 0 0 1 1 1 1 0 0 1 1 … x%2 n / m … 3 4 5 0 1 2 3 4 5 0 1 2 … y%(n)
1.由非周期连续时间信号推出DFS
• X(t)经过抽样为x(nT),对离散的时间信
号进行DTFT得到周期连续频谱密度函
数。再经过抽样,得到周期性离散频
谱密度函数即为DFS.
x(t)
取样
x(t)
D T
实验四傅里叶变换(FT)及其性质

实验四傅里叶变换(FT)及其性质一、实验目的1学会运用Matlab求连续时间信号的傅里叶2、学会运用Matlab求连续时间信号的频谱图3、学会运用Matlab分析连续时间信号的傅里叶变换的性质二、实验原理及实例分析(一)傅里叶变换的实现在曲廊讨论的刑期信号中・当WW T *〒时•周期信号就鞘化为非闻期信号・当周期<吋・周期信号的各欢锻波幅度及谱线间編将JS近于尢勢小•但類谱的相时形状像持不变・这样*象来由许多谓鎖#!眦的曲期WT号MAttlK谱Ht会连咸用、够成卄周期们号前诠纹顶讲为r有效地分析ir庇期信号的稠¥ tv h •找门引人广忙w叶交换分折法.倩号川卄的傅卑叶更换宦义为FW 士F[/h)]= [ /<Oc **dx肾堀叶反变换定义为/(I) —F * F<(w) I = f Flcube*"血X」博里叶正反变换称为博里"I変换M■简记为/(D*^F<w)#倍号的1•星叶愛換主!8包括MATLAB将号运算和MATLAB散值分析两稈方ifc・ F 而分WlifflUJL探讨.同时•探讨r if续时純信号的極谐圈・L MATLAB 号运算求解隆MATLAB If号散学Ttl箱提供了祈援求解傅里叶变换峙博屢叶反愛换的函数fouritrt) ifouricrt >4Fmiri史t 变換的ifi句格式分为二种*(])F founcrC/) i它丘符号函数_/ W Fomrirr $换•默认屯冋話关「h的瞩数, (Z h)' F-fourieK/^h它返河碉数F £关十符号时象的歯数•血木是默认的心即r -F*v) /f j}<. z 血,(3) F^fouricK/.w^J,屋对按于禺的函数/进抒變换・返叫臥敢FMt英于卫的満fa "■散.即F(r) - "*dw-,反变换的洽句祐式di分为三种.(U f ikurUHF);r的Fourier 换•迪立变址默认为占默认返岡JtJtTi-的戚数.(2)f = ifourier(F*M):它返Wi隕数丿星M的肃数■而不是JK认的工*(-i J f ifuLLrk-rt F, a tT>) *是对关T '■■'的函数F进行变换*返hd Xi J "的rfi独j・伯幫汴审;的是” ifi数(outicri、及ifourtert )KF Gift'S Eft w”嚙进片足是的笛号变址或瘠罚号我达式・例1用Matlab符号运算求解法求单边指数信号f (t) =^'1化)的FT。
测试信号分析与处理第4章 离散傅里叶变换

m0
2)频域圆卷积
若 y(n) x(n)h(n)
1 N 1
Y (k) DFT[ y(n)] N l0 X (l)H p (k l)RN (k)
❖ 实数序列奇偶性(对称性)
❖ 帕斯瓦尔定理:变换过程中能量是守恒的。
N1 x(n) 2
1 N 1
2
X (k)
n0
N k0
第二节 离散傅里叶级数(DFS)
二、离散傅里叶级数 ❖ 离散周期信号的频谱,即离散傅里叶级数(DFS)。 ❖ 离散傅里叶级数的变换对表达式
N 1
X p (k) DFS[xp (n)] xp (n)WNnk n0
xp (n)
IDFS[ X p (k)]
《测试信号分析与处理》课程
第五节 快速傅里叶变换 第六节 IDFT的快速算法(IFFT) 第七节 实序列的FFT高效算法 第八节 频率域采样理论
第一节 序列的傅里叶变换
❖ 如X(Z)在单位圆上是收敛的,则将在单位圆上的Z 变换定义为序列的傅里叶变换,即
)]
1
Y(k) 2
X(k)
k 0,1, , N 1 2
Z(k)
1 2
WN
K
-1
X(k+N/2)
第六节 IDFT的快速算法(IFFT)
x(0) 1/2
1/2
1/2
X(0)
x(1) 1/2 W80 -1 1/2
1/2
X(1)
x(2) 1/2
1/2 W80
-1
1/2
X(k)= Wnkx(n)
或
x(n)= 1 W-nkX(k)
实验四 利用DFT分析离散信号频谱

数字信号处理及实验实验报告实验题目利用DFT分析离散信号频谱姓名组别班级光电14 学号144320200206 【实验目的】应用离散傅里叶变换(DFT),分析离散信号的频谱。
深刻理解DFT分析离散信号频谱信号频谱的原理,掌握改善分析过程中产生的误差的方法。
【实验原理】根据信号傅里叶变化建立的时域与频域之间的对应关系,可以得到有限序列的离散傅里叶变换(DFT)与4种确定信号傅里叶变换之间的关系,实现由DFT分析其频谱。
【实验结果与数据处理】1、利用FFT分析信号x[k] = cos(3πk/8),k = 0,1,2……,31的频谱:(1)确定DFT计算的参数。
(2)进行理论值与计算值比较,讨论信号频谱分析过程中产生误差的原因及改善方法。
分析:信号的周期T = 16,角频率w=2π/N=π/8。
clc,clear,close allN = 16; k = 0 : N-1;x = cos(3*pi*k/8);X = fft(x,N);subplot(2,1,1);stem(k - N/2,abs(fftshift(X)));ylabel('幅度','fontsize',15);xlabel('频率(rad)','fontsize',15);subplot(2,1,2);stem(k - N/2,angle(fftshift(X)));ylabel('相位','fontsize',15);xlabel('频率(rad)','fontsize',15);2、有限长脉冲序列x[k]= [2,3,3,1,0,5;k = 0,1,2,3,4,5],利用FFT分析其频谱,并绘出其幅度谱与相位谱。
clc,clear,close allN = 6; k = 0 : N-1; w = k-3;x=[2,3,3,1,0,5];X=fft(x,N);subplot(2,1,1);stem(w,abs(fftshift(X)));ylabel('幅度','fontsize',15);xlabel('频率(rad)','fontsize',15);subplot(2,1,2);stem(w,angle(fftshift(X)));ylabel('相位','fontsize',15);xlabel('频率(rad)','fontsize',15);3、某周期序列由3个频率组成:x[k] = cos(7πk/16) + cos(9πk/16) + cos(πk/2),利用FFT分析其频谱。
离散傅里叶变换

离散傅里叶变换离散傅里叶变换(DFT),是连续傅里叶变换在时域和频域上都离散的形式,将时域信号的采样变换为在离散时间傅里叶变换(DTFT)频域的采样。
在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。
即使对有限长的离散信号作DFT,也应当将其看作经过周期延拓成为周期信号再作变换。
在实际应用中通常采用快速傅里叶变换以高效计算DFT。
目录对换实例离散傅里叶变换的基本性质对换实例离散傅里叶变换的基本性质展开编辑本段对换实例傅里叶变换的变换对对于N点序列{x[n ]} 0 ≤ n < N ,它的离散傅里叶变换(DFT)为?x[k ] = N - 1Σn = 0 e - i 2 π–––––N n k x[n ] k = 0,1, …,N-1.其中e 是自然对数的底数,i 是虚数单位。
通常以符号F表示这一变换,即?x= Fx离散傅里叶变换的逆变换(IDFT)为:x[n ] = 1––N N - 1Σk = 0 e i 2 π–––––N nk ?x[k ] n = 0,1, …,N-1.可以记为:x = F -1 ?x实际上,DFT和IDFT变换式中和式前面乘上的归一化系数并不重要。
在上面的定义中,DFT和IDFT前的系数分别为1 和1/N。
有时会将这两个系数都改成1/ √––N,这样就有x = FFx,即DFT成为酉变换。
从连续到离散连续时间信号x(t) 以及它的连续傅里叶变换(CT)?x( ω)都是连续的。
由于数字系统只能处理有限长的、离散的信号,因此必须将x 和?x都离散化,并且建立对应于连续傅里叶变换的映射。
数字系统只能处理有限长的信号,为此假设x(t)时限于[0, L],再通过时域采样将x(t) 离散化,就可以得到有限长的离散信号。
设采样周期为T,则时域采样点数N=L/T。
x discrete (t) = x (t) N - 1Σn = 0 δ(t-nT) = N - 1Σn = 0 x (nT) δ(t-nT)它的傅里叶变换为?xdiscrete ( ω) = N - 1Σn = 0 x (nT)F δ(t-nT) = 1––T N - 1Σn = 0 x (nT)e - i 2 π n ω T这就是x(t)时域采样的连续傅里叶变换,也就是离散时间傅里叶变换,它在频域依然是连续的。
实验四 离散时间系统的频域分析

实验四 离散时间系统的频域分析1.实验目的(1)理解和加深傅里叶变换的概念及其性质。
(2)离散时间傅里叶变换(DTFT)的计算和基本性质。
(3)离散傅里叶变换(DFT)的计算和基本性质。
2.实验原理对离散时间信号进行频域分析,首先要对其进行傅里叶变换,通过得到的频谱函数进行分析。
离散时间傅里叶变换(DTFT ,Discrete-time Fourier Transform)是傅立叶变换的一种。
它将以离散时间nT (其中,T 为采样间隔)作为变量的函数(离散时间信号)f (nT )变换到连续的频域,即产生这个离散时间信号的连续频谱()iw F e ,其频谱是连续周期的。
设连续时间信号f (t )的采样信号为:()()()sp n f t t nT f nT d ¥=-=-å,并且其傅里叶变换为:()()(){}sp n iwt f t f nT t nT dt e d ¥¥-=---=åòF 。
这就是采样序列f(nT)的DTFT::()()iwTinwT DTFT n F ef nT e ¥-=-=å,为了方便,通常将采样间隔T 归一化,则有:()()iwinw DTFT n F ef n e ¥-=-=å,该式即为信号f(n)的离散时间傅里叶变换。
其逆变换为:()1()2iw DTFT inw F e dw f n e ppp-=ò。
长度为N 的有限长信号x(n),其N 点离散傅里叶变换为:1()[()]()knNN n X k DFT x n x n W -===å。
X(k)的离散傅里叶逆变换为:101()[()]()knN N k x n IDFT X k X k W N --===å。
DTFT 是对任意序列的傅里叶分析,它的频谱是一个连续函数;而DFT 是把有限长序列作为周期序列的一个周期,对有限长序列的傅里叶分析,DFT 的特点是无论在时域还是频域都是有限长序列。
实验四 利用离散傅立叶变换(DFT)分析信号的频谱

实验四 利用离散傅立叶变换(DFT )分析信号的频谱一、实验目的1、通过这一实验,能够熟练掌握快速离散傅里叶变换(FFT )的原理及其用FFT 进行频谱分析的基本方法。
2、在通过计算机上用软件实现FFT 及信号的频谱分析。
3、通过实验对离散傅里叶变换的主要性质及FFT 在数字信号处理中的重要作用有进一步的了解。
二、实验原理1、离散傅里叶变换(DFT )及其主要性质DFT 表示离散信号的离散频谱,DFT 的主要性质中有奇偶对称特性,虚实特性等。
通过实验可以加深理解。
例如:实序列的DFT 具有偶对称的实部和奇对称的虚部,这可以证明如下: 由定义∑-==10)()(N n kn NW n x k X ∑∑-=-=-=1010)2sin()()2cos()(N n N n kn N n x j kn N n x ππ ∑-=-=-10)()()(N n n k N N W n x k N X∑-=-=10)(N n kn N Nn W W n x ∑-=-=10)(N n kn N W n x ∑∑-=-=+=1010)2sin()()2cos()(N n N n kn N n x j kn N n x ππ )(*)(k N X k X -=∴实序列DFT 的这个特性,在本实验中可以通过实指数序列及三角序列看出来。
对于单一频率的三角序列来说它的DFT 谱线也是单一的,这个物理意义我们可以从实验中得到验证,在理论上可以推导如下: 设:)()2sin()(n R n N n x N π=,其DFT 为: ∑-=-=102)()(N n kn N j en x k X π kn Nj N n e n N ππ210)2sin(--=∑= kn N j N n n N j n N j e e e j πππ21022)(21--=-∑-= ∑-=+----=10)1(2)1(2)(21N n k n N j k n N j e e j ππ 从而∑-=-=-=10220)(21)0(N n n N j n N j e e j X ππ∑-=--==-=10422)1(21)1(N n n N j N j j N e j X π 0)2(=X0)2(=-N X22)(21)1(102)2(2N j j N e e j N X N n n j n N N j =-=-=-∑-=--ππ以上这串式中)0(X 反映了)(n x 的直流分量,)1(x 是)(n x 的一次谐波,又根据虚实特性)1()1(*X N X =-,而其它分量均为零。
信号处理实验四离散傅里叶变换

信号处理实验四离散傅里叶变换哈尔滨工程大学实验报告实验名称:实验四:离散傅里叶变换班级:电子信息工程4班学号:姓名:实验时间: 2016年10月19日成绩:________________________________指导教师:栾晓明实验室名称: 数字信号处理实验室哈尔滨工程大学实验室与资产管理处 制实验四 离散傅里叶变换一、 实验原理1. 由DFT 定义式:10()[()]()NN knn X k DFT x n x n W -===∑ k=0,1 , … , N -1,将其写成矩阵方程表示为NX W x =利用MATLAB 的矩阵运算功能,可编写出计算DFT 的函数文件。
function [Xk] = dft(xn,N) %计算离散傅里叶变换%Xk = 在0<=k<=N-1间的DFT 系数数组 %xn = N 点有限长序列 % N = DFT 的长度 n = [0:1:N-1]; %n 的行向量 k = [0:1:N-1]; %k 的行向量WN = exp(-j*2*pi/N);%Wn 因子 nk = n'*k;%产生一个含bk 值的N 乘N 维矩阵 WNnk = WN.^nk; %DFT 矩阵 Xk = xn*WNnk; %DFT 系数的行向量由IDFT 定义式:11()[()]()N nkk x n IDFT X k X k W N--===∑ ,n= 0, 1, 2, … ,N -1,利用MATLAB 的矩阵运算功能,可编写出计算傅里叶反变换的函数文件。
function [xn] = idft(Xk,N) %计算离散傅里叶反变换 %----------------- %xn = 在0<=n<=N-1 %Xk = N 点有限长序列 % N = IDFT 的长度 k = [0:1:N-1]; %k 的行向量 n = [0:1:N-1]; %n 的行向量WN = exp(-j*2*pi/N); %Wn 因子 nk = n'*k;%产生一个含bk 值的N 乘N 维矩阵 WNnk = WN.^nk; %DFT 矩阵 xn = Xk*WNnk;%傅里叶反变换计算序列值 DFT 的快速算法FFT 利用了W nkN的三个固有特性:(1)对称性,(W )W nk nkN N*-=,(2)周期性,()()W W W nk n N k n k N N N N++==,(3)可约性,W nk nmkN mNW =和//W nk nk m N N mW =。
离散傅里叶变换及其快速算法
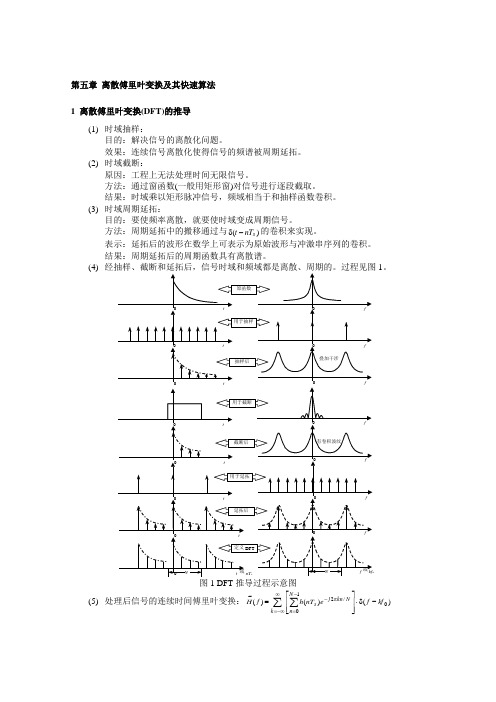
第五章 离散傅里叶变换及其快速算法 1 离散傅里叶变换(DFT)的推导(1) 时域抽样:目的:解决信号的离散化问题。
效果:连续信号离散化使得信号的频谱被周期延拓。
(2) 时域截断:原因:工程上无法处理时间无限信号。
方法:通过窗函数(一般用矩形窗)对信号进行逐段截取。
结果:时域乘以矩形脉冲信号,频域相当于和抽样函数卷积。
(3) 时域周期延拓:目的:要使频率离散,就要使时域变成周期信号。
方法:周期延拓中的搬移通过与)(s nT t -δ的卷积来实现。
表示:延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。
结果:周期延拓后的周期函数具有离散谱。
(4)1。
图1 DFT 推导过程示意图(5) 处理后信号的连续时间傅里叶变换:∑∑∞-∞=-=π--δ⋅⎥⎥⎦⎤⎢⎢⎣⎡=k N n N kn j s kf f e nT h f H )()()(~010/2(i))(~f H 是离散函数,仅在离散频率点SNT kT k kf f ===00处存在冲激,强度为k a ,其余各点为0。
(ii) )(~f H 是周期函数,周期为ss T NT N T N Nf 100===,每个周期内有N 个不同的幅值。
(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。
2 DFT 及IDFT 的定义(1) DFT 定义:设()s nT h 是连续函数)(t h 的N 个抽样值1,,1,0-=N n ,这N 个点的宽度为N 的DFT 为:[])1,...,1,0(,)()(10/2-=⎪⎪⎭⎫⎝⎛==∆-=π-∑N k NTk H enT h nT h DFT s N n Nnk j s s N (2) IDFT 定义:设⎪⎪⎭⎫⎝⎛s NT kH 是连续频率函数)(f H 的N 个抽样值1,,1,0-=N k , 这N 个点的宽度为N 的IDFT 为:())1,...,1,0(,110/21-==⎪⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛∆-=π--∑N k nT h e NTkH NNT kH DFT s N k N nk j s sN (3) N nk j e /2π-称为N 点DFT 的变换核函数,N nk j e /2π称为N 点IDFT 的变换核函数。
离散傅里叶变换

离散傅里叶变换(Discrete Fourier Transform, DFT)是一种将离散信号转换为频域表示的数学工具。
它是傅里叶变换在离散领域的推广和延伸,广泛应用于信号处理、图像处理、通信系统等领域。
在理解离散傅里叶变换之前,我们先来回顾一下傅里叶变换的概念。
傅里叶变换是一种将时域信号转换为频域信号的方法。
通过傅里叶变换,我们可以将一个信号表示为不同频率的正弦波或余弦波的叠加。
傅里叶变换可以用来分析信号的频谱特性,从而实现滤波、音频处理等操作。
而离散傅里叶变换则是将傅里叶变换应用于离散信号。
离散信号是指信号在时间(或空间)上以离散的方式采样得到的信号。
在现实应用中,信号往往是以数字的形式存储和处理的,因此离散傅里叶变换成为了非常重要的工具。
离散傅里叶变换的定义如下:给定由N个实数或复数构成的序列{x(n)},其离散傅里叶变换为:X(k) = Σ(x(n) * e^(-i2πkn/N))其中,k和n都是整数,X(k)是频谱上的一个点,对应于频率为k的分量,x(n)是原始信号上的一个点。
离散傅里叶变换的求解可以利用快速傅里叶变换(Fast Fourier Transform, FFT)算法进行高效计算。
FFT算法利用了信号的周期性和对称性,通过将计算复杂度从O(N^2)降低到O(NlogN),大大提高了计算的速度。
FFT算法的精髓在于将长度为N的DFT分解为多个长度为N/2的DFT,这样递归地进行分解,最后合并得到结果。
离散傅里叶变换在信号处理中有广泛的应用。
例如,在音频处理中,可以利用离散傅里叶变换将时域上的音频信号转换为频域上的频谱图,从而实现音频的分析和处理。
在图像处理中,可以利用离散傅里叶变换将图像转换为频域表示,进而实现图像去噪、图像压缩等操作。
离散傅里叶变换还被广泛应用于通信系统中。
在数字通信中,可以利用离散傅里叶变换将时域上的数字信号转换为频域上的信号,实现信号的调制和解调。
在无线通信中,可以利用离散傅里叶变换对信号进行频谱分析,从而实现信号的解调和信号的检测。
离散傅里叶变换(DFT)快速傅里叶变换(FFT) 实验四

实验四:DFS 、DFT 与FFT1、已知某周期序列的主值序列为x(n)=[0,1,2,3,2,1,0],编程显示2个周期的序列波形。
要求:① 用傅里叶级数求信号的幅度谱和相位谱,并画出图形 ② 求傅里叶级数逆变换的图形,并与原序列进行比较 程序清单: N=7;xn=[0,1,2,3,2,1,0]; xn=[xn,xn]; n=0:2*N-1; k=0:2*N-1;Xk=xn*exp(-1i*2*pi/N).^(n'*k); x=(Xk*exp(1i*2*pi/N).^(n'*k))/N; subplot(2,2,1);stem(n,xn);title('x(n)');axis([-1,2*N,1.1*min(xn),1.1*max(xn)]); subplot(2,2,2);stem(n,abs(x));title('IDFS|X(k)|');axis([-1,2*N,1.1*min(x),1.1*max(x)]); subplot(2,2,3),stem(k,abs(Xk));title('|X(k)|');axis([-1,2*N,1.1*min(abs(Xk)),1.1*max(abs(Xk))]); subplot(2,2,4),stem(k,angle(Xk));title('arg|X(k)|');axis([-1,2*N,1.1*min(angle(Xk)),1.1*max(angle(Xk)]);程序运行结果如下图:课程名称:数字信号处理 实验成绩:指导教师:实 验 报 告院系: 信息工程学院 班级: 学号: 姓名:日期: 2011. 10.300510123x(n)0510510IDFS|X (k)|51051015|X (k)|510-2-1012arg|X (k)|2、已知有限长序列x(n)=[1,0.5,0,0.5,1,1,0.5,0],要求: ① 求该序列的DFT 、IDFT 的图形; 程序清单:xn=[1,0.5,0,0.5,1,1,0.5,0]; N=length(xn); n=0:N-1;k=0:N-1;Xk=xn*exp(-1i*2*pi/N).^(n'*k); x=(Xk*exp(1i*2*pi/N).^(n'*k))/N; subplot(2,2,1);stem(n,xn);title('x(n)');axis([-1,N,1.1*min(xn),1.1*max(xn)]); subplot(2,2,2);stem(n,abs(x));title('IDFT|X(k)|');axis([-1,N,1.1*min(x),1.1*max(x)]); subplot(2,2,3),stem(k,abs(Xk));title('|X(k)|');axis([-1,N,1.1*min(abs(Xk)),1.1*max(abs(Xk))]); subplot(2,2,4),stem(k,angle(Xk));title('arg|X(k)|');axis([-1,N,1.1*min(angle(Xk)),1.1*max(angle(Xk))]);程序运行结果如下图:024680.51x(n)024680.51IDFT|X (k)|24681234|X (k)|2468-2-1012arg|X (k)|② 用FFT 算法求该序列的DFT 、IDFT 的图形; 程序清单:xn=[1,0.5,0,0.5,1,1,0.5,0]; N=length(xn);subplot(2,2,1);stem(n,xn); title('x(n)'); k=0:N-1;Xk=fft(xn,N);subplot(2,1,2);stem(k,abs(Xk)); title('Xk=DFT(xn)'); xn1=ifft(Xk,N);subplot(2,2,2);stem(n,xn1);title('x(n)=IDFT(Xk) 程序运行结果如下图:246800.20.40.60.81x(n)1234567012345X k=DFT(xn)246800.20.40.60.81x(n)=IDFT(X k)③ 假定采用频率Fs=20Hz ,序列长度N 分别取8、32和64,用FFT 计算其幅度谱和相位谱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四:离散傅里叶变换
实验原理:
DFT的快速算法FFT利用了的三个固有特性:(1)对称性(2)周期性(3)可约性。
FFT算法基本上可以分为两大类,即按时间抽选法(DIT,Decimation-In-Time)和按频率抽选法(DIF,Decimation-In-frequency)。
MATLAB中提供了进行快速傅里叶变换的fft函数:
X=fft(x),基2时间抽取FFT算法,x是表示离散信号的向量;X是系数向量;
X=fft(x,N),补零或截断的N点DFT,当x得长度小于N时,对补零使其长度为N,当x的长度大于N时,对x截断使其长度为N。
实验内容:
=60;
n=[0:1:k/2];
xa1=2*sin(10*pi*n/k)+cos(18*pi*n/k);
subplot(321)
stem(n,xa1)
xlabel('N');ylabel('x(n)');
xk1=fft(xa1);xk1=abs(xk1)
subplot(322)
stem(n,xk1)
xlabel('k');ylabel('X(k)');
n=[0:1:k*];
xa1=2*sin(10*pi*n/k)+cos(18*pi*n/k);
subplot(323)
stem(n,xa1)
xlabel('N');ylabel('x(n)');
xk1=fft(xa1);xk1=abs(xk1)
subplot(324)
stem(n,xk1)
xlabel('k');ylabel('X(k)');
n=[0:1:k*2];
xa1=2*sin(10*pi*n/k)+cos(18*pi*n/k);
subplot(325)
stem(n,xa1)
xlabel('N');ylabel('x(n)');
xk1=fft(xa1);xk1=abs(xk1)
subplot(326)
stem(n,xk1)
xlabel('k');ylabel('X(k)');
结果分析:当选取的采样分析长度不为周期信号周期T的整数倍时,就会发生频率泄露,如上图。
反之则不会发生频率泄露
2.
n=[0:7];
L=length(n);
x=ones(L,1);
N=32;
n1=[0:N-1];
xk=fft(x,N);
subplot(221);
n2=(2*pi/N)*[0:(N-1)]';
stem(n2,abs(xk));
xlabel('k'),ylabel('幅度');
title('N = 32');
subplot(223);
stem(n2,angle(xk));
xlabel('k'),ylabel('相位');
N=64;
n1=[0:N-1];
xk=fft(x,N);
subplot(222);
n2=(2*pi/N)*[0:(N-1)]';
stem(n2,abs(xk));
xlabel('k'),ylabel('幅度');
title('N = 64');
subplot(224);
stem(n2,angle(xk));
xlabel('k'),ylabel('相位');
结果分析:当采样点数越大时,用STEM绘制出的图形包络线越接近于真实的连续幅频和相频特性的连续曲线。
