函数的单调性与导数PPT优秀课件6
合集下载
函数的单调性课件(共17张PPT)

如果我们以x表示时间间隔(单位:h),y表示记忆保持量,则 不难看出,图3-7中,y是的函数,记这个函数为y =f(x).
这个函数反映出记忆具有什么规律?你能从中得到什么启发?
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
问题情境:我们知道,“记忆”在我们的学习过程中 扮演着非常重要的角色,因此有关记忆的规律一直都 是人们研究的课題。德国心理学家艾宾浩斯曾经对记 忆保持量进行了系统的实验研究,并给出了类似图37所示的记忆规律.
创设情境,生成问题 在在活初初动中中1,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
△x表示自变量x的增量,△y表示因变量y的增量. 这时,对于属于这个区间上的任意两个不相等的值x1,x2: 这个数是增函数的充要条件是yx >0; 这个数是增函数的充要条件是y <0.
x
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
因此,函数f(x)=3x+2在(- ,+ )上是增函数.
巩固练习,提升素养 在活初动中3,我们用过“自然数集”“有理数集”等表述,这里的“集”就是集合的简称,那么什么是集合呢?
数学Biblioteka 基础模块(上册)第三章 函数
3.1.3 函数的单调性
这个函数反映出记忆具有什么规律?你能从中得到什么启发?
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
问题情境:我们知道,“记忆”在我们的学习过程中 扮演着非常重要的角色,因此有关记忆的规律一直都 是人们研究的课題。德国心理学家艾宾浩斯曾经对记 忆保持量进行了系统的实验研究,并给出了类似图37所示的记忆规律.
创设情境,生成问题 在在活初初动中中1,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
△x表示自变量x的增量,△y表示因变量y的增量. 这时,对于属于这个区间上的任意两个不相等的值x1,x2: 这个数是增函数的充要条件是yx >0; 这个数是增函数的充要条件是y <0.
x
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
因此,函数f(x)=3x+2在(- ,+ )上是增函数.
巩固练习,提升素养 在活初动中3,我们用过“自然数集”“有理数集”等表述,这里的“集”就是集合的简称,那么什么是集合呢?
数学Biblioteka 基础模块(上册)第三章 函数
3.1.3 函数的单调性
高二数学函数的单调性与导数PPT教学课件

第三章 导数及其应用 y
3.3.1 函数的单调性与导数
o
x
观察下列图象的单调区间, 并求单调区间相应的导数.
图象是单调上升的.
y10
在x∈(-∞,0)内 图象是单调下降的.
y2x0
在x∈( 0,+∞)内 图象是单调上升的.
y2x0
图象是单调上升的.
y3x20 (当 x0 时 )
在x∈(-∞,0)内 图象是单调下降的.
当 f(x) >0,
即 x117或 x117 时,
2
2
函数单调递增;
当 f(x) <0,
即 117x1Biblioteka 7时, y22函数单调递减;
图象见右图。
o
x
练习1:确定下列函数的单调区间:
(1) f(x)=x2-2x+4 x<1时,函数单调递减, x>1时,函数单调递增。
(2) f(x)=3x-x3 x<-1或x>1时,函数单调递减, -1<x<1时,函数单调递增。
从而函数f(x)=x3+3x 在x∈R上单调递增, 见右图。
o
x
f (x) x3 3x
(2) f(x)=x2-2x-3 ;
解: f(x)=2x-2=2(x-1)>0
当 f(x)>0,即x>1时,函数单调递增;
当 f(x)<0,即x<1时, 函数单调递减;
y
f (x) x2 2x 3
图象见右图。
当 1<x< 4时,
y
o1
解:由题意可知
yf(x)
当1<x<4时, f(x)为增函数 当x>4,或x<1时,
3.3.1 函数的单调性与导数
o
x
观察下列图象的单调区间, 并求单调区间相应的导数.
图象是单调上升的.
y10
在x∈(-∞,0)内 图象是单调下降的.
y2x0
在x∈( 0,+∞)内 图象是单调上升的.
y2x0
图象是单调上升的.
y3x20 (当 x0 时 )
在x∈(-∞,0)内 图象是单调下降的.
当 f(x) >0,
即 x117或 x117 时,
2
2
函数单调递增;
当 f(x) <0,
即 117x1Biblioteka 7时, y22函数单调递减;
图象见右图。
o
x
练习1:确定下列函数的单调区间:
(1) f(x)=x2-2x+4 x<1时,函数单调递减, x>1时,函数单调递增。
(2) f(x)=3x-x3 x<-1或x>1时,函数单调递减, -1<x<1时,函数单调递增。
从而函数f(x)=x3+3x 在x∈R上单调递增, 见右图。
o
x
f (x) x3 3x
(2) f(x)=x2-2x-3 ;
解: f(x)=2x-2=2(x-1)>0
当 f(x)>0,即x>1时,函数单调递增;
当 f(x)<0,即x<1时, 函数单调递减;
y
f (x) x2 2x 3
图象见右图。
当 1<x< 4时,
y
o1
解:由题意可知
yf(x)
当1<x<4时, f(x)为增函数 当x>4,或x<1时,
高二数学-函数的单调性与导数公开课优秀课件(经典、值得收藏)

二、题型探究
3.利用导数求参数的取值范围
例.若函数f(x)=2x2+ln x-ax在定义域上单调递增,求实数a的取值范围.
解 ∵f(x)=2x2+ln x-ax的定义域为(0,+∞), 且在(0,+∞)上单调递增,
∴f′(x)=4x+1x-a≥0 在(0,+∞)上恒成立. ∴a≤4x+1x在(0,+∞)上恒成立.
单调性 割线斜率的符号 切线斜率的符号 导数
一、知识讲解:
函数单调性与导函数正负的关系
单调性 割线斜率的符号 切线斜率的符号 导数
观察下面函数的图象,探讨单调性与其导函数正负的关系:
yx
y y x3
y y 1
y
y
x
ya
x o
x o
x o
x o
导数值 >0 <0
切线的斜率 >0 <0
倾斜角 锐角 钝角
曲线的变化趋势 函数的单调性
上升
递增
下降
递减
一般地,设函数y f (x),在区间(a,b)上,思考: 若f x(x) (a0,,b)则, ff(( xx)) 在0该区函间数上f递( x增)在;区间(fa(,xb))为 0增是函f(数x)为增函数 若函f (数x)f(0x,)在则区 f(间x)(a在, b该)为区增间函上递数减。f ( x)的什0恒么成条立件(不?恒等于0)
二、题型探究
2.函数图象与导数图象的关系 (2)如果函数f(x)的图象如图,那么导函数y=f′(x)的图象可能是
解析: 由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,故选A.
二、题型探究
2.函数图象与导数图象的关系
(1)函数的单调性与其导函数的正负的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x) 在(a,b)上单调递增;如果f′(x)<0,则y=f(x)在这个区间上单调递减;若恒有f′(x)=0, 则y=f(x)是常数函数,不具有单调性. (2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x)的值越大.
函数的单调性与导数优秀ppt课件
①当1<x<4时,f’(x)>0; ②当x>4,或x<1时,f’(x)<0; ③当x=4,或x=1时,f’(x) =0. 试画出函数f(x)图象的大致形状。
y y=f(x)
O1
4
x
7/20/2024
例2 求函数 f (x) 2x3 3x2 12x 1 的单调区间
解: f '(x) 6x2 6x 12
7/20/2024
例1
设 f '( x)是函数 f ( x) 的导函数,y f '( x)的图象如
c 右图所示,则 y f ( x) 的图象最有可能的是( )
y
y f (x)
y
y f (x)
y
y f '( x)
o 1 2x o 1 2x
(A)
y y f (x)
(B)
o
2x
y y f (x)
G=(a,b)
y
y
oa
bx
oa
bx
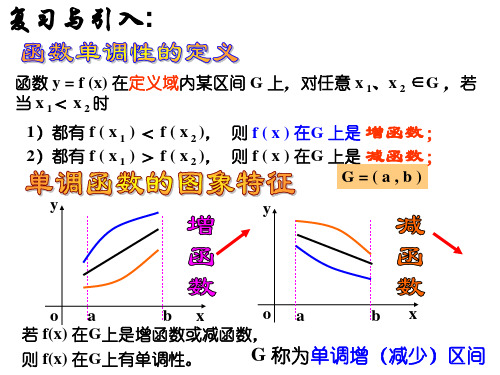
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上有单调性。
G 称为单调增(减少)区间
新授 画出下列函数的图像,并根据图像指出每个函数的单调区间
y x2
y x3
y1 x
y
y
y
ox
ox
o
x
(-∞,0) (0,+∞)
(- ∞ ,+∞) (-∞,0) (0,,+∞)
为增区间; (4)解不等式f’(x)<0,解集在定义域内的部分
为减区间.
7/20/2024
课堂练习 求下列函数的单调区间。
(1) f (x) x2 2x 3 (2) f (x) x3 3x
y y=f(x)
O1
4
x
7/20/2024
例2 求函数 f (x) 2x3 3x2 12x 1 的单调区间
解: f '(x) 6x2 6x 12
7/20/2024
例1
设 f '( x)是函数 f ( x) 的导函数,y f '( x)的图象如
c 右图所示,则 y f ( x) 的图象最有可能的是( )
y
y f (x)
y
y f (x)
y
y f '( x)
o 1 2x o 1 2x
(A)
y y f (x)
(B)
o
2x
y y f (x)
G=(a,b)
y
y
oa
bx
oa
bx
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上有单调性。
G 称为单调增(减少)区间
新授 画出下列函数的图像,并根据图像指出每个函数的单调区间
y x2
y x3
y1 x
y
y
y
ox
ox
o
x
(-∞,0) (0,+∞)
(- ∞ ,+∞) (-∞,0) (0,,+∞)
为增区间; (4)解不等式f’(x)<0,解集在定义域内的部分
为减区间.
7/20/2024
课堂练习 求下列函数的单调区间。
(1) f (x) x2 2x 3 (2) f (x) x3 3x
函数的单调性与导数 课件

探究 2 判断函数在某个区间(a,b)内的单调性可从以下几个 方面入手:
(1)利用函数单调性的定义:在定义域内任取 x1,x2(x1<x2), 通过判断 f(x1)-f(x2)的符号来确定函数 f(x)的单调性.
(2)图像法:利用函数图像的变化趋势直观判断,图像在某个 区间呈上升趋势,则函数在这个区间内是增函数;图像在某个区 间呈下降趋势,则函数在这个区间内是减函数.
探究 1 (1)利用导数求函数的单调区间和判断函数单调性的 基本步骤:
①确定函数 f(x)的定义域; ②求出函数 f(x)的导数 f′(x); ③令 f′(x)>0,在定义域内解不等式,求得 x 的相应区间为 f(x)的单调递增区间; ④令 f′(x)<0,在函数定义域内解不等式,求得 x 的相应区 间为 f(x)的单调递减区间.
解法三:∵f′(x)=2a-3x2,f(x)在(0,1)上是增函数,∴f
′(x)≥0 在(0,1)上恒成立.
又∵f′(x)为二次函数,且开口向下,
f′(0)≥0, ∴f′(1)≥0,解得a≥32.
a>0,
∴a 的取值范围是[23,+∞).
(2)f′(x)=a-1x=ax- x 1,
①当 a≤0 时,f′(x)<0,即 f(x)在(0,2)上单调递减,不合
题型一 求函数的单调区间
例 1 求下列函数的单调区间: (1)f(x)=x3-3x+1; (2)f(x)=2x-lnx; (3)f(x)=sinx-cosx+x+1,0<x<2π;
(4)f(x)= ax (a≠0)(-1<x<1). 1-x2
【解析】 (1)f′(x)=3x2-3=3(x+1)(x-1), 令 f′(x)>0,得 x<-1 或 x>1. 令 f′(x)<0,得-1<x<1. ∴f(x)的增区间是(-∞,-1),(1,+∞); f(x)的减区间是(-1,1). (2)由 x>0,得函数定义域为(0,+∞). f′(x)=2-1x.令 2-1x>0 解得 x>12;令 2-1x<0,得 0<x<12.所 以 f(x)的增区间是(12,+∞);减区间为(0,12).
导数与函数的单调性 (共36张PPT)

[小题热身] 1.函数 f(x)=cos x-x 在(0,π)上的单调性是( A.先增后减 B.先减后增 C.增函数 D.减函数 解析:∵f′(x)=-sinx-1<0. ∴f(x)在(0,π)上是减函数,故选 D.
)
答案:D
2.如图所示是函数 f(x)的导函数 f′(x)的图象,则下列判断 中正确的是( ) A.函数 f(x)在区间(-3,0)上是减函数 B.函数 f(x)在区间(-3,2)上是减函数 C.函数 f(x)在区间(0,2)上是减函数 D.函数 f(x)在区间(-3,2)上是单调函数
[解析] (1)因为 f(x)=xea x+bx, 所以 f′(x)=(1-x)ea-x+b. a-2 f 2 = 2e + 2 , 2e +2b=2e+2, 依题设, 即 a-2 +b=e-1. f′2=e-1, -e 解得 a=2,b=e.
-
(2)由(1)知 f(x)=xe2 x+ex. 由 f′(x)=e2-x(1-x+ex-1)及 e2-x>0 知,f′(x)与 1-x+ex- 1 同号. 令 g(x)=1-x+ex-1,则 g′(x)=-1+ex-1. 所以,当 x∈(-∞,1)时,g′(x)<0,g(x)在区间(-∞,1) 上单调递减; 当 x∈(1,+∞)时,g′(x)>0,g(x)在区间(1,+∞)上单调 递增. 故 g(1)=1 是 g(x)在区间(-∞,+∞)上的最小值, 从而 g(x)>0,x∈(-∞,+∞). 综上可知,f′(x)>0,x∈(-∞,+∞). 故 f(x)的单调递增区间为(-∞,+∞).
(2)a=2 时, 单调递增. (3)a>2 时,0< 当 在 x∈(0,+∞)内,f′(x)≥0,f(x) 2 a<1,
2 a)或 x∈(1,+∞)时,f′(x)>0,f(x)单调递增; 2 a,1)时,f′(x)<0,f(x)单调递减.
)
答案:D
2.如图所示是函数 f(x)的导函数 f′(x)的图象,则下列判断 中正确的是( ) A.函数 f(x)在区间(-3,0)上是减函数 B.函数 f(x)在区间(-3,2)上是减函数 C.函数 f(x)在区间(0,2)上是减函数 D.函数 f(x)在区间(-3,2)上是单调函数
[解析] (1)因为 f(x)=xea x+bx, 所以 f′(x)=(1-x)ea-x+b. a-2 f 2 = 2e + 2 , 2e +2b=2e+2, 依题设, 即 a-2 +b=e-1. f′2=e-1, -e 解得 a=2,b=e.
-
(2)由(1)知 f(x)=xe2 x+ex. 由 f′(x)=e2-x(1-x+ex-1)及 e2-x>0 知,f′(x)与 1-x+ex- 1 同号. 令 g(x)=1-x+ex-1,则 g′(x)=-1+ex-1. 所以,当 x∈(-∞,1)时,g′(x)<0,g(x)在区间(-∞,1) 上单调递减; 当 x∈(1,+∞)时,g′(x)>0,g(x)在区间(1,+∞)上单调 递增. 故 g(1)=1 是 g(x)在区间(-∞,+∞)上的最小值, 从而 g(x)>0,x∈(-∞,+∞). 综上可知,f′(x)>0,x∈(-∞,+∞). 故 f(x)的单调递增区间为(-∞,+∞).
(2)a=2 时, 单调递增. (3)a>2 时,0< 当 在 x∈(0,+∞)内,f′(x)≥0,f(x) 2 a<1,
2 a)或 x∈(1,+∞)时,f′(x)>0,f(x)单调递增; 2 a,1)时,f′(x)<0,f(x)单调递减.
函数单调性课件(公开课)ppt

函数单调性课件(公开课)
目录
• 函数单调性的定义与性质 • 判断函数单调性的方法 • 单调性在解决实际问题中的应用 • 函数单调性的深入理解 • 函数单调性的实际案例分析
01 函数单调性的定义与性质
函数单调性的定义
函数单调性是指函数在某个区间内的增减性。如果函数在某个区间内单调递增, 则表示函数值随着自变量的增加而增加;如果函数在某个区间内单调递减,则表 示函数值随着自变量的增加而减小。
的计算过程。
单调性与微分方程的关系
要点一
单调性决定了微分方程解的稳定 性
对于一阶线性微分方程,如果其系数函数在某区间内单调 递增(或递减),则该微分方程的解在此区间内是稳定的 。
要点二
单调性是研究微分方程的重要工 具
通过单调性可以判断微分方程解的存在性和唯一性,以及 研究解的动态行为。
05 函数单调性的实际案例分 析
总结词
利用单调性证明或解决不等式问题
详细描述
单调性在解决不等式问题中起到关键作用。通过分析函数的单调性,我们可以证明不等式或解决与不等式相关的 问题。例如,利用单调性可以证明数学归纳法中的不等式,或者在比较大小的问题中利用单调性进行判断。
单调性在函数极值问题中的应用
总结词
利用单调性求解函数的极值
详细描述
函数单调性的定义可以通过函数的导数来判断。如果函数的导数大于0,则函数在该 区间内单调递增;如果函数的导数小于0,则函数在该区间内单调递减。
函数单调性的性质
函数单调性具有传递性,即如果函数在区间I上单调递增,且 在区间J上单调递增,则函数在区间I和J的交集上也是单调递 增的。
函数单调性具有相对性,即如果函数在区间I上单调递增,且 另一个函数在区间J上单调递增,则这两个函数在区间I和J的 交集上也是单调递增的。
目录
• 函数单调性的定义与性质 • 判断函数单调性的方法 • 单调性在解决实际问题中的应用 • 函数单调性的深入理解 • 函数单调性的实际案例分析
01 函数单调性的定义与性质
函数单调性的定义
函数单调性是指函数在某个区间内的增减性。如果函数在某个区间内单调递增, 则表示函数值随着自变量的增加而增加;如果函数在某个区间内单调递减,则表 示函数值随着自变量的增加而减小。
的计算过程。
单调性与微分方程的关系
要点一
单调性决定了微分方程解的稳定 性
对于一阶线性微分方程,如果其系数函数在某区间内单调 递增(或递减),则该微分方程的解在此区间内是稳定的 。
要点二
单调性是研究微分方程的重要工 具
通过单调性可以判断微分方程解的存在性和唯一性,以及 研究解的动态行为。
05 函数单调性的实际案例分 析
总结词
利用单调性证明或解决不等式问题
详细描述
单调性在解决不等式问题中起到关键作用。通过分析函数的单调性,我们可以证明不等式或解决与不等式相关的 问题。例如,利用单调性可以证明数学归纳法中的不等式,或者在比较大小的问题中利用单调性进行判断。
单调性在函数极值问题中的应用
总结词
利用单调性求解函数的极值
详细描述
函数单调性的定义可以通过函数的导数来判断。如果函数的导数大于0,则函数在该 区间内单调递增;如果函数的导数小于0,则函数在该区间内单调递减。
函数单调性的性质
函数单调性具有传递性,即如果函数在区间I上单调递增,且 在区间J上单调递增,则函数在区间I和J的交集上也是单调递 增的。
函数单调性具有相对性,即如果函数在区间I上单调递增,且 另一个函数在区间J上单调递增,则这两个函数在区间I和J的 交集上也是单调递增的。
《函数单调性与导数》课件

导数在物理问题中的应用
速度与加速度
在运动学中,导数可以用来描述 物体的速度和加速度。例如,自 由落体运动中,物体的速度和加
速度可以通过求导得到。
热传导
在热力学中,导数可以用来描述 热量传递的过程。例如,通过求 导得到温度场的变化率,可以帮
助我们理解热传导的规律。
弹性力学
在弹性力学中,导数可以用来描 述物体的应力应变关系。例如, 通过求导得到物体的应力分布和 应变状态,可以帮助我们理解物
调性
利用导数的符号变化,确定函数 在某区间内的增减性
通过求解一阶导数的不等式,判 断函数的单调性
利用导数判断函数单调性的方法
直接求导
对于已知函数,直接求导并分 析导数的符号变化
利用导数的几何意义
通过导数的几何意义,绘制函 数图像,直观判断函数的单调 性
构造新函数
通过构造函数并求导,利用导 数判断新函数的单调性来研究 原函数的单调性
成本效益分析
导数可以用来分析企业的成本效益,从而制定最优的经营策略。例如,通过求导找到最小 化成本或最大化的利润点,可以帮助企业制定合理的价格和产量策略。
投资组合优化
在金融领域,导数可以用来优化投资组合,以实现最大的收益或最小的风险。例如,通过 求导找到最优的投资组合比例,可以帮助投资者实现资产配置的目标。
详细描述:导数的计算方法包括定义法、求导公式和法则、复合函数求导、隐函数求导、参数方程确定的函数求导等。
03
利用导数判断函数单调性
导数与函数单调性的关系
导数大于零,函数单 调递增
导数等于零,函数可 能为极值点或拐点
导数小于零,函数单 调递减
单调性判定定理的推导
基于极限的导数定义,通过分析 函数在某区间的变化率来判断单
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如果在某个 f'x 区 0间 ,那内 么y 恒 函 f有 x数
有什么 ? 特征
思考请同学们回顾一单 下调 函性 数的定 ,并义
思考某个区间上 y函f x数 的平均变化率的几
何意义与其导数关 正系 负 . 的
例1 已知导数f'x的下列信息: y
当1 x 4时,f'x 0;
9 . 8 t 6 . 5 的图象 .
运动员从起跳到最高点
,以
及从最高点到入水这两
段
时间的运动状态有什么
区
别?
h
Oa
bt
图 1.311
v
a
O
b t
图 1.312
通过动画演,观 示察运动员在各时段的 运动状态 .
通过观察,图 我象 们可以:发现
1运动员从起跳到,离最水高面点高 h随度 时间 t的增加而,增 即h加 t是增函.相 数应,地 vth't0.
当 x4,或 x1时 ,f'x0,这两点,比 我较 们
称它"临 们界 为 ". 点
综,函 上f数 x图象的大1.致 34所 形.示 状
例2 判断下列函数的单 ,并调 求性 出单调区 : 间
1fxx3 3x; 2fxx2 2x3y; 3fxsinxx,x0,π; 4fx2x3 3x2 24x1. fxx33x
例3 如图 1.36,水以恒(即 速单位时间内注 体入 积相)同 注入下面四种底 同面 的积 容相 器 ,请中 分别找 出与各容器对应 h与 的时 高t间 的 度函数关系. 图象
1
2
3
4
h
h
h
h
o A
t o B t o C t o D t
图1.36
y y x3
2 O
x
y y1 x
O
x
O
x
3
图1.32 4
y yfx
x1,fx1
O
x0,fx0
x
动画演示 .
图1.33
如图 1.33,导数 f'x0表示函f数 x在点 x0,fx0
处的切线的.在斜 x率 x0处,f'x00,切线"是 左 下右"上 式的 ,这时 ,函数 fx在x0 附近单调;递 在增
函 fx 数 x 2 2 x 3 的图 1 .3 5 象 2 所 .如 示
y
o1
图 1.352
fxx22x3
x
y
o
图 1.353
π
x
fxsixn x
3因f为 xsixn x,x0,π ,所以
f'x
.
因 ,函 此 fx 数 sx i n x ,x 0 ,π 内 .
如 1 .3 图 5 3 所 . 示
4 因 f x 2 x 3 为 3 x 2 2 x 1 , 所 4 f ' x 以 . 当 f ' x 0 , 即 时 , 函 f x 数 ; 当 f ' x 0 , 即 时 , 函 f x 数 .
解1因f为 xx33x,所以 o
f'x3x233x210.
x
因此 ,函数fxx3 3x在x
R上单调递 ,如增图 1.351
所示 .
图 1.351
2 因 f x x 2 2 x 为 3 , 所 f ' x 2 x 2 以 2 x 1 . 当 f'x 0 ,即 x 1 时 ,函 fx 数 x 2 2 x 3 单调 ; 当 f'x 0 ,即 x 1 时 ,函 fx 数 x 2 2 x 3 单调 .
fx 2 x 3 3 x 2 2x 4 1 的图 1 .3 5 象 4 所 .如
y
如果不用导数的方法
,
fx 2 x 3 3 x 2 2 x 4 1
直接运用单调性的定
51
O
x
图 1.354
义 , 你如何求解本题 ? 运算过程 麻烦吗 ? 你 有什么体会 ?
xx1处,f'x10,切线"是 左上右"式 下的 ,这时 ,函 数fx在x1附近单调.递减
一般,地 函数的单调性与正导负数有的如下: 关
在某个a,区 b内 ,间 如果 f'x0,那么函 yf数 x 在这个区间内 ;如单 果 f'x调 0,递 那增 么函 y 数 fx在这个区间内 . 单调递减
函数是描述客观世界变化规律的重要数学模 型.研究函数时,了解函数的增与减、增减的快 与慢以及函数的最大值或最小值等性质是非 常重要的.通过研究函数这些性质,我们可以对 数量的变化规律进行长期的研究,导致了微积 分的创立
下面 ,我们运用导数研的究性函 ,质 从数中你 可以体会导数在数研中究的函作 . 用
当x 4,或x 1时,f'x 0;
当x 4,或x 1时,f'x 0.
试画出函数fx图象的大致形状. O 1 4
x
解 当1x4时,f'x0,可
图1.34
知fx在此区间内单调;递增
当 x4,或 x1时 ,f'x0,可f知 x在这两个
内单调 ; 递减
1.3.1 函数的单调性与导数
观察 图 1 . 3 1 1 表示高
台跳水运动员的高度
h随
时间变化的函数
h t
4 . 9 t 2 6 . 5 t 10 的图度
v 随时间 t 变
化的函数 v t h ' t
分析 以容器 2为例 ,由于容器
上细下粗 ,所以水以恒速注入时 ,
开始阶段高度增加得慢 ,以后高
2从最高点到 ,运入 动水 员离水h面 随高度 时间 t的增加而,即 减 ht小 是减函 .相数应,地 vth't0.
思考 这种情况是否具有一性 般呢?
观察下面一 图 1 些 .32 函 ,探数 讨图 函象 数
调性y与其导 系 .数正 y 负的关
yx
y x2
O
x
1
有什么 ? 特征
思考请同学们回顾一单 下调 函性 数的定 ,并义
思考某个区间上 y函f x数 的平均变化率的几
何意义与其导数关 正系 负 . 的
例1 已知导数f'x的下列信息: y
当1 x 4时,f'x 0;
9 . 8 t 6 . 5 的图象 .
运动员从起跳到最高点
,以
及从最高点到入水这两
段
时间的运动状态有什么
区
别?
h
Oa
bt
图 1.311
v
a
O
b t
图 1.312
通过动画演,观 示察运动员在各时段的 运动状态 .
通过观察,图 我象 们可以:发现
1运动员从起跳到,离最水高面点高 h随度 时间 t的增加而,增 即h加 t是增函.相 数应,地 vth't0.
当 x4,或 x1时 ,f'x0,这两点,比 我较 们
称它"临 们界 为 ". 点
综,函 上f数 x图象的大1.致 34所 形.示 状
例2 判断下列函数的单 ,并调 求性 出单调区 : 间
1fxx3 3x; 2fxx2 2x3y; 3fxsinxx,x0,π; 4fx2x3 3x2 24x1. fxx33x
例3 如图 1.36,水以恒(即 速单位时间内注 体入 积相)同 注入下面四种底 同面 的积 容相 器 ,请中 分别找 出与各容器对应 h与 的时 高t间 的 度函数关系. 图象
1
2
3
4
h
h
h
h
o A
t o B t o C t o D t
图1.36
y y x3
2 O
x
y y1 x
O
x
O
x
3
图1.32 4
y yfx
x1,fx1
O
x0,fx0
x
动画演示 .
图1.33
如图 1.33,导数 f'x0表示函f数 x在点 x0,fx0
处的切线的.在斜 x率 x0处,f'x00,切线"是 左 下右"上 式的 ,这时 ,函数 fx在x0 附近单调;递 在增
函 fx 数 x 2 2 x 3 的图 1 .3 5 象 2 所 .如 示
y
o1
图 1.352
fxx22x3
x
y
o
图 1.353
π
x
fxsixn x
3因f为 xsixn x,x0,π ,所以
f'x
.
因 ,函 此 fx 数 sx i n x ,x 0 ,π 内 .
如 1 .3 图 5 3 所 . 示
4 因 f x 2 x 3 为 3 x 2 2 x 1 , 所 4 f ' x 以 . 当 f ' x 0 , 即 时 , 函 f x 数 ; 当 f ' x 0 , 即 时 , 函 f x 数 .
解1因f为 xx33x,所以 o
f'x3x233x210.
x
因此 ,函数fxx3 3x在x
R上单调递 ,如增图 1.351
所示 .
图 1.351
2 因 f x x 2 2 x 为 3 , 所 f ' x 2 x 2 以 2 x 1 . 当 f'x 0 ,即 x 1 时 ,函 fx 数 x 2 2 x 3 单调 ; 当 f'x 0 ,即 x 1 时 ,函 fx 数 x 2 2 x 3 单调 .
fx 2 x 3 3 x 2 2x 4 1 的图 1 .3 5 象 4 所 .如
y
如果不用导数的方法
,
fx 2 x 3 3 x 2 2 x 4 1
直接运用单调性的定
51
O
x
图 1.354
义 , 你如何求解本题 ? 运算过程 麻烦吗 ? 你 有什么体会 ?
xx1处,f'x10,切线"是 左上右"式 下的 ,这时 ,函 数fx在x1附近单调.递减
一般,地 函数的单调性与正导负数有的如下: 关
在某个a,区 b内 ,间 如果 f'x0,那么函 yf数 x 在这个区间内 ;如单 果 f'x调 0,递 那增 么函 y 数 fx在这个区间内 . 单调递减
函数是描述客观世界变化规律的重要数学模 型.研究函数时,了解函数的增与减、增减的快 与慢以及函数的最大值或最小值等性质是非 常重要的.通过研究函数这些性质,我们可以对 数量的变化规律进行长期的研究,导致了微积 分的创立
下面 ,我们运用导数研的究性函 ,质 从数中你 可以体会导数在数研中究的函作 . 用
当x 4,或x 1时,f'x 0;
当x 4,或x 1时,f'x 0.
试画出函数fx图象的大致形状. O 1 4
x
解 当1x4时,f'x0,可
图1.34
知fx在此区间内单调;递增
当 x4,或 x1时 ,f'x0,可f知 x在这两个
内单调 ; 递减
1.3.1 函数的单调性与导数
观察 图 1 . 3 1 1 表示高
台跳水运动员的高度
h随
时间变化的函数
h t
4 . 9 t 2 6 . 5 t 10 的图度
v 随时间 t 变
化的函数 v t h ' t
分析 以容器 2为例 ,由于容器
上细下粗 ,所以水以恒速注入时 ,
开始阶段高度增加得慢 ,以后高
2从最高点到 ,运入 动水 员离水h面 随高度 时间 t的增加而,即 减 ht小 是减函 .相数应,地 vth't0.
思考 这种情况是否具有一性 般呢?
观察下面一 图 1 些 .32 函 ,探数 讨图 函象 数
调性y与其导 系 .数正 y 负的关
yx
y x2
O
x
1
