转向梯形机构优化设计
工程机械梯形转向机构最优设计

35° 291080 291006 01073 291114 01035
40° 321632 321026 01606 321157 01457
41° 331334 321588 01747 321723 01611
42° 341035 331134 01901 331274 01761
在程序中对 Η、K 作一些限制条件, 其计算方 法、优化思想是相同的。
在图2所示梯形机构中建立直角坐标系, 当 内轮转过 Βp 角时, 外轮实际转过 Αp1角。设 Υ= Η
《建筑机械》1996年 (11)
- Βp , <= Η+ Αp , 此时 A ’、B ’坐标分别为 A ’ 根据
(N co sΥ, N sinΥ) , B ’(M - N co s<, N sin<)。
(5)
图3 转向梯形实际特性曲线
解三角方程 (5) 得
<= a rcco s〔2x z - 4x 2z 2+ 4 (x 2+ y 2) (z 2- y 2) 2 (x 2+ y 2) 〕
(6)
则 Αp1= <- Η
312 理论转向角的确定
利 用方程 (1) 不难计算出当内轮转过 Βp 时, 外轮的理论要求转向角 Αp2为
关键词: 工程机械 梯形 转向装置 优选设计
1 前言 轮式底盘工程机械其转向通常采用三种方
式: 偏转车轮转向、铰接转向和滑移转向。对载 重汽车、汽车吊等行驶速度较快的机种大多采 用第一种转向方式。在偏转车轮转向系设计中, 最为重要的是连杆转向机构参数的确定。如图1 所示, 理想的转向机构应能保证车辆转向时, 内 外两侧转向轮无侧滑, 即内、外转向轮的转向角 Βp , Αp1能够满足理论特性方程 (1) :
某型电动微型汽车转向梯形的优化设计

(4)
阿克曼梯形即为满足阿克曼转向理论特性的四连杆机构, 其底角 γ(见图 3)可由下式(5)确定:
(5)
3.2 内轮解析式
2020.01 科学技术创新 -161-
(Байду номын сангаас)
图 2 理想的内、外轮转角关系图
图 6 内轮一侧杆系运动情况 由图 6 可知:
(8)
图 3 底角 γ 其梯形臂的作用长度 m=(0.11K~0.15K); 阿克曼梯形是一个如图 4 所示的平面梯形,其特性为:(1)
;(2)梯形上底长度 AB 与两主销中心距及两主销中 心线穿地点完全一致。
因此,利用上面的公式可得出函数: 为保证梯形机构合适的传动角,应满足 l1 与 l2 的夹角
(9)
(10) (11)
以此作为约束条件,因为在 的最大值为 1,
所以 h 的取值范围为:
(12)
的全部范围内,
的最小值为
。
图 4 阿克曼梯形 3 优化设计及结果 3.1 外轮解析式
1266/1296 1867 825 475/475 337.5/412.5 155/60 R15
175/55 R15
2.2 转向盘及转向轮内外最大转角的确定 汽车转向盘应汽车转向运动完成后,具有自主保持直线行 驶的能力。根据《汽车设计》知不同汽车方向盘的直径 D 如表 2 所示[3]。
表 2 不同汽车方向盘直径
则可导出转向横拉杆 l2 表达式,齿条行程 S 与外轮转角 的 关系:
(17)
W0 为加权因子,因为在不同转角所用到的频率各不相同, (6) 故要设定一个加权因子。
由图中几何关系可得到:
(18)
-162- 科学技术创新 2020.01
转向梯形驱动机构的运动分析及优化设计

V ol 121 N o 18公 路 交 通 科 技2004年8月JOURNA L OF HIGHWAY AND TRANSPORT ATION RESEARCH AND DEVE LOPMENT文章编号:1002Ο0268(2004)08Ο0124Ο05收稿日期:2003Ο07Ο03作者简介:李玉民(1969-),男,河南南阳人,东南大学博士研究生,主要研究方向为载运工具运用工程1转向梯形驱动机构的运动分析及优化设计李玉民1,李旭宏1,过学迅2(11东南大学交通学院,江苏 南京 210096;21武汉理工大学,湖北 武汉 430070)摘要:转向梯形驱动机构的空间布置对汽车的操纵稳定性影响很大。
本文以常见的非独立悬架结构为例,建立空间几何模型进行运动分析,提出同时满足“与前悬架运动协调”和“左右转向力均匀”两方面要求的转向梯形驱动机构优化设计方法。
实践应用表明该方法可行。
关键词:汽车转向;空间连杆机构;运动分析;优化设计中图分类号:U46312 文献标识码:AK inematics Analysis and Optimal De sign of Driving Mechanismsof Ackerman Steering LinkageLI Yu Οmin 1,LI Xu Οhong 1,G UO Xue Οxun2(11T ransportation C ollege ,S outheast University ,Jiangsu Nanjing 210096,China ;21Wuhan University of T echnology ,Hubei Wuhan 430070,China )Abstract :The spatial position of driving mechanisms of Ackerman steering linkage quite in fluences the stability of vehicle maneuvering characteristics 1T aking non Οindependent suspension as an example ,this paper establishes spatial geometric analysis m odel ,then puts forward an optimal design method which meets the coordinated m otion of steering driving linkage and front suspension ,at the same time meets the uniformity of left Οand Οright steering force 1Application shows that the method is feasible 1K ey words :Autom otive steering ;S patial linkage mechanisms ;K inematics analysis ;Optimal design 如图1示,汽车转向传动机构包括转向梯形和转向梯形驱动机构,其中转向梯形驱动机构是指由转向摇臂OA 、直拉杆AB 和转向节臂BC 等组成的驱动转向梯形完成转向任务的连杆机构。
赛车转向梯形优化设计

曼警 ●1
! 』 量 童圣
l¨ l
!
I f rc i n c c q =  ̄c r g u ̄t o i . e ] l a t ) y ( i2一 x I0 . . ̄ = 0s a= 2 O 18f f  ̄ . x 2 . m m
} |3一 c s f 1 卜 c 0 m n 驰 “j o , c ,扭( , t+蠊 l , 缸
3 外观 结构 设计
在设 计汽油发电机组的外观结构时 ,我们 充分考虑和 追 求产品的差异化 。产 品差异化 , 是增强产 品竞争 力、 占领市 场
L 5 0 Y单相 汽油发 电机 组在与 同类 发电机组相 比 ,具有 W5 0 C
性 能优越 、 外观精美等 优点 , 是一款具有相 当市场竞争力 的汽 油发 电机组 产品。该款发 电机组 自上市 以来 , 深受客户欢迎 ,
式中 , 为最小传 动角 , 6 为设计变量 /及 7的函数1 7 / , " 2 1 。
在 M TA A L B软件上 编辑 目标 函数 的优化 约束 条件 的 M 7 2
赛 车优化前后理 想和实际 的汽车左 右车轮转角 的关 系 曲 线如 图 6所示 , 当外轮转 角为虽大 2 。时 。 2 出现最大理论 与实 际 A k r n转角偏差 , 38 , eema 为 .。 存在轮胎 的磨 损 , 但是在外 轮
( 下转 第 8 0页 )
Eq ime t up n Ma ua t n e h oo yNo6,01 n fcr gT c n lg . 2 0 i
到 2 0h 0 。
襄 3 可 靠性、 耐久性试验表
的一种有效方式 。朗沃德 L 5 0 Y单相汽油发电机组 由汽 W5 0 C 油发动机 、 单相发 电机 、 框架 、 面板 、 电器 仪表 、 隔热板 、 减震软 垫等零部 件组成 , 减震 性能和发 电机隔热效果非常好 , 而且采 用 目前市场上 少有的圆弧 面板 设计 ,把一些影 响外 观的螺栓 紧固件完全 隐藏起来 , 工精细 , 做 外型饱满 、 圆滑 , 获得中华 并 人 民共和 国国家知识产权局两项专利保护 。
汽车整体式转向梯形机构仿真计算与优化

汽车整体式转向梯形机构仿真计算与优化首先,需要进行操纵性能仿真计算。
操纵性能是指车辆在转向过程中的稳定性、准确性和操纵力的大小。
通过建立车辆动力学模型,可以模拟车辆在不同转向输入下的行驶状态,并计算车辆的操纵性能参数,如转向响应时间、转向幅度和操纵力矩等。
通过对不同转向梯形机构参数的变化进行仿真计算,可以评估梯形机构对操纵性能的影响,并进行优化设计。
其次,还需要进行力学性能仿真计算。
力学性能是指转向机构在不同工况下的强度、刚度和耐久性等。
通过建立转向机构的有限元模型,可以分析转向机构在不同工况下的应力、应变和位移等力学参数,评估转向机构的设计是否满足强度和刚度要求,并进行优化调整。
同时,还可以通过应用疲劳分析方法,预测转向机构在长期使用过程中的损伤、疲劳寿命和可靠性等问题,以提高整体转向机构的耐久性。
最后,需要进行优化设计。
在进行仿真计算的基础上,可以通过参数优化和结构优化方法,对转向机构的参数和结构进行调整和改进。
例如,通过对齿条、滚珠丝杠、主动齿轮和从动齿轮等关键部件的几何参数进行优化,可以减小滚动摩擦和间隙,提高转向机构的机械效率和动力传递精度。
同时,还可以通过改变转向机构的布局和材料选择,减少转向机构的质量,并提高其刚度和强度,从而提升整体转向机构的性能。
综上所述,汽车整体式转向梯形机构的仿真计算与优化是确保汽车操纵性和稳定性的重要环节,能够通过操纵性能仿真计算、力学性能仿真计算和优化设计方法,对转向机构的性能进行评估和改进,提高汽车整体转向梯形机构的性能和可靠性。
齿轮齿条式转向器双梯形转向机构的优化设计
齿轮齿条式转向器双梯形转向机构的优化设计李睿扬(学号:02000404)(东南大学机械工程系)汽车转向系统需精确地实现阿克曼转向条件,这与转向传动机构的设计密切关联。
在本文,将以与齿轮齿条式转向器配用的转向传动机构为实例,讨论机构的优化设计。
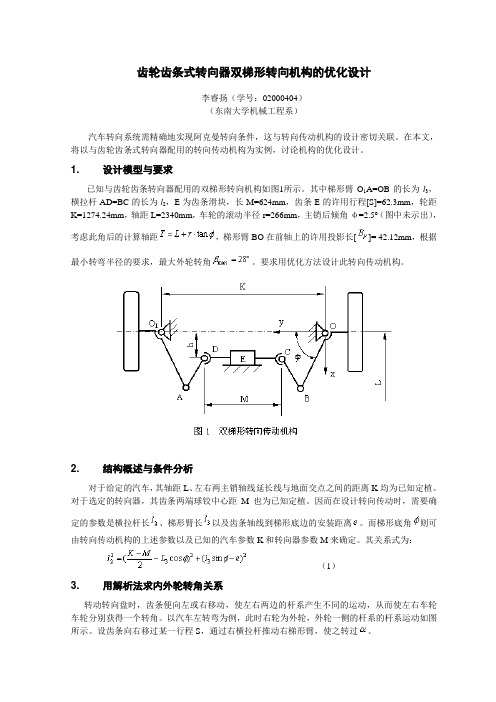
1.设计模型与要求已知与齿轮齿条转向器配用的双梯形转向机构如图1所示。
其中梯形臂O1A=OB的长为l3,横拉杆AD=BC的长为l2,E为齿条滑块,长M=624mm,齿条E的许用行程[S]=62.3mm,轮距K=1274.24mm,轴距L=2340mm,车轮的滚动半径r=266mm,主销后倾角φ=2.5o(图中未示出),考虑此角后的计算轴距,梯形臂BO在前轴上的许用投影长[]= 42.12mm,根据最小转弯半径的要求,最大外轮转角。
要求用优化方法设计此转向传动机构。
2.结构概述与条件分析对于给定的汽车,其轴距L、左右两主销轴线延长线与地面交点之间的距离K均为已知定植。
对于选定的转向器,其齿条两端球铰中心距M也为已知定植。
因而在设计转向传动时,需要确定的参数是横拉杆长、梯形臂长以及齿条轴线到梯形底边的安装距离。
而梯形底角则可由转向传动机构的上述参数以及已知的汽车参数K和转向器参数M来确定。
其关系式为:(1)3.用解析法求内外轮转角关系转动转向盘时,齿条便向左或右移动,使左右两边的杆系产生不同的运动,从而使左右车轮车轮分别获得一个转角。
以汽车左转弯为例,此时右轮为外轮,外轮一侧的杆系的杆系运动如图所示。
设齿条向右移过某一行程S,通过右横拉杆推动右梯形臂,使之转过。
图2 转向传动机构几何关系如图2所示,取梯形右底角顶点O为坐标原点,则可导出齿条行程S与外轮转角的关系:(2)另外,由图可知:(3)而,(4)(5)将(4)、(5)表达式代入(3)式。
因此,利用(2)式便可求出对应于任一外轮转角的齿条行程S,再将S代入公式(3)(4)(5),即可求相应的内轮转角。
将上述公式结合起来便可将表示为的函数,记作。
汽车断开式转向梯形机构的优化设计
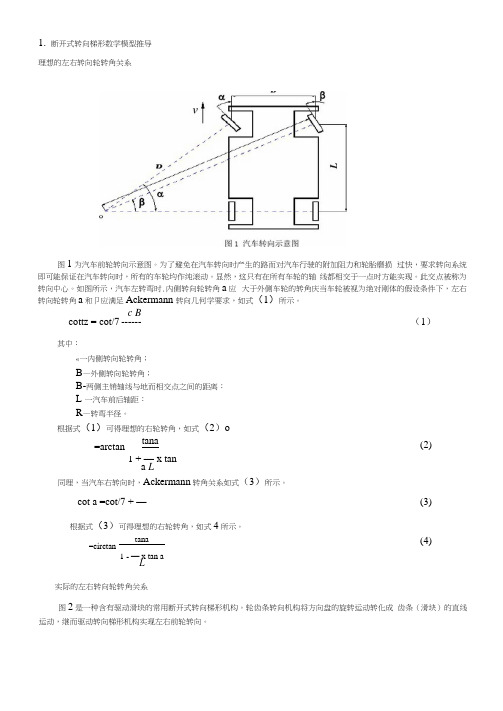
1.断开式转向梯形数学模型推导理想的左右转向轮转角关系图1为汽车前轮转向示意图。
为了避免在汽车转向时产生的路而对汽车行驶的附加阻力和轮胎磨损过快,要求转向系统即可能保证在汽车转向时,所有的车轮均作纯滚动。
显然,这只有在所有车轮的轴线都相交于一点时方能实现。
此交点被称为转向中心。
如图所示,汽车左转弯时.内侧转向轮转角a应大于外侧车轮的转角庆当车轮被视为绝对刚体的假设条件下,左右转向轮转角a和卩应满足Ackermann 转向几何学要求,如式(1)所示。
c Bcottz = cot/7 ------ (1)其中:«一内侧转向轮转角;B—外侧转向轮转角;B-两侧主销轴线与地而相交点之间的距离:L 一汽车前后轴距:R—转弯半径。
根据式(1)可得理想的右轮转角,如式(2)otana (2) =arctan1 + — x tana L同理,当汽车右转向时,Ackermann转角关系如式(3)所示。
(3)cot a =cot/7 + —根据式(3)可得理想的右轮转角,如式4所示。
tana(4)=circtan1 - — x tan aL实际的左右转向轮转角关系图2是一种含有驱动滑块的常用断开式转向梯形机构。
轮齿条转向机构将方向盘的旋转运动转化成齿条(滑块)的直线运动,继而驱动转向梯形机构实现左右前轮转向。
图中:厶一转向机齿条左右球较中心的距离;L 2 一左右横拉杆的长度;厶一左右转向节臂的长度:厶•一车轮中心至转向主销的距离:S] —转向齿条从中心位置向左的位移量: s 2 一转向齿条从中心位宜向左的位移量:y —转向齿条左右球狡中心连线与左右转向主销中心连线之偏距,图示位置取正值,反之取负值: S 。
一直线行驶时,转向齿条左球钱中心和左转向主销的水平距离:一转向节骨与汽车纵轴线的夹角。
运用余弦泄理和三角函数变换公式,经推导可得: ______________________-Cv - S xcos a = cos (ZAOB + Z.BOY )= 一;----- - ------------2厶(丁 +尸)A 点的坐标值为:v CxS-yx>jA 2 + B 2-C 2B2x (/+r )2*…Cxy + SxyjA 2 + B 2-C 2 沧=_ ------------- —zn ----------2x (/+S') 其中:A = -2LyxS,B = _2厶xy,C = 15,-1^-y 2-~s\ F —表示转向齿条弐球钱中心和左转向主销中心的实际距藹,对于直线行驶时,g = S 。
拖拉机转向梯形机构优化设计的一种方法

,
、
`
一
.
、
.
_
_
织
一
!
尽
:
}
`
“”
` “
( 5)
该式 能 较 真 实地 反 映 出 实 际 使 用 中拖 拉 机 轮 胎 转 向时 的 磨 损情况
L Z
。
约柬 亲 件
[ j 2 望里 竺 一 0
.
M
0
.
`
18
<
0
12 一
望垫 卫 <
M
,
0
(6 )
y 。。 一 2 0
<
O
一 y
<
0
集
Jou
美
rn
航
o
海
学
院
学
报1 3
1
)
11
,
19 95
(
:
8~
l a
f
Jim e i
N a 讨 ga t i o n
I n s t lt u t e
拖 拉 机 转 向 梯 形 机 构 优 化
设 计 的 一 种 方 法
陈启 发
( 轮机系 )
脚要
本文分析 了 复合 形 法 在 拖拉 机 转 向梯 形 机 构 参数 设 计中出 现
材
s
s n
i
n
(y +
a
)
创M 式中
:
+
m
Z
士 ZM m i
(y +
)
;
`
(2)
m
是转 向梯形臂 长
。
;
y
