汽车转向梯形的优化设计
转向梯形驱动机构的运动分析及优化设计

V ol 121 N o 18公 路 交 通 科 技2004年8月JOURNA L OF HIGHWAY AND TRANSPORT ATION RESEARCH AND DEVE LOPMENT文章编号:1002Ο0268(2004)08Ο0124Ο05收稿日期:2003Ο07Ο03作者简介:李玉民(1969-),男,河南南阳人,东南大学博士研究生,主要研究方向为载运工具运用工程1转向梯形驱动机构的运动分析及优化设计李玉民1,李旭宏1,过学迅2(11东南大学交通学院,江苏 南京 210096;21武汉理工大学,湖北 武汉 430070)摘要:转向梯形驱动机构的空间布置对汽车的操纵稳定性影响很大。
本文以常见的非独立悬架结构为例,建立空间几何模型进行运动分析,提出同时满足“与前悬架运动协调”和“左右转向力均匀”两方面要求的转向梯形驱动机构优化设计方法。
实践应用表明该方法可行。
关键词:汽车转向;空间连杆机构;运动分析;优化设计中图分类号:U46312 文献标识码:AK inematics Analysis and Optimal De sign of Driving Mechanismsof Ackerman Steering LinkageLI Yu Οmin 1,LI Xu Οhong 1,G UO Xue Οxun2(11T ransportation C ollege ,S outheast University ,Jiangsu Nanjing 210096,China ;21Wuhan University of T echnology ,Hubei Wuhan 430070,China )Abstract :The spatial position of driving mechanisms of Ackerman steering linkage quite in fluences the stability of vehicle maneuvering characteristics 1T aking non Οindependent suspension as an example ,this paper establishes spatial geometric analysis m odel ,then puts forward an optimal design method which meets the coordinated m otion of steering driving linkage and front suspension ,at the same time meets the uniformity of left Οand Οright steering force 1Application shows that the method is feasible 1K ey words :Autom otive steering ;S patial linkage mechanisms ;K inematics analysis ;Optimal design 如图1示,汽车转向传动机构包括转向梯形和转向梯形驱动机构,其中转向梯形驱动机构是指由转向摇臂OA 、直拉杆AB 和转向节臂BC 等组成的驱动转向梯形完成转向任务的连杆机构。
赛车转向梯形优化设计

曼警 ●1
! 』 量 童圣
l¨ l
!
I f rc i n c c q =  ̄c r g u ̄t o i . e ] l a t ) y ( i2一 x I0 . . ̄ = 0s a= 2 O 18f f  ̄ . x 2 . m m
} |3一 c s f 1 卜 c 0 m n 驰 “j o , c ,扭( , t+蠊 l , 缸
3 外观 结构 设计
在设 计汽油发电机组的外观结构时 ,我们 充分考虑和 追 求产品的差异化 。产 品差异化 , 是增强产 品竞争 力、 占领市 场
L 5 0 Y单相 汽油发 电机 组在与 同类 发电机组相 比 ,具有 W5 0 C
性 能优越 、 外观精美等 优点 , 是一款具有相 当市场竞争力 的汽 油发 电机组 产品。该款发 电机组 自上市 以来 , 深受客户欢迎 ,
式中 , 为最小传 动角 , 6 为设计变量 /及 7的函数1 7 / , " 2 1 。
在 M TA A L B软件上 编辑 目标 函数 的优化 约束 条件 的 M 7 2
赛 车优化前后理 想和实际 的汽车左 右车轮转角 的关 系 曲 线如 图 6所示 , 当外轮转 角为虽大 2 。时 。 2 出现最大理论 与实 际 A k r n转角偏差 , 38 , eema 为 .。 存在轮胎 的磨 损 , 但是在外 轮
( 下转 第 8 0页 )
Eq ime t up n Ma ua t n e h oo yNo6,01 n fcr gT c n lg . 2 0 i
到 2 0h 0 。
襄 3 可 靠性、 耐久性试验表
的一种有效方式 。朗沃德 L 5 0 Y单相汽油发电机组 由汽 W5 0 C 油发动机 、 单相发 电机 、 框架 、 面板 、 电器 仪表 、 隔热板 、 减震软 垫等零部 件组成 , 减震 性能和发 电机隔热效果非常好 , 而且采 用 目前市场上 少有的圆弧 面板 设计 ,把一些影 响外 观的螺栓 紧固件完全 隐藏起来 , 工精细 , 做 外型饱满 、 圆滑 , 获得中华 并 人 民共和 国国家知识产权局两项专利保护 。
汽车转向梯形机构在不同目标函数下的优化2010

设 计与研 究汽车转向梯形机构在不同目标函数下的优化廖林清,王金龙,谢 明,屈 翔,张 君(重庆理工大学重庆汽车学院,重庆400050)Optimization Design of t he Steering Trapezoidal Mechanism wit h Different ObjectiveFunctionsL IAO Lin 2qing ,WANG Jin 2long ,XIE Ming ,QU Xiang ,ZHANG Jun(Chongqing Automobile College ,Chongqing University of Technology ,Chongqing 400050,China ) 摘要:基于汽车转向梯形机构的平面模型,依据阿克曼原理,以外转向轮转角误差、转向中心误差Ⅰ、转向中心误差Ⅱ和转向前束误差建立4种目标函数,应用C ++Bulider6.0软件编译优化设计程序,结合优化设计实例,分析4种目标函数下的优化效果,结果表明以转向中心误差Ⅰ为目标函数最合理.关键词:转向梯形机构;目标函数;优化设计中图分类号:U463.4文献标识码:A文章编号:100122257(2010)022*******收稿日期:2009210219基金项目:重庆市科技攻关计划项目(CSTC ,2009AB6021)Abstract :According to t he Ackerman princi 2ple ,four kinds of objective f unctions including t he angular error of out side steering tire ,steering cen 2ter error Ⅰ,Ⅱ,steering toe 2in error are established based on t he planar model of t he steering trape 2zoidal mechanism in t his paper.The optimization result s under t he conditions of t he four kinds of objective f unctions are analyzed combined wit h op 2timized cases by using t he C ++Bulider6.0soft 2ware.The result s indicate t hat it ’s t he best solu 2tion when steering center error Ⅰis selected as t he objective f unction.K ey w ords :steering t rapezoidal mechanism ;objective f unction ;optimization design0 引言汽车转向梯形机构的设计对转向性能起决定性作用,在汽车设计中占重要地位,精确的转向梯形机构能够更好地满足阿克曼原理,保障良好的转向性能.转向梯形机构有整体式和断开式2种,当汽车前悬架采用非独立悬架时,采用整体式转向梯形机构.整体式转向梯形机构有结构简单,调整前束容易,制造成本低等优点[1].整体式转向梯形机构不满足阿克曼原理.汽车转向过程中,当内转向轮转过一个角度时,实际外转向轮转角与理论外转向轮转角间有误差,产生外转向轮转角误差;前轮转向中心会偏离后轮轴线,形成转向中心误差;转向前束角[2]不全为零,存在转向前束误差.目前对转向梯形机构的优化设计,目标函数有以下几种:以外转向轮的绝对误差的最大值或相对误差的极大值为目标函数[3],这种方法只考虑转向过程中的最大误差,不能对整个转向过程进行综合分析;以两转向轮轴线交点的运动轨迹为目标函数[4-5],这种方法需要将交点坐标值与轴距进行比较,才能得到优化结果,不够直观;以转向轮转角误差为目标函数[6-8],这种方法选择不同转向轮为自变量时得到的优化结果不同,并且优化后的转向梯形机构存在转角误差很小,但前轮转向中心偏离后轮轴线较远的不理想情况.本文以转向中心误差和转向前束误差建立目标函数,以整体式转向梯形机构的优化设计为例,对目标函数进行研究.1 整体式转向梯形机构优化设计的目标函数1.1 以外转向轮转角误差建立目标函数对于如图1所示的整体式转向梯形机构,传统的优化设计中常用外转向轮转角误差作为目标函数[1].设内转向轮转角α为自变量,外转向轮转角β为因变量.按照阿克曼原理可求得理论外转向轮转角β,从转向梯形机构的平面模型可推导出实际外转向轮转角β′.β′应尽可能接近β.由于小转角在使用中较频繁,大转角较少使用,所以引入加权系数ω(α).设x 为设计变量;αmax 为内转向轮的最大转角.由外转向轮转角误差建立的目标函数为:f (x )=∑αmaxα=0ω(α) arccosk -r cos (θ0-α)k 2+r 2-2k r cos (θ0-α)arccot cot α+kl+arccosr (1-2cos 2θ0)-k[cos (θ0-α)-2cos θ0]k 2+r 2-2kr cos (θ0-α)-θ0arccot cot α+kl-1×100%(1)图1 整体式转向梯形机构1.2以转向中心误差Ⅰ建立目标函数整体式转向梯形机构不满足阿克曼原理,在汽车转向时,前轮转向中心O 点不在后轮轴线上,如图2所示.此时,转向中心误差可以用O 点到后轮轴线的距离|O H |来表示.将|O H |记为转向中心误差Ⅰ,从图2可知:|O H |=kcot β-cot α-l(2)在整个转向过程中,转向中心误差Ⅰ的总和越小则表示梯形机构越好,同样引入加权系数ω(α),由转向中心误差Ⅰ建立的目标函数f (x )为:f (x )=∑αmaxα=0ω(α)‖O H ‖=∑αmax α=0ω(α)kcot β-cot α-l(3)1.3 以转向中心误差Ⅱ建立目标函数整体式转向梯形机构不满足阿克曼原理,在汽车转向时,两前轮在后轮轴线上的交点分别为O 1,O 2,如图2所示.转向中心误差也可以O 1,O 2在后轮轴线上的距离|O 1O 2|来表示.将|O 1O 2|记为转向中心误差Ⅱ,从图2可知:|O 1O 2|=l !(cot α-cot β)+k (4)在整个转向过程中,转向中心误差Ⅱ的总和越小则表示梯形机构越好,同样引入加权系数ω(α),由转向中心误差Ⅱ建立的目标函数为:f (x )=∑αmaxα=0ω(α)‖O 1O 2‖=∑αmax α=0ω(α)|l ・(cot α-cotβ)+k |(5)图2 转向中心1.4 以转向前束误差建立目标函数转向前束的定义:当满足阿克曼原理时,两前轮轴线与后轮轴线汇交于一点,此时转向前束角为0.当不满足阿克曼原理时,两前轮轴线的交点不在后轮轴线上.此时可以假想将内外转向轮回转轴线按相反方向偏移一个相等的角度Δθ,使转向轮回转轴线和后轮轴线三者交于一点,满足阿克曼原理,这个假想的偏移角度Δθ就是转向前束角[2].整体式转向梯形机构的转向前束如图3所示,则有内外转向轮转角的关系为:cot (β+Δθ)-cot (α-Δθ)=kl(6)从式(6)可得:Δθ=arccot (2+2B +A C )±(2+2B +A C )2+4(A -C )(A -B C )2(A -C )(7)A =cot β-cot α;B =cot β!cot α;C =k l在转向过程中,转向前束值越小说明梯形机构的误差越小,同样引入加权系数ω(α),由转向前束误差建立的目标函数为:f (x )=∑αmaxα=0ω(α)|Δθ|(8)图3 转向前束2 设计变量与约束条件的确定2.1 设计变量在汽车设计中,对转向梯形机构的设计主要是选择合适的梯形臂长度r 和梯形底角θ0,因此选取r 和θ0两个参数为设计变量.即x ={r ,θ0}(9)2.2 约束条件在转向过程中,其误差在最常使用的中间位置附近小转角范围内应尽量小,以减小高速行驶时轮胎的磨损;而在不经常使用且车速较低的最大转角时,可适当放宽要求.并且考虑到多数使用工况下转角θ0小于20°,且10°以内的小转角使用得更加频繁,因此取加权系数为:ω(α)=1.50°<α≤10°1.010°<α≤20°0.520°<α≤αmax(10)r 和θ0两个参数过小时,会使横拉杆上的转向力过大;当r 过大时,将使梯形布置困难;当θ0越大,梯形越接近矩形,f (x )值就越大.所以各设计变量的取值范围构成的约束条件为:r -r min ≥0r max -r ≥0θ0-θ0max ≥0(11)其中梯形臂长度r 常取为r min =0.11k 、r max =0.15k;梯形底角θ0min =70°.3 优化设计实例某种汽车的转向传动机构参数为:轴距l =4700mm ,两主销间的距离k =1480mm ,梯形臂长r =199.8mm ,梯形底角θ0=75.5°,内转向轮的最大转角αmax =42°.根据上述建立的目标函数、设计变量和约束条件,选用C ++Bulider6.0软件编译优化设计程序.对实例分别在4个目标函数下进行优化计算,得到优化前后的设计变量如表1所示,优化前后的误差曲线如图4所示.表1 优化前后的设计变量设计变量优化前优化后外转向轮转角误差转向中心误差Ⅰ转向中心误差Ⅱ转向前束误差梯形臂长度(mm )199.8162.8162.8162.8162.8梯形底角(°)75.575.674.174.376.7 从表1可以看出,整体式转向梯形机构优化设计时,选择的目标函数不同,得到的梯形底角的最优值不一致,梯形臂长度的最优值基本一致.所以选择不同的优化目标函数对梯形底角有影响,但对梯形臂长度基本没有影响.在转向梯形机构中,梯形底角的变化会改变内、外转向轮的转角关系以及前轮转向中心的运动轨迹,梯形臂长度直接影响转向梯形机构的布置,引起汽车转向性能的改变.图4 优化前后的误差曲线从图4可以看出,以外转向轮转角误差为目标函数优化后,误差值变化不大,优化效果不太明显;以转向中心误差Ⅰ为目标函数优化后,优化效果显著,而且转角小于20°的误差值都很小,转向效果最好;以转向中心误差Ⅱ为目标函数优化后,虽然误差的总和减小了,但转角大于10°的误差都比原来增大了;以转向前束误差为目标函数优化后,误差总和减小了,大转角范围内的误差也减小了,但20°转角附近的误差明显增大.所以4个目标函数中,以转向中心误差Ⅰ为目标函数,优化结果较理想.4 结束语通过以上分析和优化设计实例可知:选择的目标函数不同,求解的梯形底角的最优值不相同,梯形臂长度的最优值基本相同.4个目标函数中,传统的以外转向轮转角为目标函数,优化效果不明显.以转向中心误差Ⅰ为目标函数最合理,优化效果显著,优化后的转向梯形机构更精确,能够更好地满足阿克曼原理.参考文献:[1] 王望予.汽车设计[M ].北京:机械工业出版社,2004.[2] 吴晓建.齿轮齿条式转向机构转向特性研究[D ].重庆:重庆理工大学,2009.[3] 王国安,郝子军.轮式推土机转向梯形优化设计[J ].西安公路学院学报,1986,(9):89-112.[4] 周全申,等.车辆转向机构设计与分析[J ].河南工业大学学报(自然科学版),2006,(4):60-66.[5] Mitchell Wm C ,Staniforth Allan ,Scott Ian.Analysis ofackermann steering geometry [A ].Motorsports Engi 2neering Conference and Exhibition[C].USA.2006.[6] Leishman Robert ,Chase Kenneth.A new tool for de 2sign and analysis of optimized rack and pinion steering Mechanisms[C].USA ,2009.[7] 姚明龙,王福林.车辆转向梯形优化设计及其求解方法的研究[J ].机械设计与制造,2007,(5):24-26.[8] 陈朝阳,张代胜.汽车转向梯形最优化设计[J ].安徽工学院学报,1982,(3):28-36.作者简介:廖林清 (1966-),男,四川眉山人,教授,硕士研究生导师,主要从事现代设计法的教学与应用研究.挠性陀螺仪内外接头的质量控制贺新华,田梦君(西北工业大学机电学院,陕西西安710072)Quality Cont rol of t he J unction Between Inside and Out side of Flexible Gyro scopeHE Xin 2hu a ,TIAN meng 2jun(School of Mechanical Engineering ,Northwestern Polytechnical University ,Xi ’an 710072,China ) 摘要:从理论分析计算的角度,分析了关键尺寸(宽度和厚度)对内外挠性接头性能的影响,研究了困扰批生产的接头外观的控制等,保证了接头的质量,提高了接头加工效率和合格率,降低了生产成本.关键词:内外挠性接头;尺寸控制;外观控制中图分类号:T H123文献标识码:A文章编号:100122257(2010)022*******收稿日期:2009209203Abstract :In terms of t heoretical analysis ,t he key parameters (widt h and t hickness )impacting on t he performances of flexible junction and t he con 2t rol strategy which conf used batch p roduction were analyzed and t he result s were given at last.The st rategy not only assured t he ability of gyroscopebut also imp roved t he efficiency of processing and t he acceptance rate was improved.K ey w ords :flexible gyroscope ;size control ;ap 2pearance cont rol0 引言内外挠性接头是挠性陀螺仪的关键部位,它把飞轮转子与底座电机的驱动轴连接起来,是引起陀螺仪基本误差的元件[1].可以说挠性接头性能的好坏,从某种程度决定了整个陀螺仪性能的好坏.接头的尺寸,外观设计要求很严,材料价格昂贵,批量生产中,超差、报废较多,直接经济损失较大.挠性接头的品质因素F M 对接头的性能起决定作用,其与总漂移误差成反比,即F M 越大,表示精度越高,因此,为了提高陀螺仪的精度,应尽可能增大F M .由F M =(J Z +I e )/(2I e -I Z ),可知,F M 与陀。
汽车整体式转向梯形机构仿真计算与优化

汽车整体式转向梯形机构仿真计算与优化首先,需要进行操纵性能仿真计算。
操纵性能是指车辆在转向过程中的稳定性、准确性和操纵力的大小。
通过建立车辆动力学模型,可以模拟车辆在不同转向输入下的行驶状态,并计算车辆的操纵性能参数,如转向响应时间、转向幅度和操纵力矩等。
通过对不同转向梯形机构参数的变化进行仿真计算,可以评估梯形机构对操纵性能的影响,并进行优化设计。
其次,还需要进行力学性能仿真计算。
力学性能是指转向机构在不同工况下的强度、刚度和耐久性等。
通过建立转向机构的有限元模型,可以分析转向机构在不同工况下的应力、应变和位移等力学参数,评估转向机构的设计是否满足强度和刚度要求,并进行优化调整。
同时,还可以通过应用疲劳分析方法,预测转向机构在长期使用过程中的损伤、疲劳寿命和可靠性等问题,以提高整体转向机构的耐久性。
最后,需要进行优化设计。
在进行仿真计算的基础上,可以通过参数优化和结构优化方法,对转向机构的参数和结构进行调整和改进。
例如,通过对齿条、滚珠丝杠、主动齿轮和从动齿轮等关键部件的几何参数进行优化,可以减小滚动摩擦和间隙,提高转向机构的机械效率和动力传递精度。
同时,还可以通过改变转向机构的布局和材料选择,减少转向机构的质量,并提高其刚度和强度,从而提升整体转向机构的性能。
综上所述,汽车整体式转向梯形机构的仿真计算与优化是确保汽车操纵性和稳定性的重要环节,能够通过操纵性能仿真计算、力学性能仿真计算和优化设计方法,对转向机构的性能进行评估和改进,提高汽车整体转向梯形机构的性能和可靠性。
齿轮齿条式转向器双梯形转向机构的优化设计
齿轮齿条式转向器双梯形转向机构的优化设计李睿扬(学号:02000404)(东南大学机械工程系)汽车转向系统需精确地实现阿克曼转向条件,这与转向传动机构的设计密切关联。
在本文,将以与齿轮齿条式转向器配用的转向传动机构为实例,讨论机构的优化设计。
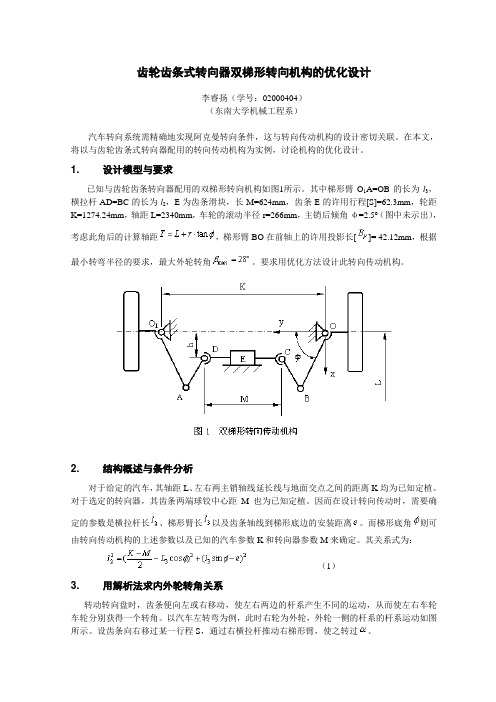
1.设计模型与要求已知与齿轮齿条转向器配用的双梯形转向机构如图1所示。
其中梯形臂O1A=OB的长为l3,横拉杆AD=BC的长为l2,E为齿条滑块,长M=624mm,齿条E的许用行程[S]=62.3mm,轮距K=1274.24mm,轴距L=2340mm,车轮的滚动半径r=266mm,主销后倾角φ=2.5o(图中未示出),考虑此角后的计算轴距,梯形臂BO在前轴上的许用投影长[]= 42.12mm,根据最小转弯半径的要求,最大外轮转角。
要求用优化方法设计此转向传动机构。
2.结构概述与条件分析对于给定的汽车,其轴距L、左右两主销轴线延长线与地面交点之间的距离K均为已知定植。
对于选定的转向器,其齿条两端球铰中心距M也为已知定植。
因而在设计转向传动时,需要确定的参数是横拉杆长、梯形臂长以及齿条轴线到梯形底边的安装距离。
而梯形底角则可由转向传动机构的上述参数以及已知的汽车参数K和转向器参数M来确定。
其关系式为:(1)3.用解析法求内外轮转角关系转动转向盘时,齿条便向左或右移动,使左右两边的杆系产生不同的运动,从而使左右车轮车轮分别获得一个转角。
以汽车左转弯为例,此时右轮为外轮,外轮一侧的杆系的杆系运动如图所示。
设齿条向右移过某一行程S,通过右横拉杆推动右梯形臂,使之转过。
图2 转向传动机构几何关系如图2所示,取梯形右底角顶点O为坐标原点,则可导出齿条行程S与外轮转角的关系:(2)另外,由图可知:(3)而,(4)(5)将(4)、(5)表达式代入(3)式。
因此,利用(2)式便可求出对应于任一外轮转角的齿条行程S,再将S代入公式(3)(4)(5),即可求相应的内轮转角。
将上述公式结合起来便可将表示为的函数,记作。
汽车断开式转向梯形机构的优化设计
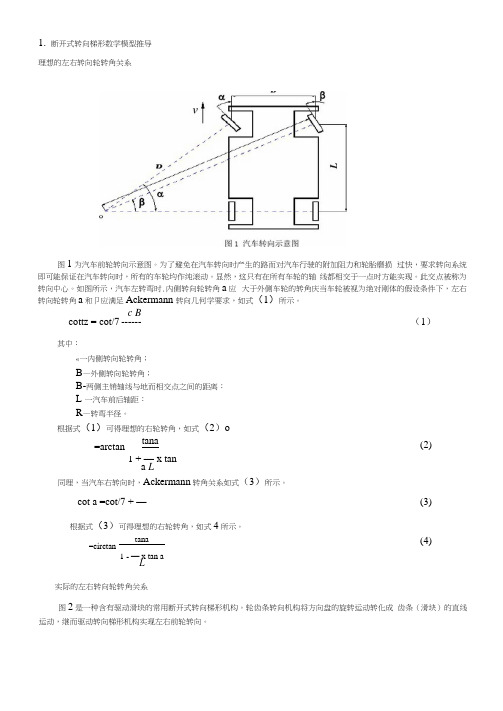
1.断开式转向梯形数学模型推导理想的左右转向轮转角关系图1为汽车前轮转向示意图。
为了避免在汽车转向时产生的路而对汽车行驶的附加阻力和轮胎磨损过快,要求转向系统即可能保证在汽车转向时,所有的车轮均作纯滚动。
显然,这只有在所有车轮的轴线都相交于一点时方能实现。
此交点被称为转向中心。
如图所示,汽车左转弯时.内侧转向轮转角a应大于外侧车轮的转角庆当车轮被视为绝对刚体的假设条件下,左右转向轮转角a和卩应满足Ackermann 转向几何学要求,如式(1)所示。
c Bcottz = cot/7 ------ (1)其中:«一内侧转向轮转角;B—外侧转向轮转角;B-两侧主销轴线与地而相交点之间的距离:L 一汽车前后轴距:R—转弯半径。
根据式(1)可得理想的右轮转角,如式(2)otana (2) =arctan1 + — x tana L同理,当汽车右转向时,Ackermann转角关系如式(3)所示。
(3)cot a =cot/7 + —根据式(3)可得理想的右轮转角,如式4所示。
tana(4)=circtan1 - — x tan aL实际的左右转向轮转角关系图2是一种含有驱动滑块的常用断开式转向梯形机构。
轮齿条转向机构将方向盘的旋转运动转化成齿条(滑块)的直线运动,继而驱动转向梯形机构实现左右前轮转向。
图中:厶一转向机齿条左右球较中心的距离;L 2 一左右横拉杆的长度;厶一左右转向节臂的长度:厶•一车轮中心至转向主销的距离:S] —转向齿条从中心位置向左的位移量: s 2 一转向齿条从中心位宜向左的位移量:y —转向齿条左右球狡中心连线与左右转向主销中心连线之偏距,图示位置取正值,反之取负值: S 。
一直线行驶时,转向齿条左球钱中心和左转向主销的水平距离:一转向节骨与汽车纵轴线的夹角。
运用余弦泄理和三角函数变换公式,经推导可得: ______________________-Cv - S xcos a = cos (ZAOB + Z.BOY )= 一;----- - ------------2厶(丁 +尸)A 点的坐标值为:v CxS-yx>jA 2 + B 2-C 2B2x (/+r )2*…Cxy + SxyjA 2 + B 2-C 2 沧=_ ------------- —zn ----------2x (/+S') 其中:A = -2LyxS,B = _2厶xy,C = 15,-1^-y 2-~s\ F —表示转向齿条弐球钱中心和左转向主销中心的实际距藹,对于直线行驶时,g = S 。
整体式转向梯形机构优化设计-2014

整体式转向梯形机构优化设计SGA3550型自卸式非公路用汽车采用整体式转向梯形机构(如图1所示) ,由转向横拉杆、转向梯形臂和汽车前轴组成。
图中,为K主销中心距,L为轴距,为转向梯形底角, W为转向臂长,为内侧车轮转角,为外侧车轮转角(以下符号意义相同) 。
这种方案的优点是结构简单,调整容易,制造成本低;主要缺点是一侧转向轮上、下跳动时,会影响另一侧转向轮。
车辆转向时,内侧车轮被迫沿着比外侧车轮小的弧线行进,因此,转向梯形应使汽车在转向时两前轮产生不同的转向角,并沿着各自的弧线滚动,同时前后四个车轮又绕着同一圆心滚动 ,从而消除轮胎的滑动。
若忽略车轮的侧偏角,车辆转向时内外轮理想转角应保持以下关系:若忽略车轮的侧偏角,车辆转向时内外轮理想转角应保持以下关系:cot-cot=K/L (1)若自变角为,则因变角的期望值为=arccot(cot-K/L) (2)现有转向梯形机构仅能近似满足上式关系。
利用余弦定理可推得转向梯形的实际因变角如下:图2(3)(4)(5)(6)由(4)(5)(6)式得出(7)(8)由(3)(7)(8)式得出:实际因变角要求:(1) 列出转向机构的优化数学模型(2) 已知轮距2900mm;轴距L= 3800 mm;主销中心距K= 2100 mm;用Matlab中lsqcurvefit(……)函数或lsqnonlin(……)函数进行优化,求取设计变量梯形底角的值(要求底角范围在60-90度之间),转向梯形臂长度的值(要求在250-450mm之间)以满足设计需求。
该优化问题可以看作是将理想的内外转向轮曲线同待优化的内外转向轮角度关系进行拟合,MATLAB优化工具箱中提供了几种可供选择的优化函数:(1) [x,resnorm]=lsqcurvefit(fun,x0,xdata,ydata,lb,ub),该函数是进行非线性曲线的二次拟合。
其中F(x)为待优化的函数,数学模型为:(2) [x,resnorm]=lsqnonlin(……),该函数求解非线性最小二乘问题,包括非线性数据拟合问题。
汽车转向梯形机构设计

汽车转向梯形机构设计及matlab/simMechanics 仿真汽车转向梯形机构设计及matlab/simMechanics 仿真Trapezoidal steering mechanism design matlab simMechanics Simulation 一、汽车转向梯形机构设计1.设计模型与要求:已知汽车梯形转向机构如下图所示。
该车车型为沃尔沃,转向节跨距M 为1305mm ,前轮距D 为1535mm ,轴距L 为2640mm 。
该车最小的转弯半径R 为5300mm ,并且具有良好的传力性能。
2.结构概述与条件分析根据题目条件,转向节跨距M ,前轮距D ,轴距L 均已知,则设计梯形转向机构只需要确定连架杆a ,连杆b 和轮与连架杆之间的夹角0α即可。
由于aM b 2cos 0-=α 根据最小转弯半径R=11000,以及公式:)(21sin max M D R L--=α求出m ax α=30.61313.两侧转向轮偏转角之间的理想关系式为了避免在汽车转向时产生的路面对汽车行驶的附加阻力和轮胎过快磨损,要求车轮作纯滚动。
显然只有在车轮轴线交于O 点才能实现。
此时的α和β满足以下关系式:LM +=βαcot cot 为此要精心地确定转向梯形机构的参数。
实际设计中,所有汽车的转向梯形都只能设计得再一定的车轮偏转角范围内,使两侧车轮偏转角的关系大体上接近于理想关系。
4.转向传动机构的优化设计4.1 传动机构连架杆与车轮轴线夹角0α的确定根据经验公式:︒±=5)34arctan(0ML α 带入数据得 0α=67.4161︒~77.4161︒,初步设计取的是72︒。
4.2 理论曲线与实际曲线焦点位置的确定以及连架杆a 的确定根据经验得交点一般发生在0.8m ax α~0.95m ax α=24.49°~29.0824°之间,实验中取α=26︒。
此时实际理论ββ==)tan tan arctan(ααM L L -=32.728°,带入实际公式,则可以确定连架杆a 值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
齿轮齿条式转向梯形的优化设计学院:车辆与能源学院专业:2012级车辆工程学号:S12085234009姓名:刘建霞日期:2014年4月15日齿轮齿条式转向器(如图1)具有结构简单紧凑,制造工艺简便等优点,不仅适用于整体式前轴也适用于前轮采用独立悬架的断开式前轴,目前被广泛地用于轿车、轻型客货车、微型汽车等车辆上。
与该转向器相匹配的转向梯形机构与传统的整体式转向梯形机构相比有其特殊之处,下面举一实例加以说明。
图1 齿轮齿条式转向梯形机构运动实体模型题目:已知某微型汽车(如图2所示)各参数如下:1274.24K mm =,0()=2.5β主销后倾角,L(轴距)=2340mm ,=mm r (车轮滚动半径)266,=oy B y 梯形臂球头销中心的()42坐标.12mm ,由最小转弯半径得最大外轮转角为28o ,许用齿条行程[]62.3S mm =,选用参数624M mm =,试设计转向传动机构。
要求:(1)用优化方法设计此转向梯形传动机构。
(2)优化后校验,压力角40o α≤。
(3)计算出l 1长度,齿条左右移动最大距离。
图2 齿轮齿条转向梯形机构一 建模由转向基本要求可知,在不计轮胎侧偏时,实现转向轮纯滚动、无侧滑转向的条件是内、外轮转角符合Arckerman 理想转角关系:cot cot /O i k L θθ-=,如图3所示。
图3 理想的内外轮转角关系(1)设计变量: 选取变量 1(,,)X l h γ=图4 外轮一侧杆系运动情况由图4内外轮转角的关系得:221o 21o l cos(r )l [sin()h]2K M S l r θθ-=-+-+-SM K h22arctan+-=ϕ (2)221222221)2(2)2(arccoshS M K l l h S M K l ++--++-+=γ (3) i r θφγ=-- (4)联立上式可得o ()i g θθ=的函数关系式。
对于给定的汽车和选定的转向器,转向梯形机构有横拉杆长l 1和梯形臂长m 两个设计变量。
在计算过程中,以梯形底角r 代替横拉杆长l 1作为设计变量,再代入式(1)得到l 1。
底角r 可按经验公式先选一个初始值43r arctan()67.88LK ==,进行优化搜索。
12(2)目标函数:()(X)ii i MinF θθ=-∑ (实际内轮转角与理想内轮转角之差) (3)约束条件:第一,要保证梯形臂不与车轮上的零部件发生干涉。
第二,要保证有足够的齿条行程来实现要求的最大转角。
第三,要保证有足够大的传动角β。
传动角β是指转向梯形臂与横拉杆所夹的锐角。
传动角过小会造成有效力过小,导致转向沉重或回正不良。
所以压力角α≤40°作为约束条件。
第四,为了保证传动良好还希望横拉杆与齿条间夹角ξ比较小,一般为m ax ξ︒≤10。
将这些约束条件表示为下述的约束方程: S.T-l 1<0;l 1-<0;;l 1-((K-M)/2-l 1*cos γ)sin10°-h<0;h-l 1*sin(γ-)+((K-M)/2-l 1*cos γ)sin10°<0;二 计算优化取初始值l=128,r=67.88°,使用MATMAB数学软件优化计算。
1优化计算程序:K=1274.24;b=2.5*pi/180; %主销后倾角L=2340;r=266; %车轮滚动半径Boy=42.12;Qomax=28*pi/180; %根据最小转弯半径求出的最大外轮转角M=624;S=62.3;j=1;T=L+r*tan(b); %计及主销后倾角b时的计算轴距%Qi=acot(cot(Qo)-0.5419); %理想的内外轮转角关系Qimax=36.756*pi/180; %根据上式求出理想的内轮最大转角R0=atan((4/3)*(T/K));%梯形臂长l1的取值范围l1min=Boy/cos(R0);l1max=S/(cos(R0)-cos(R0+Qomax));l1=128;%l1选定时,梯形底角R的取值上限Rmax=acos(Boy/l1);%l1、R选定时安装距离h的取值范围hmin=l1-((K-M)/2-l1*cos(R0))*sin(10*pi/180);hmax=l1*sin(R0-Qimax)+((K-M)/2-l1*cos(R0))*sin(10*pi/180);%取初值R0=67.88*pi/180;l1=128;h=96;for Qo1=1:28for h=hmin:hmaxfori=R0:0.1:Rmaxfor l=l1min:0.1:l1maxQo=Qo1*pi/180;l2=sqrt(((K-M)/2-l1*cos(R0))^2+(l1*sin(R0)-h)^2);S1(j)=(K-M)/2-l1*cos(R0+Qo)-sqrt(l2^2-(l1*sin(R0+Qo)-h)^2);%齿条行程Qii(j)=R0-atan(2*h/(K-M+2*S1(j)))-acos((l1^2+h^2+((K-M)/2+S1(j))^2-l2^2 )/(2*l1*sqrt(h^2+((K-M)/2+S1(j))^2)));%实际的内外轮转角关系Qi(j)=acot(cot(Qo)-0.5419);%理想的内外轮转角关系if (Qo1>0)&(Qo1<=10);Wo=1.5;elseif (Qo1>10)&(Qo1<=20);Wo=1.0;else (Qo1>20)&(Qo1<=28);Wo=0.5;endP0(j)=(Qii(j)*180/pi-Qi(j)*180/pi)^2*Wo;j=j+1;endendendend[m,c]=min(P0);P=sqrt(sum(P0)/(28)); %评价指标j=1;for Qo1=1:28for h=hmin:hmaxfori=R0:0.1:Rmaxfor l=l1min:0.1:l1maxQo=Qo1*pi/180;S1(j)=(K-M)/2-l1*cos(R0+Qo)-sqrt(l2^2-(l1*sin(R0+Qo)-h)^2);%齿条行程Qii(j)=R0-atan(2*h/(K-M+2*S1(j)))-acos((l1^2+h^2+((K-M)/2+S1(j))^2-l2^2 )/(2*l1*sqrt(h^2+((K-M)/2+S1(j))^2)));%实际的内外轮转角关系Qi(j)=acot(cot(Qo)-0.5419);%理想的内外轮转角关系if (Qo1>0)&(Qo1<=10);Wo=1.5;elseif (Qo1>10)&(Qo1<=20);Wo=1.0;else (Qo1>20)&(Qo1<=28);Wo=0.5;endP0(j)=(Qii(j)*180/pi-Qi(j)*180/pi)^2*Wo;j=j+1;if j==c-1H=h;I=i;L1=l;endendendendendl2=sqrt(((K-M)/2-L1*cos(I))^2+(L1*sin(I)-H)^2); %横拉杆长度j=1;for Qo1=1:28Qo=Qo1*pi/180;S1(j)=(K-M)/2-L1*cos(I+Qo)-sqrt(l2^2-(L1*sin(I+Qo)-H)^2);%齿条行程Qlii(j)=I-atan(2*H/(K-M+2*S1(j)))-acos((L1^2+H^2+((K-M)/2+S1(j))^2-l2^2 )/(2*L1*sqrt(H^2+((K-M)/2+S1(j))^2)));%实际的内外轮转角关系Qsi(j)=acot(cot(Qo)-0.5419);%理想的内外轮转角关系j=j+1;endplot(Qlii,'r');hold onplot(Qsi);legend('计算内轮转角','理想内轮转角');三计算结果:F(X)= 3.38*10-6l=129.8751γ=67.88h=112.91四验证压力角OF=sqrt(H^2+((K-M)/2+S1(23))^2);G=acos((L1^2+H^2+((K-M)/2+S1(23))^2-l2^2)/(2*L1*sqrt(H^2+((K-M)/2+S1(23))^2)));a23=asin(OF*sin(G)/l2)*180/pi;计算可得外轮转角为23°时的压力角为a23= 31.4°<40°符合要求。
下图为优化后转向梯形外轮转角在0~28°变化时,实际内轮转角与理想内轮转角的变化曲线。
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
