计控实验二-连续系统变换为离散系统
连续与离散控制系统教学设计 (2)

连续与离散控制系统教学设计引言控制系统是工程学科中一个重要的研究领域,其研究对象是对于物理、化学、生物等系统进行控制。
连续控制系统与离散控制系统是控制系统的两个基本方向,掌握这两种控制系统的设计与实现方法,对于广大工程类学生而言是很重要的。
本文介绍了一份连续与离散控制系统教学设计,旨在帮助学生更好地掌握这两个控制系统,并应用于实际工程设计中。
教学目的1.培养学生对控制系统的基本认识和了解。
2.掌握连续控制系统的设计与实现方法。
3.掌握离散控制系统的设计与实现方法。
4.理解连续控制系统与离散控制系统的区别与联系。
5.在工程实践中成功应用所掌握的知识和技能。
教学对象电气工程、自动化、机械工程或相关专业的大学本科生。
教学内容1.控制系统基础知识–控制系统组成和功能–控制系统常见符号与术语2.连续控制系统设计–连续控制系统的建模–连续控制系统的稳态分析–连续控制系统的设计、调试和验证3.离散控制系统设计–离散控制系统的设计方法–采样定理与离散化建模–离散控制系统的稳态分析–离散控制系统的设计、调试和验证4.连续控制系统与离散控制系统的联系与区别–正确比较两种控制系统各自的特点和应用范围5.教学实践和实验–实际运用所学知识进行任务分析、建模和设计–使用软件进行系统仿真、调试和验证–使用物理模型进行实验–进行控制效果的测试和比较教学方法1.理论课–采取教师授课、案例讲解和学生交流互动相结合的方式进行。
–大量应用MATLAB/Simulink软件进行仿真2.实验教学–学生在电气或自控实验室内完成具体的系统建模、仿真,测试和实验。
3.课程实践–学生完成实际工程任务的分析、设计和控制实现。
教材主教材:•《现代控制系统》(Richard C.Dorf and Robert H.Bishop)•《控制科学与工程导论》(皮克林)参考书目:•《控制系统工程实践》(Chee-Mun Ong)•《现代控制工程》(Ogata)•《自动控制原理》(曹毅)•《现代控制理论及其应用》(谢尔顿.罗斯)教学评估1.平时成绩占教学总成绩的40%,包括学习笔记、作业、实验报告等。
连续系统离散化方法
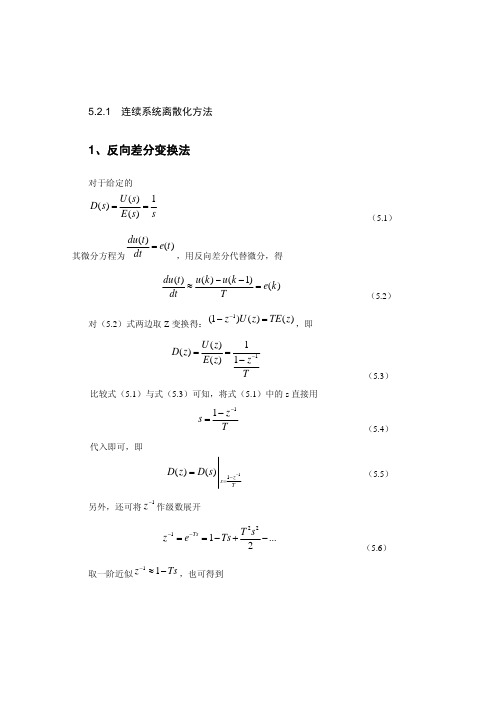
2 2 2
这相应于 z 平面单位圆内部,如图 5-6 所示。因此,双线性变换将 s 平面上整个左半平面 映射到 z 平面上以原点为圆心的单位圆内部(这是 z 平面上的稳定区) 。这和 z = e 映射是一
Ts
样的,但是离散滤波器的过渡响应及频率响应特性有显著的不同。
jω
Im
ωB
D ( z ) 不能保持 D ( s ) 的脉冲响应和频率响应。
(5) 所得的离散频率响应不产生畸变。
4、脉冲响应不变法
所谓脉冲响应不变法就是将连续滤波器 D ( s ) 离散得到离散滤波器 D ( z ) 后,它的脉冲响 应
g D ( kT ) = Z −1[ D ( z )]
与连续滤波器的脉冲响应 g (t ) = L [ D ( s )] 在各采样时刻的值是相等
上式可以写成
1⎞ ⎛ ⎛1⎞ 2 ⎜σ − ⎟ + ω < ⎜ ⎟ 2⎠ ⎝ ⎝ 2⎠
2
2
由上式可以看出, s 平面的稳定域映射到 z 平面上以 σ = 1 / 2 , ω = 0 为圆心, 1 / 2 为半 径的圆内,如图 5-3 所示。
jω
Im
ω =0
σ
Re
z =1
图 5-3 反向差分变换 s 平面与 z 平面的对应关系 反向差分变换方法的主要特点如下: ①变换计算简单; ②由图 5-3 看出, s 平面的左半平面映射到 z 平面的单位圆内部一个小圆内,因而,如果
(5.17)
还可以将式(5.14)看作采用双线性变换时由 s 平面到 z 平面的映射。应当注意到,双线
22
第 2 章 计算机控制系统的信号转换
性变换使 D ( z ) 的极、零点数目相同,且离散滤波器的阶数(即离散滤波器的极点数)与原连 续滤波器的阶数相同。 由式 (5.14) ,s 平面的左半平面 [Re( s ) < 0] 映射到 z 平面时,其关系如下:
第5章数字控制系统的连续——离散化设计

1 lim[s s0 s
10s 1 s1
]
lim[(z
z 1
1)
z
z
1
K
z
z 0.9048] z 0.3679
K z 6.6397
因此
D(z) 6.6397 z 0.9048 z 0.3679
(4)仿真检验
Gd (z)
(1
z 1 )Z[ 1 s
1 ] s(10s 1)
0.04837(z 0.9678) (z 1)(z 0.9048)
D(z) K z1 (z 1)z
(z e T )2
当R(s) 1 时,u(t) 0
u(t) lim sR(s)D(s)
t s0
s
t
当R(s) 1 时,u(t) 1
当R(z)
s
2
z
t
时 ,u(k) 0
u(k) lim(z 1)R(z)D(z)
k
z 1
z 1 k 当R(s) Tz 时 ,u(k) K z1T
(1 e T )2
(1 e T )2 (z 1)(z 1)
K z2 2T D(z) 2T
(z e T )2
(3)匹 配 到z :D(z) K z1 (z 1)(z )
(z e T )2
要 求T 1s, 1时 ,D( j ) D(e jT ) j 0.50
(1 j)2
(t)
h(t) (t) *(t)
h*(t)
D(s)
D(z)
分析脉冲不变法特点:D(s) 与 D(z)之间的近似关系。
➢ 由设计准则知,二者的脉冲响应在采样点取相同值; ➢ D(s)与D(z)极点按Z变换定义z=esT一一对应 ; ➢ 若D(s)稳定,其极点位于S左半平面,则其D(z)必稳定,
连续系统的离散化方法课件

离散化方法的意义
精确性
离散化方法可以提供对连续系统的精 确近似,特别是在计算机仿真和数字 控制系统中。
可计算性
离散化方法可以将不可计算的分析转 化为可计算的形式,便于进行数值计 算和控制器设计。
离散化方法的应用场景
01
02
03
数字控制
在数字控制系统中,连续 系统的离散化是必要的步 骤,以便在数字计算机上 进行数值计算和控制。
小波基选择
常用的小波基包括Haar小波、Daubechies小波、Morlet 小波等。
误差分析
小波变换法的误差主要来自于变换误差和离散化误差。
05
离散化方法的评估与优化
评估离散化方法优劣的标准
01
02
03
04
精度
离散化方法是否能准确代表原 连续系统。
稳定性
离散化方法在一定参数变化范 围内是否能保持稳定。
状态空间模型
用状态变量和输入、输出变量描述连续系统的动态特性。
状态空间模型通常形式为:`x'(t) = Ax(t) + Bu(t)` 和 `y(t) = Cx(t) + Du(t)`,其中 `x(t)` 表 示系统状态,`u(t)` 表示系统输入,`y(t)` 表示系统输出,`A`, `B`, `C`, `D` 是系数矩阵。
化率。
通过求解 ODE,可以得到系统 在任意时刻的状态。
传递函数
表示连续系统在输入和输出之间的传递 特性。
传递函数通常形式为:`G(s) = Y(s) / U(s)`,其中 `Y(s)` 和 `U(s)` 分别是输 出和输入的拉普拉斯变换,`s` 是复变
量。
通过分析传递函数的零点、极点和增益 ,可以得到系统的稳定性和性能特性。
计算机控制技术01-实验二 离散控制系统的性能分析(时域频域)_实验指导书

实验二离散控制系统的性能分析(时域/频域)一、实验目的:1.掌握离散闭环系统的动态性能时域参数的分析与计算方法;2.掌握离散系统稳定性的频域典型参数分析与计算方法。
二、实验工具:1.MATLAB 软件(6.5 以上版本);2.每人计算机一台。
三、实验内容:1.在Matlab 语言平台上,通过给定的闭环离散系统,深刻理解时域参数的物理意义与计算方法,内容包括如下:●阻尼比参数分析:Z平面与S 平面的极点相互转换编程实现;分析S/Z 两个平面域特殊特性(水平线、垂直线、斜线、圆周等)的极点轨迹相互映射方法;●系统阶跃响应参数:上升时间和超调量等。
2.采用频域分析方法,通过编程计算,进一步理解离散系统的稳定性参数,包括如下:●通过幅频图,进行增益裕度分析;●通过相频图,进行相位裕度分析。
四、实验步骤:% script2%Suppose that pole eq. is s=real(s)+j*imag(s) in s plane;% thus s=abs(s)*exp(j*angle(s)).%Assume that pole eq. is z=real(z)+j*imag(z) in z plane;%Thus z=abs(z)*exp(j*angle(z)).%Consequence is gotten as follows:% abs(z)*exp(j*angle(z))=exp((real(s)+j*imag(s))*ts)% =exp(real(s)*ts)*exp(j*imag(s)*ts)% abs(z)=exp(real(s)*ts),thus, real(s)=log(abs(z))/ts;% angle(z)=imag(s)*ts, thus, imag(s)=angle(z)/ts;% Assume that damp ratio is cos(theta), theta=arctan(-imag(s)/real(s));% thus in z plane, damp ratio = cos(arctan(-angle(z)/log(abs(z))))% sys_ta:% R(z)------/ -kz----/ ---->--zoh-->----gplant---> ----- Y(z)% l l% l-----------------------< < ------------------------- l%Example 1 Damping ratio computationts=0.1;gp=tf(1,[1 1 0])gz=c2d(gp,ts,'zoh')kz=tf(5*[1,-0.9],[1 -0.7],ts);sys_ta=feedback(gz*kz,1,-1)p=pole(sys_ta)π/T0.9π/T radii=abs(p);angl=angle(p)damp(sys_ta)real_s=log(radii)/tsimg_s=angl/tszeta=cos(atan(-img_s./real_s))wn=sqrt(real_s.^2+img_s.^2)%Example 2 Mapping of horizontal s-plane line to z-planexx=[0:0.05:1]'N=length(xx)s0=-xx*35;s=s0*[1 1 1 1 1]+j*ones(N,1)*[0,0.25,0.5,0.75,1]*pi/tsplot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid3530 0.762520 0.860.64 0.5 0.34 0.1630 25 201515 0.9410 100.985 5 50 -35 -30 -25 -20 -15 -10 -5 010.80.7π/T 0.6π/T 0.5π/T 0.4π/T 0.10.3π/T 0.2 0.6 0.4 0.20.8π/T 0.9π/T 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.2π/T 0.1π/T0 π/T-0.2-0.4-0.6 -0.8 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1%Example 3 Mapping of vertical s-plane line to z-plane0.6π/T 0.5π/T0.4π/T 0.3π/T 0.7π/T0.2π/T 0.8π/T0.1π/Ts0=j*xx*pi/ts;s=ones(N,1)*[0,-5,-10,-20,-30]+s0*[1 1 1 1 1]plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid35300.72250.580.44 0.3 0.14302520 0.82201515 0.9210 100.98 550 -30 -25 -20 -15 -10 -5 010.8 0.6 0.4 0.2-0.2-0.4-0.6 -0.8 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1%Example 4 Mapping of constant damping ratio s-plane lines into z-planes=s0*[1 1 1 1]-imag(s0)*[0,1/tan(67.5*pi/180),...1/tan(45*pi/180),1/tan(22.5*pi/180)]s=[s,real(s(:,4))];plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid0.6π/T 0.5π/T 0.4π/T 0.7π/T0.8π/T 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.10.3π/T 0.2π/T 0.9π/T0.1π/Tπ/T π/T0.9π/T 0.1π/T 0.8π/T0.2π/T 0.7π/T0.3π/T 0.6π/T 0.5π/T0.4π/T35 0.88 0.8 0.62 0.3530 0.9352520 0.968150.988100.99750 70 60 50 40 30 20 10 -80 -70 -60 -50 -40 -30 -20 -10 010.8 0.6 0.4 0.2-0.2-0.4-0.6 -0.8 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1%Example 5 Mapping of circle s-plane line to z-planephi=xx*pi/2s0=(pi/ts)*(-cos(phi)+j*sin(phi))s=s0*[1,0.75,0.5,0.25,0]plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v')0.6π/T 0.5π/T 0.4π/T 0.7π/T0.8π/T 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.10.3π/T 0.2π/T 0.9π/T0.1π/Tπ/T π/T0.9π/T 0.1π/T 0.8π/T0.2π/T 0.7π/T0.3π/T 0.6π/T 0.5π/T0.4π/T3530 2520151050 -35 -30 -25 -20 -15 -10 -5 010.8 0.6 0.4 0.2-0.2-0.4-0.6 -0.8 -1 -1-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1%Example 6 Step response measurek=[0:1:60];Step Response1.41.210.80.60.40.2step(sys_ta,k*ts)0 0 1 2 34 5 6 Time (sec) %Example 7 Root-locus analysis rlocus(gz*kz)0.64 0.5 0.34 0.1630 0.76250.86 20150.9410 0.985 50.6π/T 0.5π/T 0.4π/T 0.7π/T0.8π/T 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.10.3π/T 0.2π/T 0.9π/T0.1π/Tπ/T π/T0.9π/T 0.1π/T 0.8π/T0.2π/T 0.7π/T0.3π/T 0.6π/T 0.5π/T0.4π/T System: ta Rise Time (sec): 0.8 System: ta Final Value: 1System: ta Settling Time (sec): 2.7 System: ta Peak amplitude: 1.07 Overshoot (%): 6.87 At time (sec): 1.8 A m p l i t u d e%Example 8 Root-locus analysis in page 56numg=[1 0.5];deng=conv([1 -0.5 0],[1 -1 0.5]);sys_z=tf(numg,deng,-1)rlocus(sys_z)%Example 9 Root-locus analysis in page 57numg=[1];deng=[1 4 0];ts=0.25sys_s2=tf(numg,deng)sys_z2=c2d(sys_s2,ts,'imp')rlocus(sys_z2)%Example 10 Analysis of frequency response and roots locus in page 59a=1.583e-7;k=[1e7,6.32e6,1.65e6];w1=-1;w2=1;ts=0.1;v=logspace(w1,w2,100);deng=[1.638 1 0];numg1=k(1,1)*a*[-1 1]numg2=k(1,2)*a*[-1 1]numg3=k(1,3)*a*[-1 1]sys_s1=tf(numg1,deng)sys_s2=tf(numg2,deng)sys_s3=tf(numg3,deng)bode(sys_s1,sys_s2,sys_s3,v),grid onBode Diagram4020-20-40-90-135-180-225 -2701010 10 Frequency (rad/sec)% k parameter is gain value of open system%Up-bound value of k parameter is determined according to roots locusnumg=1.2e-7*[1 1]P h a s e (d e g ) M a g n i t u d e (d B )deng=conv([1 -1],[1 -0.242]);sys_z2=tf(numg,deng,ts)rlocus(sys_z2),grid on五、实验报告要求:根据实验内容进行如下分析:1.S 平面与Z 平面不同位置的映射关系分析;2.系统阶跃响应参数(时域指标)分析,如上升时间和超调量等,及其与S/Z 平面的对应关系;3.离散系统根轨迹分析;4.离散系统Bode 图分析;5.对离散系统相对稳定性的进一步思考。
连续系统离散化分析

1实验一 离散系统的分析一 实验目的1.学习利用采样控制理论;2.使用MATLAB 理论进行分析;3. 学习利用z 变换与反变换分析离散控制系统;二、实验步骤1.开机执行程序C :\matlab \bin \matlab.exe (或用鼠标双击图标)进人MATLAB 命令窗口;2.运用所学自动控制理论z 变换与反变换,使用MATLAB 的基本知识分析离散控制系统的基本性质及进行控制系统的设计。
3. MATLAB 离散系统基本命令模型转换1)连续系统离散化sysd=c2d(sys,T) T 为采样时间sysd=c2d(sys,T,method)method 有四种模式:a. ‘zoh’---采用零阶保持器,b. ‘foh’---采用一阶保持器,c. ‘tustin’---采用双线性逼近(tustin )方法,d. ‘preqarp’---采用改进的(tustin )方法,2)离散系统连续化sys=d2c(sysd,T,method) T 为采样时间例 设)1(1)(+=s s s g , T=0.1s , 求G(z) 键入命令:sys=tf([1],[1 1 0]);c2d(sys,0.1) %采样时间0.1s得到离散传递函数:当采样时间取T=1s 时:0.004837 z + 0.004679 G (z )= ---------------------------- z^2 - 1.905 z + 0.9048 0.3679 z + 0.2642 G (z )= ---------------------------- z^2 - 1.368 z + 0.36792例 系统脉冲传递函数为6322.02644.03678.0)()(2+−+=z z z z R z C ,求离散单位阶跃响应。
解. 在MATLAB 窗口键入以下程序num=[0.3678 0.2644];den=[1 -1 0.6322];dstep(num,den)结果件下图:三、实验内容有系统1)其中K =10,T =0.25s,求单位阶跃函数r(t)=1 (t)作用下的响应。
第5章数字控制系统的连续——离散化设计-PPT精品文档

说明: 连续——离散化设计是一种近似的设计方法:
由D(s)到D(z)的转换是一种近似过程; 在设计中,没有考虑保持器对系统的影响。(零保带来T/2
的相位滞后,使系统闭环性能变坏。因此连续——离散化设 计的系统,要求有较小的采样周期T。) 本章重点: 1. 由D(s)到D(z)的多种近似方法。 2. 检验所设计的数控系统的性能。
改进的双线性变换为 D (z) D (s)
(z 1) 0 s tg ( T/ 2) (z 1) 0
5.3 匹配Z变换(又称零极点匹配、根匹配)
设计准则:直接将D(s)的零极点由Z变换 z=esT 映射到Z 平面上,成为D(z)的零极点。
K ( s z K ( z z s i) z i) 1 1 D ( s ) ni D ( z ) ni ( sp ( zp i) i)
1( t )
D(s)
u(t )
1( t )
1 * (t )
u * (t )
D(z)
分析保持器等效法的特点:
D(s)与D(z)极点按Z变换定义一一对应 若D(s)稳定,D(z)稳定;
z=esT;
D(z)与T有关;
D(s)与D(z)频率特性不同; D(s)与D(z)零点不是按
z=esT 一一对应的。
设计准则为: 波 使 器 D ( s 模 ) 和 拟 数 滤 字滤 D ( z ) 波 在所要求的频 有 率 相 点 同 上 的 具 频率特性 即 D ( s )sj D ( z )z T。 0 0 ej
2 T 0 2 ( ej 1 ) T 0 j A 0 A j T 0 tg ( T /2 )2 T ( e 1 ) 0
第5章 数字控制系统的 连续——离散化设计
计算机控制实验报告-离散化方法研究解析

东南大学自动化学院实验报告课程名称:计算机控制技术第 2 次实验实验名称:实验三离散化方法研究院(系):自动化学院专业:自动化姓名:学号:实验室:416 实验组别:同组人员:实验时间:2014年4月10日评定成绩:审阅教师:一、实验目的1.学习并掌握数字控制器的设计方法(按模拟系统设计方法与按离散设计方法);2.熟悉将模拟控制器D(S)离散为数字控制器的原理与方法(按模拟系统设计方法);3.通过数模混合实验,对D(S)的多种离散化方法作比较研究,并对D(S)离散化前后闭环系统的性能进行比较,以加深对计算机控制系统的理解。
二、实验设备1.THBDC-1型控制理论·计算机控制技术实验平台2.PCI-1711数据采集卡一块3.PC机1台(安装软件“VC++”及“THJK_Server”)三、实验原理由于计算机的发展,计算机及其相应的信号变换装置(A/D和D/A)取代了常规的模拟控制。
在对原有的连续控制系统进行改造时,最方便的办法是将原来的模拟控制器离散化。
在介绍设计方法之前,首先应该分析计算机控制系统的特点。
图3-1为计算机控制系统的原理框图。
图3-1 计算机控制系统原理框图由图3-1可见,从虚线I向左看,数字计算机的作用是一个数字控制器,其输入量和输出量都是离散的数字量,所以,这一系统具有离散系统的特性,分析的工具是z变换。
由虚线II向右看,被控对象的输入和输出都是模拟量,所以该系统是连续变化的模拟系统,可以用拉氏变换进行分析。
通过上面的分析可知,计算机控制系统实际上是一个混合系统,既可以在一定条件下近似地把它看成模拟系统,用连续变化的模拟系统的分析工具进行动态分析和设计,再将设计结果转变成数字计算机的控制算法。
也可以把计算机控制系统经过适当变换,变成纯粹的离散系统,用z变化等工具进行分析设计,直接设计出控制算法。
按模拟系统设计方法进行设计的基本思想是,当采样系统的采样频率足够高时,采样系统的特性接近于连续变化的模拟系统,此时忽略采样开关和保持器,将整个系统看成是连续变化的模拟系统,用s域的方法设计校正装置D(s),再用s域到z域的离散化方法求得离散传递函数D(z)。
连续系统离散化方法

连续系统离散化方法连续系统离散化方法是一种常用的数值计算方法,它将连续系统转化为离散系统,从而使得计算机可以进行处理。
本文将从离散化方法的定义、应用、实现以及优缺点等方面进行介绍。
一、离散化方法的定义离散化方法是指将连续系统转化为离散系统的过程。
在计算机中,所有的数值都是离散的,而实际上很多系统是连续的,比如电路、机械系统、化学反应等等。
离散化方法就是将这些连续系统转化为可以在计算机中处理的离散系统。
离散化方法可以通过采样和量化来实现。
二、离散化方法的应用离散化方法在很多领域都有应用,比如电路设计、控制系统设计、信号处理等等。
在电路设计中,离散化方法可以将连续电路转化为数字电路,从而实现数字信号的处理。
在控制系统设计中,离散化方法可以将连续控制器转化为数字控制器,从而实现数字化自动控制。
在信号处理中,离散化方法可以将连续信号转化为数字信号,从而实现对信号的数字处理。
三、离散化方法的实现离散化方法的实现可以通过采样和量化来实现。
采样是指对连续信号进行离散化,将其转化为一系列的采样值。
量化是指对采样值进行离散化,将其转化为一系列的离散数值。
采样和量化的具体实现方式包括正弦采样、脉冲采样、最大值采样、平均值采样等等。
量化的具体实现方式包括线性量化、对数量化、非线性量化等等。
四、离散化方法的优缺点离散化方法的优点是可以将连续系统转化为离散系统,从而可以在计算机中进行处理。
离散系统具有稳定性、可控性、可观性等优点。
离散化方法的缺点是会引入误差,因为离散化过程中会丢失一些信息。
此外,离散化方法需要选取适当的采样周期和量化精度,否则会影响系统的性能。
离散化方法是一种常用的数值计算方法,它将连续系统转化为离散系统,从而使得计算机可以进行处理。
离散化方法的应用广泛,包括电路设计、控制系统设计、信号处理等等。
离散化方法的实现可以通过采样和量化来实现。
离散化方法既有优点,又有缺点,需要在具体应用中对其进行合理的选择和设计。
连续系统离散化

离散相似法
连续系统的离散化
首先要得到一个与被仿真系统等价的离散 模型。这个模型可以通过对连续系统的离 散化过程来获得。它分成以下五步:
① 首先对输入信号u(t)进行采样,即在输入 端加一个采样开关S1,其采样周期为T。
② 连续变化的信号u(t)经过采样开关后,变 成了一个离散信号u(kT)。为保证模型的等 价性,首先要求信号等价,因此它不能直 接进入原来的连续系统,而必须加上一只 信号重构器,它使信号u(k)重新变成一个 连续信号uh(t), uh(t)u(t)。
环节2是一阶惯性环节,其传递函数为
X (s) k0 k0 T1 U (s) T1s 1 s 1 T1 x(k 1) eT T1 x(k ) k0 (1 eT T1 )u(k )
连续系统按结构图的离散相似法仿真
环节3也是一阶惯性环节,其传递函数为
Y (s) 1 1 T2 X (s) T2s 1 s 1 T2
对上式进行拉氏反变换,求得方程的解为
t
X (t) (t) X (0) 0 (t )BU ( )d
时域解法求取离散系统差分方程
(t) L1 (sI A)1
X (t) eAt X (0) t eA(t )ΒU ( )d 0 t
X (t) (t)X (0) 0 (t )BU ( )d
采用一阶保持器描述系统的差分方程
x(k 1)T (T )x(kT) m (T ) n (T )u(kT) n (T )u(k 1)T
e(k 1) R(k 1) y(k 1)
e(k) R(k) y(k)
x1(k
1)
x1(k
)
3 4
Te(k
)
1 4
Te(k
连续系统离散化处理基本方法

连续系统离散化处理基连续系统离散化处理的基本方法在数字汁算机上对连续系统进行仿真时,首先遇到的问题是如何解决数字计算 机在数值及时间上的离散性与被仿真系统数值及时间上的连续性这一基本问题。
从根本意义上讲,数字汁算机所进行的数值计算仅仅是“数字”计算,它表示 数值的精度受限于字长,这将引入舍入误差;另一方面,这种计算是按指令一步一 步进行的,因而,还必须将时间离散化,这样就只能得到离散时间点上系统性能。
用数字仿真的方法对微分方程的数值积分是通过某种数值计算方法来实现的。
任何 一种计算方法都只能是原积分的一种近似。
因此,连续系统仿真,从本质上是对原 连续系统从时间、数值两个方面对原系统进行离散化,并选择合适的数值计算方法 来近似积分运算,山此得到的离散模型来近似原连续模型。
如何保证离散模型的计 算结果从原理上确能代表原系统的行为,这是连续系统数字仿真首先必须解决的问 题。
设系统模型为:其中U ⑴为输入变量,y ⑴为系统变量;令仿真时间 间隔为/),离散化后的输入变量为!:仇),系统变量为y 仇),其中f 女表示仁妙。
如 果力(fj yO*川即5(4)"(儿)-"仇)©0,5(4)=沪仇)-y (S )"(对所有k=o,i,2,...),则可认为两模型等价,这称为相似 原理(参见图)。
实际上,要完全保证S (4)= 0,G .(4)= 0是很困难的。
进一步分析离散化引的误差, 随着计算机技术的发展,山i 甲規桃孚长引入的舍入误差可以忽略,关键是数值积分 算法,也称为仿真建模方法。
相似原理用于仿真时,对仿真建模方法有三个基本要 求:(1) 稳定性:若原连续系统是稳定的,则离散化后得到的仿真模型也应是稳定 的。
关于稳定性的详细讨论将在节中进行。
(2) 准确性:有不同的准确性评价准则,最基本的准则是:绝对误差准则:杠(.)=其中规定精度的误差量。
相对误差准则:‘以) y(F^)-y(S) y(S) <d(3)快速性:如前所述,数字仿真是一步一步推进的,即由某一初始值y (f 。
计算机控制系统的连续域-离散化设计

(4) 以下述传递函数为例,证明预修双线性变换方法可以保证在指定频率处连续 环节与等效离散环节频率特性模值与相角相等.
D (s) 10 s 10
令关键频率为 1 10
D ( j1 ) 10 1 0.707 3db 2
频率特性 1 10 模值为 频率特性 1 10 相角为 预修正双线性变换为
D (s) s a
解:该环节没有有限极点,但认为有一个无限极点,因此可得
D( z ) k
( z e aT ) ( z 1)
根据低频增益相等方法确定增益:
D (1) k
k
1 e aT D(0) a 11
2a 1 e aT
因此有
D( z )
2a ( z e aT ) 1 e aT ( z 1)
s s 10 s
s ,取 T=0.02s,关键频率为 1 10 ,预修正双线性变 s 10
10 z 1 10 0.02 z 1 tg 2
0.909( z 1) .频率特性如图 4-1 所示.从图 4-1 可见, ( z 0.817)
低频特性相近,且可以保证在关键频率 1 10 处频率特性相等, 但高频特性相差 较多.
D( z )
12 102
1 D ( j ) tg 1 450 1 10 s 10 s 10 10 z 1 10 10T z 1 tg 2
10 z 1 10T z 1 tg 2
D (e j10T )
10 10 1 j10T 10 10T 10 e 1 jtg 10 1 j 10 j10T 10T 10T e 2 1 tg tg 2 2
计算机控制系统的连续域-离散化设计

--每种变换方法零点、极点的数目; --每种变换方法的应用特点. (2) 要注意,各种变换方法特性不同,各有优缺点. 但不管哪种方法, 变换后所 得等效环节与连续环节特性相比均有畸变,畸变程度与采样周期、环节本身特性 有关,很难说哪种是最好的.但 TUSTIN 变换方法与其它几种方法相比,由于其具 有较好特性,应用较多,一阶向后差分和匹配 z 变换方法也有较多应用。 (3) 各种变换公式本质上都是 z 变换的特殊简化形式,变换后特性优于 z 变 换。Matlab 软件提供了变换的算法和指令。 3)PID 离散方法 PID 控制器作为单输入/单输出系统的一种有效的控制方法已经沿用了很多 年,目前仍然被广泛应用着,由于它同时可以兼顾系统的动态、静态特性而受到 广大控制工程师的青睐。 对于计算机控制系统来说, 主要工作是将如何将连续域 的 PID 控制律离散化以及如何对其进行改进。主要应注意掌如下几方面问题: (1) 要牢记位置式及增量式两种基本 PID 离散公式以及各自的优缺点.一般说 采用增量式算法较为有效,较为简单,但需要增加计算机外的积分过程。应用中, 比例控制器(P 控制)较容易调节;一般很难直接采用微分(D)控制器,积分 (I)控制也需要调节. (2) 要注意利用计算机功能改进数字 PID 算法的几种方法,其中特别注意: --产生积分饱和的机理及抗积分饱和各种方法 , 其中要熟悉积分分离的具体 算法; --为克服 PID 算法中微分控制作用的缺点,常用的改进微分算法; --工程应用时所采用的其它措施. (3) 要注意工业中采用 PID 算法时,主要参数并不是通过理论计算所得,主要 是在对被控过程特性测试的条件下,依经验进行现场调试所得,所以应对几种常用 的 PID 参数整定方法有所了解. 2 重点与难点问题说明 (1) 由于将连续控制系统转换为计算机控制系统时在系统中需加入零阶保持 器,而零阶保持器是一相位滞后环节 , 因此会使系统特性变坏, 为此在连续域设计 时要检查加入零阶保持器后系统特性,如果影响较大则应加入适当的补偿,或者减
连续系统离散化方法

连续系统离散化方法一、概述连续系统离散化方法是一种将连续系统转化为离散系统的方法,常用于控制系统的设计和分析。
该方法可以将一个无限维度的连续系统转化为有限维度的离散系统,使得控制器设计和分析变得更加简单和可行。
二、连续系统模型在开始进行连续系统离散化的过程中,需要先建立一个连续系统模型。
通常情况下,这个模型可以由微分方程或者差分方程来表示。
三、离散化方法1. 时域离散化方法时域离散化方法是最基本的离散化方法之一。
它通过将时间轴上的信号进行采样,从而将一个连续时间信号转换为一个离散时间信号。
这个过程中需要确定采样周期以及采样点数目等参数。
2. 频域离散化方法频域离散化方法是一种利用傅里叶变换将一个连续时间信号转换为一个频域信号,然后再对该频域信号进行采样得到一个离散时间信号的方法。
这个过程中需要确定采样频率以及采样点数目等参数。
3. 模拟器法模拟器法是一种将连续系统转化为离散系统的方法。
这个方法的核心思想是利用一个数字模拟器来模拟连续系统的行为,从而得到一个离散时间信号。
4. 差分方程法差分方程法是一种将连续系统转化为离散系统的方法。
这个方法的核心思想是利用微分方程在离散时间点上进行近似,从而得到一个差分方程。
四、误差分析在进行离散化过程中,会产生一定的误差。
因此,需要对误差进行分析和评估,以确保离散化后的结果与原始连续系统相近。
五、应用实例1. 机械控制系统机械控制系统中通常需要对连续时间信号进行采样和处理。
通过使用离散化方法,可以将连续信号转换为数字信号,并且可以在数字域上进行控制器设计和分析。
2. 电力电子控制系统电力电子控制系统中通常需要对高频信号进行处理。
通过使用频域离散化方法,可以将高频信号转换为数字信号,并且可以在数字域上进行控制器设计和分析。
六、总结连续系统离散化方法是一种将连续系统转化为离散系统的方法。
通过使用不同的离散化方法,可以将连续时间信号转换为数字信号,并且可以在数字域上进行控制器设计和分析。
将连续系统转换为离散系统的函数为

将连续系统转换为离散系统的函数为本文旨在探讨将连续系统转换为离散系统的函数。
在进行离散系统设计的过程中,将连续系统转换为离散系统的有效方式之一是采用“函数转换”的方法。
函数转换是指将自变量的连续值变换为离散值的过程。
函数转换可以将连续系统的输入变量(如温度、电压等)转换为可操作的离散状态,从而使离散系统在系统设计方面有了更好的选择。
具体来说,将连续系统转换为离散系统的函数可以分为三类:(1)抽样转换函数;(2)阈值转换函数;(3)非线性转换函数。
(1)抽样转换函数是将连续系统的输入转换为离散系统输入的最基本方法。
其核心思想是在连续系统的输入变化较小时,通过抽取样本值,从而将连续系统转换为离散系统。
这种函数转换除了实现简单易行之外,还可以满足混合连续-离散系统(HybridContinuous-Discrete Systems)的工业应用。
(2)阈值转换函数是将连续系统转换为离散系统的另一种有效方法。
其主要原理是将系统的连续输入映射到一组预定的阈值,从而实现将连续系统转换为离散系统。
优点在于在实际应用中,该函数可以提供更精确的空间分辨,从而提高系统的状态可控性。
(3)非线性转换函数是采用曲线或其他形式,将连续系统的输入转换为离散系统输入的方法。
此类函数比上述两种方法具有更广泛的适用范围,因为它可以使用不同形式的曲线来根据需要自行调整系统的输入空间分辨率,从而更好地满足实际系统的需求。
函数转换为离散系统设计提供了一种有效的手段,但在实际应用中也会存在一些缺点。
其中包括:(1)有可能光栅化的误差;(2)时间的不同步等。
在使用函数转换的时候,应该根据实际情况,选择合适的函数,以达到良好的系统性能。
同时,还应该加以反复测试和实验,以保证函数转换达到较高的精确度。
总之,将连续系统转换为离散系统的函数是一种非常重要的技术手段,它可以提高系统的精准度,使离散系统的设计更加有效率。
但在实际应用中,也需要加以注意,以确保正确选择函数,以达到预期的性能。
计控实验二-连续系统变换为离散系统

实验二 连续系统变换为离散系统一、实验目的在对连续系统进行实时计算机控制时,往往需要把连续系统转换成离散系统。
二、实验指导为了得到连续系统的离散化数学模型,Matlab 提供了c2d()函数。
c2d()函数的调用格式为:ﻩ ﻩsys d=c2d (sys,Ts) 或ﻩﻩﻩ ﻩ sysd=c2d(sys,Ts,metho d)式中,输入参量s ys 为连续时间模型对象;Ts 为采样周期;sysd为带采样时间T s的离散时间模型。
Meth od 用来指定离散化采用的方法:ﻩ‘zoh ’——采用零阶保持器法;ﻩﻩ‘foh ’——采用一阶保持器法;ﻩ ‘tusti n’——采用双线性变换法;‘pr ewarp ’——采用改进的双线性变换法;ﻩ‘ma tche d’——采用零极点匹配法;缺省时,为‘zoh ’三、实验内容1.已知连续系统的零极点增益模型为:ﻩ ﻩ ﻩ试采用零阶保持器与零极点匹配法求其离散传递函数。
设采样周期。
程序及结果:>> k=10,z=-5,p=[-1 -3 -8];sys = z pk ( z ,p,k )sys =10 (s+5)-----------------(s +1) (s+3) (s+8)Co nt inuou s-time ze ro/p ole/g ain mod el .>> Ts=0.1Ts =0.1000>> sysd=c2d(sys,Ts,'z oh') )8)(3)(1()5(10)(++++=s s s s s G s T 1.0=sysd =0.040105 (z -0.6065) (z+0.7932)--------------------------------(z -0.9048) (z-0.7408) (z-0.4493)Sa mple tim e: 0.1 sec on dsDi scr ete -t ime zer o/pole/gain model.>> sys d=c2d (sys,Ts,'matc hed')sys d =0.035957 (z-0.6065) (z+1)--------------------------------(z -0.9048) (z-0.7408) (z -0.4493)Sample time: 0.1 seco ndsDiscrete -t ime zer o/pole /gai n mode l.2、已知系统如图1所示,被控对象 G h (s)为零阶保持器,图1(1) 若其控制器按模拟化设计方法设计,其系统框图如图2,得到的传递函数为)110(1)()()(+==s s s U s s G a θ1110)(++=s s s D试分别采用零阶保持器、双线性变换法、零极点匹配法进行控制器离散化,求系统的阶跃响应曲线和误差曲线,并与连续系统的阶跃响应曲线进行比较。
连续时间系统状态方程的离散化

x1[(k x2[(k
1)T 1)T
] ]
1 0
1
ek ek
x1(kT x2 (kT
) )
1 0
1
ek ek
u1(kT u2 (kT
) )
(2)用递推法求离散方程的近似解: 取k=0,1,2…T=0.2秒,并代入输入函数和初始条件可得近似解:
1 4
(2T e2T 1 (1 e2T )
1)
2
(4)xx
1[(k 2[(k
1)T] 1)T]
G(T)xx12
(kT) (kT)
H(kT)U(kT)
说明:(1)当T选定后(如T=0.5秒)G(t)和 H(t)都是确定的系数矩阵
(2)离散化后得状态方程,可按递推法或 Z变换法求出解
k 1
x(k) (k)x(0) (k j 1)Hu( j)
j 1
二、线性时变系统状态方程的离散化 --按导数定义近似求出,也称近似计算方法
假设T很小T≤0.1Tmin(最小时间常数),精度要 求不高时,可用差商代替微商。
1 0
T 1
t
x1(kT x2 (kT
) )
0 T
u(kT
)
u(kT ) r(kT ) x1(kT )
系统离散状态方程(T=0.1)
可见T较小时,
x1[(k x2[(k
1)T ] 1)T ]
0.9 0.1
0.1 0.9
1.37 0.63
递推求下去
x1(0.6) x2 (0.6)
连续控制器离散化方法

模拟(连续)控制器系统
计算机(离散)控制器系统
离散控制器等效控制系统
采用连续与离散控制器的系统系阶越响应的区别
例:已知某系统被控对象的传递函数为 要求设计控制器,使满足性能指标: ①闭环稳定 ②过渡过程时间Ts≤3s ③阶跃响应超调量δ≤5% 设计满足上述要求的数字控制器D(Z)(取采样周期 T=0.2秒,采用双线性近似法) 解: 模拟控制器设计过程略,得到的模拟控制器为:
D( s ) 16 s 2.1 s 8
( k 1)T kT
u ( ) d
T [u (( k 1)T ) u ( kT )] 2
T z 1 u ( kT ) 2 z 1 1 T z 1 2 z 1 , s s 2 z 1 T z 1 2 z 1 ) C ( Cd ( z ) C ( s ) T z 1
Cd ( z) 的极点为
1 aT 1
稳定
(3)Tustin法
aT aT a z 1 2 Cd ( z ) 2 2 z 1 aT aT aT aT a (1 )z ( 1) 1 1 T z 1 2 2 2 z 2 aT 1 2 ( z 1)
( s b1 )( s b2 ) ( s bm ) C (s) k ( s a1 )( s a2 ) ( s an ) ( z 1)d 1 ( z eb1T )( z eb2T ) ( z ebmT ) Cd ( z ) kd ( z e a1T )( z e a2T ) ( z e anT )
例:分别用前向差分、后向差分、Tustin法对 进行离散化 (1)前向差分
a aT z 1 a z 1 aT T Cd ( z) 的极点为 1 aT Cd ( z )
2 连续系统离散化问题
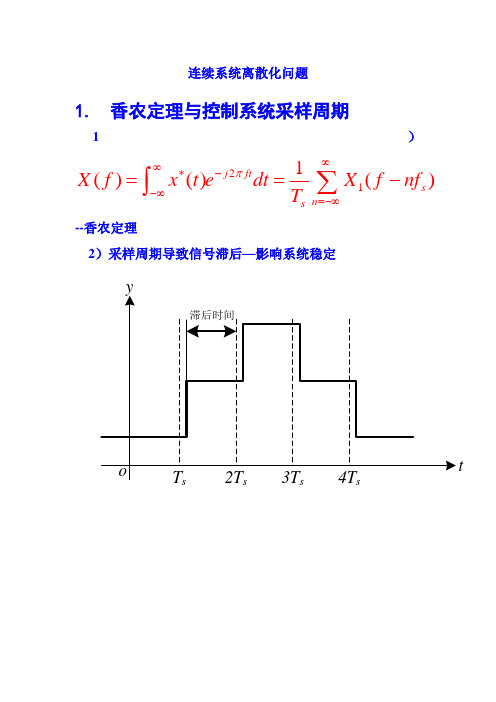
连续系统离散化问题1. 香农定理与控制系统采样周期1)211()()()j ftsn sX f x t edt X f nf T π∞∞*--∞=-∞==-∑⎰--香农定理2)采样周期导致信号滞后—影响系统稳定tss s s12f 1f 112f 1f3)超前校正的局限性4)减小采样周期对信号微分精度的影响,如由角度信号求角速度信号所出现精度问题。
2. 零阶保持器、连续系统离散化问题1)零阶保持器0()1()1()s g t t t T =--010[()]s T ss s e T L g t T s--→=−−−−→≈s()nsnf nT z∞-=-∞=∑()F z=()nsnf nT z∞-=-∞=∑()F z=保持强度非幅值T ()e t ()e t T ()E s ()E s 模拟电路{{图连续系统离散化过程图中G c(s)为原系统(连续系统)的传递函数,G h(s)为信号重构器的传递函数。
ss)s kT -(sT t kδ-∞-⎰定义:A /D 两种假定所致的结果都是正确的,可以转换器对同一物理量的采样所得,()()s s s x kT T t T k δ-是义更明确由Z 变换的理论可知:{}()()()c h c G z Z G s G s =。
表1 常用函数的Z 变换表即使是其他任何保持器,上面的过程也近似成立,因为保持器的输出是基本相同的。
2)由于调节器或执行器更必然的是被控对象具有低通滤波器特性,即系统信号的上限频率远小于采样频率:f max<<f s,故系统对采样信号的响应与对相应连续信号的响应具有相同的频谱特性,即二者只差一个比例值T s。
201()()()()()()c h c c s h m s m G s G s F s G s G s jm G s T ω∞**=-∞≠⎡⎤⎡⎢⎥⎢=++⎢⎥⎢⎢⎥⎢⎣⎦⎣∑01()()()()()()c h c s n s n G s F s G s G s F s F s jn T ω∞*=-∞≠⎡⎤⎢⎥=++⎢⎥⎢⎥⎣⎦∑3)由相应连续传递函数G c (s )获得控制器脉冲响应传递函数G c (z )脉冲传递函数与连续传递函数的关系为:1()()()()stsm sG z G s g t e dt G s jm T ω∞∞**-=-∞===+∑⎰,s T sz e=由上式可见,很难由无穷级数形式的()G s *得到()G z 的简单的分式多项式形式,但根据上述2)中的分析,可用()c G s 替代()cG s *,故有()()s c c T sG z G s z e=⎧⎨=⎩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 连续系统变换为离散系统
一、实验目的
在对连续系统进行实时计算机控制时,往往需要把连续系统转换成离散系统。
二、实验指导
为了得到连续系统的离散化数学模型,Matlab 提供了c2d()函数。
c2d()函数的调用格式为:
sysd=c2d(sys,Ts) 或 sysd=c2d(sys,Ts,method)
式中,输入参量sys 为连续时间模型对象;Ts 为采样周期;sysd 为带采样时间Ts 的离散时间模型。
Method 用来指定离散化采用的方法: ‘zoh ’——采用零阶保持器法;
‘foh ’——采用一阶保持器法;
‘tustin ’——采用双线性变换法;
‘prewarp ’——采用改进的双线性变换法;
‘matched ’——采用零极点匹配法;缺省时,为‘zoh ’
三、实验内容
1.已知连续系统的零极点增益模型为:
试采用零阶保持器与零极点匹配法求其离散传递函数。
设采样周期。
程序及结果:
>> k=10,z=-5,p=[-1 -3 -8];
sys = zpk ( z,p,k )
sys =
10 (s+5)
-----------------
(s+1) (s+3) (s+8)
Continuous -time zero/pole/gain model.
>> Ts=0.1
Ts =
0.1000
>> sysd=c2d(sys,Ts,'zoh') )
8)(3)(1()5(10)(++++=
s s s s s G s T 1.0=
sysd =
0.040105 (z -0.6065) (z+0.7932)
--------------------------------
(z -0.9048) (z -0.7408) (z -0.4493)
Sample time: 0.1 seconds
Discrete -time zero/pole/gain model.
>> sysd=c2d(sys,Ts,'matched')
sysd =
0.035957 (z -0.6065) (z+1)
--------------------------------
(z -0.9048) (z -0.7408) (z -0.4493)
Sample time: 0.1 seconds
Discrete -time zero/pole/gain model.
2、已知系统如图1所示,被控对象 G h (s)为零阶保持器,
图1
(1) 若其控制器按模拟化设计方法设计,其系统框图如图2,得到的传递函数
为
)110(1)()()(+==s s s U s s G a θ1
110)(++=s s s D
试分别采用零阶保持器、双线性变换法、零极点匹配法进行控制器离散化,求系统的阶跃响应曲线和误差曲线,并与连续系统的阶跃响应曲线进行比较。
采样周期为1秒。
(2)选择采样周期T=0.2s ,试采用零极点匹配法进行控制器离散化,求其系统的阶跃响应曲线和误差曲线,并与连续系统的阶跃响应进行比较。
(3)若在图2 中的D (s )后加一数字补偿器(该环节是一相位超前环节) 求系统的阶跃响应曲线和误差曲线,并与连续系统的阶跃响应进行比较。
要求:运用Matlab 编写命令语句或应用程序,并实现。
(1)
num=[10,1],den=[1 1];
Ds=tf(num,den);
Ts=1;
Dz=c2d(Ds,Ts,'zoh');
num=1,den=[10 1 0],Gs=tf(num,den);
Gz=c2d(Gs,Ts,'zoh');
G=feedback(Dz*Gz,1);
Dz1=c2d(Ds,Ts,'tustin');
G1=feedback(Dz1*Gz,1);
Dz2=c2d(Ds,Ts,'matched');
G2=feedback(Dz2*Gz,1);
G3=feedback(Ds*Gs,1);
figure (1)
subplot(2,2,1);step(G3);
title('连续系统单位阶跃响应');grid on;
subplot(2,2,2);step(G);
title('离散系统单位阶跃响应(零阶保持器)');grid on;
subplot(2,2,3);step(G1);
title('离散系统单位阶跃响应(双线性变化法)');grid on;
subplot(2,2,4);step(G2);
title('离散系统单位阶跃响应(零极点匹配)');grid on;
figure (2)
[y,t,x]=step(G3);
E3=1-y;subplot(2,2,1);plot(E3);title('连续系统误差曲线');grid on;
[y,t,x]=step(G);
E=1-y;subplot(2,2,2);plot(E);title('离散系统误差曲线(零阶保持器)');grid on;
1
8.05.1)(-∧-=z z D
[y,t,x]=step(G1);
E1=1-y;subplot(2,2,3);plot(E1);title('离散系统误差曲线(双线性变化法)');grid on; [y,t,x]=step(G2);
E2=1-y;subplot(2,2,4);plot(E2);title('离散系统误差曲线(零极点匹配)');grid on;
(2)
num=[10,1],den=[1 1];
Ds=tf(num,den);
Ts=0.2;
Dz=c2d(Ds,Ts,'zoh');
num=1,den=[10 1 0],Gs=tf(num,den);
Gz=c2d(Gs,Ts,'zoh');
Dz2=c2d(Ds,Ts,'matched');
G2=feedback(Dz2*Gz,1);
G3=feedback(Ds*Gs,1);
subplot(2,2,1);step(G3);
title('连续系统单位阶跃响应');grid on;
subplot(2,2,2);step(G2);
title('离散系统单位阶跃响应(零极点匹配)');grid on;
[y,t,x]=step(G3);
E3=1-y;subplot(2,2,3);plot(E3);title('连续系统误差曲线');grid on;
[y,t,x]=step(G2);
E2=1-y;subplot(2,2,4);plot(E2);title('离散系统误差曲线(零极点匹配)');grid on;
(3)
num=[10,1],den=[1 1];
Ds=tf(num,den);
Ts=1;
Dz=c2d(Ds,Ts,'zoh');
numd=[1 0];
dend=[1.5 0.8];
Dd= tf(numd,dend,1);
num=1,den=[10 1 0],Gs=tf(num,den);
Gz=c2d(Gs,Ts,'zoh');
Dz2=c2d(Ds,Ts,'matched');
G2=feedback(Dz2*Gz*Dd,1);
G3=feedback(Ds*Gs,1);
subplot(2,2,1);step(G3);
title('连续系统单位阶跃响应');grid on;
subplot(2,2,2);step(G2);
title('离散系统单位阶跃响应(零极点匹配)');grid on;
[y,t,x]=step(G3);
E3=1-y;subplot(2,2,3);plot(E3);title('连续系统误差曲线');grid on;
[y,t,x]=step(G2);
E2=1-y;subplot(2,2,4);plot(E2);title('离散系统误差曲线(零极点匹配)');grid on;
四、实验报告要求
1.编写各题实验程序;
2.给出各题程序运行结果;
3.比较题1的两种离散化方法的离散效果,得出结论;
两种方法得到的离散结果,极点相同,零点不同,增益不同。
4.根据题2(1)的结果,得出三种离散化方法的离散效果比较;
5.根据题2(2)的结果,分析采样周期选择对模拟化设计方法的影响;6.根据题2(3)的结果,分析零阶保持器对系统动态特性的影响。
