安徽省合肥市2020届高三4月第二次质量检测数学(理)试题
2020届安徽省合肥市高三第二次教学质量检测数学(理)试题(解析版)

数学(理)试题一、单选题1.设复数满足,则在复平面内的对应点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】A【解析】先对复数进行化简,进而可得到它在复平面内对应点的坐标,从而可得到答案。
【详解】由题意,,故在复平面内对应点为,在第一象限,故选A.【点睛】本题考查了复数的四则运算,及复数的几何意义,属于基础题。
2.若集合,,则()A.B.C.D.【答案】C【解析】求出集合,然后与集合取交集即可。
【详解】由题意,,,则,故答案为C.【点睛】本题考查了分式不等式的解法,考查了集合的交集,考查了计算能力,属于基础题。
3.已知双曲线的一条渐近线方程为,且经过点,则双曲线的方程是()A.B.C.D.【答案】C4.在中,,则()A.B.C.D.【答案】B5.下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:空调类冰箱类小家电类其它类营业收入占比净利润占比则下列判断中不正确的是()A.该公司2018年度冰箱类电器营销亏损B.该公司2018年度小家电类电器营业收入和净利润相同C.该公司2018年度净利润主要由空调类电器销售提供D.剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低【答案】B6.将函数的图象上各点横坐标缩短到原来的(纵坐标不变)得到函数的图象,则下列说法正确的是()A.函数的图象关于点对称B.函数的周期是C.函数在上单调递增D.函数在上最大值是1【答案】C7.已知椭圆的左右焦点分别为,,右顶点为,上顶点为,以线段为直径的圆交线段的延长线于点,若,则该椭圆离心率是()A.B.C.D.【答案】D8.某部队在一次军演中要先后执行六项不同的任务,要求是:任务必须排在前三项执行,且执行任务之后需立即执行任务;任务、任务不能相邻.则不同的执行方案共有()A.36种B.44种C.48种D.54种【答案】B9.函数的图象大致为()A.B.C.D.【答案】A10.如图,正方形网格纸中的实线图形是一个多面体的三视图,则该多面体各表面所在平面互相垂直的有()A.2对B.3对C.4对D.5对【答案】C【解析】画出该几何体的直观图,易证平面平面,平面平面,平面平面,平面平面,从而可选出答案。
安徽省合肥市2020年高三第二次质量检测理科数学试卷文字版含解析

合肥市2020年高三第二次教学质量检测数学试题(理科)(考试时间:120分钟 满分:150分)注意事项1.答题前,务必在答题卡和答题卷规定的地方填写自己的姓名、准考证号和座位号后两位.2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.3.答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卷上书写,要求字体工整、笔迹清晰.作图题可先用铅笔在答题卷规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚,必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草纸上答题元效.第I 卷(满分60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只一项是符合题目要求的.1.若集合{}{}22,0322≥=≤--=x x B x x x A ,则B A I =( ) A .]3,21[ B .]1,21[ C .]21,3[- D .]3,2[2.欧拉公式θθθsin cos i e i +=把自然对数的底数e ,虚数单位i ,三角函数θcos 和θsin 联系在一起,充分体现了数学的和谐美,被誉为“数学的天桥”若复数z 满足i z i e i =⋅+)(π,则z =( )A .1B .22C .23 D .2 3.若实数y x ,满足约束条件⎪⎩⎪⎨⎧≥-+≥+-≥-+032304042y x y x y x ,则y x z -=2的最小值是( )A .5-B .4-C .7D .164.已知)(x f 为奇函数,当0<x 时,2)(ex ex f x -=-(e 是自然对数的底数),则曲线)(x f y =在1=x 处的切线方程是( )A .e ex y +-=B .e ex y +-=C .e ex y +-=D .e ex y +-=5.若110tan 380cos =+οοm ,则m =( )A .4B .2C .2-D .4-6.已知函数)20,0)(tan()(πϕωϕω<<>+=x x f 的图象关于点)0,6(π成中心对称,且与直线y=a 的两个相邻交点间的距离为2π,则下列叙述正确的是( ) A .函数的最小正周期为πB .函数)(x f 图象的对称中心为))(0,6(Z k k ∈+ππC .函数)(x f 的图象可由2tan =y 的图象向左平移6π得到 D .函数)(x f 的递增区间为))(62,32(Z k k k ∈+-ππππ 7.《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为b 和a 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱青),将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为a+b ,宽为内接正接正方形的边长d ,由刘徽构造的图形还可以得到许多重要的结论,如图3.设D 为斜边BC 的中点,作直角三角形ABC 的内接正方形对角线AE ,过点A 作AF ⊥BC 于点F ,则下列推理正确的是( )①由图1和图2面积相等得b a ab d +=; ②由AE≥AF 可得2222b a b a +≥+; ③由AD≥AE 可得b a b a 112222+≥+; ④由AD≥AF 可得ab b a 222≥+。
安徽省合肥市2020年高三第二次教学质量检测理科数学试题(含答案)

A. -5
3.r+ 2y- 3
B. -4
C. 7
· D. 16
4.已知 f(:r) 为奇函数,当 .T < (:)时, f(�T) = e-.-r … ex2 ( e 是自然对数的底数〉 , 则曲线
Y = f(.r)在 .T = 1处的切线方程是
A. y =一 町 + e B. y = er +e
C. y =町 - e
充分体现了数学的和谐美,被誉为“数学的天桥气若复数 z 满足 (eiir +
cost)
i) •
和 sin8 联系在一起,
z = i,则 I zl =
A ....
R号
已号
nD. ..!?.
2.r+y-4 注。
时崎旧隅
; :三。 3.若实数 .T 'y 满足约束条件 x-y 十 4 ;主 0,则 z = 2x-y 的最小值是
同理得,CN 平面 ABEF ,∴ DM // CN . 又∵ DM CN ∴四边形CDMN 为平行四边形 ∴CD // MN .
∵M,N 分别是 AF,BE 的中点 ∴MN // AB
∴CD // AB .
………………………………5 分
(2)在 AB 边上取一点 P ,使得 AP DF .
由图(1)可得, ADFP 为正方形,即 AP FP . ∵M 为 AF 的中点 ∴MP MA .
合肥市 2020 年高三第二次教学质量检测
数学试题(理科)参考答案及评分标准
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分.
题号 1
2
3
4
5
6
7
8
9 10 11 12
安徽省合肥市2020届高三第二次教学质量检测(数学理)doc高中数学

安徽省合肥市2020届高三第二次教学质量检测(数学理)doc高中数学安徽省合肥市2018年高三第二次教学质量检测数学试题〔理科〕〔考试时刻:120分钟,总分值:150分〕本卷须知: 1.答卷前,考生先使用黑色字迹的签字笔将自己的学校、姓名、准考证号填写在指定位置;核对条形码上本人的姓名和准考证号码,无误后,将共粘贴在指定的方框内。
2.非选择题答题书写要工整,字迹清晰。
修改答案时禁止使用涂改液或涂改胶条。
3.请在题号指定的答题区域内作答,在题号指定区域以外答题或超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.考试结,监考人将答题卷收回,试卷不收回。
第一卷〔总分值50分〕一、选择题〔本大题共10小题,每题5分,共50分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的〕 1.集合{|06,},{1,3,6},{1,4,5}U x x x Z A B =≤≤∈==,那么()U A C B ⋂= 〔 〕A .{1}B .{3,6}C .{4,5}D .{1,3,4,5,6}2.复数32,4a i b xi =+=+〔其中i 为虚数单位〕,假设复数aR b∈,那么实数x 的值为〔 〕A .-6B .6C .83 D .-833.sin()2sin(),sin cos 2ππαααα-=-+⋅=则〔 〕A .25B .25-C .25或25- D .15-4.双曲线22221x y a b-=,F 1是左焦点,O 是坐标原点,假设双曲线上存在点P ,使1||||PO PF =,那么此双曲线的离心率的取值范畴是〔 〕A .(]1,2B .(1,)+∞C .〔1,3〕D .[)2,+∞5.某农科院在3×3的9块式验田中选出6块种植某品种水稻进行试验,那么每行每列都有一块试验田种植水稻的概率为 〔 〕A .156B .17C .114D .3146.假设随机变量(1,4),(0),X N P x m -≤=则P(0<X<2)=〔 〕A .12m -B .12m-C .122m-D .1m -7.右图是某四棱锥的三视图,那么该几何体的表面积等于〔 〕A .3465+B .66543+C .663413+D .175+8.在直角梯形ABCD 中,AB//CD ,,45AD AB B ⊥∠=°,AB=2CD=2,M 为腰BC 的中点,那么MA MD ⋅=〔 〕A .1B .2C .3D .49.R 上可导函数()f x 的图象如下图,那么不等式2(23)()0x x f x '-->的解集为〔 〕A .(,2)(1,)-∞-⋃+∞B .(,2)(1,2)-∞-⋃C .(,1)(1,0)(2,)-∞-⋃-⋃+∞D .(,1)(1,1)(3,)-∞-⋃-⋃+∞10.已右函数21(0)()(1)1(0)x x f x f x x ⎧-≤=⎨-+>⎩,把函数()()g x f x x =-的零点按从小到大的顺序排列成一个数列,那么该数列的通项公式为 〔 〕A .*(1)()2nn n an N -=∈ B .*(1)()n a n n n N =-∈ C .*1()n a n n N =-∈D .*22()n n a n N =-∈第二卷〔总分值100分〕二、填空题〔本大题共5题,每题5分,共25分。
安徽省合肥市2020年高三4月第二次教学质量检测理科综合试卷

合肥市2020年高三第二次教学质量检测理科综合试题参考答案及评分标准第Ⅰ卷 (每小题6分,共126分)题号1 2 3 4 5 6 7 8 9 10 答案C AD C B D A C C B 题号 11 12 13 14 15 16 17 18 19 20 答案D B C C B C D ABC AC BD 题号21 答案CD第Ⅱ卷22.(7分) (1)将气垫导轨调节水平 (2分)(2)②③④⑤; (1分)(3)mgL ;22211()((2d d M m t t ⎡⎤+-⎢⎥⎣⎦ (各1分) (4)气垫导轨没有水平且B 端偏低(备注:作答“由于阻力…”不给分) (2分)23.(8分) (1)9.0Ω;偏小 (各1分)(2)①如图所示(3分) ②10.0(1分) ③并联;0.05 (各1分)24.(14分)(1)只有当开关S 接1时回路中才有焦耳热产生,在导体棒上升过程,设回路中产生的焦耳热为Q ,根据能量守恒有 2012mv mgh Q =+ (2分) 又12:2:3R R =,因此电阻R 1产生的热量为 135Q Q = (1分) 21031()52Q mv mgh =-(1分)(2)当开关S 接2时,导体棒由静止开始下落,设导体棒下落的加速度为a ,由牛顿第二定律得mg ILB ma -=(1分) 又Q C U CBL v I CBLa t t t∆∆∆====∆∆∆ (2分)联立得 22mg a CB L m=+ (1分) 所以导体棒做初速度为0,加速度为a 的匀加速直线运动,设导体棒回到出发点的速度大小为v ,由22v ah = (1分)得 v = (1分)(3)当导体棒向上运动时,由于所受安培力向下且不断减小,所以导体棒做加速度逐渐减小的减速运动;当导体棒开始向下运动时做初速度为0的匀加速直线运动,由于所受安培力与重力反向,所以此过程加速度小于g(4分)25.(18分)(1)选水平向右为正方向,设甲的加速度为1a ,对甲,由牛顿第二定律11(2)m g ma μ= (1分)212m/s a = (1分)设甲速度由0v 减到0过程通过的位移为1x ,经历的时间为1t 。
安徽省合肥市2020-2021学年高三上学期期初调研性检测理科数学试题

合肥市2021届高三调研性检测数学试(理科)(考试时间:120分钟 满分:150分)第Ⅰ卷(60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数z满足1zi -=,其中i 是虚数单位,则复数z 的模为( )A.B.C.D. 3B首先根据题意得到z i =,再计算模长即可.因为1zi -=,所以221++===iz i ii.所以==z 故选:B2. 若集合{}1A xx =>∣,{}2230B x x x =--≤∣,则A B =( ) A. (1,3] B. [1,3] C. [1,1)- D. [1,)-+∞A化简集合B ,根据交集的定义,即可求解.{}2230[1,3]B x x x =--≤=-∣, {}1(1,)A x x =>=+∞∣,(1,3]A B ∴=。
故选:A.3. 若变量x ,y 满足约束条件1133x y x y x y -≤⎧⎪+≥-⎨⎪-≥⎩,则目标函数3z x y =+的最小值为( )A. 92- B. 4- C. 3- D. 1D根据变量x ,y 满足1133x y x y x y -≤⎧⎪+≥-⎨⎪-≥⎩,画出可行域,然后平移直线30x y +=,当直线在y 轴上截距最小时,目标函数取得最小值.由变量x ,y 满足1133x y x y x y -≤⎧⎪+≥-⎨⎪-≥⎩,画出可行域如图所示:平移直线30x y +=,当直线在y 轴上截距最小时,经过点1,0A ,此时目标函数取得最小值,最小值是1,故选:D4. 为了保障广大人民群众的身体健康,在新冠肺炎疫情防控期间,有关部门对辖区内15家药店所销售的A 、B 两种型号的口罩进行了抽检,每家药店抽检10包口罩(每包10只),15家药店中抽检的A 、B 型号口罩不合格数(Ⅰ、Ⅱ)的茎叶图如图所示,则下列描述不正确...的是( )A. 估计A 型号口罩的合格率小于B 型号口罩的合格率B. Ⅰ组数据的众数大于Ⅱ组数据的众数C. Ⅰ组数据的中位数大于Ⅱ组数据的中位数D. Ⅰ组数据的方差大于Ⅱ组数据的方差 D根据茎叶图中的数据计算出两种型号口罩的合格率,可判断A 选项的正误;求出两组数据的众数,可判断B 选项的正误;求出两组数据的中位数,可判断C 选项的正误;利用排除法可判断D 选项的正误. 对于A选项,由茎叶图可知,A 型号口罩的不合格数为658210124131416202130199++⨯++⨯++++++=,B 型口罩的不合格数为245682101131416212528180++++⨯++⨯+++++=,A 型号口罩的合格率为1991301115001500-=,B 型口罩的合格率为1801320115001500-=, 所以,A 型口罩的合格率小于B 型口罩的合格率,A 选项正确; 对于B 选项,Ⅰ组数据的众数为12,Ⅱ组数据的众数11,B 选项正确; 对于C 选项,Ⅰ组数据的中位数为12,Ⅱ组数据的11,C 选项正确; 由排除法可知D 选项不正确.故选:D.5. 设数列{}n a 的前n 项和为n S ,若3122n n S a =-,则5S =( )A. 81B. 121C. 243D. 364B利用递推式与等比数列求和的通项公式即可得出.31,22n n S a =-∴当2n ≥时,113122n n S a --=-,∴111313133222222n n n n n n n a S S a a a a ---⎛⎫=-=---=- ⎪⎝⎭, 化简可得:13n n a a -=, 当1n =时,1113122a S a ==-,解得:11a =. ∴数列{}n a 是等比数列,首项为1,公比为3,()()55151113121113a q S q-⨯-∴===--.故选:B.6. 函数cos ()x xx xf x e e -=+在[],ππ-上的图象大致是( )A. B.C .D.A先由函数的奇偶性定义,判断()f x 为奇函数,排除B ,D ,再由()f x 在(0,),(,)22πππ函数值的正负值判断,即可得出结论.cos (),[,]x xx xf x x e eππ-=∈-+定义域关于原点对称, cos ()(),()x xx xf x f x f x e e ---==-∴+是奇函数,图象关于原点对称,排除选项B ,D ,(0,),()0,,()022x f x x f x ππ∈>==,(,),()02x f x ππ∈<,所以选项C 不满足,选项A 满足.故选:A. 7. 周六晚上,小红和爸爸、妈妈、弟弟一起去看电影,订购的4张电影票恰好在同一排且连在一起,为安全起见,每个孩子至少有一侧有家长陪坐,则不同的坐法种数为( ) A. 8 B. 12 C. 16 D. 20C先计算出4个人的全排列,再减去不符合情况的种数即可.4个人坐四个座位,共有4424A =种坐法,当孩子坐在一起并且坐在最边上时,有一个孩子没有大人陪伴,共有222228A A =种,所以每个孩子旁边必须有大人陪着共有24-8=16种坐法. 故选:C .8. 已知函数()2)0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示,则函数()f x 的单调递减区间为( )A. 32,2()88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B. 3,()88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦C. 372,2()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D. 37,()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D由图可知,20,218822f f ππππωϕωϕ⎛⎫⎛⎫⎛⎫⎛⎫=+==+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,338288T πππ=-=,从而可求出2,4πωϕ==-,()2)4f x x π=-,进而由3222,242k x k k Z πππππ+≤-≤+∈可求得答案解:由图可知,20,218822f f ππππωϕωϕ⎛⎫⎛⎫⎛⎫⎛⎫=+==+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 所以18k πωϕπ+=,1k Z ∈,2224k ππωϕπ+=+或2232,24k k Z ππωϕπ+=+∈,因为338288T πππ=-=,所以T π=,所以2ππω=, 因为0>ω,所以2ω=, 所以14k πϕπ=-,1k Z ∈,2324k πϕπ=-+或222,4k k Z πϕπ=-+∈ 因为||2ϕπ<,所以4πϕ=-, 所以()2)4f x x π=-,由3222,242k x k k Z πππππ+≤-≤+∈, 解得37,88k x k k Z ππππ+≤≤+∈,所以()f x 的单调递减区间为37,()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,故选:D 由三视图可知,几何体为一个三棱锥A BCD -, 如下图所示:根据三视图可知,4DB =,2DC =,高为2,1182323A BCD V DC DB -∴=⨯⨯⨯⨯=,∴所求几何体体积:83,故选:C .10. 在ABC 中,D 、E 、F 分别是边BC 、CA 、AB 的中点,AD 、BE 、CF 交于点G ,则:①1122EF CA BC =-;②1122BE AB BC =-+;③AD BE FC +=; ④0GA GB GC ++=. 上述结论中,正确的是( ) A. ①② B. ②③C. ②③④D. ①③④C 分析】作出图形,利用平面向量的加法法则可判断①②③④的正误. 如下图所示:对于①,F 、E 分别为AB 、AC 的中点,111222FE BC CA BC ∴=≠-,①错误; 对于②,以BA 、BC 为邻边作平行四边形ABCO ,由平面向量加法的平行四边形法则可得2BE BO BA BC AB BC ==+=-+,1122BE AB BC ∴=-+,②正确;对于③,由②同理可得2AD AB AC =+,1122AD AB AC ∴=+,同理可得1122CF CA CB =+,()102AD BE CF AB AC BA BC CA CB ∴++=+++++=, AD BE CF FC ∴+=-=,③正确;对于④,易知点G 为ABC 的重心,所以,23GA AD =-,23GB BE =-,23GC CF =-,因此,()203GA GB GC AD BE CF ++=-++=,④正确.故选:C. 11. 双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ,M 为C 的渐近线上一点,直线2F M 交C 于点N ,且20F M OM ⋅=,2232F M F N =(O 为坐标原点),则双曲线C 的离心率为( ) A. 5 B. 2 C. 3 D. 2 A设点M 为第一象限内的点,求出直线2F M 的方程,可求得点M 的坐标,由2232F M F N =可求得点N 的坐标,再将点N 的坐标代入双曲线C 的方程,进而可求得双曲线C 的离心率.设点M 为第一象限内的点,可知直线OM 的方程为by x a=,()2,0F c ,2F M OM ⊥,所以,直线2F M 的方程为()ay x c b=--, 联立()b y x a a y x c b ⎧=⎪⎪⎨⎪=--⎪⎩,解得2a x c ab y c ⎧=⎪⎪⎨⎪=⎪⎩,即点2,a ab M c c ⎛⎫ ⎪⎝⎭,设点(),N x y ,()222,,0,a ab b ab F M c c c c c ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,()2,F N x c y =-,2232F M F N =,()23232b x c c ab y c ⎧-=-⎪⎪∴⎨⎪=⎪⎩,解得222323a c x c ab y c ⎧+=⎪⎪⎨⎪=⎪⎩,即点2222,33a c ab N c c ⎛⎫+ ⎪⎝⎭,将点N 的坐标代入双曲线C 的方程得22222222331a c ab c c a b ⎛⎫+⎛⎫ ⎪ ⎪⎝⎭⎝⎭-=, 可得22249e e e⎛⎫+-= ⎪⎝⎭,整理得25e =,1e >,解得5e =故选:A.12. 已知a 、b R ∈,函数()()3210f x ax bx x a =+++<恰有两个零点,则+a b 的取值范围( )A. (),0-∞B. (),1-∞-C. 1,4⎛⎫-∞- ⎪⎝⎭D. 1,4⎛⎫-∞ ⎪⎝⎭D利用导数分析函数()y f x =的单调性,可得出该函数的极小值()10f x =,由题意得出()()2111321111321010f x ax bx f x ax bx x ⎧=++=⎪⎨=+++='⎪⎩,进而可得23112111223a x xb x x ⎧=+⎪⎪⎨⎪=--⎪⎩,可得出32111222a b x x x +=--,令110t x =<,由0a <可得出12t <-,构造函数()32222g t t t t =--,求得函数()y g t =在区间1,2⎛⎫-∞- ⎪⎝⎭上的值域,由此可求得+a b 的取值范围.()321f x ax bx x =+++且0a <,()2321f x ax bx '=++,24120b a ∆=->, 则方程()0f x '=必有两个不等的实根1x 、2x ,设12x x <, 由韦达定理得1223bx x a+=-,12103x x a=<,则必有120x x <<,且()21113210f x ax bx '=++=,① 当1x x <或2x x >时,()0f x '<;当12x x x <<时,()0f x '>.所以,函数()y f x =的单调递增区间为()12,x x ,单调递减区间为()1,x -∞和()2,x +∞.由于()010f =>,若函数()y f x =有两个零点,则()32111110f x ax bx x =+++=,②联立①②得21132111321010ax bx ax bx x ⎧++=⎨+++=⎩,可得23112111223a x xb x x ⎧=+⎪⎪⎨⎪=--⎪⎩,所以,32111222a b x x x +=--, 令110t x =<,令()32222g t t t t =--,则()a b g t +=, ()3222210a t t t t =+=+<,解得12t <-,()()()()2264223212311g t t t t t t t '=--=--=+-.当12t <-时,()0g t '>,此时,函数()y g t =单调递增,则()321111122222224a b g t g ⎛⎫⎛⎫⎛⎫⎛⎫+=<-=⨯--⨯--⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:D.第Ⅱ卷(90分)二、填空题:本大题共4小题,每小题5分,满分20分.把答案填写在答题卡上的相应位置. 13. 若命题:p 若直线l 与平面α内的所有直线都不平行,则直线l 与平面α不平行;则命题p ⌝是________命题(填“真”或“假”).假先写出p ⌝,再判断真假即可.命题:p 若直线l 与平面α内的所有直线都不平行,则直线l 与平面α不平行; 命题p ⌝:若直线l 与平面α内的所有直线都不平行,则直线l 与平面α平行,假命题. 故答案为:假命题.14. 若直线l 经过抛物线24x y =-的焦点且与圆22(1)(2)1x y -+-=相切,则直线l 的方程为________.0x =或4330x y --=先根据抛物线方程24x y =-,求得焦点坐标()0,1F -,再分直线的斜率不存在和直线的斜率存在时,两种情况设直线方程,然后利用圆心到直线的距离等于半径求解. 因为抛物线方程为24x y =-, 所以焦点坐标为:()0,1F -,当直线的斜率不存在时,设直线方程为:0x =, 圆心到直线的距离为1d r ,符合题意,当直线的斜率存在时,设直线方程为:1y kx =-,即10kx y --=, 圆心到直线的距离为2311k d r k -===+,解得43k =, 所以直线方程为4330x y --=, 故答案为:0x =或4330x y --=15. 已知函数()cos ()f x x x x R =-∈,α,β是钝角三角形的两个锐角,则(cos )f α________(sin )f β (填写:“>”或“<”或“=”).>对函数()f x 求导判断其单调性,再由钝角三角形内角判断cos ,sin αβ的大小. 由()1sin 0f x x '=+≥,可得()f x 在R 上单调递增, 因为α,β是钝角三角形两个锐角,所以2παβ+<,022ππβα<<-<,sin y x =在0,2π⎛⎫ ⎪⎝⎭上单调增,sin sin 2πβα⎛⎫∴<- ⎪⎝⎭,sin cos βα<,所以()(cos )sin f f αβ> 故答案为:>16. 已知三棱锥P ABC -的顶点P 在底面的射影O 为ABC 的垂心,若2ABC OBC PBC S S S ⋅=△△△,且三棱锥P ABC -的外接球半径为3,则PAB PBC PAC S S S ++△△△的最大值为________. 18连AO 交BC 于D ,由顶点P 在底面的射影O 为ABC 的垂心,得AD BC ⊥,进而证明,,BC PA PC AB PD BC ⊥⊥⊥,由2ABC OBC PBC S S S ⋅=△△△。
【附加15套高考模拟试卷】安徽省“江淮十校”2020届高三4月联考数学(理科)试题含答案
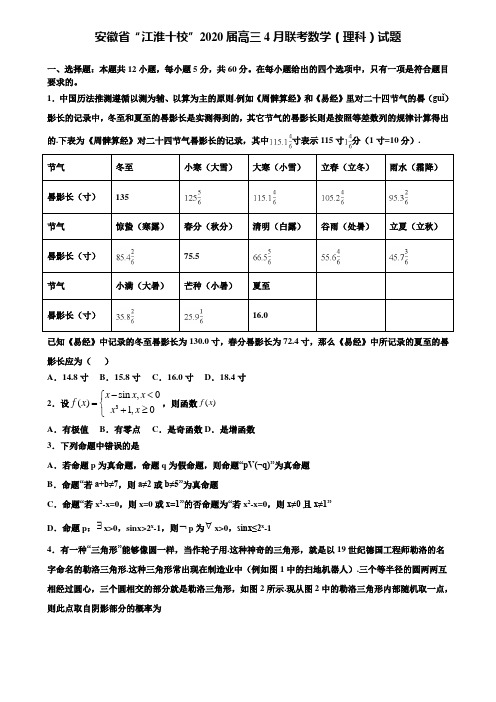
晷影长(寸)
16.0
已知《易经》中记录的冬至晷影长为 130.0 寸,春分晷影长为 72.4 寸,那么《易经》中所记录的夏至的晷
影长应为( ) A.14.8 寸 B.15.8 寸 C.16.0 寸 D.18.4 寸
x sin x, x 0
2.设 f (x)
x3 1, x 0
,则函数 f (x)
的.下表为《周髀算经》对二十四节气晷影长的记录,其中
寸表示 115 寸 分(1 寸=10 分).
节气
冬至
小寒(大雪) 大寒(小雪) 立春(立冬) 雨水(霜降)
晷影长(寸) 135
节气
惊蛰(寒露) 春分(秋分) 清明(白露) 谷雨(处暑) 立夏(立秋)
晷影长(寸)
75.5
节气
小满(大暑) 芒种(小暑) 夏至
线 AB 的方程为( )
y 1x2
y 1 x3
y 1 x3
y 1x2
A. 2
B. 4
C. 2
D. 4
7.若某几何体的三视图如图所示,则这个几何体的体积是( )
A.5 B.6 C.7 D.8 8.在学校举行一次年级排球赛比赛中,李明、张华、王强三位同学分别对比赛结果的前三名进行预测:
李明预测:甲队第一,乙队第三
D.命题 p: x>0,sinx>2x-1,则 p 为 x>0,sinx≤2x-1
4.有一种“三角形”能够像圆一样,当作轮子用.这种神奇的三角形,就是以 19 世纪德国工程师勒洛的名 字命名的勒洛三角形.这种三角形常出现在制造业中(例如图 1 中的扫地机器人).三个等半径的圆两两互 相经过圆心,三个圆相交的部分就是勒洛三角形,如图 2 所示.现从图 2 中的勒洛三角形内部随机取一点, 则此点取自阴影部分的概率为
合肥市2020届高三第二次教学质量检测(理科数学)详细解析

x x
y1 ,
∴ 的分布列为
60x y1
60
3 4
x
x
y1
60 x x y1
p
0.4
0.4
0.2
E
0.4 60x
y1
0.4
60
3 4
x
x
y1
0.2 60
x x
y1
2 3
x3
15 2
x2
50x
160
.
………………………………9 分
设f
x E
2 3
x3
15 2
x2
50x
160
,0 x 20 ,∴ f x 2x2
15x 50 .
f x 0 0 x 10 , f x 0 10 x 20 .
高三数学试题(理科)答案 第 1 页(共 4 页)
设平面 DFE 的一个法向量为m x,y,z .
由 FFDE
m m
0 0
得 xxzy00
.
令 x 1 ,则 y 1,z 1 ,∴m (1,1,-1).
由平面 ADF 是坐标平面 xMz 可得:平面 ADF 一个法向量为n (0,1,0).
由(1)知,MD 平面 ABEF ,∴MA,MP,MD 两两垂直.
以M 点为坐标原点,直线MA,MP,MD 分别为坐标轴建立空间直角坐标系M xyz ,如图.
设AF 2 ,则 D (0,0, 1), A (1,0,0), P (0,1,0), F (-1,0,0), ∴ FD (1,0,1), FE AP (-1,1,0).
∵b1 b2 b3 bn 2 2 2 2 ,∴b1 b2 b3 bn1 2 2 ( n 2 ),
华大新高考联盟2020届高三4月教学质量测评数学(理)试题及答案

机密★启用前华大新高考联盟2020届高三4月教学质量测评理科数学本试题卷共4页.23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝#试顺利★注意事项:1 .答短前.先将fl己的姓名■准考iE弓域可在答距长上.并将准琴江号条形研财在答恩K上的指定位2.逸押IS的作答:侦小应燃目的答案愫勺涂黑・耳在试K上的区域均无效.3.填空*和解答题的作答:用签字笔宜接答在容愆卡上酉应的答题IK域内.写在试题尝,草SI纸和答W卡上的菲答题区域均无效.4.选考也的作答■先把所送趣口的醴号在答粗N上指定的位置用2B松宅涂SL答宝珂在答履卞上对应的谷(SH域内" 。
在武!»■・草棉舐和答的|?上的曹咨IS风域均无效.5 .考试培束后.崎将谷曜卡上交.-、选择题:本题共12小越,每小越5分,共60分,在每小题纶出的四个选项中,只有一项是符合题目萋求的。
1.已W?»r»l+4-.则r •iA.OB.1C.72D.22.设«^A-{xlx>3}-B-Ullog>(x-a»0|.Wa=3 是8UA 的A .充分不必要条件 B.2要不充分条件C充妾条件 D.既不充分又K必要条件3.i殳等是数列修」的前〃顼和为S..已知七5s,+., 30.岫S«A.85B.97C.100D.1754.槐晋时期的数学家弟薇首创常剧术.为计算圈周率建星『严密的戒论即完脊的算法.所时割倒术.就是以间内按正多边形的而枳.来无限逼近同血枳.对澈形容他的利同术说,•割之弥细.所失弥少.割之又割.以至丁木讨刮.则勺网合体.而尤所失矣...比;I企一1盘内■一内按正I二边形•将loottSTM机撤入间盘内.发现只右I粒豆子不在正十.边形内.据此实羚估计网周宇的近似值为A-T R 16r22C T n T5.已tU^=lg2.>»-ln3.c ~ log,3•则A.《rVz VyB.Vy<rC.x<y<t\lz<T<y6 .执行如图所示程序也图.设输出教据构成集合人•从集合人中任取一个兀素m,则事件“函敢fM)=/+”rr在[0・+c>上是增雨数”的借率为理科教学忒题第1页(共4贞〉7 .设/(x).g(r)分别为定义在-5 I的奇函牧和偶函数.日/(”+g(«r) = 2e,cgr(e为自然对数的底j = /(x)-«(x)的图象大致为&某病。
2020届安徽省合肥市高三下学期4月第二次教学质量检测数学(理)试题

B.函数 图象的对称中心为
C.函数 的图象可由 的图象向左平移 得到
D.函数 的递增区间为
7.《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为 和 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为 ,宽为内接正方形的边长 .由刘徽构造的图形还可以得到许多重要的结论,如图3.设 为斜边 的中点,作直角三角形 的内接正方形对角线 ,过点 作 于点 ,则下列推理正确的是()
A. B. C. D.
10.已知抛物线 : 的焦点为 ,过点 的直线 交抛物线 于点 , ,若 ,则 ()
A. B. C. D.
11.若关于 的不等式 有且只有两个整数解,则实数 的取值范围是()
A. B.
C. D.
12.在三棱锥 中,二面角 、 和 的大小均等于 , ,设三棱锥 外接球的球心为 ,直线 与平面 交于点 .则 ()
21.已知函数 .( 是自然对数的底数)
(1)求 的单调递减区间;
(2)记 ,若 ,试讨论 在 上的零点个数.(参考数据: )
22.在直角坐标系 ,曲线 的参数方程为 ( 为参数).以坐标原点 为极点, 轴的非负半轴为极轴建立极坐标系,直线 的极坐标方程为 .
(1)写出曲线 的普通方程和直线 的直角坐标方程;
市场销售状态
畅销
平销
滞销
市场销售状态概率
预期平均年利润(单位:万元)
方案
700
400
2020届四省名校高三第二次大联考数学(理)试题(PDF版,含答案解析)

2020届四省名校高三第二次大联考理科数学注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.考试结束后,请将本试卷和答题卡一并交回。
满分150分,考试用时120分钟。
一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合{})2ln(+==x y x A ,{}13<=x x B ,则=B A A.{}02<<-x x B.{}02<≤-x x C.{}12<<-x x D.{}12<≤-x x 2.对于平面内两个非零向量a 和b ,0:>⋅b a p ,a q :和b 的夹角为锐角,则p 是q 的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件3.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入x n ,的值分别为2,4,则输出v 的值为A.24B.25C.49D.504.已知等差数列{}n a 的前n 项和为n S ,且1032=+a a ,305=S ,则数列{}n a 的公差为A.1B.2C.3D.45.42)2(xx -展开式中含5x 的项的系数为A.8B.8-C.4D.4-6.正三棱柱(底面为正三角形的直棱柱)111C B A ABC -中,AB AA =1,M 为棱1CC 的中点,则异面直线C A 1与BM 所成的角为A.6π B.4πC.3π D.2π7.2019年成都世界警察与消防员运动会期间,需安排甲、乙、丙、丁四名志愿者去CB A ,,三个场馆参与服务工作,要求每个场馆至少一人,则甲乙被安排到同一个场馆的概率为A.121 B.81C.61D.418.已知函数)sin(31)cos(33)(θθ+-+=x x x f )2|(|πθ<是偶函数,则θ的值为A.3π B.3π-C.6π D.6π-9.在ABC ∆中,点D 在BC 边上,且DB CD 3=,点M 在AD 边上,AM AD 3=,若AC AB CM μλ+=,则=+μλA.32- B.32C.67 D.67-10.抛物线)0(:2>=a ax y C 的焦点F 是双曲线12222=-x y 的一个焦点,过F 且倾斜角为︒60的直线l 交C 于B A ,,则=||AB A.2334+ B.234+C.316D.1611.下列选项中,函数1sin 2)(2+-=x x x x f 的部分图象可能是A. B.C. D.12.设点)0,1(A ,)0,4(B ,动点P 满足||||2PB PA =,设点P 的轨迹为1C ,圆2C :4)3(3(22=-++y x ,1C 与2C 交于点N M ,,Q 为直线2OC 上一点(O 为坐标原点),则=⋅MQ MN A.4 B.32C.2 D.3二、填空题(本大题共4小题,每小题5分,共20分)13.设复数|43|1i ii z +-+=,则=z _______.14.在正项等比数列{}n a 中,1011010=a ,则=++++2019321lg lg lg lg a a a a _______.15.如图,三棱锥ABC P -中,平面⊥PAC 平面ABC ,BC SB ⊥,2==BC AB ,3==PC PA ,则三棱锥ABC P -的外接球的表面积为_______.16.已知函数⎪⎩⎪⎨⎧>+≤+--=1,21ln 1,272)(2x x x x x x f 若关于x 的方程kx x f =)(恰有4个不相等的实数根,则实数k 的取值范围是_______.三、解答题(共70分。
2020届安徽省合肥市高三下学期4月第二次教学质量检测数学(理)试题(解析版)

2020届安徽省合肥市高三下学期4月第二次教学质量检测数学(理)试题一、单选题1.若集合{}2230A x x x =--≤,{2xB x =≥,则A B =I ( )A .1,32⎡⎤⎢⎥⎣⎦B .1,12⎡⎤⎢⎥⎣⎦C .13,2⎡⎤-⎢⎥⎣⎦D .[]2,3【答案】A【解析】解不等式确定集合,A B 后由交集运算得结论. 【详解】由题意13{|}A x x =-≤≤,1{|}2B x x =≥, ∴1{|3}2A B x x =≤≤I . 故选:A . 【点睛】本题考查集合的交集运算,考查解一元二次不等式和指数不等式,掌握指数函数性质和一元二次不等式求解方法是解题关键.2.欧拉公式i e cos isin θθθ=+把自然对数的底数e ,虚数单位i ,三角函数cos θ和sin θ联系在一起,充分体现了数学的和谐美,被誉为“数学的天桥”,若复数z 满足()i i i ez π+⋅=,则z =( )A .1BC D【答案】B【解析】由新定义化为复数的代数形式,然后由复数的除法运算求出z 后再求模. 【详解】 由题意(1)cos sin 1(1)(1)i i i i i i z e ii i i i i πππ--====+++-+-+--111222i i -+==-,∴z ==. 故选:B .【点睛】本题考查复数的新定义,考查复数的除法运算和求复数的模,解题关键是由新定义化i e π为代数形式,然后求解.3.若实数x ,y 满足约束条件240403230x y x y x y +-≥⎧⎪-+≥⎨⎪+-≥⎩,则2z x y =-的最小值是( )A .5-B .4-C .7D .16【答案】B【解析】作出可行域,作出目标函数对应的直线,平移该直线可得最优解. 【详解】作出可行域,如图射线BA ,线段BC ,射线CD 围成的阴影部分(含边界),作直线:20l x y -=,向上平移直线l 时2z x y =-减小,∴当l 过点(0,4)B 时,2z x y =-取得最小值-4. 故选:B .【点睛】本题考查简单的线性规划,解题关键是作出可行域,注意本题中可行域不是多边形内部,而是一个开放性区域.4.已知()f x 为奇函数,当0x <时,()2xf x e ex -=-(e 是自然对数的底数),则曲线()y f x =在1x =处的切线方程是( ) A .y ex e =-+ B .y ex e =+C .y ex e =-D .1122y e x e e e ⎛⎫=--+ ⎪⎝⎭ 【答案】C【解析】由奇函数求出0x >时,函数解析式,再求出导函数后可得切线斜率,从而得切线方程. 【详解】由于()f x 是奇函数,所以0x >时,22()()()x x f x f x e ex e ex =--=--=-+,(1)0f =,()2x f x e ex '=-+,(1)2f e e e '=-+=,所以所求切线方程为(1)y e x =-. 故选:C . 【点睛】本题考查导数的几何意义,考查函数的奇偶性,解题关键是由奇函数定义求出0x >时函数解析式后对函数的求导.5.若cos801m ︒+︒=,则m =( ) A .4 B .2C .2-D .4-【答案】A【解析】移项由切化弦化简1︒,然后可得m . 【详解】由题意1-︒12(cos10)cos10221cos10cos10cos10︒︒︒︒︒=-==︒︒︒2sin(3010)2sin 204sin10cos10cos10cos10cos10︒-︒︒︒︒===︒︒︒4sin104cos80cos80m =︒=︒=︒,所以4m =.【点睛】本题考查同角间的三角函数关系,考查两角差的正弦公式与二倍角公式、诱导公式.在三角函数式中同时出现了正弦、余弦、正切时,可用切化弦方法变形后再化简. 6.已知函数()()tan 0,02f x x ωϕωϕπ⎛⎫=+><< ⎪⎝⎭的图象关于点,06π⎛⎫⎪⎝⎭成中心对称,且与直线y a =的两个相邻交点间的距离为2π,则下列叙述正确的是( ) A .函数()f x 的最小正周期为πB .函数()f x 图象的对称中心为(),06k k Z π⎛⎫π+∈⎪⎝⎭ C .函数()f x 的图象可由tan 2y x =的图象向左平移6π得到 D .函数()f x 的递增区间为(),2326k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭【答案】D【解析】利用正切函数的性质进行判断. 【详解】由()f x 的图象与直线y a =的两个相邻交点间的距离为2π,知函数最小正周期是2π,A 错; 由此得22πωπ==,又由,06π⎛⎫⎪⎝⎭是其图象对称中心得,26k πϕπ⨯+=或262k ππϕπ⨯+=+,k Z ∈,又02πϕ<<,所以6π=ϕ. 所以()tan(2)6f x x π=+,由262k x ππ+=得412k x ππ=-,对称中心是(,0),412k k Z ππ-∈,B 错; tan 2y x =的图象向左平移6π得到tan 2()tan(2)()63y x x f x ππ=+=+≠,C 错;由2262k x k πππππ-<+<+,得2326k k x ππππ-<<+,即函数的增区间是(),2326k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭,D 正确. 故选:D .本题考查正切型函数的图象与性质,掌握正切函数的性质是解题关键.7.《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为b 和a 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为+a b ,宽为内接正方形的边长d .由刘徽构造的图形还可以得到许多重要的结论,如图3.设D 为斜边BC 的中点,作直角三角形ABC 的内接正方形对角线AE ,过点A 作AF BC ⊥于点F ,则下列推理正确的是( )①由图1和图2面积相等得abd a b=+; ②由AE AF ≥2222a b a b ++≥;③由AD AE ≥222112a b a b+≥+; ④由AD AF ≥可得222a b ab +≥. A .①②③④ B .①②④C .②③④D .①③【答案】A【解析】根据图形进行计算. 【详解】①由面积相等得()ab a b d =+,abd a b=+,正确;②在图3中,由三角形面积得AF =,又AE a b==+, 由AE AF ≥≥2a b +≥,正确;③AD =AD AE ≥≥2211ab a b a b ≥=++,正确;④由由AD AF ≥≥,所以222a b ab +≥,正确.四个推理都正确. 故选:A . 【点睛】本题考查推理,通过构造几何图形推导出基本不等式及其推论.本题考查数学文化,激发学生的学习积极性.8.为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着A ,B ,C 三个农业扶贫项目进驻某村,对该村仅有的甲、乙、丙、丁四个贫困户进行产业帮扶.经过前期实际调研得知,这四个贫困户选择A ,B ,C 三个扶贫项目的意向如下表:若每个贫困户只能从自己已登记的选择意向项目中随机选取一项,且每个项目至多有两个贫困户选择,则不同的选法种数有( ) A .24种 B .16种C .10种D .8种【答案】B【解析】按只有一个项目有2个贫困户选和只选2个项目,每个项目两个贫困户选,分类讨论. 【详解】只有一个项目有2个贫困户选:C 项目有2个贫困户选,甲乙分别选取,A B 项目,方法为22A =2种,B 项目有2个贫困户选,方法数有22114A ++=种,A 项目有2个贫困户选,不能丙丁同时选A ,方法数有111115++++=种,共2+4+5=11种,只选2个项目,每个项目两个贫困户选,先AB ,有13C =3种,选AC 只有1种,选BC 只有1种,共3+1+1=5种, 综上共有方法数11+5=16种. 故选:B . 【点睛】本题考查分布列组合的综合应用,掌握分类计数原理和分步计数原理是解题关键. 9.某几何体是由一个半球挖去一个圆柱形成的,其三视图如图所示.已知半球的半径为6,则当此几何体体积最小时,则当此几何体体积最小时,它的表面积等于( )A .24πB .(1833+πC .21πD .(1842+π【答案】D【解析】设设圆柱高为x (06)x <<,求圆柱底面半径,从而用x 表示出圆柱体积,由导数知识求得最大值,此时该几何体体积最小,再求其表面积即可. 【详解】设圆柱高为x (06)x <<,则圆柱底面半径为26r x =-,圆柱体积为223(6)(6)V r x x x x x πππ==-=-,2(63)V x π'=-,由0V '=得2x 2-舍去),当2)x ∈时,0V '>,函数3(6)V x x π=-递增,2,6)x ∈时,0V '<,函数3(6)V x x π=-递减,∴2x =时,3max [62(2)]42V ππ==,262r x -=,圆柱体积最大时,此几何体体积最小.22222(18S ππππ=⨯+⨯⨯=+全.故选:D . 【点睛】本题考查几何体的体积与表面积,考查导数在体积最值中的应用.解题关键是用圆柱的高x 表示出圆柱的体积,由圆柱体积的最大值得几何体体积的最小值.10.已知抛物线C :24y x =的焦点为F ,过点()3,0D 的直线l 交抛物线C 于点A ,B ,若FA FB -=u u u r u u u r ,则FA FB ⋅=u u u r u u u r( )A .9-B .11-C .12-D .【答案】A【解析】设直线直线l 方程为(3)y k x =-(此时中斜率k 显然存在),设1122(,),(,)A x y B x y ,直线方程代入抛物线方程后应用韦达定理得1212,x x x x +,由抛物线的定义条件FA FB -=u u u r u u u r可转化为12x x -=,从而可求得k ,再由向量数量积的坐标表示计算出结论. 【详解】抛物线24y x =中焦参数2p =,焦点为(1,0)F ,设1122(,),(,)A x y B x y∴1212(1)(1)FA FB x x x x -=+-+=-=u u u r u u u r显然直线l 不与x 轴垂直,设其方程为(3)y k x =-,由24(3)y x y k x ⎧=⎨=-⎩,得2222(64)90k x k x k -++=,∴212264k x x k ++=,129x x =. ∴2222121212264()()4()4913k x x x x x x k+-=+-=-⨯=,24k =,∴127x x +=. ∴11221212(1,)(1,)(1)(1)FA FB x y x y x x y y ⋅=-⋅-=--+u u u r u u u r22121212121212(1)(1)(3)(3)()1[3()9]x x k x x x x x x k x x x x =--+--=-+++-++9=-.故选:A . 【点睛】本题考查直线与抛物线相交问题,考查平面向量数量积的坐标表示,考查抛物线的定义,解题过程中,利用抛物线定义把已知条件FA FB -=u u u r u u u r转化继12x x -是关键.11.若关于x 的不等式22ln 4ax a x x ->--有且只有两个整数解,则实数a 的取值范围是( ) A .(]2ln3,2ln 2-- B .(),2ln 2-∞- C .(],2ln3-∞- D .(),2ln3-∞-【答案】C【解析】首先确定2是题设不等式的一个整数解,然后按1不是不等式的解和1是不等式的解分类讨论. 【详解】首先2x =时,不等式为224ln 24a a ->--,恒成立,即整数2是不等式的一个解,则由题意1或3是不等式的另一个整数解.若1不是不等式的解,则22ln14a a -≤--,2a ≥,此时不等式化为:(2)ln 24a x x a -+>-,易知函数(2)ln y a x x =-+在(0,)+∞上是增函数,则大于2的所有整数都是原不等式的解,不合题意.所以1是原不等式的解,大于3的所有整数不是原不等式的解,2a <, 所以3x ≥时,不等式22ln 4ax a x x -≤--恒成立,即24ln 2x xa x --≤-在[3,)+∞上恒成立, 设24ln ln ()222x x xg x x x --==---,则2222ln ln 1()(2)(2)x x x x x g x x x --+-'=-=--,3x ≥时,ln 1x >,()0g x '>,()g x 单调递增,所以()(3)2ln3g x g ≥=-,所以2ln3a ≤-. 综上a 的取值范围是(,2ln 3]-∞-. 故选:C . 【点睛】本题考查不等式的整数解问题,解题关键是转化为不等式在22ln 4ax a x x -≤--在[3,)+∞上恒成立,再变形转化为求函数的最值.12.在三棱锥P ABC -中,二面角P AB C --、P AC B --和P BC A --的大小均等于3π,::3:4:5AB AC BC =,设三棱锥P ABC -外接球的球心为O ,直线PO 与平面ABC 交于点Q .则POOQ=( ) A .14B .2C .3D .4【答案】D【解析】设3AB x =,由三个二面角相等得顶点P 在底面上的射影H 是ABC V 的内心,过ABC V 外心作平面ABC 的垂线,外接球球心就在这条垂直线,由外接球半径求得球心到底面的距离后利用平行线性质可得结论. 【详解】如图,作PH ⊥平面ABC ,垂足为H ,因此三个侧面,,PAB PBC PCA 与底面ABC 所成的二面角相等,所以H 是ABC V 的内心,又::3:4:5AB AC BC =,设3,4,5AB x AC x BC x ===,则222AB AC BC +=,即ABC V 是直角三角形,斜边是BC ,作HN BC ⊥于N ,连接PN ,由PH ⊥平面ABC ,BC ⊂平面ABC ,所以PH BC ⊥,PH HN H =I ,所以BC ⊥平面PHN ,PN ⊂平面PHN ,所以BC PN ⊥,所以PNH ∠是二面角P BC A --的平面角,所以3PNH π∠=,ABC V 是直角三角形,所以2AB AC BCHN x +-==,所以tan PH HN PNH =∠=,设M 是BC 中点,则M 是ABC V 的外心,连接OM ,则OM ⊥平面ABC ,所以//PH OM ,OM BC ⊥,连接HM ,如图PHMO 是直角梯形,在Rt ABC V 中可得HM x ==,若外接球球心在O '位置,如图,则在直角梯形PHMO '中,222()PO HM PH O M ''=+-,在直角O MC '△中,222O C O H MC ''=+,而O P O C ''=,所以22()HM PH O M '+-22O M MC '=+,即222255()(3)()22x x O M O M x ''+-=+,解得33O M x '=-,所以O 在平面ABC 的下方(O 与P 在平面ABC 的两侧),且3OQ x =. 直线PO 与平面ABC 交于点Q .则Q HM ∈,由//PH MO 得333PQ PHxOQ OMx===,所以4PO PQ OQ OQ OQ +==. 故选:D .【点睛】本题考查三棱锥的外接球问题,考查二面角的概念,解题关键是掌握结论:一是三棱锥三个侧面与底面所成二面角相等,则顶点在底面上的射影是底面三角形内心.二是三棱锥的外接球的球心在过各面外心且与该面垂直的直线上.本题确定球心位置时可以分类球心是在平面ABC 的哪一侧,也可以先画图假设在O '位置,计算出MO '的长,如果0MO '>,位置正确,如果0MO '<,则O 在另一侧.二、填空题13.已知向量a r 和b r满足22a a b =-=r r r ,1a b -=r r ,则a b ⋅=r r __________.【答案】1【解析】利用数量积的定义把模转化为数量积后可得. 【详解】由题意222222(2)442442a b a b a a b b a b b -=-=-⋅+=-⋅+=r r r r r r r r r r r ,①, 22222()2221a b a b a a b b a b b -=-=-⋅+=-⋅+=r r r r r r r r r r r ,②,由①②联立可解得1a b ⋅=r r.故答案为:1. 【点睛】本题考查向量的数量积的运算,解题关键是掌握向量数量积的性质,向量的模的运算转化为向量的数量积.14.三人制足球(也称为笼式足球)以其独特的魅力,吸引着中国众多的业余足球爱好者.在某次三人制足球传球训练中,A 队有甲、乙、丙三名队员参加.甲、乙、丙三人都等可能地将球传给另外两位队友中的一个人.若由甲开始发球(记为第一次传球),则第4次传球后.,球仍回到甲的概率等于__________. 【答案】38【解析】用树状图表示出传球事件,即可得概率. 【详解】画出树状图表示出传球事件:由树状图,知第四次传回甲的概率是63168P ==. 故答案为:38.【点睛】本题考查古典概型,解题方法是用树状图写出所有基本事件,从而可计算概率.15.已知双曲线C :()222210,0x y a b a b-=>>的右焦点为点F ,点B 是虚轴的一个端点,点P 为双曲线C 左支上一个动点,若BPF △周长的最小值等于实轴长的4倍,则双曲线C 的渐近线方程为__________. 【答案】2y x =±【解析】把P 到右焦点的距离转化为P 到左焦点的距离,根据最小值可建立,,a b c 的等式,从而求得ba,得渐近线方程.【详解】设1F 是双曲线的左焦点,如图,则12PF PF a =+,12BF BP PF BF BP PF a ++=+++,显然2211BP PF BF b c +≥=+,当且仅当1,,B P F 三点共线时取等号, ∴BPF △的最小值是2222b c a ++,∴222242b c a a ++=⨯,2222229a b c b b a =+=++,224b a =,2ba=,∴渐近线方程为2y x =±. 故答案为:2y x =±.16.已知ABC V 三个内角A ,B ,C 所对的边分别为a ,b ,c ,若sin A ,sin B ,sin C 成等比数列,()sin B A -,sin A ,sin C 成等差数列,则:(1)C =__________;(2)tan tan AB=__________. 【答案】π251- 【解析】(1)由已知结合等差数列和等比数列的性质列式,由正弦定理化角为边,由和差角的正弦公式化简后由余弦定理可得;(2)由(1)计算出sin ,cos A A ,然后由同角关系可计算出结果. 【详解】(1)由sin A ,sin B ,sin C 成等比数列得2sin sin sin B A C =,∴2b ac =,又()sin B A -,sin A ,sin C 成等差数列,∴2sin sin()sin A B A C =-+, 即2sin sin()sin()sin cos cos sin sin cos cos sin 2sin cos A B A A B B A B A A B A B B A=-++=-++=,∴sin sin cos A B A =,∴2222b c a a b bc+-=⋅,即222222b c a ac b +-==,∴222+=a b c ,∴2C π=;(2)由(1)可得2A B π+=,22sin sin cos cos 1sin A B A A A ===-,解得1sin cos 2A B ==,cos sin A B +=∴22tan sin cos sin 1tan cos sin cos 2A AB A B A B A ===. 【点睛】本题考查了正弦定理、余弦定理、同角间的三角函数关系在解三角形中的应用,同时还考查了诱导公式、两角和与差的正弦公式,解题中需确定选用的公式.属于中档题.三、解答题17.已知等差数列{}n a 的前n 项和为n S ,21a =,714S =,数列{}n b 满足221232n n n b b b b +⋅⋅⋅⋅⋅⋅⋅=.(1)求数列{}n a 和{}n b 的通项公式;(2)若数列{}n c 满足()cos n n n c b a =π,求数列{}n c 的前2n 项和2n T .【答案】(1)2n n a =.2nn b =.(2)()12445n n T ++-=-【解析】(1)由基本量法求出等差数列{}n a 的通项公式,用作商法可求得n b ,但要注意1b 的求法;(2)根据cos()2nπ的周期性,化简后由等比数列前n 项和公式计算. 【详解】解:(1)设{}n a 的公差为d ,由21a =,714S =得11172114a d a d +=⎧⎨+=⎩.解得112a =,12d =,所以2n n a =.∵()212212322n n n nn b b b b ++⋅⋅⋅⋅⋅⋅⋅==,∴()()12123122n n n b b b b n --⋅⋅⋅⋅⋅⋅⋅=≥,两式相除得()22nn b n =≥.当1n =时,12b =适合上式. ∴2nn b =.(2)∵()cos π2cos π2nn n n n c b a ⎛⎫==⎪⎝⎭, ∴()2342π3π2cos2cos π2cos 2cos 2π22n T =+++()()21221π2cos2cosπ2n n n n --+⋅⋅⋅++()()()24622cos π2cos 2π2cos 3π2cos πn n =+++⋅⋅⋅+()246222212nn =-+-+⋅⋅⋅+-⋅ ()()()141444145nn +---+-==-+.【点睛】本题考查求等差数列的通项公式,考查了等差数列的前n 项和公式,考查了由递推关系求数列的通项公式,考查等比数列的前n 项和,解题中求和时要注意利用余弦定理的周期性,得出新数列的公比.18.如图(1),在矩形ABCD 中,E ,F 在边CD 上,BC CE EF FD ===.沿BE ,AF 将CBE △和DAF △折起,使平面CBE 和平面DAF 都与平面ABEF 垂直,如图(2).(1)试判断图(2)中直线CD 与AB 的位置关系,并说明理由; (2)求平面ADF 和平面DEF 所成锐角二面角的余弦值.【答案】(1)CD ∥AB .见解析(2 【解析】(1)分别取AF ,BE 的中点M ,N ,连结CD ,DM ,CN ,MN ,可证得DM 与CN 都与平面ABEF 垂直,从而得它们平行且相等,得平行四边形CDMN ,得//CD MN ,在图(1)中可证得//MN AB ,从而得结论;(2)在AB 边上取一点P ,使得AP DF =,可证得MA ,MP ,MD 两两垂直.以M 点为坐标原点,直线MA ,MP ,MD 分别为坐标轴建立空间直角坐标系M xyz -,用空间向量法求二面角的余弦. 【详解】解:(1)CD AB P .理由如下:连结CD ,分别取AF ,BE 的中点M ,N ,连结DM ,CN ,MN ,由图(1) 可得,ADF V 与BCE V 都是等腰直角三角形且全等,则DM AF ⊥,CN BE ⊥,DM CN =,如图.∵平面ADF ⊥平面ABEF ,交线为AF ,DM ⊂平面ADF ,DM AF ⊥,∴DM ⊥平面ABEF .同理得,CN ⊥平面ABEF ,∴DM CN P .又∵DM CN =∴四边形CDMN 为平行四边形,∴CD MN ∥. ∵M ,N 分别是AF ,BE 的中点∴MN AB P ∴CD AB P .(2)在AB 边上取一点P ,使得AP DF =. 由图(1)可得,ADFP 为正方形,即AP FP =. ∵M 为AF 的中点∴MP MA ⊥.由(1)知,MD ⊥平面ABEF ,∴MA ,MP ,MD 两两垂直.以M 点为坐标原点,直线MA ,MP ,MD 分别为坐标轴建立空间直角坐标系M xyz -,如图.设2AF =,则()0,0,1D ,()1,0,0A ,()0,1,0P ,()1,0,0F -,∴()1,0,1FD =u u u r ,()1,1,0FE AP ==-u u u r u u u r. 设平面DFE 的一个法向量为(),,m x y z =u r. 由00FD m FE m ⎧⋅=⎨⋅=⎩u u u v vu u u v v 得00x z x y +=⎧⎨-+=⎩. 令1x =,则1y =,1z =-,∴()1,1,1m =-u r.由平面ADF 是坐标平面xMz 可得:平面ADF 一个法向量为()0,1,0n =r.设平面ADF 与平面DFE 所成的锐角二面角为θ,则3cos cos ,m n m n m nθ⋅===⋅u r r u r r u r r∴平面ADF 与平面DFE 3【点睛】本题考查线面平行的性质定理,考查用空间向量法求二面角.解题关键是找到过同一点的两两垂直的三条直线,以它们为坐标轴建立空间直角坐标系.本题考查了学生的空间想象能力,运算求解能力,属于中档题.19.已知椭圆C 的方程为22143x y +=,斜率为12的直线l 与椭圆C 交于A ,B 两点,点31,2P ⎛⎫⎪⎝⎭在直线l 的左上方. (1)若以AB 为直径的圆恰好经过椭圆右焦点2F ,求此时直线l 的方程; (2)求证:PAB △的内切圆的圆心在定直线1x =上. 【答案】(1)11127y x =-.(2)见解析【解析】(1)设直线l 的方程为12y x m =+.设()11,A x y ,()22,B x y .由直线方程与椭圆方程联立消元后应用韦达定理得1212,x x x x +,由判别式大于0得m 的一个范围,由点31,2P ⎛⎫⎪⎝⎭在直线l 的左上方再一个m 的范围,两者结合得m 的取值范围,以AB 为直径的圆恰好经过椭圆C 的右焦点2F ,说明220AF BF ⋅=u u u u r u u u u r,用坐标表示并代入1212,x x x x +可求得m ,注意m 的取值范围,即得直线方程;(2)由(1)计算0PA PN k k +=,即得直线1x =是APB ∠的内角平分线,可得结论. 【详解】解:(1)设直线l 的方程为12y x m =+.设()11,A x y ,()22,B x y . 由2214312x y y x m ⎧+=⎪⎪⎨⎪=+⎪⎩得2230x mx m ++-=,则12x x m +=-,2123x x m =-. 由()22430m m =-->△,解得22m -<<. 又∵点31,2P ⎛⎫⎪⎝⎭在直线l 的左上方,∴21m -<<. 若以AB 为直径的圆恰好经过椭圆C 的右焦点2F ,则220AF BF ⋅=u u u u r u u u u r,即()()11221,1,0x y x y --⋅--=,化简得274110m m +-=,解得117m =-,或1m =(舍). ∴直线l 的方程为11127y x =-. (2)∵1212332211PAPBy y kk x x --+=+--12123131222211x m x mx x ----=+-- ()12111111m x x ⎛⎫=+-+ ⎪--⎝⎭()()()1212122111x x m x x x x -+=+--++()222221110132m m m m m m m m +--+=+-=+=++-+-, ∴直线1x =平分APB ∠,即PAB △的内切圆的圆心在定直线1x =上. 【点睛】本题考查直线与椭圆相交问题,考查直线的对称性.直线与椭圆相交问题采取设而不求思想,即设交点坐标为1122(,),(,)x y x y ,设直线方程,代入椭圆方程后应用韦达定理得1212,x x x x +,用1212,x x x x +参与运算求解.20.某企业拟对某条生产线进行技术升级,现有两种方案可供选择:方案A 是报废原有生产线,重建一条新的生产线;方案B 是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:(1)以预期平均年利润的期望值为决策依据,问:该企业应选择哪种方案?(2)记该生产线升级后的产品(以下简称“新产品”)的年产量为x (万件),通过核算,实行方案A 时新产品的年度总成本1y (万元)为32128101603y x x x =-++,实行方案B 时新产品的年度总成本2y (万元)为32213201003y x x x =-++.已知0.2p =,20x ≤.若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价t (元)分别为60,3604x -,60x -,且生产的新产品当年都能卖出去.试问:当x 取何值时,新产品年利润ξ的期望取得最大值?并判断这一年利润能否达到预期目标.【答案】(1)当104p <<时,应选择方程A ;当1143p <≤时应选择方程B ;(2)年产量为10万件的情况下,可以达到甚至超过预期的平均年利润.【解析】(1)根据表格数据计算出两种方案的平均年利润的期望值,比较可得;(2)求出方案A ,按市场销售状态的新产品的年利润ξ的分布列,求出期望值,再用导数的知识求得最大值即可. 【详解】解:(1)∵010210131p p p <<⎧⎪<≤⎨⎪≤-<⎩,解得103p <≤.()14004001200400400200E A p p p p =+--=-, ()1200300900100300200E B p p p p =+--=+,()()104E A E B p >⇒<<; ()()14E A E B p =⇒=;()()1143E A E B p <⇒<≤. ∴当104p <<时,应选择方程A ;当1143p <≤时应选择方程B ;当14p =时,根据(1)的结果,应选择方案A ,所以新产品的年度总成本为32128101603y x x x =-++.(2)设市场行情为畅销、平销和滞销时,新产品的年利润分别为1ξ,2ξ和3ξ, 则1160x y ξ=-,213604x x y ξ⎛⎫=-- ⎪⎝⎭,()3160x x y ξ=--, ∴ξ的分布列为()()11130.4600.4600.2604E x y x x y x x y ξ⎡⎤⎛⎫=⨯-+⨯--+⨯--⎡⎤ ⎪⎢⎥⎣⎦⎝⎭⎣⎦322155016032x x x =-++-.设()322155016032f x E x x x ξ==-++-,020x <≤, ∴()221550f x x x '=-++.()0010f x x '>⇒<<,()01020f x x '<⇒<<.∴()f x 在()0,10上单调递增,在(]10,20上单调递减,∴当10x =时,()f x 取得最大值,即年产量为10万件时,()E ξ取得最大值, 此时()()max 10423.3f x f =≈(万元).由(1)知,预期平均年利润的期望()400200360E A p =-=(万元).因为423.3360>,所以在年产量为10万件的情况下,可以达到甚至超过预期的平均年利润.【点睛】本题考查了概率的性质,考查离散型随机变量的概率分布列和数学期望,用导数求出函数的最大值,考查学生的运算求解能力和实际应用能力.属于中档题型.21.已知函数()sin xf x e x =.(e 是自然对数的底数) (1)求()f x 的单调递减区间;(2)记()()g x f x ax =-,若0<<3a ,试讨论()g x 在()0,π上的零点个数.(参考数据:2 4.8e π≈)【答案】(1)()3π7π2π,2π44k k k Z ⎛⎫++∈ ⎪⎝⎭.(2)见解析 【解析】(1)求出导函数()f x ',解不等式()0f x '<,结合三角函数的性质可得解;(2)求出()(sin cos )x g x e x x a '=+-,令()()hx g x '=,由导数的知识求得()h x 的单调性,然后通过讨论(0),(),()2g g g ππ'''的正负确定()g x 的单调性的极值,确定其零点个数.【详解】解:(1)()sin xf x e x =,定义域为R . ()()πsin cos sin 4x x f x e x x x ⎛⎫'=+=+ ⎪⎝⎭. 由()0f x '<解得πsin 04x ⎛⎫+< ⎪⎝⎭,解得()3π7π2π2π44k x k k Z +<<+∈.(2)由已知()sin x g x e x ax =-,∴()()sin cos x g x e x x a '=+-.令()()h x g x '=,则()2cos xh x e x '=. ∵()0,πx ∈,∴当π0,2x ⎛⎫∈ ⎪⎝⎭时,()0h x '>; 当π,π2x ⎛⎫∈ ⎪⎝⎭时,()0h x '<, ∴()h x 在π0,2⎛⎫ ⎪⎝⎭上单调递增,在π,π2⎛⎫ ⎪⎝⎭上单调递减, 即()g x '在π0,2⎛⎫ ⎪⎝⎭上单调递增,在π,π2⎛⎫ ⎪⎝⎭上单调递减. ∵()01g a '=-,()ππ0g e a '=--<. ①当10a -≥,即01a <≤时,()00g '≥,∴π02g ⎛⎫'> ⎪⎝⎭. ∴0π,π2x ⎛⎫∃∈ ⎪⎝⎭,使得()00g x '=, ∴当()00,x x ∈时,()0g x '>;当()0,πx x ∈时,()0g x '<,∴()g x 在()00,x 上单调递增,在()0,πx 上单调递减.∵()00g =,∴()00g x >.又∵()ππ0g a =-<,∴由零点存在性定理可得,此时()g x 在()0,π上仅有一个零点.②若13a <<时,()010g a '=-<,又∵()g x '在π0,2⎛⎫ ⎪⎝⎭上单调递增,在π,π2⎛⎫ ⎪⎝⎭上单调递减,又π2π02g e a ⎛⎫'=-> ⎪⎝⎭, ∴1π0,2x ⎛⎫∃∈ ⎪⎝⎭,2π,π2x ⎛⎫∈ ⎪⎝⎭,使得()10g x '=,()20g x '=, 且当()10,x x ∈、()2,πx x ∈时,()0g x '<;当()12,x x x ∈时,()0g x '>. ∴()g x 在()10,x 和()2,πx 上单调递减,在()12,x x 上单调递增.∵ππ22ππ3π0222g e a e ⎛⎫=->-> ⎪⎝⎭,∴()20g x >. 又∵()ππ0g a =-<,由零点存在性定理可得,()g x 在()12,x x 和()2,πx 内各有一个零点,即此时()g x 在()0,π上有两个零点.综上所述,当01a <≤时,()g x 在()0,π上仅有一个零点;当13a <<时,()g x 在()0,π上有两个零点.【点睛】本题考查利用导数判断函数的单调性、求极值等问题,考查等人转化思想、分类讨论思想的综合应用,涉及构造函数、多次求导等方法,有一定的综合性,考查学生的分析问题能力和逻辑思维能力,属于难题.22.在直角坐标系xOy ,曲线C 的参数方程为3cos 4sin 129cos sin 55x y ϕϕϕϕ=-⎧⎪⎨=+⎪⎩(ϕ为参数).以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为πsin 3ρθ⎛⎫+= ⎪⎝⎭(1)写出曲线C 的普通方程和直线l 的直角坐标方程;(2)若直线l 与曲线C 交于P ,Q 两点,()2,0M ,求MP MQ +的值. 【答案】(1)221259x y +=0y +-=.(2【解析】(1)由22cos sin 1ϕϕ+=消去参数可得曲线C 的普通方程,由公式cos sin x y ρθρθ=⎧⎨=⎩可得直线l 的直角坐标方程; (2)写出直线l 以M为起点的标准参数方程1222x t y ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),代入曲线C 的普通方程,由利用参数的几何意义,由韦达定理及弦长公式可得弦长.(1)曲线C 的参数方程3cos 4sin 129cos sin 55x y ϕϕϕϕ=-⎧⎪⎨=+⎪⎩消去参数ϕ得, 曲线C 的普通方程为221259x y +=.∵πsin 3ρθ⎛⎫+= ⎪⎝⎭cos sin 0θρθ+-=, ∴直线l0y +-=.(2)设直线l的参数方程为1222x t y ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数), 将其代入曲线C 的直角坐标方程并化简得276630t t --=,∴1267t t +=,129t t =-. ∵M 点在直线l 上, ∴127MP MQ t t +=-===. 【点睛】本题考查参数方程与普通方程的互化,考查极坐标方程与直角坐标方程的互化,考查直线标准参数方程的应用,考查学生的推理能力与计算能力,属于中档题.23.已知不等式135x x m -+-<的解集为3,2n ⎛⎫⎪⎝⎭. (1)求n 的值;(2)若三个正实数a ,b ,c 满足a b c m ++=.证明:2222222b c c a a b a b c +++++≥. 【答案】(1)74n =(2)见解析 【解析】(1)根据不等式的解集与方程根的关系求出m ,然后解绝对值不等式得n . (2)首先利用基本不等式得222222222b c c a a b bc ac ab a b c a b c+++++≥++,通分后,再凑配成()()()2222222222221a b b c b c c a c a a b abc ⎡⎤+++++⎣⎦,再利用基本不等式可得.(1)由题意知,32为方程135x x m -+-=的根, ∴391522m -+-=,解得1m =. 由1351x x -+-<1x <时,1531x x -+-<,54x >,x ∈∅, 513x ≤≤时,1531x x -+-<,32x >,∴3523x <≤, 53x >时,1351x x -+-<,74x <,∴5734x <<, 综上不等式解为3724x <<,∴74n =. (2)由(1)知1a b c ++=, ∴222222222b c c a a b bc ac ab a b c a b c+++++≥++. ()2222222a b b c c a abc=++ ()()()2222222222221a b b c b c c a c a a b abc ⎡⎤=+++++⎣⎦, ()()222122222abc ab c bc a ca b a b c abc abc ≥++=++=, ∴2222222b c c a a b a b c+++++≥成立. 【点睛】本题考查解绝对值不等式,考查不等式的证明.考查推理能力与运算求解能力.证明不等式时应用基本不等式不需要考虑等号成立的条件,即使等号取不到,不等式仍然成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合肥市2020年高三第二次教学质量检测数学试题(理科)(考试时间:120分钟满分:150分)第I 卷(满分60分)一、选择题:本大题共12小题,每小题5分,满分60分在每小题给出的四个选项中,只有一项 是符合题目要求的。
1.若集合2230|2x A x x x B x --≤≥={|},={,则A B =I =A . 1,32⎡⎤⎢⎥⎣⎦B . 1,12⎡⎤⎢⎥⎣⎦C . 13,2⎡⎤-⎢⎥⎣⎦ D .[]2,3 2.欧拉公式i cos sin e θθθ=+把自然对数的底数e ,虚数单位i ,三角函数cos sin θθ和联系在一起,充分体现了数学的和谐美,被誉为“数学的天桥”若复数z 满足i (i)i e z π+=g 则z =A . 1B .2 C .2D3.若实数x ,y 满足约束条件240403230x y x y x y +-≥⎧⎪-+≥⎨⎪+-≥⎩则2z x y -=的最小值是A . 5-B . 4-C . 7D .164.已知f x ()为奇函数,当0x <时,2x f x e ex --()=(e 是自然对数的底数)则曲线y f x =()在1x =处的切线方程是A . y ex e =-+B . y ex e =+C . y ex e =-D .11(2)2y e x e e e=--+ 5.若cos801m o o=,则m = A . 4 B . 2 C . 2- D .4- 6.已知函数tan 002f x x πωϕωϕ()=(+)(>,<<)的图象关于点6π(,0)成中心对称,且与直线y a =的两个相邻交点间的距离为2π,则下列叙述正确的是 A.函数f x ()的最小正周期为π B.函数f x ()图象的对称中心为(0)6k k Z ππ∈+,() C.函数f x ()的图象可由tan 2y x =的图象向左平移6π得到D.函数f x ()的递增区间为,()2326k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭ 7.《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为b 和a 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为a b +,宽为内接正方形的边长d ,由刘构造的图形还可以得到许多重要的结论,如图3.设D 为斜边BC 的中点,作直角三角形ABC 的内接正方形对角线AE ,过点A 作AF BC ⊥于点F ,则下列推理正确的是①由图1和图2面积相等得ab d a b += ②由AE AF ≥2222a b a b ++≥ ③由AD AE ≥222112a b a b+≥+ ④由AD AF ≥可得222a b ab +≥ A . ①②③④ B . ①②④ C . ②③④ D .①③ 8.为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着A ,B ,C 三个农业扶贫项目进驻某村,对该村仅有的甲、乙、丙、丁四个贫困户进行产业帮扶经过前期实际调研得知,这四个贫困户选择A ,B ,C 三个扶贫项目的意向如下表:扶贫项目 AB C 贫困户 甲、乙、丙、丁甲、乙、丙 丙、丁若每个贫困户只能从自己已登记的选择意向项目中随机选取一项,且每个项目至多有两个贫困户选择,则不同的选法种数有A . 24种B . 16种C . 10种D .8种9.几何体是由一个半球挖去一个圆柱形成的,其三视图如图所示已知半球的半径为6,则当此几何体体积最小时,它的表面积等于A . 24πB . (1833π+C . 21πD .(182)π+ 10.已知抛物线C:24y x =的焦点为F ,过点D (3,0)的直线交抛物线C 于点A ,B ,若13FA FB -u u u r u u u r =则FA FB u u u r u u u r g =A . 9-B . 11-C . 12-D .2311.若关于x 的不等式22ln 4ax a x x --->有且只有两个整数解,则实数a 的取值范围是A . (]2ln3,2ln 2--B . (),2ln 2-∞-C . (],2ln3-∞-D .(),2ln3-∞-12.在三棱锥P ABC -中,二面角P AB C P AC B P BC A ------、和的大小均等于3π, ::3:4:5AB AC BC =,设三棱锥P ABC -外接球的球心为O ,直线PO 与平面ABC 交于点Q ,则PO OQ = A . 14B . 2C . 3D .4 第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题、第(23)题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,满分20分.第16题第一空2分,第二空3分.把答案填在答题卡上的相应位置.13.已知向量a b 和满足22,1,a a b a b --=||==则a b =g _________.14.三人制足球(也称为笼式足球)以其独特的魅力,吸引着中国众多的业余足球爱好者,在某次三人制足球传球训练中,A 队有甲、乙、丙三名队员参加。
甲、乙丙三人都等可能地将球传给另外两位队友中的一个人。
若由甲开始发球(记为第一次传球),则第4次传球后,球仍回到甲的概率等于_________.15.已知双曲线C:222210,0x y a b a b-=(>>)的右焦点为点F ,点B 是虚轴的一个端点,点P 为双曲线C 左支上一个动点,若△BPF 周长的最小值等于实轴长的4倍,则双曲线C 的渐近线方程为_____________16.已知△ABC 三个内角A ,B ,C 所对的边分别为,,a b c ,若sin ,sin ,sin A B C 成等比数列, ,sin B A sinA sinC -(),成等差数列,则:(1)C =__________ (2) tan tan A B= 三、解答题:本大题共6小题,满分70分解答应写出文字说明证明过程或演算步骤.17.(本小题满分12分)已知等差数列n a {}的前n 项和为n S ,271,14a S ==,数列n b {}满足221232n nn b b b b +⋯g g =(1)求数列n n a b {}和{}的通项公式;(2)若数列n c {}满足cos n n n c b a π=(),求数列n c {}的前2n 项和2n T .18.(本小题满分12分)如图(1),在矩形ABCD 中,E ,F 在边CD 上,BC CE EF FD ===沿,BE AF 将△CBE 和△DAF 折起,使CBE DAF ABEF 平面和平面都与平面垂直,如图(2)(1)试判断图(2)中直线CD 与AB 的位置关系,并说明理由;(2)求平面ADF 和平面DEF 所成锐角二面角的余弦值19.(本小题满分12分)已知椭圆C 的方程为22143x y +=,斜率为12的直线与椭圆C 交于A ,B 两点,点P 3(1,)2在直线l 的左上方. (1)若以AB 为直径的圆恰好经过椭圆C 的右焦点2F ,求此时直线l 的方程;(2)求证:△PAB 的内切圆的圆心在定直线1x =上.20.(本小题满分12分)某企业拟对某条生产线进行技术升级,现有两种方案可供选择:方案A 是报废原有生产线,重建一条新的生产线;方案B 是对原有生产线进行技术改造,由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:(1)以预期平均年利润的期望值为决策依据,问:该企业应选择哪种方案?(2)记该生产线升级后的产品(以下简称“新产品)的年产量为x (万件),通过核算,实行方案A 时新产品的年度总成本1y (万元)为32118101603y x x x -=++,实行方案B 时新产品的年度总成本2y (万元)为32213201003y x x x -=++.已知0.2,20p x ≤=.若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价t (元)分别为60,360,604x x --,且生产的新产品当年都能卖出去试问:当x 取何值时,新产品年利润的期望取得最大值?并判断这一年利润能否达到预期目标.21.(本小题满分12分)已知函数sin xfx e x ()=(e 是自然对数的底数) (1)求f x ()的单调递减区间(2)记,03g x f x ax a -()=()若<<,试讨论g x ()在(0,)π上的零点个数.(参考数据2 4.8e π≈)请考生在第22、23题中任选一题作答注意:只能做所选定的题目,如果多做,则按所做的第一个题目计分,作答时,请用2B 铅笔在答题卡上,将所选题号对应的方框涂黑.22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 的参数方程为3cos 4sin (129cos sin 55x y ϕϕϕϕϕ=-⎧⎪⎨=+⎪⎩为参数).以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,直线l 的极坐标方程为3in πρθ(+.(1)写出曲线C 的普通方程和直线l 的直角坐标方程;(2)若直线l 与曲线C 交于P ,Q 两点,M (2,0),求MP MQ +的值23.(本小题满分10分)选修4-5:不等式选讲 已知不等式135x x m --+<的解集为3,2n ()(1)求n 的值; (2)若三个正实数,,a b c 满足a b c m ++=,证明:2222222b c c a a b a b c ≥+++++.。
