正比例的意义ppt22页PPT
合集下载
正比例的意义演示文稿PPT教学课件
2020/12/10
6
总价 数量 =单价(一定)
总铅价笔和的数量总是价两和种数相量关成联正的比量例,吗数量? 变为化什,么总价?也随着变化。当总价和对
应数量的比的比值总是一定(也就是 单价一定)时,我们就说铅笔的总价 和数量成正比例,铅笔的总价和数量 是成正比例的量。
2020/12/10
7
y x = k(一定)
数量/枝 1 2 3 4 5 6 ……
总价/元 0.3 0.6 0.9 1.2 1.5 1.8 ……
填写写出上几表组,对说 应说 的总价是 和随数着量哪的个比, 数并量比的较变比化值而 的变 大化 小的 。?
2020/12/10
5
0.3 =0.3
1
0.6 =0.3
2
0.9 =0.3
……
3
这个比值表示的是什么?你能用 式子表示它与总价和数量之间的 关系吗?
同一时间,物体的高度和影长成 正比例吗?为什么?
2020/12/10
10
先分别按2:1、3:1和4:1的 比画出正方形放大后的图形, 再填写下表。
2020/12/10
11
PPT教学课件
谢谢观看
Thank You For Watching
12
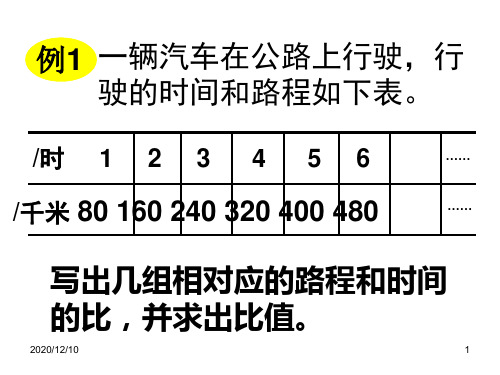
例1 一辆汽车在公路上行驶,行 驶的时间和路程如下表。
/时 1 2 3 4 5 6
……
/千米 80 160 240 320 400 480
……
写出几组相对应的路程和时间 的比,并求出比值。
2020/12/10
1
80 =80
1
160 2 =80
240 3 =80
……
这个比值80表示什么?你能用一 个式子表示这几个量之间的关系吗?
正比例和反比例ppt课件

在直角坐标系中,反比例函数图 像是一个双曲线。
正反比例的性质对照
相同点
两者都涉及到两个量的变化关系,其中一个量变化时,另一个量也相应变化。
不同点
正比例中,比值是一定的;反比例中,比值是不定的。正比例关系是一条直线,而反比例 关系是一个双曲线。
应用场景
正比例关系在物理、化学、工程等领域都有广泛应用,如速度、密度等;反比例关系在电 力、运输、通讯等领域常见,如电流与电阻、运输成本与运输距离等。
02 正比例和反比例的应用
正比例的应用
01
02
03
计算增长率
在统计学中,正比例常用 于计算某一变量的增长率 ,如GDP增长率、人口增 长率等。
猜测模型
在猜测模型中,正比例关 系可用于猜测未来趋势, 例如猜测产品销售量与广 告投入的关系。
线性回归分析
在回归分析中,正比例关 系可用于描写两个变量之 间的线性关系,例如身高 与体重的关系。
在坐标系中,反比例关系表现为一条 双曲线。
当一个量y随着另一个量x的增大而减 小,或者随着x的减小而增大时,我们 说y与x成反比。
正反比例数学表达的异同点
相同点
正比例和反比例都涉及到两个量之间的变化关系,且都存在 一个常数k来描写这种关系。
不同点
正比例是y与x之间的直接关系,而反比例是xy之间的乘积关 系;正比例关系中y随x增大而增大,而反比例关系中y随x增 大而减小或随x减小而增大;正比例在坐标系中表现为直线, 而反比例表现为双曲线。
则它们成反比例。
反比例关系在现实生活中也广泛 存在,如一定质量的物体下,压 力与面积成反比;一定速度下,
距离与时间成反比等。
正反比例的异同点
相同点
正比例和反比例都是描写两个量之间关系的比例关系,都涉及到两个变量的变 化趋势。
正反比例的性质对照
相同点
两者都涉及到两个量的变化关系,其中一个量变化时,另一个量也相应变化。
不同点
正比例中,比值是一定的;反比例中,比值是不定的。正比例关系是一条直线,而反比例 关系是一个双曲线。
应用场景
正比例关系在物理、化学、工程等领域都有广泛应用,如速度、密度等;反比例关系在电 力、运输、通讯等领域常见,如电流与电阻、运输成本与运输距离等。
02 正比例和反比例的应用
正比例的应用
01
02
03
计算增长率
在统计学中,正比例常用 于计算某一变量的增长率 ,如GDP增长率、人口增 长率等。
猜测模型
在猜测模型中,正比例关 系可用于猜测未来趋势, 例如猜测产品销售量与广 告投入的关系。
线性回归分析
在回归分析中,正比例关 系可用于描写两个变量之 间的线性关系,例如身高 与体重的关系。
在坐标系中,反比例关系表现为一条 双曲线。
当一个量y随着另一个量x的增大而减 小,或者随着x的减小而增大时,我们 说y与x成反比。
正反比例数学表达的异同点
相同点
正比例和反比例都涉及到两个量之间的变化关系,且都存在 一个常数k来描写这种关系。
不同点
正比例是y与x之间的直接关系,而反比例是xy之间的乘积关 系;正比例关系中y随x增大而增大,而反比例关系中y随x增 大而减小或随x减小而增大;正比例在坐标系中表现为直线, 而反比例表现为双曲线。
则它们成反比例。
反比例关系在现实生活中也广泛 存在,如一定质量的物体下,压 力与面积成反比;一定速度下,
距离与时间成反比等。
正反比例的异同点
相同点
正比例和反比例都是描写两个量之间关系的比例关系,都涉及到两个变量的变 化趋势。
正比例的意义PPT教学课件

2 、一列火车行驶的时间和所行路程如下表。
时间(时) 1 2 3 4 5 6 7 8 … 路程(千米) 50 100 150 200 250 300 350 400 …
(1).都有两种相关联的量 (2).相对应的两个数的比值(也就是商)
一定
说一说
观察表中的两种量是不是成正比例 的量?
石头.剪子.布游戏的情况
时间(时) 1 2 3 4 5 6 7 8 … 路程(千米) 50 100 150 200 250 300 350 400 …
观察上表,你发现了哪些信息, 你能解决哪些问题?
时间和路程是两种相关联的量
路程
=速度(一定)
时间
看一看
观察这两张表,它们有什么共同点?
1、石头.剪子.布游戏的情况
次数(次) 1 2 3 4 5 6 7 … 分数(分) 5 10 15 20 25 30 35 …
解决生活中的数学问题
现在某体育用品店声称:如果买50只 篮球以下,每只42元;如果买50只篮球以上 (包括50只),每只40元. 请问总价同篮球的 数量是不是成正比例, 如果成 正比例, 那 是 在什么情况?
SARS病毒(冠状病毒)
埃博拉病毒
病毒:
结构简单,无细胞结构,生物体由蛋白质外壳和遗传物质核酸构成。
不同类型AIDS病毒
脊髓灰质炎病毒
噬菌体是寄生在细菌细胞体内的病毒
乙 型 肝 炎 病 毒
烟草花叶病毒
爱 滋 病 病 毒
细菌:
有细胞壁、细胞膜、细胞质和核物质(无成形细胞核)。 有些细胞还有荚膜和鞭毛。
营养方式
寄生:从活的生物体内吸收营养 腐生:分解动植物的遗体而获得营养
荚膜 细胞壁 细胞膜 细胞质 核物质
时间(时) 1 2 3 4 5 6 7 8 … 路程(千米) 50 100 150 200 250 300 350 400 …
(1).都有两种相关联的量 (2).相对应的两个数的比值(也就是商)
一定
说一说
观察表中的两种量是不是成正比例 的量?
石头.剪子.布游戏的情况
时间(时) 1 2 3 4 5 6 7 8 … 路程(千米) 50 100 150 200 250 300 350 400 …
观察上表,你发现了哪些信息, 你能解决哪些问题?
时间和路程是两种相关联的量
路程
=速度(一定)
时间
看一看
观察这两张表,它们有什么共同点?
1、石头.剪子.布游戏的情况
次数(次) 1 2 3 4 5 6 7 … 分数(分) 5 10 15 20 25 30 35 …
解决生活中的数学问题
现在某体育用品店声称:如果买50只 篮球以下,每只42元;如果买50只篮球以上 (包括50只),每只40元. 请问总价同篮球的 数量是不是成正比例, 如果成 正比例, 那 是 在什么情况?
SARS病毒(冠状病毒)
埃博拉病毒
病毒:
结构简单,无细胞结构,生物体由蛋白质外壳和遗传物质核酸构成。
不同类型AIDS病毒
脊髓灰质炎病毒
噬菌体是寄生在细菌细胞体内的病毒
乙 型 肝 炎 病 毒
烟草花叶病毒
爱 滋 病 病 毒
细菌:
有细胞壁、细胞膜、细胞质和核物质(无成形细胞核)。 有些细胞还有荚膜和鞭毛。
营养方式
寄生:从活的生物体内吸收营养 腐生:分解动植物的遗体而获得营养
荚膜 细胞壁 细胞膜 细胞质 核物质
《正比例的意义》课件

3
归纳总结
对正比例的应用进行归纳总结,形成系统化的知 识体系。
THANKS
感谢观看
化学反应速率
在化学反应中,反应物的浓度和 反应速率成正比。
电磁感应
在电磁感应现象中,感应电动势与 磁通量的变化率成正比。
牛顿第二定律
在物理学中,力与加速度成正比, 质量一定时,加速度与力成正比。
03
正比例的性质
比例常数的性质
比例常数恒定
在正比例关系中,比例常数是恒 定的,不随变量的变化而改变。
比例常数的作用
比例常数决定了两个量之间的比 例关系,是正比例关系的核心。
比例常数的意义
比例常数表示两个量之间的相对 大小关系,通过比较比例常数可 以判断两个量之间的正比例关系
。
比例变量的性质
变量同向变化
在正比例关系中,当一个变量增加时,另一个变 量也相应增加,保持相同的方向变化。
变量保持等比
在正比例关系中,两个变量之间的比值是恒定的 ,即等比关系。
函数图像
03
利用函数图像的性质,通过观察图像上的点分布和变化趋势,
证明两个量之间的正比例关系。
通过几何证明正比例
相似三角形
利用相似三角形的性质,通过比较三角形各边的比例,证明两个 量之间的正比例关系。
平行线性质
利用平行线的性质,通过比较线段之间的长度和角度,证明两个 量之间的正比例关系。
坐标系
在坐标系中,通过观察点的坐标变化和分布,证明两个量之间的 正比例关系。
对于确定的物质,密度是 常数,质量和体积成正比 。
数学中的正比例应用
函数关系
在数学中,函数关系可以 表示为y=kx,其中k是常 数,x和y成正比。
正比例和反比例ppt课件

反比例的性质及证明
01 反比例的定义
当两个量的乘积恒定时,称这两个量成反比例。
02 反比例的性质
反比例的两个量具有相反的符号,当一个量增加 时,另一个量会相应减少,且它们的乘积恒定。
03 反比例的证明
可以通过绘制图表或使用代数方法证明两个量之 间的反比例关系。
正比例和反比例的练习题及
05
解析
正比例的练习题及解析
函数
正比例关系是函数关系中的一种,其中自变量和因变量之间的比例常数k称为正比例系数。通过 掌握正比例函数的性质和图像,我们可以更好地理解其他函数的关系和性质。
正比例和反比例在实际问题中的意义
资源分配
在资源分配过程中,正比例关系可以帮助我们更好地规划资 源的分配,确保各项任务能够按照比例完成。例如,在多个 部门协同工作时,通过调整各部门之间的任务分配比例,可 以更好地完成任务。
06
总结与回顾
正比例和反比例的重要性和应用价值
正比例和反比例是数学中重要的概念,对于理解 函数和变量之间的关系以及解实际问题具有重 要意义。
在实际生活中,正比例和反比例关系广泛存在, 如购物时的价格和数量、速度和时间等。掌握正 比例和反比例的概念和应用有助于解决日常生活 中的问题。
正比例和反比例的异同点及注意事项
02 正比例中,当一个量增加时,另一个量也增加; 而在反比例中,当一个量增加时,另一个量减少 。
02 正比例和反比例可以相互转化,比如时间和距离 的关系就是典型的正比例关系,但如果考虑速度 恒定的情况下,时间和距离就成反比例关系。
02
正比例和反比例的应用
在生产生活中的实际应用
生产计划
在生产过程中,企业需要制定生产计划,根据产品的需 求量和库存量来确定每日的生产量。正比例关系可以帮 助企业更好地规划生产,避免库存积压或缺货现象。
正比例的意义正比例和反比例PPT课件

时间
答:生产零件的数量和时间成正比例,因为它们的比值是一定的。
做同一种服装, 做的套数和用布的米数如下表:
服装数量/套 1
2
3
4
5
…
用数量/米 2.2
4.4 6.6
8.8
11
…
做的套数和用布的米数成正比例吗?为什么?
做的套数和用布的米数成正比例吗?为什么?
4.4 << 2.2 2
6.6 << 2.2 3
(2)写出几组相对应的总价和数量的比,并比较比值的大小。
0.4 << 0.4 1
1.6 << 0.4 4
0.8 << 0.4 2 2 << 0.4 5
1.2 << 0.4 3
2.4 << 0.4 6
…… 比值相等
购买一种铅笔的数量和总价如下表:
数量/支 1
2
3
4
5
总价/元 0.4
0.8
1.2
1.6
时间/时 1
2
3
4
5
6
7
……
路程/千米 80
160
240
320
400
480
560
80÷1 = 80 160÷2= 80 ……行驶的速度不变。
观察表中的数据,你有什么发现?
你能写出几组相对应的路程和时间的比,并求出比值吗?
80 << 80 1
160 << 80 2
240 << 80 3
320 << 80 4
8.8 << 2.2 4
11 << 2.2 5
答:生产零件的数量和时间成正比例,因为它们的比值是一定的。
做同一种服装, 做的套数和用布的米数如下表:
服装数量/套 1
2
3
4
5
…
用数量/米 2.2
4.4 6.6
8.8
11
…
做的套数和用布的米数成正比例吗?为什么?
做的套数和用布的米数成正比例吗?为什么?
4.4 << 2.2 2
6.6 << 2.2 3
(2)写出几组相对应的总价和数量的比,并比较比值的大小。
0.4 << 0.4 1
1.6 << 0.4 4
0.8 << 0.4 2 2 << 0.4 5
1.2 << 0.4 3
2.4 << 0.4 6
…… 比值相等
购买一种铅笔的数量和总价如下表:
数量/支 1
2
3
4
5
总价/元 0.4
0.8
1.2
1.6
时间/时 1
2
3
4
5
6
7
……
路程/千米 80
160
240
320
400
480
560
80÷1 = 80 160÷2= 80 ……行驶的速度不变。
观察表中的数据,你有什么发现?
你能写出几组相对应的路程和时间的比,并求出比值吗?
80 << 80 1
160 << 80 2
240 << 80 3
320 << 80 4
8.8 << 2.2 4
11 << 2.2 5
《正比例的意义》课件

正比例关系与反比例关系的应用场景比较
单击添加标题
正比例关系:在物理、化 学、生物等学科中,当两 个变量之间的关系是正比 例时,可以用正比例关系 来描述。例如,在物理学 中,物体的速度与位移之 间的关系是正比例关系。
单击添加标题
反比例关系:在物理、化 学、生物等学科中,当两 个变量之间的关系是反比 例时,可以用反比例关系 来描述。例如,在物理学 中,物体的加速度与位移 之间的关系是反比例关系。
例关系。
正比例关系与反比例关系的数学表达形式的比较
正比例关系:y=kx, 其中k为常数
反比例关系:y=k/x, 其中k为常数
正比例关系:y随x的 增大而增大,y随x的 减小而减小
反比例关系:y随x的 增大而减小,y随x的 减小而增大
正比例关系:y与x的 比值保持不变
反比例关系:y与x的 乘积保持不变
两个变量之间的关系是正比例关系,当其中一个变量不变时,另一个变量 也不变,反之亦然。
两个变量之间的关系是正比例关系,当其中一个变量变化时,另一个变量 也变化,反之亦然。
判定条件的运用
确定两个变量之 间的关系
观察两个变量是 否同时增加或减 少
计算两个变量的 比值是否恒定
判断两个变量之 间的关系是否符 合正比例关系
单击添加标题
正比例关系与反比例关系 的应用场景比较:在现实 生活中,正比例关系和反 比例关系都有广泛的应用。 例如,在商业活动中,销 售额与成本之间的关系是 正比例关系,而利润与成 本之间的关系是反比例关
系。
单击添加标题
正比例关系与反比例关系 的应用场景比较:在科学 研究中,正比例关系和反 比例关系也有广泛的应用。 例如,在生物学中,生物 体的生长速度与营养物质 之间的关系是正比例关系, 而生物体的生长速度与环 境温度之间的关系是反比
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总价 数量 =单价(一定)
0.3 =0.3
1
0.6 =0.3
2
0.9 =0.3
3
1.2 =0.3
4
……这个比值0.3表示什么?(单价)
你能用式子表示它与总价和数量之 间的关系吗?
铅笔的总价和数量成正比 例吗?为什么?
总价 数量 =单价(一定)
① 总价和数量是 两种相关联的量 ,
②数量变化,总价也随着变化。
=速度 (一定)
时间
…810…=8这0 个126比0值=8800表2示340什=么80?(3速420度=)80
你能用一个式子表示这几个量 之间的关系吗?
路程 时间
=速度(一定)
① 路程和时间是两种相关联的量 ,
② 时间变化,路程也随着变化。
③ 当路程和对应时间的比的比值总是 一定(也就是速度一定)时,我们就说 行驶的路程和时间成正比例,行驶的路 程和时间是 成正比例的量 。
正比例的意义
购买一种铅笔的数量和总价如 下表。
数量/枝 1 2 3 4 5 6 ……
总价/元 0.3 0.6 0.9 1.2 1.5 1.8 ……
填写写出上几表组,对说应说的总总价价是和随数着量哪的个比, 数并量比的较变比化值而的变大化小的。?
数量/枝 1 2 3 4 5 6 ……
总价/元 0.3 0.6 0.91.2 1.5 1.8 ……
25 =25
50 =25
100 =25
……
1
2
4
数量 因为:时间 =生产效率(一定)
所以:数量和时间成正比例。
0.6 :1=0.6 1.2 :2=0.6 1.8 :3=0.6
对应数量和时间的比值相等。
(工作效率)
因为:碾米数量
工作时间
=工作效率(一定)
所以:碾米数量和工作时间 成正比例。
下面是同一时间测得的不同物 体的高度和它的影长。
5 3
00.4.88=
5 3
……
因为:物体高度 影长
=
5 3 (一定)
所以:物体高度和影长成正比例。
时间一定,路程和速度 速度一定,路程和时间 总价一定,数量和单价 小方的身高和他的年龄 长方形的长一定,宽和面积
先分别按2∶1,3∶1和4∶1的 比画出正方形放大后的图形,再填 写下表。
正方形边长/cm 1 2 3 4 正方形周长/cm 4 8 12 16 正方形面积/cm 2 1 4 9 16
y x = k(一定)
▲正比例关系两种相关联的量的变化规律: 两种量同时扩大,同时缩小,比值不变。
张师傅生产零件的情况如下表。
时间/时 1 2 4 6 8 数量/个 25 50 100 150 200
生产零件的数量和时间成正 比例吗?为什么?
时间/时 1 2 4 6 8 数量/个 25 50 100 150 200
一辆汽车在公路上行驶,行驶的 时间和路程如下表。
时间/时 1 2 3 4 5 6 ……
路程/千米 80 160 240 320 400 480 ……
※写出几组相对应的路程和时间的 比,并求出比值。
时间/时 1 2 3 4 5 6 ……
路程/千米 80 160 240 320 400 480 ……
路程
(2)正方形的面积与边长成正比 吗?为什么?
1 :1=1 4 :2=2 9:3=3 16:4=4
因为:面积
边长
=边长(不一定)
所以:正方形面积和边长不成正比例。
物体高度/m 0.8 1 1.25 1.6 2.5 影 长/m 0.48 0.6 0.75 0.96 1.5
同一时间,物体的高度和影长成 正比例吗?为什么?
物体高度/m 0.8 1 1.25 1.6 2.5 影 长/m 0.48 0.6 0.75 0.96 1.5
0.8 0.48
=
5 3
00.4.88=
正方形边长/cm 1 2 3 4
正方形周长/cm 4 8 12 16
正方形面积/ cm ห้องสมุดไป่ตู้ 1 4 9 16
(1)正方形的周长与边长成正比 吗?为什么?
因为:周长 边长
=4(一定)
所以:正方形周长和边长成正比例。
正方形边长/cm 1 2 3 4
正方形周长/cm 4 8 12 16
正方形面积/ cm 2 1 4 9 16
③当总价和对应数量的比的比值总 是一定(也就是单价一定)时,我们 就说铅笔的总价和数量成正比例,铅 笔的总价和数量是成正比例的量。
两种相关联的量,一种量变化,另一种量
也随着变化,如果这两种量相对应的两个数 的比值(也就是商)一定,这两种量就叫做 成正比例的量,它们的关系叫做成正比例关 系。
如果用字母y和x表示两种相关联的量, 用k表示它们的比值(一定),正比例关 系可以用以下关系式表示:
