梯形面积公式推导_图文

合集下载

梯形面积推导过程

梯形面积推导过程
梯形面积公式推导过程：
1.用平行四边形推导梯形面积的方法：先将两个相等的梯形拼成一个平行四边形，设梯形上底长为a，下底长为b。

2。

则平行四边形的底长为高设为h，先算出平行四边形的面积为：底*高=（a+b）*h。

3。

然后其中一个梯形面积的则是平行四边形的一半，所以要除以2，即梯形面积公式为：（a+b）*h÷2。

4。

先连接梯形中任意一条对角线，梯形则分为两个等高的三角形。

5。

设上底为a，下底为b，高为h。

6。

其中三角形面积为：底*高÷2，则以下三角形面积分别为：a*h÷2，b*h÷2。

7。

则梯形的面积就等于两等高三角形的面积相加，其梯形面
积公式为：a*h÷2+b*h÷2=（a+b）*h÷2。

梯形面积公式的推导演示

两个完全一样的梯形拼成一个平行四边形
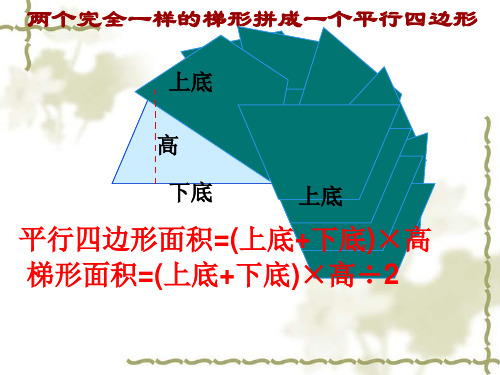
上底高下底上底
平行四边形面积=(上底+下底)×高梯形面积=(上底+下底)×高÷2
上底高
因为：大三角形的面积 =（上底+下底）×高÷2 所以：梯形的面积
下底
上底 =（上底+下底）×高÷2
把一个梯形分割成两个三角形
上底
高
下底
绿三角形面积=下底×高÷2 红三角形面积=上底×高÷2 梯形面积=绿三角形面积+红三角形面积 =下底×高÷2 +上底×高÷2 =(上底+下底)×高÷2

把一个梯形转化成一个平行四边形
因为：平行四边形的面积 =（上底+下底)×高÷2 所以：梯形的面积=（上底+下底)×高÷2
梯形的面积公式梯形的面积 = (上底＋下底)×高÷2 如果用字母s表示梯形的面积，a、b、h 分别表示梯形的上底、下底和高，哪用字母怎样表示梯形的面积公式呢？
S=(a＋b) h÷2

梯形公式推导过程

梯形公式推导过程梯形公式是计算梯形面积的常用公式，它的推导过程相对简单，我们来一起了解一下。

我们需要明确梯形的定义。

梯形是一个四边形，其中两边是平行的，另外两边不平行。

我们假设梯形的上底为a，下底为b，高为h。

接下来，我们来推导梯形的面积公式。

根据梯形的定义，我们可以将梯形分成一个矩形和两个直角三角形。

如图所示，其中矩形的长为b，宽为h，两个直角三角形的底分别为a和b，高都为h。

根据矩形的面积公式，矩形的面积可以表示为S1 = b * h。

而两个直角三角形的面积分别为S2 = 0.5 * a * h 和 S3 = 0.5 * b * h。

那么，整个梯形的面积可以表示为S = S1 + S2 + S3 = b * h + 0.5 * a * h + 0.5 * b * h。

我们可以对公式进行合并和化简，得到梯形面积公式：S = 0.5 * (a + b) * h。

至此，我们成功推导出梯形的面积公式。

需要注意的是，梯形公式适用于所有的梯形，无论上底和下底的长度如何。

同时，梯形的高也可以是负数或零，但这在实际应用中并不常见。

梯形面积公式的推导过程相对简单，但是应用范围非常广泛。

无论是在日常生活中还是在工程设计中，我们都可以通过梯形公式来计算梯形的面积，为实际问题提供解决方案。

因此，熟练掌握梯形公式是非常重要的。

除了梯形面积公式，我们还可以通过梯形的边长和角度等信息来计算其他属性，如梯形的周长、对角线的长度等。

这些计算方法在实际应用中也非常常见。

梯形公式是计算梯形面积的重要工具，它的推导过程简单明了。

通过理解和掌握梯形公式，我们可以更好地解决与梯形相关的实际问题。

希望通过本文的介绍，读者们对梯形公式的推导过程有了更深入的了解和理解。

梯形面积公式的四种推导方法

梯形面积公式的四种推导方法一、引言梯形是一个只有两对平行边的四边形，其中上底和下底是平行的，而两腰不平行。

梯形的面积公式为（上底+下底）*高/2。

本篇文档将详细介绍如何通过不同的方式推导出这个公式。

二、平行线分割法首先，我们可以将梯形分割成两个三角形。

假设上底长为a，下底长为b，高为h，那么这两个三角形的面积分别为1/2ah和1/2bh。

因此，梯形的总面积就是这两个三角形的面积之和，即1/2ah + 1/2bh = (1/2)(a+b)h，这就是梯形面积公式。

三、矩形与三角形组合法另一种方法是将梯形视为一个矩形和两个等高的三角形的组合。

假设矩形的宽为(a-b)/2，那么矩形的面积就是((a-b)/2)*h。

另外两个等高的三角形的面积分别为1/2ah和1/2bh。

所以，梯形的总面积就是这三个图形的面积之和，即((a-b)/2)*h + 1/2ah + 1/2bh = (1/2)(a+b)h。

四、割补法第三种方法是利用割补法。

我们可以在梯形中画一条平行于上底和下底的线，将其分割成一个矩形和两个等高的三角形。

假设这条线离上底的距离为x，则矩形的宽为x，面积为xh；两个等高的三角形的面积分别为1/2( a-x)h 和1/2(b-x)h。

所以，梯形的总面积就是这三个图形的面积之和，即xh + 1/2( a-x)h + 1/2(b-x)h = (1/2)(a+b)h。

五、相似三角形法最后一种方法是利用相似三角形的性质。

我们可以发现，梯形中的任意一个小三角形都与整个梯形是相似的。

因此，它们的面积比等于对应的边长的平方比。

设小三角形的面积为S，那么有S/h^2=(a+b)/2h。

解得S=1/2(a+b)h，这就是梯形的面积。

六、结论以上就是推导梯形面积公式的四种方法，分别是平行线分割法、矩形与三角形组合法、割补法以及相似三角形法。

每种方法都有其独特的思路和应用场景，希望读者能从中受益，更深入地理解和掌握梯形面积的计算方法。

梯形面积公式的推导方法

梯形面积公式的推导方法
梯形的面积公式可用以下四种方法进行推导。

推导一：甲、乙两个梯形全等，且上底为a,下底为b,高为h。

将这两个梯形拼接成一个平行四边形，则平行四边形的一条底边长为a+b,此底边上的高与梯形的高h相等，那么一个梯形的面积是平行四边形面积的一半。

(参见图一)
梯形的面积=(a+b) h* 2=1/2 (a+b) h
推导二：一个梯形上底为a,下底为b,高为h。

在梯形内连接一组对角的顶点作一虚线，将三角形沿中点旋转，拼成一个大三角形。

(参见图二)则有：
梯形的面积=(b+a) h* 2=1/2 (a+b) h
推导三：一个梯形上底为a,下底为b,高为h。

在梯形内连接顶点到一腰中点作一虚线，将梯形分为两个等高不同底的三角形。

(参见图三)则有：
第一个三角形的面积=1/2ah
第二个三角形的面积=1/2bh
梯形的面积=1/2ah+1/2bh=1/2 (a+b) h
推导四：一个梯形上底为a,下底为b,高为h。

在梯形内作一虚线，将梯形分为一个平行四边形和一个三角形。

(参见图四)则有：
平行四边形的面积=ah 三角形的面积=(b—a) h* 2=1/2bh —1/2ah
梯形的面积=ah+1/2bh —1/2ah=1/2ah+1/2bh=1/2 (a+b) h。

梯形面积计算公式的推导

高 ÷2
梯形面积公式的推导过程：
上底高下底－上底
一个梯形的面积=平行四边形的面积＋三角形的面积
底×高
＋
底×高÷2
上底×高＋（下底－上底）× 高 ÷ 2 所以：梯形的面积=（上底+下底）×
高 ÷2
梯形面积公式的推导过程：
梯形面积公式的推导过程：
梯形面积公式的推导过程：
高下底上底
一个梯形的面积=三角形的面积底×高÷2 （上底+下底）所以：梯形的面积=（上底+下底）×
S ＝ (a ＋ b ) h÷2
小试牛刀一个梯形的上底是 2cm，下底是5cm，高是3cm．求这个梯形的面积．
我是小法官：
梯形的面积是平行四边形的面积的一半。
梯形的面积是底与它上下底的和相等，高又相等的平行四边形面积的一半。
我是小法官：
S＝(a+b)h
梯形的面积公式用字母表示是
梯形的面积公式用字母表示是
观察下面的梯形，你发现了什么？
3cm 3cm 3cm
6cm
6cm
6cm
通过观察，我发现了上面三个梯形都是等底等高的，所以它们的面积也是一样的。
课堂小结
1、这节课我们学会了（） 2、这节课我们学到了（）

S＝(a+b)h÷2
我是小法官：
两个梯形的高相等，它们的面积就相等。
我是小法官：
两个面积相等的梯形可以拼成一个平行四边形。
两个完全一样的梯形可以拼成一个平行四边形。
求这个梯形的面积。
6m 5.8 m 3.6 m
一条新挖的渠道，横截面是梯形，渠口宽3.2 米，渠底宽1.8米，渠 3.2米深1.5米， 1.5米横截面的面积是多少平方米？ 1.8米

梯形的推导公式

梯形的推导公式
梯形是一个四边形，其中两边平行，而另外两边不平行。

推导梯形的面积公式可以通过将梯形划分为矩形和三角形来完成。

设梯形的上底长为a，下底长为b，高为h。

1.将梯形划分为上下两个矩形：
上矩形的面积为：a × h
下矩形的面积为：b × h
2.将梯形划分为一个矩形和两个相等的三角形：
矩形的面积为：(a + b) × h
两个三角形的面积之和为：(1/2) × a × h + (1/2) × b × h = (a + b) × (h/2)
由上述推导可知，梯形的面积公式为：
面积 = 上矩形的面积 + 下矩形的面积
= 矩形的面积 + 两个三角形的面积之和
= (a + b) × h/2
因此，梯形的面积公式为：面积 = (上底 + 下底) ×
高/2，其中上底为a，下底为b，高为h。

梯形面积计算公式的推导

梯形面积公式的推导过程：
梯形面积公式的推导过程：
旋转
梯形面积公式的推导过程：
梯形面积公式的推导过程：
梯形面积公式的推导过程：
梯形面积公式的推导过程：
平移
梯形面积公式的推导过程：
梯形面积公式的推导过程：
噢！两个完全相同的梯形拼成了一个平行
四边形。
一个梯形的面积与拼成的平行四边形的面积有什么关系
梯形的面积是底与它上下底的和相等，高又相等的平行四边形面积是
S＝(a+b)h
梯形的面积公式用字母表示是
S＝(a+b)h÷2
我是小法官：
两个梯形的高相等，它们的面积就相等。
我是小法官：
两个面积相等梯形可以拼成一个平行四边形。
两个完全一样的梯形可以拼成一个平行四边形。
梯形面积公式的推导过程：
高高下底上底
一个梯形的面积=所拼成的平行四边形的面积÷2 底
×
高
（上底+下底） × 梯形的高所以：梯形的面积=（上底+下底）×
高 ÷2
梯形面积公式的推导过程：
高
上底
B A 高
下底一个梯形的面积=三角形A的面积＋三角形B的面积
底×高÷2 下底×高÷2
＋
底×高÷2
高 ÷2
梯形的面积公式是：
梯形的面积=（上底+下底）× 高 ÷ 2
如果用S表示梯形的面积，用a、b和h分别表示梯形的上底、下底和高，那么梯形的面积公式是：
S ＝ (a ＋ b ) h÷2
一个梯形的上底是 2cm，下底是5cm，高是3cm．求这个梯形的面积．
我是小法官：
梯形的面积是平行四边形的面积的一半。

计算梯形面积的公式

计算梯形面积的公式梯形是一种特殊的四边形，它有两个平行的底边和两条不平行的侧边。

计算梯形的面积可以使用以下公式：面积 = (上底 + 下底) × 高÷ 2其中，上底和下底分别指梯形的两个平行底边的长度，高指梯形两个底边之间的垂直距离。

梯形面积公式的推导过程如下：假设梯形的上底为a，下底为b，高为h。

我们可以将梯形划分为两个三角形和一个矩形。

我们计算矩形的面积，即底边的平均长度乘以高，得到矩形的面积为ab×h。

然后，我们计算两个三角形的面积。

每个三角形的面积都可以表示为底边乘以高再除以2，即ah/2和bh/2。

将矩形和两个三角形的面积相加，得到梯形的总面积为(ab×h) + (ah/2) + (bh/2)。

化简上述表达式，得到梯形的总面积为(ab+ah+bh)/2，进一步化简为(a+b)×h/2。

根据以上推导，我们可以得出梯形面积的公式为(上底 + 下底) × 高÷ 2。

下面我们通过一个例子来演示如何使用梯形面积的公式进行计算。

假设某个梯形的上底长度为5 cm，下底长度为10 cm，高为8 cm。

我们可以根据公式进行计算：面积= (5 + 10) × 8 ÷ 2= 15 × 8 ÷ 2= 120 ÷ 2= 60 平方厘米因此，该梯形的面积为60平方厘米。

通过以上例子，我们可以看到使用梯形面积的公式可以快速准确地计算梯形的面积。

只需要知道梯形的上底、下底和高，就可以使用这个公式进行计算。

需要注意的是，公式中的长度单位要保持一致。

在计算过程中，如果是以厘米为单位，那么计算结果也应该以平方厘米为单位。

除了使用公式计算梯形面积，还可以通过将梯形分解为两个三角形和一个矩形来计算。

这种方法也能得出相同的结果，但相对来说计算过程稍微复杂一些。

总结起来，计算梯形面积的公式是(上底 + 下底) × 高÷ 2。

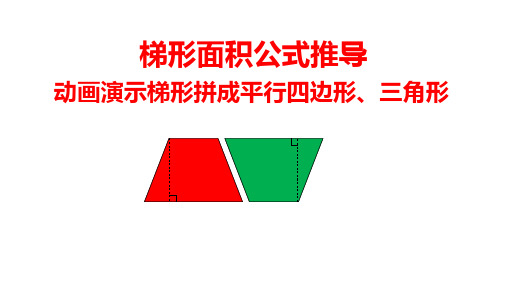
梯形面积公式推导：动画演示梯形转化成平行四边形、三角形

13 ㎝ 25 ㎝ 27 ㎝
课堂练习
1.算出下面每个梯形的面积。（单位：厘米）
5
10
20
8
8
11
12
10
8
S=(a＋b) ×h÷2 S=(a＋b) ×h÷2 S=(a＋b)×h÷2
=(5＋10) ×8÷2 =(8＋12) ×10÷2 =(8＋20) ×11÷2
=60
=100
=154
梯形的面积是平行四边形的面积的一半。
选择题
（（1）梯形的上底是4米，下底是6米，高是5米，它的面积
是（ B ）。
A. A. 45平方米 B. 25平方米 C. 25米
( 2 ) （2）一个梯形上底是80厘米,下底是12分米。高是5分米
，它的面积是（ A ）平方分米。
A A 50
B. 25
C. 230
一个梯形的上底是9厘米，比下底短 3 厘米，高是10厘米，它的面积是多少平方厘米？
b=9 + 3 = 12（厘米） S=(a＋b) ×h÷2
=（9+12）×10÷2 = 21 ×10÷2 = 105
答：梯形的面积是105平方厘米。
全课总结
1、今天课堂上我们学梯形面积公式的推导。 2、梯形的面积公式中为什么要除以2 ？
梯形面积公式推导ቤተ መጻሕፍቲ ባይዱ
动画演示梯形拼成平行四边形、三角形
自主学习：
你能仿照求三角形面积的办法，运用转化法把梯形转化成已学过的图形（平行四边形、三角形等），然后推导出梯形的面积公式吗？
上底
下底
下底
上底
上底
下底
下底
上底
想一想：
１、拼成的图形与原梯形的面积有什么关系？ 2、拼成图形的底与梯形的上底、下底有什么关系？ 3、拼成图形的高与梯形的高有什么关系？

出入相补原理推导梯形面积

出入相补原理推导梯形面积
我们要使用出入相补原理来推导梯形的面积。

首先，我们需要理解什么是出入相补原理。

出入相补原理是一个几何学原理，它告诉我们：一个平面图形可以被切割成若干小的部分，然后重新组合成另一个形状，其面积保持不变。

假设我们有一个梯形，其上底为a，下底为b，高为h。

首先，我们可以将这个梯形切割成两个三角形，一个三角形的底是a，另一个三角形的底是b。

然后，我们可以将这两个三角形重新组合成一个矩形。

这个矩形的长是(a+b)，宽是h。

根据出入相补原理，这个矩形的面积等于原始梯形的面积。

矩形的面积=长×宽=(a+b)×h
所以，梯形的面积=(a+b)×h
通过出入相补原理，我们成功推导出了梯形的面积公式：(a+b)×h。