经典:梯形面积计算公式的推导
梯形的面积推导公式

梯形的面积推导公式有多种,以下是其中四种:
1. 梯形面积公式推导一:
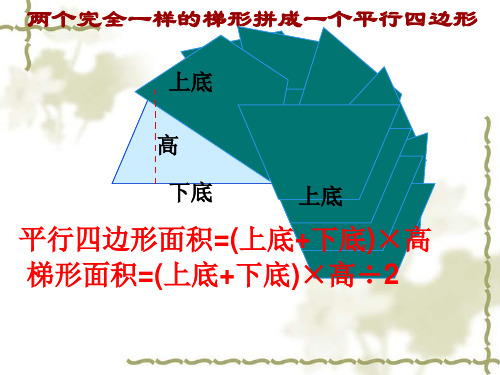
两个完全相同的梯形可以拼成一个平行四边形,这个平行四边形的底等于梯形的上底与下底的和,高等于梯形的高。
因为平行四边形的面积等于底×高,所以梯形的面积等于上底与下底和的一半乘以高,即(上底+下底)×高÷2。
2. 梯形面积公式推导二:
将梯形对角线右半部分顺次连接,可以将梯形分成两个三角形,其中一个是小三角形,另一个是大三角形的面积是小三角形的两倍。
因此,梯形的面积等于两个三角形的面积的和,即(上底+下底)×高÷2=1/2(上底+下底)×高+1/2(上底+下底)×高。
3. 梯形面积公式推导三:
在梯形内连接顶点到一腰中点的线段,将梯形分为两个等高不同底的三角形。
根据等高三角形的面积比等于底边的比,可以得出梯形的面积等于两个三角形的面积的和,即(上底+下底)×高÷2=1/2(上底+下底)×高+1/2(上底+下底)×高。
4. 梯形面积公式推导四:
在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。
根据
平行四边形和三角形的面积公式,可以得出梯形的面积等于平行四边形的面积和三角形的面积的和,即(上底+下底)×高÷2=1/2(上底+下底)×高+1/2(上底+下底)×高-1/2上底×高。
梯形面积公式的推导演示
上底 高 下底 上底
平行四边形面积=(上底+下底)×高 梯形面积=(上底+下底)×高÷2
上底 高
因为:大三角形的面积 =(上底+下底)×高÷2 所以:梯形的面积
下底
上底 =(上底+下底)×高÷2
把一个梯形分割成两个三角形
上底
高
下底
绿三角形面积=下底×高÷2 红三角形面积=上底×高÷2 梯形面积=绿三角形面积+红三角形面积 =下底×高÷2 +上底×高÷2 =(上底+下底)×高÷2
把一个梯形转化成一个平行四边形
因为:平行四边形的面积 =(上底+下底)×高÷2 所以:梯形的面积=(上底+下底)×高÷2
梯形的面积公式 梯形的面积 = (上底+下底)×高÷2 如果用字母s表示梯形的面积,a、b、h 分别表示梯形的上底、下底和 高,哪用 字母怎样表示梯形的面积公式呢?
S=(a+b) h÷2
梯形公式推导过程

梯形公式推导过程梯形公式是计算梯形面积的常用公式,它的推导过程相对简单,我们来一起了解一下。
我们需要明确梯形的定义。
梯形是一个四边形,其中两边是平行的,另外两边不平行。
我们假设梯形的上底为a,下底为b,高为h。
接下来,我们来推导梯形的面积公式。
根据梯形的定义,我们可以将梯形分成一个矩形和两个直角三角形。
如图所示,其中矩形的长为b,宽为h,两个直角三角形的底分别为a和b,高都为h。
根据矩形的面积公式,矩形的面积可以表示为S1 = b * h。
而两个直角三角形的面积分别为S2 = 0.5 * a * h 和 S3 = 0.5 * b * h。
那么,整个梯形的面积可以表示为S = S1 + S2 + S3 = b * h + 0.5 * a * h + 0.5 * b * h。
我们可以对公式进行合并和化简,得到梯形面积公式:S = 0.5 * (a + b) * h。
至此,我们成功推导出梯形的面积公式。
需要注意的是,梯形公式适用于所有的梯形,无论上底和下底的长度如何。
同时,梯形的高也可以是负数或零,但这在实际应用中并不常见。
梯形面积公式的推导过程相对简单,但是应用范围非常广泛。
无论是在日常生活中还是在工程设计中,我们都可以通过梯形公式来计算梯形的面积,为实际问题提供解决方案。
因此,熟练掌握梯形公式是非常重要的。
除了梯形面积公式,我们还可以通过梯形的边长和角度等信息来计算其他属性,如梯形的周长、对角线的长度等。
这些计算方法在实际应用中也非常常见。
梯形公式是计算梯形面积的重要工具,它的推导过程简单明了。
通过理解和掌握梯形公式,我们可以更好地解决与梯形相关的实际问题。
希望通过本文的介绍,读者们对梯形公式的推导过程有了更深入的了解和理解。
梯形面积公式四种推导方法

梯形面积公式四种推导方法梯形是一个四边形,它的两边是平行线段,而另外两边分别连接这两条平行线段的两个非相邻顶点。
梯形的面积可以通过四种不同的方法推导出来。
方法一:使用高和底边长度推导梯形面积设梯形的上底长为a,下底长为b,高为h。
可以将梯形分为两个三角形和一个矩形。
矩形的面积为a×h,两个三角形的面积之和为1/2×a×h+1/2×b×h=1/2×(a+b)×h。
将矩形的面积与两个三角形的面积相加,得到整个梯形的面积为(a+b)×h。
方法二:使用对角线和非平行边的长度推导梯形面积设梯形的对角线之和为d,非平行边的长度分别为a和b,其中a > b。
可以将梯形分为两个直角三角形和一个矩形。
两个直角三角形的面积之和为1/2×a×b + 1/2×(a-b)×b = 1/2×(a+b)×b,矩形的面积为a×(d-b)。
将两个直角三角形的面积与矩形的面积相加,得到整个梯形的面积为(a+b)×b + a×(d-b) = (a+b)×b + ad - ab = ab + bd - ab + ad = ad + bd。
方法三:使用两个非平行边和夹角的正弦推导梯形面积设梯形的两个非平行边的长度为a和b,夹角为θ。
可以将梯形分为两个直角三角形和一个矩形。
两个直角三角形的面积之和为1/2×a×b×sinθ + 1/2×(a+b)×h = 1/2×(a+b)×h,其中h为夹角θ的高。
矩形的面积为b×h。
将两个直角三角形的面积与矩形的面积相加,得到整个梯形的面积为1/2×(a+b)×h + b×h = 1/2×(a+b)×h + 1/2×(a+b)×h = (a+b)×h。
梯形面积计算公式的推导大全

梯形面积计算公式的推导大全梯形是一种具有两个平行底边的四边形。
梯形的面积计算公式可以通过各种方法推导得出。
接下来,我们将详细介绍三种方法来推导梯形的面积计算公式。
方法一:基于平行线的性质推导梯形面积计算公式首先,考虑一个梯形,假设两个底边的长度分别为a和b,高为h。
将梯形划分为一个小矩形和两个直角三角形。
根据平行线的性质可知,梯形的两个底边所在的直线是平行的。
因此,我们可以将梯形的高线延长,使其与另一条底边相交。
这样,我们得到了一个矩形和两个全等的直角三角形。
根据矩形的面积公式可知,矩形的面积等于底边b的长度乘以高h。
而两个直角三角形的面积可以通过直角三角形的面积公式得到,即面积等于底边a乘以高h的一半。
因此,整个梯形的面积等于矩形的面积加上两个直角三角形的面积,即:梯形的面积=矩形的面积+两个直角三角形的面积= bh + (ah)/2=(a+b)h/2这就是基于平行线的性质推导得到的梯形面积计算公式。
方法二:基于梯形的剖分推导梯形面积计算公式考虑一个梯形,两个底边的长度分别为a和b,高为h。
将梯形剖分为两个全等的直角三角形和一个矩形。
如前一方法所述,直角三角形的面积等于底边乘以高的一半。
由于直角三角形是全等的,所以两个直角三角形的面积之和等于一个直角三角形面积的两倍,即2(ah)/2 = ah。
而矩形的面积等于底边b的长度乘以高h。
因此,整个梯形的面积等于两个直角三角形的面积加上矩形的面积,即:梯形的面积=两个直角三角形的面积+矩形的面积= ah + bh=(a+b)h同样得到了基于梯形的剖分推导得到的梯形面积计算公式。
方法三:基于面积相等的概念推导梯形面积计算公式考虑一个梯形,两个底边的长度分别为a和b,高为h。
我们将梯形与一个等底等高的平行四边形放在一起。
根据面积相等的概念可知,梯形和平行四边形的面积相等。
平行四边形的面积可以通过底边a和高h的乘积得到,即平行四边形的面积为 ah。
而梯形的底边长度为a,高为h,因此梯形的面积等于平行四边形的面积减去两个直角三角形的面积。
推导梯形面积公式的三种方法

推导梯形面积公式的三种方法推导梯形面积公式的三种方法如下:
方法一:几何推导
考虑一个梯形,将其切割成一个矩形和两个直角三角形。
假设梯形的上底长为a,下底长为b,高为h。
我们可以将梯形分成两个等高的小梯形,分别是上底长为a和b 的梯形,这两个小梯形的面积之和等于原梯形的面积。
而每个小梯形的面积可以用矩形面积减去直角三角形面积来表示。
所以,梯形的面积可以表示为:(a+b)*h/2。
方法二:代数推导
我们可以将梯形看成是一个矩形和两个直角三角形的组合。
利用代数方法可以得到梯形的面积公式。
设梯形的上底长为a,下底长为b,高为h。
可以得到梯形的面积S =矩形的面积+两个直角三角形的面积
= (a+b)*h + (1/2)*a*h + (1/2)*b*h
= (a+h)*h/2 + (b+h)*h/2
= (a+b)*h/2。
方法三:积分推导
我们可以使用微积分中的积分原理来推导梯形的面积公式。
设梯形的上底长为a,下底长为b,高为h,可以将梯形所在的平面区域看成是y = h和y = 0之间的平面图形。
利用定积分,梯形的面积可以表示为:∫[a,b]hdx
= h∫[a,b]dx
= h[x]ₐ_ᵦ
= h(b-a)
= (a+b)*h/2。
上述三种方法是推导梯形面积公式的常见方法,可以根据需要选择使用哪种方法。
同时,我们还可以推广梯形面积公式,例如推导出等腰梯形、半个圆柱体的梯形面积公式等。
梯形面积计算公式的推导

基于三角形面积公式的推导
总结词
利用三角形面积公式推导梯形面积公式
详细描述
将梯形分成两个三角形,分别计算其面积,然后将两个面积相加得到梯形的面积。
基于矩形面积公式的推导
总结词
利用矩形分成两个矩形,分别计算其面积,然后将两个面积相加得到梯形的面积。
梯形面积计算公式的推导
xx年xx月xx日
contents
目录
• 引言 • 梯形面积计算公式的基础知识 • 梯形面积计算公式的推导过程 • 梯形面积计算公式的应用举例 • 结论与展望
01
引言
背景介绍
梯形是几何学中一个重要的基本图形,具有广泛的应用价值 。
梯形面积的计算对于几何学、工程、建筑等领域都有重要意 义。
梯形面积计算公式在土地测量中得到了广泛应用,为土地 资源评估和规划提供了重要的基础数据。
实际应用二:水利工程
在水利工程中,梯形面积计算公式被用于计算水坝、渠道等水利设施的过水面积 ,以评估水流速度和流量。
通过使用梯形面积计算公式,水利工程师可以更准确地设计和评估水利设施的效 能。
实际应用三:机械制图
应用领域
该梯形面积计算公式可以应用于各种领域,如几何学、物理学、工程学、建筑学等。
改进方向
为了更好地应用该公式,可以开发便捷的计算机软件或小程序,方便用户快速计算梯形面积。
THANKS
谢谢您的观看
公式解释
所得到的梯形面积计算公式为$S = \frac{(a + b)}{2} \times h$ ,其中$a$和$b$分别为梯形的 上底和下底长度,$h$为梯形的 高。
适用范围
该公式适用于所有具有上底、下 底和高度的梯形,不受梯形形状 、大小和位置的限制。
梯形的面积计算公式的推导

梯形的面积计算公式的推导
要推导梯形的面积计算公式,我们可以利用梯形的性质和几何知识。
下面我将详细解释这个推导过程。
首先,让我们回顾一下梯形的定义。
梯形是一个有四边的多边形,其
中有两条平行边称为底,两条非平行边称为腰。
我们可以将梯形分为两个
三角形,通过绘制一条从梯形的一个顶点到另一条平行边上的一点。
这条
线称为梯形的高。
我们假设梯形的底的长度分别为a和b,高为h。
那么梯形的面积可
以表示为两个三角形的面积之和。
让我们先计算底为a的三角形的面积。
根据三角形的面积公式,三角
形的面积等于底乘以高的一半。
因此,底为a的三角形的面积可以表示为:Area1 = (1/2) * a * h
接下来,让我们计算底为b的三角形的面积。
同样地,底为b的三角
形的面积可以表示为:
Area2 = (1/2) * b * h
如前所述,梯形的面积等于两个三角形的面积之和,即:
Area = Area1 + Area2
代入Area1和Area2的公式,得到:
Area = (1/2) * a * h + (1/2) * b * h
我们可以进行合并和整理,将公式改写为:
Area = (1/2) * h * (a + b)
这就是梯形的面积计算公式。
总结一下,梯形的面积计算公式可以通过将梯形分为两个三角形,并应用三角形的面积公式推导得出。
公式为:
Area = (1/2) * h * (a + b)
其中,h表示梯形的高,a和b表示梯形的两个底的长度。
所以,可以根据这个公式计算梯形的面积。
梯形面积计算公式的推导大全

a
24
一个梯形的上底是
2cm,下底是5cm, 高是3cm.求这个梯
形的面积.
a
25
我是小法官:
梯形的面积是平行四
边形的面积的一半。
梯形的面积是底与它上下底
的和相等,高又相等的平行
四边形面积的一半。
a
26
我是小法官:
梯形的面积公式用字母表示是
S=(a+b)h
梯形的面积公式用字母表示是
梯形的面积上底下底如果用s表示梯形的面积用ab和h分别表示梯形的上底下底和高那么梯形的面积公式是
五年级(上)
西南师范大学出版社
a
1
2厘米 3厘米
2分米 5分米
a
2
a
3
6m
3.6m
梯合 梯分
分三
合三
四三
a
4
a
5
1、拼成的图形的底与梯形的上 底与下底有什么关系?
2、拼成的图形的高与梯形的高 有什么关系?梯形的面积与拼成
米深,2米渠,底横宽1.5米3.6,米渠
截面的
2米
面积是多
少平方米? 1.5米
a
31
有一堆圆木,摆成 下图形状,该怎样 计算圆木的根数?
a
32
a
33
梯形面积公式
上底
的推导过程:
B
高A
高
下底 一个梯形的面积=三角形A的面积+三角形B的面积
底×高÷2 + 底×高÷2
下底×高÷2 + 上底×高÷2
所以:梯形的面积=(上底+下底)× 高 ÷ 2
a
17
梯形面积公式 的推导过程:
上底 高
梯形面积计算公式的推导大全

我是小法官:
梯形的面积公式用字母表示是
S=(a+b)h
梯形的面积公式用字母表示是
S=(a+b)h÷2
我是小法官:
两个梯形的高相等, 它们的面积就相等。
我是小法官:
两个面积相等梯形可以拼 成一个平行四边形。
两个完全一样的梯形 可以拼成一个平行四 边形。
高 ÷2
梯形的面积公式是:
梯形的面积=(上底+下底)× 高 ÷ 2
如果用S表示梯形的面积,用a、b和h分 别表示梯形的上底、下底和高,那么梯形的面 积公式是:
S = (a + b ) h÷2
一个梯形的上底是 2cm,下底是5cm, 高是3cm.求这个梯 形的面积.
我是小法官:
梯形的面积是平行四 边形的面积的一半。
+ 上底×高÷2
所以:梯形的面积=(上底+下底)×
高 ÷2
梯形面积公式 的推导过程:
上底 高 下底-上底
一个梯形的面积=平行四边形的面积+三角形的面积
底×高
+
底×高÷2
上底×高 + (下底-上底)× 高 ÷ 2 所以:梯形的面积=(上底+下底)×
高 ÷2
梯形面积公式的推导过程:
梯形面积公式的推导过程:
求下面梯形的面积。 3.2dm 4cm
3cm 2cm
5dm
6.4dm
一条新挖的渠道,横截 面是梯形,渠口宽3.6 米,渠底宽1.5米,渠 3.6米 深2米,横 2米 截面的 面积是多 1.5米 少平方米?
有一堆圆木,摆成 下图形状,该怎样 计算圆木的根数?
梯形面积公式的推导过程:
梯形面积公式推导的多样方法

梯形面积公式推导的多样方法课本中介绍梯形面积公式推导的方法,通常只有一种方法,那就是用两个相同梯形拼成一个平行四边形,然后用这个平行四边形的面积推得其中梯形的面积。
这种方法很简洁,实际上梯形面积公式推导还有其它方法,现介绍如下:方法一:把一个梯形剪拼成平行四边形。
把梯形两腰的中点用线连起来,顺着这一条线剪下,把上面的梯形翻转和下面的梯形拼在一起,就成了一个平行四边形。
S梯形二S平行四边形=(上底+下底)X(高十2)=(上底+下底)X高宁2方法二:把一个梯形剪拼成一个三角形。
找到BC的中点E,把D和E用线连起来,剪下,按箭头的方向翻转,就拼成一个三角形。
S梯形二S A AFD=(上底+下底)X高十2方法三:如图所示,把梯形切割成两块,一块是平行四边形,一块是三角形。
上底上底平行四边形的底就是原梯形的上底,三角形的底是梯形的下底与上底之差,而平行四边形和三角形的高都等于梯形的高所以,梯形的面积=平行四边形的面积+三角形的面积=上底X高+(下底一上底)X高宁2=(2X上底)X高宁2+(下底一上底)X高宁2=(2X上底+下底—上底)X高宁2=(上底+下底)X高宁2因此梯形的面积=(上底+下底)X高十2方法四:把梯形分成两个三角形,分别算面积,然后计算它们的和把梯形分成两个三角形,如图所示,一个在左下,一个在右上。
右上三角形的面积=上底X高* 2左下三角形的面积=下底X高宁2所以梯形的面积=上底X高十2 +下底X高十2 = (上底+下底)X高宁2因此梯形的面积=(上底+下底)X高十2方法五:如图所示,把梯形的缺角补上,正好补成一个长方形,贝长方形的面积=下底X高而补上的两个小三角形的总面积为:小三角形面积和=(下底—上底)X高* 2所以梯形面积=长方形的面积一小三角形面积和=下底X高一(下底一上底)X高宁2=[下底一(下底一上底)宁2] X高=[2 X下底一(下底一上底)]X高宁2=(上底+下底)X高宁2方法六:如图所示,分别沿梯形两腰中点向下底作垂线,与腰、下底正好围成两个直角三角形,把这两个三角形分别按逆时针或顺时针旋转1800角,使得原来的梯形被拼组成一个长方形。
梯形面积对角线计算公式

梯形面积对角线计算公式一、梯形面积的一般公式。
梯形的面积公式为S = ((a + b)h/2)(其中a和b分别为梯形的上底和下底,h为梯形的高)。
二、梯形面积的对角线计算公式推导。
设梯形ABCD,AD∥ BC,对角线AC和BD相交于点O。
1. 根据三角形面积公式S=(1/2)ah(a为底,h为高)- 因为ABC和DBC等底BC,且AD∥ BC,这两个三角形BC边上的高相等。
- 设ABC的面积为S_1,DBC的面积为S_2,则S_1 = S_2。
- 同时S_1=(1/2)BC× h_1,S_2=(1/2)BC× h_2(h_1和h_2分别是ABC和DBC中BC边上的高)。
2. 对于AOB和DOC- 因为S_ ABC-S_ BOC=S_ DBC-S_ BOC,所以S_ AOB=S_ DOC。
- 设AD = a,BC = b,AOD的高为h_3,BOC的高为h_4。
- 由AODsim BOC(因为AD∥ BC),可得(h_3/h_4)=(a/b)。
- 设S_ AOD = S_3,S_ BOC=S_4,则S_3=(1/2)ah_3,S_4=(1/2)bh_4。
- 又因为(S_3/S_4)=((1/2)ah_3)/(frac{1){2}bh_4}=<=ft((a/b))^2。
3. 梯形面积S = S_3 + S_4+ 2S_ AOB- 由S_ AOB=S_ DOC,设S_ AOB=S_ DOC=x。
- 我们可以通过相似三角形的关系以及上述等式联立求解出梯形面积与对角线相关线段的关系。
- 设AC = m,BD=n,∠ AOB=θ。
- 则S_ AOB=(1/2)AO× BO×sinθ,S_ DOC=(1/2)DO× CO×sinθ。
- 根据AODsim BOC,可得(AO/CO)=(DO/BO)=(a/b)。
- 梯形面积S=(1/2)(AC× BD)sinθ=(1/2)mnsinθ。
梯形面积计算公式的推导

梯形面积公式的推导过程:
梯形面积公式的推导过程:
旋转
梯形面积公式的推导过程:
梯形面积公式的推导过程:
梯形面积公式的推导过程:
梯形面积公式的推导过程:
平 移
梯形面积公式的推导过程:
梯形面积公式的推导过程:
噢! 两个完全相同的梯形拼成了一个平行
四边形。
一个梯形的面积与拼成的平行四边形的面积有什么关系
梯形的面积是底与它上下底 的和相等,高又相等的平行 四边形面积是
S=(a+b)h
梯形的面积公式用字母表示是
S=(a+b)h÷2
我是小法官:
两个梯形的高相等, 它们的面积就相等。
我是小法官:
两个面积相等梯形可以拼 成一个平行四边形。
两个完全一样的梯形 可以拼成一个平行四 边形。
梯形面积公式的推导过程:
高 高 下底 上底
一个梯形的面积=所拼成的平行四边形的面积÷2 底
×
高
(上底+下底) × 梯形的高 所以:梯形的面积=(上底+下底)×
高 ÷2
梯形面积公式 的推导过程:
高
上底
B A 高
下底 一个梯形的面积=三角形A的面积+三角形B的面积
底×高÷2 下底×高÷2
+
底×高÷2
高 ÷2
梯形的面积公式是:
梯形的面积=(上底+下底)× 高 ÷ 2
如果用S表示梯形的面积,用a、b和h分 别表示梯形的上底、下底和高,那么梯形的面 积公式是:
S = (a + b ) h÷2
一个梯形的上底是 2cm,下底是5cm, 高是3cm.求这个梯 形的面积.
我是小法官:
梯形的面积是平行四 边形的面积的一半。
梯形的面积公式推导

梯形的面积公式推导梯形是一种四边形,它有两条平行边,这使得它与其他四边形不同。
我们可以通过推导梯形的面积公式来更好地理解它。
首先我们假设梯形的两条平行边分别为a和b,而梯形的高为h。
接下来,我们将梯形分割成一个大三角形和一个小三角形,这样我们就能更好地处理。
我们假设大三角形的底边为a,高为h,小三角形的底边为b,高为h。
首先,我们计算大三角形的面积。
根据三角形的面积公式,我们有:大三角形的面积等于底边乘以高的一半,即S1 = (a * h) / 2。
接下来,我们计算小三角形的面积。
同样地,根据三角形的面积公式,小三角形的面积等于底边乘以高的一半,即S2 = (b * h) / 2。
现在,我们将两个三角形的面积相加,即S1 + S2 = ((a * h) / 2) + ((b * h) / 2)。
我们可以使用公因式法则将这个等式简化为S1 + S2 = (a + b) * h / 2。
我们知道,梯形的面积等于两个三角形的面积之和,所以我们可以将上述等式表示为整个梯形的面积公式,即S = (a + b) * h / 2。
通过这个推导过程,我们得到了梯形的面积公式:S = (a + b) * h / 2。
这个公式告诉我们,要计算梯形的面积,我们只需要知道它的两条平行边和高就可以了。
这个推导过程不仅帮助我们理解了梯形的面积公式,还为我们提供了一种方法,可以将梯形的计算分解为计算两个简单三角形的面积。
这使得我们能更轻松地解决与梯形相关的问题。
总之,梯形的面积公式推导为S = (a + b) * h / 2,这个公式是基于两个三角形的面积之和。
通过这个公式,我们可以更好地理解梯形以及如何计算它的面积。
希望本文的内容能对你有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形面积计算公式的推导
1
只有一组对边平行的四 边形叫做梯形。
2
梯形的各部分名称: 上底
腰
腰
高
下底
3
比一比:两个梯形有什么关系?
试一试吧!
4
5
通过旋转、平移 能拼成一个什么 图形
两个梯形完全相同。
再试一试
6
7
8
9
10
11
上底
上底
下底
高
高
下底
下底
上底
平行四边形的底
通过实验可看出,两个完全一样的梯形都可以拼成一个 ( 平行四边形)。
拼成的平行四边形的底=梯形的(上底)+(下底)
拼成的平行四边形的高=梯形的(高)。
拼成的平行四边行的面积 =(上底+下底) ×高
所以梯形的面积= (上(底+下底) ×高÷2 =
用字母表示为s=(a= +b) ×h ÷2
12
1.判断题。 (1)两个梯形都能拼成一个平行四边形。(× )
(2)两个形状一样的梯形一定能拼成一个平行四
边形。
(× )
(3)两个完全一样的梯形一定能拼成一个平行
四边形。
(√ )
(4)平行四边形的面积是梯形面积的2倍。(× )
13
有一条水渠,它的横截面是一个梯形(如图),求它 的横截面的面积。(图中单位:米)
2.4 0.9
1.6
(2.4+1.6)×0.9÷2 =4×0.9÷2 =1.8(平方米) 答:水渠横截面的面积是1.8平方米。
20
(3+6)×7 ÷2 = 9×7 ÷2 = 31.5(c㎡)
等底等高的梯形, 面积相等,形状不同。
21
8m
(30-8)×8÷2 =24 ×8÷2 =96(平方米) 答:这块菜地占地96平方米。
18
试求出下面梯形的未知项。(图中单位:厘米)
1.5
2 面积是35平方厘米,高 是多少?
6 165平方厘米 11
?
19
2
4
4
(2+4)×4 ÷2=12
2
4
4
(2+4)×4 ÷2=12
2
4
5
(2+4)×5 ÷2=15
14
任选一个图形计算它的面积。(图中单位:分米)
35
30
20 (35+20)×30÷2 =55×30÷2 =825(平方分米) 答:这个梯形的面积 是825平方分米。
7.5 11
12.5
(7 .5+12.5)×11÷2
=20×11÷2
=110(平方分米)
答:这个梯形的面积
是110平方分米。
15
选择正确的列式
13
8.5
12.5
10Байду номын сангаас
(1) (13+10) ×8.5÷2
(2) (8.5+12.5) ×13÷2
(3) (13+10) ×12.5÷2
√ (4) (8.5+12.5) ×10÷2
16
(3+7)×5÷2 =12 ×5÷2 =30(根) 答:这堆木材共有30根。
17
这是靠篱笆围成的一块菜地。篱笆总长是30米。这 块菜地占地多少平方米?
