机械动力学——任意周期激励
第7章机械动力学
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
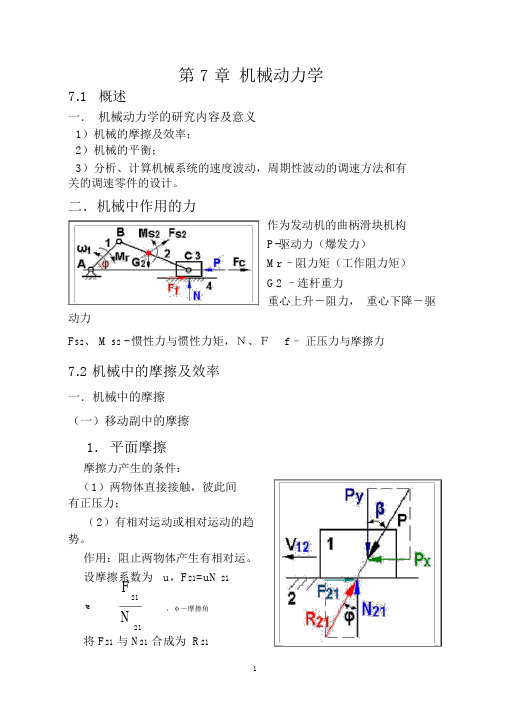
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
机械动力学——任意周期激励讲解

振幅放大因子
(s)
1
(1s 2 )2 (2 s)2
相位差 (s) tan 1 2 s
1s 2
3
任意周期激励的响应
•已知:
xc
xe
it
,x
H
(
)
F0
,H
(
)
1 k
e
i
•则可以得到:
xc
1 k
ei
F0 e it
F0 k
eit
F0 cost isint
bn
sin
nt )
任意周期激励的响应
系统的稳态响应为:
x(t) a0 an cos(nt n ) bn sin(nt n )
2k n1 k [1 (n / 0 )2 ]2 (2 n / 0 )2
其中
0
k c
周期函数F(t)可展开成Fourier级数,即可分解为无穷个谐波函 数之和。
F (t )
a0 2
(an
n1
cos nt
bn
sin nt)
其中
a0
2 T
T
F (t)dt
an
2 T
T
F (t)cos ntdt
bn
2 T
T
F (t)sin ntdt
2
2F0 T
T
2 sin ntdt
0
T
T sin ntdt
2
2F0 T
机械系统动力学

t
J
0
M()
t0
当 M ()ab 时,可解出t的值
t
t0
Jln ab b ab0
第十四章 机械系统动力学
HIGH EDUCATION PRESS
3.等效转动惯量是常数、等效力矩为等效构件速度函数的运动 方程的求解
将 d d 代入 dt d
J d M()
dt
得:Jdd M()
d J d M()
第十四章 机械系统动力学
HIGH EDUCATION PRESS
三、等效参量的计算
1. 作定轴转动的等效构件的等效参量的计算 2. 作直线移动的等效构件的等效参量的计算
第十四章 机械系统动力学
HIGH EDUCATION PRESS
1.作定轴转动的等效构件的等效参量的计算
等效转动惯量的计算:
动能:
1
A
Mi2 Fi2 G2
CF
曲柄压力机的受力分析
第十四章 机械系统动力学
HIGH EDUCATION PRESS
二、等效构件
名词术语: 1. 等效转动惯量 2. 等效质量 3. 等效力矩 4. 等效力
第十四章 机械系统动力学
HIGH EDUCATION PRESS
二、等效构件
等效构件示意图
第十四章 机械系统动力学
第十四章 机械系统动力学
HIGH EDUCATION PRESS
2.作用在机械上的驱动力
(1)驱动力为常量 (2)驱动力是位移的函数 (3)驱动力是速度的函数
第十四章 机械系统动力学
HIGH EDUCATION PRESS
解析法研究异步电动机驱动力矩特性
M
d
0 tan
机械动力学

机械动力学Copyright @ 2009 HRBEU 702All Rights Reserved绪论一、机械动力学性质1.机械:机构、机器的总称。
(机械原理)2.动力学:研究刚体运动及受力关系的学科。
动力学正问题—已知力(力矩)求运动;动力学反(逆)问题—已知运动求力(力矩)。
机械动力学:是研究机械在力作用下的运动、机械在运动中产生的力(力矩)的科学。
F ma=例:机构组成性质:曲柄、急回。
若已知力(力矩),当机构处于平衡状态时,求力矩(力)--机械静力学问题。
若已知M、F,求ω、v 时—机械动力学。
ωM Fv二、机械动力学研究内容1. 描述机械有那些基本参数1)机构参数:几何参数(杆长);物理参数(质量m,转动惯量J)。
2)运动参数:转角θ、ω、α、s、v、a。
3)力矩M、力F。
2. 内容1)已知机械的物理、几何参数进行动力学分析。
a、已知力求运动;b、已知力求运动。
可表示为:2)已知运动、受力求结构这是机械设计研究问题,一般实际做法是先设计后校核,少数情况是直接求设计参数。
例:(,)(,,,,,,)f F Mg l m J v a ωαZZ X YZ Z q求支点最佳位置。
如果梁静止为静力学问题;如果梁有惯性运动为动力学问题。
3)具体章节内容单自由度运动学方程的建立二自由度运动学方程的建立,如差动轮系、五杆机构多自由度运动学方程的建立,如机械手臂、机器人等理想情况下(无摩擦变形等)考虑摩擦,如铰链、关节处摩擦考虑弹性变形,如杆变形、并联柔性机器人变质量问题,如推土机工作过程、火箭发射过程有间隙情况下动力学研究,不详讲述三、研究对象--以机械为研究对象三大典型机构连杆机构凸轮机构齿轮机构组合机构四、其它1.学习机械动力学目的、意义学习动力学分析问题的思想和基本方法,能够解决一般动力学问题。
2.教材(见前言)3.考核方式开卷。
§1-1 利用动态静力法进行动力学分析一、思路动静法:根据达朗贝尔原理将惯性力计入静力平衡方程,求出为平衡静载荷和动载荷而需在原动件上施加的力(力矩)。
机械动力学

6.机构分析和机构综合。此项内容一般是对机构的结构和运动而言,但随着机械运转速度的提高, 机械动力学已成为分析和综合高速机构时不可缺少的内容。
理论及应用
理论及应用
1.分子机械动力学的研究:作为纳米科技的一个分支,分子机械和分子器件的研究工作受到普遍。 如何针对纳机电系统(NEMS)器件建立科学适用的力学模型,成为解决纳米尺度动力学问题的瓶颈。 分子机械是极其重要的一类NEMS器件.分为天然的与人工的两类。人工分子机械是通过对原子的 人为操纵,合成、制造出具有能量转化机制或运动传递机制的纳米级的生物机械装置。由于分子 机械具有高效节能、环保无噪、原料易得、承载能力大、速度高等特点,加之具有纳米尺度,故 在国防、航天、航空、医学、电子等领域具有十分重要的应用前景,因而受到各发达国家的高度 重视。已经成功研制出多种分子机械,如分子马达、分子齿轮、分子轴承等。但在分子机械实现 其工程化与规模化的过程中,由于理论研究水平的制约,使分子机械的研究工作受到了进一步得 制约。分子机械动力学研究的关键是建立科学合理的力学模型。分子机械动力学采用的力学模型 有两类,第一类是建立在量子力学、分子力学以及波函数理论基础上的离散原子作用模型。
阐述
对刚性转子的平衡已有较成熟的技术和方法:对工作转速接近或超过转子自身固有频率的挠性转 子平衡问题,不论是理论与方法都需要进一步研究。 平面或空间机构中包含有往复运动和平面或空间一般运动的构件,其质心沿一封闭曲线运动。根 据机构的不同结构,可以应用附加配重或附加构件等方法,全部或部分消除其振颤力。但振颤力 矩的全部平衡较难实现。 机械运转过程中能量的平衡和分配关系包括:机械效率的计算和分析,调速器的理论和设计,飞 轮的应用和设计等。 机械振动的分析是机械动力学的基本内容之一,现已发展成为内容丰富、自成体系的一门学科。 机构分析与机构综合一般是对机构的结构和运动而言,但随着机械运转速度提高,机械动力学已 成为分析与综合高速机构时不可缺少的内容。
动力学中的机械振动与周期

动力学中的机械振动与周期在动力学中,机械振动是一个重要的研究领域。
机械振动是指物体在受到外力作用时,由于其固有特性而产生的周期性运动。
周期性运动是指物体在相同时间间隔内重复出现的运动状态。
本文将介绍机械振动的基本概念、周期性运动的特征以及机械振动的应用。
一、机械振动的基本概念机械振动的基本概念包括质点振动和刚体振动。
质点振动是指物体在自由运动过程中保持形状不变,只发生位置移动的振动。
刚体振动是指在振动过程中,固体保持形状不变,整体发生平移或者旋转的振动。
机械振动的产生离不开弹性力和阻尼力的作用。
弹性力是物体受到形变作用时产生的恢复力,它使得物体回到其平衡位置。
阻尼力则是摩擦力等外力对物体振动过程中的能量损失。
二、周期性运动的特征周期性运动的特征是指物体在振动过程中重复出现的特定运动状态。
基本的周期性运动包括简谐振动和非简谐振动。
简谐振动是指物体在恢复力和质量之间满足线性关系时产生的振动。
简谐振动具有周期恒定、频率恒定和振幅恒定的特点。
非简谐振动是指物体在恢复力和质量之间不满足线性关系时产生的振动。
非简谐振动的振幅和周期会随着时间的推移而变化。
三、机械振动的应用机械振动在工程和科学领域具有广泛的应用。
以下列举几个常见的应用场景。
1. 结构物的振动分析: 在工程领域中,机械振动的分析可用于评估建筑物、桥梁等结构物的耐久性和安全性。
通过对结构物的振动特性进行测量和分析,可以判断结构物是否存在疲劳、共振等问题,从而进行相应的维修和改善措施。
2. 振动传感器: 振动传感器是一种常用的测量设备,可以用于检测和监测机械设备的振动情况。
通过对设备振动的监测,可以及时发现设备的故障和损坏,从而提前采取维修和保养措施,减少停机时间和生产损失。
3. 振动控制技术: 振动控制技术是通过对振动系统施加控制力来减小或消除振动的技术手段。
该技术广泛应用于航空航天、汽车制造、机械加工等领域。
通过振动控制技术可以提高系统的稳定性和工作效率,减少振动对设备和人体的损伤。
同等学力申硕统考-机械工程考点汇总

机械工程控制基础1.控制系统的基本性能要求:快速性、稳定性、准确性。
2.若系统的数学模型表达式是线性的,则这种系统是线性系统,线性系统最重要的特性是可以运用叠加原理。
3.方块图是系统中各环节的功能和信号流向的图解表示方法,由基本方块、相加点和分支点构成。
4.方块图包含了与系统动态性能有关的信息,与系统的物理结构无关。
5.方块图简化过程遵守的两条基本原则:(1)前向通道的传递函数保持不变(2)各反馈回路的传递函数保持不变6.数学模型是系统动态特性的数学表达式。
建立数学模型是分析、研究一个动态系统特性的前提,一个合理的数学模型应能以最简化的形式准确地描述系统的动态特性。
7.校正有串联校正和并联校正。
串联校正按校正环节的性能可分为:增益校正、相位超前校正、相位滞后校正、相位超前-滞后校正。
并联校正按校正环节并联方式分为:反馈校正、顺馈校正。
8.反馈校正是从系统某一环节的输出中取出信号,经过校正网络加到该环节前面某一环节的输入端,并与那里输入信号叠加,从而改变信号的变化规律,实现对系统进行校正的目的。
9.信息是指一切能表达一定含义的信号、密码、情报和消息。
10.信息传递,是指信息在系统及过程中以某种关系动态的传递过程。
11.系统一般指的是能完成一定任务的一些部件的组合。
12.控制系统是指系统的可变输出能按照要求由输入或控制输入进行调节的系统。
按是否存在反馈,分为开环控制系统和闭环控制系统。
13.信息的反馈就是把一个系统的输出信号不断直接的或经过中间变换后全部或部分地返回到输入端,再输入到系统中去。
如果反馈回去的信号与原系统的输入信号的方向相反或相位相差180°,则称为负反馈;如果方向或相位相同,则称之为正反馈。
14.反馈控制是指在某一行动和任务完成之后,将实际结果进行比较,从而对下一步行动的进行产生影响,起到控制的作用。
15.频率响应是系统对正弦输入的稳态响应。
16.频率特性是通过分析不同正弦输入下系统的稳态来表示系统的动态特性,它仅与系统本身参数有关。
单自由度振动系统对任意激励响应的仿真分析

Kev wor ds: br io Vi at n: Ar r y bit ar Ex t i n; Re po e; Em at ci at o s ns ul e
0 引 言
系统的等效集 巾质量为 m ,刚度为 k ,粘性 阻尼系数为
C ,振动位移 x 受外力 f t作用。 , ()
其运动微分方 程为:
从线性系统振动理论可知 , 当机械系统受到简谐激励作
用时,其响应是 同频率的筒谐 振动 。在受到非简谐的周期激 励时,可把周期激励展开成 Fu i r o re 级数,把级数的每一项 视作…简谐激励,确定其稳态响应。根据线性系统 的叠加性 把所有简谐稳态响应加起来,就得到了系统对该周期激励的
维普资讯
TeSm lto n lssQ h eonet h rirr x ia inQ ioeFedmVba inS se h iua inAa yi nteR sos oteAbtayEc tto fSn l - eo irto ytm -r
邱 英
计算机对其进行仿真分析,结果直观 明了,是一种非常有效 的振动分 析工具。
关键词: 动: 振 任意激励: 响应: 仿真 中图分类号 :0 2 34 文献标识码 :A 文章编号:1 7 — 7 2 (0 85 0 3 一 2 1 4 9 一 2 0 )— 0 8 O 6
Ab ta t B s d n h e p n e o h u i i p i e x i a i n o s n l — r e o i r t o y t m,t e s r c : a e o t e r s o s t t e n t m u s e c t t o f i g e f e d m v b a i n s s e h
动力学的一些简单概念

机械振动:机械或结构在它的静平衡位置附近的往复弹性运动。
本书涉及的振动均指机械振动。
激励、响应和系统三者之间的关系已知其中之二可求其一振动的分类线性振动:用线性微分方程描述。
在线性振动中叠加原理成立非线性振动:非线性微分方程描述系统的自由度数:描述系统运动所需要的独立坐标的数目。
•连续系统:在实际中遇到的大多数振动系统的质量和刚度都是连续分布的,通常需要无限多个自由度才能描述它们的振动,它们的运动微分方程是偏微分方程。
如等截面的梁、杆,以及板等。
•离散系统:在结构的质量和刚度分布很不均匀时或者为了解决实际问题的需要,把连续结构简化为由若干个集中质量、集中阻尼和集中刚度组成的离散系统。
所谓离散系统是指系统只有有限个自由度。
描述离散系统的振动可用常微分方程。
其他的分类:(1)按激励情况分类:自由振动:系统在初始激励下或原有的激励消失后的振动。
强迫振动:系统在持续的外界激励作用下产生的振动。
(2)按响应情况分类:简谐振动:振动的物理量为时间的正弦或余弦函数。
周期振动:振动的物理量为时间的周期函数,可用谐波分析的方法归结为一系列简谐振动的叠加。
简谐振动也是周期振动。
瞬态振动:振动的物理量为时间的非周期函数,在实际的振动中通常只在一段时间内存在。
离散振动系统三个最基本的元件:惯性元件、弹性元件和阻尼元件。
在系统振动过程中惯性元件储存和释放动能,弹性元件储存和释放势能,阻尼元件耗散振动能量。
单自由度系统:只有一个自由度的振动系统称为单自由度振动系统。
单自由度线性振动系统可以用一个常系数的二阶线性常微分方程描述它的振动规律。
自由振动:系统在初始激励下或外加激励消失后的一种振动形态。
其振动规律完全取决于系统本身的性质。
阻尼是用来度量系统自身消耗振动能量的能力的物理量。
最常用的阻尼是气体和液体的粘性阻尼,在线性振动理论中规定,由粘性阻尼引起的粘性阻尼力的大小与相对速度成正比,方向与速度方向相反。
等效阻尼方法是,假定系统做简谐振动,令原系统耗散的能量与粘性阻尼耗散的能量相同,从而求出等效阻尼系数。
机械动力学

vSjy aSjy ) J j j j ]
例题P72
§3.4 动力学方程式的求解 注意:关键是确定等效转动惯量和等效力矩的关系式(解析式、图表形式等)
一、等效转动惯量和等效力矩均为位置的函数
(Md=Md(),Mr=Mr(), Me=Me(),Je=Je())
1. 等效构件的角速度
❖
1 2
式中第二项符号的确定方法为:当Mj与ωj同向时取正号,反向时取负号。
广义力就是作用在广义坐标处的一个力或力矩,它所作的功等于系统中 全部力和力矩在同一时间内所作的功。
广义坐标为一个角位移时,广义力F为一等效力矩Me,它可按下式计算:
F
Me
m ( Fkvk
k 1
cosk
q
)
m
(M j
j 1
j )
q
Me表示式中的广义传动比 j / q、vk / q是由机构的尺度和位置决定的, Me仅仅是机构广义坐标q的函数,与广义速度 q 的变化无关。
单自由度机械系统的动力学方程:
J e q
1 2
J e q
q2
Me
三、等效力学模型
机械系统是复杂多样的,在进行动力学研究时,通常要将复杂 的机械系统,按一定的原则简化为一个便于研究的等效动力学模型。
2、等效条件 (1) 等效构件所具有的动能等于原机械系统的总动能; (2) 等效构件的瞬时功率等于原机械系统的总瞬时功率。
3、等效参数 (1) 等效质量me,等效转动惯量Je; (2) 等效力Fe,等效力矩Me。
等效动力学模型的建立
对于单自由度的机械系统,只要知道其中一个构件的运 动规律其余所有构件的运动规律就可随之求得。因此可把复杂 的机械系统简化成一个构件(称为等效构件),建立最简单的等 效动力学模型,将使研究机械真实运动的问题大为简化。当等 效构件为一个绕机架转动的构件时,模型为图a。当等效构件 为一个移动滑块时,模型为图b 。
机械动力学第1、2章

2
2
1 2 2 1 d n 根据 Td 2 k mn cc 2mn
ln(16) 2.7726
k 200 3.43382 2358.2652( N / m) cc 2 200 3.4338 1373.54( N s / m) c cc 0.4037 1373.54 554.4981( N s / m)
第一章 单自由度系统
• • • • •
常用的推导动力学方程的方法 牛顿第二定律 达朗贝尔原理 虚位移原理 能量守恒原理
无阻尼自由振动
1.无阻尼自由振动解
如果一个质点偏离其平衡位置的距离 为 xm, 则其将进行自由振动,有牛顿 定律,质点力的平衡方程为
ma F W k st x kx
高塔消振 高塔消振 台北 101 大厦内部装有阻尼耗能减振器 台北 101 大厦内部装有阻尼耗能减振器
有阻尼自由振动的应用
网球 (( 羽毛球 )) 拍消 网球 羽毛球 拍消 网球拍或羽毛球拍在击球后产生自由振动,若不在 网球拍或羽毛球拍在击球后产生自由振动,若不在 下次击球之前停止振动,将影响再次击球的方向和 下次击球之前停止振动,将影响再次击球的方向和 角度,为此在铁合金管外面绕上石墨纤维,并在其 角度,为此在铁合金管外面绕上石墨纤维,并在其 外面用塑料捆扎住,石墨纤维外表面的库仑阻尼, 外面用塑料捆扎住,石墨纤维外表面的库仑阻尼, 使球拍在击球后,以最快的时间稳定下来 使球拍在击球后,以最快的时间稳定下来
p103
【解】由于x1.5=x1/4, 因而x2=x1/16
n t2
x1 Ae nt1 sin( 1 2 n t1 ) x2 Ae
第5讲 两自由度系统的振动

(4)
,式中常数u1和u2起振幅的作用。 请
将方程(4)代入方程(3),得
m1u1 f(t)+ (k11u1 + k12u2 ) f (t ) = 0 m2u2 f (t)+ (k21u1 + k22u2 ) f (t ) = 0
2015/3/24 机械系统动力学-多自由度系统的振动
现在关心的问题是,在初值条件下,如何求解 这个方程。这里,有两个问题需要确定: 1、坐标x1和x2是否有相同的随时间的变化规律 2、x1和x2是否是简谐函数
2015/3/24
机械系统动力学-多自由度系统的振动
14
有趣的“同步化” 现象
最早观察到同步化现象的科学家是
课 件荷兰的物理学家克里斯蒂安 · 惠更斯 仅 供(Christian Huygens 1629-1695)。根据 学 习伽利略(Galileo Galilei 1564-1642)发现 复 习 的钟摆的等时性原理,他于1656年把单 之 用 ,摆引入了机械钟,研制成第一个摆钟。 请
勿标,它们能够完全描述了系统在任何时刻的运动:x1和 它 用x2不仅表示出质量m1和m2的运动,而且也描述了
弹簧
。 曹k 、k 和k 的运动。因此,该系统是一个两自由度系统。 1 2 3
2015/3/24 机械系统动力学-多自由度系统的振动 8
两自由度系统的自由振动(微分方程)
f1 f2
课 件 仅 供 x1 x2 学 k2 (x2 − x1 ) 习 k1 x1 m1 m2 k3 x2 复 习 f1 f2 之 用 设运动x1和x2是微幅的,振动系统是线性的。由牛 ,顿定律建立运动微分方程 :
引言
2015/3/24
机械系统动力学-多自由度系统的振动
结构动力学-第十章-随机振动激励响应关系

ch
0 0
0
kh(t)dt
0
0
(t)dt
0
或: m h(0 ) h(0 ) c h(0 ) h(0 ) kh( )(0 0 ) 1
即: mh(0) ch(0) 1 (1)
积分两次:
0
dt
t mhdt
0
dt
t chdt
0
dt
t
kh(t)dt
0
t
dt (t)dt
t
x(t) h(t )y( )d y(t) * h(t)
卷积积分
此式也可以由上页的(*)式推出:
y(t)
y( )
t
t
此式也可以由上页的(*)式推出:
x(t) 1
2
H
(
)
y(t)eit dteit d
1
2
H
(
)
y( )ei d eit d
1
2
y( )
H
(
)e
当t 0时, (t)=0,故有
mh ch kh 0 或 h 2nh n2h 0
其通解为: h(t) en t ( A cosd t B sin d t)
积分常数A和B由初始条件确定
则: mh ch kh (t) (*)
对(*)式两边从0-到0+积分两次
积分一次:mh 0 0
2
或: 1 e-itdt 2 ()
故: 1
2
() 或:1
2 ()
同样: 1 ei0 t
2
( 0 )
1 ei0 t
2
( 0 )
(3)脉冲响应函数
实际上,在第四章瞬态振动一章已经求过h(t)。 求h(t)的步骤如下: ①建立系统运动微分方程
《机械动力学与振动》课程教学大纲

《机械动力学与振动》课程教学大纲课程名称:机械动力学与振动课程代码:EM357学分/学时:3学分/51学时开课学期:春季学期适用专业:机械工程、热能与动力工程、核工程、航空宇航科学、建筑环境与设备及相关专业先修课程:高等数学、理论力学、线性代数后续课程:开课单位:机械与动力工程学院一、课程性质和教学目标(需明确各教学环节对人才培养目标的贡献,专业人才培养目标中的知识、能力和素质见附表)课程性质:机械动力学与振动是机械工程、热能动力工程、核科学与工程、航空航天工程等专业的一门重要专业基础课,是机械、能源动力类专业必修主干课。
教学目标:机械动力学与振动是研究机械系统的运动、振动和受力之间的关系的科学,通过本课程的学习,掌握与机械动力学和振动有关的基本理论和分析方法,具备对复杂机械系统建立动力学模型的能力,进行动力学与振动相关分析的能力及从事相关科学研究工作和相关专业技术工作的能力,也为相关工程管理工作提供重要的理论基础。
(A4.1, A5.1, A5.2, A5.3,B2,B4,C2)通过本课程教学,不仅使学生在机械动力学和振动特别是机械系统在外力作用下的响应及应用方面树立正确的概念,同时培养学生科学抽象、逻辑思维能力,进一步强化实践是检验理论的唯一标准的认识观。
具体来说,1、能够利用牛顿/欧拉方程和拉格朗日方程建立弹性体系统进行动力学方程;[A3, A4.1, A4.2,A5.1]2、能够对振动系统的自由振动和受迫振动进行求解,了解提高抗振性能所利用的基本原则和主要途径[A5.1, A5.4]3、能够运用常用的振动基本公式、图表和计算软件(如matlab)等进行一般振动特性分析和计算。
[A5.2,A5.1, A5.4]4、具备对工程中的传动机构动力学,机器人动力学、惯性力系的平衡、振动传递、隔振、动力吸振及旋转不平衡等问题进行建模和分析的能力[A5.1,A5.3, A5.4, B2, B4]5、掌握模态法对多自由度系统的求解及特征根和特征向量的物理意义[A5.1]6、强化理论来源于实践,实践是检验理论的唯一标准的认识观。
2012年机械动力学基础考试题答案解读

一、填空题(10分,每空2分)(1)、平衡位置(2)、非线性振动,非周期振动,连续系统(3)、质量、弹簧、阻尼(4)、线性(5)、质量,弹簧刚度二、判断题(10分,每题2分)(1)、√(2)、√(3)、×(4)、√(5)、×三、简答题(20分,每题5分)(1)、如何通过测量弹簧-质量系统的静变形求出系统的固有频率?解:根据弹簧的静变形s δ和质量块的重力mg 相等,即mg k s=δ,确定sgm kδ=,代入固有频率公式,sn gm k δω==。
(2)、名词解释:静力耦合(弹性耦合),动力耦合(惯性耦合)。
解:振动微分方程通过刚度项来耦合,即刚度矩阵非对角元素非零,称为静力耦合或弹性耦合。
振动微分方程通过质量项来耦合,即质量矩阵非对角元素非零,称为动力耦合或惯性耦合(3)、在周期激励作用下,把几个谐响应的总和作为系统响应的理论基础上什么?解:叠加原理,即周期激励的响应等于各谐波分量引起响应的总和。
(4)、分别举例说明振动的危害和益处。
本题属于开放题。
四、计算题(15分)某仪表模型如下图所示,刚性杆AO (质量可忽略)绕O 点转动,杆长5=L cm 。
在A 点有一集中质量025.0=m kg ,拟在B 点加一阻尼系统,其刚度4=k KN/m 的弹簧和阻尼系数为c 的阻尼器,41=l cm 。
试求:系统经过2次循环后幅值减小40%,所需要的阻尼系数,且当OA 杆初始偏角为 5,初始角速度为零,求系统做自由振动方程。
A解:(1)设刚杆在振动时的摆角为θ,由刚杆的振动微分方程可建立系统的振动微分方程:θθθ21212kl cl mL --= 0221221=++θθθmLkl mL cl (1) 系统的无阻尼固有频率:rad/s 320=1mkL l n =ω 由3540%-1131==A A 可得对数减幅系数: 2554.035ln 21ln2131===A A δ于是相对阻尼系数为0406.0)2(22=+=δπδζ根据方程(1)得:2212mL cl n =ζω由此得到阻尼系数Ns/m 1.015=1625025.03200406.022212=⨯⨯⨯⨯==l mL c n ζω(2)有阻尼系统固有频率为rad/s 319.73612=-=n d ωζω1)设系统有阻尼自由振动方程的解为:)sin(ϕωθζω+=-t Ae d t n由初始角 50=θ,00=θ 得: 5.12020=⎪⎪⎭⎫ ⎝⎛++=d n A ωθζωθθ 度 rad 1.53 =度 87.67arctan 000=⎪⎪⎭⎫⎝⎛+=θζωθθωϕn d )53.1367.319sin(1.5992.12+=-t e t θ度2)或者 设系统有阻尼自由振动方程的解为:())sin()(cos 21t A t A e d d t nωωθζω+=-其中 rad 0.08721805501====πθ A rad 0.0035319.7360.08723200.04060002=⨯⨯+=+=d n A ωθζωθ于是,())319.736sin(0.0035)319.736(0.0872cos 992.12t t e t +=-θ rad五、计算题(20分)解:梁和弹簧并联,其等效刚度系数为则系统的固有频率为:本题所示系统为无阻尼单自由度系统,即:取静平衡位置为坐标原点,则系统的动力学方程为其中,由单自由度系统在任意激励下的响应公式可得系统在外加载荷作用下在竖直方向的响应为:当时当时当时当t>t3时综上,系统在外加载荷作用下在竖直方向的响应为其中,六、计算题(10分)坐标,,分别表示,,偏离其各自平衡位置的水平位移。
机械动力学

第七章机械动力学1. 概述2. 机械中的摩擦与效率3. 机构的动态静力分析4. 机械的平衡5. 机械的运转及动力学模型6. 机械系统速度波动及其调节第七章机械动力学1. 概述2. 机械中的摩擦与效率3. 机构的动态静力分析4. 机械的平衡5. 机械的运转及动力学模型6. 机械系统速度波动及其调节第七章机械动力学第一节概述一、机械动力学的研究内容及意义机构在传递和转换运动的同时必然伴随着力的传递和转换。
机械在工作过程中受到不同性质的力的作用,这些力影响着机械的运动状态。
同时,机械的运动也影响着机械的受力。
机械系统中力和运动的相互作用决定了机械的工作状态。
机械动力学(dynamics of machinery)研究机械在运动中的力以及在各种力作用下的机械运动,分析和评价机械的动力学性能,研究提高机械动力学性能的措施。
这是机械系统分析与设计的一个十分重要的内容。
机械在运动中始终存在摩擦,其运动副中的摩擦力是一种有害阻力,它不仅造成动力的浪费,降低机械效率,而且使运动副元素受到磨损,削弱零件的强度,导致机械运动精度和工作可靠性降低,缩短机械的寿命。
研究机械中的摩擦及其对机械运行和效率的影响,通过合理设计,改善机械运转性能,提高机械效率,是机械动力学分析的重要内容。
机械系统通常由原动机、传动系统、执行系统等组成。
一般来说,原动件的运动不是匀速的,其运动规律取决于各运动构件的质量、转动惯量以及作用在机械上的各种外力。
假定原动件匀速运动进行分析的局限性分析结果与真实情况有差异。
这种假定对于低速、轻载的机械是允许的。
对于高速、重载、大质量的机械,这种分析误差可能直接影响到设计的安全性和可靠性。
实际工况机械运转时,绝大多数机械系统主轴(main shaft)的速度都是波动变化的。
过大的速度波动会影响机器的正常工作,增大运动副中的动负荷,加剧运动副的磨损,降低机器的工作精度和传动效率,缩短机器的使用寿命,激发机器振动,产生噪音等。
“机械动力学”课程教学大纲

“机械动力学”课程教学大纲英文名称:Mechanical Dynamics课程编号:MACH3441学时:32 (理论学时:32 实验学时:课外学时:2实验)学分:2适用对象:机械设计、机械制造及自动化、机械电子工程、流体机械、电机、电器、材料工程等本科生高年级。
先修课程:高等数学、一般物理学、理论力学、材料力学、线性代数利用教材及参考书:[1] 石端伟主编. 机械动力学. 北京:中国电力出版社,2007.[2] 张策主编. 机械动力学.北京:高等教育出版社, 2020.[3] 倪振华主编. 振动力学. 西安交通大学出版社,1988.一、课程性质和目的性质:专业课目的:1.了解机械动力学的研究内容、进展历史和最新研究进展。
2.培育机械系统动力学分析的大体能力。
3.了解机械系统动力学分析相关的CAE软件。
4.了解机械系统动态测试有关技术。
5.培育查阅和运用相关科技文献进行动力学分析的初步能力。
6.培育创新思维和解决工程实际问题的能力。
7.培育科学、严谨的工作作风。
二、课程内容简介三、随着现代机械装备朝着高精度、高效、大功率的方向进展,其动态性能指标的好坏愈来愈受到普遍关注和高度重视。
机械动力学已日趋成为现代机械设计与制造工程领域不可或缺的基础知识。
本课程要紧介绍机械系统动力分析的大体理论、分析方式、测试与操纵技术和典型机械系统动力学分析方式。
通过课程的学习,培育学生能够在机械系统动力分析方面具有明确的大体概念、必要的专业基础知识、必然的机械系统动力分析能力与计算能力。
四、教学大体要求1.了解相关机械系统动力学分析的新理论、新方式及进展趋向。
2. 把握有关机械系统动力学分析的大体概念、大体理论与方式。
3. 了解典型机械系统动力学分析流程,具有进行工程实际问题分析的初步能力。
4. 成立正确的机械系统动力分析的思维方式,理论联系实际,具有必然的科研创新精神;5. 课后需要查阅文献,并开展讨论,完成作业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
率的简谐激励,然后求出系统对各个频率的简谐激励的响
应,再根据线性系统的叠加原理,将各个响应逐一叠加, 即得到系统对周期激励的响应。
这种对系统响应的分析方法被称为谐波分析法。
任意周期激励的响应
假设系统受到的周期激振力为: F (t ) F (T t )
4 F0
任意周期激励的响应
系统运动方程:
cx kx F (t ) mx
把所有特解叠加起来,就得到系统在周期激振力作 用下的稳态响应:
4F0 x(t ) k
记: Bn
n 1,3,5
1 n[1 (n / 0 ) ]
2
sin(nt )
4 F0 2 n k[1 (n / 0 ) ]
则
线性系统
x1 (t )
F2 (t )
线性系统
x2 (t )
c1F1 (t ) c2 F2 (t )
线性系统
c1 x1 (t ) c2 x2 (t )
5
任意周期激励的响应
Fourier变换
周期函数F(t)可展开成Fourier级数,即可分解为无穷个谐波函 数之和。
a0 F (t ) (an cos nt bn sin nt ) 2 n1
任意周期激励的响应
对于
2 F0 2 2cos n bn T n n
当 n 取偶数时:
bn 0 n 2, 4,6
当 n 取奇数时:
1 F (t ) sin nt n1,3,5... n 1 1 (sin t sin t sin 5t ) 3 5 4 F0
Asin Acos sin t cost ky ky
18
谢 谢!
19
F0 cost k
4
任意周期激励的响应
前面各节讨论的强迫振动中,都假设了系统受到的激励为简谐激 励,但实际工程问题中遇到的大多是周期激励而很少为简谐激励。
若激励F(t) 有
F (t ) F (t T )
则F(t)为周期激励, T为周期。
线性系统满足叠加原理
若
F1 (t )
单自由度系统受迫振动
姓 名: 何江波
学 院: 机械工程学院
邮 箱:445875183@
2016/12/18
教学内容
• 简谐力激励的受迫振动
• 任意周期激励的响应
• 瞬态振动
2
任意周期激励的响应
cx kx F0 sin t 振动微分方程:mx
•令:Fc F0 cost i sin t F0 e it
x H ( ) F0
H ( ) 1 k m 2 ic
复频响应函数
(s)
1 (1 s 2 ) 2 (2 s) 2
相位差
2 s ( s ) tan 1 s 2
1
3
任意周期激励的响应
1 i it x xe , x H ( ) F , H ( ) e •已知: c 0 k
其中
2 T a0 T F (t )dt 2 T an F (t ) cos ntdt T 2 T b F (t )sin ntdt n T
频率 ω=2π/T 成为基频,T为F(t)的周期。
6
任意周期激励的响应
Ω 检测轴(y) mx ky my 驱动轴(x)
cx cy kx
16
任意周期激励的响应
科氏力的计算公式为:
Ω 检测轴(y) mx ky my 驱动轴(x)
Acos(t ) F 2my x
Ω 为角速度, ω 为驱动轴的驱动频率 求: (1)检测轴的稳态响应
cx cy kx
原理: 通过静电力驱动x轴的质量块(mx)发生周期振动。 在存在角速度(Ω )的情况下,周期振动在检测轴产 生科氏力,科氏力正比于角速度。 科氏力使检测轴的质量块 (my) 发生振动,通过测 量检测轴质量块的振动幅度便可以测量得到角速度。
a0 F (t ) (an cos nt bn sin nt ) 2 n1
前两项积分项均为奇函 数,因而积分均为零,
任意周期激励的响应
F (t ) bn sin nt
n 1
T 2 0
2 T bn F (t ) sin ntdt T
任意周期激励的响应
系统在周期激励下的响应特点:
(1)线性系统在周期激励下的响应仍为周期函数, 且响应周期与激励周期相等。
(2)线性系统在周期激励下的响应波形发生畸变。
(3)无阻尼系统,有:
H (n )
1 1 (n / 0 ) 2
H (n )
当 n / 0 ,有
当基频是自然频率的整数分之一时就可能发生共振。
•则可以得到:
F 1 xc e i F0e it 0 e it k k F0 cost i sin t k
若: F (t ) F0 sint 则: x(t )
F0 sin t k
若: F (t ) F0 cost 则: x(t )
2 其中T为周期,记 通过谐波分析 F (t ) 可写为: T
a0 F (t ) (an cos nt bn sin nt ) 2 n1
系统的运动微分方程为:
a0 cx kx (an cos nt bn sin nt ) mx 2 n1
1
Acos cost ky
(s)
1 (1 s 2 ) 2 (2 s) 2
2 s ( s ) tan 1 s 2
0
ky my
cy 2 k ymy
s
0
y t y1 (t ) y 2 (t ) A cost ky
2 2 T bn F0 sin ntdt T F0 sin ntdt T T 2
T 2 F0 T 2 0 sin ntdt T sin ntdt T 2
2 F0 2 2 cos n T n n
任意周期激励的响应
微机械陀螺仪 功能:测量角速度
原理: 通过静电力驱动x轴的质量块(mx) 发生周期振动。 在存在角速度 (Ω ) 的情况下,周 期振动在检测轴产生科氏力,科氏力 正比于角速度。 科氏力使检测轴的质量块 (my)发 生振动,通过测量检测轴质量块的振 动幅度便可以测量得到角速度。
17
任意周期激励的响应
k y y Acos(t ) Acos cos(t ) Asin sin(t ) m y y c y y
对: Asin sin(t )
y1 (t ) 则: Asin sin t ky
若: Acos cos(t ) 则: y 2 (t )
•设: xc xe it x :稳态响应的复振幅 •代入振动微分方程,有: •令: 0 则有:
k m
c 2 km
s
0
1 1 s 2 2 si 1 i H ( ) [ ] e 2 2 2 k (1 s ) (2 s) k
振幅放大因子
mx 2e it cxie it kxe it F0e it
任意周期激励的响应
系统的稳态响应为:
a0 an cos(nt n ) bn sin(nt n ) x(t ) 2k n 1 k [1 (n / 0 ) 2 ]2 (2 n / 0 ) 2
其中
k c 0 m 20 m 2 n / 0 n arctan 1 (n / 0 ) 2
任意周期激励的响应
例:质量-弹簧系统受到周
12
t -F0 T
0
0 是系统的固有频率
求:系统的稳态响应,画出响应的频谱图
任意周期激励的响应
解:
2 0 周期方波激励的基频: T 6
周期方波可以分解为:
2 T 0 a0 T F (t )dt 2 T an F (t ) cos ntdt 0 T 2 T bn T F (t ) sin ntdt
