哈工大机电系统控制第三章答案-
工厂电气控制技术第三章习题参考答案

第三章习题参考答案1、何谓编程语言?PLC常用的编程语言主要有哪几种?解:编程语言就是用户程序的表达方式。
PLC常用的编程语言主要有:梯形图、指令语句、顺序功能图(SFC)、级式编程语言(stage)、逻辑图编程语言、高级编程语言等几种方式。
2、梯形图与继电器控制线路图有哪些异同点?解:相同点:两种图的结构类似,采用类似的图形符号。
不同点:第1,继电器线路图为并行工作方式;梯形图为串行工作方式。
第2,继电器线路图中常开、常闭接点的数量有限;梯形图中各类软器件用于内部编程的常开、常闭接点使用次数不受限制。
3、为什么在梯形图中软器件接点的使用次数不受限制?解:因为PLC内部调用的常开、常闭触头实质是位元件的电平信号,而内部电子电路采用的CMOS RAM电子电路功耗极小,从而在有限的用户程序容量内其使用次数不受限制。
4、在梯形图中地址相同的输出继电器重复使用会带来什么结果?解:plc在扫描的时候,最后扫描到的状态就是输出状态,即使你开始的程序中输出为1,如果最后的扫描为0的话,输出也是零。
5、FX2系列PLC的基本指令有几条?各条指令的功能是什么?写出图3-92所示梯形图的语句表。
解:基本指令是实现PLC基本指令功能即逻辑运算、顺序控制、定时与计数控制的指令系统。
一共20条。
各指令的功能见表3-5所示。
-1--2-6、FX2系列PLC的步进指令有几条?各有什么用途?写出图3-93所示状态转移图的等效梯形图和语句表。
解:PLC的步进指令有两条:——设置表示。
SETSTL S。
的符号由步进开始指令,操作元件是状态器STL一个状态后,则另一个状态复位。
表示步进结束。
RET后必须使用步进结束指令,无操作目标元件,在一系列RET STL-3--4-7、FX2系列PLC的功能指令有多少条?其用途是什么?如何计算功能指令块的程序步?写-5-出图3-94所示梯形图的语句表。
解:FX2的PLC功能指令可分为程序流向控制、数据传送与比较、算术与逻辑运算、数据循环与移位、数据处理、高速处理、方便控制和外部设备通信等8种类型共97条。
哈尔滨工业大学自控原理习题答案(第三章)

则根据系统框图可得
代入 ,得
另 ,得到系统的干扰输出
则误差表达式为
若积分环节加在扰动点之前则
, ,
可求得 。
若积分环节加在扰动点之后,则
, ,
可求得
由此可见在扰动点之前的前向通道加入积分环节,才能消除阶跃扰动产生的稳态误差。
3.23
设
则系统的闭环传递函数为:
误差为
将 及 得
闭环特征方程为
又因为 故系统稳定,与参数a,b无关。
若
则有系统的稳态误差
则求出待定系数为
3.29
当a=0时系统的闭环传递函数为:
则根据
得 。
当 ,根据系统的闭环传递函数为
则根据
得a=0.25
3.30
由图3.30所示的单位阶跃响应 ,可得系统的超调量和峰值时间为
又有参数间的关系:
因为系统的开环传递函数为 ,则系统的闭环传递函数为
则
得到参数为
3.34
列Routh表可得
3.12
由系统框图可知系统的开环传递函数为
因为是单位反馈,可得系统的特征方程为
如果要求闭环传递函数的特征根全部位于s=-1垂线之左,可令s=z-1,并代入特征方程,得
建立Routh表
Z3115
z21140K-27
z1 0
z040K-27
令第一列的元素全部为正,可得不等式组
解得K的取值范围为
3.14
由系统框图可以求得系统的开环传递函数为
3.1
图3.1(b)所示的单位阶跃响应具有等幅振荡特性,说明系统的阻尼比 。这与系统主反馈取“-”及内反馈取“0”相对应,因为在这种情况下该二阶系统的传递函数为
图3.1(c)所示单位阶跃响应具有发散特性,说明系统不稳定。这与系统的主反馈取“-”及内反馈取“+”相对应,因为在这种情况下,该二阶系统的传递函数为:
机电控制工程基础综合练习解答

第一章 习题答案一、填空1.系统输出全部或部分地返回到输入端叫做 反馈2.有些系统中,将开环与闭环结合在一起,这种系统称为复合控制系统3.我们把输出量直接或间接地反馈到 反馈 形成闭环参与控制的系统,称作闭环控制系统4.控制的任务实际上就是形成控制作用的规律,使不管是否存在扰动,均能使被控制对象的输出量满足给定值的要求。
5.系统受扰动后偏离了原工作状态,扰动消失后,系统能自动恢复到原来的工作状态这样的系统是 稳定 系统。
6、自动控制系统主要元件的特性方程式的性质,可以分为线性控制系统和非线性控制系统。
7、为了实现闭环控制,必须对输出量进行测量,并将测量的结果反馈到输入端与输入量相减得到偏差,再由偏差产生直接控制作用去消除偏差 。
因此,整个控制系统形成一个闭合回路。
我们把输出量直接或间接地反馈到输入端,形成闭环,参与控制的系统,称作闭环控制系统8、题图由图中系统可知,输入量直接经过控制器作用于被控制对象,当出现扰动时,没有人为干预,输出量 按照输入量所期望的状态去工作,图中系统是一个控制系统。
1、不能 开环9、如果系统受扰动后偏离了原工作状态,扰动消失后,系统能自动恢复到原来的工作状态,这样的系统称为系统,否则为 系统。
任何一个反馈控制系统能正常工作,系统必须是 的。
稳定 ; 不稳定 ; 稳定二、选择1.开环与闭环结合在一起的系统称为。
( )A 复合控制系统;B 开式控制系统;C 闭环控制系统;D 连续控制系统答:A 2.当时,闭环反馈控制系统输出的实际值∞→t 与按参考输入所确定的希望值之间的差值)(∞y )(∞r y 叫 。
( )A 微分;B 差分;C 稳态误差;D 积分答:C3.把输出量反馈到系统的输入端与输入量相减称为 。
( )A 反馈;B 负反馈;C 稳态差误;D 积分答:B4.机器人手臂运动控制属于 。
( )A 闭环控制;B 开环控制C 正反馈控制D 连续信号控制答:A5.自动售货机控制属于 。
机电自动控制课后习题答案

机电自动控制课后习题答案机电自动控制课后习题答案机电自动控制是一门综合性的学科,涵盖了机械、电子、自动化等多个领域的知识。
在学习过程中,课后习题是巩固知识、提高能力的重要途径。
下面将为大家提供一些机电自动控制课后习题的答案,希望能对大家的学习有所帮助。
第一章:基础知识1. 什么是自动控制系统?答案:自动控制系统是由传感器、执行器、控制器和反馈回路组成的系统,用于实现对某个物理过程或工业过程的自动控制。
2. 什么是反馈控制?答案:反馈控制是指通过对被控对象输出的信息进行测量,并与期望输出进行比较,然后根据比较结果调整控制器的输出,以实现对被控对象的控制。
3. 什么是传感器?答案:传感器是一种能够将被测量物理量转换为电信号或其他形式的能量输出的装置。
4. 什么是执行器?答案:执行器是一种能够接受控制信号,并将其转换为相应的动作或输出的装置。
第二章:传感器与执行器1. 常见的传感器有哪些?答案:常见的传感器包括温度传感器、压力传感器、光电传感器、接近传感器等。
2. 常见的执行器有哪些?答案:常见的执行器包括电机、气缸、液压马达等。
3. 传感器的工作原理是什么?答案:传感器的工作原理基于物理量与电信号之间的相互转换。
常见的工作原理包括电阻、电容、电感、光电、压力等。
4. 执行器的工作原理是什么?答案:执行器的工作原理根据不同的类型而有所不同。
例如,电机的工作原理是利用电磁感应产生转矩,从而实现机械运动。
第三章:控制器1. 常见的控制器有哪些?答案:常见的控制器包括PID控制器、PLC控制器、单片机控制器等。
2. PID控制器的工作原理是什么?答案:PID控制器根据当前的误差、误差的变化率和误差的积分值,计算出控制器的输出信号。
其工作原理是通过比例、积分和微分三个部分的组合,实现对被控对象的控制。
3. PLC控制器的工作原理是什么?答案:PLC控制器通过输入模块获取外部信号,经过逻辑运算、计算和控制输出模块,实现对被控对象的控制。
哈工大机电系统控制第三章答案

3-1 题图3-1所示的阻容网络中,i ()[1()1(30)](V)u t t t =--。
当t =4s 时,输出o ()u t 值为多少?当t 为30s 时,输出u o (t )又约为多少?解:661(s)1111(s)1110410141o i U sCU RCs s R sC -====+⨯⨯⨯+++(4)0.632(V)o u ≈,(30)1(V)o u ≈3-2 某系统传递函数为21()56s s s s +Φ=++,试求其单位脉冲响应函数。
解:2(s)112(s)5623o i X s X s s s s +-==+++++ 其单位脉冲响应函数为23(t)(e 2e )1()t t x t δ--=-+⋅3-3 某网络如图3-3所示,当t ≤0-时,开关与触点1接触;当t ≥0+时,开关与触点2接触。
试求输出响应表达式,并画出输出响应曲线。
1V题图3-1 题图3-3解:1(s)11(s)2121()o i R U RCs s sCU RCs s R R sC++===++++ 01(t)1(2)1()(V)i i i u u u t =+=+-⋅1111212(s)(s)121212o i s s U U s s s ss ++-===-+++ 则21(t)(e 2)1()(V)t o u t -=-⋅1201(t)1(e 2)1()(V)o o o u u u t -=+=+-⋅其输出响应曲线如图3-3所示图3-3 题图3-43-4 题图3-4所示系统中,若忽略小的时间常数,可认为1d 0.5()d yB s x-=∆。
其中,ΔB 为阀芯位移,单位为cm ,令a =b (ΔB 在堵死油路时为零)。
(1) 试画出系统函数方块图,并求(s)(s)Y X 。
(2) 当i ()[0.51()0.51(4)1(40)]cm x t t t s t s =⨯+⨯---时,试求t =0s,4s,8s,40s,400s 时的y (t )值,()B ∆∞为多少? (3) 试画出x (t )和y (t )的波形。
哈工大电机学教材答案

第一章 磁路1-1 磁路的磁阻如何计算?磁阻的单位是什么?答:磁路的磁阻与磁路的几何形状(长度、面积)和材料的导磁性能有关,计算公式为AlR m μ=,单位:Wb A1-2 铁心中的磁滞损耗和涡流损耗是怎样产生的,它们各与哪些因素有关?答:磁滞损耗:铁磁材料置于交变磁场中,被反复交变磁化,磁畴间相互摩擦引起的损耗。
经验公式V fB C p nm h h =。
与铁磁材料的磁滞损耗系数、磁场交变的频率、铁心的体积及磁化强度有关;涡流损耗:交变的磁场产生交变的电场,在铁心中形成环流(涡流),通过电阻产生的损耗。
经验公式G B f C p m Fe h 23.1≈。
与材料的铁心损耗系数、频率、磁通及铁心重量有关。
1-3 图示铁心线圈,已知线圈的匝数N=1000,铁心厚度为0.025m (铁心由0.35mm 的DR320硅钢片叠成), 叠片系数(即截面中铁的面积与总面积之比)为0.93,不计漏磁,试计算:(1) 中间心柱的磁通为4105.7-⨯Wb ,不计铁心的磁位降时所需的直流励磁电流;(2) 考虑铁心磁位降时,产生同样的磁通量时所需的励磁电流。
解: 磁路左右对称∴可以从中间轴线分开,只考虑右半磁路的情况:铁心、气隙截面2422109.293.01025.1025.0m m A A --⨯=⨯⨯⨯==δ(考虑边缘效应时,通长在气隙截面边长上加一个气隙的长度;气隙截面可以不乘系数)气隙长度m l 41052-⨯==δδ铁心长度()m cm l 21045.122025.025.15225.125.7-⨯=⨯--+⨯⎪⎭⎫⎝⎛-= 铁心、气隙中的磁感应强度T T A B B 29.1109.22105.7244=⨯⨯⨯=Φ==--δ (1) 不计铁心中的磁位降: 气隙磁场强度m A m A B H 67100.110429.1⨯=⨯==-πμδδ 磁势A A l H F F I 500105100.146=⨯⋅⨯=⋅==-δδδ电流A NF I I5.0==(2) 考虑铁心中的磁位降:铁心中T B 29.1= 查表可知:m A H 700=铁心磁位降A A l H F Fe 15.871045.127002=⨯⨯=⋅=-A A A F F F Fe I 15.58715.87500=+=+=δ A NF I I59.0≈=1-4 图示铁心线圈,线圈A 为100匝,通入电流1.5A ,线圈B 为50匝,通入电流1A ,铁心截面积均匀,求PQ两点间的磁位降。
自动控制原理第三章课后习题 答案(最新)要点

3-1(1) )(2)(2.0t r t c= (2) )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4s i n 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
解法二 依题意,系统误差定义为 )()()(t c t r t e -=,应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T s Ts Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 23-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ%、峰值时间tp 和调节时间ts 。
自动控制原理第三章课后习题答案解析(最新)

完美WORD 格式格式专业整理专业整理 知识分享知识分享3-1(1) )(2)(2.0t r t c =(2) )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==F 单位脉冲响应:s s C /10)(= 010)(³=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(³=t tt c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s f单位脉冲响应:124.004.01)(2++=s s s C t et g t4sin 325)(3-=单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t et et c tt4sin 434cos 1)(33----=3-2温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=F Ts s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Ts s s s G 1)(1)()(=F -F =îíì==11vT K用静态误差系数法,当t t r ×=10)( 时,C T Ke ss°===5.21010。
第三章 自控课后答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。
解Φ()()./(.)s L k t s ==+001251253-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述,其中,1)(0<-<τT 。
试证系统的动态性能指标为T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=τln 693.0t T r=22.TT T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ解 设单位阶跃输入ss R 1)(=当初始条件为0时有:11)()(++=Ts s s R s C τ11111)(+--=⋅++=∴Ts T s sTs s s C ττC t h t T Te t T()()/==---1τ1) 当t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; Tt T T d -⎪⎭⎫ ⎝⎛-=-τln 2ln⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求tr (即)(t c 从1.0到9.0所需时间)当 Tt eTT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt eTT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s eTT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [lnTT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
哈工大机电系统控制第三章答案-汇编
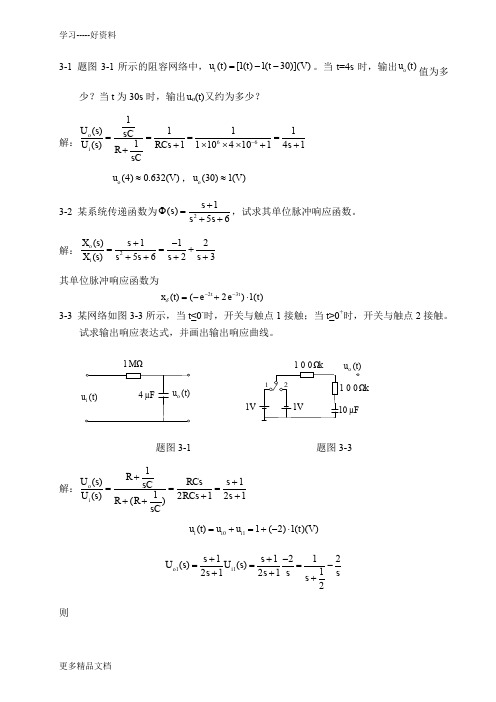
3-1 题图3-1所示的阻容网络中,i ()[1()1(30)](V)u t t t =--。
当t =4s 时,输出o ()u t 值为多少?当t 为30s 时,输出u o (t )又约为多少?解:661(s)1111(s)1110410141o i U sCU RCs s R sC -====+⨯⨯⨯+++(4)0.632(V)o u ≈,(30)1(V)o u ≈3-2 某系统传递函数为21()56s s s s +Φ=++,试求其单位脉冲响应函数。
解:2(s)112(s)5623o i X s X s s s s +-==+++++ 其单位脉冲响应函数为23(t)(e 2e )1()t t x t δ--=-+⋅3-3 某网络如图3-3所示,当t ≤0-时,开关与触点1接触;当t ≥0+时,开关与触点2接触。
试求输出响应表达式,并画出输出响应曲线。
1V题图3-1 题图3-3解:1(s)11(s)2121()o i R U RCs s sCU RCs s R R sC++===++++ 01(t)1(2)1()(V)i i i u u u t =+=+-⋅1111212(s)(s)121212o i s s U U s s s ss ++-===-+++ 则21(t)(e 2)1()(V)t o u t -=-⋅1201(t)1(e 2)1()(V)o o o u u u t -=+=+-⋅其输出响应曲线如图3-3所示图3-3 题图3-43-4 题图3-4所示系统中,若忽略小的时间常数,可认为1d 0.5()d yB s x-=∆。
其中,ΔB 为阀芯位移,单位为cm ,令a =b (ΔB 在堵死油路时为零)。
(1) 试画出系统函数方块图,并求(s)(s)Y X 。
(2) 当i ()[0.51()0.51(4)1(40)]cm x t t t s t s =⨯+⨯---时,试求t =0s,4s,8s,40s,400s 时的y (t )值,()B ∆∞为多少? (3) 试画出x (t )和y (t )的波形。
哈工大《机电系统控制器与应用》大作业三

《机电系统控制器与应用》大作业三(2015年春季学期)题目:《机电系统控制器与应用》大作业三姓名:学号:班级:专业:机械设计制造及其自动化报告提交日期:哈尔滨工业大学大作业要求1.请根据课堂内容,自己选择灯闪烁方式,题目自拟,但拒绝雷同和抄袭,否则均为零分;2.作业最后应包含自己的心得、体会或意见、建议等;3.统一用该模板撰写,每份报告字数不少于2000字,上限不限;4.正文格式:小四号字体,行距为1.25倍行距;5.用A4纸双面打印;左侧装订,1枚钉;6.需同时提交打印稿和电子文档予以存档,电子文档由班长收齐,统一发送至:chenzhg@。
7.此页不得删除。
评语:教师签名:年月日大作业题目:彩灯灯控制实验一 功能描述:本实验中利用了PLC 的Q0.0-Q0.7数字量端口控制了8个彩灯,使其每隔一秒亮一个且重复循环。
按实验接线图接通电路并载入程序之后,按下I0.0后所有的灯都熄灭了,而按下I0.1之后,所有的8个灯从Q0.0开始循环亮灭。
二 接线图: 1. I/O 口分配:2. PLC 接线图:灯控制的PLC 接线图如下所示:-+DC24V三梯形图:四连线图:五程序调试及结果分析:把编写好的程序下载到PLC中进行调试,实验结果如下图所示:结果分析:因特殊继电器SM0.0在PLC一上电后就一直保持接通。
所以T37进行延时计时,延时到后启动T38计时,T38计时到后T38常闭触点断开所以T37断开计时,T37常开触点恢复为常开所以 T38也断开计时。
此时T38的常闭触点恢复为常闭所以T37又重新计时,同时计数器C0开始计数一次。
如此的反复计数。
当计数为1时,Q0.0接通。
计数器计数为2是Q0.1接通……如此下去当计数器计数到8 时 Q0.7 接通(其中Q0.0~Q0.7分别接通8个彩灯)。
当计数器计到 9时时计数器C0清零。
当按下在线控制面板上的I0.0接通,此时计数器,和Q0.0~Q0.7都清零,即没有一个灯亮。
哈工大机电系统控制基础秋习题课第三章答案

第3章习题课答案3-1 设单位反馈系统的开环传递函数为4()(s 5)G s s =+,试求该系统的单位阶跃响应和单位脉冲响应。
解:系统闭环传递函数为24(s)44(s 5)4(s)54(s 1)(s 4)1(s 5)o i X s X s s s +===++++++ (1)当()1()i x t t =时,1()i X s s=41()41133()()()(4)(1)14o o i i X s X s X s X s s s s s s s ===-+++++则 441()1()1()1()33t tox t t e t e t --=-⋅+⋅ (2)当()()i x t t δ=时,()1i X s =44(s)433(s)(s)1(s)(s 4)(s 1)14o o i i X X X X s s ==⨯=-++++则 44()()1()3tt o x t e e t --=-⋅3-2 系统结构图如图3-70所示。
已知系统单位阶跃响应的超调量σ%3.16=%,峰值时间1=p t s 。
(1)求系统的开环传递函数)(s G ; (2)求系统的闭环传递函数)(s Φ;(3)根据已知的性能指标σ%、p t 确定系统参数K 及τ; (4)计算等速输入s t t r )(5.1)(︒=时系统的稳态误差。
解 (1) )110(10)1(101)1(10)(++=+++=ττs s K s s s s s K s G(2) 2222210)110(10)(1)()(nn n s s K s s Ks G s G s ωξωωτ++=+++=+=Φ (3)由 ⎪⎩⎪⎨⎧=-===--113.16212ξωπσςξπn p oooo t e 联立解出⎪⎩⎪⎨⎧===263.063.35.0τωξn由(2) 18.1363.31022===n K ω,得出318.1=K 。
(4) 63.31263.01018.1311010)(lim 0=+⨯=+==→τK s sG K s v 413.063.35.1===v ss K A e3-3 设图(a )所示系统的单位阶跃响应如图(b )所示。
机械控制系统工程课后习题解答

机械控制工程基础答案提示第二章 系统的数学模型2-1 试求如图2-35所示机械系统的作用力)(t F 与位移)(t y 之间微分方程和传递函数。
)(t F )(t y f图2-35 题2-1图解:依题意:()()()()22d y t dy t a m F t f ky t dt b dt⋅=⋅-⋅- 故 ()()()()t F b at ky dt t dy f dtt y d m ⋅=+⋅+22 传递函数: ()()()kfs ms b as F s Y s G ++==22-2 对于如图2-36所示系统,试求出作用力F 1(t )到位移x 2(t )的传递函数。
其中,f 为粘性阻尼系数。
F 2(t )到位移x 1(t )的传递函数又是什么?m 2m 1k 1 f k 2F 1(t )F 2(t ) x 2(t )x 1(t )图2-36 题2-2图解:依题意:对1m : ()()()()212121111dt t x d m dt t dx dtt dx f t x k F =⎥⎦⎤⎢⎣⎡---对两边拉氏变换:()()()[]()s X s m s sX s sX f x k s F 12121111=--- ①对2m : ()()()()()222222212dt t x d m t x k dt t dx dt t dx f t F =-⎥⎦⎤⎢⎣⎡-+ 对两边拉氏变换:()()()[]()()s X s m s x k s sx s sx f s F 22222212=--+ ②故: ()()()()()()()()⎩⎨⎧=+++-=-++S F s x k fs s m s fsx s F s fsx s x k fs s m 222221121121 故得:()()()()()()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧-+++++++=-+++++++⋅=22221212212122222121222211fs k fs s m k fs s m k fs s m s F s fsF s x fs k fs s m k fs s m s fsF k fs s m s F s x 故求()t F 1到()t x 2的传递函数 令:()02=s F()()()()()()()()()2122211122432121212211212x s fsG s F s m s fs k m s fs k fs fsm m s f m m s m k m k s f k k s k k ==++++-=+++++++求()t F 2到()t x 1的传递函数 令:()01=s F()()()()()()()()()1122221122432121212211212x s fsG s F s m s fs k m s fs k fs fsm m s f m m s m k m k s f k k s k k ==++++-=+++++++2-3 试求图2-37所示无源网络传递函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1 题图3-1所示的阻容网络中,i ()[1()1(30)](V)u t t t =--。
当t =4s 时,输出o ()u t 值为多少?当t 为30s 时,输出u o (t )又约为多少?解:661(s)1111(s)1110410141o i U sCU RCs s R sC -====+⨯⨯⨯+++(4)0.632(V)o u ≈,(30)1(V)o u ≈3-2 某系统传递函数为21()56s s s s +Φ=++,试求其单位脉冲响应函数。
解:2(s)112(s)5623o i X s X s s s s +-==+++++ 其单位脉冲响应函数为23(t)(e 2e )1()t t x t δ--=-+⋅3-3 某网络如图3-3所示,当t ≤0-时,开关与触点1接触;当t ≥0+时,开关与触点2接触。
试求输出响应表达式,并画出输出响应曲线。
1V题图3-1 题图3-3解:1(s)11(s)2121()o i R U RCs s sCU RCs s R R sC++===++++01(t)1(2)1()(V)i i i u u u t =+=+-⋅1111212(s)(s)121212o i s s U U s s s ss ++-===-+++ 则21(t)(e 2)1()(V)t o u t -=-⋅1201(t)1(e 2)1()(V)o o o u u u t -=+=+-⋅其输出响应曲线如图3-3所示图3-3 题图3-43-4 题图3-4所示系统中,若忽略小的时间常数,可认为1d 0.5()d yB s x-=∆。
其中,ΔB 为阀芯位移,单位为cm ,令a =b (ΔB 在堵死油路时为零)。
(1) 试画出系统函数方块图,并求(s)(s)Y X 。
(2) 当i ()[0.51()0.51(4)1(40)]cm x t t t s t s =⨯+⨯---时,试求t =0s,4s,8s,40s,400s 时的y (t )值,()B ∆∞为多少? (3) 试画出x (t )和y (t )的波形。
解:(1)依题意可画出如图3-4所示的系统函数方块图,图3-4-1则10.5(s)1210.5X(s)4112Y sss⨯==++⨯(2)该一阶惯性环节的时间常数为4(s)T=当(t)[0.51()0.51(4)1(40)](cm)x t t t=⋅+⋅---时,(0)0(cm)y=(4)0.50.6320.316(cm)y≈⨯=(8)0.50.8660.50.6320.749(cm)y≈⨯+⨯=(40)1(cm)y≈(400)0(cm)y≈()0(cm)B∆∞=(3)x(t)和y(t)的波形如图3-4-2(a)、(b)所示。
图3-4-23-5 设单位反馈系统的开环传递函数为4()(s5)G ss=+,试求该系统的单位阶跃响应和单位脉冲响应。
解:系统闭环传递函数为24(s)44(s5)4(s)54(s1)(s4)1(s5)oiX sX s ss+===++++++(1)当()1()ix t t=时,1()iX ss=41()41133()()()(4)(1)14o o i i X s X s X s X s s s s s s s ===-+++++g则441()1()1()1()33t t o x t t e t e t --=-⋅+⋅(2)当()()i x t t δ=时,()1i X s =44(s)433(s)(s)1(s)(s 4)(s 1)14o o i i X X X X s s ==⨯=-++++则44()()1()3tt o x t e e t --=-⋅ 3-6 设单位反馈系统的开环传递函数为1()(s 1)G s s =+,试求系统的上升时间、峰值时间、最大超调量和调整时间。
当()(s 1)KG s s =+时,试分析放大倍数K 对单位阶跃输入产生的输出动态过程特性的影响。
解:(1)2221(s)1(s 1)1(s)20.5111(s 1)o i X s X s s s +==+⨯⨯+++ 得1(rad/s)n ω=则0.5ζ=s)d ωω===arccos arccos0.5(rad)3πθζ===所以2.418(s)r t ππ-=≈3.628(s)r d t πω==≈16.3%p M ee==≈336(s)10.5r n t ωζ≈==⨯(进入5%误差带) (2)222(s)(s 1)1(s)12(s 1)o i KX s K X s s +==++++ 得s)n ω=则ζ=s)2d ωω===arccos θζ==则(Ⅰ)当1ζ==时,即14K =时,系统为临界阻尼,系统不产生振荡。
(Ⅱ)当1ζ=>时,即14K <时,系统为过阻尼,系统不产生振荡。
(Ⅲ)当0ζ==时,即K =∞时,系统为零阻尼,系统产生振荡。
(Ⅳ)当01ζ<<,即14K <<∞时,系统为欠阻尼,此时2r dt πθω-== K 增大时,r t 减小。
2p dt πω==K 增大时,p t 减小。
p M eee===K 增大时,p M 也增大。
336(s)1s n t ωζ===当K 较大时,s t 基本不受K 变化的影响。
3-7 已知一系统由下述微分方程描述:10x y dtdy2dt y d 2<<=++ξξ, 当x (t )=1(t )时,试求最大超调量。
解:将微分方程两边取拉氏变换得2(s)2sY(s)Y(s)X(s)s Y ζ++=则2(s)1(s)21Y X s s ζ=++,01ζ<<max ()|()()p y t y M ey -∞==∞3-8 设有一系统的传递函数为222()2nn nωG s s ξωs ω=++,为使系统对阶跃响应有5%的超调量和2 s 的调整时间,试求ζ和n ω。
解:510032ne ζω⎧⎪=⎪⎨⎪=⎪⎩ 解之,得0.69ζ≈, 2.2(rad/s)n ω=3-9 证明对于题图3-9所示系统,o i (s)(s)X X 在右半s 平面上有零点,当x i (t )为单位阶跃时,求y (t )。
解:(s)642(s 1)(s)21(s 1)(2)Y X s s s -=-=++++由上式可见,s=1是系统在右半s 平面的零点。
当(t)1(t)x =时2(s 1)1431(s)(s 1)(s 2)12Y s s s s-==--++++则2(t)(4e 3e 1)1(t)t t y --=--⋅3-10 设一单位反馈系统的开环传递函数为10()(s 1)G s s =+,该系统的阻尼比为0.157,无阻尼自振角频率为3.16 rad/s ,现将系统改变为如题图3-10所示,使阻尼比为0.5。
试确定n K 值。
题图3-9 题图3-10解: 10(s)(s 1)10(1K s)(s)1(s 1)o n i X s X s +=+++222210(110K )s 103.16(110K )s 3.16n n s s =+++=+++依题意,有110220.5 3.16 3.16n n K ζω+==⨯⨯= 解之,得0.216n K =,即为所求。
3-11 二阶系统在s 平面中有一对复数共轭极点,试在s 平面中画出与下列指标相应的极点可能分布的区域:(1) n 0.7072rad /s ξω≥>,; (2) n 00.7072rad /s ξω≤≤≤,; (3) 00.5ξ≤≤,n 2rad /s 4rad /s ω≤≤;(4) n 00.7072rad /s ξω≤≤≤,。
解:(1)所求区域为图3-11(a)中阴影部分。
(2)所求区域为图3-11(b)中阴影部分。
(3)所求区域为图3-11(c)中阴影部分。
(4)所求区域为图3-11(d)中阴影部分。
(a) (b)(c) (d)图3-113-12 设一系统如题图3-12(a)所示。
(1) 当控制器c ()1G s =时,求单位阶跃输入时系统的响应。
设初始条件为零,讨论L 和J 对响应的影响。
(2) 设c d ()1s G s T =+,J =1000,为使系统为临界阻尼,求d T 值。
(3) 现在要求得到一个没有过调的响应,输入函数形式如题图3-12(b)所示。
设c ()1G s =,L 和J 参数同前,求K 和t 1。
i ()X s +-()o X s 2s LJ c ()G s ()E s U(a)tx o (t )tx i (t )10K t 1t(b) 题图3-12解:(1)222(s)(s)1o i L L X Js J L L X s Js J==++则211(s)o L JX Ls s s J ==-+对上式进行拉氏反变换,得(t)1(t)1(t)o X =-⋅由此可知,其单位阶跃响应为等幅振荡,当L 增大、J 减小时,角频率ω增大。
(2)22(1T s)(s)(s)1(1T s)d o i d LX Js L X Js +==++为使系统为临界阻尼,需使1ζ=,即20d T === 由(1)知(s)(s)o i X X =当(t)1(t)i x =时(t)(11(t)o x =-⋅所以110t π==== 另有1(1)(1)[1)]1K K t t -+---= 当110t t π==,10L =,1000J =代入上式,得[(110)](1)[10]1K πK -+--= 解之,得0.5K =3-13 题图3-13所示为宇宙飞船姿态控制系统方块图。
假设系统中控制器时间常数T =3 s ,力矩与惯量比为22rad /9K s J =。
试求系统阻尼比。
题图3-13解:221(1)(s)1(s)1(1)o i K Ts X Js X K Ts Js+=++(1)KTs +=则3220.7072292T KJζ===≈3-14 设一伺服电动机的传递函数为()()1s KU s TsΩ=+。
假定电动机以ω的恒定速度转动,当电动机的控制电压u o突然降到0时,试求其速度响应方程式。
解:电动机的控制电压如图3-14所示图3-1422()()111o o oU KU KUK Ks U sTs Ts s ssT-Ω===-+++则2()(1)1()tTot KU e tω-=-⋅又有10()ot KUωω==所以120()()()1()tTt t t e tωωωω-=+=⋅3-15 对于题图3-15所示的系统,如果将阶跃输入iθ作用于该系统,试确定表述角度位置0θ的方程式。
假定该系统为欠阻尼系统,初始状态静止。
iθokJD题图3-15解:依题意,有[()()]()()o o i o K t t D t J t θθθθ•••--=得2()()o i t Kt Js Ds Kθθ==++则n ω=ζ= 所以,当()1()i t a t θ=⋅时()[1arccos )]1()n t o t a t ζωθωζ-=-+⋅2[1sin(1()2Dt Ja t J -=-+⋅3-16 某系统如题图3-16所示,试求单位阶跃响应的最大超调量M p 、上升时间t r 和调整时间t s 。
