求三角函数定义域和值域题型
三角函数值域的求法及例题
标题：三角函数值域的求法及其应用
一、基本概念：
三角函数是描述周期性现象的关键工具，特别是一元函数微积分中的基本函数。
它们的值域，即能够表示的函数的取值范围，对于理解函数的性质和图形至关重要。
二、求值域的方法：
1. 观察法：根据三角函数的定义，我们知道正弦、余弦和正切函数的值域分别是-1 到1（包括-1，但不包括0），0 到正无穷（包括0），以及-π/2 到π/2（包括0，但不包括π/2 和-π/2）。
当已知函数的表达式时，可以通过观察函数的定义域和函数自身的性质来求值域。
2. 三角函数不等式法：可以利用三角函数的不等式来求值域，例如：对于正弦函数，有0 <= sin(x) <= 1。
3. 反函数法：对于反三角函数，如arcsin(x) 和arctan(x)，可以通过求其反函数的定义域来得到值域。
4. 换元法：对于某些复杂的三角函数，可以通过换元法将问题简化。
5. 判别式法：对于二次或高次方程的解，可以通过判别式小于或等于零来求出函数的值域。
三、例题解析：
【例题】求函数f(x) = 3sin(2x + π/6) 的值域。
解：首先，我们可以看出函数的定义域为R（即所有实数），且函数的周期性表现为sin(x) 的形式。
由于正弦函数的值域为-1 到1（包括-1，但不包括0），因此我们可以得出f(x) 的值域为[-3, 3]。
四、总结：
求三角函数值域的方法多种多样，观察法、三角函数不等式法、反函数法、换元法以及判别式法都是常见的方法。
理解这些方法并灵活运用，可以帮助我们更好地解决实际问题。
以上就是关于三角函数值域求法的介绍以及例题解析，希望对你有所帮助。
三角函数的定义域与值域题库(精)
专题三：三角函数的定义域与值域（习题库）一、选择题1、函数f（x）的定义域为[﹣，]，则f（sinx）的定义域为（）A、[﹣，]B、[，]C、[2kπ+，2kπ+]（k∈Z）D、[2kπ﹣，2kπ+]∪[2kπ+，2kπ+]（k∈Z）分析：由题意知，求出x的范围并用区间表示，是所求函数的定义域；解答：∵函数f（x）的定义域为为[﹣，]，∴，解答（k∈Z）∴所求函数的定义域是[2kπ﹣，2kπ+]∪[2kπ+，2kπ+]（k∈Z）故选D．2、函数的定义域是（）A、.B、.C、D、.解答：由题意可得sinx﹣≥0⇒sinx≥又x∈（0，2π）∴函数的定义域是．故选B．3、函数的定义域为（）A、 B、C、 D、解答：由题意得tanx≥0，又tanx 的定义域为（kπ﹣，kπ+），∴，故选D．4、函数f（x）=cosx（cosx+sinx），x∈[0，]的值域是（）A、[1，]B、C、D、解答：∵f（x）=cosx（cosx+sinx）=cos2x+sinxcosx===又∵∴∴则1≤f（x）≤故选A．5、函数y=﹣cos2x+sinx﹣的值域为（）A、[﹣1，1]B、[﹣，1]C、[﹣，﹣1]D、[﹣1，]解答：函数y=﹣cos2x+sinx﹣=﹣（1﹣2sin2x）+sinx﹣=sin2x+sinx﹣1=﹣∵﹣1≤sinx≤1，∴当sinx=﹣时，函数y有最小值为﹣．sinx=1时，函数y 有最大值为1，故函数y 的值域为[﹣，1]，故选B．6、函数值域是（）A、 B、C、 D、[﹣1，3]解答：因为，所以sinx∈[]，2sinx+1∈故选B7、函数的最大值是（）A、5B、6C、7D、8解答：∵==∈[﹣7，7] ∴函数的最大值是78、若≤x≤，则的取值范围是（）A、[﹣2，2]B、C、D、解答：=2（sinx+cosx）=2sin（），∵≤x≤，∴﹣≤≤，∴≤﹣sin（）≤1，则函数f（x）的取值范围是：．故选C．9、若，则函数y=的值域为（）A、 B、 C、 D、解答：函数y===因为，所以sin∈（0，）∈故选D10、函数，当f（x）取得最小值时，x的取值集合为（）A、 B、C、 D、解答：∵函数，∴当 sin（﹣）=﹣1时函数取到最小值，∴﹣=﹣+2kπ，k∈Z函数，∴x=﹣+4kπ，k∈Z，∴函数取得最小值时所对应x的取值集合:为{x|x═﹣+4kπ，k∈Z} 故选A．11、函数y=sin2x﹣sinx+1（x∈R）的值域是（）A、[，3]B、[1，2]C、[1，3]D、[，3]解答：令sinx=t，则y=t2﹣t+1=（t﹣）2+，t∈[﹣1，1]，由二次函数性质，当t=时，y取得最小值．当t=﹣1时，y取得最大值3，∴y∈[，3] 故选A．12、已知函数，则f（x）的值域是（）A、[﹣1，1]B、C、D、解答：解：由题=，当 x∈[，]时，f（x）∈[﹣1，]；当 x∈[﹣，]时，f （x）∈[﹣1，]可求得其值域为．故选D．13、函数的值域为（）A、 B、 C、[﹣1，1] D、[﹣2，2]解答：=﹣sinxcosx+cos2x=cos2x ﹣sin2x=cos （2x+）∴函数的值域为[﹣1，1] 故选C ．14、若≥，则sinx 的取值范围为（ ） A 、 B 、 C 、∪D 、∪解答：∵≥，∴解得x ∈[，）∪（，] ∴sinx ∈故选B15、函数y=sin2x+2cosx 在区间[﹣，]上的值域为（ ）A 、[﹣，2]B 、[﹣，2）C 、[﹣，]D 、（﹣，] 解答：∵x ∈[﹣，] ∴cosx ∈[﹣，1]又∵y=sin2x+2cosx=1﹣cos2x+2cosx=﹣（cosx ﹣1）2+2 则y ∈[﹣，2] 故选A 二、填空题（共7小题） 16、已知，则m 的取值范围是 ．解答：∵=2（sinθ+cosθ）=2sin（θ+），∴﹣2≤≤2，∴m≥，或m≤﹣，故m的取值范围是（﹣∝，﹣]∪[，+∞）．17、函数在上的值域是___________．解答：因为，故故答案为：18、函数的值域为．解答：由题意是减函数，﹣1≤sinx≤1，从而有函数的值域为，故答案为19、（理）对于任意，不等式psin2x+cos4x≥2sin2x恒成立，则实数p的范围为．解答：∵psin2x+cos4x≥2sin2x ∴psin2x≥2sin2x﹣1﹣sin4x+2sin2x=4sin2x﹣sin4x﹣1∴p≥4﹣（sin2x+）而sin2x+≥2∴4﹣（sin2x+）的最大值为2则p≥2 故答案为：[2，+∞）20、函数的值域是．解答：令t=sinx+cosx=，t2=1+2sinxcosx∵∴x+∴从而有:f（x）==﹣2 在单调递增当t+1=2即t=1时，此时x=0或x=，函数有最小值当t+1=1+即t=时此时x=，函数有最大值2﹣2故答案为：[﹣2]21、函数的定义域为．解答：要使函数有意义，必须解得，故答案为：（0，）．三、解答题（共8小题）22.（1）已知f（x）的定义域为［0，1］，求f（cosx）的定义域；（2）求函数y=lgsin（cosx）的定义域；分析：求函数的定义域：（1）要使0≤cosx≤1，（2）要使sin （cosx）＞0，这里的cosx以它的值充当角。
三角函数的定义域、值域及单调区间(含答案)
三角函数的定义域、值域及单调区间一、单选题(共12道，每道8分)1.与函数定义域相同的一个函数是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：三角函数的定义域2.函数的定义域是( )A.B.C.D.答案：C解题思路：试题难度：三颗星知识点：三角函数的定义域3.函数的定义域是( ) A.B.C.D.答案：D解题思路：试题难度：三颗星知识点：三角函数的定义域4.的值域是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：三角函数的值域5.函数的值域是( )A.{3}B.{3，﹣1}C.{3，1，﹣1}D.{3，1，﹣1，﹣3}答案：B解题思路：试题难度：三颗星知识点：三角函数的值域6.函数的值域是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：三角函数的值域7.已知函数，则f(x)在区间上的最大值与最小值分别是( )A.1，﹣2B.2，﹣1C.1，﹣1D.2，﹣2答案：A解题思路：试题难度：三颗星知识点：三角函数的最值8.已知函数的定义域为，值域为，则函数上，( )A.有最大值2B.有最小值2C.有最大值1D.有最小值1答案：B解题思路：试题难度：三颗星知识点：三角函数的最值9.函数的单调增区间为( ) A.B.C.D.答案：A解题思路：试题难度：三颗星知识点：复合三角函数的单调性10.设函数，在区间D上单调递增，则区间D可以是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：复合三角函数的单调性11.函数的单调增区间是( )A.B.C.D.答案：A解题思路：先确定函数的定义域是全体实数，记，则，∵是递增函数，∴根据口诀“同增异减”可得，只需要找到的递增区间即可，∴．故选A试题难度：三颗星知识点：复合三角函数的单调性12.函数的单调递减区间是( ) A.B.C.D.答案：D解题思路：试题难度：三颗星知识点：复合三角函数的单调性第11页共11页。
三角函数的值域问题
y sin x
y cos x
2
(k∈z)
2
时y min 1 x 2k 时y min 1
(k∈z)
二、新课讲解
• 下列函数有最大值、最小值吗？如果有，请写出 取最大值、最小值时的自变量x的集合，并说出 最大值、最小值分别是什么？ • (1)y=2sinx, xR • (2)y=-3sinx,xR • (3)y=asinx,xR(a>0) • (4)y=asinx,xR(a<0) • (5)y=asinx,xR(a≠0)
类型二：求y A sin( x )型函数的的值域与最值
例3：求函数y 2 sin( 2 x )的最值，并求取得最值时 3 自变量x的集合。
1 变式1：函数y 3 2 sin( x )的值域为 ______ . 2 3 变式2：已知y a sin( 2 x ) b(a 0)的最大值为3, 3 最小值为 1, 求a, b的值.
当题目中有出现自变量x属于某个小区间，那么
要用换元 2 x )的范围。 3
类型三：值域与最值的应用
延伸:
0 (2014 湖北高考改编)某实验室一天的温度(单位： C)
随时间t (单位：h)的变化近似满足函数： t )，t 0,24 12 6 求实验室一天的最大温差。 f (t ) 10 2 sin(
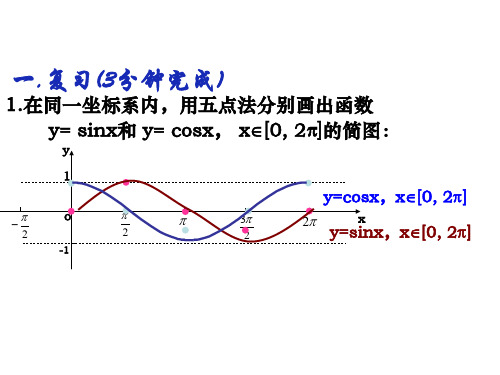
1.在同一坐标系内，用五点法分别画出函数 y= sinx和 y= cosx， x[0, 2]的简图：
y
1
一.复习
y=cosx，x[0, 2]
2
o
-1
2
3 2
三角函数的定义域与值域题库
专题三：三角函数的定义域与值域（习题库）一、选择题1、函数f（x）的定义域为[﹣，]，则f（sinx）的定义域为（）A、[﹣，]B、[，]C、[2kπ+，2kπ+]（k∈Z）D、[2kπ﹣，2kπ+]∪[2kπ+，2kπ+]（k∈Z）分析：由题意知，求出x的范围并用区间表示，是所求函数的定义域；解答：∵函数f（x）的定义域为为[﹣，]，∴，解答（k∈Z）∴所求函数的定义域是[2kπ﹣，2kπ+]∪[2kπ+，2kπ+]（k∈Z）故选D．2、函数的定义域是（）A、.B、.C、D、.解答：由题意可得sinx﹣≥0⇒sinx≥又x∈（0，2π）∴函数的定义域是．故选B．3、函数的定义域为（）A、B、C、 D、解答：由题意得tanx≥0，又tanx 的定义域为（kπ﹣，kπ+），∴，故选D．4、函数f（x）=cosx（cosx+sinx），x∈[0，]的值域是（）A、[1，]B、C、D、解答：∵f（x）=cosx（cosx+sinx）=cos2x+sinxcosx===又∵∴∴则1≤f（x）≤故选A．5、函数y=﹣cos2x+sinx﹣的值域为（）A、[﹣1，1]B、[﹣，1]C、[﹣，﹣1]D、[﹣1，]解答：函数y=﹣cos2x+sinx﹣=﹣（1﹣2sin2x）+sinx﹣=sin2x+sinx﹣1=﹣∵﹣1≤sinx≤1，∴当sinx=﹣时，函数y有最小值为﹣．sinx=1时，函数y 有最大值为1，故函数y 的值域为[﹣，1]，故选B．6、函数值域是（）A、B、 C、D、[﹣1，3]解答：因为，所以sinx∈[]，2sinx+1∈故选B7、函数的最大值是（）A、5B、6C、7D、8解答：∵==∈[﹣7，7] ∴函数的最大值是78、若≤x≤，则的取值范围是（）A、[﹣2，2]B、C、D、解答：=2（sinx+cosx）=2sin（），∵≤x≤，∴﹣≤≤，∴≤﹣sin（）≤1，则函数f（x）的取值范围是：．故选C．9、若，则函数y=的值域为（）A、B、 C、D、解答：函数y===因为，所以sin∈（0，）∈故选D10、函数，当f（x）取得最小值时，x的取值集合为（）A、 B、C、 D、解答：∵函数，∴当 sin（﹣）=﹣1时函数取到最小值，∴﹣=﹣+2kπ，k∈Z函数，∴x=﹣+4kπ，k∈Z，∴函数取得最小值时所对应x的取值集合:为{x|x═﹣+4kπ，k∈Z}故选A．11、函数y=sin2x﹣sinx+1（x∈R）的值域是（）A、[，3]B、[1，2]C、[1，3]D、[，3]解答：令sinx=t，则y=t2﹣t+1=（t﹣）2+，t∈[﹣1，1]，由二次函数性质，当t=时，y取得最小值．当t=﹣1时，y取得最大值3，∴y∈[，3] 故选A．12、已知函数，则f（x）的值域是（）A、[﹣1，1]B、C、D、解答：解：由题=，当x∈[，]时，f（x）∈[﹣1，]；当x∈[﹣，]时，f（x）∈[﹣1，] 可求得其值域为．故选D．13、函数的值域为（）A、B、 C、[﹣1，1] D、[﹣2，2]解答：=﹣sinxcosx+cos2x=cos2x﹣sin2x=cos（2x+）∴函数的值域为[﹣1，1] 故选C．14、若≥，则sinx的取值范围为（）A、 B、C、∪D、∪解答：∵≥，∴解得x∈[，）∪（，] ∴sinx∈故选B15、函数y=sin2x+2cosx在区间[﹣，]上的值域为（）A、[﹣，2]B、[﹣，2）C、[﹣，]D、（﹣，]解答：∵x∈[﹣，] ∴cosx∈[﹣，1]又∵y=sin2x+2cosx=1﹣cos2x+2cosx=﹣（cosx﹣1）2+2则y∈[﹣，2] 故选A二、填空题（共7小题）16、已知，则m的取值范围是．解答：∵=2（sinθ+cosθ）=2sin（θ+），∴﹣2≤≤2，∴m≥，或m≤﹣，故m的取值范围是（﹣∝，﹣]∪[，+∞）．17、函数在上的值域是___________．解答：因为，故故答案为：18、函数的值域为．解答：由题意是减函数，﹣1≤sinx≤1，从而有函数的值域为，故答案为19、（理）对于任意，不等式psin2x+cos4x≥2sin2x恒成立，则实数p的范围为．解答：∵psin2x+cos4x≥2sin2x ∴psin2x≥2sin2x﹣1﹣sin4x+2sin2x=4sin2x﹣sin4x ﹣1∴p≥4﹣（sin2x+）而sin2x+≥2∴4﹣（sin2x+）的最大值为2则p≥2故答案为：[2，+∞）20、函数的值域是．解答：令t=sinx+cosx=，t2=1+2sinxcosx∵∴x+∴从而有:f（x）==﹣2在单调递增当t+1=2即t=1时，此时x=0或x=，函数有最小值当t+1=1+即t=时此时x=，函数有最大值2﹣2故答案为：[﹣2]21、函数的定义域为．解答：要使函数有意义，必须解得，故答案为：（0，）．三、解答题（共8小题）22.（1）已知f（x）的定义域为［0，1］，求f（cosx）的定义域；（2）求函数y=lgsin（cosx）的定义域；分析：求函数的定义域：（1）要使0≤cosx≤1，（2）要使sin（cosx）＞0，这里的cosx以它的值充当角。
三角函数的定义域、值域和最值
三角函数的定义域、值域和最值一 知识点精讲：1 三角函数的定义域 （1）r y =αsin 定义域为R. （2）rx =αcos 定义域为R.（3）xy =αtan 定义域为 ⎭⎬⎫⎩⎨⎧∈+≠Z k k ,2|ππαα. （4）y x =αcot 定义域为{}Z k k ∈≠,|παα.2 三角函数的值域① )0(,sin ≠+=a b x a y 型当0>a 时，],[b a b a y ++-∈ ； 当0<a 时 ],[b a b a y +-+∈ ② c x b x a y ++=sin sin2型此类型的三角函数可以转化成关于sinx 的二次函数形式。
通过配方，结合sinx 的取值范围，得到函数的值域。
x sin 换为x cos 也可以。
③ x b x a y cos sin +=型 利用公式ab x b a x b x a =++=+φφtan ),sin(cos sin 22， 可以转化为一个三角函数的情形。
④x x b x x a y cos sin )cos (sin ++=型利用换元法，设x x t cos sin +=, ]2,2[-∈t ，则212cos sin -=t x x ,转化为关于t 的二次函数222122b at t b t bat y -+=-+=.⑤x x c x b x a y cos sin cos sin 22++=型这是关于x x cos ,sin 的二次齐次式，通过正余弦的降幂公式以及正弦的倍角公式，22sin cos sin ,22cos 1cos,22cos 1sin22x x x xx xx =+=-=，可转化为p x n x m y ++=2cos 2sin 的形式。
⑥ d x c bx a y ++=sin sin 型 可以分离常数，利用正弦函数的有界性。
⑦bx ax y ++=cos sin 型 可以利用反解的思想方法，把分母乘过去，整理得，a by x y x -=-cos sin ，11,1)sin(22≤+-+-=-ya by ya by x φ, 通过解此不等式可得到y的取值范围。
高三高考文科数学《三角函数》题型归纳与汇总
高三高考文科数学《三角函数》题型归纳与汇总高考文科数学题型分类汇总：三角函数篇本文旨在汇总高考文科数学中的三角函数题型，包括定义法求三角函数值、诱导公式的使用、三角函数的定义域或值域、三角函数的单调区间、三角函数的周期性、三角函数的图象变换和三角函数的恒等变换。
题型一：定义法求三角函数值这类题目要求根据三角函数的定义，求出给定角度的正弦、余弦、正切等函数值。
这类题目的难点在于熟练掌握三角函数的定义，以及对角度的准确度量。
题型二：诱导公式的使用诱导公式是指通过对已知的三角函数进行代数变形，得到新的三角函数值的公式。
这类题目需要熟练掌握各种诱导公式，以及灵活应用。
题型三：三角函数的定义域或值域这类题目要求确定三角函数的定义域或值域。
需要掌握各种三角函数的性质和图象，以及对函数的定义域和值域的概念和计算方法。
题型四：三角函数的单调区间这类题目要求确定三角函数的单调区间，即函数在哪些区间上单调递增或单调递减。
需要掌握各种三角函数的性质和图象，以及对函数单调性的判定方法。
题型五：三角函数的周期性这类题目要求确定三角函数的周期。
需要掌握各种三角函数的性质和图象，以及对函数周期的计算方法。
题型六：三角函数的图象变换这类题目要求根据给定的变换规律，确定三角函数图象的变化。
需要掌握各种三角函数的性质和图象，以及对图象变换的计算方法。
题型七：三角函数的恒等变换这类题目要求根据已知的三角函数恒等式，进行变形和推导。
需要掌握各种三角函数的恒等式，以及灵活应用。
2）已知角α的终边经过一点P，则可利用点P在单位圆上的性质，结合三角函数的定义求解．在求解过程中，需注意对角终边位置进行讨论，避免忽略或重复计算．例2已知sinα=0.8，且α∈[0,π2]，则cosα=．答案】0.6解析】∵sinα=0.8，∴cosα=±√1-sin²α=±0.6XXXα∈[0,π2]，∴cosα>0，故cosα=0.6易错点】忘记对cosα的正负进行讨论思维点拨】在求解三角函数值时，需注意根据已知条件确定函数值的正负，避免出现多解或无解的情况．同时，需根据角度范围确定函数值的取值范围，避免出现超出范围的情况．题型二诱导公式的使用例3已知tanα=√3，且α∈(0,π2)，则sin2α=．答案】34解析】∵ta nα=√3，∴α=π/30<α<π/2，∴0<2α<πsin2α=sin(π-2α)=sinπcos2α-cosπsin2α=-sin2α2sin2α=0，∴sin2α=0sin2α=3/4易错点】忘记利用诱导公式将sin2α转化为sin(π-2α)思维点拨】在解决三角函数的复合问题时，可利用诱导公式将一个三角函数转化为其他三角函数的形式，从而简化计算．同时，需注意根据角度范围确定函数值的取值范围，避免出现超出范围的情况．题型三三角函数的定义域或值域例4已知f(x)=2sinx+cosx，则f(x)的值域为．答案】[−√5,√5]解析】∵f(x)=2sinx+cosx=√5(sin(x+α)+sin(α-x))，其中tanα=-121≤sin(x+α)≤1，-1≤sin(α-x)≤15≤f(x)≤√5f(x)的值域为[−√5,√5]易错点】忘记利用三角函数的性质将f(x)转化为含有同一三角函数的形式思维点拨】在确定三角函数的定义域或值域时，可利用三角函数的性质将其转化为含有同一三角函数的形式，从而方便计算．同时，需注意对于复合三角函数，需先将其转化为含有同一三角函数的形式，再确定其定义域或值域．题型四三角函数的单调区间例5已知f(x)=sin2x，则f(x)在区间[0,π]上的单调递增区间为．答案】[0,π/4]∪[3π/4,π]解析】∵f'(x)=2cos2x=2(2cos²x-1)=4cos²x-2f'(x)>0的充要条件为cosx12f(x)在[0,π/4]∪[3π/4,π]上单调递增易错点】忘记将f'(x)化简为含有同一三角函数的形式，或对于三角函数的单调性判断不熟练思维点拨】在求解三角函数的单调区间时，需先求出其导数，并将其化简为含有同一三角函数的形式．然后，利用三角函数的单调性进行判断，得出函数的单调区间．题型五三角函数的周期性例6已知f(x)=sin(2x+π)，则f(x)的周期为．答案】π解析】∵sin(2x+π)=sin2xcosπ+cos2xsinπ=-sin2xf(x)的周期为π易错点】忘记利用三角函数的周期性质思维点拨】在求解三角函数的周期时，需利用三角函数的周期性质，即f(x+T)=f(x)，其中T为函数的周期．同时，需注意对于复合三角函数，需先将其转化为含有同一三角函数的形式，再确定其周期．题型六三角函数的图象变换例7已知f(x)=sinx，g(x)=sin(x-π4)，则g(x)的图象相对于f(x)的图象向左平移了．答案】π4解析】∵g(x)=sin(x-π4)=sinxcosπ4-cosxsinπ4g(x)的图象相对于f(x)的图象向左平移π4易错点】忘记利用三角函数的图象变换公式，或对于三角函数的图象不熟悉思维点拨】在求解三角函数的图象变换时，需利用三角函数的图象变换公式，即y=f(x±a)的图象相对于y=f(x)的图象向左（右）平移a个单位．同时，需对于各种三角函数的图象有一定的了解，以便准确判断图象的变化情况．题型七三角函数的恒等变换例8已知cosα=12，且α∈(0,π2)，则sin2α的值为．答案】34解析】∵cosα=12，∴sinα=√3/2sin2α=2sinαcosα=√3/2×1/2=3/4易错点】忘记利用三角函数的恒等变换公式思维点拨】在求解三角函数的恒等变换时，需熟练掌握三角函数的基本恒等式和常用恒等式，从而简化计算．同时，需注意根据已知条件确定函数值的正负，避免出现多解或无解的情况．已知角α的终边所在的直线方程，可以通过设出终边上一点的坐标，求出此点到原点的距离，然后利用三角函数的定义来解决相关问题。
三角函数定义域-值域-周期测试题
数学限时测试三 一、选择题1、 在同一坐标系中函数[]π2,0,sin ∈=x x y 与[]ππ4,2,sin ∈=x x y 的图象A ．重合B ．形状相同，位置不同C ．形状不同，位置相同D ．形状不同，位置不同2、函数[]π2,0,sin 1∈+=x x y 的图象与直线2=y 的交点个数为A ．0B ．1C ．2D ．33、在(02)π，内，使sin cos x x <成立的x 的取值范围是（ ）Ａ．ππ5π⎛⎫⎛⎫π ⎪⎪424⎝⎭⎝⎭，， Ｂ．π⎛⎫π ⎪4⎝⎭， Ｃ．02π5π⎛⎫⎛⎫π ⎪ ⎪44⎝⎭⎝⎭，， Ｄ．5ππ⎛⎫⎪44⎝⎭，4、若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（）A B ．1 CD ．25、当-π2≤x≤π2时，函数f(x)= sinx +3cosx 的（ ）A 、最大值是1，最小值是--1B 、最大值是1，最小值是--2C 、最大值是2，最小值是--2D 、最大值是2，最小值是--1 6、函数f (x )＝3sin x +sin(π2+x )的最大值是（ ）A ．1BCD ．27、函数y=1-sinx+3cosx 的周期是（ ）A. πB. π2C. π21D. 32π 8、求y=sin 2x+2sinxcosx+3cos 2x 的周期是（ ）A. πB. π2C. π3D. 4π 9、函数y = 12cos 2sin -+x x 的定义域是A [ 0 ,4π] B [ 42,2πππ+k k ]C [2,πππ+k k ] D [432,42ππππ++k k ]10．函数2cos 3cos 2++=x x y 的最小值为（ ）A ．2B ．0C ．1D ．6班别__________ 姓名__________二.填空题：11.如果直线m y =与函数[)π2,0,sin ∈=x x y 无交点，则∈m __________；12.求函数y ＝2cos 2x ＋5sinx －4的值域为__________；三.解答题：13.求函数)2474(cos sin 4sin 3cos 35)(22ππ≤<-+=x x x x x x f 的最值，并求取得最值时x 的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(2)要使函数有意义，必须使sin x＞
x≠
x＞－12.
得 2kπ＜x＜2kπ＋π，
∴原函数的定义域为
≠2kπ＋π， 2
－23π＜x＜2kπ＋23π， (k∈Z)．
(2kπ，2kπ＋π2)∪(2kπ＋π2，2kπ＋23π)(k∈Z)．
函数的定义域主要考虑以下几点：偶次根号下不小于 0；对数的真数大于 0，底数大于 0 且不等于 1；分母不能为 0 等．一般我们解满足这些条件的不等式求出 x 的 取值范围，再取交集即可．
•
4、越是无能的人，越喜欢挑剔别人的 错儿。 15:12:4 215:12: 4215:1 2Saturday, December 12, 2020
•
5、知人者智，自知者明。胜人者有力 ，自胜 者强。 20.12.1 220.12. 1215:1 2:4215: 12:42D ecembe r 12, 2020
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 2.1220. 12.12Sa turday, December 12, 2020
•
2、阅读一切好书如同和过去最杰出的 人谈话 。15:1 2:4215: 12:4215 :1212/ 12/2020 3:12:42 PM
•
3、越是没有本领的就越加自命不凡。 20.12.1 215:12: 4215:1 2Dec-20 12-Dec-20
解：(1)要使函数有意义，必须使{36－x2≥0.
x＞0 ，
得－6点≤x拨≤:12..列根出－据π2三图＜x角象＜不2写kπ等＋出π2式不，k等∈Z式. 的解集
由图知不等式组的解集为 [－6，－32π)∪(－π2，π2)∪(32π，6]． 故原函数的定义域为 [－6，－32π)∪(－π2，π2)∪(32π，6]．
cos
x
t2
1 2
例5：y sin x cos x sin x cos x
y
解： 设t=sinx+cosx,则t 2, 2
原式化为： y=t+ t2 1 2
= 1 t2 t 1 = 1（t 1）2 1
2
22
1
2
0
2x
t 2, 2
ymin =-1 ,
ymax
=
1 2
+
2
练习：y sin x cos x 1 sin x cos x
(2)cosx ≤1/2
解：作出余弦函数y=cosx，x∈[0，2π]的图象：
y
1
1/2
o
/2
3/2
2 x
-1
由图形可以得到，满足条件的x的集合为：
[π/3+2kπ,5 π/3+2kπ] k Z
题型二. 求三角函定义域:
【例 2】 求下列函数的定义域： (1)y＝ 36－x2＋lg cos x； (2)y＝logsin x(cos x＋12)．
y (t 1 )2 3
24
当t
1 2
时，y
min
3 4
当t=-1时，ymax =3
-1
0
1 2
1
t
练习： y cos2 x sin x 2 的值域。
点拨:统一函数名
三） 分式型 y a sin x b
c sin x d
例3： 求y sin x 的值域。 sin x 2
反表示法
•
6、意志坚强的人能把世界放在手中像 泥块一 样任意 揉捏。 2020年 12月12 日星期 六下午 3时12 分42秒1 5:12:42 20.12.1 2
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月下午 3时12 分20.12. 1215:1 2December 12, 2020
一.复习(3分钟完成)
1.在同一坐标系内，用五点法分别画出函数
y= sinx和 y= cosx， x[0, 2]的简图：
y
1
o
2
2
-1
y=cosx，x[0, 2]
3 2
2
x
y=sinx，x[0, 2]
三、解三角不等式（数形结合）
1.sin x 1 2
-
7
6
6
1 2
3.cos(2x ) 3 32
点拨: 1.反表示 2.利用 sinx 1, cos x 1有界性
解: sin x 2 y 1 y
sinx 1
| 2 y | 1 1 y
两边平方
值域为
1,
1 3
练习： y cos x 2
cos x 1
四）二合一 y a sin x b cos x
利用a sin x b cos x a2 b2 sin( x )
总结：形如y=asinx+b的函数的最大值是 a b
最小值是 a b
二)二次型 y a sin2 x bsin x c
例2：求 y sin2 x sin x 1的值域。 二次函数法
点拨:1.换元(注明新元取值)
2.运用二次函数图象性质(一看对称轴,二看区间端点)
y
解:令t sin x 1,1
二.求 三角函值域的几种典型形式
一）一次型 y=asinx+b
直接代入法
例1：求y 2sin x 1 值域。
分析：利用 sinx 1 cos x 1有界性
函数y 2sin x 1的值域为1，3
练习：口答下列函数的值域
(1)y=-2sinx+1
[－1，3]
(2) y=3cosx+2
[－1，5]
将2x 看作一个整体 3
3
2
11
6
6
返回目录
题型一：利用正弦函数和余弦函数的图象，解三角不等式
(1)sinx≥1/2
(2)cosx ≤1/2
解（1）作出正弦函数y=sinx，x∈[0，2π]的图象： y
1
1/2
o
/2
3/2
2
x
-1 由图形可以得到，满足条件的x的集合为：
[π/6+2k π,5 π/6+2k π] k Z
2
例5. y 2cos x sin( x )
2
2
3 sin2 x sin x cos x的值域.
3
1.统一角 2.降次 3.二合一
五） 其他形式：
一般一个式子中同时出现了sin x cos x和sin x cos x.
想到了
令t sin x cos x(t
2,
2
) 则sin
x
例4. y sin x 3 cos x的值域.
解：原式= 12 （ 3）2 sin( x ) 2 sin( x ）
3
3
原式的值域为2，2
练习：y 2sin x cos x的值域. 值域为 5, 5
例5. y cos2 x sin x cos x的值域.
1.降次
2.二合一
sin x cos x 1 sin 2 x cos2 x 1 cos 2x sin2 x 1 cos 2x