三角函数定义域和值域练习
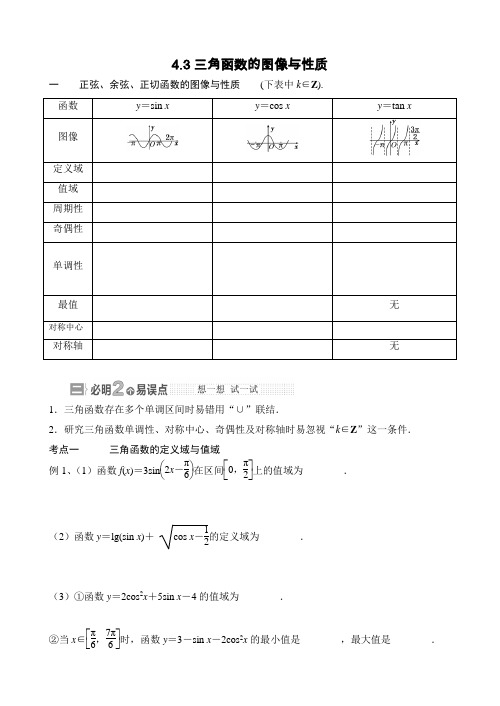
三角函数的定义域、值域

要使y 1 sin z有最小值- 1,
必须
2
z
2
2k ,k z
2
要使y 1 sin z有最大值 1,
1 x 2k
必须
2
z
2
2k ,k z
1
x
2
2k
x
4k
2 x
35
2
4k
3
使原函数取得最小值的集合是
2 32
3
y sin x
x
|
x
5
3
4k ,k
Z
y sin x
角
练习 求函数 y=cos2x+4sin x 的最值及取到最大值和最小值 时的 x 的集合.
解 y=cos2x+4sin x=1-sin2x+4sin x =-sin2x+4sin x+1=-(sin x-2)2+5.
∴当 sin x=1,即 x=2kπ+2π,k∈Z 时,ymax=4; 当 sin x=-1 时,即 x=2kπ-2π,k∈Z 时,ymin=-4. 所以 ymax=4,此时 x 的取值集合是{x|x=2kπ+π2,k∈Z}; ymin=-4,此时 x 的取值集合是{x|x=2kπ-π2,k∈Z}.
2
所以结论要相反 y sin z 最小
3.二次函数的某些知识点
例 求函数 y=sin2x-sin x+1,x∈R 的值域.
解 设 t=sin x,t∈[-1,1],f(t)=t2-t+1. ∵f(t)=t2-t+1=t-122+34. ∵-1≤t≤1, ∴当 t=-1,即 sin x=-1 时,ymax=f(t)max=3;
x x sinx
忘掉的同学再去看看课本, 后面的老师还会讲到
课堂小结
高中数学三角函数练习题附答案

高中数学三角函数练习题附答案一、填空题1.已知函数()1sin sin 34f x x x π⎛⎫=⋅+- ⎪⎝⎭定义域为[](),m n m n <,值域为11,24⎡⎤-⎢⎥⎣⎦,则n m-的最小值是________.2.已知球O 的表面积为16π,点,,,A B C D 均在球O的表面上,且,4ACB AB π∠=则四面体ABCD 体积的最大值为___________. 3.在ABC中,AB =BC =1cos 7BAC ∠=,动点D 在ABC 所在平面内且2π3BDC ∠=.给出下列三个结论:①BCD △②线段AD 的长度只有最小值,无最大值,且最小值为1;③动点D 的轨迹的长度为8π3.其中正确结论的序号为______. 4.已知)F为椭圆2222:1(0)x y C a b a b+=>>的右焦点,过点F 的直线l 与椭圆C 交于,A B 两点,P 为AB 的中点,O 为坐标原点.若△OFP 是以OF 为底边的等腰三角形,且△OFP 外接圆的面积为23π,则椭圆C 的长轴长为___________. 5.若函数()sin 12xf x x π=+,则(1)(2)(3)(2021)f f f f +++⋯⋯+=__________6.给出下列命题:①若函数()f x 的定义域为[]0,2,则函数(2)f x 的定义域为[]0,4; ②函数()tan f x x =在定义域内单调递增;③若定义在R 上的函数()f x 满足(1)()f x f x +=-,则()f x 是以2为周期的函数;④设常数a ∈R ,函数2log ,04()10,41x x f x x x ⎧<≤⎪=⎨>⎪-⎩若方程()f x a =有三个不相等的实数根1x ,2x ,3x ,且123x x x <<,则312(1)x x x +的值域为[64,)+∞.其中正确命题的序号为_____.7.已知函数()sin cos f x x x =+,()sin cos g x x x =:①函数()f x 的图象关于点(,0)4π对称;②函数|()|g x 的最小正周期是2π;③把函数f (2x )图象上所有点向右平移8π个单位长度得到的函数图象的对称轴与函数y=()g x 图象的对称轴完全相同;④函数1()()y f x g x =--在R 上的最大值为2.则以上结论正确的序号为_______________8.已知正四棱柱1111ABCD A B C D -中,2AB =,1AA =若M 是侧面11BCC B 内的动点,且AM MC ⊥,则1A M 的最小值为__________.9.在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且23,3a A π==.若mb nc +(0,0m n >>)有最大值,则nm的取值范围是__________. 10.在三棱锥P ABC -中,4AB BC ==,8PC =,异面直线PA ,BC 所成角为π3,AB PA ⊥,AB BC ⊥,则该三棱锥外接球的表面积为______.二、单选题11.在ABC 中,角,,A B C 所对应的边分别为,,a b c ,设ABC 的面积为S ,则24Sa bc+的最大值为( ) A .216B .312C .316D .21812.若函数()f x 同时满足:①定义域内任意实数x ,都有()()110f x f x ++-=;②对于定义域内任意1x ,2x ,当12x x ≠时,恒有()()()12120x x f x f x -⋅->⎡⎤⎣⎦;则称函数()f x 为“DM 函数”.若“DM 函数”满足()()2sin cos 0f f αα-+>,则锐角α的取值范围为( ) A .0,4π⎛⎫ ⎪⎝⎭B .0,3π⎛⎫ ⎪⎝⎭C .,43ππ⎛⎫ ⎪⎝⎭D .2,43ππ⎛⎫ ⎪⎝⎭13.如图所示,已知△ABC ,D 是AB 的中点,沿直线CD 将△ACD 翻折成△ACD ',所成二面角A CD B '--的平面角为α,则( )A .A DB α'∠≤ B .A DB α'∠≥C .A CB α∠'≤D .A CB α'∠≥14.已知函数()sin 22cos f x x x =-,下列说法错误的是( ) A .函数()f x 是周期函数 B .6x π=是函数()f x 图象的一条对称轴C .函数()f x 的增区间为()72,266k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z D .函数()f x 3315.已知函数()()()sin 010f x x ωϕω=+<<,若存在实数1x 、2x ,使得()()122f x f x -=,且12x x π-=,则ω的最大值为( )A .9B .8C .7D .516.已知,42ππα⎡⎤∈⎢⎥⎣⎦,,32ππβ⎡⎤∈⎢⎥⎣⎦sin αβαβ=+,则tan()αβ-=( ) AB .1C.2+D217.已知函数()()3log 911x f x x+=-,下列说法正确的是( )A .()f x 既不是奇函数也不是偶函数B .()f x 的图象与sin y x =有无数个交点C .()f x 的图象与2y =只有一个交点D .()()21f f -<-18.设锐角ABC 的内角,,A B C 所对的边分别为,,a b c,若,3A a π=2b 2c bc ++的取值范围为( ) A .(1,9] B .(3,9] C .(5,9]D .(7,9]19.设函数242,0()sin ,60x x x f x x x ⎧-+≥=⎨-≤<⎩,对于非负实数t ,函数()y f x t =-有四个零点1x ,2x ,3x ,4x .若1234x x x x <<<,则1234x x x x ++的取值范围中的整数个数为( )A .0B .1C .2D .320.已知1F 、2F 是椭椭圆和双曲线共有焦点,P 为两曲线的一个公共点,且126F PF π∠=,记椭圆和双曲线的离心率分别1e ,2e ,则1212e e e e +⋅的最大值为 A .4B .2C .83D .163三、解答题21.函数()()03f x x πωω⎛⎫=+> ⎪⎝⎭在一个周期内的图象如图所示,A 为图象的最高点,B ,C 为图象与x 轴的交点,ABC ∆为等边三角形.将函数()f x 的图象上各点的横坐标变为原来的π倍后,再向右平移23π个单位,得到函数()y g x =的图象.(Ⅰ)求函数()g x 的解析式;(Ⅱ)若不等式()23sin 324x m g x m π⋅-≤+对任意x ∈R 恒成立,求实数m 的取值范围.22.若函数()y f x =的图像上存在两个不同的点关于y 轴对称,则称函数()y f x =图像上存在一对“偶点”.(1)写出函数()sin f x x =图像上一对“偶点”的坐标;(不需写出过程) (2)证明:函数()ln(2)2g x x x =+-+图像上有且只有一对“偶点”;(3)若函数()2()x h x e mx m =--∈R 图像上有且只有一对“偶点”,求m 的取值范围. 23.如图,湖中有一个半径为1千米的圆形小岛,岸边点A 与小岛圆心C 相距3千米,为方便游人到小岛观光,从点A 向小岛建三段栈道AB ,BD ,BE ,湖面上的点B 在线段AC 上,且BD ,BE 均与圆C 相切,切点分别为D ,E ,其中栈道AB ,BD ,BE 和小岛在同一个平面上.沿圆C 的优弧(圆C 上实线部分)上再修建栈道DE .记CBD ∠为θ.()1用θ表示栈道的总长度()f θ,并确定sin θ的取值范围;()2求当θ为何值时,栈道总长度最短.24.已知()sin ,2cos a x x =,()2sin ,sin b x x =,()f x a b =⋅ (1)求()f x 的解析式,并求出()f x 的最大值;(2)若0,2x π⎡⎤∈⎢⎥⎣⎦,求()f x 的最小值和最大值,并指出()f x 取得最值时x 的值.25.已知函数22cos 3sin 2f x xx a 的最小值为0.(1)求a 的值及函数()y f x =图象的对称中心;(2)若关于x 的方程()0f x m -=在区间70,6π⎡⎤⎢⎥⎣⎦上有三个不相等的实数根1x ,2x ,3x ,求m的取值范围及()123tan 2x x x ++的值.26.如图,半圆的直径2AB =,O 为圆心,C ,D 为半圆上的点.(Ⅰ)请你为C 点确定位置,使ABC ∆的周长最大,并说明理由; (Ⅱ)已知AD DC =,设ABD θ∠=,当θ为何值时, (ⅰ)四边形ABCD 的周长最大,最大值是多少? (ⅱ)四边形ABCD 的面积最大,最大值是多少27.已知向量9(sin ,1),(sin ,cos )8a x b x x ==-, 设函数(),0,2f x a b x π⎡⎤=⋅∈⎢⎥⎣⎦.(Ⅰ)求()f x 的值域(Ⅱ)设函数()f x 的图像向左平移2π个单位长度后得到函数()h x 的图像,若不等式()()sin 20f x h x x m ++-<有解,求实数m 的取值范围.28.设函数2()cos sin 2f x x a x a =-+++(a ∈R ). (1)求函数()f x 在R 上的最小值;(2)若不等式()0f x <在[0,]2π上恒成立,求a 的取值范围;(3)若方程()0f x =在(0,)π上有四个不相等的实数根,求a 的取值范围.29.函数()()2sin f x x ωϕ=+(其中0,2πωϕ><),若函数()f x 的图象与x 轴的任意两个相邻交点间的距离为2π,且函数()f x 的图象过点()0,1. (1)求()f x 的解析式; (2)求()f x 的单调增区间:(3)求()()2sin f x x ωϕ=+在,02π⎛⎫- ⎪⎝⎭的值域. 30.已知向量33cos ,sin 22a x x ⎛⎫= ⎪⎝⎭,cos ,sin 22x x b ⎛⎫=- ⎪⎝⎭,且0,2x π⎡⎤∈⎢⎥⎣⎦(1)求a ·b 及||a b +;(2)若3()||2f x a b a b =⋅-+,求()f x 的最小值【参考答案】一、填空题1.3π2 3.①③4.5.3032 6.③④ 7.②③④89.1,22⎛⎫ ⎪⎝⎭10.80π 二、单选题 11.A 12.A 13.B 14.B 15.A 16.D 17.C 18.D 19.B 20.A 三、解答题21.(Ⅰ)()12g x x =(Ⅱ)2,23⎡⎤-⎢⎥⎣⎦【解析】 【分析】(Ⅰ)利用等边三角形的性质,根据已知,可以求出函数的周期,利用正弦型函数的最小正周期公式求出ω,最后根据正弦型函数图象的变换性质求出()y g x =的解析式; (Ⅱ)根据函数()y g x =的解析式,原不等式等价于23cos 3cos 10x m x m +++≥在x ∈R 恒成立,利用换元法,构造二次函数,分类讨论进行求解即可. 【详解】(Ⅰ)点A ABC ∆为等边三角形,所以三角形边长为2,所以24T πω==,解得2πω=,所以()23f x x ππ⎛⎫+ ⎪⎝⎭,将函数()f x 的图象上各点的横坐标变为原来的π倍后,得到()123h x x π⎛⎫=+ ⎪⎝⎭,再向右平移23π个单位,得到()12g x x =.(Ⅱ)()22g x x x ππ⎛⎫-=-= ⎪⎝⎭,所以()223sin 233cos 3cos x g x x m x π⋅-=--,原不等式等价于23cos 3cos 10x m x m +++≥在x ∈R 恒成立. 令cos x t =,[]1,1t ∈-,即23310t mt m +++≥在[]1,1t ∈-上恒成立.设()2331t t mt m ϕ=+++,对称轴2m t =-, 当12m-≤-时,即2m ≥时,()1240m ϕ-=-+≥,解得2m ≤,所以2m =; 当12m-≥时,即2m ≤-时,()1440m ϕ=+≥,解得1m ≥-(舍); 当112m -<-<时,即22m -<<时,231024m m m ϕ⎛⎫-=-++≥ ⎪⎝⎭,解得223m -≤<.综上,实数m 的取值范围为2,23⎡⎤-⎢⎥⎣⎦.【点睛】本题考查了正弦型函数的图象变换和性质,考查了利用换元法、构造法解决不等式恒成立问题,考查了数学运算能力.22.(1)()(),0,0ππ-(2)见解析(3)()1,+∞ 【解析】(1)根据题意即正弦函数的性质即可直接求解;(2)要证:函数数()2x h x e mx =--图象上有且只有一对“偶点”,只需证:())()()y Q x g x g x ==--=在(0,2)上有且只有一个零点,结合导数及函数的性质即可证明;(3)由题意,问题可转化为函数()()y h x h x =--只有一个零点,结合函数的性质及导数可求. 【详解】(1)函数()sin f x x =图像上一对“偶点”的坐标为()(),0,0ππ-, (2)设()()()()()ln 2ln 22Q x g x g x x x x =--=+--+-, 因为()y Q x =的定义域为()2,2-,且()()Q x Q x -=-, 所以函数()y Q x =为奇函数,要证:函数()ln(2)2g x x x =+-+图像上有且只有一对“偶点”, 只需证:()y Q x =在()0,2上有且只有一个零点,令()()222204x Q x x-'==-,得x =所以,函数()Q x 在(上为单调减函数,在)2上为单调增函数,(ln 30Q=+-<,4441122ln 40Q e e e ⎛⎫⎛⎫-=-+> ⎪ ⎪⎝⎭⎝⎭,所以函数()Q x 在41e ⎫-⎪⎭上有且只有一个零点,所以函数()ln(2)2g x x x =+-+图像上有且只有一对“偶点”,(3)设()()()2x xF x h x h x e e mx -=--=--,()00F =,因为()y F x =的定义域为R ,且()()F x F x -=-, 所以函数()y F x =为奇函数,因为函数()2()x h x e mx m =--∈R 图像上有且只有一对“偶点”, 所以函数()y F x =在()0,∞+有且只有一个零点, ()12x xF x e m e '=+-,()0,x ∈+∞, ①当1m 时,因为()220F x m '>-≥,所以函数()y F x =在()0,∞+上为单调增函数,所以()()00F x F >=, 所以函数()F x 在()0,∞+无零点,②当1m 时,由()212120x x xx xe me F x e m e e-+'=+-==,得:(0ln x m =,所以函数()y F x =在()00,x 上单调减函数,在()0,x +∞上单调增函数, 所以()()000F x F <=, 设()ln H x x x =-,()1xH x x-'=, 所以函数()H x 在()0,1上单调增函数,在()1,+∞上单调减函数, 所以()()110H x H ≤=-<,所以ln x x <,所以(ln ln 22m m m +<<,设()()211x m x e x x =-->,设()()2xM x m x e x '==-, 因为()220xM x e e '=->->,所以函数()M x 在()1,+∞单调增函数,所以()()120M x M e >=->,所以函数()m x 在()1,+∞单调增函数, 所以()()120m x m e >=->,所以当1x >时,21x e x >+,()22222124140m m m F m e m e m e=-->-->, 因为函数()y F x =在()0,x +∞上单调增函数,所以函数()F x 在()0,2x m 上有且仅有一个1x ,使得()10F x =, 综上:m 的取值范围为()1,+∞. 【点睛】本题中综合考查了函数的性质及导数的综合应用,体现了分类讨论思想的应用,试题具有一定的综合性. 23.()1()1232sin tan f θπθθθ=-+++,1sin ,13θ⎡⎫∈⎪⎢⎣⎭;()2当3πθ=时,栈道总长度最短.【解析】()1连CD ,CE ,由切线长定理知:1tan tan CD BE BD θθ===,1sin sin CD BC θθ==,130sin AB AC BC θ=-=-≥,1sin 3θ≥,即01sin 3θ=,00,2πθ⎛⎫∈ ⎪⎝⎭, 则()1232sin tan f θπθθθ=-+++,0,2πθθ⎡⎫∈⎪⎢⎣⎭,进而确定sin θ的取值范围; ()2根据()12cos 23sin f θθθπθ-=-++求导得()()2cos 2cos 1sin f θθθθ--'=,利用增减性算出()min 533f πθ=+,进而求θ得取值. 【详解】解:()1连CD ,CE ,由切线长定理知:1tan tan CD BE BD θθ===,1sin sin CD BC θθ==, CBE CBD θ∠=∠=,又CD BD ⊥,CE BE ⊥,故2DCE πθ∠=-,则劣弧DE 的长为2πθ-,因此,优弧DE 的长为2πθ+, 又3AC =,故130sin AB AC BC θ=-=-≥,1sin 3θ≥,即01sin 3θ=,00,2πθ⎛⎫∈ ⎪⎝⎭, 所以,()1232sin tan f θπθθθ=-+++,0,2πθθ⎡⎫∈⎪⎢⎣⎭,则1sin ,13θ⎡⎫∈⎪⎢⎣⎭; ()2()12cos 23sin f θθθπθ-=-++,0,2πθθ⎡⎫∈⎪⎢⎣⎭,其中01sin 3θ=,00,2πθ⎛⎫∈ ⎪⎝⎭,()()2cos 2cos 1sin f θθθθ--'=故3πθ=时,()min 533f πθ=+ 所以当3πθ=时,栈道总长度最短.【点睛】本题主要考查导数在函数当中的应用,属于中档题.24.(1)()f x 214x π⎛⎫=-+ ⎪⎝⎭1.(2)0x =时,最小值0.38x π=1. 【解析】 【分析】(1)利用数量积公式、倍角公式和辅助角公式,化简()f x ,再利用三角函数的有界性,即可得答案; (2)利用整体法求出32444x πππ-≤-≤,再利用三角函数线,即可得答案. 【详解】(1)()22sin 2sin cos f x x x x =+1cos2sin2x x =-+214x π⎛⎫=-+ ⎪⎝⎭∴sin 214x π⎛⎫-≤ ⎪⎝⎭,()f x ∴1.(2)由(1)得()214f x x π⎛⎫=-+ ⎪⎝⎭,∵0,2x π⎡⎤∈⎢⎥⎣⎦,32444x πππ∴-≤-≤.sin 214x π⎛⎫≤-≤ ⎪⎝⎭, ∴当244x ππ-=-时,即0x =时,()f x 取最小值0.当242x ππ-=,即38x π=时,()f x 1. 【点睛】本题考查向量数量积、二倍角公式、辅助角公式、三角函数的性质,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意整体法的应用.25.(1)1,,2212k ππ⎛⎫- ⎪⎝⎭,k Z ∈;(2)[)3,4, 【解析】(1)由题得()2sin 216f x x a π⎛⎫=+++ ⎪⎝⎭,求出a 的值即得函数()y f x =图象的对称中心;(2)作出函数()y f x =在70,6x π⎡⎤∈⎢⎥⎣⎦上的大致图象,求出123523x x x π++=即得解.【详解】(1)()cos 23sin 212sin 216x x a x a f x π⎛⎫=+++=+++ ⎪⎝⎭,由已知可得()2110a ⨯-++=,∴1a =,()2sin 226f x x π⎛⎫=++ ⎪⎝⎭,令26x k ππ+=可得()y f x =图象的对称中心为,2212k ππ⎛⎫- ⎪⎝⎭,k Z ∈. (2)()y f x =在70,6x π⎡⎤∈⎢⎥⎣⎦上的大致图象如图所示,由图可得[)3,4m ∈,所以123x x π+=,2343x x π+=,所以123523x x x π++=, 所以()1235tan 2tan33x x x π++==-.【点睛】本题主要考查三角恒等变换和三角函数的图象和性质,考查三角函数图象的综合应用,意在考查学生对这些知识的理解掌握水平和分析推理能力. 26.(Ⅰ)点C 是半圆的中点,理由见解析; (Ⅱ)(ⅰ)6πθ=时,最大值5(ⅱ)6πθ=33【解析】(Ⅰ)设BC a =,AC b =,AB c =,法一:依题意有222+=a b c ,再利用基本不等式求得2a b c +,从而得出结论;法二:由点C 在半圆上,AB 是直径,利用三角函数求出cos a c α=⋅,sin b c α=⋅,再利用三角函数的性质求出结论;(Ⅱ)(ⅰ)利用三角函数值表示四边形ABCD 的周长p ,再求p 的最大值;(ⅱ)利用三角函数值表示出四边形ABCD 的面积s ,再结合基本不等式求s 的最大值. 【详解】(Ⅰ)点C 在半圆中点位置时,ABC ∆周长最大.理由如下: 法一:因为点C 在半圆上,且AB 是圆的直径,所以2ACB π∠=,即ABC ∆是直角三角形,设BC a =,AC b =,AB c =,显然a ,b ,c 均为正数,则222+=a b c , 因为222a b ab +≥,当且仅当a b =时等号成立,所以()()2222222a b a b ab a b +≥++=+,所以()2222a b a b c +≤+=, 所以ABC ∆的周长为()21222a b c c ++≤+=+,当且仅当a b =时等号成立,即ABC ∆为等腰直角三角形时,周长取得最大值,此时点C 是半圆的中点. 法二:因为点C 在半圆上,且AB 是圆的直径, 所以2ACB π∠=,即ABC ∆是直角三角形,设BC a =,AC b =,AB c =,02ABC παα⎛⎫∠=<< ⎪⎝⎭,则cos a c α=⋅,sin b c α=⋅,a b c ++cos sin c c c αα=⋅+⋅+()2cos sin 2αα=++2224πα⎛⎫=++ ⎪⎝⎭,因为02πα<<,所以3444πππα<+<, 所以当42ππα+=,即4πα=时, ABC ∆周长取得最大值222,此时点C 是半圆的中点.(Ⅱ)(ⅰ)因为AD DC =,所以ABD DBC θ∠=∠=, 所以sin AD DC AB θ==⋅,cos2CB AB θ=⋅, 设四边形ABCD 的周长为p , 则p AD DC CB AB =+++2sin cos22AB AB θθ=++()2214sin 212sin 254sin 2θθθ⎛⎫=+-+=-- ⎪⎝⎭,显然0,4πθ⎛⎫∈ ⎪⎝⎭,所以当6πθ=时,p 取得最大值5;(ⅱ)过O 作OE BC ⊥于E ,设四边形ABCD 的面积为s ,四边形AOCD 的面积为1s ,BOC ∆的面积为2s ,则 121122s s s AC OD BC OE =+=⋅+⋅ 11sin 21cos 2sin 222AB AB θθθ=⋅+⋅ sin 2cos2sin 2θθθ=+⋅()sin 21cos2θθ=+, 所以()222sin 21cos2s θθ=+()()221cos 21cos 2θθ=-+()()31cos21cos2θθ=-+()()331cos 21cos 23θθ=-+()()()2231cos 21cos 211cos 232θθθ-++⎡⎤≤+⎢⎥⎣⎦()()()231cos 21cos 211cos 232θθθ-++⎡⎤=+⎢⎥⎣⎦()()()2231cos 21cos 21cos 21232θθθ⨯-++⎡⎤++⎢⎥≤⎢⎥⎢⎥⎢⎥⎣⎦()()()431cos 21cos 221cos 2134θθθ-++++⎡⎤=⎢⎥⎣⎦ 413273216⎛⎫==⎪⎝⎭; 当且仅当()31cos21cos2θθ-=+,即1cos 22θ=时,等号成立, 显然04πθ⎛⎫∈ ⎪⎝⎭,,所以202πθ⎛⎫∈ ⎪⎝⎭,,所以此时6πθ=,所以当6πθ=时,33s =,即四边形ABCD 33 【点睛】本题考查解三角形的应用问题,考查三角函数与基本不等式的应用,需要学生具备一定的计算分析能力,属于中档题. 27.(Ⅰ)11,88⎡⎤-⎢⎥⎣⎦(Ⅱ)9,4⎛⎫-+∞ ⎪⎝⎭(Ⅰ)根据向量的数量积的坐标运算可得函数()f x 的解析式,化成二次函数型函数,求得值域;(Ⅱ)首先根据三角函数的变换规则求得()h x 的解析式,要使()()sin 20f x h x x m ++-<在0,2x π⎡⎤∈⎢⎥⎣⎦有解,即不等式()()sin2m f x h x x >++在0,2x π⎡⎤∈⎢⎥⎣⎦有解,令()()sin2y f x h x x =++求出函数的最小值,即可得实数m 的取值范围.【详解】 解:(1)()222991sin cos 1cos cos cos cos 888f x x x x x x x =+-=-+-=-+- ()211cos 28f x x ⎛⎫∴=--+ ⎪⎝⎭,0,2x π⎡⎤∈⎢⎥⎣⎦0cos 1x ∴≤≤()1188f x ∴-≤≤ ()f x ∴的值域为11,88⎡⎤-⎢⎥⎣⎦(2)函数()21cos cos 8f x x x =-+-的图像向左平移2π个单位长度后得到函数()h x 的图像,()2211cos cos sin sin 2288h x x x x x ππ⎛⎫⎛⎫∴=-+++-=--- ⎪ ⎪⎝⎭⎝⎭,依题意,不等式()()sin2m f x h x x >++在0,2x π⎡⎤∈⎢⎥⎣⎦有解,设()()5sin2cos sin sin24y f x h x x x x x =++=--+52sin cos cos sin ,0,42y x x x x x π⎡⎤=+--∈⎢⎥⎣⎦,令[]cos sin ,0,1,142t x x x x t ππ⎛⎫⎡⎤=-=+∈∴∈- ⎪⎢⎥⎝⎭⎣⎦, 则[]2211,1,142y t t t t ⎛⎫=-+-=--∈- ⎪⎝⎭∴函数()()sin2y f x h x x =++的值域为9,04⎡⎤-⎢⎥⎣⎦.∴ min 94m y >=-故实数m 的取值范围为9,4⎛⎫-+∞ ⎪⎝⎭.本题考查正弦函数的性质,二次函数的性质以及辅助角公式,属于中档题.28.(1)2min2,2;()1,22;422,2.a af x a a a a >⎧⎪⎪=-++-≤≤⎨⎪+<-⎪⎩(2)(,1)a ∈-∞-(3)12a -<<-【解析】 【分析】(1)通过换元法将函数变形为二次函数,同时利用分类讨论的方法求解最大值; (2)恒成立需要保证max ()0f x <即可,对二次函数进行分析,根据取到最大值时的情况得到a 的范围;(3)通过条件将问题转化为二次函数在给定区间上有两个零点求a 的范围,这里将所有满足条件的不等式列出来,求解出a 的范围. 【详解】解:(1)令sin x t =,[1,1]t ∈-,则2()()1f x g t t at a ==+++,对称轴为2a t =-. ①12a -<-,即2a >,min ()(1)2f x g =-=.②112a -≤-≤,即22a -≤≤,2min ()()124a a f x g a =-=-++.③12a->,即2a <-,min ()(1)22f x g a ==+. 综上可知,2min2,2;()1,22;422,2.a af x a a a a >⎧⎪⎪=-++-≤≤⎨⎪+<-⎪⎩ (2)由题意可知,max ()0f x <,2()()1f xg t t at a ==+++,[0,1]t ∈的图象是开口向上的抛物线,最大值一定在端点处取得,所以有(0)10,(1)220,g a g a =+<⎧⎨=+<⎩故(,1)a ∈-∞-. (3)令sin x t =,(0,)x π∈.由题意可知,当01t <<时,sin x t =有两个不等实数解,所以原题可转化为2()10g t t at a =+++=在(0,1)内有两个不等实数根.所以有201,24(1)0,12(0)10,(1)220,a a a a g a g a ⎧<-<⎪⎪⎪∆=-+>⇒-<<-⎨⎪=+>⎪=+>⎪⎩【点睛】(1)三角函数中,形如2()sin sin f x a x b x c =++或者2()cos cos f x a x b x c =++都可以采用换元法求解函数最值;(2)讨论二次函数的零点的分布,最好可以采用数形结合的方法解决问题,这样很大程度上减少了遗漏条件的可能.29.(1)2sin(2)6y x π=+;(2),,36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;(3)[)2,1-【解析】 【分析】(1)依据题意可得函数周期为π,利用周期公式算出ω,又函数过定点()0,1,即可求出ϕ,进而得出解析式;(2)利用正弦函数的单调性代换即可求出函数()f x 的单调区间;(3)利用换元法,设26t x π=+,结合2sin y t =在5,66t ππ⎛⎫∈-⎪⎝⎭上的图象即可求出函数()()2sin f x x ωϕ=+在,02π⎛⎫- ⎪⎝⎭的值域【详解】(1)因为函数()f x 的图象与x 轴的任意两个相邻交点间的距离为2π,所以函数()f x 的周期为π,由2T ππω==,得2ω=,又函数()f x 的图象过点()0,1,所以(0)1f =,即2sin 1=ϕ,而,所以6π=ϕ, 故()f x 的解析式为2sin(2)6y x π=+.(2)由sin y x =的单调增区间是2,2,22k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦可得222262k x k πππππ-+≤+≤+,解得36k x k ππππ-+≤≤+故故函数()f x 的单调递增区间是,,36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.(3)设 26t x π=+,,02x π⎛⎫∈- ⎪⎝⎭,则5,66t ππ⎛⎫∈-⎪⎝⎭ ,由2sin y t =在5,66t ππ⎛⎫∈- ⎪⎝⎭上的图象知,当2t π=-时,min 2f =- 当t 趋于6π时,函数值趋于1,故()()2sin f x x ωϕ=+在,02π⎛⎫- ⎪⎝⎭的值域为[)2,1- . 【点睛】本题主要考查正弦型函数解析式的求法,正弦函数性质的应用,以及利用换元法结合图象解决给定范围下的三角函数的范围问题,意在考查学生数学建模以及数学运算能力. 30.(1)见解析; (2)178-. 【解析】 【分析】(1)运用向量数量积的坐标表示,求出a ·b ;运用平面向量的坐标运算公式求出a b +,然后求出模.(2)根据上(1)求出函数()f x 的解析式,配方,利用二次函数的性质求出最小值. 【详解】(1)33cos cos sin sin cos22222x xa b x x x ⋅=⋅-⋅=cos a b ⎛+= ⎝ =∵0,2x π⎡⎤∈⎢⎥⎣⎦∴cos 0x ∴2cos a b x +=(2)()cos23cos f x x x =- 223172cos 13cos 2cos 48x x x ⎛⎫=--=-- ⎪⎝⎭∵0,2x π⎡⎤∈⎢⎥⎣⎦∴0cos 1x ∴()min 317cos 48x f x ==-【点睛】本题考查了平面向量数量积的坐标表示,以及平面向量的坐标加法运算公式.重点是二次函数求最小值问题.。
三角函数的定义域与值域题库(精)

专题三:三角函数的定义域与值域(习题库)一、选择题1、函数f(x)的定义域为[﹣,],则f(sinx)的定义域为()A、[﹣,]B、[,]C、[2kπ+,2kπ+](k∈Z)D、[2kπ﹣,2kπ+]∪[2kπ+,2kπ+](k∈Z)分析:由题意知,求出x的范围并用区间表示,是所求函数的定义域;解答:∵函数f(x)的定义域为为[﹣,],∴,解答(k∈Z)∴所求函数的定义域是[2kπ﹣,2kπ+]∪[2kπ+,2kπ+](k∈Z)故选D.2、函数的定义域是()A、.B、.C、D、.解答:由题意可得sinx﹣≥0⇒sinx≥又x∈(0,2π)∴函数的定义域是.故选B.3、函数的定义域为()A、 B、C、 D、解答:由题意得tanx≥0,又tanx 的定义域为(kπ﹣,kπ+),∴,故选D.4、函数f(x)=cosx(cosx+sinx),x∈[0,]的值域是()A、[1,]B、C、D、解答:∵f(x)=cosx(cosx+sinx)=cos2x+sinxcosx===又∵∴∴则1≤f(x)≤故选A.5、函数y=﹣cos2x+sinx﹣的值域为()A、[﹣1,1]B、[﹣,1]C、[﹣,﹣1]D、[﹣1,]解答:函数y=﹣cos2x+sinx﹣=﹣(1﹣2sin2x)+sinx﹣=sin2x+sinx﹣1=﹣∵﹣1≤sinx≤1,∴当sinx=﹣时,函数y有最小值为﹣.sinx=1时,函数y 有最大值为1,故函数y 的值域为[﹣,1],故选B.6、函数值域是()A、 B、C、 D、[﹣1,3]解答:因为,所以sinx∈[],2sinx+1∈故选B7、函数的最大值是()A、5B、6C、7D、8解答:∵==∈[﹣7,7] ∴函数的最大值是78、若≤x≤,则的取值范围是()A、[﹣2,2]B、C、D、解答:=2(sinx+cosx)=2sin(),∵≤x≤,∴﹣≤≤,∴≤﹣sin()≤1,则函数f(x)的取值范围是:.故选C.9、若,则函数y=的值域为()A、 B、 C、 D、解答:函数y===因为,所以sin∈(0,)∈故选D10、函数,当f(x)取得最小值时,x的取值集合为()A、 B、C、 D、解答:∵函数,∴当 sin(﹣)=﹣1时函数取到最小值,∴﹣=﹣+2kπ,k∈Z函数,∴x=﹣+4kπ,k∈Z,∴函数取得最小值时所对应x的取值集合:为{x|x═﹣+4kπ,k∈Z} 故选A.11、函数y=sin2x﹣sinx+1(x∈R)的值域是()A、[,3]B、[1,2]C、[1,3]D、[,3]解答:令sinx=t,则y=t2﹣t+1=(t﹣)2+,t∈[﹣1,1],由二次函数性质,当t=时,y取得最小值.当t=﹣1时,y取得最大值3,∴y∈[,3] 故选A.12、已知函数,则f(x)的值域是()A、[﹣1,1]B、C、D、解答:解:由题=,当 x∈[,]时,f(x)∈[﹣1,];当 x∈[﹣,]时,f (x)∈[﹣1,]可求得其值域为.故选D.13、函数的值域为()A、 B、 C、[﹣1,1] D、[﹣2,2]解答:=﹣sinxcosx+cos2x=cos2x ﹣sin2x=cos (2x+)∴函数的值域为[﹣1,1] 故选C .14、若≥,则sinx 的取值范围为( ) A 、 B 、 C 、∪D 、∪解答:∵≥,∴解得x ∈[,)∪(,] ∴sinx ∈故选B15、函数y=sin2x+2cosx 在区间[﹣,]上的值域为( )A 、[﹣,2]B 、[﹣,2)C 、[﹣,]D 、(﹣,] 解答:∵x ∈[﹣,] ∴cosx ∈[﹣,1]又∵y=sin2x+2cosx=1﹣cos2x+2cosx=﹣(cosx ﹣1)2+2 则y ∈[﹣,2] 故选A 二、填空题(共7小题) 16、已知,则m 的取值范围是 .解答:∵=2(sinθ+cosθ)=2sin(θ+),∴﹣2≤≤2,∴m≥,或m≤﹣,故m的取值范围是(﹣∝,﹣]∪[,+∞).17、函数在上的值域是___________.解答:因为,故故答案为:18、函数的值域为.解答:由题意是减函数,﹣1≤sinx≤1,从而有函数的值域为,故答案为19、(理)对于任意,不等式psin2x+cos4x≥2sin2x恒成立,则实数p的范围为.解答:∵psin2x+cos4x≥2sin2x ∴psin2x≥2sin2x﹣1﹣sin4x+2sin2x=4sin2x﹣sin4x﹣1∴p≥4﹣(sin2x+)而sin2x+≥2∴4﹣(sin2x+)的最大值为2则p≥2 故答案为:[2,+∞)20、函数的值域是.解答:令t=sinx+cosx=,t2=1+2sinxcosx∵∴x+∴从而有:f(x)==﹣2 在单调递增当t+1=2即t=1时,此时x=0或x=,函数有最小值当t+1=1+即t=时此时x=,函数有最大值2﹣2故答案为:[﹣2]21、函数的定义域为.解答:要使函数有意义,必须解得,故答案为:(0,).三、解答题(共8小题)22.(1)已知f(x)的定义域为[0,1],求f(cosx)的定义域;(2)求函数y=lgsin(cosx)的定义域;分析:求函数的定义域:(1)要使0≤cosx≤1,(2)要使sin (cosx)>0,这里的cosx以它的值充当角。
三角函数定义域值域的求法

π
3
)
练习:y = 2sin x − cos x的值域.
2 ∴ 原式的值域为[ −2,]
值域为 − 5, 5
例5. y = cos 2 x + sin x cos x的值域. 2.二合一 1.降次 二 降 1 1 + cos2x sin 2 x = 1 − cos 2 x 2 sin xcos x = sin 2 x cos x = 2 2 2 π 2 例5. y = 2cos x sin( x + ) − 3 sin x + sin x cos x的值域. 3 1.统一角 2.降次 统 3.二合一 降 二
D
θ
C
A
B
1.在同一坐标系内, 1.在同一坐标系内,用五点法分别画出函数 在同一坐标系内 sinx和 cosx, 2π 的简图: y= sinx和 y= cosx, x∈[0, 2π]的简图:
y 1
π
2
-1
一.复习(3分钟完成) 复习(3分钟完成) (3分钟完成
−
o
π
2
y=cosx,x∈[0, 2π] y=cosx, 2π
t
三) 分式型 y = a sin x + b c sin x + d
点拨: 点拨 1.反表示 反表示 2y 解: sin x = 1− y
sin x 例3: 求y = 的值域。 sin x + 2
反表示法
2.利用 sinx ≤ 1, cos x ≤ 1有界性 2.利 Q sinx ≤ 1
1 两边平方 ∴ 值 域 为 − 1, 3
cos x − 2 练习: y = cos x − 1
三角函数的定义域、值域及最值(人教A版)(含答案)

三角函数的定义域、值域及最值(人教A版)一、单选题(共14道,每道7分)1.函数的定义域为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:三角函数的定义域2.若函数的定义域是,则函数的定义域是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:复合函数的定义域3.函数的定义域为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:复合函数的定义域4.函数的定义域为( )A. B.C. D.第一、三象限答案:C解题思路:试题难度:三颗星知识点:复合函数的定义域5.函数,当取得最小值时,的取值集合为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的最值6.函数的值域为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:正弦函数的定义域和值域7.函数,的值域为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:正弦函数的定义域和值域8.函数,的值域是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:复合函数的值域9.已知函数,则在区间上的最大值与最小值分别是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:复合函数的值域10.若函数在区间上的最小值为,则的值为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:正弦函数的定义域和值域11.函数的值域为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:复合函数的值域12.函数的值域是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:正切函数的值域13.若(为常数)的最大值是3,最小值是,则的值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:三角函数的最值14.若,则下列不等式中成立的是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数的图象。
三角函数的定义域、值域及单调区间(含答案)

三角函数的定义域、值域及单调区间一、单选题(共12道,每道8分)1.与函数定义域相同的一个函数是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:三角函数的定义域2.函数的定义域是( )A.B.C.D.答案:C解题思路:试题难度:三颗星知识点:三角函数的定义域3.函数的定义域是( ) A.B.C.D.答案:D解题思路:试题难度:三颗星知识点:三角函数的定义域4.的值域是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:三角函数的值域5.函数的值域是( )A.{3}B.{3,﹣1}C.{3,1,﹣1}D.{3,1,﹣1,﹣3}答案:B解题思路:试题难度:三颗星知识点:三角函数的值域6.函数的值域是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:三角函数的值域7.已知函数,则f(x)在区间上的最大值与最小值分别是( )A.1,﹣2B.2,﹣1C.1,﹣1D.2,﹣2答案:A解题思路:试题难度:三颗星知识点:三角函数的最值8.已知函数的定义域为,值域为,则函数上,( )A.有最大值2B.有最小值2C.有最大值1D.有最小值1答案:B解题思路:试题难度:三颗星知识点:三角函数的最值9.函数的单调增区间为( ) A.B.C.D.答案:A解题思路:试题难度:三颗星知识点:复合三角函数的单调性10.设函数,在区间D上单调递增,则区间D可以是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:复合三角函数的单调性11.函数的单调增区间是( )A.B.C.D.答案:A解题思路:先确定函数的定义域是全体实数,记,则,∵是递增函数,∴根据口诀“同增异减”可得,只需要找到的递增区间即可,∴.故选A试题难度:三颗星知识点:复合三角函数的单调性12.函数的单调递减区间是( ) A.B.C.D.答案:D解题思路:试题难度:三颗星知识点:复合三角函数的单调性第11页共11页。
三角函数的值域问题

y sin x
y cos x
2
(k∈z)
2
时y min 1 x 2k 时y min 1
(k∈z)
二、新课讲解
• 下列函数有最大值、最小值吗?如果有,请写出 取最大值、最小值时的自变量x的集合,并说出 最大值、最小值分别是什么? • (1)y=2sinx, xR • (2)y=-3sinx,xR • (3)y=asinx,xR(a>0) • (4)y=asinx,xR(a<0) • (5)y=asinx,xR(a≠0)
类型二:求y A sin( x )型函数的的值域与最值
例3:求函数y 2 sin( 2 x )的最值,并求取得最值时 3 自变量x的集合。
1 变式1:函数y 3 2 sin( x )的值域为 ______ . 2 3 变式2:已知y a sin( 2 x ) b(a 0)的最大值为3, 3 最小值为 1, 求a, b的值.
当题目中有出现自变量x属于某个小区间,那么
要用换元 2 x )的范围。 3
类型三:值域与最值的应用
延伸:
0 (2014 湖北高考改编)某实验室一天的温度(单位: C)
随时间t (单位:h)的变化近似满足函数: t ),t 0,24 12 6 求实验室一天的最大温差。 f (t ) 10 2 sin(
1.在同一坐标系内,用五点法分别画出函数 y= sinx和 y= cosx, x[0, 2]的简图:
y
1
一.复习
y=cosx,x[0, 2]
2
o
-1
2
3 2
三角函数的定义域与值域题库

专题三:三角函数的定义域与值域(习题库)一、选择题1、函数f(x)的定义域为[﹣,],则f(sinx)的定义域为()A、[﹣,]B、[,]C、[2kπ+,2kπ+](k∈Z)D、[2kπ﹣,2kπ+]∪[2kπ+,2kπ+](k∈Z)分析:由题意知,求出x的范围并用区间表示,是所求函数的定义域;解答:∵函数f(x)的定义域为为[﹣,],∴,解答(k∈Z)∴所求函数的定义域是[2kπ﹣,2kπ+]∪[2kπ+,2kπ+](k∈Z)故选D.2、函数的定义域是()A、.B、.C、D、.解答:由题意可得sinx﹣≥0⇒sinx≥又x∈(0,2π)∴函数的定义域是.故选B.3、函数的定义域为()A、B、C、 D、解答:由题意得tanx≥0,又tanx 的定义域为(kπ﹣,kπ+),∴,故选D.4、函数f(x)=cosx(cosx+sinx),x∈[0,]的值域是()A、[1,]B、C、D、解答:∵f(x)=cosx(cosx+sinx)=cos2x+sinxcosx===又∵∴∴则1≤f(x)≤故选A.5、函数y=﹣cos2x+sinx﹣的值域为()A、[﹣1,1]B、[﹣,1]C、[﹣,﹣1]D、[﹣1,]解答:函数y=﹣cos2x+sinx﹣=﹣(1﹣2sin2x)+sinx﹣=sin2x+sinx﹣1=﹣∵﹣1≤sinx≤1,∴当sinx=﹣时,函数y有最小值为﹣.sinx=1时,函数y 有最大值为1,故函数y 的值域为[﹣,1],故选B.6、函数值域是()A、B、 C、D、[﹣1,3]解答:因为,所以sinx∈[],2sinx+1∈故选B7、函数的最大值是()A、5B、6C、7D、8解答:∵==∈[﹣7,7] ∴函数的最大值是78、若≤x≤,则的取值范围是()A、[﹣2,2]B、C、D、解答:=2(sinx+cosx)=2sin(),∵≤x≤,∴﹣≤≤,∴≤﹣sin()≤1,则函数f(x)的取值范围是:.故选C.9、若,则函数y=的值域为()A、B、 C、D、解答:函数y===因为,所以sin∈(0,)∈故选D10、函数,当f(x)取得最小值时,x的取值集合为()A、 B、C、 D、解答:∵函数,∴当 sin(﹣)=﹣1时函数取到最小值,∴﹣=﹣+2kπ,k∈Z函数,∴x=﹣+4kπ,k∈Z,∴函数取得最小值时所对应x的取值集合:为{x|x═﹣+4kπ,k∈Z}故选A.11、函数y=sin2x﹣sinx+1(x∈R)的值域是()A、[,3]B、[1,2]C、[1,3]D、[,3]解答:令sinx=t,则y=t2﹣t+1=(t﹣)2+,t∈[﹣1,1],由二次函数性质,当t=时,y取得最小值.当t=﹣1时,y取得最大值3,∴y∈[,3] 故选A.12、已知函数,则f(x)的值域是()A、[﹣1,1]B、C、D、解答:解:由题=,当x∈[,]时,f(x)∈[﹣1,];当x∈[﹣,]时,f(x)∈[﹣1,] 可求得其值域为.故选D.13、函数的值域为()A、B、 C、[﹣1,1] D、[﹣2,2]解答:=﹣sinxcosx+cos2x=cos2x﹣sin2x=cos(2x+)∴函数的值域为[﹣1,1] 故选C.14、若≥,则sinx的取值范围为()A、 B、C、∪D、∪解答:∵≥,∴解得x∈[,)∪(,] ∴sinx∈故选B15、函数y=sin2x+2cosx在区间[﹣,]上的值域为()A、[﹣,2]B、[﹣,2)C、[﹣,]D、(﹣,]解答:∵x∈[﹣,] ∴cosx∈[﹣,1]又∵y=sin2x+2cosx=1﹣cos2x+2cosx=﹣(cosx﹣1)2+2则y∈[﹣,2] 故选A二、填空题(共7小题)16、已知,则m的取值范围是.解答:∵=2(sinθ+cosθ)=2sin(θ+),∴﹣2≤≤2,∴m≥,或m≤﹣,故m的取值范围是(﹣∝,﹣]∪[,+∞).17、函数在上的值域是___________.解答:因为,故故答案为:18、函数的值域为.解答:由题意是减函数,﹣1≤sinx≤1,从而有函数的值域为,故答案为19、(理)对于任意,不等式psin2x+cos4x≥2sin2x恒成立,则实数p的范围为.解答:∵psin2x+cos4x≥2sin2x ∴psin2x≥2sin2x﹣1﹣sin4x+2sin2x=4sin2x﹣sin4x ﹣1∴p≥4﹣(sin2x+)而sin2x+≥2∴4﹣(sin2x+)的最大值为2则p≥2故答案为:[2,+∞)20、函数的值域是.解答:令t=sinx+cosx=,t2=1+2sinxcosx∵∴x+∴从而有:f(x)==﹣2在单调递增当t+1=2即t=1时,此时x=0或x=,函数有最小值当t+1=1+即t=时此时x=,函数有最大值2﹣2故答案为:[﹣2]21、函数的定义域为.解答:要使函数有意义,必须解得,故答案为:(0,).三、解答题(共8小题)22.(1)已知f(x)的定义域为[0,1],求f(cosx)的定义域;(2)求函数y=lgsin(cosx)的定义域;分析:求函数的定义域:(1)要使0≤cosx≤1,(2)要使sin(cosx)>0,这里的cosx以它的值充当角。
三角函数定义域和值域

1.在同一坐标系内,用五点法分别画出函数 y= sinx和 y= cosx, x[0, 2]的简图:
y
1
一.复习(3分钟完成)
y=cosx,x[0, 2]
2
o
-1
2
3 2
2
y=sinx,x[0, 2]
x
2.写出y=sinx和y=cosx的定义域,值域,最值,周期
-1 0
1 2
1
t
练习: y cos x sin x 2 的值域。
点拨:统一函数名
三) 分式型
sin x 例3: 求y 的值域。 反表示法 sin x 2 点拨: 1.反表示 2.利用 sinx 1, cos x 1有界性 2y 解 : sin x sinx 1 1 y 2y 1 | | 1 两边平方 值域为 1, 3 1 y
D
C
A
B
; https:///u/5028959491
jbh68lcf
这样,想找个有骨节有肩膊的都不能。”“或者也有,只轮不着我们罢了。”“你我倒也算了,老板——”“嘘!”很怕蝶宵华听见了伤心,偷 眼看他,他端坐鞍上,双目微阖,竟似僧人入定了。苏家,全凭苏小横在,才安定下来。明柯逃跑了,谁知嘉颜是帮着明柯弄亏空贪官中银子的, 也跟了明柯逃跑,临走还卷了一票。明远据说进京去,太守家似有悔婚之意。桩桩件件,每件都要压垮老太太。苏小横只道:“有我在!你们不 必问端底,等着就好。”众人也终于静了。回道观里,裳儿拿红纸剪着玩,有一搭没一搭的,又似剪窗花,又似只糟塌纸张,见苏小横回来,嘻 嘻笑道:“爷爷也计算差了。”苏小横道:“哦?”“盗坠索银的人,爷爷先把目标锁定在大哥、五哥身上,尤以五哥嫌疑更重,五哥手里也确 实有大笔银子来路不名,叫爷爷查出来,”裳儿弄着剪子,侃侃谈道,“可他旋即却糊涂得把田庄里贪得来的银子,都输在赌局里,以至于受蕙 妹妹胁迫,坏了笙表妹名声,吃了爹爹一顿杖,爬都爬不起来,爷爷就重点去调查大哥了罢?谁知五哥买通爹爹身边行杖的,筋骨无碍,装着养 伤,悄没声儿一切都打点好,拐了嘉颜姐姐,扔嘣就走了!把爷爷可摆了一道。”“是你被摆了一道。”苏小横道。裳儿手里的剪子,停了停。 “你将是独当一面的人,特立专行,生杀予夺,非如此,不足以在宫中固宠。”苏小横道,“内外种种,我知道的,你也知道,我并未瞒你,我 所不知道的,你也应该自己想办法知道,定出方略,克敌制胜。你没有做到,就是败了。宫中败亡,你把责任怪在爷爷头上,纵然爷爷肯承担, 有用么?”裳儿默然片刻,将剪子放下,端端正正拜苏小横一礼:“孙女谨受教。”“你剪的是什么?”苏小横看着那张叠了数叠、被剪了许多 刀的红纸。裳儿将红纸展开,胡乱纵横的刀痕,并未能形成任何花样:“这是裳儿的心境。”“本应如何呢?”苏小横又问。“本应,”裳儿打 开一本书,取出里面压得平平的剪纸,是鸳鸯戏水,“送于四姐姐贴在嫁妆箱上,给四姐姐道喜。”苏小横神色不动:“你四姐姐婚事有阻 碍。”“是。”裳儿知这也是考题,“大哥既进京,四姐姐婚事就没有阻碍了。”苏小横微微叹了口气:“你会看不起你大哥吗?”“不会。” 这倒是真心话,“虽说男女分工有别,但强盗杀来,若只余妇女,那妇女也必须举刃招架;同样道理,床帷间、私室里,若只有男儿能去,那末 男儿也该去。为家族效命,诗姐姐如此,裳儿如此,大哥如此,原没什么分别。”说着伤感起来,“爷爷,你可知孙女流落在外,最困苦时,只 为一勺掺着砂子的糙豆饭,他要我做什么都可以。”苏小横抚着裳儿的头:“爷爷救你太迟。”“相比很多人来说,已经
三角函数的定义域和值域

三角函数的定义域和值域一. 求三角函定义域: 11(1) y (2) y 1sin x 1sin(2x+)6p ==++(3) y 2cos x-1 (4) y lg(2sin lg(2sinx-1)x-1)==练点拨:1.列出三角不等式2.根据图象写出不等式的解集例1.求下列函数的定义域; 二.求 三角函值域的几种典型形式 一)一次型2sin 1y x =+例1:求 值域。
1cos 1x ££分析:利用 sinx sinx 有界性y=asinx+b 练习:口答下列函数的值域 (1)y=-2sinx+1 (2) y=3cosx+2 总结:形如y=asinx+b 的函数的最大值是 最小值是 a b +a b-+直接代入法二)二次型22sin sin 1y x x =-+例:求的值域。
2cos sin 2y x x =--+练习: 的值域。
点拨:1.换元(注明新元取值)2.运用二次函数图象性质(一看对称轴,二看区间端点)点拨:统一函数名二次函数法 三) 分式型 sin sin a x by c x d+=+sin 3sin 2xy x =+例: 求的值域。
点拨: 1.反表示 1cos 1x ££2.利用sinx ,有界性cos 2cos 1x y x -=-练习: 反表示四)二合一 sin cos y a x b x =+22sin cos sin()a xb x a b x j +=++利用sin 3cos y x x =+例4. 的值域.2sin cos .y x x =-练习:的值域2cos sin cos y x x x =+例5. 的值域.1.降次2.二合一sin cos x x 1sin 22x =2cos x =1cos 22x +2sin x 1cos 22x-=22cos sin()3sin sin cos 3y x x x x x p=+-+例5. 的值域.1.统一角2.降次3.二合一2sin sin y a x b x c =++5sin cos sin cos y x x x x=++例:sin cos sin cos .x x x x +一般一个式子中同时出现了和想到了五) 其他形式:六:应用题求最值R 例6:把一段半径的圆木锯成横截面为矩形的木料,怎样锯法才能使得横截面的面积最大。
高中数学三角函数专项训练(含答案)

高中数学三角函数专项训练(含答案)一、填空题1.已知函数()1sin sin 34f x x x π⎛⎫=⋅+- ⎪⎝⎭定义域为[](),m n m n <,值域为11,24⎡⎤-⎢⎥⎣⎦,则n m-的最小值是________.2.赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了"勾股圆方图",亦称"赵爽弦图"(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成).类比"赵爽弦图",可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设 ,AD AB AC λμ=+若4AD AF =,则λ-μ的值为___________3.法国著名的军事家拿破仑.波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.在三角形ABC 中,角60A =,以,,AB BC AC 为边向外作三个等边三角形,其外接圆圆心依次为123,,O O O ,若三角形123O O O 3ABC 的周长最小值为___________4.在ABC 中,7AB =3BC =1cos 7BAC ∠=,动点D 在ABC 所在平面内且2π3BDC ∠=.给出下列三个结论:①BCD △3②线段AD 的长度只有最小值,无最大值,且最小值为1;③动点D 的轨迹的长度为8π3.其中正确结论的序号为______.5.log sin()3y x ππ=+的单调增区间为________.6.已知向量a ,b ,c 满足0a b c ++=,()()0a b a c -⋅-=,||9b c -=,则||||||a b c ++的最大值是___________.7.已知函数()()2sin 06f x x πωω⎛⎫=+> ⎪⎝⎭,若()f x 的图象关于直线3x π=对称,且在3,164ππ⎛⎫⎪⎝⎭上单调,则ω的最大值是______. 8.已知O 为△ABC 外接圆的圆心,D 为BC 边的中点,且4BC =,6AO AD ⋅=,则△ABC 面积的最大值为___________.9.在平面直角坐标系xOy 中,已知直线2y x =+与x 轴,y 轴分别交于M ,N 两点,点P 在圆22()2x a y -+=上运动.若MPN ∠恒为锐角,则实数a 的取值范围是________.10.△ABC 内接于半径为2的圆,三个内角A ,B ,C 的平分线延长后分别交此圆于1A ,1B ,1C .则111coscos cos 222sin sin sin A B C AA BB CC A B C++++的值为_____________.二、单选题11.已知双曲线2221(0)y x b b-=>的左、右焦点分别为1F ,2F ,过点2F 作直线l 交双曲线的右支于A ,B 两点.若11||::3:3:2AB AF BF =,则双曲线的离心率为( ) A 33B 2C .113D .1112.已知无穷项实数列{}n a 满足: 1a t =, 且 14111n n n a a a +=--, 则( ) A .存在1t >, 使得20111a a = B .存在0t <, 使得20211a a =C .若2211a a =, 则21a a =D .至少有2021个不同的t , 使得20211a a =13.已知点P 是曲线e 3xy =+α为曲线在点P 处的切线的倾斜角,则α的取值范围是( ) A .0,6π⎛⎤ ⎥⎝⎦B .,62ππ⎡⎫⎪⎢⎣⎭C .,63ππ⎡⎤⎢⎥⎣⎦D .0,3π⎛⎤ ⎥⎝⎦14.若函数()f x 同时满足:①定义域内任意实数x ,都有()()110f x f x ++-=;②对于定义域内任意1x ,2x ,当12x x ≠时,恒有()()()12120x x f x f x -⋅->⎡⎤⎣⎦;则称函数()f x 为“DM 函数”.若“DM 函数”满足()()2sin cos 0f f αα-+>,则锐角α的取值范围为( ) A .0,4π⎛⎫ ⎪⎝⎭B .0,3π⎛⎫ ⎪⎝⎭C .,43ππ⎛⎫ ⎪⎝⎭D .2,43ππ⎛⎫ ⎪⎝⎭15.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭,3B π=,则a c +的取值范围是( )A .⎝B .32⎛ ⎝C .⎣D .32⎡⎢⎣16.在ABC 中,,E F 分别是,AC AB 的中点,且32AB AC =,若BEt CF <恒成立,则t 的最小值为( ) A .34B .78C .1D .5417.在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,S 为ABC 的面积,且()222S a b c =--,则222b c bc+的取值范围为( )A .4359,1515⎛⎫ ⎪⎝⎭B .4315⎡⎫⎪⎢⎣⎭C .5915⎡⎫⎪⎢⎣⎭D .)⎡+∞⎣18.已知F 是椭圆2221(1)x y a a +=>的左焦点,A 是该椭圆的右顶点,过点F 的直线l (不与x 轴重合)与该椭圆相交于点M ,N .记MAN α∠=,设该椭圆的离心率为e ,下列结论正确的是( )A .当01e <<时,2πα<B .当02e <<2πα>C .当12e <<时,23πα>D 1e <<时,34πα>19.设函数()xf x mπ=,函数()f x 的对称轴为0x x =,若存在0x 满足()22200x f x m +<⎡⎤⎣⎦,则m 的取值范围为( ) A .(,6)(6,)-∞-+∞ B .(,4)(4,)-∞-⋃+∞ C .(,2)(2,)-∞-+∞D .(,1)(1,)-∞-+∞20.△ABC 中,BD 是AC 边上的高,A=4π,BD AC =( )A .14B .12C .23D .34三、解答题21.已知1l ,2l ,3l 是同一平面内自上而下的三条不重合的平行直线.(1)如图1,如果1l 与2l 间的距离是1,2l 与3l 间的距离也是1,可以把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,求这个正三角形ABC 的边长.(2)如图2,如果1l 与2l 间的距离是1,2l 与3l 间的距离是2,能否把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,如果能放,求BC 和3l 夹角θ的正切值并求该正三角形边长;如果不能,试说明理由.(3)如果边长为2的正三角形ABC 的三顶点分别在1l ,2l ,3l 上,设1l 与2l 间的距离为1d ,2l 与3l 间的距离为2d ,求12d d ⋅的取值范围.22.在直角ABC ∆中,2BAC π∠=,延长CB 至点D ,使得2CB BD =,连接AD .(1)若AC AD =,求CAD ∠的值; (2)求角D 的最大值.23.已知函数()()2sin 24sin 206x x x f πωωω⎛⎫=--+> ⎪⎝⎭,其图象与x 轴相邻的两个交点的距离为2π. (1)求函数()f x 的解析式;(2)若将()f x 的图象向左平移()0m m >个长度单位得到函数()g x 的图象恰好经过点,03π⎛-⎫ ⎪⎝⎭,求当m 取得最小值时,()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调区间. 24.如图,在ABC ∆中,90,3,1ABC AB BC ︒∠===,P 为ABC ∆内一点,90BPC ︒∠=.(1)若3PC =,求PA ; (2)若120APB ︒∠=,求ABP ∆的面积S .25.在ABC ∆中,角,,A B C 的对边分别为,,a b c . 已知10sin 2C =(1)若4a =,210c =ABC ∆的面积;(2)若ABC ∆的面积为9154,且22213sin sin sin 16A B C +=,求c 的值.26.已知两个不共线的向量a ,b 满足(1,3)a =,(cos ,sin )b =θθ,R θ∈. (1)若//a b ,求角θ的值;(2)若2a b -与7a b -垂直,求||a b +的值;(3)当0,2π⎡⎤θ∈⎢⎥⎣⎦时,存在两个不同的θ使得|3|||a b ma +=成立,求正数m 的取值范围.27.在ABC ∆中,内角,,A B C 所对的边分别是,,a b c ,已知sin tan 1cos BC B=-.(Ⅰ)求证:ABC ∆为等腰三角形;(Ⅱ)若ABC ∆是钝角三角形,且面积为24a ,求2b ac的值.28.已知向量()cos sin ,sin a m x m x x ωωω=-,()cos sin ,2cos b x x n x ωωω=--,设函数()()2n f x a b x R =⋅+∈的图象关于点,112π⎛⎫⎪⎝⎭对称,且()1,2ω∈ (I )若1m =,求函数()f x 的最小值;(II )若()4f x f π⎛⎫≤ ⎪⎝⎭对一切实数恒成立,求()y f x =的单调递增区间.29.函数()sin()f x A x ωϕ=+(其中0,0,||2A πωϕ>><)的部分图象如图所示,把函数()f x 的图像向右平移4π个单位长度,再向下平移1个单位,得到函数()g x 的图像.(1)当17,424x ππ⎡⎤∈⎢⎥⎣⎦时,求()g x 的值域 (2)令()=()3F x f x -,若对任意x 都有2()(2)()20F x m F x m -+++≤恒成立,求m 的最大值30.在锐角△ABC 中,a 、b 、c 分别为角A 、B 、C 所对的边,且32sin a c A = (Ⅰ)确定角C 的大小: (Ⅱ)若c =,且△ABC 的面积为,求a +b 的值.【参考答案】一、填空题1.3π 2.473.6 4.①③5.(2,2)(Z)36k k k ππππ-++∈6.3+37.138.9.1a 或4a10.4 二、单选题 11.A 12.D 13.A 14.A 15.A 16.B 17.C 18.A 19.C 20.A 三、解答题21.(1)2 ;(2)能放,tan θ=;(3)(]0,1 【解析】 【分析】(1)根据,A C 到直线2l 的距离相等,可得2l 过AC 的中点M ,2l AC ⊥,从而求得边长2AC AM =的值.(2)假设能放,设边长为a ,BC 与3l 的夹角θ,不妨设060θ<≤,可得sin 2a θ=,()sin 601a θ-=,两式相比化简可得sin θa 的值,从而得出结论. (3)利用两角和差的正弦、余弦公式化简()124sin 60sin d d θθ⋅=-为()2sin 2301θ+-,再根据正弦函数的定义和值域求出12d d ⋅的取值范围. 【详解】 (1),A C 到直线2l 的距离相等,∴2l 过AC 的中点M , ∴2l AC ⊥, ∴边长22AC AM ==(2)假设能放,设边长为a ,BC 与3l 的夹角θ, 由对称性,不妨设060θ<≤, ∴sin 2a θ=,()sin 601a θ-=,两式相比可得:()sin 2sin 60θθ=-,即sin sin θθθ-,2sin θθ∴=,tan θ∴=,sin θ∴=,故边长3a ==, 综上可得,能放.(3)()1214sin 60sin 4sin sin 2d d θθθθθ⎫⋅=-=-⎪⎪⎝⎭()1cos 2222sin 23012θθθ⎫+=-=+-⎪⎪⎝⎭. 060θ<≤,30230150θ∴<+≤,()1sin 23012θ≤+≤, 所以()02sin 23011θ≤+-≤, 又10d >,20d >,所以(]120,1d d ⋅∈. 【点睛】本题是一道考查三角函数应用的题目,解题的关键是掌握等边三角形的性质以及三角函数的恒等变换,属于中档题. 22.(1)23CAD π∠=;(2)6π.【解析】 【分析】(1)在ABD ∆中,由正弦定理得,sin sin BD ABDα=,再结合在直角ABC ∆中,sin AB BC C =,然后求解即可;(2)由正弦定理及两角和的余弦可得()2tan tan cos 2sin 22D D αααϕ=+=+,然后结合三角函数的有界性求解即可. 【详解】解:(1)设BAD ∠=α,在ABD ∆中,由正弦定理得,sin sin BD ABDα=, 而在直角ABC ∆中,sin AB BC C =,所以sin sin sin BD BC CDα=, 因为AC AD =,所以C D =, 又因为2CB BD =,所以1sin 2α=,所以6πα=,所以23CAD π∠=;(2)设BAD ∠=α, 在ABD ∆中,由正弦定理得,sin sin BD ABDα=, 而在直角ABC ∆中,()cos cos AB BC ABC BC D α=∠=+, 所以()()cos cos cos sin sin sin sin sin BC D BC D D BD D Dαααα+-==, 因为2CB BD =,所以2sin 2sin cos cos 2sin sin D D D ααα=-, 即22sin cos sin 2tan 12sin 2cos 2D ααααα==+-,即()2tan tan cos 2sin 22D D αααϕ=++,1≤及0,2D π⎛⎫∈ ⎪⎝⎭,解得0tan D <≤ 所以角D 的最大值为6π. 【点睛】本题考查了正弦定理,重点考查了三角函数的有界性,属中档题.23.(1)()23f x x π⎛⎫=+ ⎪⎝⎭(2)单调增区间为,612ππ⎡⎤--⎢⎥⎣⎦,57,1212ππ⎡⎤⎢⎥⎣⎦;单调减区间为5,1212ππ⎡⎤-⎢⎥⎣⎦. 【解析】 【分析】(1)利用两角差的正弦公式,降幂公式以及辅助角公式化简函数解析式,根据其图象与x 轴相邻的两个交点的距离为2π,得出周期,利用周期公式得出1ω=,即可得出该函数的解析式;(2)根据平移变换得出()223m x x g π⎛⎫=++ ⎪⎝⎭,再由函数()g x 的图象经过点,03π⎛⎫- ⎪⎝⎭,结合正弦函数的性质得出m 的最小值,进而得出()223g x x π⎛⎫=+⎪⎝⎭,利用整体法结合正弦函数的单调性得出该函数在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调区间.【详解】解:(1)()2sin 24sin 26x x x f πωω⎛⎫=--+ ⎪⎝⎭11cos22cos24222xx x ωωω-=--⨯+32cos22x x ωω=+23x πω⎛⎫=+ ⎪⎝⎭由已知函数()f x 的周期T π=,22ππω=,1ω=∴()23f x x π⎛⎫=+ ⎪⎝⎭.(2)将()f x 的图象向左平移()0m m >个长度单位得到()g x 的图象∴()223m x x g π⎛⎫=++ ⎪⎝⎭,∵函数()g x 的图象经过点,03π⎛⎫- ⎪⎝⎭22033m ππ⎡⎤⎛⎫⨯-++= ⎪⎢⎥⎝⎭⎣⎦,即sin 203m π⎛⎫-= ⎪⎝⎭∴23m k ππ-=,k Z ∈∴26k m ππ=+,k Z ∈∵0m >,∴当0k =,m 取最小值,此时最小值为6π此时,()223g x x π⎛⎫=+⎪⎝⎭. 令7612x ππ-≤≤,则2112336x πππ≤+≤当22332x πππ≤+≤或32112236x πππ≤+≤,即当612x ππ-≤≤-或571212x ππ≤≤时,函数()g x 单调递增当232232x πππ≤+≤,即51212x ππ-≤≤时,函数()g x 单调递减.∴()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调增区间为,612ππ⎡⎤--⎢⎥⎣⎦,57,1212ππ⎡⎤⎢⎥⎣⎦;单调减区间为5,1212ππ⎡⎤-⎢⎥⎣⎦.【点睛】本题主要考查了由正弦函数的性质确定解析式以及正弦型函数的单调性,属于中档题.24.(12 【解析】 【分析】(1)求出12BP ==,,36CBP ABP ππ∠=∠=,ABP ∆中由余弦定理即可求得PA ;(2)设PBA α∠=,利用正弦定理表示出()sin120sin 60AB PB =︒︒-α,求得tan α=,利用面积公式即可得解. 【详解】(1)在ABC ∆中,90,1ABC AB BC ︒∠===,2AC =P 为ABC ∆内一点,90BPC ︒∠=,PC =,所以12BP =,CBP ∆中,由余弦定理得:2221cos 22BP BC PC CBP BP BC +-∠==⋅所以,36CBP ABP ππ∠=∠=ABP ∆中,由余弦定理得:AP==; (2)120APB ︒∠=,设0,,90,602PBA PBC PAB π⎛⎫∠=α∈∠=︒-α∠=︒-α ⎪⎝⎭,在Rt PBC ∆中,sin sin PB BC =⋅α=α, 在PBA ∆中,由正弦定理()sin120sin 60AB PB=︒︒-α,即()sin 2sin 60α=︒-α,sin sin α=α-α,所以tan α=sin PB α==ABP ∆的面积11sin 22S AB PB α=⋅==. 【点睛】此题考查解三角形,对正余弦定理的综合使用,涉及两角差的正弦公式以及同角三角函数关系的使用,综合性较强.25.(1)2)c =【解析】 【分析】(1)先根据sin2C =sin C 与cos C ,再利用余弦定理求出b 边,最后利用1sin 2ABC S ab C ∆=求出答案;(2)利用正弦定理将等式化为变得关系,再利用余弦定理化为2c 与ab 的关系式,再结合面积求出c 的值. 【详解】解:(1)因为sin2C =所以2101cos 12sin122164C C =-=-⨯=-.又()0,C π∈,所以sin C =.因为4a =,c =2222cos c a b ab C =+-, 所以214016244b b ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得4b =,所以11sin 4422ABC S ab C ∆==⨯⨯= (2)因为22213sin sin sin 16A B C +=,由正弦定理,得2221316a b c +=. 又2222cos a b ab C c +-=,所以283c ab =.又1sin 2ABC S ab C ∆=,得18ab =,所以248c =,所以c = 【点睛】本题考查正余弦定理解三角形,属于基础题.26.(1),3k k Z πθθπ⎧⎫=+∈⎨⎬⎩⎭|(2(3)⎣⎭【解析】 【分析】(1)由题得tan θ=2)先求出1a b ⋅=,再利用向量的模的公式求出||7a b +=;(3)等价于2476m πθ⎛⎫+=- ⎪⎝⎭在0,2π⎡⎤θ∈⎢⎥⎣⎦有两解,结合三角函数分析得解. 【详解】(1)由题得sin 0,tan θθθ=∴=所以角θ的集合为,3k k Z πθθπ⎧⎫=+∈⎨⎬⎩⎭| . (2)由条件知2a =, 1b =,又2a b -与7a b -垂直, 所以()()2781570a b a b a b -⋅-=-⋅+=,所以1a b ⋅=. 所以222||||2||4217a b a a b b +=+⋅+=++=,故||7a b +=.(3)由3a b ma +=,得223a b ma +=,即2222233a a b b m a +⋅+=,即2434b m +⋅+=,)27cos 4m θθ+=,所以2476m πθ⎛⎫+=- ⎪⎝⎭.由0,2π⎡⎤θ∈⎢⎥⎣⎦得2,663πππθ⎡⎤+∈⎢⎥⎣⎦,又θ要有两解,结合三角函数图象可得,2647m ≤-<2134m ≤<又因为0m >m ≤<即m 的范围⎣⎭. 【点睛】本题主要考查向量平行垂直的坐标表示,考查向量的模的计算,考查三角函数图像和性质的综合应用,意在考查学生对这些知识的理解掌握水平和分析推理能力,属于中档题.27.(Ⅰ)证明见解析;(Ⅱ)2【解析】 【分析】(Ⅰ)将正切化弦,结合两角和差正弦公式可求得()sin sin C B C =+,根据三角形内角和可整理为sin sin C A =,则由正弦定理可得到结论;(Ⅱ)利用三角形面积公式可求得1sin 2B =;根据三角形为钝角三角形且(Ⅰ)中的c a =,可知B 为钝角,求得cos B ;利用余弦定理可构造方程求得,a b 之间关系,从而得到所求结果. 【详解】 (Ⅰ)由sin tan 1cos B C B =-得:sin sin cos 1cos C BC B=-则:()sin sin cos cos sin sin C B C B C B C =+=+A B C π++= ()()sin sin sin B C A A π∴+=-= sin sin C A ∴=由正弦定理可知:c a =ABC ∆∴为等腰三角形(Ⅱ)由题意得:2211sin sin 224a S ac B a B ===,解得:1sin 2B =ABC ∆为钝角三角形,且a c = B ∴为钝角 cos B ∴=由余弦定理得:(2222222cos 22b a c ac B a a =+-==+2222b b ac a ∴==【点睛】本题考查三角形形状的求解、利用余弦定理、三角形面积公式求解三角形边之间的关系问题,涉及到两角和差正弦公式、三角形内角和、诱导公式、同角三角函数值的求解等知识.28.(Ⅰ)1()22,31234k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【解析】 【分析】化简()f x 解析式可得()()22n f x x ωϕ=-+;根据图象关于,112π⎛⎫ ⎪⎝⎭可求得n ;(Ⅰ)若1m =,则()()21f x x ωϕ=-+,从而可得函数最小值;(Ⅱ)利用4x π=为对称轴,,112π⎛⎫ ⎪⎝⎭为对称中心可得()*642T T k k N π=+⋅∈,根据周期和ω的范围可求得ω;将,112π⎛⎫ ⎪⎝⎭代入解析式可求得()314f x x π⎛⎫=-+ ⎪⎝⎭,将34x π-整体放入正弦函数的单调递增区间中,解出x 的范围即可. 【详解】由题意得:()()22cos sin 2sin cos 2n f x m x x n x x ωωωω=--++()sin 2cos 2222n n n x m x x ωωωϕ=-+=-+ 其中cos ϕ=sin ϕ=图象关于点,112π⎛⎫⎪⎝⎭对称 12n ∴=,解得:2n =()()21f x x ωϕ∴=-+(Ⅰ)若1m =,则()()21f x x ωϕ=-+()min 1f x ∴=(Ⅱ)()4f x f π⎛⎪≤⎫ ⎝⎭对一切实数恒成立 ()max 4f x f π⎛⎫∴= ⎪⎝⎭()*412642T T k k N πππ∴-==+⋅∈,即:()()*223212T k N k ππω==∈+()3212k ω∴=+,又()1,2ω∈ 32ω∴=()2sin3cos31f x x m x ∴=-+,又图象关于点,112π⎛⎫⎪⎝⎭对称2sin cos 111244f m πππ⎛⎫∴=-+= ⎪⎝⎭,解得:2m =()2sin 32cos31314f x x x x π⎛⎫∴=-+=-+ ⎪⎝⎭令232242k x k πππππ-+≤-≤+,k Z ∈,解得:2212343k k x ππππ-+≤≤+,k Z ∈ ()f x ∴的单调递增区间为:()22,31234k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【点睛】本题考查三角函数图象与性质的综合应用问题,涉及到根据三角函数的性质求解函数解析式的求解、三角函数最值的求解、单调区间的求解问题.29.(1)1,0⎡⎤⎢⎥⎣⎦(2)265-【解析】 【分析】(1)根据图象的最低点求得A 的值,根据四分之一周期求得ω的值,根据点7,112π⎛⎫- ⎪⎝⎭求得ϕ的值,由此求得函数()f x 的解析式,进而根据图象平移变换求得()g x 的解析式,并由此求得17,424x ππ⎡⎤∈⎢⎥⎣⎦时()g x 的值域.(2)先求得()f x 的值域,由此求得()F x 的值域.令()[4,2]t F x =∈--对题目所给不等式换元,根据二次函数的性质列不等式组,解不等式组求得m 的取值范围,由此求得m 的最大值. 【详解】(1)根据图象可知171,4123A T ππ==- 2,2,()sin(2)T f x x Tππωϕ∴=∴===+ 代入7,112π⎛⎫-⎪⎝⎭得,7sin 1,2,63k k Z ππϕϕπ⎛⎫+=-=+∈ ⎪⎝⎭, ||,0,23k ππϕϕ<∴==()sin 23f x x π⎛⎫∴=+ ⎪⎝⎭把函数()f x 的图像向右平移4π个单位长度,再向下平移1个单位,得到函数()g x ()sin 21sin 21436g x x x πππ⎛⎫⎛⎫⎛⎫∴=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,设26t x π=-,则5,34t ππ⎡⎤∈⎢⎥⎣⎦, 此时sint ⎡⎤∈⎢⎥⎣⎦,所以值域为1,0⎡⎤⎢⎥⎣⎦. (2)由(1)可知()sin 2[1,1]3f x x π⎛⎫=+∈- ⎪⎝⎭()()3[4,2]F x f x =-∈--对任意x 都有2()(2)()20F x m F x m -+++≤恒成立 令()[4,2]t F x =∈--,2()(2)2h t t m t m =-+++,是关于t 的二次函数,开口向上则max ()0h t ≤恒成立而()h t 的最大值,在4t =-或2t =-时取到最大值则(2)0(4)0h h -≤⎧⎨-≤⎩,4(2)(2)2016(2)(4)20m m m m -+-++≤⎧⎨-+-++≤⎩, 解得103265m m ⎧≤-⎪⎪⎨⎪≤-⎪⎩所以265m ≤-,则m 的最大值为265-. 【点睛】本小题主要考查由三角函数图像求三角函数的解析式,考查三角函数图像变换,考查不等式恒成立问题,考查化归与转化的数学思想方法,属于中档题. 30.(Ⅰ)3π(Ⅱ)5 【解析】 【详解】试题分析:(12sin sin A C A =即可得sin C =60C =︒(2)∵1sin 2S ab C ==a b + 试题解析: 解:(12sin sin A C A =, ∵,A C是锐角,∴sin C =60C =︒.(2)∵1sin 2S ab C ==6ab = 由余弦定理得222222cos ()3()187c a b ab C a b ab a b =+-=+-=+-= ∴5a b +=点睛:在解三角形问题时多注意正余弦定理的结合运用,正弦定理主要用在角化边和边化角上,而余弦定理通常用来求解边长。
高考复习:三角函数的图像与性质(含参考答案与解析方法)
4.3三角函数的图像与性质一 正弦、余弦、正切函数的图像与性质 (下表中k ∈Z ).1.三角函数存在多个单调区间时易错用“∪”联结.2.研究三角函数单调性、对称中心、奇偶性及对称轴时易忽视“k ∈Z ”这一条件. 考点一 三角函数的定义域与值域例1、(1)函数f (x )=3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域为________.(2)函数y =lg(sin x )+ cos x -12的定义域为________.(3)①函数y =2cos 2x +5sin x -4的值域为________.②当x ∈⎣⎡⎦⎤π6,7π6时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________.考点二 三角函数的单调性例2、函数y =2sin ⎝⎛⎭⎫x -π4的单调递减区间为 _____________.变式训练1 (1)函数y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫x -π4的单调递减区间为_____________; (2)函数y =sin ⎝⎛⎭⎫-2x +π3的单调递减区间为_______________.考点三 三角函数的对称性与奇偶性例3、(2013·扬州期末)已知函数f (x )=-2sin 2x +23sin x · cos x +1.(1)求f (x )的最小正周期及对称中心;(2)当x ∈⎣⎡⎦⎤-π6,π3时,求f (x )的最大值和最小值.例4 (1)若函数y =3sin(2x +φ)(0<φ<π)的图像关于点⎝⎛⎭⎫π3,0中心对称,则φ=________.(2) 已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π3的一条对称轴为x =π3,一个对称中心为点⎝⎛⎭⎫π12,0,则ω的最小值为______.(3)设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图像如图所示,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则f ⎝⎛⎭⎫16的值为______.冲刺高考:1、已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是________.2、已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b 的值为________.3、(2014·北京)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________. 课堂练习1、 函数y =lg sin 2x +9-x 2的定义域为________________.2、 函数y =sin x -cos x 的定义域是________.3、 函数f (x )=2sin ⎝⎛⎭⎫x -π4,x ∈[-π,0]的单调增区间为________.4、若函数f (x )=2sin ωx (ω>0)在⎣⎡⎤-2π3,2π3上单调递增,则ω的最大值为______.5、将函数y =3cos x +sin x (x ∈R ) 的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是________.4.3三角函数的图像与性质(作业)1、已知函数f (x )=-2sin(2x +φ)(|φ|<π),若f (π8)=-2,则f (x )的单调递减区间是________.2、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是________.3、给出下列四个命题,其中不正确的命题为______.(填序号) ①若cos α=cos β,则α-β=2k π,k ∈Z ;②函数y =2cos ⎝⎛⎭⎫2x +π3的图象关于x =π12中心对称;③函数y =cos(sin x )(x ∈R )为偶函数;④若α、β均为第一象限角,且α>β,则sin α>sin β ⑤函数y =sin|x |是周期函数,且周期为2π.4、 函数y =cos 2x +sin 2x ,x ∈R 的值域是________.5、 函数y =cos(π4-2x )的单调减区间为________.6、设函数f (x )=3sin(π2x +π4),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________.7、已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)=________.8、已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间.9、设函数f (x )=sin(πx 4-π6)-2cos 2πx8+1.(1)求f (x )的最小正周期.(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时,y =g (x )的最大值.4.3三角函数的图像与性质一 正弦、余弦、正切函数的图像与性质(下表中k ∈Z ).1.三角函数存在多个单调区间时易错用“∪”联结.2.研究三角函数单调性、对称中心、奇偶性及对称轴时易忽视“k ∈Z ”这一条件. 考点一 三角函数的定义域与值域例1 (1)函数f (x )=3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域为________. 解析:当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6,sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-12,1, 故3sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-32,3, 即此时函数f (x )的值域是⎣⎡⎦⎤-32,3. (2) (2014·湛江调研)函数y =lg(sin x )+ cos x -12的定义域为________.解析:要使函数有意义必须有⎩⎪⎨⎪⎧ sin x >0,cos x -12≥0,即⎩⎪⎨⎪⎧sin x >0,cos x ≥12, 解得⎩⎪⎨⎪⎧2k π<x <π+2k π,-π3+2k π≤x ≤π3+2k π(k ∈Z ), ∴2k π<x ≤π3+2k π,k ∈Z ,∴函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π<x ≤π3+2k π,k ∈Z .(3)①函数y =2cos 2x +5sin x -4的值域为________.②当x ∈⎣⎡⎦⎤π6,7π6时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________. 解析:①y =2cos 2x +5sin x -4=2(1-sin 2x )+5sin x -4=-2sin 2x +5sin x -2 =-2(sin x -54)2+98. 故当sin x =1时,y max =1,当sin x =-1时,y min =-9,故y =2cos 2x +5sin x -4的值域为[-9,1]. ②∵x ∈⎣⎡⎦⎤π6,7π6,∴sin x ∈⎣⎡⎦⎤-12,1. 又y =3-sin x -2cos 2x =3-sin x -2(1-sin 2x )= 2⎝⎛⎭⎫sin x -142+78. ∴当sin x =14时,y min =78, 当sin x =-12或sin x =1时,y max =2.答案:(1)[-9,1] (2)78 2[类题通法]1.三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图像来求解.2.三角函数值域的不同求法 (1)利用sin x 和cos x 的值域直接求;(2)把所给的三角函数式变换成y =A sin(ωx +φ)的形式求值域; (3)把sin x 或cos x 看作一个整体,转换成二次函数求值域; (4)利用sin x ±cos x 和sin x cos x 的关系转换成二次函数求值域. 考点二 三角函数的单调性例2、求函数y =2sin ⎝⎛⎭⎫x -π4的单调递减区间 [解] 由2k π+π2≤x -π4≤2k π+3π2,k ∈Z ,得2k π+3π4≤x ≤2k π+7π4,k ∈Z .故函数y =2sin ⎝⎛⎭⎫x -π4的单调减区间为 ⎣⎡⎦⎤2k π+3π4,2k π+7π4(k ∈Z ). 变式训练1 (1)求函数y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫x -π4的单调递减区间;(2)求函数y =sin ⎝⎛⎭⎫-2x +π3的单调递减区间 解 (1)画出函数y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫x -π4的图像,易知其单调递减区间为⎣⎡⎦⎤k π+3π4,k π+5π4(k ∈Z ). (2) y =-sin ⎝⎛⎭⎫2x -π3, 它的减区间是y =sin ⎝⎛⎭⎫2x -π3的增区间. 由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故所给函数的减区间为⎣⎡⎦⎤k π-π12,k π+5π12,k ∈Z ; 例3、求函数y =sin ⎝⎛⎭⎫π3+4x +cos ⎝⎛⎭⎫4x -π6的周期、单调区间及最大、最小值. 解 ∵⎝⎛⎭⎫π3+4x +⎝⎛⎭⎫π6-4x =π2, ∴cos ⎝⎛⎭⎫4x -π6=cos ⎝⎛⎭⎫π6-4x =cos ⎣⎡⎦⎤π2-⎝⎛⎭⎫π3+4x =sin ⎝⎛⎭⎫π3+4x . ∴y =2sin ⎝⎛⎭⎫4x +π3,周期T =2π4=π2. 当-π2+2k π≤4x +π3≤π2+2k π (k ∈Z )时,函数单调递增,∴函数的递增区间为⎣⎡⎤-5π24+k π2,π24+k π2 (k ∈Z ). 当π2+2k π≤4x +π3≤3π2+2k π (k ∈Z )时,函数单调递减, ∴函数的递减区间为⎣⎡⎦⎤π24+k π2,7π24+k π2(k ∈Z ).当x =π24+k π2 (k ∈Z )时,y max =2; 当x =-5π24+k π2 (k ∈Z )时,y min =-2.考点三 三角函数的对称性与奇偶性例4、(2013·扬州期末)已知函数f (x )=-2sin 2x +23sin x · cos x +1.(1)求f (x )的最小正周期及对称中心;(2)当x ∈⎣⎡⎦⎤-π6,π3时,求f (x )的最大值和最小值. 解:(1)f (x )= 3 sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6, 所以f (x )的最小正周期为T =2π2=π.令 sin ⎝⎛⎭⎫2x +π6=0,得x =k π2-π12(k ∈Z ), 所以f (x )的对称中心为⎝⎛⎭⎫k π2-π12,0(k ∈Z ). (2)因为x ∈⎣⎡⎦⎤-π6,π3,所以-π6≤2x +π6≤5π6, 所以-12≤sin ⎝⎛⎭⎫2x +π6≤1,所以-1≤f (x )≤2. 所以当x =-π6时,f (x )的最小值为-1;当x =π6时,f (x )的最大值为2.例5 (1)若函数y =3sin(2x +φ)(0<φ<π)的图像关于点⎝⎛⎭⎫π3,0中心对称,则φ=________.解析:由题意得3sin ⎝⎛⎭⎫23π+φ=0,所以23π+φ=k π(k ∈Z ).又因为0<φ<π,所以φ=π3. (2) 已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π3的一条对称轴为x =π3,一个对称中心为点⎝⎛⎭⎫π12,0,则ω的最小值为______.解析:由题意知π3-π12≥T 4,T =2πω≤π,ω≥2.(3)设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图像如图所示,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则f ⎝⎛⎭⎫16的值为______.解析:由题意知,点M 到x 轴的距离是12,根据题意可设f (x )=12cos ωx ,又由题图知12·2πω=1,所以ω=π,所以f (x )=12cos πx ,故f ⎝⎛⎭⎫16=12cos π6=34. [类题通法]1.若f (x )=A sin(ωx +φ)为偶函数,则当x =0时,f (x )取得最大或最小值. 若f (x )=A sin(ωx +φ)为奇函数,则当x =0时,f (x )=0.2.对于函数y =A sin(ωx +φ),其对称轴一定经过图像的最高点或最低点,对称中心一定是函数的零点,因此在判断直线x =x 0或点(x 0,0)是否是函数的对称轴或对称中心时,可通过检验f (x 0)的值进行判断.三角函数的单调性、对称性、周期性例6、(1)已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是________.(2)已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b的值为________.(3)(2014·北京)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________. 思维点拨 (1)(π2,π)为函数f (x )某个单调减区间的子集;(2)由f (x +π4)=f (-x )可得函数的对称轴,应用函数在对称轴处的性质求解即可;(3)利用正弦型函数图象的对称性求周期. 解析 (1)由π2<x <π得π2ω+π4<ωx +π4<πω+π4,由题意知(π2ω+π4,πω+π4)⊆[π2,3π2], ∴⎩⎨⎧π2ω+π4≥π2,πω+π4≤3π2,∴12≤ω≤54. (2)由f (x +π4)=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3.(3)∵f (x )在⎣⎡⎦⎤π6,π2上具有单调性, ∴T 2≥π2-π6, ∴T ≥2π3. ∵f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3, ∴f (x )的一条对称轴为x =π2+2π32=7π12. 又∵f ⎝⎛⎭⎫π2=-f ⎝⎛⎭⎫π6, ∴f (x )的一个对称中心的横坐标为π2+π62=π3. ∴14T =7π12-π3=π4, ∴T =π. 答案 (1)[12,54] (2)-1或3 (3)π温馨提醒 (1)对于已知函数的单调区间的某一部分确定参数ω的范围的问题:首先,明确已知的单调区间应为函数的单调区间的子集;其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解.(2)函数y =A sin(ωx +φ)+b 的图象与其对称轴的交点是最值点. 课堂练习1、函数y =lg sin 2x +9-x 2的定义域为________________.解析 由⎩⎪⎨⎪⎧ sin 2x >0,9-x 2≥0,得⎩⎪⎨⎪⎧2k π<2x <2k π+π,k ∈Z ,-3≤x ≤3.∴-3≤x <-π2或0<x <π2. ∴函数y =lg sin 2x +9-x 2的定义域为 {x |-3≤x <-π2或0<x <π2}.2、函数y =sin x -cos x 的定义域是________. 解析 要使函数有意义,必须有sin x -cos x ≥0,即sin x ≥cos x ,同一坐标系中作出y =sin x ,y =cos x ,x ∈[0,2π]的图象如图所示.结合图象及正、余弦函数的周期是2π知, 函数的定义域为{x |2k π+π4≤x ≤2k π+5π4,k ∈Z }.3、函数f (x )=2sin ⎝⎛⎭⎫x -π4,x ∈[-π,0]的单调增区间为________. 解析:当x -π4∈⎣⎡⎦⎤2k π-π2,2k π+π2,k ∈Z 时,是f (x )的单调增区间. 又因为x ∈[-π,0],故取k =0得x ∈⎣⎡⎦⎤-π4,0 4、若函数f (x )=2sin ωx (ω>0)在⎣⎡⎦⎤-2π3,2π3上单调递增,则ω的最大值为______. 解析:依题意可知12×T ≥2×2π3,即12×2πω≥2×2π3,解得ω≤34,从而ω的最大值为34.5、将函数y =3cos x +sin x (x ∈R ) 的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是________.解析 y =3cos x +sin x =2sin(x +π3)向左平移m 个单位长度后得到y =2sin(x +π3+m ),它关于y 轴对称可得 sin(π3+m )=±1, ∴π3+m =k π+π2,k ∈Z ,∴m =k π+π6,k ∈Z , ∵m >0,∴m 的最小值为π6.4.3三角函数的图像与性质(作业)1、已知函数f (x )=-2sin(2x +φ)(|φ|<π),若f (π8)=-2,则f (x )的单调递减区间是________.解析 由f (π8)=-2得f (π8)=-2sin(2×π8+φ)=-2sin(π4+φ)=-2,所以sin(π4+φ)=1.因为|φ|<π, 所以φ=π4. 由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,解得 k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递减区间为[k π-3π8,k π+π8](k ∈Z ).2、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是________.解析 根据题意平移后函数的解析式为 y =sin ω⎝⎛⎭⎫x -π4, 将⎝⎛⎭⎫3π4,0代入得sin ωπ2=0,则ω=2k ,k ∈Z ,且ω>0, 故ω的最小值为2. 3、给出下列四个命题,其中不正确的命题为______.(填序号) ①若cos α=cos β,则α-β=2k π,k ∈Z ;②函数y =2cos ⎝⎛⎭⎫2x +π3的图象关于x =π12中心对称; ③函数y =cos(sin x )(x ∈R )为偶函数;④若α、β均为第一象限角,且α>β,则sin α>sin β⑤函数y =sin|x |是周期函数,且周期为2π. 答案 ①④⑤解析 命题①:若α=-β,则cos α=cos β,假命题;命题②:x =π12,cos ⎝⎛⎭⎫2x +π3=cos π2=0,故x =π12是y =2cos ⎝⎛⎭⎫2x +π3的对称中心;命题⑤:函数y =sin|x |不是周期函数. 4、函数y =cos 2x +sin 2x ,x ∈R 的值域是________. 解析 y =cos 2x +sin 2x =cos 2x +1-cos 2x 2=1+cos 2x2.∵cos 2x ∈[-1,1],∴y ∈[0,1].5、函数y =cos(π4-2x )的单调减区间为________.解析 由y =cos(π4-2x )=cos(2x -π4)得2k π≤2x -π4≤2k π+π(k ∈Z ),故k π+π8≤x ≤k π+5π8(k ∈Z ). 所以函数的单调减区间为[k π+π8,k π+5π8](k ∈Z ).6、设函数f (x )=3sin(π2x +π4),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________. 解析 f (x )=3sin(π2x +π4)的周期T =2π×2π=4,f (x 1),f (x 2)应分别为函数f (x )的最小值和最大值, 故|x 1-x 2|的最小值为T2=2.7、已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)=________.解析 由题中图象可知,此正切函数的半周期等于3π8-π8=π4,即最小正周期为π2, 所以ω=2.由题意可知,图象过定点(3π8,0),所以0=A tan(2×3π8+φ), 即3π4+φ=k π(k ∈Z ), 所以φ=k π-3π4(k ∈Z ),又|φ|<π2,所以φ=π4. 又图象过定点(0,1),所以A =1.综上可知,f (x )=tan(2x +π4), 故有f (π24)=tan(2×π24+π4)=tan π3= 3.8、已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1. (1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈⎣⎡⎦⎤0,π2,∴2x +π6∈⎣⎡⎦⎤π6,7π6. ∴sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, ∴-2a sin ⎝⎛⎭⎫2x +π6∈[-2a ,a ]. ∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1, ∴b =-5,3a +b =1,因此a =2,b =-5. (2)由(1)得,f (x )=-4sin ⎝⎛⎭⎫2x +π6-1, g (x )=f ⎝⎛⎭⎫x +π2=-4sin ⎝⎛⎭⎫2x +7π6-1=4sin ⎝⎛⎭⎫2x +π6-1, 又由lg g (x )>0,得g (x )>1,∴4sin ⎝⎛⎭⎫2x +π6-1>1,∴sin ⎝⎛⎭⎫2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π6,k ∈Z ,其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z ,∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时,g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z .9、设函数f (x )=sin(πx 4-π6)-2cos 2πx8+1.(1)求f (x )的最小正周期.(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时,y =g (x )的最大值.解 (1)f (x )=sin πx 4cos π6-cos πx 4sin π6-cos πx 4=32sin πx 4-32cos πx 4=3sin(πx 4-π3), 故f (x )的最小正周期为T =2ππ4=8.(2)方法一 在y =g (x )的图象上任取一点(x ,g (x )), 它关于x =1的对称点(2-x ,g (x )).由题设条件,知点(2-x ,g (x ))在y =f (x )的图象上,从而g (x )=f (2-x )=3sin[π4(2-x )-π3]=3sin[π2-πx 4-π3]=3cos(πx 4+π3).当0≤x ≤43时,π3≤πx 4+π3≤2π3,因此y =g (x )在区间[0,43]上的最大值为g (x )max =3cos π3=32.方法二 区间[0,43]关于x =1的对称区间为[23,2],且y =g (x )与y =f (x )的图象关于直线x =1对称, 故y =g (x )在[0,43]上的最大值为y =f (x )在[23,2]上的最大值.由(1)知f (x )=3sin(πx 4-π3),当23≤x ≤2时,-π6≤πx 4-π3≤π6. 因此y =g (x )在[0,43]上的最大值为g (x )max =3sin π6=32.。
求三角函数值域及最值的常用方法+练习题

求三角函数值域及最值的常用方法(一)一次函数型或利用:=+=x b x a y cos sin )sin(22ϕ+⋅+x b a化为一个角的同名三角函数形式,利用三角函数的有界性或单调性求解; (2)2sin(3)512y x π=--+,x x y cos sin =(3)函数x x y cos 3sin +=在区间[0,]2π上的最小值为 1 .(4)函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是 (,1][1,)-∞-⋃+∞(二)二次函数型利用二倍角公式,化为一个角的同名三角函数形式的一元二次式,利用配方法、 换元及图像法求解。
(2)函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于43.(3).当20π<<x 时,函数x xx x f 2sin sin 82cos 1)(2++=的最小值为 4 .(4).已知k <-4,则函数y =cos2x +k (cos x -1)的最小值是 1 .(5).若2αβπ+=,则cos 6sin y βα=-的最大值与最小值之和为____2____.(三)借助直线的斜率的关系,用数形结合求解型如dx c bx a x f ++=cos sin )(型。
此类型最值问题可考虑如下几种解法:①转化为c x b x a =+cos sin 再利用辅助角公式求其最值;②利用万能公式求解;③采用数形结合法(转化为斜率问题)求最值。
例1:求函数sin cos 2xy x =-的值域。
解法1:数形结合法:求原函数的值域等价于求单位圆上的点P(cosx , sinx )与定点Q(2, 0)所确定的直线的斜率的范围。
作出如图得图象,当过Q 点的直线与单位圆相切时得斜率便是函数sin cos 2xy x =-得最值,由几何知识,易求得过Q 的两切线得斜率分别为33-、33。
结合图形可知,此函数的值域是33[,]33-。
求三角函数值域及最值的常用方法+练习题

求三角函数值域及最值的常用方法(一)一次函数型或利用:=+=x b x a y cos sin )sin(22ϕ+⋅+x b a化为一个角的同名三角函数形式,利用三角函数的有界性或单调性求解;(2)2sin(3)512y x π=--+,x x y cos sin =(3)函数x x y cos 3sin +=在区间[0,]2π上的最小值为 1 .(4)函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是 (,1][1,)-∞-⋃+∞(二)二次函数型利用二倍角公式,化为一个角的同名三角函数形式的一元二次式,利用配方法、 换元及图像法求解。
(2)函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于43.(3).当20π<<x 时,函数x xx x f 2sin sin 82cos 1)(2++=的最小值为 4 .(4).已知k <-4,则函数y =cos2x +k (cos x -1)的最小值是 1 .(5).若2αβπ+=,则cos 6sin y βα=-的最大值与最小值之和为____2____.(三)借助直线的斜率的关系,用数形结合求解例1:求函数cos 2y x =-的值域。
解法1:数形结合法:求原函数的值域等价于求单位圆上的点P(cosx, sinx )与定点Q(2, 0)所确定的直线的斜率的范围。
作出如图得图象,当过Q 点的直线与单位圆相切时得斜率便是函数sin cos 2xy x =-得最值,由几何知识,易求得过Q 的两切线得斜率分别为3。
结合图形可知,此函数的值域是[33-。
解法2:将函数sin cos 2x y x =-变形为cos sin 2y x x y -=,∴sin()x φ+=由|sin()|1x φ+=≤22(2)1y y ⇒≤+,解得:33y -≤≤[33- 解法3:利用万能公式求解:由万能公式212sin ttx +=,221cos 1t x t -=+,代入sin cos 2x y x =-得到2213t yt=--则有2320yt t y ++=知:当0t =,则0y =,满足条件;当0t ≠,由24120y =-≥△,33y ⇒-≤≤故所求函数的值域是[,]33-。
(完整)三角函数习题及答案

第四章 三角函数§4-1 任意角的三角函数一、选择题:1.使得函数lg(sin cos )y θθ=有意义的角在( )(A)第一,四象限 (B)第一,三象限 (C)第一、二象限 (D)第二、四象限 2.角α、β的终边关于У轴对称,(κ∈Ζ)。
则(A)α+β=2κπ (B)α-β=2κπ(C)α+β=2κπ-π (D)α-β=2κπ-π 3.设θ为第三象限的角,则必有( )(A)tan cot 22θθ(B)tan cot 22θθ (C)sin cos 22θθ(D)sin cos 22θθ4.若4sin cos 3θθ+=-,则θ只可能是( )(A)第一象限角 (B)第二象限角 (C )第三象限角 (D)第四象限角5.若tan sin 0θθ且0sin cos 1θθ+,则θ的终边在( )(A)第一象限 (B)第二象限 (C)第三象限 (D )第四象限 二、填空题:6.已知α是第二象限角且4sin 5α= 则2α是第▁▁▁▁象限角,2α是第▁▁▁象限角.7.已知锐角α终边上一点A 的坐标为(2sina3,-2cos3),则α角弧度数为▁▁▁▁。
8.设1sin ,(,)sin y x x k k Z xπ=+≠∈则Y 的取值范围是▁▁▁▁▁▁▁。
9.已知cosx-sinx<-1,则x 是第▁▁▁象限角。
三、解答题:10.已知角α的终边在直线y =上,求sin α及cot α的值。
11.已知Cos(α+β)+1=0, 求证:sin (2α+β)+sin β=0。
12.已知()()cos ,5n f n n N π+=∈,求ƒ(1)+ƒ(2)+ƒ(3)+……+ƒ(2000)的值. §4-2 同角三角函数的基本关系式及诱导公式一、选择题:1.()sin 2cos 22ππ⎛⎫--- ⎪⎝⎭化简结果是( )(A)0 (B )1- (C)2sin 2 ()2sin 2D -2.若1sin cos 5αα+=,且0απ,则tan α的值为( ) ()43A - ()34B - ()34C ()43D -或34-3. 已知1sin cos 8αα=,且42ππα,则cos sin αα-的值为( )(A ()34B ()C ()D ±4. 已知4sin 5α=,并且α是第一象限角,则tan α的值是( ) ()43A - ()34B - ()34C ()43D5.的结果是( )()0cos100A ()0cos80B ()0sin80C ()0cos10D6. 若cot ,(0)m m α=≠且cos α,则角α所在的象限是( )(A )一、二象限 (B )二、三象限 (C)一、三象限 (D )一、四象限 填空题:7.化简()()()21sin 2sin 2cos αππαα+-+--=▁▁▁▁▁▁。
求三角函数定义域和值域题型
二.求 三角函值域的几种典型形式
一)一次型 y=asinx+b
直接代入法
例1:求y 2sin x 1 值域。
分析:利用 sinx 1 cos x 1有界性
函数y 2sin x 1的值域为1,3
练习:口答下列函数的值域
(1)y=-2sinx+1
[-1,3]
(2) y=3cosx+2
[-1,5]
cos
x
t2
1 2
例5:y sin x cos x sin x cos x
y
解: 设t=sinx+cosx,则t 2, 2
原式化为: y=t+ t2 1 2
= 1 t2 t 1 = 1(t 1)2 1
2, 2
ymin =-1 ,
ymax
=
1 2
+
2
练习:y sin x cos x 1 sin x cos x
(2)cosx ≤1/2
解:作出余弦函数y=cosx,x∈[0,2π]的图象:
y
1
1/2
o
/2
3/2
2 x
-1
由图形可以得到,满足条件的x的集合为:
[π/3+2kπ,5 π/3+2kπ] k Z
题型二. 求三角函定义域:
【例 2】 求下列函数的定义域: (1)y= 36-x2+lg cos x; (2)y=logsin x(cos x+12).
例4. y sin x 3 cos x的值域.
解:原式= 12 ( 3)2 sin( x ) 2 sin( x )
3
3
原式的值域为2,2
练习:y 2sin x cos x的值域. 值域为 5, 5
高中数学 1.2.1任意角的三角函数的定义及应用练习(含解析)苏教版必修4-苏教版高一必修4数学试题

1.2 任意角的三角函数1.2.1 任意角的三角函数的定义及应用在初中我们已经学了锐角三角函数,知道它们都是以锐角为自变量、边的比值为函数值的三角函数.你能用平面直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗?改变终边上的点的位置,这个比值会改变吗?把角扩充为任意角,结论成立吗?一、任意角的三角函数1.单位圆:在平面直角坐标系中,以原点O 为圆心,以单位长度为半径的圆称为________.2.三角函数的定义:设角α的顶点与原点重合,始边与x 轴非负半轴重合.在平面直角坐标系中,角α终边与单位圆交于一点P (x ,y ),则r =|OP |=1.那么:(1)y 叫做________,记作sin α,即y =sin α; (2)x 叫做________,记作cos α,即x =cos α; (3)y x 叫做________,记作tan α,即y x=tan α(x ≠0).正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们把它们统称为________.答案:1.单位圆2.(1)α的正弦 (2)α的余弦 (3)α的正切 三角函数二、三角函数值在各个象限内的符号1.由三角函数的定义,以及各象限内的点的坐标的符号,可以确定三角函数在各象限的符号.sin α=y r,其中r >0,于是sin α的符号与y 的符号相同,即:当α是第________象限角时,sin α>0;当α是第________象限角时,sin α<0.cos α=x r,其中r >0,于是cos α的符号与x 的符号相同,即:当α是第__________象限角时,cos α>0;当α是第________象限角时,cos α<0.tan α=y x,当x 与y 同号时,它们的比值为正,当x 与y 异号时,它们的比值为负,即:当α是第________象限角时,tan α>0;当α是第 ________象限角时,tan α<0.2.根据终边所在位置总结出形象的识记口诀1:“sin α=yr :上正下负横为0;cos α=x r :左负右正纵为0;tan α=y x:交叉正负.” 形象的识记口诀2:“一全正、二正弦、三正切、四余弦.” 答案:1.一、二 三、四 一、四 二、三 一、三 二、四三、诱导公式一由定义可知,三角函数值是由角的终边的位置确定的,因此,终边相同的角的同一三角函数的值________,这样就有下面的一组公式(诱导公式一):sin(2k π+α)=sin α,cos(2k π+α)=cos α,tan(2k π+α)=tan α,k ∈Z. 答案:相等四、三角函数线1.有向线段:有向线段是规定了方向(即起点、终点)的线段,它是________、 ________的.在平面直角坐标系中,和坐标轴同向的有向线段为正,反向的为负.2.正弦线、余弦线、正切线:三角函数线是用来形象地表示三角函数值的有向线段.有向线段的________表示三角函数值的________,有向线段的________表示三角函数值的绝对值的________.三角函数线的作法如下:设角α的终边与单位圆的交点为P ,过点P 作x 轴的垂线,垂足为M ,则有向线段MP ,OM 就分别是角α的正弦线与余弦线,即MP =y =sin α,OM =x =cos α.过点A (1,0)作单位圆的切线,设这条切线与角α的终边(或终边的反向延长线)交于点T ,则有向线段AT 就是角α的正切线,即AT =tan α.3.填写下表中三角函数的定义域、值域:函数定义域值域 y =sin α y =cos α y =tan α答案:1.有长度 有正负 2.方向 正负 长度 大小 3.函 数定 义 域值 域 y =sin α R [-1,1] y =cos α R[-1,1]y =tan α⎩⎨⎧⎭⎬⎫α⎪⎪⎪α≠π2+k π,k ∈ZR任意角的三角函数的定义1.正弦、余弦、正切可分别看成是从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数.2.三角函数值是比值,是一个实数.这个实数的大小和点P (x ,y )在终边上的位置无关,而是由角α的终边位置所决定.对于确定的角α,其终边的位置也是唯一确定的.因此,三角函数是角的函数.(1)三角函数值只与角α的终边所在的位置有关,与点P 在终边上的位置无关. (2)三角函数值是一个比值,没有单位.三角函数值的符号三角函数值在各象限的符号取决于终边所在的位置,具体说取决于x,y的符号,记忆时结合三角函数定义式记,也可用口诀只记正的“一全正、二正弦、三正切、四余弦”.三角函数线对于三角函数线,须明确以下几点:(1)当角α的终边在y轴上时,余弦线变成一个点,正切线不存在.(2)当角α的终边在x轴上时,正弦线、正切线都变成点.(3)正弦线、余弦线、正切线都是与单位圆有关的有向线段,所以作某角的三角函数线时,一定要先作单位圆.(4)线段有两个端点,在用字母表示正弦线、余弦线、正切线时,要先写起点字母,再写终点字母,不能颠倒;或者说,含原点的线段,以原点为起点,不含原点的线段,以此线段与x轴的公共点为起点.(5)三种有向线段的正负与坐标轴正负方向一致,三种有向线段的长度与三种三角函数值相同.三角函数的定义域1.由三角函数的定义式可以知道,无论角α终边落在哪里,sin α,cos α都有唯一的值与之对应,但对正切则要求α终边不能落在y轴上,否则正切将无意义.2.角和实数建立了一一对应关系,三角函数就可以看成是以实数为自变量的函数,所以就可以借助单位圆,利用终边相同的角的概念求出任意角的三角函数.基础巩固1.sin 810°+tan 765°+tan 1125°+cos 360°=________.答案:42.若α的终边过点P(2sin 30°,-2cos 30°),则sin α的值为________.答案:-3 23.若角α的终边过点P (3cos θ,-4cos θ)(θ为第二象限角),则sin α=________.答案:454.cos θ·tan θ<0,则角θ是________象限角. 答案:第三或第四5.已知点P (tan α,cos α)在第三象限,则角α的终边在第________象限. 答案:二6.角α的正弦线与余弦线长度相等,且符号相同,那么α(0<α<2π)的值为________.答案:π4或54π7.sin 1,sin 1.2,sin 1.5三者的大小关系是________. 答案:sin 1.5>sin 1.2>sin 1能力升级8.函数y =sin x +-cos x 的定义域是________.解析:∵⎩⎪⎨⎪⎧sin x ≥0,-cos x ≥0,∴⎩⎪⎨⎪⎧sin x ≥0,cos x ≤0,即角x 的终边落在第二象限内和两个半轴上.∴2k π+π2≤x ≤2k π+π,k ∈Z.答案:⎣⎢⎡⎦⎥⎤2k π+π2,2k π+π(k ∈Z)9.已知角α的终边在直线y =kx 上,若sin α=-255,cos α<0,则k =________.解析:∵sin α=-255,cos α<0,∴α的终边在第三象限.令角α的终边上一点的坐标为(a ,ka ),a <0,则r =-1+k 2·a ,sin α=-ka 1+k 2a=-255,∴k =2. 答案:210.在(0,2π)内,满足tan 2α=-tan α的α的取值X 围是________. 解析:由tan 2α=-tan α,知tan α≤0,在单位圆中作出角α的正切线,知π2<α≤π或3π2<α<2π. 答案:⎝ ⎛⎦⎥⎤π2,π∪⎝ ⎛⎭⎪⎫3π2,2π11.解不等式2+2cos x ≥0. 解析:2+2cos x ≥0⇔cos x ≥-22,利用单位圆,借助三角函数线(如图)可得出解集是⎣⎢⎡⎦⎥⎤2k π-34π,2k π+34π(k ∈Z).12.若π4<θ<π2,则下列不等式中成立的是( )A .sin θ>cos θ>tan θB .cos θ>tan θ>sin θC .sin θ>tan θ>cos θD .tan θ>sin θ>cos θ解析:作出角θ的三角函数线(如图),数形结合得AT >MP >OM ,即tan θ>sin θ>cosθ.答案:D13.函数y =sin x |sin x |+cos x |cos x |+tan x|tan x |的值域是( C )A .{-1,0,1,3}B .{-1,0,3}C .{-1,3}D .{-1,1}14.若0<α<π2,证明:(1)sin α+cos α>1; (2)sin α<α<tan α.证明:(1)在如图所示单位圆中, ∵0<α<π2,|OP |=1,∴sin α=MP ,cos α=OM . 又在△OPM 中,有 |MP |+|OM |>|OP |=1. ∴sin α+cos α>1.(2)如图所示,连接AP ,设△OAP 的面积为S △OAP ,扇形OAP 的面积为S 扇形OAP ,△OAT 的面积为S △OAT .∵S △OAP <S 扇形OAP <S △OAT , ∴12OA ·MP <12AP ︵·OA <12OA ·AT .∴MP <AP ︵<AT ,即sin α<α<tan α.15.已知f (n )=cosn π5(n ∈Z),求f (1)+f (2)+f (3)+…+f (2 014)的值.解析:角n5π(n =1,2,…,10)表示10个不同终边的角,这10条终边分成五组,每组互为反向延长线.∴f (1)+f (2)+…+f (10)=0,f (11)+f (12)+…+f (20)=0,…f (2 001)+f (2 002)+…+f (2 010)=0.∴f (1)+f (2)+…+f (2 010)=0.∴f (1)+f (2)+…+f (2 014)=f (2 011)+f (2 012)+f (2 013)+f (2 014)=cos π5+cos 2π5+cos 3π5+cos 4π5.由定义知cos π5与cos 4π5,cos 2π5与cos 3π5互为相反数,故f (1)+f (2)+…+f (2 014)=0.。
