宁波大学912信号与系统2020年考研专业课真题试卷

合集下载

宁波大学信息科学与工程学院《912信号与系统》历年考研真题专业课考试试题

2013年宁波大学912信号处理基础（信号与系统＋数字信号处理）
考研真题
2014年宁波大学912信号处理基础（信号与系统＋数字信号处理）
考研真题
2015年宁波大学912信号处理基础（信号与系统＋数字信号处理）
考研真题
2016年宁波大学912信号处理基础（信号与系统＋数字信号处理）
目录
2013年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研真题 2014年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研真题 2015年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研真题 2016年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研真题 2017年宁波大学912信号与系统考研真题 2018年宁波大学912信号与系统考研真题 2019年宁波大学912信号与系统考研真题
考研真题
2017年宁波大学912信号与系统考研真题
2018年宁波大学912信号与系统考研真题
2019年宁波大学9

研达考研-2017-2019宁波大学912信号与系统考研真题

2z2 z z2 1 z
1
；
24
（2）
X
(z)
(z
z3 z2 1)( z 2
2z z 1)
。
10.（24 分）已知某一离散时间因果 LTI 系统函数的差分方程为
y[n] 1 y[n 1] 1 y[n 2] x[n]
6
6
当输入 x[n] 3u[n] ，且 y[0] 6, y[1] 4 时，求系统的零输入响应 yzi[n]、零状态响应
3.（20 分）
（1）试画出题 3.1 图 x(t)与 h(t)的卷积 y(t)=x(t)*h(t)在 0 t 7 范围内的波形。
题 3.1 图（2）试计算卷积和 y[n]= x[n]* h[n]，其中
x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1)，h[n]={1, 4, 3}(n=-1, 0, 1)。
2.（14 分）试计算卷积 e2tu(t) tnu(t) [ ''(t) 3 '(t) 2 (t)]etu(t) 。
3.（14 分）一个因果 LTI 系统，其输入 x(t) 、输出 y(t) 用下列微分-积分方程表示：
d y(t) 5y(t) x( ) f (t )d x(t)
dt
其中 f (t) etu(t) 3 (t) ，试求该系统单位冲激响应 h(t) 。
科目代码： 912 总分值： 150 科目名称：
信号与系统
f1(t)
fs(t) H(j) f2(t)
p(t)
-2
p(t)
(1)
...
...
-2T -T O T 2T 3T 4T 5T t -b
题6图
F1(j) 1

2020年宁波大学数字信号处理考研复试核心题库之信号与系统填空题精编

2020年宁波大学数字信号处理考研复试核心题库之信号与系统填空题精编特别说明本书根据最新复试要求并结合历年复试经验对该题型进行了整理编写，涵盖了这一复试科目该题型常考及重点复试试题并给出了参考答案，针对性强，由于复试复习时间短，时间紧张建议直接背诵记忆，考研复试首选资料。

但由于各种原因，如资料引用时未能联系上作者或者无法确认内容来源等，因而有部分未注明作者或来源，在此对原作者或权利人表示感谢。

若使用过程中对本书有任何异议请直接联系我们，我们会在第一时间与您沟通处理。

因编撰此电子书属于首次，加之作者水平和时间所限，书中错漏之处在所难免，恳切希望广大考生读者批评指正。

重要提示本书由本机构编写组多位高分在读研究生按照考试大纲、真题、指定参考书等公开信息潜心整理编写，仅供考研复试复习参考，与目标学校及研究生院官方无关，如有侵权请联系我们立即处理。

一、2020年宁波大学数字信号处理考研复试核心题库之信号与系统填空题精编1．系统流图如下图所示，列出对应的状态方程和输出方程__________。

图【答案】2．系统的信号流图和状态变量如下图所示，列出状态方程和输出方程，并写成矩阵形式__________。

图【答案】状态方程和输出方程如下3．=__________。

【答案】4．已知离散线性系统的阶跃响应为，则冲激响应h(n)=__________。

【答案】5．周期信号的双边频谱如下图所示，写出的三角函数表示式__________。

图【答案】【解析】写出周期信号f(t)指数形式的傅里叶级数，利用欧拉公式即可求出三角函数表示式6．=____________________。

【答案】、7．差分方程的特解为__________。

宁波大学911电子线路(模拟电路+数字电路)2020年考研专业课真题

(答案必须写在考点提供的答题纸上)一、选择题（每小题5分，共5题，共25分）1. 测得 PNP 型三极管各电极对地电位分别为 VE ＝ -4V ， VB ＝-4.7V ， VC ＝-4.6V ，说明此三极管处在哪个工作区（）。

A. 放大区B. 饱和区C. 截止区D. 反向击穿区2.如下图所示单相桥式整流、电容滤波电路，电容量足够大时，已知副边电压有效值为210V U =，测得输出电压的平均值() 4.5V O AV U =，则下列描述正确的是（）。

A. 电路正常工作B. 电容C 开路C. 负载R L 开路D. 电容C 和二极管D 1同时开路3. LC 正弦波振荡电路如图所示，该电路（）。

A. 由于无选频网络不能产生正弦波振荡B. 由于不满足相位平衡条件，不能产生正弦波振荡C. 由于放大器不能正常工作，不能产生正弦波振荡D. 满足振荡条件能产生正弦波振荡科目代码： 911总分值： 150科目名称：电子线路（模拟电路+数字电路）(答案必须写在考点提供的答题纸上)4. 如图所示电路中晶体管饱和管压降的数值为│U C E S │，则最大输出功率P O M ＝( ) 。

A ．L 2CES CC 2)21(R U V -B ．L2CES CC )21(R U V - C ． L 2CES CC 2)(R U V - D.2()CC CES L V U R -5. 在图示电路中，稳压管 D Z 的稳定电压 U Z = 6V ，最小稳定电流 I Zm i n = 5 mA ，输入电压 U I =12V ，电阻 R=100，要保证输出稳定电压6V ，I L 最大不应超过 ( )。

A. 60 mAB. 55 mAC. 45 mAD. 40 mA二、简答题（每小题5分，共5题，共25分）1．用逻辑代数的基本公式和常用公式将化为最简与或式。

ABC C AB C B A BC A C B A Y ++++=2. 如图所示，请写出Y 的表达式。

考研信号与系统真题

信号与系统试题（本试题的答案必须全部写在答题纸上，写在试题及草稿纸上无效，）注意：1. t 表示连续时间，n 表示离散整数。

2. u(t)为单位阶跃函数 ⎩⎨⎧≥=0001)( t t t u u(n)为单位阶跃序列 ⎩⎨⎧≥=001)( n n n u3. )(t δ为狄拉克δ函数。

一、（每小题4分，本题共20分）判断下列系统是否为线性的、时不变的、因果的。

x(t)为系统输入信号，y(t)为输出信号。

（1）)(2)(t x et y =（2）)3()2()(t x t x t y ---= （3）tt x t y 2sin )()(=（4）)()(2t x t y =（5）⎰∞-=td x t y ττ)()(二、（每小题5分，本题共15分）说明下列信号是否为能量信号或功率信号，计算其能量或平均功率。

（1）)()(t tx t y =（2）)()5.0()(n u n y n-=（3）)()(n u n x =三、（每小题5分，本题共10分）求下列函数值。

（1）]dtt t u t t )2()(00--⎰∞∞-δ（2）dtt ⎰--112)4(δ四、（每小题5分，本题共10分）已知信号x(t)波形如图（1）所示，画出下列信号的波形图。

（1）⎰∞--t dtt x )2( （2）[]dtt x d )26(-如图2.1所示，系统由A 、B 、C 三个系统组成，∑为加法器，已知系统A 的冲激响应为)(21)(4t u et h tA-=，系统B 与系统C 的阶跃响应分别为)(2),()1(3t u eS t u eStc tB--=-=。

请用时域分析法求解下列问题。

（1）求系统的阶跃响应s(t)；（2）若输入信号x(t)如图2.2所示，求系统的零状态响应)(t yzs。

六、（本题共20分）某线性时不变系统构成如图3所示，∑为加法器，参数如下：⎥⎦⎤⎢⎣⎡=t t dt d t h c A πω2sin )(，cj Be Hωπωω/2)(-=，ttt hc Cπω3sin )(=，)()(t u t hD=、（1）求该系统冲激响应h(t)；（2）当输入为()2/cos 2sin )(t t t x c c ωω+=时，系统输出)(t y已知某系统的系统函数为4)(2+=s s s H ，若输入信号为)()(1t u et x -=，输出信号为)(t y ，1)0(=-y ，1)0(='-y ，)(t y '为)(t y 的一阶导数。

宁大912信号与系统初试试卷(A卷)

(答案必须写在考点提供的答题纸上)
科目代码： 912 总分值： 150 科目名称：
信号与系统
10.（24 分）已知一离散时间因果 LTI 系统的系统函数 H (z) K1源自1 4z1
，
K
为实常数，且当
x(n) 1时，输出 y(n) 4 3。
（1）求该系统的频率响应，画出幅频特性曲线，并说明为何种滤波器；
（2）若
y(1)
2
，
x(n)
1 2
n
u(n)
，求系统的零输入响应和零状态响应；
（3）若
y(1)
4
，
x(n)
3
1 2
n
u(n)
，求系统的完全响应；
（4）当输入
x(n)
2
cos
π 4
n
u(n)
时，求系统的稳态响应。
第3页共3页
科目代码： 912 总分值： 150 科目名称：
信号与系统
f1(t)
fs(t) H(j) f2(t)
p(t) -2
p(t)
(1)
...
...
-2T -T O T 2T 3T 4T 5T t -b
题6图
F1(j) 1
-1 O
1
H(j)
A
-a O
a
2 b
7.（14 分）已知系统函数 H (s) 的极点位于 s 3 处，零点在 s a 且 H () 1。此系统的阶跃响应中包含一项 K1e3t 。若 a 从 0 变到 5，确定相应的 K1 值如何随之改变。
8.（18 分）给定题 8 图所示连续时间因果 LTI 系统
X(s)
1 s2 2s 1
K
Y(s)

宁波大学信号与系统2018—2020年考研真题试题

2.（14 分）试计算卷积 e2tu(t) tnu(t) [ ''(t) 3 '(t) 2 (t)]etu(t) 。
3.（14 分）一个因果 LTI 系统，其输入 x(t) 、输出 y(t) 用下列微分-积分方程表示：
d y(t) 5y(t) x( ) f (t )d x(t)
dt
其中 f (t) etu(t) 3 (t) ，试求该系统单位冲激响应 h(t) 。
宁波大学 2020 年硕士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码： 912 总分值： 150 科目名称：
信号与系统
1. （10 分）试计算卷积积分： y(t) 1 * 1 tt
2. （8 分）试计算卷积和： y(n) bnu(n 1) * bnu(n 2), 其中 b 1。
x(n)
u(n)
时，输出响应
y(n)
1 2
4(2)n
5 2
(3)n
u(n)
。求此系统的差分方程。
10．（12 分）已知二阶离散时间因果 LTI 系统的框图如题 10 图所示。（1）求系统函数，并判断系统的稳定性；
（2）设抽样频率为 10kHz，输入正弦幅度为 5，频率为 1kHz，试求稳态输出幅度。
4. （18 分）一线性时不变一阶系统，在以下三种激励下，其起始状态均相同，当激励 x1(t) (t) 时，其全响应为 y1(t) (t) etu(t) ；当激励 x2 (t) u(t) 时，其全响应为 y2 (t) 3etu(t) ；当激励 x3 (t) u(t) u(t 1) 时，求系统全响应。
X (z)
2z2 z2 1 z

2020年宁波大学研究生自命题考试专业课924【水力学】

(答案必须写在考点提供的答题纸上)科目代码： 924 总分值： 150 科目名称：水力学一、判断题（正确打“ ”，错误打“ ”，所有答案须写在答题纸上，写在本试题纸或草稿纸上均无效。

每题2分，总分20分。

）1. 牛顿液体的切应力与剪切变形速度呈线性关系。

（）2. 平面上静水总压力的大小等于压力中心点的压强与受力面面积的乘积。

（）3. 均匀流一定是层流，非均匀流一定是紊流。

（）4. 水流在边壁处的流速为零，因此该处的流速梯度为零。

（）5. 紊流的沿程水头损失与断面平均流速的平方成正比。

（）6. 水力坡度就是单位长度流程上的水头损失。

（）7. 有压管道均匀流的水力坡度与管轴线坡度是相等的。

（）8. 均匀流流场内的压强分布规律与静水压强分布规律相同。

（）9. 直接水击是指阀门关闭时间大于水击相长的水击。

（）10. 水流从陡坡流到缓坡时必然发生水跃。

（）二、单项选择题（所有答案须写在答题纸上，写在本试题纸或草稿纸上均无效。

每题2分，总分20分。

）1. 液体中某点的真空度为1m 的水柱，则该点的相对压强为（）（A ） 9.8kN/m 2 （B ）-9.8kN/m 2 （C ）1kN/m 2 （D ）-1kN/m 22. 牛顿内摩擦定律表达了液体的（）（A ）切应力和速度、粘性之间的关系（B ）切应力和粘性、剪切变形率之间的关系（C ）切应力和粘性、剪切变形之间的关系（D ）切应力和粘性、流速梯度、压强之间的关系3. 水力模型实验中按重力相似设计模型，长度模型比尺=100，测得模型中某点的流速=0.8m/s ，则原型中对应的流速为（）（A ）8m/s （B ）6m/s （C ）5m/s （D ）10m/s考研专业课(答案必须写在考点提供的答题纸上)科目代码： 924 总分值： 150 科目名称：水力学4. 一平面潜没于水中，当保持其形心位置不变，而使其与水平面之间的倾角改变时，则一侧的水压力（）（A ）大小方向均不变（B ）大小改变而方向不变（C ）方向改变而大小不变（D ）大小方向均改变5. 管道的负压区是指测压管水头线（）（A ）在基准面以下的部分（B ）在下游自由水面以下的部分（C ）在管轴线以下的部分（D ）在基准面以上的部分6. 对于并联长管道，每根管道的（）（A ）流量相等（B ）切应力相等（C ）沿程水头损失相等（D ）水力坡度相等7. 在陡坡渠道上，下列哪种流动不可能发生（）（A ）均匀缓流（B ）均匀急流（C ）非均匀缓流（D ）非均匀急流8. 断面单位能量e 随水深h 的变化规律是（）（A ）e 存在极大值（B ）e 存在极小值（C ）e 随h 增加而单调增加（D ）e 随h 增加而单调减少9. 底宽b =1.5m 的矩形明渠，通过的流量Q =1.5m 3/s ，已知渠中某处水深h =0.4m ，则该处的水流流态为（）（A ）缓流（B ）急流（C ）临界流（D ）无法确定10. 圆管流的临界雷诺数（下临界雷诺数）（）（A ）随管径变化（B ）随流体的密度变化（C ）随流体的粘度变化（D ）不随以上各量变化三、填空题（所有答案须写在答题纸上，写在本试题纸或草稿纸上均无效。

宁波大学912信号与系统2020年考研专业课真题

题7图
8．（22分）已知一个连续时间稳定LTI系统的系统函数为，输入如题8图所示。
（1）说明该系统为何种滤波器；
（2）求系统的初始条件和；
（3）当时，求系统的完全响应y(t)。
题8图
9.（14分）已知二阶离散时间系统的零输入响应初始条件为，。当输入时，输出响应。求此系统的差分方程。
10．（12分）已知二阶离散时间因果LTI系统的框图如题10图所示。
（1）求系统函数，并判断系统的稳定性；
（2）设抽样频率为10kHz，输入正弦幅度为5，频率为1kHz，试求稳态输出幅度。
题10图
1.（10分）试计算卷积积分：
2.（8分）试计算卷积和：。
3．（18分）设系统的微分方程表示为：，试从时域角度求使完全响应为时的系统起始状态和，并确定常数值。
4.（18分）试求题4图所示周期信号的三角函数形式傅里叶级数表示式。
题4图
5.（16分）试求题5图所示信号的频谱函数。
题5图
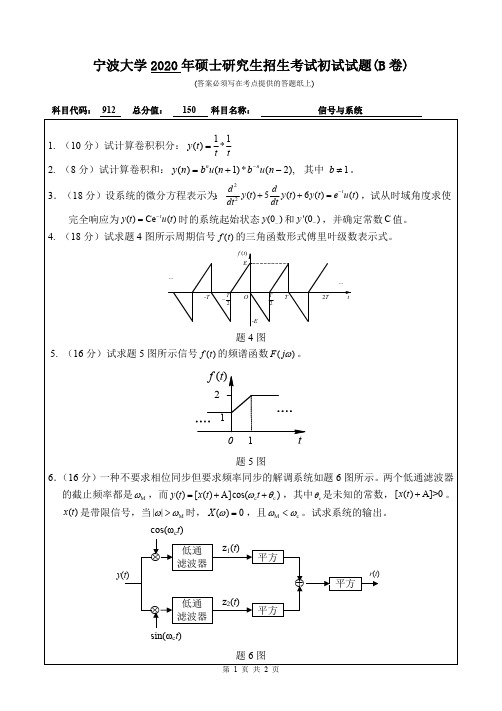
6．（16分）一种不要求相位同步但要求频率同步的解调系统如题6图所示。两个低通滤波信号，当时，，且。试求系统的输出。
题6图
7.（16分）题7图是一个低通微分器的连续时间滤波器的频率响应。当输入信号为下列时，求该滤波器的输出信号。
（1）；（2）。

宁波大学考研真题911电子线路(模拟电路+数字电路)2015年-2017年

入学考试试题(A卷)(答案必须写在答题纸上)考试科目: 电子线路（模拟电路+数字电路）科目代码：911适用专业:电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、集成电路工程、计算机技术图1入学考试试题(A 卷) (答案必须写在答题纸上)考试科目:电子线路（模拟电路+数字电路）科目代码： 911 适用专业:电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、集成电路工程、计算机技术图23、试画出用3线-8线译码器74LS138 123Y AC Y ABC Y BC =⎧⎪=⎨⎪=+⎩图3的电压波形如图5。

试画出与之对应的输出电压入学考试试题(A卷)(答案必须写在答题纸上)考试科目: 电子线路（模拟电路+数字电路）科目代码：911适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、集成电路工程、计算机技术图7所示各电路输出电压与输入电压的运算关系式。

(a) (b)图8入学考试试题(A卷)(答案必须写在答题纸上)考试科目: 电子线路（模拟电路+数字电路）科目代码：911适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、集成电路工程、计算机技术入学考试试题(A卷)(答案必须写在答题纸上)考试科目:电子线路（模拟电路+数字电路）科目代码：911适用专业:电路与系统、通信与信息系统、信号与信息处理、信息检测与智能系统、电子与通信工程、集成电路工程、计算机技术一、单项选择题（每小题5分，共5题，总计25分，将正确答案的编号填入答题纸）1.某NPN型硅三极管b-e间电压U BE=0.7V，c-b间电压U CB=0.1V，由此可判断该管工作在A、放大区B、截止区C、饱和区D、不能确定2．在放大电路中，温度上升，则A、I CBO减小，U BE减小B、I CBO增大，U BE增大C、I CBO减小，U BE增大D、I CBO增大，U BE减小3．某放大电路，要求输入电阻小，输出电压稳定，应该选用下列那一种负反馈A、电压串联B、电压并联C、电流并联D、电流串联4.在由NMOS晶体管组成的基本共源放大电路中，当输入信号为1kHz、50mV的正弦电压时，输出电压波形出现削顶的失真，这种失真是A、截止失真B、饱和失真C、交越失真D、频率失真5．共模抑制比KCMR越大表明电路A、电压放大倍数越稳定B、输出量中共模成分越大C、电压放大倍数越大D、抑制温漂能力越强大二、简答题（每小题5分，共5题，共25分）1.用逻辑代数的基本公式和常用的公式将()()()Y A B C A B C A B C=++++++化为最简与或形式2．求逻辑函数C ABF+=的对偶函数3．试说明下列反相器的输出逻辑值：1）TTL反相器的输入端接一个小电阻（0.1KΩ）2）TTL反相器的输入端接一个大电阻（100KΩ）3）TTL反相器的输入端悬空4）CMOS反相器的输入端接一个小电阻（0.1KΩ）5）CMOS反相器的输入端接一个大电阻（100KΩ）入学考试试题(A 卷)(答案必须写在答题纸上)考试科目:电子线路（模拟电路+数字电路）科目代码：911适用专业:电路与系统、通信与信息系统、信号与信息处理、信息检测与智能系统、电子与通信工程、集成电路工程、计算机技术4．在CMOS 电路中有时采用图1所示的扩展功能用法，写出Y 的逻辑式。

宁波大学《912信号与系统》考研专业课真题试卷

( ) 5. 下列各种陈述中，正确的是______。 (A) 系统函数能提供求解零输入响应所需的全部信息； (B) 系统函数的零点位置影响时域波形的衰减或增长； (C) 若零极点离虚轴很远，则它们对频率响应的影响非常小；
(D) 原点的二阶极点对应于 t2u(t) 形式的波形；
第1页共5页
宁波大学 2014 年攻读硕士学位研究生
入学考试试题(B 卷) (答案必须写在答题纸上)
考试科目: 信号处理基础(信号与系统+数字信号处理)
科目代码：912
适用专业: 通信与信息系统、信号与信息处理、电子与通信工程
(
) 6.
系统 T[x(n)]
x(n)
sin(
2 9
(n
1)
7
)
① 非线性系统 ② 移变系统
③ 因果系统
④ 稳定系统
(7) (2 分) 实现 IIR 数字滤波器时，如果想方便对系统频响的零点进行控制和调整，那么常用的 IIR 滤波器结构中，首选______________型结构来实现该 IIR 系统。
海天课堂
中国考研专业课辅导知名品牌
宁波大学考研专业课真题试卷
912 信号与系统
2014 年《912 信号与系统》专业课真题试卷 2015 年《912 信号与系统》专业课真题试卷 2016 年《912 信号与系统》专业课真题试卷 2017 年《912 信号与系统》专业课真题试卷 2018 年《912 信号与系统》专业课真题试卷 2019 年《912 信号与系统》专业课真题试卷 2020 年《912 信号与系统》专业课真题试卷
(B) Ζ y2 (n) x(n)
(C) Ζ y3 (n) x(n)
(D) Ζ y4 (n) x(n)

宁波大学912信号与系统2020年考研专业课初试大纲

2020年宁波大学硕士研究生招生考试初试科目
考　试　大　纲
科目代码、名称:912信号与系统
1、考试形式与试卷结构
（1）试卷满分值及考试时间
本试卷满分为150分，考试时间为180分钟。

（二）答题方式
答题方式为闭卷、笔试。

试卷由试题和答题纸组成；答案必须写在答题纸（由考点提供）相应的位置上。

（三）试卷内容结构
考试内容主要包括信号与系统的基本概念、线性时不变系统的时域分析、连续时间信号与系统的傅里叶分析、抽样、调制与解调、拉普拉斯变换与连续时间系统、z变换与离散时间系统。

（四）试卷题型结构
题型主要为计算或论证题。

二、考查目标
课程考试的目的在于测试考生对于信号与系统的基本概念、理论、算法、变换方法和设计方法的掌握情况。

3、考查范围或考试内容概要
(1) 信号与系统的基本概念
了解信号与系统的概念、表示与分类，了解连续时间信号与离散时间信号的概念，掌握信号的分解与运算，了解线性时不变（LTI）系统的概念与基本性质。

(2) 线性时不变系统的时域分析
掌握线性时不变系统输入输出方程的建立及解法，掌握零输入响应和零状态响应、单位冲激响应（单位样值响应）和单位阶跃响应、卷积（和）等概念及求解运
算，掌握线性时不变系统的基本性质并能用框图表示线性时不变系统。

(3) 连续时间信号与系统的傅里叶分析
掌握连续时间周期信号傅里叶级数的各种表示及系数转换关系，掌握傅里叶变
第1页，共2页。

宁波大学2018年《912信号与系统》考研专业课真题试卷

n
1 2
n
（4）当输入 x(n) = 2 + cos n u(n) 时，求系统的稳态响应。

π 4
第 3 页共 3 页
x(t) 1 -2 O -1 2 4 6 8 t
h(t) 2 -1 O 1 2 3 t
题 3.1 图（2）试计算卷积和 y[n]= x[n]* h[n]，其中 x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1)，h[n]={1, 4, 3}(n=-1, 0, 1)。 4.（12 分）试画出信号 f (t ) = sgn{sin[ 叶级数表示式。 5.（14 分）求信号 f (t ) =

2
(t − 1)]} 的波形，并求出该信号的指数函数形式傅里
sin(2t ) cos(5t ) 的傅里叶变换 F ( j) ，并画出其频谱图。 t
6. （18 分）某系统如题 6 图所示，输入 f1(t)为带限信号，H(jω)为带通滤波器。（1）当 2 = 21 ， a = 1 ， b = 2 ， T =
总分值：
150
科目名称：
信号与系统
f1(t) p(t)
fs(t)
H(j)
f2(t) -2 -1
F1(j) 1 O A
1
H(j)
2
p(t) (1) ... -2T -T O ... T 2T 3T 4T 5T t -b -a O
a
b
题6图 7.（14 分）已知系统函数 H (s) 的极点位于 s = −3 处，零点在 s = −a 且 H () = 1 。此系统的阶跃响应中包含一项 K1e
−3t
。若 a 从 0 变到 5，确定相应的 K1 值如何随之改变。