第16届中环杯决赛试卷与答案四年级_7257

合集下载

第16届中环杯四年级决赛

参赛证号（请用2B铅笔填涂）一、填空题Ⅰ（本大题共5小题，每题6分，共30分）1.计算：56.87.520.1643.228.425.321⨯+⨯+⨯+=。

2.小明在前3次测验中的分数分别为82分、86分、92分。

为了使得他四次测验的平均分达到90分，他第四次测验必须考到分。

3.小明参加投篮比赛，一共投进了10个球。

每投进一个球的得分，要么是2分，要么是3分。

小明一共得了26分，那么他一共投进个3分球。

4.数列121，1221，12221，122221，……的前2017项中，有项能被3整除。

5.如图，将一个小正方体放入一个大正方体内，小正方体的体积为5立方厘米，大正方体棱长是小正方体棱长的4倍，则两个正方体之间空白部分的体积为立方厘米。

二、填空题Ⅱ（本大题共5小题，每题8分，共40分）6.如果一个数可以表示为两个偶数的乘积，这两个偶数都不是4的倍数，并且这样的表示方法只有一种，那么这个数就称为“思维数”（比如12就是“思维数”，因为符合要求的表示方法只有2乘以6）。

不超过2017的最大“思维数”是。

7.如图，长方形XYZW由8个正方形组成，其中白色正方形的边长为1。

则XYZW的面积为。

8.小明将若干个（至少两个）连续正整数乘起来，得到一个六位数乘积4774ab，则a b+=。

9.如图，在3×3的方格中，将中间一块涂黑，在剩下的8个1×1的小方格中各填入一个数，使得每条边上3个小方格内数之和为42。

如果这8个数之和为111，并且这8个数中有且只有两种不同的值，那么这两种值之和为。

10.新新骑着自行车，以每分钟400米的速度，从816路公交车的始发站出发，沿816路车的线路前进。

当他骑出1400米时，一辆816路公交车从始发站开出。

已知这辆车每分钟行驶600米，每4分钟到达一站并停车1分钟。

那么这辆车开出分钟后能追上新新。

（请继续完成反面内容）三、填空题Ⅲ（本大题共5小题，每题10分，共50分）11.如图所示，六边形ABCDEF的对角线AD、BE、CF不交于一点。

2016第十六届中环杯四年级初赛解析

解析(初赛)第十六届“中环杯”四年级_______ 33+20.15=20.15+40.3）×1.计算题：（【分析】原式33+20.15?=(20.15+20.15?2)66+20.15?=20.15?33+20.15 1)??66?20.15?(33 2015?，要求这四个数字构成一个四位、2.abc_____这样的四位数都也a1都大互不相同，=【分析=1432134=1=2有 a2431234=1有=2,共.3一个长方体的六个面的面积之积1464，则该长方体的体积________【分析设长方体的长宽高分别则1464abaabac2222?c(a14641b)222?121acb 2121)?(abc11?abc4.小明通过2、0、1、6这四个数字构成了一个数列（不断地将2、0、1、6这四个数字按照这个顺序加在数后面）：2,20,201,2016,20162,201620,2016201,20162016,201620162，…，这个数列中，质数有______个.【分析】只有第一个2是质数，以后出现的数都不是质数，所以质数有1个.、B两地沿相同的方向行驶.甲车如果每小时行驶50甲、乙两车同时从A千米，则6小时5.可以追上前方的乙车；如果每小时行驶80千米，则2小时可以追上前方的乙车.由此可知，乙车的速度是________千米/时.?时间，速度差千米/时，由追及问题的路程差=【分析】设乙车速度为x得2?x)?x)?6?(80(50?300?6x?160?2x140?4x35?x6.右图中有_________个三角形., 【分析】分类枚举，如图个；个小三角形构成的有4 1个小三角形构成的个122345个小三角形构成的个121356个小三角形构成的个123345246个小三角形构成的个共（个.17已知四位满足下面的性质都是完全平方数（完全平方数是CBABCAB4=22,81=92481.所有满、能表示为某个整数平方的数，比如为完全平方数），则我们就称__________. 足这个性质的四位数之和为【分析】满足条件的平方数为有：ABBCCD491664 634649164861 ?ABCD?164或936或498764?和为164+936+498764=1S(123)?1?2?3?6)aS(naa.8.的各个的数码和（比如表示对于自然数，如果一个自然数S(3n)?3S(n)n_____________ 的最大值为数码都互不相同，并且，则【分析】S（3n）?3S(n)?3乘以n时不能进位，则n中最大的数字只能为3，故n最大为3210.、BCEF//BCEGFOOABCDABCD.9.若是正方形都是正方形，其中点如图，的中心，和S?S?S3.25BCEFEF________（，的长度都是正整数，并且四边形则的面积为EGFOABCDEGFO EGFO. 的面积，以此类推）表示F11._________. 【分析】结果如下：23195?115 207234485100011.克的物体，这把秤会显示其正确的重量；对神庙里有一把古老的秤，对于重量小于10001000.的随机数于重量大于等于克的物体，这把秤会显示出一个大于等于、、、S1000PRQ表示它们的重小明有五个物品，题目各自的重量都小于克，我们分别用.将这五个物品两两配对放到秤上进行称重，得到下面的结果：量700P+T=Q+R=900R+T=2100Q+T=800Q+S=1200. （克）（克）、（克）、（克）、、（克）__________.那么这五个物品的重量从重到轻的顺序为=2100⑤；Q+S=1200④；R+T=800①；Q+R=900②；P+T=700③；【分析】Q+T 所以：S>R>T>Q>P; 由②⑤得：T>Q;R>T; 由①③得：Q>P; 由②④得：S>R由①②得：0123456712.写在一个正方体的八个顶点上（每个顶点写一个数，所有的、、、、、将、、则一个面上的四个数之和最大则这相邻的两个数必然是一奇一偶可先确定枚举即可，如图，最大的和.17372pq1896n13的数表示自然满，定pq1(13332________.）和【分析】位置原理+分解质因数.pqr?190062?100nn?2?38?19?10n?2?19?(102)?n?1?101)2?19??(5?n?1499）（即，为：所以：p q r2，19110??51n?原式8??(925n?9??n17)14..四个完全相同的等腰梯形如下图进行放置，题目的下底构成了一个正方形的两条对角线PX=3XQ÷=____________.整个正方形面积，阴影部分面积若XQP1.2.515次当甲地时，两人一共相遇了.地，也算一次相遇个全程；所以乙的速度是甲，则甲走全程用时为2AB8058÷4=2014…24029×时间为2=8058，个全程，1+2014×时，次到那甲第2015B走了2=4029 （次）3+2=60442014×012…916.中的数字（方框内数字允、、在的每个方框中填入一个、、??0____________. 种填数方法许相同，任何数最高位不能为，使得算式成立，有）设ab?cd?efg 【分析】ab?10，cd可取90到99：10个：个到9911?11，cd可取89ab：可取10到99ab90个?99，cd(10+90)×81÷+90×9=4860（个）AEDAE=15DE=20.17.以，如下图所示，三角形为直角三角形，两条直角边的长度分别为，，，ACGABEFAEABFEADADABCD与交为边作平行四边形为边作正方形边于点，以FGHAGHCFH_______..的面积之差（大面积减去小面积）为与三角形交于点则三角形ABFEGHCD的面积ADEAD=25，所以正方形的边长为25，根据三角形【分析】有勾股定理可以算出：ADC 三角形，GD=16，所以GF=13，同时在AEG中用勾股定理算出AG=9可以算出EG=12，的AGH 与三角形CFH）×16÷2=304；三角形（的面积=25×25÷2=312.5，梯形CDGF=13+25CDGF=312.5-304=8.5. ADC-梯形面积之差=三角形a,b,c,d 18.满足下面的性质：四个不同的质数a+b+c+d 1—个质数；）（还是个质数；a,b,c,d中某两个数之和还是—（2）. ）a,b,c,d中某三个数之和还是一个质数（3_______ . a+b+c+d的最小值为满足条件的b+c+d只能是a=2，由于某三个数的和为质数，2【分析】有a+b+c+d为质数知必有，不妨设17. ，7，5219732为质数，所以可以从最小的尝试，的得到答案为，，，或，31. a+b+c+d 最后可得的最小值为3?3—19.个数，其中右上角的数已经填好了，的小方格内都要填一个的方格中，每个11?30.接下来填的数需要满足下列条件：为（如图）(1)每个数都能整除与它相邻的上面方格内的数（如果与它相邻的上面方格不存在，自然不；用满足这个条件）(2)每个数都能整除与它相邻的右面方格内的数（如果与它相邻的右面方格不存在，自然不._______.种不同的填法有用满足这个条件），他的上方格和右方格必，可设三列从上到下≤3种种种).1+2+3=种1+2=种种).1.).20-1A-I3?5.20.所示，如图我们可以用的方格表来表示字母20-2A-D的表中，需要满足：左表中右边的数字表示这一行中圆点个数，下边的将填入图.数字表示这一列中圆点个数，填好后的结果如右表所示20-3A-I，使其符合前面描述的要求现在，将填入图的表中（每个字母能且只能使用一次）.（只要将字母写入表格即可，不用画圆点）20-20-20-359128GABFCDHEI【分析】。

五年级上册数学试题-第十六届中环杯决赛全国通用 PDF 含答案

第十六届“中环杯”小学生思维能力训练活动第十六届“中环杯”中小学生思维能力训练活动五年级决赛2016年3月5日 12:30~14:00考试时间：90分钟满分：100分一、填空题A ：（本大题共8小题，每题6分，共48分）【第1题】计算：11112016________21422754⎛⎫⨯+--= ⎪⎝⎭。

【分析与解】计算。

1111201621422754⎛⎫⨯+-- ⎪⎝⎭1111201621422754⎡⎤⎛⎫⎛⎫=⨯+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦1120161418⎛⎫=⨯- ⎪⎝⎭11201620161418=⨯-⨯144112=-32=第十六届“中环杯”小学生思维能力训练活动若E 、U 、L 、S 、R 、T 分别表示1、2、3、4、5、6（不同的字母表示不同的数字），且满足： ⑴6E U L ++=；⑵18S R U T +++=；⑶15U T ⨯=；⑷8S L ⨯=。

则六位数________EULSRT =。

【分析与解】⑴因为6E U L ++=；而1236++=；所以{}{},,1,2,3E U L =；⑵因为18S R U T +++=；而654318+++=；所以{}{},,,6,5,4,3S R U T =；⑶因为15U T ⨯=；而1511535=⨯=⨯；所以{}{},3,5U T =；⑷因为8S L ⨯=；而81824=⨯=⨯；所以{}{},2,4S L =。

由⑴和⑶，得3U =，则5T =；由⑴和⑷，得2L =，则4S =；最后分别结合⑴和⑵，得1E =，6R =；故六位数132465EULSRT =。

第十六届“中环杯”小学生思维能力训练活动一个超过20的自然数N ，在14进制与20进制中都可以表示为回文数（回文数就是指正读与倒读都一样的数，比如12321、3443都是回文数，而12331不是回文数）。

N 的最小值为________（答案用10进制表示）。

【分析与解】数论，进制与位值。

(完整版)第十六届华杯赛总决赛试题

第十六届华罗庚金杯少年数学邀请赛总决赛小学组一试2011年7月23日中国·惠州一. 填空题：（共3题，每题10分）1. 计算 313615176413900114009144736543++++++＝_________.2. 如右图所示，正方形ABCD 的面积为12，AE ＝ED ，且EF ＝2FC ，则三角形ABF 的面积等于_________.3. 某地区的气象记录表明，在一段时间内，全天下雨共1天；白天雨夜间晴或白天晴夜间雨共9天；6个夜间和7个白天晴朗。

则这段时间有_______天，其中全天天晴有_______天。

二. 解答题：（共3题，每题10分，写出解答过程）4. 已知a 是各位数字相同的两位数，b 是各位数字相同的两位数，c 是各位数字相同的四位数，且c b a =+2。

求所有满足条件的（a ，b ，c ）。

5. 纸板上写着100、200、400三个自然数，再写上两个自然数，然后从这五个数中选出若干个数（至少两个）做只有加、减法的四则运算，在一个四则运算式子中，选出的数只能出现一次，经过所有这样的运算，可以得到k 个不同的非零自然数。

那么k 最大是多少？6. 将1，2，3，4，5，6，7，8，9填入右图的圆圈中，每个圆圈恰填一个数，满足下列条件：1）正三角形各边上的数之和相等；2）正三角形各边上的数之平方和除以3的余数相等。

问：有多少种不同的填入方法？( 注意，经过旋转和轴对称反射，排列一致的，视为同一种填法 )总决赛小学组二试2011年7月23日中国·惠州一. 填空题：（共3题，每题10分）1. 某班共36人都买了铅笔，共买了50支，有人买了1支，有人买了2支，有人买了3支。

如果买1支的人数是其余人数的2倍，则买2支的人数是_________.2. 右图中，四边形ABCD 的对角线AC 与BD 相交于O ，E 为BC 的中点，三角形ABO 的面积为45，三角形ADO 的面积为18，三角形CDO 的面积为69。

16届中环杯四年级决赛试题详解

【答案】17 7. 已知四位数 ABCD 满足下面的性质： AB 、 BC 、 CD 都是完全平方数（完全平方数是指能表示为某个整数平方的数，比如 4 22 ， 81 92 ，则我们就称 4、81 为完全平方数）。所有满足这个性质的四位数之和为________. 【答案】13462 8. 对于自然数 a ， S a 表示 a 的数码和（比如 S 123 1 2 3 6 ）。如果一个自然数 n 的各个数码都互不相同，并且 S 3n 3S n ，则 n 的最大值为________。【答案】 3210 9. 如图， ABCD 和 EGFO 都是正方形，其中点 O 是正方形 ABCD 的中心， EF // BC 。若 BC 、 EF 的长度都是正整数，并且四边形 BCEF 的面积为 3.25，则 S ABCD S EGFO _____（ S EGFO 表示 EGFO 的面积，依次类推）。
f p f q f r f pqr ________。
【答案】 8 14. 四个完全相同的等腰梯形如下图进行放置，它们的下底构成了一个正方形的两条对角线。若 PX 3 XQ ，阴影部分面积整个正方形面积 _______。
P X Q
S
R
【答案】0.375
ABCD ，以 AB、AE 为边作平行四边形 ABFE，EF 交 AD 边于点 G，AC 与 FG 交于点 H。则
AGH 与 CFH 的面积之差（大面积减去小面积）为
A
15
。
B F H
E
G
20
D
C
【答案】 8.5 18. 四个不同的质数 a、b、c、d 满足下面的性质：（1） a b c d 还是一个质数；（2） a、b、c、d 中某两个数之和还是一个质数；（3） a、b、c、d 中某三个数之和还是一个质数。满足条件的 a b c d 的最小值为______。【答案】 31

第十六届中环杯选拔赛（四年级）

第⼗六届中环杯选拔赛（四年级）第⼗六届“中环杯”⼩学⽣思维能⼒训练活动六年级组选拔赛1．计算：171720.152++2015=3203_____。

2．要使得算式()111145-1-+4=7234成⽴，⽅框内应填的数是_____。

3．把61本书分给某个班级的学⽣，如果其中⾄少有1⼈能分到⾄少3本书，那么这个班最多有_____⼈。

4．有⼀个数，除以3余数是1，除以5余数是2，那么这个数除以15的余数是_____。

5．如图，⼀个三⾓形的三个内⾓分别为(5x +3y )°、(3x +20)°、(10y +30)°，其中x 、y 都是正整数，则x +y =_____。

6．三个数两两之间的最⼤公约数分别是3、4、5，那么这三个数的和最⼩是_____。

7．对字母a ~z 进⾏编码(a =1，b =2，……，z =26)，这样每个英⽂单词(所有单词中的字母都认为是⼩写字母)都可以算出其所有字母编码的乘积p 。

⽐如单词good ，其对应的p 值为7×15×15×4=6300(因为g =7，o =15，d =4)。

如果某个合数⽆法表⽰成任何单词(⽆论这个单词是不是有意义)的p 值，这样的合数就称为“中环数”。

最⼩的三位数“中环数”为_____。

8．甲、⼄两⼈同时骑⾃⾏车从A 地道C 地，路上会经过B 地。

骑了⼀会⼉，甲问⼄：“我们已经骑了多少公⾥了？”⼄回答：“我们骑的路程相当于这⾥到B 地距离的13。

”⼜骑了10公⾥后，甲⼜问：“我们还要骑多少公⾥才能到达C地？”⼄回答：“我们还要骑的路程相当于这⾥到B地距离的13。

”A、C两地相距_____公⾥(答案写成分数形式)。

9．如果⼀个数不是11的倍数，但是移除⼀个任意位上的数码后，它就变成11的倍数了(⽐如111就是这样的数，⽆论移除其个位、⼗位或百位数码，都变成11的倍数了)，这样的数定义为“中环数”。

第十六届全国中学生物理竞赛参考解答

第十六届全国中学生物理竞赛参考解答一、参考解答1 只要有液态水存在，平衡时汽缸中气体的总压强就等于空气压强与饱和水蒸气压强之和：3.0atm p p p =+=总空饱00〔1〕第一次膨胀后102V V =2.0atm p p p =+=总空饱11〔2〕由于第一次膨胀是等温过程，所以 0102p V p V p V ==空空空011〔3〕解〔1〕、〔2〕、〔3〕三式，得 1.0atm p =饱〔4〕 2.0atm p =空0〔5〕 1.0atm p =空1〔6〕由于1.0atm p =饱，可知汽缸中气体的温度0373K T =〔7〕根据题意，经两次膨胀，气体温度未改变。

2.设水蒸气为mol γ水．经第一次膨胀，水全部变成水蒸气，水蒸气的压强仍为p 饱，这时对于水蒸气和空气分别有10p V RT γ=饱水〔8〕1002p V RT RT γ==空1空〔9〕由此二式与〔5〕、〔6〕式可得2mol γ=水〔10〕3. 在第二次膨胀过程中，混合气体可按理想气体处理，有21p V p V =总2总1〔11〕由题意知，204V V =，102V V =，再将〔2〕式代入，得 1.0atm p =总2〔12〕二、参考解答l ．在所示的光路图〔图复解16-2-1〕中，人射光AB 经透镜1L 折射后沿BC 射向2L ，经2L 折射后沿CD 出射．AB 、BC 、CD 与透镜主轴的交点分别为P 、P '和P ''，如果P 为物点，因由P 沿主轴射向1O 的光线方向不变，由透镜性质可知，P '为P 经过1L 所成的像，P ''为P '经2L 所成的像，因而图中所示的1u 、1v 、2u 、2v 之间有以下关系：111111u v f +=〔1〕222111u v f +=〔2〕 21d u v =+〔3〕当入射光线PB 与出射光线平行时，图中的αα'=，利用相似三角形关系可求得21v h h u '=, 21uh h v '=从而求得2211v u u v =〔4〕联立方程〔1〕、〔2〕、〔3〕、〔4〕，消去1v 、2u 和2v ，可得：1112()f du d f f =-+〔5〕由于d 、1f 、2f 均已给定，所以1u 为一确定值，这说明：如果入射光线与出射光线平行，那么此入射光线必须通过主轴上一确定的点，它在1L 的左方与1L 相距1112()f du d f f =-+处，又由于1u 与α无关，但凡通过该点射向1L 的入射光线都和对应的出射光线相互平行．2．由所得结果〔5〕式可以看出，当12d f f >+时，10u >，此情况下的光路图就是图复解16-2-1．当12df f =+时，1u →∞，0α=，此时入射光线和出射光线均平行于主轴，光路如图复解16-2-2．当12df f <+时，10u <，这说明P 点在1L 的右方，对1L 来说，它是虚物．由〔1〕式可知，此时10v >，由2211f u v f =可知，20u >，又由21220u vv u =<可知，20v <，所以此时的光路图如图复解16-2-3．三、参考解答根据题中所给的条件，当圆环内通过电流I 时，圆环中心的磁感应强度012B r μ=穿过圆环的磁通量可近似为02BS Ir μφπ≈=〔1〕根据法拉第电磁感应定律，电流变化产生的感生电动势的大小02Ir t tμφπ∆∆==∆∆E〔2〕圆环的电阻02r IR I I tμπ∆==∆E 〔3〕根据题设条件0.05m r =，720410N A μπ=⨯⋅－－，100A I =，61410A/s 310A/s It∆≤≈⨯∆－－,代入〔3〕式得23310R ≤⨯Ω－〔4〕由电阻与电阻率ρ、导线截面积S 、长度L 的关系LR S ρ=与导线的直径1mm d =，环半径5cm r =，得电阻率2297.510m 8S d R RL rρ===⨯Ω⋅－〔5〕四、参考解答1．双星均绕它们的连线的中点做圆周运动，设运动速率为v ，向心加速度满足下面的方程：222/2v GM M L L =〔1〕v =2〕周期：2(/2)L Tv ππ=计算＝3〕 2．根据观测结果，星体的运动周期TT <观察计算计算〔4〕这说明双星系统中受到的向心力大于本身的引力，故它一定还受到其他指向中心的作用力，按题意这一作用来源于均匀分布的暗物质，均匀分布在球体内的暗物质对双星系统的作用与一质量等于球内暗物质的总质量M '位于中点处的质量点一样．考虑暗物质作用后双星的速度即为观察到的速度v 观，那么有2222(/2)v GM MM M G L L L '=+观/2〔5〕v 观6〕因为在轨道一定时，周期和速度成反比，由〔4〕式得：1v 观1＝7〕把〔2〕、〔6〕式代入〔7〕式得14N M M -'=〔8〕设所求暗物质的密度为ρ，那么有341324L N M πρ-⎛⎫=⎪⎝⎭ 故33(1)2N ML ρπ-=〔9〕五、参考解答解法一：1．〔1〕电阻图变形．此题连好的线路的平面图如图预解16-5-1所示．现将电阻环改画成三角形，1、3、5三点为顶点，2、4、6三点为三边中点，如图预解1—5-2与图预解16-5-3所示．整个连好的线路相当于把n D 的三个顶点分别接到1n D -的三个中点上，图预解16-5-1变为图预解16-5-4．这样第1问归结为求图预解16-5-4中最外层三角环任意两顶点间的等效电阻。

2016年中环杯初赛模拟卷及答案

（新舟教育吴忠良供题）【答案】 3.75 4. 从自然数 1 ~ 20 中选出 4 个数（不重复），把所有的可能性按顺序排列如下（每种可能性中 4 个数都是从小到大的）：（1，2，3，4）、（1， 2，3，5）、（1，2，3，6）、……、（1，2，3，20）、（1，2，4， 5）、（1，2，4，6）、……、（1，2，4，20）、……、（16，18，
4 5
4 4
2 5
2016 年第 16 届中环杯七年级初赛模拟试卷填空题（共 10 题，前 5 题每题 4 分，后 5 题每题 6 分） 1. 计算： 23 2 22 2 2 1 33 2 32 2 3 1 243 2 242 2 24 1 ________.
1
x y z 20
3
y3 z3 _____. xyz
2 y 3
3
______.
5. 若 p, q 都是素数，关于 x 的方程 x4 px3 q 0 有整数根，满足要求的有序数对 p, q 有_____对 6. 现有 20 个正整数，它们依次为 12 5 、 22 5 、、 202 5 ，计算其中任意相邻两数的最大公约数，请写出所有可能出现的最大公约数： _______________. （四季教育供题） 7. 若多项式 f x 满足：对任意 x ，均有 f x 4 f x 7 x 3 ，并且 f 0 5 ，则
7. 如果一个等差数列的每一项都是整数，其中某相邻四项之和为 30，某相邻五项之和也是 30。前面所提的“相邻四项”与“相邻五项”中相同的数字最少有_____个 8. 一条直线上有两个钉子，相距 20 厘米，一根弹性均匀的白色绳子两头系在两个钉子上，甲要将这根绳子涂成红色，他每次最多可以将 2 厘米涂成红色，但乙在旁边捣乱，甲每涂 1 次，乙都将一个钉子沿直线向外移动 1 厘米，即绳子均匀的拉长 1 厘米，问甲要将绳子全部涂成红色至少要涂次（四季教育供题） 9.

16届中环杯二年级决赛试题

话遥排在队伍最前面的人说院野后面的所有人都说假话遥冶剩下的所有人都说院野排在我前面的那个人渊与说话人
相邻冤说假话遥冶这 25 个人中袁有 ___________ 人说假话遥 11. 在黑板上写有数 123456789遥在写的数中选两个相
邻的数码袁如果它们都不为 0袁则每个减 1 且交换数码的位置袁例如院123456789邛123436789邛噎遥这样操作若干次后袁能够得到的最小数是 ___________遥
3. 有一个正方体袁它的六个面分别标上了 1~
6袁图中是从三个角度观察到的图像遥野钥冶处的数字
应该是 ___________遥
4. 哆啦 A 梦和大雄玩野剪刀尧石头尧布冶的游
第2题
戏袁规定每一局的获胜者可以得到两个铜锣烧袁输的人没有铜锣烧袁如果是平局就每人各得到一个铜锣烧遥大雄知道哆啦 A 梦只能出石头袁但是他还是想要和哆啦 A 梦分享铜锣烧袁于是他决定每
三尧动手动脑题渊本大题共 2 小题袁每题 10 分袁共 20 分冤院 13. 哆啦 A 梦和大雄玩猜 4 位数的游戏遥大雄每猜一个数袁哆啦 A 梦就会告诉他其中有
几个数的数字是对的袁有几个数的数位是对的遥比如院正确答案是 5678袁大雄如果猜 4687袁那
么袁数字正确的有 3 个渊分别是野6冶尧野7冶尧野8冶冤袁数位正确的是 1 个渊因为野6冶放对位置了袁野7冶尧野8冶没有对冤遥
二年级第 2 页
第十六届野中环杯冶中小学生思维能力训练活动二年级决赛
得分院
注意院每小题前的野阴冶由阅卷人员填写袁考生请勿填写遥
一尧填空题 A院渊本大题共 8 小题袁每题 6 分袁共 48 分冤
1. 计算院3+14+27+32+58+26=___________遥

第十六届“华杯赛”小学组决赛试题A答案

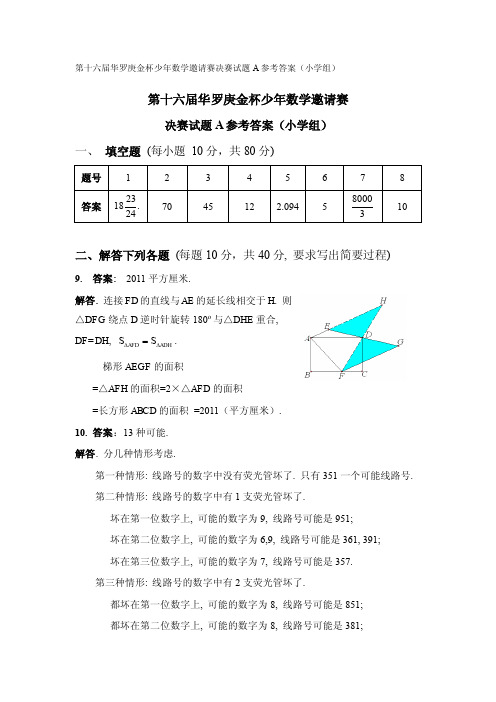
第十六届华罗庚金杯少年数学邀请赛决赛试题A 参考答案（小学组）一、填空题 (每小题 10分，共80分)二、解答下列各题 (每题10分，共40分, 要求写出简要过程)9. 答案: 2011平方厘米.解答. 连接FD 的直线与AE 的延长线相交于H . 则△DFG 绕点D 逆时针旋转180o 与△DHE 重合,DF=DH , ADH AFD S S ∆∆=.梯形AEGF 的面积=△AFH 的面积=2×△AFD 的面积=长方形ABCD 的面积 =2011（平方厘米）.10. 答案：13种可能.解答. 分几种情形考虑.第一种情形: 线路号的数字中没有荧光管坏了. 只有351一个可能线路号. 第二种情形: 线路号的数字中有1支荧光管坏了.坏在第一位数字上, 可能的数字为9, 线路号可能是951;坏在第二位数字上, 可能的数字为6,9, 线路号可能是361, 391;坏在第三位数字上, 可能的数字为7, 线路号可能是357.第三种情形: 线路号的数字中有2支荧光管坏了.都坏在第一位数字上, 可能的数字为8, 线路号可能是851;都坏在第二位数字上, 可能的数字为8, 线路号可能是381;都坏在第三位数字上, 可能的数字为4, 线路号可能是354;坏在第一、二位数字上, 第一位数字可能的数字为9，第二位数字可能的数字为6，9, 线路号可能是961， 991;坏在第一、三位数字上, 第一位数字可能的数字为9，第三位数字可能的数字为7, 线路号可能是957;坏在第二、三位数字上,第二位数字可能的数字为6，9, 第三位数字可能的数字为7，线路号可能是367, 397.所以可能的线路号有13个:351,354,357,361,367,381,391,397,851,951,957,961,991.11. 答案: 3, 5.解答. 设这个月的第一个星期日是a 日（71≤≤a ）, 则这个月内星期日的日期是a k +7, k 是自然数, 317≤+a k . 要求有三个奇数.当a =1时, 要使7k +1是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时,177+=+k a k 分别为1, 15, 29, 这时20号是星期五.当a =2时, 要使7k +2是奇数, k 为奇数, 即k 可取1, 3两个值, 7k +2不可能有三个奇数.当a =3时, 要使7k +3是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时377+=+k a k 分别为3, 17, 31, 这时20号是星期三.当74≤≤a 时, a k +7不可能有三个奇数.12. 答案: 253.解：令k m 15=, k 是自然数, 首先考虑满足下式的最大的m ,.201115151153152151≤⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡m m 于是.2011213152)1(1515)1(152151150151511531521512≤-=+-=+⨯-++⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡k k k k k kk m m 因此.402213152≤-k k 又40224114171317152>=⨯-⨯, 40223632161316152<=⨯-⨯,得知k 最大可以取16. 当16=k 时, m =240. 注意到这时312161952363220112131520112+⨯==-=--k k . 注意到20112024131618161513151615121516152151615115161515161511516152151>=⨯+=⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡-⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ 而201120081216181615121516153152151<=⨯+=⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ .所以253 是满足题目要求的n的最小值.三、解答下列各题(每小题15分，共30分，要求写出详细过程)13.答案: 312解答. 由于2+0+1+1=4 且0+1+2+3+4+6+7+8+9=40, 4≡40(mod 9), 所以, 九个不同的汉字代表的数字：0, 1, 2, 3, 4, 6, 7, 8, 9.易知：40-4=36, 36÷9=4（次）, 说明此算式共发生四次进位.“4=2+2=1+1+2=1+2+1”显然：①华=1, “4=2+2”无解②华=1, “4=1+1+2”有解A:28+937+1046=2011, 可组成算式36种（6×6×1=36）B：69+738+1204=2011, 可组成算式48种（6×4×2=48）C：79+628+1304=2011, 可组成算式48种（6×4×2=48）③华=1, “4=1+2+1”有解A：46+872+1093=2011, 可组成算式36种（6×6×1=36）B：98+673+1240=2011, 可组成算式72种（6×6×2=72）C：97+684+1230=2011, 可组成算式72种（6×6×2=72）总计：72×3+96=216+96=312（种）.14.解答. 如左下图, 设M, N, P分别为棱GC, GF, GH的中点, 'M, 'N, 'P 分别为棱AE, AD, AB的中点, O为正方体的中心(长方形BDHF的中心).(1)第一只蜘蛛甲可以把爬虫控制在右上图所示的范围内.首先蜘蛛甲做与爬虫关于点O的对称方向的移动, 不妨设爬虫由G沿棱GC 向点M移动, 蜘蛛甲由A沿棱AE向点'M移动, 爬虫被限制在GM上. 当爬虫到达点M时, 蜘蛛甲也同时到达点'M. 然后蜘蛛甲改变策略, 做与爬虫关于平面BDHF对称的方向移动.a) 当爬虫到达点B, D, F, H时, 蜘蛛甲捉住爬虫.b) 当爬虫未到达点B, D, F, H时, 爬虫被控制在左上图所示的范围内.(2) 蜘蛛乙先移动到点G, 由于右上图无环路, 蜘蛛乙可以跟在爬虫后面, 总可以捉住爬虫.。

2016第十六届中环杯四年级决赛详解

25 10 15 3 5 是合数 49 10 39 313 是合数 81 10 71 是质数故 a 最小是 71
【第 3 题】如图， C、E、B 三点共线， CB AB, AE / / DC , AB 8, CE 5 ，则 AED 的面积为______
A1 与 A3 中至少有一个是假话
但不可能为 A1 是真话， A3 是假话则 A1 是假话；则 n 12 再对 A1 是假话，则 n 12 再对 D1 进行讨论 ①若 D1 是真话，即 12 n 20 故 B1 与 B3 都是假话则 B2 是真话；则 10 n 但不存在既满足 12 n 20 ，又满足 10 n 的正整数 n ②故 D1 是假话，即 n 20 则 D2 是真话，即 n 是一个质数故 B2 、 C1 、 C3 均是假话则 C2 是真话，即 20 n 90 故 B3 是假话则 B1 是真话，即 84 n 90 注意到，符合 84 n 90 且 n 为质数的只有 n 89 ，即这个数是 89 【第 10 题】如图， ABC 是一个等边三角形，在 BC 边上取点 D、E ，使得 BC 3DE ，作等边 DEF ，联结 AF ，作 DG 平行 AF 于点 G ，作 EH 平行 AF 交边 AC 于点 H ，作。若 G I A、 FH J 、 A FH J A F BDF 的面积为 45， DEF 的面积为 30，则 GI HJ，一共有 6 道题目，每道题目的分值均为 7 分（最后每题的得分都是整数，最低为 0 分，最高为 7 分），每个参赛者的总分就是 6 道题目得分的乘积，如果两个人的得分相同，就计算 6 道题目得分之和，从而评定名次高低。如果还相同，就算两人并列。在这次比赛中，一共有 86 262144 位参赛者，这些参赛者中没有出现并列，排名为 76 117649 的参赛者的得分为________分【说明】 ⑴此题为错题若两个人 6 道题每题得分完全相同则 6 道题目得分的乘积相同，6 道题目得分的和也相同则这两个人的排名相同，即这两个人并列由题意，这 86 262144 位参赛者中没有出现并列则这 86 262144 位参赛者每题得分均不完全相同而每题的得分为 0~7 的整数，由乘法原理一共有 86 种得分情况若甲第 1~6 题得分为 0、 0、 0、 0、 0、 0、 1 ，乙第 1~6 题得分为 0、 0、 0、 0、 0、 1、 0 甲、乙两人 6 道题目得分的乘积为 0,6 道题目得分的和为 1 则甲、乙两人排名相同，即这两个人并列这与“这些参赛者中没有出现并列”矛盾故此题为错题 ⑵若将原题中“这些参赛者中没有出现并列”改为“这些参赛者中，任意两人这 6 题的各题得分不完全相同” ，则排名为 76 117649 的参赛者的得分为 1 分理由如下：若 6 题中，至少有一题得分为 0，则 6 道题目得分的乘积为 0 若 6 题中，没有一题得分为 0，则 6 道题目得分的乘积不为 0 这种情况下，每题的得分为 1~7 的整数，由乘法原理一共有 76 种得分情况故排名为 76 117649 的参赛者的得分为乘积最小的正整数而第 1~6 题得分为 1、 1、 1、 1、 1、 1 的参赛者，得分为 1 故排名为 76 117649 的参赛者的得分为 1 分【第 8 题】如图所示，两条直线与两个圆交于 9 个点，从这 9 个点中选出 4 个点，要求这 4 个点的任意 3 个点既不在一条直线上，也不在一个圆圈上，不同的选法有______种

四年级中环杯决赛模拟卷

例6. 例7.
例8.
1 AD ， AB 9cm ， AD 3 的长度是整数。 CGF 与 AEG 的面积之差的值也是整数，并且这个面积之差是 5 的倍数，则 AD 的最小值为________厘米
如图，长方形 ABCD 中， E , F 分别是 AD, BC 上的点，满足 AE BF
2016 年第 16 届中环杯四年级决赛模拟试卷填空题（共 10 题，前 5 题每题 4 分，后 5 题每题 6 分）
例1. 计算： 7.8 63 84 9 6.1126 ________.
例2. 例3.
已知 19700019d 为质数，则 d ________. 小明漂流到一个奇怪的小岛上，岛上有两种人，老实人和骗子，老实人永远说真话，骗子永远说假话。国王让编号 1 到 6 的 6 个人从前到后依次站成一列（1 在最前面，6 在最后面），后面的人可以看见前面所有人，前面的人看不见后面的人，每个人都知道另一个人是老实人还是骗子。这 6 个人每人说一句话，小明如果猜出共有几个骗子，国王就可以给他一条船离开小岛 1 号说：“我是老实人”； 2 号说：“我和 1 号至少有 1 个是老实人”； 3 号说：“我和 2 号都是老实人”； 4 号说：“我和 2 号、3 号中，骗子比老实人多”； 5 号说：“我和前面 4 个人中，骗子比老实人多”； 6 号说：“我和 4 号、5 号都是骗子”；小明为了离开小岛，他说一共有_____个骗子
11| abc 11| bcd 若五位数 abcde 满足，这样的五位数称为“中环数”，最小的“中环数”为________. 11| cde 11| abcde
例4.
例5.
一个学生旅行团一行 27 人晚上来到一家旅社，旅社有下面三种房间：三人间，每间 135 元；二人间，每间 100 元；四人间，每间 120 元。这个团男生 15 人，女生 12 人，要求男、女生必须分开住，他们最少需要花费______元若 2a 9b 2a9b （其中 2a9b 是一个四位数），则 2a9b ________. 将数字 0 或 1 填入 4 4 的方格表内，每个小方格能且只能填入一个数字，要求任一行、任一列的数字和均为 2，则B

(仅供参考)第16届中环杯决赛试卷与答案四年级-7257

第16届中环杯四年级决赛一、填空题A （本大题共8小题，每题6分，共48分）：1. 计算：0.263 1.91261969⨯+⨯+⨯=________。

【答案】20162. 一个质数a 比一个完全平方数b 小10，则a 的最小值为______。

（说明：完全平方数是指能表示为一个整数的平方的数，比如242=，293=，所以49、都是完全平方数。

）【答案】713. 如图，C 、E 、B 三点共线，CB AB ⊥，AE //DC ，8AB =，5EC =，则AED ∆的面积为______。

【答案】204. 三支蜡烛分别能燃烧30、40、50分钟（但是不是同时点燃的）。

已知这三支蜡烛同时处于燃烧状态的时间有10分钟，只有一支蜡烛处于燃烧状态的时间有20分钟。

那么正好有两支蜡烛同时处于燃烧状态的时间有_______分钟。

【答案】355. 将一个888⨯⨯的立方体的三个面染红色，三个面染蓝色（要求任意三个有公共顶点的面不能全都染同一种颜色），然后将其切割成512个111⨯⨯的小立方体。

这512个小立方体中，有_____个小立方体上既有红色面又有蓝色面。

【答案】566.在11!（11!11101k+（其中k为自然数）的最大=⨯⨯⨯）的所有因数中，可以表示为61因数为________。

【答案】3857.在某次数学比赛中，一共有6道题目，每道题目的分值均为7分（最后每题的得分都是整数，最低为0分，最高为7分），每个参赛者的总分就是6道题目得分的乘积。

如果两个人的得分相同，就计算6道题目得分之和，从而评定名次高低。

如果还相同，就算两人并列。

在这次比赛中，一共有68262144=位参赛者，这些参赛者中没有出现并列。

排名为67117649=的参赛者的得分为_____分。

【答案】本题有问题，无解。

8.如下图所示，两条直线与两个圆交于9个点。

从这9个点中选出4个点，要求这4个点中的任意3个点既不在一条直线上，也不在一个圆周上。

2016 年第16 届中环杯四年级初赛模拟试卷详解

6 6 8
同理可得 n 5 2 6 2 1 2 3 5
5 5 7
所以 m n 2.8
-6-
王洪福老师
数学
10. 将含有一些数字的表格划分为若干个区域，要求: （1）每个数字表示其所在区域的面积（这里所谓的面积就是指单位正方形的个数）；（2）两个面积相等的区域不相邻（可以有公共顶点，但是不能有公共边）；（3）每个区域内可以有多个数字（当然，这些数字必然相等）或者没有数字；如下图所示，给出了一个例子 3 3 3 3 2 2 3 2
查看更多试题资料欢迎关注王洪福老师公众号
-7-
BE =c ， DE a ， BF d ， DF b 所以 BD BE ED c a ， BD BF FD d b 所以 2 BD a b c d 10 10 20 ，所以 BD 10
因为 CE BD ，所以 S BCD BD CE 2 10 5 2 25
王洪福老师
数学
2016 年第 16 届中环杯四年级初赛模拟试卷详解
填空题（共 10 题，前 5 题每题 4 分，后 5 题每题 6 分） 1. 计算：（20.15+30.24）×72+15.12×56+564.2= 【解析】 .
（20.15 30.24） 72 15.12 56 564.2 =20.15 72+30.24 72 15.12 2 28 20.15 28 =20.15 72+30.24 72 30.24 28 20.15 28 =20.15 72+28 30.24 72+28 =2015 3024 =5039

上海中环杯小学四年级考前模拟题第一套答案详解

综合强化复习04-07 姓名：得分：一、填空题：1、计算：（1+2+3+……+2009+2010+2011）÷2011+（1+2+3+……+2010）÷2011=（）。

分析：除数一样时，可以用乘法分配率。

首先提取公因数2011，然后观察括号里的数相加规律，从1加到2011再加回1，这样的数列求和等于数列中最大的数的平方。

=（1+2+3+……+2009+2010+2011+1+2+3+……+2010）÷2011=2011×2011÷2011=20112、, x y 为两个数，规定两种新的运算“*”及“△”，,8,65*xy y x y x y x =∆+=求： (4△6)*(5△3)=（）。

分析：套用规则即可。

一般符号前面的数和后面的数分开分析。

=（8×4×6）*（8×5×3）=192*120=192×5+120×6=960+720=16803、将20条长10厘米的纸带粘合在一起，纸带之间的重合部分为2厘米，粘得的纸带长（）厘米。

分析：若把20条纸带的长全部算出来，则粘合的部分2厘米包含了2次，需要减去一次，关键是减去多少个2厘米，20条，粘合的部分有19处。

=20×10-19×2=162厘米4、100个连续自然数（按从小到大的顺序排列）的和是20150，取出其中第2个、第4个、第6个……第100个，再把剩下的50个数相加，得到的结果是（）. 分析：100个连续自然数分成了两组，取出的是双数个，留下的是单数个。

50个双数个比50个单数个的总和多50，因此这道题实质是道和差问题。

=（20150-50）÷2=100505、某天，博物馆开馆前已排了530米的长队，并且每分钟有6位参观者加入。

从开馆开始，1小时10分钟之后队列消失，到此时为止，进入博物馆的参观者人数是2010位。

中环杯数学竞赛四年级试题

中环杯数学竞赛四年级试题中环杯数学竞赛是一项面向小学生的数学竞赛，旨在激发学生的数学兴趣，提高数学素养。

以下是一份模拟的四年级中环杯数学竞赛试题，供参考：一、选择题（每题2分，共10分）1. 下列哪个数是最小的两位数？A. 10B. 98C. 100D. 992. 如果一个数的3倍是45，那么这个数是多少？A. 15B. 50C. 40D. 303. 一个长方形的长是12厘米，宽是8厘米，它的周长是多少？A. 40厘米B. 44厘米C. 48厘米D. 56厘米4. 以下哪个分数是最大的？A. 1/2B. 2/3C. 3/4D. 4/55. 一个数加上8等于23，这个数是多少？A. 15B. 21C. 17D. 19二、填空题（每空1分，共10分）6. 一个数的5倍是30，这个数是_________。

7. 把一个数增加20，得到的结果比原数大_________。

8. 一个数的2/3等于18，这个数是_________。

9. 一个班级有40名学生，其中女生占2/5，女生有_________人。

10. 如果一个数的3倍是另一个数的2倍，那么这两个数的比是_________。

三、简答题（每题5分，共20分）11. 一个长方形的长是15厘米，宽是10厘米，求它的面积。

12. 一个班级有50名学生，其中1/4是男生，这个班级有多少名男生？13. 一个数的4倍是另一个数的2倍，如果这个数是12，求另一个数。

14. 一个数的1/5加上另一个数的1/4等于9，如果另一个数是36，求这个数。

四、应用题（每题10分，共20分）15. 小明有40张邮票，他给了小红一半，然后他又给了小红剩下的一半，最后小明还剩下多少张邮票？16. 一个水果店有苹果和橙子，苹果的数量是橙子的3倍，如果苹果和橙子一共是90个，问苹果和橙子各有多少个？五、附加题（10分）17. 一个数列的前三项是1，2，3，从第四项开始，每一项都是前三项的和。

2022年第16届中环杯四年级初赛模拟试卷答案

2022年第16届中环杯四年级初赛模拟试卷答案2022,年第,16,届中环杯四年级初赛模拟试卷(篇一)2022年第十六届中环杯初赛试题（二年级）1、计算：2+3+5-6+7+1-10＝2、计算：2310-187+8÷2＝3、观察下面的三个天平，1个圆圈的重量和朵花的重量相等。

4、羊村的村长为了防范灰太狼，在正方形的羊村周围安排小羊们站岗放哨。

要求每边有4只小羊站岗，则最少需要只小羊。

5、10台拖拉机开10天需要消耗10桶油。

照此计算，20台拖拉机开20天需要消耗桶油。

6、把1-5这五个数字分别填入下图的方格中，使得横行三数之和与竖行三数之和都等于9。

7、泡泡把蓝圆片摆成一个圈，每两个蓝圆片之间再放入一个红圆片。

放完之后，泡泡数了数，一共放了70个小圆片，那么蓝圆片有个。

8、一辆洒水车给一个社区街道洒水，地图如下图，你能否设计一条洒水路线，使洒水车不重复地走遍所有街道，再回到出发点？你的为：（填能或不能）{2022,年第,16,届中环杯四年级初赛模拟试卷答案}。

9、有一个正方体木块，每个面上分别写上了1、2、3、4、5、6，并且相对两面上的和是7，这个木块按下图放置后，按照图中箭头所示方向翻动。

翻动到最后一格时，木块朝上一面的数是{2022,年第,16,届中环杯四年级初赛模拟试卷答案}。

10、小泡泡要给一些美丽的花朵涂颜色。

他有5种颜色的蜡笔，一朵花只可以用一种颜色，那么下图中这些花朵中至少有朵花的颜色相同。

11、大熊、静香、胖虎、小夫与机器猫一起举行围棋比赛，每两人要比赛一场。

到现在为止，大熊已经赛了4场，静香赛了3场，胖虎赛了2场，小夫赛了1场。

机器猫参加了场比赛。

12、香香和爸爸在比年龄，爸爸6年前的年龄比香香5年后的年龄还大18岁，香香10年后的年龄和爸爸7年前的年龄和是50岁。

则今年爸爸岁。

13、小明想要对图中的每个小三角形进行染色，要求任意一个三角形的三边都是一条染红色、一条染绿色、一条染蓝色。