2014年第十二届走美杯初赛六年级答案(B卷)

合集下载

小学六年级美术期末试卷及答案课件

大师作品
可以提高学生的审美水平，了解不同风格的绘画技巧。
同龄人作品
激发学生的创造力和竞争力，鼓励他们尝试新的绘画方式。
相关学习网站推荐
美术学习网
包含大量的美术学习资源和教程，涉及多种绘画技巧和工具。
儿童美术网
专门为儿童提供美术教育和资源，有优秀的儿童画作品展示。
艺术网
提供专业的艺术资讯和美术作品欣赏，涉及多种艺术形式。
学生作品展示
03
优秀作品展示
总结词
色彩搭配合理、创意独特、细节处理到位
详细描述
优秀作品在色彩搭配上非常合理，整体画面色彩丰富且和谐，给人留下深刻的印象。同时，这些作品具有独特的创意，能够体现学生的创造力和想象力。另外，优秀作品在细节处理上非常到位，无论是线条的勾勒还是色彩的搭配都非常精细，让人感受到作品的精致和细腻。
的艺术鉴赏水平和审美素养。
05
相关料与推荐
相关美术教学资源
美术课本
作为基础教材，包含多种绘画技巧和基础知识，适合小学生学习。
美术参考书
提供更多的实践技巧和案例，有助于学生提高绘画水平。
在线课程
提供专业的美术教育资源，方便学生在家中自学。
优秀美术作品欣赏
儿童画
色彩鲜艳，构图简单，易于理解，符合小学生的认知特点。
等方式，鼓励学生积极参与课堂活动并与他人合作。
下一步教学计划Байду номын сангаас展望
拓展绘画技巧
计划在下个学期继续拓展学生的绘画技巧，包括素描、水彩、油画等不同绘画形式的学习和实践。
加强创作指导
计划加强对学生创作的指导，通过更多样化的主题和情境设置，激发学生的创作灵感和表现力。

2014年美国“数学大联盟杯赛”(中国赛区)初赛五、六年级试卷

37. 将 1 ~ 9 九个数不重不漏地组成一个两位数、一个三位数、一个四位数。这三个数均能被 9 整除，并且 7、8、9 分别在这三个数中，三个数十位数字为三个连续的偶数，个位数字为三个连续的奇数。如果将四位数的千位移到两位数的百位，组成新的三个三位数，新的三位数也均能被 9 整除。那么题中最初的三位数是。 38. 如图为一个正方体有盖纸盒的示意图，在 1 ~ 30 的数中选出 7 个，在纸盒的每个面填一个数。将盒盖的两个数字相加后，三组相对面填的数均满足两两乘积相等。那么 x 处的数字有种可能。
姓名(签名)
A) 413 B) 1626 C) 21155 D) 161155 16. Which of the following figures has an odd number of sides? A) rhombus B) trapezoid C) pentagon D) hexagon 17. For how many integers from 55 to 66 is the ones digit greater than the tens digit? A) 4 B) 5 C) 10 D) 11 18. Lex buys 6 same-priced books and pays with a $50 bill. The change Lex receives is twice the price of a book. Each book costs A) $6.25 B) $7.14 C) $8.33 D) $12.50
14. If two consecutive whole numbers have a different number of digits, then their 一、选择题(每小题 5 分，答对加 5 分，答错不扣分，共 150 分，答案请填涂在答题卡上) 1. The band’s trombone plays 2013 notes, the trumpet plays 2014 notes, and the tuba plays 218 notes. That’s a total of ? notes. A) 6245 B) 6045 C) 4245 D) 645 2. The remainder when (999 999 999 + 666 666 + 333 + 1) is divided by 3 is A) 0 B) 1 C) 2 D) 3 3. 20 − 5 × 2 = 2 × ? A) 5 B) 15 C) 25 D) 30 C) 15 D) 100

2014年第十二届走美杯初赛小学二年级A卷(Word解析)

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学二年级试卷（A卷）填空题Ⅰ（每题8分，共40分）1．计算：1+3+5+7+9+11+15=__________．2．△+△+□=24，□+□+77=●，14+●=99，△=__________．3．找规律填数：（1）1，2，4，7，11，__________，22．（2）1，2，4，4，7，6，10，8，___________，___________．4．一个数加上9所得的和的一半是5，这个数是__________．5．甲乙两筐水果共重60千克，甲筐水果重量是乙筐水果重量的一半，甲筐水果是__________千克．填空题Ⅱ（每题10分，共50分）6．把1、2、3、4、5、6、7七个数填在右图中的七个圆圈里，每个数只能用一次，使每条线上的三个数相加之和都等于12．7．在下面的格子里填上1、3、5，使每行、每列恰好都有1、3、5三个数．8．数一数，下图中一共有__________个正方形．9．一根30厘米长的木条，要锯成5厘米的小段，需要锯__________次．53110．一个大正方体表面涂上红色后，按将下图方式切成27个小正方体，这些小正方体中，恰好有三个面涂有红色的有__________个．填空题Ⅲ（每题12分，共60分）11．将1、2、3、4四个数字填到下面的减法算式里，使得差最小，这个最小的差是__________．12．今年爸爸的年龄恰好等于姐妹俩的年龄之和，3年后，爸爸的年龄比姐妹俩的年龄之和__________（填“大”或“小”），相差__________岁．13．如下图，把左边4颗钉子围起来用去的绳子比把右边6颗钉子围起来用去的绳子短4厘米，把左边4颗钉子围起来用去绳子__________厘米．14．少先队员排队去参加科技馆，从排头数起小明是第10个；从排尾数起，小英是第13个．小明的前面就是小英，这队少先队员共有__________人．15．仔细观察下面表示数的方式，第六行表示__________．－表示5表示4表示3表示2表示1第六行第五行第四行第三行第二行第一行第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学二年级试卷（A 卷）参考答案1 2 34 5 6 7 8 64 10 (1)16；(2)13，101 20 如下图如下图109 10 11 12 13 14 15 587小，382176．7．参考解析填空题Ⅰ（每题8分，共40分）1．计算：1+3+5+7+9+11+15=___________．【考点】速算巧算【难度】☆☆ 【答案】64【解析】原式1+3+(5+15)+(7+13)+(9+11)64==2．△+△+□=24，□+□+77=●，14+●=99，△=___________．【考点】数字谜【难度】☆☆ 【答案】10【解析】●=991485-=；□=(8577)24-÷=；△(244)210=-÷=．3．找规律填数：（1）1，2，4，7，11，___________，22．（2）1，2，4，4，7，6，10，8，___________，___________．【考点】找规律【难度】☆☆ 【答案】(1)16；(2)13，10【解析】（1）从2到11，每个数与前面的差分别是1、2、3、4，故括号内的数为a ，且115a -=，所以括号内填16．（2）观察可知，奇数项1、4、7、10是一个前后两项差3的等差数列，故第一个括号内应该填13；偶数项2、4、6、8是一个前后两项差2的等差数列，故第二个括号内应该填10．4．一个数加上9所得的和的一半是5，这个数是___________．【考点】和倍问题【难度】☆☆ 【答案】1【解析】一个数加上9所得的和的一半是5，所以一个数加上9所得的和是：25=10⨯，这个是1091-=．53627145113355315．甲乙两筐水果共重60千克，甲筐水果重量是乙筐水果重量的一半，甲筐水果是___________千克．【考点】和差倍应用题【难度】☆☆ 【答案】20【解析】根据题意可知，乙筐水果重量是甲筐的2倍，故甲筐水果的重量是603=20÷．填空题Ⅱ（每题10分，共50分）6．把1、2、3、4、5、6、7七个数填在右图中的七个圆圈里，每个数只能用一次，使每条线上的三个数相加之和都等于12．【考点】几何计数【难度】☆☆☆【答案】【解析】设中间数为a ，3条线之和是12345672282=123a a +++++++=+⨯，4a =，另六个数分成三组有（1，7）、（2，6）、（3，5）．7．在下面的格子里填上1、3、5，使每行、每列恰好都有1、3、5三个数．【考点】数阵图【难度】☆☆☆【答案】【解答】第一行，第一个数是1，第二个不能是1、3，则为5，第三个则为3；第二行，同理可得一个数是5，第三个是1；第三行，第一个数是3，第二个数是18．数一数，下图中一共有___________个正方形．5362714531511335531【考点】几何计数【难度】☆☆☆ 【答案】10【解答】最外面的大正方形是1个，它被分为4个相同的中等正方形；中间有1个中等正方形，以及4个小正方形．9．一根30厘米长的木条，要锯成5厘米的小段，需要锯__________次．【考点】应用题【难度】☆☆☆ 【答案】5【解答】锯成305=6÷段，需要锯61=5-次10．一个大正方体表面涂上红色后，按将下图方式切成27个小正方体，这些小正方体中，恰好有三个面涂有红色的有__________个．【考点】立体几何【难度】☆☆☆ 【答案】8【解答】根据题意，恰好有三个面涂红色，则必然在8个顶点处所以共有8个．填空题Ⅲ（每题12分，共60分）11．将1、2、3、4四个数字填到下面的减法算式里，使得差最小，这个最小的差是__________．【考点】数字谜【难度】☆☆☆ 【答案】7【解析】由题意可知，被减数十位数要大于减数的十位数．要使差最小，被减数十位数不能是4，1也不能取，否则差小于0．当被减数十位数取2时，这个减法算式最小的情况应该是23149-=；当被减数十位数取3时，这个减法算式最小的情况应该是3124=7-．12．今年爸爸的年龄恰好等于姐妹俩的年龄之和，3年后，爸爸的年龄比姐妹俩的年龄之和__________（填“大”或“小”），相差__________岁．－【考点】年龄问题【难度】☆☆☆ 【答案】小，3【解析】已知爸爸的年龄与姐妹俩的年龄和相等，3年后，爸爸增加3岁，姐妹俩的年龄各增加3岁，共增加6岁，所以此时爸爸的年龄小于姐妹俩的年龄，相差3岁．13．如下图，把左边4颗钉子围起来用去的绳子比把右边6颗钉子围起来用去的绳子短4厘米，把左边4颗钉子围起来用去绳子__________厘米．【考点】图形规律【难度】☆☆☆ 【答案】8【解答】由图可知，右边的图形比左边的图形多用两条线段，多出来的长为4厘米，所以每一段长为2厘米，所以左边的图形用去绳子的长度为：42=8⨯(厘米)．14．少先队员排队去参加科技馆，从排头数起小明是第10个；从排尾数起，小英是第13个．小明的前面就是小英，这队少先队员共有__________人．【考点】排队问题【难度】☆☆☆ 【答案】21【解答】由题意可知，从排头数起，小英是第9个，从排尾数起，她是第13个，所以少先队员共有9+13121-=（人）．15．仔细观察下面表示数的方式，第六行表示__________．【考点】找规律【难度】☆☆☆ 【答案】7【解析】由图可知，第一列的黑点代表“4”，第二列的黑点代表“2”，第三列的黑点代表“1”．所以第六行是4+2+1=7．表示5表示4表示3表示2表示1第六行第五行第四行第三行第二行第一行。

小学奥数走美杯初赛试题及答案(六年级)

小学奥数走美杯初赛试题及答案（六年级）一、填空题Ⅰ(每题8分，共40分)1．的分母增加36后，要使分数的大小不变，分子应加______。

2．在“庆祝六一”征文竞赛活动中，某校六年级有80人获一、二、三等奖。

其中获三等奖的人数占六年级获奖人数的62.5%，获一、二等奖的人数比是1∶4。

六年级获二等奖共有______人。

3．把一些糖果平均分给10个小朋友。

其中有两个小朋友又把他们得到的全部糖果，都分给了其余的小朋友；结果，其余的小朋友每人多了3颗糖果。

一共有_______颗糖果。

4．在一个正方形里面画一个的圆，这个圆的面积是正方形面积的_______%。

(π取3.14)5．假如物价下降50%，那么原来买1件东西的钱现在就能买2件。

1件变2件增加了100%，这就相当于我手中的钱增值了100%。

假如物价上涨25%，相当于手中的钱贬值了_____%。

二、填空题Ⅱ(每题10分，共50分)6．算式的计算结果是_______。

7．如图，大等边三角形中放了三个面积都是30平方厘米的小正六边形。

大三角形的面积是______平方厘米。

8．假如 (A、B均为自然数)，那么B是______。

9．有五个互不相等的非零自然数。

假如其中一个剑少45，另外四个数都变成原先的2倍，那么得到的仍旧是这五个数。

这五个数的总和是______。

10．甲、乙两车都从A地到B地。

甲车比乙车提前30分钟动身，行到全程三分之一时，甲车发生了故障，修车花了15分钟，结果比乙车晚到B地15分钟。

甲车修车前后速度不变，全程为300千米。

那么乙车追上甲车时在距A地_______千米。

三、填空题Ⅲ(每题12分，共60分)11．在一个棱长为5厘米的正方体上如图切掉一个三棱柱。

那么体积削减_______立方厘米；外表积削减______平方厘米。

12．从0、2、4、6、8中挑出4个各不一样的数字能组成一个四位完全平方数，那么这个完全平方数是______。

13．某网络嬉戏中推出圣者套装，包含圣剑、圣盔、圣甲3件装备。

“走美杯”小学数学竞赛试卷(六年级初赛b卷)

“走美杯”小学数学竞赛试卷（六年级初赛B卷）一、填空题I（每题8分，共40分）1．（8分）183×279×361﹣182×278×360的计算结果是（）A．217017B．207217C．207216D．2170162．（8分）假设地球是个均匀的球体（半径6378千米），围绕地球赤道正上方上有一圈铁丝，铁丝的周长比地球赤道长1米，在赤道和铁丝之间会有一个缝隙，下列动物中，有种可以安全通过铁丝．①蚂蚁；②蜜蜂；③青蛙；④老鼠；⑤猫；⑥成年奶牛；⑦大象．3．（8分）将0﹣5这六个数字中的4个数字填入图的圆圈中，没条线段两端的数字作差（大或小），可以得到5个差，这5个查恰好为1﹣5．在所有满足条件的填法中，四位数ABCD （首位不能为0）的最小值是．4．（8分）一次考试中，总人数的又3人得了3分，总人数的又4人得了4分，总人数的又5得了5分，其余人都得2分．已知得2分的人数和得5分的人数一样多，则有人得了4分．5．（8分）在一个长20米、宽8米、深1.6米的长方体游泳池的四壁及地面贴磁砖，磁砖是边长为0.2米的正方形，共需磁砖块．二、填空题II（每题10分，共50分）6．（10分）如图，正方形的边长是20厘米，阴影部分面积为平方厘米．（π取3.14）7．（10分）两个相同的玻璃杯，都装满了糖水，糖与水的质量比分别是1：7和1：9，现将这两杯糖水混合，混合后糖水的含糖率是%．8．（10分）一个游戏需要8人参加，分成红、黄两队，每队各4人，一对兄弟来参加这个游戏，他们俩很想被分在同一队，但是谁被编入哪个队是完全随机的，那么这对兄弟被分进同一队的可能性是．9．（10分）将数字1～9填入如图竖式的9个方格中，每个数字只能用一次，那么和的最大值为．10．（10分）军区食堂晚饭需用1000斤大米和200斤小米，军需员到米店后发现米店正在促销，“大米1元1斤，每购10斤送1斤小米（不足10斤部分不送）；小米2元一斤，每购5斤送2斤大米（不足5斤部分不送）．”军需员至少要付元钱才能买够晚饭需用的米．三、填空题III（每题12分，共60分）11．（12分）定义a□b=（a+2）（b+2）﹣2：算式1×3×5×7×9×11×13﹣（1□3□5□7□9□11）的计算结果是．12．（12分）如图中共能数出个三角形．13．（12分）甲乙两船从一条和的A、B两个码头同时出发，相向而行，甲船的静水速度比乙船的静水速度快20%，水速为乙船静水速度的10%，两船在距离中点10千米处相遇．A、B两个码头间的距离为千米．14．（12分）一个四位数，他最小的8个约数的和是43，那么这个四位回文数是．（回文数例如：1111、4334、3210123）15．（12分）小俊掷骰子游戏，刚开始他站在起点格（如表），如果他掷出1至5点，掷出几点就前进几格，如果他掷出6点或某次前进后超出终点格，则立即返回起点格；若小俊掷了四次恰好到达终点格，掷骰子的顺序有种可能．起123456789终2013年第11届“走美杯”小学数学竞赛试卷（六年级初赛B卷）参考答案与试题解析一、填空题I（每题8分，共40分）1．（8分）183×279×361﹣182×278×360的计算结果是（）A．217017B．207217C．207216D．217016【分析】把361看作360+1，原式变为=（182+1）×（278+1）×（360+1）﹣182×278×360，然后把括号展开，通过相互抵消，把剩下的部分作进一步计算，得出结果．【解答】解：183×279×361﹣182×278×360=（182+1）×（278+1）×（360+1）﹣182×278×360=182×（278+1）×（360+1）﹣182×278×360+279×361=（182×278+182）×（360+1）﹣182×278×360+279×361=182×278×360+182×278+182×360+182﹣182×278×360+279×361=182×278+182×360+182+279×361=182×（278+360+1）+279×361=182×278+182×361+279×361=50596+（182+279）×361=50596+461×361=50596+166421=217017．故选：A【点评】通过数字拆分，运用运算技巧或运算定律，进行简算．2．（8分）假设地球是个均匀的球体（半径6378千米），围绕地球赤道正上方上有一圈铁丝，铁丝的周长比地球赤道长1米，在赤道和铁丝之间会有一个缝隙，下列动物中，有5种可以安全通过铁丝．①蚂蚁；②蜜蜂；③青蛙；④老鼠；⑤猫；⑥成年奶牛；⑦大象．【分析】根据题意，因为铁丝的周长大于地球赤道的周长，所以可把铁丝的周长和地球赤道的周长看作一个圆环理解，即外圆周长比内圆周长多1米，所以可用多出的周长长度除以2π即可得到圆环的宽度，然后再根据选项进行分析选择即可．【解答】解：铁丝与赤道的缝隙宽度为：1÷2÷3.14≈0.16（米）=16（厘米），所以宽度为16厘米的缝隙，可以通过的动物有：蚂蚁、蜜蜂、青蛙、老鼠、猫，而成年奶牛和大象则不能通过．故答案为：5．【点评】解答此题的关键是把铁丝和赤道围成的图形想象成圆环的问题进行解答即可．3．（8分）将0﹣5这六个数字中的4个数字填入图的圆圈中，没条线段两端的数字作差（大或小），可以得到5个差，这5个查恰好为1﹣5．在所有满足条件的填法中，四位数ABCD （首位不能为0）的最小值是1052．【分析】要使四位数最小，那么A为1，B为0，又因为必须有一个差为5，故C、D中有一个为5，若C为5，那么D只能为2或3；若D为5，那么C无解，因此，最小值为1052．【解答】解：因为四位数ABCD最小，因此A为1，B为0；又因为必须有一个差为5，故CD中有一个为5，若C为5，那么D只能为2或3；若D为5，那么C无解；因此，最小值为1052．故答案为：1052．【点评】此题解答的关键在于抓住“四位数ABCD的值最小”以及隐含条件“有一个差为5”，进行推理，解决问题．4．（8分）一次考试中，总人数的又3人得了3分，总人数的又4人得了4分，总人数的又5得了5分，其余人都得2分．已知得2分的人数和得5分的人数一样多，则有259人得了4分．【分析】设总人数为60份，那么3分的是20份+3人，4分的是15份加4人，5分的是12份加5人，剩下2分的是13份﹣12人，5分和2分的一样多，即：13份﹣12人=12份+5人，即1份=17人，由此即可求出得4分的人数．【解答】解：设总人数为60份，那么3分的是20份+3人，4分的是15份加4人，5分的是12份加5人，剩下2分的是13份﹣12人，5分和2分的一样多，即：13份﹣12人=12份+5人即1份=17人所以4分：15×17+4=255+4=259（人）；答：则有259人得了4分．故答案为：259．【点评】此题较难，可以运用假设法，设出总人数为60份，分别用份数表示出3分、4分、5分、2分的人数，进而根据得2分的人数和得5分的人数一样多，列出等式，求出1份的人数，是解答此题的关键．5．（8分）在一个长20米、宽8米、深1.6米的长方体游泳池的四壁及地面贴磁砖，磁砖是边长为0.2米的正方形，共需磁砖6240块．【分析】由题意可知：需要贴瓷砖的面积就是水池的4个侧面的面积加上底面积，游泳池的长、宽、高已知，代入数据即可求出需要贴瓷砖的面积，再除以每块瓷砖的面积，就是所需要的瓷砖的块数．【解答】解：（20×8+20×1.6×2+8×1.6×2）÷（0.2×0.2）=（160+64+25.6）÷0.04=249.6÷0.04=6240（块）；答：共需磁砖6240块．故答案为：6240．【点评】解答有关长方体计算的实际问题，一定要搞清所求的是什么，再进一步选择合理的计算方法进行计算解答问题．二、填空题II（每题10分，共50分）6．（10分）如图，正方形的边长是20厘米，阴影部分面积为400平方厘米．（π取3.14）【分析】阴影部分的面积=以20厘米为直径两个圆的面积﹣（一个圆的面积﹣正方形的面积）．【解答】解：3.14×（20÷2）2×2﹣（3.14×202×2÷4﹣20×20）=628﹣（628﹣400）=628﹣228=400（平方厘米）故答案为：400．【点评】考查了组合图形的面积，本题解答关键是得到圆的面积．7．（10分）两个相同的玻璃杯，都装满了糖水，糖与水的质量比分别是1：7和1：9，现将这两杯糖水混合，混合后糖水的含糖率是11.25%．【分析】把每瓶糖水的重量看作单位“1”，则2瓶中的糖的重量分别为+，混合后的总重量为2，然后根据×100%=含糖率，解答即可．【解答】解：（+）÷2×100%=××100%=11.25%答：混合后糖水的含糖率是11.25%；故答案为：11.25．【点评】解答此题的关键是把每瓶糖水的重量看作单位“1”，然后根据含糖率公式进行解答即可．8．（10分）一个游戏需要8人参加，分成红、黄两队，每队各4人，一对兄弟来参加这个游戏，他们俩很想被分在同一队，但是谁被编入哪个队是完全随机的，那么这对兄弟被分进同一队的可能性是．【分析】根据题意，可知参加游戏的人共分成红、黄两队，所以这对兄弟参加这个游戏时，分法如下：哥哥分到红队、弟弟分到黄队，哥哥分到黄队、弟弟分到红队，哥哥和弟弟都分到黄队，哥哥和弟弟都分到红队，共有4种可能，其中他们俩被分在同一队有2种可能，进而求出被分进同一队的可能性是多少．【解答】解：兄弟二人分法如下：哥哥分到红队、弟弟分到黄队，哥哥分到黄队、弟弟分到红队，哥哥和弟弟都分到黄队，哥哥和弟弟都分到红队，共有4种可能；其中他们俩被分在同一队有：哥哥和弟弟都分到黄队，哥哥和弟弟都分到红队，共2种可能，所以2=；故答案为：．【点评】本题考查了简单事件发生的可能性的求解，即用“可能性=所求情况数÷总情况数”去解答．9．（10分）将数字1～9填入如图竖式的9个方格中，每个数字只能用一次，那么和的最大值为3972．【分析】要使和最大，则百位数字是9，那么上面第三个加数的最高位是3，第二个加数的最高位是8或7，若是8，则十位上相加的和不进位，则和的十位上数字最大，是7，那么还剩下1、2、4、5、6，经过计算可得：其中2+4+6=12，向前一位进1，则1+5=6，计算进位的1，是7，则上面十位上的两个方格中的数字分别是1和5，个位上的两个方格中数字分别是4和6，据此即可解答问题．【解答】解：根据题干分析可得：答：和的最大值是3972．故答案为：3972．【点评】解答此题的关键是先明确要使和最大，则百位上数字为9，由此确定千位和百位上的数字分别是3和8，那么十位上数字最大就是7，据此再根据剩下的数字特点进行分配即可解答问题．10．（10分）军区食堂晚饭需用1000斤大米和200斤小米，军需员到米店后发现米店正在促销，“大米1元1斤，每购10斤送1斤小米（不足10斤部分不送）；小米2元一斤，每购5斤送2斤大米（不足5斤部分不送）．”军需员至少要付1168元钱才能买够晚饭需用的米．【分析】仔细观察两种米的促销方法，会发现其折扣本质是相同的（如果把“10斤大米”和“5斤小米”看做一份促销品的话，那么10元钱能买到的折扣都是份促销品），故不存在多买大米好还是多买小米好的问题，只需凑足所需重量，就一定是最省的方法；设买大米x斤，小米y斤，列方程组：来估算大米与小米应买多少斤，得到大致重量：大米买950斤，小米买105斤，此时花了1160元，已有992斤大米和200斤小米，再用8元买8斤大米即可，最少用1168元．【解答】解：设买大米x斤，小米y斤，列方程组：，得到大致重量：大米买950斤，小米买105斤，此时花了1160元，已有992斤大米和200斤小米，再用8元买8斤大米即可，最少用1168元；答：军需员至少要付1168元钱才能买够晚饭需用的米．故答案为：1168．【点评】通过分析得出把“10斤大米”和“5斤小米”看做一份促销品的话，那么10元钱能买到的折扣都是份促销品，是解答此题的关键．三、填空题III（每题12分，共60分）11．（12分）定义a□b=（a+2）（b+2）﹣2：算式1×3×5×7×9×11×13﹣（1□3□5□7□9□11）的计算结果是2．【分析】根据题意得出a□b等于a与2的和乘b与2的和，再减去2，由此用此方法计算1□3□5□7□9□11的值即可．【解答】解：1□3□5□7□9□=[（1+2）×（3+2）﹣2]□5□7□9=13□5□7□□911=[（13+2）（5+2）﹣2]□7□9□11=103□7□9□11=[（103+2）（7+2）﹣2]□9□11=943□9□11=[（943+2）（9+2）﹣2]□11=10393□11=（10393+2）（11+2）﹣2=135135﹣2=135133；1×3×5×7×9×11×13﹣（1□3□5□7□9□11）=135135﹣135133=2；故答案为：2．【点评】关键是根据给出的式子，找出新的运算方法，再利用新的运算方法解决问题．12．（12分）如图中共能数出72个三角形．【分析】首先由图形可知一个小三角形组成的三角形有24个；再由两个三角形组成的有22个；由三个三角形组成的有12个；由4个三角形组成的有10个，由中间的多边形和3个三角形组成的有2个；由中间的多边形和多个三角形组成的有2个；相加即可得出答案．【解答】解：24+22+12+10+2+2=72（个）故答案为：72．【点评】考查了组合图形中三角形的计数，解答本题的关键是掌握计数原理和不在同一直线上的三点可以构成一个三角形．13．（12分）甲乙两船从一条和的A、B两个码头同时出发，相向而行，甲船的静水速度比乙船的静水速度快20%，水速为乙船静水速度的10%，两船在距离中点10千米处相遇．A、B两个码头间的距离为110千米．【分析】设水速为“1”，则乙船静水速度为10，甲船静水速度为12，若乙顺水、甲逆水，则两船在中点相遇，不符合要求．因此甲船顺水，甲的速度是13，乙的速度是9，若全程为22份，相遇时甲走了13份．因为两船在距离中点10千米处相遇，因此，2份为10千米，进而求出全程．【解答】解：水速为“1”，则乙船静水速度为10，甲船静水速度为12，若乙顺水、甲逆水，则两船在中点相遇，不符合要求．因此甲船顺水，甲的速度是13，乙的速度是9，若全程为22份，相遇时甲走了13份，因此，2份为10千米，全程为：10÷2×22=5×22=110（千米）答：A、B两个码头间的距离为110千米．故答案为：110．【点评】此题属于较难的题目，应认真分析，采用了设数法，结合推理进行解答．14．（12分）一个四位数，他最小的8个约数的和是43，那么这个四位回文数是2772．（回文数例如：1111、4334、3210123）【分析】最小的八个约数的和为43，约数首先为自然数，首先该有1和2（如果没2的话，就不会有偶约数，最小的8个奇数的和大于43），不该有5（有5的话首末位都为0）和10，而1+2+3+4+6+7+8+9=40不够43，而回文数必然是11的倍数，所以11也是这8个约数之一，把11考虑进去，就只有下面一种情形了：1+2+3+4+6+7+9+11=43，然后求出这8个数的最小公倍数即可；由此解答．【解答】解：由分析可知：约数首先为自然数，首先该有1和2，不该有5和10，而1+2+3+4+6+7+8+9=40不够43，而回文数必然是11的倍数，所以11也是这8个约数之一，把11考虑进去，则有：1+2+3+4+6+7+9+11=43，以上数的最小公倍数为：4×7×9×11=2772，正好满足要求；答：这个四位回文数是2772；故答案为：2772．【点评】明确回文数的含义：从左往右读，还是从右往左读，都是同一个数，称这样的数为“回文数”；然后根据题意，进行推导，求出这8个约数，是解答此题的关键．15．（12分）小俊掷骰子游戏，刚开始他站在起点格（如表），如果他掷出1至5点，掷出几点就前进几格，如果他掷出6点或某次前进后超出终点格，则立即返回起点格；若小俊掷了四次恰好到达终点格，掷骰子的顺序有92种可能．起123456789终【分析】从起点到终点是10号格，也就是只要掷出的和是10即可；从起点到终点可以分成三种情况，一种是没有掷出6，那么只要1～5中选择4个数的和是10即可，掷出的顺序不同的算不相同；第二种是第一次就掷出了6，然后从1～5中选择4个数的和是10即可；第三种情况第二次掷出6，第三次和第四次都掷出5；由此找出各种情况的可能，然后相加．【解答】解：情况一，没有掷出6；①1+1+3+5=10，考虑加数的位置，有12种可能；②1+1+4+4=10，考虑加数的位置，有6种可能；③1+2+2+5=10，考虑加数的位置，有12种可能；④1+2+3+4=10，考虑加数的位置，有24种可能；⑤1+3+3+3=10，考虑加数的位置，有4种可能；⑥2+2+3+3=10，考虑加数的位置，有6种可能；⑦2+2+2+4=10，考虑加数的位置，有4种可能；一共有12+6+12+24+4+6+4=68种可能；情况二，第一次就掷出了6，剩下3个数的和是10；①1+5+4=10，考虑加数的位置，有6种可能；②2+5+3=10，考虑加数的位置，有6种可能；③2+4+4=10，考虑加数的位置，有3种可能；④3+4+3=10，考虑加数的位置，有3种可能；一共有6+6+3+3=18种可能；第三种情况第二次掷出6，第三次和第四次都掷出5；那么第一次可以是1～6，就有6种可能；68+18+6=92（种）答：掷骰子的顺序有92种可能．故答案为：92．【点评】本题较复杂，解决本题要细心，正确的分类，然后逐步根据排列的方法和加法原理进行求解．。

2014第十二届希望杯初赛六年级(含解析)

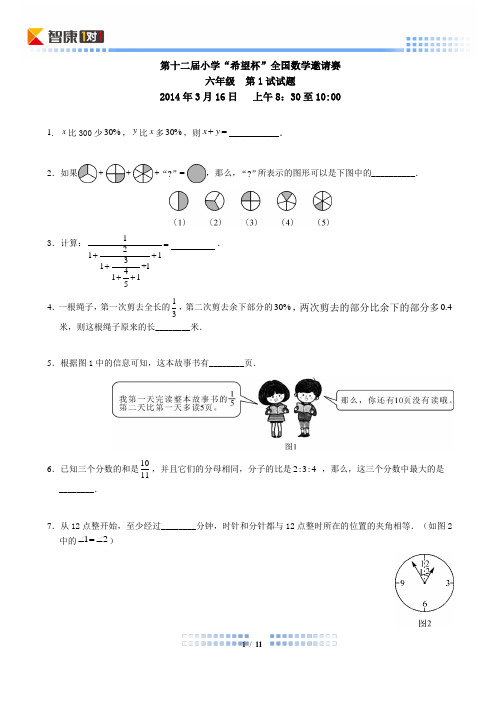
第十二届小学“希望杯”全国数学邀请赛六年级第1试试题2014年3月16日上午8：30至10:001．x 比300少30%，y 比x 多30%，则x y +=__________． 2．如果+++?“”=，那么，?“”所表示的图形可以是下图中的__________．3．计算：121131+14115=+++++ ． 4．一根绳子，第一次剪去全长的13，第二次剪去余下部分的30%，两次剪去的部分比余下的部分多0.4米，则这根绳子原来的长________米．5．根据图1中的信息可知，这本故事书有________页．6．已知三个分数的和是1011，并且它们的分母相同，分子的比是2:3:4 ，那么，这三个分数中最大的是________．7．从12点整开始，至少经过________分钟，时针和分针都与12点整时所在的位置的夹角相等．（如图2中的12∠=∠）8．若三个不同的质数的和是53，则这样的三个质数有________组．9．被11除去7，被7除去5，并且不大于200的所有自然数的和是________．10．在救灾捐款中，某公司有110的人各捐款200元，有34的人各捐款100元，其余人各捐款50元，则该公司人均捐款________元．11．如图3，圆P 的直径OA 是圆O 的半径，⊥OA BC ；10OA =,则阴影部分的面积是________．（π 取3）12．如图4，一个直径为1厘米的圆找遍长为2厘米的正方形滚动一周后回到原来的位置，在这个过程中，圆面覆盖过的区域（阴影部分）的面积是________平方厘米（π取3）13．如图5，一个长方形的长和宽的比是5:3．如果长方形的长减少5厘米，宽增加3厘米，那么，这个长方形就变成一个正方形．则原长方形的面积是________平方厘米．14．一次智力测试由5道判断对错的题目组成，答对一题得20分，答错或不答得0分．小花在答题时每道题都是随意答“对”或“错”，那么，她得60分或60分以上的概率是________%．15．如图6，一个底面直径是10厘米的圆柱形容器装满水，先将一个底面直径是8厘米的圆锥形铁块放入容器中，铁块全部浸入水中，再将铁块取出，这时水面的高度下降了3.2厘米，则圆锥形铁块高________厘米．16．甲挖了一条水渠总长度的14，第二天挖了剩下水渠长度的521，第三天挖了未挖水渠长度的12，第四天挖完了最后剩下的100米水渠．则这条水渠长________米．17．用1024个棱长是1的小正方体组成体积是1024的一个长方体，将这个长方体的六个面都涂上颜色，则六个面都没有涂色的小正方体最多有________个．18．如图7，已知2AB =，3BG =,4GD =,5ED =,BCG ∆和EFG ∆的面积和是24，AGF ∆和CDG ∆的面积和是51，则ABC ∆与DEF ∆的面积和是________．19．甲、乙两人分别从A 、B 两地同时出发，相形而行，甲、乙的速度比是5:3，两人相遇后继续行进，甲到达B 地、乙到达A 地后都立即沿原路返回．若两人第二次相遇的地点距第一次相遇的地点50千米，则A 、B 两地相距A ________千米．20．在1,2,3,50中，任取10个连续的数，则其中恰有3个质数的概率是________．第十二届小学“希望杯”全国数学邀请赛六年级第1试试题参考答案1 2 3 4 5 6 7 8 9 10483 （3）431146 25 40997201311 351 102．511 12 13 14 15 16 17 18 19 2075 11 240 50%15 350 504 23 144 2241部分详解1．x比300少30%，y比x多30%，则x y+=__________．【考点】计算，百分数计算【难度】☆【答案】483【分析】根据题意，()300130%210x=⨯-=，()130%y x=+，所以()210130%273y=⨯+=，所以210273483x y+=+=．2．如果+++?“”=，那么，?“”所表示的图形可以是下图中的__________．【考点】计算，分数计算【难度】☆【答案】（3）【分析】观察图形就可以发现，111+++=1346⨯圆圆圆未知圆，所以1111=1---=4364未知，结果为14圆．3．计算：121131+14115=+++++　．【考点】计算，繁分数计算【难度】☆【答案】43 114【分析】原式1111143====== 222281141141++11++11++11++1315434343 1++11++11414145．4．一根绳子，第一次剪去全长的13，第二次剪去余下部分的30%，两次剪去的部分比余下的部分多0.4米，则这根绳子原来的长米．【考点】应用题，分数应用题【难度】☆☆【答案】6【分析】第二次剪去了全长的11%=35⎛⎫⨯⎪⎝⎭1-30，两次共剪去了全长的118+=3515，余下8711515-=，故全长为870.461515⎛⎫÷-=⎪⎝⎭．5．根据图1中的信息可知，这本故事书有页．【考点】分数应用题【难度】☆☆【答案】25页【分析】假如这本书一共x页，则1151055x x x+++=，解得25x=页．6．已知三个分数的和是1011，并且它们的分母相同，分子的比是2:3:4，那么，这三个分数中最大的是．【考点】分数应用题，比例【难度】☆☆【答案】4099【分析】假设分数的分母为y ，分子分别为2x ，3x ，4x ，根据题意2341011x x x y y y ++=，所以解出最大分数为44099x y =．7．从12点整开始，至少经过分钟，时针和分针都与12点整时所在的位置的夹角相等（如图2中的12∠=∠【考点】时钟问题【难度】☆☆ 【答案】72013分【分析】分针走一小时为360度，时针走一小时为30度，假设所走时间为t 小时，若角度相同，则30360360t t =-，解得12720=1313t =小时分．8．若三个不同的质数的和是53，则这样的三个质数有组．【考点】计数，分类枚举，数论【难度】☆☆ 【答案】11组【分析】53以内的质数共有15个，可列举()4157++，()37313++，()37511++，()31319++，()31517++，()29519++，()29717++，()291113++，()231119++，()231317++，()4337++共11组．9．被11除去7，被7除去5，并且不大于200的所有自然数的和是．【考点】数论，余数问题【难度】☆☆ 【答案】351【分析】假设a ，b 均分别为除数，则这个数就为117a +，75b +且11775a b +=+，得到7112b a =+．通过试数，当至少3a =，5b =时可使等式成立，即当3a =，10a =，17a =时，满足题意，那么只有三个数满足题意，即40，117，194，三者的和是351．10．在救灾捐款中，某公司有110的人各捐款200元，有34的人各捐款100元，其余人各捐款50元，则该公司人均捐款元．【考点】方程解应用题，分数应用题，平均数问题【难度】☆☆ 【答案】102．5【分析】设公司共有a 人，则根据题意有该公司人家呢捐款钱数为：1313200100150102.5104104a a a a ⎡⎤⎛⎫⨯+⨯+--⨯÷= ⎪⎢⎥⎝⎭⎣⎦11．如图3，圆P 的直径OA 是圆O 的半径，⊥OA BC ；10OA =,则阴影部分的面积是．（π 取3）【考点】几何，圆与扇形【难度】☆☆ 【答案】75【分析】阴影部分的面积=大圆面积的一半-小圆面积22131035752=⨯⨯-⨯=．12．如图4，一个直径为1厘米的圆找遍长为2厘米的正方形滚动一周后回到原来的位置，在这个过程中，圆面覆盖过的区域（阴影部分）的面积是平方厘米（π 取3）【考点】圆与扇形之旋转与覆盖【难度】☆☆ 【答案】11【分析】由题意和图形可知，阴影部分的面积等于四个角的四个14圆的面积（即一个半径为1圆的面积）加上上下左右四个小长方形的面积（小长方形的长为2，宽为1）则，23121411=⨯+⨯⨯=阴影部分的面积（平方厘米）．13．如图5，一个长方形的长和宽的比是5:3 ．如果长方形的长减少5厘米，宽增加3厘米，那么，这个长方形就变成一个正方形．则原长方形的面积是平方厘米．【考点】图形变换和列方程解应用题【难度】☆☆ 【答案】240平方厘米【分析】设长方形的长为5a ，宽为3a ．则根据题意有：5533a a -=+，解方程得4a =，则长方形的长为20厘米，宽为12厘米，则原长方形的面积为2012240⨯=（平方厘米）．14．一次智力测试由5道判断对错的题目组成，答对一题得20分，答错或不答得0分．小花在答题时每道题都是随意答“对”或“错”，那么，她得60分或60分以上的概率是 % ．【考点】计数，概率【难度】☆☆☆ 【答案】50%【分析】根据题意可知，要想得到60分或60分以上则应该答对3道或4道或5道题，答对3道题的概率为：从5道题里面选3道题答对有10种情况，则概率为51102⎛⎫⨯ ⎪⎝⎭；答对4道题的概率为：从5道题里选4道答对有5种情况，则概率为5152⎛⎫⨯ ⎪⎝⎭；答对5道题的概率为：从5道题中选5道答对有1种情况，则概率为5112⎛⎫⨯ ⎪⎝⎭，则得60分或60分以上的概率为：()51105150%2⎛⎫++⨯= ⎪⎝⎭．15．如图6，一个底面直径是10厘米的圆柱形容器装满水，先将一个底面直径是8厘米的圆锥形铁块放入容器中，铁块全部浸入水中，再将铁块取出，这时水面的高度下降了3.2 厘米，则圆锥形铁块高________厘米．【考点】立体图几何，圆柱与圆锥的体积计算【难度】☆☆☆ 【答案】15厘米【分析】设圆锥形铁块的高为h 厘米，由题意知圆柱下降的体积为圆锥的体积，则有221π5 3.2π43h ⨯⨯=⨯⨯⨯，解得15h =（厘米）．16．甲挖了一条水渠总长度的14 ，第二天挖了剩下水渠长度的521 ，第三天挖了未挖水渠长度的12，第四天挖完了最后剩下的100 米水渠．则这条水渠长米．【考点】分数应用题，倒退法【难度】☆☆ 【答案】350米【分析】第四天挖的100米为第三天的11122-=，所以第三天挖时水渠共长11002002÷=（米），第三天的长度的等于第二天的51612121-=，所以第二天挖时水渠长16200262.521÷=（米），第二天的长度等于第一天的13144-=，所以第一天水渠长3262.53504÷=（米）．17．用1024个棱长是1的小正方体组成体积是1024的一个长方体，将这个长方体的六个面都涂上颜色，则六个面都没有涂色的小正方体最多有个．【考点】立体几何【难度】☆☆ 【答案】504个【分析】若想让没有染色的小正方形个数最多，则应保证组成的长方形尽可能的接近正方形，即长方形的长宽高应该尽可能的接近由于长方形的体积为1024，且长宽高都为整数，则长宽高应该分别是8,8,16在这种情况下，除了最外面一层的小正方形被染色外，里面的小正方形均未被染色,则未被染色的部分体积6614504=⨯⨯=，则，没有被染色的小正方形的个数为5041504÷=（个）18．如图7，已知2AB =，3BG =,4GD =,5ED =,BCG ∆和EFG ∆的面积和是24，AGF ∆ 和CDG ∆ 的面积和是51，则ABC ∆与DEF ∆的面积和是．【考点】平面几何，三角形等积变形【难度】☆☆☆ 【答案】23【分析】设BCG ∆的高为a ，EFG ∆的高为b ，则根据题意得()()134242195512a b a b ⎧⨯+=⎪⎪⎨⎪+=⎪⎩，解得：86a b =⎧⎨=⎩，则ABC ∆与DEF ∆的面积和11112856232222AB a ED b =⨯⨯+⨯⨯=⨯⨯+⨯⨯=．19．甲、乙两人分别从A 、B 两地同时出发，相形而行，甲、乙的速度比是5:3，两人相遇后继续行进，甲到达B 地、乙到达A 地后都立即沿原路返回．若两人第二次相遇的地点距第一次相遇的地点50千米，则A 、B 两地相距A 千米．【考点】行程，多次相遇问题【难度】☆☆☆ 【答案】100千米【分析】由于甲乙两人的速度比为5:3，若把AB 分为8份，则第一次相遇时甲乙走了一个AB 的长，其中甲走了5份，乙走了3份，此时的相遇点在下图中的C 点处；相遇之后两人继续行进，则易知第二次相遇的时候两人共走了3个AB 的全长，其中甲走了15份，乙走了9份，则可以知道甲乙第二次相遇的地点在D 处，由于15DC =(千米)，可知4份的长度为50千米，由于AB 全长为8份，则100AB =千米．20．在1,2,3,50中，任取10个连续的数，则其中恰有3个质数的概率是．【考点】质数的判断，计数综合【难度】☆☆☆ 【答案】2241【分析】在1至50的数中共有15个质数，任意连续的10个数排列的共有41种情况（以1—9为开始，41—50结束），那么列举其中的3个质数的组合分别为：11 / 116—15,7—16,8—17,9—18,12—21,13—22,14—23,15—24,16—25,17—26,22—31,23—32,28—37,29—38，34—43,35—44，36—45,37—46,38—47，39—48,40—49,41—50,共22组三个质数的连续10个数．所以概率为2244．。

【试卷】2014年第12届“走美杯”小学数学竞赛试卷(四年级初赛B卷)_234873

2014年第12届“走美杯”小学数学竞赛试卷（四年级初赛B卷）一、填空题Ⅰ（每题8分，共40分）1．（8分）计算：47167×61×7=．2．（8分）4个人排成一排，有种不同的排法．3．（8分）我们知道0、1、2、3、…叫做自然数．只能被1和自身整除的大于1的自然数叫做质数或者素数，比如2、3、5、7、11等．按照从小到大的顺序，第10个质数是．4．（8分）昊宇写好了三封信和三个信封，要将每封信放入相应的信封中，一个信封只放入一封信．三封信中至少有一封信被装错的所有可能情形有种．5．（8分）“24 点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52 张扑克牌（不包括大小王）中抽取4 张，用这4 张扑克牌上的数字（A=1，J=11，Q=12，K=13）通过加减乘除四则运算得出24，先找到算法者获胜．游戏规定4 张牌扑克都要用到，而且每张牌只能用1次，比如2、3、4，Q，则可以由算法（2×Q）×（4﹣3）得到24．如果在一次游戏中恰好抽到了9、7、3、2，则你的算法是．二、填空题Ⅱ（每题10分，共50分）6．（10分）将一个正方形纸片按照如图所示方式折叠两次后再对折，沿对折线剪开，得到个小正方形纸片．7．（10分）将一根长80厘米的细绳对折两次后，用剪刀在中点处剪开，取其中长度最长的与最短的各一段，这两段绳的绳长之和是厘米．8．（10分）图中有个平行四边形．9．（10分）古希腊的数学家们将自然数按照以下方式与多边形联系起来，定义了多边形数：三角形数：1、3、6、10、15…四边形数：1、4、9、16、25…五边形数：1、5、12、22、35…六边形数：1、6、15、28、45……则按照上面的顺序，第6个五边形数为．10．（10分）用180°与五边形的每一个内角作差，所得到的值叫做这个内角的角亏．如图所示五边形所有内角角亏之和为度．三、填空题III（每题12分，共60分）11．（12分）少年宫春季书法班、美术班、器乐班招生．书法班招收了29名学员，美术班招收了28名学员，器乐班招收了27名学员．在这些学员中，既报书法又报美术的有13名，既报书法又报器乐的有12人，既报美术又报器乐的有11名，三个科目都报的有5名．那么，只参加一个科目学习的学员有名．12．（12分）日常生活中经常使用十进制来表示数，要用10 个数码：0、1、2、3、4、5、6、7、8、9．在电子计算机中用二进制，只要用两个数码0和1．正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进1”，于是，可以得到以下自然数的十进制与二进制表示对了1+1=10，十进制的3在二进制中变成了10+1=11，…那么，二进制中的“111100”用十进制表示是．13．（12分）将图中的圆圈染色．要求有连线的两个相邻的圆圈染不同的颜色，则最少需要种颜色．14．（12分）有一个两人游戏，游戏道具为一支笔和一张白纸，游戏过程为两人轮流在白纸上写数字、用抓阄或者猜叮壳等方式确定谁先写．把先写的一方称为先手方，后写的一方称为后手方，游戏规则如下：先手方首先选择在白纸上写下1或2，先手方完成之后，后手方在先手方写下的数字上选择加1 或者加2，将选择后计算的结果写在白纸上，双方依照这个规则轮流一次写下自己的数字，先写到22的人获胜．这个游戏先手方是有必胜策略的，如果要取胜，先手方从第一轮开始到取胜分别写下的数字为．15．（12分）在如图的3×3方格中分别填入1、2、3、4、5、6、7、8、9，使横、竖、对角线上的任意三个方格中的数字之和相等．2014年第12届“走美杯”小学数学竞赛试卷（四年级初赛B卷）参考答案与试题解析一、填空题Ⅰ（每题8分，共40分）1．（8分）计算：47167×61×7=20140309．【解答】解：47167×61×7=2877187×7=20140309．故答案为：20140309．2．（8分）4个人排成一排，有24种不同的排法．【解答】解：4×3×2×1=24（种）答：有24 种不同的排法．故答案为：24．3．（8分）我们知道0、1、2、3、…叫做自然数．只能被1和自身整除的大于1的自然数叫做质数或者素数，比如2、3、5、7、11等．按照从小到大的顺序，第10个质数是29．【解答】解：质数从小到大有：2、3、5、7、11、13、17、19、23、29…．所以按照从小到大的顺序，第10个质数是29．故答案为：29．4．（8分）昊宇写好了三封信和三个信封，要将每封信放入相应的信封中，一个信封只放入一封信．三封信中至少有一封信被装错的所有可能情形有5种．【解答】解：三封信分别放入三个信封，一个信封只放一封信，一共有3×2×1=6（种），三封信对应装对的情形只有一种，至少有一封信被装错的所有可能情形有6﹣1=5（种）．故答案为：5．5．（8分）“24 点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52 张扑克牌（不包括大小王）中抽取4 张，用这4 张扑克牌上的数字（A=1，J=11，Q=12，K=13）通过加减乘除四则运算得出24，先找到算法者获胜．游戏规定4 张牌扑克都要用到，而且每张牌只能用1次，比如2、3、4，Q，则可以由算法（2×Q）×（4﹣3）得到24．如果在一次游戏中恰好抽到了9、7、3、2，则你的算法是（7﹣2）×3+9．【解答】解：（7﹣2）×3+9=15+9=24故答案为：（7﹣2）×3+9．二、填空题Ⅱ（每题10分，共50分）6．（10分）将一个正方形纸片按照如图所示方式折叠两次后再对折，沿对折线剪开，得到4个小正方形纸片．【解答】解：严格按照图中的顺序向左上对折，再右上对折，沿对折线剪开，展开得到相同4个相同的正方形；故答案为：4．7．（10分）将一根长80厘米的细绳对折两次后，用剪刀在中点处剪开，取其中长度最长的与最短的各一段，这两段绳的绳长之和是30厘米．【解答】解：对折2次，从中间剪断，绳子变成5段，即22+1=5，其中3段长的，2段短的，长的是这根绳子的的，短的是这根绳子的的；长的一段为：80××=20（厘米）短的一段为：80××=10（厘米）20+10=30（厘米）答：这两段绳的绳长之和是30厘米；故答案为：30．8．（10分）图中有13个平行四边形．【解答】解：根据题干分析可得：8+4+1=13（个）答：一共有13个平行四边形．故答案为：13．9．（10分）古希腊的数学家们将自然数按照以下方式与多边形联系起来，定义了多边形数：三角形数：1、3、6、10、15…四边形数：1、4、9、16、25…五边形数：1、5、12、22、35…六边形数：1、6、15、28、45……则按照上面的顺序，第6个五边形数为51．【解答】解：因为：5﹣1=4，12﹣5=7，22﹣12=10，35﹣22=13，所以下一个相差16，16+35=51故答案为：51．10．（10分）用180°与五边形的每一个内角作差，所得到的值叫做这个内角的角亏．如图所示五边形所有内角角亏之和为360度．【解答】解：（180°﹣∠A）+（180°﹣∠B）+（180°﹣∠C）+（180°﹣∠D）+（180°﹣∠E）=180°×5﹣（∠A+∠B+∠C+∠D+∠E）=900°﹣（5﹣2）×180°=900°﹣540°=360°故答案为：360°．三、填空题III（每题12分，共60分）11．（12分）少年宫春季书法班、美术班、器乐班招生．书法班招收了29名学员，美术班招收了28名学员，器乐班招收了27名学员．在这些学员中，既报书法又报美术的有13名，既报书法又报器乐的有12人，既报美术又报器乐的有11名，三个科目都报的有5名．那么，只参加一个科目学习的学员有27名．【解答】解：总人数为：29+28+27﹣13﹣12﹣11+5=53（人），53﹣13﹣12﹣11+5×2=27（人），答：只参加一个科目学习的学员有27名．故答案为：27．12．（12分）日常生活中经常使用十进制来表示数，要用10 个数码：0、1、2、3、4、5、6、7、8、9．在电子计算机中用二进制，只要用两个数码0和1．正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进1”，于是，可以得到以下自然数的十进制与二进制表示对了1+1=10，十进制的3在二进制中变成了10+1=11，…那么，二进制中的“111100”用十进制表示是60．【解答】解：二进制中的“111100”用十进制表示是：1×25+1×24+1×23+1×22+0×21+0=32+16+8+4+0+0=60故答案为：60．13．（12分）将图中的圆圈染色．要求有连线的两个相邻的圆圈染不同的颜色，则最少需要3种颜色．【解答】解：一方面，显然对于一个五边形，2种颜色不能保证要求；另一方面，如图所示，3种颜色是可以的．因此最少需要3种颜色．故答案为：3．14．（12分）有一个两人游戏，游戏道具为一支笔和一张白纸，游戏过程为两人轮流在白纸上写数字、用抓阄或者猜叮壳等方式确定谁先写．把先写的一方称为先手方，后写的一方称为后手方，游戏规则如下：先手方首先选择在白纸上写下1或2，先手方完成之后，后手方在先手方写下的数字上选择加1 或者加2，将选择后计算的结果写在白纸上，双方依照这个规则轮流一次写下自己的数字，先写到22的人获胜．这个游戏先手方是有必胜策略的，如果要取胜，先手方从第一轮开始到取胜分别写下的数字为2，5，8，11，14，17，20，22．【解答】解：先手方从第一轮开始到取胜，写数字2，对方如果加1，那么自己在此基础上加2，（对方如果加2，那么自己在此基础上加1）写出的数字为：2，5，8，11，14，17，20，22．故答案为：2，5，8，11，14，17，20，22．15．（12分）在如图的3×3方格中分别填入1、2、3、4、5、6、7、8、9，使横、竖、对角线上的任意三个方格中的数字之和相等．【解答】解：根据分析，可得。

2014.6六年级语文期末试卷参考答案

小学语文六年级学业水平测试评分标准与参考答案一、积累与运用(30分)1．满分为5分。

书写规范美观、行款整齐，得5～4分；书写比较规范、注意行款，得3～2；书写较差，行款不整齐，得1～0分。

2．满分为4分，每小题2分。

（1）C（2）B3．满分为4分，每小题2分。

（1）C （2）D4．满分为2分，答案是B。

5．满分为4分，写对一个得2分，答案是A和C。

6．满分为11分，每空为1分，错别字累计4个扣1分，第7小题不作评分要求。

参考答案：（1）只流清气满乾坤。

（2）燕山月似钩。

（3）家祭无忘告乃翁。

（4）醉里吴音相媚好。

（5）会当凌绝顶。

（6）闻过则喜。

（7）草茸茸。

（8）有教无类。

（9）以友辅仁。

桃花潭水深千尺，不及汪伦送我情；孤帆远影碧空尽，唯见长江天际流。

符合条件都可以。

二、阅读与理解（40分）（一）一粒橡子的奇遇（16分）7．分值为4分，每小题2分。

（1）破晓：天刚亮。

有天亮的意思即可得满分。

（2）蚕食：文中指橡树苗被森林中的虫子像蚕吃桑叶那样一点一点吃掉。

有慢慢或一点点吃掉的意思即可得满分。

8．分值为5分，每空1分。

参考答案：（1）过渡句；承上启下。

错字不扣分。

（2）不容易的事或日复一日，年复一年；藤蔓缠绕；冰天雪地；火烧火燎。

9．分值为4分。

评分要求：能具体的、语句通顺地描绘一个场景即可得满分。

10．分值3分。

参考答案：（1）“橡树只有死亡，最后变成营养丰富的泥土，为新的树提供营养，才能改变现在的衰老和疲倦。

”（2）“使它变得比现在更大的唯一方式就是奉献，将自己的生命通过死亡化成营养丰富的泥土，让下一代小树长得更茁壮。

”（3）“大橡树只有死去才会变得更大，因为它能变成营养丰富的泥土。

”（4）要想变得比现在更强大就只有死亡，这样生命才能得以轮回。

（5）“他死后就会变成大地，而土地是很大的。

”等等。

能抓住“现在”与“死亡”谈自己的理解即可得满分。

如果学生这样答只能得1~2分：“它现在正在一步步枯萎，如果想比现在更大，只有死亡”可得2分；“死亡就是它变得比现在更伟大的唯一方式”没能围绕“死亡”与“现在”谈看法只能得1分。

第十二届“走美杯”数学解题技能初赛试题及答案(三年级)

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛注意事项:1．请在密封线内填好有关信息. 总分2．不允许使用手机、计算器等电子设备.小学三年级试卷（A 卷）填空题I（每题8 分，共40 分）1. 2⨯(99981+19⨯38)=2. 3 个人排成一排，有种不同的排法？3. 我们知道0,1,2,3,……叫做自然数，只能被1 和自身整除的大于1 的自然数叫做质数或素数，比如2,3,5,7,11 等，按照从小到大的顺序，第8 个质数是.4. “24 点”游戏时很多人熟悉的数学游戏，游戏过程如下：任意从52 张扑克牌（不含大小王）中抽取4 张，用这4 张扑克牌上的数字（从1 到13，其中A=1，J=11，Q=12，K=13）通过加减乘除四则运算法则运算得出 24，最先找到算法的人获胜。

游戏规定 4 张扑克牌都要用到，而且每张牌只能用一次，比如2，3，4，Q，则可以由算法(2⨯Q)⨯(4 -3)得到24. 如果在一次游戏中恰好抽到了 4，8，8，8，则你的算法是：.5. 自然数1，2，…，50 中，被3 除余1 的数有个。

填空题II（每题10 分，共50 分）6. 下图中有个正方形。

7. 将一根长80 厘米的细绳对折一次后，用剪刀在中点处剪开，其中最长的一段绳长是厘米。

8. 将一个面积为36 平方厘米的正方形纸片按照下图所示方式折叠两次后对折，沿对折线剪开，得到的长方形纸片中面积最大的为平方厘米。

9. 古希腊的数学家们将自然数据按照以下方式与多边形联系起来，定义了多边形数：三边形数：1,3,6,10,15，…… 四边形数：1,4,9,16,25，…… 五边形数：1,5,12,22,35，…… 六边形数：1，6,15,28,45，…………则按照上面的顺序，第8 个三边形数为10. 将下图中的圆圈染色，要求有连线的两个相邻的圆圈染不同的颜色，则至少需要种颜色。

填空题III（每题12 分，共60 分）11. 2015 年1 月1 日是星期四，根据这一信息，可以算出2015 年2 月1 日是星期.12. 用1 颗红珠子，2 颗蓝珠子，2 颗绿珠子串成一个手链，可以串成种不同的手链。

第十二届“走美杯”数学解题技能初赛试题及答案(四年级)

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛注意事项:1．请在密封线内填好有关信息. 总分2．不允许使用手机、计算器等电子设备.小学四年级试卷（A 卷）填空题I（每题8 分，共40 分）1. 计算：47167×61×7=。

2. 4 个人排成一排，有种不同的排法。

3. 我们知道0,1,2,3，……叫做自然数。

只能被1 和自身整除的大于1 的自然数叫做质数或者素数，比如2,3,5,7,11 等。

按照从小到大的顺序，第10 个质数是.4. 吴宇写好了三封信和三个信封，要将每封信放入相应的信封中，一个信封只放入一封信，三封信中至少有一封信被装错的所有可能情形有种.5. “24 点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52 张扑克牌（不包括大小王）中抽取4 张，用这4 张扑克牌上的数字（A=1，J=11，Q=12，K=13）通过加减乘除四则运算得出24，先找到算法者获胜。

游戏规定4 张牌扑克都要用到，而且每张牌只能用1 次，比如 2,3,4，Q，则可以由算法（2×Q）×（4-3）得到 24.如果在一次游戏中恰好抽到了9,7,3,2，则你的算法是。

填空题II（每题10 分，共50 分）6. 将一个正方形纸片按照下图所示方式折叠两次后再对折，沿对折线剪开，得到个小正方形纸片。

7. 将一根长 80 厘米的细绳对折一次后，用剪刀在中点处剪开，取其中长度最长的与最短的各一段，这两段绳的绳长之和是厘米。

8. 下图中有个平行四边形。

9、古希腊的数学家们将自然数按照以下方式与多边形联系起来，定义了多边形数：三角形数：1,3,6,10,15…… 四边形数：1,4,9,16,25…… 五边形数：1,5,12,22,35……六边形数：1,6,15,28,45…………则按照上面的顺序，第6 个五边形数为。

10. 用 180°与四边形的每一个内角作差，所得到的值叫做这个内角的角亏。

人教部编版六年级上册数学期末检测AB卷试题及答案

期末检测A卷时间：90分钟满分：100分一、基础训练营(39分)1．用“——”给加点字选择正确的读音。

(6分)强．迫(qiǎng qiáng)模．样(mómú)倒．映(dǎo dào)晕．车(yùn yūn)提供．(gòng gōng)内蒙．古(měng méng) 2．读拼音，写词语。

(8分)3．在下列各句中的两个错别字下画横线，并改正在括号中。

(8分)(1)边源都参差如夏云头，镶着日光，发出水银色陷。

()()(2)魁悟的渔夫拖着被斯破了的渔网走进来。

()()(3)我一边想，一边在屋里走来走去，带上雨帽，又抖抖子，把雨衣弄得窸窸窣窣响。

()()(4)徽波粼粼的海面上，刹时间洒满了银光。

()()4．用“√”标出下列词语中加点字最恰当的解释。

(4分)(1)全神贯．注A．连贯。

B．贯通。

(2)居高临．下A．靠近；对着。

B．来到。

(3)一筹．莫展A．筹划。

B．计策；办法。

(4)一望无际．A．彼此之间。

B．靠边的或分界的地方。

5．下面句子中加点词使用不恰当的一句是()(2分)A．游客们常常为此陶醉不已，流连忘返．．．．。

B．西双版纳曾经有过唯我独尊．．．．的象兵。

C．“十一”长假，街上车水马龙．．．．。

．．．．，游人络绎不绝6．判断。

(对的打“√”，错的打“×”)(3分)(1)“他像一座山。

”这是一个比喻句，把“他”比作“一座山。

”()(2)“这些木雕艺术品太美了，真是________。

”横线处可以填入“余音绕梁”。

()(3)“我那时并不知道这所谓猹的是怎么一件东西——便是现在也没有知道——只是无端的觉得状如小狗而很凶猛。

”句中的破折号的作用是解释说明。

()7．按要求完成句子练习。

(8分)(1)我们只有一个地球。

我们要保护地球。

(用恰当的关联词合成一句话) _________________________________________________________ (2)这个故事怎能不使人感动得落泪呢？(改为陈述句)_________________________________________________________ (3)通过老师的介绍，使我对京剧产生了极大的兴趣。

第十二届“走美杯”数学解题技能初赛试题及答案(六年级)

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛注意事项:1．请在密封线内填好有关信息. 总分2．不允许使用手机、计算器等电子设备.小学六年级试卷（A 卷）填空题I（每题8 分，共40 分）1．计算：20140309= .7 ⨯101⨯ 4672．现有含食盐6%的盐水92 千克，如果将盐水的浓度提高到8%，需要再加入盐千克。

3．像2，3，5，7 这样的只能被1 和自身整除的大于1 的自然数叫做质数或者素数。

每一个自然数都能写成若干个（可以相同）质数的乘积，比如，4=2×2，6=2×3，8=2×2×2，9=3×3，10=2×5 等，那么 1938 写成这种形式为 .4．某班有 3 名学生参加数学解题技能展示选拔赛，那么，可能出现的入选情形一共有种.5．“24 点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52 张扑克牌（不包括大小王）中抽取4 张，用这4 张扑克牌上的数字（A=1，J=11，Q=12，K=13）通过加减乘除四则运算得出24，最先找到算法者获胜，游戏规定4 张拍扑克都要用到，而且每张牌只能用 1 次，比如 2，3，4，Q，则可以由算法(2⨯Q)⨯(4 - 3)得到 24. 王亮在一次游戏中抽到了K，9，1，1，他发现K + 9 +1+1 = 24 ，如果将这种能够直接相加得到24 的4 张牌称为“友好牌组”，那么，含有Q 的不同“友好牌组”共有组。

填空题II（每题10 分，共50 分）6．在中国古代数学中，两个形状相同的圆柱以垂直方向互相穿插，如图所示，中间重合部分所构成的几何体称为牟合方盖，从正上方俯视牟合方盖，看到的图形为。

7. 如图所示的图形由1 个大的半圆弧和6 个小的半圆弧围成，已知最大的半圆弧的直径为1，则这个图形的周长为（用圆周率π表示）。

8. 如图所示，已知大圆的半径为2，则阴影部分II 的面积为。

2014走美杯B卷试题

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学五年级试卷（B卷）填空题Ⅰ（每题8分，共40分）1．计算：20140601=13×（1000000+13397×________）2．5个人围坐在一张圆桌就餐，有_________种不同的坐法．3．像2,3,5,7 这样的只能被1和自身整除的大于1的自然数叫做质数或者素数。

每一个自然数都能写成若干个质数（可以相同）的乘积，比如，4=2×2，6=2×3，8=2×2×2，9=3×3，10=2×5等，那么2×3×5×7-1写成这种形式为_________．4．一个自然数，它是5和7的倍数，并且被3除余1，满足这些条件的最小的自然数是_________种．5．“24点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52张扑克牌(不包括大小王)中抽取4张，用这4张扑克牌上的数字（1,11,12,13====）通过加减乘除四则运算得出24，最先找到算法者A J Q K取胜．游戏规定4张扑克牌都要用到，而且每张牌只能用一次，比如2，3，4，Q，则可以由算法(2)(43)⨯⨯-Q 得到24．王亮在一次游戏中抽到了8，8，7，1，他发现887124+++=，如果将这种能够直接相加得到24 的4 张牌称为“友好牌组”，那么，含有最大数字为8 的不同“友好牌组”共有_________组．填空题Ⅱ（每题10分，共50分）6．如图由一些棱长为1的单位小立方体构成，一共有_________个小立方体．7．下图中有_________个平行四边形．8．用2种颜色对一个2×2棋盘上的4个小方格染色，有_________种不同的染色方案．9．古希腊的数学家们将自然数按照以下方式与多边形联系起来，三边形数：1，3，6，10，15，…… 四边形数：1，4，9，16，25，…… 五边形数：1，5，12，22，35，…… 六边形数：1，6，15，28，45，……按照上面的顺序，第8个六边形数为_________．10．边长为a b +的正方形纸片有以下两种剪裁方法，按照“等量减等量差相等”的原则，阴影部分所表示的三个小正形的面积之间的关系可以用,,a b c 表示为_________．填空题Ⅲ（每题12分，共60分）11．将1到16的自然数排成44⨯的方阵，每行每列以及对角线上数的和都等于34，这样的方阵称为4阶幻方，34称为4阶幻方的幻和．10阶幻方的幻和等于_________．12．吴宇写好了四封信和四个信封，要将每封信放入相应的信封中，一个信封只放入一封信，四封信全部被装错的情形有_________种．13．日常生活中经常使用十进制来表示数．要用10个数码：0，1，2，3，4，5，6，7，8，9．在电子计算机中用二进制，只要两个数码0和1，正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进cc c bababa cbaaaabbbba1”，于是，可以得到一下自然数的十进制与二进制表示对照表：十进制0 1 2 3 4 5 6 7 8 …二进制0 1 10 11 100 101 110 111 1000 …十进制的0在二进制中还是0，十进制的1在二进制中还是1，十进制的2在二进制中变成了1+1=10，十进制的3在二进制中变成了10+1=11，……熟知十进制10个2相乘等于1024，即102=1024，在二进制中就是10000000000．那么二进制中的“10110”用十进制表示是_________．14．2014年3月9日是星期日，根据这一消息，可以算出2014年全年天数最多的是星期_________．15．有一个两人游戏，22颗围棋子是游戏道具，用抓阄等方式确定谁先走，把先走的一方称为先手方，后走的一方称为后手方，游戏规则如下：先走方必须选择拿走1颗或2颗围棋子；先手完成后，后手方开始按照同样的规则取围棋子：双方轮流抓取，直到取完所有的棋子．取走最后一颗围棋子的人获胜．这个游戏先手方是有必胜策略的，如果要取胜，先手方应该留给对手的围棋子数目从第一轮开始到取胜依次为_________．。

第6-10届走美杯6年级初赛试题解析

第六届“走进每秒的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛小学六年级试卷一、填空题I(每题8分，共40分)1. 11111111 612203042567290+++++++=解：原式=11111111223349102105-+-++-=-=L L2．一个表面积为56emz的长方体如图切成27个小长方体，这27个小长方体表面积的和是______cm2．解：每一刀增加两个切面，增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后，表面积增加到原来的3倍，即表面积的和为168cm2.3．将2、4、6、8、12、18、24、36、72填人右边的九宫格，使每行每列及两条对角线上三数的积都相等．每行的三个数的积是______．解：每行三个数的积相等，所以这个积的3次方等于9个数的积，这就个数是：2130、2230、2131、2330、2231、2132、2331、2232、2332，它们的积21839，所以每行上的3个数的积为2633=1728. 4.0.2.0080.A BCC A B••••=，三位数ABC的最大值是多少？解析：2.008化为分数是251125，可以约分为251125的分数有502250、753375，所以ABC的最大值为753.5．如图所示，长方形ABCD 内的阴影部分的面积之和为70，AB=8,AD=15四边形EFGO 的面积为______．分析：根据容斥关系：四边形EFGO 的面积=三角形AFC+三角形DBF-白色部分的面积三角形AFC+三角形DBF=长方形面积的一半即60，白色部分的面积等于长方形面积减去阴影部分的面积，即120-70=50 所以四边形的面积=60-50=10二、填空题Ⅱ(每题l0分，共50分)6．如图，ABCD 是正方形．阴影部分的面积为_______．（π取3．14）分析：正方形和它的内切圆的面积比是固定的，即4：π.小正方形的面积等于（3+5）2-4×3×5÷2==34，所以其内切圆的面积等于34÷4×（4-π）=7.317．用数字l ～8各一个组成8位数，使得任意相邻三个数字组成的三位数都是3的倍数．共有种组成方法．分析：l ～8中被三除余1和余2的数各有3个，被3整除的数有两个，根据题目条件可以推导，符合条件的排列，一定符合“被三除所得余数以3位周期”，所以8个数字，第1、4、7位上的数被3除同余，第2、5、8位上的数被3除同余，第3、6位上的数被3除同余，显然第3、6位上的数被3整除，第1、4、7位上的数被3除可以余1也可以余2，第2、5、8位上的数被3除可以余2可以余1，余数的安排上共有2种方法，余数安排定后，还有同余数之间的排列，一共有3！×3！×2！=144种方法.8．N 为自然数，且1+N ，2+N 、……、9+N 与690都有大于l 的公约数．N 的最小值为_______．解析：690=2×3×5×23，连续9个数中，最多有5个是2的倍数，也有可能有4个是2的倍数，如果有5个连续奇数，这5个连续奇数中最多有2个3的倍数，1个5的倍数，1个23的倍数，所以必然有一个数不是2、3、5、23的倍数，即与690没有大于l 的公约数.所以9个数中只有4个奇数，剩下的5个数，有3个3的倍数，1个5的倍数，1个23的倍数，则1+N 、3N +、5N +、7N +、9N +是偶数，剩下的4个数中2+N 、8N +是3的倍数（5各偶数当中只有5N +是3的倍数），还有4N +、6N +一个是5的倍数，一个是23的倍数.剩下的可以用中国剩余定理求解，5N +是2和3的倍数，且相邻两个数中一个是23的倍数，另一个是5的倍数，显然524N +=是最小解，所以N 的最小值为19.9． 50位同学围成一圈，从某同学开始顺时针报数．第一位同学报l ，跳过一人第三位同学报2，跳过两人第六位同学报3，……这样下去，报到2008为止．报2008的同学第一次报的是_______．分析：将这些学生按报数方向依次编号；1、2、3、……49、50、51……2008，每一个人的编号不唯一，例如编号为2001、1951……101、51的和编号为1的为同一个人，这样第n 次报数的人的编号为()12n n +, 报2008的同学的编号为2017036，他的最小编号为36，我们知道36=1+2+3+4+5+6+7+8，所以报2008的同学第一次报8.10．用l —9填满三角形空格，一个格子只能填人一个数字，使每个数字在每一行，每一列(包括不相连的行，列)及每个粗黑线围成的区域中至多出现一次．分析：解题顺序如第二附图，依照A 、B 、C 、D ……的顺序.三、填空题Ⅲ(每题l2分，共60分)11．A 、B 两杯食盐水各有40克，浓度比是 3：2．在B 中加入60克水，然后倒人A 中________克．再在A 、B 中加人水，使它们均为100克，这时浓度比为7：3．分析：在B中加入60克水后，B盐水浓度减少为原来的25，但溶质质量不变，此时两杯盐水的盐质量比仍然为3：2，B中的盐占所有盐的质量的22325=+，但最终状态B中的盐占所有盐的质量的337310=+，也就是说B中的盐减少了32111054-÷=，也就是说从A中倒出了14的盐水，即25克.12．中午l2时，校准A、B、C三钟．当天下午A钟6点时，B钟5点50分；B钟7点时，C钟7点20分．晚上C钟11点时，A钟_____点_____分，B钟_______点_____分．分析：下午A钟6点，B钟5点50分，两钟的运行比为360：350=36：35B钟7点时，C钟7点20分，时钟运行比为420：440=21：22，A:B:C=108:105:110所以C钟11点的时候，A钟10：48，B钟10：30.13．一次，齐王与大将田忌赛马．每人有四匹马，分为四等．田忌知道齐王这次比赛马的出场顺序依次为一等，二等，三等，四等，而且还知道这八匹马跑的最快的是齐王的一等马，接着依次为自己的一等，齐王的二等，自己的二等，齐王的三等，自己的三等，齐王的四等，自己的四等．田忌有______种方法安排自己的马的出场顺序，保证自己至少能赢两场比赛．分析：枚举法，枚举出所有方法：1423、2143、2413、3124、3142、3412、3421、4123、4132、4231、4312、4321.14．机器人A、B从P出发到Q，将Q处的球搬到P点．A每次搬3个，往返一次需l5秒．8每次搬5个，往返一次需25秒．竞赛开始8立即出发，A在B后10秒出发．在竞赛开始后的420秒内，A领先的时间是_______秒，B领先的时间是______秒．(领先指搬到P的球多)．分析：对俩机器人的工作情况分别ABA-B:时间0- 25- 40- 50- 55- 70- 75- 85- 100- 115 ……个数差0 -2 1 -4 -1 2 -3 0 -2 1 ……所以从25秒开始，每隔75秒就会出现一个循环，即周期为75秒.前25秒，A、B都没有完成搬运。

第14届地方初赛6年级B卷答案

级初赛B 卷答案一、选择题。

1、B2、B3、D4、A5、A6、B7、D8、A5、甲＝3，乙＝11，丙＝177、小圆的直径为12÷3＝4，长方形的长为：12×2＋4×2＝32，长方形的宽为：12，则长方形的周长为：（32＋12）×2＝888、长方体的高是：（10＋7－26÷2）÷2＝（17－13）÷2＝2（厘米），则长方体的长是10－2＝8（厘米），宽是：7－2＝5（厘米），所以长方体的体积是：8×5×2＝80（立方厘米）。

二、填空题。

9、1∶5∶4 10、31 11、43 12、289，35 13、225 14、126 15、1500 16、612、[11，2，5]－[3，1，7]＝（11×5＋2，5）－（3×7＋1，7）＝（57，5）－（22，7）＝（57×7－5×22，5×7）＝（289，35）13、设花生糖果的重量为n 公斤，则牛奶糖果的重量为107n,那么n ＋107n=680，解得n=400，所以剩余牛奶糖果的重量为107×400－55=225（公斤）。

14、甲商店水果箱数可能为9、18、27、36、 (189)乙商店水果箱数可能为16、32、48、…、176，又126＋64＝190箱，所以甲商店分得126箱。

15、甲取380元，乙存700元后三人共有2980－380＋700＝3300（元），这时丙占总钱数的2÷（1－31）＝3份，1份是3300÷（5＋3＋3）＝300（元），现在甲有300×5＝1500（元）。

16、若取走2枚2元的硬币，此时2元硬币与1元硬币数量相同，且全部硬币总值为21元。

因2元硬币与1元硬币数量相同，故可将它们看作每枚1.5元的硬币，即1.5元与0.5元的硬币共18枚，它们的总值为21元。

小学奥数--分数裂项-精选练习例题-含答案解析(附知识点拨及考点)

本讲知识点属于计算大板块内容，其实分数裂项很大程度上是发现规律、利用公式的过程，可以分为观察、改造、运用公式等过程。

很多时候裂项的方式不易找到，需要进行适当的变形，或者先进行一部分运算，使其变得更加简单明了。

，本讲是整个奥数知识体系中的一个精华部分，列项与通项归纳是密不可分的，所以先找通项是裂项的前提，是能力的体现，对学生要求较高。

分数裂项一、“裂差”型运算将算式中的项进行拆分，使拆分后的项可前后抵消，这种拆项计算称为裂项法.裂项分为分数裂项和整数裂项，常见的裂项方法是将数字分拆成两个或多个数字单位的和或差。

遇到裂项的计算题时，要仔细的观察每项的分子和分母，找出每项分子分母之间具有的相同的关系，找出共有部分，裂项的题目无需复杂的计算，一般都是中间部分消去的过程，这样的话，找到相邻两项的相似部分，让它们消去才是最根本的。

(1)对于分母可以写作两个因数乘积的分数，即1a b ⨯形式的，这里我们把较小的数写在前面，即a b <，那么有1111()a b b a a b =-⨯- 、(2)对于分母上为3个或4个连续自然数乘积形式的分数，即：1(1)(2)n n n ⨯+⨯+，1(1)(2)(3)n n n n ⨯+⨯+⨯+形式的，我们有： 1111[](1)(2)2(1)(1)(2)n n n n n n n =-⨯+⨯+⨯+++ 1111[](1)(2)(3)3(1)(2)(1)(2)(3)n n n n n n n n n n =-⨯+⨯+⨯+⨯+⨯++⨯+⨯+ 裂差型裂项的三大关键特征：（1）分子全部相同，最简单形式为都是1的，复杂形式可为都是x(x 为任意自然数)的，但是只要将x 提取出来即可转化为分子都是1的运算。

（2）分母上均为几个自然数的乘积形式，并且满足相邻2个分母上的因数“首尾相接”（3）分母上几个因数间的差是一个定值。

$知识点拨教学目标分数裂项计算二、“裂和”型运算：常见的裂和型运算主要有以下两种形式：（1）11a b a b a b a b a b b a +=+=+⨯⨯⨯ （2）2222a b a b a b a b a b a b b a +=+=+⨯⨯⨯ 裂和型运算与裂差型运算的对比：裂差型运算的核心环节是“两两抵消达到简化的目的”，裂和型运算的题目不仅有“两两抵消”型的，同时还有转化为“分数凑整”型的，以达到简化目的。

走美杯2014六年级B真题及答案

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学六年级试卷（B卷）填空题Ⅰ（每题8分，共40分）1．计算：20140601(100000013397______)13÷+⨯=．2．有含糖量为7%的糖水600克，为了得到含糖量为10%的糖水，需要再加入糖_________克．3．像2，3，5，7这样只能被1和自身整除的大于1的自然数叫做质数或素数．每一个自然数都能写成若干个(可以相同)质数的乘积，比如，4=22⨯，6=23⨯，10=25⨯等，那么，2014写成⨯⨯，9=33⨯，8=222这种形式为_________．4．某班有4名同学参加数学解题技能展示选拔赛，那么，可能出现的入选情形一共有_________种．5．“24点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52张扑克牌(不包括大小王)中抽取4张，用这4张扑克牌上的数字（1,11,12,13====）通过加减乘除四则运算得出24，最先找到算法者A J Q K取胜．游戏规定4张扑克牌都要用到，而且每张牌只能用一次，比如2，3，4，Q，则可以由算法(2)(43)⨯⨯-Q 得到24．王亮在一次游戏中抽到了Q，9，2，1，他发现92124Q+++=，如果将这种能够直接相加得到24的4张牌称为“友好牌组”．那么，含有Q的不同“友好牌组”共有_________组．填空题Ⅱ（每题10分，共50分）6．在中国古代数学中，两个形状相同的圆柱以垂直的方向相互穿插，如图所示，中间重合部分所构成的几何体称为牟合方盖．从正上方俯视牟合方盖，呈现的图形为_________．7．如图所示的图形由1个大的半圆弧和6个小的半圆弧围成，已知最大的半圆弧的直径为20，则这个图形的周长为_________（圆周率用π表示）．8．如图所示，已知大圆的半径为2，则阴影部分I与II的面积之和为_________（圆周率用π表示）．9．将下图中的圆圈染色，要求有连线的两个相邻的圆圈染不同的颜色，则至少需要_________种颜色．填空题Ⅲ（每题12分，共60分）10．古希腊的数学家们将自然数按以下方式与多边形联系起来，定义了多边形数：三边形数:1，3，6，10，15，……四边形数:1，4，9，16，25，……五边形数:1，5，12，22，35，……六边形数:1，6，15，28，45，…………则按照上面的顺序，第6个七边形数为_________．11．日常生活中经常使用十进制来表示数．要用10个数码：0，1，2，3，4，5，6，7，8，9．在电子计算机中用二进制，只要两个数码0和1，正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进1”，于是，可以得到一下自然数的十进制与二进制表示对照表：十进制0 1 2 3 4 5 6 7 8 …二进制0 1 10 11 100 101 110 111 1000 …十进制的0在二进制中还是0，十进制的1在二进制中还是1，十进制的2在二进制中变成了1+1=10，2=1024，在二进制十进制的3在二进制中变成了10+1=11，……熟知十进制10个2相乘等于1024，即10中就是．那么，十进制中的2014用二进制表示是_________．12．用6颗颜色不同的彩色珠子串成一个手链，有_________种不同的串法．13．连续的5个自然数24，25，26，27，28有一个共同性质：它们都是合数．我们把这样5个连续自然数称为长度为5的连续合数组．试再写出一个长度为5的连续合数组_________．14．有一个两人游戏，两堆黑（10颗）白（21颗）棋子是游戏道具，用抓阄或猜叮壳等方式确定谁先走，把先走的一方称为先手方，后走的一方称为后手方，游戏规则如下：先手方必须在两堆棋子中选定一堆，至少选择一颗取走，也可以选择将这一堆全部棋子取走；先手方完成之后，后手方开始按照同样的规则取围棋子；双方轮流抓取，直到取完所有棋子．取走最后一颗围棋子的人获胜．这个游戏先手3 / 11方是有必胜策略的，如果要取胜，先手方在一开始应该取走_________．15．勾股定理又称为“毕达哥拉斯定理”，是一个有着悠悠4000多年历史的重要几何定理．它揭示了这样一个事实:对任何一个直角三角形而言，以它的两条直角边的长度为边长的正方形的面积之和，等于以斜边的长度为边长的正方形的面积．关于勾股定理，人们发现了400多种证明，甚至连美国总统也曾加入到证明一者的队伍中．在众多证明方法中，我国古代数学家刘徽给出的证明简单直观，耐人寻味（如下图所示）这个证明实际上给出了一个通过有限次直线切割，将两个正方形拼补为一个更大的正方形的方法．设两个小正方形的边长分别为3和4，按照刘徽的方法，这两个小正方形被切割成5部分，请分别计算出这5部分的面积，并按从小到大的顺序写在下面：_________．AB=CDD CBA DCBA第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学六年级试卷（B卷）参考答案1 2 3 4 5 6 7 8 41 20 201425319=⨯⨯16 12 20π2π-9 10 11 12 13 14 154 81 ．60 32,33,34,35,36．（答案不唯一）11颗白色327457768888，，，，参考解析填空题Ⅰ（每题8分，共40分）1．计算：20140601100000013397______)13÷+⨯=（．【考点】速算巧算【难度】☆【答案】41【解析】(20140601131000000)1339741÷-÷=2．有含糖量为7%的糖水600克，为了得到含糖量为10%的糖水，需要再加入糖_________克．【考点】浓度问题【难度】☆☆【答案】20【解析】600(17%)558⨯-=（克）558110%)620÷-=（（克）620600=20-（克）3．像2，3，5，7这样只能被1和自身整除的大于1的自然数叫做质数或素数．每一个自然数都能写成若5 / 11干个(可以相同)质数的乘积，比如，4=22⨯，6=23⨯，8=222⨯⨯，9=33⨯，10=25⨯等，那么，2014写成这种形式为_________．【考点】分解质因数【难度】☆ 【答案】201425319=⨯⨯．【解析】分解质因数4．某班有4名同学参加数学解题技能展示选拔赛，那么，可能出现的入选情形一共有种_________．【考点】计数问题【难度】☆☆ 【答案】16．【解析】每个人都可能考上或考不上，222216⨯⨯⨯=．5．“24点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52张扑克牌(不包括大小王)中抽取4张，用这4张扑克牌上的数字（1,11,12,13A J Q K ====）通过加减乘除四则运算得出24，最先找到算法者取胜．游戏规定4张扑克牌都要用到，而且每张牌只能用一次，比如2，3，4，Q ，则可以由算法(2)(43)Q ⨯⨯-得到24．王亮在一次游戏中抽到了Q ，9，2，1，他发现92124Q +++=，如果将这种能够直接相加得到24的4张牌称为“友好牌组”，那么，含有Q 的不同“友好牌组”共有_________组．【考点】计数问题，枚举法【难度】☆☆ 【答案】12．【解析】分别为1011Q 、、、；921Q 、、、；822Q 、、、；831Q 、、、；732Q 、、、；741Q 、、、；651Q 、、、；642Q 、、、；633Q 、、、；552Q 、、、；543Q 、、、；444Q 、、、．填空题Ⅱ（每题10分，共50分）6．在中国古代数学中，两个形状相同的圆柱以垂直的方向相互穿插，如图所示，中间重合部分所构成的几何体称为牟合方盖．从正上方俯视牟合方盖，呈现的图形为_________．【考点】立体几何，三视图【难度】☆☆7 / 11【答案】【解析】俯视图7．如图所示的图形由1个大的半圆弧和6个小的半圆弧围成，已知最大的半圆弧的直径为20，则这个图形的周长为_________（圆周率用π表示）．【考点】平面几何【难度】2星【答案】20π【解析】周长等于一个大圆的周长，20d ππ=．8．如图所示，已知大圆的半径为2，则阴影部分Ⅰ与Ⅱ的面积之和为_________（圆周率用π表示）．【考点】平面几何【难度】3星【答案】2π-【解析】Ⅰ和Ⅱ部分面积为14大圆-直角边为2的等腰直角三角形211=222242ππ⨯-⨯⨯=-9．将下图中的圆圈染色，要求有连线的两个相邻的圆圈染不同的颜色，则至少需要_________种颜色．【考点】数阵图【难度】3星【答案】4种【解析】从中间开始，逐步往外填．填空题Ⅲ（每题12分，共60分）10．古希腊的数学家们将自然数按以下方式与多边形联系起来，定义了多边形数：三边形数:1，3，6，10，15，…… 四边形数:1，4，9，16，25，…… 五边形数:1，5，12，22，35，…… 六边形数:1，6，15，28，45，…… ……则按照上面的顺序，第6个七边形数为_________．CBB CA CBDC BA9 / 11【考点】找规律【难度】3星【答案】81【解析】从上至下公差分别为0,1,3,6,10；从左到右相邻的差分别为2,3,4,5；3,5,7,9；4,7,10,13；5,9,13,17；6,11,16,21,26，所以七边形数：1,7,18,34,55,81．11．日常生活中经常使用十进制来表示数．要用10个数码：0，1，2，3，4，5，6，7，8，9．在电子计算机中用二进制，只要两个数码0和1，正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进1”，于是，可以得到一下自然数的十进制与二进制表示对照表：十进制 0 1 2 3 4 5 6 7 8 … 二进制110111001011101111000…十进制的0在二进制中还是0，十进制的1在二进制中还是1，十进制的2在二进制中变成了1+1=10，十进制的3在二进制中变成了10+1=11，……熟知十进制10个2相乘等于1024，即102=1024，在二进制中就是．那么，十进制中的2014用二进制表示是_________．【考点】进制转换【难度】3星【答案】．【解析】22014210070250312251121251262123102151271231112．用6颗颜色不同的彩色珠子串成一个手链，有_________种不同的串法．【考点】计数问题【难度】3星【答案】60．【解析】先选定一颗珠子，其他珠子在其后边开始全排列．手链可以翻转，再除以2．13．连续的5个自然数24，25，26，27，28有一个共同性质：它们都是合数．我们把这样5个连续自然数称为长度为5的连续合数组．试再写出一个长度为5的连续合数组_________．【考点】质数合数【难度】2星【答案】32,33,34,35,36．【解析】（答案不唯一，合理即可）14．有一个两人游戏，两堆黑（10颗）白（21颗）棋子是游戏道具，用抓阄或猜叮壳等方式确定谁先走，把先走的一方称为先手方，后走的一方称为后手方，游戏规则如下：先手方必须在两堆棋子中选定一堆，至少选择一颗取走，也可以选择将这一堆全部棋子取走；先手方完成之后，后手方开始按照同样的规则取围棋子；双方轮流抓取，直到取完所有棋子．取走最后一颗围棋子的人获胜．这个游戏先手方是有必胜策略的，如果要取胜，先手方在一开始应该取走_________．【考点】操作问题【难度】3星【答案】应该取走11颗白色．【解析】使白色子数量与黑色子保持一致后，如对方取黑色堆，则在白色堆取相同数量，反之亦然，必可取走最后一颗棋子．15．勾股定理又称为“毕达哥拉斯定理”，是一个有着悠悠4000多年历史的重要几何定理．它揭示了这样一个事实:对任何一个直角三角形而言，以它的两条直角边的长度为边长的正方形的面积之和，等于以斜边的长度为边长的正方形的面积．关于勾股定理，人们发现了400多种证明，甚至连美国总统也曾加入到证明一者的队伍中．在众多证明方法中，我国古代数学家刘徽给出的证明简单直观，耐人寻味（如下图所示）这个证明实际上给出了一个通过有限次直线切割，将两个正方形拼补为一个更大的正方形的方法．设两个小正方形的边长分别为3和4，按照刘徽的方法，这两个小正方形被切割成5部分，请分别计算出这5部分的面积，并按从小到大的顺序写在下面：_________．【考点】勾股定理【难度】3星【答案】327457768888，，，，AB=CDD CBAD CBA【解析】54321D CBA11 / 11。

(参考资料)2014年美国“数学大联盟杯赛”(中国赛区)初赛五、六年级试卷

A) 100
B) 160
C) 200
D) 250
二、填空题(每小题 5 分，答对加 5 分，答错不扣分，共 50 分，答案请填涂在答题卡上)
31. The sum of the digits of 2014 is 2 + 0 + 1 + 4 = 7. Let n be a natural number.
m = n + 2014. The sum of the digits of m is half the sum of the digits of n.
What is the minimum value of n?
Answer: ______.
32. The sum of 5 different prime numbers is 200. Each of the 5 prime
1
2
26. If 5 of the 200 stripes on Frank’s giant shell are blue, 5 of the remaining
stripes are brown, and the rest are white, there are ? more white stripes
D) 110
22. The average of 2014 sixes is equal to the average of 4028 ? .
A) threes
B) sixes
C) nines
D) twelves
23. What is 0.625% of 8% of 500?
A) 0.25
B) 2.5
数字为三个连续的偶数，个位数字为三个连续的奇数。如果将四位数的