人教版数学七下期末压轴题专项训练
2020-2021学年人教版 七年级数学下册期末压轴题训练(word版 含答案)
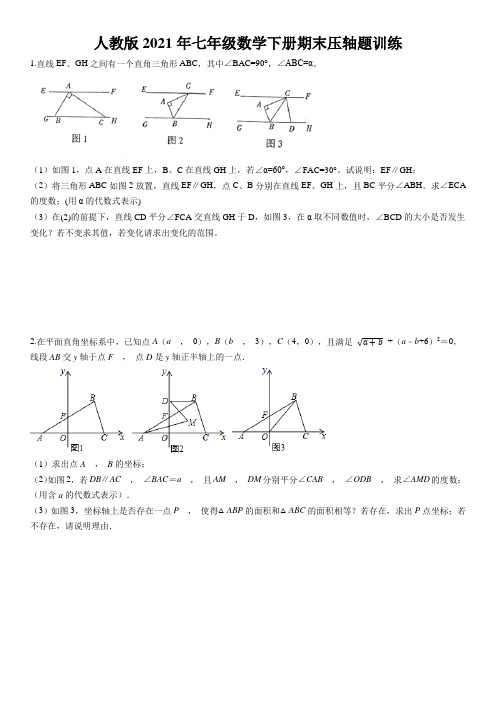
人教版2021年七年级数学下册期末压轴题训练1.直线EF、GH之间有一个直角三角形ABC,其中∠BAC=90°,∠ABC=α。
(1)如图1,点A在直线EF上,B、C在直线GH上,若∠α=60°,∠FAC=30°。
试说明:EF∥GH;(2)将三角形ABC如图2放置,直线EF∥GH,点C、B分别在直线EF、GH上,且BC平分∠ABH。
求∠ECA 的度数;(用α的代数式表示)(3)在(2)的前提下,直线CD平分∠FCA交直线GH于D,如图3,在α取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化请求出变化的范围。
2.在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足√a+b+(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.(1)求出点A,B的坐标;(2)如图2,若DB∥AC,∠BAC=a,且AM,DM分别平分∠CAB,∠ODB,求∠AMD的度数;(用含a的代数式表示).(3)如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且(a+2)2+ √b−3=0,(1)求a,b的值;(2)在坐标轴上存在一点M,使△COM的面积是△ABC的面积的一半,求出点M的坐标.(3)如图2,过点C做CD⊥y轴交y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分角∠AOP,OF⊥OE,当点P运动时,∠OPD∠DOE的值是否会改变?若不变,求其值;若改变,说明理由.4.某小区准备新建60 个停车位,以解决小区停车难的问题。
已知新建2个地上停车位和3个地下停车位共需1.7 万元:新建4 个地上停车位和2 个地下停车位共需1.4 万元。
(1)该小区新建 1 个地上停车位和1个地下停车位各需多少万元?(2)若该小区新建车位的投资金额超过14 万元而不超过15万元,问共有几种建造方案?(3)对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.5.为迎接暑假旅游高峰的到来,某旅游纪念品商店决定购进A、B两种纪念品.若购进A种纪念品7件,B种纪念品4件,需要760元;若购进A种纪念品5件.B种纪念品8件,需要800元.(1)求购进A、B两种纪念品每件各需多少元?(2)若该商店决定购进这两种纪念品共100件.考虑市场需求和资金周转,这100件纪念品的资金不少于7000元,但不超过7200元,那么该商店共有几种进货方案?(3)若销售A种纪念品每件可获利润30元,B种纪念品每件可获利润20元,用(2)中的进货方案,哪一种方案可获利最大?最大利润是多少元?6.如图,在平面直角坐标系中,直线AB与x轴交于点B(b,0),与y轴交于点A(0,a),且√a−b+2+|2a+ b−8|=0(1)求S△AOB(2)若P(x,y)为直线AB上一点①△APO的面积不大于△BPO面积的2,求P点横坐标x的取值范围3②求x与y的数量关系(3)已知点Q(m,m-2),若△ABQ的面积为6,求m7.在平面直角坐标系中,点A(0,a),B(2,b),C(4,0)且a>0.(1)若(a−2)2+√b−4=0,求点A,点B的坐标.(2)如图,在(1)的条件下,求三角形ABC面积.(3)在(2)的条件下,过点B作BD平行y轴交AC于点D,求点D的坐标.8.如图1,在平面直角坐标系中,线段AB的两个端点分别为A(0,2),B(−1,0),将线段AB向右平移3个单位长度,得到线段CD,连接AD(1)直接写出点C、点D的坐标(2)如图2,延长DC交y轴于点E,点P是线段OE上的一动点,连接BP、CP,猜想∠ABP、∠BPC、∠ECP之间的数量关系,并说明理由(3)在x轴上是否存在点Q,使ΔQBD的面积与四边形ABCD的面积相等,若存在,求出Q的坐标,若不存在,请说明理由9.在平面直角坐标系中,点A、B在坐标轴上,其中A(0,a)、B( b,0)满足:|2a−b−1|+√a+2b−8=0(1)求A、B两点的坐标;(2)将线段AB平移到CD,点A的对应点为C(-2,t),如图(1)所示.若三角形ABC的面积为9,求点D的坐标.10.在平面直角坐标系中,已知A(a,0),B(b,0),C(0,4),D(6,0).点P(m,n)为线段CD上一点(不与点C和点D重合).(1)利用三角形COP、三角形DOP及三角形COD之间的面积关系,求m与n之间的数量关系;(2)如图1,若a=﹣2,点B为线段AD的中点,且三角形ABC的面积等于四边形AOPC面积,求m的值;(3)如图2,设a,b,m满足{2a+3b+m=03a+2b+m=−5,若三角形ABP的面积小于5,求m的取值范围.11.如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE,AE交CD于H.∠DCE的平分线交AE于G.(1)求证:AD∥BC;(2)若∠BAC=∠DAE,∠AGC=2∠CAE.求∠CAE的度数;(3)(2)中条件∠BAC=∠DAE仍然成立,若∠AGC=3∠CAE,直接写出∠CAE的度数________.参考答案1.(1)证明:∵∠EAB=180°-∠BAC-∠FAC,∠BAC=90°,∠FAC=30°,∴∠EAB=60°,又∵∠ABC=60°,∴∠EAB=∠ABC,∴EF∥GH;(2)解:经过点A作AM∥GH,又∵EF∥GH,∴AM∥EF∥GH,∵BC平分∠ABH∴∠ABC=∠CBH=a∴∠MAB=180°-∠ABH=180°-2a∴∠MAC=90°-(180°-2a)=2a-90°∴∠ECA=∠MAC=2a-90°(3)解:不发生变化,由(2)得:∠ECA=2a-90°,∴∠FCA=180°-(2a-90°)=270°-2a∵CD平分∠FCA,∴∠FCD=135°-a,∵EF//GH∴∠FCB+∠CBH=180°,∴∠FCB=180°-a,∴∠BCD=180°-a-(135°-a)=452.(1)解:∵√a+b+(a﹣b+6)2=0,∴a+b=0,a﹣b+6=0,∴a=﹣3,b=3,∴A(﹣3,0),B(3,3);(2)解:如图2,过点M作MN∥DB,交y轴于点N,∴∠DMN=∠BDM,又∵DB∥AC,∴MN∥AC,∴∠AMN=∠MAC,∵DB∥AC,∠DOC=90°,∴∠BDO=90°,又∵AM,DM分别平分∠CAB,∠ODB,∠BAC=a,∴∠MAC=12a,∠BDM=45°,∴∠AMN=12a,∠DMN=45°,∴∠AMD=∠AMN+∠DMN=45°+ 12a;(3)解:存在.连结OB,如图3,设F(0,t),∵S△AOF+S△BOF=S△AOB,∴12•3•t+ 12•t•3=12×3×3,解得t=32,∴F点坐标为(0,32),△ABC的面积=12×7×3=212,当P点在y轴上时,设P(0,y),∵S△ABP=S△APF+S△BPF,∴12•|y﹣32|•3+ 12•|y﹣32|•3=212,解得y=5或y=﹣2,∴此时P点坐标为(0,5)或(0,﹣2);当P点在x轴上时,设P(x,0),则12•|x+3|•3=212,解得x=﹣10或x=4,∴此时P点坐标为(﹣10,0),∴a+2=0,b-3=0∴a=﹣2,b=3;(2)如图1,过点C作CT⊥x轴,CS⊥y轴,垂足分别为T、S.∵A(﹣2,0),B(3,0),∴AB=5,∵C(﹣1,2),∴CT=2,CS=1,∴△ABC的面积=AB•CT=5,∵△COM的面积=12△ABC的面积,∴△COM的面积=52,若点M在x轴上,即12OM•CT=52,∴OM=2.5.∴M的坐标为(2.5,0)(﹣2.5,0),若点M在y轴上,即12OM•CS=52,∴OM=5,∴点M坐标(0,5)或(0,﹣5),综上所述:点M的坐标为(0,5)或(﹣2.5,0)或(0,﹣5)或(2.5,0);(3)如图2,∠OPD∠DOE的值不变,理由如下:∵CD⊥y轴,AB⊥y轴,∴∠CDO=∠DOB=90°,∴AB∥CD,∴∠OPD=∠POB.∵OF⊥OE,∴∠POF+∠POE=90°,∠BOF+∠AOE=90°,∵OE平分∠AOP,∴∠POE=∠AOE,∴∠POF=∠BOF,∴∠OPD=∠POB=2∠BOF.∴∠OPD =2∠BOF =2∠DOE ,∴ ∠OPD ∠DOE =2.4.(1)解:设新建一个地上停车位需 x 万元,新建一个地下停车位需 y 万元,由题意得: {2x +3y =1.74x +2y =1.4, 解得 {x =0.1y =0.5, 故新建一个地上停车位需 0.1 万元,新建一个地下停车位需 0.5 万元.(2)设新建 m 个地上停车位,由题意得: 14<0.1m +0.5(60−m)≤15 ,解得 37.5≤m <40 ,因为 m 为整数,所以 m =38 或 39 ,对应的 60−m =22 或 21 ,故一共 2 种建造方案。
(完整版)人教版七年级数学下册期末复习压轴题-解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1. 仔细阅读下列解题过程:若 , 求 的值.解:2222690a ab b b ++-+=222222690()(3)003033a ab b b b a b b a b b a b ∴+++-+=∴++-=∴+=-=∴=-=,, 根据以上解题过程, 试探究下列问题:(1)已知 , 求 的值;(2)已知 , 求 的值;(3)若 , 求 的值.2. 启秀中学初一年级组计划将 本书奖励给本次期中考试中取得优异成绩的 名同学, 如果每人分 本, 那么还剩下 本;如果每人分 本, 那么最后一人分得的书不足 本, 但不少于 本. 最终, 年级组讨论后决定, 给 名同学每人发 本书, 那么将剩余多少本书?3.在南通市中小学标准化建设工程中, 某校计划购进一批电脑和电子白板, 经过市场考察得知, 购买 台电脑和 台电子白板需要 万元, 购买 台电脑和 台电子白板需要 万元.(1)求每台电脑、每台电子白板各多少万元;(2)根据学校实际, 需购进电脑和电子白板共 台, 若总费用不超过 万元, 则至多购买电子白板多少台?4.已知关于 , 的二元一次方程组 它的解是正数.(1)求m 的取值范围;(2)化简: ;5. 已知 , , 求 的平方根.6. 定义: 若实数x, y 满足 , , 且x ≠y, 则称点M(x, y)为“好点”. 例如, 点(0, -2)和 (-2, 0)是“好点”. 已知: 在直角坐标系xOy 中, 点P(m, n).(1)P1(3, 1)和P2(-3, 1)两点中, 点________________是“好点”.(2)若点P(m, n)是“好点”, 求m+n 的值.(3)若点P 是“好点”, 用含t 的代数式表示mn, 并求t 的取值范围.7. 已知有理数 满足: , 且 , 求 的值.8. 如图, 在方格纸内将 水平向右平移4个单位得到 .(1)补全 , 利用网格点和直尺画图;(2)图中 与 的位置关系是: ;(3)画出ABC ∆中AB 边上的中线CE ;(4)平移过程中, 线段 扫过的面积是: .9. 如图所示, A(2, 0), 点 B 在 y 轴上, 将三角形 OAB 沿 x 轴负方向平移, 平移后的图形为三角形 DEC, 且点 C 的坐标为(-6, 4) .(1)直接写出点E 的坐标;(2)在四边形 ABCD 中, 点 P 从点 B 出发, 沿“BC→CD”移动. 若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒, 回答下列问题:①求点 P 在运动过程中的坐标, (用含 t 的式子表示, 写出过程);②当 3 秒<t<5 秒时, 设∠CBP=x°, ∠PAD=y°, ∠BPA=z°, 试问 x, y, z 之间的数量关系能否确定?若能, 请用含 x, y 的式子表示 z, 写出过程;若不能, 说明理由.10. 问题1: 现有一张△ABC纸片, 点D.E分别是△ABC边上两点, 若沿直线DE折叠. (1)探究1: 如果折成图①的形状, 使A点落在CE上, 则∠1与∠A的数量关系是;(2)探究2: 如果折成图②的形状, 猜想∠1+∠2和∠A的数量关系是;(3)探究3:如果折成图③的形状, 猜想∠1、∠2和∠A的数量关系, 并说明理由.(4)问题2: 将问题1推广, 如图④, 将四边形ABCD纸片沿EF折叠, 使点A.B落在四边形EFCD的内部时, ∠1+∠2与∠A.∠B之间的数量关系是 .11.已知a +b=5, ab=-2.求下列代数式的值:(1) ;(2) .12.如图, 在方格纸内将 水平向右平移4个单位得到△ .(1)画出△; (2)画出边上的中线和高线;(利用网格点和直尺画图)(3) 的面积为 .13. 如果ac =b, 那么我们规定(a, b )=c. 例如;因为23=8, 所以(2, 8)=3.(1)根据上述规定填空: (3, 27)= , (4, 1)= , (2, 0.25)= ;(2)记(3, 5)=a, (3, 6)=b, (3, 30)=c. 判断a, b, c 之间的等量关系, 并说明理由.14. 先化简, 再求值:(x ﹣2y )(x +2y )﹣(x ﹣2y )2, 其中x =3, y =﹣1.15.已知: , .求下列代数式的的值.(1)xy ;(2)224x xy y ++;(3) . 16. 装饰公司为小明家设计电视背景墙时需要A.B 型板材若干块, A型板材规格是a(b, B 型板材规格是b(b.现只能购得规格是150(b 的标准板材.(单位: cm )(1)若设a(60cm, 裁法一 裁法二 裁法三b(30cm.一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法, 下图是裁法一的裁剪示意图.A型板材块数120B型板材块数3m n则上表中, m=___________, n=__________;(2)为了装修的需要, 小明家又购买了若干C型板材, 其规格是a(a, 并做成如下图的背景墙.请写出下图中所表示的等式:__________;(3)若给定一个二次三项式2a2(5ab(3b2, 试用拼图的方式将其因式分解. (请仿照(2)在几何图形中标上有关数量)17.已知关于x、y的方程组与有相同的解, 求a、b的值.18. 计算:(1)(12)﹣3﹣20160﹣|﹣5|;(2)(3a2)2﹣a2•2a2+(﹣2a3)2+a2;(3)(x+5)2﹣(x﹣2)(x﹣3);(4)(2x+y ﹣2)(2x+y+2).19. 已知关于 、 的二元一次方程组 (k 为常数).(1)求这个二元一次方程组的解(用含k 的代数式表示);(2)若 , 求k 的值;(3)若 , 设 , 且m 为正整数, 求m 的值.20. 解下列方程组或不等式组(1)24231x y x y +=⎧⎨-=⎩ (2)()211113x x x x ⎧--≤⎪⎨+>-⎪⎩【参考答案】***试卷处理标记, 请不要删除一、解答题1. (1) ;(2) ;(3) .【分析】(1)首先把第3项 裂项, 拆成 , 再用完全平方公式因式分解, 利用非负数的性质求得 代入求得数值;(2)首先把第2项 裂项, 拆成 , 再用完全平方公式因式分解, 利用非负数的性质求得 代入求得数值;(3)先把 代入 , 得到关于 和 的式子, 再仿照(1)(2)题.【详解】解: (1)2222210x xy y y y ∴-++-+=22()(1)0x y y ∴-+-=010x y y ∴-=-=,,11x y ∴==,,23x y ∴+=;(2)2254210a b ab b +--+=22244210a b ab b b ∴+-+-+=22(2)(1)0a b b ∴-+-=2010a b b ∴-=-=,21a b ∴==,;(3)4m n =+,2(4)8200n n t t ∴++-+=22448160n n t t ∴+++-+=22(2)(4)0n t ∴++-=2040n t ∴+=-=,24n t ∴=-=,42m n ∴=+=20(2)1m t n -∴=-=【点睛】本题考查的分组分解法、配方法和非负数的性质, 对于项数较多的多项式因式分解, 分组分解法是一个常用的方法.首先要观察各项特征, 寻找熟悉的式子, 熟练掌握平方差公式和完全平方公式是基础.2.38本【分析】先表示书的总量, 利用不等关系列不等式组, 求不等式组的正整数解即可得到答案.【详解】解: 由题意得:由①得:由②得:不等式组的解集是:为正整数,20,n ∴=478158,m n ∴=+=15820638.∴-⨯=答: 剩下 本书.【点睛】本题考查的是不等式组的应用, 掌握利用不等关系列不等式组是解题的关键.3.(1)电脑 万元, 电子白板 万元;(2) 台【分析】(1)设每台电脑 元, 每台电子白板 元, 根据题意列出方程组, 解方程组即可;(2)设购进电子白板 台, 则购进电脑 台, 根据总费用不超过 万元, 列出不等式, 根据 实际意义即可求解.【详解】(1)设每台电脑 元, 每台电子白板 元, 则 , 解得故每台电脑 万元, 每台电子白板 万元;(2)设购进电子白板 台, 则购进电脑 台, 由题意得1.50.5(31)30m m +-≤解得 , 又因为 是正整数, 则 , 故至多购买电子白板 台.【点睛】本题考查了二元一次方程组应用, 一元一次不等式应用, 综合性较强, 难度不大, 根据题意列出二元一次方程组、一元一次不等式是解题关键.4. (1)(2)m -【分析】(1)先解方程组, 用含m 的式子表示出x 、y, 再根据方程组的解时一对正数列出关于m 的不等式组, 解之可得;(2)根据m 的取值范围判断出m-2<0、m+1>0,m-1<0, 再根据绝对值性质去绝对值符号、合并同类项即可得.【详解】解: (1)解方程组 ,得321x m y m =+⎧⎨=-⎩因为解为正数, 则 , 解得 ;(2)原式2(1)(1)m m m m =--+--=-.【点睛】本题考查了二元一次方程组及解法、一元一次不等式组及解法. 解题的关键是根据题意列出关于m 的不等式组及绝对值的性质.5.【分析】根据题意得到三元一次方程组, 解方程组, 求出 , 最后求平方根即可.【详解】∵ , ,∴ , ,∴2113024010y x x y z -+-=⎧⎪-+=⎨⎪-=⎩,解得231x y z =⎧⎪=⎨⎪=⎩,则6x y z ++=,∴ 平方根为 .【点睛】本题考查相反数的意义, 非负数的表达, 解三元一次方程组, 求平方根等知识, 综合性较强, 解题关键是根据题意列出三元一次方程组.6. (1) ;(2) ;(3)【分析】(1)将P1(3, 1)和P2(-3, 1)分别代入等式即可得出结果;(2)将点P(m, n)代入等式即可得出m+n 的值;(3)根据“好点”的定义, 将P 点代入即可得到关于m 和n 的等式, 将两个等式结合即可得出结果.【详解】解: (1)对于 , ,对于 , , , 所以 是“好点”(2)∵点 是好点,∴222,2m n t n m t =+=+, 222()m n n m -=-,∴2m n +=-(3)∵ ,2222m n n t m t -=+--①,2222m n m t n t +=+++②,得()()2()0m n m n m n -++-=,即()(2)0m n m n -++=,由题知, ,由②得 ,∴4242,4mn t mn t -=-+=-,∵ , ∴ ,∴2()40m n mn +->,∴44(4)0t -->,所以3t >,【点睛】本题主要考查的是新定义“好点”, 正确的掌握整式的乘法解题的关键.7. 【分析】利用 将 整理求出 的值, 然后将 利用完全平方公式变形, 将各自的值代入计算即可求出值.【详解】∵221x y , ∴化简得: ,∵1x y -=,∴ 可化为: ,即有: ,∴2222313516x xy y x y xy .【点睛】此题考查了整式的混合运算 化简求值, 熟练掌握运算法则是解本题的关键.8. (1)图见详解;(2)平行且相等;(3)图见详解;(4)28.【分析】(1)根据图形平移的性质画出△A B C '''即可;(2)根据平移的性质可得出AC 与A C ''的关系;(3)先取 的中点 , 再连接 即可;(4)线段 扫过的面积为平行四边形 的面积, 根据平行四边形的底为4, 高为7, 可得线段 扫过的面积.【详解】解: (1)如图所示, △ 即为所求;(2)由平移的性质可得, 与 的关系是平行且相等;故答案为: 平行且相等;(3)如图所示, 线段 即为所求;(4)如图所示, 连接 , , 则线段 扫过的面积为平行四边形 的面积,由图可得, 线段 扫过的面积 .故答案为:28.【点睛】本题主要考查了利用平移变换进行作图, 作图时要先找到图形的关键点, 分别把这几个关键点按照平移的方向和距离确定对应点后, 再顺次连接对应点即可得到平移后的图形.9.(1) (2)1)点P 在线段BC 上时, , 2)点P 在线段CD 上时, ;(3)能确定, , 证明见解析【分析】(1)根据平移的性质即可得到结论;(2)①分两种情况: 1)点P 在线段BC 上时, 2)点P 在线段CD 上时;②如图, 作P 作 交于AB 于E, 则 , 根据平行线的性质即可得到结论.【详解】(1)∵点B 的横坐标为0, 点C 的横坐标为-6,∴将A(2, 0)向左平移6个单位长度得到点E∴()4,0E -;(2)①∵6,4BC CD ==∴1)点P 在线段BC 上时,(),4P t -;2)点P 在线段CD 上时,()6,10P t --;②能确定如图, 作P 作 交于AB 于E, 则∴1,2CBP x DAP y ==︒==︒∠∠∠∠ ∴1+2BPA x y z ==︒+︒=︒∠∠∠ ∴z x y =+.【点睛】本题考查了平行线的问题, 掌握平移的性质、代数式的用法、平行线的性质以及判定定理是解题的关键.10. (1) ;(2) ;(3)见解析;(4)【分析】(1)根据三角形外角性质可得;(2)在四边形 中, 内角和为360°, ∠BDA=∠CEA=180°, 利用这两个条件, 进行角度转化可得关系式;(3)如下图, 根据(1)可得∠1=2∠ , ∠2=2∠ , 从而推导出关系式;(4)根据平角的定义以及四边形的内角和定理, 与(2)类似思路探讨, 可得关系式.【详解】(1)∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠;(2)∵在四边形 中, 内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理, ∠A=∠∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ;(3)数量关系:理由:如下图, 连接由(1)可知: ∠1=2∠ , ∠2=2∠∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠';(4)由折叠性质知: ∠2=180°-2∠AEF, ∠1=180°-2∠BFE相加得: .【点睛】本题考查角度之间的关系, (4)问的解题思路是相同的, 主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.11. (1)29;(2)64.【分析】(1)根据完全平方公式得到 , 然后整体代入计算即可;(2)根据完全平方公式得到 , 然后整体代入计算即可.【详解】解: (1) ;(2) .【点睛】本题考查了代数式求值, 完全平方公式和整体代入的思想, 熟练掌握完全平方公式是解题的关键.12. (1)见解析; (2) 见解析;(3) 4.【解析】【分析】(1)根据图形平移的性质画出△A′B′C′即可;(2)先取AB 的中点D, 再连接CD 即可;过点C 作CD ⊥AB 交AB 的延长线于点E, CE 即为所求;(3)利用割补法计算△ABC 的面积.【详解】(1)如图所示:(2)如图所示;(3)S△BCD=20-5-1-10=4.13. (1)3, 0, ﹣2;(2)a+b=c, 理由见解析.【分析】(1)直接根据新定义求解即可;(2)先根据新定义得出关于a, b, c的等式, 然后根据幂的运算法则求解即可.【详解】(1)∵33=27,∴(3, 27)=3,∵40=1,∴(4, 1)=0,∵2﹣2=,∴(2, 0. 25)=﹣2.故答案为: 3, 0, ﹣2;(2)a+b=c.理由: ∵(3, 5)=a, (3, 6)=b, (3, 30)=c,∴3a=5, 3b=6, 3c=30,∴3a×3b=5×6=3c=30,∴3a×3b=3c,∴a+b=c.【点睛】本题考查了新定义运算, 明确新定义的运算方法是解答本题的关键, 本题也考查了有理数的乘方、同底数幂的乘法运算.14.4xy﹣8y2, ﹣20【分析】先根据整式的乘法法则和乘法公式算乘法, 再合并同类项, 最后代入求出即可.【详解】(x﹣2y)(x+2y)﹣(x﹣2y)2=x2﹣4y2﹣(x2﹣4xy+4y2)=x2﹣4y2﹣x2+4xy﹣4y2=4xy﹣8y2,当x=3, y=﹣1时,原式=4×3×(﹣1)﹣8×(﹣1)2=﹣20.【点睛】本题考查整式的化简求值, 涉及平方差公式、完全平方公式、合并同类项等知识, 熟练掌握整式的乘法运算法则和乘法公式的运用是解答的关键.15. (1)3;(2)31;(3)25.【分析】(1)把多项式乘积展开, 再将已知 代入, 即可求解;(2)根据(1)得到 , 再利用完全平方公式, 即可求解;(3)根据 将 用 来表示, 再代入 , 合并同类项即可求解.【详解】解: (1)∵ , 而 ,∴ ()=324=3254=3xy x y -++--+⨯-.故答案为 .(2)由(1)知 ,∴ ()22224=2=523=31x xy y x y xy +++++⨯. 故答案为 .(3)∵ , 得 ,则()()22225=55525105525x xy y y y y y y y y y y ++-+-+=-++-+=. 故答案为 .【点睛】本题目考查整式的乘法, 难度一般, 是常考知识点, 熟练掌握代数式之间的转化是顺利解题的关键.16.(1)m(1, n(5;(2)(a(2b )2(a2(4ab(4b2;(3)2a2(5ab(3b2((a(b)(2a(3b), 详见解析【分析】(1)结合图形和条件分析可以得出按裁法二裁剪时, 可以裁出B 型板1块, 按裁法三裁剪时, 可以裁出5块B 型板;(2)看图即可得出所求的式子;(3)通过画图能更好的理解题意, 从而得出结果. 由于构成的是长方形, 它的面积等于所给图片的面积之和, 从而因式分解.【详解】(1)按裁法二裁剪时, 2块A 型板材块的长为120cm, 150-120=30, 所以可裁出B 型板1块, 按裁法三裁剪时, 全部裁出B 型板, 150÷30=5, 所以可裁出5块B 型板; ∴m=1, n=5.故答案为:1, 5;(2)如下图:发现的等式为: (a(2b )2(a2(4ab(4b2;故答案为: (a(2b )2(a2(4ab(4b2.(3)按题意画图如下:∵构成的长方形面积等于所给图片的面积之和,∴2a 2+5ab +3b 2=(a +b )(2a +3b ).【点睛】本题考查了完全平方公式和几何图形的应用及一元一次方程的应用, 关键是根据学生的画图能力, 计算能力来解答.17.149299a b ⎧=⎪⎪⎨⎪=⎪⎩【分析】因为两个方程组有相同的解, 故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组, 求出未知数的值, 再代入另一组方程组即可.【详解】354526x y ax by -=⎧⎨+=-⎩①③ 和2348x y ax by +=-⎧⎨-=⎩②④ 解: 联立①②得:解得:12x y =⎧⎨=-⎩将 代入③④得: 解得:149299a b ⎧=⎪⎪⎨⎪=⎪⎩【点睛】此题考查了二元一次方程组的解, 方程组的解即为能使方程组中两方程都成立的未知数的值.18. (1)2;(2)7a4+4a6+a2;(3)15x+19;(4)4x2+4xy+y2﹣4【分析】(1)首先利用负整数指数幂的性质、零次幂的性质、绝对值的性质进行计算, 再算加减即可;(2)首先利用积的乘方的计算法则、单项式乘以单项式计算法则计算, 再合并同类项即可;(3)首先利用完全平方公式、多项式乘以多项式计算法则计算, 再合并同类项即可;(4)首先利用平方差计算, 再利用完全平方公式进行计算即可.【详解】解: (1)原式=8﹣1﹣5=2;(2)原式=9a4﹣2a4+4a6+a2,=7a4+4a6+a2;(3)原式=x2+10x+25﹣(x2﹣3x﹣2x+6),=x2+10x+25﹣x2+3x+2x﹣6,=15x+19;(4)原式=(2x+y)2﹣4,=4x2+4xy+y2﹣4.【点睛】本题考查的是实数的运算, 幂的运算及合并同类项, 整式的混合运算, 掌握以上知识点是解题的关键.19. (1);(2)或;(3)1或2.【分析】(1)根据题意直接利用加减消元法进行计算求解即可;(2)由题意根据和以及(n为整数)得到三个关于k的方程, 求出k即可;(3)根据题意用含m的代数式表示出k, 根据, 确定m的取值范围, 由m为正整数, 求得m的值即可.【详解】解: (1),①+②得: , 解得: ,①-②得:, 解得:,∴二元一次方程组的解为: .(2)∵, ,∴, 即, 解得: ;∵, ,∴, 即, 解得: ;∵(n为正整数), ,∴为偶数, 即, 解得: ;当时, , 为奇数, 不合题意, 故舍去.综上52k=或12k=-.(3)∵, 即,∴2114mk-=,∵14k≤,∴, 解得,∵m为正整数,∴m=1或2.【点睛】本题考查解二元一次方程组以及解一元一次不等式, 根据题意列出不等式是解题的关键.20. (1)(2)【分析】(1)运用加减消元法先消除x, 求y的值后代入方程②求x得解;(2)先分别解每个不等式, 然后求公共部分, 确定不等式组的解集.【详解】解: (1)①×2-②, 得 7y=7,∴y=1.把y=1代入②, 得 x=2.∴21 xy=⎧⎨=⎩.(2)解不等式得.解不等式得.∴不等式组的解集为.【点睛】此题考查解方程组和不等式组, 属常规基础题, 难度不大.。
人教版七年级下册数学期末解答题压轴题试卷含解析

人教版七年级下册数学期末解答题压轴题试卷含解析一、解答题1.工人师傅准备从一块面积为25平方分米的正方形工料上裁剪出一块18平方分米的长方形的工件.(1)求正方形工料的边长;(2)若要求裁下来的长方形的长宽的比为3:2,问这块正方形工料是否合格?(参考数据:2=1.414,3=1.732,5=2.236)2.张华想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.他不知能否裁得出来,正在发愁.李明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意李明的说法吗?张华能用这块纸片裁出符合要求的纸片吗?3.如图用两个边长为18cm的小正方形纸片拼成一个大的正方形纸片,沿着大正方形纸片的边的方向截出一个长方形纸片,能否使截得的长方形纸片长宽之比为3:2,且面积为30cm2请说明理由.4.求下图44⨯的方格中阴影部分正方形面积与边长.5.有一块正方形钢板,面积为16平方米.(1)求正方形钢板的边长.(2)李师傅准备用它裁剪出一块面积为12平方米的长方形工件,且要求长宽之比为3:2,问李师傅能办到吗?若能,求出长方形的长和宽;若不能,请说明理由.(参考数≈).2 1.414≈3 1.732二、解答题6.(1)如图①,若∠B+∠D=∠E,则直线AB与CD有什么位置关系?请证明(不需要注明理由).(2)如图②中,AB//CD,又能得出什么结论?请直接写出结论.(3)如图③,已知AB//CD,则∠1+∠2+…+∠n-1+∠n的度数为.7.如图1,已知直线m ∥n ,AB 是一个平面镜,光线从直线m 上的点O 射出,在平面镜AB 上经点P 反射后,到达直线n 上的点Q .我们称OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB .(1)如图1,若∠OPQ =82°,求∠OPA 的度数;(2)如图2,若∠AOP =43°,∠BQP =49°,求∠OPA 的度数;(3)如图3,再放置3块平面镜,其中两块平面镜在直线m 和n 上,另一块在两直线之间,四块平面镜构成四边形ABCD ,光线从点O 以适当的角度射出后,其传播路径为 O→P→Q→R→O→P→…试判断∠OPQ 和∠ORQ 的数量关系,并说明理由.8.如图1,MN ∥PQ ,点C 、B 分别在直线MN 、PQ 上,点A 在直线MN 、PQ 之间. (1)求证:∠CAB =∠MCA +∠PBA ;(2)如图2,CD ∥AB ,点E 在PQ 上,∠ECN =∠CAB ,求证:∠MCA =∠DCE ; (3)如图3,BF 平分∠ABP ,CG 平分∠ACN ,AF ∥CG .若∠CAB =60°,求∠AFB 的度数.9.如图,//MN PQ ,直线AD 与MN 、PQ 分别交于点A 、D ,点B 在直线PQ 上,过点B 作BG AD ⊥,垂足为点G .(1)如图1,求证:90MAG PBG ∠+∠=︒;(2)若点C 在线段AD 上(不与A 、D 、G 重合),连接BC ,MAG ∠和PBC ∠的平分线交于点H 请在图2中补全图形,猜想并证明CBG ∠与AHB ∠的数量关系;10.已知,AB∥CD.点M在AB上,点N在CD上.(1)如图1中,∠BME、∠E、∠END的数量关系为:;(不需要证明)如图2中,∠BMF、∠F、∠FND的数量关系为:;(不需要证明)(2)如图3中,NE平分∠FND,MB平分∠FME,且2∠E+∠F=180°,求∠FME的度数;(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,且EQ∥NP,则∠FEQ的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ的度数.三、解答题11.已知,如图①,∠BAD=50°,点C为射线AD上一点(不与A重合),连接BC.(1)[问题提出]如图②,AB∥CE,∠BCD=73 °,则:∠B= .(2)[类比探究]在图①中,探究∠BAD、∠B和∠BCD之间有怎样的数量关系?并用平行....线的性质....说明理由.(3)[拓展延伸]如图③,在射线BC上取一点O,过O点作直线MN使MN∥AD,BE平分OG BE交AD于G点,当C点沿着射∠ABC交AD于E点,OF平分∠BON交AD于F点,//线AD方向运动时,∠FOG的度数是否会变化?若变化,请说明理由;若不变,请求出这个不变的值.12.如图1,O 为直线AB 上一点,过点O 作射线,30OC AOC ︒∠=,将一直角三角板(30M ︒∠=)的直角顶点放在点O 处,一边ON 在射线OA 上,另一边OM 与OC 都在直线AB 的上方,将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周.(1)几秒后ON 与OC 重合?(2)如图2,经过t 秒后,//MN AB ,求此时t 的值.(3)若三角板在转动的同时,射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC 与OM 重合?请画图并说明理由.(4)在(3)的条件下,求经过多长时间OC 平分MOB ∠?请画图并说明理由. 13.已知两条直线l 1,l 2,l 1∥l 2,点A ,B 在直线l 1上,点A 在点B 的左边,点C ,D 在直线l 2上,且满足115ADC ABC ∠=∠=o .(1)如图①,求证:AD ∥BC ;(2)点M ,N 在线段CD 上,点M 在点N 的左边且满足MAC BAC ∠=∠,且AN 平分∠CAD ;(Ⅰ)如图②,当30ACD ∠=o 时,求∠DAM 的度数; (Ⅱ)如图③,当8CAD MAN ∠=∠时,求∠ACD 的度数. 14.综合与探究综合与实践课上,同学们以“一个含30角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a ,b ,且//a b ,三角形ABC 是直角三角形,90BCA ∠=︒,30BAC ∠=︒,60ABC ∠=︒操作发现:(1)如图1.148∠=︒,求2∠的度数;(2)如图2.创新小组的同学把直线a 向上平移,并把2∠的位置改变,发现21120∠-∠=︒,请说明理由. 实践探究:(3)填密小组在创新小组发现的结论的基础上,将图2中的图形继续变化得到图3,AC 平分BAM ∠,此时发现1∠与2∠又存在新的数量关系,请写出1∠与2∠的数量关系并说明理由.15.如图1,在平面直角坐标系中,()()02A a C b ,,,,且满足()240a b a b ++-+=,过C 作CB x ⊥轴于B(1)求三角形ABC 的面积.(2)发过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,若,90()CAB ACB a αββ∠=∠=+=︒,求AED ∠的度数.(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等?若存在,求出P 点坐标;若不存在;请说明理由.四、解答题16.如图,直线m 与直线n 互相垂直,垂足为O 、A 、B 两点同时从点O 出发,点A 沿直线m 向左运动,点B 沿直线n 向上运动.(1)若∠BAO 和∠ABO 的平分线相交于点Q ,在点A ,B 的运动过程中,∠AQB 的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.(2)若AP 是∠BAO 的邻补角的平分线,BP 是∠ABO 的邻补角的平分线,AP 、BP 相交于点P ,AQ 的延长线交PB 的延长线于点C ,在点A ,B 的运动过程中,∠P 和∠C 的大小是否会发生变化?若不发生变化,请求出∠P 和∠C 的度数;若发生变化,请说明理由.17.(生活常识)射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图 1,MN 是平面镜,若入射光线AO 与水平镜面夹角为∠1,反射光线OB 与水平镜面夹角为∠2,则∠1=∠2 .(现象解释)如图 2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB 经过两次反射,得到反射光线CD.求证AB∥CD.(尝试探究)如图 3,有两块平面镜OM,ON,且∠MON =55︒,入射光线AB 经过两次反射,得到反射光线CD,光线AB 与CD 相交于点E,求∠BEC 的大小.(深入思考)如图 4,有两块平面镜OM,ON,且∠MON =α ,入射光线AB 经过两次反射,得到反射光线CD,光线AB 与CD 所在的直线相交于点E,∠BED=β , α 与β 之间满足的等量关系是 .(直接写出结果)18.操作示例:如图1,在△ABC中,AD为BC边上的中线,△ABD的面积记为S1,△ADC 的面积记为S2.则S1=S2.解决问题:在图2中,点D、E分别是边AB、BC的中点,若△BDE的面积为2,则四边形ADEC的面积为 .拓展延伸:(1)如图3,在△ABC中,点D在边BC上,且BD=2CD,△ABD的面积记为S1,△ADC的面积记为S2.则S1与S2之间的数量关系为.(2)如图4,在△ABC中,点D、E分别在边AB、AC上,连接BE、CD交于点O,且BO=2EO,CO=DO,若△BOC的面积为3,则四边形ADOE的面积为 .19.如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)仔细观察,在图2中有个以线段AC为边的“8字形”;(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数;(3)在图2中,若设∠C=α,∠B=β,∠CAP=13∠CAB,∠CDP=13∠CDB,试问∠P与∠C、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为.20.阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是120°,40°,20°,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.(1)如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为__________(2)如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.【参考答案】一、解答题1.(1)正方形工料的边长是 5 分米;(2)这块正方形工料不合格,理由见解析.【详解】试题分析:(1)根据正方形的面积公式求出的值即可;(2)设长方形的长宽分别为3x分米、2x分米,得出方程3解析:(1)正方形工料的边长是 5 分米;(2)这块正方形工料不合格,理由见解析.【详解】试题分析:(125的值即可;(2)设长方形的长宽分别为3x分米、2x分米,得出方程3x•2x=18,求出3长方形的长和宽和5比较即可得出答案.试题解析:(1)∵正方形的面积是 25 平方分米,∴正方形工料的边长是 5 分米;(2)设长方形的长宽分别为 3x 分米、2x 分米,则3x•2x=18,x2=3,x13,x2=335,3,即这块正方形工料不合格.2.不同意,理由见解析.【详解】试题分析:设面积为300平方厘米的长方形的长宽分为3x厘米,2x厘米,则3x•2x=300,x2=50,解得x=,而面积为400平方厘米的正方形的边长为20厘米,由于解析:不同意,理由见解析.【详解】试题分析:设面积为300平方厘米的长方形的长宽分为3x厘米,2x厘米,则3x•2x=300,x2=50,解得x=400平方厘米的正方形的边长为20厘米,由于20,所以用一块面积为400平方厘米的正方形纸片,沿着边的方向裁不出一块面积为300平方厘米的长方形纸片,使它的长宽之比为3:2.试题解析:解:不同意李明的说法.设长方形纸片的长为3x(x>0)cm,则宽为2x cm,依题意得:3x•2x=300,6x2=300,x2=50,∵x>0,∴x∴长方形纸片的长为cm,∵50>49,∴7,∴21,即长方形纸片的长大于20cm,由正方形纸片的面积为400 cm2,可知其边长为20cm,∴长方形纸片的长大于正方形纸片的边长.答:李明不能用这块纸片裁出符合要求的长方形纸片.点睛:本题考查了算术平方根的定义:一个正数的正的平方根叫这个数的算术平方根;0的算术平方根为0.也考查了估算无理数的大小.3.不能截得长宽之比为,且面积为cm2的长方形纸片,见解析【分析】根据拼图求出大正方形的边长,再根据长方形的长、宽之比为3:2,计算长方形的长与宽进行验证即可.【详解】解:不能,因为大正方形纸解析:不能截得长宽之比为3:2,且面积为30cm2的长方形纸片,见解析【分析】根据拼图求出大正方形的边长,再根据长方形的长、宽之比为3:2,计算长方形的长与宽进行验证即可.【详解】解:不能,2+2=36(cm2),所以大正方形的边长为6cm,设截出的长方形的长为3b cm,宽为2b cm,则6b2=30,所以b所以3b所以不能截得长宽之比为3:2,且面积为30cm2的长方形纸片.【点睛】本题考查了算术平方根,理解算术平方根的意义是正确解答的关键.4.8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可.【详解】解:正方形面积=4×4-4××2×2=8; 正方形的边解析:8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可. 【详解】解:正方形面积=4×4-4×12×2×2=8;正方形的边长 【点睛】本题考查了算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x叫做a5.(1)4米 (2)见解析 【分析】(1)根据正方形边长与面积间的关系求解即可;(2)设长方形的长宽分别为米、米,由其面积可得x 值,比较长方形的长和宽与正方形边长的大小可得结论. 【详解】 解解析:(1)4米 (2)见解析 【分析】(1)根据正方形边长与面积间的关系求解即可;(2)设长方形的长宽分别为3x 米、2x 米,由其面积可得x 值,比较长方形的长和宽与正方形边长的大小可得结论. 【详解】解:(1)正方形的面积是16平方米, ∴4=米;(2)设长方形的长宽分别为3x 米、2x 米, 则3212x x •=, 22x =,x34x =,24x =<,∴长方形长是4米,所以李师傅不能办到.【点睛】本题考查了算术平方根的实际应用,灵活的利用算术平方根表示正方形和长方形的边长是解题的关键.二、解答题6.(1)AB//CD,证明见解析;(2)∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠Fn-1+∠D ;(3)(n-1)•180°【分析】(1)过点E作EF//AB,利用平行线的性质则可得出解析:(1)AB//CD,证明见解析;(2)∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D;(3)(n-1)•180°【分析】(1)过点E作EF//AB,利用平行线的性质则可得出∠B=∠BEF,再由已知及平行线的判定即可得出AB∥CD;(2)如图,过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥AB,根据探究(1)的证明过程及方法,可推出∠E+∠G=∠B+∠F+∠D,则可由此得出规律,并得出∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D;(3)如图,过点M作EF∥AB,过点N作GH∥AB,则可由平行线的性质得出∠1+∠2+∠MNG =180°×2,依此即可得出此题结论.【详解】解:(1)过点E作EF//AB,∴∠B=∠BEF.∵∠BEF+∠FED=∠BED,∴∠B+∠FED=∠BED.∵∠B+∠D=∠E(已知),∴∠FED=∠D.∴CD//EF(内错角相等,两直线平行).∴AB//CD.(2)过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥AB,∵AB∥CD,∴AB∥EM∥FN∥GH∥CD,∴∠B=∠BEM,∠MEF=∠EFN,∠NFG=∠FGH,∠HGD=∠D,∴∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D,即∠E+∠G=∠B+∠F+∠D.由此可得:开口朝左的所有角度之和与开口朝右的所有角度之和相等,∴∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠F n-1+∠D.故答案为:∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D.(3)如图,过点M作EF∥AB,过点N作GH∥AB,∴∠APM+∠PME=180°,∵EF∥AB,GH∥AB,∴EF∥GH,∴∠EMN+∠MNG=180°,∴∠1+∠2+∠MNG =180°×2,依次类推:∠1+∠2+…+∠n-1+∠n=(n-1)•180°.故答案为:(n-1)•180°.【点睛】本题考查了平行线的性质与判定,属于基础题,关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.7.(1)49°,(2)44°,(3)∠OPQ=∠ORQ【分析】(1)根据∠OPA=∠QPB.可求出∠OPA的度数;(2)由∠AOP=43°,∠BQP=49°可求出∠OPQ的度数,转化为(1)来解解析:(1)49°,(2)44°,(3)∠OPQ=∠ORQ【分析】(1)根据∠OPA=∠QP B.可求出∠OPA的度数;(2)由∠AOP=43°,∠BQP=49°可求出∠OPQ的度数,转化为(1)来解决问题;(3)由(2)推理可知:∠OPQ=∠AOP+∠BQP,∠ORQ=∠DOR+∠RQC,从而∠OPQ=∠ORQ.【详解】解:(1)∵∠OPA=∠QPB,∠OPQ=82°,∴∠OPA=(180°-∠OPQ)×12=(180°-82°)×12=49°,(2)作PC∥m,∵m∥n,∴m∥PC∥n,∴∠AOP=∠OPC=43°,∠BQP=∠QPC=49°,∴∠OPQ=∠OPC+∠QPC=43°+49°=92°,∴∠OPA=(180°-∠OPQ)×12=(180°-92°)×1244°,(3)∠OPQ=∠ORQ.理由如下:由(2)可知:∠OPQ=∠AOP+∠BQP,∠ORQ=∠DOR+∠RQC,∵入射光线与平面镜的夹角等于反射光线与平面镜的夹角,∴∠AOP=∠DOR,∠BQP=∠RQC,∴∠OPQ=∠ORQ.【点睛】本题主要考查了平行线的性质和入射角等于反射角的规定,解决本题的关键是注意问题的设置环环相扣、前为后用的设置目的.8.(1)证明见解析;(2)证明见解析;(3)120°.【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∠MCA=∠DAC,∠PBA=∠DAB,根据角的和差等量代换即可得解;(2)解析:(1)证明见解析;(2)证明见解析;(3)120°.【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∠MCA=∠DAC,∠PBA=∠DAB,根据角的和差等量代换即可得解;(2)由两直线平行,同旁内角互补得到∴、∠CAB+∠ACD=180°,由邻补角定义得到∠ECM+∠ECN=180°,再等量代换即可得解;(3)由平行线的性质得到,∠FAB=120°﹣∠GCA,再由角平分线的定义及平行线的性质得到∠GCA﹣∠ABF=60°,最后根据三角形的内角和是180°即可求解.【详解】解:(1)证明:如图1,过点A作AD∥MN,∵MN∥PQ,AD∥MN,∴AD ∥MN ∥PQ ,∴∠MCA =∠DAC ,∠PBA =∠DAB ,∴∠CAB =∠DAC +∠DAB =∠MCA +∠PBA ,即:∠CAB =∠MCA +∠PBA ;(2)如图2,∵CD ∥AB ,∴∠CAB +∠ACD =180°,∵∠ECM +∠ECN =180°,∵∠ECN =∠CAB∴∠ECM =∠ACD ,即∠MCA +∠ACE =∠DCE +∠ACE ,∴∠MCA =∠DCE ;(3)∵AF ∥CG ,∴∠GCA +∠FAC =180°,∵∠CAB =60°即∠GCA +∠CAB +∠FAB =180°,∴∠FAB =180°﹣60°﹣∠GCA =120°﹣∠GCA ,由(1)可知,∠CAB =∠MCA +∠ABP ,∵BF 平分∠ABP ,CG 平分∠ACN ,∴∠ACN =2∠GCA ,∠ABP =2∠ABF ,又∵∠MCA =180°﹣∠ACN ,∴∠CAB =180°﹣2∠GCA +2∠ABF =60°,∴∠GCA ﹣∠ABF =60°,∵∠AFB +∠ABF +∠FAB =180°,∴∠AFB =180°﹣∠FAB ﹣∠FBA=180°﹣(120°﹣∠GCA )﹣∠ABF=180°﹣120°+∠GCA ﹣∠ABF=120°.【点睛】本题主要考查了平行线的性质,线段、角、相交线与平行线,准确的推导是解决本题的关键.9.(1)证明见解析;(2)补图见解析;当点在上时,;当点在上时,.【分析】(1)过点作,根据平行线的性质即可求解;(2)分两种情况:当点在上,当点在上,再过点作即可求解.【详解】(1)证明:解析:(1)证明见解析;(2)补图见解析;当点C 在AG 上时,290AHB CBG ∠-∠=︒;当点C 在DG 上时,290AHB CBG ∠+∠=︒.【分析】(1)过点G 作//GE MN ,根据平行线的性质即可求解;(2)分两种情况:当点C 在AG 上,当点C 在DG 上,再过点H 作//HF MN 即可求解.【详解】(1)证明:如图,过点G 作//GE MN ,∴MAG AGE ∠=∠,∵//MN PQ ,∴//GE PQ .∴PBG BGE ∠=∠.∵BG AD ⊥,∴90AGB ∠=︒,∴90MAG PBG AGE BGE AGB ∠+∠=∠+∠=∠=︒.(2)补全图形如图2、图3,猜想:290AHB CBG ∠-∠=︒或290AHB CBG ∠+∠=︒.证明:过点H 作//HF MN .∴1AHF ∠=∠.∵//MN PQ ,∴//HF PQ∴2BHF ∠=∠,∴12AHB AHF BHF ∠=∠+∠=∠+∠.∵AH 平分MAG ∠,∴21MAG ∠=∠.如图3,当点C 在AG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠+∠=∠,∵//MN PQ ,∴MAG GDB ∠=∠,2212290AHB MAG PBG CBGGDB PBG CBG CBG∴∠=∠+∠=∠+∠+∠=∠+∠+∠=︒+∠即290AHB CBG ∠-∠=︒.如图2,当点C 在DG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠-∠=∠.∴2212290AHB MAG PBG CBG CBG ∠=∠+∠=∠+∠-∠=︒-∠.即290AHB CBG ∠+∠=︒.【点睛】本题考查了平行线的基本性质、角平分线的基本性质及角的运算,解题的关键是准确作出平行线,找出角与角之间的数量关系.10.(1)∠BME =∠MEN ﹣∠END ;∠BMF =∠MFN +∠FND ;(2)120°;(3)不变,30°【分析】(1)过E 作EH ∥AB ,易得EH ∥AB ∥CD ,根据平行线的性质可求解;过F 作FH ∥AB解析:(1)∠BME =∠MEN ﹣∠END ;∠BMF =∠MFN +∠FND ;(2)120°;(3)不变,30°【分析】(1)过E 作EH ∥AB ,易得EH ∥AB ∥CD ,根据平行线的性质可求解;过F 作FH ∥AB ,易得FH ∥AB ∥CD ,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME +∠END )+∠BMF -∠FND =180°,可求解∠BMF =60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∠FEQ =12∠BME ,进而可求解.【详解】解:(1)过E 作EH ∥AB ,如图1,∴∠BME =∠MEH ,∵AB ∥CD ,∴HE ∥CD ,∴∠END =∠HEN ,∴∠MEN =∠MEH +∠HEN =∠BME +∠END ,即∠BME =∠MEN ﹣∠END .如图2,过F 作FH ∥AB ,∴∠BMF=∠MFK,∵AB∥CD,∴FH∥CD,∴∠FND=∠KFN,∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN+∠MFN=180°,∴2(∠BME+∠END)+∠BMF﹣∠FND=180°,∴2∠BME+2∠END+∠BMF﹣∠FND=180°,即2∠BMF+∠FND+∠BMF﹣∠FND=180°,解得∠BMF=60°,∴∠FME=2∠BMF=120°;(3)∠FEQ的大小没发生变化,∠FEQ=30°.由(1)知:∠MEN=∠BME+∠END,∵EF平分∠MEN,NP平分∠END,∴∠FEN=12∠MEN=12(∠BME+∠END),∠ENP=12∠END,∵EQ∥NP,∴∠NEQ=∠ENP,∴∠FEQ=∠FEN﹣∠NEQ=12(∠BME+∠END)﹣12∠END=12∠BME,∵∠BME=60°,∴∠FEQ=12×60°=30°.【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键.三、解答题11.(1);(2),见解析;(3)不变,【分析】(1)根据平行线的性质求出,再求出的度数,利用内错角相等可求出角的度数;(2)过点作∥,类似(1)利用平行线的性质,得出三个角的关系; (3)运用解析:(1)23︒;(2)BCD A B ∠=∠+∠,见解析;(3)不变, 25FOG ∠=︒【分析】(1)根据平行线的性质求出50A DCE ∠=∠=︒,再求出BCE ∠的度数,利用内错角相等可求出角的度数;(2)过点C 作CE ∥AB ,类似(1)利用平行线的性质,得出三个角的关系;(3)运用(2)的结论和平行线的性质、角平分线的性质,可求出FOG ∠的度数,可得结论.【详解】(1)因为CE ∥AB ,所以50A DCE ∠=∠=︒,B BCE ∠=∠因为∠BCD =73 °,所以23BCE BCD DCE ∠=∠-∠=︒,故答案为:23︒(2)BCD A B ∠=∠+∠,如图②,过点C 作CE ∥AB ,则A DCE ∠=∠,B BCE ∠=∠.因为BCD DCE BCE ∠=∠+∠,所以BCD BAD B ∠=∠+∠,(3)不变,设ABE x ∠=,因为BE 平分ABC ∠,所以CBE ABE x ∠=∠=.由(2)的结论可知BCD BAD ABC ∠=∠+∠,且50BAD ︒∠=,则:502BCD x ∠=︒+.因为MN ∥AD ,所以502BON BCD x ∠=∠=︒+,因为OF 平分BON ∠, 所以1252COF NOF BON x ∠=∠=∠=︒+. 因为OG ∥BE ,所以COG CBE x ∠=∠=,所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒.【点睛】本题考查了平行线的性质和角平分线的定义,解题关键是熟练运用平行线的性质证明角相等,通过等量代换等方法得出角之间的关系.12.(1)10秒;(2)20秒;(3)20秒,画图见解析;(4)秒,画图见解析【分析】(1)用角的度数除以转动速度即可得;(2)求出∠AON=60°,结合旋转速度可得时间t;(3)设∠AON=3解析:(1)10秒;(2)20秒;(3)20秒,画图见解析;(4)703秒,画图见解析【分析】(1)用角的度数除以转动速度即可得;(2)求出∠AON=60°,结合旋转速度可得时间t;(3)设∠AON=3t,则∠AOC=30°+6t,由题意列出方程,解方程即可;(4)根据转动速度关系和OC平分∠MOB,由题意列出方程,解方程即可.【详解】解:(1)∵30÷3=10,∴10秒后ON与OC重合;(2)∵MN∥AB∴∠BOM=∠M=30°,∵∠AON+∠BOM=90°,∴∠AON=60°,∴t=60÷3=20∴经过t秒后,MN∥AB,t=20秒.(3)如图3所示:∵∠AON+∠BOM=90°,∠BOC=∠BOM,∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,设∠AON=3t,则∠AOC=30°+6t,∵OC与OM重合,∵∠AOC+∠BOC=180°,可得:(30°+6t)+(90°-3t)=180°,解得:t=20秒;即经过20秒时间OC与OM重合;(4)如图4所示:∵∠AON+∠BOM=90°,∠BOC=∠COM ,∵三角板绕点O 以每秒3°的速度,射线OC 也绕O 点以每秒6°的速度旋转,设∠AON=3t ,∠AOC=30°+6t ,∵∠BOM+∠AON=90°,∴∠BOC=∠COM=12∠BOM=12(90°-3t ),由题意得:180°-(30°+6t )=12( 90°-3t ), 解得:t=703秒, 即经过703秒OC 平分∠MOB . 【点睛】 此题考查了平行线的判定与性质,角的计算以及方程的应用,关键是应该认真审题并仔细观察图形,找到各个量之间的关系求出角的度数是解题的关键.13.(1)证明见解析;(2)(Ⅰ);(Ⅱ).【分析】(1)先根据平行线的性质可得,再根据角的和差可得,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得,从而可得,再根据角的和差可得 解析:(1)证明见解析;(2)(Ⅰ)5DAM ∠=︒;(Ⅱ)25ACD ∠=︒.【分析】(1)先根据平行线的性质可得65BAD ∠=︒,再根据角的和差可得180BAD ABC ∠+∠=︒,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得30BAC ACD ∠=∠=︒,从而可得30MAC ∠=︒,再根据角的和差可得35DAC ∠=︒,然后根据DAM DAC MAC ∠=∠-∠即可得;(Ⅱ)设MAN x ∠=,从而可得8CAD x ∠=,先根据角平分线的定义可得142CAN CAD x ∠=∠=,再根据角的和差可得5BAC MAC x ∠=∠=,然后根据65CAD BAC BAD ∠+∠=∠=︒建立方程可求出x 的值,从而可得BAC ∠的度数,最后根据平行线的性质即可得.【详解】(1)12//,115l l ADC ∠=︒,18065BAD ADC ∴∠=︒-∠=︒,又115ABC ∠=︒,180BAD ABC ∴∠+∠=︒,//AD BC ∴;(2)(Ⅰ)12//,30l l ACD ∠=︒,30BAC ACD ∴∠=∠=︒,MAC BAC ∠=∠,30MAC ∴∠=︒,由(1)已得:65BAD ∠=︒,35DAC BAD BAC ∴∠=∠-∠=︒,35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒;(Ⅱ)设MAN x ∠=,则8CAD x ∠=, AN 平分CAD ∠,142CAN CAD x ∴∠=∠=, 5MAC CAN MAN x ∴∠=∠+∠=,MAC BAC ∠=∠,5BAC x ∴∠=,由(1)已得:65BAD ∠=︒,65CAD BAC BAD ∴∠+∠=∠=︒,即8565x x +=︒,解得5x =︒,525BAC x ∴∠==︒,又12//l l ,25ACD BAC ∴∠=∠=︒.【点睛】本题考查了平行线的判定与性质、角的和差、角平分线的定义、一元一次方程的几何应用等知识点,熟练掌握平行线的判定与性质是解题关键.14.(1);(2)理由见解析;(3),理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠ 解析:(1)242∠=︒;(2)理由见解析;(3)12∠=∠,理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠DBC ,则∠ABD =∠ABC−∠DBC =60°−∠1,进而得出结论;(3)过点C 作CP ∥a ,由角平分线定义得∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,由平行线的性质得∠1=∠BAM =60°,∠PCA =∠CAM =30°,∠2=∠BCP =60°,即可得出结论.【详解】解:(1)如图1 148∠=︒,90BCA ∠=︒,3180142BCA ∴∠=︒-∠-∠=︒,//a b,∴∠=∠=︒;2342图1BD a,(2)理由如下:如图2.过点B作//图2ABD∴∠+∠=︒,2180a b,//b BD∴,//∴∠=∠DBC,1∴∠=∠-∠=︒-∠,601ABD ABC DBC∴∠+︒-∠=︒,2601180∴∠-∠=︒;21120(3)12∠=∠,图3CP a,理由如下:如图3,过点C作//AC平分BAM∠,∴∠=∠=︒,CAM BAC30∠=∠=︒,260BAM BACa b,又//CP b∴,//∠=∠=︒,160BAM30PCA CAM ∴∠=∠=︒,903060BCP BCA PCA ∴∠=∠-∠=︒-︒=︒,又//CP a ,260BCP ∴∠=∠=︒,12∠∠∴=.【点睛】本题是三角形综合题目,考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识;本题综合性强,熟练掌握平移的性质和平行线的性质是解题的关键.15.(1)4;(2)45°;(3)P (0,-1)或(0,3)【分析】(1)根据非负数的性质得到a =−b ,a−b +4=0,解得a =−2,b =2,则A (−2,0),B (2,0),C (2,2),即可计算出解析:(1)4;(2)45°;(3)P (0,-1)或(0,3)【分析】(1)根据非负数的性质得到a =−b ,a−b +4=0,解得a =−2,b =2,则A (−2,0),B (2,0),C (2,2),即可计算出三角形ABC 的面积=4;(2)由于CB ∥y 轴,BD ∥AC ,则∠CAB =∠ABD ,即∠3+∠4+∠5+∠6=90°,过E 作EF ∥AC ,则BD ∥AC ∥EF ,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED =∠1+∠2=12×90°=45°;(3)先根据待定系数法确定直线AC 的解析式为y =12x +1,则G 点坐标为(0,1),然后利用S △PAC =S △APG +S △CPG 进行计算.【详解】解:(1)由题意知:a =−b ,a−b +4=0,解得:a =−2,b =2,∴ A (−2,0),B (2,0),C (2,2),∴S △ABC =1AB BC=42⋅; (2)∵CB ∥y 轴,BD ∥AC ,∴∠CAB =∠ABD ,∴∠3+∠4+∠5+∠6=90°,过E 作EF ∥AC ,∵BD ∥AC ,∴BD ∥AC ∥EF ,∵AE ,DE 分别平分∠CAB ,∠ODB ,∴∠3=∠4=∠1,∠5=∠6=∠2,∴∠AED =∠1+∠2=12×90°=45°;(3)存在.理由如下:设P 点坐标为(0,t ),直线AC 的解析式为y =kx +b ,把A (−2,0)、C (2,2)代入得: -2k+b=02k+b=2⎧⎨⎩,解得1k=2b=1⎧⎪⎨⎪⎩, ∴直线AC 的解析式为y =12x +1,∴G 点坐标为(0,1),∴S △PAC =S △APG +S △CPG =12|t−1|•2+12|t−1|•2=4,解得t =3或−1,∴P 点坐标为(0,3)或(0,−1).【点睛】本题考查了绝对值、平方的非负性,平行线的判定与性质:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,内错角相等.四、解答题16.(1)∠AQB 的大小不发生变化,∠AQB =135°;(2)∠P 和∠C 的大小不变,∠P=45°,∠C=45°.【分析】第(1)题因垂直可求出∠ABO 与∠BAO 的和,由角平分线和角的和差可求出∠BA 解析:(1)∠AQB 的大小不发生变化,∠AQB =135°;(2)∠P 和∠C 的大小不变,∠P=45°,∠C=45°.【分析】第(1)题因垂直可求出∠ABO 与∠BAO 的和,由角平分线和角的和差可求出∠BAQ 与∠ABQ 的和,最后在△ABQ 中,根据三角形的内角各定理可求∠AQB 的大小.第(2)题求∠P 的大小,用邻补角、角平分线、平角、直角和三角形内角和定理等知识求解.【详解】解:(1)∠AQB 的大小不发生变化,如图1所示,其原因如下:∵m⊥n,∴∠AOB=90°,∵在△ABO中,∠AOB+∠ABO+∠BAO=180°,∴∠ABO+∠BAO=90°,又∵AQ、BQ分别是∠BAO和∠ABO的角平分线,∴∠BAQ=12∠BAC,∠ABQ=12∠ABO,∴∠BAQ+∠ABQ=12 (∠ABO+∠BAO)=190452⨯=又∵在△ABQ中,∠BAQ+∠ABQ+∠AQB=180°,∴∠AQB=180°﹣45°=135°.(2)如图2所示:①∠P的大小不发生变化,其原因如下:∵∠ABF+∠ABO=180°,∠EAB+∠BAO=180°∠BAQ+∠ABQ=90°,∴∠ABF+∠EAB=360°﹣90°=270°,又∵AP、BP分别是∠BAE和∠ABP的角平分线,∴∠PAB=12∠EAB,∠PBA=12∠ABF,∴∠PAB+∠PBA=12 (∠EAB+∠ABF)=12×270°=135°,又∵在△PAB中,∠P+∠PAB+∠PBA=180°,∴∠P=180°﹣135°=45°.②∠C的大小不变,其原因如下:∵∠AQB=135°,∠AQB+∠BQC=180°,∴∠BQC=180°﹣135°,又∵∠FBO=∠OBQ+∠QBA+∠ABP+∠PBF=180°∠ABQ=∠QBO=1∠ABO,∠PBA=∠PBF=∠ABF,2∴∠PBQ=∠ABQ+∠PBA=90°,又∵∠PBC=∠PBQ+∠CBQ=180°,∴∠QBC=180°﹣90°=90°.又∵∠QBC+∠C+∠BQC=180°,∴∠C=180°﹣90°﹣45°=45°【点睛】本题考查三角形内角和定理,垂直,角平分线,平角,直角和角的和差等知识点,同时,也是一个以静求动的一个点型题目,有益于培养学生的思维几何综合题.17.【现象解释】见解析;【尝试探究】BEC 70;【深入思考】2.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠解析:【现象解释】见解析;【尝试探究】∠BEC = 70︒;【深入思考】β= 2α.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠3+∠4=180°,即可得出∠DCB+∠ABC=180°,即可证得AB∥CD;[尝试探究]根据三角形内角和定理求得∠2+∠3=125°,根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用平角的定义得出∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,即可得出∠EBC+BCE=360°-250°=110°,根据三角形内角和定理即可得出∠BEC=180°-110°=70°;[深入思考]利用平角的定义得出∠ABC=180°-2∠2,∠BCD=180°-2∠3,利用外角的性质∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,而∠BOC=∠3-∠2=α,即可证得β=2α.【详解】[现象解释]如图2,∵OM⊥ON,∴∠CON=90°,∴∠2+∠3=90°∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,∴∠DCB+∠ABC=180°,∴AB∥CD;【尝试探究】如图3,在△OBC中,∵∠COB=55°,∴∠2+∠3=125°,∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=250°,∵∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,∴∠EBC+BCE=360°-250°=110°,∴∠BEC=180°-110°=70°;【深入思考】如图4,β=2α,理由如下:∵∠1=∠2,∠3=∠4,∴∠ABC=180°-2∠2,∠BCD=180°-2∠3,∴∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,∵∠BOC=∠3-∠2=α,∴β=2α.【点睛】本题考查了平行线的判定,三角形外角的性质以及三角形内角和定理,熟练掌握三角形的性质是解题的关键.18.解决问题:6;拓展延伸:(1)S1=2S2 (2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)解析:解决问题:6;拓展延伸:(1)S1=2S2(2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)作△ABD的中线AE,则有BE=ED=DC,从而得到△ABE的面积=△AED的面积=△ADC的面积,由此即可得到结论;(2)连接AO.则可得到△BOD的面积=△BOC的面积,△AOC的面积=△AOD的面积,△EOC的面积=△BOC的面积的一半,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,求出a、b的值,即可得到结论.试题解析:解:解决问题连接AE.∵点D、E分别是边AB、BC的中点,∴S△ADE=S△BDE,S△ABE=S△AEC.∵S△BDE =2,∴S△ADE =2,∴S△ABE=S△AEC=4,∴四边形ADEC的面积=2+4=6.拓展延伸:解:(1)作△ABD的中线AE,则有BE=ED=DC,∴△ABE的面积=△AED的面积=△ADC的面积= S2,∴S1=2S2.(2)连接AO.∵CO=DO,∴△BOD的面积=△BOC的面积=3,△AOC的面积=△AOD的面积.∵BO=2EO,∴△EOC的面积=△BOC的面积的一半=1.5,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,解得:a=6,b=4.5,∴四边形ADOE的面积为=a+b=6+4.5=10.5.。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是 .(请选择正确的选项)A .a 2﹣b 2=(a +b )(a ﹣b )B .a 2﹣2ab +b 2=(a ﹣b )2C .a 2+ab =a (a +b )(2)若x 2﹣y 2=16,x +y =8,求x ﹣y 的值;(3)计算:(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020). 2.3321130y x --=,|1|24z x y -=--+,求x y z ++的平方根.3.已知1502x x +-=,求值; (1)221x x +(2)1x x- 4.计算:(1)21122⎛⎫⎛⎫-⨯- ⎪ ⎪⎝⎭⎝⎭; (2)m 2•m 4+(﹣m 3)2;(3)(x +y )(2x ﹣3y );(4)(x +3)2﹣(x +1)(x ﹣1).5.已知,关于x 、y 二元一次方程组237921x y a x y -=-⎧⎨+=-⎩的解满足方程2x-y=13,求a 的值.6.问题1:现有一张△ABC 纸片,点D 、E 分别是△ABC 边上两点,若沿直线DE 折叠. (1)探究1:如果折成图①的形状,使A 点落在CE 上,则∠1与∠A 的数量关系是 ;(2)探究2:如果折成图②的形状,猜想∠1+∠2和∠A 的数量关系是 ; (3)探究3:如果折成图③的形状,猜想∠1、∠2和∠A 的数量关系,并说明理由.(4)问题2:将问题1推广,如图④,将四边形ABCD 纸片沿EF 折叠,使点A 、B 落在四边形EFCD 的内部时,∠1+∠2与∠A 、∠B 之间的数量关系是.7.计算:(1)022019()32020-- (2)4655x x x x ⋅+⋅8.仔细阅读下列解题过程:若2222690a ab b b ++-+=,求a b 、的值.解:2222690a ab b b ++-+=222222690()(3)003033a ab b b b a b b a b b a b ∴+++-+=∴++-=∴+=-=∴=-=,,根据以上解题过程,试探究下列问题:(1)已知2222210x xy y y -+-+=,求2x y +的值;(2)已知2254210a b ab b +--+=,求a b 、的值;(3)若248200m n mn t t =++-+=,,求2m t n -的值.9.如图①所示,在三角形纸片ABC 中,70C ∠=︒,65B ∠=︒,将纸片的一角折叠,使点A 落在ABC 内的点A '处.(1)若140∠=︒,2∠=________.(2)如图①,若各个角度不确定,试猜想1∠,2∠,A ∠之间的数量关系,直接写出结论.②当点A 落在四边形BCDE 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,A ∠,1∠,2∠之间又存在什么关系?请说明.(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的123456∠+∠+∠+∠+∠+∠和是________.10.已知:如图,直线BD 分别交射线AE 、CF 于点B 、D ,连接A 、D 和B 、C ,12180∠+∠=,A C ∠=∠,AD 平分BDF ∠,求证:()1//AD BC ;()2BC 平分DBE ∠.11.因式分解:(1)249x - (2) 22344ab a b b --12.如图,D 、E 、F 分别在ΔABC 的三条边上,DE//AB ,∠1+∠2=180º.(1)试说明:DF//AC ;(2)若∠1=120º,DF 平分∠BDE ,则∠C=______º.13.计算:(1)()()122012514--⎛⎫+-⨯-- ⎪⎝⎭; (2)52342322)(a a a a a +÷-. 14.如图,已知点E 、F 在直线AB 上,点G 在线段CD 上,ED 与FG 交于点H ,∠C =∠EFG ,∠CED =∠GHD .(1)求证:CE ∥GF ;(2)试判断∠AED 与∠D 之间的数量关系,并说明理由;(3)若∠EHF =80°,∠D =30°,求∠AEM 的度数.15.如图,在每个小正方形边长为1的方格纸中,△ABC 的顶点都在方格纸格点上.将△ABC 向左平移2格,再向上平移4格.(1)请在图中画出平移后的△A ′B ′C ′;(2)再在图中画出△ABC 的高CD ;(3)在图中能使S △PBC =S △ABC 的格点P的个数有 个(点P 异于A )16.解方程组:(1)2338y x x y =-⎧⎨-=⎩(2) 743832x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ 17.(类比学习)小明同学类比除法240÷16=15的竖式计算,想到对二次三项式x 2+3x +2进行因式分解的方法: 15162401 6 8080 0 222132 2222 0x x x x x x x x +++++++ 即(x 2+3x +2)÷(x +1)=x +2,所以x 2+3x +2=(x +1)(x +2).(初步应用)小明看到了这样一道被墨水污染的因式分解题:x 2+□x +6=(x +2)(x +☆),(其中□、☆代表两个被污染的系数),他列出了下列竖式:22262 (2)62 0x x x x x x x x +++++-++☆☆☆ 得出□=___________,☆=_________.(深入研究)小明用这种方法对多项式x 2+2x 2-x -2进行因式分解,进行到了:x 3+2x 2-x -2=(x +2)(*).(*代表一个多项式),请你利用前面的方法,列出竖式,将多项式x 3+2x 2-x -2因式分解.18.计算:(1)(y 3)3÷y 6;(2)2021()(3)2π--+-.19.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x 、y 的等式表示) ;(2)若2(32)5x y -=,2(32)9x y +=,求xy 的值;(3)若25,2x y xy +==,求2x y -的值.20.解下列方程组(1)29321x y x y +=⎧⎨-=-⎩. (2)34332(1)11x y x y ⎧+=⎪⎨⎪--=⎩.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)A ;(2)2;(3)20214040【分析】(1)由题意直接根据拼接前后的面积相等进行分析计算即可得出答案;(2)根据题意可知x 2﹣y 2=16,即(x +y )(x ﹣y )=16,又x +y =8,可求出x ﹣y 的值;(3)根据题意利用平方差公式将算式转化为分数的乘积的形式,根据数据规律得出答案.【详解】解:(1)图1的剩余面积为a 2﹣b 2,图2拼接得到的图形面积为(a +b )(a ﹣b ) 因此有,a 2﹣b 2=(a +b )(a ﹣b ),故答案为:A.(2)∵x 2﹣y 2=(x +y )(x ﹣y )=16,又∵x +y =8,∴x ﹣y =16÷8=2;(3)(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020) =(1﹣12)(1+12)(1﹣13)(1+13)(1﹣14)(1+14)……(1﹣12019)(1+12019)(1﹣12020)(1+12020) =12×32×23×43×34×54×……×20182019×20202019×20192020×20212020 =12×20212020 =20214040. 【点睛】本题考查平方差公式的几何意义及应用,掌握公式的结构特征是正确应用的前提,利用公式进行适当的变形是解题的关键.2.【分析】根据题意得到三元一次方程组,解方程组,求出x y z ++,最后求平方根即可.【详解】0=,|1|z -=,=|1|0z -=,∴2113024010y x x y z -+-=⎧⎪-+=⎨⎪-=⎩,解得231x y z =⎧⎪=⎨⎪=⎩,则6x y z ++=,∴x y z ++平方根为.【点睛】本题考查相反数的意义,非负数的表达,解三元一次方程组,求平方根等知识,综合性较强,解题关键是根据题意列出三元一次方程组.3.(1)174;(2)32±【分析】(1)利用完全平方公式(a +b)²=a ²+2ab +b ²解答;(2)利用(1)的结果和完全平方公式(a−b)²=a ²−2ab +b ²解答.【详解】解:(1)由题:152x x +=, 21254x x ⎛⎫∴+= ⎪⎝⎭即2212524x x ++=, 221174x x ∴+= (2)222111792244x x x x ⎛⎫-=+-=-= ⎪⎝⎭ 132x x ∴-=± 【点睛】此题是完全平方公式的应用;两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.4.(1)18-;(2)2m 6;(3)2x 2﹣xy ﹣3y 2;(4)6x +10. 【分析】(1)根据同底数幂的乘法法则进行计算;(2)先根据同底数幂的乘法法则和幂的乘方法则进行计算,再根据合并同类项法则进行计算;(3)根据多项式乘以多项式法则进行计算,再合并同类项;(4)先根据完全平方公式,平方差公式进行计算,再合并同类项.【详解】解:(1)21122⎛⎫⎛⎫-⨯- ⎪ ⎪⎝⎭⎝⎭=312⎛⎫- ⎪⎝⎭18=-; (2)m 2•m 4+(﹣m 3)2=m 6+m 6=2m 6;(3)(x +y )(2x ﹣3y )=2x 2﹣3xy +2xy ﹣3y 2=2x 2﹣xy ﹣3y 2;(4)(x +3)2﹣(x +1)(x ﹣1)=x 2+6x +9﹣x 2+1=6x +10.【点睛】此题考查的是幂的运算性质和整式的运算,掌握同底数幂的乘法法则、幂的乘方法则、多项式乘以多项式法则、完全平方公式和平方差公式是解决此题的关键.5.a=4【分析】先联立x+2y=−1与2x−y=13解出x ,y ,再代入2x−3y=7a−9即可求出a 值.【详解】依题意得21213x y x y +=-⎧⎨-=⎩解得53x y =⎧⎨=-⎩, 代入2x−3y=7a−9,得:a=4,故a 的值为4.【点睛】此题主要考查二元一次方程组的解,解题的关键是熟知二元一次方程组的解法.6.(1)12A ∠=∠;(2)122A ∠+∠=∠;(3)见解析;(4)1222360A B ∠+∠=∠+∠-︒【分析】(1)根据三角形外角性质可得;(2)在四边形A EAD '中,内角和为360°,∠BDA=∠CEA=180°,利用这两个条件,进行角度转化可得关系式;(3)如下图,根据(1)可得∠1=2∠DAA ',∠2=2∠EAA ',从而推导出关系式; (4)根据平角的定义以及四边形的内角和定理,与(2)类似思路探讨,可得关系式.【详解】(1)∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠;(2)∵在四边形A EAD '中,内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理,∠A=∠A '∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ;(3)数量关系:212A ∠-∠=∠理由:如下图,连接AA '由(1)可知:∠1=2∠DAA ',∠2=2∠EAA '∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠';(4)由折叠性质知:∠2=180°-2∠AEF ,∠1=180°-2∠BFE相加得:123602(360)22360A B A B ∠+∠=︒-︒-∠-∠=∠+∠-︒.【点睛】本题考查角度之间的关系,(4)问的解题思路是相同的,主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.7.(1)89;(2)102x ; 【分析】 (1)根据零指数幂和负整数指数幂的运算法则即可计算;(2)根据同底数幂的乘法法则和合并同类项即可计算.【详解】(1)原式=1-19=89; (2)原式=x 10+x 10=2x 10.【点睛】本题考查整式的混合运算,负整数指数幂,零指数幂,解答本题的关键是明确各法则的计算方法.8.(1)23x y +=;(2)21a b ==,;(3)21m t n -=.【分析】(1)首先把第3项22y 裂项,拆成22y y +,再用完全平方公式因式分解,利用非负数的性质求得x y 、代入求得数值;(2)首先把第2项25b 裂项,拆成224b b +,再用完全平方公式因式分解,利用非负数的性质求得a b 、代入求得数值;(3)先把4m n =+代入28200mn t t +-+=,得到关于n 和 t 的式子,再仿照(1)(2)题.【详解】解:(1)2222210x xy y y -+-+=2222210x xy y y y ∴-++-+=22()(1)0x y y ∴-+-=010x y y ∴-=-=,,11x y ∴==,,23x y ∴+=;(2)2254210a b ab b +--+=22244210a b ab b b ∴+-+-+=22(2)(1)0a b b ∴-+-=2010a b b ∴-=-=,21a b ∴==,;(3)4m n =+,2(4)8200n n t t ∴++-+=22448160n n t t ∴+++-+=22(2)(4)0n t ∴++-=2040n t ∴+=-=,24n t ∴=-=,42m n ∴=+=20(2)1m t n -∴=-=【点睛】本题考查的分组分解法、配方法和非负数的性质,对于项数较多的多项式因式分解,分组分解法是一个常用的方法. 首先要观察各项特征,寻找熟悉的式子,熟练掌握平方差公式和完全平方公式是基础.9.(1)50°;(2)①见解析;②见解析;(3)360°.【分析】(1)根据题意,已知70C ∠=︒,65B ∠=︒,可结合三角形内角和定理和折叠变换的性质求解;(2)①先根据折叠得:∠ADE=∠A ′DE ,∠AED=∠A ′ED ,由两个平角∠AEB 和∠ADC 得:∠1+∠2等于360°与四个折叠角的差,化简得结果;②利用两次外角定理得出结论;(3)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'GF+∠B'FG)以及(∠C'DE+∠C'ED)和(∠A'HL+∠A'LH),再利用三角形的内角和定理即可求解.【详解】解:(1)∵70C ∠=︒,65B ∠=︒,∴∠A ′=∠A=180°-(65°+70°)=45°,∴∠A ′ED+∠A ′DE =180°-∠A ′=135°,∴∠2=360°-(∠C+∠B+∠1+∠A ′ED+∠A ′DE )=360°-310°=50°;(2)①122A ∠+∠=∠,理由如下由折叠得:∠ADE=∠A ′DE ,∠AED=∠A ′ED ,∵∠AEB+∠ADC=360°,∴∠1+∠2=360°-∠ADE-∠A ′DE-∠AED-∠A ′ED=360°-2∠ADE-2∠AED ,∴∠1+∠2=2(180°-∠ADE-∠AED )=2∠A ;②221A ∠=∠+∠,理由如下:∵2∠是ADF 的一个外角∴2A AFD ∠=∠+∠.∵AFD ∠是A EF '△的一个外角∴1AFD A '∠=∠+∠又∵A A '∠=∠∴221A ∠=∠+∠(3)如图由题意知,∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'GF+∠B'FG)-(∠C'DE+∠C'ED)-(∠A'HL+∠A'LH)=720°-(180°-∠B')-(180°-C')-(180°-A')=180°+(∠B'+∠C'+∠A')又∵∠B=∠B',∠C=∠C',∠A=∠A',∠A+∠B+∠C=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°.【点睛】题主要考查了折叠变换、三角形、四边形内角和定理.注意折叠前后图形全等;三角形内角和为180°;四边形内角和等于360度.10.(1)见解析;(2)见解析.【解析】【分析】()1求出1BDC ∠=∠,根据平行线的判定得出//AB CF ,根据平行线的性质得出C EBC ∠=∠,求出A EBC ∠=∠,根据平行线的判定得出即可;()2根据角平分线定义求出FDA ADB ∠=∠,根据平行线的性质得出FDA C ∠=∠,ADB DBC ∠=∠,C EBC ∠=∠,求出EBC DBC ∠=∠即可.【详解】()12180BDC ∠+∠=,12180∠+∠=,1BDC ∴∠=∠,//AB CF ∴,C EBC ∴∠=∠,A C ∠=∠,A EBC ∴∠=∠,//AD BC ∴;()2AD 平分BDF ∠,FDA ADB ∴∠=∠,//AD BC ,FDA C ∴∠=∠,ADB DBC ∠=∠,C EBC ∠=∠,EBC DBC ∴∠=∠,BC ∴平分DBE ∠.【点睛】本题考查了平行线的性质和判定,角平分线定义的应用,考查了学生运用性质进行推理的能力,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.11.(1)()()2323x x +-;(2)()22--b a b . 【分析】(1)直接利用平方差公式因式分解即可;(2)先提取公因式,然后利用完全平方公式分解因式即可.【详解】(1) ()()249=2323x x x -+-; (2)()223224444ab a b b b a ab b--=--+=()22--b a b .【点睛】 本题考查了用提公因式法和公式法进行因式分解.注意先提公因式,再利用公式法分解,同时因式分解要彻底,直到不能分解为止.12.(1)见解析;(2)60.【分析】(1)根据平行线的性质得出∠A=∠2,求出∠1+∠A=180°,根据平行线的判定得出即可.(2)根据平行线的性质解答即可.【详解】证明:(1)∵DE∥AB,∴∠A=∠2,∵∠1+∠2=180°.∴∠1+∠A=180°,∴DF∥AC;(2)∵DE∥AB,∠1=120°,∴∠FDE=60°,∵DF平分∠BDE,∴∠FDB=60°,∵DF∥AC,∴∠C=∠FDB=60°【点睛】本题考查了平行线的性质和判定定理,解题的关键是能灵活运用平行线的判定和性质定理进行推理.13.(1)7;(2)55a.【分析】(1)直接利用负整数指数幂的性质、零指数幂的性质分别化简得出答案;(2)直接利用积的乘方运算法则、整式的除法运算法则计算得出答案.【详解】解:(1)(14)﹣1+(﹣2)2×50﹣(﹣1)﹣2;=4+4×1﹣1=4+4﹣1=7;(2)2a5﹣a2•a3+(2a4)2÷a3=2a5﹣a5+4a8÷a3=2a5﹣a5+4a5=5a5.【点睛】此题主要考查了整式乘除和乘法运算,以及有理数乘方的运算,熟练掌握运算法则是解本题的关键.14.(1)证明见解析;(2)∠AED+∠D=180°,理由见解析;(3)110°【分析】(1)依据同位角相等,即可得到两直线平行;(2)依据平行线的性质,可得出∠FGD=∠EFG,进而判定AB∥CD,即可得出∠AED+∠D=180°;(3)依据已知条件求得∠CGF的度数,进而利用平行线的性质得出∠CEF的度数,依据对顶角相等即可得到∠AEM的度数.【详解】(1)∵∠CED=∠GHD,∴CB∥GF;(2)∠AED+∠D=180°;理由:∵CB∥GF,∴∠C=∠FGD,又∵∠C=∠EFG,∴∠FGD=∠EFG,∴AB∥CD,∴∠AED+∠D=180°;(3)∵∠GHD=∠EHF=80°,∠D=30°,∴∠CGF=80°+30°=110°,又∵CE∥GF,∴∠C=180°﹣110°=70°,又∵AB∥CD,∴∠AEC=∠C=70°,∴∠AEM=180°﹣70°=110°.【点睛】本题主要考查了平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.15.(1)见解析;(2)见解析;(3)4.【分析】整体分析:(1)根据平移的要求画出△A´B´C´;(2)延长AB,过点C作AB延长线的垂线段;(3)过点A作BC的平行线,这条平行线上的格点数(异于点A)即为结果.【详解】(1)如图所示(2)如图所示.(3)如图,过点A作BC的平行线,这条平行线上的格点数除点A外有4个,所以能使S△ABC=S△PBC的格点P的个数有4个,故答案为4.16.(1)57xy=⎧⎨=⎩;(2)6024xy=⎧⎨=-⎩【分析】(1)2338y xx y=-⎧⎨-=⎩①②,由①得2x-y=3③,②-③可求得x,将x值代入①可得y值,即可求得方程组的解.(2)743832x yx y⎧+=⎪⎪⎨⎪+=⎪⎩①②,先将①×12去分母,将分式方程化为整式方程,得3x+4y=84③,将②×6,由分式方程化为整式方程,得2x+3y=48④,③和④再利用加减消元法即可求解方程组的解.【详解】(1)23 38 y xx y=-⎧⎨-=⎩①②由①,得2x-y=3③②-③,得x=5将x=5代入①,得2×5-y=3∴y=7故方程组的解为:57x y =⎧⎨=⎩故答案为:57x y =⎧⎨=⎩(2)743832x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩①② ①×12,得3x+4y=84③②×6,得2x+3y=48④③×2,得6x+8y=168⑤④×3,得6x+9y=144⑥⑤-⑥,得y=-24将y=-24代入①,得874x -= ∴x=60 故方程组的解为:6024x y =⎧⎨=-⎩故答案为:6024x y =⎧⎨=-⎩【点睛】本题考查了一元二次方程的解法—加减消元法,将方程组中的各个方程化简成标准形式,方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等,把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程,解这个一元一次方程,求出一个未知数的值;17.[初步应用]5,3;[深入研究]x 3+2x 2-x -2=(x +2)(x +1)(x -1);详见解析;【分析】[初步应用]列出竖式结合已知可得:2☆-6=0,2-=☆,求出□与☆即可.[深入研究]列出竖式可得x 3+2x 2-x -2÷(x +2),即可将多项式x 3+2x 2-x -2因式分解.【详解】[初步应用]∵多项式x 2+□x +6能被x +2整除,∴2☆-6=0,2-=☆,∴☆= 3,□=5,故答案为:5,3;[深入研究]∵2323212222 22 0x x x x x x x x x -++--+----, ∴()()()()()3222221211x x x x x x x x +--=+-=++-. 【点睛】本题考查整式的除法;理解题意,仿照整数的除法列出竖式进行运算是解题的关键.18.(1)y 3;(2)12.【分析】(1)先计算幂的乘方,然后计算同底数幂除法;(2)分别利用负整数指数幂、零次幂、乘方计算,然后合并.【详解】解:(1)原式=y 9÷y 6=y 3;(2)原式=4﹣1+9=12.【点睛】本题考查了整式的运算与实数的运算,熟练运用公式是解题的关键.19.(1)224()()xy x y x y =+--;(2)16xy =;(3)23x y -=±. 【分析】(1)阴影部分的面积可以由边长为x+y 的大正方形的面积减去边长为x-y 的小正方形面积求出,也可以由4个长为x ,宽为y 的矩形面积之和求出,表示出即可;(2)先利用完全平方公式展开,然后两个式子相减,即可求出答案;(3)利用完全平方变形求值,即可得到答案.【详解】解:(1)图中阴影部分的面积为: 224()()xy x y x y =+--;故答案为:224()()xy x y x y =+--;(2)∵2(32)5x y -=, ∴2291245x xy y -+=①,∵2(32)9x y +=,∴2291249x xy y ++=②,∴由②-①,得 24954xy =-=, ∴16xy =;(3)∵25,2x y xy +==,∴222(2)4425x y x xy y +=++=,∴224254217x y +=-⨯=,∴222(2)4417429x y x y xy -=+-=-⨯=;∴23x y -=±;【点睛】本题考查了完全平方公式的几何背景,准确识图,以及完全平方公式变形求值,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键. 20.(1)272x y =⎧⎪⎨=⎪⎩;(2)692x y =⎧⎪⎨=⎪⎩【分析】(1)根据加减消元法,即可求解;(2)先去分母,去括号,移项,合并同类项,再通过加减消元法,即可求解.【详解】(1)29321x y x y +=⎧⎨-=-⎩①②, +①②得:48x =.解得:2x =, 把2x =代入①得:229y +=,解得:72y =, ∴方程组的解为272x y =⎧⎪⎨=⎪⎩; (2)原方程可化为3436329x y x y +=⎧⎨-=⎩①②, ①-②得:627y =,解得:92y =, 把92y =代入②得:399x -=,解得:6x =, ∴方程组的解为692x y =⎧⎪⎨=⎪⎩. 【点睛】本题主要考查解二元一次方程组,掌握加减消元法,是解题的关键.。
数学人教版(七年级)初一下册数学期末复习压轴题 解答题测试题及答案

∴∠A=∠F.
考点:平行线的判定与性质;对顶角、邻补角.
3.(1) ;(2)
【分析】
(1)利用加减消元法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【详解】
(1)① ,得
.③
② ③,得
把 代入①,得
所以S=22010﹣1即1+2+22+23+24+…+22009=22010﹣1
请依照此法,求:1+5+52+53+54+…+52020的值.
16.计算:
(1)( )﹣3﹣20160﹣|﹣5|;
(2)(3a2)2﹣a2•2a2+(﹣2a3)2+a2;
(3)(x+5)2﹣(x﹣2)(x﹣3);
(4)(2x+y﹣2)(2x+y+2).
15.阅读理解并解答:
为了求1+2+22+23+24+…+22009的值.
可令S=1+2+22+23+24+…+22009
则2S=2+22+23+24+…+22009+22010
因此2S﹣S=(2+22+23+24+…+22009+22010)﹣(1+22+23+24&#(2)若方程组的解满足 , ,求 的取值范围.
4.如图,点D、E、F分别是△ 三边上的点,DF∥AC,∠BFD=∠CED,请写出∠B与∠CDE之间的数量关系,并说明理由.
人教版七年级数学下《压轴题培优》期末复习专题含答案

人教版七年级数学期末复习专题 -- 压轴题培优1.已知 AM∥ CN,点 B 为平面内一点, AB⊥ BC于 B.( 1)如图 1,直接写出∠ A 和∠ C之间的数目关系;(2)如图 2,过点 B 作 BD⊥ AM于点 D,求证:∠ ABD=∠ C;(3)如图 3,在( 2)问的条件下,点 E、F 在 DM上,连结 BE、BF、 CF,BF均分∠ DBC,BE 均分∠ABD,若∠ FCB+∠ NCF=180°,∠ BFC=3∠DBE,求∠ EBC的度数 .2.如图,已知两条射线 OM∥ CN,动线段 AB的两个端点 A.B 分别在射线 OM、 CN上,且∠ C=∠OAB=108°,F在线段 CB上, OB均分∠ AOF, OE均分∠ COF.(1)请在图中找出与∠ AOC相等的角,并说明原因;(2)若平行挪动 AB,那么∠ OBC与∠ OFC的度数比能否跟着 AB地点的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;(3)在平行挪动 AB 的过程中,能否存在某种状况,使∠ OEC=2∠ OBA?若存在,恳求出∠ OBA度数;若不存在,说明原因 .3.已知 AB∥ CD,线段 EF分别与 AB、 CD订交于点 E、 F.(1)如图①,当∠ A=25° , ∠ APC=70°时,求∠ C的度数;(2)如图② , 当点 P在线段 EF上运动时(不包含 E、F两点) , ∠ A.∠ APC与∠ C之间有什么确立的相等关系?试证明你的结论.( 3)如图③,当点P在线段 FE的延伸线上运动时, ( 2)中的结论还建立吗?假如建立, 说明原因;假如不建立,尝试究它们之间新的相等关系并证明.4. 如图1, 在平面直角坐标系中,A(a,0 )是x 轴正半轴上一点,C 是第四象限一点,CB⊥y轴 ,交y 轴负半轴于2B( 0,b ) , 且 (a-3) +|b+4|=0,S四边形AOBC=16.(1)求 C点坐标;(2)如图 2, 设 D为线段 OB上一动点 , 当 AD⊥ AC时 , ∠ ODA的角均分线与∠ CAE的角均分线的反向延伸线交于点 P, 求∠ APD的度数.(3)如图 3, 当 D 点在线段 OB上运动时 , 作 DM⊥ AD交 BC于 M点 , ∠ BMD、∠ DAO的均分线交于 N 点 , 则 D 点在运动过程中 , ∠ N的大小能否变化?若不变 , 求出其值 , 若变化 , 说明原因.5.已知 BC∥ OA,∠ B=∠A=100° . 试回答以下问题:(1)如图 1 所示 , 求证: OB∥AC;(2)如图 2, 若点 E、 F在 BC上, 且知足∠ FOC=∠ AOC,而且 OE均分∠ BOF.试求∠ EOC的度数;(3)在( 2)的条件下,若平行挪动 AC,如图 3,那么∠ OCB:∠ OFB的值能否随之发生变化?若变化,试说明原因;若不变,求出这个比值。
人教版七7年级下册数学期末解答题压轴题题(含答案)
人教版七7年级下册数学期末解答题压轴题题(含答案)一、解答题1.已知足球场的形状是一个长方形,而国际标准球场的长度a 和宽度b (单位:米)的取值范围分别是100110a ≤≤,6475b ≤≤.若某球场的宽与长的比是1:1.5,面积为7350平方米,请判断该球场是否符合国际标准球场的长宽标准,并说明理由. 2.如图,用两个面积为2200cm 的小正方形拼成一个大的正方形. (1)则大正方形的边长是___________;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为5:4,且面积为2360cm ?3.如图,8块相同的小长方形地砖拼成一个大长方形,(1)每块小长方形地砖的长和宽分别是多少?(要求列方程组进行解答)(2)小明想用一块面积为7平方米的正方形桌布,沿着边的方向裁剪出一块新的长方形桌布,用来盖住这块长方形木桌,你帮小明算一算,他能剪出符合要求的桌布吗?4.如图,用两个边长为152的小正方形拼成一个大的正方形, (1)求大正方形的边长?(2)若沿此大正方形边的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为720cm 25.如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.(1)阴影正方形的面积是________?(可利用割补法求面积) (2)阴影正方形的边长是________?(3)阴影正方形的边长介于哪两个整数之间?请说明理由.二、解答题6.如图,直线AB ∥直线CD ,线段EF ∥CD ,连接BF 、CF . (1)求证:∠ABF +∠DCF =∠BFC ;(2)连接BE 、CE 、BC ,若BE 平分∠ABC ,BE ⊥CE ,求证:CE 平分∠BCD ;(3)在(2)的条件下,G 为EF 上一点,连接BG ,若∠BFC =∠BCF ,∠FBG =2∠ECF ,∠CBG =70°,求∠FBE 的度数.7.如图,已知AM //BN ,点P 是射线AM 上一动点(与点A 不重合),BC BD 、分别平分ABP ∠和PBN ∠,分别交射线AM 于点,C D .(1)当60A ∠=︒时,ABN ∠的度数是_______;(2)当A x ∠=︒,求CBD ∠的度数(用x 的代数式表示);(3)当点P 运动时,ADB ∠与APB ∠的度数之比是否随点P 的运动而发生变化?若不变化,请求出这个比值;若变化,请写出变化规律.(4)当点P 运动到使ACB ABD =∠∠时,请直接写出14DBN A +∠∠的度数.8.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由; (2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AENCDG∠∠的值; (3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.9.如图1,把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上. (1)根据图1填空:∠1= °,∠2= °; (2)现把三角板绕B 点逆时针旋转n °.①如图2,当n =25°,且点C 恰好落在DG 边上时,求∠1、∠2的度数;②当0°<n <180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n 的值和对应的那两条垂线;如果不存在,请说明理由.10.已知AB ∥CD ,线段EF 分别与AB ,CD 相交于点E ,F .(1)请在横线上填上合适的内容,完成下面的解答:如图1,当点P 在线段EF 上时,已知∠A =35°,∠C =62°,求∠APC 的度数; 解:过点P 作直线PH ∥AB , 所以∠A =∠APH ,依据是 ; 因为AB ∥CD ,PH ∥AB , 所以PH ∥CD ,依据是 ; 所以∠C =( ),所以∠APC =( )+( )=∠A +∠C =97°. (2)当点P ,Q 在线段EF 上移动时(不包括E ,F 两点): ①如图2,∠APQ +∠PQC =∠A +∠C +180°成立吗?请说明理由;②如图3,∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠M +∠MPQ +∠PQM =180°,请直接写出∠M ,∠A 与∠C 的数量关系.三、解答题11.阅读下面材料:小颖遇到这样一个问题:已知:如图甲,//,AB CD E 为,AB CD 之间一点,连接,,35,37BE DE B D ∠=︒∠=︒,求BED ∠的度数.她是这样做的: 过点E 作//,EF AB 则有,BEF B ∠=∠ 因为//,AB CD 所以//.EF CD ① 所以,FED D ∠=∠所以,BEF FED B D ∠+∠=∠+∠ 即BED ∠=_ ; 1.小颖求得BED ∠的度数为__ ; 2.上述思路中的①的理由是__ ; 3.请你参考她的思考问题的方法,解决问题:已知:直线//,a b 点,A B 在直线a 上,点,C D 在直线b 上,连接,,AD BC BE 平分,ABC DE ∠平分,ADC ∠且,BE DE 所在的直线交于点E .(1)如图1,当点B 在点A 的左侧时,若,ABC ADC αβ∠=∠=,则BED ∠的度数为 ;(用含有,αβ的式子表示).(2)如图2,当点B 在点A 的右侧时,设,ABC ADC αβ∠=∠=,直接写出BED ∠的度数(用含有,αβ的式子表示).12.已知ABC ,//DE AB 交AC 于点E ,//DF AC 交AB 于点F .(1)如图1,若点D 在边BC 上, ①补全图形; ②求证:A EDF ∠=∠.(2)点G 是线段AC 上的一点,连接FG ,DG .①若点G 是线段AE 的中点,请你在图2中补全图形,判断AFG ∠,EDG ∠,DGF ∠之间的数量关系,并证明;②若点G 是线段EC 上的一点,请你直接写出AFG ∠,EDG ∠,DGF ∠之间的数量关系. 13.如图,已知AM ∥BN ,∠A =64°.点P 是射线AM 上一动点(与点A 不重合),BC 、BD 分别平分∠ABP 和∠PBN ,分别交射线AM 于点C ,D .(1)①∠ABN 的度数是 ;②∵AM ∥BN ,∴∠ACB =∠ ; (2)求∠CBD 的度数;(3)当点P 运动时,∠APB 与∠ADB 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律; (4)当点P 运动到使∠ACB =∠ABD 时,∠ABC 的度数是 .14.如图1,在平面直角坐标系中,()()02A a C b ,,,,且满足()240a b a b ++-+=,过C 作CB x ⊥轴于B(1)求三角形ABC 的面积.(2)发过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,若,90()CAB ACB a αββ∠=∠=+=︒,求AED ∠的度数.(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等?若存在,求出P 点坐标;若不存在;请说明理由.15.如图1,//AB CD ,在AB 、CD 内有一条折线EPF .(1)求证:AEP CFP EPF ∠+∠=∠;(2)在图2中,画BEP ∠的平分线与DFP ∠的平分线,两条角平分线交于点Q ,请你补全图形,试探索EQF ∠与EPF ∠之间的关系,并证明你的结论;(3)在(2)的条件下,已知BEP ∠和DFP ∠均为钝角,点G 在直线AB 、CD 之间,且满足1BEG BEP n ∠=∠,1DFG DFP n∠=∠,(其中n 为常数且1n >),直接写出EGF ∠与EPF ∠的数量关系.四、解答题16.如图①,将一副直角三角板放在同一条直线AB 上,其中∠ONM =30°,∠OCD =45°.(1)将图①中的三角板OMN 沿BA 的方向平移至图②的位置,MN 与CD 相交于点E ,求∠CEN 的度数;(2)将图①中的三角板OMN 绕点O 按逆时针方向旋转,使∠BON =30°,如图③,MN 与CD 相交于点E ,求∠CEN 的度数;(3)将图①中的三角板OMN 绕点O 按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第____________秒时,直线MN 恰好与直线CD 垂直.(直接写出结果) 17.己知:如图①,直线MN ⊥直线PQ ,垂足为O ,点A 在射线OP 上,点B 在射线OQ 上(A 、B 不与O 点重合),点C 在射线ON 上且2OC =,过点C 作直线//l PQ .点D 在点C 的左边且3CD =(1)直接写出的BCD ∆面积 ;(2)如图②,若AC BC ⊥,作CBA ∠的平分线交OC 于E ,交AC 于F ,试说明CEF CFE ∠=∠;(3)如图③,若ADC DAC ∠=∠,点B 在射线OQ 上运动,ACB ∠的平分线交DA 的延长线于点H ,在点B 运动过程中HABC∠∠的值是否变化?若不变,求出其值;若变化,求出变化范围. 18.操作示例:如图1,在△ABC 中,AD 为BC 边上的中线,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1=S 2.解决问题:在图2中,点D 、E 分别是边AB 、BC 的中点,若△BDE 的面积为2,则四边形ADEC 的面积为 . 拓展延伸:(1)如图3,在△ABC 中,点D 在边BC 上,且BD =2CD ,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1与S 2之间的数量关系为 .(2)如图4,在△ABC 中,点D 、E 分别在边AB 、AC 上,连接BE 、CD 交于点O ,且BO =2EO ,CO =DO ,若△BOC 的面积为3,则四边形ADOE 的面积为 .19.已知,如图1,直线l 2⊥l 1,垂足为A ,点B 在A 点下方,点C 在射线AM 上,点B 、C 不与点A 重合,点D 在直线11上,点A 的右侧,过D 作l 3⊥l 1,点E 在直线l 3上,点D 的下方.(1)l2与l3的位置关系是;(2)如图1,若CE平分∠BCD,且∠BCD=70°,则∠CED=°,∠ADC=°;(3)如图2,若CD⊥BD于D,作∠BCD的角平分线,交BD于F,交AD于G.试说明:∠DGF=∠DFG;(4)如图3,若∠DBE=∠DEB,点C在射线AM上运动,∠BDC的角平分线交EB的延长线于点N,在点C的运动过程中,探索∠N:∠BCD的值是否变化,若变化,请说明理由;若不变化,请直接写出比值.20.如图,已知直线a∥b,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧,线段EF沿射线AD的方向平移,在平移的过程中BD所在的直线与EF所在的直线交于点P.问∠1的度数与∠EPB的度数又怎样的关系?(特殊化)(1)当∠1=40°,交点P在直线a、直线b之间,求∠EPB的度数;(2)当∠1=70°,求∠EPB的度数;(一般化)(3)当∠1=n°,求∠EPB 的度数(直接用含n 的代数式表示).【参考答案】一、解答题1.符合,理由见解析 【分析】根据宽与长的比是1:1.5,面积为7350平方米,列方程求出长和宽,比较得出答案. 【详解】解:符合,理由如下:设宽为b 米,则长为1.5b 米,由题意得, 1.5b×b解析:符合,理由见解析 【分析】根据宽与长的比是1:1.5,面积为7350平方米,列方程求出长和宽,比较得出答案. 【详解】解:符合,理由如下:设宽为b 米,则长为1.5b 米,由题意得, 1.5b×b=7350,∴b=70,或b=-70(舍去), 即宽为70米,长为1.5×70=105米, ∵100≤105≤110,64≤70≤75, ∴符合国际标准球场的长宽标准. 【点睛】本题考查算术平方根的意义,列出方程求出长和宽是得出正确答案的前提.2.(1);(2)不能剪出长宽之比为5:4,且面积为的大长方形,理由详见解析 【分析】(1)根据已知得到大正方形的面积为400,求出算术平方根即为大正方形的边长;(2)设长方形纸片的长为,宽为,根据解析:(1)20cm ;(2)不能剪出长宽之比为5:4,且面积为2360cm 的大长方形,理由详见解析 【分析】(1)根据已知得到大正方形的面积为4002cm ,求出算术平方根即为大正方形的边长;(2)设长方形纸片的长为5xcm ,宽为4xcm ,根据面积列得54360x x ⋅=,求出x =得到520x =>,由此判断不能裁出符合条件的大正方形. 【详解】(1)∵用两个面积为2200cm 的小正方形拼成一个大的正方形, ∴大正方形的面积为4002cm ,∴20cm =故答案为:20cm ;(2)设长方形纸片的长为5xcm ,宽为4xcm ,54360x x ⋅=,解得:x520x =,答:不能剪出长宽之比为5:4,且面积为2360cm 的大长方形. 【点睛】此题考查利用算术平方根解决实际问题,利用平方根解方程,正确理解题意是解题的关键.3.(1) 长是1.5m,宽是0.5m.;(2)不能. 【解析】 【分析】(1)设每块小长方形地砖的长为xm,宽为ym,列方程组求解即可; (2)把正方形的边长与大长方形的长比较即可. 【详解】 解:解析:(1) 长是1.5m,宽是0.5m.;(2)不能. 【解析】 【分析】(1)设每块小长方形地砖的长为xm,宽为ym,列方程组求解即可; (2)把正方形的边长与大长方形的长比较即可. 【详解】解:(1)设每块小长方形地砖的长为xm,宽为ym,由题意得:32x yx y =⎧⎨+=⎩, 解得: 1.50.5x y =⎧⎨=⎩, ∴长是1.5m,宽是0.5m.(2)∵正方形的面积为7平方米, ∴米,∵∴他不能剪出符合要求的桌布. 【点睛】本题考查了二元一次方程组的应用,算术平方根的应用,找出等量关系列出方程组是解(1)的关键,求出正方形的边长是解(2)的关键.4.(1)30;(2)不能. 【解析】【分析】(1)根据已知正方形的面积求出大正方形的面积,即可求出边长;(2)先求出长方形的边长,再判断即可.【详解】解:(1)∵大正方形的面积是:∴大正解析:(1)30;(2)不能.【解析】【分析】(1)根据已知正方形的面积求出大正方形的面积,即可求出边长;(2)先求出长方形的边长,再判断即可.【详解】2⨯解:(1)∵大正方形的面积是:(2∴=30;(2)设长方形纸片的长为4xcm,宽为3xcm,则4x•3x=720,解得:x,4x>30,所以沿此大正方形边的方向剪出一个长方形,不能使剪出的长方形纸片的长宽之比为4:3,且面积为720cm2.故答案为(1)30;(2)不能.【点睛】本题考查算术平方根,解题的关键是能根据题意列出算式.5.(1)5;(2);(3)2与3两个整数之间,见解析【分析】(1)通过割补法即可求出阴影正方形的面积;(2)根据实数的性质即可求解;(3)根据实数的估算即可求解.【详解】(1)阴影正方形的解析:(1)5;(23)2与3两个整数之间,见解析【分析】(1)通过割补法即可求出阴影正方形的面积;(2)根据实数的性质即可求解;(3)根据实数的估算即可求解.【详解】(1)阴影正方形的面积是3×3-4×121 2⨯⨯=5故答案为:5;(2)设阴影正方形的边长为x,则x2=5∴x(3)∵∴23<<∴阴影正方形的边长介于2与3两个整数之间.【点睛】本题考查了无理数的估算能力和不规则图形的面积的求解方法:割补法.通过观察可知阴影部分的面积是5个小正方形的面积和.会利用估算的方法比较无理数的大小.二、解答题6.(1)证明见解析;(2)证明见解析;(3)∠FBE=35°.【分析】(1)根据平行线的性质得出∠ABF=∠BFE,∠DCF=∠EFC,进而解答即可;(2)由(1)的结论和垂直的定义解答即可;解析:(1)证明见解析;(2)证明见解析;(3)∠FBE=35°.【分析】(1)根据平行线的性质得出∠ABF=∠BFE,∠DCF=∠EFC,进而解答即可;(2)由(1)的结论和垂直的定义解答即可;(3)由(1)的结论和三角形的角的关系解答即可.【详解】证明:(1)∵AB∥CD,EF∥CD,∴AB∥EF,∴∠ABF=∠BFE,∵EF∥CD,∴∠DCF=∠EFC,∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;(2)∵BE⊥EC,∴∠BEC=90°,∴∠EBC+∠BCE=90°,由(1)可得:∠BFC=∠ABE+∠ECD=90°,∴∠ABE+∠ECD=∠EBC+∠BCE,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ECD=∠BCE,∴CE平分∠BCD;(3)设∠BCE=β,∠ECF=γ,∵CE平分∠BCD,∴∠DCE=∠BCE=β,∴∠DCF=∠DCE﹣∠ECF=β﹣γ,∴∠EFC=β﹣γ,∵∠BFC=∠BCF,∴∠BFC=∠BCE+∠ECF=γ+β,∴∠ABF=∠BFE=2γ,∵∠FBG=2∠ECF,∴∠FBG=2γ,∴∠ABE+∠DCE=∠BEC=90°,∴∠ABE=90°﹣β,∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,∵BE平分∠ABC,∴∠CBE=∠ABE=90°﹣β,∴∠CBG=∠CBE+∠GBE,∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,整理得:2γ+β=55°,∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.【点睛】本题主要考查平行线的性质,解决本题的关键是根据平行线的性质解答.7.(1)120°;(2)90°-x°;(3)不变,;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN=180°-x°,根据角平分线的定义知∠解析:(1)120°;(2)90°-12x°;(3)不变,12;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN=180°-x°,根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=180°-x°,即∠CBD=∠CBP+∠DBP=90°-12x°;(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB:∠ADB=2:1;(4)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据角平分线的定义可得∠ABP=∠PBN=12∠ABN=2∠DBN,由平行线的性质可得12∠A+12∠ABN=90°,即可得出答案.【详解】解:(1)∵AM∥BN,∠A=60°,∴∠A+∠ABN=180°,∴∠ABN=120°;(2)∵AM∥BN,∴∠ABN+∠A=180°,∴∠ABN=180°-x°,∴∠ABP+∠PBN=180°-x°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=180°-x°,∴∠CBD=∠CBP+∠DBP=12(180°-x°)=90°-12x°;(3)不变,∠ADB:∠APB=12.∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1,∴∠ADB:∠APB=12;(4)∵AM∥BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠ABC,∠PBN=2∠DBN,∴∠ABP=∠PBN=2∠DBN=12∠ABN,∵AM∥BN,∴∠A+∠ABN=180°,∴12∠A+12∠ABN=90°,∴12∠A+2∠DBN=90°,∴14∠A+∠DBN=12(12∠A+2∠DBN)=45°.【点睛】本题主要考查平行线的性质和角平分线的定义,熟练掌握平行线的性质是解题的关键.8.(1)见解析;(2);(3)75°【分析】(1)根据平行线的性质、余角和补角的性质即可求解.(2)根据平行线的性质、对顶角的性质和平角的定义解答即可.(3)根据平行线的性质和角平分线的定义以解析:(1)见解析;(2)12;(3)75°【分析】(1)根据平行线的性质、余角和补角的性质即可求解.(2)根据平行线的性质、对顶角的性质和平角的定义解答即可.(3)根据平行线的性质和角平分线的定义以及三角形内角和解答即可.【详解】解:(1)∠C=∠1+∠2,证明:过C作l∥MN,如下图所示,∵l∥MN,∴∠4=∠2(两直线平行,内错角相等),∵l∥MN,PQ∥MN,∴l∥PQ,∴∠3=∠1(两直线平行,内错角相等),∴∠3+∠4=∠1+∠2,∴∠C=∠1+∠2;(2)∵∠BDF=∠GDF,∵∠BDF=∠PDC,∴∠GDF=∠PDC,∵∠PDC+∠CDG+∠GDF=180°,∴∠CDG+2∠PDC=180°,∴∠PDC=90°-12∠CDG,由(1)可得,∠PDC+∠CEM=∠C=90°,∴∠AEN=∠CEM,∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠,(3)设BD交MN于J.∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,∵PQ∥MN,∴∠BJA=∠PBD=50°,∴∠ADB=∠AJB-∠JAD=50°-∠JAD=50°-∠CAM,由(1)可得,∠ACB=∠PBC+∠CAM,∴∠ACB+∠ADB=∠PBC+∠CAM+50°-∠CAM=25°+50°=75°.【点睛】本题考查了平行线的性质、余角和补角的性质,解题的关键是根据平行找出角度之间的关系.9.(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相解析:(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相等可得∠1=∠ABE,根据两直线平行,同旁内角互补求出∠BCG,然后根据周角等于360°计算即可得到∠2;②结合图形,分A B、B C、AC三条边与直尺垂直讨论求解.【详解】解:(1)∠1=180°-60°=120°,∠2=90°;故答案为:120,90;(2)①如图2,∵∠ABC=60°,∴∠ABE=180°-60°-n°=120°-n°,∵DG∥EF,∴∠1=∠ABE=120°-n°,∠BCG=180°-∠CBF=180°-n°,∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-∠BCG=360°-90°-(180°-n°)=90°+n°;②当n=30°时,∵∠ABC=60°,∴∠ABF=30°+60°=90°,AB⊥DG(EF);当n=90°时,∠C=∠CBF=90°,∴BC⊥DG(EF),AC⊥DE(GF);当n=120°时,∴AB⊥DE(GF).【点睛】本题考查了平行线角的计算,垂线的定义,主要利用了平行线的性质,直角三角形的性质,读懂题目信息并准确识图是解题的关键.10.(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.解析:(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.【分析】(1)根据平行线的判定与性质即可完成填空;(2)结合(1)的辅助线方法即可完成证明;(3)结合(1)(2)的方法,根据∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,即可证明∠PMQ,∠A与∠C的数量关系.【详解】解:过点P作直线PH∥AB,所以∠A=∠APH,依据是两直线平行,内错角相等;因为AB∥CD,PH∥AB,所以PH∥CD,依据是平行于同一条直线的两条直线平行;所以∠C=(∠CPH),所以∠APC=(∠APH)+(∠CPH)=∠A+∠C=97°.故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①如图2,∠APQ+∠PQC=∠A+∠C+180°成立,理由如下:过点P作直线PH∥AB,QG∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG,∴∠A =∠APH ,∠C =∠CQG ,∠HPQ +∠GQP =180°,∴∠APQ +∠PQC =∠APH +∠HPQ +∠GQP +∠CQG =∠A +∠C +180°.∴∠APQ +∠PQC =∠A +∠C +180°成立;②如图3,过点P 作直线PH ∥AB ,QG ∥AB ,MN ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥PH ∥QG ∥MN ,∴∠A =∠APH ,∠C =∠CQG ,∠HPQ +∠GQP =180°,∠HPM =∠PMN ,∠GQM =∠QMN ,∴∠PMQ =∠HPM +∠GQM ,∵∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠PMQ +∠MPQ +∠PQM =180°,∴∠APM +∠CQM =∠A +∠C +∠PMQ =2∠MPQ +2∠MQP =2(180°﹣∠PMQ ), ∴3∠PMQ +∠A +∠C =360°.【点睛】考核知识点:平行线的判定和性质.熟练运用平行线性质和判定,添加适当辅助线是关键.三、解答题11.;2.平行于同一条直线的两条直线平行;3.(1);(2).【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;(2)根据B解析:1.72;2.平行于同一条直线的两条直线平行;3.(1)1122αβ+;(2)1118022αβ-+. 【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;(2)根据BE 平分,ABC DE ∠平分,ADC ∠求出11,22ABE CDE αβ∠=∠=,过点E 作EF ∥AB ,根据平行线的性质求出∠BEF =12α,11801802DEF CDE β∠=︒-∠=︒-,再利用周角求出答案.【详解】1、过点E 作//,EF AB则有,BEF B ∠=∠因为//,AB CD所以//.EF CD ①所以,FED D ∠=∠所以,BEF FED B D ∠+∠=∠+∠即BED ∠=72;故答案为:72;2、过点E 作//,EF AB则有,BEF B ∠=∠因为//,AB CD所以EF ∥CD (平行于同一条直线的两条直线平行),故答案为:平行于同一条直线的两条直线平行;3、(1)∵BE 平分,ABC DE ∠平分,ADC ∠∴1111,2222ABE ABC CDE ADC αβ∠=∠=∠=∠=, 过点E 作EF ∥AB ,由1可得∠BED =BEF FED ABE CDE ∠+∠=∠+∠,∴∠BED =1122αβ+, 故答案为:1122αβ+;(2)∵BE 平分,ABC DE ∠平分,ADC ∠∴1111,2222ABE ABC CDE ADC αβ∠=∠=∠=∠=, 过点E 作EF ∥AB ,则∠ABE =∠BEF =12α, ∵//,AB CD∴EF ∥CD ,∴180CDE DEF ∠+∠=︒, ∴11801802DEF CDE β∠=︒-∠=︒-, ∴11360360(180)22BED DEF BEF βα∠=︒-∠-∠=︒-︒--=1118022αβ-+.【点睛】此题考查平行线的性质:两直线平行内错角相等,两直线平行同旁内角互补,平行线的推论,正确引出辅助线是解题的关键.12.(1)①见解析;②;见解析(2)①∠AFG+∠EDG=∠DGF ;②∠AFG-∠EDG=∠DGF【分析】(1)①根据题意画出图形;②依据DE ∥AB ,DF ∥AC ,可得∠EDF+∠AFD=180°,∠解析:(1)①见解析;②;见解析(2)①∠AFG +∠EDG =∠DGF ;②∠AFG -∠EDG =∠DGF【分析】(1)①根据题意画出图形;②依据DE ∥AB ,DF ∥AC ,可得∠EDF +∠AFD =180°,∠A +∠AFD =180°,进而得出∠EDF =∠A ;(2)①过G 作GH ∥AB ,依据平行线的性质,即可得到∠AFG +∠EDG =∠FGH +∠DGH =∠DGF ;②过G 作GH ∥AB ,依据平行线的性质,即可得到∠AFG -∠EDG =∠FGH -∠DGH =∠DGF .【详解】解:(1)①如图,②∵DE ∥AB ,DF ∥AC ,∴∠EDF +∠AFD =180°,∠A +∠AFD =180°,∴∠EDF =∠A ;(2)①∠AFG +∠EDG =∠DGF .如图2所示,过G作GH∥AB,∵AB∥DE,∴GH∥DE,∴∠AFG=∠FGH,∠EDG=∠DGH,∴∠AFG+∠EDG=∠FGH+∠DGH=∠DGF;②∠AFG-∠EDG=∠DGF.如图所示,过G作GH∥AB,∵AB∥DE,∴GH∥DE,∴∠AFG=∠FGH,∠EDG=∠DGH,∴∠AFG-∠EDG=∠FGH-∠DGH=∠DGF.【点睛】本题考查了平行线的判定和性质:两直线平行,内错角相等.正确的作出辅助线是解题的关键.13.(1)① ②;(2);(3)不变,,理由见解析;(4)【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;(2)由角平分线的解析:(1)①116,︒②CBN;(2)58︒;(3)不变,:2:1APB ADB∠∠=,理由见解析;(4)29.︒【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;∠ABN,即可求出结果;(2)由角平分线的定义可以证明∠CBD=12(3)不变,∠APB:∠ADB=2:1,证∠APB=∠PBN,∠PBN=2∠DBN,即可推出结论;(4)可先证明∠ABC=∠DBN,由(1)∠ABN=116°,可推出∠CBD=58°,所以∠ABC+∠DBN=58°,则可求出∠ABC的度数.【详解】解:(1)①∵AM//BN,∠A=64°,∴∠ABN=180°﹣∠A=116°,故答案为:116°;②∵AM//BN,∴∠ACB=∠CBN,故答案为:CBN;(2)∵AM//BN,∴∠ABN+∠A=180°,∴∠ABN=180°﹣64°=116°,∴∠ABP+∠PBN=116°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=116°,∴∠CBD=∠CBP+∠DBP=58°;(3)不变,∠APB:∠ADB=2:1,∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM//BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN∴∠ABC=∠DBN,由(1)∠ABN=116°,∴∠CBD=58°,∴∠ABC+∠DBN=58°,∴∠ABC=29°,故答案为:29°.【点睛】本题考查了角平分线的定义,平行线的性质等,解题关键是能熟练运用平行线的性质并能灵活运用角平分线的定义等.14.(1)4;(2)45°;(3)P(0,-1)或(0,3)【分析】(1)根据非负数的性质得到a =−b ,a−b +4=0,解得a =−2,b =2,则A (−2,0),B (2,0),C (2,2),即可计算出解析:(1)4;(2)45°;(3)P (0,-1)或(0,3)【分析】(1)根据非负数的性质得到a =−b ,a−b +4=0,解得a =−2,b =2,则A (−2,0),B (2,0),C (2,2),即可计算出三角形ABC 的面积=4;(2)由于CB ∥y 轴,BD ∥AC ,则∠CAB =∠ABD ,即∠3+∠4+∠5+∠6=90°,过E 作EF ∥AC ,则BD ∥AC ∥EF ,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED =∠1+∠2=12×90°=45°;(3)先根据待定系数法确定直线AC 的解析式为y =12x +1,则G 点坐标为(0,1),然后利用S △PAC =S △APG +S △CPG 进行计算.【详解】解:(1)由题意知:a =−b ,a−b +4=0,解得:a =−2,b =2,∴ A (−2,0),B (2,0),C (2,2),∴S △ABC =1AB BC=42⋅; (2)∵CB ∥y 轴,BD ∥AC ,∴∠CAB =∠ABD ,∴∠3+∠4+∠5+∠6=90°,过E 作EF ∥AC ,∵BD ∥AC ,∴BD ∥AC ∥EF ,∵AE ,DE 分别平分∠CAB ,∠ODB ,∴∠3=∠4=∠1,∠5=∠6=∠2,∴∠AED =∠1+∠2=12×90°=45°;(3)存在.理由如下:设P 点坐标为(0,t ),直线AC 的解析式为y =kx +b ,把A (−2,0)、C (2,2)代入得: -2k+b=02k+b=2⎧⎨⎩,解得1k=2b=1⎧⎪⎨⎪⎩,∴直线AC 的解析式为y =12x +1,∴G 点坐标为(0,1),∴S △PAC =S △APG +S △CPG =12|t−1|•2+12|t−1|•2=4,解得t =3或−1,∴P 点坐标为(0,3)或(0,−1).【点睛】本题考查了绝对值、平方的非负性,平行线的判定与性质:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,内错角相等.15.(1)见解析;(2);见解析;(3)【分析】(1)过点作,根据平行线性质可得;(2)由(1)结论可得:,,再根据角平分线性质可得;(3)由(2)结论可得:.【详解】(1)证明:如图1,过解析:(1)见解析;(2)2360EPF EQF ∠+∠=︒;见解析;(3)360EPF n EGF ∠+∠=︒【分析】(1)过点P 作//PG AB ,根据平行线性质可得;(2)由(1)结论可得:EPF AEP CFP ∠=∠+∠,EQF BEQ DFQ ∠=∠+∠,再根据角平分线性质可得EQF BEQ DFQ ∠=∠+∠()13602EPF =︒-∠; (3)由(2)结论可得:()1EGF BEG DFG BEP DFP n ∠=∠+∠=∠+∠()1360EPF n =︒-∠. 【详解】(1)证明:如图1,过点P 作//PG AB ,∵//AB CD ,∴//PG CD ,∴1AEP ∠=∠,2CFP ∠=∠,又∵12EPF ∠+∠=∠,∴AEP CFP EPF ∠+∠=∠;(2)如图2,由(1)可得:EPF AEP CFP ∠=∠+∠,EQF BEQ DFQ ∠=∠+∠,∵BEP ∠的平分线与DFP ∠的平分线相交于点Q , ∴1()2EQF BEQ DFQ BEP DFP ∠=∠+∠=∠+∠ []()11360()36022AEP CFP EPF =︒-∠+∠=︒-∠, ∴2360EPF EQF ∠+∠=︒;(3)由(2)可得:EPF AEP CFP ∠=∠+,EGF BEG DFG ∠=∠+∠,∵1BEG BEP n ∠=∠,1DFG DFP n∠=∠, ∴1()EGF BEG DF nG BEP DFP ∠=∠+∠=∠+∠ []()11360()360AEP CFP EPF n n=︒-∠+∠=︒-∠, ∴360EPF n EGF ∠+∠=︒;【点睛】考核知识点:平行线性质和判定的综合运用.熟练运用平行线性质和判定是关键.四、解答题16.(1)105°;(2)135°;(3)5.5或11.5.【分析】(1)在△CEN中,用三角形内角和定理即可求出;(2)由∠BON=30°,∠N=30°可得MN∥CB,再根据两直线平行,同旁内角解析:(1)105°;(2)135°;(3)5.5或11.5.【分析】(1)在△CEN中,用三角形内角和定理即可求出;(2)由∠BON=30°,∠N=30°可得MN∥CB,再根据两直线平行,同旁内角互补即可求出∠CEN的度数.(3)画出图形,求出在MN⊥CD时的旋转角,再除以30°即得结果.【详解】解:(1)在△CEN中,∠CEN=180°-∠ECN-∠CNE=180°-45°-30°=105°;(2)∵∠BON=30°,∠N=30°,∴∠BON=∠N,∴MN∥CB.∴∠OCD+∠CEN=180°,∵∠OCD=45°∴∠CEN=180°-45°=135°;(3)如图,MN⊥CD时,旋转角为360°-90°-45°-60°=165°,或360°-(60°-45°)=345°,所以在第165°÷30°=5.5或345°÷30°=11.5秒时,直线MN恰好与直线CD垂直.【点睛】本题以学生熟悉的三角板为载体,考查了三角形的内角和、平行线的判定和性质、垂直的定义和旋转的性质,前两小题难度不大,难点是第(3)小题,解题的关键是画出适合题意的几何图形,弄清求旋转角的思路和方法,本题的第一种情况是将旋转角∠DOM放在四边形DOMF中,用四边形内角和求解,第二种情况是用周角减去∠DOM的度数. 17.(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD的高为OC,所以S△BCD=CD•OC,(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠解析:(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD的高为OC,所以S△BCD=12CD•OC,(2)利用∠CFE+∠CBF=90°,∠OBE +∠OEB =90°,求出∠CEF =∠CFE .(3)由∠ABC +∠ACB =2∠DAC ,∠H +∠HCA =∠DAC ,∠ACB =2∠HCA ,求出∠ABC =2∠H ,即可得答案.详解:(1)S △BCD =12CD •OC =12×3×2=3. (2)如图②,∵AC ⊥BC ,∴∠BCF =90°,∴∠CFE +∠CBF =90°.∵直线MN ⊥直线PQ ,∴∠BOC =∠OBE +∠OEB =90°.∵BF 是∠CBA 的平分线,∴∠CBF =∠OBE .∵∠CEF =∠OBE ,∴∠CFE +∠CBF =∠CEF +∠OBE ,∴∠CEF =∠CFE .(3)如图③,∵直线l ∥PQ ,∴∠ADC =∠PAD .∵∠ADC =∠DAC∴∠CAP =2∠DAC .∵∠ABC +∠ACB =∠CAP ,∴∠ABC +∠ACB =2∠DAC .∵∠H +∠HCA =∠DAC ,∴∠ABC +∠ACB =2∠H +2∠HCA ∵CH 是,∠ACB 的平分线,∴∠ACB =2∠HCA ,∴∠ABC =2∠H ,∴H ABC ∠∠=12.点睛:本题主要考查垂线,角平分线和三角形面积,解题的关键是找准相等的角求解. 18.解决问题:6; 拓展延伸:(1)S1=2S2 (2)10.5【解析】试题分析:解决问题:连接AE ,根据操作示例得到S △ADE=S △BDE ,S △ABE=S △AEC ,从而得到结论;拓展延伸:(1)解析:解决问题:6; 拓展延伸:(1)S 1=2S 2 (2)10.5【解析】试题分析:解决问题:连接AE ,根据操作示例得到S △ADE =S △BDE ,S △ABE =S △AEC ,从而得到结论;拓展延伸:(1)作△ABD 的中线AE ,则有BE =ED =DC ,从而得到△ABE 的面积=△AED 的面积=△ADC 的面积,由此即可得到结论;(2)连接AO .则可得到△BOD 的面积=△BOC 的面积,△AOC 的面积=△AOD 的面积,△EOC 的面积=△BOC 的面积的一半, △AOB 的面积=2△AOE 的面积.设△AOD 的面积=a ,△AOE 的面积=b ,则a +3=2b ,a =b +1.5,求出a 、b 的值,即可得到结论.试题解析:解:解决问题连接AE.∵点D、E分别是边AB、BC的中点,∴S△ADE=S△BDE,S△ABE=S△AEC.∵S△BDE =2,∴S△ADE =2,∴S△ABE=S△AEC=4,∴四边形ADEC的面积=2+4=6.拓展延伸:解:(1)作△ABD的中线AE,则有BE=ED=DC,∴△ABE的面积=△AED的面积=△ADC的面积= S2,∴S1=2S2.(2)连接AO.∵CO=DO,∴△BOD的面积=△BOC的面积=3,△AOC的面积=△AOD的面积.∵BO=2EO,∴△EOC的面积=△BOC的面积的一半=1.5,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,解得:a=6,b=4.5,∴四边形ADOE的面积为=a+b=6+4.5=10.5.19.(1)互相平行;(2)35,20;(3)见解析;(4)不变,【分析】(1)根据平行线的判定定理即可得到结论;(2)根据角平分线的定义和平行线的性质即可得到结论;(3)根据角平分线的定义和平行解析:(1)互相平行;(2)35,20;(3)见解析;(4)不变,12【分析】(1)根据平行线的判定定理即可得到结论;(2)根据角平分线的定义和平行线的性质即可得到结论;(3)根据角平分线的定义和平行线的性质即可得到结论;(4)根据角平分线的定义,平行线的性质,三角形外角的性质即可得到结论.【详解】解:(1)直线l2⊥l1,l3⊥l1,∴l2∥l3,即l2与l3的位置关系是互相平行,故答案为:互相平行;(2)∵CE平分∠BCD,∴∠BCE=∠DCE=1BCD,2∵∠BCD=70°,∴∠DCE=35°,∵l2∥l3,∴∠CED=∠DCE=35°,∵l2⊥l1,∴∠CAD=90°,∴∠ADC=90°﹣70°=20°;故答案为:35,20;(3)∵CF平分∠BCD,∴∠BCF=∠DCF,∵l2⊥l1,∴∠CAD=90°,∴∠BCF+∠AGC=90°,∵CD⊥BD,∴∠DCF+∠CFD=90°,∴∠AGC=∠CFD,∵∠AGC=∠DGF,∴∠DGF=∠DFG;;理由如下:(4)∠N:∠BCD的值不会变化,等于12∵l2∥l3,∴∠BED=∠EBH,∵∠DBE=∠DEB,∴∠DBE=∠EBH,∴∠DBH=2∠DBE,∵∠BCD+∠BDC=∠DBH,∴∠BCD+∠BDC=2∠DBE,∵∠N+∠BDN=∠DBE,∴∠BCD+∠BDC=2∠N+2∠BDN,∵DN平分∠BDC,∴∠BDC=2∠BDN,。
人教版七年级下册数学期末复习压轴题 解答题试卷及答案百度文库doc

人教版七年级下册数学期末复习压轴题 解答题试卷及答案百度文库doc一、解答题1.因式分解:(1)x 4﹣16;(2)2ax 2﹣4axy +2ay 2.2.已知1502x x +-=,求值; (1)221x x +(2)1x x- 3.平面内的两条直线有相交和平行两种位置关系.①如图a ,若//AB CD ,点P 在AB 、CD 外部,则BPD ∠、B 、D ∠之间有何数量关系?解:BPD B D ∠=∠-∠.证明:∵//AB CD ,∴B BOD ∠=∠,又∵POD BOD ∠+∠=______,在POD 中,由三角形内角和定理可得____________180POD ∠+∠+∠=︒, 故______BPD D ∠=∠+∠,从而得BPD B D ∠=∠-∠.②若//AB CD ,将点P 移到AB 、CD 内部,如图b ,以上结论是否成立?若成立,说明理由;若不成立,则BPD ∠、B 、D ∠之间有何数量关系?请证明你的结论; ③在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图c ,则BPD ∠、B 、D ∠、BQD ∠之间有何数量关系?请证明你的结论;4.好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在ABC ∆中,点I 是ABC ∠、ACB ∠的平分线的交点,点D 是MBC ∠、NCB ∠平分线的交点,,BI DC 的延长线交于点E .(1)若50BAC ∠=︒,则BIC ∠= °;(2)若BAC x ∠=︒ (090x <<),则当ACB ∠等于多少度(用含x 的代数式表示)时,//CE AB ,并说明理由;(3)若3D E ∠=∠,求BAC ∠的度数.5.已知a +a 1-=3, 求(1)a 2+21a(2)a 4+41a 6.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是 .(请选择正确的选项)A .a 2﹣b 2=(a +b )(a ﹣b )B .a 2﹣2ab +b 2=(a ﹣b )2C .a 2+ab =a (a +b )(2)若x 2﹣y 2=16,x +y =8,求x ﹣y 的值;(3)计算:(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020). 7.如图1,在ABC 中,BD 平分ABC ∠,CD 平分ACB ∠.(1)若80A ∠=︒,则BDC ∠的度数为______;(2)若A α∠=,直线MN 经过点D .①如图2,若//MN AB ,求NDC MDB ∠-∠的度数(用含α的代数式表示); ②如图3,若MN 绕点D 旋转,分别交线段,BC AC 于点,M N ,试问在旋转过程中NDC MDB ∠-∠的度数是否会发生改变?若不变,求出NDC MDB ∠-∠的度数(用含α的代数式表示),若改变,请说明理由:③如图4,继续旋转直线MN ,与线段AC 交于点N ,与CB 的延长线交于点M ,请直接写出NDC ∠与MDB ∠的关系(用含α的代数式表示).8.如图,已知ABC 中,,AD AE 分别是ABC 的高和角平分线.若44B ∠=︒,12DAE ∠=︒,求C ∠的度数.9.如图①所示,在三角形纸片ABC 中,70C ∠=︒,65B ∠=︒,将纸片的一角折叠,使点A 落在ABC 内的点A '处.(1)若140∠=︒,2∠=________.(2)如图①,若各个角度不确定,试猜想1∠,2∠,A ∠之间的数量关系,直接写出结论.②当点A 落在四边形BCDE 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,A ∠,1∠,2∠之间又存在什么关系?请说明.(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的123456∠+∠+∠+∠+∠+∠和是________.10.先化简,再求值:(2x+2)(2﹣2x )+5x (x+1)﹣(x ﹣1)2,其中x =﹣2.11.先化简,再求值:()()()()2212112,x x x x x --+---其中2230x x --=.12.(问题背景)(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B =∠C+∠D(简单应用)(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=28°,∠ADC=20°,求∠P的度数(可直接使用问题(1)中的结论)(问题探究)(3)如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,若∠A=30°,∠C=18°,则∠P的度数为(拓展延伸)(4)在图4中,若设∠C=x,∠B=y,∠CAP=14∠CAB,∠CDP=14∠CDB,试问∠P与∠C、∠B之间的数量关系为(用x、y表示∠P)(5)在图5中,BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论.13.装饰公司为小明家设计电视背景墙时需要A、B型板材若干块,A型板材规格是a⨯b,B型板材规格是b⨯b.现只能购得规格是150⨯b的标准板材.(单位:cm)(1)若设a=60cm,b=30cm.一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法,下图是裁法一的裁剪示意图.裁法一裁法二裁法三A型板材块数120B型板材块数3m n则上表中,m=___________,n=__________;(2)为了装修的需要,小明家又购买了若干C型板材,其规格是a⨯a,并做成如下图的背景墙.请写出下图中所表示的等式:__________;(3)若给定一个二次三项式2a 2+5ab +3b 2,试用拼图的方式将其因式分解.(请仿照(2)在几何图形中标上有关数量)14.要说明(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc 成立,三位同学分别提供了一种思路,请根据他们的思路写出推理过程.(1)小刚说:可以根据乘方的意义来说明等式成立;(2)小王说:可以将其转化为两数和的平方来说明等式成立;(3)小丽说:可以构造图形,通过计算面积来说明等式成立;15.在校运动会中,篮球队和排球队共有24支,其中篮球队每队10名队员,排球队每队12名队员,共有260名队员.请问篮球队、排球队各有多少支?(利用二元一次方程组解决问题)16.把下列各式分解因式:(1)4x 2-12x 3(2)x 2y +4y -4xy(3)a 2(x -y )+b 2(y -x )17.四边形ABCD 中,∠A=140°,∠D=80°.(1)如图①,若∠B=∠C ,试求出∠C 的度数;(2)如图②,若∠ABC 的角平分线交DC 于点E ,且BE ∥AD ,试求出∠C 的度数;(3)如图③,若∠ABC 和∠BCD 的角平分线交于点E ,试求出∠BEC 的度数.18.已知关于x 、y 的二元一次方程组21322x y x y k +=⎧⎪⎨-=-⎪⎩(k 为常数). (1)求这个二元一次方程组的解(用含k 的代数式表示);(2)若()2421y x +=,求k 的值; (3)若14k ≤,设364m x y =+,且m 为正整数,求m 的值.19.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x 、y 的等式表示) ;(2)若2(32)5x y -=,2(32)9x y +=,求xy 的值;(3)若25,2x y xy +==,求2x y -的值.20.如图,直线MN ∥GH ,直线l 1分别交直线MN 、GH 于A 、B 两点,直线l 2分别交直线MN 、GH 于C 、D 两点,且直线l 1、l 2交于点E ,点P 是直线l 2上不同于C 、D 、E 点的动点.(1)如图①,当点P 在线段CE 上时,请直写出∠NAP 、∠HBP 、∠APB 之间的数量关系: ;(2)如图②,当点P 在线段DE 上时,(1)中的∠NAP 、∠HBP 、∠APB 之间的数量关系还成立吗?如果成立,请说明成立的理由;如果不成立,请写出这三个角之间的数量关系,并说明理由.(3)如果点P 在直线l 2上且在C 、D 两点外侧运动时,其他条件不变,请直接写出∠NAP 、∠HBP 、∠APB 之间的数量关系 .【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)2(4)(2)(2)x x x ++- (2)22()a x y -【分析】(1)原式利用平方差公式分解即可;(2)原式提取公因式,再利用完全平方公式分解即可.【详解】解:(1)原式=(x 2+4)(x 2﹣4)=(x 2+4)(x +2)(x ﹣2);(2)原式=2a (x 2﹣2xy +y 2)=2a (x ﹣y )2.【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.2.(1)174;(2)32± 【分析】 (1)利用完全平方公式(a +b)²=a ²+2ab +b ²解答;(2)利用(1)的结果和完全平方公式(a−b)²=a ²−2ab +b ²解答.【详解】解:(1)由题:152x x +=, 21254x x ⎛⎫∴+= ⎪⎝⎭ 即2212524x x ++=, 221174x x ∴+= (2)222111792244x x x x ⎛⎫-=+-=-= ⎪⎝⎭ 132x x ∴-=± 【点睛】此题是完全平方公式的应用;两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.3.①见解析;②BPD B D ∠=∠+∠,证明见解析;③BPD B D BQD ∠=∠+∠+∠,证明见解析.【分析】①先根据平行线的性质可得B BOD ∠=∠,再根据平角的定义可得180POD BOD ∠+∠=︒,然后根据三角形的内角和定理可得180POD BPD D ∠+∠+∠=︒,最后根据等量代换即可得证;②如图(见解析),先根据平行线的性质可得B BQD ∠=∠,再根据三角形的外角性质可得BPD BQD D ∠=∠+∠,然后根据等量代换即可得;③如图(见解析),先根据三角形的外角性质可得BED B BQD ∠=∠+∠,BPD D BED ∠=∠+∠,再根据等量代换即可得.【详解】①BPD B D ∠=∠-∠.证明:∵//AB CD ,∴B BOD ∠=∠,又∵180POD BOD ∠+∠=︒,在POD 中,由三角形内角和定理可得180POD BPD D ∠+∠+∠=︒,故BOD BPD D ∠=∠+∠,从而得BPD B D ∠=∠-∠;②BPD B D ∠=∠+∠,证明如下:如图,延长BP ,交CD 于点Q ,∵//AB CD ,B BQD ∴∠=∠,由三角形的外角性质得:BPD BQD D ∠=∠+∠,BPD B D ∴∠=∠+∠;③BPD B D BQD ∠=∠+∠+∠,证明如下:如图,延长BP ,交CD 于点E ,由三角形的外角性质得:BED B BQD BPD D BED ∠=∠+∠⎧⎨∠=∠+∠⎩, 则BPD B D BQD ∠=∠+∠+∠.【点睛】本题考查了平行线的性质、三角形的内角和定理、三角形的外角性质等知识点,熟练掌握三角形的外角性质是解题关键.4.(1)115;(2)180-2x ,理由见解析;(3)45°.【分析】(1)已知点I 是两角∠ABC 、∠ACB 平分线的交点,故()()()11118018018018090222BIC IBC ICB ABC ACB A BAC ∠=︒-∠+∠=︒-∠+∠=︒-︒-∠=+∠ ,由此可求∠BIC ;(2)当CE ∥AB 时, ∠ACE=∠A=x °,根据∠ACE=∠A=x °,根据CE 是∠ACG 的角平分线,推出∠ACG=2x °,∠ABC=∠BAC=x °,即可求出ACB ∠的度数.(3)由题意知:△BDE 是直角三角形∠D+∠E=90°,可求出若∠D=3∠E 时,∠BEC=22.5°,再推理出12BEC BAC ∠=∠,即可求出BAC ∠的度数. 【详解】(1)∵点I 是两角∠ABC 、∠ACB 平分线的交点,∴()180BIC IBC ICB ∠=︒-∠+∠ ()11802ABC ACB =-∠+∠︒ ()11801802A =-︒︒-∠ 1901152BAC =+∠=︒; 故答案为:115.(2)当∠ACB 等于(180-2x )°时,CE ∥AB .理由如下:∵CE ∥AB ,∴∠ACE=∠A=x °,∵∠ACE=∠A=x °,CE 是∠ACG 的角平分线,∴∠ACG=2∠ACE=2x °,∴∠ABC=∠ACG-∠BAC=2x °-x °=x °,∴∠ACB=180°-∠BAC-∠ABC=(180-2x )°;(3)由题意知:△BDE 是直角三角形∠D+∠E=90°若∠D=3∠E 时∠BEC=22.5°,∵90BEC BDC ∠=︒-∠190902BAC ⎛⎫=︒-︒-∠ ⎪⎝⎭ 12BAC =∠, ∴45BAC ∠=︒.【点睛】本题考查了三角形的内角、外角平分线的夹角大小与原三角形内角的关系,要充分运用三角形内角和定理,角平分线性质转换.5.(1)7;(2)47.【分析】(1)根据13a a -+=得出13a a +=,进而得出219a a ⎛⎫+= ⎪⎝⎭,从而可得出结论;(2)根据(1)中的结论可知2217a a +=,故2221()49a a +=,从而得出441a a +的值. 【详解】解:(1)∵13a a -+=, ∴13a a+=, ∴21()9a a +=,即:22129a a++=, ∴2217a a+=; (2)由(1)知:2217a a +=, ∴2221()49a a +=,即:441249a a++=, ∴44147a a +=. 【点睛】本题主要考查的是负整数指数幂和分式的运算,解题的关键是熟练掌握完全平方公式的灵活应用.6.(1)A ;(2)2;(3)20214040 【分析】(1)由题意直接根据拼接前后的面积相等进行分析计算即可得出答案;(2)根据题意可知x 2﹣y 2=16,即(x +y )(x ﹣y )=16,又x +y =8,可求出x ﹣y 的值;(3)根据题意利用平方差公式将算式转化为分数的乘积的形式,根据数据规律得出答案.【详解】解:(1)图1的剩余面积为a 2﹣b 2,图2拼接得到的图形面积为(a +b )(a ﹣b ) 因此有,a 2﹣b 2=(a +b )(a ﹣b ),故答案为:A.(2)∵x 2﹣y 2=(x +y )(x ﹣y )=16,又∵x +y =8,∴x ﹣y =16÷8=2;(3)(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020) =(1﹣12)(1+12)(1﹣13)(1+13)(1﹣14)(1+14)……(1﹣12019)(1+12019)(1﹣12020)(1+12020)=12×32×23×43×34×54×……×20182019×20202019×20192020×20212020=12×20212020=2021 4040.【点睛】本题考查平方差公式的几何意义及应用,掌握公式的结构特征是正确应用的前提,利用公式进行适当的变形是解题的关键.7.(1)130°;(2)①90︒-α;②不变,90︒-α;③∠NDC+∠MDB=90︒-1α2.【分析】(1)根据已知,以及三角形内角和等于180︒,即可求解;(2)①根据平行线的性质可以证得∠ABD=∠BDM=∠MBD,∠CND=∠A=α,再利用含有α的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;②延长BD交AC于点E,则∠NDE=∠MDB,因此∠NDC-∠MDB=∠NDC-∠NDE=∠EDC,再利用三角形内角和为180︒,即可求解;③如图可知,∠NDC+∠MDB=180︒-∠BDC,利用平角的定义,即可求解代数式.【详解】解:(1)∵∠A=80︒∴∠ABC+∠ACB=180︒-80︒=100︒又∵ BD平分∠ABC,CD平分∠ACB,∴∠DBC+∠DCB=12⨯100︒=50︒.∴∠BDC=180︒-50︒=130︒.(2)①∵MN//AB,BD平分∠ABC,CD平分∠ACB,∴∠ABD=∠BDM=∠MBD,∠CND=∠A=α,∴∠NDC=180︒-α-12∠ACB,∠MDB=12∠ABC,∴∠NDC-∠MDB=180︒-α-12∠ACB-12∠ABC=180︒-α-12(∠ACB+∠ABC)=180︒-α-12(180︒-α)=90︒-α.②不变;延长BD交AC于点E,如图:∴∠NDE=∠MDB ,∵∠BDC=180︒-12(∠ACB+∠ABC )=180︒-12(180︒-α)=90︒+1α2, ∴∠NDC-∠MDB=∠NDC-∠NDE=∠EDC=180︒-∠BDC=180︒-(90︒+1α2)=90︒-α, 同①,说明MN 在旋转过程中∠NDC-∠MDB 的度数只与∠A 有关系,而∠A 始终不变, 故:MN 在旋转过程中∠NDC-∠MDB 的度数不会发生改变.③如图可知,∠NDC+∠MDB=180︒-∠BDC ,由②知∠BDC=90︒+1α2, ∴∠NDC+∠MDB=180︒-(90︒+1α2)=90︒-1α2. 故∠NDC 与∠MDB 的关系是∠NDC+∠MDB=90︒-1α2. 【点睛】本题目考查平行线与三角形的综合,涉及知识点有平行线的性质,三角形内角和等于180°等,是中考的常考知识点,难度一般,熟练掌握以上知识点的综合运用是顺利解题的关键.8.68︒【分析】根据已知首先求得∠BAD 的度数,进而可以求得∠BAE ,而∠CAE=∠BAE ,在△ACD 中利用内角和为180°,即可求得∠C .【详解】解:∵AD 是△ABC 的高,∠B=44︒,∴∠ADB=∠ADC =90︒,在△ABD 中,∠BAD=180︒-90︒-44︒=46︒,又∵ AE 平分∠BAC ,∠DAE=12︒,∴∠CAE=∠BAE=46︒-12︒=34︒,而∠CAD=∠CAE-∠DAE=34︒-12︒=22︒,在△ACD 中,∠C=180︒-90︒-22︒=68︒.故答案为68︒.【点睛】本题考查三角形中角度的计算,难度一般,熟记三角形内角和为180°是解题的关键.9.(1)50°;(2)①见解析;②见解析;(3)360°.【分析】(1)根据题意,已知70C ∠=︒,65B ∠=︒,可结合三角形内角和定理和折叠变换的性质求解;(2)①先根据折叠得:∠ADE=∠A ′DE ,∠AED=∠A ′ED ,由两个平角∠AEB 和∠ADC 得:∠1+∠2等于360°与四个折叠角的差,化简得结果;②利用两次外角定理得出结论;(3)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'GF+∠B'FG)以及(∠C'DE+∠C'ED)和(∠A'HL+∠A'LH),再利用三角形的内角和定理即可求解.【详解】解:(1)∵70C ∠=︒,65B ∠=︒,∴∠A ′=∠A=180°-(65°+70°)=45°,∴∠A ′ED+∠A ′DE =180°-∠A ′=135°,∴∠2=360°-(∠C+∠B+∠1+∠A ′ED+∠A ′DE )=360°-310°=50°;(2)①122A ∠+∠=∠,理由如下由折叠得:∠ADE=∠A ′DE ,∠AED=∠A ′ED ,∵∠AEB+∠ADC=360°,∴∠1+∠2=360°-∠ADE-∠A ′DE-∠AED-∠A ′ED=360°-2∠ADE-2∠AED ,∴∠1+∠2=2(180°-∠ADE-∠AED )=2∠A ;②221A ∠=∠+∠,理由如下:∵2∠是ADF 的一个外角∴2A AFD ∠=∠+∠.∵AFD ∠是A EF '△的一个外角∴1AFD A '∠=∠+∠又∵A A '∠=∠∴221A ∠=∠+∠(3)如图由题意知,∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'GF+∠B'FG)-(∠C'DE+∠C'ED)-(∠A'HL+∠A'LH)=720°-(180°-∠B')-(180°-C')-(180°-A')=180°+(∠B'+∠C'+∠A')又∵∠B=∠B',∠C=∠C',∠A=∠A',∠A+∠B+∠C=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°.【点睛】题主要考查了折叠变换、三角形、四边形内角和定理.注意折叠前后图形全等;三角形内角和为180°;四边形内角和等于360度.10.73x +;-11【分析】根据整式的运算法则即可求出答案.【详解】解:22222511xx x x x 222445521x x x x x73x 当2x =-时,原式14311. 【点睛】本题考查整式化简求值,熟练运用运算法则是解题的关键.11.6【解析】试题分析:先根据乘法公式和单项式乘以多项式的法则计算化简,根据化简的结果,将2230x x --=变形后整体代入计算即可.试题解析:原式=()()222441212x x x x x -+---- 222441222x x x x x =-+-+-+223x x =-+∵2230x x --=,∴223x x -=,∴原式=3+3=6.12.(1)证明见解析;(2)24°;(3)24°;(4)∠P=34x+14y ;(5)∠P=180()2A C ︒-∠+∠ 【分析】 (1)根据三角形内角和为180°,对顶角相等,即可证得∠A+∠B=∠C+∠D(2)由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC ①,∠PAD+∠P=∠PCD+∠ADC ②,将两个式子相加,已知AP 、CP 分别平分∠BAD 、∠BCD ,可得∠BAP=∠PAD ,∠BCP=∠PCD ,可证得∠P=12(∠ABC+∠ADC),即可求出∠P 度数. (3)已知直线BP 平分∠ABC 的外角∠FBC ,DP 平分∠ADC 的外角∠ADE ,可得∠1=∠2,∠3=∠4,由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1,∠A+∠4=∠P+∠2,两式相加即可求出∠P 的度数.(4)由(1)的结论得:14∠CAB+∠C=∠P+14∠CDB ,34∠CAB+∠P=∠B+34∠CDB ,第一个式子乘以3,得到的式子减去第二个式子即可得出用x、y表示∠P(5)延长AB交DP于点F,标注出∠1,∠2,∠3,∠4,由(1)的结论得:∠A+2∠1=∠C+180°-2∠3,其中根据对顶角相等,三角形内角和,以及外角的性质即可得到∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P,代入∠A+2∠1=∠C+180°-2∠3,即可得出∠P与∠A、∠C的关系.【详解】(1)如图1,∠A+∠B+∠AOB=∠C+∠D+∠COD=180°∵∠AOB=∠COD∴∠A+∠B=∠C+∠D(2)∵AP、CP分别平分∠BAD、∠BCD∴∠BAP=∠PAD,∠BCP=∠PCD,由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC①,∠PAD+∠P=∠PCD+∠ADC②①+②,得2∠P+∠PAD+∠BCP=∠BAP+∠ABC +∠PCD+∠ADC∴∠P=12(∠ABC+∠ADC)∴∠ABC=28°,∠ADC=20°∴∠P=12(28°+20°)∴∠P=24°故答案为:24°(3)∵如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,∴∠1=∠2,∠3=∠4由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1①,∠A+∠4=∠P+∠2②①+②,得∠C+180°-∠3+∠A+∠4=∠P+180°-∠1+∠P+∠2∴30°+18°=2∠P∴∠P=24°故答案为:24°(4)由(1)的结论得:14∠CAB+∠C=∠P+14∠CDB①,34∠CAB+∠P=∠B+34∠CDB②①×3,得34∠CAB+3∠C=3∠P+34∠CDB③②-③,得∠P-3x=y-3∠P∴∠P=34x+14y故答案为:∠P=34x+14y(5)如图5所示,延长AB交DP于点F由(1)的结论得:∠A+2∠1=∠C+180°-2∠3∵∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P ∴∠A+360°-2∠A-2∠3-2∠P=∠C+180°-2∠3解得:∠P=180()2A C︒-∠+∠故答案为:∠P=180()2A C︒-∠+∠【点睛】本题是考查了角平分线性质及三角形内角和定理,对顶角相等,三角形任一外角等于不相邻的两个内角和等知识点,本题是典型的拓展延伸题,一般第一问得出基本结论,后面的问题将基本结论作为解题基础,进行拓展延伸.13.(1)m=1,n=5;(2)(a+2b)2=a2+4ab+4b2;(3)2a2+5ab+3b2=(a+b)(2a+3b),详见解析【分析】(1)结合图形和条件分析可以得出按裁法二裁剪时,可以裁出B型板1块,按裁法三裁剪时,可以裁出5块B型板;(2)看图即可得出所求的式子;(3)通过画图能更好的理解题意,从而得出结果.由于构成的是长方形,它的面积等于所给图片的面积之和,从而因式分解.【详解】(1)按裁法二裁剪时,2块A型板材块的长为120cm,150-120=30,所以可裁出B型板1块,按裁法三裁剪时,全部裁出B型板,150÷30=5,所以可裁出5块B型板;∴m=1,n=5.故答案为:1,5;(2)如下图:发现的等式为:(a+2b)2=a2+4ab+4b2;故答案为:(a+2b)2=a2+4ab+4b2.(3)按题意画图如下:∵构成的长方形面积等于所给图片的面积之和,∴2a 2+5ab +3b 2=(a +b )(2a +3b ).【点睛】本题考查了完全平方公式和几何图形的应用及一元一次方程的应用,关键是根据学生的画图能力,计算能力来解答.14.(1)详见解析;(2)详见解析;(3)详见解析【分析】(1)利用乘方的意义求解,即可;(2)将式子变形,利用完全平方公式计算,即可;(3)化成边长为a+b+c 的正方形,即可得出答案.【详解】(1)小刚:(a +b +c )2=(a +b +c )(a +b +c )=a 2+ab +ac +ba +b 2+bc +ca +cb +c 2=a 2+b 2+c 2+2ab +2ac +2bc(2)小王:(a +b +c )2=[(a +b )+c ]2=(a +b )2+2(a +b )c +c 2=a 2+b 2+2ab +2ac +2bc +c 2(3)小丽:如图【点睛】本题考查了整式的运算法则的应用,能正确根据整式的运算法则进行化简是解此题的关键,也培养了学生的动手操作能力.15.篮球队14支,排球队10支【分析】根据题意可知,本题中的等量关系是“有24支队”和“260名运动员”,列方程组求解即可.【详解】设篮球队x 支,排球队y 支,由题意可得:241012260x y x y +=⎧⎨+=⎩解的:1410x y =⎧⎨=⎩答:设篮球队14支,排球队10支【点睛】解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.16.(1)4x 2(1-3x )(2)y (x -2)2(2)(x -y )(a +b )(a -b )【分析】(1)直接利用提公因式法分解因式即可;(2)先提取公因式,然后利用完全平方公式分解因式即可;(3)先提取公因式,然后利用平方差公式分解因式即可.【详解】(1)()232412413x x x x =--; (2)()()22244442x y y xy y x x y x +-=+-=-; (3)()()()()()2222()()a x y b y x x y a b x y a b a b =--=-+--+-.【点睛】本题考查了分解因式,解题的关键是熟练掌握提取公因式法和公式法分解因式.17.(1)70°;(2)60°;(3)110°【分析】(1)根据四边形的内角和是360°,结合已知条件就可求解;(2)根据平行线的性质得到∠ABE 的度数,再根据角平分线的定义得到∠ABC 的度数,进一步根据四边形的内角和定理进行求解;(3)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB 的度数,再进一步求得∠BEC 的度数.【详解】(1)在四边形ABCD 中,∵∠A+∠B+∠C+∠D=360°, 又∠A=140°,∠D=80°,∠B=∠C,∴140°+∠C+∠C+80°=360°,即∠C=70°.(2)∵BE ∥AD ,∠A=140°,∠D=80°,∴∠BEC=∠D ,∠A+∠ABE=180°.∴∠BEC=80°,∠ABE=40°.∵BE 是∠ABC 的平分线,∴∠EBC=∠ABE=40°.∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.(3)在四边形ABCD 中, 有∠A+∠ABC+∠BCD+∠D=360°, ∠A=140°,∠D=80°,所以∠ABC+∠BCD=140°,从而有12∠ABC+12∠BCD=70°. 因为∠ABC 和∠BCD 的角平分线交于点E,所以有∠EBC=12∠ABC,∠ECB=12∠BCD. 故∠C=180°-(∠EBC +∠ECB)=180°-(12∠ABC+12∠BCD)=180°-70°=110°.18.(1)218524k x ky -⎧=⎪⎪⎨-⎪=⎪⎩;(2)52k =或12k =-;(3)1或2. 【分析】(1)根据题意直接利用加减消元法进行计算求解即可;(2)由题意根据01(0)a a =≠和11n =以及2(1)1n -=(n 为整数)得到三个关于k 的方程,求出k 即可;(3)根据题意用含m 的代数式表示出k ,根据14k ≤,确定m 的取值范围,由m 为正整数,求得m 的值即可.【详解】 解:(1)21322x y x y k ⎧+=⎪⎪⎨⎪-=-⎪⎩①②, ①+②得:3412x k =+-,解得:218k x -=, ①-②得:3212y k =-+,解得:524k y -=, ∴二元一次方程组的解为:218524k x ky -⎧=⎪⎪⎨-⎪=⎪⎩. (2)∵01(0)a a =≠,2(42)1y x +=,∴20y =,即52204k -⨯=,解得:52k =; ∵11n =,2(42)1y x +=,∴421x +=,即214218k -⨯+=,解得:12k =-; ∵2(1)1n -=(n 为正整数),2(42)1y x +=, ∴4212x y +=-,为偶数,即214218k -⨯+=-,解得:52k =-; 当52k =-时,3532115222y k =-+=++=,为奇数,不合题意,故舍去. 综上52k =或12k =-. (3)∵215213643647842k k m x y k --=+=⨯+⨯=+,即172m k =+,∴2114m k -=, ∵14k ≤, ∴211144m k -=≤,解得94m ≤, ∵m 为正整数,∴m=1或2.【点睛】本题考查解二元一次方程组以及解一元一次不等式,根据题意列出不等式是解题的关键.19.(1)224()()xy x y x y =+--;(2)16xy =;(3)23x y -=±. 【分析】(1)阴影部分的面积可以由边长为x+y 的大正方形的面积减去边长为x-y 的小正方形面积求出,也可以由4个长为x ,宽为y 的矩形面积之和求出,表示出即可;(2)先利用完全平方公式展开,然后两个式子相减,即可求出答案;(3)利用完全平方变形求值,即可得到答案.【详解】解:(1)图中阴影部分的面积为: 224()()xy x y x y =+--;故答案为:224()()xy x y x y =+--;(2)∵2(32)5x y -=, ∴2291245x xy y -+=①,∵2(32)9x y +=,∴2291249x xy y ++=②,∴由②-①,得 24954xy =-=, ∴16xy =; (3)∵25,2x y xy +==, ∴222(2)4425x y x xy y +=++=,∴224254217x y +=-⨯=,∴222(2)4417429x y x y xy -=+-=-⨯=;∴23x y -=±;【点睛】本题考查了完全平方公式的几何背景,准确识图,以及完全平方公式变形求值,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键.20.(1)∠APB=∠NAP+∠HBP;(2)见解析;(3)∠HBP=∠NAP+∠APB【分析】(1)过P点作PQ∥GH,根据平行线的性质即可求解;(2)过P点作PQ∥GH,根据平行线的性质即可求解;(3)根据平行线的性质和三角形外角的性质即可求解.【详解】解:(1)如图①,过P点作PQ∥GH,∵MN∥GH,∴MN∥PQ∥GH,∴∠APQ=∠NAP,∠BPQ=∠HBP,∵∠APB=∠APQ+∠BPQ,∴∠APB=∠NAP+∠HBP,故答案为:∠APB=∠NAP+∠HBP;(2)如图②,过P点作PQ∥GH,∵MN∥GH,∴MN∥PQ∥GH,∴∠APQ+∠NAP=180°,∠BPQ+∠HBP=180°,∵∠APB=∠APQ+∠BPQ,∴∠APB=(180°﹣∠NAP)+(180°﹣∠HBP)=360°﹣(∠NAP+∠HBP);(3)如备用图,∵MN∥GH,∴∠PEN=∠HBP,∵∠PEN=∠NAP+∠APB,∴∠HBP=∠NAP+∠APB.故答案为:∠HBP=∠NAP+∠APB.【点睛】此题考查了平行公理的推论:平行于同一条直线的两直线平行,以及平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,熟记定理是解题的关键.。
人教版七7年级下册数学期末解答题压轴题卷(附答案)
人教版七7年级下册数学期末解答题压轴题卷(附答案)一、解答题1.如图,用两个面积为2200cm的小正方形拼成一个大的正方形.(1)则大正方形的边长是;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为4:3,且面积为2360cm?2.观察下图,每个小正方形的边长均为1,(1)图中阴影部分的面积是多少?边长是多少?(2)估计边长的值在哪两个整数之间.3.如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.(1)拼成的正方形的面积与边长分别是多少?(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长4.数学活动课上,小新和小葵各自拿着不同的长方形纸片在做数学问题探究.(1)小新经过测量和计算得到长方形纸片的长宽之比为3:2,面积为30,请求出该长方形纸片的长和宽;(2)小葵在长方形内画出边长为a,b的两个正方形(如图所示),其中小正方形的一条边在大正方形的一条边上,她经过测量和计算得到长方形纸片的周长为50,阴影部分两个长方形的周长之和为30,由此她判断大正方形的面积为100,间小葵的判断正确吗?请说明理由.5.求下图44的方格中阴影部分正方形面积与边长.二、解答题6.已知:AB//CD.点E在CD上,点F,H在AB上,点G在AB,CD之间,连接FG,EH,GE,∠GFB=∠CEH.(1)如图1,求证:GF//EH;(2)如图2,若∠GEH=α,FM平分∠AFG,EM平分∠GEC,试问∠M与α之间有怎样的数量关系(用含α的式子表示∠M)?请写出你的猜想,并加以证明.7.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.(1)求证:∠ABF+∠DCF=∠BFC;(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.8.如图1,点E 在直线AB 、DC 之间,且180DEB ABE CDE ∠+∠-∠=︒. (1)求证://AB DC ;(2)若点F 是直线BA 上的一点,且BEF BFE ∠=∠,EG 平分DEB ∠交直线AB 于点G ,若20D ∠=︒,求FEG ∠的度数;(3)如图3,点N 是直线AB 、DC 外一点,且满足14CDM CDE ∠=∠,14ABN ABE ∠=∠,ND 与BE 交于点M .已知()012CDM αα∠=︒<<︒,且//BN DE ,则NMB ∠的度数为______(请直接写出答案,用含α的式子表示).9.综合与实践课上,同学们以“一个直角三角形和两条平行线”为背景开展数学活动,如图,已知两直线,a b ,且,a b ABC //是直角三角形,90BCA ∠=︒,操作发现:(1)如图1.若148∠=︒,求2∠的度数;(2)如图2,若30,1A ∠=︒∠的度数不确定,同学们把直线a 向上平移,并把2∠的位置改变,发现21120∠-∠=︒,请说明理由.(3)如图3,若∠A =30°,AC 平分BAM ∠,此时发现1∠与2∠又存在新的数量关系,请写出1∠与2∠的数量关系并说明理由.10.点A ,C ,E 在直线l 上,点B 不在直线l 上,把线段AB 沿直线l 向右平移得到线段CD .(1)如图1,若点E 在线段AC 上,求证:∠B +∠D =∠BED ;(2)若点E 不在线段AC 上,试猜想并证明∠B ,∠D ,∠BED 之间的等量关系; (3)在(1)的条件下,如图2所示,过点B 作PB //ED ,在直线BP ,ED 之间有点M ,使得∠ABE =∠EBM ,∠CDE =∠EDM ,同时点F 使得∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,其中n ≥1,设∠BMD =m ,利用(1)中的结论求∠BFD 的度数(用含m ,n 的代数式表示).三、解答题11.如图1,由线段,,,AB AM CM CD 组成的图形像英文字母M ,称为“M 形BAMCD ”.(1)如图1,M 形BAMCD 中,若//,50AB CD A C ∠+∠=︒,则M ∠=______; (2)如图2,连接M 形BAMCD 中,B D 两点,若150,B D AMC α∠+∠=︒∠=,试探求A ∠与C ∠的数量关系,并说明理由;(3)如图3,在(2)的条件下,且AC 的延长线与BD 的延长线有交点,当点M 在线段BD 的延长线上从左向右移动的过程中,直接写出A ∠与C ∠所有可能的数量关系.12.(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a 从空气中射入水中,再从水中射入空气中,形成光线b ,根据光学知识有12,34∠=∠∠=∠,请判断光线a 与光线b 是否平行,并说明理由.(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等,如图2有一口井,已知入射光线α与水平线OC 的夹角为40︒,问如何放置平面镜MN ,可使反射光线b 正好垂直照射到井底?(即求MN 与水平线的夹角) (3)如图3,直线EF 上有两点A 、C ,分别引两条射线AB 、CD .105BAF ∠=︒,65DCF ∠=︒,射线AB 、CD 分别绕A 点,C 点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t ,在射线CD 转动一周的时间内,是否存在某时刻,使得CD 与AB 平行?若存在,求出所有满足条件的时间t . 13.综合与探究(问题情境)王老师组织同学们开展了探究三角之间数量关系的数学活动.(1)如图1,EF ∥MN ,点A 、B 分别为直线EF 、MN 上的一点,点P 为平行线间一点,请直接写出∠PAF 、∠PBN 和∠APB 之间的数量关系; (问题迁移)(2)如图2,射线OM 与射线ON 交于点O ,直线m ∥n ,直线m 分别交OM 、ON 于点A 、D ,直线n 分别交OM 、ON 于点B 、C ,点P 在射线OM 上运动.①当点P 在A 、B (不与A 、B 重合)两点之间运动时,设∠ADP =∠α,∠BCP =∠β.则∠CPD ,∠α,∠β之间有何数量关系?请说明理由;②若点P 不在线段AB 上运动时(点P 与点A 、B 、O 三点都不重合),请你画出满足条件的所有图形并直接写出∠CPD ,∠α,∠β之间的数量关系.14.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况,如图,灯A 射线自AM 顺时针旋转至AN 便立即回转,灯B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视,若灯A 转动的速度是a °/秒,灯B 转动的速度是b °/秒,且a 、b 满足()2450a b a b -++-=.假定这一带长江两岸河堤是平行的,即//PQ MN ,且60BAN ∠=︒(1)求a 、b 的值;(2)若灯B 射线先转动45秒,灯A 射线才开始转动,当灯B 射线第一次到达BQ 时运动停止,问A 灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A 射线到达AN 之前.若射出的光束交于点C ,过C 作CD AC ⊥交PQ 于点D ,则在转动过程中,BAC ∠与BCD ∠的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.15.(感知)如图①,//,40,130AB CD AEP PFD ︒︒∠=∠=,求EPF ∠的度数.小明想到了以下方法:解:如图①,过点P 作//PM AB ,140AEP ︒∴∠=∠=(两直线平行,内错角相等)//AB CD (已知),//∴PM CD (平行于同一条直线的两直线平行),2180PFD ︒∴∠+∠=(两直线平行,同旁内角互补). 130PFD ︒∠=(已知),218013050︒︒︒∴∠=-=(等式的性质). 12405090︒︒︒∴∠+∠=+=(等式的性质).即90EPF ︒∠=(等量代换).(探究)如图②,//AB CD ,50,120AEP PFC ︒︒∠=∠=,求EPF ∠的度数.(应用)如图③所示,在(探究)的条件下,PEA ∠的平分线和PFC ∠的平分线交于点G ,则G ∠的度数是_______________︒.四、解答题16.(1)如图1,∠BAD 的平分线AE 与∠BCD 的平分线CE 交于点E ,AB ∥CD ,∠ADC =50°,∠ABC =40°,求∠AEC 的度数;(2)如图2,∠BAD 的平分线AE 与∠BCD 的平分线CE 交于点E ,∠ADC =α°,∠ABC =β°,求∠AEC 的度数;(3)如图3,PQ ⊥MN 于点O ,点A 是平面内一点,AB 、AC 交MN 于B 、C 两点,AD 平分∠BAC 交PQ 于点D ,请问ADPACB ABC∠∠-∠的值是否发生变化?若不变,求出其值;若改变,请说明理由.17.如图,在ABC 中,AD 是高,AE 是角平分线,20B ∠=︒,60C ∠=°.(1)求CAD ∠、AEC ∠和EAD ∠的度数.(2)若图形发生了变化,已知的两个角度数改为:当30B ∠=︒,60C ∠=°,则EAD ∠=__________︒.当50B ∠=︒,C 60∠=︒时,则EAD ∠=__________︒. 当60B ∠=︒,60C ∠=°时,则EAD ∠=__________︒. 当70B ∠=︒,60C ∠=°时,则EAD ∠=__________︒.(3)若B 和C ∠的度数改为用字母α和β来表示,你能找到EAD ∠与α和β之间的关系吗?请直接写出你发现的结论.18.如图所示,已知射线//,//,100CB OA AB OC C OAB ︒∠=∠=.点E 、F 在射线CB 上,且满足FOB AOB ∠=∠,OE 平分COF ∠ (1)求EOB ∠的度数;(2)若平行移动AB ,那么:OBC OFC ∠∠的值是否随之发生变化?如果变化,找出变化规律.若不变,求出这个比值;(3)在平行移动AB 的过程中,是否存在某种情况,使OEC OBA ∠=∠?若存在,求出其度数.若不存在,请说明理由.19.在ABC 中,射线AG 平分BAC ∠交BC 于点G ,点D 在BC 边上运动(不与点G 重合),过点D 作//DE AC 交AB 于点E .(1)如图1,点D 在线段CG 上运动时,DF 平分EDB ∠.①若100BAC ︒∠=,30C ︒∠=,则AFD ∠=_____;若40B ︒∠=,则AFD ∠=_____; ②试探究AFD ∠与B 之间的数量关系?请说明理由;(2)点D 在线段BG 上运动时,BDE ∠的角平分线所在直线与射线AG 交于点F .试探究AFD ∠与B 之间的数量关系,并说明理由.20.己知:如图①,直线MN ⊥直线PQ ,垂足为O ,点A 在射线OP 上,点B 在射线OQ 上(A 、B 不与O 点重合),点C 在射线ON 上且2OC =,过点C 作直线//l PQ .点D 在点C 的左边且3CD =(1)直接写出的BCD ∆面积 ;(2)如图②,若AC BC ⊥,作CBA ∠的平分线交OC 于E ,交AC 于F ,试说明CEF CFE ∠=∠;(3)如图③,若ADC DAC ∠=∠,点B 在射线OQ 上运动,ACB ∠的平分线交DA 的延长线于点H ,在点B 运动过程中HABC∠∠的值是否变化?若不变,求出其值;若变化,求出变化范围. 【参考答案】一、解答题1.(1);(2)无法裁出这样的长方形.【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解; (2)设长方形长为cm ,宽为cm ,根据题意列出方程,解方程比较4x 与20的大小 解析:(1)20;(2)无法裁出这样的长方形. 【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解;(2)设长方形长为4x cm ,宽为3x cm ,根据题意列出方程,解方程比较4x 与20的大小即可. 【详解】解:(1)由题意得,大正方形的面积为200+200=400cm 2, ∴cm ;()2根据题意设长方形长为4x cm ,宽为3x cm ,由题:43360x x ⋅= 则230x =0xx ∴=∴长为43020>∴无法裁出这样的长方形.【点睛】本题考查了算术平方根,根据题意列出算式(方程)是解决此题的关键.2.(1)图中阴影部分的面积17,边长是;(2)边长的值在4与5之间 【分析】(1)由图形可以得到阴影正方形的面积等于原来大正方形的面积减去周围四个直角三角形的面积,由正方形的面积等于边长乘以边长,可解析:(1)图中阴影部分的面积17;(2)边长的值在4与5之间 【分析】(1)由图形可以得到阴影正方形的面积等于原来大正方形的面积减去周围四个直角三角形的面积,由正方形的面积等于边长乘以边长,可以得到阴影正方形的边长;(2 【详解】(1)由图可知,图中阴影正方形的面积是:5×5−1442=17答:图中阴影部分的面积17(2)∵所以45∴边长的值在4与5之间;【点睛】本题主要考查了无理数的估算及算术平方根的定义,解题主要利用了勾股定理和正方形的面积求解,有一定的综合性,解题关键是无理数的估算.3.(1)5;;(2);;(3)能,.【分析】(1)易得5个小正方形的面积的和,那么就得到了大正方形的面积,求得面积的算术平方根即可为大正方形的边长.(2)求出斜边长即可.(3)一共有10个小正解析:(1)5;5;(2)51-;(3)能,10.-;15【分析】(1)易得5个小正方形的面积的和,那么就得到了大正方形的面积,求得面积的算术平方根即可为大正方形的边长.(2)求出斜边长即可.(3)一共有10个小正方形,那么组成的大正方形的面积为10,边长为10的算术平方根,画图.【详解】试题分析:解:(1)拼成的正方形的面积与原面积相等1×1×5=5,边长为5,如图(1)(2)斜边长=222222+=,故点A表示的数为:222-;点A表示的相反数为:222-(3)能,如图拼成的正方形的面积与原面积相等1×1×10=1010考点:1.作图—应用与设计作图;2.图形的剪拼.4.(1)长为,宽为;(2)正确,理由见解析【分析】(1)设长为3x,宽为2x,根据长方形的面积为30列方程,解方程即可;(2)根据长方形纸片的周长为50,阴影部分两个长方形的周长之和为30列方程解析:(1)长为,宽为2)正确,理由见解析【分析】(1)设长为3x,宽为2x,根据长方形的面积为30列方程,解方程即可;(2)根据长方形纸片的周长为50,阴影部分两个长方形的周长之和为30列方程组,解方程组求出a即可得到大正方形的面积.【详解】解:(1)设长为3x,宽为2x,则:3x•2x=30,∴x∴3x=,2x=答:这个长方形纸片的长为(2)正确.理由如下:根据题意得:()()250 4230a b ab a b⎧⎡⎤++=⎪⎣⎦⎨+-=⎪⎩,解得:105ab=⎧⎨=⎩,∴大正方形的面积为102=100.【点睛】本题考查了算术平方根,二元一次方程组,解二元一次方程组的基本思路是消元,把二元方程转化为一元方程是解题的关键.5.8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可.【详解】解:正方形面积=4×4-4××2×2=8;正方形的边解析:8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可.【详解】解:正方形面积=4×4-4×12×2×2=8; 正方形的边长=8=22.【点睛】本题考查了算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x 叫做a 的算术平方根.记为a . 二、解答题6.(1)见解析;(2),证明见解析.【分析】(1)由平行线的性质得到,等量代换得出,即可根据“同位角相等,两直线平行”得解;(2)过点作,过点作,根据平行线的性质及角平分线的定义求解即可.【详解析:(1)见解析;(2)902FME α∠=︒-,证明见解析. 【分析】(1)由平行线的性质得到CEH EHB ∠=∠,等量代换得出GFB EHB ∠=∠,即可根据“同位角相等,两直线平行”得解;(2)过点M 作//MQ AB ,过点G 作//GP AB ,根据平行线的性质及角平分线的定义求解即可.【详解】(1)证明://AB CD ,CEH EHB ∴∠=∠,GFB CEH ∠=∠,GFB EHB ∴∠=∠,//GF EH ∴;(2)解:902FME α∠=︒-,理由如下:如图2,过点M 作//MQ AB ,过点G 作//GP AB ,//AB CD ,//MQ CD ∴,AFM FMQ ∴∠=∠,QME MEC ∠=∠,FME FMQ QME AFM MEC ∴∠=∠+∠=∠+∠,同理,FGE FGP PGE AFG GEC ∠=∠+∠=∠+∠, FM 平分AFG ∠,EM 平分GEC ∠,2AFG AFM ∴∠=∠,2GEC MEC ∠=∠,2FGE FME ∴∠=∠,由(1)知,//GF EH ,180FGE GEH ∴∠+∠=︒,GEH α∠=,180FGE α∴∠=︒-,2180FME α∴∠=︒-,902FME α∴∠=︒-.【点睛】此题考查了平行线的判定与性质,熟记平行线的判定与性质及作出合理的辅助线是解题的关键.7.(1)证明见解析;(2)证明见解析;(3)∠FBE =35°.【分析】(1)根据平行线的性质得出∠ABF =∠BFE ,∠DCF =∠EFC ,进而解答即可; (2)由(1)的结论和垂直的定义解答即可;解析:(1)证明见解析;(2)证明见解析;(3)∠FBE =35°.【分析】(1)根据平行线的性质得出∠ABF =∠BFE ,∠DCF =∠EFC ,进而解答即可;(2)由(1)的结论和垂直的定义解答即可;(3)由(1)的结论和三角形的角的关系解答即可.【详解】证明:(1)∵AB ∥CD ,EF ∥CD ,∴AB ∥EF ,∴∠ABF =∠BFE ,∵EF ∥CD ,∴∠DCF =∠EFC ,∴∠BFC =∠BFE +∠EFC =∠ABF +∠DCF ;(2)∵BE ⊥EC ,∴∠BEC =90°,∴∠EBC +∠BCE =90°,由(1)可得:∠BFC =∠ABE +∠ECD =90°,∴∠ABE +∠ECD =∠EBC +∠BCE ,∵BE 平分∠ABC ,∴∠ABE =∠EBC ,∴∠ECD =∠BCE ,∴CE 平分∠BCD ;(3)设∠BCE =β,∠ECF =γ,∵CE 平分∠BCD ,∴∠DCE =∠BCE =β,∴∠DCF =∠DCE ﹣∠ECF =β﹣γ,∴∠EFC =β﹣γ,∵∠BFC =∠BCF ,∴∠BFC =∠BCE +∠ECF =γ+β,∴∠ABF =∠BFE =2γ,∵∠FBG =2∠ECF ,∴∠FBG =2γ,∴∠ABE +∠DCE =∠BEC =90°,∴∠ABE =90°﹣β,∴∠GBE =∠ABE ﹣∠ABF ﹣∠FBG =90°﹣β﹣2γ﹣2γ,∵BE 平分∠ABC ,∴∠CBE =∠ABE =90°﹣β,∴∠CBG =∠CBE +∠GBE ,∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,整理得:2γ+β=55°,∴∠FBE =∠FBG +∠GBE =2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.【点睛】本题主要考查平行线的性质,解决本题的关键是根据平行线的性质解答.8.(1)见解析;(2)10°;(3)【分析】(1)过点E 作EF ∥CD ,根据平行线的性质,两直线平行,内错角相等,得出结合已知条件,得出即可证明;(2)过点E 作HE ∥CD ,设 由(1)得AB ∥CD解析:(1)见解析;(2)10°;(3)18015α︒-【分析】(1)过点E 作EF ∥CD ,根据平行线的性质,两直线平行,内错角相等,得出,CDE DEF ∠=∠结合已知条件180DEB ABE CDE ∠+∠-∠=︒,得出180,FEB ABE ∠+∠=︒即可证明;(2)过点E 作HE ∥CD ,设,,GEF x FEB EFB y ∠=∠=∠= 由(1)得AB ∥CD ,则AB ∥CD ∥HE ,由平行线的性质,得出20,DEF D EFB y ∠=∠+∠=︒+再由EG 平分DEB ∠,得出,DEG GEB GEF FEB x y ∠=∠=∠+∠=+则2DEF DEG GEF x y ∠=∠+∠=+,则可列出关于x 和y 的方程,即可求得x ,即GEF ∠的度数;(3)过点N 作NP ∥CD ,过点M 作QM ∥CD ,由(1)得AB ∥CD ,则NP ∥CD ∥AB ∥QM ,根据14CDM CDE ∠=∠和CDM α∠=,得出3,MDE α∠=根据CD ∥PN ∥QM ,DE ∥NB ,得出,PND CDM DMQ α∠=∠=∠=3,EDM BNM α∠=∠=即4,BNP α∠=根据NP ∥AB ,得出4,PNB ABN α∠=∠=再由14ABN ABE ∠=∠,得出16,ABM α∠=由AB ∥QM ,得出18016,QMB α∠=︒-因为NMB NMQ QMB ∠=∠+∠,代入α的式子即可求出BMN ∠.【详解】(1)过点E 作EF ∥CD ,如图,∵EF ∥CD ,∴,CDE DEF ∠=∠∴,DEB CDE DEB DEF FEB ∠-∠=∠-∠=∠∵180DEB ABE CDE ∠+∠-∠=︒,∴180,FEB ABE ∠+∠=︒∴EF ∥AB ,∴CD ∥AB ;(2)过点E 作HE ∥CD ,如图,设,,GEF x FEB EFB y ∠=∠=∠=由(1)得AB ∥CD ,则AB ∥CD ∥HE ,∴20,,D DEH HEF EFB y ∠=∠=︒∠=∠=∴20,DEF DEH HEF D EFB y ∠=∠+∠=∠+∠=︒+又∵EG 平分DEB ∠,∴,DEG GEB GEF FEB x y ∠=∠=∠+∠=+∴2,DEF DEG GEF x y x x y ∠=∠+∠=++=+即220,x y y +=︒+解得:10,x =︒即10GEF ∠=︒;(3)过点N 作NP ∥CD ,过点M 作QM ∥CD ,如图,由(1)得AB ∥CD ,则NP ∥CD ∥AB ∥QM ,∵NP ∥CD ,CD ∥QM ,,CDM α∠=∴PND CDM DMQ α∠=∠=∠=,又∵14CDM CDE ∠=∠, ∴33,MDE CDM α∠=∠=∵//BN DE ,∴3,MDE BNM α∠=∠=∴34,PNB PND BNM ααα∠=∠+∠=+=又∵PN ∥AB ,∴4,PNB NBA α∠=∠= ∵14ABN ABE ∠=∠, ∴44416,ABM ABN αα∠=∠=⨯=又∵AB ∥QM ,∴180,ABM QMB ∠+∠=︒∴18018016,QMB ABM α∠=︒-∠=︒-∴1801618015NMB NMQ QMB ααα∠=∠+∠=+︒-=-.【点睛】本题考查平行线的性质,角平分线的定义,解决问题的关键是作平行线构造相等的角,利用两直线平行,内错角相等,同位角相等来计算和推导角之间的关系.9.(1)42°;(2)见解析;(3)∠1=∠2,理由见解析【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD=180°解析:(1)42°;(2)见解析;(3)∠1=∠2,理由见解析【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠DBC ,则∠ABD =∠ABC -∠DBC =60°-∠1,进而得出结论;(3)过点C 作CP ∥a ,由角平分线定义得∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,由平行线的性质得∠1=∠BAM =60°,∠PCA =∠CAM =30°,∠2=∠BCP =60°,即可得出结论.【详解】解:(1)∵∠1=48°,∠BCA =90°,∴∠3=180°-∠BCA -∠1=180°-90°-48°=42°,∵a∥b,∴∠2=∠3=42°;(2)理由如下:过点B作BD∥a.如图2所示:则∠2+∠ABD=180°,∵a∥b,∴b∥BD,∴∠1=∠DBC,∴∠ABD=∠ABC-∠DBC=60°-∠1,∴∠2+60°-∠1=180°,∴∠2-∠1=120°;(3)∠1=∠2,理由如下:过点C作CP∥a,如图3所示:∵AC平分∠BAM∴∠CAM=∠BAC=30°,∠BAM=2∠BAC=60°,又∵a∥b,∴CP∥b,∠1=∠BAM=60°,∴∠PCA=∠CAM=30°,∴∠BCP=∠BCA-∠PCA=90°-30°=60°,又∵CP∥a,∴∠2=∠BCP=60°,∴∠1=∠2.【点睛】本题是三角形综合题目,考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识;本题综合性强,熟练掌握平移的性质和平行线的性质是解题的关键.10.(1)见解析;(2)当点E在CA的延长线上时,∠BED=∠D-∠B;当点E 在AC的延长线上时,∠BED=∠BET-∠DET=∠B-∠D;(3)【分析】(1)如图1中,过点E作ET∥AB.利用平行解析:(1)见解析;(2)当点E在CA的延长线上时,∠BED=∠D-∠B;当点E在AC的延长线上时,∠BED=∠BET-∠DET=∠B-∠D;(3)()12m nn-【分析】(1)如图1中,过点E作ET∥A B.利用平行线的性质解决问题.(2)分两种情形:如图2-1中,当点E在CA的延长线上时,如图2-2中,当点E在AC的延长线上时,构造平行线,利用平行线的性质求解即可.(3)利用(1)中结论,可得∠BMD=∠ABM+∠CDM,∠BFD=∠ABF+∠CDF,由此解决问题即可.【详解】解:(1)证明:如图1中,过点E作ET∥A B.由平移可得AB∥CD,∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠BET+∠DET=∠B+∠D.(2)如图2-1中,当点E在CA的延长线上时,过点E作ET∥A B.∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠DET-∠BET=∠D-∠B.如图2-2中,当点E在AC的延长线上时,过点E作ET∥A B.∵AB ∥ET ,AB ∥CD ,∴ET ∥CD ∥AB ,∴∠B =∠BET ,∠TED =∠D ,∴∠BED =∠BET -∠DET =∠B -∠D .(3)如图,设∠ABE =∠EBM =x ,∠CDE =∠EDM =y ,∵AB ∥CD ,∴∠BMD =∠ABM +∠CDM ,∴m =2x +2y ,∴x +y =12m ,∵∠BFD =∠ABF +∠CDF ,∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,∴∠BFD =()111n n n x y x y n n n ---+=+=112n m n -⨯=()12m n n -. 【点睛】本题属于几何变换综合题,考查了平行线的性质,角平分线的定义等知识,解题的关键是学会条件常用辅助线,构造平行线解决问题,属于中考常考题型. 三、解答题11.(1)50°;(2)∠A+∠C=30°+α,理由见解析;(3)∠A-∠DCM=30°+α或30°-α【分析】(1)过M 作MN ∥AB ,由平行线的性质即可求得∠M 的值.(2)延长BA ,DC 交于E ,解析:(1)50°;(2)∠A +∠C =30°+α,理由见解析;(3)∠A -∠DCM =30°+α或30°-α【分析】(1)过M 作MN ∥AB ,由平行线的性质即可求得∠M 的值.(2)延长BA ,DC 交于E ,应用四边形的内角和定理与平角的定义即可解决问题. (3)分两种情形分别求解即可;【详解】解:(1)过M作MN∥AB,∵AB∥CD,∴AB∥MN∥CD,∴∠1=∠A,∠2=∠C,∴∠AMC=∠1+∠2=∠A+∠C=50°;故答案为:50°;(2)∠A+∠C=30°+α,延长BA,DC交于E,∵∠B+∠D=150°,∴∠E=30°,∵∠BAM+∠DCM=360°-(∠EAM+∠ECM)=360°-(360°-∠E-∠M)=30°+α;即∠A+∠C=30°+α;(3)①如下图所示:延长BA、DC使之相交于点E,延长MC与BA的延长线相交于点F,∵∠B+∠D=150°,∠AMC=α,∴∠E=30°由三角形的内外角之间的关系得:∠1=30°+∠2∠2=∠3+α∴∠1=30°+∠3+α∴∠1-∠3=30°+α即:∠A-∠C=30°+α.②如图所示,210-∠A=(180°-∠D CM)+α,即∠A-∠DCM=30°-α.综上所述,∠A-∠DCM=30°+α或30°-α.【点睛】本题考查了平行线的性质.解答该题时,通过作辅助线准确作出辅助线l∥AB,利用平行线的性质(两直线平行内错角相等)将所求的角∠M与已知角∠A、∠C的数量关系联系起来,从而求得∠M的度数.12.(1)平行,理由见解析;(2)65°;(3)5秒或95秒【分析】(1)根据等角的补角相等求出∠3与∠4的补角相等,再根据内错角相等,两直线平行即可判定a∥b;(2)根据入射光线与镜面的夹角与反解析:(1)平行,理由见解析;(2)65°;(3)5秒或95秒【分析】(1)根据等角的补角相等求出∠3与∠4的补角相等,再根据内错角相等,两直线平行即可判定a∥b;(2)根据入射光线与镜面的夹角与反射光线与镜面的夹角相等可得∠1=∠2,然后根据平角等于180°求出∠1的度数,再加上40°即可得解;(3)分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据两直线平行,内错角相等列式计算即可得解;②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据两直线平行,同位角相等列式计算即可得解;③CD旋转到与AB都在EF 的左侧,分别表示出∠DCF与∠BAC,然后根据两直线平行,同位角相等列式计算即可得解.【详解】解:(1)平行.理由如下:如图1,∵∠3=∠4,∴∠5=∠6,∵∠1=∠2,∴∠1+∠5=∠2+∠6,∴a∥b(内错角相等,两直线平行);(2)如图2:∵入射光线与镜面的夹角与反射光线与镜面的夹角相等,∴∠1=∠2,∵入射光线a与水平线OC的夹角为40°,b垂直照射到井底,∴∠1+∠2=180°-40°-90°=50°,∴∠1=1×50°=25°,2∴MN与水平线的夹角为:25°+40°=65°,即MN与水平线的夹角为65°,可使反射光线b正好垂直照射到井底;(3)存在.如图①,AB与CD在EF的两侧时,∵∠BAF=105°,∠DCF=65°,∴∠ACD=180°-65°-3t°=115°-3t°,∠BAC=105°-t°,要使AB∥CD,则∠ACD=∠BAC,即115-3t=105-t,解得t=5;如图②,CD旋转到与AB都在EF的右侧时,∵∠BAF=105°,∠DCF=65°,∴∠DCF=360°-3t°-65°=295°-3t°,∠BAC=105°-t°,要使AB∥CD,则∠DCF=∠BAC,即295-3t=105-t,解得t=95;如图③,CD旋转到与AB都在EF的左侧时,∵∠BAF=105°,∠DCF=65°,∴∠DCF=3t°-(180°-65°+180°)=3t°-295°,∠BAC=t°-105°,要使AB∥CD,则∠DCF=∠BAC,即3t-295=t-105,解得t=95,此时t>105,∴此情况不存在.综上所述,t为5秒或95秒时,CD与AB平行.【点睛】本题考查了平行线的判定与性质,光学原理,读懂题意并熟练掌握平行线的判定方法与性质是解题的关键,(3)要注意分情况讨论.13.(1)∠PAF +∠PBN +∠APB =360°;(2)①,见解析;②或【分析】(1)作PC ∥EF ,如图1,由PC ∥EF ,EF ∥MN 得到PC ∥MN ,根据平行线的性质得∠PAF +∠APC =180°,∠解析:(1)∠PAF +∠PBN +∠APB =360°;(2)①CPD αβ∠=∠+∠,见解析;②CPD βα∠=∠-∠或CPD αβ∠=∠-∠【分析】(1)作PC ∥EF ,如图1,由PC ∥EF ,EF ∥MN 得到PC ∥MN ,根据平行线的性质得∠PAF +∠APC =180°,∠PBN +∠CPB =180°,即有∠PAF +∠PBN +∠APB =360°;(2)①过P 作PE ∥AD 交ON 于E ,根据平行线的性质,可得到EPD α∠=∠,CPE β∠=∠,于是CPD αβ∠=∠+∠;②分两种情况:当P 在OB 之间时;当P 在OA 的延长线上时,仿照①的方法即可解答.【详解】解:(1)∠PAF +∠PBN +∠APB =360°,理由如下:作PC ∥EF ,如图1,∵PC ∥EF ,EF ∥MN ,∴PC ∥MN ,∴∠PAF +∠APC =180°,∠PBN +∠CPB =180°,∴∠PAF +∠APC +∠PBN +∠CPB =360°,∴∠PAF +∠PBN +∠APB =360°;(2)①CPD αβ∠=∠+∠,理由如下:如答图,过P 作PE ∥AD 交ON 于E ,∵AD ∥BC ,∴PE ∥BC ,∴EPD α∠=∠,CPE β∠=∠,∴CPD αβ∠=∠+∠②当P 在OB 之间时,CPD αβ∠=∠-∠,理由如下:如备用图1,过P 作PE ∥AD 交ON 于E ,∵AD ∥BC ,∴PE ∥BC ,∴EPD α∠=∠,CPE β∠=∠,∴CPD αβ∠=∠-∠;当P 在OA 的延长线上时,CPD βα∠=∠-∠,理由如下:如备用图2,过P 作PE ∥AD 交ON 于E ,∵AD ∥BC ,∴PE ∥BC ,∴EPD α∠=∠,CPE β∠=∠,∴CPD βα∠=∠-∠;综上所述,∠CPD ,∠α,∠β之间的数量关系是CPD βα∠=∠-∠或CPD αβ∠=∠-∠.【点睛】本题考查了平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.难点是分类讨论作平行辅助线.14.(1),;(2)15秒或63秒;(3)不发生变化,【分析】(1)利用非负数的性质解决问题即可.(2)分三种情形,利用平行线的性质构建方程即可解决问题.(3)由参数表示,即可判断.【详解】解析:(1)4a =,1b =;(2)15秒或63秒;(3)不发生变化,34BAC BCD ∠=∠【分析】(1)利用非负数的性质解决问题即可.(2)分三种情形,利用平行线的性质构建方程即可解决问题.(3)由参数t 表示BAC ∠,BCD ∠即可判断.【详解】解:(1)∵()2450a b a b -++-=, ∴4050a b a b -=⎧⎨+-=⎩, 4a ∴=,1b =;(2)设A 灯转动t 秒,两灯的光束互相平行,①当045t <<时,4(45)1t t =+⨯,解得15t =;②当4590t <<时,()418018045t t -=-+,解得63t =;③当90135t <<时,436045t t -=+,解得135t =,(不合题意)综上所述,当t =15秒或63秒时,两灯的光束互相平行;(3)设A 灯转动时间为t 秒,1804CAN t ∠=︒-,60(1804)4120BAC t t ∴∠=︒-︒-=-︒,又//PQ MN ,18041803BCA CBD CAN t t t ∴∠=∠+∠=+︒-=︒-,而90ACD ∠=︒,9090(1803)390BCD BCA t t ∴∠=︒-∠=︒-︒-=-︒,:4:3BAC BCD ∴∠∠=,即34BAC BCD ∠=∠.【点睛】本题考查平行线的性质和判定,非负数的性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,属于中考常考题型.15.[探究] 70°;[应用] 35【分析】[探究]如图②,根据AB ∥CD ,∠AEP=50°,∠PFC=120°,即可求∠EPF 的度数.[应用]如图③所示,在[探究]的条件下,根据∠PEA 的平分线解析:[探究] 70°;[应用] 35【分析】[探究]如图②,根据AB ∥CD ,∠AEP=50°,∠PFC=120°,即可求∠EPF 的度数.[应用]如图③所示,在[探究]的条件下,根据∠PEA 的平分线和∠PFC 的平分线交于点G ,可得∠G的度数.【详解】解:[探究]如图②,过点P作PM∥AB,∴∠MPE=∠AEP=50°(两直线平行,内错角相等)∵AB∥CD(已知),∴PM∥CD(平行于同一条直线的两直线平行),∴∠PFC=∠MPF=120°(两直线平行,内错角相等).∴∠EPF=∠MPF-MPE=120°50°=70°(等式的性质).答:∠EPF的度数为70°;[应用]如图③所示,∵EG是∠PEA的平分线,PG是∠PFC的平分线,∴∠AEG=12∠AEP=25°,∠GCF=12∠PFC=60°,过点G作GM∥AB,∴∠MGE=∠AEG=25°(两直线平行,内错角相等)∵AB∥CD(已知),∴GM∥CD(平行于同一条直线的两直线平行),∴∠GFC=∠MGF=60°(两直线平行,内错角相等).∴∠G=∠MGF-MGE=60°-25°=35°.答:∠G的度数是35°.故答案为:35.【点睛】本题考查了平行线的判定与性质、平行公理及推论,解决本题的关键是掌握平行线的判定与性质.四、解答题16.(1)∠E=45°;(2)∠E=;(3)不变化,【分析】(1)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD ,∠B+∠EAB=∠E+∠ECB ,由角平分线的性质,可得∠ECD=∠ECB=∠解析:(1)∠E =45°;(2)∠E =2βα-;(3)不变化,12【分析】(1)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD ,∠B+∠EAB=∠E+∠ECB ,由角平分线的性质,可得∠ECD=∠ECB=12∠BCD ,∠EAD=∠EAB=12∠BAD ,则可得∠E= 12(∠D+∠B ),继而求得答案;(2)首先延长BC 交AD 于点F ,由三角形外角的性质,可得∠BCD=∠B+∠BAD+∠D ,又由角平分线的性质,即可求得答案.(3)由三角形内角和定理,可得90ADP ACB DAC ∠+︒=∠+∠ADP DFO ABC OEB ∠+∠=∠+∠,利用角平分线的性质与三角形的外角的性质可得答案.【详解】解:(1)∵CE 平分∠BCD ,AE 平分∠BAD∴∠ECD=∠ECB=12∠BCD ,∠EAD=∠EAB=12∠BAD , ∵∠D+∠ECD=∠E+∠EAD ,∠B+∠EAB=∠E+∠ECB ,∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB∴∠D+∠B=2∠E ,∴∠E=12(∠D+∠B ), ∵∠ADC=50°,∠ABC=40°,∴∠AEC=12×(50°+40°)=45°;(2)延长BC 交AD 于点F ,∵∠BFD=∠B+∠BAD ,∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D ,∵CE 平分∠BCD ,AE 平分∠BAD∴∠ECD=∠ECB=12∠BCD ,∠EAD=∠EAB=12∠BAD , ∵∠E+∠ECB=∠B+∠EAB ,∴∠E=∠B+∠EAB -∠ECB=∠B+∠BAE -12∠BCD =∠B+∠BAE -12(∠B+∠BAD+∠D ) = 12(∠B -∠D ), ∠ADC =α°,∠ABC =β°,即∠AEC=.2βα-(3)ADP ACB ABC ∠∠-∠的值不发生变化,1.2ADP ACB ABC ∠∴=∠-∠ 理由如下:如图,记AB 与PQ 交于E ,AD 与CB 交于F ,,PQ MN ⊥90,DOC BOE ∴∠=∠=︒90ADP ACB DAC ∠+︒=∠+∠①,ADP DFO ABC OEB ∠+∠=∠+∠②,∴ ①-②得:90,DFO ACB ABC DAC OEB ︒-∠=∠-∠+∠-∠90,DFO OEB DAC ACB ABC ∴︒-∠+∠-∠=∠-∠90,,ADP DFO OEB EAD ADP ∠=︒-∠∠-∠=∠AD 平分∠BAC ,,BAD CAD ∴∠=∠,OEB CAD ADP ∴∠-∠=∠2,ADP ACB ABC ∠=∠-∠1.2ADP ACB ABC ∠∴=∠-∠【点睛】此题考查了三角形内角和定理、三角形外角的性质以及角平分线的定义.此题难度较大,注意掌握整体思想与数形结合思想的应用.17.(1)30°,70°,20°;(2)15°,5°,0°,5°;(3)当时,;当时,.【分析】(1)先利用三角形内角和定理求出的度数,再根据角平分线和高的性质分别得出和的度数,进而可求和的度数;解析:(1)30°,70°,20°;(2)15°,5°,0°,5°;(3)当αβ<时,1()2EAD βα∠=-;当αβ>时,1()2EAD αβ∠=-. 【分析】(1)先利用三角形内角和定理求出BAC ∠的度数,再根据角平分线和高的性质分别得出EAC ∠和DAC ∠的度数,进而可求AEC ∠和EAD ∠的度数;(2)先利用三角形内角和定理求出BAC ∠的度数,再根据角平分线和高的性质分别得出EAC ∠和DAC ∠的度数,则前三问利用EAD EAC DAC ∠=∠-∠即可得出答案,第4问利用EAD DAC EAC ∠=∠-∠即可得出答案;(3)按照(2)的方法,将相应的数换成字母即可得出答案.【详解】(1)∵20B ∠=︒,60C ∠=°,∴180100BAC B C ∠=-∠-∠=︒︒ .∵AE 平分BAC ∠, ∴1502EAC BAC ∠=∠=︒. ∵AD 是高,90ADC ADE ∴∠=∠=︒ ,9030CAD C ∴∠=︒-∠=︒ ,。
(完整版)人教版初一下册数学期末压轴题试题培优试题

一、解答题1.如图,A 点的坐标为(0,3),B 点的坐标为(﹣3,0),D 为x 轴上的一个动点且不与B ,O 重合,将线段AD 绕点A 逆时针旋转90°得线段AE ,使得AE ⊥AD ,且AE =AD ,连接BE 交y 轴于点M .(1)如图,当点D 在线段OB 的延长线上时, ①若D 点的坐标为(﹣5,0),求点E 的坐标. ②求证:M 为BE 的中点. ③探究:若在点D 运动的过程中,OMBD的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.(2)请直接写出三条线段AO ,DO ,AM 之间的数量关系(不需要说明理由).2.已知AB ∥CD ,∠ABE 与∠CDE 的角分线相交于点F .(1)如图1,若BM 、DM 分别是∠ABF 和∠CDF 的角平分线,且∠BED =100°,求∠M 的度数;(2)如图2,若∠ABM =13∠ABF ,∠CDM =13∠CDF ,∠BED =α°,求∠M 的度数;(3)若∠ABM =1n ∠ABF ,∠CDM =1n∠CDF ,请直接写出∠M 与∠BED 之间的数量关系3.已知//AM CN ,点B 为平面内一点,AB BC 于B .(1)如图1,求证:90A C ∠+∠=︒;(2)如图2,过点B 作BD MA ⊥的延长线于点D ,求证:ABD C ∠=∠;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,且BF 平分DBC ∠,BE 平分ABD ∠,若AFC BCF ∠=∠,3BFC DBE ∠=∠,求EBC ∠的度数.4.点A ,C ,E 在直线l 上,点B 不在直线l 上,把线段AB 沿直线l 向右平移得到线段CD .(1)如图1,若点E 在线段AC 上,求证:∠B +∠D =∠BED ;(2)若点E 不在线段AC 上,试猜想并证明∠B ,∠D ,∠BED 之间的等量关系; (3)在(1)的条件下,如图2所示,过点B 作PB //ED ,在直线BP ,ED 之间有点M ,使得∠ABE =∠EBM ,∠CDE =∠EDM ,同时点F 使得∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,其中n ≥1,设∠BMD =m ,利用(1)中的结论求∠BFD 的度数(用含m ,n 的代数式表示). 5.如图1,已知直线m ∥n ,AB 是一个平面镜,光线从直线m 上的点O 射出,在平面镜AB 上经点P 反射后,到达直线n 上的点Q .我们称OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB .(1)如图1,若∠OPQ =82°,求∠OPA 的度数;(2)如图2,若∠AOP =43°,∠BQP =49°,求∠OPA 的度数;(3)如图3,再放置3块平面镜,其中两块平面镜在直线m 和n 上,另一块在两直线之间,四块平面镜构成四边形ABCD ,光线从点O 以适当的角度射出后,其传播路径为O→P→Q→R→O→P→…试判断∠OPQ 和∠ORQ 的数量关系,并说明理由. 6.已知,//AE BD ,A D ∠=∠. (1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.7.阅读下面文字:对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭可以如下计算:原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭114=-上面这种方法叫拆项法,你看懂了吗? 仿照上面的方法,计算: (1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭(2)235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭8.下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,将以上三个等式两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯. (1)观察发现:1n(1)n =+__________1111122334n(1)n ++++=⨯⨯⨯+ . (2)初步应用:利用(1)的结论,解决以下问题“①把112拆成两个分子为1的正的真分数之差,即112= ;②把112拆成两个分子为1的正的真分数之和,即112= ; ( 3 )定义“⊗”是一种新的运算,若1112126⊗=+,11113261220⊗=++,111114*********⊗=+++,求193⊗的值.9.我们知道,任意一个正整数x 都可以进行这样的分解:x m n =⨯(m ,n 是正整数,且m n ≤),在x 的所有这种分解中,如果m ,n 两因数之差的绝对值最小,我们就称m n⨯是x 的最佳分解,并规定:()=nf x m.例如:18可分解成118⨯,29⨯或36⨯,因为1819263->->-,所以36⨯是18的最佳分解,所以()311862f == (1)填空:()6f = ;()16=f ;(2)一个两位正整数t (10t a b =+,19a b ≤≤≤,a ,b 为正整数),交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54,求出所有的两位正整数;并求()f t 的最大值; (3)填空:①()22357f ⨯⨯⨯= ;②()42357f ⨯⨯⨯= ;10.a 是不为1的有理数,我们把11a-称为a 的差倒数.如:2的差倒数是1112=--,现已知a 1=12,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数,… (1)求a 2,a 3,a 4的值;(2)根据(1)的计算结果,请猜想并写出a 2016•a 2017•a 2018的值; (3)计算:a 33+a 66+a 99+…+a 9999的值. 11.探究与应用: 观察下列各式: 1+3= 2 1+3+5= 2 1+3+5+7= 2 1+3+5+7+9= 2 ……问题:(1)在横线上填上适当的数; (2)写出一个能反映此计算一般规律的式子;(3)根据规律计算:(﹣1)+(﹣3)+(﹣5)+(﹣7)+…+(﹣2019).(结果用科学记数法表示)12.对非负实数x “四舍五入”到各位的值记为x <>.即:当n 为非负整数时,如果12n x -≤<1n 2+,则x n <>=;反之,当n 为非负整数时,如果x n <>=,则1122n x n -<+≤.例如: 00.480<>=<>=,0.64 1.491, 3.5 4.124<>=<>=<>=<>=. (1)计算: 1.87<>= ;π= ; (2)①求满足12x <->=的实数x 的取值范围, ②求满足43x x <>=的所有非负实数x 的值; (3)若关于x 的方程21122a x x -<>+-=-有正整数解,求非负实数a 的取值范围. 13.如图1,在平面直角坐标系中,A (a ,0)是x 轴正半轴上一点,C 是第四象限内一点,CB ⊥y 轴交y 轴负半轴于B (0,b ),且|a ﹣3|+(b+4)2=0,S 四边形AOBC =16.(1)求点C 的坐标.(2)如图2,设D 为线段OB 上一动点,当AD ⊥AC 时,∠ODA 的角平分线与∠CAE 的角平分线的反向延长线交于点P ,求∠APD 的度数;(点E 在x 轴的正半轴).(3)如图3,当点D 在线段OB 上运动时,作DM ⊥AD 交BC 于M 点,∠BMD 、∠DAO 的平分线交于N 点,则点D 在运动过程中,∠N 的大小是否会发生变化?若不变化,求出其值;若变化,请说明理由.14.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结FA 、FB ,E 是射线FA 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.15.如图1,C 点是第二象限内一点, CB y ⊥轴于B ,且()0,B b 是y 轴正半轴上一点,(),0A a 是x 轴负半x 轴上一点,且()2230, 9AOBC a b S ++-==四边形.(1)A( ),B ( )(2)如图2,设D 为线段OB 上一动点,当AD AC ⊥时,ODA ∠的角平分线与CAE ∠的角平分线的反向延长线交于点P ,求APD ∠的度数: (注: 三角形三个内角的和为180) (3)如图3,当D 点在线段OB 上运动时,作DM AD ⊥交CB 于,,M BMD DAO ∠∠的平分线交于N ,当D 点在运动的过程中,N ∠的大小是否变化?若不变,求出其值;若变化,请说明理由.16.如图,数轴上两点A 、B 对应的数分别是﹣1,1,点P 是线段AB 上一动点,给出如下定义:如果在数轴上存在动点Q ,满足|PQ |=2,那么我们把这样的点Q 表示的数称为连动数,特别地,当点Q 表示的数是整数时我们称为连动整数.(1)﹣3,0,2.5是连动数的是 ;(2)关于x 的方程2x ﹣m =x +1的解满足是连动数,求m 的取值范围 ;(3)当不等式组11212()3x x a +⎧>-⎪⎨⎪+-⎩的解集中恰好有4个解是连动整数时,求a 的取值范围.17.在平面直角坐标系中,(,1)A a ,(,3)B b 满足()2120a b ++-=. (1)直接写出a 、b 的值:a = ;b = ;(2)如图1,若点(3,)P n 满足ABP △的面积等于6,求n 的值;(3)设线段AB 交y 轴于C ,动点E 从点C 出发,在y 轴上以每秒1个单位长度的速度向下运动,动点F 从点(8,0)-出发,在x 轴上以每秒2个单位长度的速度向右运动,若它们同时出发,运动时间为t 秒,问t 为何值时,有2ABEABFSS=?请求出t 的值.18.如图所示,在直角坐标系xoy 中,已知()6,0A ,()8,6B ,将线段OA 平移至CB ,连接OC 、AB 、CD 、BD ,且//OC AB ,点D 在x 轴上移动(不与点O 、A 重合).(1)直接写出点C 的坐标;(2)点D 在运动过程中,是否存在ODC △的面积是ABD △的面积的3倍,如果存在请求出点D 的坐标,如果不存在请说明理由;(3)点D 在运动过程中,请写出OCD ∠、ABD ∠、BDC ∠三者之间存在怎样的数量关系,并说明理由.19.历史上的数学巨人欧拉最先把关于x 的多项式用记号f(x)来表示.例如f(x)=x 2+3x -5,把x =某数时多项式的值用f(某数)来表示.例如x =-1时多项式x 2+3x -5的值记为f(-1)=(-1)2+3×(-1)-5=-7.(1)已知g(x)=-2x 2-3x +1,分别求出g(-1)和g(-2);(2)已知h(x)=ax 3+2x 2-ax -6,当h(12)=a ,求a 的值;(3)已知f(x)=2+3kx a -6x bk --2(a ,b 为常数),当k 无论为何值,总有f(1)=0,求a ,b 的值.20.某公园的门票价格如下表所示:某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如 果两个班联合起来,作为一个团体购票,则需付 1078 元. (1)列方程求出两个班各有多少学生;(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮 他们买票呢?请给出最省钱的方案.21.如图,//CD EF ,AE 是CAB ∠的平分线,α∠和β∠的度数满足方程组2250(1)3100(2)αβαβ∠+∠=︒⎧⎨∠-∠=︒⎩,(1)求α∠和β∠的度数; (2)求证://AB CD . (3)求C ∠的度数.22.数轴上有两个动点M ,N ,如果点M 始终在点N 的左侧,我们称作点M 是点N 的“追赶点”.如图,数轴上有2个点A ,B ,它们表示的数分别为-3,1,已知点M 是点N 的“追赶点”,且M ,N 表示的数分别为m ,n .(1)由题意得:点A 是点B 的“追赶点”,AB =1-(-3)=4(AB 表示线段AB 的长,以下相同);类似的,MN =____________.(2)在A ,M ,N 三点中,若其中一个点是另外两个点所构成线段的中点,请用含m 的代数式来表示n .(3)若AM =BN ,MN =43BM ,求m 和n 值.23.如果3个数位相同的自然数m ,n ,k 满足:m +n =k ,且k 各数位上的数字全部相同,则称数m 和数n 是一对“黄金搭档数”.例如:因为25,63,88都是两位数,且25+63=88,则25和63是一对“黄金搭档数”.再如:因为152,514,666都是三位数,且152+514=666,则152和514是一对“黄金搭档数”.(1)分别判断87和12,62和49是否是一对“黄金搭档数”,并说明理由;(2)已知两位数s 和两位数t 的十位数字相同,若s 和t 是一对“黄金搭档数”,并且s 与t 的和能被7整除,求出满足题意的s .24.在平面直角坐标系xOy 中,把线段AB 先向右平移h 个单位,再向下平移1个单位得到线段CD (点A 对应点C ),其中()(),,,A a b B m n 分别是第三象限与第二象限内的点.(1)若|3|10,2a b h ++=,求C 点的坐标;(2)若1b n =-,连接AD ,过点B 作AD 的垂线l ①判断直线l 与x 轴的位置关系,并说明理由;②已知E 是直线l 上一点,连接DE ,且DE 的最小值为1,若点B ,D 及点(),s t 都是关于x ,y 的二元一次方程(0)px qy k pq +=≠的解(),x y 为坐标的点,试判断()()s m t n -+-是正数、负数还是0?并说明理由.25.某小区准备新建60个停车位,以解决小区停车难的问题.已知新建2个地上停车位和3个地下停车位共需1.7万元:新建4个地上停车位和2个地下停车位共需1.4万元, (1)该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)若该小区新建车位的投资金额超过14万元而不超过15万元,问共有几种建造方案? (3)对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额. 26.阅读材料:关于x ,y 的二元一次方程ax+by=c 有一组整数解00x x y y =⎧⎨=⎩,则方程ax+by=c 的全部整数解可表示为00x x bty y at =-⎧⎨=+⎩(t 为整数).问题:求方程7x+19y=213的所有正整数解.小明参考阅读材料,解决该问题如下:解:该方程一组整数解为0069x y =⎧⎨=⎩,则全部整数解可表示为61997x ty t =-⎧⎨=+⎩(t 为整数).因为61909+70.t t ->⎧⎨>⎩,解得96719t -<<.因为t 为整数,所以t =0或-1.所以该方程的正整数解为69x y =⎧⎨=⎩和252x y =⎧⎨=⎩. (1)方程3x-5y=11的全部整数解表示为:253x ty t θ=+⎧⎨=+⎩(t 为整数),则θ= ;(2)请你参考小明的解题方法,求方程2x+3y=24的全部正整数解; (3)方程19x+8y=1908的正整数解有多少组? 请直接写出答案.27.在平面直角坐标系xOy 中,已知点M (a ,b ).如果存在点N (a ′,b ′),满足a ′=|a +b |,b ′=|a ﹣b |,则称点N 为点M 的“控变点”. (1)点A (﹣1,2)的“控变点”B 的坐标为 ;(2)已知点C (m ,﹣1)的“控变点”D 的坐标为(4,n ),求m ,n 的值;(3)长方形EFGH 的顶点坐标分别为(1,1),(5,1),(5,4),(1,4).如果点P (x ,﹣2x )的“控变点”Q 在长方形EFGH 的内部,直接写出x 的取值范围.28.请阅读求绝对值不等式3x <和3x >的解的过程.对于绝对值不等式3x <,从图1的数轴上看:大于3-而小于3的数的绝对值小于3,所以3x <的解为33x -<<;对于绝对值不等式3x >,从图2的数轴上看:小于3-或大于3的数的绝对值大于3,所以3x >的解为3x <-或3x >.(1)求绝对值不等式32x ->的解(2)已知绝对值不等式21x a -<的解为3b x <<,求2a b -的值(3)已知关于x ,y 的二元一次方程组234461x y m x y m -=-⎧⎨+=-+⎩的解满足2x y +≤,其中m 是负整数,求m 的值.29.阅读理解:定义:A ,B ,C 为数轴上三点,若点C 到点A 的距离是它到点B 的时距离的n (n 为大于1的常数)倍,则称点C 是(),A B 的n 倍点,且当C 是(),A B 的n 倍点或(),B A 的n 倍点时,我们也称C 是A 和B 两点的n 倍点.例如,在图1中,点C 是(),A B 的2倍点,但点C 不是(),B A 的2倍点.(1)特值尝试.①若2n =,图1中,点______是(),D C 的2倍点.(填A 或B )②若3n =,如图2,M ,N 为数轴上两个点,点M 表示的数是2-,点N 表示的数是4,数______表示的点是(),M N 的3倍点.(2)周密思考:图2中,一动点P 从N 出发,以每秒2个单位的速度沿数轴向左运动t 秒,若P 恰好是M 和N 两点的n 倍点,求所有符合条件的t 的值.(用含n 的式子表示)(3)拓展应用数轴上两点间的距离不超过30个单位长度时,称这两点处于“可视距离”.若(2)中满足条件的M 和N 两点的所有n 倍点P 均处于点N 的“可视距离”内,请直接写出n 的取值范围.(不必写出解答过程)30.在平面直角坐标系中,点A ,B 的坐标分别为(﹣1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积S 四边形ABDC ;(2)在y 轴上是否存在一点P ,连接PA ,PB ,使S △PAB =S 四边形ABDC ?若存在这样一点,求出点P 的坐标;若不存在,试说明理由;(3)点P 是直线BD 上一个动点,连接PC 、PO ,当点P 在直线BD 上运动时,请直接写出∠OPC 与∠PCD 、∠POB 的数量关系【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)①E (3,﹣2)②见解析;③12OM BD =,理由见解析;(2)OD+OA =2AM 或OA ﹣OD =2AM【分析】(1)①过点E 作EH ⊥y 轴于H .证明△DOA ≌△AHE (AAS )可得结论.②证明△BOM ≌△EHM (AAS )可得结论.③是定值,证明△BOM ≌△EHM 可得结论.(2)根据点D 在点B 左侧和右侧分类讨论,分别画出对应的图形,根据全等三角形的判定及性质即可分别求出结论.【详解】解:(1)①过点E作EH⊥y轴于H.∵A(0,3),B(﹣3,0),D(﹣5,0),∴OA=OB=3,OD=5,∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∴△DOA≌△AHE(AAS),∴AH=OD=5,EH=OA=3,∴OH=AH﹣OA=2,∴E(3,﹣2).②∵EH⊥y轴,∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴BM=EM.③结论:OMBD=12.理由:∵△DOA≌△AHE,∴OD=AH,∵OA=OB,∴BD=OH,∵△BOM≌△EHM,∴OM=MH,∴OM=12OH=12BD.(2)结论:OA+OD=2AM或OA﹣OD=2AM.理由:当点D在点B左侧时,∵△BOM≌△EHM,△DOA≌△AHE∴OM=MH,OD=AH∴OH=2OM,OD-OB=AH-OA∴BD=OH∴BD=2OM,∴OD ﹣OA =2(AM ﹣AO ),∴OD+OA =2AM .当点D 在点B 右侧时,过点E 作EH ⊥y 轴于点H∵∠AOD =∠AHE =∠DAE =90°,∴∠DAO+∠EAH =90°,∠EAH+∠AEH =90°,∴∠DAO =∠AEH ,∵AD=AE∴△DOA ≌△AHE (AAS ),∴EH=AO=3=OB ,OD=AH∴∠EHO =∠BOH =90°,∵∠BMO =∠EMH ,OB =EH =3,∴△BOM ≌△EHM (AAS ),∴OM =MH∴OA +OD= OA +AH=OH=OM +MH=2MH=2(AM +AH )=2(AM +OD )整理可得OA ﹣OD =2AM .综上:OA+OD =2AM 或OA ﹣OD =2AM .【点睛】此题考查的是全等三角形的判定及性质、旋转的性质和平面直角坐标系,掌握全等三角形的判定及性质、旋转的性质和点的坐标与线段长度的关系是解决此题的关键.2.(1)65°;(2)3606α︒-︒;(3)2n ∠M +∠BED =360° 【分析】(1)首先作EG ∥AB ,FH ∥AB ,连结MF ,利用平行线的性质可得∠ABE +∠CDE =260°,再利用角平分线的定义得到∠ABF +∠CDF =130°,从而得到∠BFD 的度数,再根据角平分线的定义和三角形外角的性质可求∠M 的度数;(2)先由已知得到∠ABE =6∠ABM ,∠CDE =6∠CDM ,由(1)得∠ABE +∠CDE =360°-∠BED ,∠M =∠ABM +∠CDM ,等量代换即可求解;(3)由(2)的方法可得到2n ∠M +∠BED =360°.【详解】解:(1)如图1,作//EG AB ,//FH AB ,连结MF ,//AB CD ,//////EG AB FH CD ∴,ABF BFH ∴∠=∠,CDF DFH ∠=∠,180ABE BEG ∠+∠=︒,180GED CDE ∠+∠=︒, 360ABE BEG GED CDE ∴∠+∠+∠+∠=︒,100BED BEG DEG ∠=∠+∠=︒,260ABE CDE ∴∠+∠=︒,ABE ∠和CDE ∠的角平分线相交于E ,130ABF CDF ∴∠+∠=︒,130BFD BFH DFH ∴∠=∠+∠=︒, BM 、DM 分别是ABF ∠和CDF ∠的角平分线,12MBF ABF ∴∠=∠,12MDF CDF ∠=∠, 65MBF MDF ∴∠+∠=︒,1306565BMD ∴∠=︒-︒=︒;(2)如图1,13ABM ABF ∠=∠,13CDM CDF ∠=∠, 3ABF ABM ∴∠=∠,3CDF CDM ∠=∠,ABE ∠与CDE ∠两个角的角平分线相交于点F ,6ABE ABM ∴∠=∠,6CDE CDM ∠=∠,66360ABM CDM BED ∴∠+∠+∠=︒,BMD ABM CDM ∠=∠+∠,6360BMD BED ∴∠+∠=︒,3606BMD α︒-︒∴∠=; (3)由(2)结论可得,22360n ABM n CDM E ∠+∠+∠=︒,M ABM CDM ∠=∠+∠, 则2360n M BED ∠+∠=︒.【点睛】本题主要考查了平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.3.(1)见解析;(2)见解析;(3)︒=∠105EBC .【分析】(1)先根据平行线的性质得到C BDA ∠=∠,然后结合AB BC ⊥即可证明;(2)过B 作//BH DM ,先说明ABD CBH ∠=∠,然后再说明//BH NC 得到CBH C ∠=∠,最后运用等量代换解答即可;(3)设∠DBE =a ,则∠BFC =3a ,根据角平分线的定义可得∠ABD =∠C =2a ,∠FBC =12∠DBC =a +45°,根据三角形内角和可得∠BFC +∠FBC +∠BCF =180°,可得∠AFC =∠BCF 的度数表达式,再根据平行的性质可得∠AFC +∠NCF =180°,代入即可算出a 的度数,进而完成解答.【详解】(1)证明:∵//AM CN ,∴C BDA ∠=∠,∵AB BC ⊥于B , ∴90B ∠=︒,∴90A BDA ∠+∠=︒,∴90A C ∠+∠=︒;(2)证明:过B 作//BH DM ,∵BD MA ⊥,∴90ABD ABH ∠+∠=︒,又∵AB BC ⊥,∴90ABH CBH ∠+∠=︒,∴ABD CBH ∠=∠,∵//BH DM ,//AM CN∴//BH NC ,∴CBH C ∠=∠,∴ABD C ∠=∠;(3)设∠DBE =a ,则∠BFC =3a ,∵BE 平分∠ABD ,∴∠ABD =∠C =2a ,又∵AB ⊥BC ,BF 平分∠DBC ,∴∠DBC =∠ABD +∠ABC =2a +90,即:∠FBC =12∠DBC =a +45°又∵∠BFC +∠FBC +∠BCF =180°,即:3a +a +45°+∠BCF =180°∴∠BCF =135°-4a ,∴∠AFC =∠BCF =135°-4a ,又∵AM//CN,∴∠AFC+∠NCF=180°,即:∠AFC+∠BCN+∠BCF=180°,∴135°-4a+135°-4a+2a=180,解得a=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点睛】本题主要考查了平行线的性质、角平分线的性质及角的计算,熟练应用平行线的性质、角平分线的性质是解答本题的关键.4.(1)见解析;(2)当点E在CA的延长线上时,∠BED=∠D-∠B;当点E在AC的延长线上时,∠BED=∠BET-∠DET=∠B-∠D;(3)()12m nn-【分析】(1)如图1中,过点E作ET∥A B.利用平行线的性质解决问题.(2)分两种情形:如图2-1中,当点E在CA的延长线上时,如图2-2中,当点E在AC的延长线上时,构造平行线,利用平行线的性质求解即可.(3)利用(1)中结论,可得∠BMD=∠ABM+∠CDM,∠BFD=∠ABF+∠CDF,由此解决问题即可.【详解】解:(1)证明:如图1中,过点E作ET∥A B.由平移可得AB∥CD,∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠BET+∠DET=∠B+∠D.(2)如图2-1中,当点E在CA的延长线上时,过点E作ET∥A B.∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠DET-∠BET=∠D-∠B.如图2-2中,当点E在AC的延长线上时,过点E作ET∥A B.∵AB ∥ET ,AB ∥CD ,∴ET ∥CD ∥AB ,∴∠B =∠BET ,∠TED =∠D ,∴∠BED =∠BET -∠DET =∠B -∠D .(3)如图,设∠ABE =∠EBM =x ,∠CDE =∠EDM =y ,∵AB ∥CD ,∴∠BMD =∠ABM +∠CDM ,∴m =2x +2y ,∴x +y =12m ,∵∠BFD =∠ABF +∠CDF ,∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,∴∠BFD =()111n n n x y x y n n n ---+=+=112n m n -⨯=()12m n n-. 【点睛】本题属于几何变换综合题,考查了平行线的性质,角平分线的定义等知识,解题的关键是学会条件常用辅助线,构造平行线解决问题,属于中考常考题型.5.(1)49°,(2)44°,(3)∠OPQ =∠ORQ【分析】(1)根据∠OPA =∠QP B .可求出∠OPA 的度数;(2)由∠AOP =43°,∠BQP =49°可求出∠OPQ 的度数,转化为(1)来解决问题; (3)由(2)推理可知:∠OPQ =∠AOP +∠BQP ,∠ORQ =∠DOR +∠RQC ,从而∠OPQ =∠ORQ .【详解】解:(1)∵∠OPA =∠QPB ,∠OPQ =82°,∴∠OPA =(180°-∠OPQ )×12=(180°-82°)×12=49°,(2)作PC ∥m ,∵m ∥n ,∴m ∥PC ∥n ,∴∠AOP =∠OPC =43°,∠BQP =∠QPC =49°,∴∠OPQ =∠OPC +∠QPC =43°+49°=92°,∴∠OPA =(180°-∠OPQ )×12=(180°-92°)×1244°,(3)∠OPQ =∠ORQ .理由如下:由(2)可知:∠OPQ =∠AOP +∠BQP ,∠ORQ =∠DOR +∠RQC ,∵入射光线与平面镜的夹角等于反射光线与平面镜的夹角,∴∠AOP =∠DOR ,∠BQP =∠RQC ,∴∠OPQ =∠ORQ .【点睛】本题主要考查了平行线的性质和入射角等于反射角的规定,解决本题的关键是注意问题的设置环环相扣、前为后用的设置目的.6.(1)见解析;(2)72︒【分析】(1)根据平行线的性质得出180A B ∠+∠=︒,再根据等量代换可得180B D ∠+∠=︒,最后根据平行线的判定即可得证;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB ,根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠,再根据平角的含义得出ECF CFG ∠=∠,然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠;设,FAB CFH αβ∠=∠=,根据角的和差可得出2AEC AFH ∠=∠,结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒,最后根据垂线的含义及平行线的性质,即可得出答案.【详解】(1)证明://AE BD180A B ∴∠+∠=︒A D ∠=∠180B D ∴∠+∠=︒//AB CD ∴;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB//AB CDQCA CAB ∴∠=∠,BGM DFG ∠=∠,CFH BHF ∠=∠,CFA FAG ∠=ACE BAC BGM ∠=∠+∠ECQ QCA BAC BGM ∴∠+∠=∠+∠ECQ BGM DFG ∴∠=∠=∠180,180ECQ ECD DFG CFG ∠+=︒∠+=︒ECF CFG ∴∠=∠//AB CD//AB EP ∴,PEA EAB PEC ECF ∴∠=∠∠=∠AEC PEC PEA ∠=∠-∠AEC ECF EAB ∴∠=∠-∠ECF AEC EAB ∴∠=∠+∠AF 平分BAE ∠12EAF FAB EAB ∴∠=∠=∠ FH 平分CFG ∠12CFH HFG CFG ∴∠=∠=∠ //CD AB,BHF CFH CFA FAB ∴∠=∠∠=∠设,FAB CFH αβ∠=∠=AFH CFH CFA CFH FAB ∠=∠-∠=∠-∠AFH βα∴∠=-,BHF CFH β∠=∠=222ECF AFH AEC EAB AFH AEC β∴∠+∠=∠+∠+∠=∠+22ECF AFH E BHF ∴∠+∠=∠+∠2AEC AFH ∴∠=∠35180AEC AFH ∠-∠=︒18AFH ∴∠=︒FH HM ⊥90FHM ∴∠=︒90GHM β∴∠=︒-180CFM NMF ∠+∠=︒90HMB HMN β∴∠=∠=︒-EAF FAB ∠=∠18EAF CFA CFH AFH β∴∠=∠=∠-∠=-︒189072EAF GMH ββ∴∠+∠=-︒+︒-=︒72EAF GMH ∴∠+∠=︒.【点睛】本题考查了平行线的判定及性质,角平分线的定义,能灵活根据平行线的性质和判定进行推理是解此题的关键.7.(1)14-(2)124- 【分析】(1)根据例子将每项的整数部分相加,分数部分相加即可解答;(2)根据例子将每项的整数部分相加,分数部分相加即可解答.【详解】(1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭ 104⎛⎫=+- ⎪⎝⎭ 14=- (2)原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭ 124⎛⎫=-+- ⎪⎝⎭ 124=- 【点睛】此题考察新计算方法,正确理解题意是解题的关键,根据例子即可仿照计算.8.(1)111n n -+;1n n +;(2)①1341-;②112424+;( 3 )14. 【分析】(1)利用材料中的“拆项法”解答即可;(2)①先变形为111234=⨯,再利用(1)中的规律解题;②先变形为121224=,再逆用分数的加法法则即可分解;(3)按照定义“⊗”法则表示出193⊗,再利用(1)中的规律解题即可. 【详解】解:(1)观察发现:()11n n =+111n n -+, 1111122334(1)n n ++++⨯⨯⨯+ =11111111223341n n -+-+-+⋯+-+ =111n -+ =1n n +; 故答案是:111n n -+;1n n +. (2)初步应用: ①111234=⨯=1134-; ②121112242424==+; 故答案是:1134-;112424+. ( 3 )由定义可知:193⊗=11111111112203042567290110132++++++++ =455111111611311412-+-+-+⋯+- =13211- =14. 故193⊗的值为14. 【点睛】考查了有理数运算中的规律型问题:数字的变化规律,有理数的混合运算.本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.9.(1)23,1;(2)两位正整数为39,28,17,()f t 的最大值为47;(3)①2021;②2021【分析】(1)仿照样例进行计算即可;(2)由题设可以看出交换前原数的十位上数字为a ,个位上数字为b ,则原数可以表示为10a+b ,交换后十位上数字为b ,个位上数字为a ,则交换后数字可以表示为10b+a ,根据“交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54”确定出a 与b 的关系式,进而求出所有的两位数,然后求解确定出()f t 的最大值即可;(3)根据样例分解计算即可.【详解】解:(1)61623=⨯=⨯,∵6132->-,∴()263f =; 161162844=⨯=⨯=⨯∵1618244->->-,∴()161f =, 故答案为:23;1; (2)由题意可得:交换后的数减去交换前的数的差为:10109()54b a a b b a +--=-=,∴6b a -=,∵19a b ≤≤≤,∴93b a ==,或82b a ==,或71b a ==,,∴t 为39,28,17;∵39=1×39=3×13,∴()33913f =; 28=1×28=2×14=4×7,∴()28f =47; 17=1×17,∴()11717f =; ∴()f t 的最大值47. (3)①∵223572021⨯⨯⨯=⨯∴()220235721f ⨯⨯⨯=; ②423574042⨯⨯⨯=⨯∴()4402023574221f⨯⨯⨯==;故答案为:2021;2021【点睛】本题主要考查了有理数的运算,理解最佳分解的定义,并将其转化为有理数的运算是解题的关键.10.(1)a2=2,a3=-1,a4=1 2(2)a2016•a2017•a2018= -1(3)a33+a66+a99+…+a9999=-1【分析】(1)将a1=12代入11a-中即可求出a2,再将a2代入求出a3,同样求出a4即可.(2)从(1)的计算结果可以看出,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2然后计算a2016•a2017•a2018的值;(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,即可求出结果.【详解】(1)将a1=12,代入11a-,得21=211-2a=;将a2=2,代入11a-,得31=-11-2a=;将a3=-1,代入11a-,得411=1--12a=().(2)根据(1)的计算结果,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2所以,a2016•a2017•a2018=(-1)×12×2= -1(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,a33+a66+a99+…+a9999=(-1)3+(-1)6+(-1)9+…+(-1)99=(-1)+1+(-1)+…(-1)=-1【点睛】此类问题考查了数字类的变化规律,解题的关键是要严格根据定义进行解答,同时注意分析循环的规律.11.(1)2、3、4、5;(2)第n个等式为1+3+5+7+…+(2n+1)=n2;(3)﹣1.008016×106.【分析】(1) 根据从1开始连续n 各奇数的和等于奇数的个数的平方即可得到.(2) 根据规律写出即可.(3) 先提取符号,再用规律解题.【详解】解:(1)1+3=221+3+5=321+3+5+7=421+3+5+7+9=52……故答案为:2、3、4、5;(2)第n 个等式为1+3+5+7+…+(2n+1)=2(1)n +(3)原式=﹣(1+3+5+7+9+ (2019)=﹣10102=﹣1.0201×106.【点睛】本题考查数字变化规律,解题的关键是找到第一个的规律,然后加以运用即可.12.(1)2,3 (2)①5722x ≤<②330,,42 (3)00.5a ≤< 【分析】(1)根据新定义的运算规则进行计算即可;(2)①根据新定义的运算规则即可求出实数x 的取值范围;②根据新定义的运算规则和43x 为整数,即可求出所有非负实数x 的值; (3)先解方程求得22x a =-<>,再根据方程的解是正整数解,即可求出非负实数a 的取值范围.【详解】 (1) 1.87<>=2;π=3;(2)①∵12x <->= ∴1121222x --<+≤ 解得5722x ≤<; ②∵43x x <>=∴41413232x x x -<+≤ 解得3322x -<≤ ∵43x 为整数∴333,0,,442x =- 故所有非负实数x 的值有330,,42; (3)21122a x x -<>+-=- 1241a x x -<>+-=-22x a =-<>∵方程的解为正整数∴21a -<>=或2①当21a -<>=时,2x =是方程的增根,舍去②当22a -<>=时,00.5a ≤<.【点睛】本题考查了新定义下的运算问题,掌握新定义下的运算规则是解题的关键.13.(1) C (5,﹣4);(2)90°;(3)见解析.【详解】分析:(1)利用非负数的和为零,各项分别为零,求出a ,b 即可;(2)用同角的余角相等和角平分线的意义即可;(3)利用角平分线的意义和互余两角的关系简单计算证明即可.详解:(1)∵(a ﹣3)2+|b+4|=0,∴a ﹣3=0,b+4=0,∴a=3,b=﹣4,∴A (3,0),B (0,﹣4),∴OA=3,OB=4,∵S 四边形AOBC =16.∴0.5(OA+BC )×OB=16,∴0.5(3+BC )×4=16,∴BC=5,∵C 是第四象限一点,CB ⊥y 轴,∴C (5,﹣4);(2)如图,延长CA ,∵AF 是∠CAE 的角平分线,∴∠CAF=0.5∠CAE ,∵∠CAE=∠OAG ,∴∠CAF=0.5∠OAG,∵AD⊥AC,∴∠DAO+∠OAG=∠PAD+∠PAG=90°,∵∠AOD=90°,∴∠DAO+∠ADO=90°,∴∠ADO=∠OAG,∴∠CAF=0.5∠ADO,∵DP是∠ODA的角平分线,∴∠ADO=2∠ADP,∴∠CAF=∠ADP,∵∠CAF=∠PAG,∴∠PAG=∠ADP,∴∠APD=180°﹣(∠ADP+∠PAD)=180°﹣(∠PAG+∠PAD)=180°﹣90°=90°即:∠APD=90°(3)不变,∠ANM=45°理由:如图,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∵DM⊥AD,∴∠ADO+∠BDM=90°,∴∠DAO=∠BDM,∵NA是∠OAD的平分线,∴∠DAN=0.5∠DAO=0.5∠BDM,∵CB⊥y轴,∴∠BDM+∠BMD=90°,∴∠DAN=0.5(90°﹣∠BMD),∵MN是∠BMD的角平分线,∴∠DMN=0.5∠BMD,∴∠DAN+∠DMN=0.5(90°﹣∠BMD)+0.5∠BMD=45°在△DAM中,∠ADM=90°,∴∠DAM+∠DMA=90°,在△AMN中,∠ANM=180°﹣(∠NAM+∠NMA)=180°﹣(∠DAN+∠DAM+∠DMN+∠DMA)=180°﹣[(∠DAN+DMN)+(∠DAM+∠DMA)] =180°﹣(45°+90°)=45°,∴D点在运动过程中,∠N的大小不变,求出其值为45°点睛:此题是四边形综合题,主要考查了非负数的性质,四边形面积的计算方法,角平分线的意义,解本题的关键是用整体的思想解决问题,也是本题的难点.14.(1)100;(2)75°;(3)n =3.【分析】(1)如图:过O 作OP //MN ,由MN //OP //GH 得∠NAO +∠POA =180°,∠POB +∠OBH =180°,即∠NAO +∠AOB +∠OBH =360°,即可求出∠AOB ;(2)如图:分别延长AC 、CD 交GH 于点E 、F ,先根据角平分线求得58NAC ∠=︒,再根据平行线的性质得到58CEF ∠=︒;进一步求得18DBF ∠=︒,17DFB ∠=︒,然后根据三角形外角的性质解答即可;(3)设BF 交MN 于K ,由∠NAO =116°,得∠MAO =64°,故∠MAE =641n n ︒⨯+,同理∠OBH =144°,∠HBF =n ∠OBF ,得∠FBH =1441n n ︒⨯+,从而=n BKA FBH n ∠∠=⨯︒+1441,又∠FKN =∠F +∠FAK ,得144606411n n n n ︒︒︒⨯=+⨯++,即可求n . 【详解】解:(1)如图:过O 作OP //MN ,∵MN //GHl∴MN //OP //GH∴∠NAO +∠POA =180°,∠POB +∠OBH =180°∴∠NAO +∠AOB +∠OBH =360°∵∠NAO =116°,∠OBH =144°∴∠AOB =360°-116°-144°=100°;(2)分别延长AC 、CD 交GH 于点E 、F ,∵AC 平分NAO ∠且116NAO ∠=︒,∴58NAC ∠=︒,又∵MN //GH ,∴58CEF ∠=︒;∵144OBH ∠=︒,36OBG ∠=︒∵BD 平分OBG ∠,∴18DBF ∠=︒,又∵,CDB ∠=︒35∴351817DFB CDB DBF ∠=∠-∠=-=︒;∴175875ACD DFB AEF ∠=∠+∠=︒+︒=︒;(3)设FB 交MN 于K ,∵116NAO ∠=︒,则MAO ∠=︒64; ∴641n MAE n ∠=⨯︒+ ∵144OBH ∠=︒, ∴+1n FBH n ∠=⨯︒144,=n BKA FBH n ∠∠=⨯︒+1441, 在△FAK 中,64601n BKA FKA F n ∠=∠+∠=⨯︒+︒+, ∴144646011n n n n ⨯︒=⨯︒+︒++, ∴3n =.经检验:3n =是原方程的根,且符合题意.【点睛】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.15.(1)A (-2,0)、B (0,3);(2)∠APD=90°;(3)∠N 的大小不变,∠N=45°【分析】(1)利用非负数的和为零,各项分别为零,求出a ,b 的值;(2)如图,作DM ∥x 轴,结合题意可设∠ADP=∠OAP=x ,∠EAF=∠CAF=∠OAP=y ,根据平角的定义可知∠OAD=90°-2y ,由平行线的性质可得∠OAD+∠ADM=180°,即90-2y+2x+90°=180°,进而可得出x=y ,再结合图形即可得出∠APD 的度数;(3)∠N 的大小不变,∠N=45°,如图,过D 作DE ∥BC ,过N 作NF ∥BC ,根据平行线的性质可知∠BMD+∠OAD=∠ADM=90°,然后根据角平分线的定义和平行线的性质,可得∠ANM=12∠BMD+12∠OAD ,据此即可得到结论. 【详解】(1)由()2230a b ++-=,可得20a 和230b ,解得2,3a b =-=∴A 的坐标是(-2,0)、B 的坐标是(0,3);(2)如图,作DM ∥x 轴根据题意,设∠ADP=∠OAP=x,∠EAF=∠CAF=∠OAP=y,∵∠CAD=90°,∴∠CAE+∠OAD=90°,∴2y+∠OAD=90°,∴∠OAD=90°-2y,∵DM∥x轴,∴∠OAD+∠ADM=180°,∴90-2y+2x+90°=180°,∴x=y,∴∠APD=180°-(∠PAD+∠ADP)=180°-(y+90°-2y+x)=180°-90°=90°(3)∠N的大小不变,∠N=45°理由:如图,过D作DE∥BC,过N作NF∥BC.∵BC∥x轴,∴DE∥BC∥x轴,NF∥BC∥x轴,∴∠EDM=∠BMD,∠EDA=∠OAD,∵DM⊥AD,∴∠ADM=90°,∴∠BMD+∠OAD=∠EDM+∠EDA=∠ADM=90°,∵MN平分∠BMD,AN平分∠DAO,∴∠BMN=12∠BMD,∠OAN=12∠OAD,∴∠ANM=∠BMN+∠OAN=12∠BMD+12∠OAD=12×90°=45°.【点睛】本题考查了坐标与图形性质:利用点的坐标计算出相应的线段的长和判断线段与坐标轴的位置关系.也考查了三角形内角和定理和三角形外角性质.16.(1)﹣3,2.5;(2)﹣4<m <﹣2或0<m <2;(3)1≤a <2.【分析】(1)根据连动数的定义逐一判断即得答案;(2)先求得方程的解,再根据连动数的定义得出相应的不等式组,解不等式组即可求出结果;(3)先解不等式组中的每个不等式,再根据连动整数的概念得到关于a 的不等式组,解不等式组即可求得答案.【详解】解:(1)设点P 表示的数是x ,则11x -≤≤,若点Q 表示的数是﹣3,由2PQ =可得()32x --=,解得:x =﹣1或﹣5,所以﹣3是连动数;若点Q 表示的数是0,由2PQ =可得02x -=,解得:x =2或﹣2,所以0不是连动数; 若点Q 表示的数是2.5,由2PQ =可得 2.52x -=,解得:x =﹣0.5或4.5,所以2.5是连动数;所以﹣3,0,2.5是连动数的是﹣3,2.5,故答案为:﹣3,2.5;(2)解关于x 的方程2x ﹣m =x +1得:x =m +1,∵关于x 的方程2x ﹣m =x +1的解满足是连动数,∴112112m m ---<⎧⎨-->⎩或112112m m +-<⎧⎨++>⎩, 解得:﹣4<m <﹣2或0<m <2;故答案为:﹣4<m <﹣2或0<m <2;(3)()112123x x a +⎧>-⎪⎨⎪+-≤⎩①②, 解不等式①,得x >﹣3,解不等式②,得x ≤1+a ,∵不等式组()112123x x a +⎧>-⎪⎨⎪+-≤⎩的解集中恰好有4个解是连动整数, ∴四个连动整数解为﹣2,﹣1,1,2,∴2≤1+a <3,解得:1≤a <2,∴a 的取值范围是1≤a <2.【点睛】本题是新定义试题,以数轴为载体,主要考查了一元一次不等式组,正确理解连动数与连动整数、列出相应的不等式组是解题的关键.17.(1)1-,2;(2)233n =或13-;(3)225t =或2。
人教版初一数学下册期末几何压轴题试题含答案(13)

一、解答题1.如图1,在平面直角坐标系中,(,0),(,2)A a C b ,且满足2(2)|2|0a b ++-=,过C 作CB x ⊥轴于B .(1)求ABC ∆的面积.(2)若过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,求AED ∠的度数.(3)在y 轴上存在点P 使得ABC ∆和ACP ∆的面积相等,请直接写出P 点坐标.2.已知AB ∥CD ,∠ABE 与∠CDE 的角分线相交于点F .(1)如图1,若BM 、DM 分别是∠ABF 和∠CDF 的角平分线,且∠BED =100°,求∠M 的度数;(2)如图2,若∠ABM =13∠ABF ,∠CDM =13∠CDF ,∠BED =α°,求∠M 的度数;(3)若∠ABM =1n ∠ABF ,∠CDM =1n∠CDF ,请直接写出∠M 与∠BED 之间的数量关系3.直线AB ∥CD ,点P 为平面内一点,连接AP ,CP .(1)如图①,点P 在直线AB ,CD 之间,当∠BAP =60°,∠DCP =20°时,求∠APC 的度数;(2)如图②,点P 在直线AB ,CD 之间,∠BAP 与∠DCP 的角平分线相交于K ,写出∠AKC 与∠APC 之间的数量关系,并说明理由;(3)如图③,点P 在直线CD 下方,当∠BAK =23∠BAP ,∠DCK =23∠DCP 时,写出∠AKC 与∠APC 之间的数量关系,并说明理由.4.如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.(1)根据图1填空:∠1=°,∠2=°;(2)现把三角板绕B点逆时针旋转n°.①如图2,当n=25°,且点C恰好落在DG边上时,求∠1、∠2的度数;②当0°<n<180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.5.综合与实践背景阅读:在同一平面内,两条不重合的直线的位置关系有相交、平行,若两条不重合的直线只有一个公共点,我们就说这两条直线相交,若两条直线不相交,我们就说这两条直线互相平行两条直线的位置关系的性质和判定是几何的重要知识,是初中阶段几何合情推理的基础.已知:AM∥CN,点B为平面内一点,AB⊥BC于B.问题解决:(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,则∠EBC=.6.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由; (2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AENCDG∠∠的值; (3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.7.数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试: ①3310001000000100==,又1000593191000000<<,31059319100∴,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又39729=,∴能确定59319的立方根的个位数是9. ③如果划去59319后面的三位319得到数59,33327596433594<<,可得3305931940<<, 由此能确定59319的立方根的十位数是3 因此59319的立方根是39.(1)现在换一个数195112,按这种方法求立方根,请完成下列填空. ①它的立方根是_______位数. ②它的立方根的个位数是_______. ③它的立方根的十位数是__________. ④195112的立方根是________.(2)请直接填写....结果: ①313824=________. ②3175616=________.8.新定义:对非负数x“四舍五入”到个位的值记为<x>, 即当n 为非负数时,若1122n x n -≤<+,则<x>=n . 例如<0>=<0.49>=0,<0.5>=<(1)49>=1,<2>=2,<(3)5>=<(4)23>=4,… 试回答下列问题:(1)填空:<9.6>=_________;如果<x>=2,实数x 的取值范围是________________.(2)若关于x 的不等式组24130x x m x -⎧≤-⎪⎨⎪->⎩的整数解恰有4个,求<m>的值;(3)求满足65x x =的所有非负实数x 的值. 9.观察下面的变形规律:;;;….解答下面的问题: (1)仿照上面的格式请写出= ;(2)若n 为正整数,请你猜想= ;(3)基础应用:计算:.(4)拓展应用1:解方程: =2016 (5)拓展应用2:计算:.10.阅读材料:求值:2342017122222+++++⋯+, 解答:设2342017122222S =+++++⋯+,①将等式两边同时乘2得:2342018222222S =++++⋯+,②将-②①得:201821S =-,即2342017201812222221S =+++++⋯+=-. 请你类比此方法计算:()234201122222+++++⋯+.()2342133333(n +++++⋯+其中n 为正整数)11.数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试: ①3310001000000100==,又1000593191000000<<,31059319100∴<<,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又39729=,∴能确定59319的立方根的个位数是9. ③如果划去59319后面的三位319得到数59,而333275964<<,则33594<<,可得3305931940<<, 由此能确定59319的立方根的十位数是3 因此59319的立方根是39.(1)现在换一个数195112,按这种方法求立方根,请完成下列填空. ①它的立方根是_______位数. ②它的立方根的个位数是_______. ③它的立方根的十位数是__________. ④195112的立方根是________. (2)请直接填写....结果: ①313824=________. ②3175616=________. 12.观察下面的变形规律:;;;….解答下面的问题: (1)仿照上面的格式请写出= ;(2)若n 为正整数,请你猜想= ;(3)基础应用:计算:.(4)拓展应用1:解方程: =2016 (5)拓展应用2:计算:.13.如图,已知点()0,0O ,()2,0A ,()1,2B -.(1)求OAB 的面积;(2)点C 是在坐标轴上异于点A 的一点,且OBC 的面积等于OAB 的面积,求满足条件的点C 的坐标;(3)若点D 的坐标为()m,2,且1m <-,连接AD 交OB 于点E ,在x 轴上有一点F ,使BDE 的面积等于BEF 的面积,请直接写出点F 的坐标__________(用含m 的式子表示).14.如图1,AB //CD ,点E 、F 分别在AB 、CD 上,点O 在直线AB 、CD 之间,且100EOF ∠=︒.(1)求BEO OFD ∠+∠的值;(2)如图2,直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ,直接写出EMN FNM ∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG m OEG ∠=∠;FH 在DFO ∠内,DFH m OFH ∠=∠,直线MN 分别交EG 、FH 分别于点M 、N ,且50FMN ENM ∠-∠=︒,直接写出m 的值.15.如图,在平面直角坐标系中,点的坐标分别是,现同时将点分别向上平移2个单位长度,再向右平移2个单位长度,得到的对应点.连接.(1)写出点的坐标并求出四边形的面积. (2)在轴上是否存在一点,使得的面积是面积的2倍?若存在,请求出点的坐标;若不存在,请说明理由. (3)若点是直线上一个动点,连接,当点在直线上运动时,请直接写出与的数量关系.16.在平面直角坐标系中,点(),1A a ,(),6B b ,(),3C c ,且a ,b ,c 满足231321b c a a c b +=+⎧⎨+=+⎩.(1)请用含a 的式子分别表示B ,C 两点的坐标;(2)当实数a 变化时,判断ABC 的面积是否发生变化?若不变,求其值;若变化,求其变化范围;(3)如图,已知线段AB 与y 轴相交于点E ,直线AC 与直线OB 交于点P ,若2PA PC ≤,求实数a 的取值范围.17.在平面直角坐标系xOy 中,对于给定的两点P ,Q ,若存在点M ,使得△MPQ 的面积等于1,即S △MPQ =1,则称点M 为线段PQ 的“单位面积点”,解答下列问题: 如图,在平面直角坐标系xOy 中,点P 的坐标为(1,0).(1)在点A (1,2),B (﹣1,1),C (﹣1,﹣2),D (2,﹣4)中,线段OP 的“单位面积点”是 ;(2)已知点E (0,3),F (0,4),将线段OP 沿y 轴向上平移t (t >0)个单位长度,使得线段EF 上存在线段OP 的“单位面积点”,直接写出t 的取值范围 .(3)已知点Q (1,﹣2),H (0,﹣1),点M ,N 是线段PQ 的两个“单位面积点”,点M 在HQ 的延长线上,若S △HMN 2△PQN ,求出点N 纵坐标的取值范围.18.在平面直角坐标系中,点(,1)A a ,(,3)B b 满足关系式2(1)|2|0++-=a b .(1)求a ,b 的值;(2)若点(3,)P n 满足ABP △的面积等于6,求n 的值;(3)线段AB 与y 轴交于点C ,动点E 从点C 出发,在y 轴上以每秒1个单位长度的速度向下运动,动点F 从点(8,0)-M 出发,以每秒2个单位长度的速度向右运动,问t 为何值时有2ABEABFSS=,请直接写出t 的值.19.某工厂接受了20天内生产1200台GH 型电子产品的总任务.已知每台GH 型产品由4个G 型装置和3个H 型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G 型装置或3个H 型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G 、H 型装置数量正好全部配套组成GH 型产品.(1)按照这样的生产方式,工厂每天能配套组成多少套GH 型电子产品?请列出二元一次方程组解答此问题.(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工4个G 型装置.设原来每天安排x 名工人生产G 型装置,后来补充m 名新工人,求x 的值(用含m 的代数式表示) 20.如图,//CD EF ,AE 是CAB ∠的平分线,α∠和β∠的度数满足方程组2250(1)3100(2)αβαβ∠+∠=︒⎧⎨∠-∠=︒⎩,(1)求α∠和β∠的度数; (2)求证://AB CD . (3)求C ∠的度数.21.平面直角坐标系中,A (a ,0),B (0,b ),a ,b 满足2(25)220a b a b ++++-=,将线段AB 平移得到CD ,A ,B 的对应点分别为C ,D ,其中点C 在y 轴负半轴上.(1)求A ,B 两点的坐标;(2)如图1,连AD 交BC 于点E ,若点E 在y 轴正半轴上,求BE OEOC-的值; (3)如图2,点F ,G 分别在CD ,BD 的延长线上,连结FG ,∠BAC 的角平分线与∠DFG 的角平分线交于点H ,求∠G 与∠H 之间的数量关系. 22.阅读下列文字,请仔细体会其中的数学思想.(1)解方程组321327x y x y -=-⎧⎨+=⎩,我们利用加减消元法,很快可以求得此方程组的解为 ;(2)如何解方程组()()()()3523135237m n m n ⎧+-+=-⎪⎨+++=⎪⎩呢?我们可以把m +5,n +3看成一个整体,设m +5=x ,n +3=y ,很快可以求出原方程组的解为 ; (3)由此请你解决下列问题:若关于m ,n 的方程组722am bn m bn +=⎧⎨-=-⎩与351m n am bn +=⎧⎨-=-⎩有相同的解,求a 、b 的值.23.如果3个数位相同的自然数m ,n ,k 满足:m +n =k ,且k 各数位上的数字全部相同,则称数m 和数n 是一对“黄金搭档数”.例如:因为25,63,88都是两位数,且25+63=88,则25和63是一对“黄金搭档数”.再如:因为152,514,666都是三位数,且152+514=666,则152和514是一对“黄金搭档数”.(1)分别判断87和12,62和49是否是一对“黄金搭档数”,并说明理由;(2)已知两位数s 和两位数t 的十位数字相同,若s 和t 是一对“黄金搭档数”,并且s 与t 的和能被7整除,求出满足题意的s .24.如图,在平面直角坐标系中,点O 为坐标原点,A 点的坐标为()1A m n -,,B 点的坐标为()0n -,,其中,m n 是二元一次方程组2202m n m n +=⎧⎨-=-⎩的解,过点A 作x 轴的平行线交y 轴于点C .(1)求点,A B 的坐标;(2)动点P 从点B 出发,以每秒4个单位长度的速度沿射线BO 的方向运动,连接PC ,设点P 的运动时间为t 秒,三角形OPC 的面积为()0S S ≠,请用含t 的式子表示S (不用写出相应的t 的取值范围);(3)在(2)的条件下,在动点P 从点B 出发的同时,动点Q 从点C 出发以每秒1个单位长度的速度沿线段CA 的方向运动.过点O 作直线PC 的垂线,点G 为垂足;过点Q 作直线PC 的垂线,点H 为垂足.当2OG QH =时,求t 的值.25.如图,在平面直角坐标系中,已知,0,0,A a B b 两点,且a 、b 满足()224210a b a b ++++-=点(),0C m 在射线AO 上(不与原点重合).将线段AB 平移到DC ,点D 与点A 对应,点C 与点B 对应,连接BC ,直线AD 交y 轴于点E .请回答下列问题:(1)求A 、B 两点的坐标;(2)设三角形ABC 面积为ABC S ∆,若4<ABC S ∆≤7,求m 的取值范围; (3)设,BCA AEB αβ∠=∠=,请给出,αβ,满足的数量关系式,并说明理由. 26.阅读材料:形如2213x <+<的不等式,我们就称之为双连不等式.求解双连不等式的方法一,转化为不等式组求解,如221213x x <+⎧⎨+<⎩;方法二,利用不等式的性质直接求解,双连不等式的左、中、右同时减去1,得122x <<,然后同时除以2,得1112x <<. 解决下列问题:(1)请你写一个双连不等式并将它转化为不等式组; (2)利用不等式的性质解双连不等式2235x ≥-+>-; (3)已知532x -≤<-,求35x +的整数值.27.在平面直角坐标系xOy 中,已知点M (a ,b ).如果存在点N (a ′,b ′),满足a ′=|a +b |,b ′=|a ﹣b |,则称点N 为点M 的“控变点”. (1)点A (﹣1,2)的“控变点”B 的坐标为 ;(2)已知点C (m ,﹣1)的“控变点”D 的坐标为(4,n ),求m ,n 的值;(3)长方形EFGH 的顶点坐标分别为(1,1),(5,1),(5,4),(1,4).如果点P (x ,﹣2x )的“控变点”Q 在长方形EFGH 的内部,直接写出x 的取值范围.28.小语爸爸开了一家茶叶专卖店,包装设计专业毕业的小语为爸爸设计了一款纸质长方体茶叶包包装盒(纸片厚度不计).如图,阴影部分是裁剪掉的部分,沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处长方形形状的“接口”用来折叠后粘贴或封盖.(1)若小语用长40cm ,宽34cm 的长方形纸片,恰好能做成一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?(2)小语爸爸的茶叶专卖店以每盒200元购进一批茶叶,按进价增加18%作为售价,第一个月由于包装粗糙,只售出不到一半但超过三分之一的量;第二个月采用了小语的包装后,马上售完了余下的茶叶,但每盒成本增加了6元,售价仍不变,已知在整个买卖过程中共盈利1800元,求这批茶叶共进了多少盒?29.某加工厂用52500元购进A 、B 两种原料共40吨,其中原料A 每吨1500元,原料B 每吨1000元.由于原料容易变质,该加工厂需尽快将这批原料运往有保质条件的仓库储存.经市场调查获得以下信息:①将原料运往仓库有公路运输与铁路运输两种方式可供选择,其中公路全程120千米,铁路全程150千米;②两种运输方式的运输单价不同(单价:每吨每千米所收的运输费); ③公路运输时,每吨每千米还需加收1元的燃油附加费;④运输还需支付原料装卸费:公路运输时,每吨装卸费100元;铁路运输时,每吨装卸费220元.(1)加工厂购进A 、B 两种原料各多少吨?(2)由于每种运输方式的运输能力有限,都无法单独承担这批原料的运输任务.加工厂为了尽快将这批原料运往仓库,决定将A 原料选一种方式运输,B 原料用另一种方式运输,哪种方案运输总花费较少?请说明理由.30.在平面直角坐标系中,已知线段AB ,点A 的坐标为()1,2-,点B 的坐标为()3,0,如图1所示.(1)平移线段A B 到线段C D ,使点A 的对应点为,点B 的对应点为C ,若点C 的坐标为()2,4-,求点D 的坐标;(2)平移线段A B 到线段C D ,使点C 在y 轴的正半轴上,点D 在第二象限内(A 与D 对应, B 与C 对应),连接BC BD ,,如图2所示.若(7BCD BCD S S ∆∆=表示△BCD 的面积),求点C 、D 的坐标;(3)在(2)的条件下,在y 轴上是否存在一点P ,使(23PCD PCD BCD S S S ∆∆∆=表示△PCD 的面积)?若存在,求出点P 的坐标; 若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)4;(2)45︒;(2)(0,3)P 或(0,1)-. 【分析】(1)根据非负数的性质易得2a =-,2b =,然后根据三角形面积公式计算; (2)过E 作//EF AC ,根据平行线性质得////BD AC EF ,且1312CAB ∠=∠=∠,1422ODB ∠=∠=∠,所以112()2AED CAB ODB ∠=∠+∠=∠+∠;然后把90CAB ODB ∠+∠=︒ 代入计算即可;(3)分类讨论:设(0,)P t ,当P 在y 轴正半轴上时,过P 作//MN x 轴,//AN y 轴,//BM y 轴,利用4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形可得到关于t 的方程,再解方程求出t ;当P 在y 轴负半轴上时,运用同样方法可计算出t . 【详解】解:(1)2(2)20a b ++-=,20a ∴+=,20b -=, 2a ∴=-,2b =,CB AB ⊥(2,0)A ∴-,(2,0)B ,(2,2)C ,ABC ∆∴的面积12442=⨯⨯=;(2)解://CB y 轴,//BD AC ,5CAB ∴∠=∠,又∵590ODB ∠+∠=︒, ∴90CAB ODB ∠+∠=︒, 过E 作//EF AC ,如图①,//BD AC ,////BD AC EF ∴,31∴∠=∠,42∠=∠AE ∵,DE 分别平分CAB ∠,ODB ∠,即:132CAB ∠=∠,142ODB ∠=∠,112()452AED CAB ODB ∴∠=∠+∠=∠+∠=︒;(3)(0,1)P -或(0,3).解:①当P 在y 轴正半轴上时,如图②,设(0,)P t ,过P 作//MN x 轴,//AN y 轴,//BM y 轴,4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形,∴4(2)(2)42t t t t -+---=,解得3t =, ②当P 在y 轴负半轴上时,如图③4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形∴4(2)(2)42t t t t -+-+--=,解得1t =-, 综上所述:(0,3)P 或(0,1)-. 【点睛】本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.构造矩形求三角形面积是解题关键. 2.(1)65°;(2)3606α︒-︒;(3)2n ∠M +∠BED =360° 【分析】(1)首先作EG ∥AB ,FH ∥AB ,连结MF ,利用平行线的性质可得∠ABE +∠CDE =260°,再利用角平分线的定义得到∠ABF +∠CDF =130°,从而得到∠BFD 的度数,再根据角平分线的定义和三角形外角的性质可求∠M 的度数;(2)先由已知得到∠ABE =6∠ABM ,∠CDE =6∠CDM ,由(1)得∠ABE +∠CDE =360°-∠BED ,∠M =∠ABM +∠CDM ,等量代换即可求解; (3)由(2)的方法可得到2n ∠M +∠BED =360°. 【详解】解:(1)如图1,作//EG AB ,//FH AB ,连结MF ,//AB CD ,//////EG AB FH CD ∴,ABF BFH ∴∠=∠,CDF DFH ∠=∠,180ABE BEG ∠+∠=︒,180GED CDE ∠+∠=︒,360ABE BEG GED CDE ∴∠+∠+∠+∠=︒,100BED BEG DEG ∠=∠+∠=︒,260ABE CDE ∴∠+∠=︒,ABE ∠和CDE ∠的角平分线相交于E ,130ABF CDF ∴∠+∠=︒, 130BFD BFH DFH ∴∠=∠+∠=︒,BM 、DM 分别是ABF ∠和CDF ∠的角平分线,12MBF ABF ∴∠=∠,12MDF CDF ∠=∠,65MBF MDF ∴∠+∠=︒, 1306565BMD ∴∠=︒-︒=︒;(2)如图1,13ABM ABF ∠=∠,13CDM CDF ∠=∠,3ABF ABM ∴∠=∠,3CDF CDM ∠=∠,ABE ∠与CDE ∠两个角的角平分线相交于点F ,6ABE ABM ∴∠=∠,6CDE CDM ∠=∠, 66360ABM CDM BED ∴∠+∠+∠=︒,BMD ABM CDM ∠=∠+∠, 6360BMD BED ∴∠+∠=︒,3606BMD α︒-︒∴∠=; (3)由(2)结论可得,22360n ABM n CDM E ∠+∠+∠=︒,M ABM CDM ∠=∠+∠, 则2360n M BED ∠+∠=︒. 【点睛】本题主要考查了平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.3.(1)80°;(2)∠AKC =12∠APC ,理由见解析;(3)∠AKC =23∠APC ,理由见解析【分析】(1)先过P 作PE ∥AB ,根据平行线的性质即可得到∠APE =∠BAP ,∠CPE =∠DCP ,再根据∠APC =∠APE +∠CPE =∠BAP +∠DCP 进行计算即可;(2)过K 作KE ∥AB ,根据KE ∥AB ∥CD ,可得∠AKE =∠BAK ,∠CKE =∠DCK ,进而得到∠AKC =∠AKE +∠CKE =∠BAK +∠DCK ,同理可得,∠APC =∠BAP +∠DCP ,再根据角平分线的定义,得出∠BAK +∠DCK =12∠BAP +12∠DCP =12(∠BAP +∠DCP )=12∠APC ,进而得到∠AKC =12∠APC ;(3)过K 作KE ∥AB ,根据KE ∥AB ∥CD ,可得∠BAK =∠AKE ,∠DCK =∠CKE ,进而得到∠AKC =∠BAK ﹣∠DCK ,同理可得,∠APC =∠BAP ﹣∠DCP ,再根据已知得出∠BAK ﹣∠DCK =23∠BAP ﹣23∠DCP =23∠APC ,进而得到∠BAK ﹣∠DCK =23∠APC .【详解】(1)如图1,过P 作PE ∥AB , ∵AB ∥CD ,∴PE∥AB∥CD,∴∠APE=∠BAP,∠CPE=∠DCP,∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;(2)∠AKC=12∠APC.理由:如图2,过K作KE∥AB,∵AB∥CD,∴KE∥AB∥CD,∴∠AKE=∠BAK,∠CKE=∠DCK,∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,过P作PF∥AB,同理可得,∠APC=∠BAP+∠DCP,∵∠BAP与∠DCP的角平分线相交于点K,∴∠BAK+∠DCK=12∠BAP+12∠DCP=12(∠BAP+∠DCP)=12∠APC,∴∠AKC=12∠APC;(3)∠AKC=23∠APC理由:如图3,过K作KE∥AB,∵AB∥CD,∴KE∥AB∥CD,∴∠BAK=∠AKE,∠DCK=∠CKE,∴∠AKC=∠AKE﹣∠CKE=∠BAK﹣∠DCK,过P作PF∥AB,同理可得,∠APC=∠BAP﹣∠DCP,∵∠BAK=23∠BAP,∠DCK=23∠DCP,∴∠BAK﹣∠DCK=23∠BAP﹣23∠DCP=23(∠BAP﹣∠DCP)=23∠APC,∴∠AKC=23∠APC.【点睛】本题考查了平行线的性质和角平分线的定义,解题的关键是作出平行线构造内错角相等计算.4.(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相等可得∠1=∠ABE,根据两直线平行,同旁内角互补求出∠BCG,然后根据周角等于360°计算即可得到∠2;②结合图形,分A B、B C、AC三条边与直尺垂直讨论求解.【详解】解:(1)∠1=180°-60°=120°,∠2=90°;故答案为:120,90;(2)①如图2,∵∠ABC=60°,∴∠ABE=180°-60°-n°=120°-n°,∵DG∥EF,∴∠1=∠ABE=120°-n°,∠BCG=180°-∠CBF=180°-n°,∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-∠BCG=360°-90°-(180°-n°)=90°+n°;②当n=30°时,∵∠ABC=60°,∴∠ABF=30°+60°=90°,AB⊥DG(EF);当n=90°时,∠C=∠CBF=90°,∴BC ⊥DG (EF ),AC ⊥DE (GF );当n =120°时, ∴AB ⊥DE (GF ).【点睛】本题考查了平行线角的计算,垂线的定义,主要利用了平行线的性质,直角三角形的性质,读懂题目信息并准确识图是解题的关键. 5.(1)90A C ∠+∠=︒;(2)见解析;(3)105° 【分析】(1)通过平行线性质和直角三角形内角关系即可求解. (2)过点B 作BG ∥DM ,根据平行线找角的联系即可求解. (3)利用(2)的结论,结合角平分线性质即可求解. 【详解】解:(1)如图1,设AM 与BC 交于点O ,∵AM ∥CN , ∴∠C =∠AOB , ∵AB ⊥BC , ∴∠ABC =90°, ∴∠A +∠AOB =90°, ∠A +∠C =90°,故答案为:∠A +∠C =90°;(2)证明:如图2,过点B 作BG ∥DM ,∵BD ⊥AM ,∴DB⊥BG,∴∠DBG=90°,∴∠ABD+∠ABG=90°,∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,∴∠C=∠CBG,∴∠ABD=∠C;(3)如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)知∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=∠AFB=β,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°得:2α+β+3α+3α+β=180°,∵AB⊥BC,∴β+β+2α=90°,∴α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.故答案为:105°.【点睛】本题考查平行线性质,画辅助线,找到角的和差倍分关系是求解本题的关键.6.(1)见解析;(2)1;(3)75°2【分析】(1)根据平行线的性质、余角和补角的性质即可求解.(2)根据平行线的性质、对顶角的性质和平角的定义解答即可.(3)根据平行线的性质和角平分线的定义以及三角形内角和解答即可.【详解】解:(1)∠C=∠1+∠2,证明:过C作l∥MN,如下图所示,∵l∥MN,∴∠4=∠2(两直线平行,内错角相等),∵l∥MN,PQ∥MN,∴l∥PQ,∴∠3=∠1(两直线平行,内错角相等),∴∠3+∠4=∠1+∠2,∴∠C=∠1+∠2;(2)∵∠BDF=∠GDF,∵∠BDF=∠PDC,∴∠GDF=∠PDC,∵∠PDC+∠CDG+∠GDF=180°,∴∠CDG+2∠PDC=180°,∴∠PDC=90°-12∠CDG ,由(1)可得,∠PDC+∠CEM=∠C=90°,∴∠AEN=∠CEM,∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠,(3)设BD交MN于J.∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,∵PQ∥MN,∴∠BJA=∠PBD=50°,∴∠ADB=∠AJB-∠JAD=50°-∠JAD=50°-∠CAM,由(1)可得,∠ACB=∠PBC+∠CAM,∴∠ACB+∠ADB=∠PBC+∠CAM+50°-∠CAM=25°+50°=75°.【点睛】本题考查了平行线的性质、余角和补角的性质,解题的关键是根据平行找出角度之间的关系.7.(1)①两;②8;③5;④58;(2)①24;②56.【分析】(1)①根据例题进行推理得出答案;②根据例题进行推理得出答案;③根据例题进行推理得出答案;④根据②③得出答案;(2)①先判断它的立方根是几位数,再判断个位、十位上的数字,即可得到结论;②先判断它的立方根是几位数,再判断个位、十位上的数字,即可得到结论.【详解】<<,(1)①31000100=,10001951121000000∴10100<<,∴能确定195112的立方根是一个两位数,故答案为:两;②∵195112的个位数字是2,又∵38512=,∴能确定195112的个位数字是8,故答案为:8;③如果划去195112后面三位112得到数195,<∴<,56可得5060<,由此能确定195112的立方根的十位数是5,故答案为:5;④根据②③可得:195112的立方根是58,故答案为:58;(2)①13824的立方根是两位数,立方根的个位数是4,十位数是2,∴13824的立方根是24,故答案为:24;②175616的立方根是两位数,立方根的个位数是6,十位数是5,∴175616的立方根是56,故答案为:56.【点睛】此题考查立方根的性质,一个数的立方数的特点,正确理解题意仿照例题解题的能力,掌握一个数的立方数的特点是解题的关键.8.(1)10;1.5 2.5x ≤<(2)3m =(3):0,1,2 【详解】分析:(1)①利用对非负数x“四舍五入”到个位的值为<x>,进而求解即可; (2)首先将<m>看做一个字母,解不等式,进而根据整数解的个数得出m 的取值; (3)利用65x x =得出关于x 的不等式,求解即可. 详解:(1)①10,②1.5 2.5x ≤<; (2)解不等式组得:1x m -≤<由不等式组的整数解恰有4个得,23m <≤, ∴3m =; (3)∵65x x =, ∴161252x x x -≤<+,0x ≥, ∴0 2.5x ≤<, ∵x 为非负整数, ∴x 的值为:0,1,(2)点睛:此题主要考查了理解题意的能力,关键是看到所得值是个位数四舍五入后的值,问题得解. 9.(1) ;(2);(3);(4)x=2017;(5)【分析】(1)类比题目中方法解答即可;(2)根据题目中所给的算式总结出规律,解答即可;(3)利用总结的规律把每个式子拆分后合并即可解答;(4)方程左边提取x 后利用(3)的方法计算后,再解方程即可;(5)类比(3)的方法,拆项计算即可. 【详解】 (1)故答案为:;(2)=故答案为:;(3)计算:==1﹣=;(4)=2016=2016, x=2017; (5).=+()+()+…+().=(1﹣).=. 【点睛】本题是数字规律探究题,解决问题基本思路是正确找出规律,根据所得的规律解决问题. 10.(1)2121-;(2)()n 11312+-. 【解析】 【分析】()1设23420S 122222=+++++⋯+,两边乘以2后得到关系式,与已知等式相减,变形即可求出所求式子的值;()2同理即可得到所求式子的值.【详解】解:()1设23420S 122222=+++++⋯+,将等式两边同时乘2得:2345212S 222222=++++⋯+, 将下式减去上式得:212S S 21-=-,即21S 21=-, 则234202112222221+++++⋯+=-;()2设234n S 133333=+++++⋯+①,两边同时乘3得:234n n 13S 333333+=++++⋯++②, -②①得:n 13S S 31+-=-,即()n 11S 312+=-, 则()234nn 11133333312++++++⋯+=-. 【点睛】本题考查了规律型:数字的变化类,有理数的混合运算,解题的关键是明确题意,运用题目中的解题方法,运用类比的数学思想解答问题.11.(1)①两;②8;③5;④58;(2)①24;②56.【分析】(1)①根据例题进行推理得出答案;②根据例题进行推理得出答案;③根据例题进行推理得出答案;④根据②③得出答案;(2)①先判断它的立方根是几位数,再判断个位、十位上的数字,即可得到结论;②先判断它的立方根是几位数,再判断个位、十位上的数字,即可得到结论.【详解】<<,(1)①33100010,1000000100==,10001951121000000∴3<<,10195112100∴能确定195112的立方根是一个两位数,故答案为:两;②∵195112的个位数字是2,又∵38512=,∴能确定195112的个位数字是8,故答案为:8;③如果划去195112后面三位112得到数195,而333<<,125211956∴3<<,51956可得3<<,5019511260由此能确定195112的立方根的十位数是5,故答案为:5;④根据②③可得:195112的立方根是58,故答案为:58;(2)①13824的立方根是两位数,立方根的个位数是4,十位数是2,∴13824的立方根是24,故答案为:24;②175616的立方根是两位数,立方根的个位数是6,十位数是5,∴175616的立方根是56,故答案为:56.【点睛】此题考查立方根的性质,一个数的立方数的特点,正确理解题意仿照例题解题的能力,掌握一个数的立方数的特点是解题的关键.12.(1) ;(2) ;(3);(4)x=2017;(5)【分析】(1)类比题目中方法解答即可;(2)根据题目中所给的算式总结出规律,解答即可;(3)利用总结的规律把每个式子拆分后合并即可解答;(4)方程左边提取x 后利用(3)的方法计算后,再解方程即可;(5)类比(3)的方法,拆项计算即可. 【详解】 (1)故答案为:;(2)=故答案为:;(3)计算:==1﹣=;(4)=2016=2016, x=2017; (5).=+()+()+…+().=(1﹣).=. 【点睛】本题是数字规律探究题,解决问题基本思路是正确找出规律,根据所得的规律解决问题. 13.(1)2;(2)(0,4),(0,4),(2,0)--;(3)1(1,0)F m +或2(1,0)F m -- 【分析】(1)直接利用以OA 为底,进行求面积;(2)OBC 的面积等于OAB 的面积,需要分三种情况进行分类讨论; (3)根据BDEBEFSS=推导出OBDOBFSS=,然后分两种情况进行讨论,即当F 位于x 轴负半轴上时与F 位于x 轴正半轴上时.【详解】 解:(1)1122222OABB SOA y =⋅⋅=⨯⨯=. (2)作如下图形,进行分类讨论:①当点C 在y 轴正半轴上时,111||22OBC B SOC x =⋅⋅=, 114,(0,4)OC C ∴=;②当点C 在y 轴负半轴上时,221||22OBC B SOC x =⋅⋅=, 224,(0,4)OC C ∴=-;③当点C 在x 轴负半轴上时, 33122OBC B SOC y =⋅⋅=, 332,(2,0)OC C ∴=-;因此符合条件的C 点坐标有3个,分别是(0,4),(0,4),(2,0)--. (3)BDEBEFSS=,1122D F BE h BE h ∴⋅⋅=⋅⋅, D F h h ∴=,即D 与F 点到OB 的距离相等,12OBDD S OB h =⋅⋅, 12OBFF SOB h =⋅⋅, OBDOBFSS∴=, ∴由BDEBEFSS=可推出OBDOBFSS=,①F 位于x 轴负半轴上时,11(1)2122OBDB S BD y m m =⋅⋅=⨯--⨯=--, 11111122BOF B B SOF y OF y OF =⋅⋅=⋅⋅=, 11OF m ∴=--, 1(1,0)F m ∴+;②F 位于x 轴正半轴上时,222112BOF B SOF y OF m =⋅⋅==--, 2(1,0)F m ∴--,综上:点F 的坐标为1(1,0)F m +或2(1,0)F m --. 【点睛】本题考查了坐标与图形、三角形的面积、动点问题,解题的关键是要作适当辅助线,进行分类讨论求解.14.(1)260BEO DFO ∠+∠=︒ ;(2)EMN FNM ∠-∠的值为40°;(3)53.【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解;(2)过点M 作MK ∥A B ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM =∠OEM =x ,∠CFN =∠OFN =y ,由∠BEO +∠DFO =260°可求x -y =40°,进而求解;(3)设直线FK 与EG 交于点H ,FK 与AB 交于点K ,根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒,可得50KFD AEG ∠-∠=︒,结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒,,,可得11180100AEG AEG KFD KFD n n ∠+∠+︒-∠-∠=︒,即可得关于n 的方程,计算可求解n 值. 【详解】证明:过点O 作OG ∥AB ,∵AB ∥CD , ∴AB ∥OG ∥CD ,∴180180BEO EOG DFO FOG ∠+∠=︒∠+∠=︒,, ∴360BEO EOG DFO FOG ∠+∠+∠+∠=︒, 即360BEO EOF DFO ∠+∠+∠=︒, ∵∠EOF =100°,∴∠260BEO DFO +∠=︒;(2)解:过点M 作MK ∥AB ,过点N 作NH ∥CD ,∵EM 平分∠BEO ,FN 平分∠CFO , 设BEM OEM x CFN OFN y ∠=∠=∠=∠=,, ∵260BEO DFO ∠+∠=︒∴21802260BEO DFO x y ∠+∠=+︒-=︒, ∴x -y =40°,∵MK ∥AB ,NH ∥CD ,AB ∥CD , ∴AB ∥MK ∥NH ∥CD ,∴EMK BEM x HNF CFN y KMN HNM ∠=∠=∠=∠=∠=∠,,, ∴EMN FNM EMK KMN HNM HNF ∠+∠=∠+∠-∠+∠() x KMN HNM y =+∠-∠-=x -y =40°,EMN FNM ∠-∠的值为40°;(3)如图,设直线FK 与EG 交于点H ,FK 与AB 交于点K ,∵AB ∥CD , ∴AKF KFD ∠=∠,∵AKF EHK HEK EHK AEG ∠=∠+∠=∠+∠, ∴KFD EHK AEG ∠=∠+∠, ∵50EHK NMF ENM ∠=∠-∠=︒, ∴50KFD AEG ∠=︒+∠, 即50KFD AEG ∠-∠=︒,∵AEG n OEG ∠=∠,FK 在∠DFO 内,DFK n OFK ∠=∠.∴1180180CFO DFK OFK KFD KFD n∠=︒-∠-∠=︒-∠-∠ ,1AEO AEG OEG AEG AEG n ∠=∠+∠=∠+∠,∵260BEO DFO ∠+∠=︒, ∴100AEO CFO ∠+∠=︒,∴11180100AEG AEG KFD KFD n n ∠+∠+︒-∠-∠=︒,即(180)1KFD AEG n ⎛⎫⎪⎝∠⎭+-∠︒=, ∴115080n ⎛⎫⎪⨯⎭︒︒⎝+=, 解得53n = . 经检验,符合题意, 故答案为:53.【点睛】本题主要考查平行线的性质,角平分线的定义,灵活运用平行线的性质是解题的关键. 15.(1)点,点;12;(2)存在,点的坐标为和;(3) ∠OFC=∠FOB-∠FCD ,见解析.。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案doc

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案doc一、解答题1.先化简,再求值:(a -1)(2a +1)+(1+a )(1-a ),其中a =2.2.已知:如图EF ∥CD ,∠1+∠2=180°.(1)试说明GD ∥CA ;(2)若CD 平分∠ACB ,DG 平分∠CDB ,且∠A =40°,求∠ACB 的度数.3.已知:方程组2325x y a x y +=-⎧⎨+=⎩,是关于x 、y 的二元一次方程组. (1)求该方程组的解(用含a 的代数式表示);(2)若方程组的解满足0x <,0y >,求a 的取值范围.4.因式分解:(1)16x 2-9y 2(2)(x 2+y 2)2-4x 2y 25.如图,△ABC 的顶点都在方格纸的格点上,将△ABC 向下平移3格,再向右平移4格.(1)请在图中画出平移后的△A′B′C′;(2)在图中画出△A′B′C′的高C′D′.6.疫情初期,武汉物资告急,全国一心,各地纷纷运送物资到武汉.已知3辆大货车与2辆小货车可以一次运货17吨,5辆大货车与4辆小货车可以一次运货29吨,则2辆大货车与1辆小货车可以一次运货多少吨?7.计算(1)(π-3.14)0-|-3|+(12)1--(-1)2012 (2) (-2a 2)3+(a 2)3-4a .a 5(3)x (x+7)-(x-3)(x+2)(4)(a-2b-c )(a+2b-c )8.阅读下列各式:(a•b )2=a 2b 2,(a•b )3=a 3b 3,(a•b )4=a 4b 4…回答下列三个问题:(1)验证:(2×12)100= ,2100×(12)100= ; (2)通过上述验证,归纳得出:(a•b )n = ; (abc )n = .(3)请应用上述性质计算:(﹣0.125)2017×22016×42015.9.在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元;(2)根据学校实际,需购进电脑和电子白板共31台,若总费用不超过30万元,则至多购买电子白板多少台?10.如图,在边长为1个单位长度的小正方形网格中,ΔABC 经过平移后得到ΔA B C ''',图中标出了点B 的对应点B ',点A '、C '分别是A 、C 的对应点.(1)画出平移后的ΔA B C ''';(2)连接BB '、CC ',那么线段BB '与CC '的关系是_________;(3)四边形BCC B ''的面积为_______.11.计算:(1)2201(2)3()3----÷- (2)22(21)(21)x x -+ 12.如图1是一个长为 4a ,宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).(1)图2中的阴影部分的面积为 ;(2)观察图2请你写出 ()2a b +,()2a b -,ab 之间的等量关系是 ;(3)根据(2)中的结论,若 6x y +=,114x y ⋅=,则 x y -= ;(4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式()()2222252a b a b a ab b ++=++.在图形上把每一部分的面积标写清楚. 13.(问题背景)(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B =∠C+∠D(简单应用)(2)如图2,AP 、CP 分别平分∠BAD 、∠BCD ,若∠ABC =28°,∠ADC =20°,求∠P 的度数(可直接使用问题(1)中的结论)(问题探究)(3)如图3,直线BP 平分∠ABC 的外角∠FBC ,DP 平分∠ADC 的外角∠ADE ,若∠A =30°,∠C =18°,则∠P 的度数为(拓展延伸)(4)在图4中,若设∠C =x ,∠B =y ,∠CAP =14∠CAB ,∠CDP =14∠CDB ,试问∠P 与∠C 、∠B 之间的数量关系为 (用x 、y 表示∠P )(5)在图5中,BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论.14.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;(2)根据(1)中的结论,若x+y=5,x•y=94,则x﹣y=;(3)拓展应用:若(2019﹣m)2+(m﹣2020)2=15,求(2019﹣m)(m﹣2020)的值.15.(类比学习)小明同学类比除法240÷16=15的竖式计算,想到对二次三项式x2+3x+2进行因式分解的方法:15 162401 680802221322222xx x xx xxx+++++++即(x 2+3x +2)÷(x +1)=x +2,所以x 2+3x +2=(x +1)(x +2).(初步应用)小明看到了这样一道被墨水污染的因式分解题:x 2+□x +6=(x +2)(x +☆),(其中□、☆代表两个被污染的系数),他列出了下列竖式: 22262 (2)62 0x x x x x x x x +++++-++☆☆☆ 得出□=___________,☆=_________.(深入研究)小明用这种方法对多项式x 2+2x 2-x -2进行因式分解,进行到了:x 3+2x 2-x -2=(x +2)(*).(*代表一个多项式),请你利用前面的方法,列出竖式,将多项式x 3+2x 2-x -2因式分解.16.已知关于x 、y 的方程组354526x y ax by -=⎧⎨+=-⎩与2348x y ax by +=-⎧⎨-=⎩有相同的解,求a 、b 的值.17.先化简,再计算:(2a +b )(b -2a )-(a -b )2,其中a =-1,b =-218.计算:(1)(12)﹣3﹣20160﹣|﹣5|; (2)(3a 2)2﹣a 2•2a 2+(﹣2a 3)2+a 2;(3)(x+5)2﹣(x ﹣2)(x ﹣3);(4)(2x+y ﹣2)(2x+y+2).19.如图,边长为1的正方形ABCD 被两条与边平行的线段EF ,GH 分割成四个小长方形,EF 与GH 交于点P ,设BF 长为a ,BG 长为b ,△GBF 的周长为m ,(1)①用含a ,b ,m 的式子表示GF 的长为 ;②用含a ,b 的式子表示长方形EPHD 的面积为 ;(2)已知直角三角形两直角边的平方和等于斜边的平方,例如在图1,△ABC 中,∠ABC=900,则222AB BC AC +=,请用上述知识解决下列问题:①写出a,b,m满足的等式;②若m=1,求长方形EPHD的面积;③当m满足什么条件时,长方形EPHD的面积是一个常数?20.水果商贩老徐上水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元.老徐购得草莓和苹果共60箱,刚好花费3100元.(1)问草莓、苹果各购买了多少箱?(2)老徐有甲、乙两家店铺,每出售一箱草莓或苹果,甲店分别获利15元和20元,乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓a箱,苹果b箱,其余均分配给乙店,由于他口碑良好,两家店都很快卖完了这批水果.①若老徐在甲店获利600元,则他在乙店获利多少元?+=?②若老徐希望获得总利润为1000元,则a b【参考答案】***试卷处理标记,请不要删除一、解答题1.a2-a,2【分析】分别根据多项式的乘法法则和平方差公式计算每一项,再合并同类项,然后把a的值代入化简后的式子计算即可.【详解】解:(a-1)(2a+1)+(1+a)(1-a)=2a2-a-1+1-a2= a2-a,当a=2时,原式=22-2=2.【点睛】本题考查了整式的混合运算和代数式求值,属于基本题型,熟练掌握多项式的乘法法则是解题的关键.2.(1)见解析;(2)∠ACB=80°【分析】(1)利用同旁内角互补,说明GD∥CA;(2)由GD∥CA,得∠A=∠GDB=∠2=40°=∠ACD,由角平分线的性质可求得∠ACB的度数.【详解】解:(1)∵EF ∥CD∴∠1+∠ECD =180°又∵∠1+∠2=180°∴∠2=∠ECD∴GD ∥CA ;(2)由(1)得:GD ∥CA ,∴∠BDG =∠A =40°,∠ACD =∠2,∵DG 平分∠CDB ,∴∠2=∠BDG =40°,∴∠ACD =∠2=40°,∵CD 平分∠ACB ,∴∠ACB =2∠ACD =80°.【点睛】本题考查了角平分线的性质和平行线的性质.解决本题的关键熟练利用所学的性质进行解题.3.(1)1213x a y a=+⎧⎨=-⎩;(2)12a <- 【分析】(1)利用加减消元法求解可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】(1)①2⨯,得 2242x y a +=-.③②-③,得12x a =+把12x a =+代入①,得13y a =-所以原方程组的解是1213x a y a =+⎧⎨=-⎩(2)根据题意,得 120130a a +<⎧⎨->⎩解不等式组,得,12a <- 所以a 的取值范围是:12a <-. 【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.4.(1)(43)(4-3)x y x y +;(2)22()(-y)x y x +.【分析】(1)直接利用平方差公式22()()a b a b a b +-=-分解即可; (2)先利用平方差公式,再利用完全平方公式222()2a b a ab b ±=±+即可.【详解】(1)原式2243))((x y =-(43)(43)x y x y =+-;(2)原式2222)()(2x y xy =-+2222(2)(2)x y x y xy y x ++=+-22()()x y x y =+-.【点睛】本题考查了利用平方差公式和完全平方公式进行因式分解,熟记公式是解题关键.5.(1)图见解析;(2)图见解析.【详解】解:(1)△A′B′C′如下图;(2)高C′D′如下图.6.2辆大货车与1辆小货车可以一次运货11吨【分析】设1辆大货车一次运货x 吨,1辆小货车一次运货y 吨,根据“3辆大货车与2辆小货车可以一次运货17吨,5辆大货车与4辆小货车可以一次运货29吨”,即可得出关于x ,y 的二元一次方程组,解之即可得出x ,y 的值,将其代入(2)x y +中即可求出结论.【详解】设1辆大货车一次运货x 吨,1辆小货车一次运货y 吨由题意得:32175429x y x y +=⎧⎨+=⎩解得:51x y =⎧⎨=⎩则225111x y +=⨯+=答:2辆大货车与1辆小货车可以一次运货11吨.【点睛】本题考查了二元一次方程组的实际应用,理解题意,正确列出方程组是解题关键.7.(1)-1;(2)611a -;(3)86x +;(4)222a ac c -+ -24b【分析】(1)直接利用零指数幂,绝对值,负指数幂,乘方法则运算.(2)先利用幂的运算法则,再合并同类项.(3)利用整式的乘法法则进行运算.(4)利用平方差公式进行运算.【详解】解:(1)原式=1-3+2-1=-1(2)原式=68a - +6a -64a =611a -(3)原式=27x x + -()26x x -- =27x x +26x x -++ =86x +(4)原式=()2a c - -()22b =222a ac c -+ -24b【点睛】本题主要考查了数的计算,整式的加减与乘法,解题的关键要对零指数幂,绝对值,负指数幂以及幂的运算和整式的乘法法则熟悉.8.(1)1, 1, (2)a n b n , a n b n c n ,(3)132-. 【解析】【分析】(1)先算括号内的乘法,再算乘方;先乘方,再算乘法;(2)根据有理数乘方的定义求出即可;(3)根据同底数幂的乘法计算,再根据积的乘方计算,即可得出答案.【详解】 解:(1)(2×12)100=1,2100×(12)100=1; (2)(a•b )n =a n b n ,(abc )n =a n b n c n , (3)原式=(﹣0.125)2015×22015×42015×[(﹣0.125)×(﹣0.125)×2]=(﹣0.125×2×4)2015×132 =(﹣1)2015×132 =﹣1×132=﹣132. 【点睛】 本题主要考查了同底数幂的乘法和积的乘方,掌握运算法则是解答此题的关键.9.(1)电脑0.5万元,电子白板1.5万元;(2)14台【分析】(1)设每台电脑x 元,每台电子白板y 元,根据题意列出方程组,解方程组即可;(2)设购进电子白板m 台,则购进电脑()31m -台,根据总费用不超过30万元,列出不等式,根据m 实际意义即可求解.【详解】(1)设每台电脑x 元,每台电子白板y 元,则2 3.52 2.5x y x y +=⎧⎨+=⎩,解得0.51.5x y =⎧⎨=⎩故每台电脑0.5万元,每台电子白板1.5万元;(2)设购进电子白板m 台,则购进电脑()31m -台,由题意得 1.50.5(31)30m m +-≤解得14.5m ≤,又因为m 是正整数,则14m ≤,故至多购买电子白板14台.【点睛】本题考查了二元一次方程组应用,一元一次不等式应用,综合性较强,难度不大,根据题意列出二元一次方程组、一元一次不等式是解题关键.10.(1)见解析;(2)平行且相等;(3)28【分析】(1)根据平移的性质画出点A 、C 平移后的对应点A '、C '即可画出平移后的△A B C '''; (2)根据平移的性质解答即可;(3)根据平行四边形的面积解答即可.【详解】解:(1)如图,ΔA B C '''即为所求;(2)根据平移的性质可得:BB '与CC '的关系是平行且相等;故答案为:平行且相等;(3)四边形BCC B ''的面积为4×7=28.故答案为:28.【点睛】本题主要考查了平移的性质和平移作图,属于常考题型,熟练掌握平移的性质是解题关键.11.(1)374-.(2)16x 4−8x 2+1. 【分析】(1)原式利用负整数指数幂,零指数幂、平方的计算法则得到1914--÷,再计算即可得到结果;(2)原式逆用积的乘方运算法则变形,再利用平方差公式及完全平方公式化简即可得到结果.【详解】(1)2201(2)3()3----÷-= 1914--÷=374-. (2)原式=[(2x−1)(2x +1)]2=(4x 2−1)2=16x 4−8x 2+1.【点睛】本题考查零指数幂、负整数指数幂 、平方差公式及完全平方公式,熟练掌握运算法则是解本题的关键.12.(1)2()b a -;(2)22()()4a b a b ab +=-+;(3)±5;(4)详见解析 【分析】(1)表示出阴影部分正方形的边长,然后根据正方形的面积公式列式即可;(2)根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可; (3)将(x -y )2变形为(x +y )2—4xy ,再代入求值即可;(4)由已知的恒等式,画出相应的图形,如图所示.【详解】解:(1)阴影部分为一个正方形,其边长为b -a ,∴其面积为:2()b a -,故答案为:2()b a -;(2)大正方形面积为:()2a b +小正方形面积为:2()b a -=2()a b -, 四周四个长方形的面积为:4ab ,∴22()()4a b a b ab +=-+,故答案为:22()()4a b a b ab +=-+;(3)由(2)知,22()()4x y x y xy +=-+, ∴22()()4x y x y xy -=+-,∴x y -=5=±,故答案为:±5;(4)符合等式()()2222252a b a b a ab b ++=++的图形如图所示,【点睛】本题考查了完全平方公式的几何背景,此类题目关键在于同一个图形的面积用两种不同的方法表示.13.(1)证明见解析;(2)24°;(3)24°;(4)∠P=34x+14y ;(5)∠P=180()2A C ︒-∠+∠ 【分析】 (1)根据三角形内角和为180°,对顶角相等,即可证得∠A+∠B=∠C+∠D(2)由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC ①,∠PAD+∠P=∠PCD+∠ADC ②,将两个式子相加,已知AP 、CP 分别平分∠BAD 、∠BCD ,可得∠BAP=∠PAD ,∠BCP=∠PCD ,可证得∠P=12(∠ABC+∠ADC),即可求出∠P 度数. (3)已知直线BP 平分∠ABC 的外角∠FBC ,DP 平分∠ADC 的外角∠ADE ,可得∠1=∠2,∠3=∠4,由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1,∠A+∠4=∠P+∠2,两式相加即可求出∠P 的度数.(4)由(1)的结论得:14∠CAB+∠C=∠P+14∠CDB ,34∠CAB+∠P=∠B+34∠CDB ,第一个式子乘以3,得到的式子减去第二个式子即可得出用x 、y 表示∠P (5)延长AB 交DP 于点F ,标注出∠1,∠2,∠3,∠4,由(1)的结论得:∠A+2∠1=∠C+180°-2∠3,其中根据对顶角相等,三角形内角和,以及外角的性质即可得到∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P ,代入∠A+2∠1=∠C+180°-2∠3,即可得出∠P 与∠A 、∠C 的关系.【详解】(1)如图1,∠A+∠B+∠AOB=∠C+∠D+∠COD=180°∵∠AOB=∠COD∴∠A+∠B=∠C+∠D(2)∵AP、CP分别平分∠BAD、∠BCD∴∠BAP=∠PAD,∠BCP=∠PCD,由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC①,∠PAD+∠P=∠PCD+∠ADC②①+②,得2∠P+∠PAD+∠BCP=∠BAP+∠ABC +∠PCD+∠ADC∴∠P=12(∠ABC+∠ADC)∴∠ABC=28°,∠ADC=20°∴∠P=12(28°+20°)∴∠P=24°故答案为:24°(3)∵如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,∴∠1=∠2,∠3=∠4由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1①,∠A+∠4=∠P+∠2②①+②,得∠C+180°-∠3+∠A+∠4=∠P+180°-∠1+∠P+∠2∴30°+18°=2∠P∴∠P=24°故答案为:24°(4)由(1)的结论得:14∠CAB+∠C=∠P+14∠CDB①,34∠CAB+∠P=∠B+34∠CDB②①×3,得34∠CAB+3∠C=3∠P+34∠CDB③②-③,得∠P-3x=y-3∠P∴∠P=34x+14y故答案为:∠P=34x+14y(5)如图5所示,延长AB交DP于点F由(1)的结论得:∠A+2∠1=∠C+180°-2∠3∵∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P ∴∠A+360°-2∠A-2∠3-2∠P=∠C+180°-2∠3解得:∠P=180()2A C︒-∠+∠故答案为:∠P=180()2A C︒-∠+∠【点睛】本题是考查了角平分线性质及三角形内角和定理,对顶角相等,三角形任一外角等于不相邻的两个内角和等知识点,本题是典型的拓展延伸题,一般第一问得出基本结论,后面的问题将基本结论作为解题基础,进行拓展延伸.14.(1)(a+b)2-(a-b)2=4ab;(2)±4;(3)-7【分析】(1)由图可知,图1的面积为4ab,图2中白色部分的面积为(a+b)2-(b-a)2=(a+b)2-(a-b)2,图1的面积和图2中白色部分的面积相等即可求解.(2)由(1)知,(x+y)2-(x-y)2=4xy,将x+y=5,x•y=94代入(x+y)2-(x-y)2=4xy,即可求得x-y的值(3)因为(2019﹣m)+(m﹣2020)=-1,等号两边同时平方,已知(2019﹣m)2+(m﹣2020)2=15,即可求解.【详解】(1)由图可知,图1的面积为4ab,图2中白色部分的面积为(a+b)2-(b-a)2=(a+b)2-(a-b)2∵图1的面积和图2中白色部分的面积相等∴(a+b)2-(a-b)2=4ab故答案为:(a+b)2-(a-b)2=4ab(2)由(1)知,(x+y)2-(x-y)2=4xy∵x+y=5,x•y=9 4∴52-(x-y)2=4×9 4∴(x-y)2=16∴x-y=±4故答案为:±4(3)∵(2019﹣m)+(m﹣2020)=-1∴[(2019﹣m)+(m﹣2020)]2=1∴(2019﹣m)2+2(2019﹣m)(m﹣2020)+ (m﹣2020)2=1∵(2019﹣m)2+(m﹣2020)2=15∴2(2019﹣m)(m﹣2020)=1-15=-14∴(2019﹣m)(m﹣2020)=-7故答案为:-7【点睛】本题考查了完全平方公式的几何背景,运用几何直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.15.[初步应用]5,3;[深入研究]x3+2x2-x-2=(x+2)(x+1)(x-1);详见解析;【分析】[初步应用]列出竖式结合已知可得:2☆-6=0,2-=☆,求出□与☆即可.[深入研究]列出竖式可得x 3+2x 2-x -2÷(x +2),即可将多项式x 3+2x 2-x -2因式分解.【详解】[初步应用]∵多项式x 2+□x +6能被x +2整除,∴2☆-6=0,2-=☆,∴☆= 3,□=5,故答案为:5,3;[深入研究]∵2323212222 22 0x x x x x x x x x -++--+----, ∴()()()()()3222221211x x x x x x x x +--=+-=++-. 【点睛】本题考查整式的除法;理解题意,仿照整数的除法列出竖式进行运算是解题的关键.16.149299a b ⎧=⎪⎪⎨⎪=⎪⎩【分析】因为两个方程组有相同的解,故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组,求出未知数的值,再代入另一组方程组即可.【详解】354526x y ax by -=⎧⎨+=-⎩①③ 和2348x y ax by +=-⎧⎨-=⎩②④ 解:联立①②得:35234x y x y -=⎧⎨+=-⎩解得:12x y =⎧⎨=-⎩将12x y =⎧⎨=-⎩代入③④得:4102628a b a b -=-⎧⎨+=⎩解得:149299a b ⎧=⎪⎪⎨⎪=⎪⎩【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.17.-5a 2+2ab ,-1【分析】先利用平方差公式和完全平方公式进行计算,然和合并同类项,最后把a ,b 的值代入即可.【详解】()()()22222()=4222b a a a b b a ab b a b --++----2222=42b a a b ab ---+252a ab =-+,当a =-1,b =-2时,原式=-1.【点睛】本题考查了整式的化简求值,解题的关键是熟练掌握混合运算的顺序和整式的乘法公式.18.(1)2;(2)7a 4+4a 6+a 2;(3)15x+19;(4)4x 2+4xy+y 2﹣4【分析】(1)首先利用负整数指数幂的性质、零次幂的性质、绝对值的性质进行计算,再算加减即可;(2)首先利用积的乘方的计算法则、单项式乘以单项式计算法则计算,再合并同类项即可;(3)首先利用完全平方公式、多项式乘以多项式计算法则计算,再合并同类项即可; (4)首先利用平方差计算,再利用完全平方公式进行计算即可.【详解】解:(1)原式=8﹣1﹣5=2;(2)原式=9a 4﹣2a 4+4a 6+a 2,=7a 4+4a 6+a 2;(3)原式=x 2+10x+25﹣(x 2﹣3x ﹣2x+6),=x 2+10x+25﹣x 2+3x+2x ﹣6,=15x+19;(4)原式=(2x+y )2﹣4,=4x 2+4xy+y 2﹣4.【点睛】本题考查的是实数的运算,幂的运算及合并同类项,整式的混合运算,掌握以上知识点是解题的关键.19.(1)①m a b --;②1a b ab --+;(2)①22220m ma mb ab --+=;②12;③m=1 【分析】(1)①直接根据三角形的周长公式即可;②根据BF 长为a ,BG 长为b ,表示出EP ,PH 的长,根据求长方形EPHD 的面积;(2)①直接根据直角三角形两直角边的平方和等于斜边的平方,表示出a ,b ,m 之间的关系式;②根据线段之间的关系利用勾股定理求出长方形EPHD 的面积的值;③结合①的结论和②的作法即可求解.【详解】(1)①∵BF 长为a ,BG 长为b ,△GBF 的周长为m ,∴GF m a b =--,故答案为:m a b --;②∵正方形ABCD 的边长为1 ,∴AB=BC=1,∵BF 长为a ,BG 长为b ,∴AG=1-b ,FC=1-a ,∴EP=AG=1-b ,PH=FC=1-a ,∴长方形EPHD 的面积为:(1)(1)1a b a b ab --=--+,故答案为:1a b ab --+;(2)①△ABC 中,∠ABC=90°,则222AB BC AC +=,∴在△GBF 中, GF m a b =--,∴()222m a b a b --=+, 化简得,22220m ma mb ab --+=故答案为:22220m ma mb ab --+=;②∵BF=a ,GB=b ,∴FC=1-a ,AG=1-b ,在Rt △GBF 中,22222GF BF BG a b ==+=+,∵Rt △GBF 的周长为1, ∴1BF BG GF a b ++=+=即1a b =--,即222212(()b a b a b a +=-+++),整理得12220a b ab --+= ∴12a b ab +-=, ∴矩形EPHD 的面积••S PH EP FC AG ==()()11a b =--1a b ab =--+11122=-=.③由①得: 22220m ma mb ab --+=, ∴212ab ma mb m =+-. ∴矩形EPHD 的面积••S PH EP FC AG ==()()11a b =--1a b ab =--+2112ma mb a m b +-=--+ ()()211121m a m m b =--+-+, ∴要使长方形EPHD 的面积是一个常数,只有m=1.【点睛】本题考查了正方形的特殊性质和勾股定理,根据正方形的特殊性质和勾股定理推出22220m ma mb ab --+=是解题的关键.20.(1)草莓35箱,苹果25箱;(2)①340元,②53或52【分析】(1)抓住题中关键的已知条件,老徐购得草莓和苹果共60箱,刚好花费3100元,设未知数列方程组,求解方程即可;(2)①由题意列二元一次方程,可得到34120a b +=,列式求出他在乙店获利;②根据老徐希望获得总利润为1000元,建立关于a 、b 的二元一次方程,整理可得18034a b -=,再根据a 、b 的取值范围及a 一定是4的整数倍,即可求出结果; 【详解】 (1)解:设草莓购买了x 箱,苹果购买了y 箱,根据题意得:6060403100x y x y ⎧+=⎨+=⎩, 解得3525x y ⎧=⎨=⎩.答:草莓购买了35箱,苹果购买了25箱;(2)解:①若老徐在甲店获利600元,则1520600ab +=, 整理得:34120a b +=,他在乙店的获利为:()()12351625a b -+-, =()820434a b -+,=820-4120⨯,=340元;②根据题意得:()()1520123516251000a b a b ++-+-=,整理得:34180ab +=, 得到18034ab -=,∵a、b 均为正整数,∴a 一定是4的倍数,∴a 可能是0,4,8…,∵035a ≤≤,025b ≤≤, ∴当且仅当a=32,b=21或a=25,b=24时34180a b +=成立, ∴322153a b +=+=或28+24=52. 故答案为340元;53或52.【点睛】本题主要考查了二元一次方程组的应用,根据题意列式是解题的关键.。
人教版七年级下数学期末复习不等式压轴题训练(含答案)

人教版七年级下数学期末复习不等式压轴题训练(含答案)七年级下数学期末复习不等式压轴题训练(含答案)1.定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2′(2-5)+1=2′(-3)+1=-6+1=-5.(1)求(-2)⊕3的值(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.2.例题试确定实数a的取值范围,使不等式组恰有两个整数解.解:由不等式两边同乘以6得到3x+2(x+1)>0,可以求出x>-,由不等式两边都乘以3得到3x+5a+4>4x+4+3a可以解出x<2a,所以不等式组的解集为,因为该不等式组恰有有两个整数解,所以1<2a≤2,所以<a≤1.仿照例题完成下题试确定实数a的取值范围,使不等式组恰有两个整数解.3.阅读材料,并回答问题如图,有一根木棒MN放置在数轴上,它两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5.(单位:cm)由此可得,木棒长为__________cm .借助上述方法解决问题:一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,116岁了,哈哈!”美羊羊纳闷,村长爷爷到底是多少岁?(1)请你画出示意图,求出村长爷爷和美羊羊现在的年龄.(2)若羊村中的小羊均与美羊羊同岁,老羊均与村长爷爷同岁.灰太狼计划为全家抓5只羊,综合考虑口感和生长周期等因素,决定所抓羊的年龄之和不超过112岁且高于34岁.请问灰太狼有几种抓羊方案?4.x取哪些正整数时,不等式x+3>6与2x-1<10都成立?5.已知多项式a2-5a-7减去多项式a2-11a+9的差等于不等式5-4x<0的最小正整数解,求a的值.6..一件由黄金与白银制成的首饰重a克,商家称其中黄金含量不低于90%,黄金和白银的密度分别是19.3和10.5,列出不等式表示这件首饰的体积应满足什么条件.(提示:质量=密度×体积.)7.某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆0.5元,一般车保管费是每辆0.3元.(1)若设一般车停放辆次数为x,总的保管费收入为y元,试写出y与x的关系式.(2)若估计前来停放3500辆自行车中,变速车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的取值范围.答案:1定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2′(2-5)+1=2′(-3)+1=-6+1=-5.(1)求(-2)⊕3的值(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.【22题答案】【答案】(1)11(2)x>-1.数轴表示如图所示:【解析】【详解】分析:(1)按照定义新运算a⊕b=a(a-b)+1,求解即可.(2)先按照定义新运算a⊕b=a(a-b)+1,得出3⊕x,再令其小于13,得到一元一次不等式,解不等式求出x的取值范围,即可在数轴上表示.不等式的解集在数轴上表示的方法:>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.解:(1)∵a⊕b=a(a-b)+1,∴(-2)⊕3=-2(-2-3)+1=10+1=11.(2)∵3⊕x<13,∴3(3-x)+1<13,9-3x+1<13,-3x<3,∴x>-1.数轴表示如图所示:2.例题试确定实数a的取值范围,使不等式组恰有两个整数解.解:由不等式两边同乘以6得到3x+2(x+1)>0,可以求出x>-,由不等式两边都乘以3得到3x+5a+4>4x+4+3a可以解出x<2a,所以不等式组的解集为,因为该不等式组恰有有两个整数解,所以1<2a≤2,所以<a≤1.仿照例题完成下题试确定实数a的取值范围,使不等式组恰有两个整数解.【23题答案】【答案】<a≤【解析】【详解】试题分析:先求出不等式组的解集,再根据整数解的情况,得到a的取值范围.试题解析:解不等式组得:2-3a 以<a≤.3.阅读材料,并回答问题如图,有一根木棒MN放置在数轴上,它的两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5.(单位:cm)由此可得,木棒长为__________ cm.借助上述方法解决问题:一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,116岁了,哈哈!”美羊羊纳闷,村长爷爷到底是多少岁?(1)请你画出示意图,求出村长爷爷和美羊羊现在的年龄.(2)若羊村中的小羊均与美羊羊同岁,老羊均与村长爷爷同岁.灰太狼计划为全家抓5只羊,综合考虑口感和生长周期等因素,决定所抓羊的年龄之和不超过112岁且高于34岁.请问灰太狼有几种抓羊方案?【24题答案】【答案】(1)村长64岁,美羊羊12岁(2)抓四只小羊一只老羊或抓五只小羊【解析】【详解】试题分析:(1)在求村长爷爷年龄时,借助数轴,把美羊羊与村长爷爷的年龄差看做木棒MN,类似村长爷爷比美羊羊大时看做当N点移动到A点时,此时M点所对应的数为-40,美羊羊比村长爷爷大时看做当M点移动到B点时,此时N点所对应的数为116,所以可知爷爷比美羊羊大[116-(-40)]÷3=52,可知爷爷的年龄.(2)设抓小羊x只,则老羊为(5-x)只,再根据抓羊的年龄之和不超过112岁且高于34岁,列不等式组,解不等式组,得出其整数解即可试题解析:(1)如图:点A表示美羊羊现在的年龄,点B表示村长爷爷现在的年龄,木棒MN的两端分别落在点A、B.由题意可知,当点N移动到点A时,点M所对应的数为-40,当点M移动到点B时,点N所对应的数为116.可求MN=52.所以点A所对应的数为12,点B所对应的数为64.即美羊羊今年12岁,村长爷爷今年64岁.(2)设抓小羊x只,则老羊为(5-x)只,依题意得:解得:,则x=4或x=5,即抓四只小羊一只老羊或抓五只小羊【点睛】此题考查了数轴,解题的关键是把村长爷爷与美羊羊的年龄差看做一个整体(木棒MN),而后把此转化为上一题中的问题.4.x取哪些正整数时,不等式x+3>6与2x-1<10都成立?【20题答案】【答案】4或5【解析】【详解】试题分析:解x+3>6和2x-1<10,求出解集的公共部分,再从解集中找出正整数即可.解x+3>6得,x>3;解2x-1<10得,x<5.5;∴3,∴x=4或5.5.已知多项式a2-5a-7减去多项式a2-11a+9的差等于不等式5-4x<0的最小正整数解,求a的值.【21题答案】【答案】a=3【解析】【详解】试题分析:先解不等式5-4x<0,求出解集,从而从解集中找出最小正整数,然后列方程求解.∵5-4x<0,∴,∴不等式5-4x<0的最小正整数解是2,∴(a2-5a-7)-(a2-11a+9)=a2-5a-7-a2+11a-9=6a-16=2,∴6a=18,∴a=3.6..一件由黄金与白银制成的首饰重a克,商家称其中黄金含量不低于90%,黄金和白银的密度分别是19.3和10.5,列出不等式表示这件首饰的体积应满足什么条件.(提示:质量=密度×体积.)【22题答案】【答案】【解析】【详解】试题分析:由质量=密度×体积可得,据此表示出当黄金含量为90%时V的取值范围,进而得出答案.解:如果其中黄金的含量为90%,则首饰的体积V()为.如果其中黄金的含量为100%(注意仅仅是如果!),则首饰的体积V()为.∴主要考查了由实际问题抽象出一元一次不等式,根据质量、密度、体积之间的关系表示出V的最大值是解题关键.7.某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆0.5元,一般车保管费是每辆0.3元.(1)若设一般车停放的辆次数为x,总的保管费收入为y元,试写出y与x的关系式.(2)若估计前来停放的3500辆自行车中,变速车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的取值范围.【23题答案】【答案】(1)y=-0.2x+1750;(2)这个星期天保管费的收入在1225元至1330元之间.【解析】【分析】(1)根据总的保管费y=一般车辆人保管费+变速车的保管费列出方程,化简即可.(2)根据3500辆自行车中,变速车的辆次不小于25%,但不大于40%可确定变速车的辆数范围,再根据辆数确定保管费收费范围即可.【小问1详解】由题意,得y=0.3x+0.5(3500-x),即y=-0.2x+1750.【小问2详解】∵变速车停放的辆次不小于3500的25%,但不大于3500的40%,∴一般自行车停放的辆次是在3500×60%与3500×75%之间.当x=3500×60%=2100时,y=-0.2×2100+1750=1330;当x=3500×75%=2625时,y=-0.2×2625+1750=1225;∴这个星期天保管费的收入在1225元至1330元之间.【点睛】本题主要考查了一次函数的实际应用,准确根据题意求解析式是解题的关键.。
人教版中学七年级数学下册期末解答题压轴题(及答案)(1)

人教版中学七年级数学下册期末解答题压轴题(及答案)(1)一、解答题1.(1)小丽计划在母亲节那天送份礼物妈妈,特设计一个表面积为12dm2的正方体纸盒,则这个正方体的棱长是.(2)为了增加小区的绿化面积,幸福公园准备修建一个面积121πm2的草坪,草坪周围用篱笆围绕.现从对称美的角度考虑有甲,乙两种方案,甲方案:建成正方形;乙方案:建成圆形的.如果从节省篱笆费用的角度考虑,你会选择哪种方案?请说明理由;(3)在(2)的方案中,审批时发现修如此大的草坪,目的是亲近自然,若按上方案就没达到目的,因此建议用如图的设计方案:正方形里修三条小路,三条小路的宽度是一样,这样草坪的实际面积就减少了21πm2,请你根据此方案求出各小路的宽度(π取整数).2.如图是一块正方形纸片.(1)如图1,若正方形纸片的面积为1dm2,则此正方形的对角线AC的长为dm.(2)若一圆的面积与这个正方形的面积都是2πcm2,设圆的周长为C圆,正方形的周长为C正,则C圆C正(填“=”或“<”或“>”号)(3)如图2,若正方形的面积为16cm2,李明同学想沿这块正方形边的方向裁出一块面积为12cm2的长方形纸片,使它的长和宽之比为3:2,他能裁出吗?请说明理由?3.有一块面积为100cm2的正方形纸片.(1)该正方形纸片的边长为cm(直接写出结果);(2)小丽想沿着该纸片边的方向裁剪出一块面积为90cm2的长方形纸片,使它的长宽之比为4:3.小丽能用这块纸片裁剪出符合要求的纸片吗?4.小丽想用一块面积为236cm的正方形纸片,如图所示,沿着边的方向裁出一块面积为220cm的长方形纸片,使它的长是宽的2倍.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?你认为小丽能用这块纸片裁出符合要求的纸片吗?为什么?5.求下图44的方格中阴影部分正方形面积与边长.二、解答题6.已知,//AE BD ,A D ∠=∠.(1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.7.已知直线AB //CD ,点P 、Q 分别在AB 、CD 上,如图所示,射线PB 按逆时针方向以每秒12°的速度旋转至PA 便立即回转,并不断往返旋转;射线QC 按逆时针方向每秒3°旋转至QD 停止,此时射线PB 也停止旋转.(1)若射线PB 、QC 同时开始旋转,当旋转时间10秒时,PB '与QC '的位置关系为 ; (2)若射线QC 先转15秒,射线PB 才开始转动,当射线PB 旋转的时间为多少秒时,PB ′//QC ′.8.如图1,MN ∥PQ ,点C 、B 分别在直线MN 、PQ 上,点A 在直线MN 、PQ 之间. (1)求证:∠CAB =∠MCA +∠PBA ;(2)如图2,CD ∥AB ,点E 在PQ 上,∠ECN =∠CAB ,求证:∠MCA =∠DCE ;(3)如图3,BF 平分∠ABP ,CG 平分∠ACN ,AF ∥CG .若∠CAB =60°,求∠AFB 的度数.9.直线AB ∥CD ,点P 为平面内一点,连接AP ,CP .(1)如图①,点P 在直线AB ,CD 之间,当∠BAP =60°,∠DCP =20°时,求∠APC 的度数;(2)如图②,点P 在直线AB ,CD 之间,∠BAP 与∠DCP 的角平分线相交于K ,写出∠AKC 与∠APC 之间的数量关系,并说明理由;(3)如图③,点P 在直线CD 下方,当∠BAK =23∠BAP ,∠DCK =23∠DCP 时,写出∠AKC 与∠APC 之间的数量关系,并说明理由.10.已知//AB CD ,点E 在AB 与CD 之间.(1)图1中,试说明:BED ABE CDE ∠=∠+∠;(2)图2中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请利用(1)的结论说明:2BED BFD ∠=∠.(3)图3中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请直接写出BED ∠与BFD ∠之间的数量关系.三、解答题11.已知//AM CN ,点B 为平面内一点,AB BC ⊥于B .(1)如图1,点B 在两条平行线外,则A ∠与C ∠之间的数量关系为______;(2)点B 在两条平行线之间,过点B 作BD AM ⊥于点D .①如图2,说明ABD C ∠=∠成立的理由;②如图3,BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E .若180,3FCB NCF BFC DBE ∠∠∠∠+=︒=,求EBC ∠的度数.12.(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a 从空气中射入水中,再从水中射入空气中,形成光线b ,根据光学知识有12,34∠=∠∠=∠,请判断光线a 与光线b 是否平行,并说明理由.(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等,如图2有一口井,已知入射光线α与水平线OC的夹角为40︒,问如何放置平面镜MN,可使反射光线b正好垂直照射到井底?(即求MN与水平线的夹角)(3)如图3,直线EF上有两点A、C,分别引两条射线AB、CD.105BAF∠=︒,∠=︒,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转DCF65动,设时间为t,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.13.课题学习:平行线的“等角转化”功能.阅读理解:如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.(1)阅读并补充下面推理过程解:过点A作ED∥BC,∴∠B=∠EAB,∠C=又∵∠EAB+∠BAC+∠DAC=180°∴∠B+∠BAC+∠C=180°解题反思:从上面推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.方法运用:(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.(提示:过点C作CF∥AB)深化拓展:(3)如图3,已知AB∥CD,点C在点D的右侧,∠ADC=70°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间,求∠BED的度数.14.已知点A,B,O在一条直线上,以点O为端点在直线AB的同一侧作射线OC,OD,OE使60∠=∠=.BOC EOD(1)如图①,若OD 平分BOC ∠,求AOE ∠的度数;(2)如图②,将EOD ∠绕点O 按逆时针方向转动到某个位置时,使得OD 所在射线把BOC ∠分成两个角.①若:1:2COD BOD ∠∠=,求AOE ∠的度数;②若:1:COD BOD n ∠∠=(n 为正整数),直接用含n 的代数式表示AOE ∠. 15.如图1,D 是△ABC 延长线上的一点,CE //AB .(1)求证:∠ACD =∠A+∠B ;(2)如图2,过点A 作BC 的平行线交CE 于点H ,CF 平分∠ECD ,FA 平分∠HAD ,若∠BAD =70°,求∠F 的度数.(3)如图3,AH //BD ,G 为CD 上一点,Q 为AC 上一点,GR 平分∠QGD 交AH 于R ,QN 平分∠AQG 交AH 于N ,QM //GR ,猜想∠MQN 与∠ACB 的关系,说明理由.四、解答题16.小明在学习过程中,对教材中的一个有趣问题做如下探究:(习题回顾)已知:如图1,在ABC 中,90ACB ∠=︒,AE 是角平分线,CD 是高,AE 、CD 相交于点F .求证:CFE CEF ∠=∠;(变式思考)如图2,在ABC 中,90ACB ∠=︒,CD 是AB 边上的高,若ABC 的外角BAG ∠的平分线交CD 的延长线于点F ,其反向延长线与BC 边的延长线交于点E ,则CFE ∠与CEF ∠还相等吗?说明理由;(探究延伸)如图3,在ABC 中,AB 上存在一点D ,使得ACD B ∠=∠,BAC ∠的平分线AE 交CD 于点F .ABC 的外角BAG ∠的平分线所在直线MN 与BC 的延长线交于点M .直接写出M ∠与CFE ∠的数量关系.17.如图,△ABC 中,∠ABC 的角平分线与∠ACB 的外角∠ACD 的平分线交于A 1.(1)当∠A 为70°时,∵∠ACD -∠ABD =∠______∴∠ACD -∠ABD =______°∵BA 1、CA 1是∠ABC 的角平分线与∠ACB 的外角∠ACD 的平分线∴∠A 1CD -∠A 1BD =12(∠ACD -∠ABD ) ∴∠A 1=______°;(2)∠A 1BC 的角平分线与∠A 1CD 的角平分线交于A 2,∠A 2BC 与A 2CD 的平分线交于A 3,如此继续下去可得A 4、…、A n ,请写出∠A 与∠A n 的数量关系______;(3)如图2,四边形ABCD 中,∠F 为∠ABC 的角平分线及外角∠DCE 的平分线所在的直线构成的角,若∠A +∠D =230度,则∠F =______.(4)如图3,若E 为BA 延长线上一动点,连EC ,∠AEC 与∠ACE 的角平分线交于Q ,当E 滑动时有下面两个结论:①∠Q +∠A 1的值为定值;②∠Q -∠A 1的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.18.如图1,已知AB ∥CD ,BE 平分∠ABD ,DE 平分∠BDC .(1)求证:∠BED =90°;(2)如图2,延长BE 交CD 于点H ,点F 为线段EH 上一动点,∠EDF =α,∠ABF 的角平分线与∠CDF 的角平分线DG 交于点G ,试用含α的式子表示∠BGD 的大小;(3)如图3,延长BE 交CD 于点H ,点F 为线段EH 上一动点,∠EBM 的角平分线与∠FDN 的角平分线交于点G ,探究∠BGD 与∠BFD 之间的数量关系,请直接写出结论: .19.如图①所示,在三角形纸片ABC 中,70C ∠=︒,65B ∠=︒,将纸片的一角折叠,使点A 落在ABC 内的点A '处.(1)若140∠=︒,2∠=________.(2)如图①,若各个角度不确定,试猜想1∠,2∠,A ∠之间的数量关系,直接写出结论. ②当点A 落在四边形BCDE 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,A ∠,1∠,2∠之间又存在什么关系?请说明.(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的123456∠+∠+∠+∠+∠+∠和是________.20.问题情境:如图1,AB ∥CD ,∠PAB=130°,∠PCD=120°.求∠APC 度数.小明的思路是:如图2,过P 作PE ∥AB ,通过平行线性质,可得∠APC=50°+60°=110°. 问题迁移:(1)如图3,AD ∥BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD 、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出∠CPD 、∠α、∠β间的数量关系.【参考答案】一、解答题1.(1)dm ;(2)从节省篱笆费用的角度考虑,选择乙方案建成圆形;(3)根据此方案求出小路的宽度为【分析】(1)先求得正方体的一个面的面积,然后依据算术平方根的定义求解即可;(2)根据正方形的周解析:(12;(2)从节省篱笆费用的角度考虑,选择乙方案建成圆形;(3)根据3m【分析】(1)先求得正方体的一个面的面积,然后依据算术平方根的定义求解即可;(2)根据正方形的周长公式以及圆形的周长公式即可求出答案;(3)根据图形的平移求解.【详解】解:(1)∵正方体有6个面且每个面都相等,∴正方体的一个面的面积=2 dm2.∴正方形的棱长=2dm;故答案为:2dm;(2)甲方案:设正方形的边长为xm,则x2 =121π∴x =11π∴正方形的周长为:4x=44πm乙方案: 设圆的半径rm为,则πr2==121π∴r =11∴圆的周长为:2rπ= 22πm∴ 44π-22π=22π(2-)π∵ 4>π∴ 2π>∴20π->∴正方形的周长比圆的周长大故从节省篱笆费用的角度考虑,选择乙方案建成圆形;(3)依题意可进行如图所示的平移,设小路的宽度为ym ,则(π–y)2=121π-21π∴π–yπ∴yπ∵π取整数∴y33m;【点睛】本题主要考查的是算术平方根的定义,熟练掌握正方形的性质以及平移的性质是解题的关键;2.(1);(2)<;(3)不能;理由见解析.【分析】(1)由正方形面积,易求得正方形边长,再由勾股定理求对角线长;(2)由圆面积公式,和正方形面积可求周长,比较两数大小可以采用比商法; (3)采解析:(12)<;(3)不能;理由见解析.【分析】(1)由正方形面积,易求得正方形边长,再由勾股定理求对角线长;(2)由圆面积公式,和正方形面积可求周长,比较两数大小可以采用比商法; (3)采用方程思想求出长方形的长边,与正方形边长比较大小即可.【详解】解:(1)由已知AB 2=1,则AB =1,由勾股定理,AC ;(2,周长为2.1C C <圆正;即C 圆<C 正; 故答案为:<(3)不能;由已知设长方形长和宽为3xcm 和2xcm∴长方形面积为:2x •3x =12解得x∴长方形长边为>4∴他不能裁出.【点睛】本题主要考查了算术平方根在正方形、圆、长方形面积中的应用,灵活的进行算术平方根的计算与无理数大小比较是解题的关键.3.(1)10;(2)小丽不能用这块纸片裁出符合要求的纸片.【分析】(1)根据算术平方根的定义直接得出;(2)直接利用算术平方根的定义长方形纸片的长与宽,进而得出答案.【详解】解:(1)根据算解析:(1)10;(2)小丽不能用这块纸片裁出符合要求的纸片.【分析】(1)根据算术平方根的定义直接得出;(2)直接利用算术平方根的定义长方形纸片的长与宽,进而得出答案.【详解】解:(1)根据算术平方根定义可得,该正方形纸片的边长为10cm ;故答案为:10;(2)∵长方形纸片的长宽之比为4:3,∴设长方形纸片的长为4xcm,则宽为3xcm,则4x•3x=90,∴12x2=90,∴x2=30,4解得:x或x=∴长方形纸片的长为,∵56,∴10<∴小丽不能用这块纸片裁出符合要求的纸片.【点睛】本题考查了算术平方根.解题的关键是掌握算术平方根的定义:一个正数的正的平方根叫这个数的算术平方根;0的算术平方根为0.也考查了估算无理数的大小.4.不同意,理由见解析【分析】先求得正方形的边长,然后设设长方形宽为,长为,然后依据矩形的面积为20列方程求得的值,从而得到矩形的边长,从而可作出判断.【详解】解:不同意,因为正方形的面积为,解析:不同意,理由见解析【分析】先求得正方形的边长,然后设设长方形宽为x,长为2x,然后依据矩形的面积为20列方程求得x的值,从而得到矩形的边长,从而可作出判断.【详解】解:不同意,因为正方形的面积为236cm,故边长为6cm设长方形宽为x,则长为2x长方形面积2x x x=⋅==2220∴210x=,解得x=长为6cm>即长方形的长大于正方形的边长,所以不能裁出符合要求的长方形纸片【点睛】本题主要考查的是算术平方根的性质,熟练掌握算术平方根的性质是解题的关键.5.8;用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可.【详解】解:正方形面积=4×4-4××2×2=8;正方形的边解析:8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可.【详解】解:正方形面积=4×4-4×12×2×2=8;正方形的边长【点睛】本题考查了算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x叫做a 二、解答题6.(1)见解析;(2)【分析】(1)根据平行线的性质得出,再根据等量代换可得,最后根据平行线的判定即可得证;(2)过点E 作,延长DC 至Q ,过点M 作,根据平行线的性质及等量代换可得出,再根据平角的解析:(1)见解析;(2)72︒【分析】(1)根据平行线的性质得出180A B ∠+∠=︒,再根据等量代换可得180B D ∠+∠=︒,最后根据平行线的判定即可得证;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB ,根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠,再根据平角的含义得出ECF CFG ∠=∠,然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠;设,FAB CFH αβ∠=∠=,根据角的和差可得出2AEC AFH ∠=∠,结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒,最后根据垂线的含义及平行线的性质,即可得出答案.【详解】(1)证明://AE BD180A B ∴∠+∠=︒180B D ∴∠+∠=︒//AB CD ∴;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB//AB CDQCA CAB ∴∠=∠,BGM DFG ∠=∠,CFH BHF ∠=∠,CFA FAG ∠=ACE BAC BGM ∠=∠+∠ECQ QCA BAC BGM ∴∠+∠=∠+∠ECQ BGM DFG ∴∠=∠=∠180,180ECQ ECD DFG CFG ∠+=︒∠+=︒ECF CFG ∴∠=∠//AB CD//AB EP ∴,PEA EAB PEC ECF ∴∠=∠∠=∠AEC PEC PEA ∠=∠-∠AEC ECF EAB ∴∠=∠-∠ECF AEC EAB ∴∠=∠+∠AF 平分BAE ∠12EAF FAB EAB ∴∠=∠=∠ FH 平分CFG ∠12CFH HFG CFG ∴∠=∠=∠ //CD AB,BHF CFH CFA FAB ∴∠=∠∠=∠设,FAB CFH αβ∠=∠=AFH CFH CFA CFH FAB ∠=∠-∠=∠-∠AFH βα∴∠=-,BHF CFH β∠=∠=222ECF AFH AEC EAB AFH AEC β∴∠+∠=∠+∠+∠=∠+22ECF AFH E BHF ∴∠+∠=∠+∠2AEC AFH ∴∠=∠35180AEC AFH ∠-∠=︒18AFH ∴∠=︒FH HM ⊥90FHM ∴∠=︒90GHM β∴∠=︒-180CFM NMF ∠+∠=︒90HMB HMN β∴∠=∠=︒-EAF FAB ∠=∠18EAF CFA CFH AFH β∴∠=∠=∠-∠=-︒189072EAF GMH ββ∴∠+∠=-︒+︒-=︒72EAF GMH ∴∠+∠=︒.【点睛】本题考查了平行线的判定及性质,角平分线的定义,能灵活根据平行线的性质和判定进行推理是解此题的关键.7.(1)PB′⊥QC′;(2)当射线PB 旋转的时间为5秒或25秒或45秒时,PB′∥QC′【分析】(1)求出旋转10秒时,∠BPB′和∠CQC′的度数,设PB′与QC′交于O ,过O 作OE ∥AB ,根解析:(1)PB ′⊥QC ′;(2)当射线PB 旋转的时间为5秒或25秒或45秒时,PB ′∥QC ′【分析】(1)求出旋转10秒时,∠BPB ′和∠CQC ′的度数,设PB ′与QC ′交于O ,过O 作OE ∥AB ,根据平行线的性质求得∠POE 和∠QOE 的度数,进而得结论;(2)分三种情况:①当0<t ≤15时,②当15<t ≤30时,③当30<t <45时,根据平行线的性质,得出角的关系,列出t 的方程便可求得旋转时间.【详解】解:(1)如图1,当旋转时间30秒时,由已知得∠BPB ′=10°×12=120°,∠CQC ′=3°×10=30°,过O 作OE ∥AB ,∵AB ∥CD ,∴AB ∥OE ∥CD ,∴∠POE =180°﹣∠BPB ′=60°,∠QOE =∠CQC ′=30°,∴∠POQ =90°,∴PB′⊥QC′,故答案为:PB′⊥QC′;(2)①当0<t≤15时,如图,则∠BPB′=12t°,∠CQC′=45°+3t°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠PEC=∠CQC′,即12t=45+3t,解得,t=5;②当15<t≤30时,如图,则∠APB′=12t﹣180°,∠CQC'=3t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠BEQ=∠CQC′,即12t﹣180=45+3t,解得,t=25;③当30<t≤45时,如图,则∠BPB′=12t﹣360°,∠CQC′=3t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠BEQ=∠CQC′,即12t﹣360=45+3t,解得,t=45;综上,当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′.【点睛】本题主要考查了平行线的性质,第(1)题关键是作平行线,第(2)题关键是分情况讨论,运用方程思想解决几何问题.8.(1)证明见解析;(2)证明见解析;(3)120°.【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∠MCA=∠DAC,∠PBA=∠DAB,根据角的和差等量代换即可得解;(2)解析:(1)证明见解析;(2)证明见解析;(3)120°.【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∠MCA=∠DAC,∠PBA=∠DAB,根据角的和差等量代换即可得解;(2)由两直线平行,同旁内角互补得到∴、∠CAB+∠ACD=180°,由邻补角定义得到∠ECM+∠ECN=180°,再等量代换即可得解;(3)由平行线的性质得到,∠FAB=120°﹣∠GCA,再由角平分线的定义及平行线的性质得到∠GCA﹣∠ABF=60°,最后根据三角形的内角和是180°即可求解.【详解】解:(1)证明:如图1,过点A作AD∥MN,∵MN∥PQ,AD∥MN,∴AD∥MN∥PQ,∴∠MCA=∠DAC,∠PBA=∠DAB,∴∠CAB=∠DAC+∠DAB=∠MCA+∠PBA,即:∠CAB=∠MCA+∠PBA;(2)如图2,∵CD∥AB,∴∠CAB+∠ACD=180°,∵∠ECM+∠ECN=180°,∵∠ECN=∠CAB∴∠ECM=∠ACD,即∠MCA+∠ACE=∠DCE+∠ACE,∴∠MCA=∠DCE;(3)∵AF∥CG,∴∠GCA+∠FAC=180°,∵∠CAB=60°即∠GCA+∠CAB+∠FAB=180°,∴∠FAB=180°﹣60°﹣∠GCA=120°﹣∠GCA,由(1)可知,∠CAB=∠MCA+∠ABP,∵BF平分∠ABP,CG平分∠ACN,∴∠ACN=2∠GCA,∠ABP=2∠ABF,又∵∠MCA=180°﹣∠ACN,∴∠CAB=180°﹣2∠GCA+2∠ABF=60°,∴∠GCA﹣∠ABF=60°,∵∠AFB+∠ABF+∠FAB=180°,∴∠AFB=180°﹣∠FAB﹣∠FBA=180°﹣(120°﹣∠GCA)﹣∠ABF=180°﹣120°+∠GCA﹣∠ABF=120°.【点睛】本题主要考查了平行线的性质,线段、角、相交线与平行线,准确的推导是解决本题的关键.9.(1)80°;(2)∠AKC=∠APC,理由见解析;(3)∠AKC=∠APC,理由见解析【分析】(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠解析:(1)80°;(2)∠AKC=12∠APC,理由见解析;(3)∠AKC=23∠APC,理由见解析【分析】(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得出∠BAK+∠DCK=12∠BAP+12∠DCP=12(∠BAP+∠DCP)=12∠APC,进而得到∠AKC=12∠APC;(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠BAK﹣∠DCK,同理可得,∠APC=∠BAP﹣∠DCP,再根据已知得出∠BAK﹣∠DCK=23∠BAP﹣23∠DCP=23∠APC,进而得到∠BAK﹣∠DCK=23∠APC.【详解】(1)如图1,过P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠APE=∠BAP,∠CPE=∠DCP,∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;(2)∠AKC=12∠APC.理由:如图2,过K作KE∥AB,∵AB∥CD,∴KE∥AB∥CD,∴∠AKE=∠BAK,∠CKE=∠DCK,∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,过P作PF∥AB,同理可得,∠APC=∠BAP+∠DCP,∵∠BAP与∠DCP的角平分线相交于点K,∴∠BAK+∠DCK=12∠BAP+12∠DCP=12(∠BAP+∠DCP)=12∠APC,∴∠AKC=12∠APC;(3)∠AKC=23∠APC理由:如图3,过K作KE∥AB,∵AB∥CD,∴KE∥AB∥CD,∴∠BAK=∠AKE,∠DCK=∠CKE,∴∠AKC=∠AKE﹣∠CKE=∠BAK﹣∠DCK,过P作PF∥AB,同理可得,∠APC=∠BAP﹣∠DCP,∵∠BAK=23∠BAP,∠DCK=23∠DCP,∴∠BAK﹣∠DCK=23∠BAP﹣23∠DCP=23(∠BAP﹣∠DCP)=23∠APC,∴∠AKC=23∠APC.【点睛】本题考查了平行线的性质和角平分线的定义,解题的关键是作出平行线构造内错角相等计算.10.(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED=360°-2∠BFD.【分析】(1)图1中,过点E作EG∥AB,则∠BEG=∠ABE,根据AB∥CD,EG∥AB,所以CD∥EG,解析:(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED=360°-2∠BFD.【分析】(1)图1中,过点E作EG∥AB,则∠BEG=∠ABE,根据AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,进而可得∠BED=∠ABE+∠CDE;(2)图2中,根据∠ABE的平分线与∠CDE的平分线相交于点F,结合(1)的结论即可说明:∠BED=2∠BFD;(3)图3中,根据∠ABE的平分线与∠CDE的平分线相交于点F,过点E作EG∥AB,则∠BEG+∠ABE=180°,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG+∠CDE=180°,再结合(1)的结论即可说明∠BED与∠BFD之间的数量关系.【详解】解:(1)如图1中,过点E作EG∥AB,则∠BEG=∠ABE,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,所以∠BEG+∠DEG=∠ABE+∠CDE,即∠BED=∠ABE+∠CDE;(2)图2中,因为BF平分∠ABE,所以∠ABE=2∠ABF,因为DF平分∠CDE,所以∠CDE=2∠CDF,所以∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF),由(1)得:因为AB∥CD,所以∠BED=∠ABE+∠CDE,∠BFD=∠ABF+∠CDF,所以∠BED=2∠BFD.(3)∠BED=360°-2∠BFD.图3中,过点E作EG∥AB,则∠BEG+∠ABE=180°,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG+∠CDE=180°,所以∠BEG+∠DEG=360°-(∠ABE+∠CDE),即∠BED=360°-(∠ABE+∠CDE),因为BF平分∠ABE,所以∠ABE=2∠ABF,因为DF平分∠CDE,所以∠CDE=2∠CDF,∠BED=360°-2(∠ABF+∠CDF),由(1)得:因为AB∥CD,所以∠BFD=∠ABF+∠CDF,所以∠BED=360°-2∠BFD.【点睛】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.三、解答题11.(1)∠A+∠C=90°;(2)①见解析;②105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)①过点B作BG∥DM,根据平行线找角的联系即可求解;②先过点B作BG∥解析:(1)∠A+∠C=90°;(2)①见解析;②105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)①过点B作BG∥DM,根据平行线找角的联系即可求解;②先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得2α+β+3α+3α+β=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.【详解】解:(1)如图1,AM与BC的交点记作点O,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠A+∠AOB=90°,∴∠A+∠C=90°;(2)①如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,∴∠DBG=90°,∴∠ABD+∠ABG=90°,∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥DM,BG CN//,∴∠C=∠CBG,∠ABD=∠C;②如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)知∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=∠AFB=β,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°得:2α+β+3α+3α+β=180°,∵AB⊥BC,∴β+β+2α=90°,∴α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点睛】本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角(补角)相等进行推导.余角和补角计算的应用,常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.12.(1)平行,理由见解析;(2)65°;(3)5秒或95秒【分析】(1)根据等角的补角相等求出∠3与∠4的补角相等,再根据内错角相等,两直线平行即可判定a∥b;(2)根据入射光线与镜面的夹角与反解析:(1)平行,理由见解析;(2)65°;(3)5秒或95秒【分析】(1)根据等角的补角相等求出∠3与∠4的补角相等,再根据内错角相等,两直线平行即可判定a∥b;(2)根据入射光线与镜面的夹角与反射光线与镜面的夹角相等可得∠1=∠2,然后根据平角等于180°求出∠1的度数,再加上40°即可得解;(3)分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据两直线平行,内错角相等列式计算即可得解;②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据两直线平行,同位角相等列式计算即可得解;③CD旋转到与AB都在EF 的左侧,分别表示出∠DCF与∠BAC,然后根据两直线平行,同位角相等列式计算即可得解.【详解】解:(1)平行.理由如下:如图1,∵∠3=∠4,∴∠5=∠6,∵∠1=∠2,∴∠1+∠5=∠2+∠6,∴a∥b(内错角相等,两直线平行);(2)如图2:∵入射光线与镜面的夹角与反射光线与镜面的夹角相等,∴∠1=∠2,∵入射光线a与水平线OC的夹角为40°,b垂直照射到井底,∴∠1+∠2=180°-40°-90°=50°,∴∠1=1×50°=25°,2∴MN与水平线的夹角为:25°+40°=65°,即MN与水平线的夹角为65°,可使反射光线b正好垂直照射到井底;(3)存在.如图①,AB与CD在EF的两侧时,∵∠BAF=105°,∠DCF=65°,∴∠ACD=180°-65°-3t°=115°-3t°,∠BAC=105°-t°,要使AB∥CD,则∠ACD=∠BAC,即115-3t=105-t,解得t=5;如图②,CD旋转到与AB都在EF的右侧时,∵∠BAF=105°,∠DCF=65°,∴∠DCF=360°-3t°-65°=295°-3t°,∠BAC=105°-t°,要使AB∥CD,则∠DCF=∠BAC,即295-3t=105-t,解得t=95;如图③,CD旋转到与AB都在EF的左侧时,∵∠BAF=105°,∠DCF=65°,∴∠DCF=3t°-(180°-65°+180°)=3t°-295°,∠BAC=t°-105°,要使AB∥CD,则∠DCF=∠BAC,即3t-295=t-105,解得t=95,此时t>105,∴此情况不存在.综上所述,t为5秒或95秒时,CD与AB平行.【点睛】本题考查了平行线的判定与性质,光学原理,读懂题意并熟练掌握平行线的判定方法与性质是解题的关键,(3)要注意分情况讨论.13.(1)∠DAC;(2)360°;(3)65°【分析】(1)根据平行线的性质即可得到结论;(2)过C作CF∥AB根据平行线的性质得到∠D=∠FCD,∠B=∠BCF,然后根据已知条件即可得到结论;解析:(1)∠DAC;(2)360°;(3)65°【分析】(1)根据平行线的性质即可得到结论;(2)过C作CF∥AB根据平行线的性质得到∠D=∠FCD,∠B=∠BCF,然后根据已知条件即可得到结论;(3)过点E作EF∥AB,然后根据两直线平行内错角相等,即可求∠BED的度数.【详解】解:(1)过点A作ED∥BC,∴∠B=∠EAB,∠C=∠DCA,又∵∠EAB+∠BAC+∠DAC=180°,∴∠B+∠BAC+∠C=180°.故答案为:∠DAC;(2)过C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠D=∠FCD,∵CF∥AB,∴∠B =∠BCF ,∵∠BCF +∠BCD +∠DCF =360°,∴∠B +∠BCD +∠D =360°;(3)如图3,过点E 作EF ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥EF ,∴∠ABE =∠BEF ,∠CDE =∠DEF ,∵BE 平分∠ABC ,DE 平分∠ADC ,∠ABC =60°,∠ADC =70°,∴∠ABE =12∠ABC =30°,∠CDE =12∠ADC =35°,∴∠BED =∠BEF +∠DEF =30°+35°=65°.【点睛】此题考查了平行线的判定与性质,解题的关键是正确添加辅助线,利用平行线的性质进行推算. 14.(1);(2)①;②.【分析】(1)依据角平分线的定义可求得,再依据角的和差依次可求得和,根据邻补角的性质可求得结论;(2)①根据角相等和角的和差可得∠EOC=∠BOD ,再根据比例关系可得,最 解析:(1)90AOE ∠=︒;(2)①80AOE ∠=︒;②60(120)1n AOE n -+∠=︒. 【分析】(1)依据角平分线的定义可求得30COD ∠=︒,再依据角的和差依次可求得EOC ∠和∠BOE ,根据邻补角的性质可求得结论;(2)①根据角相等和角的和差可得∠EOC=∠BOD ,再根据比例关系可得BOD ∠,最后依据角的和差和邻补角的性质可求得结论;②根据角相等和角的和差可得∠EOC=∠BOD ,再根据比例关系可得BOD ∠,最后依据角的和差和邻补角的性质可求得结论.【详解】解:(1)∵OD 平分BOC ∠,60BOC EOD ∠=∠=︒, ∴1302COD BOC ∠=∠=︒, ∴30EOC EOD COD ∠=∠-∠=︒,∴90BOE EOC BOC ∠=∠+∠=︒,∴18090AOE BOE ∠=︒-∠=︒;(2)①∵BOC EOD ∠=∠,∴∠EOC+∠COD=∠BOD+∠COD ,∴∠EOC=∠BOD ,∵60BOC ∠=︒,:1:2COD BOD ∠∠=, ∴260403BOD ∠=︒⨯=︒, ∴40EOC BOD ∠=∠=︒,∴100BOE EOC BOC ∠=∠+∠=︒,∴18080AOE BOE ∠=︒-∠=︒;②∵BOC EOD ∠=∠,∴∠EOC+∠COD=∠BOD+∠COD ,∴∠EOC=∠BOD ,∵60BOC ∠=︒,:1:COD BOD n ∠∠=, ∴6060()11n n BOD n n ∠=︒⨯=︒++, ∴60()1n EOC BOD n ∠=∠=︒+, ∴60(60)1BOE EOC BOC n n ∠=∠+∠+=︒+, ∴18060(120)1AOE BO n E n ∠=︒-∠=-︒+. 【点睛】本题考查邻补角的计算,角的和差,角平分线的有关计算.能正确识图,利用角的和差求得相应角的度数是解题关键.15.(1)证明见解析;(2)∠F=55°;(3)∠MQN =∠ACB ;理由见解析.【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案;(2)首先根据角解析:(1)证明见解析;(2)∠F=55°;(3)∠MQN =12∠ACB ;理由见解析.【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案;(2)首先根据角平分线的定义得出∠FCD =12∠ECD ,∠HAF =12∠HAD ,进而得出∠F =12(∠HAD+∠ECD ),然后根据平行线的性质得出∠HAD+∠ECD 的度数,进而可得出答案;(3)根据平行线的性质及角平分线的定义得出12QGR QGD ∠=∠,12NQG AQG ∠=∠,180MQG QGR ∠+∠=︒ ,再通过等量代换即可得出∠MQN =12∠ACB .【详解】解:(1)∵CE //AB ,∴∠ACE =∠A ,∠ECD =∠B ,∵∠ACD =∠ACE+∠ECD ,∴∠ACD =∠A+∠B ;(2)∵CF 平分∠ECD ,FA 平分∠HAD ,∴∠FCD =12∠ECD ,∠HAF =12∠HAD ,∴∠F =12∠HAD+12∠ECD =12(∠HAD+∠ECD ),∵CH //AB ,∴∠ECD =∠B ,∵AH //BC ,∴∠B+∠HAB =180°,∵∠BAD =70°, 110B HAD ∴∠+∠=︒,∴∠F =12(∠B+∠HAD )=55°;(3)∠MQN =12∠ACB ,理由如下: GR 平分QGD ∠,12QGR QGD ∴∠=∠. GN 平分AQG ∠,12NQG AQG ∴∠=∠. //QM GR ,180MQG QGR ∴∠+∠=︒ .∴∠MQN =∠MQG ﹣∠NQG=180°﹣∠QGR ﹣∠NQG=180°﹣12(∠AQG+∠QGD )=180°﹣12(180°﹣∠CQG+180°﹣∠QGC ) =12(∠CQG+∠QGC ) =12∠ACB .【点睛】本题主要考查平行线的性质和角平分线的定义,掌握平行线的性质和角平分线的定义是解题的关键. 四、解答题16.[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸]。
(完整版)人教版初一数学下册期末压轴题试题(带答案) (一)
一、解答题1.对于平面直角坐标系xOy 中的图形G 和图形G 上的任意点P (x ,y ),给出如下定义: 将点P (x ,y )平移到P '(x +t ,y ﹣t )称为将点P 进行“t 型平移”,点P '称为将点P 进行“t 型平移”的对应点;将图形G 上的所有点进行“t 型平移”称为将图形G 进行“t 型平移”.例如,将点P (x ,y )平移到P '(x +1,y ﹣1)称为将点P 进行“l 型平移”,将点P (x ,y )平移到P '(x ﹣1,y +1)称为将点P 进行“﹣l 型平移”.已知点A (2,1)和点B (4,1).(1)将点A (2,1)进行“l 型平移”后的对应点A '的坐标为 .(2)①将线段AB 进行“﹣l 型平移”后得到线段A 'B ',点P 1(1.5,2),P 2(2,3),P 3(3,0)中,在线段A ′B ′上的点是 .②若线段AB 进行“t 型平移”后与坐标轴有公共点,则t 的取值范围是 .(3)已知点C (6,1),D (8,﹣1),点M 是线段CD 上的一个动点,将点B 进行“t 型平移”后得到的对应点为B ',当t 的取值范围是 时,B 'M 的最小值保持不变.2.如图1,点E 在直线AB 、DC 之间,且180DEB ABE CDE ∠+∠-∠=︒.(1)求证://AB DC ;(2)若点F 是直线BA 上的一点,且BEF BFE ∠=∠,EG 平分DEB ∠交直线AB 于点G ,若20D ∠=︒,求FEG ∠的度数;(3)如图3,点N 是直线AB 、DC 外一点,且满足14CDM CDE ∠=∠,14ABN ABE ∠=∠,ND 与BE 交于点M .已知()012CDM αα∠=︒<<︒,且//BN DE ,则NMB ∠的度数为______(请直接写出答案,用含α的式子表示).3.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.4.如图,∠EBF =50°,点C 是∠EBF 的边BF 上一点.动点A 从点B 出发在∠EBF 的边BE 上,沿BE 方向运动,在动点A 运动的过程中,始终有过点A 的射线AD ∥BC .(1)在动点A 运动的过程中, (填“是”或“否”)存在某一时刻,使得AD 平分∠EAC ? (2)假设存在AD 平分∠EAC ,在此情形下,你能猜想∠B 和∠ACB 之间有何数量关系?并请说明理由;(3)当AC ⊥BC 时,直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系.5.已知,//AE BD ,A D ∠=∠.(1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.6.如图,直线HD //GE ,点A 在直线HD 上,点C 在直线GE 上,点B 在直线HD 、GE 之间,∠DAB =120°.(1)如图1,若∠BCG =40°,求∠ABC 的度数;(2)如图2,AF 平分∠HAB ,BC 平分∠FCG ,∠BCG =20°,比较∠B ,∠F 的大小; (3)如图3,点P 是线段AB 上一点,PN 平分∠APC ,CN 平分∠PCE ,探究∠HAP 和∠N 的数量关系,并说明理由.7.请观察下列等式,找出规律并回答以下问题.111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,…… (1)按照这个规律写下去,第5个等式是:______;第n 个等式是:______. (2)①计算:11111223344950⨯⨯⨯⨯++++. ②若a 30b -=,求:()()()()()()()()111111122339797ab a b a b a b a b +++++++++++++. 8.阅读理解:计算1111234⎛⎫+++ ⎪⎝⎭×11112345+++⎛⎫ ⎪⎝⎭﹣111112345⎛⎫++++ ⎪⎝⎭×111234++⎛⎫ ⎪⎝⎭时,若把11112345+++⎛⎫ ⎪⎝⎭与111234++⎛⎫ ⎪⎝⎭分别各看着一个整体,再利用分配律进行运算,可以大大简化难度.过程如下:解:设111234++⎛⎫ ⎪⎝⎭为A ,11112345+++⎛⎫ ⎪⎝⎭为B , 则原式=B (1+A )﹣A (1+B )=B+AB ﹣A ﹣AB=B ﹣A=15.请用上面方法计算: ①11111123456⎛⎫+++++ ⎪⎝⎭×111111234567⎛⎫+++++ ⎪⎝⎭-1111111234567⎛⎫++++++ ⎪⎝⎭×1111123456⎛⎫++++ ⎪⎝⎭②111123n ⎛⎫++++ ⎪⎝⎭111231n ⎛⎫+++ ⎪+⎝⎭-1111231n ⎛⎫++++ ⎪+⎝⎭11123n ⎛⎫+++ ⎪⎝⎭. 9.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.(1)图2中A 、B 两点表示的数分别为___________,____________;(2)请你参照上面的方法:①把图3中51⨯的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a=___________.(注:小正方形边长都为1,拼接不重叠也无空隙)②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及3a-.(图中标出必要线段的长)10.我们知道,任意一个正整数n都可以进行这样的分解:n p q=⨯(p,q是正整数,且p q≤),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:()pF nq=.例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=31 62 =.(1)F(13)=,F(24)=;(2)如果一个两位正整数t,其个位数字是a,十位数字为1b-,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;(3)在(2)所得“和谐数”中,求F(t)的最大值.11.如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).(1)观察一个等比列数1,1111,,,24816,…,它的公比q=;如果a n(n为正整数)表示这个等比数列的第n项,那么a18=,a n=;(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:令S=1+2+4+8+16+…+230…①等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②由② ﹣①式,得2S﹣S=231﹣1即(2﹣1)S=231﹣1所以3131212121S-==--请根据以上的解答过程,求3+32+33+…+323的值;(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,a n,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示a n;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+a n.12.阅读下列材料:小明为了计算22019202012222+++++的值,采用以下方法:设22019202012222s=+++++①则22020202122222s=++++②②-①得,2021221s s s-==-请仿照小明的方法解决以下问题:(1)291222++++=________;(2)220333+++=_________;(3)求231na a a a++++的和(1a>,n是正整数,请写出计算过程).13.如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.(1)直接写出点C的坐标.(2)在y轴上是否存在点P,使得S△POB=23S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.14.已知点C在射线OA上.(1)如图①,CD//OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD 与∠BO′E′的关系(用含α的代数式表示)(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.15.在平面直角坐标系xOy 中,如图正方形ABCD 的顶点A ,B 坐标分别为()1,0A -,()3,0B ,点E ,F 坐标分别为(),0E m ,()3,0F m ,且12m -<≤,以EF 为边作正方形EFGH .设正方形EFGH 与正方形ABCD 重叠部分面积为S .(1)①当点F 与点B 重合时,m 的值为______;②当点F 与点A 重合时,m 的值为______.(2)请用含m 的式子表示S ,并直接写出m 的取值范围.16.阅读下列材料:我们知道||x 的几何意义是在数轴上数x 对应的点与原点的距离,即|||0|x x =-,也就是说,12||x x -表示在数轴上数1x 与数2x 对应的点之间的距离;例 1.解方程||2x =,因为在数轴上到原点的距离为2的点对应的数为2±,所以方程||2x =的解为2x =±.例 2.解不等式|1|2x ->,在数轴上找出|1|2x -=的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为1-或3,所以方程|1|2x -=的解为1x =-或3x =,因此不等式|1|2x ->的解集为1x <-或3x >.参考阅读材料,解答下列问题:(1)方程|3|5x +=的解为 ;(2)解不等式:|2|3x -≤;(3)解不等式:428x x -++>.17.在如图所示的平面直角坐标系中,A(1,3),B(3,1),将线段A平移至CD,C (m,-1),D(1,n)(1)m=_____,n=______(2)点P的坐标是(c,0)①设∠ABP=α,请写出∠BPD和∠PDC之间的数量关系(用含α的式子表示,若有多种数量关系,选择一种加以说明)②当三角形PAB的面积不小于3且不大于10,求点p的横坐标C的取值范围(直接写出答案即可)18.如图1,已知,点A(1,a),AH⊥x轴,垂足为H,将线段AO平移至线段BC,点B(b,0),其中点A与点B对应,点O与点C对应,a、b满足24(3)0a b-+-=.(1)填空:①直接写出A、B、C三点的坐标A(________)、B(________)、C(________);②直接写出三角形AOH的面积________.(2)如图1,若点D(m,n)在线段OA上,证明:4m=n.(3)如图2,连OC,动点P从点B开始在x轴上以每秒2个单位的速度向左运动,同时点Q从点O开始在y轴上以每秒1个单位的速度向下运动.若经过t秒,三角形AOP与三角形COQ的面积相等,试求t的值及点P的坐标.19.题目:满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2,求k的值.按照常规方法,顺着题目思路解关于x,y的二元一次方程组,分别求出xy的值(含有字母k),再由x+y=2,构造关于k的方程求解,从而得出k值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x+y”这个整体,或者对方程组的两个方程进行加减变形得到“x+y”整体值,从而求出k值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x=k,5y=1解得y=15,3x+y=2,∴x=95∴k=3×95=275把x=95,y=15代入方程②得k=﹣35所以k的值为275或﹣35.请诊断分析并评价“小勇同学的解答”.20.某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G 型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)21.(1)阅读下列材料并填空:对于二元一次方程组4354{336x yx y+=+=,我们可以将x,y的系数和相应的常数项排成一个数表4354 () 1336,求得的一次方程组的解{x ay b==,用数表可表示为10)01ab(.用数表可以简化表达解一次方程组的过程如下,请补全其中的空白:从而得到该方程组的解为x=,y=.(2)仿照(1)中数表的书写格式写出解方程组236{2x yx y+=+=的过程.22.在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|25a b-+0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.(1)请直接写出A、B、C、D四点的坐标.(2)点E在坐标轴上,且S△BCE=S四边形ABDC,求满足条件的点E的坐标.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在线段BD 上移动时(不与B ,D 重合)求:DCP BOP CPO∠+∠∠的值.23.某校为了丰富同学们的课外活动,决定给全校20个班每班配4副乒乓球拍和若干乒乓球,两家体育用品商店对同一款乒乓球拍和乒乓球推出让利活动,甲商店买一副乒乓球拍送10个乒乓球,乙商店所有商品均打九折(按标价的90%)销售,已知2副乒乓球拍和10个乒乓球110元,3副乒乓球拍和20个乒乓球170元。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1.解方程或不等式(组)(1)24231x y x y +=⎧⎨-=⎩ (2)2151132x x -+-≥ (3)312(2)15233x x x x +<+⎧⎪⎨-≤+⎪⎩ 2.利用多项式乘法法则计算:(1)()()22+-+a b a ab b = ;()()22a b a ab b -++ = .在多项式的乘法公式中,除了平方差公式,完全平方公式之外,如果把上面计算结果作为结论逆运用,则成为因式分解中的立方和与立方差公式.已知2,1a b ab -==,利用自己所学的数学知识,以及立方和与立方差公式,解决下列问题:(2)22a b += ;(直接写出答案)(3)33a b -= ;(直接写出答案)(4)66a b += ;(写出解题过程)3.先化简,再求值(x-2)2+2(x+2)(x-4)-(x-3)(x+3);其中x=1.4.解方程组(1)21325x y x y +=⎧⎨-=⎩ (2)111231233x y x y ⎧-=⎪⎪⎨⎪--=⎪⎩ 5.某口罩加工厂有,A B 两组工人共150人,A 组工人每人每小时可加工口罩70只,B 组工人每小时可加工口罩50只,,A B 两组工人每小时一共可加工口罩9300只.(1)求A B 、两组工人各有多少人?(2)由于疫情加重,A B 、两组工人均提高了工作效率,一名A 组工人和一名B 组工人每小时共可生产口罩200只,若A B 、两组工人每小时至少加工15000只口罩,那么A 组工人每人每小时至少加工多少只口罩?6.因式分解:(1)()()36x m n y n m ---;(2)()222936x x +-7.解下列方程组 (1)29321x y x y +=⎧⎨-=-⎩.(2)34332(1)11x y x y ⎧+=⎪⎨⎪--=⎩.8.阅读下列各式:(a•b )2=a 2b 2,(a•b )3=a 3b 3,(a•b )4=a 4b 4…回答下列三个问题:(1)验证:(2×12)100= ,2100×(12)100= ; (2)通过上述验证,归纳得出:(a•b )n = ; (abc )n = .(3)请应用上述性质计算:(﹣0.125)2017×22016×42015. 9.解下列方程组:(1)32316x y x y -=⎧⎨+=⎩ (2)234229x y z x y z ⎧==⎪⎨⎪-+=-⎩ 10.如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,三角形ABC 的三个顶点均在格点上.(1)将三角形ABC 先向右平移6个单位长度,再向上平移3个单位长度,得到三角形A 1B 1C 1,画出平移后的三角形A 1B 1C 1;(2)建立适当的平面直角坐标系,使得点A 的坐标为(-4,3),并直接写出点A 1的坐标; (3)求三角形ABC 的面积.11.已知关于x 、y 的二元一次方程组21322x y x y k +=⎧⎪⎨-=-⎪⎩(k 为常数). (1)求这个二元一次方程组的解(用含k 的代数式表示);(2)若()2421y x +=,求k 的值; (3)若14k ≤,设364m x y =+,且m 为正整数,求m 的值. 12.疫情初期,武汉物资告急,全国一心,各地纷纷运送物资到武汉。
人教版七年级下册数学期末复习:动点问题压轴题

人教版七年级下册数学期末复习: 动点问题压轴题1. 如图, 点A在x轴的负半轴上, 点D在y轴的正半轴上, 将三角形AOD沿x轴向右平移, 平移后得到三角形BEC, 点A的对应点是点B. 已知点A的坐标为(a, 0), 点C 的坐标为(b, c), 且a, b, c满足.(1)求点B的坐标;(2)求证: ∠DAE=∠BCD;(3)点P是线段BC上一动点(不与点B、C重合), 连接DP、AP, 在点P运动过程中, ∠CDP、∠DPA、∠PAE之间是否存在永远不变的数量关系?若存在, 写出它们之间的数量关系, 并请证明;若不存在, 请说明理由.2. 已知, 直线, 直线和, 分别交于C, D点, 点A, B分别在直线, 上, 且位于直线的左侧, 动点P在直线上, 且不和点C, D重合.(1)如图1, 当动点P在线段CD上运动时, 求证: ∠APB=∠CAP+∠DBP;(2)如图2, 当动点P在点C上方运动时(P, A, B不在同一直线上), 请写出∠APB, ∠CAP, ∠DBP之间的数量关系, 并选择其中一种的数量关系说明理由.3. 如图①, 平直角坐标系中, 已知点A(a, 0), B(0, b), 其中a, b满足|2a﹣3b﹣39|=0, 将点B向右平移24个单位长度得到点C.(1)点A和点C的坐标;(2)如图①, 点D为线段BC上一动点, 点D从点C以2个单位长度/秒的速度向点B运动, 同时点E为线段OA上一动点, 从点O以3个单位长度/秒的速度向点A运动, 设运动的时间为t秒(0<t<10), 四边形BOED的面积记为S四边形BOED(以下同理表示), 若S四边形BOEDS四边ACDE, 求t的取值范围;(3)如图②, 在(2)的条件下, 在点D, E运动的过程中, DE交OC于点F, 求证:S△OEF>S△DCE总成立.4. 在平面直角坐标系中, O为原点, 点A(0, 2), B(﹣2, 0), C(4, 0).(1)如图1, △ABC的面积为;(2)如图2, 将点B向右平移7个单位长度, 再向上平移4个单位长度, 得到对应点D.①求①ACD的面积;②点P是x轴上一动点, 若△PAO的面积等于3, 请求出点P的坐标.5. 在平面直角坐标系中, O为原点, 点A(0, −3), B(−2, 0).(1)如图①, 则三角形OAB的面积为_______;(2)如图②, 将线段AB向右平移5个单位长度, 再向上平移4个单位长度, 得到平移后的线段A′B′.连接OA′, OB′.①求三角形OA′B′的面积;②P(−1, m)(m>0)是一动点, 若SΔPOB′=10, 请直接写出点P坐标.6. 在平面直角坐标系中, , 满足.(1)直接写出、的值: ;;(2)如图1, 若点满足的面积等于6, 求的值;(3)设线段交轴于C, 动点E从点C出发, 在轴上以每秒1个单位长度的速度向下运动, 动点F从点出发, 在轴上以每秒2个单位长度的速度向右运动, 若它们同时出发, 运动时间为秒, 问为何值时, 有?请求出的值.7. 如图1, ABCD, 定点E, F分别在直线AB, CD上, 在平行线AB, CD之间有一动点P, 满足0°<∠EPF<180°.(1)试问∠AEP, ∠EPF, ∠PFC满足怎样的数量关系?解: 由于点P是平行线AB, CD之间有一动点, 因此需要对点P的位置进行分类讨论: 如图1, 当P点在EF的左侧时, ∠AEP, ∠EPF, ∠PFC满足数量关系为, 如图2, 当P点在EF的右侧时, ∠AEP, ∠EPF, ∠PFC满足数量关系为.(2)如图3, EQ, FQ分别平分∠PEB和∠PFD, 且点P在EF左侧.①若∠EPF=60°, 则∠EQF=.②猜想∠EPF与∠EQF的数量关系, 并说明理由;③如图4, 若∠BEQ与∠DFQ的角平分线交于点Q1, ∠BEQ1与∠DFQ1的角平分线交于点Q2, ∠BEQ2, 与∠DFQ2的角平分线交于点Q3;此次类推, 则∠EPF与∠EQ2021F满足怎样的数量关系?(直接写出结果)8. 已知直线、, 直线与直线、分别交于点C和点D, 在直线上有动点P(点P与点C.D 不重合), 点A在直线上, 点B在直线上.(1)如图①, 如果点P在C.D之间运动时, 且满足∠1+∠3=∠2, 请写出与之间的位置关系并说明理由;(2)如图②, 如果, 点P在直线的上方运动时, 请写出∠1, ∠2与∠3之间的数量关系并说明理由;(3)如图③, 如果, 点P在直线的下方运动时, 请直接写出∠PAC、∠PBD、∠APB之间的关系(不需说明理由).9. 如图, , 平分, 设为, 点E是射线上的一个动点.(1)若时, 且, 求的度数;(2)若点E运动到上方, 且满足, , 求的值;(3)若, 求的度数(用含n和的代数式表示).10. 如图所示, 已知, 点P是射线AM上一动点(与点A不重合), BC.BD分别平分和, 分别交射线AM于点C.D, 且(1)求的度数.(2)当点P运动时, 与之间的数量关系是否随之发生变化?若不变化, 请写出它们之间的关系, 并说明理由;若变化, 请写出变化规律.(3)当点P运动到使时, 求的度数.11. 已知点D在∠ABC内, E为射线BC上一点, 连接DE, CD. (1)如图1, 点E在线段BC上, 连接AE, ∠AED=∠A+∠D.①求证AB①CD;②过点A作AM∥ED交直线BC于点M, 请猜想∠BAM与∠CDE的数量关系, 并加以证明;(2)如图2, 点E在BC的延长线上, ∠AED=∠A﹣∠D.若M平面内一动点, MA∥ED, 请直接写出∠MAB与∠CDE的数量关系.12. 如图1, 在平面直角坐标系中, 点A, B的坐标分别为(1, 0), (4, 0), 现同时将点A, B分别向上平移3个单位长度, 再向左平移1个单位长度, 分别得到A, B的对应点C, D, 连接AC, BD, CD.图1图2(1)求点C, D的坐标.(2)P是x轴上(除去B点)的动点.①连接PC, BC, 使S△PBC=2S△ABC, 求符合条件的P点坐标.②如图2, Q是线段BD上一定点, 连接PQ, 请直接写出∠BPQ+∠PQB与∠CDB的数量关系.13. 如图, 在长方形ABCD中, AB=8cm, BC=6cm, 点E是CD边上的一点, 且DE=2cm, 动点P从A点出发, 以2cm/s的速度沿A→B→C→E运动, 最终到达点E. 设点P运动的时间为t秒.(1)请以A点为原点, AB所在直线为x轴, 1cm为单位长度, 建立一个平面直角坐标系, 并用t表示出点P在不同线段上的坐标.(2)在(1)相同条件得到的结论下, 是否存在P点使△APE的面积等于20cm2时,若存在, 请求出P点坐标;若不存在, 请说明理由.14. 如图, 直线PQ∥MN, 点C是PQ、MN之间(不在直线PQ, MN上)的一个动点.(1)若∠1与∠2都是锐角, 如图甲, 请直接写出∠C与∠1, ∠2之间的数量关系;(2)若把一块三角尺(∠A=30°, ∠C=90°)按如图乙方式放置, 点D, E, F是三角尺的边与平行线的交点, 若∠AEN=∠A, 求∠BDF的度数;(3)将图乙中的三角尺进行适当转动, 如图丙, 直角顶点C始终在两条平行线之间, 点G在线段CD上, 连接EG, 且有∠CEG=∠CEM, 求值.15. 如图,在直角坐标系中,点A. C分别在x轴、y轴上,CB∥OA, OA=8,若点B的坐标为.(1)直接写出点A, C的坐标;(2)动点P从原点O出发沿x轴以每秒2个单位的速度向右运动, 当直线PC把四边形OABC分成面积相等的两部分时停止运动, 求P点运动时间;(3)在(2)的条件下, 点P停止运动时, 在y轴上是否存在一点Q, 连接PQ, 使三角形CPQ的面积与四边形OABC的面积相等?若存在, 求点Q的坐标;若不存在, 请说明理由.16. 如图, 已知点, 且, 满足.过点分别作轴、轴, 垂足分别是点、.(1)求出点B的坐标;(2)点是边上的一个动点(不与点重合), 的角平分线交射线于点, 在点运动过程中, 的值是否变化?若不变, 求出其值;若变化, 说明理由.(3)在四边形的边上是否存在点, 使得将四边形分成面积比为1:4的两部分?若存在, 请直接写出点的坐标;若不存在, 说明理由.17. 如图, 在平面直角坐标系中, 点A, B的坐标分别为A(0, a), B(b, a), 且a、b满足(a﹣2)2+|b﹣4|=0, 现同时将点A, B分别向下平移2个单位, 再向左平移1个单位, 分别得到点A, B的对应点C, D, 连接AC, BD, AB.(1)求点C, D的坐标及四边形ABDC的面积S四边形ABCD;(2)在y轴上是否存在一点M, 连接MC, MD, 使S△MCD=S四边形ABDC?若存在这样一点, 求出点M的坐标, 若不存在, 试说明理由;(3)点P是直线BD上的一个动点, 连接PA, PO, 当点P在BD上移动时(不与B, D 重合), 直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.18. 如图1, 在平面直角坐标系中, A(a, 0)是x轴正半轴上一点, C是第四象限内一点, CB⊥y轴交y轴负半轴于B(0, b), 且|a﹣3|+(b+4)2=0, S四边形AOBC=16.(1)求点C的坐标.(2)如图2, 设D为线段OB上一动点, 当AD⊥AC时, ∠ODA的角平分线与∠CAE 的角平分线的反向延长线交于点P, 求∠APD的度数;(点E在x轴的正半轴). (3)如图3, 当点D在线段OB上运动时, 作DM⊥AD交BC于M点, ∠BMD、∠DAO的平分线交于N点, 则点D在运动过程中, ∠N的大小是否会发生变化?若不变化, 求出其值;若变化, 请说明理由.19. 如图1, 在平面直角坐标系中, 点A为x轴负半轴上一点, 点B为x轴正半轴上一点, C(0, a), D(b, a), 其中a, b满足关系式: |a+3|+(b-a+1)2=0.(1)a=___, b=___, △BCD的面积为______;(2)如图2, 若AC⊥BC, 点P线段OC上一点, 连接BP, 延长BP交AC于点Q, 当∠CPQ=∠CQP时, 求证:BP平分∠ABC;(3)如图3, 若AC⊥BC, 点E是点A与点B之间一动点, 连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时, 的值是否变化?若不变, 求出其值;若变化, 请说明理由.20. 已知: 在平面直角坐标系中, 四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°, AB∥CD, AB=CD=8, AD=BC=6, D点与原点重合, 坐标为(0, 0).(1)直接写出点B的坐标__________.(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动, 若P, Q两点同时出发, 设运动时间为t秒, 当t为何值时, PQ∥y轴?(3)在Q的运动过程中, 当Q运动到什么位置时, 使△ADQ的面积为9?求出此时Q 点的坐标?。
部编数学七年级下册期末考试压轴题模拟训练(一)(解析版)(人教版)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!期末考试压轴题模拟训练(一)解得:6b =,1266-=,故:()6,6B 在第一象限,AB y ^Q 轴,6a \=,12a b \+=,故选:D .【点睛】本题考查了坐标系内点的特点;解题的关键是结合题意得到(),12B b b -在一、三象限或二、四象限的平分线上,从而求解.三、填空题6.若方程组111222a x b y c a x b y c +=ìí+=î的解是42x y =ìí=-î,则方程组111122223232a x b y a c a x b y a c +=-ìí+=-î的解是______.【答案】11x y =-ìí=î【分析】由方程组111222a x b y c a x b y c +=ìí+=î的解是42x y =ìí=-î得1112224242a b c a b c -=ìí-=î,两式相加得()()12121242a a b b c c +-+=+,对111122223232a x b y a c a x b y a c +=-ìí+=-î两式相加变形得()()()()1212121232a a x b b y a a c c +++=+-+即()()()()121212123232a a x b b y a a b b +++=-+++,对方程进行比较即可求解.【详解】解:111222a xb yc a x b y c +=ìí+=îQ 的解是42x y =ìí=-î,1112224242a b c a b c -=ì\í-=î①②,由+①②得:()()12121242a a b b c c +-+=+,111122223232a x b y a c a x b y a c +=-ìí+=-î③④,③+④得:()()()()1212121232a a x b b y a a c c +++=+-+,则()()()()()12121212123242a a x b b y a a a a b b éù+++=+-+--ëû,即()()()()121212123232a a x b b y a a b b +++=-+++,1x \=-,1y =,【答案】①②③④【分析】根据平行线的性质,角平分线和垂线的定义逐个分析计算即可.【详解】∵CGE a Ð=,AB CD ∥,∴CGE GEB a Ð=Ð=,∴180AEG a =°-Ð,【答案】30度/30°【分析】根据AB CD ∥(12PEF EFP EFD Ð+Ð=Ð进而可得EHG QFP Ð=ÐEPK EPF FPH Ð=Ð+Ð1452QPK EPK Ð=Ð=°+解.【答案】()506506,【分析】观察图形,由第四象限点的坐标的变化可得出【详解】解:观察图形可知:点1A 的坐标为()1,1--,点2A 的坐标为()11-,,点3A 的坐标为()11,,点4A 的坐标为()11-,,点5A 的坐标为()22--,,点6A 的坐标为()22-,,……\点41n A +的坐标为()11n n ----,(n 为非负整数),点42n A +的坐标为()11n n --+,(n 为非负整数),点43n A +的坐标为()11n n ++,(n 为非负整数),点44n A +的坐标为()11n n +--,(n 为非负整数),202345053=´+Q ,\点2023A 的坐标为()506506,,故答案为:()506506,.【点睛】本题主要考察了规律型:点的坐标,由第四象限点的坐标的变化可得出“点43n A +的坐标为()11n n ++,(n 为非负整数)”是解题的关键.(1)如图1,求证:AB CD P ;(2)如图2,点M N 、分别在射线、GE HF 上,点P Q 、分别在射线、GA MP NQ ,,且90MPG NQH Ð+Ð=°,分别延长MP NQ ,交于点K ,求证:(3)如图3,在(2)的条件下,连接,KH KH 平分MKN Ð,且HE 平分177DHG MPG Ð=Ð,直接写出MPG Ð的度数.(2)见解析(3)50KMN Ð=°【分析】(1)利用CHG DHF Ð=Ð,再利用等量代换,即可解决;(2)过K 作KR AB ∥,因为AB CD P ,所以RK AB CD ∥∥,则MPG MKR Ð=Ð,NQH RKN Ð=Ð代入即可解决.(3)过M 作MT AB ∥,过K 作KR AB ∥,可以得到MT AB CD KR ∥∥∥,设17DHG x Ð=,7MPG x Ð=,利用平行线的性质,用含x 的代数式表示出各个角,利用方程思想解决问题.【详解】(1)证明:CHG DHF Ð=ÐQ ,180AGH DHF Ð+Ð=°,180AGH CHG \Ð+Ð=°,AB CD \∥;(2)证明:过点K 作KR AB ∥,如图,∥Q AB CD ,KR AB ∥,RK AB CD \∥∥,MPG MKR \Ð=Ð,NQH RKN Ð=Ð,90MPG NQH Ð+Ð=°Q ,90MKR NKR \Ð+Ð=°,即90MKN Ð=°,MK NK \^;(3)50KMN Ð=°.理由如下:过M 作MT AB ∥,过K 作KR AB ∥,如图,∥Q AB CD ,KR AB ∥,MT AB ∥,MT AB CD KR \∥∥∥,(1)求三角形ABC 的面积.(2)若过B 作BD AC ∥交y 轴于D ,且AE ,DE 分别平分CAB Ð,ODB Ð,如图2,求AED Ð的度数.(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等,若存在,求出P 点坐标:若不存在,请说明理由.【答案】(1)4;(2)45°;(3)解:假设存在点P使得三角形当在负半轴时,连接OC ,∵PAC PAO PCO ACO S S S S =++=V V V V ∴422m =-+,解得:1m =-,∴2(0,1)P -,综上所述P 点坐标为:1(0,3)P 【点睛】本题考查平面直角坐标系中点到直线的距离问题、解题的关键是作辅助线及根据题意假设存在列式求解.12.已知:AB CD ∥,E 、G(1)如图1,求证:EF GH ∥;(2)如图2,过F 点作FM GH ^交GH 延长线于点M ,作BEF Ð、DFM Ð的角平分线交于点N ,EN 交GH 于点P ,求证:45N Ð=°;(3)如图3,在(2)的条件下,作AGH Ð的角平分线交CD 于点Q ,若34FEN HFM Ð=Ð,直接写出GQH MPNÐÐ的值.(1)(2)解:如图2,过点N 作∵AB CD P ,∴AB CD NK ∥∥,4KNE \Ð=Ð,67Ð=Ð,设4x Ð=,7y Ð=,(3)解:34FEN HFM Ð=ÐQ ,即83x y \=,8453x y y y \-=-=°27y \=°,72x =°,又EN Q 和GQ 是角平分线,(1)列出方程(组),求出图1中a与b的值.(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.①两种裁法共产生A型板材张,B型板材张;②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:竖式无盖(个)横式无盖(个)礼品盒板材x yA型(张)4x3y①如图1,连接BD 交x 轴于点E ,求三角形CED 的面积;②如图2,点M 从原点O 出发以2个单位长度/秒的速度沿x 轴正方向运动,过点的平行线交y 轴于点N ,点P 在直线CD 上,设点M 运动时间为t 秒,当三角形积等于三角形PMN 面积的两倍时,直接写出t 的值.【答案】(1)()4,0A -,()0,2B ,()0,4C -(2)①6;②2t =或10t =【分析】(2)①根据平移的性质得出()4,2D -,AC BD ∥,得出EBC ABE S S =V V∴EBC ABES S =V V 设(),0E x ,则4AE x =+,∵2BO =∴1122AE OB BC OE ´=´即()1142622x x ´+´=´´当()10,0N -时,则5ON OB =,同理可得OM 则()20,0M ,∴20210t =¸=综上所述,2t =或10t =,【点睛】本题考查了平移,算术平方根的非负性,坐标与图形,平行线间的距离相等,等面积法,数形结合,分类讨论是解题的关键.15.某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过105400元购进40台电脑,其中A 型电脑每台进价2500元,B 型电脑每台进价2800元,A 型每台售价3000元,B 型每台售价3200元,预计销售额不低于123200元.设A 型电脑购进x 台、商场的总利润为y (元).(1)请你设计出所有的进货方案;(2)在上述的进货方案中,哪种方案的利润最大,最大利润是多少元?(3)商场准备拿出(2)中的最大利润的一部分再次购进A 型和B 型电脑至少各两台,另一部分为地震灾区购买单价为500元的帐篷若干顶.在钱用尽三样都购买的前提下请直接写出购买A 型电脑、B 型电脑和帐篷的方案.【答案】(1)有3种购买方案,方案1:购A 型电脑22台,B 型电脑18台;方案2:购A 型电脑23台,B 型电脑17台;方案3:购A 型电脑24台,B 型电脑16台(2)购A 型电脑24台,B 型电脑16台利润最大,为18400元(3)有2种购买方案,方案1:购A 型电脑2台,B 型电脑3台,帐篷10顶;方案2:购A 型电脑3台,B 型电脑3台,帐篷5顶【分析】(1)设A 型电脑购进x 台,则B 型电脑购进()40x -台,由题意列依云一次不等式组()()25002800401054003000320040123200x x x x ì+-£ïí+-³ïî,计算求解,然后作答即可; (2)对(1)中的各方案分别求解利润,然后进行比较作答即可;(3)设再次购买A 型电脑a 台,B 型电脑b 台,帐篷c 顶,2a ³,2b ³,1c ³,且a 、b 、c 为整数,根据条件建立方程运用讨论法求出其解即可.【详解】(1)解:设A 型电脑购进x 台,则B 型电脑购进40x -()台.根据题意得:()()25002800401054003000320040123200x x x x ì+-£ïí+-³ïî,解得:2224x ££.∵x 为整数,∴x 的值为22,23,24 ,∴有3种购买方案:方案1:购A 型电脑22台,B 型电脑18台;方案2:购A 型电脑23台,B 型电脑17台;方案3:购A 型电脑24台,B 型电脑16台;【推广应用】(1)如图③,AB CD P ,点M 在直线AB 、CD 之间,线交于点N ,96M Ð=°,则N Ð=______°;(2)如图④,AB CD P ,点M 与直线CD 分别在的平分线交于点N ,25N Ð=°,则M Ð=______°;(3)如图⑤,AB CD P ,ABG Ð的平分线与CDE Ð64F Ð=°,64E Ð=°,则M Ð=______°.【答案】【问题原型】见解析;【问题迁移】M B D Ð+Ð=Ð;【推广应用】((2)50;(3)39【分析】【问题原型】作∥MN AB ,根据平行线的性质解答即可;【问题迁移】根据平行线的性质解答即可;【推广应用】(1)由【问题原型】的结论可得:96,M ABM CDM N ABN CDN Ð=Ð+Ð=°Ð=Ð+,然后结合角平分线的定义和等量代换即可解答;【问题迁移】M B D Ð+Ð=Ð,理由如下:如图,∵AB CD P ,∴MGA D Ð=Ð,∴D MGA M B Ð=Ð=Ð+Ð;【推广应用】(1)由【问题原型】的结论可得:∵ABM Ð的平分线与CDM Ð∴1,2ABN ABM CDN Ð=ÐÐ∴(1ABN CDN ABM Ð+Ð=Ð【点睛】本题考查了平行线的判定和性质、是解题的关键.。
人教版数学七下期末压轴题专项训练

初一下学期期末考试综合题训练1.善于思考的小军在解方程组时, 采用了一种“整体代换”的解法:将方程②变形: 即把方程①代入③ , 得把代入① , 得∴原方程组的解为请你解决以下问题:模仿小军的“整体代换法”解方程组(2)已知满足方程组求与的值.2.阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y 的取值范围”有如下解法:解∵ x﹣y=2,∴ x=y+2又∵x>1,∵y+2>1.∴y>﹣1.又∵ y<0,∴﹣1<y<0.⋯① 同理得:1<x< 2.⋯②由① +②得﹣1+1<y+x<0+2∴x+y 的取值范围是0<x+y<2 请按照上述方法,完成下列问题:(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围.(2)已知y>1,x<﹣1,若x﹣y=a成立,求x+y 的取值范围(结果用含a的式子表示).3. 已知,,为三个非负实数,满足(1)用含的代数式分别表示,;(2)求的取值范围;(3)设,求的取值范围.4. 定义:对任意一个两位数,如果满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与的商记为.例如:,对调个位数字与十位数字得到新两位数,新两位数与原两位数的和为,和与的商为,所以.根据以上定义,回答下列问题:(1)填空:①下列两位数:,,中,“迥异数”为.② 计算:,.(2)如果一个“迥异数” 的十位数字是,个位数字是,且,请求出“迥异数”.(3)如果一个“迥异数” 的十位数字是,个位数字是,另一个“迥异数” 的十位数字是,个位数字是,且满足,请直接写出满足条件的的值.5. 如果一元一次方程的解也是一元一次不等式组的解, 则称该一元一次方程为 该不等式组的关联方程.因为 , 所 以, 称 方程 为不 等 式组的关联方程.号)的关联方程,求 的取值范围.例如:方程的解为 ,不等式组的解集为 1)在方程①,②,③ 中,不等式组的关联方程是 ;(填序2)若不等式组的一个关联方程的根是整数,则这 个关联方程可以是;(写出一个即可)3)若方程,都是关于 的不等式6. 如图,在平面直角坐标系中,, , 三点的坐标分别为 , , .1);2)若点是第二象限内一点,且的面积不大于的面积,求的取值范围;3)若将线段向左平移个单位长度,点为轴上一点,为第一象限内一动点,连,,,若的面积等于由,,,四条线段围成图形的面积,则点的坐标为(用含的式子表示).7. 对于数,符合表示不大于的最大整数.例如:,,.请解答下列问题:(1),;(2)如果,那么的取值范围是;3)如果,求满足条件的所有负整数的值.8. 对任意一个三位数,如果满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数” 的各个数位上的数字之和记为.例如时,.(1)对于“相异数” ,若,请你写出一个的值;(2)若,都是“相异数”,其中,(,,,都是正整数),规定:,当时,求的最小值.9..在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c 满足关系式a 2+(b-3)2=0,(c-4)2≤0(1)求a、b、c 的值;1(2)如果在第二象限内有一点P(m,2),请用含m 的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP 的面积与△ABC的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.10..如图,已知长方形ABCO 中,边AB=8 ,BC=4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一下学期期末考试综合题训练
1.善于思考的小军在解方程组时,采用了一种“整体代换”的解法:
将方程②变形:即
把方程①代入③,得
把代入①,得∴原方程组的解为
请你解决以下问题:
模仿小军的“整体代换法”解方程组
(2)已知满足方程组求与的值.
2.阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解∵x﹣y=2,∴x=y+2
又∵x>1,∵y+2>1.∴y>﹣1.
又∵y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围.
(2)已知y>1,x<﹣1,若x﹣y=a成立,求x+y的取值范围(结果用含a的式子表示).
3. 已知,,为三个非负实数,满足
(1)用含的代数式分别表示,;
(2)求的取值范围;
(3)设,求的取值范围.
4. 定义:对任意一个两位数,如果满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与的商记为.
例如:,对调个位数字与十位数字得到新两位数,新两位数与原两位数的和为,和与的商为,所以.
根据以上定义,回答下列问题:
(1)填空:①下列两位数:,,中,“迥异数”为.
②计算:,
.
(2)如果一个“迥异数”的十位数字是,个位数字是,且,请求出“迥异数”.
(3)如果一个“迥异数”的十位数字是,个位数字是,另一个“迥异数”的十位数字是,个位数字是,且满足
,请直接写出满足条件的的值.
5. 如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程的解为,不等式组的解集为,因为,所以,称方程为不等式组的关联方程.
(1)在方程①,②,③中,不等式组的关联方程是;(填序号)
(2)若不等式组的一个关联方程的根是整数,则这
个关联方程可以是;(写出一个即可)(3)若方程,都是关于的不等式
组的关联方程,求的取值范围.
6. 如图,在平面直角坐标系中,,,三点的坐标分别为,,.
(1);
(2)若点是第二象限内一点,且的面积不大于的面积,求的取值范围;
(3)若将线段向左平移个单位长度,点为轴上一点,为第一象限内一动点,连,,,若的面积等于由,,,四条线段围成图形的面积,则点的坐标为(用含的式子表示).
7. 对于数,符合表示不大于的最大整数.例如:,,
.请解答下列问题:
(1),;
(2)如果,那么的取值范围是;
(3)如果,求满足条件的所有负整数的值.
8. 对任意一个三位数,如果满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”的各个数位上的数字之和记为.例如
时,.
(1)对于“相异数”,若,请你写出一个的值;
(2)若,都是“相异数”,其中,(,,,都是正整数),规定:,当时,求的最小值.
9..在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,
其中a、b、c满足关系式2 a+(b-3)2=0,(c-4)2≤0
(1)求a、b、c的值;
1),请用含m的式子表示四边形ABOP (2)如果在第二象限内有一点P(m,
2
的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
10..如图,已知长方形ABCO中,边AB=8,BC=4。
以O为原点,OAOC所在的直线为y 轴和x轴建立直角坐标系。
(1)点A的坐标为(0,4),写出B、C两点的坐标;
(2)若点P从C点出发,以2单位/秒的速度向CO方向移动(不超过点O),点Q从原点O出发,以1单位/秒的速度向OA方向移动(不超过点Array A),设P、Q两点同时出发,在他们移动过程中,四边
形OPBQ的面积是否发生变化?若不变,求其值;若变
化,求变化的范围。
