第4章_振动与波动(1)
大学物理——第4章-振动和波

合成初相 与计时起始时刻有关.
v A 2
ω
v A
2
O
x2
1
v A 1
x1
xx
分振动初相差2 1与计时起始时刻无关,但它对合成振幅 是相长还是相消合成起决定作用.
20
讨 论
2 A = A2 + A2 + 2A A2 cos(2 1) 1 1
F = kx
3
l0
k
m
A
F = kx = ma
k 令ω = m
2
A x = Acos(ωt +)
o
x
积分常数,根据初始条件确定
a = ω2 x
dx = ω2 x dt 2
2
dx υ = = Aω sin( ωt +) dt
dx 2 a = 2 = Aω cos(ωt +) dt
4
2
x = Acos(ωt +)
15
π
例 4-3 有两个完全相同的弹簧振子 A 和 B,并排的放在光滑 的水平面上,测得它们的周期都是 2s ,现将两个物体从平衡 位置向右拉开 5cm,然后先释放 A 振子,经过 0.5s 后,再释 放 B 振子,如图所示,如以 B 释放的瞬时作为时间的起点, (1)分别写出两个物体的振动方程; (2)它们的相位差是多少?分别画出它们的 x—t 图.
5cm
O
x
16
解: (1)振动方程←初始条件
x0 = 0.05m, υ0 = 0 , T = 2s
2π ω= = π rad/s T
2 υ0 2 A = x0 + 2 = 0.05m ω υ0 对B振子: tan B = = 0 B = 0 x0ω
第4章_振动与波动 (1)
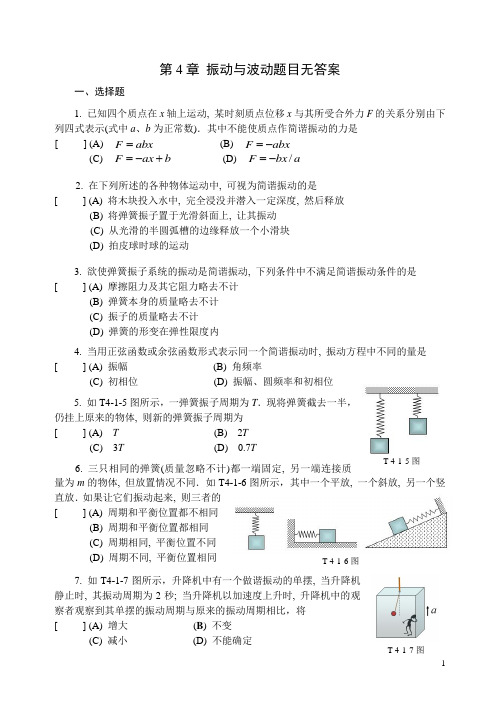
第4章 振动与波动题目无答案一、选择题1. 已知四个质点在x 轴上运动, 某时刻质点位移x 与其所受合外力F 的关系分别由下列四式表示(式中a 、b 为正常数).其中不能使质点作简谐振动的力是[ ] (A) abx F = (B) abx F -=(C) b ax F +-= (D) a bx F /-=2. 在下列所述的各种物体运动中, 可视为简谐振动的是[ ] (A) 将木块投入水中, 完全浸没并潜入一定深度, 然后释放(B) 将弹簧振子置于光滑斜面上, 让其振动(C) 从光滑的半圆弧槽的边缘释放一个小滑块(D) 拍皮球时球的运动3. 欲使弹簧振子系统的振动是简谐振动, 下列条件中不满足简谐振动条件的是[ ] (A) 摩擦阻力及其它阻力略去不计(B) 弹簧本身的质量略去不计(C) 振子的质量略去不计(D) 弹簧的形变在弹性限度内4. 当用正弦函数或余弦函数形式表示同一个简谐振动时, 振动方程中不同的量是[ ] (A) 振幅 (B) 角频率(C) 初相位 (D) 振幅、圆频率和初相位5. 如T4-1-5图所示,一弹簧振子周期为T .现将弹簧截去一半,仍挂上原来的物体, 则新的弹簧振子周期为[ ] (A) T (B) 2T(C) 3T (D) 0.7T6. 三只相同的弹簧(质量忽略不计)都一端固定, 另一端连接质量为m 的物体, 但放置情况不同.如T4-1-6图所示,其中一个平放, 一个斜放, 另一个竖直放.如果让它们振动起来, 则三者的[ ] (A) 周期和平衡位置都不相同(B) 周期和平衡位置都相同(C) 周期相同, 平衡位置不同 (D) 周期不同, 平衡位置相同7. 如T4-1-7图所示,升降机中有一个做谐振动的单摆, 当升降机静止时, 其振动周期为2秒; 当升降机以加速度上升时, 升降机中的观察者观察到其单摆的振动周期与原来的振动周期相比,将[ ] (A) 增大 (B ) 不变(C) 减小 (D) 不能确定T 4-1-6图T 4-1-7图 T 4-1-5图8. 在简谐振动的运动方程中,振动相位)(ϕω+t 的物理意义是[ ] (A) 表征了简谐振子t 时刻所在的位置(B) 表征了简谐振子t 时刻的振动状态(C) 给出了简谐振子t 时刻加速度的方向(D) 给出了简谐振子t 时刻所受回复力的方向9. 如T4-1-9图所示,把单摆从平衡位置拉开, 使摆线与竖直方向成 θ 角, 然后放手任其作微小的摆动.若以放手时刻为开始观察的时刻,用余弦函数表示这一振动, 则其振动的初位相为 [ ] (A) θ (B) 2π 或π23 (C) 0 (D) π 10. 两质点在同一方向上作同振幅、同频率的简谐振动.在振动过程中, 每当它们经过振幅一半的地方时, 其运动方向都相反.则这两个振动的位相差为[ ] (A) π (B) π32 (C) π34 (D) π54 11. 在简谐振动的速度和加速度表达式中,都有一个负号, 这是意味着[ ] (A) 速度和加速度总是负值(B) 速度的相位比位移的相位超前π21, 加速度的位相与位移的相位相差π (C) 速度和加速度的方向总是相同(D) 速度和加速度的方向总是相反12. 一质点作简谐振动, 振动方程为)cos(ϕω+=t A x . 则在2T t =(T 为振动周期) 时, 质点的速度为[ ] (A) ϕωsin A - (B) ϕωsin A(C) ϕωcos A - (D) ϕωcos A13. 一物体作简谐振动, 其振动方程为)4πcos(+=t A x ω.则在2T t = (T 为周期)时, 质点的加速度为(A) 222ωA - (B) 222ωA (C) 223ωA - (D) 223ωA 14. 一质点以周期T 作简谐振动, 则质点由平衡位置正向运动到最大位移一半处的最短时间为[ ] (A) 6T (B) 8T (C) 12T (D) T 127 15. 某物体按余弦函数规律作简谐振动, 它的初相位为2π3, 则该物体振动的初始状态为[ ] (A) x 0 = 0 , v 0 > 0 (B) x 0 = 0 , v 0<0(C) x 0 = 0 , v 0 = 0 (D) x 0 = -A , v 0 = 0T 4-1-9图16. 一作简谐运动质点的振动方程为π)21π2cos(5+=t x , 它从计时开始, 在运动一个周期后[ ] (A) 相位为零 (B) 速度为零(C) 加速度为零 (D) 振动能量为零17. 沿x 轴振动的质点的振动方程为)1π3cos(1032-⨯=-t x (SI 制), 则[ ] (A) 初相位为1° (B) 振动周期为T =3 s(C) 振幅A = 3 m (D) 振动频率 23=νHz 18. 有一谐振子沿x 轴运动, 平衡位置在x = 0处, 周期为T , 振幅为A ,t = 0时刻振子过2A x =处向x 轴正方向运动, 则其运动方程可表示为 [ ] (A) )21cos(t A x ω= (B) )cos(2t A x ω= (C) )3π2sin(--=T t A x ω (D) )3π2cos(-=T t A x ω 19. 一质点作简谐振动, 其速度随时间变化的规律为t A v ωωcos -=, 则质点的振动方程为[ ] (A) t A x ωsin = (B) t A x ωcos =(C) π)sin(+=t A x ω (D) π)cos(+=t A x ω20. 当一质点作简谐振动时, 它的动能和势能随时间作周期变化.如果f 是质点振动的频率, 则其动能变化的频率为[ ] (A) 4f (B) 2f (C) f (D) f /221. 已知一简谐振动系统的振幅为A , 该简谐振动动能为其最大值之半的位置是[ ] (A) 12A (B) 22A (C) 32A (D) A 22. 一弹簧振子作简谐振动, 其振动方程为: π)21cos(+=t A x ω.则该物体在t = 0时刻的动能与t = T /8 (T 为周期)时刻的动能之比为[ ] (A) 1:4 (B) 2:1 (C) 1:1 (D) 1:223. 一作简谐振动的质点某时刻位移为x , 系统的振动势能恰为振动动能的n 倍, 则该振动的振幅为[ ] (A) A n x =+⎛⎝ ⎫⎭⎪11 (B) A n x =-⎛⎝ ⎫⎭⎪11 (C) A n x =-11 (D) A n x =+1124. 一弹簧振子作简谐振动, 当其偏离平衡位置的位移大小为振幅的1/4时, 其动能为振动总能量的[ ] (A) 167 (B) 1615 (C) 169 (D) 1613 25. 一长为l 、质量为m 的单摆, 与一劲度系数为k 、质量为m 的弹簧振子周期相等.则k 、l 、m 、g 之间的关系为[ ] (A) lmg k = (B) g ml k = (C) gl m k = (D) 不能确定 26. 一轻质弹簧, 上端固定, 下端挂有质量为m 的重物, 其自由端振动的周期为T . 已知振子离开平衡位置为x 时其振动速度为v , 加速度为a , 且其动能与势能相等.试判断下列计算该振子劲度系数的表达式中哪个是错误的?[ ] (A) a mg k = (B) 22xm k v = (C) x ma k = (D) 22π4T m k = 27. 简谐振动的振幅由哪些因素决定?[ ] (A) 谐振子所受的合外力 (B) 谐振子的初始加速度(C) 谐振子的能量和力常数 (D) 谐振子的放置位置28. 设卫星绕地球作匀速圆周运动.若卫星中有一单摆, 下述哪个说法是对的?[ ] (A) 它仍作简谐振动, 周期比在地面时大(B) 它仍作简谐振动, 周期比在地面时小(C) 它不会再作简谐振动(D) 要视卫星运动速度决定其周期的大小29. 已知一单摆装置, 摆球质量为m ,摆的周期为T .对它的摆动过程, 下述说法中错误的是[ ] (A) 按谐振动规律, 摆线中的最大张力只与振幅有关, 而与m 无关(B) T 与m 无关(C) 按谐振动规律, T 与振幅无关(D) 摆的机械能与m 和振幅都有关30. 弹簧振子在光滑水平面上作谐振动时, 弹性力在半个周期内所作的功为[ ] (A) 2kA (B)221kA (C) 241kA (D) 0 T 4-1-26图31. 如果两个同方向同频率简谐振动的振动方程分别为π)433cos(73.11+=t x cm 和 π)413cos(2+=t x cm, 则它们的合振动方程为 [ ] (A) π)433cos(73.0+=t x cm (B) π)413cos(73.0+=t x cm (C) π)1273cos(2+=t x cm (D) π)1253cos(2+=t x cm32. 拍现象是由怎样的两个简谐振动合成的?[ ] (A) 同方向、同频率的两个简谐振动(B) 同方向、频率很大但相差甚小的两个简谐振动(C) 振动方向互相垂直、同频率的两个简谐振动(D) 振动方向互相垂直、频率成整数倍的两个简谐振动合成33. 两个同方向、同频率、等振幅的谐振动合成, 如果其合成振动的振幅仍不变, 则此二分振动的相位差为[ ] (A) 2π (B) 3π2 (C) 4π (D) π 34. 二同频率相互垂直的振动方程分别为)cos(11αω+=t A x 和)cos(22αω+=t A y .其合振动的轨迹[ ] (A) 不会是一条直线(B) 不会为一个圆(C) 不能是一封闭曲线(D) 曲线形状要由相位差和两振动振幅而定35. 下面的结论哪一个可以成立?[ ] (A) 一个简谐振动不可以看成是两个同频率相互垂直谐振动的合振动(B) 一个简谐振动只可以看成是两个同频率同方向谐振动的合振动(C) 一个简谐振动可以是两个同频率相互垂直谐振动的合振动(D) 一个简谐振动只可以是两个以上同频率谐振动的合振动36. 一质点同时参与两个相互垂直的简谐振动, 如果两振动的振动方程分别为π)π2cos(+=t x 和)π2sin(t y =, 则该质点的运动轨迹是[ ] (A) 直线 (B) 椭圆 (C) 抛物线 (D) 圆37. 将一个弹簧振子分别拉离平衡位置1厘米和2厘米后, 由静止释放(弹簧形变在弹性范围内), 则它们作谐振动的[ ] (A) 周期相同 (B) 振幅相同(C) 最大速度相同 (D) 最大加速度相同38. 谐振子作简谐振动时, 速度和加速度的方向[ ] (A) 始终相同(B) 始终相反(C) 在某两个1/4周期内相同, 另外两个1/4周期内相反(D) 在某两个1/2周期内相同, 另外两个1/2周期内相反39. 下列说法正确的是[ ] (A) 谐振子从平衡位置运动到最远点所需的时间为T 81(B) 谐振子从平衡位置运动到最远点的一半距离所需时间为8T (C) 谐振子从平衡位置出发经历T 121,运动的位移是A 31 (D) 谐振子从平衡位置运动到最远点所需的时间为T 4140. 关于振动和波, 下面几句叙述中正确的是[ ] (A) 有机械振动就一定有机械波(B) 机械波的频率与波源的振动频率相同(C) 机械波的波速与波源的振动速度相同(D) 机械波的波速与波源的振动速度总是不相等的41. 关于波,下面叙述中正确的是[ ] (A) 波动方程中的坐标原点一定要放在波源位置(B) 机械振动一定能产生机械波(C) 质点振动的周期与波的周期数值相等(D) 振动的速度与波的传播速度大小相等42. 按照定义,振动状态在一个周期内传播的距离就是波长.下列计算波长的方法中错误的是[ ] (A) 用波速除以波的频率(B) 用振动状态传播过的距离除以这段距离内的波数(C) 测量相邻两个波峰的距离(D) 测量波线上相邻两个静止质点的距离43. 一正弦波在海面上沿一定方向传播, 波长为λ, 振幅为A , 波的传播速率为u . 假设海面上漂浮的一块木块随水波上下运动, 则木块上下运动的周期是[ ] (A) u π2λ (B) uλ (C) λπ2u (D) λu 1 44. 当x 为某一定值时, 波动方程)π(2cos λx T t A x -=所反映的物理意义是 [ ] (A) 表示出某时刻的波形 (B) 说明能量的传播(C) 表示出x 处质点的振动规律 (D) 表示出各质点振动状态的分布45. 下列方程和文字所描述的运动中,哪一种运动是简谐振动?[ ] (A) x A t =1cos ω(B) x A t A t =+123cos cos ωω(C) d d 2222xt x =-ω(D) 两个同方向、频率相近的谐振动的合成46. 下列方程和文字所描述的运动中,哪一种运动是简谐波?[ ] (A) t xA y ωλcos π2cos =(B) )sin(2x cx bt A y ++=(C) 波形图始终是正弦或余弦曲线的平面波(D) 波源是谐振动但振幅始终衰减的平面波47. 下列函数f ( x , t )可以用来表示弹性介质的一维波动, 其中a 和b 是正常数.则下列函数中, 表示沿x 轴负方向传播的行波是[ ] (A) )sin(),(bt ax A t x f += (B) )sin(),(bt ax A t x f -=(C) )cos()cos(),(bt ax A t x f = (D) )sin()sin(),(bt ax A t x f =48. 已知一波源位于x = 5m 处, 其振动方程为: )cos(ϕω+=t A y m .当这波源产生的平面简谐波以波速u 沿x 轴正向传播时, 其波动方程为[ ] (A) )(cos u x t A y -=ω (B) ])(cos[ϕω+-=ux t A y (C) ])5(cos[ϕω++-=u x t A y (D) ])5(cos[ϕω+--=u x t A y 49. 一平面简谐波的波动方程为)2π(sin 5.0x t y --=m, 则此波动的频率、波速及各质点的振幅依次为[ ] (A)21、21、05.0- (B) 21、1、05.0- (C) 21、21、0.05 (D)2、2、0.0550. 已知一列机械波的波速为u , 频率为ν, 沿着x 轴负方向传播.在x 轴的正坐标上有两个点x 1和x 2.如果x 1<x 2 , 则x 1和x 2的相位差为[ ] (A) 0 (B) )(π221x x u -ν (C) π (D) )(π212x x u-ν51. 已知一平面余弦波的波动方程为)01.05.2π(cos 2x t y -=, 式中 x 、y 均以厘米计.则在同一波线上, 离x = 5cm 最近、且与 x = 5cm 处质元振动相位相反的点的坐标为[ ] (A) 7.5 cm (B) 55 cm (C) 105 cm (D) 205 cm52. 两端固定的一根弦线, 长为2m, 受外力作用后开始振动.已知此弦产生了一个波腹的波, 若该振动的频率为340 Hz, 则此振动传播的速度是____m ⋅s -1.[ ] (A) 0 (B) 170 (C) 680 (D) 136053. 一波源在XOY 坐标系中(3, 0)处, 其振动方程是)π120cos(t y = cm, 其中 t 以秒计, 波速为50 cm.s -1 .设介质无吸收, 则此波在x <3 cm 的区域内的波动方程为[ ] (A) )50π(120cos x t y +=cm (B) π]2.7)50π(120cos[-+=x t y cm (C) )50π(120cos x t y -=cm (D) π]2.1)50π(120cos[-+=x t y cm54. 若一平面简谐波的波动方程为)cos(cx bt A y -=, 式中A 、b 、c 为正值恒量.则[ ] (A) 波速为c (B) 周期为b 1 (C) 波长为c π2 (4) 角频率为bπ2 55. 一平面简谐横波沿着OX 轴传播.若在OX 轴上的两点相距8λ(其中λ为波长), 则在波的传播过程中, 这两点振动速度的[ ] (A) 方向总是相同 (B) 方向有时相同有时相反(C) 方向总是相反 (D) 大小总是不相等56. 一简谐波沿Ox 轴正方向传播,t =0时刻波形曲线如左下图所示,其周期为2 s .则P 点处质点的振动速度v 与时间t 的关系曲线为:[ ]57. 当波动方程为)01.05.2π(cos 20x t y +=cm 的平面波传到x =100cm 处时, 该处质点的振动速度为[ ] (A) )π5.2sin(50t cm.s -1 (B) )π5.2sin(50t -cm.s -1(C) )π5.2sin(π50t cm.s -1 (D) )π5.2sin(π50t -cm.s -1Aω)D ω)ω-ω-))58. 平面简谐机械波在弹性媒质中传播时, 在传播方向上某媒质元在负的最大位移处, 则它的能量是[ ] (A) 动能为零, 势能最大 (B) 动能为零, 势能为零(C) 动能最大, 势能最大 (D) 动能最大, 势能为零59. 一平面简谐波在弹性媒质中传播, 在媒质元从最大位移处回到平衡位置的过程中[ ] (A) 它的势能转换成动能(B) 它的动能转换成势能(C) 它从相邻的一段媒质元中获得能量, 其能量逐渐增大(D) 它把自己的能量传给相邻的一媒质元, 其能量逐渐减小60. 已知在某一媒质中两列相干的平面简谐波的强度之比是421=I I ,则这两列波的振幅之比21A A 是 [ ] (A) 4 (B) 2 (C) 16 (D) 861. 一点波源发出的波在无吸收媒质中传播, 波前为半球面, 该波强度I 与离波源距离r 之间的关系是[ ] (A) r I 1∝ (B) 31r I ∝ (C) r I 1∝ (D) 21r I ∝ 62. 当机械波在媒质中传播时, 某一媒质元的最大形变发生在(其中A 是振幅)[ ] (A) 媒质质元离开其平衡位置的最大位移处(B) 媒质质元离开平衡位置2/2A 处(C) 媒质元在其平衡位置处(D) 媒质元离开平衡位置2/A 处63. 假定汽笛发出的声音频率由 400 Hz 增加到1200 Hz, 而波幅保持不变, 则1200 Hz 声波对400 Hz 声波的强度比为[ ] (A) 1:3 (B) 3:1 (C) 1:9 (D) 9:164. 为了测定某个音叉C 的频率, 另选取二个频率已知而且和C 音叉频率相近的音叉A 和B, 音叉A 的频率为400 Hz, B的频率为397 Hz, 并进行下列实验: 使A 和C 同时振动每秒听到声音加强二次; 再使B 和C 同时振动, 每秒钟听到声音加强一次, 由此可知音叉C 的振动频率为[ ] (A) 401 Hz (B) 402 Hz (C) 398 Hz (D) 399 Hz65. 人耳能分辨同时传来的不同声音, 这是由于[ ] (A) 波的反射和折射 (B) 波的干涉(C) 波的独立传播特性 (D) 波的强度不同66. 两列波在空间P 点相遇, 若在某一时刻观察到P 点合振动的振幅等于两波的振幅之和, 则这两列波[ ] (A) 一定是相干波 (B) 不一定是相干波(C) 一定不是相干波 (D) 一定是初相位相同的相干波67. 有两列波在空间某点P 相遇, 某时刻观察到P 点的合振幅等于两列波的振幅之和, 由此可以判定这两列波[ ] (A) 是相干波 (B) 相干后能形成驻波(C) 是非相干波 (D) 以上三种情况都有可能68. 已知两相干波源所发出的波的相位差为π, 到达某相遇点P 的波程差为半波长的两倍, 则P 点的合成情况是[ ] (A) 始终加强(B) 始终减弱(C) 时而加强, 时而减弱, 呈周期性变化(D) 时而加强, 时而减弱, 没有一定的规律69. 两个相干波源连线的中垂线上各点[ ] (A) 合振动一定最强(B) 合振动一定最弱(C) 合振动在最强和最弱之间周期变化(D) 只能是在最强和最弱之间的某一个值70. 两初相位相同的相干波源, 在其叠加区内振幅最小的各点到两波源的波程差等于[ ] (A) 波长的偶数倍 (B) 波长的奇数倍(C) 半波长的偶数倍 (D) 半波长的奇数倍71. 在驻波中, 两个相邻波节间各质点的振动是[ ] (A) 振幅相同, 相位相同 (B) 振幅不同, 相位相同(C) 振幅相同, 相位不同 (D) 振幅不同, 相位不同72. 两列完全相同的余弦波左右相向而行, 叠加后形成驻波.下列叙述中, 不是驻波特性的是[ ] (A) 叠加后, 有些质点始终静止不动(B) 叠加后, 波形既不左行也不右行(C) 两静止而相邻的质点之间的各质点的相位相同(D) 振动质点的动能与势能之和不守恒73. 平面正弦波)π3π5sin(4y t x +=与下面哪一列波相叠加后能形成驻波?[ ] (A) )2325π(2sin 4x t y += (B) )2325π(2sin 4x t y -=(C) )2325π(2sin 4y t x += (D) )2325π(2sin 4y t x -= 74. 方程为)π100cos(01.01x t y -=m 和)π100cos(01.02x t y +=m 的两列波叠加后, 相邻两波节之间的距离为[ ] (A) 0.5 m (B) 1 m (C) π m (D) 2π m75. 1S 和2S 是波长均为λ的两个相干波的波源,相距3λ/4,1S 的相位比2S 超前2π.若两波单独传播时,在过1S 和2S 的直线上各点的强度相同,不随距离变化,且两波的强度都是0I ,则在1S 、2S 连线上1S 外侧和2S 外侧各点,合成波的强度分别是[ ] (A) 04I ,04I ; (B) 0,0;(C) 0,04I ; (D) 04I ,0.76. 在弦线上有一简谐波,其表达式为⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+⨯=-3π420π100cos 100.221x t y (SI)为了在此弦线上形成驻波,并且在x =0处为一波腹,此弦线上还应有一简谐波,其表达式为:[ ] (A) ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⨯=-3π20π100cos 100.222x t y (SI) (B) ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⨯=-3π420π100cos 100.222x t y (SI) (C) ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯=-3π20π100cos 100.222x t y (SI)(D) ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯=-3π420π100cos 100.222x t y (SI) 二、填空题1. 一质点沿x 轴作简谐振动,平衡位置为x 轴原点,周期为T ,振幅为A , (1) 若t = 0 时质点过x = 0处且向x 轴正方向运动,则振动方程为x = . (2) 若t = 0时质点在x = A /2处且向x 轴负方向运动,则质点方程为x = .2. 据报道,1976年唐山大地震时,当地居民曾被猛地向上抛起2m 高.设此地震横波为简谐波,且频率为1Hz ,波速为3km ⋅s -1, 它的波长是 ,振幅是 .3. 一质点沿x 轴作简谐振动, 其振动方程为: π)31π2cos(4-=t x cm .从t =0时刻起, 直到质点到达 2-=x cm 处、且向 x 轴正方向运动的最短时间间隔为 .4. 一个作简谐振动的质点,其谐振动方程为π)23cos(π1052+⨯=-t x (SI 制).它从计时开始到第一次通过负最大位移所用的时间为 .5. 一单摆的悬线长l =1.3m, 在顶端固定点的铅直下方0.45m 处有一小钉,如T4-2-5图所示.设两方摆动均较小,则单摆的左右两方角振幅之比21θθ的近似值为 . 6. 一质点作简谐振动, 频率为2Hz .如果开始时质点处于平衡位置, 并以π m.s -1的速率向x 轴的负方向运动, 则该质点的振动方程为 .7. 一谐振动系统周期为0.6s, 振子质量为200g .若振子经过平衡位置时速度为12cm.s -1, 则再经0.2s 后该振子的动能为 .8.劲度系数为100N ⋅m -1的轻质弹簧和质量为10g 的小球组成一弹簧振子. 第一次将小球拉离平衡位置4cm, 由静止释放任其振动; 第二次将小球拉离平衡位置2cm 并给以2m.s -1的初速度任其振动.这两次振动的能量之比为 .9. 将一个质量为20g 的硬币放在一个劲度系数为40N.m -1的竖直放置的弹簧上, 然后向下压硬币使弹簧压缩 1.0cm, 突然释放后, 这个硬币将飞离原来位置的高度为 .10. 质量为0.01 kg 的质点作简谐振动, 振幅为0.1m, 最大动能为0.02 J .如果开始时质点处于负的最大位移处, 则质点的振动方程为 .11. 一物体放在水平木板上,这木板以Hz 2=ν的频率沿水平直线作简谐运动,物体和水平木板之间的静摩擦系数50.0=s μ,物体在木板上不滑动的最大振幅max A = .12. 如果两个同方向同频率简谐振动的振动方程分别为π)3110sin(31+=t x cm 和)π6110sin(42-=t x cm, 则它们的合振动振幅为 [ ] (A) 1 cm (B) 5 cm (C) 7 cm (D) 3 cm13. 已知由两个同方向同频率的简谐振动合成的振动, 其振动的振幅为20cm, 与第一个简谐振动的相位差为6π.若第一个简谐振动的振幅为cm 3.17310=, 则第二个简小钉m45.0l1lT 4-2-5图T 4-1-32图谐振动的振幅为 cm ,两个简谐振动的相位差为 .14. 已知一平面简谐波的方程为: )π(2cos λνxt A y -=, 在ν1=t 时刻λ411=x 与 λ432=x 两点处介质质点的速度之比是 . 15. 一观察者静止于铁轨旁, 测量运行中的火车汽笛的频率.若测得火车开来时的频率为2010 Hz, 离去时的频率为1990 Hz, 已知空气中的声速为330m.s -1, 则汽笛实际频率ν是 .16. 已知一入射波的波动方程为)4π4πcos(5xt y +=(SI 制), 在坐标原点x = 0处发生反射, 反射端为一自由端.则对于x = 0和x = 1米的两振动点来说, 它们的相位关系是相位差为 .17. 有一哨子, 其空气柱两端是打开的, 基频为5000 Hz, 由此可知,此哨子的长度最接近 厘米.18. 一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为)4π/cos(05.01+=t x ω (SI) )12π/19cos(05.02+=t x ω(SI)其合成运动的运动方程为=x .(SI)19. 已知一平面简谐波沿x 轴正向传播,振动周期T = 0.5 s ,波长λ = 10m , 振幅A = 0.1m .当t = 0时波源振动的位移恰好为正的最大值.若波源处为原点,则沿波传播方向距离波源为2/λ处的振动方程为 .当 t = T / 2时,4/λ=x 处质点的振动速度为 .20. T4-2-20图表示一平面简谐波在 t = 2s 时刻的波形图,波的振幅为 0.2m ,周期为4s .则图中P 点处质点的振动方程为 .21. 一简谐波沿BP 方向传播,它在B 点引起的振动方程为t A y π2cos 11=.另一简谐波沿CP 方向传播,它在C 点引起的振动方程为()ππ2cos 22+=t A y .P 点与B 点相AT4-2-20图 T4-2-21图PB1r 2r ...C距0.40m ,与C 点相距0.50m(如T4-2-21图).波速均为u =0.20m ⋅s -1.则两波在P 的相位差为 .22. 如T4-2-22图所示,一平面简谐波沿Ox 轴正方向传播,波长为λ,若1P 点处质点的振动方程为()ϕ+=vt A y π2cos 1,则2P 点处质点的振动方程为 ,与1P 点处质点振动状态相同的那些点的位置是 .23. 一个点波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为1R 和2R .在两个球面上分别取相等的面积1S ∆和2S ∆,则通过它们的平均能流之比21/P P =_______.24. 一列平面简谐波在截面积为S 的圆管中传播, 其波的表达为)π2(cos λωxt A y -=,管中波的平均能量密度是w , 则通过截面积S 的平均能流是 .25. 两相干波源1S 和2S 的振动方程分别是t A y ωcos 1=和π)21(cos 2+=t A y ω.1S 距P 点3个波长,2S 距P 点421个波长.两波在P 点引起的两个振动的相位差的绝对值是 .26. 如T4-2-26图所示,1S 和2S 为同相位的两相干波源,相距为L ,P 点距1S 为r ;波源1S 在P 点引起的振动振幅为1A ,波源2S 在P 点引起的振动振幅为2A ,两波波长都是λ,则P 点的振幅A = .27. 21S S 、为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23为波长)(λ如图.已知1S 的初相位为π21. (1) 若使射线C S 2上各点由两列波引起的振动均干涉相消,则2S 的初位相应为:_______________________.(2) 若使21S S 连线的中垂线M N 上各点由两列波引起的振动均干涉相消,则2S 的初位相应为:________________________________________.12T4-2-26图•••MN1S 2S CT4-2-27图x12T4-2-22图三、计算题1. 如T 4-3-1图所示,将一个盘子挂在劲度系数为k 的弹簧下端,有一个质量为m 的物体从离盘高为h 处自由下落至盘中后不再跳离盘子,由此盘子和物体一起开始运动(设盘子与弹簧的质量可忽略,如图取平衡位置为坐标原点,选物体落到盘中的瞬间为计时零点).求盘子和物体一起运动运动时的运动方程.2. 一质量为10g 的物体在x 方向作简谐振动,振幅为24cm ,周期为4s .当t =0时该物体位于x = 24cm 处.求:(1) 当t =0.5s 时物体的位置及作用在物体上力的大小.(2) 物体从初位置到x =-12cm 处所需的最短时间,此时物体的速度.3. 作简谐振动的小球,速度的最大值为-1m ax s cm 3⋅=v ,振幅为2cm =A .若令速度具有正最大值的某时刻为计时器点,求该小球运动的运动方程和最大加速度.4如T4-3-4图所示,定滑轮半径为R ,转动惯量为J ,轻弹簧劲度系数为k ,物体质量为m ,将物体从平衡位置拉下一极小距离后放手,不计一切摩擦和空气阻力,试证明该系统将作谐振动并求其振动周期.5. 如T 4-3-5图所示,有一水平弹簧振子,弹簧的劲度系数k =241-m N ⋅,重物的质量m =6kg .最初重物静止在平衡位置上,一水平恒力F =10N 向左作用于物体,(不计摩擦),使之由水平位置向左运动了0.05m ,此时撤去力F .当重物运动到左方最远位置时开始计时,求该弹簧振子的运动方程.6. 已知某质点振动的初始位置为20Ax =,初始速度00>v (或说质点正向x 正向运动),求质点的振动初相位.7. 如T4-3-7图所示,一半径为R 的匀质圆盘绕边缘上一点作微角摆动, 如果其周期与同样质量单摆的周期相同, 求单摆的摆线长度.8. 某人欲了解一精密摆钟的摆长, 他将摆锤上移了1 mm, 测出此钟每分钟快0.1s .这钟的摆长是多少?T 4-3-5图T 4-3-1图T 4-3-7图T 4-3-4图9. 已知一简谐振子的振动曲线如T3-4-9图所示,求其运动方程.10. 如T4-3-10图所示,一劲度系数为k 的轻弹簧,一端固定在墙上,另一端连结一质量为m 1的物体,放在光滑的水平面上.将一质量为m 2的物体跨过一质量为M ,半径为R 的定滑轮与m 相连,求此系统的振动圆频率.11. 一个质量为m 的小球在一个光滑的半径为R 的球形碗底作微小振动,如T4-3-11图所示.设0=t 时,0=θ,小球的速度为0v ,向右运动.试求在振幅很小情况下,小球的振动方程.12. 如T4-3-12图所示,一质点作简谐振动,在一个周期内相继通过距离为12cm 的两点A 、B ,历时2s ,并且在A 、B 两点处具有相同的速度;再经过2s 后,质点又从另一方向通过B 点.试求质点运动的周期和振幅.13. 如T4-3-13图所示,在一轻质刚性杆AB 的两端,各附有一质量相同的小球,可绕通过AB 上并且垂直于杆长的水平轴O 作振幅很小的振动.设OA = a , OB = b , 且b > a ,试求振动周期.14. 有两个振动方向相同的简谐振动,其振动方程分别为(cm)2ππ2cos 3(cm)π)π2cos(421⎪⎭⎫⎝⎛+=+=t x t x (1) 求它们的合振动方程;(2) 另有一同方向的简谐振动cm )π2cos(233ϕ+=t x ,问当3ϕ为何值时,31x x +的振幅为最大值?当3ϕ为何值时,31x x +的振幅为最小值?T4-3-9 T4-3-10图RT4-3-11图OθT4-3-12图AT4-3-13图OθBba15. 一质量为M 的全息台放置在横截面均匀的密封气柱上(见T4-3-15题图).平衡时气柱高度为h .今地基作上、下振动,规律为t A x G ωcos =,其中A 为振幅,ω为振动圆频率.忽略大气压强和阻尼,试求全息台振动的振幅.16. 假设地球的密度是均匀的,如果能沿着地球直径挖通一穿过地球的隧道,试证明落入隧道的一个质点的运动是简谐运动,并求出其振动周期.17. 已知波线上两点A 、B 相距1m, B 点的振动比A 点的振动滞后121s, 相位落后30, 求此波的波速.18. 一简谐波,振动周期21=T s ,波长λ =10m ,振幅A = 0.1m. 当t = 0时刻,波源振动的位移恰好为正方向的最大值.若坐标原点和波源重合,且波沿Ox 轴正方向传播,求:(1) 此波的表达式;(2) 4/1T t =时刻,4/1λ=x 处质点的位移;(3) 2/2T t =时刻,4/1λ=x 处质点振动速度.19. 一列平面简谐波在介质中以波速u = 5m ⋅s -1沿x 轴正向传播,原点O 处质元的振动曲线如图所示.(1) 画出x =25m 处质元的振动曲线. (2) 画出t =3s 时的波形曲线.20. 如T4-3-20图所示为一平面简谐波在t =0时刻的波形图,设此简谐波的频率为250Hz ,且此时质点P 的运动方向向下,求(1) 该波的波动方程.(2) 在距原点O 为100m 处质点的振动方程与振动速度表达式.21. 已知一平面简谐波的方程为 (SI))24(πcos x t A y +=(1) 求该波的波长λ,频率ν和波速度u 的值;(2) 写出t = 4.2s 时刻各波峰位置的坐标表达式,并求出此时离坐标原点最近的那个波峰的位置;(3) 求t = 4.2s 时离坐标原点最近的那个波峰通过坐标原点的时刻t .T4-3-19图20()cm y 42)s (t m1002/2A ()m y O A-P()m xT4-3-20图T4-3-15图h。
第4章《振动》选择题解答与分析

4振动4.1旋转矢量1. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为答案:(B)参考解答:简谐振动可以用一个旋转矢量的投影来表示。
这一描述简谐振动的几何方法称为旋转矢量法。
以坐标原点o 为始端作一矢量A,该矢量以角速度ω绕o 点逆时针匀速转动。
0=t 时,旋转矢量与x 轴正向的夹角等于ϕ,则在转动过程中的任意时刻t ,矢量A与x 轴正向的夹角为)(ϕω+t ,其端点M 在坐标轴上的投影P 的坐标为)cos(ϕω+=t A x ,P 所代表的运动正是简谐振动。
本题(B)图中,旋转矢量端点在坐标轴上投影点的坐标与运动方向符合题设的要求,即为答案。
对所有选择,均给出参考解答,直接进入下一题。
2. 一质点作简谐振动,周期为T .当它由平衡位置向x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12. (B) T /8. (C) T /6. (D) T /4. 答案:(C) 参考解答:根据旋转矢量法,以坐标原点o 为始端作一矢量A,该矢量以角速度ω绕o 点逆时针匀速转动。
0=t 时,旋转矢量与x 轴正向的夹角等于ϕ,则在转动过程中的任意时刻t ,矢量A与x 轴正向的夹角为)(ϕω+t ,其端点在坐标轴上的投影的坐标为)cos(ϕω+=t A x 所代表的运动正是简谐振动。
本题按题意画旋转矢量图,由,3πωθ==t πω2=T 两式联立,解出.6Tt =对所有选择,均给出参考解答,直接进入下一题。
4.2振动曲线、初相1. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A) π/6. (B) 5π/6. (C) -5π/6.(D) -π/6. (E) -2π/3.答案:(C)参考解答:令简谐振动的表达式:)cos(ϕω+=t A x ,)(ϕω+t 称为振动系统在t 时刻的位相。
柴森高中物理题型方法只有上册

柴森高中物理题型方法只有上册柴森高中物理题型方法书籍是一套专门为高中生编写的物理学习辅助教材。
本文将详细介绍该书上册的内容,包括每一章的题型和解题方法。
柴森高中物理题型方法只有上册是一本很有用的物理学习辅助教材。
通过学习上册的内容,学生可以系统地掌握不同类型的物理题型和解题方法,提高物理学习的效果。
值得一提的是,本文对每一章的内容进行了详细描述,以确保读者能够全面了解该书上册的特点和优势。
第一章:运动物理题型与解题方法第一章主要介绍了与运动相关的物理题型和解题方法。
这包括匀速直线运动、自由落体运动、抛体运动等。
其中,每种运动方式的题型以及相应的解题方法都被详细阐述。
例如,在匀速直线运动中,我们可以利用速度、位移和时间的关系来解决问题;在自由落体运动中,我们可以利用重力加速度和时间的关系来解决问题。
第二章:力学与解题方法第二章着重介绍了与力学相关的物理题型和解题方法。
其中,包括牛顿第一、二、三定律的应用、摩擦力与力的分解等内容。
这些问题的解题思路和方法都被明确地给出,并配有具体的例题供读者参考。
例如,当我们遇到一个需要分解力的问题时,可以根据受力分析法将力拆解为水平方向和垂直方向的分量,从而更好地理解和解决问题。
第三章:能量与解题方法第三章主要涵盖了与能量相关的物理题型和解题方法。
这包括动能、势能、机械能守恒和功与能等内容。
通过学习本章的内容,读者可以更好地理解能量的转化和守恒原理,并能够灵活运用这些知识来解决不同类型的能量问题。
例如,当我们遇到一个关于机械能守恒的题目时,可以通过计算初始机械能和最终机械能的差异来求解问题。
第四章:振动与波动题型与解题方法第四章主要围绕振动和波动相关的物理题型展开。
本章介绍了简谐振动、波动传播、声音和光的特性等内容。
读者将学会如何解决与振动和波动有关的问题,例如相位差、波速和频率的计算等。
通过阅读本章,读者将对振动和波动的基本概念和规律有更深入的了解。
第五章:电磁题型与解题方法第五章重点讲解了与电磁有关的物理题型和解题方法。
大学物理学振动与波动习题答案

大学物理学(上)第四,第五章习题答案第4章振动P174.4.1 一物体沿x轴做简谐振动,振幅A = 0.12m,周期T = 2s.当t = 0时,物体的位移x= 0.06m,且向x轴正向运动.求:(1)此简谐振动的表达式;(2)t = T/4时物体的位置、速度和加速度;(3)物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间.[解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m,角频率ω = 2π/T = π.当t = 0时,x = 0.06m,所以cosφ = 0.5,因此φ = ±π/3.物体的速度为v = d x/d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sinφ,由于v > 0,所以sinφ < 0,因此φ = -π/3.简谐振动的表达式为x = 0.12cos(πt –π/3).(2)当t = T/4时物体的位置为x = 0.12cos(π/2–π/3)= 0.12cosπ/6 = 0.104(m).速度为v = -πA sin(π/2–π/3)= -0.12πsinπ/6 = -0.188(m·s-1).加速度为a = d v/d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s-2).(3)方法一:求时间差.当x= -0.06m 时,可得cos(πt1 - π/3) = -0.5,因此πt1 - π/3 = ±2π/3.由于物体向x轴负方向运动,即v < 0,所以sin(πt1 - π/3) > 0,因此πt1 - π/3 = 2π/3,得t1 = 1s.当物体从x = -0.06m处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt2 - π/3) = 0,可得πt2 - π/3 = -π/2或3π/2等.由于t2 > 0,所以πt2 - π/3 = 3π/2,可得t2 = 11/6 = 1.83(s).所需要的时间为Δt = t2 - t1 = 0.83(s).方法二:反向运动.物体从x= -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间就是它从x = 0.06m,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x0/A),(-π < φ≦π),初位相的取值由速度决定.由于v = d x/d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sinφ,当v > 0时,sinφ < 0,因此φ = -arccos(x0/A);当v < 0时,sinφ > 0,因此φ = arccos(x0/A).可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x0 = A时,φ = 0;当初位置x0 = -A时,φ = π.4.2 已知一简谐振子的振动曲线如图所示,试由图求:(1)a,b,c,d,e各点的位相,及到达这些状态的时刻t各是多少?已知周期为T;(2)振动表达式;(3)画出旋转矢量图.[解答]方法一:由位相求时间.(1)设曲线方程为x = A cosΦ,其中A表示振幅,Φ = ωt + φ表示相位.由于x a = A,所以cosΦa = 1,因此Φa = 0.由于x b = A/2,所以cosΦb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t增加,b点位相就应该大于a点的位相,因此Φb = π/3.由于x c = 0,所以cosΦc = 0,又由于c点位相大于b位相,因此Φc = π/2.同理可得其他两点位相为Φd = 2π/3,Φe = π.c点和a点的相位之差为π/2,时间之差为T/4,而b点和a点的相位之差为π/3,时间之差应该为T/6.因为b点的位移值与O时刻的位移值相同,所以到达a点的时刻为t a = T/6.到达b点的时刻为t b = 2t a = T/3.到达c点的时刻为t c = t a + T/4 = 5T/12.到达d点的时刻为t d = t c + T/12 = T/2.到达e点的时刻为t e = t a + T/2 = 2T/3.(2)设振动表达式为x = A cos(ωt + φ),当t = 0时,x = A/2时,所以cosφ = 0.5,因此φ =±π/3;由于零时刻的位相小于a点的位相,所以φ = -π/3,因此振动表达式为cos(2)3tx ATπ=π-.另外,在O时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t轴相交于f点,由于x f = 0,根据运动方程,可得cos(2)03tTππ-=所以232ftTπππ-=±.图6.2显然f 点的速度大于零,所以取负值,解得t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为t a = T /4 + t f = T /6,其位相为203a a t T Φπ=π-=.由图可以确定其他点的时刻,同理可得各点的位相.4.3如图所示,质量为10g 的子弹以速度v = 103m ·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k= 8×103N ·m -1,木块的质量为 4.99kg ,不计桌面摩擦,试求:(1)振动的振幅; (2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即mv = (m + M )v 0.解得子弹射入后的速度为v 0 = mv/(m + M ) = 2(m ·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得(m + M ) v 02/2 = kA 2/2,所以振幅为A v =×10-2(m). (2)振动的圆频率为ω=·s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为x = A cos(ωt + φ).当t = 0时,x = 0,可得φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为x = 5×10-2cos(40t - π/2)(m). 4.4 如图所示,在倔强系数为k 的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为v =物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为0m v v m M ==+这也是它们振动的初速度. 设振动方程为x = A cos(ωt + φ),其中圆频率为ω=物体没有落下之前,托盘平衡时弹簧伸长为x 1,则x 1 = Mg/k .物体与托盘碰撞之后,在新的平衡位置,弹簧伸长为x 2,则x 2 = (M + m )g/k .取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k . 因此振幅为A ==图4.3图4.4= 初位相为00arctanv x ϕω-==4.5重量为P 的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)可以证明:当两根弹簧串联时,总倔强系数为k = k 1k 2/(k 1 + k 2),因此固有频率为2πων===.(2)因为当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为2πων===4.6 一匀质细圆环质量为m ,半径为R ,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]方法一:用转动定理.通过质心垂直环面有一个轴,环绕此轴的转动惯量为 I c = mR 2. 根据平行轴定理,环绕过O点的平行轴的转动惯量为I = I c + mR 2 = 2mR 2.当环偏离平衡位置时,重力的力矩为M = -mgR sin θ,方向与角度θ增加的方向相反.根据转动定理得I β = M ,即 22d sin 0d I mgR tθθ+=,由于环做小幅度摆动,所以sin θ≈θ,可得微分方程22d 0d mgRt Iθθ+=. 摆动的圆频率为ω=周期为2πT ω=22==方法二:用机械能守恒定律.取环的质心在最底点为重力势能零点,当环心转过角度θ时,重力势能为E p = mg (R - R cos θ), 绕O 点的转动动能为212k E I =ω, 总机械能为21(cos )2E I mg R R =+-ωθ. 环在转动时机械能守恒,即E 为常量,将上式对时间求导,利用ω = d θ/d t ,β = d ω/d t ,得0 = I ωβ + mgR (sin θ) ω,由于ω ≠ 0,当θ很小有sin θ≈θ,可得振动的微分方程22d 0d mgRt Iθθ+=, 从而可求角频率和周期.[注意]角速度和圆频率使用同一字母ω,不要将两者混淆.(b)图4.54.7 横截面均匀的光滑的U 型管中有适量液体如图所示,液体的总长度为L ,求液面上下微小起伏的自由振动的频率。
大学物理课后习题答案详解

第一章质点运动学1、(习题:一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线(2)质点的位置 : 22(48)r ti t j =+-r r r由d /d v r t =r r 则速度: 28v i tj =+r r r由d /d a v t =r r 则加速度: 8a j =r r则当t=1s 时,有 24,28,8r i j v i j a j =-=+=rr r rrrrr当t=2s 时,有 48,216,8r i j v i j a j =+=+=r r r r r rr r2、(习题): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dtdv-= ⎰⎰-=t v v kdt dv v 001 t k e v v -=0t k e v dtdx-=0 dt e v dx t k tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a 4t (SI),已知t 0时,质点位于x 10 m处,初速度v0.试求其位置和时间的关系式.解: =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程;(3)落地前瞬时小球的d d r t v ,d d v t v,tvd d .解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+v v v(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t=v v v 而落地所用时间 gh2t =所以0d d r v i j t =v vd d v g j t=-v v 2202y 2x )gt (v v v v -+=+=2120212202)2(2])([gh v gh g gt v t g dt dv +=+= 5、 已知质点位矢随时间变化的函数形式为22r t i tj =+v vv,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
普通物理A(1) 课程指导 第4章《振动》

N
2
cost
N 1
2
2
14
7. 分别敲击某待测音叉和标准音叉,使它们同时发音,听到时强时弱 的拍音.若测得在20 s内拍的次数为180次,标准音叉的频率为300 Hz, 则待测音叉的频率为______________.
拍频: 单位时间内强弱变化的次数 2 1 ( 2 1)
设1 300 Hz 则有: 2 1 9,或者1 2 9 2 309 Hz,或者 2 291Hz
0.08
O
-0.04
1
x1 t (s)
2 x2
x1
0.08 c os (t
2
),
x2
0.04 c os (t
) 2
A2
0
x
A
A1
10
6. N个同方向、同频率的简谐振动,它们的振幅相等,初相分别为0, , 2, ..., 依次差一个恒量 ,求合振动的振幅。
x1 Acost x2 Acos(t ) x3 Acos(t 2)
4
1. 一质点作简谐振动,周期为T.当它由平衡位置向x轴正方向运 动时,从二分之一最大位移处到最大位移处这段路程所需要的时 间为
(A) T /12. (B) T /8. (C) T /6. (D) T /4.
旋转矢量法
[C ]
首先画出二分之一最大位移处旋转矢量图,
然后,再画最大位移处旋转矢量图。
设所求的时间为t,则有
(1) 质点的振动方程; (2) 质点在A点处的速率.
AB
x
解: 3
4
4
t = 0时, x 5cm Acos
A 5 5 2 cm
cos(3 / 4)
∴ 振动方程
x 5 2 102 cos(t 3) (SI) 44
振动与波动的实验教案

振动与波动的实验教案实验目的:通过本实验,让学生了解振动与波动的基本概念,掌握简谐振动和波动的特点,并能够通过实验观察和测量,验证相关的物理原理。
实验器材:1. 弹簧振子:弹簧、质量块、固定支架、标尺、计时器等。
2. 水波装置:水槽、振荡器、液面单色和波源等。
实验原理:1. 弹簧振子实验:当弹簧在垂直方向上遵循胡克定律时,可以简化为简谐振动系统。
振子在平衡位置附近发生的微小振动即为简谐振动。
2. 水波实验:振动源通过水面的波的传播,构成波动。
波动可分为横波和纵波。
实验步骤:1. 弹簧振子实验:a. 将弹簧固定在支架上,并将质量块悬挂在弹簧下方。
b. 将质量块向下拉开一定距离,释放后观察振子的振动情况。
c. 使用计时器记录振子完整振动的时间,并根据记录的数据计算振动周期、频率和角频率。
2. 水波实验:a. 在水槽中加入适量的水,平静后放置液面单色。
b. 将振荡器放入水槽中,并打开振荡器使其产生波动。
c. 观察波的传播情况,注意观察波的波长、振幅等特征。
d. 使用测量工具测量波的波长和振幅,并根据相关公式计算波速。
实验注意事项:1. 弹簧振子实验:a. 振子的振幅应该较小,避免弹簧过度伸缩,影响振动的准确性。
b. 在记录振动时间时,要保证计时器的准确性,尽量减小误差。
c. 实验中要保持其他因素的恒定,避免外部因素对振子振动的影响。
2. 水波实验:a. 按照实验要求调整振荡器的频率,以保证波动的稳定和连续性。
b. 在测量波长时,要注意测量的起点和终点的位置,保证测量的准确性。
c. 实验中要避免产生过多的阻尼,确保波动的传播得到清晰的观察结果。
实验结果分析:1. 弹簧振子实验:a. 根据记录的数据,计算振动周期、频率和角频率,并进行比较和分析。
b. 探究振子质量、弹簧劲度系数等对振子振动特性的影响。
2. 水波实验:a. 根据测量的数据,计算波的波长和振幅,进一步计算波速。
b. 探究波源频率、水深、水温等因素对波动特性的影响。
高中物理的振动与波动教案

高中物理的振动与波动教案教学目标:1. 理解振动和波动的概念,掌握相关词汇和定义。
2. 掌握振动和波动的特点和分类。
3. 理解振动和波动在日常生活中的应用。
4. 训练学生观察、实验和逻辑思维能力。
教学重点与难点:1. 振动和波动的概念及其特点。
2. 振动和波动的分类及日常应用。
教学准备:1. 教师准备:教案、教学PPT、实验器材、振动和波测量仪器等。
2. 学生准备:学习笔记、实验记录本等。
教学过程:一、引入振动和波动概念(10分钟)1.1师生互动,讨论振动和波动的概念及特点。
1.2通过图片、实物等展示振动和波动的例子,引导学生理解概念。
二、振动的特点与分类(20分钟)2.1讲解振动的定义、特点及种类。
2.2进行实验观察不同种类的振动现象,让学生亲自实验、感受振动。
三、波动的特点与分类(20分钟)3.1讲解波动的定义、特点及种类。
3.2展示各种类型的波动实例,帮助学生理解波动的本质及分类。
四、振动和波动在日常生活中的应用(15分钟)4.1探讨振动和波动在日常生活中的各种应用,如声波、光波的传播与应用等。
4.2展示相关实例,让学生体会振动和波动的实际应用价值。
五、实验操作与总结(15分钟)5.1学生根据教师指导进行相关实验操作。
5.2总结振动和波动的知识点,检查学生对概念的掌握程度。
六、课堂讨论与提升(10分钟)6.1师生讨论振动和波动相关问题,梳理知识点,解决学生疑问。
6.2鼓励学生展示自己对振动和波动的理解,提出自己的见解。
教学反馈:1. 收集学生对本节课程的反馈意见,帮助教师改进教学方法与内容。
2. 师生共同总结学生在振动和波动方面的学习成果和不足之处,为下节课的教学做准备。
布置作业:1. 作业:根据本节课内容,写一篇关于振动和波动的简单作文。
2. 预习:预习下节课的内容,做好相关概念的准备。
教学反思:通过本节课的教学,学生对振动和波动的概念有了更深入的理解,实验操作增加了学生的学习兴趣与参与度。
第4章习题解答

第四章 机械振动和机械波4.1什么是简谐振动?分别从运动学和动力学两方面作出解释。
并说明下列运动是不是简谐振动;(1)小球在地面上做完全弹性的上下跳动;(2)小球在半径很大的光滑凹球面底部做小幅度的摆动; (3)曲柄连杆机构使活塞做往复运动。
4.2 若弹簧振子中弹簧本身的质量不可忽略,其振动周期是增加还是减小? 这相当于增加了系统的惯性,振动周期将增加。
4.3 将单摆拉到与竖直方向成ϕ角后,放手任其摆动,则ϕ是否就是其初相位?为什么?单摆的角速度是否是谐振动的圆频率?4.4判断以下说法是否正确?说明理由。
“质点作简谐振动时,从平衡位置运动到最远点需要1/4周期,因此走过该段距离的一半需时1/8周期。
”4.5两个相同的弹簧挂着质量不同的物体,当它们以相同的振幅做简谐运动时,问振动的能量是否相同?4.6什么是波动?振动与波动有什么区别和联系? 4.7试判断下列几种关于波长的说法是否正确. (1)在波传播方向上相邻两个位移相同点的距离; (2)在波传播方向上相邻两个运动速度相同点的距离; (3)在波传播方向上相邻两个振动相位相同点的距离。
4.8当波从一种媒质透入另一种媒质时,下面那些量会改变,哪些量不会改变:波长、频率、波速、振幅。
4.9有人认为频率不同、振动方向不同、相位差不恒定的两列波不能叠加,所以它们不是相干波,这种看法对不对?说明理由。
4.10 波的能量与振幅的平方成正比,两个振幅相同的相干波在空间叠加时,干涉加强的点的合振幅为原来的两倍,能量为原来的四倍,这是否违背能量守恒定律?4.11 一质点作简谐振动)7.0100cos(6ππ+=t x cm 。
某时刻它在23=x cm 处,且向X 轴负向运动,它要重新回到该位置至少需要经历的时间为( ) A 、s 1001 B 、s 2003 C 、s 501 D 、 s 503答案:(B)4.12 一个单摆,如果摆球的质量增加为原来的四倍,摆球经过平衡位置时的速度减为原来的一半,则单摆( )A 、频率不变,振幅不变;B 、频率不变,振幅改变;C 、频率改变,振幅不变;D 、频率改变,振幅改变; B4.13 以频率ν作简谐振动的系统,其动能和势能随时间变化的频率为( ) A 、2/ν B 、ν C 、ν2 D 、ν4 答案:(C)4.14 劲度系数为m N /100的轻弹簧和质量为10g 的小球组成的弹簧振子,第一次将小球拉离平衡位置4cm ,由静止释放任其运动;第二次将小球拉离平衡位置2cm 并给以2cm/s 的初速度任其振动。
第四章-机械振动
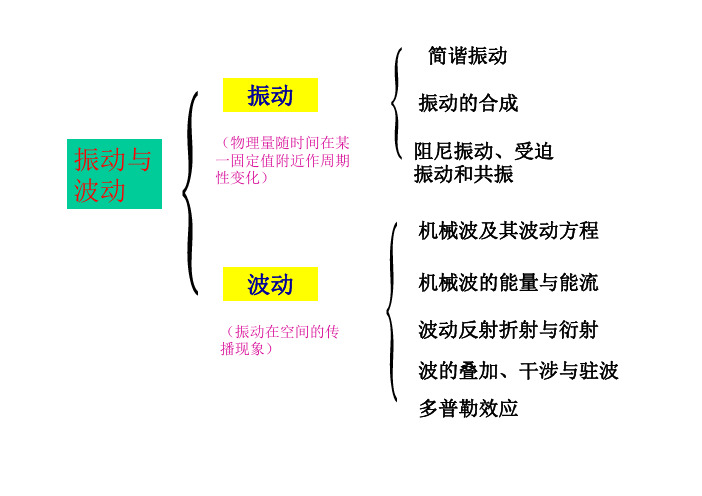
x(m)
t
A
曲线2曲线1
-A
t
t
t2
t1
1
2
当:t t2 t1 0, 2 1 0
振动2比振动1超前
t(s)
§4.1 简谐振动
例1.如图的谐振动x-t 曲线,试求其谐振方程
解:由图知
x(m)
A 2m T 2s 2
可得: 2 T O
振动表达式为
1
2t (s)
x Acos( t )
dt 2 l
谐振方程为:
设 2 2T
ml
x Acos(t )
§4.2 简谐振动的实例分析
(5)U形管中液体无粘滞振荡
x x
l
为管内液体密度,
l为液体在管内的长度。
动力学方程为:
l
d2 dt
x
2
2gx
0
谐振方程为:
2 2g
l
x Acos(t )
§4.2 简谐振动的实例分析
(6)LC谐振电路
P sin m dv
dt
v l
P
sin 1 3 (小角度时)
6
g 0
l
令 2 g
l
2 0
结论: 小角度摆动时,单摆的运动是谐振动.
周期和角频率为:T 2 l
g
g
l
§4.2 简谐振动的实例分析
(2) 复摆(物理摆)
以物体为研究对象
设 角沿逆时针方向为正
mghsin JZ
10
即: Asin( ) 0 sin( ) 0
6
2
x
1
cos(
t 2 )(m)
10 6 3
§4.1 简谐振动
大学物理实验中的波动与振动分析

大学物理实验中的波动与振动分析波动与振动是大学物理课程中的重要内容之一。
通过物理实验的手段,可以更好地理解和研究波动与振动的特性和规律,从而提升对物理学的理解和应用能力。
本文将对大学物理实验中的波动与振动进行分析。
一、实验背景和目的波动与振动是物理学的基本概念,广泛应用于多个领域。
通过进行波动与振动的实验,可以更好地理解其特性和规律,为理论的学习打下坚实的基础。
本实验旨在通过实验手段,探索波动与振动的相关原理,深入了解其性质和特征。
二、实验器材和步骤1. 实验器材:- 弹簧:用于研究弹性振动的特性,可以选择不同大小和材质的弹簧。
- 振动装置:用于产生振动,例如弹簧振子、简谐振子等。
- 高频发生器:产生高频信号,用于产生波动。
- 波动绳:用于研究波动传播的特性。
- 频率计:用于测量振动或波动的频率。
- 振动传感器:用于测量或检测振动的特征参数。
- 示波器:用于显示振动或波动的图像。
- 实验台和支架:用于固定实验器材。
2. 实验步骤:a. 振动实验:1) 根据实验要求选择合适的振动装置。
2) 将振动装置固定在实验台上。
3) 通过高频发生器产生振动信号,并调节频率。
4) 使用振动传感器测量振动的频率和振幅。
5) 使用示波器观察振动的图像,并记录关键数据和观察现象。
b. 波动实验:1) 将波动绳固定在实验台上,并保持一定的张力。
2) 通过高频发生器产生波动信号,并调节频率。
3) 使用示波器观察波动的传播和幅度变化。
4) 使用频率计测量波动的频率。
5) 记录关键数据和观察现象。
三、实验结果与分析1. 振动实验:- 通过调节高频发生器的频率,可以观察到振动信号的频率变化,并通过示波器显示出振动的图像。
- 随着频率的增加,振动的幅度可能发生变化。
- 使用振动传感器进行测量,可以得到振动的频率和振幅。
2. 波动实验:- 通过高频发生器产生波动信号,并使用波动绳进行传播实验。
- 使用示波器观察波动的传播和幅度变化。
《工程试验技术》第四章-振动与波动理论基础(下-波动理论)

此即为原方程的通解。
其中 x0 为任意一点,而k 为积分常数,
F ( x) + G( x) = ϕ ( x) 1 x C − F ( x) + G( x) = ∫ ψ (α )dα − a x0 a
1 1 x C F ( x) = ϕ ( x) − ∫ ψ (α )dα + 2 2a x0 2a 1 x C 1 G( x) = ϕ ( x) + ∫ ψ (α )dα − 2 2a x0 2a
∂ 2u = 0 ∂ξ∂η
⎞ ⎟ ⎟ (C) ⎠
∂ u = 0 ∂ξ∂η
2
函数 F,G具体形式,由初值 条件确定:
∂u = F * (ξ ) ∂ξ
u (ξ , η ) =
* F ∫ (ξ )d ξ + G (η )
u( x,0) = ϕ ( x)
(初始位移)
F ( x) + G( x) = ϕ ( x)
速度幅值谱
时域测试曲线
加速度功率谱
速度功率谱
速度幅值谱
2、嵌岩桩的检测
嵌岩桩的桩尖反射应为反向,同向应作为异常,需要进行验证
台州某工程检测结果
台州某工程检测结果
台州某工程检测结果—对同类型桩已进行静载验证
临安某工程检测结果
临安某工程检测结果-已进行取芯验证
3、浅层缺陷检测与分析
宜进行开挖验证
上行的力波和速度波的关系为:
− EA p ↑= ⋅ v ↑= − ρAC ⋅ v ↑= − Z ⋅ v ↑ c
结论:杆件(桩)中的一维波动(振动)可以分解为两个传播方向相反, 但传播速度相同的两列独立的“行波”,波形由初始条件决定。
4、波在杆件端部的反射情况
医用物理学课件:第4章 振动和波、声

s Acos(t 0 )
1 f
T
周期T :物体作一次完全振动所需的时间。
频率f :周期的倒数f,单位时间内物体所作 的完全振动的次数。
cos((t T ) 0) cos(t T 0)
T 2π cos(t 0)
角频率(angular
frequency):频率的2 倍
2π 2πf
s Acos(dt d )
稳定后的振动频率由 驱动力的频率决定
A
Fd 0
m
(02
d2
)2
4
2 2 d
d
arctan 2 d
2 0
2 d
共振resonance
A
Fd 0
m
(02
d2
)2
4
2 2 d
dA 0
d d
d r 02 2 2
Ar
2m
Fd 0
02 2
共振频率由系统的固 有频率决定
s Acos(t 0 )
s
tan 0
A1 sin 10 A1 cos10
A2 sin 20 A2 cos20
A A12 A22 2A1A2 cos(20 10 )
分析
A A12 A22 2A1A2 cos(20 10 )
20 10 2kπ 合振幅最大: A A1 A2
20 1,0 (2k 1)π
波线 wave ray:表示波传播方向的线。
波阵面、波线 wave surface , wave ray
波线
波阵面
波前wave
front
平面波plane wave
在各向同性的均匀介质中,波线为直线并与波面垂直。
波长 wave length:同一波线上相位差为2π的质点之间的 距离。波速 velocity
大学物理期末复习题---填空-计算题

第4章 振动与波动填空题(1)一质点在X 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取作坐标原点。
若t =0时质点第一次通过x =-2cm 处且向x 轴负方向运动,则质点第二次通过x =-2cm 处的时刻为__ __s 。
[答案:23s ](2)一水平弹簧简谐振子的振动曲线如题4.2(2)图所示。
振子在位移为零,速度为-ωA 、加速度为零和弹性力为零的状态,对应于曲线上的____________点。
振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力为-KA 的状态,则对应曲线上的____________点。
习题4.2(2) 图[答案:b 、f ; a 、e](3)一质点沿x 轴作简谐振动,振动范围的中心点为x 轴的原点,已知周期为T ,振幅为A 。
(a )若t=0时质点过x=0处且朝x 轴正方向运动,则振动方程为x=___________________。
(b )若t=0时质点过x=A/2处且朝x 轴负方向运动,则振动方程为x=_________________。
[答案:cos(2//2)x A t T ππ=−; cos(2//3)x A t T ππ=+](4)一横波的波动方程是))(4.0100(2sin 02.0SI x t y −=π,则振幅是____,波长是____,频率是____,波的传播速度是____。
[答案:0.02;2.5;100;250/m m Hz m s ](5)产生机械波的条件是 和 。
[答案:波源;有连续的介质](6)两列波叠加产生干涉现象必须满足的条件是 , 和 。
[答案:频率相同,振动方向相同,在相遇点的位相差恒定。
]计算题 振动4.3 质量为kg 10103−⨯的小球与轻弹簧组成的系统,按20.1cos(8)(SI)3x t ππ=+的规律作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差;解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,相比较则有:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m −⋅ 51.2=1s m −⋅2.632==A a m ω2s m −⋅(2) 0.63N m m F ma ==J 1016.32122−⨯==m mv E J 1058.1212−⨯===E E E k p当p k E E =时,有p E E 2=, 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=−=−=∆t t4.4 一质量为kg 10103−⨯的物体作谐振动,振幅为cm 24,周期为s 0.4,当0=t 时位移为cm 24+.求:(1)s 5.0=t 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到cm 12=x 处所需的最短时间; (3)在cm 12=x 处物体的总能量. 解:由题已知 s 0.4,m 10242=⨯=−T A∴ 1s rad 5.02−⋅==ππωT又,0=t 时,0,00=∴+=φA x 故振动方程为m )5.0cos(10242t x π−⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=−t x πN102.417.0)2(10103232−−⨯−=⨯⨯⨯−=−=−=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=φ,t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt (3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222−−⨯=⨯⨯⨯===πωA m kA E4.6 题4.6图为两个谐振动的t x −曲线,试分别写出其谐振动方程.习题4.6图解:由题4.6图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2−⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4.6图(b)∵0=t 时,35,0,2000πφ=∴>=v A x01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65=故 m t x b )3565cos(1.0ππ+=波动4.11 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4−),式中x ,y 以米计,t 以秒计.求:(1)绳子上各质点振动时的最大速度和最大加速度;(2)求x =0.2m 处质点在t =1s 时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点? 解: (1)将题给方程与标准式2cos()y A t x πωλ=−相比,得振幅05.0=A m ,圆频率10ωπ=,波长5.0=λm ,波速2.52u ωλυλπ===1s m −⋅.绳上各点的最大振速,最大加速度分别为ππω5.005.010max =⨯==A v 1s m −⋅222max 505.0)10(ππω=⨯==A a 2s m −⋅(2)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x ),在92.008.010=−=t s 时的位相,即 2.9=φπ. 设这一位相所代表的运动状态在25.1=t s 时刻到达x 点,则825.0)0.125.1(5.22.0)(11=−+=−+=t t u x x m4.12 一列平面余弦波沿x 轴正向传播,波速为5m ·s -1,波长为2m ,原点处质点的振动曲线如题4.12图所示.(1)写出波动方程;(2)作出t =0时的波形图及距离波源0.5m 处质点的振动曲线. 解: (1)由题4.14(a)图知,1.0=A m ,且0=t 时,0,000>=v y ,∴230πφ=, 又5.225===λυuHz ,则ππυω52==习题4.12图(a)取 ])(cos[0φω+−=ux t A y , 则波动方程为30.1cos[5()]52x y t ππ=−+m(2) 0=t 时的波形如题4.12(b)图习题4.12图(b) 习题4.12图(c)将5.0=x m 代入波动方程,得该点处的振动方程为50.530.1cos[5]0.1cos(5)52y t t πππππ⨯=−+=+m 如题4.12(c)图所示.第7章静电场7.2 填空题(1)在静电场中,电势不变的区域,场强必定为 。
第四章(第1节)两自由度系统的振动介绍

4.1 自由振动
有趣的“同步化” 现象
◆同步化现象虽然是耦合振动体最简单的运动形态,
但这并不意味着耦合振动体只能做同步运动。耦合振动 体的运动形态是多种多样的。 让我们来看看奔跑在澳洲平原上的袋鼠以及追逐在 袋鼠后面的土著人吧。袋鼠跳跃的时候,两只脚做的是 位移相同的移动。但土著人在走路时,左脚与右脚所做 的却是位移相反的移动。如果将袋鼠的跳跃看成同步化 的结果的话,那么土著人的走路则是反同步化的结果。
取加速度的正方向与坐标轴的正方向一致,根据牛 顿运动定律有
m1 x 1 k1x1 k2 ( x2 x1 ) m2 x 2 k2 ( x2 x1 ) k3 x2
4.1 自由振动
两自由度系统的微分方 程 移项得
m1 x 1 (k1 k2 ) x1 k2 x2 0 m2 x (k2 k3 ) x2 0 2 k2 x1
由系数矩阵组成的常数矩阵 M和K分别称为质量矩阵和 刚度矩阵,向量x称为位移向量。
4.1 自由振动
两自由度系统的微分方 程 设
k1 k2 k11 , k2 k12 k21 , k2 k3 k22 (4.1-3)
则方程(4.1-1)可以写成
m1 x 1 k11x1 k12 x2 0 m2 x 2 k21x1 k22 x2 0
4.1 自由振动
有趣的“同步化” 现象
四只脚的动物: 兔子在奔跑的时候,两只前脚 移动的位移相同,但两只后脚移动 的位移却和前脚的相反。 长颈鹿,是同侧的前后两只脚 一起移动。左前脚和左后脚一起动, 右前脚和右后脚一起动。 马的走路方式有些特别,做位 移相同移动的是对角线上的两只脚, 即左前脚和右后脚一起动,而右前 脚则和左后脚一起动。
第4章 受迫振动

第 4 章 受迫振动
62
E (t ) = K cos ΩT0
我们采用多尺度方法求近似解。设解形式为
u (t , ε ) = u 0 (T0 , T1 ) + εu1 (T0 , T1 ) + L
并代入受迫振动方程,计算方程两段ε0 和ε的系数,得到方程组:
2 D02 u 0 + ω 0 u 0 = K cos ΩT0 2 3 D02 u1 + ω 0 u1 = −2 D0 D1u 0 − 2µD0 u 0 − αu 0
2 3αa 0 − a0 − σ 8ω 0
−µ −λ 1 a0
2 9αa 0 − σ 8ω 0
=0
−µ −λ
将特征行列式展开,得到
2 2 3αa 0 9αa 0 σ − =0 − λ2 + 2µλ + µ 2 + σ 8ω 0 8ω 0
图 4-1 频率响应曲线
第 4 章 受迫振动
59
无论是响应振幅曲线还是相位曲线, 非线性都使得振幅和相位产生多值, 这种多值导致 了响应发生跳跃现象,图中箭头指示了跳跃点。 图 4-2 显示了非线性对频率响应曲线的弯曲程度,硬弹簧( α > 0 )将曲线向右弯曲, 而软弹簧( α < 0 )则将曲线向左弯曲。图 4-3 显示了硬弹簧系统频率响应曲线关于激励幅 值 k 的变化情况,随着激励幅值的增大,频率响应曲线偏离 σ = 0 轴而弯曲,响应幅值的峰 值轨迹为抛物线
第 4 章 受迫振动
55
4. 受迫振动
前面几章我们讨论的问题是所谓的自由振动问题, 即系统仅受初始扰动所产生的振动响 应问题,不考虑外界对系统的激励或能量输入。本章讨论外界对系统存在激励的情况,此时 的振动系统称为受迫振动系统。 外界对系统的激励通常有 2 种形式, 一种是激励在运动方程 中以非齐次项的形式出现, 这种激励称为外激励; 另一种则是在方程中以变系数的形式出现, 称为参数激励。本章中讨论的激励是外激励。 考虑系统由下列方程所控制:
振动与波动

T = 2π
L g
2.(P42思1.3) 2.(P42思1.3) 当一个弹簧振子的振幅增大到期原来的 2 倍时,则 振动的周期,能量以及最大速度, 振动的周期,能量以及最大速度,最大加速度各会 发生什么变化? 发生什么变化? 周期不变; 增大到原来的4倍 周期不变; 能量 增大到原来的 倍; 最大速度和最大加速度均增大到原来的2倍 最大速度和最大加速度均增大到原来的 倍. 3. 振动方向相同,频率相同的两个简谐振动合成后仍 振动方向相同, 然是简谐振动吗?其振动方向和频率有何特点? 然是简谐振动吗?其振动方向和频率有何特点?其 频率和初相位如何计算? 频率和初相位如何计算?
六,多普勒效应(波源和接收器在同一直线上运动) 波源和接收器在同一直线上运动) 1.波源和接收器都静止 波源和接收器静止时,接收器接收到的频率不变. 波源和接收器静止时,接收器接收到的频率不变. 2.波源和接收器运动 波源和接收器接近时,接收器接收到的频率变高. 波源和接收器接近时,接收器接收到的频率变高. 波源和接收器远离时,接收器接收到的频率变小. 波源和接收器远离时,接收器接收到的频率变小. 七,惠更斯原理与波的衍射,折射和反射 惠更斯原理与波的衍射,
由振动曲线确定. 由振动曲线确定.
g L
ω =
由振动曲线确定. 由振动曲线确定.
如:例2. . 二,已知振动参量,求振动方程. 已知振动参量,求振动方程. 如:例1,例2,习1.5. , , . 已知振动方程,求振动参量. 三,已知振动方程,求振动参量. 如:习1.1,例2. , .
x = Acos(ωt +)
1 2 1 2 EP = kx = kA cos2 (ωt +) 2 2 1 1 Ek = E Ep Ek = mv2 = kA2 sin 2 (ωt +) 2 2 1 2 2E 2E0 E = Ek + Ep = kA 振幅 A = = 2 k k
理论力学中的波动与振动分析

理论力学中的波动与振动分析波动与振动是理论力学中重要的研究方向,涉及到许多实际应用和科学理论。
本文将从经典力学和量子力学两个方面,对波动与振动进行深入分析。
一、经典力学中的波动与振动在经典力学中,波动可以用以下形式的波动方程来描述:ψ(x, t) = A * sin(kx - ωt + φ)其中,ψ是波函数,A代表振幅,k是波数,x表示位置变量,ω代表角频率,t为时间变量,φ为相位角。
振动是波动的一种特殊形式,当振动发生在一维系统中时,可以用简谐振动方程来描述:x(t) = A * cos(ωt + φ)其中,x为位移,A为最大位移量,ω为角频率,t为时间,φ为初相位角。
二、量子力学中的波动与振动在量子力学中,粒子的波动性由波函数来描述,而波函数的演化满足薛定谔方程:i * ℏ * ∂ψ/∂t = -Ĥψ其中,Ĥ为哈密顿算符,ℏ为普朗克常数除以2π。
量子力学中的波动性表现为粒子的波粒二象性,即既具有粒子性又具有波动性。
粒子的波函数通过薛定谔方程得到后,可以用波包的形式表示。
波包是一个由多个简谐波组合而成的波动形式,可以用高斯波包表达。
对于振动来说,在量子力学中,可以用谐振子模型进行描述。
谐振子模型是量子力学中的一个重要模型,它是简谐振动的量子版本。
谐振子的哈密顿算符表达式为:Ĥ = (ℏω/2) * (a^†a + aa^†)其中,a和a^†分别是谐振子的湮灭算符和产生算符,ℏ是普朗克常数除以2π,ω为角频率。
谐振子的能级由能量本征值给出。
三、波动与振动的应用波动和振动在物理学、工程学和其他学科中有广泛的应用。
以下是一些常见的应用领域:1.声学:声音是通过空气中的波动传播的,声学研究了声音的起源、传播和感知。
声波的频率和振幅可以影响我们对声音的感知。
2.光学:光是一种电磁波,光学研究了光的传播、反射、折射等现象。
波动光学理论可以解释光的干涉、衍射等现象。
3.无线通信:通过调制载波的振幅和频率,可以实现无线信号的传输。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 振动与波动题目无答案一、选择题1. 已知四个质点在x 轴上运动, 某时刻质点位移x 与其所受合外力F 的关系分别由下列四式表示(式中a 、b 为正常数).其中不能使质点作简谐振动的力是[ ] (A) abx F = (B) abx F -=(C) b ax F +-= (D) a bx F /-=2. 在下列所述的各种物体运动中, 可视为简谐振动的是[ ] (A) 将木块投入水中, 完全浸没并潜入一定深度, 然后释放(B) 将弹簧振子置于光滑斜面上, 让其振动(C) 从光滑的半圆弧槽的边缘释放一个小滑块(D) 拍皮球时球的运动3. 欲使弹簧振子系统的振动是简谐振动, 下列条件中不满足简谐振动条件的是[ ] (A) 摩擦阻力及其它阻力略去不计(B) 弹簧本身的质量略去不计(C) 振子的质量略去不计(D) 弹簧的形变在弹性限度内4. 当用正弦函数或余弦函数形式表示同一个简谐振动时, 振动方程中不同的量是[ ] (A) 振幅 (B) 角频率(C) 初相位 (D) 振幅、圆频率和初相位5. 如T4-1-5图所示,一弹簧振子周期为T .现将弹簧截去一半,仍挂上原来的物体, 则新的弹簧振子周期为[ ] (A) T (B) 2TT 4-1-5图(C) 3T (D)6. 三只相同的弹簧(质量忽略不计)都一端固定, 另一端连接质量为m 的物体, 但放置情况不同.如T4-1-6图所示,其中一个平放, 一个斜放, 另一个竖直放.如果让它们振动起来, 则三者的[ ] (A) 周期和平衡位置都不相同 (B) 周期和平衡位置都相同(C) 周期相同, 平衡位置不同(D) 周期不同, 平衡位置相同7. 如T4-1-7图所示,升降机中有一个做谐振动的单摆, 当升降机静止时, 其振动周期为2秒; 当升降机以加速度上升时, 升降机中的观察者观察到其单摆的振动周期与原来的振动周期相比,将[ ] (A) 增大 (B ) 不变(C) 减小 (D) 不能确定8. 在简谐振动的运动方程中,振动相位)(ϕω+t 的物理意义是[ ] (A) 表征了简谐振子t 时刻所在的位置(B) 表征了简谐振子t 时刻的振动状态(C) 给出了简谐振子t 时刻加速度的方向(D) 给出了简谐振子t 时刻所受回复力的方向9. 如T4-1-9图所示,把单摆从平衡位置拉开, 使摆线与竖直方向成角, 然后放手任其作微小的摆动.若以放手时刻为开始观察的时刻,用余弦函数表示这一振动, 则其振动的初位相为 T 4-1-6图T 4-1-7图 θ+T 4-1-9图[ ] (A) (B) 2π 或π23 (C) 0 (D) π 10. 两质点在同一方向上作同振幅、同频率的简谐振动.在振动过程中, 每当它们经过振幅一半的地方时, 其运动方向都相反.则这两个振动的位相差为[ ] (A) (B) π32 (C) π34 (D) π54 11. 在简谐振动的速度和加速度表达式中,都有一个负号, 这是意味着[ ] (A) 速度和加速度总是负值(B) 速度的相位比位移的相位超前π21, 加速度的位相与位移的相位相差 (C) 速度和加速度的方向总是相同(D) 速度和加速度的方向总是相反12. 一质点作简谐振动, 振动方程为)cos(ϕω+=t A x . 则在2T t =(T 为振动周期) 时, 质点的速度为[ ] (A) ϕωsin A - (B) ϕωsin A(C) ϕωcos A - (D) ϕωcos A13. 一物体作简谐振动, 其振动方程为)4πcos(+=t A x ω.则在2T t = (T 为周期)时, 质点的加速度为(A) 222ωA - (B) 222ωA (C) 223ωA - (D) 223ωA 14. 一质点以周期T 作简谐振动, 则质点由平衡位置正向运动到最大位移一半处的最短时间为[ ] (A) 6T (B) 8T (C) 12T (D) T 127 15. 某物体按余弦函数规律作简谐振动, 它的初相位为2π3, 则该物体振动的初始状态为[ ] (A) x 0 = 0 , v 0 0 (B) x 0 = 0 , v 0<0(C) x 0 = 0 , v 0 = 0 (D) x 0 = A , v 0 = 016. 一作简谐运动质点的振动方程为π)21π2cos(5+=t x , 它从计时开始, 在运动一个周期后[ ] (A) 相位为零 (B) 速度为零(C) 加速度为零 (D) 振动能量为零17. 沿x 轴振动的质点的振动方程为)1π3cos(1032-⨯=-t x (SI 制), 则[ ] (A) 初相位为1° (B) 振动周期为T =3 s(C) 振幅A = 3 m (D) 振动频率 23=νHz 18. 有一谐振子沿x 轴运动, 平衡位置在x = 0处, 周期为T , 振幅为A ,t = 0时刻振子过2A x =处向x 轴正方向运动, 则其运动方程可表示为 [ ] (A) )21cos(t A x ω= (B) )cos(2t A x ω= (C) )3π2sin(--=T t A x ω (D) )3π2cos(-=T t A x ω 19. 一质点作简谐振动, 其速度随时间变化的规律为t A v ωωcos -=, 则质点的振动方程为[ ] (A) t A x ωsin = (B) t A x ωcos =(C) π)sin(+=t A x ω (D) π)cos(+=t A x ω20. 当一质点作简谐振动时, 它的动能和势能随时间作周期变化.如果f 是质点振动的频率, 则其动能变化的频率为[ ] (A) 4f (B) 2f (C) f (D) f /221. 已知一简谐振动系统的振幅为A , 该简谐振动动能为其最大值之半的位置是[ ] (A) 12A (B) 22A (C) 32A (D) A 22. 一弹簧振子作简谐振动, 其振动方程为: π)21cos(+=t A x ω.则该物体在t = 0时刻的动能与t = T /8 (T 为周期)时刻的动能之比为[ ] (A) 1:4 (B) 2:1 (C) 1:1 (D) 1:223. 一作简谐振动的质点某时刻位移为x , 系统的振动势能恰为振动动能的n 倍, 则该振动的振幅为[ ] (A) A n x =+⎛⎝ ⎫⎭⎪11 (B) A n x =-⎛⎝ ⎫⎭⎪11 (C) A n x =-11 (D) A nx =+11 24. 一弹簧振子作简谐振动, 当其偏离平衡位置的位移大小为振幅的1/4时, 其动能为振动总能量的[ ] (A) 167 (B) 1615 (C) 169 (D) 1613 25. 一长为l 、质量为m 的单摆, 与一劲度系数为k 、质量为m 的弹簧振子周期相等.则k 、l 、m 、g 之间的关系为[ ] (A) lmg k = (B) g ml k = (C) gl m k = (D) 不能确定 26. 一轻质弹簧, 上端固定, 下端挂有质量为m 的重物, 其自由端振动的周期为T . 已知振子离开平衡位置为x 时其振动速度为v , 加速度为a , 且其动能与势能相等.试判断下列计算该振子劲度系数的表达式中哪个是错误的[ ] (A) a mg k = (B) 22xm k v = (C) x ma k = (D) 22π4Tm k = T 4-1-26图27. 简谐振动的振幅由哪些因素决定[ ] (A) 谐振子所受的合外力 (B) 谐振子的初始加速度(C) 谐振子的能量和力常数 (D) 谐振子的放置位置28. 设卫星绕地球作匀速圆周运动.若卫星中有一单摆, 下述哪个说法是对的[ ] (A) 它仍作简谐振动, 周期比在地面时大(B) 它仍作简谐振动, 周期比在地面时小(C) 它不会再作简谐振动(D) 要视卫星运动速度决定其周期的大小29. 已知一单摆装置, 摆球质量为m ,摆的周期为T .对它的摆动过程, 下述说法中错误的是[ ] (A) 按谐振动规律, 摆线中的最大张力只与振幅有关, 而与m 无关(B) T 与m 无关(C) 按谐振动规律, T 与振幅无关(D) 摆的机械能与m 和振幅都有关30. 弹簧振子在光滑水平面上作谐振动时, 弹性力在半个周期内所作的功为[ ] (A) 2kA (B)221kA (C) 241kA (D) 0 31. 如果两个同方向同频率简谐振动的振动方程分别为π)433cos(73.11+=t x cm 和 π)413cos(2+=t x cm, 则它们的合振动方程为 [ ] (A) π)433cos(73.0+=t x cm (B) π)413cos(73.0+=t x cm (C) π)1273cos(2+=t x cm (D) π)1253cos(2+=t x cm32. 拍现象是由怎样的两个简谐振动合成的[ ] (A) 同方向、同频率的两个简谐振动(B) 同方向、频率很大但相差甚小的两个简谐振动(C) 振动方向互相垂直、同频率的两个简谐振动(D) 振动方向互相垂直、频率成整数倍的两个简谐振动合成33. 两个同方向、同频率、等振幅的谐振动合成, 如果其合成振动的振幅仍不变, 则此二分振动的相位差为[ ] (A) 2π (B) 3π2 (C) 4π (D)34. 二同频率相互垂直的振动方程分别为)cos(11αω+=t A x 和)cos(22αω+=t A y .其合振动的轨迹[ ] (A) 不会是一条直线(B) 不会为一个圆(C) 不能是一封闭曲线(D) 曲线形状要由相位差和两振动振幅而定35. 下面的结论哪一个可以成立[ ] (A) 一个简谐振动不可以看成是两个同频率相互垂直谐振动的合振动(B) 一个简谐振动只可以看成是两个同频率同方向谐振动的合振动(C) 一个简谐振动可以是两个同频率相互垂直谐振动的合振动(D) 一个简谐振动只可以是两个以上同频率谐振动的合振动36. 一质点同时参与两个相互垂直的简谐振动, 如果两振动的振动方程分别为π)π2cos(+=t x 和)π2sin(t y =, 则该质点的运动轨迹是[ ] (A) 直线 (B) 椭圆 (C) 抛物线 (D) 圆37. 将一个弹簧振子分别拉离平衡位置1厘米和2厘米后, 由静止释放(弹簧形变在弹性范围内), 则它们作谐振动的[ ] (A) 周期相同 (B) 振幅相同(C) 最大速度相同 (D) 最大加速度相同38. 谐振子作简谐振动时, 速度和加速度的方向[ ] (A) 始终相同(B) 始终相反(C) 在某两个1/4周期内相同, 另外两个1/4周期内相反(D) 在某两个1/2周期内相同, 另外两个1/2周期内相反39. 下列说法正确的是[ ] (A) 谐振子从平衡位置运动到最远点所需的时间为T 81(B) 谐振子从平衡位置运动到最远点的一半距离所需时间为8T (C) 谐振子从平衡位置出发经历T 121,运动的位移是A 31 (D) 谐振子从平衡位置运动到最远点所需的时间为T 4140. 关于振动和波, 下面几句叙述中正确的是[ ] (A) 有机械振动就一定有机械波(B) 机械波的频率与波源的振动频率相同(C) 机械波的波速与波源的振动速度相同(D) 机械波的波速与波源的振动速度总是不相等的41. 关于波,下面叙述中正确的是[ ] (A) 波动方程中的坐标原点一定要放在波源位置(B) 机械振动一定能产生机械波(C) 质点振动的周期与波的周期数值相等(D) 振动的速度与波的传播速度大小相等42. 按照定义,振动状态在一个周期内传播的距离就是波长.下列计算波长的方法中错误的是[ ] (A) 用波速除以波的频率(B) 用振动状态传播过的距离除以这段距离内的波数(C) 测量相邻两个波峰的距离(D) 测量波线上相邻两个静止质点的距离43. 一正弦波在海面上沿一定方向传播, 波长为, 振幅为A , 波的传播速率为u . 假设海面上漂浮的一块木块随水波上下运动, 则木块上下运动的周期是[ ] (A) u π2λ (B) uλ (C) λπ2u (D) λu 1 44. 当x 为某一定值时, 波动方程)π(2cos λx T t A x -=所反映的物理意义是 [ ] (A) 表示出某时刻的波形 (B) 说明能量的传播(C) 表示出x 处质点的振动规律 (D) 表示出各质点振动状态的分布45. 下列方程和文字所描述的运动中,哪一种运动是简谐振动[ ] (A) x A t =1cos ω(B) x A t A t =+123cos cos ωω(C) d d 2222xt x =-ω(D) 两个同方向、频率相近的谐振动的合成46. 下列方程和文字所描述的运动中,哪一种运动是简谐波[ ] (A) t xA y ωλcos π2cos =(B) )sin(2x cx bt A y ++=(C) 波形图始终是正弦或余弦曲线的平面波(D) 波源是谐振动但振幅始终衰减的平面波47. 下列函数f ( x , t )可以用来表示弹性介质的一维波动, 其中a 和b 是正常数.则下列函数中, 表示沿x 轴负方向传播的行波是[ ] (A) )sin(),(bt ax A t x f += (B) )sin(),(bt ax A t x f -=(C) )cos()cos(),(bt ax A t x f = (D) )sin()sin(),(bt ax A t x f =48. 已知一波源位于x = 5m 处, 其振动方程为: )cos(ϕω+=t A y m .当这波源产生的平面简谐波以波速u 沿x 轴正向传播时, 其波动方程为[ ] (A) )(cos u x t A y -=ω (B) ])(cos[ϕω+-=ux t A y (C) ])5(cos[ϕω++-=u x t A y (D) ])5(cos[ϕω+--=u x t A y 49. 一平面简谐波的波动方程为)2π(sin 5.0x t y --=m, 则此波动的频率、波速及各质点的振幅依次为[ ] (A)21、21、05.0- (B) 21、1、05.0- (C) 21、21、 (D)2、2、50. 已知一列机械波的波速为u , 频率为ν, 沿着x 轴负方向传播.在x 轴的正坐标上有两个点x 1和x 2.如果x 1<x 2 , 则x 1和x 2的相位差为[ ] (A) 0 (B) )(π221x x u -ν (C) (D) )(π212x x u-ν 51. 已知一平面余弦波的波动方程为)01.05.2π(cos 2x t y -=, 式中 x 、y 均以厘米计.则在同一波线上, 离x = 5cm 最近、且与 x = 5cm 处质元振动相位相反的点的坐标为[ ] (A) 7.5 cm (B) 55 cm (C) 105 cm (D) 205 cm52. 两端固定的一根弦线, 长为2m, 受外力作用后开始振动.已知此弦产生了一个波腹的波, 若该振动的频率为340 Hz, 则此振动传播的速度是____ms -1.[ ] (A) 0 (B) 170 (C) 680 (D) 136053. 一波源在XOY 坐标系中(3, 0)处, 其振动方程是)π120cos(t y = cm, 其中 t 以秒计, 波速为50 cm.s -1 .设介质无吸收, 则此波在x <3 cm 的区域内的波动方程为 [ ] (A) )50π(120cos x t y +=cm (B) π]2.7)50π(120cos[-+=xt y cm (C) )50π(120cos x t y -=cm (D) π]2.1)50π(120cos[-+=xt y cm54. 若一平面简谐波的波动方程为)cos(cx bt A y -=, 式中A 、b 、c 为正值恒量.则 [ ] (A) 波速为c (B) 周期为b 1 (C) 波长为c π2 (4) 角频率为bπ255. 一平面简谐横波沿着OX 轴传播.若在OX 轴上的两点相距8λ(其中λ为波长), 则在波的传播过程中, 这两点振动速度的[ ] (A) 方向总是相同 (B) 方向有时相同有时相反 (C) 方向总是相反 (D) 大小总是不相等56. 一简谐波沿Ox 轴正方向传播,t =0时刻波形曲线如左下图所示,其周期为2 s .则P 点处质点的振动速度v 与时间t 的关系曲线为: [ ]vxuY P0A 012Aωv()t D 20ωv15.0()A 12()t ()Aω-12vAω-05.0()C ()s t ()s t57. 当波动方程为)01.05.2π(cos 20x t y +=cm 的平面波传到x =100cm 处时, 该处质点的振动速度为[ ] (A) )π5.2sin(50t (B) )π5.2sin(50t - (C) )π5.2sin(π50t (D) )π5.2sin(π50t -58. 平面简谐机械波在弹性媒质中传播时, 在传播方向上某媒质元在负的最大位移处, 则它的能量是[ ] (A) 动能为零, 势能最大 (B) 动能为零, 势能为零 (C) 动能最大, 势能最大 (D) 动能最大, 势能为零59. 一平面简谐波在弹性媒质中传播, 在媒质元从最大位移处回到平衡位置的过程中 [ ] (A) 它的势能转换成动能 (B) 它的动能转换成势能(C) 它从相邻的一段媒质元中获得能量, 其能量逐渐增大 (D) 它把自己的能量传给相邻的一媒质元, 其能量逐渐减小60. 已知在某一媒质中两列相干的平面简谐波的强度之比是421=I I ,则这两列波的振幅之比21A A 是 [ ] (A) 4 (B) 2 (C) 16 (D) 861. 一点波源发出的波在无吸收媒质中传播, 波前为半球面, 该波强度I 与离波源距离r 之间的关系是 [ ] (A) r I 1∝(B) 31r I ∝ (C) r I 1∝ (D) 21r I ∝62. 当机械波在媒质中传播时, 某一媒质元的最大形变发生在(其中A 是振幅) [ ] (A) 媒质质元离开其平衡位置的最大位移处2A处(B) 媒质质元离开平衡位置2/(C) 媒质元在其平衡位置处(D) 媒质元离开平衡位置2/A处63. 假定汽笛发出的声音频率由400 Hz增加到1200 Hz, 而波幅保持不变, 则1200 Hz 声波对400 Hz声波的强度比为[ ] (A) 1:3 (B) 3:1 (C) 1:9 (D) 9:164. 为了测定某个音叉C的频率, 另选取二个频率已知而且和C音叉频率相近的音叉A和B, 音叉A的频率为400 Hz, B的频率为397 Hz, 并进行下列实验: 使A和C同时振动每秒听到声音加强二次; 再使B和C同时振动, 每秒钟听到声音加强一次, 由此可知音叉C 的振动频率为[ ] (A) 401 Hz (B) 402 Hz (C) 398 Hz (D) 399 Hz65. 人耳能分辨同时传来的不同声音, 这是由于[ ] (A) 波的反射和折射(B) 波的干涉(C) 波的独立传播特性(D) 波的强度不同66. 两列波在空间P点相遇, 若在某一时刻观察到P点合振动的振幅等于两波的振幅之和, 则这两列波[ ] (A) 一定是相干波(B) 不一定是相干波(C) 一定不是相干波(D) 一定是初相位相同的相干波67. 有两列波在空间某点P相遇, 某时刻观察到P点的合振幅等于两列波的振幅之和, 由此可以判定这两列波[ ] (A) 是相干波(B) 相干后能形成驻波(C) 是非相干波(D) 以上三种情况都有可能68. 已知两相干波源所发出的波的相位差为, 到达某相遇点P的波程差为半波长的两倍, 则P点的合成情况是[ ] (A) 始终加强(B) 始终减弱(C) 时而加强, 时而减弱, 呈周期性变化(D) 时而加强, 时而减弱, 没有一定的规律69. 两个相干波源连线的中垂线上各点[ ] (A) 合振动一定最强(B) 合振动一定最弱(C) 合振动在最强和最弱之间周期变化(D) 只能是在最强和最弱之间的某一个值70. 两初相位相同的相干波源, 在其叠加区内振幅最小的各点到两波源的波程差等于[ ] (A) 波长的偶数倍(B) 波长的奇数倍(C) 半波长的偶数倍(D) 半波长的奇数倍71. 在驻波中, 两个相邻波节间各质点的振动是[ ] (A) 振幅相同, 相位相同(B) 振幅不同, 相位相同(C) 振幅相同, 相位不同(D) 振幅不同, 相位不同72. 两列完全相同的余弦波左右相向而行, 叠加后形成驻波.下列叙述中, 不是驻波特性的是[ ] (A) 叠加后, 有些质点始终静止不动(B) 叠加后, 波形既不左行也不右行(C) 两静止而相邻的质点之间的各质点的相位相同(D) 振动质点的动能与势能之和不守恒73. 平面正弦波)π3π5sin(4y t x +=与下面哪一列波相叠加后能形成驻波[ ] (A) )2325π(2sin 4x t y += (B) )2325π(2sin 4x t y -= (C) )2325π(2sin 4y t x += (D) )2325π(2sin 4yt x -=74. 方程为)π100cos(01.01x t y -=m 和)π100cos(01.02x t y +=m 的两列波叠加后, 相邻两波节之间的距离为[ ] (A) 0.5 m (B) 1 m (C) m (D) 2 m75. 1S 和2S 是波长均为λ的两个相干波的波源,相距3λ/4,1S 的相位比2S 超前2π.若两波单独传播时,在过1S 和2S 的直线上各点的强度相同,不随距离变化,且两波的强度都是0I ,则在1S 、2S 连线上1S 外侧和2S 外侧各点,合成波的强度分别是 [ ] (A) 04I ,04I ; (B) 0,0;(C) 0,04I ; (D) 04I ,0.76. 在弦线上有一简谐波,其表达式为⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+⨯=-3π420π100cos 100.221x t y (SI)为了在此弦线上形成驻波,并且在x =0处为一波腹,此弦线上还应有一简谐波,其表达式为:[ ] (A) ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⨯=-3π20π100cos 100.222x t y (SI) (B) ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⨯=-3π420π100cos 100.222x t y (SI) (C) ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯=-3π20π100cos 100.222x t y (SI) (D) ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯=-3π420π100cos 100.222x t y (SI) 二、填空题1. 一质点沿x 轴作简谐振动,平衡位置为x 轴原点,周期为T ,振幅为A , (1) 若t = 0 时质点过x = 0处且向x 轴正方向运动,则振动方程为x =. (2) 若t = 0时质点在x = A /2处且向x 轴负方向运动,则质点方程为x = . 2. 据报道,1976年唐山大地震时,当地居民曾被猛地向上抛起2m 高.设此地震横波为简谐波,且频率为1Hz ,波速为3km s -1, 它的波长是 ,振幅是 .3. 一质点沿x 轴作简谐振动, 其振动方程为: π)31π2cos(4-=t x cm .从t =0时刻起, 直到质点到达 2-=x cm 处、且向 x 轴正方向运动的最短时间间隔为 .4. 一个作简谐振动的质点,其谐振动方程为π)23cos(π1052+⨯=-t x (SI 制).它从计时开始到第一次通过负最大位移所用的时间为 .5. 一单摆的悬线长l =1.3m, 在顶端固定点的铅直下方0.45m 处有一小钉,如T4-2-5图所示.设两方摆动均较小,则单摆的左右两方角振幅之比21θθ的近似值为 . 6. 一质点作简谐振动, 频率为2Hz .如果开始时质点处于平衡位置, 并以 的速率向x 轴的负方向运动, 则该质点的振动方程为 .7. 一谐振动系统周期为, 振子质量为200g .若振子经过平衡位置时速度为12cm.s -1, 则再经后该振子的动能为 .8.劲度系数为100N m -1的轻质弹簧和质量为10g 的小球组成一弹簧振子. 第一次将小球拉离平衡位置4cm, 由静止释放任其振动; 第二次将小球拉离平衡位置2cm 并给以2m.s -1的初速度任其振动.这两次振动的能量之比为 .小钉m45.0l1lT 4-2-5图T 4-1-32图9. 将一个质量为20g 的硬币放在一个劲度系数为的竖直放置的弹簧上, 然后向下压硬币使弹簧压缩1.0cm, 突然释放后, 这个硬币将飞离原来位置的高度为 .10. 质量为0.01 kg 的质点作简谐振动, 振幅为0.1m, 最大动能为 J .如果开始时质点处于负的最大位移处, 则质点的振动方程为 .11. 一物体放在水平木板上,这木板以Hz 2=ν的频率沿水平直线作简谐运动,物体和水平木板之间的静摩擦系数50.0=s μ,物体在木板上不滑动的最大振幅max A = .12. 如果两个同方向同频率简谐振动的振动方程分别为π)3110sin(31+=t x cm 和)π6110sin(42-=t x cm, 则它们的合振动振幅为 [ ] (A) 1 cm (B) 5 cm (C) 7 cm (D) 3 cm13. 已知由两个同方向同频率的简谐振动合成的振动, 其振动的振幅为20cm, 与第一个简谐振动的相位差为6π.若第一个简谐振动的振幅为cm 3.17310=, 则第二个简谐振动的振幅为 cm ,两个简谐振动的相位差为 .14. 已知一平面简谐波的方程为: )π(2cos λνxt A y -=, 在ν1=t 时刻λ411=x 与 λ432=x 两点处介质质点的速度之比是 . 15. 一观察者静止于铁轨旁, 测量运行中的火车汽笛的频率.若测得火车开来时的频率为2010 Hz, 离去时的频率为1990 Hz, 已知空气中的声速为330m.s -1, 则汽笛实际频率是 .16. 已知一入射波的波动方程为)4π4πcos(5xt y +=(SI 制), 在坐标原点x = 0处发生反射, 反射端为一自由端.则对于x = 0和x = 1米的两振动点来说, 它们的相位关系是相位差为 .17. 有一哨子, 其空气柱两端是打开的, 基频为5000 Hz, 由此可知,此哨子的长度最接近 厘米.18. 一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为)4π/cos(05.01+=t x ω (SI) )12π/19cos(05.02+=t x ω(SI)其合成运动的运动方程为=x .(SI)19. 已知一平面简谐波沿x 轴正向传播,振动周期T = s ,波长= 10m , 振幅A =0.1m .当t = 0时波源振动的位移恰好为正的最大值.若波源处为原点,则沿波传播方向距离波源为2/λ处的振动方程为 .当 t = T / 2时,4/λ=x 处质点的振动速度为 .20. T4-2-20图表示一平面简谐波在 t = 2s 时刻的波形图,波的振幅为 0.2m ,周期为4s .则图中P 点处质点的振动方程为 .21. 一简谐波沿BP 方向传播,它在B 点引起的振动方程为t A y π2cos 11=.另一简谐波沿CP 方向传播,它在C 点引起的振动方程为()ππ2cos 22+=t A y .P 点与B 点相距0.40m ,与C 点相距0.50m(如T4-2-21图).波速均为u =0.20m s -1.则两波在P 的相位差为 .22. 如T4-2-22图所示,一平面简谐波沿Ox 轴正方向传播,波长为λ,若1P 点处质点的振动方程为()ϕ+=vt A y π2cos 1,则2P 点处质点的振动方程为 ,与1P 点处质点振动状态相同的那些点的位置是 .23. 一个点波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为1R 和2R .在两个球面上分别取相等的面积1S ∆和2S ∆,则通过它们的平均能流之比21/P P =_______.P(m)y A 传播方向(m)xT4-2-20图 T4-2-21图PB1r 2r ...Cx1P2P O 1L 2LT4-2-22图24. 一列平面简谐波在截面积为S 的圆管中传播, 其波的表达为)π2(cos λωxt A y -=,管中波的平均能量密度是w , 则通过截面积S 的平均能流是 .25. 两相干波源1S 和2S 的振动方程分别是t A y ωcos 1=和π)21(cos 2+=t A y ω.1S 距P 点3个波长,2S 距P 点421个波长.两波在P 点引起的两个振动的相位差的绝对值是 .26. 如T4-2-26图所示,1S 和2S 为同相位的两相干波源,相距为L ,P 点距1S 为r ;波源1S 在P 点引起的振动振幅为1A ,波源2S 在P 点引起的振动振幅为2A ,两波波长都是λ,则P 点的振幅A = .27. 21S S 、为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23为波长)(λ如图.已知1S 的初相位为π21. (1) 若使射线C S 2上各点由两列波引起的振动均干涉相消,则2S 的初位相应为:_______________________.(2) 若使21S S 连线的中垂线M N 上各点由两列波引起的振动均干涉相消,则2S 的初位相应为:________________________________________. 三、计算题1. 如T 4-3-1图所示,将一个盘子挂在劲度系数为k 的弹簧下端,有一个质量为m 的物体从离盘高为h 处自由下落至盘中后不再跳离盘子,由此盘子和物体一起开始运动(设盘子与弹簧的质量可忽略,如图取平衡位置为坐标原点,选物体落到盘中的瞬间为计时零点).求盘子和物体一起运动运动时的运动方程.T 4-3-1图L r1S P2ST4-2-26图•••MN1S 2S CT4-2-27图2. 一质量为10g 的物体在x 方向作简谐振动,振幅为24cm ,周期为4s .当t =0时该物体位于x = 24cm 处.求:(1) 当t =时物体的位置及作用在物体上力的大小.(2) 物体从初位置到x =-12cm 处所需的最短时间,此时物体的速度.3. 作简谐振动的小球,速度的最大值为-1m ax s cm 3⋅=v ,振幅为2cm =A .若令速度具有正最大值的某时刻为计时器点,求该小球运动的运动方程和最大加速度.4如T4-3-4图所示,定滑轮半径为R ,转动惯量为J ,轻弹簧劲度系数为k ,物体质量为m ,将物体从平衡位置拉下一极小距离后放手,不计一切摩擦和空气阻力,试证明该系统将作谐振动并求其振动周期.5. 如T 4-3-5图所示,有一水平弹簧振子,弹簧的劲度系数k =241-m N ⋅,重物的质量m =6kg .最初重物静止在平衡位置上,一水平恒力F =10N 向左作用于物体,(不计摩擦),使之由水平位置向左运动了0.05m ,此时撤去力F .当重物运动到左方最远位置时开始计时,求该弹簧振子的运动方程.6. 已知某质点振动的初始位置为20Ax =,初始速度00>v (或说质点正向x 正向运动),求质点的振动初相位.7. 如T4-3-7图所示,一半径为R 的匀质圆盘绕边缘上一点作微角摆动, 如果其周期与同样质量单摆的周期相同, 求单摆的摆线长度.8. 某人欲了解一精密摆钟的摆长, 他将摆锤上移了1 mm, 测出此钟每分钟快.这钟的摆长是多少T 4-3-5图T 4-3-7图T 4-3-4图9. 已知一简谐振子的振动曲线如T3-4-9图所示,求其运动方程.10. 如T4-3-10图所示,一劲度系数为k 的轻弹簧,一端固定在墙上,另一端连结一质量为m 1的物体,放在光滑的水平面上.将一质量为m 2的物体跨过一质量为M ,半径为R 的定滑轮与m 相连,求此系统的振动圆频率.11. 一个质量为m 的小球在一个光滑的半径为R 的球形碗底作微小振动,如T4-3-11图所示.设0=t 时,0=θ,小球的速度为0v ,向右运动.试求在振幅很小情况下,小球的振动方程.12. 如T4-3-12图所示,一质点作简谐振动,在一个周期内相继通过距离为12cm 的两点A 、B ,历时2s ,并且在A 、B 两点处具有相同的速度;再经过2s 后,质点又从另一方向通过B 点.试求质点运动的周期和振幅.13. 如T4-3-13图所示,在一轻质刚性杆AB 的两端,各附有一质量相同的小球,可绕通过AB 上并且垂直于杆长的水平轴O 作振幅很小的振动.设OA = a , OB = b , 且b > a ,试求振动周期.14. 有两个振动方向相同的简谐振动,其振动方程分别为T4-3-9 T4-3-10图RT4-3-11图OθT4-3-12图AT4-3-13图OθBba(cm)2ππ2cos 3(cm)π)π2cos(421⎪⎭⎫⎝⎛+=+=t x t x (1) 求它们的合振动方程;(2) 另有一同方向的简谐振动cm )π2cos(233ϕ+=t x ,问当3ϕ为何值时,31x x +的振幅为最大值当3ϕ为何值时,31x x +的振幅为最小值15. 一质量为M 的全息台放置在横截面均匀的密封气柱上(见T4-3-15题图).平衡时气柱高度为h .今地基作上、下振动,规律为t A x G ωcos =,其中A 为振幅,ω为振动圆频率.忽略大气压强和阻尼,试求全息台振动的振幅.16. 假设地球的密度是均匀的,如果能沿着地球直径挖通一穿过地球的隧道,试证明落入隧道的一个质点的运动是简谐运动,并求出其振动周期.17. 已知波线上两点A 、B 相距1m, B 点的振动比A 点的振动滞后121s, 相位落后ο30, 求此波的波速.18. 一简谐波,振动周期21=T s ,波长 =10m ,振幅A = 0.1m. 当t = 0时刻,波源振动的位移恰好为正方向的最大值.若坐标原点和波源重合,且波沿Ox 轴正方向传播,求:(1) 此波的表达式;(2) 4/1T t =时刻,4/1λ=x 处质点的位移;(3) 2/2T t =时刻,4/1λ=x 处质点振动速度.19. 一列平面简谐波在介质中以波速u = 5m s -1沿x 轴正向传播,原点O 处质元的振动曲线如图所示.(1) 画出x =25m 处质元的振动曲线.T4-3-19图20()cm y 42)s (tT4-3-15图h。
