实验二网孔电流和节点电压分析法仿真
电路分析网孔分析法和节点分析

将电路中的某些单口用其等效电路代替,可以简化 电路的分析和计算。
一、线性电阻的串联和并联
1.线性电阻的串联(见第一章)
2.线性电阻的并联(见第一章)
3.线性电阻的串并联 由若干个线性电阻的串联和并联所形成的单口网
络,就端口特性而言,等效于一个线性二端电阻。
i5 R2 i+2 R5 ib uS-2
支路电流: i1,i2,i3,i4,i5,i6 网孔电流:
假想沿网孔边沿流动的电流,
i4
R4 ic R6 i6
如图中ia,ib,ic
R3 +uS3-i3 参考方向可以任意选取。
若以网孔电流为求解变量, 所需方程数将大大减少。(重点)
一、网孔电流
设想电流i1、i2和i3沿每个
图中 节点1与公共点O间电阻称为R1 节点2与公共点O间电阻称为R2 节点3与公共点O间电阻称为R3
二、Δ形联接
当三个电阻依次联成一个 闭合电路,且三个联接点再 分别与外电路相联,叫Δ形 联接。
图中:
节点1与2间电阻称为R12 节点2与3间电阻称为R23 节点3与1间电阻称为R31
方法: Y-变换
R2
R12
R23 R12 R 23 R31
特例:当三电阻相等时,则
R 3RY
或
RY
1 3
R
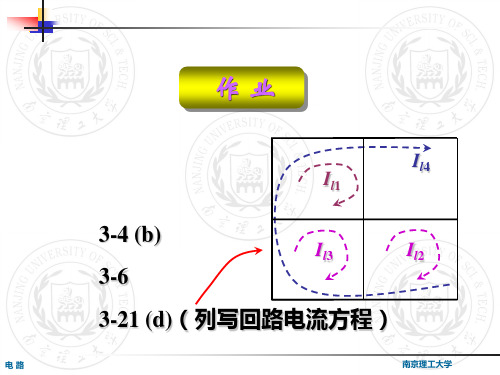
历年考题:
9、图示电路,求u 。(2V)
10、图示电路,求i 。(9/13A)
3Ω
6Ω
i
+ 18V
+u–
1A
3Ω 2A 2Ω 4Ω
–
2Ω
6Ω
3Ω
第三章网孔分析法和结点分析法
节点和网孔分析法

根据基尔霍夫电压定律(KVL),可以建立每个网孔的电压方程。对于每个网孔,其电压降等于该网 孔上所有元件电压降的代数和。通过列写网孔电压方程,可以得到一组以网孔电流为未知数的线性方 程组。
网孔阻抗矩阵形成与求解
阻抗矩阵形成
在列写网孔电压方程时,需要将电路中 的电阻、电感、电容等元件用阻抗表示 。将各元件的阻抗按照网孔电流的流向 排列成矩阵形式,即可得到网孔阻抗矩 阵。该矩阵是一个方阵,其阶数等于网 孔数。
在多个领域进行了实际应用验证,证明了 节点和网孔分析法的有效性和实用性。
未来发展趋势预测
跨领域应用拓展
随着节点和网孔分析法的不断完善,其应用领域将进一步拓展,包括 社交网络、交通网络、生物网络等多个领域。
动态网络分析
未来研究将更加注重动态网络的分析,探索网络结构和行为的动态演 化规律。
多层网络分析
节点导纳矩阵形成与求解
形成节点导纳矩阵
将节点电压方程中的系数按照一定规则排列成矩阵形式,得到节点导纳矩阵。 矩阵中的元素表示各节点之间的电导连接关系。
求解节点电压
根据节点导纳矩阵和给定的电流源,可以求解出各节点的电压值。一般采用高 斯消元法或迭代法进行求解。
03
网孔分析法
网孔定义及分类
网孔定义
随着多层网络研究的兴起,节点和网孔分析法将进一步拓展到多层网 络分析领域,揭示不同层级网络之间的相互作用和影响。
算法优化与创新
针对现有算法存在的问题和不足,未来研究将致力于算法的优化和创 新,提高节点和网孔分析法的准确性和效率。
THANKS。
05
节点和网孔分析法在电路中的 应用
复杂电路分析
01
02
03
节点分析法
网孔电流法和节点电压法例题分析

课题8:支路电流法、网孔电流法和节点电压法课型:讲授教学目的:(1)利用支路电流法求解复杂直流电路(2)利用网孔电流法求解支路数目较多的电路。
(3)利用节点电压法求解节点较少而网孔较多的电路重点、难点:重点:支路电流法、网孔电流法、节点电压法求解复杂直流电路难点:列方程过程中电压、电流参考方向及符号的确定。
教学分析:本节主要还是在巩固基尔霍夫定律的基础上,利用实例分析支路电流法、网孔电流法、节点电压法并将其用于实践案例中。
复习、提问:(1)节点的概念和判别?(2)网孔的概念和判别?教学过程:导入:求解复杂电路的方法有多种,我们可以根据不同电路特点,选用不同的方法去求解。
其中最基本、最直观、手工求解最常用的就是支路电流法。
一、支路电流法利用支路电流法解题的步骤:(1)任意标定各支路电流的参考方向和网孔绕行方向。
(2)用基尔霍夫电流定律列出节点电流方程。
有n个节点,就可以列出n-1个独立电流方程。
(3)用基尔霍夫电压定律列出L=b-(n-1)个网孔方程。
说明:L指的是网孔数,b指是支路数,n指的是节点数。
(4)代入已知数据求解方程组,确定各支路电流及方向。
例1试用支路电流法求图1中的两台直流发电机并联电路中的负载电流I及每台发电机的输出电流I1、和I2。
已知:R1=1Ω,R2=0.6Ω,R=24Ω,E1=130V,E2=117V。
解:(1)假设各支路电流的参考方向和网孔绕行方向如图示。
图1(2)根据KCL,列节点电流方程该电路有A、B两个节点,故只能列一个节点电流方程。
对于节点A有:I1+I2=I ①(3)列网孔电压方程该电路中共有二个网孔,分别对左、右两个网孔列电压方程:I1R1-I2R2+E2-E1=0 ②(沿回路循行方向的电压降之和为零,如果在I R+I2R2-E2=0 ③该循行方向上电压升高则取负号)(4)联立方程①②③,代入已知条件,可得:-I1-I2+I=0I1-0.6I2=130-1170.6I2+24I=117解得各支路电流为:I1=10A I2=-5A I=5A从计算结果,可以看出发电机E1输出10A的电流,发电机E2输出-5A的电流,负载电流为5A。
第二章 网孔分析和节点分析

un3 20 50 105 175V U un3 1 20 195V
I ( un 2 90) / 1 120 A
返 回 上 页 下 页
+
un1 100V
1 - U 20A + 3 2 2
-
100V
1
5.节点分析和网孔分析的比较:
1.网孔分析只适于平面电路;
+ : 流过互电阻的两个回路电流方向相同
Rkk:自电阻(为正)
Rjk =Rkj :互电阻
- : 流过互电阻的两个回路电流方向相反 0 : 无关
返 回 上 页 下 页
2. 网孔分析法的一般步骤(只适于平面电路):
(1) 选定m=b-(n-1)个网孔,并确定其绕行方向;
(2) 对m 个网孔,列写网孔方程(实质是KVL方程); 自电阻、互电阻、电压升。方程个数为b-(n-1)。 (3) 求解上述方程,得到m个网孔电流; (4) 求各支路电流(用网孔电流表示); (5) 其它分析。
(2) 用节点电压表示控制量。
u3 un 3 i un 2 R2
返 回 上 页 下 页
I
例
求U和I 。 应用节点法。
1
- 90V + 2
un 2 100 110 210V
注:与电流源串接的 电阻不参与列方程
0.5un1 0.5un 2 un3 20
+ - 110V
b ( n 1)
a i1 R1 uS1 + – i2 R2 + – iM2 i3
与支路电流法相比, 方程数减少n-1个。
(R1+ R2) iM1-R2iM2=uS1-uS2
i M1
R3
uS2
实践二 简单电路原理仿真综合实践(二)

韶关学院学生实践报告册实践课程名称:电路原理与仿真实践实践项目名称:简单电路原理仿真综合实践(二)实践类型(打√):(基础 、综合□、设计□)院系:教育学院专业班级:16数字媒体技术姓名: 林美露组员詹晓茹学号: 16114091037 指导老师彭浩韶关学院教务处编制实践报告内容实践报告内容原则上应包含主要实践步骤、实践数据计算(实践操作)结果、实践结果(疑问)分析等项目。
实践内容仿真实践1 实际电压源与实际电流源的等效变换一、实践目的(1)掌握EWB软件的使用方法。
(2)通过实践理解电压源和电流源的概念和各自的外部特性。
(3)理解理想电压源与实际电压源的区别及理想电流源与实际电流源的区别。
(4)掌握电压源与电流源进行等效变换的条件。
二、实践原理(1)理想电压源是指能输出恒定电压的电源。
输出电压的大小U与负载的大小无关,输出的电流I 可以是0~∞的任意值,完全由外电路的负载决定。
(2)理想电流源是指能输出恒定电流的电源。
输出电流的大小I与负载的大小无关,输出的电流U 可以是0~∞的任意值,完全由外电路的负载决定。
(3)理想电压源与理想电流源在实际中并不存在。
一个实际电源可以用理想电压源Us与电阻Rs串联的电压源表示,也可以用理想电流源Is与电阻Rs并联的电流源表示。
(4)电压源与电流源都是用来表示一个实际电源的,所以他们之间可以进行等效变换,其等效变换的条件为U s=I s R s或I s=U s/R s。
三、实践内容及步骤(1)在EWB软件中按图2.64连接电压源实践,其中电压源的电压为10V,电压源内阻为1kΩ。
外电路为1kΩ可调电位器,外电路中接入电流表和电压表。
图2.64 电压源实践电路图(2)单击仿真运行开关按钮,并通过键盘按钮调节电位器阻值的百分比,使阻值分别为0Ω,250Ω,500Ω,750Ω,1000Ω,将所测的的电流与电压值记录在实践数据表2.1中。
实践数据表2.1可调电阻(Ω)0 250 500 750 1000外电路电流(mA)10.000 8.000 6.667 5.715 5.000外电路电压(V) 1.000μ 2.000 3.333 4.285 4.999(3)按图2.65连接电流源实践电路。
电路仿真实验报告

电路仿真MATLAB实验报告班级:学号:姓名:学院:实验一直流电路(1)一、实验目的1、加深对直流电路的节点电压法和网孔电流法的理解2、学习使用MATLAB的矩阵运算的方法二、实验示例1、节点分析电路如图所示(见书本12页),求节点电压V1,V2,V3.根据电路图得到矩阵方程,根据矩阵方程使用matlab命令为Y =0.1500 -0.1000 -0.0500-0.1000 0.1450 -0.0250-0.0500 -0.0250 0.0750节点v1,v2和v3:v =404.2857350.0000412.85712、回路分析电路如图所示(见书本13页),使用解析分析得到同过电阻RB的电流,另外求10V电压源的输出功率。
分析电路得到节点方程,根据节点方程得到矩阵方程,根据矩阵方程,使用matlab的命令为z=[40,-10,-30;-10,30,-5;-30,-5,65];v=[10,0,0]';I=inv(z)*v;IRB=I(3)-I(2);fprintf('the current through R is %8.3f Amps \n',IRB)ps=I(1)*10;fprintf('the power supplied by 10v source is %8.4f watts\n',ps)结果为:the current through R is 0.037 Ampsthe power supplied by 10V source is 4.7531 watts三、实验内容1 根据书本15页电路图,求解电阻电路,已知:R1=2Ω,R2=6Ω,R3=12Ω,R4=8Ω,R5=12Ω,R6=4Ω,R7=2Ω如果Us=10V,求i3,u4,u7如果U4=4V,求Us,i3,i7使用matlab命令为clear% 初始化阻抗矩阵Z=[20 -12 0;-12 32 -12;0 -12 18];% 初始化电压矩阵V=[10 0 0]';% 解答回路电流I=inv(Z)*V;% I3的计算I3=I(1)-I(2);fprintf('the current I3 is %8.2f Amps\n',I3) % U4的计算U4=8*I(2);fprintf('the voltage U4 is %8.2f Vmps\n',U4) % U7的计算U7=2*I(3);fprintf('the voltage U7 is %8.2f Vmps\n',U7)结果the current I3 is 0.36 Ampsthe voltage U4 is 2.86 Vmpsthe voltage U7 is 0.48 Vmpsclear% 初始化矩阵XX=[20 -1 0;-12 0 -12;0 0 18];% 初始化矩阵YY=[6 -16 6]';% 进行解答A=inv(X)*Y;% 计算各要求量Us=A(2)I3=A(1)-0.5I7=A(3)结果Us = 14.0000I3 = 0.5000I7 =0.33332 求解电路里的电压如图1-4(书本16页),求解V1,V2,V3,V4,V5使用matlab命令为clear% 初始化节点电压方程矩阵Z=[0.725 -0.125 -0.1 -5 -1.25;-0.1 -0.2 0.55 0 0;-0.125 0.325 -0.2 0 1.25;1 0 -1 -1 0;0 0.2 -0.2 0 1];I=[0 6 5 0 0]';% 解答节点电压U1,U3,U4与Vb,IaA=inv(Z)*I;% 最终各电压计算V1=A(1)V2=A(1)-10*A(5)V3=A(2)V4=A(3)V5=24结果V1 =117.4792V2 = 299.7708V3 =193.9375V4 =102.7917V5 = 243、如图1-5(书本16页),已知R1=R2=R3=4Ω,R4=2Ω,控制常数k1=0.5,k2=4,is=2A,求i1和i2.使用matlab命令为clear% 初始化节点电压方程矩阵Z=[0.5 -0.25 0 -0.5;-0.25 1 -1 0.5;0 0.5 0 -1;1 -1 -4 0];I=[2 0 0 0]';% 解答节点电压V1,V2及电流I1,I2A=inv(Z)*I;% 计算未知数V1=A(1)V2=A(2)I1=A(3)I2=A(4)结果如下:V1 =6V2 =2I1 = 1I2 =1实验二直流电路(2)一、实验目的1、加深多戴维南定律,等效变换等的了解2、进一步了解matlab在直流电路中的作用二、实验示例如图所示(图见书本17页2-1),分析并使用matlab命令求解为clear,format compactR1=4;R2=2;R3=4;R4=8;is1=2;is2=0.5;a11=1/R1+1/R4;a12=-1/R1;a13=-1/R4;a21=-1/R1;a22=1/R1+1/R2+1/R3;a23=-1/R3;a31=-1/R4;a32=-1/R3;a33=1/R3+1/R4;A=[a11,a12,a13;a21,a22,a23;a31,a32,a33];B=[1,1,0;0,0,0;0,-1,1];X1=A\B*[is1;is2;0];uoc=X1(3);X2=A\B*[0;0;1];Req=X2(3);RL=Req;P=uoc^2*RL/(Req+RL)^2;RL=0:10,p=(RL*uoc./(Req+RL)).*uoc./(Req+RL),figure(1),plot(RL,p),gridfor k=1:21ia(k)=(k-1)*0.1;X=A\B*[is1;is2;ia(k)];u(k)=X(3);endfigure(2),plot(ia,u,'x'),gridc=polyfit(ia,u,1);%ua=c(2)*ia=c(1) , 用拟合函数术,c(1),c(2)uoc=c(1),Req=c(2) RL =0 1 2 3 4 5 6 7 8 9 10 p =Columns 1 through 70 0.6944 1.0204 1.1719 1.2346 1.2500 1.2397Columns 8 through 111.2153 1.1834 1.1480 1.1111A 、功率随负载变化曲线 B.电路对负载的输出特性0123456789100.20.40.60.811.21.400.20.40.60.81 1.2 1.4 1.6 1.82三、实验内容1、图见书本19页2-3,当RL从0改变到50kΩ,校验RL为10kΩ的时候的最大功率损耗使用matlab命令为clear% 定义电压源和电阻值Us=10;Rs=10000;RL=0:20000;p=(Us^2.*RL)./(RL+Rs).^2;plot(RL,p);输出结果为Maximum power occur at 10000.00hmsMaximum power dissipation is 0.0025Watts2、在图示电路里(书本20页2-4),当R1取0,2,4,6,10,18,24,42,90和186Ω时,求RL 的电压UL,电流IL 和RL 消耗的功率。
运用节点法和网孔法进行电路分析

(4.25)
(4.26)
图7所示电路包含两个电压源,而且经我们指定参考节点,电压源 V 2 是一个浮动电压源。 如图中所示,超节点包括电压源和与它并联的电阻元件 R 4 。
图7 另一个超节点例子
首先,我们注意到通过电阻 R 4 的电流 I 4 由公式(4.27)给出:
R R1 R3
这种形式。如
果对角线上的某个元素由正、负两部分组成,那么一定有一个符号是错误的。 · 所有的对角线上的元素都是正的,其它元素都是负的,而且矩阵是对称的 Aij = A ji 。如果矩 阵不具有这个特性,那一定存在错误。 用上面的形式列写电路方程式,一定存在一组由真实电流值构成的解。 一旦我们把方程式变为矩阵形式,对结果进行逐条的检验。如果 det A = 0 ,那么就能得出 一组解。 未知电压 VK 为:
运用节点法和网孔法进行电路分析运用节点法和网孔法进行电路分析众所周知运用基尔霍夫定律和欧姆定律我们可以对任何一个电路进行分析以确定其运行条件电流和电压值
运用节点法和网孔法进行电路分析
众所周知,运用基尔霍夫定律和欧姆定律,我们可以对任何一个电路进行分析,以确定其 运行条件(电流和电压值)。一般电路分析的难点在于用最少的联立方程描述电路的运行特性。 在这一讲里,我们将介绍两种非常有效的可用于对任意电路进行分析的方法:节点法和网 孔法。这些方法是建立在对基尔霍夫定律的系统应用基础上的,我们将通过图1的例子电路来说 明求解的步骤。
图10 标注网孔电流方向 现在,让我们把注意力转移到标记各个支路上的元件电压。 电阻上电压极性与指定的网孔电流的方向一致。万一某一处支路被两个网孔共用,就像例 子中含有电阻 R 2 的支路,电压的极性与各自网孔中指定的网孔电流的方向一致。 在这个电路中,我们进行网孔分析的第一步是单独分析每个网孔,根据定义的网孔电流方 向在回路上应用KVL定律。 考虑网孔1 为了分析更方便,我们把网孔1从图11所示的电路中分离出来。这么做的时候,必须注意要 包括共享支路的所有信息。在这里,我们给出了网孔电流 I 2 在共享支路上的方向。
04 网孔和回路电流法、节点电压法
I m1 I m3 5
南京理工大学
3.2 网孔电流法和回路电流法
1Ω 2Ω Im1 I
20V _ +
+ U1 5A + _
10A
Im2
2Ω _
40V
U
Im3
_ 10V +
+ _
解得:I m1 6A I m3 1A I I m1 I m 2 4A U 2( I m 2 I m3 ) 40 22V
3.2 网孔电流法和回路电流法
例: 求受控电压源发出的功率
.
9Ω 3Ω Im2 1.5U _ 5A I + m1 . + I 1Ω U Im3 _
Is R1 R2 R3 +
.
+
Us
_
Is
R3Is
电路
_
南京理工大学
3.2 网孔电流法和回路电流法
第2类情况:含理想电流源支路 理想电流源位于边沿支路 R1 R2
. .
+ Us _
Im1
R3
Im2
Is
a: 选取网孔电流绕行方向,其中含理想电流源支路的 网孔电流为已知量: Im2=-Is
b: 对不含有电流源支路的网孔根据直接观察法列方程 :
R2 I m1 ( R2 R3 ) I m2 U 0 c: 添加约束方程: m2 I m1 I s I d: 求解
电路 南京理工大学
3.2 网孔电流法和回路电流法
电路中含受控源的网孔法
R1
.
I
R3 Im2
+
Us _ Im1
+ _ rI
a: 选取网孔电流绕行方向 b: 先将受控源作独立电源处理,利用直接观察法列方程: ( R1 R2 ) I m1 R2 I m2 U s
2-2节点分析

练习
(1S)u1 5A - i
解:选定6V电压源电流i的
(0.5S)u2 2A i
参考方向。计入电流变量i
列出两个结点方程:
补充方程 u1 u2 6V
解得 u1 4V,u2 2V,i 1A
28
练习
用结点分析法求图 所示电路的结点电 压。
u1=14V (1S)u1 (1S 0.5S)u2 3A - i6 (0.5S)u1 (1S 0.5S)u3 i6
自电导是各节点上所有 电导的总和。
自电导总是正的。
i4
3
G4
2
is2
1
G3 i3
is1
G2
G1
i2
i1
4
二、节点方程组
节点1:G1 G 4 u N 1 G 4 u N 3 iS 2 节点2:G 2 G 3 u N 2 G 3u N 3 iS 2 节点3: G 4 u N 1 G 3u N 2 G 3 G 4 u N 3 iS 1
22
四、含有电压源网络的节点方程
情况2:当网络中含有多个无伴电压源,且这些电压源 无公共节点时。
此时无法将理想电压源的端电压设定为节点电压,可 设流过无伴电压源电流为未知量,按前述方法先列节点方 程,再用补充方程将该电压源的电压用节点电压表示。
23
四、含有电压源网络的节点方程
例5: 试列出节点电压方程。
i4
节点1 : i1 i4 iS2
3
G4
2
is2
1
节点2: i2 i3 iS2 节点3: i4 i3 iS1
is1
由欧姆定律i=Gu,得:
G3 i3
G2
i2
G1
i1
G1u14 G4u31 iS2 G2u24 G3u23 iS2
第二章-网孔分析和节点分析

网孔分析和节点分析
——网络方程分析法
如何选择更少的求解量, 问题: 减少联立方程数?
这些量必须具备以下性质: 1.完备性:一旦这些量被求出,其它 变量便迎刃而解;(KVL或KCL)
2.独立性:不受KVL或KCL约束,即它们 对KVL或KCL是独立的;(不相关)
本章主要内容:
1、网孔电流分析法;
KVL回路绕行方向选择与网孔电流方向一致。
——即电压降
电压降=电压升:
( R 1 R 4 R 5 ) i m 1 R 5 i m 2 R 4 i m 3 u S1 u S4 R 5 im 1 ( R 2 R 5 R 6 )im 2 R 6 im 3 u S 2 R 4 i m 1 R 6 i m 2 ( R 3 R 4 R 6 ) i m 3 u S 3 u S4
归纳 网孔分析法的计算步骤如下:
1.在电路图上标明网孔电流及参考方向;
2.列解网孔KVL方程; 3.求得各支路电流或电压。
例2-1
用网孔分析法求 I1,I2,I3和U。
I1 I2
2 I1
+ U _
I3
4
2 I2
20V
10V
I1 + U _
I2 2 10V
2 20V
4
6 I 1 4 I 2 20 4 I 1 6 I 2 10
I3
20 I1 1 10 6 4
4 6 4 6 120 40 36 16 4A I2 2 4 6 60 80 20 1A
解得: I3=I1-I2=3A
U= 4I3=12V
三、网孔方程的特殊处理方法
电路分析基础2网孔和节点分析

三、网孔分析法的计算步骤
1.在电路图上标明网孔电流及其参考方向。若全部网
孔电流均选为顺时针(或逆时针)方向,则网孔方程的全部
互电阻项均取负号。 2.用观察电路图的方法直接列出各网孔方程。 3.求解网孔方程,得到各网孔电流。 4.假设支路电流的参考方向。根据支路电流与网孔电 流的线性组合关系,求得各支路电流。 5.用VCR方程,求得各支路电压。
整理为
5i1 2i2 i3 12A 2i1 11 i2 6i3 6A i1 6i2 10 i3 19A
解得:
i 1 A i 2 A i 3 A 1 2 3 i i i 4 A i i i 3 A i i i 1 A 4 3 1 5 1 2 6 3 2
a a b a a 11 1 ,j 1 1 1 ,j 1 1 n
其中
D j a a b a a n 1 n ,j 1 n n ,j 1 nn
例 用网孔分析法求 电路各支路电流。
解:选定各网孔电流的参考方向。列出网孔方程:
( 2 1 2 ) i ( 2 ) i ( 1 ) i 6 V 18 V 1 2 3 ( 2 ) i ( 2 6 3 ) i ( 6 ) i 18 V 12 V 1 2 3 ( 1 ) i ( 6 ) i ( 3 6 1 ) i 25 V 6 V 1 2 3
i i2 7 A 1
3 A i 4 A u 2 V 求解以上方程得到: i 1 2
例
用网孔分析法求解电路的网孔电流。
解:当电流源出现在电路外围边界上时,该网孔电流等于 电流源电流,成为已知量,此例中为i3=2A。此时不必
电路(第二章 网孔分析与节点分析)

(1)i1 u 5V (2)i 2 u 10V
补充方程
i1 2i2 5A i1 i2 7 A
i1 i 2 7A
1
求解以上方程得到: i
3A
返 回
i2 4A
u 2V
上一页 下一页
电路分析基础
例4 电路如下图所示,试求流经30Ω(R3)电阻的电流i3。 已知:us=40V,is=2A,R1=20Ω,R2=50Ω,R3=30Ω。 解:假定两网孔电流iM1和iM2都为顺时针方向。
返 回 上一页 下一页
电路分析基础
整理为
5i1 2i 2 i3 12A 2i1 11i 2 6i3 6A i1 6i 2 10i3 19A
解得:
i1 1A i2 2A
i3 3A
i4 i3 i1 4A i5 i1 i2 3A i6 i3 i2 1A
电路分析基础
小结
网孔电流是一组独立的电流变量,具有 完备性和独立性,其个数为m=b-(n-1)<b;
网孔电流方程根据电路可以直接写出, 所以网孔电流法比1b法更方便;网孔方程 的实质就是关于网孔的KVL方程 含电压源支路多且网孔数少的电路宜用 网孔电流分析法。
返 回 上一页 下一页
电路分析基础
解:选定各支路电路的参考方向。
R1 i1 i3 R3
R2
+
假定两网孔电流iM1、iM2都是 + us1 顺时针方向。
i2 u s2
自电阻: R11 R1 R3 5 20 25, R22 R2 R3 10 20 30。 互电阻:R12 R21 R3 20
EDA2.1.2 支路电流法和节点电压分析法仿真
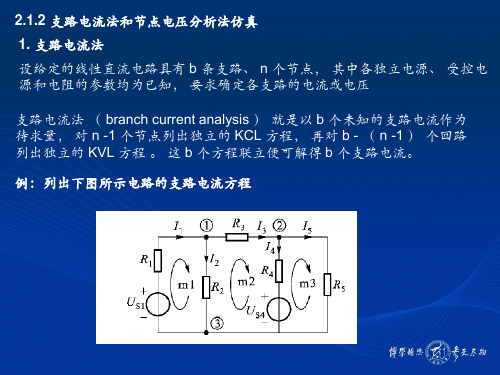
5个支路电流,需列出5个独立方程;两个独立节点,列出两个 个支路电流,需列出 个独立方程 两个独立节点,列出两个KCL方程; 个独立方程; 方程; 个支路电流 方程 三个网孔,列出三个KVL方程 三个网孔,列出三个 方程
课堂练习:列写下图所示电路的支路电流方程, 课堂练习:列写下图所示电路的支路电流方程,并通过实验测量各支路电流
2.1.2 支路电流法和节点电压分析法仿真 1. 支路电流法 设给定的线性直流电路具有 b 条支路、 n 个节点, 其中各独立电源、 受控电 源和电阻的参数均为已知, 要求确定各支路的电流或电压 支路电流法 ( branch current analysis ) 就是以 b 个未知的支路电流作为 待求量, 对 n -1 个节点列出独立的 KCL 方程, 再对 b - ( n -1 ) 个回路 列出独立的 KVL 方程 。 这 b 个方程联立便可解得 b 个支路电流。 例:列出下图所示电路的支路电流方程
练习:用节点电压法求图示电路的电流 练习:用节点电压法求图示电路的电流I
(a)
1 1 2 1 1 1 + U n1 − U n 2 − U n3 = − + 0.5 2 5 1 0.5 2 1 1 1 1 − + U n 2 − U n 3 = I U ቤተ መጻሕፍቲ ባይዱ1 + 0.5 1 0.5 1 1 1 1 1 − U n1 − U n 2 + + U n 3 2 20 20 10 U n 2 = 10
戴维南定理图示
例: 计算图 ( a )电桥中 R x 分别等于 0 该支路的电流
、0.8
、1.6
时,
① 求开路电压 U oc 。 将 R x 支路断开时, 电路如图( b ) 所示。 源电流 5 A 分流成 I 1 和 I 2 , 由分流公式求得
电路基础课件第三章:电阻性网络分析的一般方法(节点电压法、网孔电流法)

第三章:电阻性网络分析的一般方法(节点电压法、网孔电流法)3.1 节点电压法参考点:在电路中任意选择的一点,假设该点的电压为零。
节点电压:其他独立节点与参考点之间的电压。
节点电压法:节点电压法是以节点电压为求解电路的未知量,利用基尔霍夫电流定律和欧姆定律导出(n-1)个独立节点电压为未知量的方程,联立求解,得出各节点电压。
适用范围:结构复杂、非平面电路、独立回路选择麻烦,以及节点少、回路多的电路。
一、节点电压方程式的一般形式步骤:1、选择最佳参考点,标在电路图中。
2、按照节点电压方程的一般形式,根据实际电路直接列出个节点电压方程。
3、联立求解,解出各节点电压。
4、根据节点电压,再求其他待求量。
注意: 1、自电导一定为正,互电导一定为负。
2、方程右边流入节点的电流为正,流出为负。
3、电路中有电压源支路:(1)只有一个电压源支路,把参考节点选在电压源支路的一端,以充分利用已知电压。
(2)有两个以上电压源支路时,对于跨接于两个独立节点之间的电压源支路,一定要假设电流。
或者将电压源与电阻的串联等效成电流源与电阻的并联。
4、电路中含有受控源支路时,一定要写补充方程,即控制量与节点电压的关系式。
例3.3 试用节点电压法求(图8.1)所示电路中的各支路电流。
7 A I(图8.1)解 取节点O 为参考节点, 节点 1、2的节点电压为U 1、U 2, 列出节点方程,得 解之得取各支路电流的参考方向, 如图2.23所示。
根据支路电流与节点电压的关系, 有二、电路中含有理想电压源支路的处理方法例3.4 用节点电压法求(图8.2)所示电路中电流源两端电压u S 和电压源支路中的电流i S 。
解:适当选择参考点,使理想电压源正好跨接在参考点与某一节点之间,该节点电压就是理想电压源的电压。
选择节点4作为参考点,理想电压源正好跨接在参考点与节点之间,各节点电压方程为:节点1: (1/3+1/4)u 1-1/3u 2=-1A7)3121(21321)2111(2121=++-=-+U U U U VU V U 12,621==AU I AU U I AU I 4312332126261612321211===-=-=-====节点1: u2=10V节点1: -1/4 u2+(1/3+1/4)u3=1A联立求解,得:u 1=4V u3=6V电流源两端电压为:u S =u1-u3=-2V八.课堂小结:这节课主要学习了节点电压法的求解过程,在使用节点电压法时,一定要注意电压、电流的参考方向,以及电流源电流的流向。
电路分析基础第5版第2章 网孔分析和节点分析

§2-3 含运算放大器的电阻电路
2.3.1 集成运放的结构和符号
运算放大器 (简称运放或集成运放) 是一种集成电路, 是具有很高开环电压放大倍数的放大器。
在集成运放发展的早期,主要用于模拟计算机的加、 减、乘、除、积分、微分、对数和指数等各种运算,故将 “运算放大器”的名称保留至今。
R11iA+R12iB+R13iC=uS11 R21iA+R22iB+R23iC=uS22 R31iA+R32iB+R33iC=uS33
等号左端是网孔中全部电阻上电压降代数和, 等号右端为该网孔中全部电压源电压升代数和。
(R1+R4+R5)iA+R5iB-R4ic= uS1- uS4 R5iA+(R2+R5+R6) iB+ R6iC = uS2
1. 自电导×节点电位 + 互电导×相邻节点电位 = 流进 该节点的电流源电流代数和。 2. 自电导均为正值,互电导均为负值。
[例] 列出图示电路的节点电位方程组。
R3
解:选d点作为参考点,有Vd = 0
节点电位方程组为
a
R1 b R2
c
Va= E
+ E
-
(1)
R4
IS
d
–R1—1 Va+ (R1—1 + R—12 + —R14)Vb– —R12Vc= 0
i1 1
G5 2
i5 i3 3
iS G1
i2 G3
i4
2.独立性:节点电位不受 KVL的约束,节点电位彼此 独立无关。
由KVL,对图中上网孔,有
G2
G4
4
选4为参考点
武汉大学 电路仿真实验报告

Matlab程序: Z1=3j;Z2=5;Z3=-2j;Uc=10*exp(30j*pi/180); Z23=Z2*Z3/(Z2+Z3);Z=Z1+Z23; Ic=Uc/Z3,Ir=Uc/Z2,I=Ic+Ir,U1=I*Z1,Us=I*Z; disp('Uc Ir Ic I u1 Us') disp('·ùÖµ'),disp(abs([Uc,Ir,Ic,I,U1,Us])) disp('Ïà½Ç'),disp(angle([Uc,Ir,Ic,I,U1,Us])*180/pi) ha=compass([Uc,Ir,Ic,I,Us,Uc]); set(ha,'linewidth',3) 仿真结果: Ic = -2.5000 + 4.3301i Ir = 1.7321 + 1.0000i I= -0.7679 + 5.3301i U1 = -15.9904 - 2.3038i Uc Ir Ic I u1 Us 幅值 10.0000 2.0000 5.0000 5.3852 16.1555 7.8102 相角 30.0000 30.0000 120.0000 98.1986 -171.8014 159.8056 2、如图所示电路,已知C1=0.5F,R2=R3=2Ω, L4=1H;Us(t)=10+10cost,Is(t)=5+5cos2t,求b,d两点时间的电压 U(t)。 MATLAB仿真: clear,format compact w=[eps,1,2];Us=[10,10,0];Is=[5,0,5]; Z1=1./(0.5*w*j);Z4=1*w*j; Z2=[2,2,2];Z3=[2,2,2]; Uoc=(Z2./(Z1+Z2)-Z4./(Z3+Z4)).*Us; Zeq=Z3.*Z4./(Z3+Z4)+Z1.*Z2./(Z1+Z2);
网孔分析法和节点分析法

网孔方程是描述网孔的KVL方程,当两个网孔共有 一个电流源(独立源或受控源)时就产生超级网孔。
4Ω
网孔1和网孔2看
i
+ 4V _
成一个网孔,即
3
超级网孔
2Ω 2Ω
4Ω
2Ω
+ 12V_
i
i
2A
1
2
+
超级网孔
6_V
KVL 方程
4i1 6i2 6i3 12 6 4
2i1 4i2 10i3 4
20V
_
i3
ia R3
ib
+ _10V
20 20
10 ia 25
30 8 1.143A 20 7
20 30
i1 = ia = 1.143A
25 20 ib 25 20
20 10 3 0.429A 20 7 30
i2 = ib =0.429A i3 = ia - ib
=0.714A
(G1+G4)u1-G1u2-G4u3= iS1 -G1u1 +(G1+ G2+G3) u2-G3u3= 0 网孔分-析法G和4节u点1-分析G法3u2+ (G3 +G4 ) u3 = iS2
i1 R1
R2 i2
+ u_s1
i5 ia R5
ib
R4
R6
+ _us2
i4
_ us4 + ic
i6
i3 R3
+ us3 _
网孔① -uS1+i1R1+i5R5+uS4+i4R4 = 0
网孔② 网孔③
i2R2+ uS2-i6R6-i5R5 = 0 i6R6-uS3+i3R3-i4R4-uS4 = 0
网孔分析法和节点分析

§3-1 网孔分析法(重点)
本章介绍利用独立电流或 独立电压作变量来建立电路方 程的分析方法,可以减少联立 求解方程的数目,适合于求解 稍微复杂一点的线性电阻电路, 是求解线性电阻电路最常用的 分析方法。
例1 电路如图,求i1,i2,i3 .
+ i1 1Ω 5V
-
i3 2Ω 1Ω
i2 + -10V
第三章 网孔分析法和节点分析
科学家研究世界 工程师创造崭新世界
西奥多•冯•卡曼 (Theodore von Karman) 美籍匈牙利力学家,近代力学奠基人之一。
第二章 用网络等效简化电路分析
2b法的缺点是需要联立求解的方程数目 太多,给求解带来困难。
本章通过两个途径来解决这个问题:
1. 利用单口网络的等效电路来减小电路规模, 从而减少方程数目。
二、网孔方程
i1 R1 +
以网孔电流为变量,结合 VCR列写网孔的KVL方程。
-uS1 ia -uS+4
R2 i5
i+2
R5 ib uS-2
例如网孔a,ia 的箭头方 i4
向,既代表ia 的参考方向, 也代表列写KVL的绕行方向。
R4
R6 i6
ic
R3 +uS3-i3
问题: 如果我们假定网孔电流方向:同为顺时针 或逆时针, 网孔的互电阻正﹑负是否有规律?
网孔电流的实质—— 用网孔电流来表示的KVL方程。
网孔分析法不仅 使独立方程数目减 少,而且很容易列 写方程。
——具有普遍性, 程序化,系统化的 分析方法。
四、含独立电流源电路的网孔方程
1. 若有电流源与电阻并联单口,则可先将其等效为电 压源和电阻串联单口,将电路变为仅由电压源和电阻构成 的电路,再建立网孔方程。
电路分析基础ppt网孔分析和节点分析

由此得标准形式的方程: R11iM1+R12iM2=uSM1 R21iM1+R22iM2=uSM2
一般情况,对于具有 m=b-(n-1) 个网孔的电路,有
其中
R11iM1+R12iM2+ …+R1m iMm=uSM1 R21iM1+R22iM2+ …+R2m iMm=uSM2
… Rm1iM1+Rm2iM2+ …+Rmm iMm=uSMm
un1 R1
i2
un2 R2
iS1
i3 i4
un1 un2 un1 R3un2
R4
i5
un2 R5
iS3
un1 1 i3
R3
un2 2
i1
i2
i5
R1 iS2
R2 i4 R4
R5
0
若电路中含电压
源与电阻串联的
支路:
+ uS1
-
iS3
i1 un1 1 i3
un2 R3 2
R1
i2
i5
iS2
R2 i4 R4
电路,只需对网孔列写KVL方程。
可见,网孔电流法的独立方程数为b-(n-1)。
与支路电流法相比,方程数可减少n-1个。
i1 R1
+ uS1
–
a
i2 R2 iM1 + iM2 uS2
–
b
网孔1:
i3
R1 iM1-R2(iM2- iM1)-uS1+uS2=0 R3 网孔2:
R2(iM2- iM1)+ R3 iM2 -uS2=0
4 8V a +–
1
2 2 bc
实验二网孔电流和节点电压分析法仿真

实验二网孔电流和节点电压分析法仿真一、实验目的1.加深对网孔和节点分析法的理解;2.熟练利用网孔和节点分析电路;3.验证网孔电流法和节点电压法。
二、实验仪器及元器件Windows7、Multisim10三、实验内容1. 实验原理网孔电流分析法简称网孔电流法,是根据KVL定律,用网孔电流为未知量,列出各网孔回路电压(KVL)方程,并联立求解出网孔电流,再进一步求解出各支路电流以求解电路的方法。
节点电压(节点电位)是节点相对于参考点的电压降。
对于具有n个节点的电路一定有n-1个独立节点的KCL方程。
节点电压分析法是以节点电压为变量,列节点电流(KCL)方程求解电路的方法。
2. 实验步骤(1)网孔电流分析法仿真实验A.搭建仿真实验电路如图2-1所示,并设网孔电流I1、I2、I3在网孔中按顺时针方向流动。
图2-1 网孔电流法仿真实验电路B.用网孔电流法列KVL方程,求解网孔电流。
C.在Multisim中,打开仿真开关,读出3个电流表的数据,记录并将测量值填入表2-1中,比较测量值和计算值,验证网孔电流分析法。
(2)节点电压分析法仿真实验A.搭建仿真实验电路如图2-2所示。
图2-2 节点电压分析电路B.用节点电压法求解流经电阻R3的电流。
C.在Multisim中,打开仿真开关,读出电压表和电流表的数据,记录并将测量值填入表2-2中,比较测量值和计算值,验证节点电压分析法。
表2-2 节点电压法实验数据与理论计算结果对比(3)能力提升对图2-3所示电路,分别用网孔电流法分析和实验测量各网孔电流(选顺时针方向),填入表2-3中,验证正确性。
表2-3 网孔电流法实验数据与理论计算结果对比将以上所有实验结果整理、分析,写入实验报告。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二网孔电流和节点电压分析法仿真
一、实验目的
1.加深对网孔和节点分析法的理解;
2.熟练利用网孔和节点分析电路;
3.验证网孔电流法和节点电压法。
二、实验仪器及元器件
Windows7、Multisim10
三、实验内容
1. 实验原理
网孔电流分析法简称网孔电流法,是根据KVL定律,用网孔电流为未知量,列出各网孔回路电压(KVL)方程,并联立求解出网孔电流,再进一步求解出各支路电流以求解电路的方法。
节点电压(节点电位)是节点相对于参考点的电压降。
对于具有n个节点的电路一定有n-1个独立节点的KCL方程。
节点电压分析法是以节点电压为变量,列节点电流(KCL)方程求解电路的方法。
2. 实验步骤
(1)网孔电流分析法仿真实验
A.搭建仿真实验电路如图2-1所示,并设网孔电流I1、I2、I3在网孔中按顺时针方向流动。
图2-1 网孔电流法仿真实验电路
B.用网孔电流法列KVL方程,求解网孔电流。
C.在Multisim中,打开仿真开关,读出3个电流表的数据,记录并将测量值填入表2-1中,比较测量值和计算值,验证网孔电流分析法。
(2)节点电压分析法仿真实验
A.搭建仿真实验电路如图2-2所示。
图2-2 节点电压分析电路
B.用节点电压法求解流经电阻R3的电流。
C.在Multisim中,打开仿真开关,读出电压表和电流表的数据,记录并将测量值填入表2-2中,比较测量值和计算值,验证节点电压分析法。
表2-2 节点电压法实验数据与理论计算结果对比
(3)能力提升
对图2-3所示电路,分别用网孔电流法分析和实验测量各网孔电流(选顺时针方向),填入表2-3中,验证正确性。
表2-3 网孔电流法实验数据与理论计算结果对比
将以上所有实验结果整理、分析,写入实验报告。
