精品 2014年九年级数学圆的基本性质 圆周角圆心角讲义+同步练习题
2014年圆的基本性质综合训练(含答案)

第24章 圆的有关性质综合训练1.下列命题中,正确的个数是( )⑴直径是弦,但弦不一定是直径; ⑵半圆是弧,但弧不一定是半圆;⑶圆周角等于圆心角的一半;⑷一条弦把圆分成的两段弧中,至少有一段是优弧。
A .1个B .2个C .3个D .4个2.⊙O 中∠AOB =∠84°则弦AB 所对圆周角的度数为( )A .42°B .138°C .69°D .42°或138° 3.如图1,⊙O 的直径CD 垂直于弦EF ,垂足为G ,若∠EOD=40°,则∠CDF 等于( )A .80°B . 70°C . 40°D . 20°图1 图2 图3 图44.如图2,AB 是⊙O 的直径,弦CD ⊥AB,垂足为E,如果AB=20,CD=16, 那么线段OE 的长为( ) A 、10 B 、8 C 、 6 D 、4 5.已知O 的半径为5cm ,弦AB ∥CD ,且6AB cm =,8CD cm =,则弦AB,CD 间的距离为( ).A .1cmB .7cmC .5cmD .7cm 或1cm6.如图3, AD ⊥BC 于点D ,AD=4cm ,AB=8cm ,AC=6cm ,则⊙O 的直径是( )A .4cmB .12cmC .8cmD .16cm7.如图4,矩形与O 相交,若AB=4,BC=5,DE=3,则EF 的长为( ) A . 3.5 B .6.C .7 D .8 8. 若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于( )A . 45°B . 90°C . 135°D . 270° 9.已知,如图5,在ABC 中,70A ∠=,O 截ABC 的三边所得的弦长相等,则BOC ∠=( ) A . 140B . 135C . 130D . 12510.如图6,AB 是⊙O 的直径,点C ,D 在⊙O 上,OD ∥AC ,下列结论错误的是 ( )A .∠BOD =∠BACB .∠BOD =∠COD C .∠BAD =∠CAD D .∠C=∠D图5图6 图711.在平面内到定点A 的距离等于3cm 的点组成的图形是 .12.如图7,在圆O 中,AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E ,若AC=2cm ,则圆O 的半径为____________cm 。
精品 2014年九年级数学圆的基本性质 圆周角圆心角讲义+同步练习题

九年级数学 圆周角 圆心角知识点:圆心角: 弧度:圆周角:圆心角与圆周角的关系: 同圆或等圆中,同弧或等弧所对的圆周角等于它所对的圆心角的一半. 圆周角定理:直径所对的圆周角是直角,反过来,90°的圆周角所对的弦是直径。
例1.如图,已知P 是O 外任意一点,过点P 作直线PAB ,PCD ,分别交O 于点A ,C ,D . 求证:12P ∠=(BD 的度数AC -的度数).例2.如图①,点A 、B 、C 在⊙O 上,连结OC 、OB :⑴ 求证:∠A=∠B+∠C ;⑵ 若点A 在如图②的位置,以上结论仍成立吗?说明理由。
例3.如图,⊙O 的直径AB=8cm,∠CBD=300,求弦DC 的长.30︒DCBAO例4.如图所示,已知AB 为⊙O 的直径,CD 是弦,且AB CD 于点E .连接AC 、OC 、BC .(1)求证:∠ACO=∠BCD ;(2)若EB=8cm ,CD=24cm ,求⊙O 的直径.例5.如图,在⊙O 中,AB 是直径,CD 是弦,AB ⊥CD.(1)P 是CAD 上一点(不与C 、D 重合),试判断∠CPD 与∠COB 的大小关系, 并说明理由. (2)点P /在劣弧CD 上(不与C 、D 重合时),∠CP /D 与∠COB 有什么数量关系?请证明你的结论.DCBPAO例6.如图,A 、B 、C 、D 四点都在⊙O 上,AD 是⊙O 的直径,且AD=6cm,若∠ABC=∠CAD,求弦AC 的长.DCBA O例7.如图所示,在△ABC 中,∠BAC 与∠ABC 的平分线AE 、BE 相交于点E ,延长AE 交△ABC 的外接圆于D 点,连接BD 、CD 、CE ,且∠BDA=600.(1)求证△BDE 是等边三角形;(2)若∠BDC=1200,猜想BDCE 是怎样的四边形,并证明你的猜想。
同步练习:1.在⊙O 中同弦所对的圆周角( )A.相等B.互补C.相等或互补D.以上都不对 2.下列说法正确中的是( )A.顶点在圆周上的角称为圆周角B.相等的圆周角所对的弧相等C.若三角形一边上的中线等于这边的一半,则这一边必为此三角形外接圆的直径D.圆周角等于圆心角的一半3.如图,∠1、∠2、∠3、∠4的大小关系是( )A.∠4<∠1<∠2<∠3B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3∠2D.∠4<∠1<∠3=∠2CBA ODCBAO4.如图,已知圆心角∠BOC=1000,则圆周角∠BAC 的度数是( )A.50°B.100°C.130°D.200°5.如图,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对 6.如图,D 是AC 的中点,则图中与∠ABD 相等的角的个数是( )A.4个B.3个C.2个D.1个DCBACBAO7.如图,∠AOB=100°,则∠A+∠B 等于( )A.100°B.80°C.50°D.40° 8.如图,A 、B 、C 三点都在⊙O 上,点D 是AB 延长线上一点,∠AOC=140°, ∠CBD 的度数是( ) A.40° B.50° C.70° D.110° 9.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120° 10.半径为R 的⊙O 中,弦AB=2R ,弦CD=R ,若两弦的弦心距分别为OE 、OF ,则OE ∶OF 等于( )A.2∶1B.3∶2C.2∶3D.0 11.点P 为⊙O 内一点,且OP=4,若⊙O 的半径为6,则过点P 的弦长不可能为 ( )A 302B 12C 8D 10.512.如图所示,⊙O的半径为5,弧AB所对的圆心角为1200,则弦AB的长为()A.1033 B.532C.8D.5313.如图所示,正方形ABCD内接于⊙O中,P是弧AD上任意一点,则∠ABP+∠DCP等于()A.90°B.45°C.60°D.30°14.如图,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )A.3∶2B.5∶2C.5∶2D.5∶415.如图,AB是⊙O的直径,BC CD DE==,∠COD=35°,则∠AOE的度数为_________.16.如图所示,已知AB、CD是⊙O的两条直径,弦DE∥AB,∠DOE=70°,则∠BOD=__________17.如图,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.18.如图所示,在△ABC中,∠ACB=900,∠B=250,以C为圆心,CA为半径的圆交AB于点D,则∠ACD=______19.如图, AB是⊙O的直径,点C在⊙O上,∠BAC=300,点P在线段OB上运动.设∠ACP=x,则x的取值范围是20.如图,CD是圆的直径,O是圆心,E是圆上一点且∠EOD=450,A是DC延长线上一点,AE交圆于B,如果AB=OC,则∠EAD=______21.弦心距是弦的一半时,弦与直径的比是____________,弦所对的圆心角是__________22.如图,CD 是半圆的直径,O 为圆心,E 是半圆上一点,且93EOD ∠=,A 是DC 延长线上一点,AE 与半圆相交于点B ,如果AB=OC ,则EAD ∠=,EOB ∠=,ODE ∠=.23.如图,将某月手机费中各项费用的情况制成扇形统计图,则表示短信费的扇形圆心角的度数为______ 24.⊙O 中,弦AB 垂直直径CD 于点P ,半径OA=4cm ,OP=2cm ,则∠AOB=__________,∠ADC=__________,弧BD 度数为__________,△ADC 周长为__________ cm 。
精品 九年级数学上册 圆的基本性质讲义+同步练习题

圆的基本性质知识点圆的定义几何定义:线段OA,绕O点旋转一周得到的图形,叫做圆。
其中,O为圆心,OA为半径。
集合定义:到定点等于定长的所有点的集合。
其中,定点为圆心,定长为半径。
圆的书写格式:圆的对称性(1)圆是轴对称图形,它的对称轴是直径所在的直线。
(2)圆是中心对称图形,它的对称中心是圆心。
(3)圆是旋转对称图形。
与圆有关的线段半径:圆上一点与圆心的连线段。
确定一个圆的要素是圆心和半径。
弦:连结圆上任意两点的线段叫做弦。
直径:经过圆心的弦叫做直径。
弦心距:圆心到弦的垂线段的长。
弧:圆上任意两点间的部分叫做圆弧,简称弧。
劣弧:小于半圆周的圆弧叫做劣弧。
表示方法:优弧:大于半圆周的圆弧叫做优弧。
表示方法:在同圆或等圆中,能够互相重合的弧叫做等弧。
注意:同弧或等弧对应的弦相等。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
注意: 定理中的“垂直于弦的直径”可以是直径,也可以是半径,深圳可以是过圆心的直线或线段;该定理也可以理解为:若一条直线具有两条性质:①过圆心;②垂直于一条弦,则此直线具有另外三条性质:①平分此弦;②平分此弦所对的优弧;③平分此弦所对的劣弧.推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
在下列五个条件中:①CD是直径;②CD⊥AB;③AM=BM;④AC=BC;⑤AD=BD.只要具备其中两个条件,就可推出其余三个结论.注意:(1)在圆中,与已知弦(非直径)相等的弦共有条;共端点且相等的弦共有条。
(2)在圆中,与已知弦(非直径)平行的弦共有条;平行且相等的弦共有条。
例1.如图:OA、OB为⊙O的半径,C、D分别为OA、OB的中点,求证:AD=BC.例2.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足是E,如果AB=10cm,CD=8cm,求AE的长。
人教版九年级数学上学期(第一学期)第24章《圆的基本性质》同步练习及答案(3).docx

24.1 圆(第四课时 )--------圆周角知识点1、圆周角定义:顶点在 ,并且两边都和圆 的角叫圆周角。
2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角 ,都等于这条弧所对的圆心角的 。
推论1、在同圆或等圆中,如果两个圆周角 ,那么它们所对的弧 。
推论2、半圆(或直径)所对的圆周角是 ; 900的圆周角所对的弦是 。
3、圆内接四边形:定义:如果一个多边形的所有顶点都在圆上,这个多边形叫做 ,这个圆叫做 。
性质:圆内接四边形的对角一、选择题1.如图,在⊙O 中,若C 是BD 的中点,则图中与∠BAC 相等的角有( )A.1个B.2 个C.3个D.4个2.如图,△ABC 内接于⊙O ,∠A=40°,则∠BOC 的度数为( )A. 20°B. 40°C. 60°D.80°C · BD OA3.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40 º,则∠B的度数为()A.80 ºB.60 ºC.50 ºD.40 º4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为()A.50°B.60°C.70°D.80°5.如图,AB、CD是⊙O的两条弦,连接AD、BC,若∠BAD=60°,则∠BCD的度数为()A.40°B.50°C.60°D.70°A CBO6.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为()A.6 B.5 C.3 D.327、如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=23,则⊙O的半径为()A.43B.63C.8 D.128、如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()B.A F=BF C.O F=CF D.∠DBC=90°A.AD BD二、填空题1.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是.2.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB= 度.3.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE= .4.如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD= ..5、如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB= .6、如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC= cm.7、如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为.8、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .9、如图,圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD= .10、如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是度.A BC D O三、解答题1、如图,⊙O 的直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D ,求BC ,AD ,BD 的长.2. 如图,AB 是⊙O 的直径,C 是BD 的中点,CE ⊥AB 于 E ,BD 交CE 于点F .(1)求证:CF ﹦BF ;(2)若CD ﹦6, AC ﹦8,则⊙O 的半径为 ,CE 的长是 .3、如图,A ,P ,B ,C 是半径为8的⊙O 上的四点,且满足∠BAC=∠APC=60°,(1)求证:△ABC 是等边三角形; A CBDE FO(2)求圆心O到BC的距离OD.4、如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.5、如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.24.1 圆(第四课时)--------圆周角知识点1.圆上相交2.相等一半相等一定相等直角直径3.圆内接多边形这个多边形的外接圆互补一、选择题1.C2.D3.C4.C5. C6.C7、A8、C二、填空题1.150°2.25°3.60°4. 40° .5、20°6、57、50° 8.239、30°10、144°三、解答题1、A B CD O2222222BC AB AC 1068cm CD ACBACD BCD 45AD BDAD BDBD AB 100100AD BD 52cm 2∴∠∠︒∴=-=-=∠∴∠=∠=︒∴=∴=+==∴===解:AB 是O 的直径ACB=ADB=90在Rt ABC 中,AB=10cm,AC=6cm,平分在Rt ADC 中,AB=10cmAD 2.解:(1) 证明:∵AB 是⊙O 的直径,∴∠ACB ﹦90° 又∵CE ⊥AB , ∴∠CEB ﹦90° ∴∠2﹦90°-∠A ﹦∠1又∵C 是弧BD 的中点,∴∠1﹦∠A ∴∠1﹦∠2,∴ CF ﹦BF ﹒(2) ⊙O 的半径为5 , CE 的长是524﹒3、解:(1)在△ABC 中,∵∠BAC=∠APC=60°,又∵∠APC=∠ABC ,∴∠ABC=60°, ACB D E FO 1 2∴△ABC是等边三角形;(2)∵△ABC为等边三角形,⊙O为其外接圆,∴O为△ABC的外心,∴BO平分∠ABC,∴∠OBD=30°,∴OD=8×12=4.4、证明:(1)∵OD⊥AC OD为半径,∴CD AD,∴∠CBD=∠ABD,∴BD平分∠ABC;(2)∵OB=OD,∴∠OBD=∠0DB=30°,∴∠AOD=∠OBD+∠ODB=30°+30°=60°,又∵OD⊥AC于E,∴∠OEA=90°,又∵AB为⊙O的直径,∴∠ACB=90°,在Rt△ACB中,BC=12 AB,∵OD=CD ADAB,∴BC=OD.5、(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,∵DC=CB,∴AD=AB,∴∠B=∠D;(2)解:设BC=x,则AC=x﹣2,在Rt△ABC中,AC2+BC2=AB2,∴(x﹣2)2+x2=42,解得:x1=1+,x2=1﹣(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,∵CD=CB,∴CE=CB=1+.。
新人教版九年级数学上册 24.1 圆的基本性质(3)同步练习(含答案)

24.1 圆(第三课时 )--------- 弧、弦、圆心角知识点1、圆心角定义:顶点在 的角叫做圆心角2、定理:在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量 ,它们所对应的其余各组量也分别 。
一、选择题1.如果两个圆心角相等,那么( )A .这两个圆心角所对的弦相等;B .这两个圆心角所对的弧相等C .这两个圆心角所对的弦的弦心距相等;D .以上说法都不对2.下列语句中不正确的有( )①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③圆是轴对称图形,任何一条直径所在直线都是它的对称轴 ④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3.已知、是同圆的两段弧,且=2,则弦AB 与CD 之间的关系为( )A.AB=2CDB.AB<2CDC.AB>2CDD.不能确定4. 如图,AB 是 ⊙O 的直径,C ,D 是BE 上的三等分点,∠AOE=60°,则∠COE 是( )A . 40° B. 60° C. 80° D. 120 °OED C B A5、如图,半圆O 的直径AB=10cm ,弦AC=6cm ,AD 平分∠BAC ,则AD 的长为( ). cm . cm cmA.4B.82C.24D.16二、填空题1.已知圆O 的半径为5,弦AB 的长为5,则弦AB 所对的圆心角∠AOB = .2. 如图,AB 是 ⊙O 的直径,BC ⌒ =BD ⌒ ,∠A=25°, 则∠BOD= .OD CBA3.在⊙O 中,弦AB 所对的劣弧为圆周的41,圆的半径等于12,则圆心角∠AOB = ;弦AB 的长为 .4.如图,在⊙O 中,AB AC ,∠B =70°,则∠A 等于 .5.如图,AB 和DE 是⊙O 的直径,弦AC ∥DE ,若弦BE=3,则弦CE=___ _____.6. 等腰△ABC 的顶角∠A =120°,腰AB =AC =10,△ABC 的外接圆半径等于 .A三、解答题 1、如图,在⊙O 中 ,AB =AC ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC .2、如图,在⊙O 中,AB 、CD 是两条弦,OE ⊥AB ,OF ⊥CD ,垂足分别为EF .(1)如果∠AOB=∠COD ,那么OE 与OF 的大小有什么关系?为什么?(2)如果OE=OF ,那么AB 与CD 的大小有什么关系?AB 与CD 的大小有什么关系?为什么?∠AOB 与∠COD 呢?D3.如图,在⊙O 中,C 、D 是直径AB 上两点,且AC=BD ,MC ⊥AB ,ND ⊥AB ,M 、N •在⊙O 上.(1)求证:AM =BN ;(2)若C 、D 分别为OA 、OB 中点,则AM MN NB ==成立吗?BA4.如图,∠AOB=90°,C 、D 是AB 三等分点,AB 分别交OC 、OD 于点E 、F ,求证:AE=BF=CD .5、如图,以⊙O 的直径BC 为一边作等边△ABC,AB 、AC 交⊙O 于D 、E,求证:BD=DE=ECO F E D C24.1 圆(第三课时 )--------- 弧、弦、圆心角知识点1.圆心2.相等 相等一、选择题1.D2.C 下列语句中不正确的有( )①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③圆是轴对称图形,任何一条直径所在直线都是它的对称轴 ④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3.B 已知、是同圆的两段弧,且=2,则弦AB 与CD 之间的关系为( )A.AB=2CDB.AB<2CDC.AB>2CDD.不能确定4. C 如图,AB 是 ⊙O 的直径,C ,D 是BE 上的三等分点,∠AOE=60°,则∠COE 是( )A . 40° B. 60° C. 80° D. 120 °OED C B A5、A6.B二、填空题1. 60°2.50°3.90°, 122 .4. 40° .5.36. 10 三、解答题1∠︒∴∴∴∠∠∠、证明:AB=AC,ACB=60ABC 是等边三角形AB=AC=BCAOB=AOC=BOC2、D解:(1)如果∠AOB=∠COD ,那么OE=OF理由是:∵∠AOB=∠COD∴AB=CD∵OE ⊥AB ,OF ⊥CD∴AE=12AB ,CF=12CD ∴AE=CF又∵OA=OC∴Rt △OAE ≌Rt △OCF∴OE=OF(2)如果OE=OF ,那么AB=CD ,AB =CD ,∠AOB=∠COD理由是:∵OA=OC ,OE=OF∴Rt △OAE ≌Rt △OCF∴AE=CF又∵OE ⊥AB ,OF ⊥CD∴AE=12AB ,CF=12CD ∴AB=2AE ,CD=2CF∴AB=CD∴AB =CD ,∠AOB=∠COD3.(1)连结OM 、ON ,在Rt △OCM 和Rt △ODN 中OM=ON ,OA=OB ,∵AC=DB ,∴OC=OD ,∴Rt △OCM ≌Rt △ODN ,∴∠AOM=∠BON ,∴AM NB =(2)AM MN NB ==BA4.AOFE DC连结AC 、BD ,∵C 、D 是AB 三等分点,∴AC=CD=DB ,且∠AOC=13×90°=30°, ∵OA=OC ,∴∠OAC=∠OCA=75°,又∠AEC=∠OAE+∠AOE=45°+30°=75°, ∴AE=AC ,同理可证BF=BD ,∴AE=BF=CD5,OEC ∴∠∠︒∴∴∠︒∠︒∴∠︒∠∠︒∴∠∠∠∴、证明:连接OD 、OEABC 是等边三角形B=C=60OB=OD,OE=OCOBD是等边三角形是等边三角形BOD=60,EOC=60DOE=180-BOD-EOC=60BOD=DOE=EOCBD=DE=EC。
九年级数学练习题(圆的基本性质)5
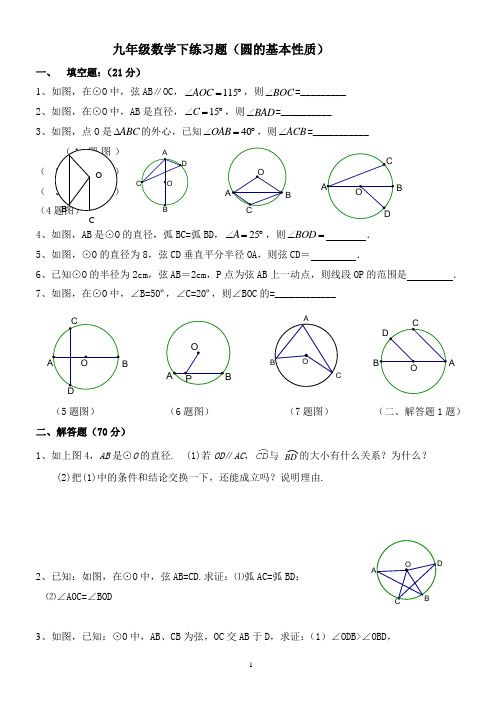
九年级数学下练习题(圆的基本性质)一、 填空题:(21分)1、如图,在⊙O 中,弦AB ∥OC ,115AOC ∠=︒,则BOC ∠=_________2、如图,在⊙O 中,AB 是直径,15C ∠=︒,则BAD ∠=__________3、如图,点O 是ABC ∆的外心,已知40OAB ∠=︒,则ACB ∠=___________(((44、如图,AB 是⊙O 的直径,弧BC=弧BD ,25A ∠=︒,则BOD ∠= . 5、如图,⊙O 的直径为8,弦CD 垂直平分半径OA ,则弦CD = .6、已知⊙O 的半径为2cm ,弦AB =2cm ,P 点为弦AB 上一动点,则线段OP 的范围是 .7、如图,在⊙O 中,∠B=50º,∠C=20º,则∠BOC 的=____________(5题图) (6题图) (7题图) (二、解答题1题) 二、解答题(70分)1、如上图4,AB 是⊙O 的直径. (1)若OD ∥AC ,与 的大小有什么关系?为什么? (2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.2、已知:如图,在⊙O 中,弦AB=CD.求证:⑴弧AC=弧BD ; ⑵∠AOC=∠BOD3、如图,已知:⊙O 中,AB 、CB 为弦,OC 交AB 于D ,求证:(1)∠ODB>∠OBD ,BBBDCA(2)∠ODB =∠OBC ;4、已知如图,AB 为⊙O 的弦,半径OE 、OF 分别交AB 于点C 、D ,且AC=BD 。
求证:CE=DF5、已知如图,,AB 、AC 为弦,OM ⊥AB 于M ,ON ⊥AC 于N ,MN 是△ABC 的中位线吗?6、已知⊙O 中,M 、N 分别是不平行的两条弦AB 和CD 的中点,且AB = CD , 求证:∠AMN=∠CNM7、已知如图,AB 、CD 是⊙O 的直径,DF 、BE 是弦,且DF=BE ,CDC求证:∠D=∠B8、已知如图,AB 是⊙O 的直径,C 是⊙O 上的一点,CD ⊥AB 于D ,CE 平分∠DCO ,交⊙O 于E , 求证:弧AE=弧EB9、已知如图,以等腰△ABC 的一腰AB 为直径的⊙O 交另一腰于F ,交底边BC 于D ,则BC 与DF 的关系,证明你的观点。
九年级数学: 圆周角圆心角综合练习题

圆的定义、垂径定理、弦、弧、圆心角、圆周角练习1. 如下图,已知CD 是⊙O 的直径,过点D 的弦DE 平行于半径OA ,若∠D 的度数是50o ,则∠C 的度数是( )A )50oB )40oC )30oD )25o第1题图 第2题图 第4题图2. 如上图,两正方形彼此相邻,且大正方形内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( ).A ) (45)+ cmB ) 9 cmC ) 45cmD ) 62cm 3. ⊙O 中,M 为的中点,则下列结论正确的是( )A .AB >2AM B .AB =2AMC .AB <2AMD .AB 与2AM 的大小不能确定4. 如上图,⊙C 过原点,且与两坐标轴分别交于点A ,点B ,点A 的坐标为(0,3),M 是第三象限内上一点,,则⊙C 的半径为( ) A. 6 B. 5 C 3 D.5. 如下图,P 为⊙O 的弦AB 上的点,PA =6,PB =2,⊙O 的半径为5,则OP =______.第5题图 第6题图 第7题图6. 如上图,扇形的半径是cm 2,圆心角是︒40,点C 为弧AB 的中点,点P 在直线OB 上,则PCPA +的最小值为 cm 7. 如图,在半径为5的⊙O 中,弦AB=6,点C 是优弧上一点(不与A 、B 重合),则的值为 .8. 圆的一条弦长等于它的半径,求这条弦所对的圆周角的度数为: .OB BMO ∠=12032AB cos C9. 如图,点A 、B 、C 、D 在⊙O 上,O 点在∠D 的内部,四边形OABC 为平行四边形,则∠OAD+∠OCD=________°.第9题图 第10题图 第11题图10. 如图,点D 为边AC 上一点,点O 为边AB 上一点,AD =DO .以O 为圆心,OD 长为半径作半圆,交AC 于另一点E ,交AB 于点F ,G ,连接EF .若∠BAC =22º,则∠EFG =_____.11. 如图,以原点O 为圆心的圆交x 轴于点A 、B 两点,交y 轴的正半轴于点C ,D 为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____________.12. 已知:如图,AB 是⊙O 的直径,CD 是⊙O 的弦,AB ,CD 的延长线交于E ,若AB =2DE ,∠E =18°,求∠C 及∠AOC 的度数.13. 已知:如图,AB 是⊙O 的直径,弦CD 交AB 于E 点,BE =1,AE =5,∠AEC =30°,求CD 的长.14. 如图,AB 为⊙O 的弦,C 、D 为弦AB 上两点, 且OC=OD ,延长OC 、OD 分别交⊙O 于E 、F ,证明:AE=BF.FE DOBAC15.已知:如图,P是∠AOB的角平分线OC上的一点,⊙P与OA相交于E,F点,与OB相交于G,H点,试确定线段EF与GH之间的大小关系,并证明你的结论.16.已知:⊙O的半径OA=1,弦AB、AC的长分别为2,3,求∠BAC的度数.17.已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离.18.已知:△ABC的三个顶点在⊙O 上,AB=AC,圆心O到BC的距离为3cm,圆的半径为7cm,求:AB的长.19.⊙O的直径为10,弦AB=8,连接弦AB的中点C与⊙O上一动点M作线段CM,求线段CM的范围..20.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF AD1)证明:E 是OB 的中点; 2)若8AB =,求CD 的长.21. 如图,射线PG 平分∠EPF ,O 为射线PG 上一点,以O 为圆心,10为半径作⊙O ,分别与∠EPF两边相交于A 、B 和C 、D ,连结OA ,此时有OA ∥PE . 1)求证:AP =AO ;2)若弦AB =12,求tan∠OPB 的值;3)若以图中已标明的点(即P 、A 、B 、C 、D 、O )构造四边形,则能构成菱形的四个点为,能构成等腰梯形的四个点为 或 或 .22. 如图,内接于⊙O ,过点的直线交⊙O 于点,交的延长线于点,且AB 2=AP ·AD(1) 求证:;(2) 如果,⊙O 的半径为1,且P 为弧AC 的中点,求AD 的长.23. 如图,内接于⊙O ,过点的直线交⊙O 于点,交的延长线于点,且AB 2=AP ·ADABC △A P BC D AB AC =60ABC ∠=ABC △A P BC D OP DC B A(1)求证:;(2)如果,⊙O的半径为1,且P为弧AC的中点,求AD的长.24.如图,F是以O为圆心,BC为直径的半圆上任意一点,A是BF的中点,AD⊥BC于D,a)求证:AD =12BF.AB AC=60ABC∠=B。
九年级数学上册圆心角与圆周角练习题

九年级数学上册圆⼼⾓与圆周⾓练习题 九年级数学上册圆⼼⾓与圆周⾓的练习积累越多,掌握越熟练。
下⾯是店铺为⼤家带来的关于九年级数学上册圆⼼⾓与圆周⾓的练习题,希望会给⼤家带来帮助。
九年级数学上册圆⼼⾓与圆周⾓练习题⽬ ⼀、选择题 1.在同圆中,同弦所对的圆周⾓ ( )A.相等 B.互补 C.相等或互补 D.互余 2.3-63所⽰,A,B,C,D在同⼀个圆上,四边形ABCD的两条对⾓线把四个内⾓分成的8个⾓中,相等的⾓共有 ( )A.2对 B.3对 C.4对 D.5对 3.3-64所⽰,⊙O的半径为5,弦AB,C是圆上⼀点,则∠ACB的度数是. 4.四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为( )A.50°B.80°C.100°D.130° 5.是中国共产主义青年团团旗上的案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是( )A.180°B.15 0°C.135°D.120° 6.下列命题中,正确的命题个数是( ) ①顶点在圆周上的⾓是圆周⾓; ②圆周⾓度数等于圆⼼⾓度数的⼀半; ③900的圆周⾓所对的弦是直径; ④圆周⾓相等,则它们所对的弧也相等。
A、1个B、2个C、3个D、4个 ⼆、填空题 7.3-65所⽰,在⊙O中,∠AOB=100°,C为优弧ACB的中点,则∠CAB= 8.3-66所⽰,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC= . 9.3-67所⽰,AB是⊙O的直径,∠BOC=120°,CD⊥AB,求∠ABD的度数. 10.已知AB是⊙O的直径,AD ∥ OC弧AD的度数为80°,则∠BOC=_________ 11.⊙O内接四边形ABCD中,AB=CD则中和∠1相等的⾓有______。
12.弦AB的长等于⊙O的半径,点C在AB上,则∠C的度数是________-. 三、解答题 13.3-68所⽰,在△ABC中,AB=AC,∠C=70°,以AB为直径的半圆分别交AC,BC于D,E,O为圆⼼,求∠DOE的度数. 14.(2014年天津市,第21题10分)已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D. (Ⅰ)①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长; (Ⅱ)②,若∠CAB=60°,求BD的长. 15.3-70所⽰,在⊙O中,AB是直径,弦AC=12 cm,BC=16 cm,∠ACB的平分线交⊙O于点D,求AD的长. 16.3-71所⽰,AB是半圆O的直径,C是半圆上⼀点,D是 AC的中点,DH⊥AB,H是垂⾜,AC分别交BD,DH于E,F,试说明DF=EF. 九年级数学上册圆⼼⾓与圆周⾓练习题答案 1.C 2.C 3.60°[提⽰:3-72所⽰,作OD⊥AB,垂⾜为D,则BD sin∠BOD BOD=60°,∴∠BOA=120°,∴∠BCA BOA=60°.故填60°.] 4.分析:因为∠BOD=100°,所以∠C=50°,所以∠A=130°,因为圆内接四边形的对⾓互补。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
A.16
0
B.32
0
C.48
0
D.64
0
4.如图,⊙O 是△ABC 的外接圆,已知∠AB0=50 ,则∠ACB 的大小为( A.400 B.300 C.450
0
) D.500
5.在同圆中,下列四个命题:(1)圆心角是顶点在圆心的角;(2)两个圆心角相等,它们所对的弦也相等; (3)两条弦相等,它们所对的弧也相等;(4)等弧所对的圆心角相等.其中真命题有( A.4 个 B.3 个 C.2 个 D.1 个 )
19.如图, AB 是⊙O 的直径,点 C 在⊙O 上,∠BAC=30 ,点 P 在线段 OB 上运动.设∠ACP=x,则 x 的取值 范围是 20.如图,CD 是圆的直径,O 是圆心,E 是圆上一点且∠EOD=45 ,A 是 DC 延长线上一点,AE 交圆于 B,如果 AB=OC,则∠EAD=______ 21.弦心距是弦的一半时,弦与直径的比是____________,弦所对的圆心角是__________
29.如图,AB 为⊙O 的弦,P 是 AB 上一点,AB=10cm,OP=5cm,PA=4cm,求⊙O 的半径.
30.⊙O 的直径为 50 cm,弦 AB∥CD,且 AB=40 cm,CD=48 cm,求弦 AB 和 CD 之间的距离.
第 6 页 共 8 页
九年级数学上册同步讲义
圆周角 圆心角同步练习题
C D
C O
A
B
A
)
B
7.如图,∠AOB=100°,则∠A+∠B 等于( A.100° B.80°
C.50°
D.40° )
8.如图,A、B、C 三点都在⊙O 上,点 D 是 AB 延长线上一点,∠AOC=140°, ∠CBD 的度数是( A.40° B.50° C.70° ) D.110°
9.在半径为 R 的圆中有一条长度为 R 的弦,则该弦所对的圆周角的度数是( A.30° B.30°或 150° C.60°
A O B D C
例 7.如图所示,在△ABC 中,∠BAC 与∠ABC 的平分线 AE、BE 相交于点 E,延长 AE 交△ABC 的外接圆于 0 D 点,连接 BD、CD、CE,且∠BDA=60 . 0 (1)求证△BDE 是等边三角形;(2)若∠BDC=120 ,猜想 BDCE 是怎样的四边形,并证明你的猜想。
第 3 页 共 8 页
九年级数学上册同步讲义
12.如图所示,⊙O 的半径为 5,弧 AB 所对的圆心角为 1200,则弦 AB 的长为( A. 10 3 3 B. 5 3 2 C.8 D. 5 3
)
13.如图所示,正方形 ABCD 内接于⊙O 中,P 是弧 AD 上任意一点,则∠ABP+∠DCP 等于( A.90° B.45° C.60° D.30°
)
14.如图,同心圆中,大圆的弦 AB 交小圆于 C、D,已知 AB=4,CD=2,AB 的弦心距等于 1,那么两个同 心圆的半径之比为( A.3∶2 ) B. 5 ∶2 C. 5 ∶ 2 D.5∶4
CD DE ,∠COD=35°,则∠AOE 的度数为_________. 15.如图,AB 是⊙O 的直径, BC
第 7 页 共 8 页
0
九年级数学上册同步讲义
10.如图,A、B、C 为⊙O 上三点,若∠OAB=46 ,则∠ACB=_______度.
0
C
O A B C
C
A
O D
B
A O
E D B
BD ,∠A=250,则∠BOD 的度数为________. 11.如图,AB 是⊙O 的直径, BC
12.如图,AB 是半圆 O 的直径,AC=AD,OC=2,∠CAB= 30°, 则点 O 到 CD 的距离 OE=______. 13.一条弦把圆分成 1:3 两部分,则弦所对的圆心角为____________ 14.如图,已知 O 是△ABC 的外接圆,∠BAC=500,∠ABC=470,求∠AOB 的度数.
A O B
0
A D O
C
B
C
4.如图,已知圆心角∠BOC=100 ,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200° 5.如图,A、B、C、D 四个点在同一个圆上,四边形 ABCD 的对角线把四个内角分成的八个角中,相等的角 有( ) A.2 对 B.3 对 C.4 对 D.5 对 6.如图,D 是 AC 的中点,则图中与∠ABD 相等的角的个数是( A.4 个 B.3 个 C.2 个 ) D.1 个
26.如图,如图在⊙O 中,弧 DE=2 弧 DC,DE=2BC,∠EOD=64 ,求∠A 的度数.
0
27.已知半径为 1 的圆中,弦 AB、AC 的长分别为 3和 2 ,求∠BAC 的度数。
第 5 页 共 8 页
九年级数学上册同步讲义
28.如图,已知以点 O 为公共圆心的两个同心圆,大圆的弦 AB 交小圆于 C、D. (1)求证:AC=DB; (2)如果 AB=6cm,CD=4cm,求圆环的面积.
6.在同一个圆中 ,同弧所对的圆周角和圆心角的关系是
0 7.如图,直径 AB 垂直于 弦 CD,垂足为 E,∠AOC=130 ,则 AD 的度数为
的度数为 , CBD
,
CAD 的度数为
, ACD 的度数为
.
A D O B C
B O A D
C
8.如图,等边△ABC 的三个顶点都在⊙O 上,D 是 AC 上任一点(与 A、C 不重合),则∠ADC 的度数是_____. 9.已知,如图,∠BAC 的对角∠BAD=100 ,则∠BOC=_______度.
第 2 页 共 8 页
九年级数学上册同步讲义
同步练习:
1.在⊙O 中同弦所对的圆周角( ) A.相等 B.互补 C.相等或互补 D.以上都不对 2.下列说法正确中的是( ) A.顶点在圆周上的角称为圆周角 B.相等的圆周角所对的弧相等 C.若三角形一边上的中线等于这边的一半,则这一边必为此三角形外接圆的 直径 D.圆周角等于圆心角的一半 3.如图,∠1、∠2、∠3、∠4 的大小关系是( ) A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2
满分:100 分 时间:25 分钟 ) B.等弧所对的弦相等 D.弦相等所对的圆心角相等 ) 姓名: 得分: 1.下列说法中,正确的是( A.等弦所对的弧相等 C.圆心角相等,所对的弦相等 2.下列命题中,正确的命题是(
A. 平分一条弦的直径,垂直平分这条弧所对的弦 B. 平分弦的直径垂直于弦,并平分弦所对的弧 C. 在⊙O 中,AB、CD 是弦,若弧 AC=弧 BD,则 AB∥CD D. 圆是轴对称图形, CD 是 O 的两条弦, 且 AB∥CD. 如果∠BAC=32 , 则∠AOD 的度数是 (
16.如图所示,已知 AB、CD 是⊙O 的两条直径,弦 DE∥AB,∠DOE=70°,则∠BOD=__________ 17.如图,A、B 是⊙O 的直径,C、D、E 都是圆上的点,则∠1+∠2=_______. 18.如图所示, 在△ABC 中, ∠ACB=900, ∠B=250, 以 C 为圆心, CA 为半径的圆交 AB 于点 D, 则∠ACD=______
九年级数学上册同步讲义
九年级数学 圆周角 圆心角
知识点: 圆心角: 弧度: 圆周角: 圆心角与圆周角的关系: 同圆或等圆中,同弧或等弧所对的圆周角等于它所对的圆心角的一半. 圆周角定理:直径所对的圆周角是直角,反过来,90°的圆周角所对的弦是直径。 例 1.如图,已知 P 是 O 外任意一点,过点 P 作直线 PAB,PCD,分别交 O 于点 A,C,D. 求证: P
1 AC 的度数) ( BD 的度数 . 2
例 2.如图①,点 A、B、C 在⊙O 上,连结 OC、OB: ⑴ 求证:∠A=∠B+∠C;⑵ 若点 A 在如图②的位置,以上结论仍成立吗?说明理由。
例 3.如图,⊙O 的直径 AB=8cm,∠CBD=30 ,求弦 DC 的长.
0
C D
30
A
D.60°或 120° )
10.半径为 R 的⊙O 中,弦 AB=2R,弦 CD=R,若两弦的弦心距分别为 OE、OF,则 OE∶OF 等于( A.2∶1 B.3∶2 C.2∶3 ( D.0 )
11.点 P 为⊙O 内一点,且 OP=4,若⊙O 的半径为 6,则过点 P 的弦长不可能为 A 2 30 B 12 C 8 D 10.5
15.点 O 是同心圆的圆心,大圆半径 OA、OB 交小圆于点 C、D。求证:AB∥CD.
16.如图,AB 是⊙O 的弦,C、D 为弦 AB 上两点,OC=OD,延长 OC、OD,交⊙O 于点 E、F.求证:弧 AE=弧 BF.
17.如图,AB 是⊙O 的直径,且 AD∥OC,若弧 AD 的度数为 80 .求弧 CD 的度数.
上一点(不与 C、D 重合),试判断∠CPD 与∠COB 的大小关系, 并说明理由. (1)P 是 CAD
(2)点 P 在劣弧 CD 上(不与 C、D 重合时),∠CP D 与∠COB 有什么数量关系?请证明你的结论.
A P
/ /
O C B D
例 6.如图,A、B、C、D 四点都在⊙O 上,AD 是⊙O 的直径,且 AD=6cm,若∠ABC=∠CAD,求弦 AC 的长.
0
第 8 页 共 8 页
第 4 页 共 8 页
0
0
九年级数学上册同步讲义
22.如图,CD 是半圆的直径,O 为圆心,E 是半圆上一 点,且 EOD 93 ,A 是 DC 延长线上一点,AE 与 半圆相交于点 B,如果 AB=OC,则 EAD , EOB , ODE .
