Mechanics(1)
机械工程专业英语(施平版)Lesson 1

• 2. A complete assembly that performs a specific function in a larger machine • 传动装置:一套装置,在一个更大机器中有具体的功能
2015/9/22 《机械工程专业英语教程》 2
V belt and pulley
V带和带轮
2015/9/22
《机械工程专业英语教程》
10
Some of the terms used in mechanics are defined below. Force Our earliest ideas concerning forces arose because of our desire to push, lift, or pull various objects. So force is the action of one body on another. Our intuitive concept of force includes such ideas as place of application , direction, and magnitude, and these are called the characteristics of a force.
2015/9/22
《机械工程专业英语教程》
9
For example, if the force operating on a journal bearing becomes too high, it will squeeze out the oil film and cause metal-to-metal contact, overheating, and rapid failure of the bearing.
工程管理专业本科生培养方案

工程管理专业本科生培养方案一、培养目标本专业培养具备管理学、经济学和土木工程技术基本知识,掌握现代管理科学理论、方法和手段,熟悉相关法规,能在国内外工程建设领域从事全过程项目策划、管理和实务运作;以及房地产投资与经营管理、物业管理等方面的复合型高级管理人才。
二、培养基本规格要求(一)品德和政治思想要求热爱社会主义祖国、拥护中国共产党的领导;坚持四项基本原则,努力学习马列主义、毛泽东思想和邓小平理论;熟悉国家有关方针、政策和法规;爱祖国、爱劳动、遵纪守法;团结同志、关心集体,政治思想素质高;热爱专业,有较强的事业心、责任感和勇于开拓创新精神;品行端正、道德品质优良。
(二)主要知识和能力要求以马列主义、毛泽东思想基本原理以及邓小平理论为指导,通过四年的学习,掌握本专业的基本理论、基本知识和基本技能。
较系统地掌握必要的经济管理科学的基本理论、建筑工程技术的基本知识;了解本专业范围内科学技术的新发展;掌握本专业所必需的现代数理方法,受到必要的技术经济分析能力和决策能力的训练,以及建筑施工管理、工程概预算方面的基本训练。
具有独立获取新知识的意识和能力;具有初步的投资项目管理能力,较强的计算机应用能力,结合所学知识解决理论与实际问题的能力,掌握一门外语。
具体是:1.掌握工程管理的组织理论、计划方法和实施目标控制的基本技能;掌握建设投资经济活动的基本规律和技术经济评价分析与项目决策的原理、方法;2.熟悉建筑土木工程技术知识;熟悉工程项目建设的方针、政策和法规;熟悉房地产基本制度与政策、房地产金融、投资、估价和经纪等基本业务;3.了解国内外工程管理的理论和实践的发展动态;4.具有运用计算机辅助解决工程管理问题的能力;具有工程造价管理(或建筑工程概预算)能力;具有从事工程项目决策与全过程管理的基本能力;具有初步的房地产投资与经营管理能力;具有准确、精练的口头与文字表达能力;外语达到四级以上,具有阅读和翻译专业书刊的能力和较强的听说能力。
力学专业英语资料(一)考研必备
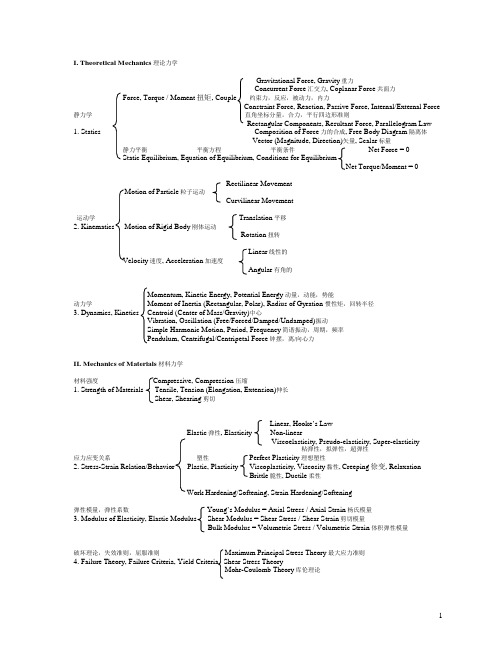
I. Theoretical Mechanics理论力学Gravitational Force, Gravity重力Concurrent Force汇交力, Coplanar Force共面力Force, Torque / Moment扭矩, Couple 约束力,反应,被动力,内力Constraint Force, Reaction, Passive Force, Internal/External Force 静力学直角坐标分量,合力,平行四边形准则Rectangular Components, Resultant Force, Parallelogram Law 1. Statics Composition of Force力的合成, Free Body Diagram隔离体Vector (Magnitude, Direction)矢量, Scalar标量静力平衡平衡方程平衡条件Net Force = 0Static Equilibrium, Equation of Equilibrium, Conditions for EquilibriumNet Torque/Moment = 0Rectilinear MovementMotion of Particle粒子运动Curvilinear Movement运动学 Translation平移2. Kinematics Motion of Rigid Body刚体运动Rotation扭转Linear线性的Velocity速度, Acceleration加速度Angular有角的Momentum, Kinetic Energy, Potential Energy动量,动能,势能动力学Moment of Inertia (Rectangular, Polar), Radius of Gyration惯性矩,回转半径3. Dynamics, Kinetics Centroid (Center of Mass/Gravity)中心Vibration, Oscillation (Free/Forced/Damped/Undamped)振动Simple Harmonic Motion, Period, Frequency简谐振动,周期,频率Pendulum, Centrifugal/Centripetal Force钟摆,离/向心力II. Mechanics of Materials材料力学材料强度 Compressive, Compression压缩1. Strength of Materials Tensile, Tension (Elongation, Extension)伸长Shear, Shearing剪切Linear, Hooke’s LawElastic弹性, Elasticity Non-linearViscoelasticity, Pseudo-elasticity, Super-elasticity粘弹性,拟弹性,超弹性应力应变关系塑性 Perfect Plasticity理想塑性2. Stress-Strain Relation/Behavior Plastic, Plasticity Viscoplasticity, Viscosity黏性, Creeping徐变, RelaxationBrittle脆性, Ductile柔性Work Hardening/Softening, Strain Hardening/Softening弹性模量,弹性系数 Young’s Modulus = Axial Stress / Axial Strain杨氏模量3. Modulus of Elasticity, Elastic Modulus Shear Modulus = Shear Stress / Shear Strain剪切模量Bulk Modulus = Volumetric Stress / Volumetric Strain体积弹性模量破坏理论,失效准则,屈服准则 Maximum Principal Stress Theory最大应力准则4. Failure Theory, Failure Criteria, Yield Criteria Shear Stress TheoryMohr-Coulomb Theory库伦理论Shear Force剪力, Bending Moment弯矩, Flexural Load弯曲荷载梁 Bending Stress弯曲应力, Normal Stress正应力, Shear Stress剪应力 (Horizontal/Longitudinal, Vertical/Transverse)5. Beam Neutral Axis中性轴, Flexure屈曲, Deflection挠曲Cantilever Beam悬臂梁, Simply Supported Beam简支梁, Pin-end, Fixed End固定端Uniformly/Linearly Distributed Load均布荷载, Concentrated Load集中荷载Buckling屈曲系数, Euler’s Equation欧拉方程6. Column 长细比,有效长度,临界荷载,偏心率Slenderness Ratio, Effective Length, Critical Load/Stress, Eccentricity RatioTension弹力, Compression压缩, Uniaxial/Axial Load单轴荷载7. Shaft杆, Rod长杆, Bar Inner/Outer Diameter内/外径Torsion扭转, Torque扭矩, TwistingRadial Distance辐射距离平面应变平面应力双向应力(单轴,三轴)应变能最大/小主应力8. Plane Strain, Plane Stress, Biaxial Stress (Uniaxial, Triaxial), Strain Energy, Major (Minor) Principal Stress Deformation变形, Displacement位移, Deflection偏向Stiffness, Rigidity刚度, Hardness硬度, Flexibility弹性, ComplianceDynamic Loading动力荷载, Cyclic/Fluctuating Loading脉冲荷载, Fatigue疲劳度Thermal Stress热应力/Strain/Deformation, Coefficient of Thermal Expansion热膨胀系数Factor of Safety安全系数, Safety FactorLimit State Design极限状态设计 (Ultimate Limit State极限状态, Serviceability Limit State正常使用极限状态), Probabilistic Design概率设计III. Structural Mechanics, Structural AnalysisRod, Shaft, Bar构件Beam, Girder1. Structural Element Column, PillarPlate, Shell, MembraneShear Wall, Shear Panel2. Truss构架, 3-hinge Arch, Rigid Frame刚性框架 (Joint节点, Pin-Joint, Hinge, Node)3. Statically Determinate静定, Statically Indeterminate超静定, Degree of Static Indeterminacy, N-fold Statically Indeterminate, Degree of Freedom自由度虚功原理 Virtual Displacement, (Matrix) Displacement Method, Stiffness Method4. Virtual Work Principle Virtual Force, (Matrix) Force Method, Flexibility MethodFinite Element MethodIV. Theory of Elasticity(Differential) Equilibrium Equation, Physical Equation, Compatibility/Geometrical EquationBoundary Conditions。
材料力学(1)

wA
M el 2 2EI
l
F
A
A
Fl 2 2EI
Fl3 wA 3EI
l
q
A
A
ql 3 6EI
wA
ql 4 8EI
l
简单模型---简支梁 表7-1—5,7,8
F
A
C
l
l
2
2
q
A C
B
A
Fl 2
16EI
Fl3
wC
杆支撑,许用应力为[]1=140MPa,试确定其直径。
解:
h
Wz
Iz ymax
bh3
12 h
bh2
b 2 h 3
h3
69
F
2
b
Fl
A
B
M max
Wz
22 h3
1m
t max
3 2
FQ A
3 2
FQ bh
F h 3b 2 Q b2
3106
40 103 b2
w = ∑wi
叠加原理
在材料服从胡克定律和小变形的条件 下,几个力共同作用引起梁的变形 ,等于 这几个力分别单独作用时引起梁的变形的 代数和。
三、方法 1.分解——每种情况都是简单模型; 2.分别计算——查表; 3.叠加。
简单模型--- 悬臂梁 表7-1—1,3,4
Me
A
A
M el EI
l
B
l 2
理论力学英文版Chapter 1

• Law of Inertia(惯性定律):A body in motion and free from external forces will keep moving at a constant speed and in a straight line. • A particle (质点):is a body whose size e forces acting on it. P3 • A rigid body(刚体) means a body does not deform under the action of forces. It is an ideal mechanical model. P4
Chapter 1 Review of Concepts in Mechanics Equilibrium(平衡)defines as a body at rest or P2 moving with constant velocity. Resultant(合力)is the sum of forces. Parallellogram Law (平行四边形法则) Vector(失量)Scalar (标量)Projection(投影) Principal of Virtual Work (虚功原理) P3 •Load(荷载) :the forces acting on a body. It includes concentrated load and distributed load.
Mechanical Model
Newton’s Laws of Motion
First Law: In the absence of applied forces, a particle originally at rest or moving with a constant speed in a straight line will remain at rest or continue to move with constant speed in a straight line. Second Law: If a particle is subjected to a force, the particle will be accelerated . The acceleration of the particle will be proportional to the magnitude of the net force and inversely proportional to the mass of the particle. Third Law: For every action, there is an equal and opposite reaction. Or, the mutual forces exerted by particles on each other are always equal and oppositely directed.
理论力学 第一章 点的运动学

已知速度的投影求速度
大小
v v v v
2 x 2 y
2 z
方向由方向余弦确定
cosv , i v x v cosv , j v y v cosv , k v z v
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§ 1.1点的运动矢量分析方法
加
速
度
t 瞬时: 速度 v(t) t+ t 瞬时:速度 v(t + t ) 或v
t 时间间隔内速度的改变量
v ( t ) = v ( t + t ) - v( t )
点在 t 瞬时的加速度
§ 1.2 点的运动的直角坐标法
加速度
a ax i a y j az k
dv x d 2 x ax 2 dt dt dv y d 2 y ay 2 dt dt dv z d 2 z az 2 dt dt
dv y dv x dv z d2 y d2x d2z a i j k 2 i 2 j 2 k dt dt dt dt dt dt
方 cosa, i a x a, 向 cosa, j a y a, 余 弦 cosa, k a z a
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§1.3 点的运动的自然坐标法
在点的运动轨迹已知的情况下,可建立弧
坐标和自然轴系来描述该点的运动,这种方
点的切线所组成的 平面,称为P点的密 切面。
P P
lim a1 a
《连续介质力学(一)》课程教学大纲

二选教材:《弹性力学》程昌钧等高教出版社1999
《弹性力学》徐芝纶高教出版社1994(第三版)
参考书目:《弹性力学》吴家龙高教出版社2001
6.考核形式:1、开卷闭卷相结合2、笔试口试相结合3、考试与平时成绩相结合
7.教学环境:课堂
(三)长度和角度的变化;应变分量的坐标变换式;主应变和应变主方向;应变张量的不变量(6学时)
(四)变形协调条件;多连通域、位移周期性条件;有限变形简介;小结(6学时)
(五)热力学定律、应变能;Green公式;各向异性弹性材料的广义胡克定律;各向同性弹性材料的广义胡克定律;弹性常数及其测定;小结(6学时)
教学要求:
本课程是连续介质力学(二)的姐妹篇,在那里将系统介绍流体力学的基本理论。为提高学生自学能力,在本课程中将安排4~6小时课堂讨论。
课
程
内
容
及
学
时
分
配
课
程
内
容
及
学
时
分
配
(一)绪论;外力和内力;应力和应力张量;应力分量的坐标变换式(6学时)
(二)主应力和主方向;应力张量的不变量;最大剪应力;平衡微分方程和力的边界条件;小结。位移与变形;应变张量与转动张量(6学时)
课
程
教
学
目
的
及
要
求
教学目的:
本课程将系统介绍弹性力学的最基本的概念和理论,要求学生系统理解和掌握弹性力学的基本假设,建立弹性力学边值问题的三条主线:应力、应变、应力与应变关系等,基本概念及相关公式的推导方法,掌握弹性力学三类边值问题的正确提法并会灵活应用,掌握弹性力学基本原理的叙述、证明及应用,掌握平面弹性力学问题的基本假设及分类,能用应力函数表达平面问题的边值问题,掌握有关的求解方法。
常用物理英语词汇(全)

常用物理英语词汇(全)力学(Mechanics)1. Force(力)2. Acceleration(加速度)3. Momentum(动量)4. Kinetic Energy(动能)5. Potential Energy(势能)6. Gravity(重力)7. Friction(摩擦力)8. Torque(扭矩)9. Angular Momentum(角动量)10. Work(功)热学(Thermodynamics)11. Temperature(温度)12. Heat(热量)13. Internal Energy(内能)14. Entropy(熵)15. Boyle's Law(波义耳定律)16. Charles's Law(查理定律)17. GayLussac's Law(盖吕萨克定律)18. Ideal Gas Law(理想气体定律)19. First Law of Thermodynamics(热力学第一定律)20. Second Law of Thermodynamics(热力学第二定律)电磁学(Electromagnetism)21. Electric Charge(电荷)22. Electric Field(电场)23. Magnetic Field(磁场)24. Current(电流)25. Voltage(电压)26. Resistance(电阻)27. Capacitance(电容)28. Inductance(电感)29. Ohm's Law(欧姆定律)30. Ampère's Law(安培定律)光学(Optics)31. Light(光)32. Refraction(折射)33. Reflection(反射)34. Diffraction(衍射)35. Interference(干涉)36. Polarization(偏振)37. Lens(透镜)38. Prism(棱镜)39. Spectrum(光谱)40. Wave Optics(波动光学)现代物理(Modern Physics)41. Quantum Mechanics(量子力学)42. Relativity(相对论)43. Photon(光子)44. Electron(电子)45. Proton(质子)46. Neutron(中子)47. Quark(夸克)48. Black Hole(黑洞)49. Higgs Boson(希格斯玻色子)50. String Theory(弦理论)这些词汇仅为物理学中常用术语的一小部分。
费恩曼的物理学讲义第一卷

费恩曼的物理学讲义第一卷
费恩曼的物理学讲义是一系列物理学教材,由美国物理学家理
查德·费曼(Richard Feynman)编写。
其中,第一卷是《费恩曼物
理学讲义第一卷,力学》(The Feynman Lectures on Physics, Volume 1: Mainly Mechanics, Radiation, and Heat)。
这本书主要涵盖了力学、辐射和热学等内容。
费恩曼以其独特
的教学风格和生动的讲解方式,将复杂的物理概念解释得浅显易懂,深受学生和物理爱好者的喜爱。
在《费恩曼物理学讲义第一卷,力学》中,费恩曼首先介绍了
物理学的基本原理和方法,然后详细探讨了力、运动、动量、能量、引力、静力学、动力学等力学的基本概念和定律。
同时,他还涉及
了流体力学、弹性力学和振动等内容。
费恩曼在书中注重培养读者的物理直觉和思维方式,通过丰富
的例子和实验来帮助读者理解物理学的基本原理。
他还引入了一些
历史背景和趣闻轶事,使得内容更加生动有趣。
这本教材对于物理学学习者来说是一本非常重要的参考书。
它
不仅可以帮助初学者建立坚实的物理基础,还可以帮助高级学习者深入理解和应用物理学的各个领域。
总之,费恩曼的物理学讲义第一卷是一本涵盖力学、辐射和热学等内容的经典物理学教材。
它以其独特的教学风格和深入浅出的讲解,帮助读者全面理解物理学的基本原理和概念。
无论是对于学生还是物理爱好者,这本书都是一本不可或缺的参考书。
《Mechanics 1历年考试真题分类汇编》

Section A Velocity and Acceleration(Chapter 1)1.A man runs in a straight line. He passes through a fixed point A with constantvelocity 7ms_1at time t = 0. At time t s his velocity is v ms_1. The diagram shows the graph of v against t for the period 0 ≤t ≤ 40. (02w)(i) Show that the man runs more than 154m in the first 24 s. [2](ii)Given that the man runs 20m in the interval 20 ≤t ≤ 24, find how far he is from A when t = 40.[2]2The diagram shows the velocity-time graphs for the motion of two cyclists P and Q, who travel in the same direction along a straight path. Both cyclists start from rest at the same point O and both accelerate at 2ms−2 up to a speed of 10ms−1. Both then continue at a constant speed of 10ms−1.(03s)Q starts his journey T seconds after P.(i) Show in a sketch of the diagram the region whose area represents thedisplacement of P, from O,at the instant when Q starts. [1]Given that P has travelled 16m at the instant when Q starts, find(ii) the value of T, [3](iii)the distance between P and Q when Q’s speed reaches 10ms−1. [2]3A boy runs from a point A to a point C. He pauses at C and then walks back towardsA until reaching the point B, where he stops. The diagram shows the graph ofv against t, where v ms−1 is the boy,s velocity at time t seconds after leavingA. The boy runs and walks in the same straight line throughout. (04s)(i) Find the distances AC and AB. [3](ii) Sketch the graph of x against t, where x metres is the boy,s displacement from A. Show clearly the values of t and x when the boy arrives at C, when he leaves C, and when he arrives at B. [3]4Particles P and Q start from points A and B respectively, at the same instant, and move towards each other in a horizontal straight line. The initial speeds of P and Q are 5ms−1 and 3ms−1 respectively. The accelerations of P and Q are constant and equal to 4ms−2 and 2ms−2 respectively (see diagram).(04w)(i) Find the speed of P at the instant when the speed of P is 1.8 times the speedof Q. [4](ii) Given that AB = 51 m, find the time taken from the start until P and Q meet.5The diagram shows the velocity-time graph for a lift moving between floors ina building. The graph consists of straight line segments. In the first stagethe lift travels downwards from the ground floor for 5 s, coming to rest atthe basement after travelling 10 m. (05s)(i) Find the greatest speed reached during this stage. [2]The second stage consists of a 10 s wait at the basement. In the third stage,the lift travels upwards until it comes to rest at a floor 34.5m above the basement,arriving 24.5 s after the start of the first stage. The lift accelerates at 2ms−2 for the first 3 s of the third stage, reaching a speed of V ms−1. Find(ii) the value of V, [2](iii) the time during the third stage for which the lift is moving at constant speed, [3](iv) the deceleration of the lift in the final part of the third stage. [2]6 A car travels in a straight line with constant acceleration a ms−2. It passesthe points A, B and C, in this order, with speeds 5ms−1, 7ms−1and 8ms−1respectively.The distances AB and BC are d1 m and d2 m respectively.(i) Write down an equation connecting (a) d1 and a,(b) d2 and a. [2](ii) Hence find d1 in terms of d2. [2]7、 The diagram shows the displacement-time graph for a car’s journey. The graphconsists of two curved parts AB and CD, and a straight line BC. The line BC isa tangent to the curve AB at B and a tangent to the curve CD at C. The gradientof the curves at t = 0 and t = 600 is zero, and the acceleration of the car is constant for 0 < t < 80 and for 560 < t < 600. The displacement of the car is 400m when t = 80. (05w)(i) Sketch the velocity-time graph for the journey. [3](ii) Find the velocity at t = 80. [2](iii) Find the total distance for the journey. [2](iv) Find the acceleration of the car for 0 < t < 80. [2]8The diagram shows the velocity-time graph for the motion of a small stone which falls vertically from rest at a point A above the surface of liquid in a container.The downward velocity of the stone t s after leaving A is v ms−1. The stone hits the surface of the liquid with velocity7ms−1when t = 0.7. It reaches the bottom of the container with velocity 5ms−1 whent = 1.2. (06s)(i) Find(a) the height of A above the surface of the liquid,(b) the depth of liquid in the container.[3](ii) Find the deceleration of the stone while it is moving in the liquid. [2](iii)Given that the resistance to motion of the stone while it is moving in the liquid has magnitude 0.7N, find the mass of the stone. [3]9 A train travels from A to B, a distance of 20 000m, taking 1000 s. The journeyhas three stages. In the first stage the train starts from rest at A andaccelerates uniformly until its speed is V ms−1. In the second stage the traintravels at constant speed V ms−1 for 600 s. During the third stage of the journeythe train decelerates uniformly, coming to rest at B. (08w)(i) Sketch the velocity-time graph for the train’s journey. [2](ii) Find the value of V. [3](iii) Given that the acceleration of the train during the first stage of thejourney is 0.15 ms−2, find the distance travelled by the train during thethird stage of the journey. [4]10A train starts from rest at a station and travels in a straight line until itcomes to rest again at the next station. The displacement-time graph above refersto the journey. (01w)(i) The speed of the train is constant from t = 120 to t = 440. Find this speed.[2](ii) Given that the acceleration of the train is constant from t = o tot= 120 and from t = 440 to t = 480, make a sketch of the velocity-timegraph for the journey, showing the maximum speed of the train. [3]。
物理专业英语_科大版 (1)

中国科技大学物理学院物理学专业英语仅供内部学习参考!2014目录1 Physics 物理学 (1)Introduction to physics (1)Classical and modern physics (2)Research fields (4)V ocabulary (7)2 Classical m echanics 经典力学 (10)Introduction (10)Description of classical mechanics (10)Momentum and collisions (14)Angular momentum (15)V ocabulary (16)3 Thermodynamics 热力学 (18)Introduction (18)Laws of thermodynamics (21)System models (22)Thermodynamic processes (27)Scope of thermodynamics (29)V ocabulary (30)4 Electromagnetism 电磁学 (33)Introduction (33)Electrostatics (33)Magnetostatics (35)Electromagnetic induction (40)V ocabulary (43)5 Optics 光学 (45)Introduction (45)Geometrical optics (45)Physical optics (47)Polarization (50)V ocabulary (51)6 Atomic ph ysics 原子物理 (52)Introduction (52)Electronic configuration (52)Excitation and ionization (56)V ocabulary (59)7 Statistical m echanics 统计力学 (60)Overview (60)Fundamentals (60)Statistical ensembles (63)V ocabulary (65)8 Quantum m echanics 量子力学 (67)Introduction (67)Mathematical formulations (68)Quantization (71)Wave-particle duality (72)Quantum entanglement (75)V ocabulary (77)9 Special r e lativity 狭义相对论 (79)Introduction (79)Relativity of simultaneity (80)Lorentz transformations (80)Time dilation and length contraction (81)Mass-energy equivalence (82)Relativistic energy-momentum relation (86)V ocabulary (89)正文标记说明:蓝色Arial字体(例如energy):已知的专业词汇蓝色Arial字体加下划线(例如electromagnetism):新学的专业词汇黑色Times New Roman字体加下划线(例如postulate):新学的普通词汇1 Physics 物理学Introduction to physicsPhysics is a part of natural philosophy and a natural science that involves the study of matter and its motion through space and time, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic disciplines, perhaps the oldest through its inclusion of astronomy. Over the last two millennia, physics was a part of natural philosophy along with chemistry, certain branches of mathematics, and biology, but during the Scientific Revolution in the 17th century, the natural sciences emerged as unique research programs in their own right. Physics intersects with many interdisciplinary areas of research, such as biophysics and quantum chemistry,and the boundaries of physics are not rigidly defined. New ideas in physics often explain the fundamental mechanisms of other sciences, while opening new avenues of research in areas such as mathematics and philosophy.Physics also makes significant contributions through advances in new technologies that arise from theoretical breakthroughs. For example, advances in the understanding of electromagnetism or nuclear physics led directly to the development of new products which have dramatically transformed modern-day society, such as television, computers, domestic appliances, and nuclear weapons; advances in thermodynamics led to the development of industrialization; and advances in mechanics inspired the development of calculus.Core theoriesThough physics deals with a wide variety of systems, certain theories are used by all physicists. Each of these theories were experimentally tested numerous times and found correct as an approximation of nature (within a certain domain of validity).For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These theories continue to be areas of active research, and a remarkable aspect of classical mechanics known as chaos was discovered in the 20th century, three centuries after the original formulation of classical mechanics by Isaac Newton (1642–1727) 【艾萨克·牛顿】.These central theories are important tools for research into more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them. These include classical mechanics, quantum mechanics, thermodynamics and statistical mechanics, electromagnetism, and special relativity.Classical and modern physicsClassical mechanicsClassical physics includes the traditional branches and topics that were recognized and well-developed before the beginning of the 20th century—classical mechanics, acoustics, optics, thermodynamics, and electromagnetism.Classical mechanics is concerned with bodies acted on by forces and bodies in motion and may be divided into statics (study of the forces on a body or bodies at rest), kinematics (study of motion without regard to its causes), and dynamics (study of motion and the forces that affect it); mechanics may also be divided into solid mechanics and fluid mechanics (known together as continuum mechanics), the latter including such branches as hydrostatics, hydrodynamics, aerodynamics pneumatics.Acoustics is the study of how sound is produced, controlled, transmitted and received. Important modern branches of acoustics include ultrasonics, the study of sound waves of very high frequency beyond the range of human hearing; bioacoustics the physics of animal calls and hearing, and electroacoustics, the manipulation of audible sound waves using electronics.Optics, the study of light, is concerned not only with visible light but also with infrared and ultraviolet radiation, which exhibit all of the phenomena of visible light except visibility, e.g., reflection, refraction, interference, diffraction, dispersion, and polarization of light.Heat is a form of energy, the internal energy possessed by the particles of which a substance is composed; thermodynamics deals with the relationships between heat and other forms of energy.Electricity and magnetism have been studied as a single branch of physics since the intimate connection between them was discovered in the early 19th century; an electric current gives rise to a magnetic field and a changing magnetic field induces an electric current. Electrostatics deals with electric charges at rest, electrodynamics with moving charges, and magnetostatics with magnetic poles at rest.Modern PhysicsClassical physics is generally concerned with matter and energy on the normal scale ofobservation, while much of modern physics is concerned with the behavior of matter and energy under extreme conditions or on the very large or very small scale.For example, atomic and nuclear physics studies matter on the smallest scale at which chemical elements can be identified.The physics of elementary particles is on an even smaller scale, as it is concerned with the most basic units of matter; this branch of physics is also known as high-energy physics because of the extremely high energies necessary to produce many types of particles in large particle accelerators. On this scale, ordinary, commonsense notions of space, time, matter, and energy are no longer valid.The two chief theories of modern physics present a different picture of the concepts of space, time, and matter from that presented by classical physics.Quantum theory is concerned with the discrete, rather than continuous, nature of many phenomena at the atomic and subatomic level, and with the complementary aspects of particles and waves in the description of such phenomena.The theory of relativity is concerned with the description of phenomena that take place in a frame of reference that is in motion with respect to an observer; the special theory of relativity is concerned with relative uniform motion in a straight line and the general theory of relativity with accelerated motion and its connection with gravitation.Both quantum theory and the theory of relativity find applications in all areas of modern physics.Difference between classical and modern physicsWhile physics aims to discover universal laws, its theories lie in explicit domains of applicability. Loosely speaking, the laws of classical physics accurately describe systems whose important length scales are greater than the atomic scale and whose motions are much slower than the speed of light. Outside of this domain, observations do not match their predictions.Albert Einstein【阿尔伯特·爱因斯坦】contributed the framework of special relativity, which replaced notions of absolute time and space with space-time and allowed an accurate description of systems whose components have speeds approaching the speed of light.Max Planck【普朗克】, Erwin Schrödinger【薛定谔】, and others introduced quantum mechanics, a probabilistic notion of particles and interactions that allowed an accurate description of atomic and subatomic scales.Later, quantum field theory unified quantum mechanics and special relativity.General relativity allowed for a dynamical, curved space-time, with which highly massivesystems and the large-scale structure of the universe can be well-described. General relativity has not yet been unified with the other fundamental descriptions; several candidate theories of quantum gravity are being developed.Research fieldsContemporary research in physics can be broadly divided into condensed matter physics; atomic, molecular, and optical physics; particle physics; astrophysics; geophysics and biophysics. Some physics departments also support research in Physics education.Since the 20th century, the individual fields of physics have become increasingly specialized, and today most physicists work in a single field for their entire careers. "Universalists" such as Albert Einstein (1879–1955) and Lev Landau (1908–1968)【列夫·朗道】, who worked in multiple fields of physics, are now very rare.Condensed matter physicsCondensed matter physics is the field of physics that deals with the macroscopic physical properties of matter. In particular, it is concerned with the "condensed" phases that appear whenever the number of particles in a system is extremely large and the interactions between them are strong.The most familiar examples of condensed phases are solids and liquids, which arise from the bonding by way of the electromagnetic force between atoms. More exotic condensed phases include the super-fluid and the Bose–Einstein condensate found in certain atomic systems at very low temperature, the superconducting phase exhibited by conduction electrons in certain materials,and the ferromagnetic and antiferromagnetic phases of spins on atomic lattices.Condensed matter physics is by far the largest field of contemporary physics.Historically, condensed matter physics grew out of solid-state physics, which is now considered one of its main subfields. The term condensed matter physics was apparently coined by Philip Anderson when he renamed his research group—previously solid-state theory—in 1967. In 1978, the Division of Solid State Physics of the American Physical Society was renamed as the Division of Condensed Matter Physics.Condensed matter physics has a large overlap with chemistry, materials science, nanotechnology and engineering.Atomic, molecular and optical physicsAtomic, molecular, and optical physics (AMO) is the study of matter–matter and light–matter interactions on the scale of single atoms and molecules.The three areas are grouped together because of their interrelationships, the similarity of methods used, and the commonality of the energy scales that are relevant. All three areas include both classical, semi-classical and quantum treatments; they can treat their subject from a microscopic view (in contrast to a macroscopic view).Atomic physics studies the electron shells of atoms. Current research focuses on activities in quantum control, cooling and trapping of atoms and ions, low-temperature collision dynamics and the effects of electron correlation on structure and dynamics. Atomic physics is influenced by the nucleus(see, e.g., hyperfine splitting), but intra-nuclear phenomena such as fission and fusion are considered part of high-energy physics.Molecular physics focuses on multi-atomic structures and their internal and external interactions with matter and light.Optical physics is distinct from optics in that it tends to focus not on the control of classical light fields by macroscopic objects, but on the fundamental properties of optical fields and their interactions with matter in the microscopic realm.High-energy physics (particle physics) and nuclear physicsParticle physics is the study of the elementary constituents of matter and energy, and the interactions between them.In addition, particle physicists design and develop the high energy accelerators,detectors, and computer programs necessary for this research. The field is also called "high-energy physics" because many elementary particles do not occur naturally, but are created only during high-energy collisions of other particles.Currently, the interactions of elementary particles and fields are described by the Standard Model.●The model accounts for the 12 known particles of matter (quarks and leptons) thatinteract via the strong, weak, and electromagnetic fundamental forces.●Dynamics are described in terms of matter particles exchanging gauge bosons (gluons,W and Z bosons, and photons, respectively).●The Standard Model also predicts a particle known as the Higgs boson. In July 2012CERN, the European laboratory for particle physics, announced the detection of a particle consistent with the Higgs boson.Nuclear Physics is the field of physics that studies the constituents and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those in nuclear medicine and magnetic resonance imaging, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology.Astrophysics and Physical CosmologyAstrophysics and astronomy are the application of the theories and methods of physics to the study of stellar structure, stellar evolution, the origin of the solar system, and related problems of cosmology. Because astrophysics is a broad subject, astrophysicists typically apply many disciplines of physics, including mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic and molecular physics.The discovery by Karl Jansky in 1931 that radio signals were emitted by celestial bodies initiated the science of radio astronomy. Most recently, the frontiers of astronomy have been expanded by space exploration. Perturbations and interference from the earth's atmosphere make space-based observations necessary for infrared, ultraviolet, gamma-ray, and X-ray astronomy.Physical cosmology is the study of the formation and evolution of the universe on its largest scales. Albert Einstein's theory of relativity plays a central role in all modern cosmological theories. In the early 20th century, Hubble's discovery that the universe was expanding, as shown by the Hubble diagram, prompted rival explanations known as the steady state universe and the Big Bang.The Big Bang was confirmed by the success of Big Bang nucleo-synthesis and the discovery of the cosmic microwave background in 1964. The Big Bang model rests on two theoretical pillars: Albert Einstein's general relativity and the cosmological principle (On a sufficiently large scale, the properties of the Universe are the same for all observers). Cosmologists have recently established the ΛCDM model (the standard model of Big Bang cosmology) of the evolution of the universe, which includes cosmic inflation, dark energy and dark matter.Current research frontiersIn condensed matter physics, an important unsolved theoretical problem is that of high-temperature superconductivity. Many condensed matter experiments are aiming to fabricate workable spintronics and quantum computers.In particle physics, the first pieces of experimental evidence for physics beyond the Standard Model have begun to appear. Foremost among these are indications that neutrinos have non-zero mass. These experimental results appear to have solved the long-standing solar neutrino problem, and the physics of massive neutrinos remains an area of active theoretical and experimental research. Particle accelerators have begun probing energy scales in the TeV range, in which experimentalists are hoping to find evidence for the super-symmetric particles, after discovery of the Higgs boson.Theoretical attempts to unify quantum mechanics and general relativity into a single theoryof quantum gravity, a program ongoing for over half a century, have not yet been decisively resolved. The current leading candidates are M-theory, superstring theory and loop quantum gravity.Many astronomical and cosmological phenomena have yet to be satisfactorily explained, including the existence of ultra-high energy cosmic rays, the baryon asymmetry, the acceleration of the universe and the anomalous rotation rates of galaxies.Although much progress has been made in high-energy, quantum, and astronomical physics, many everyday phenomena involving complexity, chaos, or turbulence are still poorly understood. Complex problems that seem like they could be solved by a clever application of dynamics and mechanics remain unsolved; examples include the formation of sand-piles, nodes in trickling water, the shape of water droplets, mechanisms of surface tension catastrophes, and self-sorting in shaken heterogeneous collections.These complex phenomena have received growing attention since the 1970s for several reasons, including the availability of modern mathematical methods and computers, which enabled complex systems to be modeled in new ways. Complex physics has become part of increasingly interdisciplinary research, as exemplified by the study of turbulence in aerodynamics and the observation of pattern formation in biological systems.Vocabulary★natural science 自然科学academic disciplines 学科astronomy 天文学in their own right 凭他们本身的实力intersects相交,交叉interdisciplinary交叉学科的,跨学科的★quantum 量子的theoretical breakthroughs 理论突破★electromagnetism 电磁学dramatically显著地★thermodynamics热力学★calculus微积分validity★classical mechanics 经典力学chaos 混沌literate 学者★quantum mechanics量子力学★thermodynamics and statistical mechanics热力学与统计物理★special relativity狭义相对论is concerned with 关注,讨论,考虑acoustics 声学★optics 光学statics静力学at rest 静息kinematics运动学★dynamics动力学ultrasonics超声学manipulation 操作,处理,使用infrared红外ultraviolet紫外radiation辐射reflection 反射refraction 折射★interference 干涉★diffraction 衍射dispersion散射★polarization 极化,偏振internal energy 内能Electricity电性Magnetism 磁性intimate 亲密的induces 诱导,感应scale尺度★elementary particles基本粒子★high-energy physics 高能物理particle accelerators 粒子加速器valid 有效的,正当的★discrete离散的continuous 连续的complementary 互补的★frame of reference 参照系★the special theory of relativity 狭义相对论★general theory of relativity 广义相对论gravitation 重力,万有引力explicit 详细的,清楚的★quantum field theory 量子场论★condensed matter physics凝聚态物理astrophysics天体物理geophysics地球物理Universalist博学多才者★Macroscopic宏观Exotic奇异的★Superconducting 超导Ferromagnetic铁磁质Antiferromagnetic 反铁磁质★Spin自旋Lattice 晶格,点阵,网格★Society社会,学会★microscopic微观的hyperfine splitting超精细分裂fission分裂,裂变fusion熔合,聚变constituents成分,组分accelerators加速器detectors 检测器★quarks夸克lepton 轻子gauge bosons规范玻色子gluons胶子★Higgs boson希格斯玻色子CERN欧洲核子研究中心★Magnetic Resonance Imaging磁共振成像,核磁共振ion implantation 离子注入radiocarbon dating放射性碳年代测定法geology地质学archaeology考古学stellar 恒星cosmology宇宙论celestial bodies 天体Hubble diagram 哈勃图Rival竞争的★Big Bang大爆炸nucleo-synthesis核聚合,核合成pillar支柱cosmological principle宇宙学原理ΛCDM modelΛ-冷暗物质模型cosmic inflation宇宙膨胀fabricate制造,建造spintronics自旋电子元件,自旋电子学★neutrinos 中微子superstring 超弦baryon重子turbulence湍流,扰动,骚动catastrophes突变,灾变,灾难heterogeneous collections异质性集合pattern formation模式形成2 Classical mechanics 经典力学IntroductionIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces. The study of the motion of bodies is an ancient one, making classical mechanics one of the oldest and largest subjects in science, engineering and technology.Classical mechanics describes the motion of macroscopic objects, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft, planets, stars, and galaxies. Besides this, many specializations within the subject deal with gases, liquids, solids, and other specific sub-topics.Classical mechanics provides extremely accurate results as long as the domain of study is restricted to large objects and the speeds involved do not approach the speed of light. When the objects being dealt with become sufficiently small, it becomes necessary to introduce the other major sub-field of mechanics, quantum mechanics, which reconciles the macroscopic laws of physics with the atomic nature of matter and handles the wave–particle duality of atoms and molecules. In the case of high velocity objects approaching the speed of light, classical mechanics is enhanced by special relativity. General relativity unifies special relativity with Newton's law of universal gravitation, allowing physicists to handle gravitation at a deeper level.The initial stage in the development of classical mechanics is often referred to as Newtonian mechanics, and is associated with the physical concepts employed by and the mathematical methods invented by Newton himself, in parallel with Leibniz【莱布尼兹】, and others.Later, more abstract and general methods were developed, leading to reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances were largely made in the 18th and 19th centuries, and they extend substantially beyond Newton's work, particularly through their use of analytical mechanics. Ultimately, the mathematics developed for these were central to the creation of quantum mechanics.Description of classical mechanicsThe following introduces the basic concepts of classical mechanics. For simplicity, it oftenmodels real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it.In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron, is more accurately described by quantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseball can spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle.Classical mechanics uses common-sense notions of how matter and forces exist and interact. It assumes that matter and energy have definite, knowable attributes such as where an object is in space and its speed. It also assumes that objects may be directly influenced only by their immediate surroundings, known as the principle of locality.In quantum mechanics objects may have unknowable position or velocity, or instantaneously interact with other objects at a distance.Position and its derivativesThe position of a point particle is defined with respect to an arbitrary fixed reference point, O, in space, usually accompanied by a coordinate system, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle.In general, the point particle need not be stationary relative to O, so r is a function of t, the time elapsed since an arbitrary initial time.In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumes Euclidean geometry for the structure of space.Velocity and speedThe velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time. In classical mechanics, velocities are directly additive and subtractive as vector quantities; they must be dealt with using vector analysis.When both objects are moving in the same direction, the difference can be given in terms of speed only by ignoring direction.AccelerationThe acceleration , or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time).Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both . If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration , but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.Inertial frames of referenceWhile the position and velocity and acceleration of a particle can be referred to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames .An inertial frame is such that when an object without any force interactions (an idealized situation) is viewed from it, it appears either to be at rest or in a state of uniform motion in a straight line. This is the fundamental definition of an inertial frame. They are characterized by the requirement that all forces entering the observer's physical laws originate in identifiable sources (charges, gravitational bodies, and so forth).A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious forces that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame.A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are un-accelerated with respect to the distant stars are regarded as good approximations to inertial frames.Forces; Newton's second lawNewton was the first to mathematically express the relationship between force and momentum . Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":a m t v m t p F ===d )(d d dThe quantity m v is called the (canonical ) momentum . The net force on a particle is thus equal to rate of change of momentum of the particle with time.So long as the force acting on a particle is known, Newton's second law is sufficient to。
materialmechanics1-精选文档

b
e
f
强化阶段
屈服阶段过后,材料以恢复了低抗变形的能力,要它 继续变形必须增加拉力,这种现象称为材料的强化。其最
高点e所对应的应力是材料所能承受的最大应力 b ,称为 强度极限。它是衡量材料强度的另一重要指标。
局部变形阶段
过e点后,在某一局部范围内,横向尺寸突然缩小, 形成颈缩现象。其横截面面积迅速减小,试样变形所需拉 力P也相应减小。曲线降落到f 点,试样被拉断。曲线ef其 段称为局部变形阶段。
p
1 u 2
变形比能的应用:
or
2 u 2E
§7 拉压静不定
静不定问题的解法:
列平衡方程; 变形协调方程;
例题分析:
例:图示,BD=L=3m,E1=210Gpa,截面面积为A1。 BC为钢索,截面面积为A2, E2=177Gpa ,设P=30KN。 求:B点的垂直和水平位移。
由此可得:
Nl l EA
EA:抗拉压刚度。
为泊松比。
横向应变:
§6 轴向拉压时的变形能
变形能:当杆件受拉时,拉力和伸长的关系如图所示。 力P所作的功为: p
dw Pd ( l)
2
线弹性范围内便为:
l
l 变形比能:单位体积内的变形能,称为比能。即:
1 Pl w P l U 2 2 EA
延伸率和断面收缩率
试件拉断后,残余变形与标距之比的百分比称为材料 的百分比称为材料的Байду номын сангаас伸率。用 表示。即:
100 %
l0 l0
工程上把材料分为两大类: 按照延伸率 的大小, 的材料称为脆性材 5 % 5 %的材料称为塑性材料;
0801力学一级学科简介

0807力学一级学科简介一级学科(中文)名称:力学(英文)名称: Mechanics一、学科概况力学是关于力、运动及其关系的科学。
其发展历史可追溯到古希腊时代,阿基米德曾对杠杆平衡、物体重心位置、物体在水中受到的浮力等,作了系统研究,确定了它们的基本规律,初步奠定了静力学,即平衡理论的基础。
伽利略通过对抛体和落体的研究,提出了惯性定律并用以解释地面上的物体和天体的运动。
17世纪末牛顿提出了力学运动的三条基本定律,使经典力学形成系统的理论。
此后,力学的研究对象由单个的自由质点,转向受约束的质点和受约束的质点系。
这方面的标志是达朗贝尔原理和拉格朗日分析力学。
其后,欧拉又进一步把牛顿运动定律用于刚体和理想流体的运动方程,这是连续介质力学创立的开端。
纳维、柯西、泊松、斯托克斯等人将运动定律和物性定律两者结合,促使弹性固体力学基本理论和粘性流体力学基本理论建立,使得力学逐渐脱离物理学而成为独立学科。
到20世纪初,在流体力学和固体力学中,实际应用跟数学理论的互相结合,使力学蓬勃起来,创立了许多新理论,同时也解决了工程技术中大量关键性问题。
从20世纪60年代起,计算机的应用日益广泛,力学无论在应用上或理论上都有了新的进展。
力学学科现设固体力学、流体力学、动力学与控制、基础力学与力学交叉、工程力学5个研究方向。
发展至今,力学学科已具有严谨的理论、实验、计算体系。
在20世纪,力学的发展取得了巨大的突破,不仅完备了学科体系,同时与其它学科的交叉与融合推动了交叉学科的形成和发展。
为了适应学科发展的要求,培养人才不应仅限于科学研究,还必须具有独立开展高水平研究的能力,具有力学学科理论、计算和实验研究的基本能力且在其中至少一个方面达到精深的专业水平。
二、学科内涵力学研究介质运动、变形、流动的宏微观行为,揭示力学过程及其与物理、化学、生物学等过程的相互作用规律。
力学既是基础科学,又是技术科学。
力学探索自然界运动的普遍规律,它以机理性、定量化地认识自然、生命与工程中的规律为目标。
工程力学第1章(静力学基本概念与物体受力分析)

五、光滑球形铰链
1.约束性质 1.约束性质 限制物体在空间上任意移动,不限制绕此点任意转动。 限制物体在空间上任意移动,不限制绕此点任意转动。 2.约束力特点 2.约束力特点 通过接触点和球心指向物体,通常用互相垂直的分力F 通过接触点和球心指向物体,通常用互相垂直的分力 x、 Fy 、Fz表示。 表示。
公理5告诉我们: 公理5告诉我们:处于平衡 状态的变形体, 状态的变形体,可用刚体静 力学的平衡理论来求解问题。 力学的平衡理论来求解问题。
§1-3
约束和约束力
自由体:位移不受限制的物体。 自由体:位移不受限制的物体。 非自由体:位移受限制的物体。 非自由体:位移受限制的物体。 约束:限制非自由体某些位移的条件或装置。 约束:限制非自由体某些位移的条件或装置。 约束力:约束施予被约束物体的力。 约束力:约束施予被约束物体的力。
第一章 静力学基本概念与 物体受力分析 §1-1
一、刚体的概念
在力的作用下不变形的物体。理想的力学模型。 在力的作用下不变形的物体。理想的力学模型。
静力学基本概念
二、平衡的概念
物体相对惯性参考系静止或作匀速直线平移。 物体相对惯性参考系静止或作匀速直线平移。 相对性、暂时性) (相对性、暂时性)
三、力和力系的概念
注意: 对刚体来说, 注意:①对刚体来说,上面的条件是充要条件 ②对变形体(或多体)来说,上面的条件只是必要条件 对变形体(或多体)来说,
③二力体:只在两个力作用下处于平衡的刚体叫二力体。 二力体:只在两个力作用下处于平衡的刚体叫二力体。
二力杆
二力杆
公理2 公理2
加减平衡力系公理
在已知力系上加上或减去任意一个平衡力系, 在已知力系上加上或减去任意一个平衡力系,并不改变 原力系对刚体的作用。该公理是力系简化的理论基础。 原力系对刚体的作用。该公理是力系简化的理论基础。 推论1 推论1:力的可传性原理 作用于刚体上的力可沿其作用线滑移到同一刚体内的任 一点,而不改变该力对刚体的作用效应。 一点,而不改变该力对刚体的作用效应。
内燃机专业英语一

在该部分内容中主要讲述内燃机、汽油发动机、柴油发动机等的相关知识。
包括:1. Engine Classification and Overall Mechanics,发动机的分类和总体结构;2. Four-stage-engine Operation,四行程发动机工作过程;3. Two-stage-engine Operation,二行程发动机工作过程;4. Diesel Engine Operating Features,柴油发动机工作特点;5. Engine Cylinder Block Crankcase,发动机气缸体曲轴箱;6. Piston Connecting Rod,活塞连杆;7.Crankshaft Flywheel,曲轴飞轮;8.Valves and Vales Train,气门与气门传动组;9. Engine Fuel System,发动机燃油系统;10. Engine Lubricating System,发动机润滑系统;11. Engine Cooling System,发动机冷却系统;12. Engine Ignition System,发动机点火系统;13. Engine Starting System,发动机起动系统;14. Locomotives,机车;15. Diesel Traction,内燃牵引。
二、教学时数:共占用18学时。
1. Engine Classification and Overall Mechanics(1学时)发动机的分类和总体结构2. Four-stage-engine Operation(1学时)四行程发动机工作过程3. Two-stage-engine Operation(1学时)二行程发动机工作过程4. Diesel Engine Operating Features(1学时)柴油发动机工作特点5. Engine Cylinder Block Crankcase(1学时)发动机气缸体曲轴箱6. Piston Connecting Rod(1学时)活塞连杆7. Crankshaft Flywheel(1学时)曲轴飞轮8.Valves and Vales Train(1学时)气门与气门传动组9. Engine Fuel System(1学时)发动机燃油系统10.Engine Lubricating System(1学时)发动机润滑系统11. Engine Cooling System(1学时)发动机冷却系统12.Engine Ignition System(1学时)发动机点火系统13.Engine Starting System(1学时)发动机起动系统14. Locomotives(2学时)机车15. Diesel Traction(3学时)内燃牵引三、教学难点与重点:重点内容有:1. Engine Classification and Overall Mechanics,发动机的分类和总体结构;2. Four-stage-engine Operation,四行程发动机工作过程;4. Diesel Engine Operating Features,柴油发动机工作特点;5. Engine Cylinder Block Crankcase,发动机气缸体曲轴箱;7.Crankshaft Flywheel,曲轴飞轮;8.Valves and Vales Train,气门与气门传动组;9. Engine Fuel System,发动机燃油系统;10. Engine Lubricating System,发动机润滑系统;11. Engine Cooling System,发动机冷却系统;13. Engine Starting System,发动机起动系统;14. Locomotives,机车;15. Diesel Traction,内燃牵引。
工程力学工程静力学(一)例题及其解答

主
要
内
容
1.1 静力学基本概念 1.2 静力学基本原理 1.3 约束和约束力 受力分析
1.1 静力学基本概念
1.1.1 力的概念 力系及分类 力——是物体之间的相互机械作用。
这种作用使物体的运动状态发生变化,以及使物体发生变形。 运动效应 变形效应 力的三要素:
力的大小:表示物体间相互机械作用的强弱,用运动 状态的变化情况或物体变形大小来体现。
若使物体处于平衡状态,作用在物体上的力系必须满足一定 的条件——力系的平衡条件。
恰使物体处于平衡状态的力系称为平衡力系
或:满足平衡条件的力系称为平衡力系。
1.1 静力学基本概念
1.1.3 刚体的概念
理想化的静力学力学模型 刚体——是指在力的作用下,其内部任意两点之间的距 离始终保持不变。
实际物体在力的作用下,都会产生程度不同的变形。工
程实际中的构件受力后的变形一般都很小,对讨论力的运动 效应影响甚微,可以忽略不计,故抽象为刚体。这样可使问
题的研究大为简化。
在讨论物体受力后的变形和破坏时,需要把物体视为变形体。
1.1.4 力的投影
1.1 静力学基本概念
力在坐标轴上的投影与力沿轴的分解 已知力 F (作用点A) 与坐标轴 x、y 夹角为,求力 F在x、y 轴上的投影。 b’ y 投影: Fx F cos
1. 2 静力学基本原理
1.2.2 二力平衡公理
作用在刚体上的两个力,使刚体保持平衡的必要和充分条 件是这两个力的大小相等,方向相反,且在同一直线上。 如图所示。
F1 F2
F1
F2
必要性:刚体、受二力、平衡 二力等值、反向、共线。 充分性:刚体、受等值、反向、共线二力 刚体平衡。
理论力学第一章英文精品PPT课件

(1)The representation of force in space:
g b
O
q
Fxy
a force is given by its magnitude, its direction and its point (line) of application magnitude: F F
point of application: the point at which the force acts onto the object.
Chapter 1: Fundamental principles of statics and force analysis
§1.1 Fundamental concepts in statics §1.2 Principles of statics §1.3 Constraints and their reaction forces §1.4 Force analysis and force diagrams
direction: it can be determined by the three angles , b, g or by the angle of inclination q and the angle of depression .
(2) The method of direct projection
Force system
coplanar force system Force system in space
Coplanar force system: 1 coplanar system of concurrent forces 2 coplanar system of parallel forces 3 general case of a force system in a plane
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18
Pretorque
20 Ncm for abutments:
188,3 N connecting force implant/abutment
187,2 N abutment/screw
10 Ncm for occlusal screw:
Octagon for abutment position
Support ring Base screw
STRAUMANN
精品课件
4
Straumann® synOcta abutments
Second Morse Taper 15°
STRAUMANN
精品课件
5
Characteristics of Morse Taper
1,00
1,00
0,75
0,75
0,50
0,50
0,25
0,25
0,22 0,47 0,70 0,87
The International Journal of Periodontics & Restorative Dentistry,
Vol.13 5 93
STRAUMANN
精品课
M determines the
pretension
精品课件
6
Cyclic testing at Straumann
Unit immersed in Ringer solution during test
2 mio. cycles
Simulated bone resorpion of 2,0 mm
Tightening torque M, 35 Ncm
Friction µ
A function of cone angle, friction, radii, type of thread
M = Mc + Mt
Mc = torque in cone (91%) Mt = torque in thread (9%)
8° Morse Taper
8° or less angle will
yield a mechanically
locking, friction fit
The International Journal of Periodontics & Restorative Dentistry,
Vol.13 5 93
Mechanics
Implant-to-abutment connection
Morse Taper
STRAUMANN
精品课件
2
Morse Taper / Straumann® synOcta
STRAUMANN
精品课件
3
Straumann® synOcta abutments
Abutment body
9
Reduction of gap due to 45° shoulder
7,07 µm 10,0 µm
The International Journal of Periodontics & Restorative Dentistry, Vol.13 5
93
STRAUMANN
精品课件
10
Non-rotation through mechanical lock
STRAUMANN
精品课件
16
Take-home message
▪ Proven validity and function since 1986 ▪ Stability against rotational loosening due
to friction fit: loosening torque is higher
STRAUMANN
精品课件
Less than 10 µm Takes no functional load
11
The Finite Element Method (FEM)
Coarse mesh in uncritical areas Fine mesh in critical areas
STRAUMANN
精品课件
17
Pretorque Interfaces
Prosthetic coping/ prosthetic retaining
screw interface
Prosthetic coping/ abutment interface
Abutment screw/
prosthetic retaining
Technovit
STRAUMANN
精品课件
7
Cyclic testing at Straumann
Implant testing
Abutment testing
STRAUMANN
精品课件
8
Removal torque
Tightening torque (Nm) Tightening torque (Nm)
精品课件
12
Load step 1: Tightening at 35 Ncm
STRAUMANN
精品课件
13
Load step 2: Load from 0°
STRAUMANN
精品课件
14
Load step 3: Load from 15°
STRAUMANN
精品课件
15
Load step 4: Load from 30°
Abutment screw/ implant fixture
interface
Pretorque Sakaguchi & Bogersen 1993 STRAUMANN
精品课件
Components
Prosthetic retaining scre Prosthetic coping Abutment Abutment screw
Dental implant
screw interface
consists of
Abutment/
five components
implant
that are united
fixture
and form six
interface
interfaces
Abutment screw/
abutment interface
than tightening torque
▪ Resistance against long-term cyclic loading: force distribution on large surface
▪ Standardized tightening torque 35 Ncm
STRAUMANN
