五年级数学下册数学拓展提高题doc资料
五年级下册数学列方程解决问题拓展提升专项练习

五年级数学下册列方程解决问题提优专项训练一、填空题(每题5分,共45分)1.有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。
笼中鸡有()只,兔有()只。
2.动物园里有一群鸵鸟和大象,它们共有36只眼睛和52只脚。
鸵鸟有()只,大象有()只。
3.动物园里养了一些梅花鹿和鸵鸟,共有脚208只,鸵鸟比梅花鹿多20只。
梅花鹿有()只,鸵鸟有()只。
4.一个养殖园内,鸡比兔多36只,共有脚792只,养殖园内鸡有()只,兔有()只。
5.在一个停车场上,现有车辆41辆,其中汽车有4个轮子,摩托车有3个轮子,这些车共有127个轮子。
停车场上汽车有()辆,摩托车有()辆。
6.体育老师买了运动服上衣和裤子共21件,共用了 439元,其中上衣每件24元、裤子每件19元。
老师买了()件上衣,买了()件裤子。
7.壮壮和雷雷做仰卧起坐,壮壮先做了 3分钟,然后两人各做了 5分钟,一共做仰卧起坐136次。
已知每分钟壮壮比雷雷平均多做4次,那么壮壮比雷雷多做了()次。
8.一百个和尚刚好喝一百碗粥,一个大和尚喝三碗粥,三个小和尚喝一碗粥,那么大和尚有()人,小和尚有()人。
9.孙阿姨有2元人民币和5元人民币共62张,合计226元,孙阿姨2元和5元人民币各有()张和()张。
二、解答题(第10题15分,第11~13题20分,共75分)10.列方程组解答:松鼠妈妈采松子。
晴天每天可以采20个,雨天每天只能采12个。
它一连几天共采了 112个松子,平均每天采14个。
这几天当中有几天是雨天?11.列方程组解答:一车间派56名工人做衣服,每个工人每天平均能缝制6件上衣或 8条裤子,问:应分配多少人缝制上衣,有多少人缝制裤子?12.列方程组解答:同学们去植树,如果每天栽6棵,那么还剩下14棵树苗;如果每人栽8棵,那么少16棵树苗,问:一共有多少个同学去栽树?13.列方程组解答:今年父亲的年龄是儿子的6倍,6年后父亲的年龄是儿子的3倍, 问:现在父亲和儿子的年龄各是多少?三、选做题(每题15分,共30分)14.有蜘蛛、蜻蜓、蝉三种动物共20只,共有腿130条,翅膀22对(蜘蛛8条腿;蜻蜓 6条腿,2对翅膀;蝉6条腿,1对翅膀),问:蜻蜓有多少只?15.在一次考试中有选择题、填空题和解答题三类题共22道。
沪教版五年级下册数学 第三单元 简易方程(二) 拓展提高卷

沪教版五年级下册数学第三单元简易方程(二)拓展提高卷第一部分计算部分(共30分)1、直接写出下面各方程的解(6分)8.2一x=0.5 x= x÷1.2=1.2 x=x÷3= 3 x= 12-5y=8.5 y=0.6x=3.1+2.3 x= y÷4-8=1.6 y=2、解方程(打*的要检验)(18分)(1)2.5(x-4)=3.5+x (2)8.5(x-1.2)÷2=68(3)3.4x÷2=4.8×5.1*(4)0.8(x+3)÷2=6.25×0.4 (5)64x+52(5-x)=296 *(6)5(x+2)=2(2x+7)3、列方程解文字题(6分)(1)一个数的3倍减去6.2,等于这个数的2倍加上9.8,求这个数。
(2)一个数的3.2倍减去3.4与20的积,等于这个数的1.5倍,求这个数。
第二部分概念部分(共8分)填空题1、王师傅a天做m个零件,平均每天做()个零件,做一个零件要()天。
2、用80厘米的铁丝围成一个长方形,要使它的宽为16厘米,长应该是多少厘米?解:设长x厘米。
列出的方程是()。
3、小明买5支铅笔,小新买3支同样的铅笔,小明比小新多付1.6元,每支铅笔售价多少元?解:设每支铅笔售ェ元。
列出的方程是()。
4、甲数的小数点向右移动两位就和乙数相等,甲数比乙数小86.13,求甲数。
解:设甲数是x。
列出的方程是( )。
第三部分应用部分(共60分)列方程解应用题1、甲、乙两班学生的平均人数是23人,甲班比乙班多2人,甲、乙两班各有多少人?2、甲仓存粮32吨,乙仓存粮57吨。
以后甲仓每天存入9吨,乙仓每天存入4吨,几天后乙仓存粮与甲仓相等?3、如右图所示,在平行四边形ABCD中,三角形ABE的面积比梯形EBCD的面积小40平方厘米。
求梯形上底ED的长。
4、体育室老师去买45只乒乓球和12只羽毛球,共要付173元,如果用一只羽毛球去换2只乒兵球,那么还可找回0.4元。
五年级下册数学思维拓展训练用方程解应用题 (2)

AB距离:(40+25)×3=195(米)
答:A、B两地相距195米。
例6:有大、中、小三种包装的筷子27盒, 它们分别装有18双、12双、8双筷子,一共装有 330双筷子,其中小盒的数量是中盒的两倍。问: 三种盒各有多少?
例2:搬运工搬运1000只玻璃瓶,规定搬运一只 可得搬运费3角,但打碎一只要赔5角。如果运完后 搬运工共得搬运费260元,问搬运时打碎了几只玻 璃瓶?
好瓶子的个数+打碎瓶子的个数=1000
搬运好瓶子得的钱-打碎瓶子赔的钱=260元
解:设打碎x只玻璃瓶,则好瓶有(1000-x)只。 0.3×(1000-x)-0.5x =260 300-0.3x-0.5x=260 300-260=0.3x+0.5x 40=0.8x x=50
例7:一个三位数,个位上的数字是5,十位 上的数字是百位上数字的2倍,如果把它的个位数 字与百位上的数字对调,则新的三位数比原数大 396,原三位数是多少?
新数-原数=396 解:设百位上数字是x,则十位上数字是2x。
原数、新数怎么表示呢?
可以利用位值原理来表示, 例如: 234=2×100+3×10+4。
则一辆客车空车。一共有多少辆车?一共有学生
多少人? 解:设一共有x辆车。
45x+15= 60×(x-1) 45x+15=60x-60
15+60=60x-45x
75=15x x=5
学生:60×(5-1)=240(人)
答:一共有5辆车,一共有学生240人。
例4:小华从家到学校,如果每分钟走50米, 就会比计划时间晚到校3分钟;如果每分钟走60米, 就会比计划时间提前2分钟到校。小华家距学校多 少米?
苏教版小学五年级下册数学奥数题带答案图文百度文库

苏教版小学五年级下册数学奥数题带答案图文百度文库一、拓展提优试题1.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有种不同的围法(边长相同的矩形算同一种围法).2.若2副网球拍和7个网球一共220元,且1副网球拍比1个网球贵83元.求网球的单价.3.某数学竞赛有10道题,规定每答对一题得5分,答错或不答扣2分.A、B 两人各自答题,得分之和是58分,A比B多得14分,则A答对道题.4.四位数的所有因数中,有3个是质数,其它39个不是质数.那么,四位数有个因数.5.(8分)如果两个质数的差恰好是2,称这两个质数为一对孪生质数.例如3和5是一对孪生质数,29和31也是一对孪生质数.在数论研究中,孪生质数是最热门的研究课题之一.华裔数学家张益唐在该课题的研究中取得了令人瞩目的成就,他的事迹激励着更多的青年学子投身数学研究.在不超过100的整数中,一共可以找到对孪生质数.6.(8分)6个同学约好周六上午8:00﹣11:30去体育馆打乒乓球,他们租了两个球桌进行单打比赛每段时间都有4 个人打球,另外两人当裁判,如此轮换到最后,发现每人都打了相同的时间,请问:每人打了分钟.7.(8分)图中所示的图形是迎春小学数学兴趣小组的标志,其中,ABCDEF 是正六边形,面积为360,那么四边形AGDH的面积是.8.一次数学竞赛中,某小组10个人的平均分是84分,其中小明得93分,则其他9个人的平均分是分.9.将100按“加15,减12,加3,加15,减12,加3,…”的顺序不断重复运算,运算26步后,得到的结果是.(1步指每“加”或“减”一个数)10.如果2头牛可以换42只羊,3只羊可以换26只兔,2只兔可以换3只鸡,则3头牛可以换多少只鸡?11.(8分)有四个人甲、乙、丙、丁,乙欠甲1元,丙欠乙2元,丁欠丙3元,甲欠丁4元.要想把他们之间的欠款结清,只因要甲拿出元.12.(8分)彤彤和林林分别有若干张卡片:如果彤彤拿6张给林林,林林变为彤彤的3倍;如果林林给彤彤2张,则林林变为彤彤的2倍.那么,林林原有张.13.(8分)一个大于1的正整数加1能被2整除,加2能被3整除,加3能被4整除,加4能被5整除,这个正整数最小是.14.(8分)在如图每个方框中填入一个数字,使得乘法竖式成立.那么,两个乘数的和是.15.定义新运算:θa=,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是.16.如图六角星的6个顶点恰好是一个正六边形的6个顶点,那么阴影部分面积是空白部分面积的倍.17.观察下面数表中的规律,可知x=.18.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有块.19.松鼠A、B、C共有松果若干,松鼠A原有松果26颗,从中拿出10颗平分给B、C,然后松鼠B拿出自己的18颗松果平均分给A、C,最后松鼠C把自己现有松果的一半平分给A、B,此时3只松鼠的松果数量相同,则松鼠C原有松果颗.20.大于0的自然数n是3的倍数,3n是5的倍数,则n的最小值是.21.(8分)在长方形ABCD中,BE=5,EC=4,CF=4,FD=1,如图所示,那么△AEF的面积是;22.如图,7×7的表格中,每格填入一个数字,使得相同的数字所在的方格都连在一起(相连的两个方格必须有公共边),现在已经给出了1,2,3,4,5各两个,那么,表格中所有数的和是.125334215423.如图所示,P为平行四边形ABDC外一点。
小学五年级数学 拓展应用题 例题+练习 带详细答案

小学五年级数学拓展应用题(带答案)例题一、甲、乙两工人生产同样的零件,原计划每天共生产700个。
由于改进技术,甲每天多生产100个,乙的日产量提高了1倍,这样二人一天共生产1020个。
甲、乙原计划每天各生产多少个零件?解答:二人实际每天比原计划多生产1020-700=320(个)。
这320个零件中,有100个是甲多生产的,那么320-100=220(个)就是乙日产量的1倍,即乙原来的日产量,甲原来每天生产700-220=480(个)。
练习一1、工厂里有2个锅炉,原来每月烧煤5.6吨。
进行技术改造后,1号锅炉每月节约1吨煤,2号锅炉每月烧煤量减少了一半,现在每月共烧煤3.5吨。
原来两个锅炉每月各烧煤多少吨?解答:一共节约:5.6-3.5=2.1(吨)2号节约:2.1-1=1.1(吨)2号原来每月:1.1+1.1=2.2(吨)1号原来每月:5.6-2.2=3.4(吨)2、甲、乙两人生产同样的零件,原计划每天共生产80个。
由于更换了机器,甲每天多做40个,乙每天生产的是原来的4倍,这样二人一天共生产零件300个。
甲、乙原计划每天各生产多少个零件?解答:一共多生产:300-80=220(个)乙每天多做:220-40=180(个)乙原来每天:180÷(4-1)=60(个)甲每天原来:80-60=20(个)3、甲、乙两队合挖一条水渠,原计划两队每天共挖100米,实际甲队因有人请假,每天比计划少挖15米,而乙队由于增加了人,每天挖的是原计划的2倍,这样两队每天一共挖了150米。
求两队原计划每天各挖多少米?解答:每天一共多挖:150-100=50(米)乙每天多挖:50+15=65(米)乙原来每天:65米甲原来每天:100-65=35(米)例题二、把一根竹竿插入水底,竹竿湿了40厘米,然后将竹竿倒转过来插入水底,这时,竹竿湿的部分比它的一半长13厘米。
求竹竿的长。
解答:因为竹竿先插了一次,湿了40厘米,倒转过来再插一次又湿了40厘米,所以湿了的部分是40×2=80(厘米)。
【典型习题系列】人教版小学数学五年级下册典型习题系列之期中复习拓展篇(原卷版)

五年级数学下册典型例题系列之期中复习拓展篇(原卷版)编者的话:《2021-2022学年五年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
本专题是期中复习拓展篇。
本部分内容考察第一单元至第四单元的拓展性内容及题型,考点和题型相对困难,偏于思维理解,建议作为根据学生情况选择性进行讲解,一共划分为八个考点,欢迎使用。
【考点一】倍数特征的应用。
【方法点拨】个位上是0、2、4、6、8的数是2的倍数。
个位上是0或5的数是5的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【典型例题1】如果五位数□436□是45的倍数,那么这个五位数是多少?【典型例题2】一个大于2的自然数,除以3余2,除以5余2,除以7也余2,那么这个自然数最小是多少?【典型例题3】三个数的和是 555,这三个数分别能被3、5、7 整除,而且商都相同,这三个数分别是多少?【考点二】分解质因数的应用。
【方法点拨】分解质因数指的就是把一个合数用几个质数乘积的形式表示出来。
例:15=3×5,24=2×2×2×3,这就是分解质因数。
【典型例题1】四个连续偶数的乘积是5760,求这四个数各是多少?【典型例题2】有168颗糖,平均分成若干份,每份不得少于10颗,也不能多于50颗。
共有多少种分法?【考点三】长方体表面积的三种增减变化方式。
【方法点拨】长方体表面积的增减变化问题主要有三种形式,即切片问题,拼接问题,高的变化引起的表面积增减变化,根据题目不同变化方式采用不同的方法解决问题。
【典型例题1】把一根长40厘米的长方体木条锯成两段,表面积增加了18平方厘米。
五年级数学拓展题

五年级数学拓展题1.小丹从家去学校,如果每分钟走60米,就要迟到5分钟;如果每分钟走90米,就能提前4分钟,小丹家到学校的路程是多少米?2.一桶油连桶共重10.6千克,用去油的一半后,连桶还重5.5千克,这桶油重多少千克?这个油桶重多少千克?3.把一根木料锯3段要3.6分钟,锯9段要多少分钟?4.甲堆煤比乙堆煤多2.5吨,现在两堆煤都运走0.5吨后,甲堆是乙堆的3倍,原来甲、乙两堆煤各有多少吨?5.有两个水池共储存水40吨,甲池注进水4吨,乙池放出水8吨,甲池中水的吨数就与乙池中水的吨数相等。
两个水池原来各有水多少吨?6.毕业生在礼堂入座,每条长椅坐3人,有25人坐不下,每条长椅坐4人,正好空出4条长椅,毕业生有多少人?7.一箱苹果连箱重8千克,卖出一半苹果后,连箱还重4.5千克。
如果每千克苹果2.5元,这箱苹果能卖多少元?7. 小宝家4月份每天预订了袋装保鲜奶,保鲜奶零售价为1.10元,按批发价共付28.5元,这样每袋比零售价便宜多少元?8. 有一个四位数,给它加上小数点后,再与原数相加,和是3248.16,这个四位数是多少?9. 一根长2.4米的铁丝,折成四条边都相等的平行四边形,它任意一边上的高是0.5米,这时这个平行四边形的面积是多少平方米?10. 六一班有学生46人,其中会骑自行车的17人,会游泳的14人,既会骑车又会游泳的4人,问两样都不会的有多少人?11. 有8个数字排成一列,它们的平均数是9.3,已知前5个数的平均数是10.5,后4个数的平均数是11.3,第5个数是多少?12. 两辆汽车同时从水泥厂出发,将一批水泥运到距这里165千米的工地上,甲车比乙车早到0.8小时,当甲车到达时,乙车还离工地24千米,甲车行驶全程用了多少小时?13. 甲、乙两人分别从相距36千米的两地出发相向而行,经过4小时相遇。
如果甲比乙先走4.5小时,那么乙出发后2小时,二人相遇.甲、乙二人每小时各行多少千米?13. 甲乙两站的路程为354千米,一辆慢车从甲站开往乙站,慢车走了一个半小时后,另有一列快车从乙站开往甲站,已知慢车的速度为每小时46千米,快车每小时走68千米,问两车各走多少小时后相遇?14. 一列火车以每分钟180米的速度穿过一条长200米的大桥(从车头开进桥面直至车尾离开桥面)用2分钟,求这列火车的车身长多少米?15. “小马虎”人如其名,总是马马虎虎。
五年级下册数学思维拓展训练环形跑道问题

900÷(130-120)=90(分)
反向:相遇时间=跑道长度÷ቤተ መጻሕፍቲ ባይዱ度和
900÷(130+120)=3.6(分)
答:至少经过90分钟,爸爸从小奥身后追上小奥; 如果他们两人反向而行,3.6分钟相遇。
例2:一个环形操场的周长是400米,甲每分钟走 80米,乙每分钟走50米,现在两人同时从同一地点同 向出发,沿操场走,多少分钟后两人又在原出发地相 遇?
例3:两人骑自行车沿着900米长的环形跑道行 驶,他们从同一地点反向而行,那么经过18分钟后就 相遇一次,若他们同向而行,那经过180分钟后快车 追上慢车一次,求两人骑自行车的速度?
反向:速度和=跑道长度÷相遇时
间900÷18=50(米/分)
同向:速度差=跑道长度÷追及时
间900÷180=5(米/分)
可以求出
两车的速度和
例4:花山果园地形是个近似的圆,周长约180千 米,两辆汽车同时从同地背向出发绕果园行驶了2.5 小时相遇,如果其中一辆车先出发了72千米,那么在 另一辆车出发几小时后,两车相遇?
速度和:180÷2.5=72(千米/小时) (180-72)÷72=1.5(小时)
答:在另一辆车出发1.5小时后,两车相遇。
例2:一个环形操场的周长是400米,甲每分钟走 80米,乙每分钟走50米,现在两人同时从同一地点同 向出发,沿操场走,多少分钟后两人又在原出发地相 遇?
甲跑一圈回到原出发地:
400÷80=5(分)
乙跑一圈回到原出发地:
400÷50=8(分)
两人同时回到原出发地:
[5,8]=40
答:40分钟后两人又在原出发地相遇。
同一地点同向而行:路程差=跑道一圈的长度 (追及问题) 追及时间=跑道长度÷速度差
小学数学五年级下册《思考题拓展延伸题》专项练习(附参考答案)

五年级数学下册思考题拓展延伸题练习班级考号姓名总分(一)(二)(三)1. a和b都是大于0的整数若a=b+1,则a和b的最大公因数是(),最小公倍数是();若a=5b,则a和b的最大公因数是(),最小公倍数是()。
2. 有一个长acm,宽bcm的长方形(a>b),可以正好剪成若干个边长是2cm的正方形,也可以正好剪成若干个边长是3cm的正方形,那么这个长方形的面积最小是多少平方厘米?1.如下图,红色三角形的面积是蓝色三角形的几分之几?黄色三角形与蓝色三角形面积之和是整个梯形面积的几分之几?2. 已知右图中梯形的下底是6厘米,且蓝色三角形的面积是梯形面积的2/3,求梯形的上底是多少厘米?(五)若a 和b 是两个自然数,,且 a是最小合数,则b可能是多少?1.猴妈妈摘了一些桃,小猴第一天吃了总数的1/9,第二天吃了剩下的一半。
这些桃还剩下总数的几分之几?2. 一根彩带全长4/5米,第一次用去全长的1/4,第二次用去全长的3/8,用了两次后,这根彩带还剩下全长的几分之几?(七)(八)1.如图,正方形的面积是10平方厘米,圆的面积是多少平方厘米?2.小正方形面积是200平方厘米,大圆的面积是多少平方厘米?(九)1.如下图,一块草坪被4条2米宽的小路平均分成了9小块,草坪的面积是多少平方米?2.求图中阴影部分面积。
(十)附:参考答案(一)思路分析解法(二)方法1:【解答】因为两个方框里填的是相同的数,上面的算式可以运用乘法分配律进行变形,即:【解答】因为两个方框里填的是相同的数,所以我们可以把方框里的数都用字母x表示,这样我们就可以得到24x-15x=18这个方程,通过解方程即可得到x=2,因此方框里填入的数是2。
方法3:【解答】根据“两个方框里填的是相同的数,进行有序列举,找出答案。
【分析】36的因数有:1、2、3、4、6、9、12、18、36,这两个数可能会有两种组合。
组合1:36和它的因数的组合;组合2:因数4的倍数和9的倍数的组合。
五年级数学下册典型例题系列之第五单元分数除法的拓展应用专项练习(解析版)北师大版

五年级数学下册典型例题系列之第五单元分数除法的拓展应用专项练习(解析版)1.甲、乙两班各有一个图书室,共有296本书。
已知甲班图书的513和乙班图书的14合在一起是95本,那么甲班图书有多少本?【答案】156本【解析】【分析】此题可以设甲班有图书x本,乙班有图书(296-x)本,甲班图书的513可表示成513x,乙班图书的14可表示成:(296-x)×14,两个加起来是95本,列出方程,求解即可。
【详解】解:设甲班图书有x本。
5 13x+(296-x)×14=955 13x-14x+296×14=9520 52x-1352x=95-74752x=21x=156答:甲班图书有156本。
【点睛】此题的解题关键是弄清题意,把甲班图书设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
2.妈妈买了2袋大米,第一袋是第二袋的78,如果从第二袋中取出3.5千克的大米放入第一袋中,那么这两袋的重量就一样多了。
这两袋大米原来各重多少千克?【答案】第一袋重49千克,第二袋重56千克【解析】【分析】根据题意,从第二袋中取出3.5千克的大米放入第一袋中,两袋的重量相同,可知第二袋比第一袋中3.5×2千克,把第二袋的重量看成单位“1”,第二袋比第一袋多出来的重量占第二袋的1-78,根据除法的意义计算出第二袋的重量,然后根据已知分数乘法的意义求出第一袋的重量即可。
【详解】3.5×2÷(1-78)=7÷1 8=56(千克)56×78=49(千克)答:第一袋重49千克,第二袋重56千克。
【点睛】此题主要考查分数乘、除法应用题的实际应用。
3.有三筐同样重的苹果,售货员从这三筐苹果中分别取出了一部分。
称一称后,他发现这三筐苹果中一共取出了100千克。
同时他还发现甲筐取出的苹果与乙筐中剩下的苹果同样重,丙筐取出的是该筐苹果的14,你知道每筐苹果有多少千克吗?【答案】80千克【解析】【分析】三筐同样重的苹果,甲筐取出的苹果与乙筐中剩下的苹果同样重,即从甲、乙两筐合取了一整筐,将每筐苹果的重量看作单位“1”,根据三筐苹果中一共取出了100千克,可知100千克对应的分率是1+14,已知一个数的几分之几是多少求这个数用除法。
五年级数学思维训练:应用题拓展(五年级)竞赛测试.doc

五年级数学思维训练:应用题拓展(五年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________一、xx 题(每空xx 分,共xx 分)【题文】(4分)水果店运来了西瓜和哈密瓜共234个,如果西瓜和哈密瓜的个数比为5:4,那么水果店运来西瓜和哈密瓜各多少个?【答案】西瓜和哈密瓜各是130个及104个. 【解析】试题分析:把234平均分成5+4=9(份),求出一份有多少个,用一份的个数乘以5就是西瓜的个数,总个数减去西瓜的个数就是哈密瓜的个数. 解:234÷(5+4)×5 =26×5 =130(个) 234﹣130=104(个)答:水果店运来西瓜和哈密瓜各是130个及104个.点评:本题关键求出一份有多少个,进一步求出西瓜的个数,用总个数减去西瓜的个数即可得到哈密瓜的个数.【题文】(4分)有429名小学生参加数学冬令营,其中男生和女生的人数比为7:6.后来又有一些女生报名参赛,这时男生和女生的人数比变为11:10.请问:后来报名的女生有多少人? 【答案】有12人. 【解析】试题分析:运用和比问题的解答方法,先求出男生的人数,因为男生的人数没有发生变化,由男生的人数求出总共的人数,然后运用总共的人数减去429人,即可得到后来报名的女生的人数. 解:429÷(7+6)×7÷11×(11+10)﹣429 =33×7÷11×21﹣429 =21×21﹣429 =12(人)答:后来报名的女生有12人.点评:本题运用和比问题的解答方法进行解答,先求出男生人数,进一步取消最后的总人数,最后求出问题.【题文】(4分)松鼠一家三口出门采摘松果,松鼠爸爸采得最快,他每采摘7颗松果,松鼠妈妈只能采摘6颗;松鼠宝宝采得最慢,他每采摘2颗,松鼠妈妈已经采摘了3颗.一天下来,他们一共采摘了340颗松果.试问:其中有多少颗是松鼠宝宝采的?【答案】80颗【解析】试题分析:由于松鼠爸爸每采摘7颗松果,松鼠妈妈采摘6颗;松鼠宝宝采每采摘2颗,松鼠妈妈采摘3颗.依此可知松鼠爸爸采摘松果颗数:松鼠妈妈采摘松果颗数:松鼠宝宝采摘松果颗数=7:6:4,再根据按比例分配即可求得松鼠宝宝采摘松果颗数.解:3:2=6:4鼠爸爸采摘松果颗数:松鼠妈妈采摘松果颗数:松鼠宝宝采摘松果颗数=7:6:4340×=340×=80(颗).答:其中有80颗是松鼠宝宝采的.点评:本题关键是得到松鼠爸爸采摘松果颗数:松鼠妈妈采摘松果颗数:松鼠宝宝采摘松果颗数=7:6:4.【题文】(4分)育才小学五年级学生分成三批去参观博物馆,第一批与第二批的人数比是5:4,第二批与第三批的人数比是3:2.已知第一批的人数比第二、三批的总和少55人.请问:育才小学五年级一共有多少人?【答案】385人.【解析】试题分析:第一批与第二批的人数比是5:4,第二批与第三批的人数比是3:2,据此设第二批有x人,则第一批有x人,第三批有x人.根据第一批的人数比第二、三批的总和少55人,列出方程x+x﹣55=x,解答即可.解:设第二批有x人,则第一批有x人,第三批有x人.x+x﹣55=xx﹣x=55x=55x=132x=×132=165x=×132=88132+165+88=385(人)答:育才小学五年级一共有385人.点评:本题含有3个未知数,设出其中一个,然后用含x的代数式,表示出另外两个,根据题意列出方程解答即可.【题文】(4分)小明将100枚棋子分成三堆,已知第一堆比第二堆的2倍还多,第二堆比第三堆的2倍也要多.请问:第三堆最多有多少枚棋子?【答案】13枚【解析】试题分析:设第三堆最多有x枚棋子,则第二堆至少有2x+1枚棋子,第一堆至少有2(2x+1)+1枚棋子,然后根据三堆的数量总和是100,求出x的值,进而判断出出第三堆最多有多少枚棋子即可.解:设第三堆最多有x枚棋子,则第二堆至少有2x+1枚棋子,第一堆至少有2(2x+1)+1枚棋子,则x+(2x+1)+2(2x+1)+1=1007x+4=1007x=967x÷7=96÷7x=13所以第三堆最多有13枚棋子.答:第三堆最多有13枚棋子.点评:此题主要考查了最大与最小问题的应用,解答此题的关键是弄清楚三堆棋子数量的关系.【题文】(4分)博雅小学五年级有200人,在一次数学竞赛中,参赛人数的获得优胜奖,获得鼓励奖,其余的人没有得奖.试问:该校五年级学生中有多少人没有参加这次数学竞赛?【答案】96人.【解析】试题分析:由于参赛人数的获得优胜奖,获得鼓励奖,可以通过求8和13的最小公倍数确定参赛人数,再用五年级的人数﹣参赛人数,列式计算即可求解.解:因为8和13的最小公倍数是8×13=104,五年级有200人所以参赛人数为104人,200﹣104=96(人)答:该校五年级学生中有96人没有参加这次数学竞赛.点评:此题属于公约数和公倍数问题,解答此题的关键是通过分析,确定范围,进而根据公倍数知识进行解答.【题文】(4分)甲、乙、丙三堆棋子总共有100多枚.先从甲堆分一些棋子给另外两堆,使得乙、丙两堆的棋子数增加1倍;接着,从乙堆分一些棋子给另外两堆,使得甲、丙两堆各增加2倍;最后,从丙堆分一些棋子给另外两堆,使得甲、乙两堆各增加3倍,此时甲、乙、丙三堆棋子数的比是1:2:3.请问:原来三堆棋子各有多少枚?【答案】甲、乙、丙原来各有73、50和21枚.【解析】试题分析:首先由丙分之后甲、乙、丙三堆棋子数的比是1:2:3,根据比的基本性质变形,进一步得到丙分之前,乙分之前,甲分之前甲、乙、丙三堆棋子数的比,再根据甲、乙、丙三堆棋子总共有100多枚即可求解.解:丙分之后甲、乙、丙三堆棋子数的比是1:2:3=4:8:124÷(3+1)=18÷(3+1)=212+(4﹣1)+(8﹣2)=21丙分之前是1:2:21=3:6:633÷(2+1)=163÷(2+1)=216+(3﹣1)+(63﹣21)=50乙分之前是1:50:21=2:100:42100÷(1+1)=5042÷(1+1)=212+(100﹣50)+(42﹣21)=73甲分之前是73:50:21又因为甲、乙、丙三堆棋子总共有100多枚,73+50+21=144(枚),所以甲、乙、丙原来各有73、50和21枚.点评:考查了按比例分配应用题和逆推问题,解题的关键是得到甲分之前甲、乙、丙三堆棋子数的比是73:50:21.【题文】(4分)今年,爷爷的年龄是小明年龄的6倍.若干年后,爷爷的年龄将是小明年龄的5倍.再过若干年,爷爷的年龄将是小明年龄的4倍.求爷爷今年的年龄.【答案】72岁.【解析】试题分析:由题意,可设爷爷今年x岁,则小明今年y岁,第一过了a年,第二次又过了b年,根据“爷爷的年龄是小明年龄的6倍.若干年后,爷爷的年龄将是小明年龄的5倍,再过若干年,爷爷的年龄将是小明年龄的4倍”列方程解答即可.解:设爷爷今年x岁,则小明今年y岁,第一过了a年,第二次又过了b年,x=6yx+a=5(y+a) x=5y+4ax+a+b=4(y+a+b) x=4y+3a+3b解x=24ay=4ab=根据实际a=3 b=5y=12x=72答:爷爷今年72岁.点评:此题等量关系较复杂,要求学生要审清题意找准等量关系,列出方程解答.【题文】(4分)甲、乙、丙三人各有一些书,甲、乙共有54本,乙、丙共有79本,已知三人中书最多的那个人书的数量是书最少的人的2倍.请问:乙有多少本书?【答案】乙有32本或乙有32本.【解析】试题分析:三人有书由少到多的情况有以下6种:(1)甲乙丙,(2)甲丙乙,(3)乙甲丙,(4)乙丙甲,(5)丙甲乙,(6)丙乙甲;又由于甲和乙的本数和小于乙和丙的本数和,故此可得:甲的本数一定小余丙的本数,故此(4)(5)(6)三种情况不可能会有,在其余的三种情况里,设最少的有x本,那么最多的就有2x本,中间数量的有y本,根据甲有的本数+乙有的本数=54本,以及乙有的本数+丙有的本数=79本,分别列出方程,依据等式的性质即可求解.解:设最少的有x本,那么最多的就有2x本,中间数量的有y本情况(1):x+y=54y+2x=79故此可得:x=2254﹣22=32(本)答:乙有32本.情况(2):x+2x=543x=543x÷3=54÷3x=1818×2=36(本)答:乙有乙有32本情况(3):x+2x=793x=793x÷3=79÷3x=26由于书的本数只能是整数,所以情况(3)不存在.点评:解答本题要明确三人有数多少的情况,再判断出不可能情况,根据可能情况列方程解答即可.【题文】(4分)某乡水电站按户收取电费,具体规定是:如果每月用电不超过24度,就按每度9分钱收费;如果超过24度,超出的部分按每度2角钱收费.已知在某月中,甲家比乙家多交了电费9角6分钱(用电按整度计算),问甲、乙两家各交了、电费.【答案】2元7角6分,1元8角.【解析】试题分析:如果甲、乙两家用电均超过24度,那么他们两家的电费差应是2角钱的整数倍;如果甲、乙两家用电均不超过24度,那么他们两家的电费差应是9分钱的整数倍.现在9角6分既不是2角钱的整数倍,又不是9分钱的整数倍,所以甲家的用电超过了24度,乙家的用电不超过24度.设甲家用了24+x度电,乙家用了24﹣y度电,有20x+9y=96,得x=3,y=4.即甲家用了27度电,乙家用了20度电,那么乙家应交电费20×9=180分=1元8角,则甲家交了180+96=276分=2元7角6分.即甲、乙两家各交电费2元7角6分,1元8角.解:设甲家用了24+x度电,乙家用了24﹣y度电,有20x+9y=96,得x=3,y=4.即甲家用了27度电,乙家用了20度电,那么乙家应交电费20×9=180分=1元8角,则甲家交了180+96=276分=2元7角6分.答:甲家交电费2元7角6分,乙家交电费1元8角.故答案为:2元7角6分,1元8角.点评:完成此题,关键是根据整数倍来确定两家的用电范围,进一步解决问题.【题文】(4分)红旗小学共有师生1081人,其中老师与学生的人数之比为2:45,男生与女生的人数之比为5:4.请问:红旗小学的老师、男生和女生各有多少人?【答案】老师46人,男生575人,女生460人.【解析】试题分析:设男生的人数人数为x人,则女生为0.8x人.男女生总人数是x+0.8x=1.8x人.又老师与学生的人数之比为2:45,所以老师人数是×1.8x人.然后根据师生总数1081,列出方程为x+0.8x+×(x+0.8x )=1081,解答即可.解:设男生的人数人数为x人,则女生为0.8x人,由题意得:x+0.8x+×(x+0.8x)=10811.8x+0.08x=10811.88x=1081x=5750.8x=0.8×575=460(人).×(x+0.8x)=×(575+460)=×1035=46(人).答:老师46人,男生575人,女生460人.点评:本题设男生的人数为x人,用含x的代数式表示出女生人数和老师人数是解答此题的关键.【题文】(4分)小悦去商店买了4斤水果糖、2斤奶糖和3斤巧克力糖,如果每块糖果的重量都相同,奶糖和巧克力糖一共有160块,那么水果糖有多少块?【答案】128块.【解析】试题分析:由题意,先求1进糖有多少块,即160÷(2+3),再求4斤水果糖有多少块;据此解答.解:160÷(2+3)×4=32×4=128(块)答:水果糖有128块.点评:此题考查了简单的归一问题,先求单一量是关键.【题文】(4分)万泉小学的师生在植树节栽种柳树、杨树和槐树共860棵,其中柳树和杨树棵数的比为3:4,杨树与槐树棵数的比为5:2.请问:这三种树各栽种了多少棵?【答案】杨树400棵,柳树300棵,槐树160棵.【解析】试题分析:设杨树有x棵.根据柳树和杨树棵数的比为3:4,杨树与槐树棵数的比为5:2,表示出柳树的棵数为x,槐树的棵数为x.根据柳树、杨树和槐树共860棵,列出方程为x+x+x=860,解出x,进而求出柳树和槐树的棵数即可.解:设杨树有x棵,由题意得:x+x+x=8602.15x=860x=400x=×400=300(棵)860﹣400﹣300=160(棵)答:杨树400棵,柳树300棵,槐树160棵.点评:本题须设其中一个未知数为x,用含x的代数式表示出另外两个.然后根据等量关系列出方程即可.【题文】(4分)某厂一月份与二月份生产零件的个数比为4:5.后来改进生产技术,三月份生产的零件个数与前丽个月的总产量之比为4:3,且三月份比二月份多生产了1610个零件.请问:这家工厂第一季度共生产多少个零件?【答案】4830个.【解析】试题分析:设二月份生产零件x个,则一月份生产零件x个.三月份生产的零件个数与前丽个月的总产量之比为4:3,所以三月份生产零件(x+x)个.根据三月份比二月份多生产了1610个零件,列出方程为(x+x)﹣x=1610,解答即可.解:设二月份生产零件x个,则一月份生产零件x个.由题意得:(x+x)﹣x=1610x+x﹣x=16101.4x=1610x=11501150+1150×+(1150+1150×)=1150+920+2760=4830(个)答:这家工厂第一季度共生产4830个零件.点评:对应这种较为复杂的数量关系的题目,设未知数列方程解答较好.【题文】(4分)有48本书分给两组小朋友,已知第二组比第一组多5人.如果把书全都分给第一组,一部分小朋友每人能拿到5本,其他小朋友每人能拿到4本;如果把书全都分给第二组,一部分小朋友每人能拿到4本,其他小朋友每人能拿到3本,问:两组一共有多少人?【答案】25人.【解析】试题分析:如果把书全部分给第一组,那么每人有4本的,每人有5本的.说明第一组人数少于48÷4=12人,多于48÷5=9…3,即9人;如果把书全分给第二组,那么每人有3本的,每人有4本的.说明第二组人数少于48÷3=16人,多于48÷4=12人;因为已知第二组比第一组多5人,所以,第一组只能是10人,第二组15人.由此解决问题.解:由于48÷4=12人,48÷5=9人…3本,所以,第一组少于12人,多于9人;由于48÷3=16,48÷4=12,所以第二组多于12人,少于16人;又已知第二组比第一组多5人,所以,第一组只能是10人,第二组只能是10+5=15人.两组一共有:10+15=25(人)答:两组一共有25人.点评:根据题意得出两组人数的取值范围是完成本题的关键.【题文】(4分)22名家长(爸爸或妈妈,他们都不是老师)和老师陪同一些小学生参加某次数学竞赛,已知家长比老师多,妈妈比爸爸多,女老师比妈妈多2人,至少有一名男老师,那么在这22人中,共有爸爸多少人?【答案】5人.【解析】试题分析:本题根据已知条件进行推敲,得出各类人数的范围,进而求出爸爸的人数.具体解题步骤如下:解:家长比老师多,所以老师少于22÷2=11人,也就是不超过10人,家长就不少于12人.在至少12个家长中,妈妈比爸爸多,所以妈妈要多于12÷2=6人,也就是不少于7人.因为女老师比妈妈多2人,所以女老师不少于9人,但老师最多就10个,并且还至少有1个男老师,所以老师必须是10个(9个女老师,1个男老师),家长12个人中,有7个妈妈,那么爸爸就有12﹣7=5人.答:在这22人中,爸爸有5人.点评:本题多次运用最值问题思考方法,且巧借半差关系,得出不等式的范围.【题文】(4分)志远中学有三个年级,共900多名学生,其中初一的学生数恰好占学生总数的,初三的学生恰好占学生总数的,请问:志远中学初二有多少名学生?【答案】376名.【解析】试题分析:因为8和15的最小公倍数是120,因此三个年级总人数应为120的公倍数,因为共900多名学生,所以总人数应是120×8=960人.因此志远中学初二有学生:960×(1﹣﹣),解决问题.解:三个年级总人数应为8和15的最小公倍数120的倍数,因此总人数应为:120×8=960(人).初二有学生:960×(1﹣﹣)=960×=376(人)答:志远中学初二有376名学生.点评:此题解答的关键在于根据分母的最小公倍数确定出总人数,进而解决问题.【题文】(4分)把100个人分成四队,第一队人数是第二队人数的1倍,是第三队人数的1倍,求第四队的人数.【答案】49人.【解析】试题分析:根据题意,可得前三队的人数比是:1::=20:15:16,因为20+15+16=51,四个队的总人数为100人,所以前三队的人数只能是20人,15人,16人,第四队人数为:100﹣20﹣15﹣16=49人,据此解答即可.解:根据题意,可得前三队的人数比是:1:(1÷1):(1÷1)=1::=20:15:16,因为20+15+16=51,四个队的总人数为100人,所以前三队的人数只能是20人,15人,16人,故第四队人数为:100﹣20﹣15﹣16=49(人).答:第四队的人数是49人.点评:解答此题的关键是首先求出前三队的人数比是多少,进而判断出前三队的人数.【题文】(4分)甲、乙、丙三人各有一些棋子,其中棋子数最多的人比最少的人多出60多枚棋子,甲先拿出自己的一半平分给乙、丙,然后乙拿出自己的平分给甲、丙,最后丙拿出自己的平分给甲、乙.这时三人的棋子数正好相同.请问:三个人一共有多少枚棋子?【答案】432枚.【解析】试题分析:反过来想:最后三人都是X枚,之前丙应该是X,乙和甲都是X;再之前乙为X,丙为X,甲为X;开始为甲X,乙为X,丙为X;从这看出X一定是48的倍数,又甲X减去丙等于60多,即X=60多,所以应该等于63(7的倍数),所以X=144,三人一共为432枚棋子.解:设最后三人都是X枚,之前丙应该是X,乙和甲都是X;再之前乙为X,丙为X,甲为X;开始为甲X,乙为X,丙为X;X﹣X=63X=63X=144144×3=432(枚)答:三个人一共有432枚棋子.点评:解决此类问题的关键是抓住最后得到的数量,从后向前进行推理,根据逆运算思维进行解答.【题文】(4分)有两堆石头,如果从第一堆中取出20块石头放进第二堆,那么第二堆的石头是第一堆的2倍;如果从第二堆中取出一些石头放进第一堆,那么第一堆的石头是第二堆的6倍.问:第一堆中最少可能有多少块石头?【答案】34块.【解析】试题分析:设第一堆有x块石头,第二堆有y块石头,从第二堆取出z块放进第一堆,然后根据“从第一堆中取出20块石头放进第二堆,那么第二堆的石头是第一堆的2倍”以及“从第二堆中取出一些石头放进第一堆,那么第一堆的石头是第二堆的6倍”这两个等量关系,列出三元一次方程组,求解即可.解:设第一堆有x块石头,第二堆有y块石头,从第二堆取出z块放进第一堆,则,由①,可得y=2x﹣60…③,把③代入②,整理得11x﹣7z=360,所以x=32;又因为x,z都是自然数,所以7z+8是11的倍数,当z=2时,x有最小值为:x=32=34,即第一堆中最少可能有34块石头.答:第一堆中最少可能有34块石头.点评:此题主要考查了多元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程组是解答此类问题的关键.【题文】(4分)北京市出租车的起步价是33公里以内10元,公里后按每公里2元计费,当里程超过15公里后,超出部分按每公里3元计费.小悦、冬冬两人都从游乐园分别坐出租车回家,小悦比冬冬多花了23元,请问:小悦家距离游乐园最远是多少公里?(不足1公里按1公里计,假定两人回家一路上没有红绿灯,也没有堵车)【答案】22公里.【解析】试题分析:3公里以内10元,而公里后按每公里2元计费,所以在15公里之内车费都是偶数,小悦比比冬冬多花23元,23不是2的倍数,也不是3的倍数,说明小悦里程超过15公里,冬冬不超过15公里,然后把23进行分解,得到一部分2的倍数和一部分3的倍数组成,从而解决问题.解:在3~15公里内花的车费都是偶数,小悦比比冬冬多花23元,23不是2的倍数,也不是3的倍数,说明小悦里程超过15公里,冬冬不超过15公里,23是由一部分2的倍数和一部分3的倍数组成,23=2×10+323=2×7+3×323=2×4+3×523=2×1+3×7当小悦里程超过15公里越多,里程越远,因此小悦里程最远是15+7=22(公里)答:小悦家距离游乐园最远是22公里.点评:本题需要根据每公里车费的情况,得出小悦里程超过15公里,冬冬不超过15公里,再把23进行拆分即可求解.【题文】(4分)(2012•仙游县)某公园对团体游园购买门票的规定如下表:购票人数 50人以下 51~100人 100人以上每人门票价 12元 10元 8元今有甲、乙两个旅游团,若分别购票,两团总计应付门票费1142元.如合在一起作为一个团体购票,总计只应付门票费864元.问:这两个旅游团各有多少人?【答案】甲旅游团有31 人,乙旅游团有77人.【解析】试题分析:根据两个团合在一起作为一个团体购票,总计只应付门票费864元.这样就可以求此两个团一共有多少人,用864÷8=108人,设甲团有x人,则乙团有(108﹣x)人,已知分别购票,两团总计应付门票费1142元,由此列方程解答.解:两个团的总人数;864÷8=108(人),设甲团有x人,则乙团有(108﹣x)人,12x+(108﹣x)×10=1142,12x+1080﹣10x=1142,2x+1080=1142,2x+1080﹣1080=1142﹣1080,2x=62,2x÷2=62÷2,x=31;108﹣31=77(人);答:甲旅游团有31 人,乙旅游团有77人.点评:此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可【题文】(4分)植物园里菊花与月季花的盆数之比是3:4,兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.如果月季比兰花多50多盆,那么菊花比郁金香少多少盆?【答案】48盆.【解析】试题分析:兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.我们设郁金香有x盆,则兰花有x盆,菊花有x盆.又菊花与月季花的盆数之比是3:4,所以月季有×(x)盆.根据月季比兰花多50多盆,列出方程50<×(x)﹣x<60,解出x,然后再求出菊花的盆数,用郁金香的盆数减去菊花的盆数即可.解:设郁金香有x盆,月季比兰花多m盆.且50<m<60根据题意得:×(x)﹣x=mx﹣x=mx=mx=因为x代表花的盆数,不能是分数,30不能被7整除.所以m应是7的倍数,有50<m<60,所以m=56.x===240(盆)x﹣x=240﹣×240=240﹣192=48(盆)答:菊花比郁金香少48盆.点评:本题含有多个未知数,要设其中的一个,然后用含x的代数式,表示出另外几个,根据题目中的等量关系列出方程解答.【题文】(4分)甲、乙、丙、丁包揽了班里期中考试的前四名.甲、乙的得分之和是108分,乙、丙的得分之和是149分,丙、丁的得分之和是121分,并且知道其中第一名的得分是第三名的2倍,那么第二名的得分是多少?【答案】67分.【解析】试题分析:由题意,甲、乙的得分之和是108分,乙、丙的得分之和是149分,丙、丁的得分之和是121分,相比得到:丙﹣甲=41,乙﹣丁=28,所以第一名是乙或者丙;分乙是第一或丙是第一两种情况来推理得出第二名的得分即可.解:相比得到:丙﹣甲=41,乙﹣丁=28,所以第一名是乙或者丙:(1)若乙是第一,则因为149不能被3整除,所以丙不为第三,只能是第二,丁第三,因为乙﹣丁=28,所以乙=56,但丙=149﹣56=93>乙,矛盾;(2)若丙第一,则因为149不能被3整除,乙只能是第二,又因为121不能被3整除,所以丁只能是第四,所以甲第三,丙﹣甲=41,即丙=82,甲=41,最后得:第二名乙=108﹣41=67;答:第二名的得分是67分.点评:此题考查利用整除性解决问题.【题文】(4分)有四位好朋友的体重都是整千克数.他们两两合称体重,共称了五次.称得的千克数分别是99、113、125、130、144.其中两人没有一起合称过,那么这两人中较重一人的体重是千克.【答案】66.【解析】试题分析:设四人体重分别是A、B、C、D,其中A、B没同时称重,而(A+C)+(B+D)=(A+D)+(B+C)(每个括号表示两人合称重量),注意到五个重量中只有99+144=113+130,因此得到C+D=125,这样就可以求出A+B=118.由此知A、B同奇偶,C、D必一奇一偶,故四人重量中必有三人同奇偶,由此即可求出A 、B、C,也就求出了这两人体重较大的体重.解:设四人是A、B、C、D,其中A、B没同时称重,于是必有(A+C)+(B+D)=(A+D)+(B+C)(每个括号表示两人合称重量),注意到五个重量中只有:99+144=113+130,故剩下的125必是C、D的重量和,即有C+D=125,所以A+B=99+144﹣125=118.由此知A、B同奇偶,C、D必一奇一偶,故四人重量中必有三人同奇偶,不妨令A、B、C同奇偶,于是A+C与B+C的值也是偶数,即有:A+C=144,B+C=130,或A+C=130,B+C=144,由前者求得:A=66,B=52,C=78,由后者求得:A=52,B=66,C=78,故合称的两人体重较大的是66kg.故答案为:66.点评:此题主要考查了多元一次方程组的应用,解题的关键是正确理解题意,把握题目中的数量关系,然后列出方程组解决问题.【题文】(4分)有若干盒卡片,每盒中卡片数一样多.把这些卡片分给一些小朋友,如果只分一盒,每人至少可以得到7张;如果每人分8张卡片,则还缺少5张.现在把所有卡片都分完,每人分到60张,而且还多出4张.问:共有多少个小朋友?【答案】11个.【解析】试题分析:由题意,60÷7=8…4,60÷8=7…4,说明卡片的盒数是8盒,“若都分8张则还缺少5张”,即如果我们在每盒中加5张(8盒共加40张),每人就可以得到8×8=64张,现在实际每人得到60张,即每人需要退出4张,其中要有4张是每人60张后多下来的,还有40张是我们一开始借来的要还出去,即要退出44张,44÷4═11,说明有11人.解:60÷7=8…4,60÷8=7…4,说明卡片的盒数是8盒,(4+5×8)÷4=44÷4=11(人),答:共有11个小朋友.点评:根据“只分一盒,每人至少可以得到7张;如果每人分8张卡片,则还缺少5张”推出共有8盒卡片是解题的关键.【题文】(4分)某次考试共有100道题,每题一分,做错不扣分,甲、乙、丙三位同学分别得90分、70分、50分,其中3个人都做出来的题叫作“容易题”,只有1个人做出来的题目叫作“较难题”,没人做出来的题目叫作“特难题”,且“较难题”是“特难题”的3倍,又已知丙同学做出的题中超过80%的是“容易题”,但又不全是“容易题”,请问:“特难题”共有多少道?【答案】7道.【解析】试题分析:通过分析,可设特难题a道,较难题有3a道,容易题有b道,则有2人做出的题有(100﹣4a ﹣b)道,易知3a+2(100﹣4a﹣b)+3b=210,可知b=5a+10>40,则有a≥7,又a<100﹣90=10,则有a ≤9,所以a=7,8,9,解得a=7,b=45;a=8,b=50;a=9,b=55,由于b<50,所以只有a=7,b=45满足条件,据此解答即可.解:设特难题a道,较难题有3a道,容易题有b道,则有2人做出的题有(100﹣4a﹣b)道:可得方程:3a+2(100﹣4a﹣b)+3b=210。
苏教版五年级(下册)数学思维拓展训练
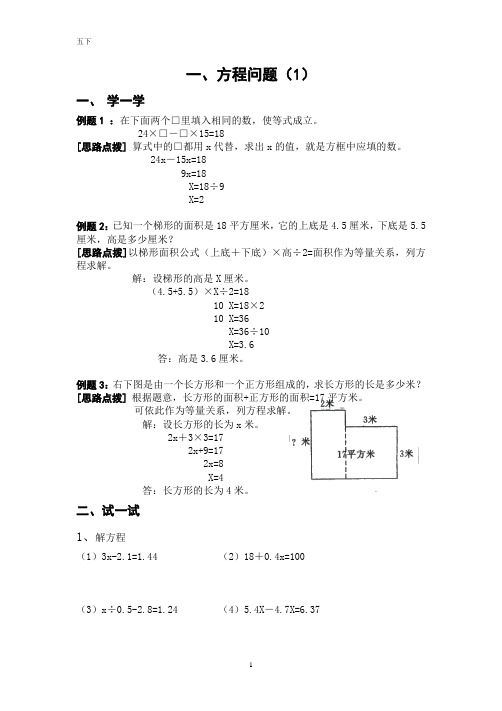
一、方程问题(1)一、学一学例题1:在下面两个□里填入相同的数,使等式成立。
24×□-□×15=18[思路点拨]算式中的□都用x代替,求出x的值,就是方框中应填的数。
24x-15x=189x=18X=18÷9X=2例题2:已知一个梯形的面积是18平方厘米,它的上底是4.5厘米,下底是5.5厘米,高是多少厘米?[思路点拨]以梯形面积公式(上底+下底)×高÷2=面积作为等量关系,列方程求解。
解:设梯形的高是X厘米。
(4.5+5.5)×X÷2=1810 X=18×210 X=36X=36÷10X=3.6答:高是3.6厘米。
例题3:右下图是由一个长方形和一个正方形组成的,求长方形的长是多少米?[思路点拨]根据题意,长方形的面积+正方形的面积=17平方米。
可依此作为等量关系,列方程求解。
解:设长方形的长为x米。
2x+3×3=172x+9=172x=8X=4答:长方形的长为4米。
二、试一试1、解方程(1)3x-2.1=1.44 (2)18+0.4x=100(3)x÷0.5-2.8=1.24 (4)5.4X-4.7X=6.37(5)4X+0.5X=18 (6) X-0.8X-6=16(7)0.72×3-7X=0.06 (8)0.5x-4×0.25=1.25(9)8x÷(1.8+3)=1.5 (10)5x+3×(x-2)=1506(11)2.7x-25+75=212 (12)x ÷1.52-12.5-2.5=4.52、□表示相同的数,□÷3×9-(5×□-3×□)=1,求□内的值。
三、练一练(列方程解答)1、已知一个长方形的周长是18平方厘米,它的长是5.6厘米,宽是多少厘米?2、已知一个三角形的面积是2.4平方厘米,它的高是0.8厘米,底是多少厘米?3、下图是由一个平行四边形和一个三角形组成的,它的总面积是171平方厘米,求三角形底是多少厘米?15厘米9厘米厘米二、方程问题(2)一、学一学例题1、鸡兔共100只,有脚280只,鸡兔各多少只?[思路点拨]此题是鸡兔同笼问题。
(完整版)五年级数学下册数学拓展提高题

五年级数学下册数学提高题
1、有四只盒子,共装了45个小球.如变动一下,第一盒减少2个;第二盒增加2个;第三盒增加一倍;第四盒减少一半,那么这四只盒子里的球就一样多了.原来每只盒子中各有几个球?
2、一个两位数,十位上的数字比个位上的数字小1,十位上的数字与个位上的数字的和是这个两位数的0.2倍.求这个两位数.
3、一个工程队由6个粗木工和1个细木工组成,完成某项任务后,粗木工每人得200元,细木工每人工资比全队的平均工资多30元,求细木工每人得多少元?
4、一个两位数,个位上的数字是十位上数字的2倍,如果把十位上的数字与个位上的数字对调,那么得到的新两位数比原两位数大36.求原两位数.
5、买4支钢笔和9支圆珠笔共付24元,已知买2支钢笔的钱可买3支圆珠笔,两种笔的价钱各是多少元?
6、电视机厂装配一批电视机,计划25天完成,如每天多装35台,24天能超额完成60台.求原计划每天装配多少台.
7、老师在黑板上写了若干个从1开始的持续自然数1,2,3,……,后来擦掉其中一个,剩下的数的平均数是10.8,擦掉的自然数是多少?
1/ 1。
【一日一题思维拓展训练】小学五年级数学下册思维拓展训练(第3套)附答案-人教版

五年级数学下册思维拓展训练(第3套)班级姓名得分【资料使用建议】:每日1题,坚持训练1.有一个两位数,把数码1加在它的前面可以得到一个三位数,加在它的后面也可以得到一个三位数,这两个三位数相差666。
原来的两位数是多少?2.在三角形ABC内有100个点,以三角形的顶点和这100点为顶点,可把三角形剖分成多少个小三角形?3.甲乙两列火车同时从AB两地相对开出,相遇时,甲.乙两车未行的路程比为4:5,已知乙车每小时行72千米,甲车行完全程要10小时,问AB两地相距多少千米?4.甲、乙两列火车同时从A地开往B地,甲车8小时可以到达,乙车每小时比甲车多行20千米,比甲车提前2小时到达。
求A、B两地间的距离。
5.将一个四位数的数字顺序颠倒过来,得到一个新的四位数。
如果新数比原数大7992,那么所有符合这样条件的四位数中原数最大的是_____。
6.数学竞赛后,小明、小华、小强各获得一枚奖牌,其中一人得金牌,一人得银牌,一人得铜牌.王老师猜测:“小明得金牌;小华不得金牌;小强不得铜牌.”结果王老师只猜对了一个.那么小明得什么牌,小华得什么牌,小强得什么牌?7.甲、乙两地公路长74千米,8:15一辆汽车从甲地到乙地,半个小时后,又有一辆同样速度的汽车从甲地开往乙地.王叔叔8:25从乙地骑摩托车出发去甲地,在差5分不到9点时,他遇到了第一辆汽车,9:16遇到第二辆汽车,王叔叔骑摩托车的速度是多少?8.牧场上一片青草,每天牧草都匀速生长.这片牧草可供10头牛吃20天,或者可供15头牛吃10天.问:可供25头牛吃几天?9.余数相同求除数有一个不等于1的整数,用它去除967、1000、2001,得到的余数相同,这个整数是多少?10.梯形的上底长12cm,高15cm。
阴影面积是15cm2,求梯形的面积。
参考答案1.【答案】解:设原来的两位数是x,由题意得:(10x+1)﹣(100+x)=666,9x=765,x=85答:原来的两位数是85。
五年级下册数学扩展专题练习:行程 .多次相遇和追及问题 (B级)全国通用

多次相遇与追及问题知识框架一、由简单行程问题拓展出的多次相遇问题所有行程问题都是围绕“路程速度时间”这一条基本关系式展开的,多人相遇与追及问题虽然较复杂,但只要抓住这个公式,逐步表征题目中所涉及的数量,问题即可迎刃而解.二、多次相遇与全程的关系1. 两地相向出发:第1次相遇,共走1个全程;第2次相遇,共走3个全程;第3次相遇,共走5个全程;…………,………………;第N次相遇,共走2N-1个全程;注意:除了第1次,剩下的次与次之间都是2个全程。
即甲第1次如果走了N米,以后每次都走2N 米。
2. 同地同向出发:第1次相遇,共走2个全程;第2次相遇,共走4个全程;第3次相遇,共走6个全程;…………,………………;第N次相遇,共走2N个全程;3、多人多次相遇追及的解题关键多次相遇追及的解题关键几个全程多人相遇追及的解题关键路程差三、解多次相遇问题的工具——柳卡柳卡图,不用基本公式解决,快速的解法是直接画时间-距离图,再画上密密麻麻的交叉线,按要求数交点个数即可完成。
折线示意图往往能够清晰的体现运动过程中“相遇的次数”,“相遇的地点”,以及“由相遇的地点求出全程”,使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。
如果不画图,单凭想象似乎对于像我这样的一般人儿来说不容易。
例题精讲【例1】甲、乙两车同时从A地出发,不停的往返行驶于A,B两地之间。
已知甲车的速度比乙车快,并且两车出发后第一次和第二次相遇都在途中C地。
问:甲车的速度是乙车的多少倍?【巩固】甲、乙二人从相距60千米的两地同时相向而行,6时后相遇。
如果二人的速度各增加1千米/时,那么相遇地点距前一次相遇地点1千米。
问:甲、乙二人的速度各是多少?【例2】如图,甲和乙两人分别从一圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动,当乙走了100米以后,他们第一次相遇,在甲走完一周前60米处又第二次相遇.求此圆形场地的周长.【巩固】A、B是圆的直径的两端,甲在A点,乙在B点同时出发反向而行,两人在C点第一次相遇,在D 点第二次相遇.已知C离A有75米,D离B有55米,求这个圆的周长是多少米?【例3】甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离是多少千米?【巩固】甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地4千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地3千米处第二次相遇,求两次相遇地点之间的距离.【例4】A、B两地相距2400米,甲从A地、乙从B地同时出发,在A、B间往返长跑。
青岛版六三学制五年级数学下册课本拓展题

五年级下册课本拓展题1.食品包装袋上标着1205克,这袋食品最重()克,最轻()克,都算合格。
2.今年第一季度的天数占全年的()3.把3米长的铁丝平均分成4份,每份占全长的(),每份长()米,每份占1米的()。
两份长()米。
4.甲乙丙三人各买了一本同样的书,甲花了自己钱数的13,乙花了自己钱数的14,丙花了自己钱数的15,()的钱最多。
5.一个正方形的周长是3分米,它的边长是()分米。
6.小华15分钟走2千米,他平均每分钟走()千米。
走1千米需()分钟。
7.把3千米长的铁丝平均截成7段,每段长()米,每段占全长的()。
8.一副扑克牌中红桃的张数占总张数的()大王和小王的张数是梅花张数的()9.有43面同样大小的红、黄、绿色小旗,按1面红旗、2面黄旗、3面绿旗的顺序排列。
三种颜色的旗各占总数的几分之几?10.13a b=(a、b都是非0自然数),当a=2、3、4、…时,b分别是几?A与b之间有什么关系?为什么?11.你能找出2个大于25又小于35的分数吗?12.把30吨小麦分4次运完,平均每次运这些小麦的()(),每次运()吨。
13.34里面有()个14,有()个1814.找出每组数的最大公因数。
42和54 的最大公因数(),57和38的最大公因数(),36和54的最大公因数(),52和78的最大公因数()15.把这16cm长、32cm长、56cm长的三段彩条截成同样长的几段且没有剩余,每段彩条最长几厘米(),可以分()段。
16.一个最简分数,若将它的分子加上2,则等于12。
这个分数可能是多少?17.一个最简分数,分子减1,分母减3,则等于34。
这个分数是()18.一个最简分数,分子加上2,分母减去3,则等于23。
这个分数是()19.一个分数分母加上8后,约分后是14这个分数可能是()20.分子分母的和是49,分子加1分母减2约分后是25原分数是()21.有一些物品,如果3个3个地数,最后剩2个;如果5个5个地数,最后剩3个;如果7个7个地数,最后剩2个。
五年级下册数学拓展作业

一、填空。
1、下面的现象中是平移的画“△”,是旋转的画“□”。
(1)索道上运行的观光缆车。
()(2)推拉窗的移动。
()(3)钟面上的分针。
()(4)飞机的螺旋桨。
()(5)工作中的电风扇。
()(6)拉动抽屉。
()二、判断题。
正确的在题后的括号里画“√”,错的画“×”。
(1)正方形是轴对称图形,它有4条对称轴。
……………()(2)圆不是轴对称图形。
……………………………………()(3)利用平移、对称和旋转变换可以设计许多美丽的镶嵌图案。
………………()(4)风吹动的小风车是旋转现象。
…………………………()三、解决问题(1)有一块平行四边形钢板,底是6.5分米,高是3.4分米。
如果每平方分米钢板重0.75千克,这块钢板重多少千克?(2)一间会议室长12米,宽7.2米,如果用边长3分米的正方形地面砖铺地,一共需要多少块?1.认真思考,对号入座(1)在26、12和13这三个数中,()是()的倍数,()是()的约数,()和()是互质数。
(2)一个数,千位上是最小的质数,百位上是最小的奇数,个位是最小的合数,其余数位上的数字是0,这个数写作()。
(3)根据要求写出三组互质数。
两个数都是质数()和()。
两个数都是合数()和()。
两个数中一个数是质数,一个数是合数()。
(4)一个数的最大约数是36 ,这个数是(),它的所有约数有(),这个数的最小倍数是()。
(5)a=2×3×5,b=2×5×11,a和b的最大公约数是(),a和b的最小公倍数是()。
(6)把210分解质因数:210=()。
(7)一个两位数同时能被2、5、3整除,这个两位数最大是(),最小是()。
(9)把下面的合数写成两个质数和的形式。
15=()+()20=()+()=()+()一填空1、一个数的倍数的个数是(),最小的倍数是()。
2、在数字5、0、6组成的三位数中,2的倍数有(),5的倍数有(),同时是2和5的倍数有()。
五年级下册数学提升练习第四周

五年级下册数学提升练习(第四周)
班级:姓名:学号:
1.三个质数A,B,C,其中A+B=33,B+C=44,C+D=66。
求A,B,C,D。
2.一个正方体木块的表面积是96cm²,把它锯成体积相等的8个小正方体。
表面积增加了多少?
3.如下图,从一个长7cm、宽5cm、高4cm的长方体的上方挖去了一个长7cm、宽2cm、高2cm的长方体。
剩下部分的表面积是多少平方厘米?
4.下面是由若干个棱长为1cm的小正方体组成的立体图形,求这个立体图形的体积。
5.下面是一个长方体容器,里面水深为5.6dm。
把一个南瓜放入后(南瓜浸没在水中),从容器里溢出4L的水。
这个南瓜的体积是多少?
6.一个无水观赏鱼缸中放有一块高为28cm,体积为4200cm³的假山石,如果水管以每分钟8dm³的流量向鱼缸内注水,那么至少需要多长时间才能将假山石完全淹没?
7.“绿水青山就是金山银山”,植树节这天,李老师带领同学们排成两路人数相等的纵队去植树。
已知李老师植树的棵数与每名同学植树的棵数相等,每人植树棵数大于1,而且一共植了111棵树。
你知道有多少名同学吗?。
人教版数学五年级下册期末试卷检测(提高,Word版含解析)

人教版数学五年级下册期末试卷检测(提高,Word 版含解析)一、选择题1.把一个正方体切开,分成两个长方体,表面积( )。
A .不变B .增加了C .减少了2.把顺时针旋转90°后的图形是( )。
A . B . C .3.一个两位数,个位上的数既是质数又是偶数,十位上的数既是奇数又是合数。
这个数是( )。
A .52B .72C .29D .924.小林和小红都去参加游泳训练。
小林每6天去一次,小红每8天去一次。
7月31日两人同时参加游泳训练后,( ),他们又再次相遇。
A .8月23日B .8月24日C .8月25日D .9月17日 5.分数单位是110的最简真分数的和是( )。
A .3 B .4.5C .2 6.长都是1米的两根铁丝,第一根用去12,第二根用去12米,剩下的相比( )。
A .两根同样长B .第一根长C .第二根长D .无法判断 7.有23位男士到宾馆住宿,住3人间和2人间(每个房间不能有空床位),有( )种不同的安排。
A .3B .4C .58.如下图,把一个六面都涂上颜色的正方体木块切成125个大小相同的小正方体,其中两面涂色的小正方体有( )个。
A .8B .54C .36二、填空题9.37.3dm =(________)3m 6.2L =(________)mL23m 5=(________)2dm 23时=(________)分 10.a b 、都是大于0的自然数。
当a ________时,b a是真分数。
这样的真分数有________个(用含有字母的式子表示)。
11.一个四位数○67○同时是2、3、5的倍数,这个数最大是(________),最小是(________)。
12.如果a b的分数值是最小的质数(a 、b 都是不为0的自然数),那么a 和b 的最大公因数是(________),最小公倍数是(________)。
13.学校分发一批口罩,每班9盒或每班14盒都正好分完,这批口罩至少有(______)盒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学下册数学提高题
1、有四只盒子,共装了45个小球.如变动一下,第一盒减少2个;第二盒增加2个;第三盒增加一倍;第四盒减少一半,那么这四只盒子里的球就一样多了.原来每只盒子中各有几个球?
2、一个两位数,十位上的数字比个位上的数字小1,十位上的数字与个位上的数字的和是这个两位数的0.2倍.求这个两位数.
3、一个工程队由6个粗木工和1个细木工组成,完成某项任务后,粗木工每人得200元,细木工每人工资比全队的平均工资多30元,求细木工每人得多少元?
4、一个两位数,个位上的数字是十位上数字的2倍,如果把十位上的数字与个位上的数字对调,那么得到的新两位数比原两位数大36.求原两位数.
5、买4支钢笔和9支圆珠笔共付24元,已知买2支钢笔的钱可买3支圆珠笔,两种笔的价钱各是多少元?
6、电视机厂装配一批电视机,计划25天完成,如每天多装35台,24天能超额完成60台.求原计划每天装配多少台.
7、老师在黑板上写了若干个从1开始的连续自然数1,2,3,……,后来擦掉其中一个,剩下的数的平均数是10.8,擦掉的自然数是多少?。
