章末复习与测评 (3)
二年级最新 阅读理解复习巩固专讲专练(章末复习+综合测评+答案)经典

最新阅读理解复习巩固专讲专练(章末复习+综合测评+答案)经典一、二年级语文下册阅读理解训练1.阅读短文,回答问题。
仙人掌和凤尾草沙漠里下了一阵稀有的雨。
一棵刚萌芽不久的凤尾草,叶子还是黄绿色的。
它看见旁边长着一株碧绿的仙人掌。
凤尾草带着厌恶的神情看了看仙人掌,嘲笑说:“喂,朋友,你满身长刺,像一个什么东西?难道你一点儿也不觉得自己太丑吗?”仙人掌平心静气地说:“我长刺不仅使动物不敢来啃咬我,更重要的是我的刺就是叶子,在干燥的环境中,不会使身体内的水分大量蒸发掉,所以,我能在沙漠里生存下来。
”黄绿的凤尾草似乎不屑和仙人掌争辩,哼了一声,再不理睬它。
过了好多天,_________________________________。
(1)从第二自然段中摘抄词语。
描写事物颜色的:________描写动作的:________ (2)为什么仙人掌身上长了刺就能在沙漠中生存?(3)过几天会怎么样,请你展开想像,写在文中的横线上。
【答案】(1)黄绿色,碧绿;看见,看了看(2)仙人掌长刺不仅使动物不敢来啃咬它,更重要的是它的刺就是叶子,在干燥的环境中,不会使身体内的水分大量蒸发掉,所以,它能在沙漠里生存下来。
(3)略【解析】2.阅读短文,回答问题。
晚饭后,我和姐姐正在门口乘凉。
忽然飞来一只大蜻蜓,落在一棵小树上,我悄悄地跑去,把它捉住。
大蜻蜓真漂亮!两只眼珠像小玻璃球,亮晶晶的。
一对红翅膀不住地扇着。
我真喜欢它,就拿着玩起来。
姐姐看见了,大声喊:“快把它放了,它是益虫!”我听了姐姐的话,想到益虫的好处,就把它放了。
(1)给划线的字选择正确的音节忽然________(yán rán)扇________着(shān shàn)乘________凉(chèng chéng)捉________住(zhuōzuō)(2)写出下面词语的反义词。
漂亮________ 喜欢________(3)作者在描写大蜻蜓的外形时,具体地写了蜻蜓的________和________的特点。
高中数学人教A版必修三 第三章 概率 章末综合测评及答案

会,估计运动会期间不.下.雨.的概率. 【解】 (1)在容量为 30 的样本中,不下雨的天数是 26,以频率
估计概率,4 月份任选一天,西安市不下雨的概率为 2360=1153. (2)称相邻的两个日期为“互邻日期对”(如,1 日与 2 日,2 日与 3
日等).这样,在 4 月份中,前一天为晴天的互邻日期对有 16 个,其中 后一天不下雨的有 14 个,所以晴天的次日不下雨的频率为 78.
(2)该班成绩在[60,100]内的概率是 P(A∪B∪C∪D)=P(A)+P(B)
+P(C)+P(D)=0.17+0.36+0.25+0.15=0.93.
19.(本小题满分 12 分)小王、小李两位同学玩掷骰子(骰子质地均 匀)游戏,规则:小王先掷一枚骰子,向上的点数记为 x;小李后掷一 枚骰子,向上的点数记为 y.
【答案】 C
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分,把答案填在
题中横线上).
13.一个袋子中有 5 个红球,3 个白球,4 个绿球,8 个黑球,如
果随机地摸出一个球,记 A={摸出黑球},B={摸出白球},C={摸出
绿球},D={摸出红球},则 P(A)=________;P(B)=________;P(C∪D)
A,B,C 和 3 名女同学 X,Y,Z,其年级情况如下表:
一年级 二年级 三年级
男同学 A
=________.
【解析】 由古典概型的算法可得 P(A)=280=25,P(B)=230,P(C∪D)
=P(C)+P(D)=240+250=290.
【答案】
2 5
3 20
9 20
14.在区间(0,1)内任取一个数 a,能使方程 x2+2ax+12=0 有两
一年级2020-2021年 阅读理解复习巩固专讲专练(章末复习+综合测评+答案)

2020-2021年阅读理解复习巩固专讲专练(章末复习+综合测评+答案)一、一年级语文上册阅读理解练习1.阅读儿歌,完成练习。
蚂蚁搬虫虫小蚂蚁,搬虫虫。
一个搬,搬不动。
两个搬,掀条缝。
三个搬,动一动。
四个五个六七个,大家一起搬进洞。
(1)找出儿歌中表示数目的汉字。
(2)读儿歌,选一选。
(填序号)①虫虫那么大,小蚂蚁最后把它搬回家了吗?( )A.搬回家了。
B.没有搬回家。
②这首儿歌告诉我们( )A.人多力量大。
B.个人的力量是无穷的。
(3)读读上面的儿歌,再学着做做下面的数字手指操。
【答案】(1)一;两;三;四;五;六;七(2)A|A(3)略【考点】儿歌【解析】2.快乐阅读小贝壳小贝壳,小贝壳,请你告诉我:为啥你长得这样美,身上五颜六色的?小贝壳,笑呵呵,悄悄对我说:那是大海妈妈给我画的花。
小贝壳,小贝壳,请你告诉我:为啥你长得这样怪,身子像个大耳朵?小贝壳,笑呵呵,悄悄对我说:那是我在听大海妈妈唱歌。
(1)为什么小贝壳身上五颜六色的?(2)小贝壳的身子像个大耳朵,是因为________。
【答案】(1)那是大海妈妈给我画的花。
(2)那是它在听大海妈妈唱歌【考点】项链【解析】3.读课文《小小的船》完成题目。
(1)弯弯的________ 的船,________ 的船________ 。
________ 的船________ ,________ 看见________ 的________ 蓝蓝的________ 。
(2)这首诗的作者是________【答案】(1)月儿小小;小小;两头尖;我在小小;坐;只;闪闪;星星;天(2)叶圣陶【考点】课文内容理解,小小的船【解析】【分析】这类题目是主要考查了学生对课文内容的掌握。
这首诗歌的内容是:弯弯的月儿小小的船。
小小的船儿两头尖。
我在小小的船里坐,只看见闪闪的星星蓝蓝的天。
这首诗的作者是叶圣陶。
【点评】此题考查学生对课文内容的掌握,学生需要掌握。
4.读儿歌,回答问题。
七年级英语阅读理解复习巩固专讲专练(章末复习+综合测评+答案)

七年级英语阅读理解复习巩固专讲专练(章末复习+综合测评+答案)一、七年级英语阅读理解1.阅读理解John is a middle school student. He is sixteen years old now. One day he had a terrible cold and a fever. He felt bad and couldn't eat anything. So he went to see a doctor. The doctor gave him a bottle of medicine. These are the words on the bottle of the medicine.Cold medicineYou must shake(摇晃)it before you take it. Take it three times a day after meals.Dose(剂量):Age: over 15 2 teaspoons(茶匙)a day8—14 1 teaspoon a day5—7 1/2 teaspoon a dayThe children under 4 years old can't take this medicine.Please put it in a cold place. Use it before December 1st,2008.(1)John should take _________a day.A. 1 teaspoonB. 2 teaspoonsC. 1/2 teaspoonD. 4 teaspoons(2)John should keep the medicine in ________.A. any placeB. hot waterC. a cold placeD. the sun(3)When children are ________years old, they can't take this medicine.A. eightB. thirteenC. twelveD. two(4)John will ________ the rest of the medicine after December is, 2008.A. have to throw awayB. begin to takeC. take two times a dayD. take three times more(5)How many times a day should you take the medicine after meals?A. OneB. TwoC. ThreeD. Four【答案】(1)B(2)C(3)D(4)A(5)C【解析】【分析】大意:本文介绍了约翰患感冒发烧看医生。
八年级英语下册语法填空复习巩固专讲专练(章末复习+综合测评+答案)经典

八年级英语下册语法填空复习巩固专讲专练(章末复习+综合测评+答案)经典一、八年级英语下册语法填空专项练习(含答案解析)1.用所给单词的适当形式填空,未提供单词的限填一词,将答案写在答题卷上。
(共10小题,每小题1分)On Friday 15 June, the students from Futian Junior High School went to Shenzhen Nursing Home to put________a concert after school. Futian Nursing Home is a home for old people who need to________( take) care of. The concert included popular songs like You Are My Sunshine and Over the Rainbow.Miss Xu,________music teacher, said the concert went very well. "We have prepared for it all this term, and the students sang________(beautiful).Mrs. Wang, who had lived in the nursing home for 11 years, said the concert made a good________(impress) on her. "I often listen to music on the radio, but it was very special to have these________(teenage) come and sing for us."From 3 p.m. to 4 p. m, the students________(stay) at the nursing home for afternoon tea. Mike Lee, a Grade 8 student, said, "We were________(please) to meet the old people. They told us what life was like________theywere young. It is good for us________(communicate )with each other."【答案】 A;A;A;A;A;A;A;A;A;A【解析】【分析】大意:六月15日,星期五,来自福田高中的学生放学后去深圳养老院举行音乐会。
课件3:章末复习与测试

3.要注意:否命题与命题的否定是不同的,否命题既否 定条件又否定结论,而命题的否定只否定结论,例如, 原命题是“若∠A=∠B,则a=b”,其否命题是“若 ∠A≠∠B,则a≠b”,而原命题的否定是“存在∠A、∠B, 虽然∠A=∠B,但a≠b”. 4.充要条件的判断是通过判断命题“若p则q”的真假来判 断的.因此,充要条件与命题的四种形式之间的关系密 切,可相互转化.
5.命题“∃x∈(-1,1),2x+a=0”是真命题,则a的取值 范围为________.
【解析】设f(x)=2x+a,由题意得函数f(x)在(-1,1)内有 零点, ∴(a+2)(a-2)<0, ∴-2<a<2. 【答案】(-2,2)
6.命题 p:过原点 O 可以作两条直线与圆 x2+y2+x -3y+54(m2+m)=0 相切,命题 q:直线(m+23)x-y +m-21=0 不过第二象限,若命题“p∧q”为真命题, 求实数 m 的取值范围.
知识结构
题型探究 题型1 四种命题的关系 例1 设原命题为“若a<b,则a+c<b+c”.(其中a、b、 c∈R) (1)写出它的逆命题、否命题、逆否命题; (2)判断这四个命题的真假; (3)写出原命题的否定.
解:(1)逆命题:若a+c<b+c,则a<b. 否命题:若a≥b,则a+c≥b+c. 逆否命题:若a+c≥b+c,则a≥b. (2)∵a<b,∴a+c<b+c,∴原命题是真命题,则其逆否 命题也是真命题. ∵a≥b,∴a+c≥b+c,∴其否命题是真命题,则其逆命题 是真命题. (3)原命题的否定是:∃a,b满足a<b,使a+c≥b+c.
点评 命题的否定形式与命题的否命题不同,前者只 否定原命题的结论,而后者同时否定条件和结论.
第一章 章末小结与测评
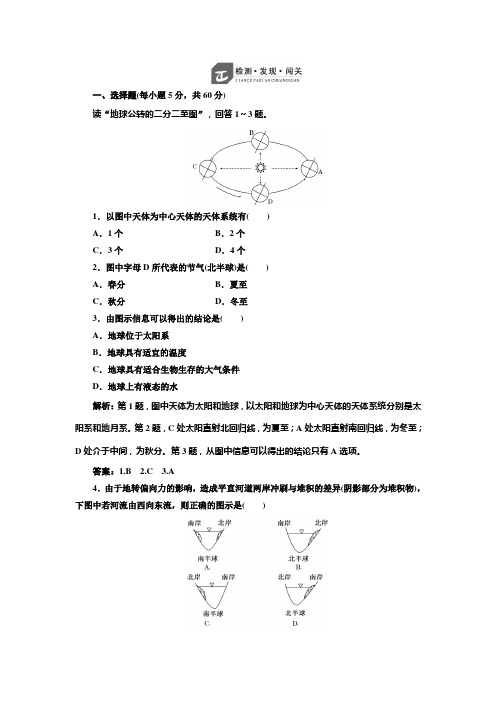
一、选择题(每小题5分,共60分)读“地球公转的二分二至图”,回答1~3题。
1.以图中天体为中心天体的天体系统有()A.1个B.2个C.3个D.4个2.图中字母D所代表的节气(北半球)是()A.春分B.夏至C.秋分D.冬至3.由图示信息可以得出的结论是()A.地球位于太阳系B.地球具有适宜的温度C.地球具有适合生物生存的大气条件D.地球上有液态的水解析:第1题,图中天体为太阳和地球,以太阳和地球为中心天体的天体系统分别是太阳系和地月系。
第2题,C处太阳直射北回归线,为夏至;A处太阳直射南回归线,为冬至;D处介于中间,为秋分。
第3题,从图中信息可以得出的结论只有A选项。
答案:1.B 2.C 3.A4.由于地转偏向力的影响,造成平直河道两岸冲刷与堆积的差异(阴影部分为堆积物),下图中若河流由西向东流,则正确的图示是()解析:对平直河流而言,受地转偏向力影响,偏向一侧的河岸以冲刷作用为主,另一侧河岸以堆积作用为主。
此题重点在于判断图中河流的流向,再结合地转偏向力北半球往右偏、南半球往左偏进行判断,确定B选项正确。
答案:B我国某校地理小组,根据当地楼房各朝向外墙面接受太阳辐射热量的实测值,计算出1月和7月的“太阳辐射热日总量变化方位图”。
据此完成5~6题。
5.读图,下列判断正确的是()A.L1表示1月太阳辐射热日总量变化曲线B.L2表示7月太阳辐射热日总量变化曲线C.该地可能位于深圳D.该地可能位于北京6.为充分利用太阳能,该地房屋主墙面应朝向()A.南方B.北方C.东南方D.西南方解析:本题组考查太阳辐射的分布及应用。
第5题,我国太阳辐射相对较强的季节为夏季,根据图中太阳辐射热日总量变化曲线可以判断出,曲线L1代表7月,曲线L2代表1月;从图中可以看出,该地在7月份来自南北方向的太阳辐射小于来自东西两侧的太阳辐射,故该地应位于回归线附近,出现太阳直射现象,推测该地可能位于深圳。
第6题,为充分利用太阳能,该地房屋主墙应朝向南方。
课件5:章末复习与测试

【解析】 由于“若b2-4ac≤0,则ax2+bx+c≥0”是假命 题,所以“ax2+bx+c≥0”的充分条件不是“b2-4ac≤0”, A错;∵ab2>cb2,且b2>0,∴a>c.而a>c时,若b2=0, 则ab2>cb2不成立,由此知“ab2>cb2”是“a>c”的充分 不必要条件,B错;“对任意x∈R,有x2≥0”的否定是 “存在x∈R,有x2<0”,C错;由l⊥α,l⊥β,可得α∥β, 理由是:垂直于同一条直线的两个平面平行,D正确. 【答案】 D
所以只需a>10即可. 故实数a的取值范围是(10,+∞).
名师指导 在本题的解答过程中,用到了两次化归思想,在第一 次通过换元,化归为一元二次不等式恒成立时,要特 别注意新元的取值范围.
跟踪训练 4.已知命题p:“至少存在一个实数x0∈[1,2],使不等式x2 +2ax+2-a>0成立”为真,试求参数a的取值范围.
例 2 已知 p:xx+-21≥0≤0,0, q:{x|1-m≤x≤1+m,m>0}, 若﹁p 是﹁q 的必要条件,求实数 m 的取值范围.
解:法一 由题意,得﹁p:A={x|x<-2 或 x>10}, ﹁q:B={x|x<1-m 或 x>1+m,m>0}, ∵﹁p 是﹁q 的必要条件, ∴﹁q⇒﹁p,﹁p⇒/ ﹁q.
解:﹁p:∀x∈[1,2],x2+2ax+2-a≤0,是假命题, 令 f(x)=x2+2ax+2-a,
则ff((12))≤≤00,, 即14+ +24aa+ +22- -aa≤≤00., 解得 a≤-3.
故命题 p 中,a>-3. 即参数 a 的取值范围为(-3,+∞).
课堂检测
1.设x>0,y∈R,则“x>y”是“x>|y|”的( )
第三章 章末小结与测评

一、选择题(每小题5分,共60分)读下图,回答1~2题。
1.该区域河流的主要补给形式是()A.大气降水B.沙漠凝结水C.冰雪融水D.湖泊水2.该区域河流径流量变化特征一般有()①流量较平稳,没有明显的汛期②流量变化受气温的影响,丰水期出现在夏季③冬季出现明显的断流现象④季节变化小,年际变化大A.①②B.②③C.③④D.①④解析:第1题,由图示信息可知此地区位于我国西北地区,该区河流主要补给水源为冰川或永久性积雪融水。
第2题,该区河流流量的变化和气温的变化基本一致,表现出水量变化的连续性、较平稳、年际变化小、季节变化大、丰水期与高温期一致、冬季有断流现象等一般特征。
答案:1.C 2.B读“水循环示意图”,回答3~4题。
3.能正确反映陆地内循环的是()A.g→b→c→d B.a→b→c→dC.f→a→c→e D.g→e→f→a4.水循环对图示地区除提供水资源外,还直接提供的资源有()A.土壤B.水能C.潮汐D.波浪解析:第3题,陆地内循环发生在陆地上,所以能正确表示陆地内循环的是g→b→c→d。
第4题,水循环形成降水发生在落差大的地区,还能提供水能资源。
答案:3.A 4.B读“某中低纬度大洋环流局部示意图(图甲)”及“世界某地区图(图乙)”,回答5~7题。
5.读甲、乙两图判断下列说法正确的是()A.甲图所示海域与乙图所示地区都位于北半球B.甲图中①洋流与乙图中M洋流成因、性质都相同C.甲图中③洋流与乙图中M洋流成因、性质都相同D.乙图中M洋流对沿岸气候有增温、增湿的作用6.如果甲图表示北印度洋的季风洋流,则此时()A.全球陆地等温线向南弯曲B.地球公转速度较慢C.巴西高原草木一片枯黄D.北京正午太阳高度角达到一年中的最小值7.若甲海域位于大西洋,则③洋流的名称是()A.本格拉寒流B.厄加勒斯暖流C.巴西暖流D.秘鲁寒流解析:第5题,甲图所示海域位于中低纬度,并且洋流逆时针流动,所以甲海域位于南半球,①洋流为暖流,③洋流为寒流,③洋流的成因和性质都与乙图中M洋流(加那利寒流)相同。
二年级2020-2021年 阅读理解复习巩固专讲专练(章末复习+综合测评+答案)

2020-2021年阅读理解复习巩固专讲专练(章末复习+综合测评+答案)一、二年级语文下册阅读理解练习1.课外阅读。
王羲(xī)之(zhī)的故事有一次,王羲之外出散步(sàn bù),看见路边有一个老婆婆在卖扇(shàn)子。
她叫了半天,还是没有人来买扇子。
王羲之看到她那失望的样子,十分同情她,便随(suí)手取过扇子,在上面写了些字,叫老婆婆再拿到市场上去卖。
老婆婆来到市场,那里的人认得扇子上的字是王羲之写的,争着要买扇子。
不一会儿,所有的扇子就卖光了。
(1)老婆婆在路边________。
(2)王羲之是怎样帮助老婆婆的?(从文中找出这个句子)(3)后来,扇子为什么再市场上一下子就卖光了呢?()A. 扇子很便宜。
B. 扇子很漂亮。
C. 人们喜欢王羲之的字。
【答案】(1)卖扇子(2)王羲之看到她那失望的样子,十分同情她,便随(suí)手取过扇子,在上面写了些字,叫老婆婆再拿到市场上去卖。
(3)C【解析】【分析】这类题目是考查学生的课外阅读理解能力。
老婆婆在路边卖扇子,卖不出去,王羲之看到她那失望的样子,十分同情她,便随(suí)手取过扇子,在上面写了些字,叫老婆婆再拿到市场上去卖,人们因为喜欢他的字,就买了扇子。
【点评】考查学生的课外阅读理解能力,对学生的能力是一定的提升。
二、语段阅读2.读一读,写一写。
(9分)春天春天来了,大地都被上了新装。
小草绿绿的,桃花红红的,柳枝青青的,小溪亮亮的。
山林里可热闹了。
小鸟,又唱又跳;蜜蜂,忙着采蜜;蝴蝶,飞来飞去。
(1)这段话共有________句话。
请用横线在文中画出第3句话(2)找出文中描写颜色的词,用横线画出来。
(3)照样子写词语。
绿绿的:________ ________飞来飞去:________ ________【答案】(1)4。
山林里可热闹了。
(2)绿绿的;红红的;青青的(3)红红的;白白的;走来走去;跳来跳去【解析】3.阅读短文,回答问题。
2019精选教育章末综合测评 第3章.doc

章末综合测评(三)(时间:60分钟满分:100分)一、选择题(本题共10小题,每小题6分.在每小题给出的四个选项中,第1~7题只有一项符合题目要求,第8~10题有多项符合题目要求.全部选对的得6分,选对但不全的得3分,有选错的得0分)1.在物理学建立、发展的过程中,许多物理学家的科学发现推动了人类历史的进步.关于科学家和他们的贡献,下列说法中错误的是() A.德国天文学家开普勒对他的导师——第谷观测的行星数据进行了多年研究,得出了开普勒三大行星运动定律B.英国物理学家卡文迪许利用“卡文迪许扭秤”首先较准确的测定了万有引力常量C.伽利略用“月—地检验”证实了万有引力定律的正确性D.牛顿认为在足够高的高山上以足够大的水平速度抛出一物体,物体就不会再落在地球上【解析】根据物理学史可知C错,A、B、D正确.【答案】C2.宇航员王亚平在“天宫1号”飞船内进行了我国首次太空授课,演示了一些完全失重状态下的物理现象.若飞船质量为m,距地面高度为h,地球质量为M,半径为R,引力常量为G,则飞船所在处的重力加速度大小为()A.0 B.GM (R+h)2C.GMm(R+h)2D.GMh2【解析】飞船受的万有引力等于在该处所受的重力,即GMm(R+h)2=mg,得g=GM(R+h)2,选项B正确.【答案】 B3.假设地球和火星都绕太阳做匀速圆周运动,已知地球到太阳的距离小于火星到太阳的距离,那么( )A .地球公转周期大于火星的周期公转B .地球公转的线速度小于火星公转的线速度C .地球公转的加速度小于火星公转的加速度D .地球公转的角速度大于火星公转的角速度【解析】 根据G Mm r 2=m ⎝ ⎛⎭⎪⎫2πT 2r =m v 2r =ma n =mω2r 得,公转周期T =2πr 3GM ,故地球公转的周期较小,选项A 错误;公转线速度v =GMr ,故地球公转的线速度较大,选项B 错误;公转加速度a n =GM r 2,故地球公转的加速度较大,选项C 错误;公转角速度ω=GM r 3,故地球公转的角速度较大,选项D正确.【答案】 D4.如图1所示,A 为静止于地球赤道上的物体,B 为绕地球沿椭圆轨道运行的卫星,C 为绕地球做圆周运动的卫星,P 为B 、C 两卫星轨道的交点.已知A 、B 、C 绕地心运动的周期相同,相对于地心,下列说法中正确的是( )图1A .物体A 和卫星C 具有相同大小的线速度B .物体A 和卫星C 具有相同大小的加速度C .卫星B 在P 点的加速度与卫星C 在该点的加速度一定不相同D .可能出现在每天的某一时刻卫星B 在A 的正上方【解析】 物体A 和卫星B 、C 周期相同,故物体A 和卫星C 角速度相同,但半径不同,根据v =ωR 可知二者线速度不同,A 项错;根据a =Rω2可知,物体A 和卫星C 向心加速度不同,B 项错;根据牛顿第二定律,卫星B 和卫星C在P 点的加速度a =GM r 2,故两卫星在P 点的加速度相同,C 项错误;对于D 选项,物体A 是匀速圆周运动,线速度大小不变,角速度不变,而卫星B 的线速度是变化的,近地点最大,远地点最小,即角速度发生变化,而周期相等,所以如图所示开始转动一周的过程中,会出现A 先追上B ,后又被B 落下,一个周期后A 和B 都回到自己的起点.所以可能出现:在每天的某一时刻卫星B 在A 的正上方,则D 正确.【答案】 D5.同步卫星位于赤道上方,相对地面静止不动.如果地球半径为R ,自转角速度为ω,地球表面的重力加速度为g .那么,同步卫星绕地球的运行速度为( ) A.Rg B.R ωg C. R 2ωg D.3R 2ωg【解析】 同步卫星的向心力等于地球对它的万有引力G Mm r 2=m ω2r ,故卫星的轨道半径r =3GM ω2.物体在地球表面的重力约等于所受地球的万有引力G Mm R 2=mg ,即GM =gR 2.所以同步卫星的运行速度v =r ω=ω·3gR 2ω2=3gR 2ω,D 正确.【答案】 D6.宇宙中两个星球可以组成双星,它们只在相互间的万有引力作用下,绕两星球球心连线的某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( )【导学号:35390054】A .双星相互间的万有引力增大B .双星做圆周运动的角速度不变C .双星做圆周运动的周期增大D .双星做圆周运动的速度增大【解析】 双星间的距离在不断缓慢增加,根据万有引力定律,F =G m 1m 2L 2,知万有引力减小,故A 错误.根据G m 1m 2L 2=m 1r 1ω2,G m 1m 2L 2=m 2r 2ω2,知m 1r 1=m 2r 2,v 1=ωr 1,v 2=ωr 2,轨道半径之比等于质量的反比,双星间的距离变大,则双星的轨道半径都变大,根据万有引力提供向心力,知角速度变小,周期变大,线速度变小,故B 、D 错误,C 正确.【答案】 C7.恒星演化发展到一定阶段,可能成为恒星世界的“侏儒”——中子星.中子星的半径较小,一般在7~20 km ,但它的密度大得惊人.若某中子星的半径为10 km ,密度为1.2×1017 kg/m 3,那么该中子星上的第一宇宙速度约为( )A .7.9 km/sB .16.7 km/sC .2.9×104 km/sD .5.8×104 km/s【解析】 中子星上的第一宇宙速度即为它表面处的卫星的环绕速度,此时卫星的轨道半径近似地认为是该中子星的球半径,且中子星对卫星的万有引力充当向心力,由G Mm r 2=m v 2r ,得v =GM r ,又M =ρV =ρ4πr 33,得v =r 4πGρ3=1×104× 4×3.14×6.67×10-11×1.2×10173m/s =5.8×107 m/s =5.8×104 km/s.故选D.【答案】 D8.北京时间2005年7月4日下午1时52分(美国东部时间7月4日凌晨1时52分)探测器成功撞击“坦普尔一号”彗星,投入彗星的怀抱,实现了人类历史上第一次对彗星的“大对撞”,如图2所示.假设“坦普尔一号”彗星绕太阳运行的轨道是一个椭圆,其运动周期为5.74年,则关于“坦普尔一号”彗星的下列说法中正确的是( )图2A.绕太阳运动的角速度不变B.近日点处线速度大于远日点处线速度C.近日点处加速度大于远日点处加速度D.其椭圆轨道半长轴的立方与周期的平方之比是一个与太阳质量有关的常数【解析】由开普勒第二定律知近日点处线速度大于远日点处线速度,B正确;由开普勒第三定律可知D正确;由万有引力提供向心力得C正确.【答案】BCD9.2013年6月11日17时38分,我国利用“神舟十号”飞船将聂海胜、张晓光、王亚平三名宇航员送入太空.设宇航员测出自己绕地球做匀速圆周运动的周期为T,离地高度为H,地球半径为R,则根据T、H、R和引力常量G,能计算出的物理量是()图3A.地球的质量B.地球的平均密度C.飞船所需的向心力D.飞船线速度的大小【解析】由GMm(R+H)2=m4π2T2(R+H),可得:M=4π2(R+H)3GT2,选项A可求出;又根据ρ=M43πR3,选项B可求出;根据v=2π(R+H)T,选项D可求出;由于飞船的质量未知,所以无法确定飞船的向心力.【答案】ABD10.迄今发现的二百余颗太阳系外行星大多不适宜人类居住,绕恒星“Gliese581”运行的行星“G1-581c”却很值得我们期待.该行星的温度在0 ℃到40 ℃之间,质量是地球的6倍、直径是地球的1.5倍,公转周期为13个地球日.“Gliese581”的质量是太阳质量的0.31倍.设该行星与地球均视为质量分布均匀的球体,绕其中心天体做匀速圆周运动,则() A.在该行星和地球上发射卫星的第一宇宙速度相同B.如果人到了该行星,其体重是地球上的22 3倍C.该行星与“Gliese581”的距离是日地距离的13 365倍D.由于该行星公转速度比地球大,地球上的物体如果被带上该行星,其质量会稍有变化【解析】解题关键是明确中心天体对行星的万有引力提供了行星的向心力,对行星的卫星有G Mmr2=mv2r,得v=GMr,将质量关系和半径关系代入得第一宇宙速度关系为v行v地=2,选项A错误;由GMmr2=mg得,人在该行星上的体重是地球上的223倍,选项B正确;对行星应用万有引力定律GMmr2=mr4π2T2,得r=3GMT24π2,r1r2=3M1M2·T21T22=30.31×1323652,选项C错误.根据爱因斯坦的狭义相对论可判D选项正确.【答案】BD二、计算题(共3小题,共40分)11.(12分) 已知太阳的质量为M,地球的质量为m1,月球的质量为m2,当发生日全食时,太阳、月球、地球几乎在同一直线上,且月球位于太阳与地球之间,如图4所示.设月球到太阳的距离为a,地球到月球的距离为b,则太阳对地球的引力F1和对月球的吸引力F2的大小之比为多少?【导学号:35390055】图4【解析】由太阳对行星的引力满足F∝m r2知太阳对地球的引力F 1=G Mm 1(a +b )2太阳对月球的引力F 2=G Mm 2a 2故F 1/F 2=m 1a 2m 2(a +b )2. 【答案】 m 1a 2m 2(a +b )212.(12分)2007年10月24日18时,“嫦娥一号”卫星星箭成功分离,卫星进入绕地轨道.在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④.11月5日11时,当卫星经过距月球表面高度为h 的A 点时,再一次实施变轨,进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T 的月球极月圆轨道⑦.如图5所示.已知月球半径为R .图5(1)请回答:“嫦娥一号”在完成三次近地变轨时需要加速还是减速?(2)写出月球表面重力加速度的表达式.【解析】 (1)加速.(2)设月球表面的重力加速度为g 月,在月球表面有G Mm R 2=mg 月卫星在极月圆轨道有G Mm (R +h )2=m (2πT )2(R +h ) 解得g 月=4π2(R +h )3T 2R 2.【答案】 (1)加速 (2)4π2(R +h )3T 2R 213.(16分)我国志愿者王跃曾与俄罗斯志愿者一起进行“火星-500”的实验活动.假设王跃登陆火星后,测得火星的半径是地球半径的12,质量是地球质量的19.已知地球表面的重力加速度是g ,地球的半径为R ,忽略火星以及地球自转的影响,求:(1)火星表面的重力加速度g ′的大小;(2)王跃登陆火星后,经测量发现火星上一昼夜的时间为t ,如果要发射一颗火星的同步卫星,它正常运行时距离火星表面将有多远?【解析】 (1)在地球表面,万有引力与重力相等,GMm 0R 2=m 0g对火星GM ′m 0R ′2=m 0g ′ 联立解得g ′=49g .(2)火星的同步卫星做匀速圆周运动的向心力由火星的万有引力提供,且运行周期与火星自转周期相同.设卫星离火星表面的高度为h ,则GM ′m 0(R ′+h )2=m 0(2πt )2(R ′+h ) 解出同步卫星离火星表面高度h =3gR 2t 236π2-12R .【答案】 (1)49g (2)3gR 2t 236π2-12R。
二年级最新 阅读理解复习巩固专讲专练(章末复习+综合测评+答案)经典

最新阅读理解复习巩固专讲专练(章末复习+综合测评+答案)经典一、二年级语文下册阅读理解练习1.阅读短文,回答问题。
____________夜,来临了,这是一个非常美丽的海滨夏夜。
夕阳西下,天空中燃烧着一片红色的晚霞。
大海,也被这霞光染成了红色。
因为它是流动的,所以比天空的景色更壮观。
每当一排排波浪涌起的时候,那映照在浪峰上的霞光,又红又亮,还没等你欣赏完,后面的一排则又闪烁着、滚动着涌了上来。
夜幕降临,天空中出现了长庚星。
它是那么大,那么亮,那么令人注目,活像一盏挂在高空的明灯。
夜色加浓,城市各处的灯火也陆续亮了起来,尤其是山坡上的那一片灯光,它们从半空中倒映在乌蓝的海面上,像一串流动着的珍珠。
踏着软绵绵的沙滩,望着这夏夜的景色,我怎能不感到兴奋和愉快呢?(1)给短文加一个合适的标题。
(2)找出文中的比喻句。
(3)全文是围绕哪句话写的?(4)作者写夏夜的海滨,按时间顺序,先写了夕阳西下时天空中的________,后写________时,天空中的________,最后写________时的________。
【答案】(1)海滨夏夜(2)它是那么大,那么亮,那么令人注目,活像一盏挂在高空的明灯。
夜色加浓,城市各处的灯火也陆续亮了起来,尤其是山坡上的那一片灯光,它们从半空中倒映在乌蓝的海面上,像一串流动着的珍珠。
(3)夜,来临了,这是一个非常美丽的海滨夏夜。
(4)晚霞;夜幕降临;长庚星;夜色加浓;灯光【解析】【分析】(1)考查拟定标题。
阅读短文,梳理段落,就可以概括出短文的主要内容,再进一步提炼标题。
(2)考查比喻句。
比喻句:就是打比方,用浅显、具体、生动的事物来代替抽象、难理解的事物。
比喻句的基本结构分为三部分:本体(被比喻的事物)、喻词(表示比喻关系的词语)和喻体。
本体、喻体有相似点,但不是同一类事物。
如:它是那么大,那么亮,那么令人注目,活像一盏挂在高空的明灯。
(3)考查找中心句的方法。
中心句是一段文章中处于中心地位的句子。
课件4:章末复习与测试

解得 a>2.
∵ 2x+1<1+ax 对一切正实数均成立,
令 t= 2x+1>1,则 x=t2-2 1,
∴2(t-1)<a(t2-1)对一切 t>1 均成立.
∴2<a(t+1),∴a>t+2 1,∴a≥1. ∵“p 或 q”为真,“p 且 q”为假,∴p,q 一真一假. 若 p 真 q 假,则 a>2 且 a<1,∴a 值不存在. 若 p 假 q 真,则 a≤2 且 a≥1,∴1≤a≤2. 故 a 的取值范围为 1≤a≤2.
2.含有一个量词的命题否定的关注点 全称命题的否定是特称命题,特称命题的否定是全称命 题.否定时既要改写量词,又要否定结论.
例 3 判断下列命题是特称命题还是全称命题,用符号 写出其否定并判断命题的否定的真假性. (1)有一个实数 α,sin2α+cos2α≠1; (2)任何一条直线都存在斜率; (3)存在实数 x,使得x2-1x+1=2.
变式训练 判断p:x≠2或y≠3是q:x+y≠5的什么条件.
解:若 p,则 q 的逆否命题是若¬q,则¬p. 由于¬q:x+y=5;¬p:x=2 且 y=3, 于是¬p⇒¬q,而¬q ¬p. 故 q⇒p,p q,即 p 是 q 成立的必要不充分条件.
变式训练
已知命题 p:∃x0∈R,使 sin x0=23,命题 q:x2-2x+3<
0 的解集为∅,下列结论:①命题“p∧q”是真命题;②命
题“p∧¬q”是真命题;③命题“¬p∨q”是真命题;④命题“¬p
∨¬q”是真命题.其中正确的是( )
A.①③④
B.②③
C.③④
D.①②③④
【解析】 命题 Байду номын сангаас:∃x0∈R,使 sin x0=23是假命题,命题 q:x2-2x+3<0 的解集是∅是真命题, 则¬p 为真命题,¬q 为假命题. ∴“p∧q”是假命题,“p∧¬q”是假命题,“¬p∨q”与“¬p∨ ¬q”均为真命题. 因此③④正确. 【答案】 C
高一级物理教学进度表
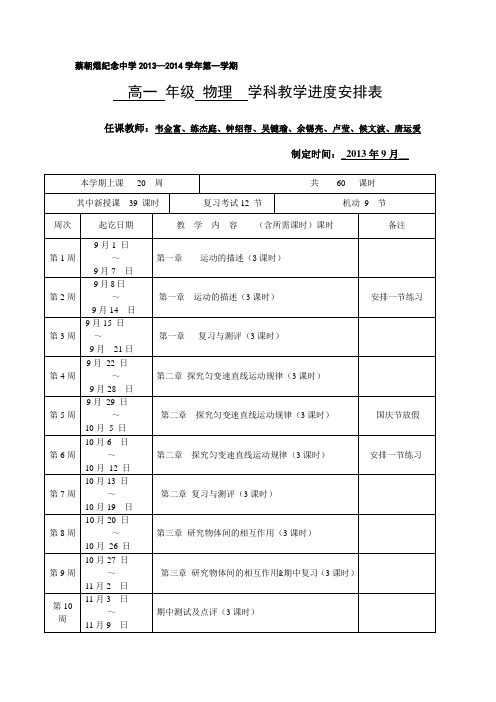
高一年级物理学科教学进度安排表
任课教师:韦金富、练杰庭、钟绍帮、吴键瑜、余锡亮、卢莹、候文波、唐运爱制定时间:_2013年9月__
本学期上课20周
共60课时
其中新授课39课时
复习考试12节
机动9节
周次
起讫日期
教学内容 (含所需课时)课时
备注
第1周
9月1日
~
10月6日
~
10月12日
第二章 探究匀变速直线运动规律(3课时)
安排一节练习
第7周
10月13日
~
10月19日
第二章 复习与测评(3课时)
第8周
10月20日
~
10月26日
第三章 研究物体间的相互作用(3课时)
第9周
10月27日
~
11月2日
第三章研究物体间的相互作用&期中复习(3课时)
第10周
11月3日
9月7日
第一章运动的描述(3课时)
第2周
9月8日
~
9月14日
第一章运动的描述(3课时)
安排一节练习
第3周
9月15日
~
9月21日
第一章 复习与测评(3课时)
第4周
9月22日
~
9月28日
第二章探究匀变速直线ቤተ መጻሕፍቲ ባይዱ动规律(3课时)
第5周
9月29日
~
10月5日
第二章 探究匀变速直线运动规律(3课时)
国庆节放假
第6周
第20周
1月12日
~
1月18日
期末复习及考试
第21周
月日
~
月日
第22周
教学设计3:章末复习与测试

章末复习与测试导入新课思路1.(直接导入)请同学们回忆上一节复习的内容,教师点出,上一节我们一起复习了本章向量的基本概念、运算性质及重要定理、公式,这一节我们将通过例题分析,继续探讨向量的有关应用,重点是复习向量的一些独特方法和应用.思路2.(投影导入)投影展示上节布置的、同学们搜集到的一道向量应用题或创新题,教师选出最有代表性的、最典型的题目引导学生进行探讨,由此展开新课.推进新课知识巩固提出问题①请同学们回忆上节列出的本章知识网络结构图.②讨论下列统考题解法的错因,并给出正确解法.原题:设向量e 1、e 2满足|e 1|=2,|e 2|=1,e 1、e 2的夹角为60°,若向量2t e 1+7e 2与向量e 1+t e 2的夹角为钝角,求实数t 的取值范围.解:由题意,得e 1·e 2=|e 1||e 2|cos60°=1,∴(2t e 1+7e 2)·(e 1+t e 2)=2t e 21+(2t 2+7)e 1·e 2+7t e 22=2t 2+15t +7.∵向量2t e 1+7e 2与向量e 1+t e 2的夹角为钝角,∴2t 2+15t +7<0,即-7<t <-12. 活动:引导学生回忆向量的数量积概念,点拨学生结合钝角考虑:向量的数量积是一个数.当两个向量的夹角是锐角时,它们的数量积大于0;当两个向量的夹角是钝角时,它们的数量积小于0;当两个向量的夹角是90°时,它们的数量积等于0.零向量与任何向量的数量积等于0.向量的数量积,可以计算向量的长度、平面内两点间的距离、两个向量的夹角、判断相应的两条直线是否垂直.教师引导学生探究讨论:对于两个非零向量a 、b ,若a 与b 的夹角θ为钝角,则a·b <0,反之,却不一定成立.因为当a·b =|a||b |cos θ<0时,a 与b 的夹角也可能为π,因此,a 与b 的夹角为钝角的充要条件是a·b <0且a ≠λb (λ<0),所以正确的解答应在上述t 的范围中去掉夹角为π的情形,即设2t e 1+7e 2=λ(e 1+t e 2)(λ<0),∴⎩⎪⎨⎪⎧2t =λ,7=λt ,其中λ<0,解得t =-142. 故所求实数t 的取值范围为(-7,-142)∪(-142,-12). 比较是最好的老师,反例更能澄清概念的本质,使我们深刻理解概念的内涵和外延,教师应引导学生多做这方面的探讨.如由a·b =0不能推出a =0或b =0,尽管由ab =0⇒a =0或b =0.又如|a·b|≤|a||b |,尽管|ab |=|a ||b |.再如(a·b )c≠a (b·c ),尽管(ab )c =a (bc ).因此,学习向量的数量积应与代数中实数间的乘积严加区分,切勿混淆.讨论结果:略.应用示例例1 已知向量a 是以点A (3,-1)为起点,且与向量b =(-3,4)垂直的单位向量.求a 的终点坐标.活动:关于向量的坐标与表示此有向线段的点的坐标,概念虽小,学生却极易混淆.教师引导学生回忆思考:一个向量的坐标与表示此向量的有向线段的点的坐标是什么关系.对此题来说,若要利用两向量垂直的充要条件,则需假设a 的终点坐标,然后表示a 的坐标,再根据两向量垂直的充要条件建立方程.解:设a 的终点坐标为(m ,n ),则a =(m -3,n +1),由题意⎩⎪⎨⎪⎧ -3(m -3)+4(n +1)=0,(m -3)2+(n +1)2=1, ①②由①,得n =14(3m -13),代入②,得25m 2-150m +209=0. 解得⎩⎨⎧ m 1=195,n 1=-25或⎩⎨⎧ m 2=115,n 2=-85.∴a 的终点坐标是(195,-25)或(115,-85). 点评:通过训练要使学生明了,一个向量的坐标等于表示此向量的有向线段的终点坐标减去起始坐标,所以向量的坐标与点的坐标既有联系又有区别,二者不能混淆.向量的概念较多,且容易混淆,在复习中教师要引导学生理清主线,分清、理解各概念的本质属性. 变式训练1.已知点A (-3,-4)、B (5,-12),(1)若OC →=OA →+OB →,OD →=OA →-OB →,求OC →及OD →的坐标;(2)求OA →·OB →.解:(1)OC →=(2,-16),OD →=(-8,8).(2)OA →·OB →=33.2.如图4所示,AB →=(6,1),BC →=(x ,y ),CD →=(-2,-3).图4(1)若BC →∥DA →,求x 与y 间的关系式;(2)若又有AC →⊥BD →,求x 、y 的值及四边形ABCD 的面积.例2 设向量a =(cos α,sin α),b =(cos β,sin β),且a 、b 满足|k a +b |=3|a -k b |(k 为正实数).(1)求证:(a +b )⊥(a -b );(2)设a 与b 的数量积表示为关于k 的函数f (k ),求f (k );(3)求函数f (k )的最小值及取得最小值时a 与b 的夹角.活动:本题是一道向量应用的经典例题,难度不大但综合性较强,体现平面向量与函数、与三角函数的交汇,是近几年高考的热点问题.解决这类问题必须熟知平面向量的概念、运算性质、定理、公式等基础知识.教师可以充分让学生自己去探究解决.对感到困难的学生,教师引导其回忆相关的知识,并适时地点拨学生注意条件的转化及解答的规范.(1)证明:|a |=cos 2α+sin 2α=1,|b |=cos 2β+sin 2β=1,∵(a +b )·(a -b )=|a|2-|b|2=0,∴(a +b )⊥(a -b ).(2)解:由|k a +b |=3|a -k b |,得(k a +b )2=3(a -k b )2,化简,得a·b =k 2+14k, 故f (k )=k 2+14k(k >0). (3)解:由y =k 2+14k(y >0),得k 2-4k +1=0. ∵k >0,方程有解,∴Δ=16y 2-4≥0.解得y ≥12,即k =1时,f (k )取最小值为12. 这时,设a 与b 的夹角为θ,则cos θ=a·b |a||b |=12. 又0≤θ≤π,∴a 与b 的夹角为π3. 点评:解决本题,我们首先要根据题意画出图形,借助对图形的观察,实现实际问题向数学问题的转化.转化与化归思想是解决数学问题的一种重要的策略和方法.以向量为工具,通过转化,可以为函数中的许多问题提供新颖、简捷的解法,请同学们注意体会.例3 有两根柱子相距20 m ,分别位于电车的两侧,在两柱之间连接一条水平的绳子,电车的送电线就悬挂在绳子的中点,如果送电线在这点垂直向下的作用力是17.8 N ,则这条成水平的绳子的中点下降0.2 m ,求此时绳子所受的张力.活动:教师应引导学生回忆向量的应用举例的处理方法:向量起源于物理,是从物理学中抽象出来的数学概念.物理学中的许多问题,如位移、速度、加速度等都可以利用向量来解决.用数学知识解决物理问题,首先要把物理问题转化为数学问题,即根据题目的条件建立数学模型,再转化为数学中的向量运算来完成.本题仍可由学生自己去探究,点拨学生先画出受力分析图,认真分析题意,创建数学模型,对感到困难的学生教师给予指导,帮助其复习相关的知识,逐步提高分析问题及解决问题的能力.解:如图5所示,设重力作用点为C ,绳子AC 、BC 所承受的力分别记为CE →、CF →,重力记为CG →.图5由C 为绳子的中点,知|CE →|=|CF →|.由CE →+CF →=CG →,知四边形CFGE 为菱形.又∵cos ∠FCG =cos ∠DCB =0.2102+(0.2)2≈0.02, ∴|CE →|=|CF →|=12|CG →|cos ∠FCG =8.90.02=445, 即绳子所受的张力为445 N.点评:本题是向量知识在物理中的应用,培养了学生动手操作绘图能力、分析问题及解决问题的能力.对学生来说这是一个难点,突破这个难点的关键是教师引导学生把物理问题转化为数学问题.知能训练课本本章复习参考题 B 组1、2、3.课堂小结1.先由学生回顾本节都复习了哪些主要内容,用到了哪些数学思想方法.向量在函数、三角函数中的重要作用,两向量的数量积的应用,向量平行与垂直条件在解题中的重要作用,向量的几何运算在解决平面几何问题和物理问题中的重要作用.2.教师点睛,要注意解题方法的灵活性,尤其是向量的坐标化思路在解题时的应用,将几何与代数知识沟通起来,同时注意向量与其他学科的联系.作业如图6,已知AC 、BD 是梯形ABCD 的对角线,E 、F分别为BD 、AC 的中点,求证:EF ∥BC .图6证明:设AB →=a ,AD →=b ,∵AD ∥BC ,∴BC →=λAD →=λb ,则BD →=AD →-AB →=b -a .∵E 为BD 中点,BE →=12BD →=12(b -a ),F 为AC 中点, BF →=BC →+CF →=BC →+12CA →=BC →+12(BA →-BC →)=12(BA →+BC →)=12(BC →-AB →)=12(λb -a ). ∴EF →=BF →-BE →=12(λb -a )-12(b -a )=(12λ-12)b . ∵b =1λBC →, ∴EF →=[(12λ-12)·1λ]BC →. ∴EF →∥BC →,即EF ∥BC .点评:证明线段平行,也就是证明向量共线.证明a 、b 向量共线,即是想办法证明a =λb ,进而想办法找到λ.设计感想1.本教案的设计思想是以向量的两种运算思路为主线,以向量的代数几何双重特点的应用为平台,将向量体现的思想方法贯穿其中,巩固加强本章向量知识.2.平面向量是中学数学的重要内容,它与函数、三角函数等多个知识点相联系,因此它与其他知识点的交汇也就成了近几年来高考命题的热点.尤其是向量体现的思想方法,几乎包括了中学的全部.如数形结合思想,例3中函数与方程思想,解决物理问题的转化与化归思想,对向量共线与否中的分类讨论思想.因此我们应给予足够的重视,充分利用向量解题的优化特点,并注意掌握解平面向量题常用的数学思想方法,以提高学生综合应用能力,也适应高考对平面向量的考查要求.。
章末综合测评(三) 推理与证明

章末综合测评(三) 推理与证明章末综合测评(三)推理与证明(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面四个推理不是合情推理的是()A.由圆的性质类比推出球的有关性质B.由直角三角形、等腰三角形、等边三角形的内角和都是180°,归纳出所有三角形的内角和都是180°C.某次考试张军的成绩是100分,由此推出全班同学的成绩都是100分D.蛇、海龟、蜥蜴是用肺呼吸的,蛇、海龟、蜥蜴是爬行动物,所以所有的爬行动物都是用肺呼吸的【解析】逐项分析可知,A项属于类比推理,B项和D项属于归纳推理,而C项中各个学生的成绩不能类比,不是合情推理.【答案】 C2.用反证法证明命题“若直线AB,CD是异面直线,则直线AC,BD也是异面直线”的过程归纳为以下三个步骤:①则A,B,C,D四点共面,所以AB,CD共面,这与AB,CD是异面直线矛盾;②所以假设错误,即直线AC,BD也是异面直线;③假设直线AC,BD是共面直线.则正确的序号顺序为()A.①②③B.③①②C.①③②D.②③①【解析】结合反证法的证明步骤可知,其正确步骤为③①②.【答案】 B3.下列推理是归纳推理的是()A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆B.由a1=1,a n=3n-1,求出S1,S2,S3,猜想出数列的前n项和S n的表=i,故错误;②在类比等差数列性质推理等比数列性质时,一般思路有:由加法类比推理为乘法,由减法类比推理为除法,由算术平均数类比推理为几何平均数等,故正确;③由于向量的数量积运算结合律不成立,错误;④若圆的半径为a,则圆的面积为πa2;类比推出,若椭圆长半轴长为a,短半轴长为b,则椭圆面积为πab,正确.【答案】 D6.将平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:①a·b=b·a;②(a·b)·c=a·(b·c);③a·(b+c)=a·b+a·c;④由a·b=a·c(a≠0)可得b=c.以上通过类比得到的结论正确的个数为()A.1B.2C.3 D.4【解析】平面向量的数量积的运算满足交换律和分配律,不满足结合律,故①③正确,②错误;由a·b=a·c(a≠0)得a·(b-c)=0,从而b-c=0或a⊥(b -c),故④错误.故选B.【答案】 B7.已知{b n}为等比数列,b5=2,则b1·b2·b3·b4·b5·b6·b7·b8·b9=29.若{a n}为等差数列,a5=2,则{a n}的类似结论为()A.a1a2a3…a9=29B.a1+a2+a3+…+a9=29C.a1a2a3…a9=2×9D.a1+a2+a3+…+a9=2×9【解析】根据等差、等比数列的特征知,a1+a2+…+a9=2×9.【答案】 D8.袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则()A.乙盒中黑球不多于丙盒中黑球B.乙盒中红球与丙盒中黑球一样多C.乙盒中红球不多于丙盒中红球D.乙盒中黑球与丙盒中红球一样多【解析】取两个球往盒子中放有4种情况:①红+红,则乙盒中红球数加1;②黑+黑,则丙盒中黑球数加1;③红+黑(红球放入甲盒中),则乙盒中黑球数加1;④黑+红(黑球放入甲盒中),则丙盒中红球数加1.因为红球和黑球个数一样多,所以①和②的情况一样多,③和④的情况完全随机.③和④对B选项中的乙盒中的红球数与丙盒中的黑球数没有任何影响.①和②出现的次数是一样的,所以对B选项中的乙盒中的红球数与丙盒中的黑球数的影响次数一样.综上,选B.【答案】 B9.在等差数列{a n}中,若a10=0,则有等式a1+a2+…+a n=a1+a2+…+a19-n(n<19且n∈N+)成立,类比上述性质,在等比数列{b n}中,若b11=1,则有()A.b1·b2·…·b n=b1·b2·…·b19-nB.b1·b2·…·b n=b1·b2·…·b21-nC.b1+b2+…+b n=b1+b2+…+b19-nD.b1+b2+…+b n=b1+b2+…+b21-n【解析】令n=10时,验证即知选B.【答案】 B10.将石子摆成如图1的梯形形状.称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2 016项与5的差,即a2 016-5=()图1A.2 018×2 014 B.2 018×2 013C.1 010×2 012 D.1 011×2 015【解析】a n-5表示第n个梯形有n-1层点,最上面一层为4个,最下面一层为n+2个.∴a n-5=(n-1)(n+6)2,∴a2 016-5=2 015×2 0222=2 015×1 011.【答案】 D11.在直角坐标系xOy中,一个质点从A(a1,a2)出发沿图2中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此规律一直运动下去,则a2 015+a2 016+a2 017=()图2A.1 006 B.1 007C.1 008 D.1 009【解析】依题意a1=1,a2=1;a3=-1,a4=2;a5=2,a6=3;…,归纳可得a1+a3=1-1=0,a5+a7=2-2=0,…,进而可归纳得a2 015+a2 017=0,a2=1,a4=2,a6=3,…,进而可归纳得a2 016=12×2 016=1 008,a2 015+a2 016+a2 017=1 008.故选C.【答案】 C12.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或是丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖了.”四位歌手的话只有两句是对的,则获奖歌手是()A.甲B.乙C.丙D.丁【解析】甲乙丙丁甲获奖××××乙获奖√√×√丙获奖√×√×丁获奖×√××【答案】 C二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横线上)13.已知圆的方程是x 2+y 2=r 2,则经过圆上一点M (x 0,y 0)的切线方程为x 0x +y 0y =r 2.类比上述性质,可以得到椭圆x 2a 2+y 2b 2=1类似的性质为__________. 【解析】 圆的性质中,经过圆上一点M (x 0,y 0)的切线方程就是将圆的方程中的一个x 与y 分别用M (x 0,y 0)的横坐标与纵坐标替换.故可得椭圆x 2a 2+y 2b 2=1类似的性质为:过椭圆x 2a 2+y 2b 2=1上一点P (x 0,y 0)的切线方程为x 0x a 2+y 0yb2=1.【答案】 经过椭圆x 2a 2+y 2b 2=1上一点P (x 0,y 0)的切线方程为x 0x a 2+y 0yb 2=114.观察下列等式: 13=1, 13+23=9, 13+23+33=36, 13+23+33+43=100,照此规律,第n 个等式可为__________.【解析】 依题意,注意到13=⎣⎢⎡⎦⎥⎤12×1×(1+1)2,13+23=⎣⎢⎡⎦⎥⎤12×2×(2+1)2=9,13+23+33=⎣⎢⎡⎦⎥⎤12×3×(3+1)2=36,…,照此规律,第n 个等式可为13+23+33+…+n 3=⎣⎢⎡⎦⎥⎤12n (n +1)2.【答案】13+23+33+…+n 3=⎣⎢⎡⎦⎥⎤12n (n +1)2 15.当n =1时,有(a -b )(a +b )=a 2-b 2,当n =2时,有(a -b )(a 2+ab +b 2)=a 3-b 3,当n =3时,有(a -b )(a 3+a 2b +ab 2+b 3)=a 4-b 4,当n ∈N +时,你能得到的结论是__________.【解析】 根据题意,由于当n =1时,有(a -b )(a +b )=a 2-b 2,当n =2时,有(a -b )(a 2+ab +b 2)=a 3-b 3,当n =3时,有(a -b )(a 3+a 2b +ab 2+b 3)=a 4-b 4,当n ∈N +时,左边第二个因式可知为a n +a n -1b +…+ab n -1+b n ,那么对应的表达式为(a -b )·(a n +a n -1b +…+ab n -1+b n )=a n +1-b n +1.【答案】 (a -b )(a n +a n -1b +…+ab n -1+b n )=a n +1-b n +116.如图3,如果一个凸多面体是n (n ∈N +)棱锥,那么这个凸多面体的所有顶点所确定的直线共有________条,这些直线共有f (n )对异面直线,则f (4)=________,f (n )=__________.(答案用数字或n 的解析式表示)图3【解析】 所有顶点所确定的直线共有棱数+底边数+对角线数=n +n +n (n -3)2=n (n +1)2.从题图中能看出四棱锥中异面直线的对数为f (4)=4×2+4×12×2=12,所以f (n )=n (n -2)+n (n -3)2·(n -2)=n (n -1)(n -2)2.【答案】n (n +1)2 12 n (n -1)(n -2)2三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)用综合法或分析法证明: (1)如果a ,b >0,则lg a +b 2≥lg a +lg b2;(2)6+10>23+2.【证明】 (1)当a ,b >0时,有a +b2≥ab , ∴lg a +b2≥lg ab ,∴lg a +b 2≥12lg ab =lg a +lg b 2.(2)要证6+10>23+2, 只要证(6+10)2>(23+2)2, 即260>248,这是显然成立的, 所以,原不等式成立.18.(本小题满分12分)观察以下各等式: sin 230°+cos 260°+sin 30°cos 60°=34,sin 220°+cos 250°+sin 20°cos 50°=34,sin 215°+cos 245°+sin 15°cos 45°=34.分析上述各式的共同特点,猜想出反映一般规律的等式,并对等式的正确性作出证明.【解】 猜想:sin 2α+cos 2(α+30°)+sin αcos(α+30°)=34.证明如下:sin 2α+cos 2(α+30°)+sin αcos(α+30°) =sin 2α+⎝ ⎛⎭⎪⎫32cos α-12sin α2+sin α⎝ ⎛⎭⎪⎫32cos α-12sin α=sin 2α+34cos 2α-32sin αcos α+14sin 2α+ 32sin α·cos α-12sin 2α =34sin 2α+34cos 2α =34. 19.(本小题满分12分)点P 为斜三棱柱ABC -A 1B 1C 1的侧棱BB 1上一点,PM ⊥BB 1交AA 1于点M ,PN ⊥BB 1交CC 1于点N .(1)求证:CC 1⊥MN ;(2)在任意△DEF 中有余弦定理:DE 2=DF 2+EF 2-2DF ·EF ·cos ∠DFE .扩展到空间类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.【解】 (1)证明:因为PM ⊥BB 1,PN ⊥BB 1,又PM ∩PN =P , 所以BB 1⊥平面PMN ,所以BB 1⊥MN . 又CC 1∥BB 1,所以CC 1⊥MN .(2)在斜三棱柱ABC -A 1B 1C 1中,有S 2ABB 1A 1=S 2BCC 1B 1+S 2ACC 1A 1-2SBCC 1B 1SACC 1A 1cos α.其中α为平面BCC1B1与平面ACC1A1所成的二面角.证明如下:因为CC1⊥平面PMN,所以上述的二面角的平面角为∠MNP.在△PMN中,因为PM2=PN2+MN2-2PN·MN cos∠MNP,所以PM2·CC21=PN2·CC21+MN2·CC21-2(PN·CC1)·(MN·CC1)cos∠MNP,由于SBCC1B1=PN·CC1,SACC1A1=MN·CC1,SABB1A1=PM·BB1=PM·CC1,所以S2ABB1A1=S2BCC1B1+S2ACC1A1-2SBCC1B1·SACC1A1·cos α.20.(本小题满分12分)如图4,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:图4(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.【证明】(1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.又因为P A⃘平面DEF,DE平面DEF,所以直线PA∥平面DEF.(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=12PA=3,EF=12BC=4.又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90°,即DE⊥EF.又PA⊥AC,DE∥PA,所以DE⊥AC.因为AC∩EF=E,AC平面ABC,EF平面ABC,所以DE⊥平面ABC.又DE平面BDE,所以平面BDE⊥平面ABC.21.(本小题满分12分)在数列{a n}中,a1=1,a2=14,且a n+1=(n-1)a nn-a n(n≥2).(1)求a 3,a 4,猜想a n 的表达式,并加以证明;(2)设b n =a n ·a n +1a n +a n +1, 求证:对任意的n ∈N +,都有b 1+b 2+…+b n <n 3. 【解】 (1)容易求得:a 3=17,a 4=110. 故可以猜想a n =13n -2,n ∈N +. 下面利用数学归纳法加以证明:①显然当n =1,2,3,4时,结论成立,②假设当n =k (k ≥4,k ∈N +)时,结论也成立,即a k =13k -2. 那么当n =k +1时,由题设与归纳假设可知:a k +1=(k -1)a k k -a k =(k -1)×13k -2k -13k -2=k -13k 2-2k -1=k -1(3k +1)(k -1)=13k +1=13(k +1)-2. 即当n =k +1时,结论也成立,综上,对任意n ∈N +,a n =13n -2成立. (2)证明:b n =a n ·a n +1a n +a n +1 =13n -2·13n +113n -2+13n +1 =13n +1+3n -2=13(3n +1-3n -2), 所以b 1+b 2+…+b n =13[(4-1)+(7-4)+(10-7)+…+(3n +1-3n -2)]=13(3n +1-1), 所以只需要证明13(3n +1-1)<n 3⇔3n +1<3n +1⇔3n +1<3n +23n +1⇔0<23n (显然成立),所以对任意的n ∈N +,都有b 1+b 2+…+b n <n 3. 22.(本小题满分12分)已知函数f (x )=x cos x -sin x +1(x >0). 【导学号:67720192】(1)求f (x )的单调区间;(2)记x i 为f (x )的从小到大的第i (i ∈N *)个零点,证明:对一切n ∈N *,有1x 21+1x 22+…+1x 2n <23. 【解】 (1)f ′(x )=cos x -x sin x -cos x =-x sin x .令f ′(x )=0,得x =k π(k ∈N *).当x ∈(2k π,(2k +1)π)(k ∈N)时,sin x >0,此时f ′(x )<0;当x ∈((2k +1)π,(2k +2)π)(k ∈N)时,sin x <0,此时f ′(x )>0.故f (x )的单调递减区间为(2k π,(2k +1)π)(k ∈N),单调递增区间为((2k +1)π,(2k +2)π)(k ∈N).(2)由(1)知,f (x )在区间(0,π)上单调递减.又f ⎝ ⎛⎭⎪⎫π2=0,故x 1=π2. 当n ∈N *时,因为f (n π)·f ((n +1)π)=[(-1)n n π+1]×[(-1)n +1(n +1)π+1]<0,且函数f (x )的图像是连续不断的,所以f (x )在区间(n π,(n +1)π)内至少存在一个零点.又f (x )在区间(n π,(n +1)π)上是单调的,故n π<x n +1<(n +1)π.因此,当n =1时,1x 21=4π2<23;当n =2时,1x 21+1x 22<1π2(4+1)<23; 当n ≥3时,1x 21+1x 22+…+1x 2n <1π2⎣⎢⎡⎦⎥⎤4+1+122+…+1(n -1)2<1π2⎣⎢⎡⎦⎥⎤5+11×2+…+1(n -2)(n -1)= 1π2⎣⎢⎡⎦⎥⎤5+⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -2-1n -1=1π2⎝ ⎛⎭⎪⎫6-1n -1<6π2<23.综上所述,对一切n ∈N *,1x 21+1x 22+…+1x 2n <23.。
课时作业3:章末复习与测试

章末复习与测试1.在两个学习基础相当的班级实行某种教学措施的实验,测试结果见下表,则实验效果与教学措施( )A.有关 C .关系不明确D .以上都不正确2.下列说法中正确的有:( ) ①若r >0,则x 增大时,y 也相应增大; ②若r <0,则x 增大时,y 也相应增大;③若r =1或r =-1,则x 与y 的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上. A .①② B .②③ C .①③ D .①②③3.有下列数据:A .y =3×2x -1 B .y =log 2x C .y =3xD .y =x 24.若两个变量的残差平方和是325, i =1n(y i -y )2=923,则随机误差对预报变量的贡献率约为( ) A .64.8% B .60%C .35.2%D .40%5.为了解儿子身高与其父亲身高之间的关系,随机抽取5对父子的身高数据如下:则y 关于x A.y ^=x -1B.y ^=x +1C.y ^=88+12xD.y ^=1766.收集一只棉铃虫的产卵数y 与温度x 的几组数据后发现两个变量有相关关系,并按不同的曲线来拟合y 与x 之间的回归方程,并算出了对应相关指数R 2如下表:A.y ^=19.8x -463.7 B.y ^=e 0.27x -3.84 C.y ^=0.367x 2-202D.y ^=(x -0.78)2-17.某学校对课程《人与自然》的选修情况进行了统计,得到如下数据:8.某研究机构对高中学段学生的记忆能力x 和识图能力y 进行统计分析,得到如下表数据:若y 与x 的回归直线方程y ^=3x -32,则实数m 的值是________.9.某医疗研究所为了检验某种血清预防感冒的作用,把500名使用过血清的人与另外500名未使用过血清的人一年中的感冒记录作比较,提出假设H 0:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算得k ≈3.918,经查临界值表知P (χ2≥3.841)≈0.05.对此,有以下四个结论:①有95%的把握认为“这种血清能起到预防感冒的作用”;②若某人未使用该血清,那么他在一年中有95%的可能性得感冒; ③这种血清预防感冒的有效率为95%; ④这种血清预防感冒的有效率为5%. 其中所有正确结论的序号是________.10.某地最近十年粮食需求量逐年上升,下表是部分统计数据:(1)利用所给数据求年需求量与年份之间的回归直线方程y=b x+a;(2)利用(1)中所求出的回归直线方程预测该地2018年的粮食需求量.11.在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:表一:男生表二:女生(1)人测评等级为合格的概率;(2)由表中统计数据填写下面的列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.参考临界值表:参考答案1.【答案】A【解析】随机变量χ2=100×(48×12-38×2)250×50×86×14≈8.306>6.635,则有99%的把握认为“实验效果与教学措施有关”. 2.【答案】C【解析】若r >0,表示两个相关变量正相关,x 增大时,y 也相应增大,故①正确.r <0,表示两个变量负相关,x 增大时,y 相应减小,故②错误.|r |越接近1,表示两个变量相关性越高,|r |=1表示两个变量有确定的关系(即函数关系),故③正确. 3.【答案】A【解析】分别把x =1,2,3,代入求值,求最接近y 的值.即为模拟效果最好. 4.【答案】C【解析】由题意可知随机误差对预报变量的贡献率约为325923≈0.352.5.【答案】C【解析】由表中数据可知x =176,y =176,代入选项知C 正确. 6.【答案】B【解析】用相关指数R 2来刻画回归效果,R 2的值越大,说明模型的拟合效果越好. 7.【答案】0.001 【解析】χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=163.794>10.828,即在犯错误的概率不超过0.001的前提下认为选修《人与自然》与性别有关. 8.【答案】4【解析】由题意,x =32,y =8+m 4,所以样本中心点坐标为⎝⎛⎭⎫32,8+m 4,因为回归直线必过样本中心点,y 与x 的回归直线方程为y ^=3x -32,所以8+m 4=3×32-32,所以m =4. 9.【答案】①【解析】由题意,因为χ2≈3.918,P (χ2≥3.841)≈0.05,所以只有①正确,即有95%以上的把握认为这种血清能起到预防感冒的作用.10.解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,为此对数据预处理如下:对预处理后的数据,容易算得,x =0,y =3.2, 又-4×(-21)+(-2)×(-11)+0×0+2×19+4×29=260, (-4)2+(-2)2+02+22+42=40, 所以b ^=26040=6.5,a ^=y -b ^x =3.2.由上述计算结果,知所求回归直线方程为 y ^-257=b ^(x -2012)+a ^=6.5(x -2012)+3.2, 即y ^=6.5(x -2012)+260.2.(2)利用回归直线方程,可预测2018年的粮食需求量为y ^=6.5(2018-2012)+260.2=6.5×6+260.2=299.2(万吨).11.解:(1)设从高一年级男生中抽出m 人, 则m 500=45500+400, 解得m =25,则从女生中抽取20人, 所以x =25-15-5=5,y =20-15-3=2.表二中非优秀学生共5人,记测评等级为合格的3人为a ,b ,c ,尚待改进的2人为A ,B , 则从这5人中任选2人的所有可能结果为(a ,b ),(a ,c ),(b ,c ),(A ,B ),(a ,A ),(a ,B ),(b ,A ),(b ,B ),(c ,A ),(c ,B ),共10种.记事件C 表示“从表二的非优秀学生中随机选取2人,恰有1人测评等级为合格”,则C 的结果为(a ,A ),(a ,B ),(b ,A ),(b ,B ),(c ,A ),(c ,B ),共6种. 所以P (C )=610=35,故所求概率为35.(2)列联表如下:因为1-0.9=0.1,P (K 2而K 2=45×(15×5-15×10)230×15×25×20=1.125<2.706,所以没有90%的把握认为“测评结果优秀与性别有关”.。
课件2:章末复习与测试

专题一 空间几何体的直观图与三视图
画空间几何体的直观图 与三视图主要依据它们的概 念及画法规则.
[例1] 如图所示的是一 个空间几何体的三视图,试 用斜二测画法画出它的直观 图.
[分析] 由几何体三视图可知,它是一个正六棱台,上、 下底边长与高可以根据三视图比例确定,我们可以先画出下 底正六边形,再画出上底正六边形,然后连接侧棱.
(1)求证:平面ABE⊥平面B1BCC1; (2)求证:C1F∥平面ABE; (3)求三棱锥E-ABC的体积.
[解] (1)在三棱柱ABC-A1B1C1中,BB1⊥底面ABC, 所以BB1⊥AB, 又因为AB⊥BC,
所以AB⊥平面B1BCC1. 所以平面ABE⊥平面B1BCC1.
(2)取 AB 中点 G,连接 EG、FG. 因为 E、F 分别是 A1C1、BC 的中点. 所以 FG∥AC,且 FG=12AC. 因为 AC∥A1C1,且 AC=A1C1, 所以 FG∥EC1,且 FG=EC1. 所以四边形 FGEC1 为平行四边形.所以 C1F∥EG. 又因为 EG⊂平面 ABE,C1F⊄平面 ABE, 所以 C1F∥平面 ABE.
PQMN.
专题4 探索性问题 立体几何中的探索性问题在近几年高考中经常出现,这 种题型主要以平行、垂直、距离和角的问题等为背景,有利 于空间想象能力、分析判断能力的考查,也有利于创新意识 的培养,因此应注意高考中立体几何探索性命题的考查趋 势.立体几何探索性命题的类型主要有:一、探索条件,即 探索能使结论成立的条件是什么;二、探索结论,即在给定 的条件下命题的结论是什么.
(3)因为 AA1=AC=2,BC=1,AB⊥BC, 所以 AB= AC2-BC2= 3,
所以三棱锥 E-ABC 的体积
课件5:章末复习与测试

条件概率 条件概率是学习相互独立事件的前提和基础,计算条件概率时 欲求的条件概率是在什么条件下发生的概率. 求条件概率的主要方法有:
-1,2x2-1,…,2x10-1 的标准差为( )
A.8
B.15
C.16
D.32
【解析】 已知样本数据 x1,x2,…,x10 的标准差为 s=8, 则 s2=64,数据 2x1-1,2x2-1,…,2x10-1 的方差为 22s2 =22×64,所以其标准差为 22×64=2×8=16,故选 C. 【答案】 C
(2)恰有 2 人被选中的概率 P2=P(A∩B∩ C )+ P(A∩ B ∩C)+P( A ∩B∩C)=2630. (3)3 人中至少有 1 人被选中的概率 P3=1-P( A ∩ B ∩ C )=1-35×14×32=190.
跟踪训练 2.某同学参加科普知识竞赛,需回答 3 个问题,竞赛规 则规定:答对第 1,2,3 个问题分别得 100 分,100 分,200 分,答错得零分.假设这名同学答对第 1,2,3 个问题的概 率分别为 0.8,0.7,0.6.且各题答对与否相互之间没有影响. (1)求这名同学得 300 分的概率; (2)求这名同学至少得 300 分的概率.
(2)ξ 的可能取值为 0,3,6. 当 ξ=0 时,甲队两场比赛皆输,其概率为 P(ξ=0)=1-23×1-14=41; 当 ξ=3 时,甲队两场只胜一场,其概率为 P(ξ=3)=23×1-14+14×1-23=172; 当 ξ=6 时,甲队两场皆胜,其概率为 P(ξ=6)=23×14=16.
课件2:章末复习与测试

(2)在平面几何中,对于Rt△ABC,AC⊥BC,设AB=c,AC=b,BC= a,则 ①a2+b2=c2; ②cos2A+cos2B=1;
2.用反证法证明命题:“设a,b为实数,则方程x3+ax+b=0至少有一个 实根”时,要做的假设是 A.方程x3+ax+b=0没有实根 B.方程x3+ax+b=0至多有一个实数 C.方程x3+ax+b=0至多有两个实根 D.方程x3+ax+b=0恰好有两个实根
【解析】方程x3+ax+b=0至少有一个实根的反面是方程x3+ax+b=0没 有实根,故选A. 【答案】A
4.数学归纳法 数学归纳法主要用于解决与正整数有关的数学命题.证明时,它的两个步骤 缺一不可,它的第一步(归纳奠基)是证当n=n0 时结论成立;第二步(归纳 递推)是假设当n= k (k≥n0且k∈N+)时结论成立,推得当n= k+1 时结论 也成立.
类型一 合情推理的应用
例1 (1)有一个奇数列1,3,5,7,9,…,现在进行如下分组:第一组含一个 数{1};第二组含两个数{3,5};第三组含三个数{7,9,11};第四组含四个 数{13,15,17,19};…,试观察每组内各数之和并猜想f(n)(n∈N+)与组的 编号数n的关系式为________.
跟踪训练 数列{an}满足:a1=1,an+1=12an+1. (1)写出a2,a3,a4; 解 因为 a1=1,an+1=21an+1, 所以 a2=12a1+1=12+1=32. a3=12a2+1=21×23+1=47. a4=12a3+1=21×47+1=185.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
技术环 电磁波→收集→ 节(工 传输→处理→分 作流程) 析→成果
工具
第3章 地理信息技术应用
栏目导引
遥感技术 范围大、速度 特征 快(实时传输)、 周期短、限制 少、应用广 较短时间内获 作用 得全面资料,
地理信息系统 ①采集、管理、分析、
全球定位系统 全能性、全球 性、全天候、 连续性、实时 性 能为各类用户 提供精密的三
RS和 信息获取和空间 GIS 结合 分析结合
评价,指导防灾活动;灾中:实况监 测并作出评价,指导抗灾活动;灾后: 评估损失,指导救灾活动
工具
第3章 地理信息技术应用
栏目导引
2.GPS应用
(1)GPS接收机的解读
工具
第3章 地理信息技术应用
栏目导引
①该图表示接收机所在的经度为 116°18′50.2″E 、纬度为
(3)北斗卫星导航系统是我国数字中国建设的重要组成部分, 说说数字中国对我国国土整治的意义。
工具
第3章 地理信息技术应用
栏目导引
解析:
第(1)题,北斗导航系统是全球定位系统(GPS),具
有全能性、全球性、全天候、连续性和实时性的特点。RS的关 键装置是传感器,GIS是一种专门处理空间数据的计算机系统;
RS广泛应用于资源、环境监测、自然灾害防御监测等。第(2)题,
实时监测台风的位置,主要采用数字地球系统。第 (3)题,数字 地球是由计算机网络来管理的技术系统,能为复杂的生产、研 究活动提供实验条件和试验基地。
工具
第3章 地理信息技术应用
栏目导引
答案:
(1)C
(2)A
(3)数字中国是将不同空间、时间的自然、人文的大量信息, 按地理坐标,从区域到全国的整合,并进行立体的、动态的显
第3章 地理信息技术应用
栏目导引
主要功能 对信息进行综合 地理 处理和空间数据 信息 分析,具有空间 系统 (GIS) 定位、定性和定 量分析的功能
在自然灾害监测中的作用 对自然灾害进行预报预警、动态监测、 灾害发生原因与规律分析、灾害损失 调查、灾情评估等,还可以为制订减 灾预案和指导灾后重建工作提供依据 灾前:圈定危险区,对危险程度作出
工具
第3章 地理信息技术应用
栏目导引
工具
第3章 地理信息技术应用
应用
栏目导引
工具
第3章 地理信息技术应用
栏目导引
工具
第3章 地理信息技术应用
栏目导引
1.如何区分“3S”技术 遥感技术 别称 人的视力的延伸 地理信息系统 地图的延伸 信息源→数据处 理→数据库→空 间分析→表达 全球定位系统
39°58′27.9″N。
②接收机所在的高度为109米,误差为5.7米。 ③卫星分布图描绘了在你所处位置 (圆心)仰望天空能搜索到 的8颗卫星,大圆表示地平线,小圆为抬头以45°角仰望天空的 范围,越靠近中心,卫星信号越强。 ④数字表示被接收到信号的卫星编号,黑色柱的长短表示 信号强弱,一般收到4~8颗卫星的信号。
输出地理空间信息;②
空间分析、多要素、综 合、动态预测;③计算
机系统支持
能对地理空间数据进行 输入、管理、分析和表 达
以便及时安排
防灾、救灾
维坐标、速度
和时间
栏目导引
工具
第3章 地理信息技术应用
2.RS、GIS和GPS之间的关系
工具
第3章 地理信息技术应用
栏目导引
阅读材料,完成下列问题。 北京时间 2010 年 11 月 1 日 11 分,我国西昌卫星发射中心用 “长征三号丙 ”运载火箭,成功将第六颗北斗导航卫星送入太
D.广泛应用于资源、环境监测、自然灾害防御监测等
工具
第3章 地理信息技术应用
栏目导引
(2)2008 年 11月 16 日,第 20 号台风“海神”横扫中国南部, 造成大量人员伤亡、财物损失,为实时监测“海神”的位置, 我国采用的主要技术手段是( )
A.数字地球系统
C.全球定位系统
B.人工拍摄
D.多媒体技术
工具
第3章 地理信息技术应用
栏目导引
(2)GPS的应用举例 ①车载GPS的应用 信息接收 通过车载GPS可以 信息发射 应用领域
车载电台把定位信 城市公共汽车调度管
在显示屏上及时查 息发送给监控中心, 理,旅游区车辆报警
看车辆的经纬度、 在电子地图上显示 与调度,海关、公安、
运行轨迹、速度、 出来,可对车辆进 海防等部门对车辆调 行进方向等 行调度指挥 度与监控
工具
第3章 地理信息技术应用
栏目导引
⑤接收机往往可以锁住 4颗以上的卫星,这时,接收机可按
卫星的星座分布分成若干组,挑选出误差最小的一组用作定位, 从而提高精度。
为提高定位精度,普遍采用差分 GPS(DGPS)技术,建立基
准站(差分台)进行GPS的基准站精确坐标,与观测值进行比较, 从而得出一修正数,并对外发布。接收机收到该修正数后,与 自身比较,消去大部分误差,得到一个比较准确的位置。实验 表明,利用差分GPS,定位精度可提高到5米。
空。 目前美国的GPS、欧洲的“伽利略”、俄罗斯的“格洛纳
斯”和中国的北斗卫星导航四大定位系统齐聚太空。
工具
第3章 地理信息技术应用
栏目导引
(1)有关北斗导航系统的叙述,正确的是( A.北斗导航系统的关键装置是传感器 B.是一种专门处理空间数据的计算机系统
)
C.具有全能性、全球性、全天候、连续性、实时性的特点
示,为复杂的生产、研究活动提供实验条件和试验基地。
工具
第3章 地理信息技术应用
栏目导引
1.遥感技术和地理信息系统在自然灾害监测中的作用 主要功能 总体上:观 测范围广、 信息获取量 遥感 大、速度快 技术 空间上:多 (RS) 波段、多时 相和全天候 时间上:同 步观测
工具
在自然灾害监测中的作用 ①除能看到电视屏幕上的常规大气云图外, 还可看到沙尘暴、台风、暴雨等灾害性天 气的形成过程;②利用遥感影像可以迅速 地发现一些初发时肉眼难以察觉的突发性 灾害,如森林火灾、赤潮等;③在交通不 便、人迹罕至的地区可展现遥感作为灾害 监测“千里眼”的优越性;④在灾害发展 过程中和消除后,对灾害发生的规模、速 度以及是否复发进行监测
工具
第3章 地理信息技术应用
栏目导引
②GPS在航海、航空导航中的作用
应用类型 应用领域 向用户提供船舶位置、航 速、航向、时间信息、海 航海应用 图、海迹显示 把自己的位置和航向发送 到航海管理中心 空域航路、着陆、机场监 视和管理 应用作用
