高考物理常见难题大盘点力矩有固定转动轴

合集下载

2019高考物理常见难题大盘点力矩有固定转动轴物体的平衡

2019高考物理常见难题大盘点力矩有固定转动轴物体的平衡1、如图1-50所示是单臂斜拉桥的示意图,均匀桥板ao 重为G ,三根平行钢索与桥面成30°,间距ab =bc =cd =do ,假设每根钢索受力相同，左侧桥墩对桥板无作用力，那么每根钢索的拉力大小是〔〕。

(A)G (B)3G ∕6(C)G ∕3(D)2G ∕3解答设aO 长为4L ，每根钢索受力为T ，以O 点为转轴，由力矩平衡条件得23sin302sin30sin30G L T L T L T L ︒︒︒⨯=⨯+⨯+⨯，解得23T G=。

此题的正确选项为〔D 〕。

2、图1-51为人手臂骨骼与肌肉的生理结构示意图，手上托着重量为G 的物体，〔1〕在方框中画出前臂受力示意图〔手、手腕、尺骨和挠骨看成一个整体，所受重力不计，图中O 点看作固定转动轴，O 点受力可以不画〕、〔2〕根据图中标尺估算出二头肌此时的收缩力约为、解答前臂的受力如图1-52所示，以O 点为转轴，由力矩平衡条件得18F N ⨯=⨯，其中N =G ，可得F =8G 。

此题的正确答案为“8G ”。

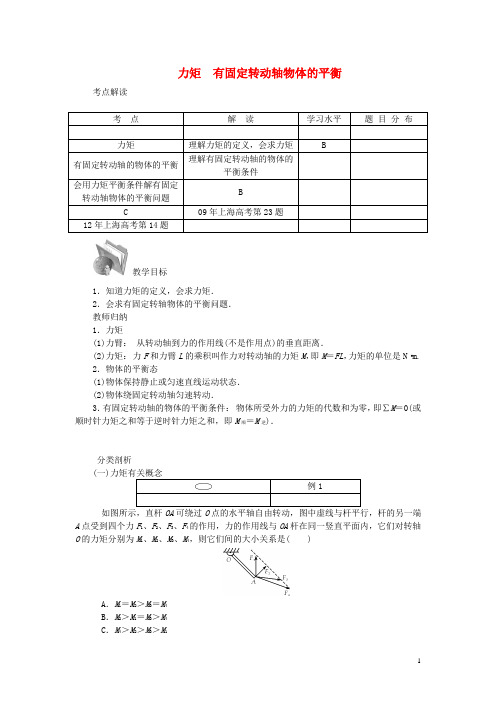
3、如图1-53所示，直杆OA 可绕O 轴转动，图中虚线与杆平行、杆的A 端分别受到F 1、F 2、F 3、F 4四个力作用，它们与OA 杆在同一竖直平面内，那么它们对O 点的力矩M 1、M 2、M 3、M 4的大小关系是〔〕。

(A)M 1＝M 2＞M 3＝M 4 (B)M 1＞M 2＞M 3＞M 4 (C)M 2＞M 1＝M 3＞M 4(D)M 1＜M 2＜M 3＜M 4解答把四个力都分解为垂直于OA 方向和沿OA 方向的两个分力，其中沿OA 方向的力对O 点的力矩都为零，而垂直于OA 方向的力臂都相等，所以四个力的力矩比较等效为垂直方向的力的比较。

从图中不难看出力大小关系为F 2⊥>F 1⊥=F 3⊥>F 4⊥，所以力矩大小关系为M 2>M 1=M 3>M 4。

高三物理力矩平衡经典试题

有固定转动轴的物体的平衡1、如图所示是一种手控制动器，a 是一个转动着的轮子，b 是摩擦制动片，c 是杠杆，O 是其固定转动轴.手在A 点施加一个作用力F 时，b 将压紧轮子，使轮子制动.若使轮子制动所需的力矩是一定的，则下列说法正确的是（）A.轮a 逆时针转动时，所需的力F 较小B.轮a 顺时针转动时，所需的力F 较小C.无论逆时针还是顺时针转动，所需的力F 相同D.无法比较F 的大小2、如图所示，两个等重等长质料均匀直棒AC 和BC ，其各自一端分别通过转轴与墙壁绞结，其另一端相连于C 点，AC 棒与竖直墙夹角为45°，BC 棒水平放置，当两棒均处于平衡状态时，则BC 棒对AC 棒作用力方向可能处于哪一区域（）A.甲区域B.乙区域C.丙区域D.丁区域3、如图所示，AC 为竖直墙面，重为G 的AB 均匀横梁处于水平位置。

BC 为支撑横梁的轻杆，它与竖直方向的夹角为α，A 、B 、C 三处均用铰链连接，轻杆所受的力为（）A 、αcos GB 、αcos 2G C 、αcos G D 、αcos 2G4、如图所示，竖直杆AB 在绳AC 拉力作用下使整个装置处于平衡状态，若绳AC 加长，使点C 缓慢向左移动，杆AB 仍竖直，且处于平衡状态，那么绳AC的拉力T 和杆AB 所受的压力N 与原来相比，下列说法中正确的是（）A 、T 增大，N 减小B 、T 减小，N 增大C 、T 和N 均增大D 、T 和N 均减小5、如图所示，一根轻质木棒AO ，A 端用光滑铰链固定于墙上，在O 端下面吊一个重物，上面用细绳BO 系于顶板上，现将B 点逐渐向右移动，并使棒AOA ．BO 绳上的拉力大小不变。

B ．BO 绳上的拉力先变大后变小。

C ．BO 绳上的拉力对轻杆的力矩先变大后变小。

D ．BO 绳上的拉力对轻杆的力矩不变。

6、如图所示，重为Ｇ的圆盘与一轻杆相连，杆与盘恰相切，支于Ｏ点.现用力F 竖直向下拉杆的另一端，使该端缓慢向下转动，则杆转到竖直之前，拉力F 及其力矩Ｍ的变化情况是（）Ａ.Ｍ变小，F 不变. Ｂ.Ｍ、F 均变小.Ｃ.Ｍ先变大再变小，F 始终变大. Ｄ.Ｍ变小，F 变大.7、如图所示，重为Ｇ的均匀棒，可绕上端Ｏ在竖直平面内转动.今在棒的下端用水平力F 拉，使棒缓慢转动，直至转到水平方向为止，则拉力F 和它的力矩Ｍ的变化情况是（）Ａ.都增大. Ｂ.都减小.Ｃ.F 增大，Ｍ减小. Ｄ.F 减小，Ｍ增大.8、质量均匀的木板，对称地支承于P 和Q 上，一个物体在木板上从P 处运动到Q 处，则Q 处对板的作用力N 随x 变化的图线是（）9、如图所示，均匀木棒AB 的一端N 支在水平地面上，将另一端用水平拉力F 拉住，使木棒处于平衡状态，则地面对木棒AB 的作用力的方向为（）A 、总是竖直向上的，如F 1B 、总是偏向木棒的右侧，如F 2C 、总是沿着木棒的方向，如F 3D 、总是偏向木棒的左侧，如F 410、如图所示，足够长的均匀木棒ＡＢ的Ａ端铰于墙上，悬线一端固定，另一端套在木棒上跟棒垂直，并使棒保持水平.如改变悬线的长度使套逐渐向右移动，但仍保持木棒水平，则悬线所受拉力大小将（）Ａ.逐渐变小. Ｂ.先逐渐变大后又逐渐变小.Ｃ.逐渐变大. Ｄ.先逐渐变小后又逐渐变大.11、如图所示，均匀细杆AB 质量为M ，A 端装有转轴，B 端连接细线通过滑轮和质量为m 的重物C 相连，若杆AB 呈水平，细线与水平方向夹角为θ 时恰能保持平衡，则杆对轴A 有作用力大小下面表达式中正确的有（） A ．mg B ．Mg 2 sin θC ．M2－2Mm sin θ＋m2 gD ．Mg －mg sin θ12、如图所示，均匀板一端搁在光滑墙上，另一端搁在粗糙地面上，人站在板上，人和板均静止，则（）A.人对板的总作用力就是人所受的重力.B.除重力外板受到三个弹力和两个摩擦力作用.C.人站得越高，墙对板的弹力就越大.D.人站得越高，地面对板的弹力就越小.13、如图所示,一端可绕O 点自由转动的长木板上方放一个物块,手持木板的另一端,使木板从水平位置沿顺时针方向缓慢转动,转动过程中，手对木板的力始终竖直向上，则在物块相对于木板滑动前（）A ．物块对木板的作用力减小B ．手对木板的作用力不变C ．手对木板的作用力增大D ．手对木板的作用力的力矩不变14、如图丙所示，一质量分布均匀的梯子，重为G ，斜搁在光滑的竖直墙上，重为P 的人沿梯子从梯子的底端A 开始匀速向上走，人的重心离地的高度h 逐渐增大，整个过程梯子不滑动。

物理学难题集萃难度分级表

第一部分力学难度备注标注为1的，要求做完第一章运动学标注为2的，看懂题11标注为3的，不看第三章电磁感应题21题11题33题22题41题32题51题41题61题51题71题61题8.13题71题8.22题81题91题91题102题101题111题111题122题121题133题131题141题141题151题151题162第二章牛顿运动定律题171题11题181题21题191题31题202题41题21 2.5题52题223题61题23 2.5题71题81第四章电离、直流电路题91题11题103题23题113题3.11题123题3.21题133题3.33题142题3.43题151题43题161题5 2.5题171题62题182题71题192题82题202听蔡子星讲题91题101第三章功、能和动量题112题11题121题21题131题31题141题42题152题51题16 2.5题61题171题71题183题81题193题92题201题101题211题111题221题122题231题131题241题141题251题151题261题161题273题171题281题181题291题191题301题201题311题211题321题222题331题231题341题241题351题251题261第五章交流电路，暂态过程及其他题271题11题281题22题291题31题302题41题311题51题321题61题331题73题341题81题352题92题361题101题373题113题382题122题39 2.5题133题143第四章角动量，有心运动题153题12题163题22题173题31题181题41题193题51题20.11题61题20.21题72题20.32题81题91第四部分光学题101第一章几何光学题111题11题12 2.5题21题132题31题142题41题51第五章题61题11题72题21题82题31题93题41题103题51题112题61题122题71题131题81题141题92题151题101题161题112题171题123题181题191第六章刚体动力学题201题11题211题2 2.5题221题3 2.5题231题4 2.5题241题5 2.5题251题6 2.5题262题71题272题82题281题91题29题103题302题112题312题122题321题13 2.5题332题14 2.5题34 2.5题152题352题162题363题172题373题182题381题191题393题20 2.5题403题212题41 2.5题222题423题233题242第二章光的干涉题253题11题262题23题272题31题41第七章振动与波动题53题11题61题21题71题31题83题41题93题52题101题62题111题73题122题8 2.5题132题93题143题102题151题111题162题122题172题132题182题142题192题152题203题163题213题172题223题183题233题191题242题20 1.5题253题212题263题222题273题233题242第三章光的衍射题252题13题262题23题273题33题282题43题293题53题303题63题313题73题323题83题332题93题342题103题352题113题362题123题372题133题383题143题391题153题401题163题41 2.5题173题421题182题431题193题203第二部分热学题213第一章平衡态理想气体状态方程题223题12题21第四章光的偏振题32题11题41题22题51题33题61题43题71题53题81题63题91题73题103题83题112题93题121题103题131题113题141题123题151题133题161题143题153第二章热力学第一、第二定律题163题12题173题23题183题31题193题42题203题51题212题62题222题71题233题81题243题91题253题101题263题111题272题122题283题132题292题142题30 2.5题152题312题162题323题171题333题183题343题191题35 2.5题202题212第五章光的色散，散射和吸收题221题12题233题2 2.5题243题33题253题42题53第三章气体动理论题63题11题73题21题83题32题93题41题103题5 2.5题112题63题73第五部分近代物理题82第一章量子物理题93题11题102题21题11 2.5题31题122题41题131题51题142题63题152题7.11题163题7.23题173题81题182题91题193题101题202题111题213题121题221题1311题232题1411题242题152题253题161题263题172题273题181题283题192题293题203题303第二章狭义相对论第四章范德瓦耳斯气体液体固体相变题11题13题21题23题31题33题41题41题5 2.5题52题63题61题73题71题82题81题93题93题102题101题113题113题123题12.11题133题12.21题14.11题12.32题14.22题13 2.5题151题141题163题152题172题161题181题173题191第三部分电磁学第六部分试题第一章静电场，导体与介质力学试题（一）题11题11题21题21题33题31题41题41题51题51题61题62题71力学试题（二）题8.11题11题8.22题2 1.5题91题31题102题43题111题53题121题6 2.5题132热学试题（一）题142题13题151题2.11题161题2.23题171题32题181题42题191题53题202热力学试题（二）题212题11题223题23题232题31题241题43题252题5 2.5题261电磁学试题（一）题271题11题281题22题291题31题302题41题313题52题321电磁学试题（二）题333题12题341题22题352题33题36 2.5题41题371题51题381电磁学试题（三）电路题391题12题401题21题413题3 2.5题421题41题431题53题443电磁学试题（四）电路题45 2.5题13题461题22题32第二章磁场，磁介质题43题11题53题23光学试题题32听蔡子星讲题11题43题21题51题31题61题41题72题52题82题62题91近代物理试题题103题12题113题21题101题31题111题41题121题51题131综合试题（一）题142题11题152题21题16.11题33题16.21题42题16.33题52题172题61题18.11综合试题（二）题18.21题12题18.33题21题191题32题201题41题211题51题223题6.11题233题6.22题241题6.32题253综合试题（三）题26 2.5题11题27 2.5题21题32题4 2.5题51题61综合试题（四）题13题21题33题42题52题6 2.5综合试题（五）题11题21题31题41题51题63听蔡子星讲（某个公式）过程及其他和吸收。

研究有固定转动轴物体平衡条件专题

研究有固定转动轴物体平衡条件专题前言：力矩平衡是高中物理静力学部分的内容，在全国高考中只有上海有明确的考试要求，因此也成为了每年上海高考的特色之一，研究有固定转动轴物体的平衡条件的实验也是在上海实验考试中有特色的一块。

【实验目的】通过实验研究有固定转动轴的物体在外力作用下平衡的条件，进一步明确力矩的概念。

【实验器材】力矩盘（带有金属轴的圆木板），刻度尺，弹簧秤，几个等质量的钩码，带有铁夹的铁架台，带有几个套环的横杆，大头针，两端有套环的丝线四条。

【准备工作】1．实验中力矩盘的固定转动轴应水平地固定在铁架台上，这样才能使力矩盘的平面调节在竖直平面内。

这是因为实验中主要是利用钩码对细线产生竖直向下的拉力使力矩盘转动，所以细线应与力矩盘保持平行。

2．如果被弹簧秤拉紧的细线方向通过转动轴O ，那么弹簧秤的拉力对力矩盘产生的力矩等于 0 ，该力对力矩盘转动将不起作用，所以在实验中被弹簧秤拉紧的细线方向不能通过转动轴O 。

【实验步骤】1．将力矩盘和一横杆安装在支架上，使盘可绕水平轴自由灵活地转动，调节盘面使其在竖直平面内。

在盘面上贴一张白纸。

2．取四枚图钉，将四根细线固定在盘面上，固定的位置可任意选定，但相互间距离不可取得太小。

在三根细绳的末端挂上不同质量的钩码，第四个钉子用细线与弹簧秤的钩子相连，弹簧秤的另一端则挂在水平横杆的套环上。

使它对盘的拉力斜向上方。

3. 当力矩盘在四个力的作用下处于平衡时，测出各力的大小及它们的力臂，将力和力臂的数据记录在表格中。

4．改变钉子位置重复实验一次。

5. 分析数据得出结论。

【数据处理】把实验结果记在下面的表内并计算出各个力的力矩以及力矩和。

顺时针方向逆时针方向力力臂力矩力矩和力力臂力矩力矩和结论: 通过实验得出，有固定转动轴物体的平衡条件是：。

【注意事项】1．实验前要确保力矩盘位于竖直平面内，力矩盘不在竖直平面，导致测量值大于真实值C2. 检查力矩盘的重心应位于转轴中心：轻拨力矩盘，看是否在任何位置都能平衡，如果达不到这个要求表明盘的重心偏离转轴，必须另加配重，校正后方能使用。

高一物理有固定转动轴物体的平衡知识精讲

高一物理有固定转动轴物体的平衡【本讲主要内容】有固定转动轴物体的平衡1. 了解转动平衡的概念，理解力臂和力矩的概念。

2. 理解有固定转动轴物体的平衡条件，会应用平衡条件处理简单的转动平衡问题【知识掌握】前面学习共点力平衡知识时，同学们知道“共点力”其实并不是说各力的作用点必须相同或相等的作用线必定交于一点。

很多情况下，在物体可当作质点且不会转动的情况下，我们也把物体受的外力都视为共点力。

若满足物体所受的共点力的合力为零，则物体处于静止或匀速直线运动状态，即平衡状态。

若物体在外力作用下可能发生转动，当然此时物体所受外力不能称为共点力，那么物体还能否保持平衡状态呢?物体若要保持平衡状态需要什么条件呢?【知识点精析】我们生活中常见到下列现象：（1）两个同学一里一外推门，门静止不动。

（2）手提一根一端固定在墙上的铁杆不动（或缓慢转动），如图所示。

（3）电动机的转子匀速转动。

（匀速转动情况下的平衡问题不要求）1. 转动平衡：一个有固定转动轴的物体，在力的作用下，如果保持静止（或匀速转动），这个物体就处于转动平衡状态。

2. 力矩（1）固定转动轴的含义（做转动的物体，物体上的各点都沿圆周运动，如果圆周的中心在同一直线上，这条直线就叫做转动轴。

）①实际转轴：如门的转轴、力矩盘的转轴、电风扇的转轴、自行车悬空转动时的车轴等。

②等效转轴：实际上并不存在的固定转轴，是人们为解决问题而假想的转轴。

（2）力臂（L）：从转动轴到力的作用线的距离。

如下图：OA不是力F的力臂，OB才是力F的力臂。

（3）力矩（M）：力和力臂的乘积。

M＝FL。

理解：①力矩是表示力对物体的转动作用的物理量。

力矩越大，力对物体的转动作用就越强；力矩为零，力对物体不会有转动作用。

②力矩是对某一转轴而言的。

同一个力，对不同的转轴，力矩不同。

③力矩的正负。

力矩的正负是根据力矩的作用效果而人为规定的。

一般规定使物体向逆时针方向转动的力矩为正，使物体向顺时针方向转动的力矩为负。

2014—2015高考物理总复习(知识回忆+跟踪练习+即时检测)第二章第9讲力矩有固定转动轴物体的平衡(1)

力矩有固定转动轴物体的平衡知识回忆1．力矩：作用在有固定转轴物体上的力所产生的转动效果，不仅与力的大小有关，而且还与转轴到力的作用线的__________有关，力的转动效果是由力和力臂两个因素决定的，用力F和力臂L的乘积来量度力的转动效果，并称之为力矩M，即：M＝FL；逆时针力矩使物体作逆时针转动，顺时针力矩使物体作顺时针转动．力矩的单位是__________．2．有固定转轴物体的平衡条件：力矩可以使物体向不同的方向转动．有固定转动轴的物体的平衡条件是：使物体向顺时针方向转动的力矩之和__________使物体向逆时针方向转动的力矩之和；也就是合力矩等于零，即∑M＝0.跟踪练习1．如图，轻杆A端用光滑水平铰链装在竖直墙面上，B端吊一重物P，并用水平绳结在墙C处，在水平向右力F缓缓拉起重物P过程中杆AB所受压力 ( )第1题图A．变大 B．变小C．先变小再变大 D．不变2．如图所示，重为G的圆盘与一轻杆相连，杆与盘恰相切，支于O点．现用力F竖直向下拉杆的另一端，使该端缓慢向下转动，则杆转到竖直之前，拉力F及其力矩M的变化情况是( )第2题图A．M变小，F不变B．M、F均变小C．M先变大再变小，F始终变大D．M变小，F变大第3题图3．如图所示，一均匀直角三角形木板abc，可绕垂直纸面通过c点的水平轴转动．现用一始终沿直角边ba的作用于a点的力F，使bc边缓慢地由水平位置转至竖直位置，在此过程中，力F的大小随α角变化的图线是图中的( )4．如图所示，质量为m 的匀质木杆，上端可绕固定水平光滑轴O 转动，下端搁在木板上，木板置于光滑水平地面上，杆与竖直方向成45°角，杆与木板间的滑动摩擦系数为1/2，为使木板向右做匀速运动，所加的水平拉力F 等于( )第4题图A.12mgB.13mgC.14mgD.16mg5．如图所示，是一种手动控制器，a 是一个转动着的轮子，b 是摩擦制动片，c 是杠杆，O 是其固定转动轴，手在A 点施加一个作用力F 时，b 将压紧轮子，使轮子制动．若使轮子制动所需的力矩是一定的，则下列说法正确的是( )第5题图A ．轮a 逆时针转动时，所需的力F 较小B ．轮a 顺时针转动时，所需的力F 较小C ．无论a 逆时针还是顺时针转动，所需的力F 相同D ．无法比较F 的大小6．A 、B 为相同大小的两正三角形板块，如图所示铰接于M 、N 、P 三处并静止．M 、N 在同一水平天花板上，A 板较厚，质量分布均匀，重力为G .B 板较薄，重力不计．三角形的竖直边垂直于天花板．那么，B 板对铰链P 的作用力的方向为________；作用力的大小为________．第6题图7．如图所示，是人手臂骨骼与肌肉的生理结构示意图，手上托着重为G的物体．(1)在方框中画出前臂受力示意图(把手、手腕、尺骨和桡骨看成一个整体，它们所受重力不计，图中O点看作固定转动轴，O点受力可以不画)；(2)根据图中标尺估算出手臂的二头肌此时的收缩力大小约为__________．第7题图8．如图所示，AOB为三角支架，质量M＝19.2kg，A端搁在铁块上，支架可绕过O点的水平轴自由转动，支架重心在C点，C点距O点的水平距离d＝0.2m，AO＝L＝0.8m，支架的斜面AD的倾角θ＝37°.质量m＝10kg的物体放在支架底端A处，物体在平行于AD方向的力F作用下由静止开始运动，F＝85N，物体与AD间的滑动摩擦系数μ＝0.25，求：(1)物体运动多长时间，运动到何处时支架开始翻倒？(2)如果这个物体在AD上某点由静止开始向下滑动，为使支架不翻倒，物体距A端的最大距离为多少？(g取10m/s2)第8题图即时检测1．如图所示，用与木棒垂直的力F作用于A端，使木棒缓慢拉起，木棒只能绕O端转动，拉力F及F的力矩大小变化是( )第1题图A．F变小，力矩变小B．F变大，力矩变大C．F不变，力矩变小D．F变小，力矩不变2．如图所示，要使圆柱体滚上台阶，则在圆柱体最高点作用的力中最省力的是( )第2题图A．F1 B．F2C．F3 D．F43．均匀木棒的质量为m，可绕固定轴O点转动，另一端放在木块上，木块的质量为m木，木块放在光滑桌面上，如图所示，如果木块在一个水平推力F作用下仍保持静止，则木棒所受力矩的个数和原来相比( )第3题图A．由1个变为2个B．由2个变为3个C．和原来一样D．以上说法均不正确4．如图所示，质量为m架且均匀分布的直角架ABC放在水平桌面上，已知AB＝AC＝L，在C点用线悬挂一个半径为R的球，球的质量分布均匀，若使直角架不向右翻倒，则球的质量m应满足的关系式__________．第4题图5．如图所示，质量为3kg的A球和质量为3kg的B球，被轻质细线连接后，挂在光滑的圆柱面上恰好处于静止状态，已知∠AOB＝90°，OB与竖直方向的夹角为________．第5题图6．如图所示，均质板AB的A端用铰链与竖直墙连接，B端用水平轻绳系于墙上．光滑球夹于墙、板之间，已知板长为l，球半径为R，板与墙夹角为θ，球重为G1，板重为G2，试求：(1)球对板压力的力矩；(2)板重力的力矩；(3)绳拉力的力矩及拉力．第6题图7.在验证“有固定转动轴的物体的平衡条件”实验中，某同学操作步骤如下：(1)①将力矩盘的金属轴O固定在铁架台上，把力矩盘套在轴上并使盘面保持竖直．同时在铁架台上固定一横杆．力矩盘上画上若干同心圆，供确定力臂时参考；②将钉子固定在力矩盘的四个任意位置上，四个钉子上分别用细线悬挂不同个数的钩码；③当力矩盘在这四个力的作用下处于平衡状态时，测出各个力的力臂，将力和力臂的数据记录在数据表中；④改变钉子的位置，重复实验一次．改正其中的错误：________________________________________________________________________ ________________________________________________________________________.(2)如果实验结果中顺时针与逆时针力矩不相等，有明显误差，其原因可能为________________________________________________________________________ ________________________________________________________________________.力矩有固定转动轴物体的平衡知识回忆1.垂直距离(称为力臂) N ·m2.等于跟踪练习1.D2.C 【解析】重力的力臂先变大后变小，判断F 的变化时应画出图线来分析，如图，当OA 转至水平时力臂最大．第2题图3.D4.D5.A 【解析】要考虑摩擦力的力矩相对O 点是逆时针还是顺时针．6.沿PN 方向向上，G3 【解析】 B 板重力不计，B 板对铰链P 的作用力的方向沿PN方向向上，以M 为轴，32L ×13G ＝F×32L ，F ＝13G. 7.(1)第7题图(2)8G8.(1)2s ，距A 点1m 处 (2)1.24m【解析】小物体向上滑动和向下滑动时支架的斜面所受摩擦力方向相反．即时检测1.A 【解析】木棒除O 点受力外，对木棒转动有贡献的力是重力G 和拉力F ，设木棒长为l ，木棒与地面夹角为α，由平衡条件有 M 逆＝M 顺＝mg×l2cos α，因cos α随α增大而减小，则F 的力矩减小，又因M 逆＝F·l，故F 减小，故选A .2.C 【解析】圆柱体以A 点为转轴滚上台阶，在这一过程中，对圆柱体转动有贡献的力是重力mg和拉力F，由平衡条件M F＝M G，要使作用在圆柱体上的力最小，则需F的力臂最大，因为F3力的力臂最大，所以F3最小，故选C.3.B【解析】当水平推力作用前，对木棒转动有贡献的力有重力和木块对它的支持力，两力均有力矩，处于力矩平衡状态，当水平推力F作用后，木块仍保持静止，说明木棒给木块一个水平向左的静摩擦力大小为F，根据作用力与反作用力的关系，木块给木棒一个水平向右的静摩擦力作用，所以此时木棒共受3个力的力矩作用，即木棒所受力矩的个数变化是由2个变为3个，且重力矩不变，支持力矩变小，因增加的静摩擦的力矩与支持力矩同向．故选B.4.m≤L4Rm架【解析】当直角架刚好没翻倒时，系统对地面的压力全部落在支点A 处，以A点为转轴，有m架g2L2＝mgR，故m＝L4Rm架，则直角架若不翻倒应满足的关系式为m≤L4R m架．5.30°【解析】把A、B两球连同细线作为一个整体，以柱的柱轴为转轴研究系统力矩平衡．因为柱面支持力N A、N B通过转轴，细线张力为内力，所以力矩平衡关系为m A gR cos α＝m B gR sinα，所以tanα＝m Am B＝33，即α＝30°.第5题图6.(1)G1R2sin2θ2(2)G2l2sinθ(3)G1R2sin2θ2＋G2l sin2θ22G1R cotθ2＋G2l sin2θ2l sinθcosθ【解析】(1)如图所示，球受重力G1，板的支持力N1和墙的支持力N2三个力的作用而平衡，从图中可得N1＝G1sinθ，故球对板的压力大小为N′＝G1sinθ.设N′的力臂为l1，则l1＝R cotθ2，则M N′＝N′l1＝G1sinθR cotθ2＝G1R2sin2θ2.第6题图(2)设板重力的力臂为l2，l2＝l2sinθ，则MG2＝G2l2＝G2l2sinθ. (3)由平衡条件，M顺＝M 逆，则M T ＝M N ′＋MG 2＝G 1R 2sin2θ2＋G 2l2sin θ.又M T ＝Tl cos θ，故T ＝G 1R2sin2θ2＋G 2l sin θ2l cos θ＝2G 1R cot θ2＋G 2l sin 2θ2l sin θcos θ.7.(1)②四个钉子应该一个用弹簧秤拉，其余三个钉子上分别用细线悬挂不同个数的钩码 (2)力矩盘重心不在中心，轴处摩擦大【解析】 “有固定转动轴的物体的平衡条件”实验中，注意事项有：转动轴要水平固定在铁架台上，力矩盘要处于竖直平面内，横杆与力矩盘在同一竖直面内，检验重心是否在转动轴上，钩码不能搁在力矩盘上，弹簧秤调零，拉力与力矩盘平行．。

高考物理必考难点力矩平衡条件及应用

高考物理必考难点力矩平衡条件及应用力矩平衡以其广泛的实用性，再次被考纲列为考查的内容，且以此知识点为素材的高考命题屡次再现于近几年高考上海卷及全国理综卷中.其难点分布于：（1）从实际背景中构建有固定转动轴的物理模型.（2）灵活恰当地选取固定转动轴.（3）将转动模型从相关系统（连结体）中隔离分析等.●难点磁场1.（★★★★）如图3-1所示，一根长为L 的轻杆OA ，可绕水平轴O 在竖直平面内自由转动，左端A 挂一质量为m 的物体，从杆上一点B 系一不可伸长的细绳，将绳跨过光滑的钉子C 与弹簧K 连接，弹簧右端固定，这时轻杆在水平位置保持平衡，弹簧处于伸长状态，已知OB =OC =32L ，弹簧伸长量恰等于BC ，由此可知，弹簧的劲度系数等于______.2.（★★★★★）（1997年上海，6）如图3-2所示是一种手控制动器，a 是一个转动着的轮子，b 是摩擦制动片，c 是杠杆，O 是其固定转动轴.手在A 点施加一个作用力F 时，b 将压紧轮子，使轮子制动.若使轮子制动所需的力矩是一定的，则下列说法正确的是A.轮a 逆时针转动时，所需的力F 较小B.轮a 顺时针转动时，所需的力F 较小C.无论逆时针还是顺时针转动，所需的力F 相同D.无法比较F 的大小●案例探究［例1］（★★★★★）如图3-3所示，长为L 质量为m的均匀木棒，上端用绞链固定在物体上，另一端放在动摩擦因数为μ的小车平台上，小车置于光滑平面上，棒与平台的夹角为θ，当：（1）小车静止时，求棒的下端受小车的支持力；（2）小车向左运动时，求棒的下端受小车的支持力；（3）小车向右运动时，求棒的下端受小车的支持力. 命题意图：题目出示的物理情境，来考查考生受力分析能力及力矩平衡条件的应用能力.B 级要求.错解分析：对“车的不同运动状态使棒所受摩擦力大小方向的变化”理解分析不透，从而错列力矩平衡方程.解题方法与技巧：（1）取棒为研究对象.选绞链处为固定转动轴，除转动轴对棒的作用力外，棒的受力情况如图3-4所示，由力矩平衡条件知：F N 1Lc os θ=mg2L c os θF N 1=21mg图3-1 图3-2图3-3（2）小车向左运动，棒另外受到一个水平向左的摩擦力F 1作用，受力如图3-5所示，则有2N F Lc os θ=mg 2L cos θ+μ2N F L sin θ 所以2N F =)tan 1(2θμ-m g ,则2N F ＞1N F （3）小车向右运动时，棒受到向右的摩擦力F 2作用，受力如图3-6所示，有 3N F L cos θ+μ3N F L sin θ=mg2L cos θ 解得3N F =)tan 1(2θμ+mg 所以3N F ＜1N F 本题的关键点是取棒作为研究对象，由于车有不同的运动方向，故棒所受摩擦力的方向也不同，从而导致弹力的不同.［例2］（★★★★★）（2002年上海卷）如图3-7所示，一自行车上连接脚踏板的连杆长R 1，由脚踏板带动半径为r 1的大齿盘，通过链条与半径为r 2的后轮齿盘连接，带动半径为R 2的后轮转动.图3—7（1）设自行车在水平路面上匀速行进时，受到的平均阻力为f ，人蹬脚踏板的平均作用力为F ，链条中的张力为T ，地面对后轮的静摩擦力为f s .通过观察，写出传动系统中有几个转动轴，分别写出对应的力矩平衡表达式；（2）设R 1=20 cm ，R 2=33 cm ，脚踏大齿盘与后轮齿盘的齿数分别为48和24，计算人蹬脚踏板的平均作用力与平均阻力之比；（3）自行车传动系统可简化为一个等效杠杆.以R 1为一力臂，在框中画出这一杠杆示意图，标出支点，力臂尺寸和作用力方向.图3—6命题意图：以生活中的自行车为背景，设立情景，考查运用力矩、力矩平衡条件解决实际问题的能力，尤其是构建物理模型的抽象、概括能力.B 级要求.错解分析：（1）尽管自行车是一种常见的交通工具，但多数考生缺少抽象概括的能力，无法构建传动系统简化的杠杆模型.（2）不能再现自行车的工作过程，无法将r 1/r 2之比与两个齿盘的齿数之比加以联系，导致中途解题受阻.解题方法与技巧：（1）自行车传动系统中的转动轴个数为2，设脚踏齿轮、后轮齿轮半径分别为r 1、r 2，链条中拉力为T .对脚踏齿盘中心的转动轴可列出：FR 1=Tr 1 对后轮的转动轴可列出：Tr 2=f s R 2（2）由FR 1=Tr 1,Tr 2=f s R 2 及f s =f （平均阻力）可得24482121==r r R f FR s 所以1033202433481221=⨯⨯==R r R r f F =3.3 （3）如图3-8所示图3-8●锦囊妙计一、高考走势随着中学新课程方案推广与实施，“有固定转动轴物体的平衡”以其在现实生活中应用的广泛性，再次被列为高考命题考查的重要内容之一.近几年高考上海卷及2002年全国综合卷的命题实践充分证明了这一点.可以预言：以本知识点为背景的高考命题仍将再现.二、物体平衡条件实际上一个物体的平衡，应同时满足F 合=0和M 合=0.共点力作用下的物体如果满足 F 合=0，同时也就满足了M 合=0，达到了平衡状态；而转动的物体只满足M 合=0就不一定能达到平衡状态，还应同时满足F 合=0方可.三、有固定转动轴物体平衡问题解题步骤1.明确研究对象，即明确绕固定转动轴转动的是哪一个物体.2.分析研究对象所受力的大小和方向，并画出力的示意图.3.依题意选取转动轴，并找出各个力对转动轴的力臂，力矩的大小和方向.4.根据平衡条件（使物体顺时针方向转动的力矩之和等于使物体逆时针方向转动的力矩之和）列方程，并求解.●歼灭难点训练1.（★★★）（1992年全国，25）如图3-9所示，AO是质量为m 的均匀细杆，可绕O 轴在竖直平面内自由转动.细杆上的P 点与放在水平桌面上的圆柱体接触，圆柱体靠在竖直的挡板上而保持平衡.已知杆的倾角为θ，AP 长度是杆长的41，各处的摩擦都不计，则挡板对圆柱体的作用力等于____________.2.（★★★★）一根木料长5.65 m ，把它左端支在地上，竖直向上抬起它的右端时，用力480 N ，用相似的方法抬起它的左端时，用力650 N ，该木料重___________N.3.（★★★★）如图3-10所示，两个等重等长质料均匀直棒AC 和BC ，其各自一端分别通过转轴与墙壁绞结，其另一端相连于C 点，AC 棒与竖直墙夹角为45°，BC 棒水平放置，当两棒均处于平衡状态时，则BC 棒对AC 棒作用力方向可能处于哪一区域A.甲区域B.乙区域C.丙区域D.丁区域 4.（★★★★）如图3-11所示，长为l 的均匀横杆BC 重为100 N ，B 端用铰链与竖直的板MN 连接，在离B 点54l 处悬吊一重为50 N 的重物测出细绳AC 上的拉力为150 N ，现将板MN 在△ABC 所在平面内沿顺时针方向倾斜30°，这时AC绳对MN 板的拉力是多少？图3-9 图3-10图3-115.（★★★★★）如图3-12所示，均匀木板AB 长12 m ，重200 N ，在距A 端3 m 处有一固定转动轴O ，B 端被绳拴住，绳与AB 的夹角为30°，板AB 水平.已知绳能承受的最大拉力为200 N ，那么重为600 N 的人在该板上安全行走，离A 端的距离应在什么范围？6.（★★★★★）如图3-13所示，梯与墙之间的摩擦因数为μ1，梯与地之间的摩擦因数为μ2，梯子重心在中央，梯长为L .当梯子靠在墙上而不倾倒时，梯与地面的最小夹角θ由下式决定：tan θ=22121μμμ-，试证之.图13—3图3-12参考答案：［难点磁场］1.9mg /4L 2.A［歼灭难点训练］1.31mg sin2θ 2.1130 3.D 4.130 N 5.作出AB 板的受力图3′-1人在O 轴左端x 处，绳子拉直拉力为零.由力矩平衡可得：G 人×x -G ×CO =0x =人G CO G ⨯=6003200⨯=1 m.即离A 端2 m 处. 人在O 轴右端y 处，绳子的拉力T =200 N ，由力矩平衡得：T sin30°×BO -G 人y -G ×CO =0.y =6003200921200sin30人⨯-⨯⨯=⨯-⨯G CO G BO T =0.5 m 即离A 端3.5 m.所以人在板上安全行走距A 端的距离范围为2 m ≤x ≤3.5 m6.略图3′—1。

高中物理奥林匹克竞赛专题力矩刚体定轴转动定律 (共15张PPT)

解：以转台和二人为研究对象，所受外力只有重
力及轴的支撑力，诸力对转轴的合力矩为零，所
以系统角动量守恒．各转动惯量分别为
J 1 m R2 ，2
JA
1 mR2 2
JB
1mR/22
2
以，地面为参照系，A处的人走动的角速度为
＋(v / R)，B处的人走动的角速度为
(2v1R)-(4v/R)
2
由角动量守恒定律
0
0
mg x k x 2
0 .2
2
J
2
4
0
2
12 .6 故： v R 1 .26 m / s
3、质量为M的匀质圆盘，可绕通过盘中心垂直于盘的固定光滑轴转动，转动惯量为Mr2/2，绕过盘的边缘挂有质量为m，长为l的匀质柔软绳索（如图）．设绳与圆盘无相对滑动，试求当圆盘两侧绳长之差为S时，绳的加速度的大小．
大小： M z F2rsin F 2 d
方向：
M
方向:
z
OZ
3、总力矩的大小= 所有外力力矩的代数和
M
正方向的规定：促进转动的力矩为正
z
1
§3-3 力矩刚体定轴转动定律
二、定轴转动定律
F=mam d v
dt
dp
F=
dt
牛二
类比法
M z J
J
dw dt
已知： m i : p 点质量
M
z
dL dt
r
M
a
S
解：选坐标如图所示，任一时刻圆盘两侧的绳长
分别为x1、x2 选长度为x1、x2的两段绳和绕着绳的盘为研究对象．设a为绳的加速度，β为盘的
角加速度，r为盘的半径，为绳的线密度，且在

高考物理力矩和力矩平衡专题训练

力矩和力矩平衡一．内容黄金组.1．了解转动平衡的概念，理解力臂和力矩的概念。

2．理解有固定转动轴物体平衡的条件 3．会用力矩平衡条件分析问题和解决问题二．要点大揭秘1．转动平衡：有转动轴的物体在力的作用下，处于静止或匀速转动状态。

明确转轴很重要：大多数情况下物体的转轴是容易明确的，但在有的情况下则需要自己来确定转轴的位置。

如：一根长木棒置于水平地面上，它的两个端点为AB ，现给B 端加一个竖直向上的外力使杆刚好离开地面，求力F 的大小。

在这一问题中，过A 点垂直于杆的水平直线是杆的转轴。

象这样，在解决问题之前，首先要通过分析来确定转轴的问题很多，只有明确转轴，才能计算力矩，进而利用力矩平衡条件。

2．力矩：力臂：转动轴到力的作用线的垂直距离。

力矩：力和力臂的乘积。

计算公式：M ＝FL 单位： Nm 效果：可以使物体转动（1）力对物体的转动效果力使物体转动的效果不仅跟力的大小有关，还跟力臂有关，即力对物体的转动效果决定于力矩。

①当臂等于零时，不论作用力多么大，对物体都不会产生转动作用。

②当作用力与转动轴平行时，不会对物体产生转动作用，计算力矩，关键是找力臂。

需注意力臂是转动轴到力的作用线的距离，而不是转动轴到力的作用点的距离。

（2）大小一定的力有最大力矩的条件： ①力作用在离转动轴最远的点上；②力的方向垂直于力作用点与转轴的连线。

（3）力矩的计算：①先求出力的力臂，再由定义求力矩M ＝FL如图中，力F 的力臂为L F =Lsin θ力矩M ＝F •L sin θ②先把力沿平行于杆和垂直于杆的两个方向分解，平行于杆的分力对杆无转动效果，力矩为零；平行于杆的分力的力矩为该分力的大小与杆长的乘积。

如图中，力F 的力矩就等于其分力F 1产生的力矩，M＝F sin θ•L两种方法不同，但求出的结果是一样的，对具体的问题选择恰当的方法会简化解题过程。

3．力矩平衡条件：力矩的代数和为零或所有使物体向顺时针方向转动的力矩之和等于所有使物体向逆时针方向转动的力矩之和。

物理竞赛讲义(三)力矩、定轴转动物体的平衡条件、重心

郑梁梅高级中学高一物理竞赛辅导讲义第三讲：力矩、定轴转动物体的平衡条件、重心【知识要点】（一）力臂：从转动轴到力的作用线的垂直距离叫力臂。

（二）力矩：力和力臂的乘积叫力对转动轴的力矩。

记为M=FL ，单位“牛·米”。

一般规定逆时针方向转动为正方向，顺时针方向转动为负方向。

（三）有固定转轴物体的平衡条件作用在物体上各力对转轴的力矩的代数和为零或逆时针方向力矩总是与顺时针方向力矩相等。

即ΣM=0，或ΣM 逆=ΣM 顺。

（四）重心：物体所受重力的作用点叫重心。

计算重心位置的方法：1、同向平行力的合成法：各分力对合力作用点合力矩为零，则合力作用点为重心。

2、割补法：把几何形状不规则的质量分布均匀的物体分割或填补成形状规则的物体，再由同向（或反向）平行力合成法求重心位置。

3、公式法：如图所示，在平面直角坐标系中，质量为m 1和m 2的A 、B 两质点坐标分别为A （x 1，y 1），B （x 2，y 2）则由两物体共同组成的整体的重心坐标为： 212211m m x m x m x C ++= 212211m m y m y m y C ++= 一般情况下，较复杂集合体，可看成由多个质点组成的质点系，其重心C 位置由如下公式求得：i i i C m x m x ∑∑= i i i C m y m y ∑∑= ii i C m z m z ∑∑= 本节内容常用方法有：①巧选转轴简化方程：选择未知量多，又不需求解结果的力线交点为轴，这些力的力矩为零，式子简化得多；②复杂的物体系平衡问题有时巧选对象：选整体分析，常常转化为力矩平衡问题求解；③无规则形状的物体重心位置计算常用方法是通过割补思想，结合平行力合成与分解的原则处理，或者助物体重心公式计算。

【典型例题】【例题1】如图所示，光滑圆弧形环上套有两个质量不同的小球A 和B 两球之间连有弹簧，平衡时圆心O 与球所在位置的连线与竖直方向的夹角分别为α和β，求两球质量之比。

力矩和定轴转动平衡+答案xs

高二物理【11】力矩定轴转动物体的平衡2012．61．力矩(1)力臂：转动轴到力的作用线的垂直距离叫力臂。

其最大可能值为力到转动轴的距离。

M ，单位：N·m。

在中学里只研究固定转动轴物体的平衡，所以力矩只(2)力矩：FL有顺时针和逆时针两种方向。

2．力矩计算中的两种等效转化（1）在计算某个力的力矩时，若将此力的作用点与转轴连起来，常可将此力分解为沿连线方向的和垂直于连线方向的两个分力，沿此连线方向的分力没有力矩，因而就转化为求垂直于此连线方向的分力的力矩了。

(2)在计算某物体重力的力矩时，可把物体看成一个整体，受到一个总重力，作用在其总重心；也可以把物体分成几块，每一块所受重力都作用在该块的重心上，然后计算这些重力的力矩和。

两种方法的结果是一致的。

3．定轴转动物体的平衡条件物体处于静止或匀速转动状态时称为力矩平衡状态。

物体所受合外力矩为零。

也可以表述为顺时针力矩之和等于逆时针力矩之和。

4．力矩最大的条件大小一定的力，其力矩最大的条件是：①力作用在离转动轴最远的点上；②力的方向垂直于力的作用点和转动轴的连线。

一、力臂和力矩1．如图所示，T字形架子A BO可绕过O点且垂直于纸面的转动轴自由转动．现在其A 端与B端分别施以图示方向的力F1、和F2，则关于F1和F2的力矩M1和M2，下列说法中正确的是( )A．都是顺时针的B．都是逆时针的C．M1是顺时针的．M2是逆时针的D．M1是逆时针的．M2是顺时针的2．如图甲、乙所示，相同的两球分别固定在相同的轻杆的一端，另一端用光滑铰链分别铰于墙面(如图甲所示)和地面(如图乙所示)。

球都搁在一粗糙的长木板上，木板放在水平地面上。

若用相同的力F分别将木板向右拉动。

那么板对球的摩擦力的力距方向各如何？二、有固定转动轴物体的平衡3．如图所示，用单位长度质量为ρ的材料制成的长方形框架A BCD ，已知AB =a ，BC =ｂ，可绕过AB 边的水平轴自由转动．现在CD 边的中点施加一个水平力F ，为使框架静止时与竖直方向成α角，则力F 的大小应为 ( )A ．ρg (a ＋b )tgα．B ．ρg (a +b )ctgα．C ．ρg （a ＋2b ）tgα/2．D ．ρg （a ＋2b ）ctgα4．如图所示，重为G 的L 形匀质杆的一端O 点通过铰链与墙连接，另一端B 点作用着一个力F ，当F 与水平面成α＝45o 角时，杆OA 边呈水平而平衡。

高三物理总复习(考点解读+教学归纳+分类解析)第二章第9讲力矩有固定转动轴物体的平衡

力矩有固定转动轴物体的平衡考点解读考点解读学习水平题目分布力矩理解力矩的定义，会求力矩 B有固定转动轴的物体的平衡理解有固定转动轴的物体的平衡条件会用力矩平衡条件解有固定转动轴物体的平衡问题BC09年上海高考第23题12年上海高考第14题教学目标1．知道力矩的定义，会求力矩．2．会求有固定转轴物体的平衡问题．教师归纳1．力矩(1)力臂：从转动轴到力的作用线(不是作用点)的垂直距离．(2)力矩：力F和力臂L的乘积叫作力对转动轴的力矩M，即M＝FL，力矩的单位是N·m.2．物体的平衡态(1)物体保持静止或匀速直线运动状态．(2)物体绕固定转动轴匀速转动．3．有固定转动轴的物体的平衡条件：物体所受外力的力矩的代数和为零，即∑M＝0(或顺时针力矩之和等于逆时针力矩之和，即M顺＝M逆)．分类剖析(一)例1如图所示，直杆可绕过点的水平轴自由转动，图中虚线与杆平行，杆的另一端A点受到四个力F1、F2、F3、F4的作用，力的作用线与OA杆在同一竖直平面内，它们对转轴O的力矩分别为M1、M2、M3、M4，则它们间的大小关系是( )A．M1＝M2＞M3＝M4B．M2＞M1＝M3＞M4C．M4＞M2＞M3＞M1D ．M 2＞M 1＞M 3＞M 4【解析】将各力分解成沿杆方向和垂直于杆方向的两个力，只比较后者的力矩即可，选B.(二) 力矩平衡简单应用例2如图(1)所示，均匀杆AC 长2 m ，重10 N ，在竖直平面内，A 端有水平固定转动轴，C 端挂一重70 N 的重物，水平细绳BD 系在杆上B 点，且AB ＝3AC /4.要使绳BD 的拉力是100N ，则∠ABD ＝________；要使BD 绳的拉力最小，且B 点位置不变，改变BD 的长度，则需BD 与AC 呈________状态．(1)(2)【解析】取AC 杆为研究对象，以A 为转轴，对AC 杆产生转动作用的力是AC 杆的重力G 0、BD 绳的拉力T 、竖直向下的细绳的拉力F ，F 在数值上等于重力G ；再由力矩的平衡条件∑M ＝0求解．对AC 受力分析如图(2)所示，由力矩的平衡条件G 0·12AC ·cos α＋F ·AC ·cos α＝ T ·AB ·sin α10·12·2·cos α＋70·2·cos α＝100·34·2·sin α∴tan α＝1，α＝∠ABD ＝45°因为重力的力矩、竖直向下的细绳拉力的力矩为一定值，若要使BD .例3B 处，可以使重锤升高，放开脚重锤落下打击稻谷．若脚用力方向始终竖直向下且转动保持平衡状态，则在重锤升起过程中，脚踩B 端向下的力F 和力矩M 将( )A ．F 增大，M 增大B ．F 先增大后减小，M 不变C ．F 不变，M 先增大后减小D ．F 不变，M 先减小后增大【解析】以O 为轴，以舂米杠杆为研究对象，在重锤自下向上升起的过程中，重锤的力臂是先增大后减小，所以重锤的力矩先增大后减小．同时脚的力臂也是先增大后减小的，所以根据力矩的平衡条件，设杆与水平方向夹角为α，有mg ·AO ·cos α＝F ·BO ·cos α∴F ＝AO BOmg无论杆在何位置F 的大小始终不变．M F ＝mgAO cos α，M F 先增大后减小，所以正确答案选C.(三)例4r 的一半，如图(1)所示(图为横截面)，柱体与台阶接触处图中P 点，要在图中柱体的最上方A 处施加一最小的力，使柱体刚能以P 为轴向台阶上滚(g 取10m/s 2)．求： (1)所加力的大小；(2)台阶对柱体的作用力的大小．(1) (2)【解析】 (1)以P 点为轴，欲在A 处施最小的力，必须使这个力的力臂最长，那么该力的方向应垂直于PA ，如图(2)所示．要使柱体刚能以P 为轴向台阶上滚，即意味着此时地面对柱体的支持力恰好为零．这样由作用力F 与重力mg 对P 点的力矩平衡可得mg ·BP ＝F ·AP 由几何关系得∠POB ＝60°，∠PAO ＝30°所以BP ＝r sin60°，AP ＝2r cos30°，解得F ＝250N.(2)柱体刚能以P 为轴向台阶上滚时，它受到在同一平面内三个非平行力的作用，即重力mg ，作用在A 点的外力F 和台阶P 点对柱体的作用力T .三力平衡必共点，据此可延长重力作用线与F 交于A 点，那么台阶对柱体的作用力T 的延长线必定通过A 点，即T 的方向垂直于F 的方向，所以T 的大小必等于重力在AP 上的分力，因此有T ＝mg cos30°＝433N.【点评】 T 是台阶P 点对柱体的作用力，其指向球心的分力即为对柱体的支持力，而沿P 点切线方向的分力则为对柱体的摩擦力．显然，对于光滑的接触点，是无法用此题给出例5＝37°；在A 、B 两顶角处各固定一个大小不计的小球，质量均为1kg.支架可绕过O 的水平轴在竖直平面内无摩擦地转动．(sin37°＝0．6，cos37°＝0.8，重力加速度g 取10m/s 2)(1)为使支架静止时AB 边水平，求在支架上施加的最小力； (2)若将支架从AB 位于水平位置开始由静止释放，求支架转动过程中A 处小球速度的最大值．【解析】施加的最小力满足的条件是：力臂最大，所以该力的作用点在A 点，方向垂直OA 向上 mg ·OA ·cos37°＝mg ·OB ·cos53°＋F min ·OA OA ＝0.16m ，OB ＝0.12m ，可解得F min ＝3.5N.(2)如图(1)(2)当支架到达平衡位置时，A 球的速度最大，根据杠杆原理，此时A 、B 距O 点垂线的距离相等，如图(2)所示，AE ＝BD ＝AB sin37°cos37°＝0.096mCD ＝CE ＝AC 2－AE 2＝0.028m OF ＝AB sin37°cos37°＝AE h 1＝OE －OF ＝0.032m h 2＝OF －OD ＝0.024mmg (h 1－h 2)＝12mv 2＋12m (v ·tan37°)2 v ＝0.32m/s.例6质量M ＝2.0kg 的小铁块静止于水平轨道的端．导轨及支架形状及尺寸如图所示，质量m ＝4.0kg.它只能绕通过支架D 点垂直于纸面水平转动，其中心在图中的O 点，现有一细线沿导轨拉小铁块，拉力F ＝12N ，小铁块和导轨之间的动摩擦因数μ＝0.50.从小铁块运动时起，导轨(及支架)能保持静止的最长时间是多少？(g 取10m/s 2)【解析】当导轨刚要不能维持平衡时，C 端受的力为零，此时导轨(及支架)受四个力作用：滑块对导轨的压力F N ＝Mg ，竖直向下，滑块对导轨的摩擦力F f ＝μMg ＝10N ，重力G ＝mg ，作用在O 点，方向竖直向下，作用于轴D 端的力．设此时的铁块走过的路程S ，根据有固定转动轴物体平衡条件及图中尺寸，有： mg ×0.1＋Mg (0.7－s )＝F f ×0.8＝μMg ×0.8 40×0.1＋20(0.7－s )＝10×0.8 s ＝0.5m铁块受的摩擦力F f ＝10N ，方向向右． F －F f ＝Ma a ＝1.0m/s 2∵s ＝1/2at 2∴t ＝1.0s【点评】此题是一道典型的力学综合题，考查面较广，从静力学，运动学到动力学，由于质量为m 的铁块和T 形支架不具有相同的运动状态，故必须采用隔离法．本章小结知识网络力⎩⎪⎪⎪⎨⎪⎪⎪⎧概念⎩⎪⎨⎪⎧定义：力是物体对物体的作用，不能离开施力物体与受力物体而存在效果⎩⎪⎨⎪⎧使物体发生形变改变物体运动状态要素：大小、方向、作用点（力的图示）分类⎩⎪⎨⎪⎧效果：拉力、动力、阻力、支持力、压力性质⎩⎪⎨⎪⎧重力：方向、作用点（关于重心的位置）弹力：产生条件、方向、大小（胡克定律）摩擦力：（静摩擦与动摩擦）产生条件、方向、大小运算——平行四边形定则⎩⎪⎨⎪⎧力的合成力的分解 |F 1－F 2|≤F 合≤F 1＋F 2物体平衡⎩⎪⎨⎪⎧共点力作用下物体平衡有固定转动轴物体平衡考题解析考题1 如图所示，用两根细线把A 、B 两小球悬挂在天花板上的同一点O ，并用第三根细线连接A 、B 两小球，然后用某个力F 作用在小球A 上，使三根细线均处于直线状态，且OB 细线恰好沿竖直方向，两小球均处于静止状态，则该力可能为图中的( )A．F1 B．F2C．F3 D．F4【解析】本题考查平衡物体的受力情况分析，属于基础知识．A、B两个小球用细线连接，且整个系统处在静止状态，在所提供的四个力中，能使系统保持静止的只能是F2和F3而不能是F1和F4，这是因为，若取F1，则F1可分解为水平向右和竖直向下两个分力，向下的分力将使A球向下运动，破坏了系统保持静止的前提；同样若取F4，则F4可分解为竖直向上和水平向左两个分力，向左的分力将使A球向左运动，且B 球不再在竖直位置上．答案为选项B、C.考题2 对如图所示的皮带传动装置，下列说法中正确的是( )A．A轮带动B轮沿逆时针方向旋转B．B轮带动A轮沿逆时针方向旋转C．C轮带动D轮沿顺时针方向旋转D．D轮带动C轮沿顺时针方向旋转【解析】本题主要考查考生灵活运用知识分析具体问题的能力．虽然涉及摩擦力概念，但重要的是如何运用摩擦力的概念分析与平常习题不同情境的问题．根据题目中呈示的图片，分别研究皮带绷紧的最高部分，结合摩擦力的概念，可以判断B、D为正确选项．考题3 如图所示，在竖直平面内的直角坐标系中，一个质量为m的质点在外力F的作用下，从坐标原点O由静止沿直线ON斜向下运动，直线ON与y轴负方向成θ角(θ＜π/4)．则F大小至少为__________；若F＝mg tanθ，则质点机械能大小的变化情况是______________________________．【解析】考题考查力的最小值．该质点受到重力和外力F从静止开始做直线运动，说明质点做匀加速直线运动，如图中显示，当F力的方向为a方向(垂直于ON)时，F力最小为mg sinθ；若F＝mg tanθ，即F力可能为b方向或c方向，故F力的方向可能与运动方向相同，也可能与运动方向相反，除重力外的F力对质点做正功，也可能做负功，故质点机械能增加、减少都有可能．考题4 如图所示，一根木棒AB 在O 点被悬挂起来，AO ＝OC ，在A 、C两点分别挂有两个和三个钩码，木棒处于平衡状态．如在木棒的A 、C 点各增加一个同样的钩码，则木棒DA ．绕O 点顺时针方向转动B ．绕O 点逆时针方向转动C ．平衡可能被破坏，转动方向不定D ．仍能保持平衡状态【解析】设木板AO 段重力G 1，重心离O 点L 1，木板BO 段重力G 2，重心离O 点L 2，AO 长度l ，由力矩平衡条件：G 1L 1＋2Gl ＝ G 2L 2＋3Gl ，当两边各挂一个钩码后，等式依然成立：G 1L 1＋3Gl ＝ G 2L 2＋4Gl ，即只要两边所增加挂钩码个数相同，依然能平衡．故选D. 考题5 如图所示，半径分别为r 和2r 的两个质量不计的圆盘，共轴固定连结在一起，可以绕水平轴O 无摩擦转动，大圆盘的边缘上固定有一个质量为m 的质点，小圆盘上绕有细绳．开始时圆盘静止，质点处在水平轴O 的正下方位置．现以水平恒力F 拉细绳，使两圆盘转动，若恒力 F ＝mg ，两圆盘转过的角度θ＝________时，质点m 的速度最大．若圆盘转过的最大角度θ＝π/3，则此时恒力F ＝________.【解析】此题若用函数极值法，由动能定理有：12mv 2＝Frθ－mg (2r －2r cos θ)，可得v ＝2gr （θ＋2cos θ－2），然后求极值，很难求．换用力矩平衡条件，对盘、质点整体，以O 为轴，当Fr ＝mg 2r sin θ时，转速最大即质点速度最大，得sin θ＝12，所以有θ＝π6.当圆盘转过最大角度θ＝π3时，由动能定理有Fr π3－2mgr (1－cos π3)＝0，可得F ＝3mg π.。

高考物理必考难点总结归纳

高考物理必考难点总结归纳在高考物理考试中，总有一些内容被视为难点，让考生感到头疼。

针对这些难点，本文将对高考物理必考的一些难点进行总结归纳，帮助考生更好地应对物理考试。

一、力学部分1. 动能定理：动能定理是解决物体的动能与其速度、质量以及作用力关系的重要定律。

根据动能定理，当一个物体受到合外力作用时，它的动能会发生改变。

2. 动量守恒定律：动量守恒定律是解决碰撞问题的基础，它表明一个孤立系统内的总动量守恒。

在碰撞问题中，可以利用动量守恒定律求解物体的速度和碰撞后的动量变化。

3. 牛顿定律：牛顿定律是解决力与物体运动之间关系的基本定律。

特别地，牛顿第一定律描述了物体在没有受到外力作用时的运动状态，牛顿第二定律描述了物体的加速度与受力的关系，牛顿第三定律描述了相互作用力的平衡。

二、电磁部分1. 安培定律：安培定律是解决电流与磁场之间关系的重要定律。

根据安培定律，电流会产生磁场，而磁场会对电流产生力的作用。

2. 法拉第电磁感应定律：法拉第电磁感应定律是解决电磁感应现象的基本定律。

根据法拉第电磁感应定律，当磁通量发生变化时，会在电路中产生感应电动势，从而引起电流的产生。

3. 麦克斯韦方程组：麦克斯韦方程组是数学表达电磁场理论的一组基础方程。

其中包括电场与电荷之间的关系、磁场与电流之间的关系以及电场和磁场相互之间的关系。

三、光学部分1. 光的折射定律：光的折射定律是解决光在介质中传播时的偏折问题的基本定律。

根据折射定律，光线从一种介质传播到另一种介质时，会发生折射现象。

2. 球面反射与球面折射：球面反射与球面折射是解决球面镜成像问题和透镜成像问题的关键。

在球面反射中，光线通过反射在球面上形成像；在球面折射中，光线通过折射在球面上形成像。

3. 构成光的颜色的现象：光的颜色是由光的频率决定的。

在光的颜色的现象中，包括色散现象、衍射现象和干涉现象等，这些现象都是基于光的波动性进行解释的。

综上所述，高考物理中的必考难点主要集中在力学、电磁和光学等部分。

高中物理经典高考难题集锦(解析版)

高中物理经典高考难题集锦(解析版)本文档收集了高中物理经典的高考难题，同时提供了详细的解析，帮助学生提高解题能力和应对高考。

题目一题目描述：一个小球自动上坡，它的重力做功与摩擦力做的功之和等于零。

求小球的加速度是多少？解析：我们知道，重力做功与摩擦力做的功之和等于零，说明小球的动能没有增加，也没有减少。

因此，小球的加速度为零，即小球保持匀速上坡。

题目二题目描述：一辆汽车以20 m/s的速度行驶，在制动的过程中，制动力为3500 N，制动距离为50 m。

汽车的质量是多少？解析：根据牛顿第二定律，制动力等于质量乘以加速度。

由于速度从20 m/s减小到零，汽车在制动过程中减速度为20 m/s。

将制动力和减速度代入公式可得：3500 = 质量 × (-20)解得质量为175 kg。

题目三题目描述：一根绳子贴在重力平衡两边的墙壁上，绳子的长度为5 m。

如果绳子的线密度为0.1 kg/m，那么绳子的质量是多少？解析：绳子的质量可以通过线密度乘以长度来计算。

将线密度0.1 kg/m和长度5 m代入计算公式可得：质量 = 0.1 × 5 = 0.5 kg。

题目四题目描述：一枚小球从高度为20 m的位置自由下落，求小球下落2秒后的速度是多少？解析：小球自由下落的加速度为9.8 m/s^2，根据速度与时间的关系公式v = u + at，将初始速度u设为0，加速度a设为9.8 m/s^2，时间t设为2 s，代入公式可得：v = 0 + 9.8 × 2 = 19.6 m/s。

题目五题目描述：一台电梯上行，在上升过程中，电梯门意外打开，此时电梯的加速度是多少？解析：电梯上行时，会受到重力的阻力。

当电梯上升过程中，电梯门打开，意味着接触到外界空气，会受到空气阻力。

所以此时电梯的加速度受到重力和空气阻力的共同作用，而具体数值需要具体情况具体分析。

以上是部分高中物理经典的高考难题及其解析，希望对学生们的物理学习有所帮助。

高中物理：第二章力矩有固定转动轴物体的平衡

第二章力矩有固定转动轴物体的平衡本章学习提要1．理解力矩概念和定义，会运用力臂和力矩的定义计算力矩。

2．会利用力矩盘进行实验，探究有固定转动轴的物体的平衡条件。

3．理解有固定转动轴的物体的平衡，知道有固定转动轴的物体的“力矩平衡条件”，能运用力矩平衡条件求解有关问题，解释生活和生产中的实际问题。

本章内容从基础型物理课程中的质点问题（质点受力、共点力平衡条件）拓展到刚体问题（力矩、力矩平衡条件）。

在日常生活和生产中所见到的物体的运动，以及分子、原子这样的微观粒子和宇宙天体的运动都包括转动，因此关于力矩和力矩平衡条件的讨论具有普遍意义。

认识怎样根据实际需要引进力矩，以及力矩的定义方法和它的物理意义。

通过力矩和力矩平衡条件的学习和应用，体会物理学与技术、社会的联系，了解运用力矩平衡条件设计出各类工具，以及千姿百态、风格迥异的各种桥梁和大型建筑，领略科学美。

A 力矩一、学习要求理解力臂和力矩概念，会用力臂和力矩的定义计算力矩。

从实际例子的分析中，明白引进力矩的必要性；认识力矩的定义方法以及力矩的物理意义。

通过从实际需要中引进力矩概念，了解力矩概念与常用工具和生活、生产的联系，体会物理学与实际的密切关系。

二、要点辨析1．为什么要引进力矩力对质点运动的作用效果取决于它的大小和方向。

而力对物体转动的作用效果不仅与力的大小和方向有关，还与力的作用点的位置有关，为了描写力的大小、方向和作用点对物体转动的作用效果，需要引进力矩这个物理量。

力臂：力的作用线与转动轴之间的距离称为力臂。

力矩：力（F）和力臂（L）的乘积称为力对转动轴的力矩。

2．关于力的作用线与转动轴的距离力的作用线是力的方向上的一条假想的直线。

力的作用线与转动轴的距离实际上涉及到两条线之间的距离。

一般情况下确定空间中任意两条直线间的距离比较麻烦。

我们所讨论的仅限于力的作用线都在同一个与转动轴相垂直的平面内，若该平面与转动轴的交点称为O，那么我们需考虑的空间中两条直线（力的作用线与转动轴线）间距离的问题便简化为一个点（O点）与一条直线（力的作用线）间距离的问题。

高考物理练习题库4(力矩有固定转动轴物体的平衡)

高考物理练习题库4(力矩有固定转动轴物体的平衡)1.如图所示，轻杆BC 的C 端铰接于墙，B 点用绳子拉紧，在BC 中点O挂重物G .当以C 为转轴时，绳子拉力的力臂是( ).【0.5】(A )OB (B )BC (C )AC (D )CE答案:D2.关于力矩，下列说法中正确的是( ).【1】(A )力对物体的转动作用决定于力矩的大小和方向(B )力矩等于零时，力对物体不产生转动作用(C )力矩等于零时，力对物体也可以产生转动作用(D )力矩的单位是“牛·米”，也可以写成“焦”答案:AB3.有固定转动轴物体的平衡条件是______.【0.5】答案:力矩的代数和为零4.有大小为F 1=4N 和F 2=3N 的两个力，其作用点距轴O 的距离分别为L 1=30cm 和L 2=40cm ，则这两个力对转轴O 的力矩M 1和M 2的大小关系为( ).【1.5】(A )因为F 1>F 2，所以M 1>M 2 (B )因为F 1<F 2，所以M 1<M 2(C )因为F 1L 1=F 2L 2，所以M 1=M 2 (D )无法判断M 1和M 2的大小答案:D5.火车车轮的边缘和制动片之间的摩擦力是5000N .如果车轮的半径是0.45m ，求摩擦力的力矩.【2】答案:2.25×103N ·m6.如图所示是一根弯成直角的杆，它可绕O 点转动.杆的OA 段长30cm ，AB 段长40cm .现用F =10N 的力作用在杆上，要使力F 对轴O 逆时针方向的力矩最大，F 应怎样作用在杆上?画出示意图，并求出力F 的最大力矩.【2.5】答案:图略，5N ·m7.如图所示是单臂斜拉桥的示意图，均匀桥板aO 重为G ，三根平行钢索与桥面成30°角，间距ab =bc =cd =dO .若每根钢索受力相同，左侧桥墩对桥板无作用力，则每根钢索的拉力大小是( ).【3】(A )G (B )6G 3 (C )3G (D )32G 答案:D8.右图为人手臂骨骼与肌肉的生理结构示意图，手上托着重为G 的物体.(1)在虚线框中画出前臂受力的示意图(手、手腕、尺骨和挠骨看成一个整体，所受重力不计，图中O 点看作固定转动轴，O 点受力可以不画).(2)根据图中标尺估算出二头肌此时的收缩力约为___________.(2000年上海高考试题)【5】答案:(1)图略(2)8G9.如图所示，直杆OA 可绕O 轴转动，图中虚线与杆平行.杆的A 端分别受到F 1、F 2、F 3、F4四个力的作用，它们与OA 杆在同一竖直平面内，则它们对O点的力矩M 1、M 2、M 3、M 4的大小关系是( ).【4】(A )M 1=M 2>M 3=M 4(B )M 1>M 2>M 3>M 4 (C )M 1>M 2=M 3>M 4(D )M 1<M 2<M 3<M 4 答案:C10.如图所示的杆秤，O 为提纽，A 为刻度的起点，B 为秤钩，P 为秤砣.关于杆秤的性能，下列说法中正确的是( ).【4】(A )不称物时，秤砣移至A 处，杆秤平衡(B )不称物时，秤砣移至B 处，杆秤平衡(C )称物时，OP 的距离与被测物的质量成正比(D )称物时，AP 的距离与被测物的质量成正比答案:AD11.如图所示，A 、B 是两个完全相同的长方形木块，长为l ，叠放在一起，放在水平桌面上，端面与桌边平行.A 木块放在B 上，右端有4l 伸出，为保证两木块不翻倒，木块B 伸出桌边的长度不能超过().【4】(A )2l (B )83l (C )4l (D )8l 12.如图所示，ABC 为质量均匀的等边直角曲尺，质量为2M ，C 端由铰链与墙相连，摩擦不计.当BC 处于水平静止状态时，施加在A 端的最小作用力的大小为______，方向是______.【4】答案:Mg 423，垂直于CA 的连线斜向上 13.如图所示，将粗细均匀、直径相同的均匀棒A 和B 粘合在一起，并在粘合处用绳悬挂起来，恰好处于水平位置而平衡，如果A 的密度是B 的2倍，那么A 的重力大小是B 的______倍.【5】答案:214.如图所示，一个质量为m 、半径为R 的球，用长为R 的绳悬挂在L 形的直角支架上，支架的重力不计，AB 长为2R ，BC 长为R 32，为使支架不会在水平桌面上绕B 点翻倒，应在A 端至少加多大的力?【6】答案:2mg 15.如图所示，重为600N 的均匀木板搁在相距为2.0m 的两堵竖直墙之间，一个重为800N 的人站在离左墙0.5m 处，求左、右两堵墙对木板的支持力大小.【7】答案:900N ,500N16.棒AB 的一端A 固定于地面，可绕A 点无摩擦地转动，B 端靠在物C 上，物C 靠在光滑的竖直墙上，如图所示.若在C 物上再放上一个小物体，整个装置仍保持平衡，则B 端与C 物之间的弹力大小将( ).【4】(A )变大 (B )变小 (C )不变 (D )无法确定答案:A17.如图所示，质量为m 的运动员站在质量为m 的均匀长板AB 的中点，板位于水平地面上，可绕通过A 点的水平轴无摩擦转动.板的B 端系有轻绳，轻绳的另一端绕过两个定滑轮后，握在运动员的手中.当运动员用力拉绳子时，滑轮两侧的绳子都保持在竖直方向，则要使板的B 端离开地面，运动员作用于绳的最小拉力是______.【5】答案:32mg18.如图所示，半径是0.1m 、重为N 310的均匀小球，放在光滑的竖直墙和长为1m 的光滑木板(不计重力)OA 之间，小板可绕轴O 转动，木板和竖直墙的夹角θ=60°，求墙对球的弹力和水平绳对木板的拉力.【5】答案:10N ,6.92N19.如图所示，均匀杆AB 每米重为30N ，将A 端支起，在离A 端0.2m的C 处挂一重300N 的物体，在B 端施一竖直向上的拉力F ，使杆保持水平方向平衡，问杆长为多少时，所需的拉力F 最小?最小值为多大?【6】答案:2m ,60N20.右图所示是用电动砂轮打磨工件的装置，砂轮的转轴通过图中O 点垂直于纸面，AB 是一长度l =0.60m 、质量m 1=0.50kg 的均匀刚性细杆，可绕过A 端的固定轴在竖直面(图中纸面)内无摩擦地转动，工件C 固定在AB 杆上，其质量m 2=1.5kg ，工件的重心、工件与砂轮的接触点P以及O 点都在过AB 中点的竖直线上，P 到AB 杆的垂直距离d =0.1m ，AB 杆始终处于水平位置，砂轮与工件之间的动摩擦因数μ=0.6.(1)当砂轮静止时，要使工件对砂轮的压力F 0=100N ，则施于B 端竖直向下的力F B 应是多大?(2)当砂轮逆时针转动时，要使工件对砂轮的压力仍为F 0=100N ，则施于B 端竖直向下的力F B ′应是多大?(2000年天津、江西高考试题)p .9【9】答案:(1)40N (2)30N21.两个所受重力大小分别为G A 和G B 的小球A 和B ，用细杆连接起来，放置在光滑的半球形碗内.小球A 、B 与碗的球心O 在同一竖直平面内，如图所示.若碗的半径为R ，细杆的长度为R 2，G A >G B ，则连接两小球的AB 细杆静止时与竖直方向的夹角为多大?【10】答案:4G G arctan A B π+ 22.如图所示，一根重为G 的均匀硬杆AB ，杆的A 端被细绳吊起，在杆的另一端B 作用一水平力F ，把杆拉向右边，整个系统平衡后，细线、杆与竖直方向的夹角分别为α、β求证:tanβ=2tanα.【15】答案:略23.半径为R 、质量为M 1的均匀圆球与一质量为M 2的重物分别用细绳AD 和ACE 悬挂于同一点A ，并处于平衡状态，如图所示.已知悬点A 到球心O 的距离为L ，不考虑绳的质量和绳与球的摩擦，试求悬挂圆球的绳AD 与竖直方向AB 间的夹角θ.(第十届全国中学生物理竞赛预赛试题)【15】答案:LM M (R M arcsin 212）+=θ 24.在一些重型机械和起重设备上，常用双块式电磁制动器，它的简化示意图如图所示，O 1和O 2为固定铰链.在电源接通时，A 杆被往下压，通过铰链C 1、C 2、C 3使弹簧S 被拉伸，制动块B 1、B 2与转动轮D 脱离接触，机械得以正常运转.当电源被切断后，A 杆不再有向下的压力(A 杆及图中所有连杆及制动块所受重力皆忽略不计)，于是弹簧回缩，使制动块产生制动效果.此时O 1C 1和O 2C 2处于竖直位置.已知欲使正在匀速转动的D 轮减速从而实现制动，至少需要M =1100N ·m 的制动力矩，制动块与转动轮之间的摩擦因数μ=0.40，弹簧不发生形变时的长度为L =0.300m ，转动轮直径d =0.400m ，图示尺寸a =0.065m ，h 1=0.245m ，h 2=0.340m ，问选用的弹簧的劲度系数k 最小要多大?(第十三届全国中学生物理竞赛预赛试题)【15】答案:k =1.24×104N /m25.如图所示，在竖直墙上有两根相距为2a 的水平木桩A 和B ，有一细棒置于A 上、B 下与水平方向成θ角，细棒与木桩之间的静摩擦因数为μ，求要使细棒静止，其重心与木桩A 之间距离应满足的条件.【25】答案:重心到木桩之间距离⎪⎩⎪⎨⎧<≥-≥时，当时当μθμθμθμαtan 0tan ),tan (x。

高考物理重点难点100个归纳

高考物理重点难点100个归纳基础篇难点1 运动图像的区别与联系难点2 运动图像的分析与运用难点3 匀变速直线运动规律的灵活选用难点4 追及和相遇问题的分析难点5 自由落体运动和竖直上抛运动的分析难点6 杆上弹力方向的分析难点7 绳上死结和活结问题的分析难点8 摩擦力的分析与计算难点9 对物体进行受力分析的方法难点10 力的矢量三角形的灵活应用难点11 整体法和隔离法在多物体平衡问题中的运用难点12 牛顿第二定律的瞬时问题的分析难点13 与牛顿第二定律相关的临界问题的分析难点14 与超重、失重相关联的问题的分析难点15 牛顿运动定律中的图像问题的分析难点16 整体法和隔离法在连接体类问题中的运用难点17 牛顿运动定律在滑块—滑板类问题中的运用难点18 牛顿运动定律在传送带类问题中的运用难点19 小船渡河类问题的分析与求解难点20 绳或杆相关联物体运动的合成与分解难点21 平抛运动规律的综合应用难点22 圆锥摆模型问题的分析难点23 类圆锥摆模型的分析难点24 轻绳或内轨道模型在竖直平面内圆周运动的临界问题难点25 轻杆或管模型在竖直平面内圆周运动的临界问题难点26 水平面内圆周运动的临界问题难点27 天体质量和密度的估算难点28 卫星稳定运行中线速度v、角速度ω、周期T和加速度a与轨道半径r的关系难点29 卫星的变轨问题难点30 人造卫星和宇宙速度难点31 万有引力定律和其他运动规律的综合应用难点32 双星问题的分析难点33 三星(质量相等)问题的分析难点34 机车启动问题的讨论——以恒定功率启动难点35 机车启动问题的讨论——以恒定加速度启动难点36 变力做功的计算难点37 动能定理在多过程问题中的运用难点38 对机械能守恒定律的理解难点39 对机械能守恒定律的应用难点40 动能定理与机械能守恒定律的比较与运用难点41 对功能关系的理解难点42 传送带模型中的能量问题难点43 碰撞结果可能性问题的分析难点44 动量守恒在子弹打木块模型中的应用难点45 动量守恒在“人船模型”(反冲问题)中的应用难点46 动量守恒在弹簧类问题中的运用难点47 动量守恒在多体多过程问题中的运用电磁学篇难点48 电场线和等势面的特点难点49 对电场性质的理解与应用难点50 带电粒子在匀强电场中做直线运动问题的分析难点51 带电粒子在匀强电场中偏转问题的分析难点52 带电粒子在电场中做其他运动问题的分析难点53 电容器充电后断开电源类问题的分析难点54 电容器充电后始终与电源相连类问题的分析难点55 电路动态问题的分析难点56 与电功、电功率、电热相关的问题的综合分析难点57 含容电路问题的综合分析难点58 伏安特性曲线的理解与运用难点59 安培力作用下导体在磁场中运动问题的分析难点60 安培力作用下通电导体平衡与加速问题的分析难点61 带电粒子在磁场中的运动情况分析难点62 画轨迹、定圆心、求半径、求时间难点63 带电粒子在有界磁场中运动的临界问题难点64 带电粒子在磁场中运动的多解问题分析难点65 带电粒子在含磁场的组合场中运动问题的分析难点66 带电粒子在含磁场的叠加场中运动情况的分析难点67 带电粒子在含磁场的叠加场中运动时粒子重力问题难点68 对楞次定律的理解与应用难点69 对法拉第电磁感应定律的理解与应用难点70 电磁感应中图像问题的分析难点71 电磁感应中电路问题的分析难点72 电磁感应中力学问题的综合分析难点73 交变电流的产生与表达难点74 交流电“四值”的理解及运用难点75 变压器的分析与计算——基本规律难点76 变压器的分析与计算——动态问题分析难点77 输电电路的基本分析难点78 远距离高压输电问题的分析实验篇难点79 秒表的使用与读数难点80 游标卡尺的使用与读数难点81 螺旋测微器的使用与读数难点82 打点计时器的使用难点83 电流表、电压表的使用与读数难点84 多用电表的使用与读数难点85 传感器的简单使用难点86 研究匀变速直线运动难点87 探究弹力与弹簧伸长的关系难点88 验证力的平行四边形定则难点89 验证牛顿运动定律难点90 探究动能定理难点91 验证机械能守恒定律难点92 力学经典演示实验难点93 伏安法测电阻的电路设计难点94 测定金属的电阻率难点95 描绘小电珠的伏安特性曲线难点96 测定电源的电动势和内阻难点97 实验原理的迁移设计难点98 实验方案的创新设计难点99 实验方法的迁移设计难点100 数据处理的迁移设计。

高考物理知识点难题汇总

高考物理知识点难题汇总在高考中，物理一直以来都是学生们的一大难题。

它既需要掌握基本的理论知识，又要善于运用这些知识解决实际问题。

下面，我将梳理一些高考物理知识点中的难题，并分析其中的解题技巧。

一、力学知识点难题1. 如何利用力学原理解决力的合成问题？力的合成问题是力学中的一个重要知识点。

往往需要用到三角函数和向量运算。

在解决这类问题时，我们可以先将力按照其分解方向分解成两个分力，然后根据力的三角函数关系求出其大小和方向。

最后再进行合力的计算。

这样可以简化问题，并减少计算难度。

2. 如何应用动力学公式解决物体的运动问题？动力学是力学的一个重要分支，涉及到物体在受到力的作用下的运动状态。

在解决物体的运动问题时，我们可以运用动力学公式，如速度、加速度、加速度的大小与方向之间的关系等。

通过将问题中给出的条件和所求的量代入公式，可以解算出所需要的答案。

同时，还要注意合理选择参考系，简化计算过程。

二、热学知识点难题1. 如何运用热力学公式解决热传导问题？热传导是热学中的一个重要概念，涉及物体的热量传递问题。

在解决热传导问题时，我们可以利用热传导的基本公式，如热传导定律、热传导方程等。

根据题目所给的条件和所求的量，代入相应的公式进行计算。

同时，要注意正确选择适当的单位，以保证计算结果的准确性。

2. 如何运用热力学定律解决热力学循环问题？热力学循环是热学中的一个重要概念，涉及到热能的转化和传递问题。

在解决热力学循环问题时，我们可以运用热力学定律，如热力学第一定律、热力学第二定律等。

通过分析题目中给出的条件和所求的量，代入相应的定律进行计算。

此外，还需要注意能量守恒和熵增原理等基本原理的运用。

三、电学知识点难题1. 如何运用电路分析方法解决复杂电路问题？电路分析是电学中的一个重要知识点，涉及到电流、电压、电阻等的分析和计算。

在解决复杂电路问题时，我们可以运用电路分析方法，如串并联电路的等效电阻、基尔霍夫定律等。

通过将电路进行简化和等效，逐步分析和计算出所需要的量。

高考物理难点讲解与练习

高考物理难点讲解与练习高考物理一直是许多考生心中的“拦路虎”，其中存在着一些具有挑战性的难点。

本文将对部分高考物理难点进行详细讲解，并提供相应的练习，帮助同学们更好地应对高考。

一、牛顿运动定律与受力分析牛顿运动定律是力学的基础，也是高考物理的重点和难点。

在解决相关问题时，正确的受力分析是关键。

首先，要明确各种力的特点。

重力总是竖直向下，大小为 mg；弹力的方向总是垂直于接触面，支持力和压力是常见的弹力；摩擦力要分清静摩擦力和滑动摩擦力，静摩擦力的大小和方向需要根据物体的受力情况和运动状态来判断，滑动摩擦力的大小与正压力和动摩擦因数有关，方向与相对运动方向相反。

其次，在进行受力分析时，要按照一定的顺序，通常先分析重力，然后是弹力，最后是摩擦力。

同时，要注意不要漏力或添力。

例 1：一个质量为 m 的物体放在粗糙水平面上，现用一个与水平方向成θ角的力 F 拉物体，物体处于静止状态。

求物体所受摩擦力的大小和方向。

解析：对物体进行受力分析，物体受到重力 mg、支持力 N、拉力 F 和摩擦力 f。

将拉力 F 分解为水平方向和竖直方向的分力，水平分力为Fcosθ，竖直分力为Fsinθ。

因为物体静止，所以在水平方向上，摩擦力f 与拉力的水平分力Fcosθ大小相等，方向相反；在竖直方向上，N ＝mg ＋Fsinθ。

练习 1：一个质量为 2kg 的物体放在倾角为 30°的斜面上，用平行于斜面向上的力 F ＝ 10N 拉物体，物体沿斜面匀速向上运动，动摩擦因数为 02。

求摩擦力的大小和方向。

二、机械能守恒定律与动能定理机械能守恒定律和动能定理是解决能量问题的重要工具。

机械能守恒定律的条件是只有重力或弹力做功，在这种情况下，机械能的总量保持不变。

动能定理则指出合外力对物体做功等于物体动能的变化。

在解题时，要注意区分这两个定理的适用条件。

如果系统内只有重力或弹力做功，优先考虑机械能守恒定律；如果涉及到多个力做功，或者做功过程比较复杂，一般使用动能定理。

力矩有固定转动轴物体的平衡

.
F1
Θ O
G1
F3
mgR - F (2R) 0 F mg
2
R 2R
mg
F
.
应用转动平衡求解重心
如图所示，边长为a的均匀正方形木板，被挖去一个半径为a/4的圆孔，圆孔的边缘和正方形右边缘相切，圆心在对称轴PQ 上，求该木板剩余部分的重心。
P
O2 C
O1
Q
x a/4 G1
P
Q
G2
G1
a 4
力所在的平面与转轴不垂直
把力分解到沿转轴方向，和垂直转轴方向。
沿转轴方向的力，不能使物体绕轴转动，该力对转轴的力矩为0
.
转动平衡条件：M合=0 或： M顺=M逆
.
已知：杆重G1=80N，物重G2=240N
θ=30°
求：钢绳对杆OB的拉力F1
F1lsin-G1
l 2
-G2l
0
A
由此得：F1=G21+si2nG2 560N B
力矩有固定转动轴物
体的平衡
.
1．转动平衡：有固定转动轴的物体，如果保持静止（或匀速转动状态），则这个物体处于转动平衡状态
２．转轴：物体转动时，它的各点都沿圆周运动，圆周的中心在同一直线上，这一条直线叫转动轴
３．力臂：转动轴到力的作用线的距离
.
４．力矩
• 引入意义：力对物体转动作用的描述 • 定义：力臂L和力F的乘积叫做力对转动轴的力矩
DC杆受拉力，大小为T
D
C
BD杆受压力，大小为 2 T
.
平面力系： FX =0
Fy =0
r
M 0
该力矩可取任意垂直平面的直线为轴

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2013高考物理常见难题大盘点：力矩有固定转动轴物体的平衡1．如图1-50所示是单臂斜拉桥的示意图,均匀桥板ao 重为G ,三根平行钢索与桥面成30°,间距ab =bc =cd =do ,若每根钢索受力相同，左侧桥墩对桥板无作用力，则每根钢索的拉力大小是（）。

本题的正确选项为（D ）。

2．图1-51为人手臂骨骼与肌肉的生理结构示意图，手上托着重量为G 的物体，（1）在方框中画出前臂受力示意图（手、手腕、尺骨和挠骨看成一个整体，所受重力不计，图中O 点看作固定转动轴，O 点受力可以不画）．（2）根据图中标尺估算出二头肌此时的收缩力约为．解答前臂的受力如图1-52所示，以O点为转轴，由力矩平衡条件得 18F N ⨯=⨯，其中N =G ，可得F =8G 。

本题的正确答案为“8G ”。

3．如图1-53所示，直杆OA 可绕O 轴转动，图中虚线与杆平行．杆的A 端分别受到F 1、F 2、F 3、F 4四个力作用，它们与OA 杆在同一竖直平面内，则它们对O 点的力矩M 1、M 2、M 3、M 4的大小关系是（）。

(A)M 1＝M 2＞M 3＝M 4 (B)M 1＞M 2＞M 3＞M 4 (C)M 2＞M 1＝M 3＞M 4(D)M 1＜M 2＜M 3＜M 4解答把四个力都分解为垂直于OA 方向和沿OA 方向的两个分力，其中沿OA 方向的力对O 点的力矩都为零，而垂直于OA 方向的力臂都相等，所以四个力的力矩比较等效为垂直图1-50图1-511图1-53方向的力的比较。

从图中不难看出力大小关系为F 2⊥>F 1⊥=F 3⊥>F 4⊥，所以力矩大小关系为M 2>M 1=M 3>M 4。

本题的正确选项为（C ）。

4．如图1-54所示的杆秤，O 为提扭，A 为刻度的起点，B 为秤钩，P 为秤砣，关于杆秤的性能，下述说法中正确的是（）。

(A)不称物时，秤砣移至A 处，杆秤平衡 (B)不称物时，秤砣移至B 处，杆秤平衡 (C)称物时，OP 的距离与被测物的质量成正比 (D)称物时，AP 的距离与被测物的质量成正比解答当不称物体时，秤砣应在零刻度线，即在A 点，此时对O 点的力矩平衡，设杆秤本身的重为G 0，重心离开O 点距离为OC ，根据力矩平衡条件得0P AO G OC ⨯=⨯，①当称物体为G 时，设秤砣在D 点时杆秤平衡，如图1-55所示，根据力矩平衡条件有0G OB G OC P OD ⨯=⨯+⨯，②由①②式得()G OB P AO OD P AD ⨯=⨯+=⨯。

本题的正确选项为（A ）（D ）。

5.．如图1-56所示，A 、B 是两个完全相同的长方形木块，长为l ，叠放在一起，放在水平桌面上，端面与桌边平行．A 木块放在B 上，右端有4l伸出，为保证两块不翻倒，木块B 伸出桌边的长度不能超过（）。

(A)l /2(B)3l /8 (C)l /4(D)l /8解答把A 、B 当作一个整体，其重心位置在两个木块的中点，根据几何关系可知在距B 右边38l 处。

为了不翻倒，它们的重心不能超过桌边，即B 伸出桌边长度不超过38l 。

本题的正确选项为（B ）。

6．如图1-57所示，将粗细均匀、直径相同的均匀棒A 和B 粘合在一起，并在粘合处用绳悬挂起来，恰好处于水平位置而平衡，如果A 的密度是B 的两倍，那么A 的重力大小是B 的 _______倍．解答假设A 的长度为x ，B 的长度为y ，横截面积为S ，B 的密度为ρ，则A 的密度为2ρ，有2A G xSg ρ=,B G ySg ρ=,根据力矩平衡条件得图1-54图1-56AB图1-5722A B x y G G ⨯=⨯，代入得x y =所以22A B G xSg x G ySg yρρ===。

本题的正确答案为“2”。

7．如图1-58所示，一个质量为m 、半径为R 的球，用长为R的绳悬挂在L 形的直角支架上，支架的重力不计，AB 长为2R ，BC 长为R 32，为使支架不会在水平桌面上绕B 点翻倒，应在A 端至少加多大的力？解答要使加在A 端的力最小，力臂应最大，即为AB 的长度。

以球和直角支架整体作为研究对象，球所受重力和A 端所受作用力对B 点力矩平衡，有2mg R F R ⨯=⨯,可得F =21mg , 所以应在A 端至少加21mg 的力作用。

8．如图1-59所示，重为600N 的均匀木板搁在相距为2.0m 的两堵竖直墙之间，一个重为800N 的人站在离左墙0.5m 处，求左、右两堵墙对木板的支持力大小．解答木板的受力分析如图1-60所示，以左边墙的交点为支点，根据力矩平衡条件得130.512N G N ⨯+⨯=⨯，①以右边墙的交点为支点，根据力矩平衡条件得212 1.51N N G ⨯=⨯+⨯，②其中N 1=G 人=800N ，G =600N ，代入①②式得N 2=900N ，N 3=500N 。

所以左、右两堵墙对木板的支持力大小分别为900N 、500N 。

9．棒AB 的一端A 固定于地面,可绕A 点无摩擦地转动,B 端靠在物C 上,物C 靠在光滑的竖直墙上,如图1-61所示.若在C 物上再放上一个小物体,整个装置仍保持平衡,则B 端与C 物之间的弹力大小将（）。

(A)变大(B)变小(C)不变(D)无法确定解答AB 棒及C 物体在竖直方向的受力分析如图1-62所示，对于C 物体，由平衡条件得图1-58图1-59图1-61图1-60N 图1-62NffG C Gf =G C ，①对于AB 棒，根据力矩平衡条件得G f N M M M +=，②在C 上加一小物体后，G C 增加，由①式可知f 也将增大，则M f 增大。

由②式可知M N 随之增大，则N 也增大。

本题的正确选项为（A ）。

10．如图1-63所示，质量为m 的运动员站在质量为m 的均匀长板AB 的中点，板位于水平地面上，可绕通过A 点的水平轴无摩擦转动，板的B 端系有轻绳，轻绳的另一端绕过两个定滑轮后，握在运动员的手中，当运动员用力拉绳子时，滑轮的两侧的绳子都保持在竖直方向，则要使板的B 端离开地面，运动员作用于绳的最小拉力是_________．解答设板长为2L ，对板进行受力分析如图1-64所示，以A 为转轴，根据力矩平衡条件得 M N +M G =M T ，即2N L mg L T L ⨯+⨯=⨯,① 以人为研究对象，有 T +N =mg ，②由①②式得T =32mg , 本题的正确答案为“32mg ”。

11．如图1-65所示，半径是0.1m ，重为310N 的均匀小球，放在光滑的竖直墙和长为1m 的光滑木板（不计重力）OA 之间，木板可绕轴O 转动，木板和竖直墙的夹角为θ=60°，求墙对球的弹力和水平绳对木板的拉力．解答对木板OA 受力分析如图1-66所示，由力矩平衡条件得1ctgcos 2N R T L θθ⨯=⨯,①对球受力分析如图1-67所示，根据平衡条件得1sin N G θ=,②12cos N N θ=, ③由①②式得2sin cos GRctgT L θθθ=，其中G =310N ，R =0.1m ，θ=60°，L =1m ，代入可得N 2N 图1-67T =34N=6.93N 。

由②③式可得N 2=10N 。

所以墙对球的弹力为10N ，水平绳对木板的拉力为6.93N 。

12．如图1-68所示，均匀杆AB 每米重为30N ，将A 端支起，在离A 端0.2m 的C 处挂一重300N 的物体，在B 端施一竖直向上的拉力F ，使杆保持水平方向平衡，求杆长为多少时，所需的拉力F 最小，最小值为多少？解答设杆长为x m ，则重为30x N ，由力矩平衡条件得3000.2302xx F x ⨯+⨯=⨯, 即215600x Fx -+=,①要使方程有解，则2415600F ∆=-⨯⨯≥，即F ≥60N ，取F =60N ，代入①式可得x =2m 。

所以杆长为2m 时，所需的拉力F 最小，最小值为60N 。

12．两个所受重力大小分别为G A 和G B 的小球A 和B ，用细杆连接起来，放置在光滑的半球形碗内．小球A 、B 与球心O 在同一竖直平面内，如图1-69所示．若碗的半径为R ，细杆的长度为R 2，G A >G B ，则连接两小球的AB 细杆静止时与竖直方向的夹角为多大?解答以A 、B 整体为研究对象，A 、B 物体所受的支持力通过球心，所以以O 为转动轴，只有A 和B 的重力矩．如图1-70所示，由力矩平衡条件可得sin sin A B G R G R αβ⋅=⋅，①由几何关系知：090αβ+=②解①②式得arctanBAG G α=，所以细杆与竖直方向的夹角γ为arctan4B A G G π+。

13．如图1-71所示，重为G 的一根均匀硬棒AB ，杆的A 端被细绳吊起，在杆的另一端B 作用一水平力F ，把杆拉向右边，整个系统平衡后，细线、棒与竖直方向的夹角分别为α、β．求证：tg β=2tg α．证明硬棒受到三个力作用平衡，则三个力的作用线必交于一点，如图1-72所示。

AB所以O 为AB 的中点，则由几何关系可得C 为BD 而tan BD AD β=，tan CDADα=，图1—68 图1-72所以tan 2tan βα=。

14．半径为R 、质量为M 1的均匀圆球与一质量为M 2的重物分别用细绳AD 和ACE 悬挂于同一点A ，并处于平衡，如图1-73所示．已知悬点A 到球心O 的距离为L ，不考虑绳的质量和绳与球的摩擦，试求悬挂圆球的绳AD 与竖直方向AB 的夹角θ．解答如图1-74所示，以球为研究对象，球受到重力、绳子ACE 对球的压力及AD 绳的拉力作用，因为不考虑绳对球的摩擦，则绳对球的压力N 必然通过球心，球是均匀的，重心必在球心，所以第三个力AD 绳的拉力必过球心，即O 、A 、D 三点在同一直线上。

以球、重物和绳作为一个系统，以A 为转动轴，由力矩平衡条件可得120M g OB M g BC ⋅-⋅=而sin ,sin OB L BC R L θθ==-，代入上式可得悬挂圆球的绳AD 与竖直方向AB 的夹角LM M RM )(arcsin 212+=θ。

15．在一些重型机械和起重设备上，常用双块式电磁制动器，它的简化示意图如图1-75所示，O 1和O 2为固定铰链．在电源接通时，A 杆被往下压，通过铰链C 1、C 2、C 3使弹簧S 被拉伸，制动块B 1、B 2与制动轮D 脱离接触，机械得以正常运转．当电源被切断后，A 杆不再有向下的压力(A 杆及图中所有连杆及制动块所受重力皆忽略不计)，于是弹簧回缩，使制动块产生制动效果．此时O 1C 1和O 2C 2处于竖直位置．已知欲使正在匀速转动的D 轮减速从而实现制动，至少需要M =1100N •m 的制动力矩，制动块与制动轮之间的摩擦系数μ＝0.40，弹簧不发生形变时的长度为L =0.300m ，制动轮直径d =0.400m ，图示尺寸a =0.065m ，h 1=0.245m ，h 2=0.340m ，试求选用弹簧的倔强系数k 最小要多大．解答如图1-76所示，制动时制动块B 1、B 2对D 的正压力分别为N 1和N 2，滑动摩擦力分别为μN 1和μN 2。