(05)分式加减法专项练习60题(有答案)ok教学提纲
分式加减法专项练习60题含答案

分式加减法专项练习60题(有答案)1.2.a(a﹣1)+3.4..5. +.6..7.=_________.8..6yue289..10..11..12.13.14..15.16.(1);(2)17.18.1+ 19.﹣+20.21.+.22.23..24.,25.26.++.27.+﹣.28.29.(式中a,b,c两两不相等):30.31.(1);(2)….32.+﹣33.化简分式:.34..35.计算:﹣.36.计算:.37.计算:.38..39.计算化简:.40.计算:+++.41.计算.42.计算:.43.化简:.44..45.计算:.zuoguo46..55.化简:.47.化简:.48..49..50.计算:﹣.51.计算:.52.计算:1﹣•.53.计算:.54.化简56.先观察下列等式,然后用你发现的规律解答下列问题:由,,…(1)计算++++++=_________(n为正整数);(2)化简:+…+.57.化简:﹣.60.求和.58.请你阅读下列计算过程,再回答所提出的问题:题目计算:解:原式=(A)=(B)=a﹣3﹣6(C)=a﹣9(D)(1)上述计算过程中,从哪一步开始出现错误:_________.(2)从B到C是否正确,若不正确,错误的原因是_________.(3)请你把正确解答过程写下来.59.观察下面的变形规律:=1﹣;=﹣;=﹣;…解答下面的问题:(1)若n为正整数,请你猜想=_________;(2)证明你猜想的结论;(3)求和:+++…+.参考答案:1.原式===1+1=2.2.原式=a2﹣a+=a2﹣a+a=a2.3.==.4.原式===.5.原式=+==.6.原式===.7.==.8.原式===a﹣1.9.原式==.10.+=+=+==1.11.原式=﹣==.12.原式=﹣=﹣=.13.原式=+===14.原式=+==.15.=﹣=﹣==﹣1.16.(1)原式=;(2)原式=17.====.18.原式=1﹣====.19.原式=﹣•==.20.===0.21.原式=+==.22.原式=﹣==.23.原式=====1.24.原式====;x的取值范围是x≠﹣2且x≠1的实数.25.原式==.26.====027.原式=﹣﹣==28.=.29.原式=++=+++++=0.30.原式=+﹣==.31.(1),=,=;(2)+…+=﹣+﹣+…+﹣=﹣=.32.==﹣2 33.=(2a+1)+﹣(a﹣3)﹣﹣(3a+2)++(2a﹣2)﹣=[(2a+1)﹣(a﹣3)﹣(3a+2)+(2a﹣2)]+(﹣+﹣)=﹣+﹣=﹣=.34.原式=﹣=﹣===35.原式====﹣36.原式====37.原式==38.原式=+﹣==39.原式=++=+﹣==== 40.原式=+++=++ =++=+=+=.41.设2x2+3x=y,则原式=﹣+===.42.原式=﹣a+2=a+1﹣a+2=3.43. 原式====.44.原式===,===45.=﹣===46.=== ==47.原式=,=﹣+,=+﹣﹣++,=048.原式=2a﹣a﹣1+a+1=2a.49.原式====.50.原式====.51.原式===.52.原式=1﹣×=1﹣==﹣.53.原式=+﹣====54.原式=++=+++++=﹣+﹣+﹣=0+0+0=055.原式===156.(1)原式=1﹣+﹣+…+﹣=1﹣=;(2)原式=﹣+…+﹣=﹣=57.原式=﹣=﹣=158.(1)A(2)不正确,不能去分母(3)原式===59.(1)=﹣;(2)﹣=﹣==;(3)+++…+=1﹣+﹣+﹣+…+﹣=1﹣=60.原式=++++…+﹣=+++…+﹣=+﹣=﹣=.。
分式加减乘除综合练习题

----分式加减乘除综合练习题1、分式基本性质:MB MA MB M A B A ÷÷=⨯⨯=(其中 M 为不等于0的整式 ); 2、运算法则:(1)同分母分式相加减法则:b c a b c b a ±=±;(2)异分母分式相加减法则:bdbcad bd ad d c b a ±==± 注意:1、类比分数的通分得到分式的通分:把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.注意:通分保证(1)各分式与原分式相等;(2)各分式分母相等。
2.通分的依据:分式的基本性质.3.通分的关键:确定几个分式的最简公分母,其步骤如下:(1).将各个分式的分母分解因式;(2).取各分母系数的最小公倍数;(3).凡出现的字母或含有字母的因式为底的幂的因式都要取;(4).相同字母或含字母的因式的幂的因式取指数最大的;(5).将上述取得的式子都乘起来,就得到了最简公分母;(6). 原来各分式的分子和分母同乘一个适当的整式,使各分式的分母都化为最简公分母。
计算 (1)x y x y x y 232323-+- (2))31)(122(--+xx (3)x x x x x x x x -÷+----+4)44122(22 (4)x x x -+--+93261623(5)x x x x x 22)242(2+÷-+- (6))11()(ba ab b b a a -÷--- (7))2122()41223(2+--÷-+-a a a a (8))1)(1(y x x y x y +--+(9)22242)44122(a aa a a a a a a a -÷-⋅+----+ (10)zx yz xy xy z y x ++⋅++)111(二、先化简,再求值.1—— 2222244x y x y x y x xy y --÷+++,其中x,y=2。
列分式方程解应用题专项练习60题(有答案)ok

列分式方程解应用题60题(有答案)1.A、B两地的距离是80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.2.轮船顺水航行80千米所需要的时间和逆水航行60千米所用的时间相同.已知水流的速度是3千米/时,求轮船在静水中的速度.3.甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合作2天就完成了全部工程.已知甲队单独完成工程所需的天数是乙队单独完成所需天数的,求甲、乙两队单独完成各需多少天?4.甲,乙两组学生去距学校4.5km的敬老院打扫卫生,甲组学生步行出发半小时后,乙组学生骑自行车开始出发,结果两组学生同时到达敬老院,如果步行的速度是骑自行车的速度的,求步行和骑自行车的速度各是多少.5.甲、乙两个工程队共同完成一项工程,乙队先单独做1天,再由两队合作2天就完成全部工程,已知甲队与乙队的工作效率之比是3:2,求甲、乙两队单独完成此项工程各需多少天?6.某校师生为爱心基金捐款,已知第一天捐款4800元,第二天捐款6000元,第二天捐款人数比第一天多50人,且两天人均捐款数相等.问这两天共有多少人捐款?人均捐款额是多少?7.甲做90个零件所用的时间和乙做120个零件所用的时间相同,又知每小时甲、乙两人共做35个机器零件.求甲、乙每小时各做多少个零件.8.甲、乙两个工程队合做一项工程,需要16天完成,现在两队合做9天,甲队因有其他任务调走,乙队再做21天完成任务.甲、乙两队独做各需几天才能完成任务?9.甲,乙两地相距19km,某人从甲地出发去乙地,先步行7km,然后骑自行车,共行2h到达乙地.已知这个人骑自行车的速度是步行速度的4倍,求步行速度和骑自行车的速度.10.甲乙两地相距360km,新修的高速公路开通后,在甲乙两地行驶的汽车的平均速度提高了50%,而从甲地到乙地的时间缩短了2h.求汽车提速后的平均车速?11.现要装配30台机器,在装配好6台以后,采用了新的技术,每天的工作效率提高了一倍,结果共用了3天完成任务,问原来每天装配机器有多少台?12.一个工人生产奥运会吉祥物“福娃欢欢”,计划30天完成,若每天多生产5个,则在26天完成且多生产了14个.则这个工人原计划每天生产多少个福娃欢欢?13.孙明与李丽共同帮助校图书馆清点图书,李丽平均每分钟比孙明多清点10本.已知孙明清点完200本图书所用的时间与李丽清点完300本所用的时间相同,求孙明平均每分钟清点图书多少本.14.某人骑自行车的速度比步行的速度每小时多走8千米,已知步行12千米所用的时间和骑自行车36千米所用的时间相等,这个人步行每小时走多少千米?15.甲、乙两班同学参加“绿化祖国”植树活动,已知乙班每小时比甲班多种2棵,甲班种60棵树所用的时间与乙班种66棵所用的时间相等,问:甲、乙两班每小时各种多少棵树?16.甲、乙合打一份稿件,4小时后,甲有事离去,由乙继续打6小时完成.已知甲打4小时的稿件乙需5小时完成.求甲、乙独打这份稿件各需多少小时?17.某中学到离学校15千米的某地旅游,先遣队和大队同时出发,行进速度是大队的1.2倍,以便提前半小时到达目的地做准备工作.求先遣队和大队的速度各是多少?18.甲乙两人分别从距目的地6千米和10千米的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20分钟到达目的地,求甲、乙两人的速度.19.一项工程要在限期内完成,如果第一组单独做,恰好按规定日期完成,如果第二组单独做,超过规定日期4天才能完成,如果两组合做3天后剩下的工程由第二组单独做,正好在规定日期内完成,问规定日期是多少天?20.某货车在发生交通事故后,沿一条小路向高速公路逃离,交警巡逻车立即沿另一公路向高速追击,在货车刚进入高速公路路口时,将它截住.已知警车的速度比货车快40千米/时,警车驶到高速公路行驶的路程是货车的2倍,求警车的速度.21.某煤矿现在平均每天比原计划多采330吨煤,已知现在采33000吨煤所需的时间和原计划采23100吨煤所需的时间相同.问现在平均每天采煤多少吨?22.甲、乙两人从学校出发,前往距学校12千米的新华书店.甲每小时比乙多走2千米,乙比甲提前1小时出发,结果两人同时到达.求甲、乙两人每小时各走多少千米?23.甲、乙两地相距828千米,一列普通列车与一列直快列车都由甲地开往乙地,直快列车的平均速度是普通列车的平均速度的1.5倍,直快列车比普通列车晚出发2小时,比普通列车早到4小时,求两列火车的平均速度.24.某工厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,则每天应多做多少件?25.某工程要在规定日期内完成.若由甲单独做,则刚好如期完成;若由乙单独做,则要超过3天完成,现在先由甲、乙合做2天,剩下的工程由乙单独做,结果刚好按时完成.求规定的天数.26.“要致富,先修路!”甲乙两地相距360千米,为更好的促进甲、乙两地经济往来,新修的高速公路开通后,在甲乙两地间行驶的客运车辆平均车速提高了50%,而从甲到乙的时间比原来缩短了2小时,求原来车辆的平均速度是多少?27.2010年春季我国西南五省持续干旱,灾情牵动全国人民的心,“一方有难、八方支援”.某厂计划生产1500桶纯净水支援灾区人民,在生产了300桶纯净水后,由于救灾需要工作效率提高到原来的1.5倍,结果提前4天完成了任务.求原来每天生产多少桶纯净水?28.小颖和几位同学去文具店购买练习本,该文具店规定,如果购买达到一定的数量,则可以按批发价购买,于是他们凑到60元钱以批发价购买,这样购得的练习本数量比用零售价购得的练习本数量多30本,若每本练习本的批发价是零售价的,问每本练习本的零售价是多少元?29.某工厂引进新技术后,平均每小时比原来多生产30个零件.若现在生产900个零件所需时间与原来生产600个零件所需时间相等,现在平均每小时生产多少个零件?30.为了帮助灾区重建家园,学校号召同学们自愿捐款.已知第一次捐款总数为4 800元,第二次捐款总数为5 000元,第二次捐款人数比第一次捐款人数多20人,且恰好相等.问第一次捐款人数是多少?31.某公园在2008年北京奥运花坛的设计中,有一个造型需要摆放1800盆鲜花,为奥运作奉献的精神促使公园园林队的工人们以原计划1.2倍的速度,提前一小时完成了任务,工人们实际每小时摆放多少盆鲜花?32.某顾客第一次在商店买若干件小商品花去4元,第二次再去买该小商品时,发现每一打(12件)降价0.8元,购买一打以上可以拆零买,这样,第二次花去4元买同样小商品的件数量是第一次的1.5倍.问他第一次买的小商品是多少件?33.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同,现在平均每天生产多少台机器?34.某工厂加工495件产品,在加工了90件后进行了技术改造,使每天生产的产品数量是原来的1.5倍,结果共用了12天圆满完成了任务,问原来每天加工多少件产品?35.阅读下面一段文字:高圆带了9元去商店买笔记本,她想买一种软面抄,正好需付9元,但售货员建议她买另一种质量更好的硬面抄,只是这种笔记本的价格比软面抄要高出一半,因此她只能少买一本笔记本.请你根据以上信息确定:这种软面抄和硬面抄的价格各是多少?高圆原来打算买多少本笔记本?36.为加强防汛工作,市工程队准备对长江堤岸一段长为2500米的江堤进行加固,在加固了1000米后,由于采用新的加固模式,现在计划每天加固的长度比原计划增加了50%,因而完成此段加固工程所需天数将比原计划缩短5天,那么现在每天加固的长度是多少米?37.甲、乙两名志愿者为灾后重建搬运物资.已知甲、乙两人每小时共搬运1500 kg物资,且甲搬运300 kg物资的时间与乙搬运200 kg物资所用的时间相同.求甲每小时比乙多搬运多少物资?38.今年全国“助残日”期间,某中学学生踊跃捐款,奉献自己的一份爱心、其中八年级一班学生共捐款450元,二班学生共捐款390元.已知一班平均每人捐款金额是二班平均每人捐款金额的1.2倍,且二班比一班多2人,那么这两个班各有多少人?39.一件工程甲单独做15天可以完成,乙单独做12天可以完成,甲,乙,丙三人合作4天可以完成,那么丙单独做,几天可以完成?40.2009年12月,相距1050公里的A、B两市的高速铁路建成通车,高速铁路上的旅客列车时速是原普通铁路的3.5倍,运行在两市间的旅客列车运行时间因此缩短7.5小时,求高速铁路的时速.41.应用题:已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米?42.某市教育局向一贫困山区县赠送3600个学生用的科学记算器以满足学生学习的需要、现用A,B两种不同的包装箱进行包装,单独用B型包装箱比单独用A型包装箱少用15个,已知每个B型包装箱装计算器的个数是A型包装箱的1.5倍,求A,B两种包装箱每个各能装计算器多少个?43.某市为处理污水需要铺设一条长为3000米的管道、为了尽量减少施工对交通所造成的影响,实际施工时每天铺设管道的长度为原计划的1.5倍,结果提前25天完成任务,求实际施工时每天铺设管道的长度.44.今年我国西南地区遭受严重旱灾,受灾人口达6130多万.为了帮助灾区重建家园,某学校号召师生自愿捐款,第一次捐款总额为20000元,第二次捐款总额为56000元,已知第二次捐款人数是第一次的2倍,而且人均捐款额比第一次多20元.求第一次捐款的人数.45.甲乙两站相距480千米,货车与客车同时从甲站出发开往乙站,已知客车的速度是货车的2.5倍,结果客车比货车早6小时到达乙站,求两种车的速度各是多少?46.某养鱼专业户要想估计鱼塘里大概有多少条鱼,他进行了如下操作:先从鱼塘里捞上来200条鱼,分别做上记号后,又放回鱼塘,一段时间后,他又从鱼塘捞上来200条鱼,发现有4条是做了记号的,由此他就知道了鱼塘大概有多少条鱼,请你说明其中的道理,并求出该鱼塘里大概多少条?47.1罐咖啡甲、乙两人一起喝10天喝完,甲单独喝则需12天喝完,1包茶叶甲、乙两人一起喝12天喝完,乙单独喝则需20天喝完,假如甲在有茶叶的情况下决不喝咖啡,而乙在有咖啡的情况下决不喝茶,问两人一起喝完1包茶叶和1罐咖啡需要多少天?48.西南地区遭受干旱已经近三个季度,造成数千万群众生活饮水困难;为了解决对口学校的学生饮水问题,实验中学学生会号召同学们自愿捐款活动.已知七年级捐款总额为4800元,八年级捐款总额为5000元,八年级捐款人数比七年级多20人,而且两个年级人均捐款数相等.试求七、八年级捐款的人数.49.某商店销售一种书包,七月份的销售额为6000元.为了让附近的孩子们在新学期能背上新书包,店主决定让利销售,在八月份将每个书包按原价的8折销售,结果销售量比七月份增加了50个,销售额比七月份增加了800元.求七月份每个书包的售价.50.“我国水资源形势非常严峻”,为了节约用水.某市今年3月1日起调整居民用水价格,每立方水费上涨25%.已51.某小组学生准备外出春游,预计共需费用120元,临出发时,有2人因故不能参加,但总费用不变,这样春游的学生人均费用增加,问原计划每人付费多少元?52.某厂将总价值为2000元的甲种原料与总价值为4800元的乙种原料混合,其平均价值比甲种原料每斤少3元,比乙种原料每斤多1元,问混合后的单价每斤多少元?53.先锋中学九年级学生由距江南10km的学校出发前往参观,一部分同学骑自行车先走,过了20min后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.(1)设骑车同学的速度为xkm/h,利用速度,时间,路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(2)列出方程,并求出问题的解.速度(千米/时)所用时间(时)所走的路程(千米)骑自行车x 10乘汽车1054.阅读下面对话:小红妈:“售货员,请帮我买些梨.”售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”对照前后两次的电脑小票,小红妈发现:每千克苹果的价是梨的1.5倍,苹果的重量比梨轻2.5千克.试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.55.2008年初,我国南方地区遭受雪灾,为保持道路畅通,市政府决定用铲雪机铲去扬威大道上的积雪.如果只用﹣台A型铲雪机单独工作,需要10小时才能全部铲完,在该铲雪机工作2小时后,一台B型铲雪机加入合作,然后一起工作了3小时将扬威大道上的积雪全部铲完,求B型铲雪机单独工作需要多少小时铲完?56.北京时间2010年4月14日7时49分,青海玉树发生7.1级地震,灾情牵动着全国各族人民的心.无为县某中心校组织了捐款活动.小华对八年级(1)(2)班捐款的情况进行了统计,得到如下三条信息:信息一:(1)班共捐款540元,(2)班共捐款480元.请你根据以上三条信息,求出八(1)班平均每人捐款多少元?57.码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系;(2)原计划若干天卸载完这批货物,但由于后一批货物要提前2天到达,则实际每天卸货数量比原计划每天多20%,恰好按时卸载完毕,求原计划每天卸载多少货物?58.2008年夏季奥运会的主办国于2001年7月13日揭晓.当时,为了支持北京申奥,红、绿两支宣传北京申奥万里行车队在距北京3000千米处会合,并同时向北京进发,绿队走完2000千米时,红队走完1800千米,随后红队的速度比原来提高20%,两车队继续同时向北京进发.(1)求红队提速前红、绿两队的速度比.(2)问红绿两支车队能否同时到达北京并说明理由.(3)若红、绿两支车队不能同时到达北京,那么,哪支车队先到达北京求出第一支车队到达北京时,两支车队的距离.(单位:千米)59.列方程或方程组解应用题:某商场销售某种商品,第一个月将此商品的进价加价20%作为销售价,共获利6000元,第二个月商场搞促销活动,将商品的进价加价10%作为销售价,第二个月的销售量比第一个增加了100件,并且商场第二个月比第一个月多获利2000元,问此商品进价是多少元商场第二个月共销售多少件?60.阅读并解答:先阅读下列计算方法:某商店将甲乙两种糖果混合销售,并按以下公式确定混合糖果的单价:单价=(元/千克),其中m1、m2分别为甲乙两种糖果的重量(千克),a1、a2分别为甲乙两种糖果的单价(元/千克).再解答下列问题:已知甲种糖果单价为20元/千克,乙种糖果单价为16元/千克.(1)现将10千克乙种糖果和一箱甲种糖果混合(搅拌均匀)销售,已知混合糖果的单价为18.4元/千克,问:这箱甲种糖果有多少千克?(2)现将10千克乙种糖果和一箱甲种糖果混合(搅拌均匀)销售,售出5千克后,又在混合糖果中加入5千克乙种糖果,再出售时,混合糖果的单价为17.5元/千克.问:这箱甲种糖果有多少千克?参考答案:1.解:设公共汽车的速度为x公里/小时,则小汽车的速度是3x公里/小时.依题意,得,解,得x=20.经检验x=20是原方程的根,且符合题意.∴3x=60.答:公共汽车和小汽车的速度分别是20公里/时,60公里/时2.解:设船在静水中的速度是x千米/时.由题意得:.解得:x=21.经检验:x=21是原方程的解.答:船在静水中的速度是21千米/时3.解:设乙队单独完成所需天数x 天,则甲队单独完成需x天,由题意,得即=1 解得x=6 经检验,x=6是原方程的根x=6时,x=4答:甲、乙两队单独完成分别需4天、6天4.解:设甲组速度为xkm/小时,则乙组速度为3xKm/小时.列方程:.解得:x=6.经检验:x=6是方程的解.∴3x=18.答:步行速度为6km/小时,骑自行车的速度为18km/小时5.解:设甲队单独完成此项工程需2x天,则乙队需要3x天.由题意得:.解之得:x=2.经检验;x=2是所列分式方程的根.∴2x=2×2=4,3x=3×2=6.答:甲队单独完成需4天,乙队需6天6.解:设第一天捐款x人,则第二天捐款(x+50)人,由题意列方程.解得x=200.检验:当x=200时,x(x+50)≠0,∴x=200是原方程的解.两天捐款人数x+(x+50)=450,人均捐款=24(元).答:两天共参加捐款的有450人,人均捐款24元7.解:设甲每小时做x个零件,则乙每小时做(35﹣x)个零件.根据题意列方程得:.解得:x=15.经检验,x=15是原方程的解.答:甲每小时做15个零件,乙每小时做20个零件8.解:设甲独做需要x天完成任务,根据题意得:×9+(﹣)×(9+21)=1,解得:x=24,经检验:x=24是方程的解,∴1÷(﹣)=48,答:甲、乙两队独做分别需要24天和48天完成任务9.解:设步行速度为x千米/时,那么骑车速度是4x千米/时,10.解:设提速前的平均车速为x km/h,根据题意得:﹣=2 解得:x=60 经检验:x=60是原方程的解,所以,(1+50%)x=90(km/h)答:汽车提速后的平均车速为90km/h.11.解:设原来每天装配机器x台,依题意得:,解这个方程得:x=6,经检验:x=6是原方程的解,答:原来每天装配机器6台12.解:设原计划每天生产x个零件.依题意可列:,解得x=29.经检验,x=29是原方程的根.答:这个工人原计划每天生产29个福娃欢欢13.解:设孙明平均每分钟清点图书x本.根据题意得:.解这个方程得:x=20.经检验:x=20是原方程的解.答:孙明平均每分钟清点图书20本14.解:设这个人步行每小时走x千米.依题意得:=.方程两边同乘以x(x+8)得:12(x+8)=36x.解得:x=4.经检验:x=4是原分式方程的解.(6分)答:这个人步行每小时走4千米.15.解:设甲班每小时种x棵树,则乙班每小时种(x+2)棵,根据题意得:,解这个方程得:x=20,经检验:x=20是原方程的根.所以当x=20时,x+2=20+2=22.所以甲班每小时种20棵树,乙班每小时种22棵树16.解:设甲单独打这份稿件需要4x小时,则乙单独打这份稿件需要5x小时.依题意,列方程:()×=1.解方程得:x=3.经检验:x=3符合题意.∴4x=12,5x=15.答:独打这份稿件,甲需12小时,乙需15小时.17.解:设大队的速度是x千米/时,先遣队的速度是1.2x千米/时,由题意得,解得x=5,经检验,x=5是原方程的解,∴1.2x=6,答:先遣队和大队的速度分别是6千米/时,5千米/时18.解:设甲的速度为3x千米/时,则乙的速度为4x千米/时.根据题意,得,解得x=1.5.经检验,x=1.5是原方程的根.所以甲的速度为3x=4.5千米/时,乙的速度为4x=6千米/时.答:甲的速度为4.5千米/时,乙的速度为6千米/时19.解:设规定日期是x天.根据题意得:+=1.解这个分式方程得:x=12.经检验:x=12是原方程的解,并且符合题意.由题意得:=.解之得:x=80.经检验:x=80是原方程的解.答:警车的速度为80千米/时21.解:设现在平均每天采煤x吨,依题意得,解得x=1100经检验,x=1100是方程的解.答:现在平均每天采煤1100吨22.解:设甲每小时走x千米,根据题意列方程得:=﹣1 整理得:x2﹣2x﹣24=0(3分)解这个方程得:x1=6x2=﹣4 经检验,x1x2是原方程的解,但x2<0不符合题意舍去,取x=6∴x﹣2=4(1分)答:甲每小时走6千米,乙每小时走4千米.(1分)23.解:设普通列车的平均速度为x千米∕时,则直快列车的平均速度为1.5x千米∕时,由题意得解得x=46经检验,x=46是原分式方程的解 1.5x=1.5×46=69(千米∕时)答:普通列车的平均速度为46千米∕时,直快列车的平均速度为69千米∕时24.解:设每天应多做x件,则依题意得:=5,解之得:x=24.经检验x=24是方程的根,答:每天应多做24件25.解:设规定天数为x天,依题意得,2×(+)+(x﹣2)×=1,解得:x=6,经检验x=6是原方程的解,答:规定的天数是6天26.解:设原来车辆的平均速度为x千米/小时.由题意可得:.解这个方程得:x=60.经检验:x=60是原方程的解.答:原来车辆的平均速度为60千米/小时27.解:设原来每天生产x桶纯净水,依题意得:,解这个方程,得x=100,经检验,x=100是原方程的解.答:原来每天生产100桶纯净水.28.解:设每本练习本的零售价是x元,则每本练习本的批发价是x,根据题意得:,解得x=0.5.将x=0.5代入检验得是方程的解.答:每本练习本的零售价是0.5元.29.解:设现在平均每小时生产x个零件,依题意得:解得:x=90 经检验,x=90是方程的解且符合题意.答:现在平均每小时生产90个零件.30.解:设第一次捐款人数是x,则第二次捐款人数是(x+20).依题意得:.解方程得:x=480.经检验:x=480是原方程的解.答:第一次捐款人数是48031.解:设工人原计划每小时摆放x盆鲜花,则实际每小时摆放1.2x盆鲜花.依题意得:=+1,解这个方程得:x=300.经检验:x=300是原方程的解.∴1.2x=360.答:工人们实际每小时摆放360盆鲜花32.解:设他第一次买的小商品是x 件.﹣=,解得:x=20,经检验x=20是原方程的解.答:他第一次买的小商品是20件33.解:设:现在平均每天生产x台机器,则原计划可生产(x﹣50)台.依题意得:.解得:x=200.检验:当x=200时,x(x﹣50)≠0.∴x=200是原分式方程的解.答:现在平均每天生产200台机器.34.解:设:原来每天加工x件,则进行技术改造后,每天生产的产品数量为1.5x件.依题意列出方程:=12,解得:x=30,经检验,x=30是原分式方程的解.答:原来每天加工30件产品35.解:设每本软面抄的价格为x元,则每本硬面抄的价格为1.5x元.由题意得:.解之得:x=3.∴1.5×3=4.5(元),9÷3=3(本).答:软面抄单价3元/本,硬面抄单价4.5元/本,高原原计划买3本笔记本36.解:设原计划每天加固的长度是x米,则现在每天加固的长度是x(1+50%)=米列方程:∴x=100 经检验:x=100是原方程的解.所以x(1+50%)==150米答:现在每天加固的长度是150米37.解:设甲、乙每小时搬运物资分别为xkg和(1500﹣x)kg,由题意得,解得x=900,经检验x=900是原方程的解,也符合实际意义.由900﹣(1500﹣900)=300(千克∕小时),知甲比乙每小时多搬运300kg物资38.解:设一班有x 人,根据题意得,解得:x=50,经检验,x=50是原分式方程的解,答:一班有50人,二班有52人39.解:设丙单独做x天可以完成.依题意列方程得:4(++)=1.解得:x=10.经检验,x=10是方程的根,也符合题意.答:丙单独做10天可以完成40.解:设普通列车时速为x公里/时,则,解之得:x=100,经检验:x=100是原方程的解,∴3.5x=350.答:高速铁路的时速为350公里/时41.解:设江水每小时的流速是x千米.根据题意,得,解得x=4.经检验,x=4是原方程的根.则江水每小时的流速是4千米42.解:设每个A型包装箱能够装x个计算器,则B型包装箱能装1.5x个计算器,依题意有:解这个方程,得x=80,经检验x=80是原方程的根,∴1.5x=120,答:每个A型包装箱能装80个计算器,每个B型包装箱能装120个计算器.43.解:设原计划施工时每天铺设管道xm,则实际施工时每天铺设管道1.5xm.据题意得:=25 解得x=40.经检验x=40是原方程的解. 1.5x=60答:实际施工时每天铺设管道60m.44.解:设第一次捐款人数为x,则解得x=400 经检验x=400是方程的解,答:第一次捐款人数为40045.解:设货车的速度为x千米/时,则客车的速度为2.5x千米/时,根据题意可列关于时间的方程式:﹣=6,解得:x=48(千米/时)故可知,货车的速度为48千米/时,客车的速度是120千米/时46.解:设该鱼塘里大概有x条鱼,依题意得,解之得:x=10000,经检验x=10000是方程的解,答:该鱼塘里大概有10000条鱼47.解:设甲单独喝茶叶的时间为x天,乙单独喝咖啡的时间为y天,根据题意列方程得,,解得y=60;,解得x=30.因此30天后甲喝完茶叶而乙只喝完咖啡的一半(),故剩下的咖啡变成两人合喝,由题意可知,他们两人还能喝÷()=5天.所以两人用30+5=35天才全部喝完.答:两人一起喝完1包茶叶和1罐咖啡需要35天48.解:设七年级捐款的人数为x人,则八年级捐款的人数为(x+20)人由题意得:解这个方程,得x=480 经检验,x=480是原方程的解∴x+20=500(人)答:七年级捐款的人数为480人,则八年级捐款的人数为500人49.解:设7月份每个书包售价为x元,则8月份每个书包售价为0.8x元,根据题意得﹣=50,解得x=50(元),经检验:x=50是所列方程的根且符合题意,答;7月份每个书包售价为50元。
分式运算加减法练习题

分式运算加减法练习题分式运算是代数中的一个重要部分,掌握分式加减法对于解决更复杂的代数问题至关重要。
以下是一些分式加减法的练习题,帮助学生巩固和提高他们的计算能力。
1. 计算下列分式的和:\(\frac{3}{4} + \frac{1}{6}\)2. 求出以下分式的差:\(\frac{5}{8} - \frac{3}{10}\)3. 计算并简化以下表达式:\(\frac{2}{5} + \frac{1}{3} - \frac{3}{10}\)4. 解决以下问题:如果 \(\frac{a}{b} + \frac{c}{d} = \frac{e}{f}\),且 \(a = 6\),\(b = 9\),\(c = 4\),\(d = 7\),求 \(e\) 和 \(f\) 的值。
5. 计算以下分式的和,并简化结果:\(\frac{2x}{3y} + \frac{3x}{4y}\)6. 求出以下分式的差,并简化:\(\frac{5}{x+1} - \frac{3}{x-1}\)7. 计算以下表达式的值:\(\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}\)8. 解决以下问题:如果 \(\frac{m}{n} - \frac{p}{q} = \frac{r}{s}\),且 \(m = 12\),\(n = 15\),\(p = 8\),\(q = 10\),求 \(r\) 和 \(s\) 的值。
9. 计算以下分式的和,并简化结果:\(\frac{3}{x} + \frac{2}{x-1}\)10. 求出以下分式的差,并简化:\(\frac{4}{y+2} - \frac{1}{y-2}\)解决这些练习题的关键是找到分母的最小公倍数,然后将分子相加减,最后简化结果。
通过这些练习,学生可以提高他们对分式运算的理解和应用能力。
请注意,这些练习题的答案需要根据具体的数学规则来计算,例如找到公共分母,进行分数的加减运算,以及简化结果。
分式加减法练习题答案

分式加减法练习题答案分式加减法是数学中的一个重要概念,它在解决实际问题时起到了重要的作用。
本文将通过一系列练习题的答案来帮助读者更好地理解和掌握分式加减法。
1. 练习题1:计算 1/2 + 1/3。
解答:首先要找到两个分母的最小公倍数,即6。
然后将分子按照最小公倍数进行等比放大,得到 3/6 + 2/6 = 5/6。
2. 练习题2:计算 3/4 - 1/5。
解答:同样地,找到两个分母的最小公倍数,即20。
然后将分子按照最小公倍数进行等比放大,得到 15/20 - 4/20 = 11/20。
3. 练习题3:计算 2/3 + 1/4 - 1/6。
解答:首先计算前两个分数的和,得到 8/12 + 3/12 = 11/12。
然后再减去最后一个分数,得到 11/12 - 2/12 = 9/12 = 3/4。
通过以上三个练习题的答案,我们可以看到分式加减法的基本原理。
首先要找到分母的最小公倍数,然后按照最小公倍数进行等比放大,最后进行相应的加减运算。
除了以上的基本原理,还有一些特殊情况需要注意。
比如当分数的分母相同,只需要对分子进行加减运算即可。
另外,当分数的分母是1时,可以直接将分子作为结果。
4. 练习题4:计算 2/3 + 4。
解答:由于分数的分母是1,所以可以直接将分子作为结果,得到 2/3 + 4 =2/3 + 12/3 = 14/3。
5. 练习题5:计算 3/4 - 2。
解答:同样地,由于分数的分母是1,所以可以直接将分子作为结果,得到 3/4 - 2 = 3/4 - 8/4 = -5/4。
通过以上两个练习题的答案,我们可以看到当分数的分母是1时,可以直接将分子作为结果。
这是因为分数的分母是1时,实际上是整数的一种表达形式。
练习题的答案不仅仅是为了得到正确的结果,更重要的是通过实际操作来加深对分式加减法的理解。
通过练习题的答案,我们可以发现其中的规律和特点,从而更好地掌握这一概念。
分式加减法在实际生活中有着广泛的应用。
(05)分式加减法专项练习60题(有答案)ok

分式加减法专项练习60题(有答案)6yue281 12a41|a 2-l[13 nx-:3 x ( X-3)5.6.2 a ..] a+1.i '.8.1 ID - 5 in2 _ in 2ID 2 _ 214.9.10. ab b:I.7'-'-.11.2m _ 1 m 2 -4 时2x 2 2x .K 2+X -2 /-4X £+4X +412.a - 1a 2+a- 2a+l¥-115.13.16 .(1)x+x | - 9X2+6I+917 .n m ^2_2L珂0jm_ 2n n, - 4im+4n*18.1+a2+ab+ b 2?-b319 .b2ab+ b2 - 2ab+ b2'a2 - b22a * b ~ e , 2b ~ c - a _ 2e - a - b~2I 5' oa - ab - ac+bc b - ab - bc+ac c - ac - bc+ab23.ir^+2ni+l V 7?(i-l)(K +2)-1 ,r 12.L2IE 2 - 9 TS;_ IT 26.25.27.2y+z —■+28 卅9b _ a+3b.:.- --29.(式中a , b , c 两两不相等)231. (1) ^― ■出;x+y2曰'+3*2 _ 己2 _ 廿 _ 5 _ 3 a? _ 4邑- § 2护 - 3时5 a+1af2 a - 2 + a - 3:, 1 … K (xfl) T (计1)(計刃 (x+2005) (x+2006)(2) b 2a+c b-ca 一 b+c|b ' a _ c b -耳-百 32.33.化简分式:34. 72x y+xy35 .计算:2x+2y36. 计算: 37•计算:3K - 4y40. 38. 39.计算化简:一X2+3X +2 X 2+K -2 1- T 21124 1-X|i+d1+/计算:41 . 1 2 12X 2+31-1 2 K 2+3X +1 2X 2+3I ^3计算45•计算:f「二47.化简:2a_ b-c _ 2b _c _a , 2c _a ~ b (a-b) ta_c) * (b_c) Cb - a)亠(G_(G_b)42•计算: 7s +2a+l a+148. ::-■-a- 1 49.a2-l51 •计算:2JS' y _z 2y _ _2 2z _K_y~~5 "I o "I- Ky- xz+yz y^- xy - yz+xz z^-KZ- yz+sy54.化简(2)化简:1 + + + +■ ++=1X^ 2X3 3X4 4X5 5X6|6X7 7X8 _—□__________ 1______ .L[(n为正整数);+・・+1(x+2QQ8) C K+2009)50.计算:56.先观察下列等式,然后用你发现的规律解答下列问题:由 __ _!—丄_J_一_!_! _J__1X2 2 1 2 2X3 6 2 3 3Xq 12 3 4 (1)计算(K+2) (X+3)(x+1)(x+1) (x+2)解答下面的问题:(1 )若n 为正整数,请你猜想一.1.= _|n Cn+1)(2) 证明你猜想的结论;(3) ------------------------------------------------------------- 求和: 一=—+—=—+—=—+ •- +=1X2 2X3 3X4 2011X2012解:原式= ----- ------------ ' (A )a+3(a+3)(a - 3)= a-3_6(a+3)_3)((a - 3)58•请你阅读下列计算过程,再回答所提岀的问题:题目计算:(B)=a — 3- 6 (C ) =a - 9 ( D )(1 )上述计算过程中,从哪一步开始岀现错误: _ _ •(2)从B 到C 是否正确,若不正确,错误的原因是 __________________ (3 )请你把正确解答过程写下来.59 •观察下面的变形规律:=11X21::;L1 1 1 |1 12|3|;3X4 3 4;参考答案:1 原式=• .' . -1 - I =1 + 1=2 .a _ ba _b a _ ba 2 - abb a (a b) n = • a + b a+b|Pt/a+b(a+b) (a _b)a+b a +h| a+ba+b|m _ 2 2m (mH)4. 5. 6. 2x1x 11(xH) (K--1) x-1 (計 1) (x-1) x+1-+a+1 (aH )2冷-1)a- 1+2 _ (aH)〔耳 T) 1 1 1-1 X3x _ 3 1 1x (x _3) x (x-3)"x Cs _ 3) x1 . 2_l+2_3 a da a T a14.十「、2自(已+1)222 .原式=a — a+ =a - a+a=a .nfl3.原式=原式= 原式=7. 10.(ID - 1 ) (ID - 2)2m (ID - 1) (nrl-1)a _ 1_ 3.^+0| a-1 |a (a+1) | 1 |a 1 _ a □ -l =a-la 2 - 2a+l a 2 - T'(a -D 旷(a -1) (a+1)〜1 一-11 _ 4 _ - a+2 _41□ _ 2 (at2) Ca _ 2) (af2)冷-2)(a+2) (a _ 2)(寸2〕_ 2)16.17.18. 19. 20.21 .22.23.24.25. 26.27.28. 29.D 2,1血G+l ) 2(x+1)(x-1)(xH) (K-1)(xH) C K -1)K-l 原式 2xy y (旳)= ¥ a - y) y (K _ y) (K +Y ) (K _ y) Cx+y)(富一 y ) 〔盂+y )(nrFl ) 22 itd-1 2 | irr^L - 2 ra _1 A (1□- 1) (nrbl) m - 1 m _ 1 m _ 1 m _ 1 m _ 1x (x+2)5 _(X- n (X42) _x 2+2x-3 - X 2-X +2 (K- 1) (x+2)(K-1;(x+2)〔耳「1)(計2)_ (i-l )(计2)原式原式原式 ;x 的取值范围是x a 2且x 的实数.K - 12m -n nr^n m n _ ID n ~ IT ] 原式-- ・ 1 _ 12 -2 (m+3)皿2 _ 9 _ in 「nr+3 (ml-3) (ID - 3i 丁 (nrl-3) Cm - 3)12-2 (昭引 +2 57)L2-2u- -&+2m - 61 J -■ i :(nrf 3) ■i 02 Cm - 3) +(nH-3)~_ 3)2y+xy2x2y+z - y - 2iy x",(xfy) (K _y)1 x+ya 2= 1(ad-2) Ca _2)nt - n (m - 2n ) in - 2n (mi-n) (m 一 n)a 2+ab+ b 2m _ 2n _rrH ■口 - ( m _ 2n) jirl-n _ irrl^2n _irr^nrn^n m+n— b 24_ 1 _ b_1 -b(a -b) 2| b ( a+b)'□-b(旦-b) ~a+l+a 1 2a 0 且一 1 8+1 /-I(a - 1) (a+1) (a+1) fa _ 1)a+9b a +3t 廿9b =~ (a-K3b) ■仙 23ab3ab - 3ab 3ab a原式=1 -=0.(a~b) ( a^+ab+ b 2)原式=原式34.…氏+F )'原式x - y x+y-莖+y 2y 2xy xy xy x36. / - 2xy+ y 2 - 2Z 3 - 2y 2z+y2 (x+y) (K -y) =b 【葢-y)J s+2y y -1yi+2y - y+1 - yx+1 | 1 |_l-x 2 1-S 2l-,21 1*1 - :, 1 -.37. 原式2-y 238. 原式三買丄玄-丄?x 2 (x _ 1)(2)「| J +••+^亠亠 + 亠——+ ••+ -s (xfl) (K +1) (X +2) (X +2005) (r+2006)同莎直+1 越 x+200EL =. 200& 丈我006=x (x+200G)” b2a^c b - c b 2a+c - b-+c - b 2a - M2c 2a - 2b+2<na " t+cb _ a _ cb _ a _ ca" b+cb _ a _ Gb _ a _G b _ a - G b 一且一 E2a 2+3a+2 __ 3a 2_4a~^ 2 a 2 _ Sa+Sarbla+2 a _ 2 + a - 3=(2a+1)-( a - 3)--( 3a+2) +—'a+1a+2a-=[(2a+1)-( a - 3)-( 3a+2) + ( 2a - 2) ]+ (-—r ■丁arl a+Z a _ J 耳一/ 丄-一 :-• = . •. -a+1 a+2 □ _ 2 a _ 3 (aH 〕(a+2)(a _ 2) (a _ 3)-盼4(a-bl)( a+2) (a - 2)(a _ 3)x+2006-40x+40 (x-2) (K -4)31. (1)x+ysy (x - y)35.原式22 - K - 3yJy+ x 2C K - 1)(y+1)(y+3) -2 (y 1? (y+3) + (y■-1D (y+1) rs(y-1) Cy+1)Cy+3) =(厂⑴(y+D (y+3)8(2x ?+3i- 1)(2 x 2+3X +1 )(2 x 2+3x+3)'2c - a - k>4 (1+/) 4 (1+ J)—丄8 (1-』)(Hx 4) (1-/) (1+/)1-x 8 2 41 .设2x +3x=y ,则原式=X J y 2 2 _ * y _xK ( K ~ y) y(y _z) K ( K ~ y) y (K_ y) xy (K _ y) xy (K _y)_ 2 . y K -(旳)Cx -y)s+y xy -y)xy (h -y)XV44.原式 2y 严2 y2X1 y 2-x 2(y+莖)Cy x) /-/y-xx (K - y)K (x - y) x U - y) x (s - y) 45.2KVx _ xE M 什貨(x - y) +x (x+y) 992zy+ z - XV+ 92sy+2 x 凤2 -x+y ^-y _ ]宀/ I'_2 _ 2K y(x _y) (x+y)46. 2工(旳)n (旳)「2工m 一y39.原式=JS ( 1 - 1 )X (x+1) 2 (x+2)(K +2) (X +1 } (x _ 1)( K +2) C X H) (s-1) | | (K +2) C K H)(; cl)K ?K + K2+X 2x - 4=2x 2 2x 4J 2 ( 英-2〕(x+1)2K - 4 (計刃(?-n 丨丘+对a+D G — i ) (xf2) (x+1) (x-1)X2+K - 240.原式=14■覽(1 - x)~(1 十辺2 (1+ x 2) 2 (1- J)丄+ 4 =44 I(1 -4 (H x £)(1-?) (1+?)1十 J 1- J 1+J+ -+ ■-1+x 2 1+J42 .原式=■-+ 乩一x - x+y 1K +X (s+y)(盖—y)(s+y) (x-y) (x+y) (K - y)K _ y47 .原式=.一: - 1〔 一 ,,++(x+2) &十 1)(1 十小(1 -X ) (2 (x-1)2+4(1-X )(1+G(1-X )(1卄)43.原式-a+2=a+1 - a+2=3.48.49.50.(a-k>) + (且-c)—(h* - c? + (b - s) +(c-a) +〔匚-b)(a- b) (a~ c)(b-c) (a-b) 〔£-辺)(c - b)+++]—,=0a+ (3a+l) ・(2a+3) a+3a4-l -•岛・3 2 (a- 1? .2 I宀1a-1a+1'=1 3x+5=h 1 ③+5)-2:計孑(X-HS) ( K _ 1 )(K+3)(K-D(K+3)G-1)原式原式原式=2a - a _1+a+仁2a.4 x- 81 3 x+612= 7 x- 14(x+2 ) ( x-2 )(x+2 ) ( x-2 )(x+2 ) ( x -2 )](也)(K-2 )51.原式乂且(# 3)52.原式=1 -2a+12a+b 2b^2a- (2a+b) 2b+2a 2a b=1..--2ab2ab Znb 2ab=1 -(曲)Ca_ 1)a+3a+153. 原式-I- , 1-L2ab 2ab1 1r 1 亠1-L 1 4.1 1x _ z z _ y y _s 1y _ m 12 _y i Z _I X _z55.原式X2-1+2(好1) (x+L ) 2= 4+1 )戈=_(田)2=1M -—+ •-+3118 =1 -+ - - + 1L56. (1)原式=1 -12=』;11= 2009灶2009K (計20Q9)=157 .原式=■K (x+2) 2 XK-2'_X- 2K+2008 K+200^y- 一a-3 ’£寸畀(arf3) G - 3)(a+3)(且- 3)丁(af3) Ca_ 3)a - 3+6 十1(时3) (a-3) (a+3) ( □ _3) a.-3(x+2) (x _2)58. (1) A (2)不正确,不能去分母(3)原式=1 ]11n (汩1)=n n+1;59. (1)-=.n+1 n .n+1 - n 1n+1 n (n+1)n (n+1) n (nil) b 5+i)(2) 2岛说九X4=14墙4 i弓-—+ ••+2011X20121feOll2012 =20122011 2012—=1.=2 +」+4+ ••+ 「1 ] 1 - X 1-x 2l+i 21出1+4|1-』60•原式叮・+.「.。
分式加减练习题及答案

分式加减练习题及答案在学习分式加减的过程中,练习题是不可或缺的一部分。
通过大量的练习,我们可以更好地理解和掌握分式加减的方法和技巧。
下面是一些分式加减练习题及其答案,希望对你的学习有所帮助。
练习题一:1. 计算:2/3 + 1/42. 计算:3/5 - 1/63. 计算:4/7 + 2/74. 计算:5/8 - 3/85. 计算:1/2 + 2/3 - 1/4答案一:1. 2/3 + 1/4 = (8/12) + (3/12) = 11/122. 3/5 - 1/6 = (18/30) - (5/30) = 13/303. 4/7 + 2/7 = (4+2)/7 = 6/74. 5/8 - 3/8 = (5-3)/8 = 2/8 = 1/45. 1/2 + 2/3 - 1/4 = (6/12) + (8/12) - (3/12) = 11/12练习题二:1. 计算:7/8 + 1/22. 计算:5/6 - 1/33. 计算:2/9 + 4/94. 计算:9/10 - 1/55. 计算:3/4 + 1/6 - 1/8答案二:1. 7/8 + 1/2 = (7/8) + (4/8) = 11/8 = 1 3/82. 5/6 - 1/3 = (5/6) - (2/6) = 3/6 = 1/23. 2/9 + 4/9 = (2+4)/9 = 6/9 = 2/34. 9/10 - 1/5 = (9/10) - (2/10) = 7/105. 3/4 + 1/6 - 1/8 = (6/8) + (2/8) - (1/8) = 7/8练习题三:1. 计算:3/4 + 2/32. 计算:4/5 - 1/103. 计算:5/6 + 1/34. 计算:8/9 - 2/95. 计算:1 + 1/2 - 1/4答案三:1. 3/4 + 2/3 = (9/12) + (8/12) = 17/12 = 1 5/122. 4/5 - 1/10 = (8/10) - (1/10) = 7/103. 5/6 + 1/3 = (5/6) + (2/6) = 7/6 = 1 1/64. 8/9 - 2/9 = (8-2)/9 = 6/9 = 2/35. 1 + 1/2 - 1/4 = (4/4) + (2/4) - (1/4) = 5/4 = 1 1/4通过以上的练习,我们可以看到分式加减的方法其实并不难,主要是要熟练掌握分式的基本运算规则,并善于化简分式。
分式的加减法练习题

分式的加减法练习题分式的加减法练习题分式是数学中的一个重要概念,在我们的日常生活中也经常会用到。
它可以帮助我们解决一些实际问题,比如分配资源、计算比例等等。
在学习分式的过程中,掌握分式的加减法是非常关键的一步。
本文将通过一些练习题来帮助大家巩固和提高对分式加减法的理解和运用能力。
1. 加法练习题(1) 计算:1/3 + 2/5 = ?解答:首先需要找到这两个分式的公共分母,即3和5的最小公倍数,为15。
然后,将两个分式的分母都改为15,得到1/3 = 5/15,2/5 = 6/15。
最后,将分子相加,得到答案为11/15。
(2) 计算:2/7 + 3/8 = ?解答:同样地,我们需要找到这两个分式的公共分母,即7和8的最小公倍数,为56。
然后,将两个分式的分母都改为56,得到2/7 = 16/56,3/8 = 21/56。
最后,将分子相加,得到答案为37/56。
2. 减法练习题(1) 计算:2/3 - 1/4 = ?解答:同样地,我们需要找到这两个分式的公共分母,即3和4的最小公倍数,为12。
然后,将两个分式的分母都改为12,得到2/3 = 8/12,1/4 = 3/12。
最后,将分子相减,得到答案为5/12。
(2) 计算:5/6 - 2/9 = ?解答:同样地,我们需要找到这两个分式的公共分母,即6和9的最小公倍数,为18。
然后,将两个分式的分母都改为18,得到5/6 = 15/18,2/9 = 4/18。
最后,将分子相减,得到答案为11/18。
通过以上的练习题,我们可以发现,分式的加减法实际上就是将分子相加或相减,而分母保持不变。
所以,只需要找到公共分母,将分子进行相应的运算即可。
当然,有时候需要进行分数的化简,比如将11/18化简为5/9,这需要我们熟练掌握分数化简的方法。
除了加减法,我们还可以进行分式的乘法和除法运算。
分式的乘法就是将两个分式的分子相乘,分母相乘,得到的结果即为乘法的结果。
分式加减法专项练习60题ok
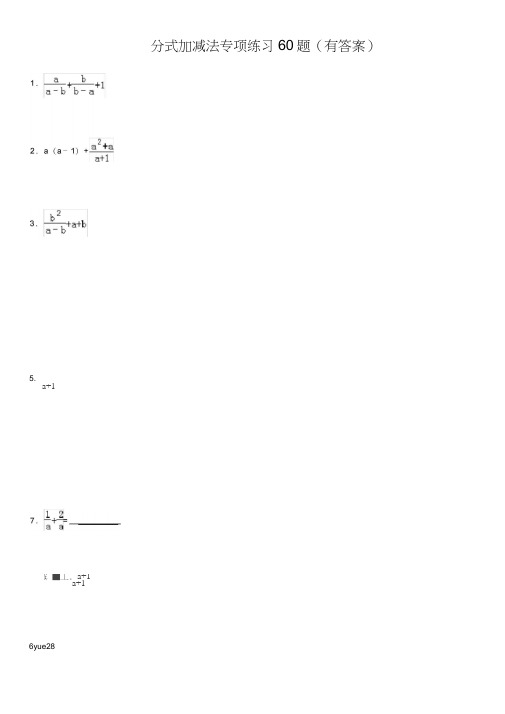
分式加减法专项练习60题(有答案)5.a+1£ ■丄. a+1a+16yue289.10.且‘ - ab b ,-/烏状11 .2mm2 - 4x2 2x .X2+X-2/ -4 K£+4T+412.16.(1)21 .17. 12 _ 2 ; ID 2- 9 皿_3'(2)+X 2~9X 2+3I x 2f6x+91 _ 4a-2 a 2 _4n _ rri2_2l111nm _ 2n- 4mn+4ii"18. 1 + a 2-hab+ b 2b 21ab+b ,a 3-b 3b 2 - 2ab+ b 2+a 2-b 219. 20 .M 11 .4垃K +L+ x 2-l32a ' b - c2b _ c _ a 2c ~ a - b~2 "I 2 2a ~ ab~ ac+bcb - ab - bc+ac 匚 一吕c 一 bc+ab9ID +2nri-l2Hi IT - 123. 24.12 + 23 ir| 26 .+亠n^32y+iy2丈+y 2-x 227. 28. aH-9ba+3b 3ab25.29.(式中a , b , c 两两不相等)5 7K- 10------------ 十---------------- -- ---------------x2+x - 6 X2- x _ 12 s 2 _ 6x+8231 . (1) ^―・旳;xfy33 .化简分式:2a2+3a+2 _ a2- a-S _ 3a2 _ 4a- 5( 2a2_ Sa+5 afl a+2 a_ 2「a-3:, 1 … -K (xfl) T (计1)(計刃(x+2005) (x+2006) b2a+c厅 - b+c +b _ 己_ €32.39 •计算化简:—X 2+3X +2 I H-X -2 1- x241•计算..-_2I 2+3I -12/十 3计1Z X 2+3X +336. x^+2sy+ y K 2- 2sy+y 22 , 2 X y+xyy 2y-Ky 234. 35 .计算:2x+2y计算:37 .计算:40. 1 + 1 | I 2 +41-x 1+r1+s 21+J38.计算:47 .化简:2a _ b _c , 2b _c ~ a , 2c _a -b (a-b) (a-G)" (b _c) (b _a) "(G_a) (c _b)42 •计算: 9a+1(3-2) •43 .化简:2y寸44.45 .计算:zuoguo46.55 .化简:"9x z+2z+L2- 1 . 248.■i- 149.0 3a+l 绝+31 3莖+5 1 1 150 .计算:时3 x 2+3£-l 351 •计算:52 .计算:1 -53 .计算: 54 .化简 2^~ y - z 2y _ x _ z 2z ~ x _ ,y ~" 5 ~o - xy- xz4yz y £- xy - yz+xz z £ - xz - yz+sy56 •先观察下列等式,然后用你发现的规律解答下列问(1)计算1J-1 -L 11」 .1丄丄 ,11X212X3I3X4 4X5 5X6 6XT2L : -1 1 1 _ 1 3X4_12_3 4(n 为正整数);(2)化简:- ----------------- X --------------------------- -------- -------- X --- -- ---------- ------------------------(K +1)(x+1) (t+2)(z+2) (x+3)+・・+ (K +2008)(計 3TO9)2 57. 化简:58•请你阅读下列计算过程,再回答所提岀的问题:题目计算:K 16*:原式=—--- ------- -- (A) ( ar+LJ ) (a-3)a - 36 n(a+3) (a - 3)(a+3) (a _ 3)=a — 3 - 6 (C ) =a — 9 ( D )(1 )上述计算过程中,从哪一步开始岀现错误: ________________ . (2)从B 到C 是否正确,若不正确,错误的原因是 __________________ (3 )请你把正确解答过程写下来.解答下面的问题:(2)证明你猜想的结论;460 .求和(1 )若n 为正整数,请你猜想n Cn+1)11 1 ■ . . . 111X2 + 1T2X3 3X4+…+2011X2012(3)求和:59.观察下面的变形规律:11X2 115. =-1.a — 1 _ a^+aa- 1 a (a+1) J 1a1 a - 2a+1/ - 1 (a-1 ) 2 (a - 1) (aH) 'a-1a-la-1参考答案:原式=^^ —」_扌1=^^+1=1+1=2 a _ b a _ b a _b-+2r a-1+2 J 1 1a+1(a+1)冷-1)(a+1} (a - 1} a _ 13 "1 L ^-3111x (x _ 3)x J7)K (x - 3) H'1+23 计 a a 3a|a 2-l.(al-1) (a 1)a+1a+12xy葢(,^-y)2xy+ x 2 _ _ K (x+y) _ y(沈+y) (x~ y)(計y) (y _y)(K _ y) (x+y 〕 ( x - y) ( s+y) x _ y10.a 2 - ab2mIT - 2m+2 I 1 ](nrl-2) Cm - 2)(nrl-2) (m _ 2) (nri-2) Cm" 2)TW~Zx (x 2)3・1) (^2)Xx - 1(K _ 2) (x+2)(我)2x+I :-■ :■=> ::'2 (in+1)ID Cm - 5)in 一 3nd-2 (ID - 1) (m - 2)2m (in - 1) (iir+1)2m (in _ 1)Ml) 2m (m 「1)(nH-1)2. 2 2 2原式=a - a+=a - a+a=a .ar+15. 原式=原式=7.原式==a -1 .原式=+丄= +亠 +丄亠=1 .且(且-b ) 2 a+t> (乩+b 〕(a _ b) a+b a+b a4b a+l>11 .原式12.原式13 .原式14 .原式=1 1+a'1 ________ 4 _______ W ________ 4 _______ = 曲 a -2 (a+2) (a _ 2) (a+2) (□ - 2) (a+2) (□ _ 2) (a+2)( _______ 自-2 =「1 (n+2) (a - 2) a+2 m _ n - ■2n) 2 m - 2n irr^n- —1 —■ — (in - 2n) m4-n in+2n m _2n (irr^n) Cm _n) m+n nrin m+n原式=1 - b 2 c (a+b) (a - b) _ 1 Ca b) 2 b (arhb) a _ b<+日b+b , (a- b) ( a?+eib+ b 2) =0 .i ia+l+a 1 - 2a 1 0且一1 a+l a 2 -](a -1) (a+l)(a+l) (a~ 1) 原式= 原式 + Cx+1 ) 2K - 1 ) 2 (XH ) 〔55-1) 原式 y (x+y)y Cx ~ y) y(K - y)(旳)(K ~ y) (x+y) x+y2 _ irH -! _ 2 nM-L - 2 m _ 1(孟+D GT) (x+1) (K-1) (K ~ y) (sc+y) m _ 1 ni _ 1 m _ 1 ni 一 1 原式= X (x+2) _ s (x - 1) (x+2) 才+2x - 3-(K-1) (x+2) (K-1) (K +2) 0-1) (H2) (x-n V 1 1 x ^- 2且x 力的实数.;x 口的取值范围是 (K -1) (x+2) |x+2 原式=2ID _ n _ nr+n mn _ m n _ ir12,2 , 2 | | 12 ,- -2 CiH-3; 2 缶-3) 原式 (nrtS) (IP 7) n+3 (ITJ 4-3) (m _ 3) (nri-3) (m _ 3) m 2 -9 3-m (nrHl)」 (io - 1) (nr+1) m 一 x 2 - x+2 (x+2)12-2 (nH-3) +2 Cm- 3) 1 12 - 2nt - 64缶-6 (nrF3) Cm 3) (卅孑)(m~ 3j原式= ¥-泳2y+x y 2xy _ x- x 2-y 2(s+y) (K _ y)計ya+9b a+3b a+9b * -(a+3b) 6b 2 3ab 3ab = 3ab 3ab ax 2-y 2+ ta _ c)(b>- c) + ( b - a) (c _ a) + Cc _ t>) '■ i1+H ■ b - 〔£ - 卫)(G - b)原式=4a - 2)3n nr+n _ = L-b16.17.18.19.20. 21 . 22. 23. 24.25.26.27.28.29.2a 2+3a+2 . J -耳 -5. 3a.' —4可-52a 2 _ Sa+Sa+1 a+2 a _ 2" a - 3=■+■+'+□ _ G a _ b b _ □1+ + b _ 4 G _I? r i c _ □=0 .= '>;T (rl-3) C K - 2) 2x- 5 ]r 7x-io (x+3) C K -4) ]P (K -2) (K -4) 5K (s 4) + (2x - 5) (i-2)-(i 10) G+3) = -40/4Q(rl-3) Cs _ 2) (K -4)(K +3) (X -2) (X -4)30 .原式] z+2006=1 1 =2006 n 』疋+200E K (x+20Q6)'b b 2a^cb - Qb 2a+< 一 l?+c -b 2a _ b-+2c 2a - 2L+2<n ~ b+c b _ a _c b _ a _b+u b ~ a~ c b 一a - cb _ a _c b 一石一亏33.34. 36. 37. 38. =(2a+1 ) +a+1 -(a - 3)a42-(3a+2)---+ --:=1a+1 a+ 2 □ 2 □ _ 3 (a+1)(寸2) -8a+^(afl)( a+2) (a _ 2j(a-3)1 Q~ 2]+ ( + (2a - 2)----------------1 ------- a41 a+2 a - 21a _ 3‘•)己一 d(x-y)[ _M _ yx+y - x+y2xy (x _yJiyxyXK2- 2xy+ y 2-2K 2-2y 22 &+y) (、耳 _ y)i+2y _ y 1 _ y x-F2y - y+1 - yi+l1 1- / 1- i 21- i 2'=1-z 21-?1 - X原式=叙 t^-1) | |6/ + —X 2 Cx - 1) X 2 ( K' - 1 )3x (K- 1) +6 s 2-(廿5)Cx - 1)g 异- T 工+5 X 2(K - ID/(K - 1)31 . (1)1+ ••+K +200532.=-2(孟+]〉" (孟+1) ―(x+2) 1(K +2005) (X-F2006)=[(2a+1 )-( a - 3)-( 3a+2) + (2a - 2) (a - 2) (a - 3)原式=U+y ) 2Jty (x+y)35.Z (K-y)原式=7s+2y 3y(K +5)(愛・1)原式=47.(什 1) Cy+3) -2 (y-n (y+3) + (y-13 (y+1) 18(y-1) Cy+l) (yf3) (y-1) (y+1)(y+3)8(2j+3x-l)(2X 2+3X +1) (2X 2+3I +3)|• ■ j1;- :. ■-•• 'I ,> -‘: + ■' + :(K +刃(s+1) (s+2) (x _ 1) | | (1+x) (1-翼)X ( X 1) 直 Cx+D 2 (x+2)(x+2)(計1) (x _ 1} (x+2) Cx+1) 0-1) (xf2) G+l) GT)39.K + K^+x 2x 4= 2 宀4_ I 2 (K -2) (M +,1 ) 1 =2M - 4〔計刀〔*-1)■ l ■ 1 1 ■ 1 ::.- (x+2) CH-1) (X -1) x Z +x-2+=2y , H 2 r2 K— (y+丈) (V - X ) 9 + - x 2-xy y —*K (x - y)x (x - y)K (K _ x (x -y)45. 2zy z _ x (s - y) 4*s C«+yD 9 b 9 2xy+ x" - xy+ 92xy+2 x 冥2 — / x+y s-y __2 _ 2 ' 工 y(x _y) (x+y)46. I+K丄1 ■XI £ + 4 =2 ]d-x)(i 十工)(i-x ;)〔1+“if x 21+/ (1 - x) (Bi)2 C1+ x 2) ,2 (1- x 2) -L4 =4 Cf-?) (1+x 2) C) (i+显)I1+/1-S 4|4 (H J)4 (1十 J j-J_呂(1- x 4) (1+/)Cl - /) (1+/)l-x S42 .原式=(◎+1 )'aPl-a+2=a+1 - a+2=3 .43.原式=x - y+2yK -yK+y T <s+y) 1 d ~y)(旳)(v $yK ( K _y? y(y - 工) & (s~ yJ/ - 2 1 - y K =-(x+y? (K - y)xy (x - y)xy ( K -y)(x+y) C K _y)1瓦一y2sy (x _ y) uy (s ~y)'2z 3y) 2x (x - y) (x+y) _K _ y心一 2a_t ,_c40 .原式=41 .设 2x 2+3x=y ,则原式=1 y+32y 44 .原式 y (x _y)( 2) — == + - - + + , =048 .原式=2a — a — 1+a+仁2a . 49 .原式 ===50 .原式 =51 . 原式53. 原式 =+ — =54. 原式 =++ + + + +55 .原式 = = =157.原式 = — = — =158 .( 1 ) A ( 2)不正确,不能去分母 ( 3)原式 =59 .( 1 )(3)+++ •• +52 .原式=1 — X=1 —=0+0+0=056 . (1)原式=1 —+ — +•• + =1 —=1原式= -------- + +1 - K 1+1C2 + 4+ —+2n1+s2 1 + J1+3】=・—|1F+1+x4+2n__ L1 _x单纯的课本内容,并不能满足学生的需要,通过补充,达到内容的完善教育之通病是教用脑的人不用手,不教用手的人用脑,所以一无所能。
分式加减综合练习题

分式加减综合练习题1、分式基本性质:MB MA MB M A B A÷÷=⨯⨯=(其中 M 为不等于0的整式 ); 2、运算法则:(1)同分母分式相加减法则:bc a b c b a ±=±; (2)异分母分式相加减法则:bdbcad bd ad d c b a ±==±注意:1、类比分数的通分得到分式的通分:把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分. 注意:通分保证(1)各分式与原分式相等;(2)各分式分母相等。
2.通分的依据:分式的基本性质.3.通分的关键:确定几个分式的最简公分母,其步骤如下: 1.将各个分式的分母分解因式; 2.取各分母系数的最小公倍数;3.凡出现的字母或含有字母的因式为底的幂的因式都要取;4.相同字母或含字母的因式的幂的因式取指数最大的;5.将上述取得的式子都乘起来,就得到了最简公分母;6. 原来各分式的分子和分母同乘一个适当的整式,使各分式的分母都化为最简公分母。
一、计算2223221(1)(2)(1)(3)23322214313(3)()(4)24426629y x x y y x x x x x x x x x x xx x x +----++---÷-+--++--2223221(1)(2)(1)(3)23322214313(3)()(4)24426629y x x y y x x x x x x x x x x xx x x +----++---÷-+--++--(5)x x x x x 22)242(2+÷-+-(6))11()(ba ab b b a a -÷---(7))2122()41223(2+--÷-+-a a a a(8))1)(1(y x x y x y +--+(922242)44122(aaa a a a a a a a -÷-⋅+----+ (10)zx yz xy xyz y x ++⋅++)111(二、化简24)2121(aa a ÷--+,并求出当=a -1的值先化简,再求值.1-2222244x y x yx y x xy y--÷+++,其中y=2三、计算(1)111xx x++-(2)231()11x x xx x x---+(3)22()a b a b a b b a ab++÷--(4) 22226211962x x x x x x x x -++++÷-+--(5)23()224x x x x x x -÷++-四、综合计算题22222222222612411.:4463932.:333.:68334.:521525.:936.:1117.:969x xx x x x x a b a b ab ab c ab a bb cc axx y m m maa a xx x x --÷+++--++-++----------++计算计算计算计算计算计算计算。
(完整版)分式的加减专项练习20题答案

八年级数学专项提高分式的加减专项练习20题答案1.化简:.考点:分式的加减法.分析:首先将原分式化为同分母的分式,然后再利用同分母的分式的加减运算法则求解即可求得答案.解答:解:====x﹣2.点评:此题考查了分式的加减运算法则.解题的关键是要注意通分与化简.2.化简的结果是a+b.考点:分式的加减法.专题:计算题.分析:根据同分母的分数相加,分母不变,分子相加减.解答:解:原式===a+b,故答案为a+b.点评:本题考查了分式的加减法,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.3.计算:.考点:分式的加减法.专题:计算题.分析:先找出最小公倍数,再通分,最后计算即可.解答:解:原式==.点评:本题考查了分式的加减法,解题的关键是找出各分母的最小公倍数.4.考点:分式的加减法.专题:计算题.分析:观察发现,只需对第二个分母提取负号,就可变成同分母.然后进行分子的加减运算.最后注意进行化简.解答:解:原式===.点评:注意:m﹣n=﹣(n﹣m).分式运算的最后结果应化成最简分式或整式.5.计算:.考点:分式的加减法.分析:首先把分子分解因式,再约分,合并同类项即可.解答:解:原式=,=a﹣2+a+2,=2a.点评:此题主要考查了分式的加减法,关键是掌握计算方法,做题时先注意观察,找准方法再计算.6.化简:考点:分式的加减法.专题:计算题.分析:首先把各分式进行约分,然后进行加减运算.解答:解:原式==x﹣y﹣=x﹣y﹣2x+y=﹣x.点评:本题不必要把两式子先通分,约分后就能加减运算了.7.计算:.考点:分式的加减法.专题:计算题.分析:先通分,再把分子相加减即可.解答:解:原式=+﹣====.点评:本题考查的是分式的加减法,异分母分式的加减就转化为同分母分式的加减.8.化简:考点:分式的加减法.专题:计算题.分析:(1)几个分式相加减,根据分式加减法则进行运算;(2)当整式与分式相加减时,一般可以把整式看作分母为1的分式,与其它分式进行通分运算.解答:解:原式===1+1=2.点评:归纳提炼:分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.9.按要求化简:.考点:分式的加减法.分析:首先通分,把分母化为(a+1)(a﹣1),再根据同分母分数相加减,分母不变,分子相加减进行计算,注意最后结果要化简.解答:解:原式=﹣===.点评:此题主要考查了分式的加减,关键是掌握异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.10.化简﹣考点:分式的加减法.专题:计算题.分析:此题分子、分母能分解的要先分解因式,经过约分再进行计算.解答:解:原式===1.点评:此题的分解因式、约分起到了关键的作用.11.化简:考点:分式的加减法.专题:计算题.分析:把异分母分式转化成同分母分式,然后进行化简.解答:解:原式====.点评:分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.12.计算:.考点:分式的加减法.分析:根据异分母分式相加减,先通分,再加减,可得答案.解答:解:原式=﹣+====.点评:本题考查了分式的加减,先通分花成同分母分时,再加减.13.)已知:,求A、B的值.考点:分式的加减法;解二元一次方程组.专题:计算题.分析:此题可先右边通分,使结果与相等,从而求出A、B的值.解答:解:∵=,∴,比较等式两边分子的系数,得,解得.点评:此题考查了分式的减法,比较灵活,需要熟练掌握分式的加减运算.14.化简:考点:分式的加减法.专题:计算题.分析:通过观察分式可知:将分母分解因式,找最简公分母,把分式通分,再化简即可.解答:解:原式=﹣=﹣=.点评:解答本题时不要盲目的通分,先化简后运算更简单.15.计算:(x﹣)+.考点:分式的加减法.分析:将括号里通分,再进行同分母的运算.解答:解:(x﹣)+=+=.点评:本题考查了分式的加减运算.关键是由同分母的加减法法则运算并化简.16.计算:考点:分式的加减法.专题:计算题.分析:根据分式的加减运算法则,先通分,再化简.解答:解:原式=+===.点评:本题考查了分式的加减运算.解决本题首先应通分,最后要注意将结果化为最简分式.17.化简﹣.考点:分式的加减法.专题:计算题.分析:原式两项通分并利用同分母分式的减法法则计算,约分即可得到结果.解答:解:原式=﹣===.点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.18.化简:﹣+考点:分式的加减法.专题:计算题.分析:首先将各式的分子、分母分解因式,约分、化简后再进行分式的加减运算.解答:解:原式=﹣•(2分)=(3分)=.(4分)点评:分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减;如果分式的分子、分母中含有公因式的,需要先约分、化简,然后再进行分式的加减运算.19.计算:考点:分式的加减法.专题:计算题.分析:先通分,把异分母分式加减运算转化为同分母分式加减运算,求解即可.解答:解:原式====.点评:本题主要考查异分母分式加减运算,先通分,把异分母分式化为同分母分式,然后再相加减.20.化简:.考点:分式的加减法.分析:本题需先根据分式的运算顺序及法则,分别对每一项进行整理,再把每一项合并即可求出答案.解答:解:原式=,=,=,=,=.点评:本题主要考查了分式的加减,在解题时要根据分式的运算顺序及法则进行计算这是本题的关键.21.计算:.考点:分式的加减法.专题:计算题.分析:先找到最简公分母,通分后再约分即可得到答案.解答:解:原式====.点评:本题考查了分式的加减,会通分以及会因式分解是解题的关键.22..考点:分式的加减法.专题:计算题.分析:观察各个分母,它们的最简公分母是x(x﹣3),先通分把异分母分式化为同分母分式,然后再加减.解答:解:===.点评:本题主要考查异分母分式加减,通分是解题的关键.。
(完整版)八年级数学上册分式加减运算计算题练习(含答案)

(完整版)八年级数学上册分式加减运算计算题练习(含答案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)八年级数学上册分式加减运算计算题练习(含答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)八年级数学上册分式加减运算计算题练习(含答案)(word版可编辑修改)的全部内容。
八年级数学上册 分式加减运算 计算题练习1、化简:.2、化简:。
)2(2222abb a b a b a ++÷--421444122++--+-x x x x x 3、化简:。
4、化简:。
a a a a 21222-÷-+a a ---1115、化简:。
6、化简:. 22222(n m mnm m n mn m --⋅++1224422-+÷--x x x x 7、化简:。
8、化简:。
)111(111(2+-÷-+a a 1)12111(2-÷+-+-+x xx x x x 9、化简:. 10、化简:.a a a a a -+-÷--2244)111(144)14(2-+-÷---x x x x x x 11、化简:。
12、化简:.962966322--+++⋅+a a a a a a 112222+---x xx x x 13、化简:. 14、化简:。
1231621222+-+÷-+-+x x x x x x x 12)121(22+-+÷-+x x xx x 15、化简:. 16、化简:。
分式的加减法练习分式的加减运算

分式的加减法练习分式的加减运算分式是数学中的一种运算形式,可以进行加法、减法、乘法和除法等运算。
本文将着重练习分式的加法和减法运算。
一、分式的加法对于分式的加法,我们需要满足分母相同的条件下进行运算。
下面将通过例子来详细说明:例1:计算1/4 + 3/4。
解:由于两个分数的分母相同,可以直接将分子相加,分母保持不变。
1/4 + 3/4 = (1 + 3)/4 = 4/4 = 1例2:计算2/3 + 1/5。
解:这里分母不同,我们需要先找到它们的最小公倍数(LCM),然后对分子进行相应的放大。
最小公倍数(LCM) = 3 * 5 = 15将分母为3的分数2/3转化为分母为15的分数:(2/3) * (5/5) = 10/15将分母为5的分数1/5转化为分母为15的分数:(1/5) * (3/3) = 3/15现在两个分数的分母相同,可以直接将分子相加。
10/15 + 3/15 = 13/15二、分式的减法对于分式的减法,也需要满足分母相同的条件下进行运算。
下面继续通过例子来说明:例3:计算5/8 - 1/8。
解:由于两个分数的分母相同,可以直接将分子相减,分母保持不变。
5/8 - 1/8 = (5 - 1)/8 = 4/8 = 1/2例4:计算2/3 - 1/5。
解:同样,这里分母不同,我们需要先找到它们的最小公倍数(LCM),然后对分子进行相应的放大。
最小公倍数(LCM) = 3 * 5 = 15将分母为3的分数2/3转化为分母为15的分数:(2/3) * (5/5) = 10/15将分母为5的分数1/5转化为分母为15的分数:(1/5) * (3/3) = 3/15现在两个分数的分母相同,可以直接将分子相减。
10/15 - 3/15 = 7/15三、总结通过以上例子,我们可以总结出分式的加法和减法规则:1. 加法规则:分母相同,直接将分子相加,分母保持不变。
2. 减法规则:分母相同,直接将分子相减,分母保持不变。
分式加减乘除混合运算练习题及答案

分式加减乘除混合运算练习题及答案1. 运算题:计算并化简下列分式:a) $ \frac{3}{4} + \frac{2}{5} $b) $ \frac{2}{3} - \frac{1}{6} $c) $ \frac{7}{8} \times \frac{3}{4} $d) $ \frac{5}{6} \div \frac{2}{5} $e) $ \frac{1}{2} + \frac{3}{4} \div \frac{5}{6} - \frac{1}{3} $2. 答案及解析:a) $ \frac{3}{4} + \frac{2}{5} = \frac{15}{20} + \frac{8}{20} =\frac{23}{20} $b) $ \frac{2}{3} - \frac{1}{6} = \frac{4}{6} - \frac{1}{6} = \frac{3}{6} = \frac{1}{2} $c) $ \frac{7}{8} \times \frac{3}{4} = \frac{21}{32} $d) $ \frac{5}{6} \div \frac{2}{5} = \frac{5}{6} \times \frac{5}{2} =\frac{25}{12} $e) $ \frac{1}{2} + \frac{3}{4} \div \frac{5}{6} - \frac{1}{3} =\frac{1}{2} + \frac{3}{4} \times \frac{6}{5} - \frac{1}{3} = \frac{1}{2} + \frac{18}{20} - \frac{1}{3} = \frac{1}{2} + \frac{9}{10} - \frac{1}{3} =\frac{90}{180} + \frac{135}{180} - \frac{60}{180} = \frac{165}{180} =\frac{11}{12} $3. 总结:以上是分式加减乘除混合运算的练习题及答案。
分式加减法混合运算测试题及答案

分式加减法混合运算测试题及答案测试题:
1. 将3/4和2/5相加,结果为多少?
2. 将5/6和1/3相减,结果为多少?
3. 将2/3和4/9相加,结果为多少?
4. 将7/8和3/4相减,结果为多少?
5. 将4/5和3/10相加,结果为多少?
答案:
1. 首先将两个分数的分母求最小公倍数,最小公倍数为20。
将3/4
和2/5转化为通分后的分数为15/20和8/20。
将分子相加,得到23/20。
然后将结果化简为最简分数形式,即为1 3/20。
2. 首先将两个分数的分母求最小公倍数,最小公倍数为6。
将5/6
和1/3转化为通分后的分数为5/6和2/6。
将分子相减,得到3/6。
然后
将结果化简为最简分数形式,即为1/2。
3. 首先将两个分数的分母求最小公倍数,最小公倍数为9。
将2/3
和4/9转化为通分后的分数为6/9和4/9。
将分子相加,得到10/9。
然
后将结果化简为最简分数形式,即为1 1/9。
4. 首先将两个分数的分母求最小公倍数,最小公倍数为8。
将7/8
和3/4转化为通分后的分数为7/8和6/8。
将分子相减,得到1/8。
5. 首先将两个分数的分母求最小公倍数,最小公倍数为10。
将4/5
和3/10转化为通分后的分数为8/10和3/10。
将分子相加,得到11/10。
然后将结果化简为最简分数形式,即为1 1/10。
(05)分式加减法专项练习60题(有答案)ok之欧阳理创编

分式加减法专项练习60题(有答案)时间:2021.03.05 创作:欧阳理1.2.a(a﹣1)+3.4..5. +.6..7.=_________.8..6yue289..10..11..12.13.14..15.16.(1);(2)17.18.1+19.﹣+20.21.+.22.23..24.,25.26.++.27.+﹣.28.29.(式中a,b,c两两不相等):30.31.(1);(2)….32.+﹣33.化简分式:.34.. 35.计算:﹣.36.计算:. 37.计算:.38.. 39.计算化简:.40.计算:+++. 41.计算.42.计算:. 43.化简:.44.. 45.计算:.zuoguo46.. 55.化简:.47.化简:.48.. 49..50.计算:﹣. 51.计算:.52.计算:1﹣•. 53.计算:.54.化简56.先观察下列等式,然后用你发现的规律解答下列问题:由,,…(1)计算++++++=_________(n为正整数);(2)化简:+…+.57.化简:﹣. 60.求和.58.请你阅读下列计算过程,再回答所提出的问题:题目计算:解:原式=(A)=(B)=a﹣3﹣6(C)=a﹣9(D)(1)上述计算过程中,从哪一步开始出现错误:_________.(2)从B到C是否正确,若不正确,错误的原因是_________.(3)请你把正确解答过程写下来.59.观察下面的变形规律:=1﹣;=﹣;=﹣;…解答下面的问题:(1)若n为正整数,请你猜想=_________;(2)证明你猜想的结论;(3)求和:+++…+.参考答案:1.原式===1+1=2.2.原式=a2﹣a+=a2﹣a+a=a2.3.==.4.原式===.5.原式=+==.6.原式===.7.==.8.原式===a﹣1.9.原式==.10.+=+=+==1.11.原式=﹣==.12.原式=﹣=﹣=.13.原式=+===14.原式=+==.15.=﹣=﹣==﹣1.16.(1)原式=;(2)原式=17.====.18.原式=1﹣====.19.原式=﹣•==.20.===0.21.原式=+==.22.原式=﹣==.23.原式=====1.24.原式====;x的取值范围是x≠﹣2且x≠1的实数.25.原式==.26.====027.原式=﹣﹣==28.=.29.原式=++=+++++=0.30.原式=+﹣==.31.(1),=,=;(2)+…+=﹣+﹣+…+﹣=﹣=.32.==﹣233.=(2a+1)+﹣(a﹣3)﹣﹣(3a+2)++(2a﹣2)﹣=[(2a+1)﹣(a﹣3)﹣(3a+2)+(2a﹣2)]+(﹣+﹣)=﹣+﹣=﹣=.34.原式=﹣=﹣=== 35.原式====﹣36.原式==== 37.原式==38.原式=+﹣==39.原式=++=+﹣====40.原式=+++=++=++=+ =+=.41.设2x2+3x=y,则原式=﹣+===.42.原式=﹣a+2=a+1﹣a+2=3.43. 原式====.44.原式===,===45.=﹣===46.=====47.原式=,=﹣+,=+﹣﹣++,=048.原式=2a﹣a﹣1+a+1=2a.49.原式====.50.原式====.51.原式===.52.原式=1﹣×=1﹣==﹣.53.原式=+﹣====54.原式=++=+++++=﹣+﹣+﹣=0+0+0=055.原式===156.(1)原式=1﹣+﹣+…+﹣=1﹣=;(2)原式=﹣+…+﹣=﹣=57.原式=﹣=﹣=1 58.(1)A(2)不正确,不能去分母(3)原式 ===59.(1)=﹣;(2)﹣=﹣==;(3)+++…+=1﹣+﹣+﹣+…+﹣=1﹣=60.原式=++++…+﹣=+++…+﹣=+﹣=﹣=.时间:2021.03.05 创作:欧阳理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 05) 分式加减法专项练习60 题( 有答案) ok分式加减法专项练习60题(有答案)2.4.2丄a(a- 1)二5.2 a .a+1 .i'.8.6yue2810.靳_ 1m2 -4 应.K2+X-2 x2 2x12.X£+4X+4 13.214a - 1 a2+a15.- 2a+l ¥-116. (1) J+S] /-9x~+3i x 2+6K4-917.a- m2 2iri nin - 2n ID?- 4mn-F4 r 2 18.21. a2+ab+ b 2b2ab+?-b3b2 - 2ab+ b2+a2 - 1: 219.x _1---- +计12a - b _ c i 2b - c _ a ’ 2c _ a.-b~2 "I 2 "I 2 a _ ab _ ac+bc b _ ab _ bc+ac c _ ac _ bc+ab 23. ir^+2ni+l V 7? 2 24 . 25. 26. --+ 亠一 叩丄一 g 3 _ IT m+3 2y+z y — 2玄 ・;:. /J 27. 28. r+9b _ a+3b 3ab Sab 29. (式中a , b , c 两两不相等)31.( 1)——一;心;2曰'+3*2 _ 己2 _ 廿 _ 5 _ 3 a? _ 4邑- § 2护 - 3时5a+1 af2 a - 2 + a -3:, 1 … K (xfl) T (计1)(計刃 (x+2005) (x+2006) (2) b 2a+< b-c a 一 b+c |b ~ a - c b _ a - c32.33.化简分式:34.x 2+2sy+ y 2 _ x 2- 2sy+y 236.计算:38. 1 12 4 1-X |i+1十/ 1+/ 40•计算: 39 .计算化简: 37•计算: ", 3x- 4y 1 2 1/+旳-1 2x +3K +1 2X 2+3I +341 .计算47.化简:2a_ b- c _ 2b _ c _ a , 2c _ a ~ b (a-b) ta_c) * (b_c) Cb - a)亠(G_(G_b)42•计算:7s +2a+la+1(a- 2)43 .化简:1 2y45 .计算:2zuoguo55 .化简: F2-! ! 2 x2+2y+l 时148. 〔話口4£1—1a- 149.a3a+l . 2a+3a2-l 1- a252•计算: 54. 化简 56. 50.计算: 1 - 51 •计算: 53 .计算: 丄占樂 a b 2ab2JS ' y _ z 2y __ 2 2z _ K _ y~~5 "I o "I- Ky- xz+yz y^- xy - yz+xz z^- KZ - yz+sy 1 1 1 .1 2X3- 6~2 3 ]二丄二丄_1 1 1 - 1 _, (2)化简: 1 + + + + + + = IX 刃 2X3 3X4 4X5 5X^ 6X7 7X8 '—□ _________ 1 ________ L [ (1)计算 (K +2) (X +3) 先观察下列等式,然后用你发现的规律解答下列问题:]二丄二丄_ 1 ,3X4^12^3 1 (n 为正整数); (x+1) (x+1) (x+2) +・・+ 1 (x+2QQ8) C K +2009)60.求和58•请你阅读下列计算过程,再回答所提岀的问题:题目计算:解:原式=一-' (A)a+3 (a+3) (a- 3)= a-3 _ 6(a+3) (□- 3)((a - 3)=a— 3- 6 (C)=a- 9 ( D)(1 )上述计算过程中,从哪一步开始岀现错误:_ _ .(2)从B到C是否正确,若不正确,错误的原因是___________________(3 )请你把正确解答过程写下来.59.观察下面的变形规律:L=[丄丄—-丄丄;解答下面的问题:(1 )若n为正整数,请你猜想一.1 一 = _ _ ;n (n+1)(2)证明你猜想的结论;(3) ---------------------------------------------------------- 求和:一=—+—=—+—=—+ •- + ------------------------------------------ = ------- .1X2 2X3 3X4 3011X2012参考答案:1 原式=• .' . -1 - I =1 + 1=2 .a _b a _ b a _ b十「、 2 自(已+1) 2 22 .原式=a — a+ =a - a+a=a .nfl3.4.2x _ 1X 1.1(汁1) (K- 1) X-1 「(計1) (Li) 1工+1原式=5.6.7.-+a+12 =(a+1) Ca_1)a -(aH)1+2Ca--.1a-1x _ 3x 一 3 I丄K ( 3:-3) x (x-3)X (x ~3)=X.1+23a a原式=原式=1 . 210.a2 - ab b = a (a b) + b = a + b a a+l>Pt/ a+b (a+b) (a _b) a+b a+b|a+b a4b(m-1) (m- 2)2m (ID-1) (nrl-1) m_ 22m Cnrf-1)15.a — 1 _ a^+a厂a- 1 a (a+1) 1 I— 2a+l _ 1 '(a-l)2(a~ 1) Cff+1)=a-l18. 19. 21 . 22. 23. 」12-2 (昭3) -2 (m 3) 2 (耐3) (m _ 3) (nrl-3) (m _3)(w+3)16.( 1)原式 (2)原式=—^亠—丄—亠—丄. 1 4 a+2 -4=甜27□ -2 (a+2) Ca _ 2) (a+2)冷- 2)(a+2) (a _2)(s+Z 〕(□ _2)a -2 = 1 |(a+2) (a - 2) a+217. 2(H +3) 2(7+3) (K -H 3) K +3原式=1 - D - n (m - 2n ) in -2n (mi-n) (m 一 n)a 2+ab+b 2rn _2n1 -------rrH-n - ( m _2n ) _rn^n - n^2n _ j n—b 24(卅)(a~b) _ 1 _ b_1 -b(a -b) 2| b ( a+b)'□-b (旦-b) ~irri nirr^n rn^nnH-n=0.. a+l+a 1 2a 0且一 1 8+1 /-I(a - 1) (a+1) (a+1) fa _1)20.(a~b)( a^+ab+ b 2)原式= 原式 (D 21G+l ) 2=计1(X+1) (K-1) T(K H) (X -1)(计 1)C K -1)K-1, 2xyy (x+y) y (x - y) =y (K _ y) (K +Y )(x - y) Cx+y) (K - y)(旳)x4y原式 2=1 .(nrfl ) 2itd-1 2 计 1 - 2 ra~ 1原式(i □- 1〕(nrbl ) m _m -1 m _1 m _1x 的取值范围是 x a 2且x 的实数.24•原式 26.12 . 2 2 112-2 (m+3) 2 Cm - 3)珈 2 - g 丁3一 jn 「n+3 ([[H-3) (ID - 3i 亠(nrl-3) Cm - 3) # (nH-3) (m _3) 12_2 (m+3) 42 Cm - 3) 12_ 2m _加f (in^3) (n - 3)(nrt3) (ro _3)27. 2y+xy=・・—2y+x y -2iy K■丄|,/=x 2-y 2m (x -y)x+ya+9b a+3b a+9b * ~ (a-K3b) ■仙23ab 3ab - 3ab3ab a原式 28.111111+++++a _ c □-1>b _刁bn c- t> C ~□5工30.原式=(x+3) (x~ 2) (K+引(K_4)7x-102) (K-4)5(-4) + (滋-5) (A-2)- (7x-10) (^+3)Cx-4)(d-3) (x_2)31.( 1)x2. _ K2 ~y2x+y x+yy3(2) +・・+32.(计刃a —2)d-小亠亠+亠-(x+2005)(计2006), 齢1 直+l x+2-_ + ••七1 =. 200&^+2006'x (x+2006)1b2a^c=丄(孟+]〉" (孟+1) ―(x+2)2a+c - b-+c‘--L …亠-L = - 24 二■!■二a" b+c b _ a _G b _ a _G b _ a-G b 一且2a2+3a+2 _ _ 3a2_4a~^ 2 a2 _ Sa+Sarbl a+2 a_ 2 + a-3=(2a+1) (a— 3) —-(3a+2)+ (2a- 2)=[(2a+1)-( a- 3)-( 3a+2) + (2a- 2)111,1亘*1a+2( a _2[_□ _ 3 (afl) (a+2)(1a+11 \| 1a+2 a- 21(□- 2) (a~ 3)1a _ 2]+1(aH) tar+2) (a- 2) (a _3)'34 .原式=& - y \ 2垃4y耳_ y x+y - at+y 2y 2sy (x_ y) xy sy xy xy xG+y) 2 sy(x+y)35.K2 - 2sy+ y^-2z2-2y32 (x+y) (x ~ y)38. 原式x2C K - 1)叙(K-1) +6 it2- &十5) (x- 1?8 Trl-5X2(M _ 1)x2(x - 1)+39 .原式= ------ —■——+.'(x+2) (K +1)(汁 2) (x+2 (1-幻-1) ■ (1+C£ ( X 1 ) Z (i+1) ―|「 2 (x+2)](x+2)(計1〕〔=-1) (K +2)(x+1) (K - 1) 「(x+2)(时1) (K - 1)/ 玄十 t 2x 4 2X 2-2X - 4 =2 2) (x+L) 2s - 4〔計小〔/-1) (x+2)〔耳+1) (x-1) ](K +刀 <z+l)(蛊T) X 2+X -240 •原式=+• 2 +十 1+护 1+J1 - X (1 — “ (1+G 14■覽 (1 - X)~( 1 十辺 ,4 =2 |HX4(1-x) <l+x) 4 1= ±JLAJ十4 (1+ J) _L4 (1+J) 8 ] (1+ J) (1-x 4) (Bx 4) l-x S+ + (1 - I 2) (1+ x 2) 2 (1+^2) □」)(1+/) 241 .设2x +3x=y ,则原式= (yM) Cy+3) -2 (y-1) (y+3) + Cy-1)(列4) 厂 S (y-1) (y+1)(什引(y-1) <y+D (y+3)8(2/+旳-1) (2X 2+3I +1) (2X 2+3X +3)' 42 .原式= 1 , 2y i - y^2y1・s+y (x+y) (s _y) (s+y) (K _y) (s+y) (K _y?K_y ■ J ys2 y2 s K ( K ~ y) y (y _ z)K ( K ~ y)F (; s _ y ) xy (K _yiK 、r (K ~y) -a+2=a+1 - a+2=3. 43.原式= 44.原式 ?Z ) 2y 2 ~ K 2-(垃+y) (x- y) _ x+ysy (x -y) xy (K~y)iy2 y 十H2 y2X1 y 2-x 2(y+工)(y x),-/y-*x (K - y)K (x - y) x U - y)K (K - y)45.2KV x _ x E M 什貨(x - y) +x (x+y) 9 92zy+ z - XV+ 92sy+2 x 凤2 - x+y ^-y _]宀/ I'_2 _ 2K y(x _y) (x+y)46. 2s (i+y)(s -y) ( x+y} s - y 47 .原式=2c - a - b.一: - 1■,48.49.50.51.(已〜-b? + (a-<) (b - c)+ (b - a)(a-b) (a-c) (b-c) (□-!>)1+ 1 丨—1 1 —i n TU 1 =0a _<;n -b a _ b+ + , =0c _ l> c _ b c _□(c - a) (G - b)+.原式c- a) + (a+ (3a+l) ■ (2a+3)a+3a4-l - 2a 3 2 (a-1) 2= 厂1=^-1 [_宀1 |a+1原式=2a - a _ 1+a+仁2a.52.原式=1 —卞-1 一〔3时5) -2K6(K+3)G-l)=&+3)(K—1)=(x+3) (n「1)4 x- 83x+6 12 一)(x -2 )'(x+2 )(x-2 ) ( x+2)(x-2)=(=1- 1 1 ax -----(寸3)=1站3=(曲) -(o+3)=—2原式7 x- IE(x+2(a+1)冷T)a+1a原式n+2 )__( K-2) K+2=I ,,2a2ab2屈53.原式2b-^2a 12a+b) 2b+2a - 2a b_ b .J H2ab =2ab2ab 2aba+1(x - y) 4 (K- z) (y- x) + (y-z)(z-x) + (z y)(x ~ y)〔皐一込)(y - x) z)(z _ x) (E_y)1+1 111 1 ]111瓦-y y _z1y _ z12 - y忑一蓋54.原式55.原式1+ -1•x - y —y _z|=0+0+0=0 X2-1+2(好1)(x+L ) 2= 4+1 )戈=_(田)21 1 1-- +…+ —:1S =8=1=l—+••+,1—1 =1 ―=2009|x sfl|x+2008 x+2009 』工+2009 i E (jd-2009)=1(2)原式7 356.("原式=1 -丄―工57 .原式=2 KK-2'K- 22(1)59. —;(x+2) (x _2)58.( 1) A ( 2)不正确,不能去分母(3)原式=1 in(2)-=.n+1 n .n+1 - n 1n+1口(n+1)n (nH) 口(n+1)n (n+1)I 1 + 1 + 1〔+••』 1 =1 —1」1」1|+1-l|+j 1_ 1 =1 | 1 =20111X22X3 3X4 |2011 X 2012 ' |2]2 |3 3 4 |201112012 2012 2012.1+ :+.2 1 -X 1+x1+y2+ —+••+:f1+ ? 1+工加+21L —亠2n12剧1-^ 1+直加—X 1-訶60.原式。
