导数的运算练习题一
导数的运算专项练习(含答案)

导数的运算一、单选题(共33题;共66分)′(x)是函数f(x)=x3+2x+1的导函数,则f′(-1)的值为()A. 0B.3 C.4 D. -2.函数的导数为()A. B.C. D.3.设函数,若,则等于()A. B.C.D.4.设则等于( )A. B.C. D.5.已知函数的导函数,且满足,则=( )A.B.C. 1D.6.已知函数的导函数为,且,则()A. 2B. 3C. 4D. 57.下列求导运算的正确是()A. 为常数B. C. D.8.已知函数的值为()A.B. C .D.9.下列求导运算正确的是()A. B.C. D.10.已知函数f(x)=sinx-cosx,则f'()=()A. B.C. D .11.若函数f(x)=2+xcos2x,则f'(x)=()A. cos 2x-xsin 2xB. x-sin2x C. 1-2sin2x D. cos2x-2sin2x12.函数的导数为()A. =2B. =C. =2D.=13.设函数的导函数为,且,则=( )A. 0B.-4 C. -2 D. 2 14.设,若,则()C.D.15.已知函数,则其导数()A. B.C.D.16.若函数,则的值为()A. 0 B . 2 C.1 D.-117.已知函数,且,则的值为()A. B.C.D.18.已知函数,为的导函数,则的值为()A.B.C.D.19.下列求导运算正确的是()A. B.C. D.20.已知函数的导函数为,且满足,则()A. B . C.21.若,则函数的导函数()A. B.C. D.22.函数的导数为()A. B.C.D.23.下列导数式子正确的是()A. B.C. D.24.已知,则等于()A. -2B. 0C. 2D. 425.已知函数,则()A. B.C.D.26.已知,则()A.B.C.D.27.设,,则x0=( )A. e2B.e C.D. ln 228.下列求导数运算正确的是()A. B.C. D.29.若f(x)=x2-2x-4ln x,则f′(x)>0的解集为()A. (0,+∞)B. (-1,0)∪(2,+∞) C. (-1,0) D. (2,+∞)30.下列求导运算正确的是( )A. B. C.D.31.已知,则( )A. B.C.D. 以上都不正确32.设f(x)=xln x,若f′(x0)=2,则x0等于( )A. e2B.e C.D. ln 233.下列导数运算正确的是()A. B.C. D.二、填空题(共11题;共11分)34.已知函数的导函数为,若,则的值为________.35.若函数,则的值为________.36.已知,则________.37.若函数,则________.38.已知函数,则________.39.已知函数,是的导函数,则________.40.若f(x)=x3,f′(x0)=3,则x0的值为________.41.已知在上可导,,则________.42.已知函数的导函数为,且,则________.43.已知f(x)=2x+3xf′(0),则f′(1)=________.44.已知函数f(x)=2e x﹣x的导数为,则的值是________.三、解答题(共6题;共60分)45.求下列函数的导函数.①②③④⑤⑥46.求下列函数的导函数①②③④⑤⑥47.求下列函数的导数:(1);(2).48.求下列函数的导数:(1);(2);(3);(4).49.求下列函数的导数.(1);(2).50.求下列函数的导数.(1)y=3x2+xcos x;(2)y=lgx-;答案解析部分一、单选题1.【答案】 B【考点】导数的运算【解析】【解答】解:因为,则,所以,故答案为:B.【分析】先由函数,求得导函数,再求即可得解.2.【答案】 D【考点】导数的运算【解析】【解答】因为,则函数的导函数,故答案为:D.【分析】先根据完全平方公式对展开,再运用常见初等函数的求导公式和求导运算法则可求解.3.【答案】 D【考点】导数的运算【解析】【解答】,,,解得,故答案为:D,【分析】对函数求导,再由可求出实数的值.4.【答案】 D【考点】导数的运算【解析】【解答】由,得.故答案为:D.【分析】由已知利用导数的运算性质进行计算,即可得结果.5.【答案】 B【考点】导数的运算【解析】【解答】对函数进行求导,得把代入得,直接可求得。
导数的运算练习题

导数的运算练习题在微积分学中,导数是非常重要的概念之一,它用于描述函数在某一点附近的变化率。
掌握导数的运算是学习微积分的基础,本文将为大家提供一些导数的运算练习题,帮助读者巩固掌握导数的计算方法。
1. 计算下列函数的导数:(1)f(x) = x^3 + 2x^2 - 5x + 1(2)g(x) = sin(x) - cos(x)(3)h(x) = e^x + ln(x)(4)i(x) = √(x^2 + 1)2. 计算下列函数的导数:(1)f(x) = 2x^3 - 3x^2 + 4x - 1(2)g(x) = cos(x) + sin(x) + tan(x)(3)h(x) = ln(x^2) - e^(2x)(4)i(x) = √x + 1/x3. 计算下列函数的导数:(1)f(x) = x^4 + 2x^3 - 3x^2 + 4x - 1(2)g(x) = sin(2x) - cos(2x)(3)h(x) = e^(x^2) + ln(x^3)(4)i(x) = ln(x) + e^x4. 计算下列函数的导数:(1)f(x) = x^5 + 2x^4 - 3x^3 + 4x^2 - 5x + 1(2)g(x) = sin(x)cos(x)(3)h(x) = ln(x) + e^x - x(4)i(x) = e^(2x) + ln(x^2)通过以上的练习题,读者可以熟悉导数的计算方法,掌握常用函数的导数运算规则。
在计算导数时,读者需要注意以下几点:1. 基本函数的导数规则:对于多项式函数,求导后,指数降低1,系数不变;对于三角函数,求导后,正弦变余弦,余弦变负正弦;对于指数函数,求导后,底数不变,指数变形式的导数。
2. 乘法法则:若函数为两个函数的乘积,则导数等于其中一个函数的导数乘以另一个函数,再加上另一个函数的导数乘以第一个函数。
3. 除法法则:若函数为两个函数的商,则导数等于分子函数的导数乘以分母函数,减去分母函数的导数乘以分子函数,再除以分母函数的平方。
(word完整版)导数的运算练习题

导数的运算练习一、常用的导数公式(1)'C = (C 为常数); (2)()'n x = ; (3)(sin )'x = ; (4)(cos )'x = ; (5)()'x a = ; (6)()'x e = ; (7)_____________; (8)_____________;二、导数的运算法则 1、(1) ; (2);(3)______________________________________; (4)=___________________________________;(C 为常数)2、复合函数的导数设 .三、练习1、已知()2f x x =,则()3f '等于( )A .0B .2xC .6D .9 2、()0f x =的导数是( )A .0B .1C .不存在D .不确定 3、32y x = ) A .23xB .213x C .12- D 33x4、曲线n y x =在2x =处的导数是12,则n 等于( )A .1B .2C .3D .45、若()f x =()1f '等于( )A .0B .13- C .3 D .136、2y x =的斜率等于2的切线方程是( ) A .210x y -+=B .210x y -+=或210x y --=C .210x y --=D .20x y -= 7、在曲线2y x =上的切线的倾斜角为4π的点是( ) A .()0,0 B .()2,4 C .11,416⎛⎫ ⎪⎝⎭ D .11,24⎛⎫⎪⎝⎭8、设()sin y f x =是可导函数,则x y '等于( )A .()sin f x 'B .()sin cos f x x '⋅C .()sin sin f x x '⋅D .()cos cos f x x '⋅ 9、函数()22423y x x=-+的导数是( )A .()2823x x -+B .()2216x -+ C .()()282361x x x -+-D .()()242361x x x -+-10、曲线34y x x =-在点()1,3--处的切线方程是( ) A .74y x =+B .72y x =+C .4y x =-D .2y x =-11、点P 在曲线323y x x =-+上移动,设点P 处切线的倾斜角为α,则角α的取值范围是( )A .0,2π⎡⎤⎢⎥⎣⎦B .30,,24πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭C .3,4ππ⎡⎫⎪⎢⎣⎭ D .3,24ππ⎛⎤ ⎥⎝⎦12、求函数212y x =-在点1x =处的导数。
函数求导练习题(含解析)

一.解答题(共15小题)1.请默写基础初等函数的导数公式:(1)(C)′=,C为常数;(2)(xα)′=,α为常数;(3)(a x)′=,a为常数,a>0且a≠1;(4)(log a x)′=,a为常数,a>0且a≠1;(5)(sin x)′=;(6)(cos x)′=.2.求下列函数的导数(1)y=x2﹣7x+6;(2)y=x+2sin x,x∈(0,2π).3.求下列函数的导数:(1)f(x)=3x4+sin x;(2).4.求下列函数的导数:(1)y=ln(2x+1);(2).5.求下列函数的导数:(1);(2)g(x)=(8﹣3x)7;(3)p(x)=5cos(2x﹣3);(4)w(x)=ln(5x+6)2.6.求下列函数的导数.(Ⅰ);(Ⅱ).7.求下列函数的导数.(1)f(x)=sin x cos x;(2)y=.8.求下列函数的导数.(1)y=;(2)y=(2x2+3)(3x﹣2).9.求下列函数的导数:(1);(2).10.求下列函数的导数:(1)S(t)=;(2)h(x)=(2x2+3)(3x﹣2).11.求下列函数的导数.(1);(2).12.求下列函数的导数:(1)y=;(2)y=.13.求下列函数的导数:(1)y=sin x+lnx;(2)y=cos x+x;(3)y=x sin x;(4);(5)y=3x2+x cos x;(6).14.求下列函数的导数.(1)y=x3﹣2x+3;(2)y=x sin(2x+5).15.求下列函数的导数:(1)y=(x2+3x+3)e x+1;(2)解析一.解答题(共15小题)1.请默写基础初等函数的导数公式:(1)(C)′=0,C为常数;(2)(xα)′=αxα﹣1,α为常数;(3)(a x)′=a x lna,a为常数,a>0且a≠1;(4)(log a x)′=,a为常数,a>0且a≠1;(5)(sin x)′=cos x;(6)(cos x)′=﹣sin x.分析:根据初等函数的导数公式,直接求解即可.解答:解:(1)(C)′=0,(2)(xα)′=αxα﹣1,(3)(a x)′=a x lna,(4)(log a x)′=,(5)(sin x)′=cos x,(6)(cos x)′=﹣sin x.故答案为:(1)0;(2)αxα﹣1;(3)a x lna;(4);(5)cos x;(6)﹣sin x.点评:本题主要考查初等函数的导数公式,比较基础.2.求下列函数的导数(1)y=x2﹣7x+6;(2)y=x+2sin x,x∈(0,2π).分析:利用导数的运算性质逐个化简即可求解.解答:解:(1)由已知可得y′=2x﹣7;(2)由已知可得y′=1+2cos x.点评:本题考查了导数的运算性质,属于基础题.3.求下列函数的导数:(1)f(x)=3x4+sin x;(2).分析:(1)(2)由基本初等函数的导数公式及导数加减、乘法法则求导函数即可.解答:解:(1)f(x)=3x4+sin x则f′(x)=12x3+cos x;(2),则f′(x)=+﹣2e2x﹣1.点评:本题主要考查导数的基本运算,比较基础.4.求下列函数的导数:(1)y=ln(2x+1);(2).分析:根据导数的公式即可得到结论.解答:解:(1)∵y=ln(2x+1),∴y′=×2=,(2)∵,∴y′=﹣sin(﹣2x)×(﹣2)=2sin(﹣2x)=﹣2sin(2x﹣).点评:本题主要考查导数的基本运算,比较基础.5.求下列函数的导数:(1);(2)g(x)=(8﹣3x)7;(3)p(x)=5cos(2x﹣3);(4)w(x)=ln(5x+6)2.分析:根据复合函数的求导法则、基本初等函数的求导公式求导计算即可.解答:解:(1)∵,∴.(2)∵g(x)=(8﹣3x)7,∴g'(x)=7(8﹣3x)6⋅(8﹣3x)'=﹣21(8﹣3x)6.(3)∵p(x)=5cos(2x﹣3),∴p'(x)=﹣5sin(2x﹣3)⋅(2x﹣3)'=﹣10sin(2x﹣3).(4)∵w(x)=ln(5x+6)2,∴点评:本题考查导数的计算,注意复合函数的导数计算,属于基础题.(Ⅰ);(Ⅱ).分析:根据导数的公式即可得到结论.解答:解:(Ⅰ)=.(Ⅱ).点评:本题主要考查导数的基本运算,比较基础.7.求下列函数的导数.(1)f(x)=sin x cos x;(2)y=.分析:利用导数的运算性质化简即可求解.解答:解:(1)因为f(x)=sin x cos x=sin2x,所以f′(x)=cos2x×=cos2x,(2)∵y=,∴y′==.点评:本题考查了导数的运算性质,考查了学生的运算求解能力,属于基础题.8.求下列函数的导数.(1)y=;(2)y=(2x2+3)(3x﹣2).分析:根据导数的公式,即可依次求解.解答:解:(1)y'==.(2)因为y=(2x2+3)(3x﹣2)=6x3﹣4x2+9x﹣6,所以y′=18x2﹣8x+9.点评:本题主要考查导数的运算,属于基础题.(1);(2).分析:(1)先展开f(x),然后求导即可;(2)根据基本初等函数和商的导数的求导公式求导即可.解答:解:(1),;(2).点评:本题考查了基本初等函数和商的导数的求导公式,考查了计算能力,属于基础题.10.求下列函数的导数:(1)S(t)=;(2)h(x)=(2x2+3)(3x﹣2).分析:结合基本初等函数的求导公式及求导法则求解即可.解答:解:(1)S(t)==t+,所以S′(t)=1﹣;(2)h(x)=(2x2+3)(3x﹣2),所以h′(x)=4x(3x﹣2)+3(2x2+3)=18x2﹣8x+9.点评:本题主要考查了基本初等函数的求导公式及求导法则,属于基础题.11.求下列函数的导数.(1);(2).分析:利用复合函数的导函数的求法,结合导数的运算求解即可.解答:解:(1),所以;(2)所以.点评:本题考查了导函数的求法,重点考查了导数的运算,属基础题.12.求下列函数的导数:(1)y=;(2)y=.分析:直接利用基本初等函数的导数公式,复合函数的导数公式以及导数的四则运算求解即可.解答:解:(1)令t=1﹣2x2,则,所以;(2).点评:本题考查了导数的运算,解题的关键是掌握基本初等函数的导数公式,复合函数的导数公式以及导数的四则运算,考查了运算能力,属于基础题.13.求下列函数的导数:(1)y=sin x+lnx;(2)y=cos x+x;(3)y=x sin x;(4);(5)y=3x2+x cos x;(6).分析:由已知结合函数的求导公式即可求解.解答:解:(1)y′=cos x+;(2)y′=﹣sin x+1;(3)y′=sin x+x cos x;(4)y′==;(5)y′=6x+cos x﹣x sin x;(6)y′==﹣.点评:本题主要考查了函数的求导公式的应用,属于基础题.14.求下列函数的导数.(1)y=x3﹣2x+3;(2)y=x sin(2x+5).分析:根据基本初等函数和复合函数的求导公式求导即可.解答:解:(1)y′=3x2﹣2;(2)y′=sin(2x+5)+2x cos(2x+5).点评:本题考查了基本初等函数和复合函数的求导公式,考查了计算能力,属于基础题.15.求下列函数的导数:(1)y=(x2+3x+3)e x+1;(2).分析:利用导数的运算法则以及常见函数的导数进行求解即可.解答:解:(1)因为y=(x2+3x+3)e x+1,所以y'=[(x2+3x+3)e x+1]'=(x2+3x+3+2x+3)e x+1=(x2+5x+6)e x+1=(x+2)(x+3)e x+1;(2)因为,所以.点评:本题考查了导数的运算,主要考查了导数的运算法则以及常见函数的导数公式,考查了化简运算能力,属于基础题.。
《导数的四则运算法则练习题一

《导数的四则运算法则练习题一各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢篇一:导数公式以及四则运算法则练习导数的计算一、选择题cosx的导数是()C xsinxxsinx?cosxxcosx?cosx? A?2B?sinx C?D xx2x21、函数y?2、曲线y?x?ex在以下哪个点处的切线斜率等于0 ()AA (0,-1)B(1,0)C (0,1)D(-1,0)3、函数y?sinx(cosx?1)的导数是()C2 A cos2x?cosx B cos2x?sinxC cos2x?cosxD cosx?cosx4、曲线y?x?3x上切线平行于x轴的点的坐标是()DA(-1,2)B (1,-2)C(1,2)D (-1,2)或(1,-2)5、设y??a??x,则y/等于()DA312?a?12?x B 12?xC 12?a?12?xD?12?x6、若f(x)?2sin(3x??),则f/()等于()B 44?A 6B -6C 2D -237、曲线y?x?x?2在P点处的切线平行于直线y?4x?1,则此切线方程是()DA y?4x By?4x?4C y?4x?8D y=4x或y=4x-42f(x)-8x的值是()B x?1x-1A 5B2 C 4D 不存在8、已知f(1)=4,f’(1)=5 则lim二、填空题9、函数y?xtanx的导数是_______________________.sinxcosx?x2cosx5210、设f(x)?x?4x?5,则f[f/(=___________________.2 2211、函数y?(x?1)(x?1)在x?1处的导数是__________.412、函数y=log2的导数是_________________________________.三、解答题13、求函数y?sin(x?14、求函数y?3ex+13(ex+x)ln2 1)的导数。
xx?sinxxcosx?cosx?sinx?xsinx?1的导数。
2023届全国高考数学复习:专题(导数的运算)重点讲解与练习(附答案)

2023届全国高考数学复习:专题(导数的运算)重点讲解与练习1.基本初等函数的导数公式2.导数的运算法则若f ′(x ),g ′(x )存在,则有[cf (x )]′=cf ′(x );[f (x )±g (x )]′=f ′(x )±g ′(x );[f (x )g (x )]′=f ′(x )g (x )+f (x )g ′(x );⎣⎡⎦⎤f (x )g (x )′=f ′(x )g (x )-f (x )g ′(x )[g (x )]2(g (x )≠0); 3.复合函数的定义及其导数(1)一般地,对于两个函数y =f (u )和u =g (x ),如果通过中间变量u ,y 可以表示成x 的函数,那么称这个函数为函数y =f (u )与u =g (x )的复合函数,记作y =f (g (x )).(2)复合函数y =f (g (x ))的导数和函数y =f (u ),u =g (x )的导数间的关系为y ′x =y ′u ꞏu ′x ,即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积.【方法总结】导数运算的原则和方法基本原则:先化简、再求导; 具体方法:(1)连乘积形式:先展开化为多项式的形式,再求导;(2)分式形式:观察函数的结构特征,先化为整式函数或较为简单的分式函数,再求导; (3)对数形式:先化为和、差的形式,再求导; (4)根式形式:先化为分数指数幂的形式,再求导;(5)三角形式:先利用三角函数公式转化为和或差的形式,再求导; (6)复合函数:由外向内,层层求导. 【例题选讲】[例1] 求下列函数的导数: (1)y =x 2sin x ;(2)y =cos x e x ;(3)y =x sin ⎝⎛⎭⎫2x +π2cos ⎝⎛⎭⎫2x +π2; (4)y =ln(2x -5).[例2] (1) (2020ꞏ全国Ⅲ)设函数f (x )=e x x +a .若f ′(1)=e4,则a =________.(2)已知函数f (x )的导函数为f ′(x ),f (x )=2x 2-3xf ′(1)+ln x ,则f (1)= .(3)已知f 1(x )=sin x +cos x ,f n +1(x )是f n (x )的导函数,即f 2(x )=f 1′(x ),f 3(x )=f 2′(x ),…,f n +1(x )=f n ′(x ),n ∈N *,则f 2 022(x )等于( )A .-sin x -cos xB .sin x -cos xC .-sin x +cos xD .sin x +cos x (4)(多选)给出定义:若函数f (x )在D 上可导,即f ′(x )存在,且导函数f ′(x )在D 上也可导,则称f (x )在D 上存在二阶导函数,记f ″(x )=(f ′(x ))′,若f ″(x )<0在D 上恒成立,则称f (x )在D 上为凸函数.以下四个函数在⎝⎛⎭⎫0,π2上是凸函数的是( ) A .f (x )=sin x +cos x B .f (x )=ln x -2x C .f (x )=x 3+2x -1 D .f (x )=x e x(5)已知f (x )的导函数为f ′(x ),若满足xf ′(x )-f (x )=x 2+x ,且f (1)≥1,则f (x )的解析式可能是( ) A .x 2-x ln x +x B .x 2-x ln x -x C .x 2+x ln x +x D .x 2+2x ln x +x 【对点训练】1.下列求导运算正确的是( )A .⎝⎛⎭⎫x +1x ′=1+1x 2B .(log 2x )′=1x ln 2C .(5x )′=5x log 5xD .(x 2cos x )′=-2x sin x 2.函数y =x cos x -sin x 的导数为( )A .x sin xB .-x sin xC .x cos xD .-x cos x 3.(多选)下列求导运算正确的是( )A .(sin a )′=cos a (a 为常数)B .(sin 2x )′=2cos 2xC .(x )′=12xD .(e x -ln x +2x 2)′=e x -1x +4x4.已知函数f (x )=sin x cos x +1x 2,则f ′(x )= .5.已知函数f (x )的导函数为f ′(x ),记f 1(x )=f ′(x ),f 2(x )=f ′1(x ),…,f n +1(x )=f ′n (x )(n ∈N *),若f (x )=x sin x ,则f 2 019(x )+f 2 021(x )=( )A .-2cos xB .-2sin xC .2cos xD .2sin x 6.f (x )=x (2 021+ln x ),若f ′(x 0)=2 022,则x 0等于( )A .e 2B .1C .ln 2D .e7.已知函数f (x )=1ax -1+e x cos x ,若f ′(0)=-1,则a = .8.已知函数f (x )=ln(2x -3)+ax e -x ,若f ′(2)=1,则a = .9.已知函数f (x )的导函数为f ′(x ),且满足关系式f (x )=x 2+3xf ′(2)+ln x ,则f ′(2)的值等于( )A .-2B .2C .-94D .94 10.已知f (x )=x 2+2xf ′(1),则f ′(0)=________.11.设函数f (x )在(0,+∞)内可导,其导函数为f ′(x ),且f (ln x )=x +ln x ,则f ′(1)= . 12.已知f ′(x )是函数f (x )的导数,f (x )=f ′(1)ꞏ2x +x 2,则f ′(2)=( )A .12-8ln 21-2ln 2B .21-2ln 2C .41-2ln 2 D .-213.(多选)若函数f (x )的导函数f ′(x )的图象关于y 轴对称,则f (x )的解析式可能为( )A .f (x )=3cos xB .f (x )=x 3+xC .f (x )=x +1x D .f (x )=e x +x 14.f (x )=3e x+1+x 3,其导函数为f ′(x ),则f (2020)+f (-2020)+f ′(2019)-f ′(-2019)的值为( ) A .1 B .2 C .3 D .4 15.已知f (x )=ax 4+b cos x +7x -2.若f ′(2 020)=6,则f ′(-2 020)=______. 16.分别求下列函数的导数:(1)y =e xln x ;(2)y =x ⎝⎛⎭⎫x 2+1x +1x 3;(3)y =x -sin x 2cos x2;(4)y =ln 1+2x .(5)f (x )=x 3+2x -x 2ln x -1x 2.参考答案【例题选讲】[例1] 求下列函数的导数: (1)y =x 2sin x ; (2)y =cos x e x ;(3)y =x sin ⎝⎛⎭⎫2x +π2cos ⎝⎛⎭⎫2x +π2; (4)y =ln(2x -5).解析 (1)y ′=(x 2)′sin x +x 2(sin x )′=2x sin x +x 2cos x .(2)y ′=⎝⎛⎭⎫cos x e x ′=(cos x )′e x -cos x (e x )′(e x )2=-sin x +cos x e x . (3)∵y =x sin ⎝⎛⎭⎫2x +π2cos ⎝⎛⎭⎫2x +π2=12x sin(4x +π)=-12sin4x , ∴y ′=-12sin 4x -12x ꞏ4cos 4x =-12sin 4x -2x cos 4x . (4)令u =2x -5,y =ln u .则y ′=(ln u )′u ′=12x -5ꞏ2=22x -5,即y ′=22x -5. [例2] (1) (2020ꞏ全国Ⅲ)设函数f (x )=e xx +a.若f ′(1)=e 4,则a =________. 答案 1 解析 f ′(x )=e x (x +a )-e x (x +a )2=e x (x +a -1)(x +a )2,则f ′(1)=a e (a +1)2=e 4,整理可得a 2-2a +1=0,解得a =1.(2)已知函数f (x )的导函数为f ′(x ),f (x )=2x 2-3xf ′(1)+ln x ,则f (1)= .答案 -74 解析 ∵f (x )=2x 2-3xf ′(1)+ln x ,∴f ′(x )=4x -3f ′(1)+1x x =1代入,得f ′(1)=4-3f ′(1)+1,得f ′(1)=54.∴f (x )=2x 2-154x +ln x ,∴f (1)=2-154=-74.(3)已知f 1(x )=sin x +cos x ,f n +1(x )是f n (x )的导函数,即f 2(x )=f 1′(x ),f 3(x )=f 2′(x ),…,f n +1(x )=f n ′(x ),n ∈N *,则f 2 022(x )等于( )A .-sin x -cos xB .sin x -cos xC .-sin x +cos xD .sin x +cos x 答案 C 解析 ∵f 1(x )=sin x +cos x ,∴f 2(x )=f 1′(x )=cos x -sin x ,f 3(x )=f 2′(x )=-sin x -cos x ,f 4(x )=f 3′(x )=-cos x +sin x ,f 5(x )=f 4′(x )=sin x +cos x ,∴f n (x )的解析式以4为周期重复出现,∵2 022=4×505+2,∴f 2 022(x )=f 2(x )=cos x -sin x .故选C .(4)(多选)给出定义:若函数f (x )在D 上可导,即f ′(x )存在,且导函数f ′(x )在D 上也可导,则称f (x )在D 上存在二阶导函数,记f ″(x )=(f ′(x ))′,若f ″(x )<0在D 上恒成立,则称f (x )在D 上为凸函数.以下四个函数在⎝⎛⎭⎫0,π2上是凸函数的是( )A .f (x )=sin x +cos xB .f (x )=ln x -2xC .f (x )=x 3+2x -1D .f (x )=x e x答案 AB 解析 对于A :f ′(x )=cos x -sin x ,f ″(x )=-sin x -cos x ,∵x ∈⎝⎛⎭⎫0,π2,∴f ″(x )<0,f (x )在⎝⎛⎭⎫0,π2上是凸函数,故A 正确.对于B :f ′(x )=1x -2,f ″(x )=-1x 2<0,故f (x )在⎝⎛⎭⎫0,π2上是凸函数,故B 正确;对于C :f ′(x )=3x 2+2,f ″(x )=6x >0,故f (x )在⎝⎛⎭⎫0,π2上不是凸函数,故C 错误;对于D :f ′(x )=(x +1)e x ,f ″(x )=(x +2)e x >0,故f (x )在⎝⎛⎭⎫0,π2上不是凸函数,故D 错误.故选AB . (5)已知f (x )的导函数为f ′(x ),若满足xf ′(x )-f (x )=x 2+x ,且f (1)≥1,则f (x )的解析式可能是( ) A .x 2-x ln x +x B .x 2-x ln x -x C .x 2+x ln x +x D .x 2+2x ln x +x 答案 C 解析 由选项知f (x )的定义域为(0,+∞),由题意得xf ′(x )-f (x )x 2=1+1x ,即⎣⎡⎦⎤f (x )x ′=1+1x ,故f (x )x =x +ln x +c (c 为待定常数),即f (x )=x 2+(ln x +c )x .又f (1)≥1,则c ≥0,故选C .【对点训练】1.下列求导运算正确的是( )A .⎝⎛⎭⎫x +1x ′=1+1x 2B .(log 2x )′=1x ln 2C .(5x )′=5x log 5xD .(x 2cos x )′=-2x sin x 1.答案 B 解析 (log 2x )′=1x ln 2,故B 正确. 2.函数y =x cos x -sin x 的导数为( )A .x sin xB .-x sin xC .x cos xD .-x cos x 2.答案 B 解析 y ′=x ′cos x +x (cos x )′-(sin x )′=cos x -x sin x -cos x =-x sin x . 3.(多选)下列求导运算正确的是( )A .(sin a )′=cos a (a 为常数)B .(sin 2x )′=2cos 2xC .(x )′=12xD .(e x -ln x +2x 2)′=e x -1x +4x3.答案 BCD 解析 ∵a 为常数,∴sin a 为常数,∴(sin a )′=0,故A 错误.由导数公式及运算法则知B ,C ,D 正确,故选BCD .4.已知函数f (x )=sin x cos x +1x 2,则f ′(x )= .4.答案 1cos 2x -2x 3 解析 f ′(x )=(sin x )′ꞏcos x -sin x ꞏ(cos x )′cos 2x+(x -2)′=cos 2x +sin 2x cos 2x +(-2)x -3=1cos 2x -2x 3. 5.已知函数f (x )的导函数为f ′(x ),记f 1(x )=f ′(x ),f 2(x )=f ′1(x ),…,f n +1(x )=f ′n (x )(n ∈N *),若f (x )=x sin x ,则f 2 019(x )+f 2 021(x )=( )A .-2cos xB .-2sin xC .2cos xD .2sin x5.答案 D 解析 由题意,f (x )=x sin x ,f 1(x )=f ′(x )=sin x +x cos x ,f 2(x )=f ′1(x )=cos x +cos x -x sin x =2cos x -x sin x ,f 3(x )=f ′2(x )=-3sin x -x cos x ,f 4(x )=f ′3(x )=-4cos x +x sin x ,f 5(x )=f ′4(x )=5sin x +x cos x ,…,据此可知f 2 019(x )=-2 019sin x -x cos x ,f 2 021(x )=2 021sin x +x cos x ,所以f 2019(x )+f 2 021(x )=2sin x ,故选D .6.f (x )=x (2 021+ln x ),若f ′(x 0)=2 022,则x 0等于( )A .e 2B .1C .ln 2D .e6.答案 B 解析 f ′(x )=2 021+ln x +x ×1x =2 022+ln x ,又f ′(x 0)=2 022,得2 022+ln x 0=2 022,则ln x 0 =0,解得x 0=1.7.已知函数f (x )=1ax -1+e x cos x ,若f ′(0)=-1,则a = .7.答案 2 解析 f ′(x )=-(ax -1)′(ax -1)2e x cos x -e x sin x =-a (ax -1)2+e x cos x -e xsin x ,∴f ′(0)=-a +1=-1, 则a =2.8.已知函数f (x )=ln(2x -3)+ax e -x ,若f ′(2)=1,则a = .8.答案 e 2解析 f ′(x )=12x -3ꞏ(2x -3)′+a e -x +ax ꞏ(e -x )′=22x -3+a e -x -ax e -x ,∴f ′(2)=2+a e -2-2a e -2=2-a e -2=1,则a =e 2.9.已知函数f (x )的导函数为f ′(x ),且满足关系式f (x )=x 2+3xf ′(2)+ln x ,则f ′(2)的值等于( )A .-2B .2C .-94D .949.答案 C 解析 因为f (x )=x 2+3xf ′(2)+ln x ,所以f ′(x )=2x +3f ′(2)+1x 所以f ′(2)=2×2+3f ′(2)+12,解得f ′(2)=-94.10.已知f (x )=x 2+2xf ′(1),则f ′(0)=________.10.答案 -4 解析 ∵f ′(x )=2x +2f ′(1),∴f ′(1)=2+2f ′(1),∴f ′(1)=-2,∴f ′(0)=2f ′(1)=2×(-2)=-4. 11.设函数f (x )在(0,+∞)内可导,其导函数为f ′(x ),且f (ln x )=x +ln x ,则f ′(1)= .11.答案 1+e 解析 因为f (ln x )=x +ln x ,所以f (x )=x +e x ,所以f ′(x )=1+e x ,所以f ′(1)=1+e 1=1+e .12.已知f ′(x )是函数f (x )的导数,f (x )=f ′(1)ꞏ2x +x 2,则f ′(2)=( )A .12-8ln 21-2ln 2B .21-2ln 2C .41-2ln 2 D .-212.答案 C 解析 因为f ′(x )=f ′(1)ꞏ2x ln 2+2x ,所以f ′(1)=f ′(1)ꞏ2ln 2+2,解得f ′(1)=21-2ln 2,所以f ′(x )=21-2ln 2ꞏ2x ln 2+2x ,所以f ′(2)=21-2ln 2×22ln 2+2×2=41-2ln 2. 13.(多选)若函数f (x )的导函数f ′(x )的图象关于y 轴对称,则f (x )的解析式可能为( )A .f (x )=3cos xB .f (x )=x 3+xC .f (x )=x +1x D .f (x )=e x +x13.答案 BC 解析 对于A ,f (x )=3cos x ,其导数f ′(x )=-3sin x ,其导函数为奇函数,图象不关于y轴对称,不符合题意;对于B ,f (x )=x 3+x ,其导数f ′(x )=3x 2+1,其导函数为偶函数,图象关于y 轴对称,符合题意;对于C ,f (x )=x +1x ,其导数f ′(x )=1-1x 2,其导函数为偶函数,图象关于y 轴对称,符合题意;对于D ,f (x )=e x +x ,其导数f ′(x )=e x +1,其导函数不是偶函数,图象不关于y 轴对称,不符合题意. 14.f (x )=3e x+1+x 3,其导函数为f ′(x ),则f (2020)+f (-2020)+f ′(2019)-f ′(-2019)的值为( ) A .1 B .2 C .3 D .414.答案 C 解析 f ′(x )=-3e x (e x +1)2+3x 2,f ′(-x )=-3e x (e x +1)2+3x 2,所以f ′(x )为偶函数,f ′(2019)-f ′(-2019) =0,因为f (x )+f (-x )=31+e x+x 3+31+e -x -x 3=31+e x +3e x 1+e x =3,所以f (2020)+f (-2020)+f ′(2019)-f ′(-2019)=3.故选C .15.已知f (x )=ax 4+b cos x +7x -2.若f ′(2 020)=6,则f ′(-2 020)=______.15.答案 8 解析 因为f ′(x )=4ax 3-b sin x +7,所以f ′(-x )=4a (-x )3-b sin(-x )+7=-4ax 3+b sin x +7.所以f ′(x )+f ′(-x )=14.又f ′(2 020)=6,所以f ′(-2 020)=14-6=8. 16.分别求下列函数的导数:(1)y =e xln x ;(2)y =x ⎝⎛⎭⎫x 2+1x +1x 3;(3)y =x -sin x 2cos x2;(4)y =ln 1+2x .(5)f (x )=x 3+2x -x 2ln x -1x 2. 16.解析 (1)y ′=(e x )′ln x +e x (ln x )′=e x ln x +e x ꞏ1x =⎝⎛⎭⎫ln x +1x e x . (2)∵y =x 3+1+1x 2,∴y ′=3x 2-2x 3. (3)∵y =x -12sin x ,∴y ′=1-12cos x .(4)∵y =ln 1+2x =12ln(1+2x ),∴y ′=12ꞏ11+2x ꞏ(1+2x )′=11+2x.(5)由已知f (x )=x -ln x +2x -1x 2.所以f ′(x )=1-1x -2x 2+2x 3=x 3-x 2-2x +2x 3.。
基本初等函数的导数公式及导数运算法则练习

word 格式-可编辑-感谢下载支持基本初等函数的导数公式及导数运算法则练习姓名 班级 1.曲线y =13x 3-2在点⎝⎛⎭⎪⎫-1,-73处切线的倾斜角为( ) A .30° B .45° C .135° D .60° 2.设f (x )=13x 2-1x x,则f ′(1)等于( )A .-16B.56 C .-76 D.763.若曲线y =x 4的一条切线l 与直线x +4y -8=0垂直,则l 的方程为( )A .4x -y -3=0B .x +4y -5=0C .4x -y +3=0D .x +4y +3=04.已知f (x )=ax 3+9x 2+6x -7,若f ′(-1)=4,则a 的值等于( )A.193B.163C.103D.1335.已知物体的运动方程是s =14t 4-4t 3+16t 2(t 表示时间,s 表示位移),则瞬时速度为0的时刻是( )A .0秒、2秒或4秒B .0秒、2秒或16秒C .2秒、8秒或16秒D .0秒、4秒或8秒6.(2010·新课标全国卷文,4)曲线y =x 3-2x +1在点(1,0)处的切线方程为( )A .y =x -1B .y =-x -1C .y =2x -2D .y =-2x -27.若函数f (x )=e xsin x ,则此函数图象在点(4,f (4))处的切线的倾斜角为( )A.π2B .0C .钝角D .锐角8.曲线y =x sin x 在点⎝ ⎛⎭⎪⎫-π2,π2处的切线与x 轴、直线x =π所围成的三角形的面积为 ( )A.π22B .π2C .2π2 D.12(2+π)29.设f 0(x )=sin x ,f 1(x )=f 0′(x ),f 2(x )=f 1′(x ),…,f n +1(x )=f n ′(x ),n ∈N ,则f 2011(x )等于( )A .sin xB .-sin xC .cos xD .-cos x10.f (x )与g (x )是定义在R 上的两个可导函数,若f (x )、g (x )满足f ′(x )=g ′(x ),则f (x )与g (x )满足( )A .f (x )=g (x )B .f (x )-g (x )为常数C .f (x )=g (x )=0D .f (x )+g (x )为常数11.函数y =(x +1)2(x -1)在x =1处的导数等于( )A .1B .2C .3D .412.若对任意x ∈R ,f ′(x )=4x 3,f (1)=-1,则f (x )=( )word 格式-可编辑-感谢下载支持A .x 4B .x 4-2 C .4x 3-5D .x 4+213.设函数f (x )=x m+ax 的导数为f ′(x )=2x +1,则数列{1f (n )}(n ∈N *)的前n 项和是( ) A.nn +1 B.n +2n +1 C.n n -1 D.n +1n14.二次函数y =f (x )的图象过原点,且它的导函数y =f ′(x )的图象是过第一、二、三象限的一条直线,则函数y =f (x )的图象的顶点在( )A .第一象限B .第二象限C .第三象限D .第四象限15.函数y =(2+x 3)2的导数为( )A .6x 5+12x 2B .4+2x 3C .2(2+x 3)2D .2(2+x 3)·3x16.(2010·江西文,4)若函数f (x )=ax 4+bx 2+c 满足f ′(1)=2,则f ′(-1)=( )A .-1B .-2C .2D .017.设函数f (x )=(1-2x 3)10,则f ′(1)=( )A .0B .-1C .-60D .6018.函数y =sin2x -cos2x 的导数是( )A .22cos ⎝⎛⎭⎪⎫2x -π4B .cos2x -sin2xC .sin2x +cos2xD .22cos ⎝⎛⎭⎪⎫2x +π419.(2010·高二潍坊)已知曲线y =x 24-3ln x 的一条切线的斜率为12,则切点的横坐标为( )A .3B .2C .1D.1220.设函数f (x )是R 上以5为周期的可导偶函数,则曲线y =f (x )在x =5处的切线的斜率为( )A .-15B .0 C.15D .521.设f (x )=ax 2-b sin x ,且f ′(0)=1,f ′⎝ ⎛⎭⎪⎫π3=12,则a =________,b =________.22.设f (x )=x 3-3x 2-9x +1,则不等式f ′(x )<0的解集为________. 23.曲线y =cos x 在点P ⎝⎛⎭⎪⎫π3,12处的切线的斜率为______.24.已知函数f (x )=ax +b e x图象上在点P (-1,2)处的切线与直线y =-3x 平行,则函数f (x )的解析式是____________.25.若f (x )=x ,φ(x )=1+sin2x ,则f [φ(x )]=_______,φ[f (x )]=________. 26.设函数f (x )=cos(3x +φ)(0<φ<π),若f (x )+f ′(x )是奇函数,则φ=________. 27.函数y =(1+2x 2)8的导数为________. 28.函数y =x 1+x 2的导数为________. 三、解答题29.求下列函数的导数:(1)y =x (x 2+1x +1x 3);(2)y =(x +1)(1x -1);(3)y =sin 4x 4+cos 4x 4;(4)y =1+x 1-x +1-x 1+x .30.求下列函数的导数:(1)y =x sin 2x ; (2)y =ln(x +1+x 2); (3)y =e x+1e x -1; (4)y =x +cos xx +sin x..31.求下列函数的导数:(1)y =cos 2(x 2-x ); (2)y =cos x ·sin3x ; (3)y =x log a (x 2+x -1); (4)y =log 2x -1x +1.32.设f (x )=2sin x 1+x 2,如果f ′(x )=2(1+x 2)2·g (x ),求g (x ).33.求下列函数的导数:(其中f (x )是可导函数)(1)y =f ⎝ ⎛⎭⎪⎫1x;(2)y =f (x 2+1).34.已知两条曲线y=sin x、y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.17.已知曲线C1:y=x2与C2:y=-(x-2)2.直线l与C1、C2都相切,求直线l的方程.18.求满足下列条件的函数f(x):(1)f(x)是三次函数,且f(0)=3,f′(0)=0,f′(1)=-3,f′(2)=0;(2)f′(x)是一次函数,x2f′(x)-(2x-1)f(x)=1.基本初等函数的导数公式及导数运算法则答案一、选择题1.曲线y =13x 3-2在点⎝ ⎛⎭⎪⎫-1,-73处切线的倾斜角为( ) A .30° B .45° C .135°D .60°[答案] B[解析] y ′|x =-1=1,∴倾斜角为45°. 2.设f (x )=13x 2-1x x,则f ′(1)等于( )A .-16B.56 C .-76D.76[答案] B3.若曲线y =x 4的一条切线l 与直线x +4y -8=0垂直,则l 的方程为( ) A .4x -y -3=0 B .x +4y -5=0 C .4x -y +3=0D .x +4y +3=0[答案] A[解析] ∵直线l 的斜率为4,而y ′=4x 3,由y ′=4得x =1而x =1时,y =x 4=1,故直线l 的方程为:y -1=4(x -1)即4x -y -3=0.4.已知f (x )=ax 3+9x 2+6x -7,若f ′(-1)=4,则a 的值等于( ) A.193 B.163 C.103D.133[答案] B[解析] ∵f ′(x )=3ax 2+18x +6,∴由f ′(-1)=4得,3a -18+6=4,即a =163.∴选B.5.已知物体的运动方程是s =14t 4-4t 3+16t 2(t 表示时间,s 表示位移),则瞬时速度为0的时刻是( )A .0秒、2秒或4秒B .0秒、2秒或16秒C .2秒、8秒或16秒D .0秒、4秒或8秒[答案] D[解析] 显然瞬时速度v =s ′=t 3-12t 2+32t =t (t 2-12t +32),令v =0可得t =0,4,8.故选D. 6.(2010·新课标全国卷文,4)曲线y =x 3-2x +1在点(1,0)处的切线方程为( ) A .y =x -1B .y =-x -1C .y =2x -2D .y =-2x -2[答案] A[解析] 本题考查了导数的几何意义,切线方程的求法,在解题时应首先验证点是否在曲线上,然后通过求导得出切线的斜率,题目定位于简单题.由题可知,点(1,0)在曲线y =x 3-2x +1上,求导可得y ′=3x 2-2,所以在点(1,0)处的切线的斜率k =1,切线过点(1,0),根据直线的点斜式可得过点(1,0)的曲线y =x 3-2x +1的切线方程为y =x -1,故选A.7.若函数f (x )=e xsin x ,则此函数图象在点(4,f (4))处的切线的倾斜角为( ) A.π2 B .0C .钝角D .锐角[答案] C[解析] y ′|x =4=(e xsin x +e xcos x )|x =4=e 4(sin4+cos4)=2e 4sin(4+π4)<0,故倾斜角为钝角,选C.8.曲线y =x sin x 在点⎝ ⎛⎭⎪⎫-π2,π2处的切线与x 轴、直线x =π所围成的三角形的面积为 ( )A.π22 B .π2C .2π2D.12(2+π)2[答案] A[解析] 曲线y =x sin x 在点⎝ ⎛⎭⎪⎫-π2,π2处的切线方程为y =-x ,所围成的三角形的面积为π22. 9.设f 0(x )=sin x ,f 1(x )=f 0′(x ),f 2(x )=f 1′(x ),…,f n +1(x )=f n ′(x ),n ∈N ,则f 2011(x )等于( )A .sin xB .-sin xC .cos xD .-cos x[答案] D[解析] f 0(x )=sin x ,f 1(x )=f 0′(x )=(sin x )′=cos x ,f2(x)=f1′(x)=(cos x)′=-sin x,f3(x)=f2′(x)=(-sin x)′=-cos x,f4(x)=f3′(x)=(-cos x)′=sin x,∴4为最小正周期,∴f2011(x)=f3(x)=-cos x.故选D.10.f(x)与g(x)是定义在R上的两个可导函数,若f(x)、g(x)满足f′(x)=g′(x),则f(x)与g(x)满足( )A.f(x)=g(x) B.f(x)-g(x)为常数C.f(x)=g(x)=0 D.f(x)+g(x)为常数[答案] B[解析] 令F(x)=f(x)-g(x),则F′(x)=f′(x)-g′(x)=0,∴F(x)为常数.11.函数y=(x+1)2(x-1)在x=1处的导数等于( )A.1 B.2C.3 D.4[答案] D[解析] y′=[(x+1)2]′(x-1)+(x+1)2(x-1)′=2(x+1)·(x-1)+(x+1)2=3x2+2x-1,∴y′|x=1=4.12.若对任意x∈R,f′(x)=4x3,f(1)=-1,则f(x)=( )A.x4B.x4-2C.4x3-5 D.x4+2[答案] B[解析] ∵f′(x)=4x3.∴f(x)=x4+c,又f(1)=-1∴1+c=-1,∴c=-2,∴f(x)=x4-2.13.设函数f(x)=x m+ax的导数为f′(x)=2x+1,则数列{1f(n)}(n∈N*)的前n项和是( )A.nn+1B.n+2n+1C.nn-1D.n+1n[答案] A[解析] ∵f(x)=x m+ax的导数为f′(x)=2x+1,∴m=2,a=1,∴f(x)=x2+x,即f(n)=n2+n=n(n+1),∴数列{1f(n)}(n∈N*)的前n项和为:S n =11×2+12×3+13×4+…+1n (n +1)=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1 =1-1n +1=nn +1, 故选A.14.二次函数y =f (x )的图象过原点,且它的导函数y =f ′(x )的图象是过第一、二、三象限的一条直线,则函数y =f (x )的图象的顶点在( )A .第一象限B .第二象限C .第三象限D .第四象限[答案] C[解析] 由题意可设f (x )=ax 2+bx ,f ′(x )=2ax +b ,由于f ′(x )的图象是过第一、二、三象限的一条直线,故2a >0,b >0,则f (x )=a ⎝ ⎛⎭⎪⎫x +b 2a 2-b 24a, 顶点⎝ ⎛⎭⎪⎫-b2a,-b 24a 在第三象限,故选C.15.函数y =(2+x 3)2的导数为( ) A .6x 5+12x 2B .4+2x 3C .2(2+x 3)2D .2(2+x 3)·3x[答案] A[解析] ∵y =(2+x 3)2=4+4x 3+x 6, ∴y ′=6x 5+12x 2.16.(2010·江西文,4)若函数f (x )=ax 4+bx 2+c 满足f ′(1)=2,则f ′(-1)=( ) A .-1 B .-2 C .2D .0[答案] B[解析] 本题考查函数知识,求导运算及整体代换的思想,f ′(x )=4ax 3+2bx ,f ′(-1)=-4a -2b =-(4a +2b ),f ′(1)=4a +2b ,∴f ′(-1)=-f ′(1)=-2要善于观察,故选B.17.设函数f (x )=(1-2x 3)10,则f ′(1)=( ) A .0B .-1C .-60D .60[答案] D[解析] ∵f ′(x )=10(1-2x 3)9(1-2x 3)′=10(1-2x 3)9·(-6x 2)=-60x 2(1-2x 3)9,∴f ′(1)=60.18.函数y =sin2x -cos2x 的导数是( )A .22cos ⎝ ⎛⎭⎪⎫2x -π4B .cos2x -sin2xC .sin2x +cos2xD .22cos ⎝⎛⎭⎪⎫2x +π4[答案] A[解析] y ′=(sin2x -cos2x )′=(sin2x )′-(cos2x )′ =2cos2x +2sin2x =22cos ⎝⎛⎭⎪⎫2x -π4.19.(2010·高二潍坊检测)已知曲线y =x 24-3ln x 的一条切线的斜率为12,则切点的横坐标为( )A .3B .2C .1D.12[答案] A[解析] 由f ′(x )=x 2-3x =12得x =3.20.设函数f (x )是R 上以5为周期的可导偶函数,则曲线y =f (x )在x =5处的切线的斜率为( ) A .-15B .0 C.15D .5[答案] B[解析] 由题设可知f (x +5)=f (x ) ∴f ′(x +5)=f ′(x ),∴f ′(5)=f ′(0) 又f (-x )=f (x ),∴f ′(-x )(-1)=f ′(x ) 即f ′(-x )=-f ′(x ),∴f ′(0)=0 故f ′(5)=f ′(0)=0.故应选B. 二、填空题21.设f (x )=ax 2-b sin x ,且f ′(0)=1,f ′⎝ ⎛⎭⎪⎫π3=12,则a =________,b =________.[答案] 0 -1[解析] f ′(x )=2ax -b cos x ,由条件知 ⎩⎪⎨⎪⎧-b cos0=12π3a -b cos π3=12,∴⎩⎪⎨⎪⎧b =-1a =0.22.设f (x )=x 3-3x 2-9x +1,则不等式f ′(x )<0的解集为________. [答案] (-1,3)[解析] f ′(x )=3x 2-6x -9,由f ′(x )<0得3x 2-6x -9<0,∴x 2-2x -3<0,∴-1<x <3.23.曲线y =cos x 在点P ⎝ ⎛⎭⎪⎫π3,12处的切线的斜率为______.[答案] -32[解析] ∵y ′=(cos x )′=-sin x , ∴切线斜率k =y ′|x =π3=-sin π3=-32.24.已知函数f (x )=ax +b e x图象上在点P (-1,2)处的切线与直线y =-3x 平行,则函数f (x )的解析式是____________.[答案] f (x )=-52x -12e x +1[解析] 由题意可知,f ′(x )|x =-1=-3, ∴a +b e -1=-3,又f (-1)=2,∴-a +b e -1=2,解之得a =-52,b =-12e ,故f (x )=-52x -12e x +1.25.若f (x )=x ,φ(x )=1+sin2x ,则f [φ(x )]=_______,φ[f (x )]=________. [答案]2⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎫x +π4,1+sin2x[解析] f [φ(x )]=1+sin2x =(sin x +cos x )2=|sin x +cos x |=2⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎫x +π4.φ[f (x )]=1+sin2x .26.设函数f (x )=cos(3x +φ)(0<φ<π),若f (x )+f ′(x )是奇函数,则φ=________. [答案]π6[解析] f ′(x )=-3sin(3x +φ),f (x )+f ′(x )=cos(3x +φ)-3sin(3x +φ)=2sin ⎝⎛⎭⎪⎫3x +φ+5π6. 若f (x )+f ′(x )为奇函数,则f (0)+f ′(0)=0, 即0=2sin ⎝ ⎛⎭⎪⎫φ+5π6,∴φ+5π6=k π(k ∈Z ). 又∵φ∈(0,π),∴φ=π6.27.函数y =(1+2x 2)8的导数为________.word 格式-可编辑-感谢下载支持 [答案] 32x (1+2x 2)7[解析] 令u =1+2x 2,则y =u 8,∴y ′x =y ′u ·u ′x =8u 7·4x =8(1+2x 2)7·4x=32x (1+2x 2)7.28.函数y =x 1+x 2的导数为________. [答案] (1+2x 2)1+x 21+x 2 [解析] y ′=(x 1+x 2)′=x ′1+x 2+x (1+x 2)′=1+x 2+x 21+x 2=(1+2x 2)1+x 21+x2.三、解答题29.求下列函数的导数:(1)y =x (x 2+1x +1x 3);(2)y =(x +1)(1x -1);(3)y =sin 4x4+cos 4x4;(4)y =1+x 1-x +1-x1+x .[解析] (1)∵y =x ⎝ ⎛⎭⎪⎫x 2+1x +1x 3=x 3+1+1x 2,∴y ′=3x 2-2x 3;(3)∵y =sin 4x 4+cos 4x4=⎝ ⎛⎭⎪⎫sin 2x 4+cos 2x 42-2sin 2x 4cos 2x4=1-12sin 2x2=1-12·1-cos x2=34+14cos x ,∴y ′=-14sin x ;(4)∵y =1+x 1-x +1-x 1+x =(1+x )21-x +(1-x )21-x=2+2x1-x =41-x -2,∴y ′=⎝ ⎛⎭⎪⎫41-x -2′=-4(1-x )′(1-x )2=4(1-x )2.word 格式-可编辑-感谢下载支持30.求下列函数的导数:(1)y =x sin 2x ; (2)y =ln(x +1+x 2);(3)y =e x +1e x -1; (4)y =x +cos x x +sin x. [解析] (1)y ′=(x )′sin 2x +x (sin 2x )′=sin 2x +x ·2sin x ·(sin x )′=sin 2x +x sin2x .(2)y ′=1x +1+x 2·(x +1+x 2)′ =1x +1+x 2(1+x 1+x 2)=11+x 2 . (3)y ′=(e x +1)′(e x -1)-(e x +1)(e x -1)′(e x -1)2=-2e x (e x -1)2 . (4)y ′=(x +cos x )′(x +sin x )-(x +cos x )(x +sin x )′(x +sin x )2 =(1-sin x )(x +sin x )-(x +cos x )(1+cos x )(x +sin x )2 =-x cos x -x sin x +sin x -cos x -1(x +sin x )2. 31.求下列函数的导数:(1)y =cos 2(x 2-x ); (2)y =cos x ·sin3x ;(3)y =x log a (x 2+x -1); (4)y =log 2x -1x +1. [解析] (1)y ′=[cos 2(x 2-x )]′=2cos(x 2-x )[cos(x 2-x )]′=2cos(x 2-x )[-sin(x 2-x )](x 2-x )′=2cos(x 2-x )[-sin(x 2-x )](2x -1)=(1-2x )sin2(x 2-x ).(2)y ′=(cos x ·sin3x )′=(cos x )′sin3x +cos x (sin3x )′=-sin x sin3x +3cos x cos3x =3cos x cos3x -sin x sin3x .(3)y ′=log a (x 2+x -1)+x ·1x 2+x -1log a e(x 2+x -1)′=log a (x 2+x -1)+2x 2+x x 2+x -1log a e. (4)y ′=x +1x -1⎝ ⎛⎭⎪⎫x -1x +1′log 2e =x +1x -1log 2e x +1-x +1(x +1)2 =2log 2e x 2-1. 32.设f (x )=2sin x 1+x 2,如果f ′(x )=2(1+x 2)2·g (x ),求g (x ).word 格式-可编辑-感谢下载支持[解析] ∵f ′(x )=2cos x (1+x 2)-2sin x ·2x (1+x 2)2 =2(1+x 2)2[(1+x 2)cos x -2x ·sin x ], 又f ′(x )=2(1+x 2)2·g (x ). ∴g (x )=(1+x 2)cos x -2x sin x .33.求下列函数的导数:(其中f (x )是可导函数) (1)y =f ⎝ ⎛⎭⎪⎫1x ;(2)y =f (x 2+1). [解析] (1)解法1:设y =f (u ),u =1x ,则y ′x =y ′u ·u ′x =f ′(u )·⎝ ⎛⎭⎪⎫-1x 2=-1x 2f ′⎝ ⎛⎭⎪⎫1x . 解法2:y ′=⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫1x ′=f ′⎝ ⎛⎭⎪⎫1x ·⎝ ⎛⎭⎪⎫1x ′=-1x 2f ′⎝ ⎛⎭⎪⎫1x . (2)解法1:设y =f (u ),u =v ,v =x 2+1,34.已知两条曲线y =sin x 、y =cos x ,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.[解析] 由于y =sin x 、y =cos x ,设两条曲线的一个公共点为P (x 0,y 0),∴两条曲线在P (x 0,y 0)处的斜率分别为若使两条切线互相垂直,必须cos x 0·(-sin x 0)=-1,即sin x 0·cos x 0=1,也就是sin2x 0=2,这是不可能的,∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.17.已知曲线C 1:y =x 2与C 2:y =-(x -2)2.直线l 与C 1、C 2都相切,求直线l 的方程.[解析] 设l 与C 1相切于点P (x 1,x 21),与C 2相切于点Q (x 2,-(x 2-2)2). 对于C 1:y ′=2x ,则与C 1相切于点P 的切线方程为y -x 21=2x 1(x -x 1),即y =2x 1x -x 21.① 对于C 2:y ′=-2(x -2),与C 2相切于点Q 的切线方程为y +(x 2-2)2=-2(x 2-2)(x -x 2), 即y =-2(x 2-2)x +x 22-4.② ∵两切线重合,∴2x 1=-2(x 2-2)且-x 21=x 22-4,解得x 1=0,x 2=2或x 1=2,x 2=0.∴直线l 的方程为y =0或y =4x -4.18.求满足下列条件的函数f (x ):(1)f (x )是三次函数,且f (0)=3,f ′(0)=0,f ′(1)=-3,f ′(2)=0;(2)f ′(x )是一次函数,x 2f ′(x )-(2x -1)f (x )=1.[解析] (1)设f (x )=ax 3+bx 2+cx +d (a ≠0)则f ′(x )=3ax 2+2bx +c由f (0)=3,可知d =3,由f ′(0)=0可知c =0,由f ′(1)=-3,f ′(2)=0可建立方程组⎩⎪⎨⎪⎧ f ′(1)=3a +2b =-3f ′(2)=12a +4b =0, 解得⎩⎪⎨⎪⎧a =1b =-3, 所以f (x )=x 3-3x 2+3.(2)由f ′(x )是一次函数可知f (x )是二次函数,则可设f (x )=ax 2+bx +c (a ≠0) f ′(x )=2ax +b ,把f (x )和f ′(x )代入方程,得x 2(2ax +b )-(2x -1)(ax 2+bx +c )=1整理得(a -b )x 2+(b -2c )x +c =1若想对任意x 方程都成立,则需 ⎩⎪⎨⎪⎧ a -b =0b -2c =0c =1解得⎩⎪⎨⎪⎧ a =2b =2c =1, 所以f (x )=2x 2+2x +1.。
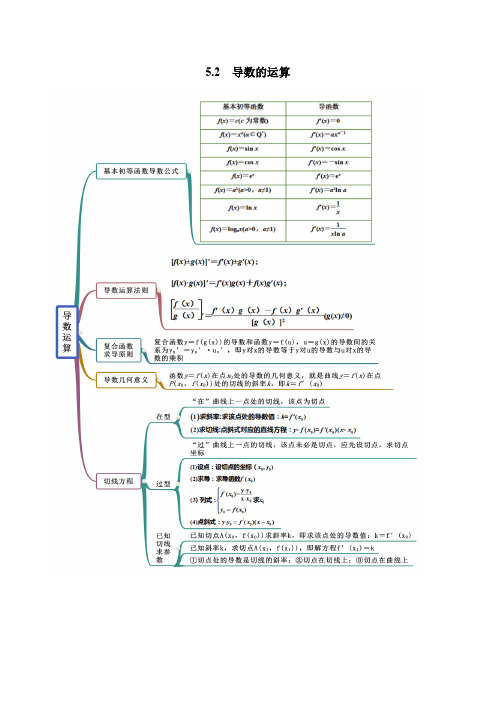
高中数学选择性必修二 精讲精炼 5 导的运算(精练)(含答案)

5.2 导数的运算(精练)【题组一 基本函数的求导】1(2021·全国)给出下列结论:①若y =31x ,则y ′=-43x ;①若y ,则y ′=13;①若f (x )=3x ,则f ′(1)=3.其中正确的个数是( ) A .1 B .2 C .3 D .0【答案】B【解析】对于①,y ′=(x -3)′=43x -,正确; 对于①,121'331133y x x --==,不正确;对于①,f ′(x )=3,故f ′(1)=3,正确. 故选:B2.(2021·全国高二课时练习)下列结论中,不正确的是( )A .若31y x =,则43y x '=- B .若y =y 'C .若21y x=,则32y x -'=- D .若()3f x x =,则()13f '=【答案】B【解析】对于A ,()3434133y x x x x --'⎛⎫''===-=- ⎪⎝⎭,A 正确;对于B ,112212y x x -'⎛⎫''=== ⎪⎝⎭,B 错误; 对于C ,()23212y x x x --'⎛⎫''===- ⎪⎝⎭,C 正确;对于D ,()3f x '=,()13f '∴=,D 正确. 故选:B.3.(2021·全国高二课时练习)已知f (x )=x a ,若f ′(-1)=-4,则a 的值等于( ) A .4 B .-4 C .5 D .-5【答案】A【解析】①()1a f x ax -'=,()()1114a f a -'∴-=⨯-=-,解得a =4.故选:A.4.(2021·全国高二课时练习)函数f (x )f ′(3)等于( )AB .0CD 【答案】A【解析】①()f x '=①()3f '==故选:A. 5.(2021·全国高二专题练习)f 0(x )=sin x ,f 1(x )=f ′0(x ),f 2(x )=f ′1(x ),…,f n +1(x )=f ′n (x ),n ①N ,则f 2 017(x )=( ) A .sin x B .-sin x C .cos x D .-cos x【答案】C【解析】因为1()(sin )cos f x x x '==,2()(cos )sin f x x x '==-,3()(sin )cos f x x x '=-=-,4()(cos )sin f x x x '=-= 5()(sin )cos f x x x '==,所以循环周期为4,因此20171()()cos f x f x x ==.故选:C.【题组二 导数的运算法则】1.(2021·全国高二课时练习)求下列函数的导数.(1)y =(x 2+1)(x -1);(2)y =3x+lg x ;(3)y =x 2+tan x ;(4)y =1xe x +.【答案】(1)'2321y x x =-+;(2)'13ln 3ln10x y x =⋅+;(3)'212cos y x x =+;(4)()'21x xe y x =+.【解析】(1)()()'22211321y x x x x x =-++=-+.(2)'13ln 3ln10x y x =⋅+. (3)222'22sin cos sin 1,22cos cos cos x x x y x y x x x x x +=+=+=+. (4)()()()'22111x xxe x e xe y x x +-==++.2.(2021·全国高二课时练习)求下列函数的导数:(1) y (2)y =41x ;(3)y =22sin (12cos )24x x -⋅-;(4)y =log 2x 2-log 2x .【答案】(1)2535x -;(2)54x -;(3)cos x ;(4)1ln 2x .【解析】(1)33215553355y x x x --'⎛⎫'==== ⎪⎝⎭';(2)()4415451444y x x x x x ----'⎛⎫'==='-=-=- ⎪⎝⎭; (3)222sin 12cos 2sin 2cos 12sin cos sin 242422x x x x x xy x ⎛⎫⎛⎫=--=-== ⎪ ⎪⎝⎭⎝⎭,()sin cos y x x ''∴==.(4)①2222log log log y x x x =-=,()21log ln 2y x x ''∴==. 3(2021·全国)求下列函数的导函数.(1)y =(2)y =;(3)222log log y x x =-;(4)22sin 12cos 24x x y ⎛⎫=-- ⎪⎝⎭.【答案】(1)y '=(2)y '=(3)1ln 2y x '=;(4)cos y x '=.【解析】((1)(3312232y x x -'⎛⎫''==== ⎪⎝⎭(2)33215553355x x y x --'⎛⎫===''=⎪⎝⎭=(3)①2222log log log y x x x =-=, ①()21log ln 2y x x ''==. (4)①222sin 12cos 2sin 2cos 12sin cos sin 242422x x x xx x y x ⎛⎫⎛⎫=--=-== ⎪ ⎪⎝⎭⎝⎭,①()sin cos y x x ''==. 【题组三 复合函数的求导】1.(2021·全国高二课时练习)求下列函数的导数.(1)f (x )=(-2x +1)2;(2)f (x )=ln (4x -1);(3)f (x )=23x +2;(4)f (x )(5)f (x )=sin (3)6x π+;(6)f (x )=cos 2x .【答案】(1)y ′=-4(-2x +1)=8x -4;(2)y ′=441x -;(3)y ′=3ln 2·23x +2;(4)y ′= (5)y ′=3cos 36x π⎛⎫+ ⎪⎝⎭;(6)f ′(x )=-sin 2x .【解析】((1)设y =u 2,u =-2x +1,则y ′=y u ′·u x ′=2u ·(-2)=-4(-2x +1)=8x -4. (2)设y =ln u ,u =4x -1,则y ′=y u ′·u x ′=1u ·4=441x -.(3)设y =2u ,u =3x +2,则y ′=y u ′·u x ′=2u ln 2·3=3ln 2·23x +2.(4)设y u =5x +4,则y ′=y u ′·u x ′·5.(5)设y =sin u ,u =3x +6π,则y ′=y u ′·u x ′=cos u ·3=3cos 36x π⎛⎫+ ⎪⎝⎭.(6)法一:设y =u 2,u =cos x ,则y ′=y u ′·u x ′=2u ·(-sin x )=-2cos x ·sin x =-sin 2x ; 法二:①f (x )=cos 2x =1cos22x +=12+12cos 2x ,所以f ′(x )=11cos 222x ⎛⎫+ ⎪⎝⎭′=0+12·(-sin 2x )·2=-sin 2x . 2.(2021·全国高二课时练习)求下列函数的导数.(1)y =41(13)x -;(2)y =cos x 2;(3)y = sin(2x -3π);(4)y 【答案】(1)512(13)x -;(2)-2x sin x 2;(3)2cos(2x -3π); 【解析】((1)令u =1-3x ,则y =41u =4u-,①y ′u =-4u -5,u ′x =-3.①y ′x =y ′u ·u ′x =12u -5=512(13)x -. (2)令u =x 2,则y =cos u ,①y ′x =y ′u ·u ′x =-sin u ·2x =-2x sin x 2. (3)令u =2x -3π,则y =sin u ,①y ′x =y ′u ·u ′x =cos u ·2=2cos(2x -3π). (4)令u =1+x 2,则y =12u ,①y ′x =y ′u ·u ′x =1122122u x x u --⋅=⋅= 3.(2021·全国高二课时练习)写出下列各函数的中间变量,并利用复合函数的求导法则,求出函数的导数. (1)y =41(34)x -;(2)cos 2008+()8y x =;(3)132x y -=;(4)ln 8()+6y x =. 【答案】(1)中间变量:()34u x x ϕ==- 函数的导数:'516(34)y x -=(2)中间变量:()20088u x x ϕ+== 函数的导数:'2008sin 2008()8y x =-+(3)中间变量:()13u x x ϕ-==函数的导数:1'33ln22x y ⋅=-- (4)中间变量:()86u x x ϕ+== 函数的导数:'443y x =+ 【解析】((1)引入中间变量()34u x x ϕ==-. 则函数41(34)y x =-是由函数441()f u u u-==与()34u x x ϕ==-复合而成的. 查导数公式表可得()5544u u f u '=--=-,()4x ϕ'=-. 根据复合函数求导法则可得()()()5'55'4116(34)(3)64414y f u x u u x x ϕ⎡⎤==''⎢⎥--⎣⎦=-⋅-==.(2)引入中间变量()20088u x x ϕ+==,则函数cos 2008)8(y x =+是由函数()f u cosu =与()2008+8u x x ϕ==复合而成的,查导数公式表可得()sin f u u '=-,()2008x ϕ'=.根据复合函数求导法则可得()()20088sin 2008[c 2008sin 20os()]()()08sin 20088x f u x u u x ϕ'''-⨯++===-=- (3)引入中间变量()13u x x ϕ-==, 则函数132x y -=是由函数()2uf u =与()13u x x ϕ==-复合而成的, 查导数公式表得()2 2uf u ln '=,()3x ϕ'=-,根据复合函数求导法则可得()()1313232ln 23()()2ln 232ln2x u u x f u x ϕ'''⨯⨯⨯--==-=-=-.(4)引入中间变量()86u x x ϕ+==,则函数ln 8()6y x +=是由函数()ln f u u =与()86u x x ϕ+==复合而成的. 查导数公式表可得()1f u u'=,()8x ϕ'=. 根据复合函数求导法则可得()()88486?86[ln()]43x f u x u x x ϕ+'''==++==.4.(2021·全国高二专题练习)求下列函数的导数:(1)y (2)y =e 2x +1;(3)y =ln(3x -1);(4)y =sin (2)3x π+;(5)y =e sin(ax +b );(6)y =5log 2(2x +1).【答案】(2)2e 2x +1;(3)331x -;(4)2cos 23x π⎛⎫+ ⎪⎝⎭;(5)()sin cos()ax b a ax b e ++⋅ ;(6)10(21)ln 2x +.【解析】((1)设y =23u x x =-,则(32)x u x y y u x '''=⋅=-= (2)设,21,u y e u x ==+则2122u x x u x y y u e e '''+=⋅=⋅=.(3)设ln ,31y u u x ==-,则(ln )(31)x u x y y u u x '''''=⋅=⋅-13331u x =⋅=-(4)设sin ,23y u u x π==+,则(sin )23x u x y y u u x π''''⎛⎫=⋅=⋅+ ⎪⎝⎭cos 22cos 23u x π⎛⎫=⋅=+ ⎪⎝⎭(5)设,sin ,u y e u v v ax b ===+,则()sin cos cos()b v ax u xu x y y u v e v a a ax b e +''''=⋅⋅=⋅⋅=+⋅;(6)设25log ,21y u u x ==+,则()210105log (21)ln 2(21)ln 2y u x u x '''=⋅+==+【题组四 求导数值】1.(2021·全国高二课时练习)已知f (x )=2x ,g (x )=ln x ,则方程f (x )+1=()'g x 的解为( ) A .1 B .12C .-1或12D .-1【答案】B【解析】(由g (x )=ln x ,得x >0,且1()g x x '=.故2x +1=1x,即2x 2+x -1=0,解得x =12或x =-1. 又因x >0,故x =12(x =-1舍去)故选:B.2(2021·全国高二课时练习)已知函数f (x )的导函数为f ′(x ),且满足f (x )=2xf ′(e )+ln x ,则f ′(e )=( ) A .e -1 B .-1 C .-e -1 D .-e【答案】C【解析】(①f (x )=2xf ′(e )+ln x ,①''1()2()f x f e x =+, ①''1()2()f e f e e =+,解得'1()f e e=-,故选:C.3.(2021·河南高三月考(文))已知函数()f x 的导函数为()f x ',且满足()()32121f x x x f x '=++-,则()2f '=( ) A .1 B .9- C .6- D .4【答案】C【解析】(因为()()32121f x x x f x '=++-,所以()()23212f x x xf ''=++,把1x =代入()'f x ,得()()2213121f f ''=⨯++,解得:()15f '=-,所以()23102f x x x '=-+,所以()26f '=-.故选:C.4.(2021·全国高二课前预习)设f (x )=cos 2x -3x ,则f ′()2π=( )A .-5B .-3C .-4D .-32π 【答案】B【解析】(f ′(x )=-2sin 2x -3,f ′()2π=-2sin π-3=-3.故选:B.5.(2021·全国高二课时练习)设函数()()320202019f x x -=,则()1f '=( )A .6057B .6057-C .2019D .2019-【答案】B 【解析】(()2()3(2019)20202019f x x '=⨯--则()2(1)3(2019)2020201916057f -⨯=-'=⨯-.故选:B6.(2021·全国高二课时练习)已知函数()()221sin 1x xf x x ++=+,其导函数记为()f x ',则()()()()389389389389f f f f ''++---=( )A .2B .2-C .3D .3-【答案】A【解析】(由已知得()22sin 11x xf x x +=++,则()()()()()2222cos 12sin 21x x x x xxf x ++-+'+=⋅,显然()f x '为偶函数.令()()22sin 11x xg x f x x +=-=+,显然()g x 为奇函数.又()f x '为偶函数,所以()()3893890f f ''--=,()()()()389389389138912f f g g +-=++-+=, 所以()()()()3893893893892f f f f ''++---=. 故选:A.【题组五切线方程】1.(2021·全国高二课时练习)设函数()()2f xg x x =+,曲线()y g x =在点1,1g 处的切线方程为21y x =+,则曲线()y f x =在点()()1,1f 处的切线的斜率为( ) A .4 B .14-C .2D .12-【答案】A【解析】因为()()2f xg x x =+,所以()()2f x g x x ''=+.又曲线()y g x =在点1,1g 处的切线方程为21y x =+,所以()12g '=,所以()()11214f g ''=+⨯=,即曲线()y f x =在点()()1,1f 处的切线的斜率为4.故选:A.2.(2021·韩城市西庄中学(理))曲线31233y x x =-+在点41,3⎛⎫⎪⎝⎭处的切线的倾斜角α为( )A .π4B .π3C .2π3D .3π4【答案】D【解析】由31233y x x =-+得22y x '=-,于是当1x =时,1y '=-,由导数的几何意义知,曲线31233y x x =-+在点41,3⎛⎫⎪⎝⎭处的切线斜率tan 1k α==-,而切线的倾斜角[)0,απ∈,所以3π4α=.故选:D 3(2021·江苏扬州·高二期中)曲线2x y x e x =⋅+在0x =处的切线方程为( ) A .1y x =+ B .2y x =C .y x =D .31y x【答案】C【解析】由题意知0x =时,02000y e =⨯+=,所以切点为()0,0,而()12x y x e x '=++,所以切线的斜率为()010201e +⨯+⨯=,则所求的切线方程为y x =, 故选:C.4.(2021·全国高二课时练习)函数()ln 23y x =+的导数为y '=______,其函数图象在点1,ln 22⎛⎫- ⎪⎝⎭处的切线的倾斜角为______. 【答案】223x + π4【解析】令23u x =+,则ln y u =,()()12ln 23223y u x u x '''=⋅+=⋅=+.当12x =-时,2131y '==-,所以函数()ln 23y x =+的图象在点1,ln 22⎛⎫- ⎪⎝⎭处的切线的斜率为1,所以倾斜角为π4.故答案为:223x + π45.(2021·浙江路桥中学高二开学考试)已知函数()cos f x x x =,则()f x '=________________,曲线()y f x =在点()0,0处的切线的倾斜角是_________. 【答案】cos sin x x x - 45【解析】可得()()cos sin cos sin f x x x x x x x '=+-=-;由导数的几何意义可得曲线()y f x =在点()0,0处的切线斜率为()0cos001f '=-=, 设切线的倾斜角为α,则0180α≤<, 因为tan 1α=,所以45α=, 故答案为:cos sin x x x -;45.6.(2021·全国高二课时练习)与直线2x -y -4=0平行且与曲线y =ln x 相切的直线方程是________. 【答案】2x -y -1-ln2=0【解析】①直线2x -y -4=0的斜率为k =2, 又①y ′=(ln x )′=1x ,①1x=2,解得x =12. ①切点的坐标为1(,ln 2)2-. 故切线方程为y +ln 2=21()2x -.即2x -y -1-ln 2=0. 故答案为:2x -y -1-ln 2=07(2021·全国高二课时练习)曲线y =1x 在点M 1(3,)3处的切线方程是________.【答案】x +9y -6=0 【解析】①y ′=-21x ,①在点M 1(3,)3处的斜率k =-19,①在点1(3,)3的斜率为-19的切线方程为:y -13=-19(x -3),即x +9y -6=0.故答案:x +9y -6=0.8(2021·全国高二课时练习)曲线()ln f x x x =在点()()1,1f 处的切线的方程为________. 【答案】10x y --=【解析】()()()''10,ln 1,11f f x x f ==+=,所以切线方程为110y x x y =-⇒--=. 故答案为:10x y --=9.(2021·东城·北京一七一中高二月考)函数()sin x f x e x =的图象在点()()0,0f 处切线的方程为___________. 【答案】0x y -= 【解析】切点为()0,0,()()()''sin cos ,01x f x x x e f =+⋅=,故切线方程为y x =,即0x y -=. 故答案为:0x y -=10.(2021·全国高二课时练习)已知点M 是曲线3212313y x x x =-++上任意一点,求曲线在点M 处的斜率最小的切线方程.【答案】33110x y +-=.【解析】①()224321y x x x '=-+=--, ①当2x =时,min1y '=-,此时53y =, ①斜率最小的切线过点2,3⎛⎫⎪⎝⎭5,且斜率1k =-,①所求切线方程为33110x y +-=. 【题组六 已知切线方程求参数】1.(2021·曲靖市沾益区第四中学高二月考(理))若存在过点()0,0的直线与曲线2y x x =+和1e x y ax -=+都相切,则a =( ) A .0 B .1- C .1 D .e【答案】A【解析】设切线方程为y kx =,与2y x x =+联立,得()210x k x +-=,所以()210k ∆=-=,解得1k =,所以切线方程为y x =.设y x =与1e x y ax -=+的图像相切于点()11,x y ,1ex y a -'=+,则111111e 1,e ,x x a ax x --⎧+=⎨+=⎩解得0a =.2.(2021·全国高二课时练习)若曲线y =x 3+ax 在(0,0)处的切线方程为2x -y =0,则实数a 的值为__________. 【答案】2【解析】曲线y =x 3+ax 的切线斜率k =y ′=3x 2+a , 又曲线在坐标原点处的切线方程为2x -y =0, ①3×02+a =2,可得a =2. 故答案为:23.(2021·全国高二课时练习)已知函数f (x )=ln +xk xe (k 为常数,e =2.718 28…是自然对数的底数),曲线y =f (x )在点(1,f (1))处的切线与x 轴平行,则k 的值为__________. 【答案】1【解析】由题设,1l (n )xkx x x x f xe --'=,x ①(0,+∞). 又y =f (x )在点(1,f (1))处的切线与x 轴平行,①f ′(1)=1k e-=0,可得k =1. 故答案为:14(2021·全国高二单元测试)设曲线y =ax 3+x 在(1,a )处的切线与直线2x ﹣y ﹣6=0平行,则实数a 的值为______. 【答案】13【解析】解:根据题意,曲线y =ax 3+x ,其导函数y ′=3ax 2+1,则有y ′|x =1=3a +1,若曲线y =ax 3+x 在(1,a )处的切线与直线2x ﹣y ﹣6=0平行,则有3a +1=2,解可得:a =13; 故答案为:135(2021·全国高二课时练习)已知函数()()2ln 1f x x ax bx =+-+,曲线()y f x =在点()()1,1f 处的切线方程为322ln 23x y -+-0=,则a b +=______.【答案】2【解析】由题知:()121f x a bx x'=-++. 又因为直线322ln 230x y -+-=的斜率为32,且过点()1,ln 2, ①()()1ln 2312f f ⎧='⎪⎨=⎪⎩,即021b a b a -=⎧⎨-=⎩,解得11a b =⎧⎨=⎩,①2a b +=. 故答案为:2.6.(2021·全国高二课时练习)已知曲线C :()3f x x ax a =-+,若过曲线C 外一点1,0A 引曲线C 的两条切线,它们的倾斜角互补,则实数a 的值为______. 【答案】278【解析】设切点坐标为()3,t t at a -+.由题意,知()23f x x a '=-,切线的斜率为23k t a =-①,所以切线的方程为()()()323y t at a t a x t --+=--①.将点()1,0代入①式,得()()()3231t at a t a t --+=--,解得0t =或32t =.分别将0t =和32t =代入①式,得k a =-和274k a =-.由题意,得274a a ⎛⎫-=-- ⎪⎝⎭,得278a =. 故答案为:278. 7.(2021·浙江海曙·效实中学高二期中)已知直线21y x =-与曲线ln(3)y x t =+相切,则实数t 的值为__________. 【答案】33ln 22- 【解析】依题意,设切点坐标为00(,ln(3))x x t +,由ln(3)y x t =+求导得:33y x t'=+, 于是得000323ln(3)21x t x t x ⎧=⎪+⎨⎪+=-⎩,即00332321ln 2x t x ⎧+=⎪⎪⎨⎪=+⎪⎩,解得:33ln 22t =-, 所以实数t 的值为33ln 22-. 故答案为:33ln 22- 8.(2021·全国高二课时练习)已知函数f (x )=2ax x b+,且f (x )的图象在x =1处与直线y =2相切. (1)求函数f (x )的解析式; (2)若P (x 0,y 0)为f (x )图象上的任意一点,直线l 与f (x )的图象切于P 点,求直线l 的斜率k 的取值范围.【答案】(1)()241x f x x =+;(2)1,42⎡⎤-⎢⎥⎣⎦. 【解析】(1)()()()()22'22222a x b x axax ab f x x b x b +-⋅-+==++,依题意可知()()'12,10f f ==,所以()()()2101121a ab f b a f b -+⎧==⎪+⎪⎨⎪==+⎩'⎪,解得 4,1a b ==. 所以()241x f x x =+ (2)()()()()()22'2222222418448141111x x f x x x x x -++-+===-++++221118142x ⎛⎫=-- ⎪+⎝⎭, 由于(]22111,0,11x x +≥∈+, 221111814,8004242⎛⎫⎛⎫--=--= ⎪ ⎪⎝⎭⎝⎭, 所以2211118,41422x ⎛⎫⎡⎤--∈- ⎪⎢⎥+⎝⎭⎣⎦, 所以切线l 的斜率的取值范围是1,42⎡⎤-⎢⎥⎣⎦. 9.(2021·全国高二课时练习)已知函数f (x )=ax 2+ln x 的导数为()'f x ,(1)求(1)(1)'+f f ;(2)若曲线y =f (x )存在垂直于y 轴的切线,求实数a 的取值范围.【答案】(1)3a +1;(2)(,0)-∞.【解析】(1)依题意,f (x )=ax 2+ln x 的定义域为(0,+∞),由f (x )=ax 2+ln x 求导得:1()2f x ax x '=+, 于是得(1)21f a '=+,而(1)f a =,所以(1()1)31f f a '+=+;(2)因曲线y =f (x )存在垂直于y 轴的切线,则此时切线斜率为0,由导数的几何意义知,方程()0f x '=在(0,)+∞内有解, 于是得方程120ax x +=,即212a x=-在(0,)+∞内有解,则0a <, 所以实数a 的取值范围是(,0)-∞.。
(完整版)导数的运算经典习题

(完整版)导数的运算经典习题1. 概述本文档列举了一些有关导数的运算的经典题,以帮助读者巩固和提高对该知识点的理解和应用能力。
2. 题集2.1 一阶导数1. 计算函数 $f(x) = 3x^2 + 2x + 1$ 的导函数 $f'(x)$。
2. 求函数 $g(x) = \sqrt{x}$ 的导数 $g'(x)$。
3. 计算函数 $h(x) = e^x - \sin(x)$ 在 $x = 0$ 处的导数 $h'(0)$。
4. 求函数 $k(x) = \ln(x)$ 的导函数 $k'(x)$。
2.2 高阶导数1. 计算函数 $f(x) = \cos(x)$ 的二阶导数 $f''(x)$。
2. 求函数 $g(x) = \frac{1}{x^2}$ 的二阶导数 $g''(x)$。
3. 计算函数 $h(x) = e^x \cos(x)$ 的二阶导数 $h''(x)$。
4. 求函数 $k(x) = \ln(x^2)$ 的二阶导数 $k''(x)$。
2.3 乘积法则和商积法则1. 使用乘积法则计算函数 $f(x) = (3x^2 + 2x + 1)(4x + 1)$ 的导函数 $f'(x)$。
2. 使用商积法则计算函数 $g(x) = \frac{x^2 + 1}{x}$ 的导数$g'(x)$。
2.4 链式法则1. 使用链式法则计算函数 $f(x) = \sin(3x^2 + 2x + 1)$ 的导数$f'(x)$。
2. 使用链式法则计算函数 $g(x) = e^{2x^3}$ 的导函数 $g'(x)$。
3. 总结本文档提供了一些有关导数的运算的经典习题,涵盖了一阶导数、高阶导数、乘积法则和商积法则、链式法则等知识点。
通过完成这些习题,读者可以巩固对导数运算的理解,并提高应用能力。
希望这些习题对您有所帮助!。
导数定义运算练习

导数练习题一第I 卷(选择题)一、选择题1.函数2()4f x x =的导函数是( )A .'()2f x x =B .'()4f x x =C .'()8f x x =D .'()16f x x =2.函数f (x )=sin 2x 的导数f′(x )=( )A .2sinxB .2sin 2xC .2cosxD .sin2x3.函数y=x cos x ﹣sin x 的导数为( )A .x sin xB .﹣x sin xC .x cos xD .﹣xcos x4.已知函数f (x )=sinx+lnx ,则f′(1)的值为( )A .1﹣cos1B .1+cos1C .cos1﹣1D .﹣1﹣cos15..若f′(x 0)=2,则k 2)x(f )k x (f 000k lim --→等于( )A .﹣1B .﹣2C .1D .6.下列各函数的导数:①;②(a x )′=a 2lnx ;③(sin2x )′=cos2x;④()′=.其中正确的有( )A .0个B .1个C .2个D .3个7.下列求导运算正确的是( )A .(x )′=1B .(x 2cosx )′=﹣2xsinxC .(3x )′=3x log 3eD .(log 2x )′=8.设x x y sin 12-=,则='y ( ).A .x x x x x 22sin cos )1(sin 2---B .x xx x x 22sin cos )1(sin 2-+-C .x x x x sin )1(sin 22-+-D .xx x x sin )1(sin 22---9.过抛物线y=x 2上的点的切线的倾斜角( ) A .30° B .45° C .60° D .135°9.若()sin cos f x x α=-,则'()f α等于( )A .sin αB .cos αC .sin cos αα+D .2sin α10.已知f(x)=xln x ,若f ′(x 0)=2,则x 0等于 ( ).A .e 2B .eC .ln 22D .ln 211.已知函数f (x )=2ln (3x )+8x+1,则的值为( )A .10B .﹣10C .﹣20D .2012.已知函数,则其导函数f′(x )的图象大致是( )A .B .C .D .二、填空题13.已知函数y=f (x )在定义域内可导,其图象如图,记y=f (x )的导函数为y=f′(x ),则不等式f′(x )≥0的解集为 ______________14.已知函数=+=)4(,cos sin )2()('ππf x x f x f 则_______. 15.函数()ln 1f x x =+在点(1,1)处的切线方程为 .16.若函数()(1)(2)(3)(4)f x x x x x =----,则(2)=f ' .三、解答题17. 用导数的定义求函数121)(+=x x f 在0x x =处的导数18. 用导数公式求函数121)(+=x x f 的导数)('x f ,并求)(0'x f19.已知函数2321)(x x x f +=.(1)求)(x f 在))34(,34(--f 处的切线方程; (2)函数x e x f y )(=的导数.20.已知函数f(x)=ae x+bxlnx图象上x=1处的切线方程为y=2ex﹣e.求实数a和b的值;21.已知函数f(x)=(2x﹣1)2+5x(1)求f′(x)(2)求曲线y=f(x)在点(2,19)处的切线方程.22.已知抛物线1=xfx(2+2)(1)抛物线上哪一点处的切线的倾斜角是︒45。
新人教版高中数学选择性必修第二册培优班精讲《导数的运算》练习含答案解析
5.2 导数的运算考点一 初等函数求导【例1】(2020·林芝市第二高级中学高二期末(文))求下列函数的导函数.(1)()3224f x x x =-+(2)()32113f x x x ax =-++(3)()cos ,(0,1)f x x x x =+∈ (4)2()3ln f x x x x =-+-(5)sin y x = (6)11x y x +=-【答案】(1)2()68f x x x =-+ (2)2()2f x x x a '=-+ (3)()sin 1f x x '=-+ (4)1()23f x x x'=--+ (5)cos y x '= (6)22(1)y x '=--【解析】(1)由()3224f x x x =-+,则()'268f x x x =-+;(2)由()32113f x x x ax =-++,则()'22f x x x a =-+;(3)由()cos ,(0,1)f x x x x =+∈ ,则()1sin ,(0,1)f x x x =-∈;(4)由2()3ln f x x x x =-+-,则'1()23f x x x=-+-;(5)由sin y x =,则 'cos y x =;(6)由11x y x +=-,则'''22(1)(1)(1)(1)2(1)(1)x x x x y x x +⨯--+⨯-==---.【一隅三反】1.(2020·西藏高二期末(文))求下列函数的导数.(1)2sin y x x =;(2)n 1l y x x=+;(3)322354y x x x =-+-.【答案】(1)22sin cos y x x x x '=+(2)211y x x'=-(3)2665y x x '=-+【解析】(1)2sin y x x =22sin cos y x x x x '=+(2)n 1l y x x =+211y x x'=-(3)322354y x x x x =-+-2665y x x '=-+2.(2020·通榆县第一中学校高二月考(理))求下列函数的导数:(Ⅰ)22ln cos y x x x =++;(Ⅱ)3e x y x =.【答案】(Ⅰ)14sin x x x+-;(Ⅱ)()233e xx x +.【解析】(Ⅰ)由导数的计算公式,可得()212(ln )(cos )4sin y x x x x x x'=++=+-'''.(Ⅱ)由导数的乘法法则,可得()()()3323e e 3e x xx y x x xx ''=+=+'.3.(2020·山东师范大学附中高二期中)求下列函数在指定点的导数:(1)4ln(31)y x =++ ,1x =; (2)2cos 1sin x y x=+,π2x =.【答案】(1)12x y ='=(2)21ln 2x y π==+'【解析】(1)321231y x x -'=-++,12x y ='=(2)21sin y x+'=,21ln2x y π==+'考点二 复合函数求导【例2】.(2020·凤阳县第二中学高二期末(理))求下列函数的导数:(1)2=e x y ;(2)()313y x =-.【答案】(1)22x e ;(2)29(13)x --或281549y x x '=-+-.【解析】(1)2'22e (2)e 22e x x x y x =⋅=⋅=';(2)()()22'313(13)913y x x x =--=--'.或281549y x x '=-+-. 【一隅三反】1.(2020·陕西碑林·西北工业大学附属中学高二月考(理))求下列函数的导数:(1)()*()2+1ny x n N ∈=,;(2)(ln y x =+;(3)11x x e y e +=-;(4)2)2(+5y xsin x =.【答案】(1)()1'221n y n x -=+;(2)'y =;(3)()221xxe y e-'=-;(4)2sin(25)4cos(25)y x x x '=+++.【解析】(1)()()()11'2121'221n n y n x x n x ⋅--=++=+;(2)1y ⎛=+= ⎝'(3)∵12111xx xe y e e +==+--∴()()222211xxx xe e y e e'-=-=--;(4)()()2sin 254cos 25y x x x =+'++.2.(2020·横峰中学高二开学考试(文))求下列各函数的导数:(1)ln(32)y x =-;(2)()212x x f x ee e -+=++(3)y【答案】(1)332y x '=-;(2)21()2x x f x e e -+'=-+.(3)y '=【解析】(1)因为ln(32)y x =-令32t x =-,ln y t =所以()()1332ln 332y x t t x '''=-⋅=⋅=-(2)()21221,()2x x x x f x e f x ee e e -+-+∴'=-+++= .(3)令212t x =-,则12y t =,所以112211()(4)22y t t t x -'''==⋅=-=;考点三 求导数值【例3】.(2020·甘肃城关·兰州一中高二期中(理))已知函数()f x 的导函数为()'f x ,且满足()3(1)ln f x xf x '=+,则(1)f '=A .12-B .12C .1-D .e【答案】A【解析】()()31ln f x xf x '=+ ,求导得()()131f x f x''=+,则()()1311f f ''=+,解得()112f '=-.故选:A.【一隅三反】1.(2020·广东湛江·高二期末(文))已知函数()cos x f x x =,则2f π⎛⎫= ⎪⎝⎭'( )A .2π-B .2πC .3πD .3π-【答案】A【解析】()cos x f x x = ,()2sin cos x x x f x x --'∴=,因此,2sin 22222f πππππ⎛⎫⎛⎫--- ⎪ ⎪⎛⎫⎝⎭⎝⎭'-==- ⎪⎝⎭⎛⎫- ⎪⎝⎭.故选:A.2.(2020·四川高二期中(理))若函数()()22co 102s x f x x f x '=++,则6f π⎛⎫' ⎪⎝⎭的值为( )A .0B .6πC .3πD .π【答案】B【解析】因为()()20sin 1f x x f x ''=-+,所以令0x =,则()01f '=,所以()2sin 1f x x x '=-+,则66f ππ⎛⎫'=⎪⎝⎭,故选: B.3.(2020·广西桂林·高二期末(文))已知函数2()f x x x =+,则()1f '=( )A .3B .0C .2D .1【答案】A【解析】由题得()21(1)3f x x f ''=+∴=,.故选:A 考点四 求切线方程【例4】.(2020·郸城县实验高中高二月考(理))已知曲线31433y x =+(1)求曲线在点(2,4)P 处的切线方程;(2)求曲线过点(2,4)P 的切线方程【答案】(1)440x y --=;(2)20x y -+=或440x y --=.【解析】(1)∵2y x '=,∴在点()2,4P 处的切线的斜率2|4x k y ='==,∴曲线在点()2,4P 处的切线方程为()442y x -=-,即440x y --=.(2)设曲线31433y x =+与过点()2,4P 的切线相切于点30014,33A x x ⎛⎫+ ⎪⎝⎭,则切线的斜率020|x x k y x =='=,∴切线方程为()320001433y x x x x ⎛⎫-+=-⎪⎝⎭,即23002433y x x x =⋅-+.∵点()2,4P 在该切线上,∴2300244233x x =-+,即320340x x -+=,∴322000440x x x +-+=,∴()()()2000014110x x x x +-+-=,∴()()200120x x +-=,解得01x =-或02x =.故所求切线方程为440x y --=或20x y -+=.【一隅三反】1.(2020·黑龙江大庆实验中学高三月考(文))曲线2xy x =-在点()1,1-处的切线方程为A .21y x =-+B .32y x =-+C .23y x =-D .2y x =-【答案】A【解析】2xy x =-的导数为22'(2)y x =--,可得曲线22y x =-在点()1,1-处的切线斜率为1'|2x k y ===-,所以曲线2xy x =-在点()1,1-处的切线方程为12(1)y x +=--,即21y x =-+,故选A.2.(2020·河南高三其他(理))曲线()21ln 22y x x =-在某点处的切线的斜率为32-,则该切线的方程为()A .3210x y +-=B .3210x y ++=C .6450x y +-=D .12870x y +-=【答案】D【解析】求导得1y x x '=-,根据题意得132y x x '=-=-,解得2x =-(舍去)或12x =,可得切点的坐标为11,28⎛⎫⎪⎝⎭,所以该切线的方程为131822y x ⎛⎫-=-- ⎪⎝⎭,整理得12870x y +-=.故选:D.3.(2020·北京高二期末)过点P (0,2)作曲线y =1x 的切线,则切点坐标为( )A .(1,1)B .(2,12)C .(3,13)D .(0,1)【答案】A【解析】设切点001(,)x x ,022001112(0)y x x x x '=-∴-=--Q 01x ∴=,即切点(1,1)故选:A4.(2020·吉林洮北·白城一中高二月考(理))已知函数f(x)=x 3-4x 2+5x -4.(1)求曲线f(x)在点(2,f(2))处的切线方程;(2)求经过点A(2,-2)的曲线f(x)的切线方程.【答案】(1)x -y -4=0(2)x -y -4=0或y +2=0【解析】(1)∵f′(x)=3x 2-8x +5,∴f′(2)=1,又f(2)=-2,∴曲线f(x)在点(2,f(2))处的切线方程为y -(-2)=x -2,即x -y -4=0.(2)设切点坐标为(x 0,x 03-4x 02+5x 0-4),∵f′(x 0)=3x 02-8x 0+5,∴切线方程为y -(-2)=(3x 02-8x 0+5)(x -2),又切线过点(x 0,x 03-4x 02+5x 0-4),∴x 03-4x 02+5x 0-2=(3x 02-8x 0+5)(x 0-2),整理得(x 0-2)2(x 0-1)=0,解得x 0=2或x 0=1,∴经过A(2,-2)的曲线f(x)的切线方程为x -y -4=0或y +2=0.考点五 利用切线求参数【例5】.(2020·全国高三其他(理))已知曲线()ln xy e ax x =-在点()1,ae 处的切线方程为y kx =,则k =()A .1-B .0C .1D .e【答案】D【解析】令()()ln xy f x eax x ==-,则()()1ln x xf x e ax x e a x'=-+-(,所以()12f ea e ='-,因为曲线()ln xy eax x =-在点()1,ae 处的切线方程为y kx =,所以该切线过原点,所以()12f ea e ae ='-=,解得1a =,即k e =.故选:D.【一隅三反】1.(2020·岳麓·湖南师大附中月考)已知函数()2ln xf x ax x=-,若曲线()y f x =在()()1,1f 处的切线与直线210x y -+=平行,则a =______.【答案】12-【解析】因为函数()2ln x f x ax x =-,所以()21ln 2xf x ax x-'=-,又因为曲线()y f x =在()()1,1f 处的切线与直线210x y -+=平行,所以()1122f a '=-=,解得12a =-,故答案为:12-2.(2020·安徽庐阳·合肥一中高三月考(文))曲线(1)x y ax e =+在点(0,1)处的切线的斜率为2,则a =_____.【答案】1【解析】 (1)x y ax e =+,∴(1)x y ax a e '=++ 012x y a =∴=+=',1a \=.故答案为:1.3.(2020·山东莱州一中高二月考)已知直线y x b =+是曲线3x y e =+的一条切线,则b =________.【答案】4【解析】设()3xf x e =+,切点为()00,+3xx e ,因为()xf x e '=,所以01x e =,解得00x =,所以0034y e =+=,故切点为(0,4),又切点在切线y x b =+上,故4b =.故答案为:4。
高中数学专题练习《导数的四则运算法则》含详细解析

5.2.2导数的四则运算法则基础过关练题组一导数的四则运算法则1.函数f(x)=x 2x+3的导数f'(x)=()A.x 2+6xx+3B.-2x(x+3)2C.x2+6x(x+3)2D.3x2+6x(x+3)22.函数y=x2cos x的导数为()A.y'=2xcos x-x2sin xB.y'=2xcos x+x2sin xC.y'=x2cos x-2xsin xD.y'=xcos x-x2sin x3.已知f(x)=x2+e x,则f'(0)=()A.0B.-4 C.-2 D.14.对于函数f(x)=e xx2+ln x-2kx,若f'(1)=1,则实数k等于()A.e2B.e3C.-e2D.-e35.(2020浙江宁波余姚中学高二下月考)设f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f'(x)=g'(x),则f(x)与g(x)满足() A.f(x)=g(x) B.f(x)=g(x)=0C.y=f(x)-g(x)为常数函数D.y=f(x)+g(x)为常数函数6.若函数f(x)=x 2e x,则f'(x)=.7.已知函数f(x),g(x)满足f(5)=5,f'(5)=3,g(5)=4,g'(5)=1,若h(x)=f(x)+2g(x),则h'(5)=.8.求下列函数的导数.(1)y=x-2+x2;(2)y=3x e x-2x+e;(3)y=lnxx2+1;(4)y=x2-4sin x2cos x2.题组二求导法则的综合应用9.已知函数f(x)=f'(1)+xln x,则f(e)=()A.1+eB.eC.2+eD.310.已知定义在R上的函数f(x)=e x+x2-x+sin x,则曲线y=f(x)在点(0,f(0))处的切线方程为()A.y=3x-2B.y=x+1C.y=2x-1D.y=-2x+311.(2020浙江嘉兴高三上期末)设曲线y=x+1x-2在点(1,-2)处的切线与直线ax+by+c=0(b≠0)垂直,则ab=()A.13B.-13C.3D.-312.(2020河北保定高二上期末)设曲线f(x)=ae x-ln x(a≠0)在x=1处的切线为l,则l在y轴上的截距为()A.1B.2C.aeD.ae-113.若质子的运动方程为s=tsin t,其中s的单位为m,t的单位为s,则质子在t=2s时的瞬时速度为m/s.14.曲线y=x3+3x2+6x-10的所有切线中,斜率最小的切线方程为.15.(2020江西南昌三中高二下期中)已知函数f(x)=x-2ln x,求曲线y=f(x)在点A(1,f(1))处的切线方程.能力提升练题组导数的四则运算法则及其应用1.()设函数f(x)=sinθ3x3+√3cosθ2x2+tanθ,其中θ∈[0,5π12],则导数f'(1)的取值范围是()A.[-2,2]B.[√2,√3]C.[√3,2]D.[√2,2]2.(2020湖南长沙长郡中学高二上期末,)下面四个图象中,有一个是函数f(x)=13x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)=()A.13B.-23C.73D.-13或533.(2019河北衡水中学高三二调,)已知f'(x)是函数f(x)的导函数,且对任意的实数x都有f'(x)=e x(2x-2)+f(x)(e是自然对数的底数),f(0)=1,则(易错)A.f(x)=e x(x+1)B.f(x)=e x(x-1)C.f(x)=e x(x+1)2D.f(x)=e x(x-1)24.()设函数f(x)=xsin x+cos x的图象在点(t,f(t))处切线的斜率为g(t),则函数y=g(t)图象的一部分可以是()5.(多选)()给出定义:若函数f(x)在D上可导,即f'(x)存在,且导函数f'(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f'(x))',若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,π)上不是凸函数的是()2A.f(x)=sin x-cos xB.f(x)=ln x-2xC.f(x)=-x3+2x-1D.f(x)=xe x6.()对于三次函数f(x)=ax3+bx2+cx+d(a≠0),现给出定义:设f'(x)是函数f(x)的导数,f″(x)是f'(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数f(x)=ax3+bx2+cx+d(a≠0)的“拐点”.经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=2x3-3x2+1,则g(1100)+g(2100)+…+g(99100)=.7.(2020湖南长沙长郡中学高二上期末,)已知函数f(x)=13x3-2x2+3x(x∈R)的图象为曲线C.(1)求曲线C上任意一点的切线的斜率的取值范围;(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C 的切点的横坐标的取值范围.8.()已知直线x+2y-4=0与抛物线y2=4x相交于A,B两点,O是坐标原点,试在抛物线的AOB⏜上求一点P,使△ABP的面积最大.9.()已知函数f(x)(x∈(0,+∞))的导函数为f'(x),且满足xf'(x)-2f(x)=x3e x,f(1)=e-1,求f(x)在点(2,f(2))处的切线方程.答案全解全析基础过关练1.C f'(x)=(x 2)'(x+3)−x2(x+3)′(x+3)2=2x(x+3)−x 2(x+3)2=2x2+6x-x2(x+3)2=x2+6x(x+3)2.故选C.2.A对函数y=x2cos x求导,得y'=2xcos x+x2·(-sin x)=2xcos x-x2sin x.故选A.3.D由题意,得f'(x)=2x+e x,则f'(0)=1,故选D.4.A因为f'(x)=e x(x-2)x3+1x+2kx2,所以f'(1)=-e+1+2k=1,解得k=e2,故选A.5.C取f(x)=x,g(x)=x+1,满足f'(x)=g'(x),可以验证A、B、D错误;由f'(x)=g'(x),得f'(x)-g'(x)=0,即[f(x)-g(x)]'=0,所以f(x)-g(x)=c(c为常数),C 正确.故选C.6.答案2x-x 2e x解析f'(x)=2xe x-x2e x(e x)2=2x-x2e x.7.答案516解析由题意得,h'(x)=f'(x)g(x)-[f(x)+2]g'(x)[g(x)]2,由f(5)=5,f'(5)=3,g(5)=4,g'(5)=1,得h'(5)=f'(5)g(5)-[f(5)+2]g'(5)[g(5)]2=3×4−(5+2)×142=516.8.解析(1)y'=2x-2x-3. (2)y'=(ln3+1)·(3e)x-2x ln2.(3)y'=x 2+1−2x 2lnx x(x 2+1)2.(4)∵y=x 2-4sin x2cos x 2=x 2-2sin x,∴y'=2x-2cos x.9.A ∵f'(x)=ln x+1,∴f'(1)=ln 1+1=1,则f(x)=1+xln x,∴f(e)=1+eln e=1+e.10.B ∵f'(x)=e x +2x-1+cos x,∴切线的斜率k=f'(0)=1,又f(0)=1,∴切线方程为y=x+1. 11.B 依题意得y'=x -2-(x+1)(x -2)2=-3(x -2)2,则y'x=1=-3,由于曲线y=x+1x -2在点(1,-2)处的切线与直线ax+by+c=0(b ≠0)垂直,所以(-3)·(-ab)=-1,解得a b=-13.故选B.12.A 因为函数f(x)=ae x -ln x(a ≠0), 所以f'(x)=ae x -1x ,将x=1代入,得k=ae-1,又f(1)=ae,所以曲线f(x)在x=1处的切线l 的方程为y-ae=(ae-1)(x-1), 整理得y=(ae-1)x+1,令x=0,得y=1. 所以l 在y 轴上的截距为1.故选A. 13.答案 sin 2+2cos 2解析 ∵s'=(tsin t)'=sin t+tcos t, ∴所求瞬时速度为(sin 2+2cos 2)m/s. 14.答案 3x-y-11=0解析 ∵y'=3x 2+6x+6=3(x 2+2x+2) =3(x+1)2+3≥3,∴当x=-1时,y'最小,即此时切线的斜率最小,此时切点为(-1,-14), ∴切线方程为y+14=3(x+1), 即3x-y-11=0.15.解析 ∵函数f(x)=x-2ln x 的导函数为f'(x)=1-2x ,∴曲线y=f(x)在点A(1,f(1))处的切线斜率为f'(1)=1-2=-1,又f(1)=1,∴曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),即x+y-2=0.能力提升练1.D f'(x)=sin θ·x 2+√3cos θ·x, ∴f'(1)=sin θ+√3cos θ=2sin (θ+π3),∵θ∈[0,5π12],∴θ+π3∈[π3,3π4],∴sin (θ+π3)∈[√22,1],∴f'(1)=2sin (θ+π3)∈[√2,2].故选D.2.D 因为f'(x)=x 2+2ax+a 2-1,所以y=f'(x)的图象开口向上,排除②④.若y=f'(x)的图象为①,则a=0,f(-1)=53;若y=f'(x)的图象为③,则a 2-1=0,得a=±1.又对称轴x=-a>0,所以a=-1,所以f(-1)=-13.3.D 由f'(x)=e x (2x-2)+f(x), 得f'(x)-f(x)e x =2x-2,即[f(x)e x]'=2x-2,所以f(x)e x=x 2-2x+c(c 为常数),所以f(x)=(x 2-2x+c)e x , 又因为f(0)=1,所以c=1,所以函数f(x)的解析式是f(x)=e x (x-1)2.故选D.易错警示 已知原函数可求出唯一的导函数,已知导数求原函数,则结论不唯一,如本题中由y'=2x-2可以得到y=x 2-2x+c(c 为常数),解题时容易将c 遗漏导致解题错误. 4.A 由f(x)=xsin x+cos x,可得f'(x)=sin x+xcos x-sin x=xcos x. 则g(t)=f'(t)=tcos t,易知函数g(t)是奇函数,排除选项B,D; 当t ∈(0,π2)时,g(t)>0,排除选项C.故选A.5.AD 对于A,f'(x)=cos x+sin x, f″(x)=-sin x+cos x,当x ∈(0,π4)时,f″(x)>0,故f(x)=sin x-cos x 不是凸函数;对于B,f'(x)=1x-2,f″(x)=-1x2<0,故f(x)=ln x-2x 是凸函数; 对于C,f'(x)=-3x 2+2,f″(x)=-6x,当x ∈(0,π2)时,f″(x)<0,故f(x)=-x 3+2x-1是凸函数;对于D,f'(x)=(x+1)e x ,f″(x)=(x+2)e x ,当x ∈(0,π2)时,f″(x)>0,故f(x)=xe x 不是凸函数.故选AD.6.答案992解析 依题意得,g'(x)=6x 2-6x,g″(x)=12x -6,令g″(x)=0,解得x=12, ∵g (12)=12,∴函数g(x)的对称中心为(12,12),则g(1-x)+g(x)=1,∵1100+99100=2100+98100=…=49100+51100=1,∴g (1100)+g (99100)=g (2100)+g (98100)=…=g (49100)+g (51100)=1,∴g (1100)+g (2100)+…+g (99100) =[g (1100)+g (99100)]+[g (2100)+g (98100)] +…+[g (49100)+g (51100)]+g (12) =49+12=992.7.解析 (1)由题意得f'(x)=x 2-4x+3,则f'(x)=(x-2)2-1≥-1,即曲线C 上任意一点的切线的斜率的取值范围是[-1,+∞).(2)设曲线C 的其中一条切线的斜率为k,则由条件和(1)中结论可知, {k ≥−1,-1k ≥−1,解得-1≤k<0或k ≥1,故由-1≤x 2-4x+3<0或x 2-4x+3≥1,得x ∈(-∞,2-√2]∪(1,3)∪[2+√2,+∞).8.解析 因为|AB|为定值,所以要使△PAB 的面积最大,只要点P 到AB 的距离最大即可,即点P 是抛物线的切线中平行于AB 的切线的切点,设P(x,y).由题图知,点P 在x 轴下方的图象上,所以y=-2√x ,所以y'=-√x . 因为k AB =-12,所以-√x =-12,解得x=4.由y=-2√x ,得y=-4, 所以点P 的坐标为(4,-4).9.解析 ∵xf'(x)-2f(x)=x 3e x ,x ∈(0,+∞),∴xf'(x)-2f(x)x 3=e x . 令g(x)=f(x)x 2,则g'(x)=xf'(x)-2f(x)x 3=e x , ∴g(x)=f(x)x 2=e x +c(c 为常数),∴f(x)=x 2(e x +c).又f(1)=e+c=e-1,∴c=-1.∴f(x)=x 2(e x -1),∴f'(x)=2x(e x -1)+x 2e x =(x 2+2x)e x -2x,∴f'(2)=8e 2-4.又f(2)=4(e 2-1),∴所求切线方程为y-4(e 2-1)=(8e 2-4)·(x-2),即y=(8e 2-4)x-12e 2+4.。
导数的运算——综合练习(解析版)

导数的运算——综合练习一.选择题(共40小题)1.若f′(x)是函数f(x)=x3+2x+1的导函数,则f′(﹣1)的值为()A.1 B.3 C.1或3 D.42.若f(x)=x5,f′(x0)=20,则x0的值为()A.B.±C.﹣2 D.±23.下列求导运算正确的是()A.(cosx)'=sinx B.(3x)'=3x log3eC.D.(x2cosx)′=﹣2xsinx4.已知函数f(x)=sinx﹣cosx,且f′(x)=2f(x),则tan2x的值是()A.﹣B.C.﹣D.5.已知函数f(x)=,若f′(1)=,则实数a的值为()A.2 B.4 C.6 D.86.已知函数f(x)=6﹣x3,g(x)=e x﹣1,则这两个函数的导函数分别为()A.f′(x)=6﹣3x2,g′(x)=e x B.f′(x)=﹣3x2,g′(x)=e x﹣1C.f′(x)=﹣3x2,g′(x)=e x D.f′(x)=6﹣3x2,g′(x)=e x﹣17.已知f(x)=lnx,则f′(e)的值为()A.1 B.﹣1 C.e D.8.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(2)=()A.B.1 C.﹣1 D.﹣9.已知,则f'(2)=()A.B.C.2 D.﹣210.下列求导运算正确的是()A.(log2x)′=B.(x+)′=1+C.(cosx)′=sinx D.()′=11.若f(x)=,f'(x)为f(x)的导函数,则f'(x)=()A.f'(x)= B.f'(x)=C.f'(x)= D.f'(x)=12.已知函数f(x)=x2+2xf′(2017)﹣2017lnx,则f′(2017)=()A.2016 B.﹣2016 C.2017 D.﹣201713.已知f'(x)是f(x)=sinx+acosx的导函数,且f'()=,则实数a的值为()A.B.C.D.114.已知函数f(x)的导函数f'(x),且满足f(x)=2xf'(1)+lnx,则f′(1)=()A.﹣1 B.﹣e C.1 D.e15.下列函数在点x=0处没有切线的是()A.y=3x2+cosx B.y=xsinx C.D.16.f'(x)是函数f(x)的导函数,且f(x)=﹣x2+2x f'(2017)+2017㏑x,则f'(1)=()A.2016 B.6045 C.2017 D.604817.已知函数f(x)=f´()cosx+sinx,则f()=()A.B.﹣1 C.1 D.018.函数y=sin(lnx)的导数y′=()A.ln(cosx)B.cos(lnx)C.﹣cos(lnx)D.cos(lnx)19.已知函数f(x)=ln(ax﹣1)的导函数是f'(x),且f'(2)=2,则实数a的值为()A.B.C.D.120.设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,f n+1(x)=f n′(x),n∈N,则f2017(x)=()A.sinx B.﹣sinx C.cosx D.﹣cosx21.已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,f n(x)=f n﹣1′(x),则f2015(x)等于()A.sinx B.﹣sinx C.cosx D.﹣cosx22.函数(x>0),若x0满足f'(x0)=0,设m∈(0,x0),n∈(x0,+∞),则()A.f'(m)<0,f'(n)<0 B.f'(m)>0,f'(n)>0 C.f'(m)<0,f'(n)>0 D.f'(m)>0,f'(n)<023.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)﹣f(a)=f'(m)(b﹣a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数在[0,b]上恰有两个“中值点”,则实数b的取值范围是()A.,B.(3,+∞)C.,D.,24.设函数f(x)=x3﹣ax2+2bx+1的导函数为f′(x),若函数f′(x)的图象关于直线x=对称,且当x∈[1,π]时,恒有f(x)≥1,则实数b的取值范围为()A.(,+∞)B.[,1]C.(﹣∞,]D.[,+∞)25.已知定义在(0,+∞)上的单调函数f(x),对∀x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是()A.(0,) B.(1,2) C.(,1) D.(2,3)26.已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x,有,则的最小值为()A.2 B.C.3 D.27.已知函数f(x)及其导数f'(x),若存在x0使得f(x0)=f'(x0),则称x0是f(x)的一个“巧值点”.给出下列五个函数:①f(x)=x2,②f(x)=e﹣x,③f(x)=lnx,④f(x)=tanx,其中有“巧值点”的函数的个数是()A.1 B.2 C.3 D.428.已知函数,其导函数记为f'(x),则f(2017511)+f'(2017511)+f(﹣2017511)﹣f'(﹣2017511)=()A.0 B.1 C.2 D.201751129.[x]表示不超过x的最大整数,若f′(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)f′(x),则函数f=[g(x)]+[g(﹣x)]的值域是()A.{﹣1,0}B.{0,1}C.{0}D.{偶数}30.定义:如果函数f(x)在[m,n]上存在x1,x2(m<x1<x2<n)满足f′(x1)=,f′(x2)=,则称函数f(x)是[m,n]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,则实数a的取值范围是()A.(,)B.(,3) C.(,1) D.(,1)31.已知函数f(x)=asinx+bx3+1(a,b∈R),f′(x)为f(x)的导函数,则f(2016)+f(﹣2016)+f′(2017)﹣f′(﹣2017)=()A.2017 B.2016 C.2 D.032.已知f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则f'(0)=()A.n B.n﹣1 C.D.n(n+1)33.设函数f(x)=x3+x2+,其中θ∈(﹣,),则导数f′(1)的取值范围是()A.(﹣,1]B.(﹣,1)C.(﹣,)D.(﹣,]34.已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…f n+1(x)=f′n(x),n∈N,那么f2017=()A.cosx﹣sinx B.sinx﹣cosx C.sinx+cosx D.﹣sinx﹣cosx35.定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=x3﹣1,h(x)=2x,φ(x)=ln(x+1)的“新驻点”分别为α,β,γ,则α,β,γ的大小关系为()A.α>β>γ B.β>α>γ C.γ>α>β D.β>γ>α36.设f1(x)=sinx,定义f n+1(x)为f n(x)的导数,即f(x)=f n′(x),n∈N*,若△ABC的内角A满足f1(A)+f2(A)+…+f2018(A)=0,则cosA的值为()A.1 B.﹣1 C.D.﹣37.已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则x0称为f(x)的一个“巧值点”,则下列函数中有“巧值点”的是()①f(x)=x2;②f(x)=e﹣x;③f(x)=lnx;④f(x)=tanx;⑤f(x)=.A.①③⑤B.①③④C.②③④D.②⑤38.设函数f n′(x)是f n(x)的导函数,f0(x)=e x(cosx+sinx),f1(x)=,f2(x)=,…,(n∈N),则f2016(x)=()A.e x(cosx+sinx)B.e x(cosx﹣sinx)C.﹣e x(cosx+sinx)D.e x(sinx﹣cosx)39.已知函数f(x)=e x﹣2ax,函数g(x)=﹣x3﹣ax2.若不存在x1,x2∈R,使得f′(x1)=g′(x2),则实数a的取值范围为()A.(﹣2,3)B.(﹣6,0)C.[﹣2,3]D.[﹣6,0]40.已知函数f(x)=lnx+tanα(α∈(0,))的导函数为f′(x),若使得f′(x0)=f(x0)成立的x0<1,则实数α的取值范围为()A.(,)B.(0,)C.(,)D.(0,)二.填空题(共6小题)41.已知在R上可导,F(x)=f(x3﹣1)+f(1﹣x3),则F′(1)=.42.已知f(x)=f(4﹣x),当x≤2时,f(x)=e x,f′(3)+f(3)=.43.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,若x0是方程f(x)﹣f′(x)=4的一个解,且x0∈(a,a+1)(a∈N*),则实数a=.44.已知函数y=f(x)的导函数为f'(x)=cosx﹣5,且f(0)=0,如果f(1﹣ax)+f(1﹣ax2)<0恒成立,则实数a的取值范围是.45.已知函数f(x)满足f(0)=﹣1,其导函数f′(x)满足f′(x)>k>1,则下列结论中正确的是.(1)f()>﹣1;(2)f()>;(3)f()<;(4)f()<f()46.若函数f(x)的导数f′(x)存在导数,记f′(x)的导数为f n(x).如果f(x)对任意x∈(a,b),都有f n(x)<0成立,则f(x)有如下性质:f()≥.其中n∈N*,x1,x2,…,x n∈(a,b).若f(x)=sinx,则f n(x)=;根据上述性质推断:当x1+x2+x3=π且x1,x2,x3∈(0,π)时,根据上述性质推断:sinx1+sinx2+sinx3的最大值为.导数的运算——综合练习参考答案与试题解析一.选择题(共40小题)1.若f′(x)是函数f(x)=x3+2x+1的导函数,则f′(﹣1)的值为()A.1 B.3 C.1或3 D.4【分析】先求函数f(x)的导函数,然后在导函数解析式中把x代﹣1求值.【解答】解:因为函数f(x)=x3+2x+1,所以其导函数f′(x)=x2+2,所以f′(﹣1)=(﹣1)2+2=3.故选B.2.若f(x)=x5,f′(x0)=20,则x0的值为()A.B.±C.﹣2 D.±2【分析】根据函数的导数公式解方程即可.【解答】解:函数的导数f′(x)=5x4,∵f′(x0)=20,∴5x04=20,得x04=4,则x0=±,故选:B.3.下列求导运算正确的是()A.(cosx)'=sinx B.(3x)'=3x log3eC.D.(x2cosx)′=﹣2xsinx【分析】根据函数的导数公式进行判断即可.【解答】解:(cosx)'=﹣sinx,A不正确;(3x)'=3x ln3,B不正确(lgx)′=,C正确;(x2cosx)′=2xcosx﹣x2sinx,D不正确故选:C.4.已知函数f(x)=sinx﹣cosx,且f′(x)=2f(x),则tan2x的值是()A.﹣B.C.﹣D.【分析】求出f(x)的导函数,根据f′(x)=2f(x)列出关系式,计算即可求出tan2x的值.【解答】解:求导得:f′(x)=cosx+sinx,∵f′(x)=2f(x),∴cosx+sinx=2(sinx﹣cosx),即3cosx=sinx,∴tanx=3,则tan2x===﹣.故选C5.已知函数f(x)=,若f′(1)=,则实数a的值为()A.2 B.4 C.6 D.8【分析】根据导数的公式即可得到结论【解答】解:函数f(x)=,则f′(x)=∵f′(1)=,即f′(1)==,∴a=4.故选:B6.已知函数f(x)=6﹣x3,g(x)=e x﹣1,则这两个函数的导函数分别为()A.f′(x)=6﹣3x2,g′(x)=e x B.f′(x)=﹣3x2,g′(x)=e x﹣1C.f′(x)=﹣3x2,g′(x)=e x D.f′(x)=6﹣3x2,g′(x)=e x﹣1【分析】根据导数的运算法则求导即可.【解答】解:f′(x)=﹣3x2,g′(x)=e x,故选:C7.已知f(x)=lnx,则f′(e)的值为()A.1 B.﹣1 C.e D.【分析】利用导数的运算法则即可得出.【解答】解:∵,∴.故选D.8.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(2)=()A.B.1 C.﹣1 D.﹣【分析】已知函数f(x)的导函数为f′(x),利用求导公式对f(x)进行求导,再把x=1代入,x=2代入求解即可.【解答】解:∵函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,(x>0)∴f′(x)=2f′(1)+,把x=1代入f′(x)可得f′(1)=2f′(1)+1,解得f′(1)=﹣1,∴f′(2)=2f′(1)+=﹣2+=﹣.故选D.9.已知,则f'(2)=()A.B.C.2 D.﹣2【分析】把给出的函数求导,在其导函数中取x=2,则f′(2)可求.【解答】解:∵f′(x)=﹣+3f′(2),∴f′(2)=﹣+3f′(2),解得:f′(2)=,故选:A.10.下列求导运算正确的是()A.(log2x)′=B.(x+)′=1+C.(cosx)′=sinx D.()′=【分析】利用导数的运算法则即可得出.【解答】解:=,=1﹣,(cosx)′=﹣sinx,=,可知:只有A正确.故选:A.11.若f(x)=,f'(x)为f(x)的导函数,则f'(x)=()A.f'(x)= B.f'(x)=C.f'(x)= D.f'(x)=【分析】根据导数的运算法则计算即可.【解答】解:∵f(x)=,∴f'(x)=,故选:B12.已知函数f(x)=x2+2xf′(2017)﹣2017lnx,则f′(2017)=()A.2016 B.﹣2016 C.2017 D.﹣2017【分析】对函数f(x)的解析式求导,得到其导函数,把x=2017代入导函数中,列出关于f'(2017)的方程,进而得到f'(2017)的值【解答】解:求导得:f′(x)=x+2f′(2017)﹣令x=2017,得到f′(2017)=2017+2f′(2017)﹣1,解得:f′(2017)=﹣2016,故选:B13.已知f'(x)是f(x)=sinx+acosx的导函数,且f'()=,则实数a的值为()A.B.C.D.1【分析】求出f(x)的导数,由条件解方程,即可得到所求a的值.【解答】解:由题意可得f'(x)=cosx﹣asinx,由可得,解之得.故选:B.14.已知函数f(x)的导函数f'(x),且满足f(x)=2xf'(1)+lnx,则f′(1)=()A.﹣1 B.﹣e C.1 D.e【分析】已知函数f(x)的导函数为f′(x),利用求导公式对f(x)进行求导,再把x=1代入,即可求解;【解答】解:∵函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,(x>0),∴f′(x)=2f′(1)+,把x=1代入f′(x)可得f′(1)=2f′(1)+1,解得f′(1)=﹣1,故选A15.下列函数在点x=0处没有切线的是()A.y=3x2+cosx B.y=xsinx C.D.【分析】根据导数的定义可得答案.【解答】解:∵在x=0处不可导.故选D.16.f'(x)是函数f(x)的导函数,且f(x)=﹣x2+2x f'(2017)+2017㏑x,则f'(1)=()A.2016 B.6045 C.2017 D.6048【分析】根据导数的运算法则求导,代值计算即可.【解答】解:∵f′(x)=﹣x+2f'(2017)+,∴f′(2017)=﹣2017+2f'(2017)+1,解得f′(2017)=2016,∴f′(1)=﹣1+2×2016+2017=6048,故选:D.17.已知函数f(x)=f´()cosx+sinx,则f()=()A.B.﹣1 C.1 D.0【分析】先求导,再代值计算即可.【解答】解:∵f(x)=f´()cosx+sinx,∴f′(x)=﹣f´()sinx+cosx,∴f′()=﹣f´()×+,∴f′()=﹣1,∴f(π)=(﹣1)×(﹣)+=﹣1,故选:B18.函数y=sin(lnx)的导数y′=()A.ln(cosx)B.cos(lnx)C.﹣cos(lnx)D.cos(lnx)【分析】根据题意,令t=lnx,则y=sint,根据复合函数的导数公式进行求导即可答案.【解答】解:根据题意,令t=lnx,则y=sint,则其导数y′=cos(t)•(lnx)′=cos(lnx)•(lnx)′=cos(lnx),故选:D.19.已知函数f(x)=ln(ax﹣1)的导函数是f'(x),且f'(2)=2,则实数a的值为()A.B.C.D.1【分析】利用导数的运算法则即可得出.【解答】解:由f(x)=ln(ax﹣1)可得,由f'(2)=2,可得,解之得.故选:B.20.设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,f n+1(x)=f n′(x),n∈N,则f2017(x)=()A.sinx B.﹣sinx C.cosx D.﹣cosx【分析】由题意对函数的变化规律进行探究,发现呈周期性的变化,且其周期是4,故只须研究清楚f2010(x)是一个周期中的第几个函数即可得出其解析式.【解答】解:由题意f0(x)=sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=﹣sinx,f3(x)=f2′(x)=﹣cosx,f4(x)=f3′(x)=sinx,由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,∵2017=4×504+1,f2010(x)是一周中的第三个函数,故f2017(x)=cosx.故选:C.21.已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,f n(x)=f n﹣1′(x),则f2015(x)等于()A.sinx B.﹣sinx C.cosx D.﹣cosx【分析】对函数连续求导研究其变化规律,可以看到函数解析式呈周期性出现,以此规律判断求出f2015(x)【解答】解:由题意f1(x)=cosx,f2(x)=f1′(x)=﹣sinx,f3(x)=f2′(x)=﹣cosx,f4(x)=f3′(x)=sinx,f5(x)=f4′(x)=cosx,…由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,∵2015=4×503+3,故f2015(x)=f3(x)=﹣cosx故选:D22.函数(x>0),若x0满足f'(x0)=0,设m∈(0,x0),n∈(x0,+∞),则()A.f'(m)<0,f'(n)<0 B.f'(m)>0,f'(n)>0 C.f'(m)<0,f'(n)>0 D.f'(m)>0,f'(n)<0【分析】根据题意,对f(x)求导可得f′(x),若f'(x0)=0,则有=1,将m、n的值代入计算可得答案.【解答】解:根据题意,函数(x>0),其导数f′(x)=e x﹣=,若f'(x0)=0,则有=1,当m∈(0,x0),即m<x0,f'(m)=<0,n∈(x0,+∞),即n>x0,f'(n)=>0,故选:C.23.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)﹣f(a)=f'(m)(b﹣a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数在[0,b]上恰有两个“中值点”,则实数b的取值范围是()A.,B.(3,+∞)C.,D.,【分析】根据新定义得到x1,x2为方程x2﹣2x﹣b2+b=0在(0,b)上有两个不同根,构造函数g(x)=x2﹣2x﹣b2+b,列出不等式组,解得即可【解答】解:f′(x)=x2﹣2x,设=b2﹣b,由已知可得x1,x2为方程x2﹣2x﹣b2+b=0在(0,b)上有两个不同根,令g(x)=x2﹣2x﹣b2+b,则>>>>,解得<b<3,故选:C24.设函数f(x)=x3﹣ax2+2bx+1的导函数为f′(x),若函数f′(x)的图象关于直线x=对称,且当x∈[1,π]时,恒有f(x)≥1,则实数b的取值范围为()A.(,+∞)B.[,1]C.(﹣∞,]D.[,+∞)【分析】根据f′(x)的图象判断f(x)在[1,π]上的单调性,列出不等式解出.【解答】解:f′(x)=3x2﹣2ax+2b,∵函数f′(x)的图象关于直线x=对称,∴=,即a=2.∴f(x)=x3﹣2x2+2bx+1,f′(x)=3x2﹣4x+2b,△=16﹣24b,(1)若△=16﹣24b≤0,即b时,f′(x)≥0,∴f(x)在[1,π]上是增函数,∴f min(x)=f(1)=2b≥1,解得b≥,∴b≥.排除B,C.(2)若△=16﹣24b>0,即b<时,令f′(x)=0,解得x=.①若1≥,即b<时,f′(x)在[1,π]上恒大于或等于0,∴f(x)在[1,π]上是增函数,∴f min(x)=f(1)=2b≥1,解得b≥,∴≤b<.排除A.故选:D.25.已知定义在(0,+∞)上的单调函数f(x),对∀x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是()A.(0,) B.(1,2) C.(,1) D.(2,3)【分析】设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得t的值,可得f (x)的解析式,由二分法分析可得h(x)的零点所在的区间为(1,2),结合函数的零点与方程的根的关系,即可得答案.【解答】解:根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,又由f(x)是定义在(0,+∞)上的单调函数,则f(x)﹣log2x为定值,设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得,t=2;则f(x)=log2x+2,f′(x)=,将f(x)=log2x+2,f′(x)=代入f(x)﹣f′(x)=2,可得log2x+2﹣=2,即log2x﹣=0,令h(x)=log2x﹣,分析易得h(1)=﹣<0,h(2)=1﹣>0,则h(x)=log2x﹣的零点在(1,2)之间,则方程log2x﹣=0,即f(x)﹣f′(x)=2的根在(1,2)上,故选:B.26.已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x,有,则的最小值为()A.2 B.C.3 D.【分析】由对于任意实数x,f(x)≥0成立求出a的范围及a,b c的关系,求出f(1)及f′(0),作比后放缩去掉c,通分后利用基本不等式求最值.【解答】解:∵f(x)≥0,知>,∴c.又f′(x)=2ax+b,∴f′(0)=b>0,f(1)=a+b+c.∴≥1+=≥1+=2.当且仅当4a2=b2时,“=”成立.故选A.27.已知函数f(x)及其导数f'(x),若存在x0使得f(x0)=f'(x0),则称x0是f(x)的一个“巧值点”.给出下列五个函数:①f(x)=x2,②f(x)=e﹣x,③f(x)=lnx,④f(x)=tanx,其中有“巧值点”的函数的个数是()A.1 B.2 C.3 D.4【分析】根据题意,依次分析四个函数,分别求函数的导数,根据条件f(x0)=f′(x0),确实是否有解即可.【解答】解:根据题意,依次分析所给的函数:①、若f(x)=x2;则f′(x)=2x,由x2=2x,得x=0或x=2,这个方程显然有解,故①符合要求;②、若f(x)=e﹣x;则f′(x)=﹣e﹣x,即e﹣x=﹣e﹣x,此方程无解,②不符合要求;③、f(x)=lnx,则f′(x)=,若lnx=,利用数形结合可知该方程存在实数解,③符合要求;④、f(x)=tanx,则f′(x)=()′=,即sinxcosx=1,变形可sin2x=2,无解,④不符合要求;故选:B.28.已知函数,其导函数记为f'(x),则f(2017511)+f'(2017511)+f(﹣2017511)﹣f'(﹣2017511)=()A.0 B.1 C.2 D.2017511【分析】先求导,再判断导函数f'(x)的奇偶性,f(x)=1+,设g(x)=,判断其奇偶性,即可求出答案.【解答】解:f(x)=1+,∴f′(x)=,∴f′(﹣x)==f′(x),∴f′(x)为偶函数,∴f'(2017511)﹣f'(﹣2017511)=0,设g(x)=,则g(﹣x)=﹣=﹣g(x),∴g(x)为奇函数,∴f(2017511)+f(﹣2017511)=1+g(2017511)+1+g(﹣2017511)=2,∴f(2017511)+f'(2017511)+f(﹣2017511)﹣f'(﹣2017511)=2,故选:C29.[x]表示不超过x的最大整数,若f′(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)f′(x),则函数f=[g(x)]+[g(﹣x)]的值域是()A.{﹣1,0}B.{0,1}C.{0}D.{偶数}【分析】先对函数g(x)进行化简,根据[x]表示不超过x的最大整数,针对x进行分类讨论,发现规律,问题得以解决.【解答】解:由题意可知g(x)=f(x)•f′(x)=,>,<,不妨设x>0,则y=[g(x)]+[g(﹣x)]=[]+[]当∈(0,1),则∈(﹣1,0),[]=0,[]=﹣1,y=[g(x)]+[g(﹣x)]=﹣1当=0,则=0,[]=0,[]=0,y=[g(x)]+[g(﹣x)]=0依此类推可得y=[g(x)]+[g(﹣x)]的值域是{﹣1,0},故选A.30.定义:如果函数f(x)在[m,n]上存在x1,x2(m<x1<x2<n)满足f′(x1)=,f′(x2)=,则称函数f(x)是[m,n]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,则实数a的取值范围是()A.(,)B.(,3) C.(,1) D.(,1)【分析】令f′(x)=3x2﹣2x==a2﹣a,a2﹣a=3x2﹣2x,x∈[0,a].令g(x)=3x2﹣2x﹣a2+a,根据函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,可得方程3x2﹣2x﹣a2+a=0在x∈(0,a)有两个不等实数根.必须满足:g(0)>0,<0,g(a)>0.解出即可得出.【解答】解:令f′(x)=3x2﹣2x==a2﹣a,∴a2﹣a=3x2﹣2x,x∈[0,a].令g(x)=3x2﹣2x﹣a2+a,∵函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,∴方程3x2﹣2x﹣a2+a=0在x∈(0,a)有两个不等实数根.∴g(0)>0,<0,g(a)>0.解得<<1.∴实数a的取值范围是,.故选:C.31.已知函数f(x)=asinx+bx3+1(a,b∈R),f′(x)为f(x)的导函数,则f(2016)+f(﹣2016)+f′(2017)﹣f′(﹣2017)=()A.2017 B.2016 C.2 D.0【分析】根据函数的解析式求出函数的导数,结合函数的奇偶性建立方程关系进行求解即可.【解答】解:函数的导数f′(x)=acosx+3bx2,则f′(x)为偶函数,则f′(2017)﹣f′(﹣2017)=f′(2017)﹣f′(2017)=0,由f(x)=asinx+bx3+1得f(2016)=asin2016+b•20163+1,f(2016)=asin2016+b•20163+1,f(﹣2016)=﹣asin2016﹣b•20163+1,则f(2016)+f(﹣2016)=2,则f(2016)+f(﹣2016)+f′(2017)﹣f′(﹣2017)=2+0=2,故选:C32.已知f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则f'(0)=()A.n B.n﹣1 C.D.n(n+1)【分析】根据题意,对函数f(x)求导,计算可得f′(x),将x=0代入计算可得答案.【解答】解:根据题意,f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则其导数f′(x)=1+2(1+x)+3(1+x)2+4(1+x)3+…+n(1+x)n﹣1,则f'(0)=1+2+3+4+…+n=;故选:D.33.设函数f(x)=x3+x2+,其中θ∈(﹣,),则导数f′(1)的取值范围是()A.(﹣,1]B.(﹣,1)C.(﹣,)D.(﹣,]【分析】求导,当x=1时,f′(1)=+=sin(θ+),由θ∈(﹣,),即可求得θ+∈(﹣,),根据正弦函数的性质,即可求得导数f′(1)的取值范围.【解答】解:f(x)=x3+x2+,f′(x)=x2+x,f′(1)=+=sin(θ+),由θ∈(﹣,),则θ+∈(﹣,),则sin(θ+)∈(﹣,1],∴导数f′(1)的取值范围(﹣,1],故选A.34.已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…f n+1(x)=f′n(x),n∈N,那么f2017=()A.cosx﹣sinx B.sinx﹣cosx C.sinx+cosx D.﹣sinx﹣cosx【分析】根据题意,利用导数的运算法则依次计算f1(x)、f2(x)、f2(x)…的值,分析可得f n(x)+4=f n(x),即可得f2017(x)=f504×4+1(x)=f1(x),即可得答案.【解答】解:根据题意,∵f0(x)=sinx+cosx,∴f1(x)=f0′(x)=cosx﹣sinx,f2(x)=f1′(x)=﹣sinx﹣cosx,f3(x)=﹣cosx+sinx,f4(x)=sinx+cosx,以此类推,可得出f n(x)=f n(x)+4(x)=f1(x)=cosx﹣sinx;∴f2017(x)=f504×4+1故选:A35.定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=x3﹣1,h(x)=2x,φ(x)=ln(x+1)的“新驻点”分别为α,β,γ,则α,β,γ的大小关系为()A.α>β>γ B.β>α>γ C.γ>α>β D.β>γ>α【分析】由题设中所给的定义,对三个函数所对应的方程进行研究,分别计算求出α,β,γ的值或存在的大致范围,再比较出它们的大小即可选出正确选项【解答】解:①∵g(x)=x3﹣1,∴g′(x)=3x2,由g(x)=g′(x),得x3﹣1=2x2,∵2x2>0,(x=0时不成立),∴x3﹣1>0,∴x>1,∴α>1.②∵h(x)=2x,∴h′(x)=2,由h(x)=h′(x),解得x=1,∴β=1.③∵φ(x)=ln(x+1),∴φ′(x)=,由φ(x)=φ′(x),得到ln(x+1)=,令m(x)=ln(x+1)﹣,则m′(x)=+,因此函数m(x)在(﹣1,+∞)单调递增.∵m(0)=﹣1<0,m(1)=ln2﹣>0,∴0<γ<1.综上可知:α>β>γ.故选:A.36.设f1(x)=sinx,定义f n+1(x)为f n(x)的导数,即f(x)=f n′(x),n∈N*,若△ABC的内角A满足f1(A)+f2(A)+…+f2018(A)=0,则cosA的值为()A.1 B.﹣1 C.D.﹣【分析】根据导数公式直接进行求导,得到函数f n(x)具备周期性,然后根据周期性将条件进行化简,即可得到结论.(x)=f′n(x),【解答】解:∵f1(x)=sinx,f n+1∴f2(x)=f′1(x)=cosx,f3(x)=f′2(x)=﹣sinx,f4(x)=f'3(x)=﹣cosx,f5(x)=f′4(x)=sinx,f6(x)=f′5(x)=cosx,(x)=f′n(x),具备周期性,周期性为4.∴f n+1且f1(x)+f2(x)+f3(x)+f4(x)=cosx﹣sinx+sinx﹣cosx=0,∵f1(A)+f2(A)+…+f2018(A)=0,∴f1(A)+f2(A)=sinA+cosA=0,∴A=135°,故cosA=﹣,故选:D.37.已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则x0称为f(x)的一个“巧值点”,则下列函数中有“巧值点”的是()①f(x)=x2;②f(x)=e﹣x;③f(x)=lnx;④f(x)=tanx;⑤f(x)=.A.①③⑤B.①③④C.②③④D.②⑤【分析】求出函数的导数,使f(x)=f′(x),如果有解,则存在存在“巧值点”.【解答】解:①中的函数f(x)=x2,f′(x)=2x.要使f(x)=f′(x),则x2=2x,解得x=0或2,可见函数有巧值点;对于②中的函数,要使f(x)=f′(x),则e﹣x=﹣e﹣x,由对任意的x,有e﹣x>0,可知方程无解,原函数没有巧值点;对于③中的函数,要使f(x)=f′(x),则lnx=,由函数f(x)=lnx与y=的图象知,它们有交点,因此方程有解,原函数有巧值点;对于④中的函数,f (x)=tanx,f′(x)=,要使f(x)=f′(x),则tanx=,即sinxcosx=1,即sin2x=2,无解,∴原函数没有巧值点,故④错误;对于⑤中的函数,要使f(x)=f′(x),则=﹣,解得x=﹣1,原函数有巧值点;故有“巧值点”的函数为①③⑤.故选:A.38.设函数f n′(x)是f n(x)的导函数,f0(x)=e x(cosx+sinx),f1(x)=,f2(x)=,…,(n∈N),则f2016(x)=()A.e x(cosx+sinx)B.e x(cosx﹣sinx)C.﹣e x(cosx+sinx)D.e x(sinx﹣cosx)【分析】我们易得到f n(x)表达式以8为周期,呈周期性变化,由于2016÷8余0,故f2008(x)=f0(x),进而得到答案【解答】解:∵f0(x)=e x(cosx+sinx),∴f0′(x)=e x(cosx+sinx)+e x(﹣sinx+cosx)=2e x cosx,∴f1(x)==e x cosx,∴f1′(x)=e x(cosx﹣sinx),∴f2(x)==e x(cosx﹣sinx),∴f2′(x)=e x(cosx﹣sinx)+e x(﹣sinx﹣cosx)=﹣2e x sinx,∴f3(x)=﹣e x sinx,∴f3′(x)=﹣e x(sinx+cosx),∴f4(x)=﹣e x(cosx+sinx),∴f4′(x)=﹣2e x cosx,∴f5(x)=﹣e x cosx,∴f6(x)=﹣e x(cosx﹣sinx),∴f7(x)=e x sinx,∴f8(x)=e x(cosx+sinx),…,∴f2016(x)=f(0)=e x(cosx+sinx),故选:A.39.已知函数f(x)=e x﹣2ax,函数g(x)=﹣x3﹣ax2.若不存在x1,x2∈R,使得f′(x1)=g′(x2),则实数a的取值范围为()A.(﹣2,3)B.(﹣6,0)C.[﹣2,3]D.[﹣6,0]【分析】先求导,分别求出导函数的最值,再根据不存在x1,x2∈R,使得f′(x1)=g′(x2),得到关于a的不等式解得即可.【解答】解:∵函数f(x)=e x﹣2ax,函数g(x)=﹣x3﹣ax2,∴f′(x)=e x﹣2a>﹣2a,g′(x)=﹣3x2﹣2ax=﹣3(x+)2+≤,∵不存在x1,x2∈R,使得f′(x1)=g′(x2),∴﹣2a≥,解得﹣6≤a≤0,故选:D.40.已知函数f(x)=lnx+tanα(α∈(0,))的导函数为f′(x),若使得f′(x0)=f(x0)成立的x0<1,则实数α的取值范围为()A.(,)B.(0,)C.(,)D.(0,)【分析】由于f′(x)=,f′(x0)=,f′(x0)=f(x0),可得=ln x0+tan α,即tan α=﹣ln x0,由0<x0<1,可得﹣ln x0>1,即tan α>1,即可得出.【解答】解:∵f′(x)=,f′(x0)=,f′(x0)=f(x0),∴=ln x0+tan α,∴tan α=﹣ln x0,又∵0<x0<1,∴可得﹣ln x0>1,即tan α>1,∴α∈(,).故选:A.二.填空题(共6小题)41.已知在R上可导,F(x)=f(x3﹣1)+f(1﹣x3),则F′(1)=0.【分析】根据题意,由F(x)的解析式对其求导可得F'(x),将x=0代入,化简变形即可得答案.【解答】解:根据题意,F(x)=f(x3﹣1)+f(1﹣x3),则F'(x)=3x2f'(x3﹣1)﹣3x2f'(1﹣x3),则F'(1)=3f'(0)﹣3f'(0)=0.故答案为:0.42.已知f(x)=f(4﹣x),当x≤2时,f(x)=e x,f′(3)+f(3)=0.【分析】由f(x)=f(4﹣x)可得,函数f(x)的图象关于直线x=2对称,则f(3)=f(1),f′(3)=﹣f′(1),进而得到答案.【解答】解:由f(x)=f(4﹣x)可得,函数f(x)的图象关于直线x=2对称,当x≤2时,f(x)=e x,f′(x)=e x,∴f(3)=f(1)=e,f′(3)=﹣f′(1)=﹣e,故f′(3)+f(3)=0,故答案为:0.43.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,若x0是方程f(x)﹣f′(x)=4的一个解,且x0∈(a,a+1)(a∈N*),则实数a=1.【分析】由题意可得f(x)﹣log2x为定值,设为t,代入可得t=4,进而可得函数的解析式,化方程有解为函数F(x)=f(x)﹣f′(x)﹣4=log2x﹣有零点,易得F(1)<0,F(2)>0,由零点的判定可得答案.【解答】解:根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,又由f(x)是定义在(0,+∞)上的单调函数,则f(x)﹣log2x为定值,设t=f(x)﹣log2x,则f(x)=t+log2x,又由f(t)=6,可得t+log2t=6,可解得t=4,故f(x)=4+log2x,f′(x)=,又x0是方程f(x)﹣f′(x)=4的一个解,所以x0是函数F(x)=f(x)﹣f′(x)﹣4=log2x﹣的零点,分析易得F(1)=﹣<0,F(2)=1﹣=1﹣>0,故函数F(x)的零点介于(1,2)之间,故a=1,故答案为:144.已知函数y=f(x)的导函数为f'(x)=cosx﹣5,且f(0)=0,如果f(1﹣ax)+f(1﹣ax2)<0恒成立,则实数a的取值范围是(﹣8,0] .【分析】由题意函数的导函数f'(x)=cosx﹣5<0恒成立,故函数是减函数,再由函数是奇函数将不等式f(1﹣ax)+f(1﹣ax2)<0转化为f(1﹣ax)<f(ax2﹣1),由单调性及定义转化为不等式,再分类讨论即可求出a的取值范围【解答】解:∵﹣1≤cosx≤1,∴f'(x)=cosx﹣5<0,∴函数f(x)在R上单调递减,∵f′(x)=cosx﹣5为偶函数及f(0)=0可得f(x)为奇函数由f(1﹣ax)+f(1﹣ax2)<0可得,f(1﹣ax)<﹣f(1﹣ax2)=f(ax2﹣1)即1﹣ax>ax2﹣1∴a(x2+x)<2,当x<﹣1或x>0时,x2+x>0,则a<=∵>0,∴a≤0,当﹣1<x<0时,x2+x<0,则a>=当x=﹣时,(x+)2﹣有最小值,则有最大值﹣8,∴a>﹣8,当x2+x=0时,恒成立,综上所述a的取值范围为(﹣8,0],故答案为(﹣8,0].45.已知函数f(x)满足f(0)=﹣1,其导函数f′(x)满足f′(x)>k>1,则下列结论中正确的是(1),(2),(4).(1)f()>﹣1;(2)f()>;(3)f()<;(4)f()<f()【分析】根据导数的概念得出>k>1,(1),(2)分别取x=,x=判断即可,(4)根据函数的单调性判断即可.【解答】解:∵f′(x)=,且f′(x)>k>1,∴>k>1,即>k>1,对于(1),令x=,即有f()+1>•k=1,即为f()>0,故(1)正确;对于(2),当x=时,f()+1>•k=,即f()>﹣1=,故f()>,故(2)正确;对于(3),由(2)可得f()>>﹣1=,故(3)不正确,对于(4),函数递增,故(4)正确.故正确个数为3,故选;(1)(2)(4)46.若函数f(x)的导数f′(x)存在导数,记f′(x)的导数为f n(x).如果f(x)对任意x∈(a,b),都有f n(x)<0成立,则f(x)有如下性质:f()≥.其中n∈N*,x1,x2,…,x n∈(a,b).若f(x)=sinx,则f n(x)=﹣sinx;根据上述性质推断:当x1+x2+x3=π且x1,x2,x3∈(0,π)时,根据上述性质推断:sinx1+sinx2+sinx3的最大值为.【分析】构造函数f(x)=sinx,x∈(0,π),求导,则f″(x)=﹣sinx,由正弦函数的图象可知f″(x)<0成立,根据函数的性质sinx1+sinx2+sinx3≤3sin(),即可求得sinx1+sinx2+sinx3的最大值.【解答】解:设f(x)=sinx,x∈(0,π),则f′(x)=cosx,则f″(x)=﹣sinx,x∈(0,π),f(x)有如下性质:f()≥.则sinx1+sinx2+sinx3≤3sin()=3×sin=,∴sinA+sinB+sinC的最大值为,故答案为:﹣sinx,。
高中数学选择性必修二 5 2 导数的运算(精练)(含答案)

5.2 导数的运算【题组一 初等函数求导】1.(2018·全国高二课时练习)求函数()2y f x x x==+在下列各点处的导数. (1)0x x =; (2)1x =; (3)2x =-.【答案】(1) 2021x -+ (2)-1 (3) 12【解析】∵()2f x x x =+,∴()221f x x=-'+. (1)当0x x =时,()02021f x x =-'+. (2)当1x =时,()221111f '=-+=-. (3)当2x =-时,()()2212122f -=-+=-'.2.求下列函数的导数:(1)y =;(2)cos 2y x π⎛⎫=-⎪⎝⎭;(3)xy =.【答案】(1)1232x ;(2)cos x ;(3)1ln 32x【解析】(1)y′=(32x )′=1232x(2)∵y =cos =sin x ,∴y′=(sin x)′=cos x.(3)y′=[()x]′=()xln=()13ln32x.3.(2020·海林市朝鲜族中学高二课时练习)求下列函数的导数:(1)cos y x=; (2)2311y x x x x ⎛⎫=++ ⎪⎝⎭. 【答案】(1)(2)2332x x-【解析】(1)y′=′=′cos x + (cos x)′=′cos x -sin x =-x -cos x -sin x =--sin x =-.(2)∵y =x =x 3+1+,∴y′=3x 2-.4.(2020·海林市朝鲜族中学高二课时练习)求下列函数的导数. (1)()3411632f x x x =-+; (2)f(x)=(5x -4)cos x; (3)()ln xf x x=. 【答案】(1)232x x -;(2)5cos 5sin 4sin x x x x -+;(3)21ln xx- 【解析】(1)∵()3411632f x x x =-+,∴()23'2f x x x =-. (2)∵f(x)=(5x -4)cos x ,∴()()'5x 4cos?x '5cos 5sin 4sin f x x x x x ⎡⎤=-=-+⎣⎦.(3)∵()ln xf x x =,∴()()221ln x lnx lnx x f x x x '--==,. 【题组二 复合函数求导】1.(2020·宁县第二中学高二期中(理))求下列函数的导数:(1)cos3xy = (2)n xy x e =【答案】(1)'1sin33x y =-;(2)()'1x n y e x x n -=+ 【解析】(1)cos 3x y =,∴''1sin sin 3333x x xy ⎛⎫=-⋅=- ⎪⎝⎭. (2)n x y x e =,∴()'11n x n x x n y nx e x e e x x n --=+=+2.(2020·江苏徐州·高二月考)求下列函数的导数. (1)()ln xf x x=(2)()()239f x x x x ⎛⎫=+-⎪⎝⎭(3)()()2ln 51xf x x =+-【答案】(1)()'21ln x fx x -=;(2)()'222736f x x x =++;(3)()'52ln 251xf x x =+- 【解析】(1)()'''22(ln )ln ()1ln x x x x xf x x x⋅-⋅-==;(2)()()''239f x x x x ⎛⎫=+-+ ⎪⎝⎭()'239x x x ⎛⎫+- ⎪⎝⎭ 2222233272()(9)(1)2639x x x x x x x x =-+++=-++++=222736x x ++; (3)()()''12ln 25151x fx x x =+⨯-=-52ln 251x x +-. 3.(2020·江苏省如东高级中学高二期中)求下列函数的导函数. (1)()521y x =+(2)1log 32ay x =+ 【答案】(1)410(21)y x '=+;(2)3(32)ln y x a'=-+【解析】(1)445(21)210(21)y x x '=+⨯=+;(2)log (32)a y x =-+,133(32)ln (32)ln y x a x a'=-⨯=-++.4.(2020·陕西泾阳·高二期中(理))求下列函数的导数: (Ⅰ)2sin y x x =;(Ⅱ))22y =.【答案】(Ⅰ)22sin cos y x x x x '=+(Ⅱ)1y'= 【解析】(Ⅰ)()()222sin sin 2sin cos y x x x x x x x x '''=+=+.(Ⅱ)))222221y ''===-. 5.(2020·长春兴华高中高二期末(文))求下列函数的导数:(1)sin xy e x = ;(2)y =2311x x x x ⎛⎫++ ⎪⎝⎭; (3)sincos 22x y x x =-; 【答案】(1)y ′=e x sinx +e x cosx .(2)y ′=3x 2-32x.(3)y ′=1-12cosx . 【解析】(1)y ′=(e x )′sinx +e x (sinx )′=e x sinx +e x cosx ..(2)因为y =x 3+21x +1,所以y ′=3x 2-32x. (3)因为y =x -12sinx ,所以y ′=1-12cosx . 6.(2020·江西南昌·高二期末(理))求出下列函数的导数. (1)tan xy e x = (2)()3ln 45y x +=(3)2311y x x x x ⎛⎫=++ ⎪⎝⎭(4)y =sin nx x(5)()5221x y e x ++﹣=【答案】(1)'2tan cos x xe y e x x=+;(2)'1245y x =+;(3)'2332x y x =-; (4)'1cos sin n x x n x y x+-=;(5)()4'29221()x y x x e +=+﹣﹣ 【解析】(1)由tan xy e x =,则()''2'tan tan t cos ()an x x xxe y e x e x e x x+==+, 即'2tan cos xxe y e x x=+(2)由3ln 45y x +=(),则'1245y x =+(3)由2323111y x x x x x x ⎛⎫=++=++ ⎪⎝⎭﹣,则'2332xy x =-, (4)由sin n x y x =,则'1cos sin n x x n x y x+-=, (5)由()5221x y e x +=+﹣,则()4'29221()x y x x e +=+﹣﹣. 【题组三 求导数值】1.(2020·四川高二期中(理))已知()sin 2f x x =,则()()limx f x x f x x∆→+∆-=∆( )A .cos2xB .cos2x -C .2cos2xD .2cos2x -【答案】C【解析】由()()()()0limcos 222cos 2x f x x f x f x x x x∆→+∆-'==⋅=∆.故选:C.2.(2020·江西高二期末(理))若函数()f x 的导数()f x '满足()()121ln f x f x x '=+,则12f ⎛⎫'= ⎪⎝⎭( )A .eB .2C .1D .0【答案】D【解析】∵()()121ln f x f x x'=+,∴()()21121f x f x x ''=⨯-,令1x =,可得(1)2(1)1f f ''=-,解得(1)1f '=,因此()221f x x x '=-,14402f ⎛⎫'∴=-= ⎪⎝⎭,故选:D 3.(2020·四川省南充市白塔中学高二开学考试(文))已知函数()f x 的导函数为()f x ',且满足关系式()()232x f x x xf e '=++,则()2f '的值等于( )A .2-B .222e -C .22e -D .222e --【答案】D【解析】依题意()()''232xf x x f e =++,令2x =得()()''22432f f e =++,()2'222e f =--,故选D.4.(2020·四川棠湖中学高二月考(文))若函数f (x )满足f (x )=13x 3-f ′(1)·x 2-x ,则f ′(1)的值为( ) A .1 B .2 C .0D .-1【答案】C 【解析】依题意()()'3'211fx x f x =--,令1x =得()()''11211f f =--,解得()'10f =,故选C.5.(2020·河南商丘·高二期末(理))已知函数()()2ln 31f x x x f x '=-+,则()1f =( )A .2B .1C .0D .1-【答案】D【解析】因为()()2ln 31f x x x f x '=-+,则()()1321f x f x x''=-+, 所以()()'1132'1f f =-+,则()12f '=,所以()2ln 32f x x x x =-+,所以()1ln1321f =-+=-.故选:D.6.(2020·江西高二期末(文))已知函数()f x 的导函数为()f x ',且满足()()2322f x x xf '=+,则()2f '=______. 【答案】12-【解析】因为()()2322f x x xf '=+,所以()()622f x x f ''=+,将2x =代入得()()21222f f ''=+,解得()212f '=-,故答案为:12-.7.(2020·四川内江·高二期末(文))已知2()x f x e x =+,则(1)(1)f f '+=________.【答案】23e +【解析】因为2()xf x e x =+,所以()2xf x e x '=+所以(1)1,(1)2f e f e '=+=+所以(1)(1)23f f e '+=+.故答案为:23e +. 【题组四 求切线方程】1.(2020·湖南高二期末)曲线sin x xy e=在点()0,0处的切线方程为______.【答案】0x y -=【解析】因为()cos sin x xxe x xef x e-'=,所以切线斜率()01k f '==,所以曲线()sin xf x e x =在点()0,0处的切线方程为:0x y -=.故答案为:0x y -=2.(2020·江西高二期末(理))已知函数()xxf x e ae -=+为偶函数,则()f x 在其图象上的点()()ln3,ln3f 处的切线的斜率为______.【答案】83【解析】函数()xxf x e ae -=+为偶函数,()()f x f x ∴-=,即x x x x e ae e ae --+=+,解得1a =,则'()x x f x e e -=-,∴()f x 在点()()ln3,ln3f 处的切线的斜率ln3ln318'(ln 3)333kf e e.故答案为:83.3.(2020·陕西西安·高新一中高三期末(文))曲线(sin )e xy x x =+在点(0,0)处的切线方程为________.【答案】2y x =【解析】0(sin cos 1)e ,|2xx y x x x y =''=+++=,所以切线方程为2y x =.故答案为:2y x =.4.(2020·重庆八中高三月考)已知函数()f x 为奇函数,当0x >时,3()ln =- f x x x ,则曲线()y f x =在点(1,(1))-- f 处的切线方程为________.【答案】210x y -+=【解析】∵函数()f x 是奇函数,()()f x f x ∴-=-, 当0x >时,3()ln =- f x x x ,不妨设0x <,则0x ->, 故()3()ln () f x xx f x -=---=-,故0x <时,()3()ln f x x x +=-,故'2()31 f x x x=+,故(1)1ln11 f -+=-=-,'(1)312 f -=-=,故切线方程是:2(1)1y x =+-,整理得:210x y -+=,故答案为:210x y -+=.5.(2020·重庆高三期中(文))曲线()2ln 2f x x x =-在点()()1,1f 处的切线与坐标轴围成的三角形的面积为____________.【答案】16【解析】()2ln 2f x x x =-,()()'14,0f x x x x∴=->, ()'13f ∴=-,12f ,∴切线方程为:()231y x +=--即31y x =-+,当0x =,时1y =,当0y =,时13x =, ∴三角形面积为:1111236⨯⨯=.故答案为:16. 6.(2020·五华·云南师大附中高三月考(理))曲线()21ln y x x =+在()1,0处的切线方程为______.【答案】220x y --=【解析】2n '12l x x x xy +=+,当1x =时,切线斜率'2k y ==,故切线方程为()21y x =-,即220x y --=.故答案为:220x y --=7.(2020·江西高三月考(理))1()e x f x -=+的图像在1x =处的切线方程为________.【答案】210x y -+=【解析】112()e 2x f x x -=+,则()112x f x e x --'=+,且()12f '=()13,f =∴切线方程为()321y x -=-,即210x y -+=故答案为:210x y -+=8.(2020·五华·云南师大附中高三月考(文))过原点与曲线ln y x =相切的切线方程为______. 【答案】x y e= 【解析】设切点坐标为()00,x y ,切线方程为y kx =,由ln y x =,则1y x'=,则001|x x y x ='=, 则0001y x x =,即000ln 1x x x =,即0ln 1x =,解得0x e =,所以01|x x k y e='==, 所以原点与曲线ln y x =相切的切线方程为x y e=. 故答案为:x y e= 9.(2020·黑龙江萨尔图·大庆实验中学高二期末(文))已知()2f x x =,则曲线()y f x =过点()1,0P -的切线方程是______.【答案】0y =或440x y ++=【解析】设切点为(,)m n ,2()f x x =的导数为()2f x x '=,可得切线的斜率为2k m =, 又20211n m m m m -==++,解得0m =或2m =-, 当0m =时,0k =;2m =-时,4k =-;曲线()y f x =过点(1,0)P -的切线方程为(1)y k x =+,则切线的方程为0y =或44y x =--.故答案为:0y =或44y x =--.10.(2020·黑龙江道里·哈尔滨三中(文))过函数()33f x x x =-上的点()2,2M --的切线方程是_________.【答案】2y =-或9160x y -+=【解析】因为()233f x x ='- 设切点为00,x y ,则()20033k f x x '==-, 所以切线方程为:()()()320000333y x x x x x --=--, 因为()2,2M --在切线方程上,所以()()()32000023332x x x x ---=---,解得:01x =或02x =-. 当01x =时,20330k x =-=,此时切线方程为2y =-;当02x =-时,20339k x =-=,此时切线方程为9160x y -+=.所以,切线方程为:2y =-或9160x y -+=.故答案为:2y =-或9160x y -+=.11.(2020·辽宁省本溪满族自治县高级中学高三其他(文))过点(0,1)-作曲线ln f x =(0x >)的切线,则切点坐标为________.【答案】【解析】由ln f x =(0x >),则2()ln ,0f x x x =>,化简得()2ln ,0f x x x =>, 则2()f x x'=,设切点为00(,2ln )x x ,显然(0,1)-不在曲线上, 则0002ln 12x x x +=,得0x =,则切点坐标为.故答案为:.12.(2020·石嘴山市第三中学高二期末(理))过点(1,1)--与曲线x y e x =+相切的直线方程为______________.【答案】21y x =+.【解析】设切点坐标为()000,e x x x +, 由x y e x =+得e 1x y '=+,∴切线方程为()()0000e 1e x x y x x x =+-++, 切线过点()1,1--,∴()()00001e 11e x x x x -=+--++,即00e 0x x =, ∴00x =,即所求切线方程为21y x =+.故答案为:21y x =+.13.(2020·吉林净月高新技术产业开发区·东北师大附中高二月考(理))过点()1,1作曲线3y x =的切线,则切线方程是______.【答案】3410x y -+=和320x y --=【解析】设切点坐标为()3,t t ,对函数3y x =求导得23y x '=,则所求切线的斜率为23t , 所以,曲线3y x =在点()3,t t 处的切线方程为()323y t t x t -=-,由于该直线过点()1,1,即()32131t t t -=-,整理得()()22110t t +-=,解得12t =-或1t =. 当12t =-时,所求切线的方程为131842y x ⎛⎫+=+ ⎪⎝⎭,即3410x y -+=; 当1t =时,所求切线的方程为()131y x -=-,即320x y --=.故答案为:3410x y -+=和320x y --=.【题组五 利用切线求参数】1.(2020·辽宁高二期末)已知函数()21f x ax x =-+,若()()011lim 3x f x f x∆→+∆-=∆,则实数a 的值为( ) A .2B .1C .1-D .2- 【答案】A 【解析】根据题意,函数()21f x ax x =-+,其导数()21f x ax ='-,则()121f a '=-,又由()()011lim 3x f x f x∆→+∆-=∆,即()1213f a '=-=,解可得2a =; 故选:A.2.(2020·湖北省天门中学高二月考)曲线3()2f x x x =+-在0P 处的切线平行于直线41y x =-,则0P 点的坐标为( )A .(1, 0)B .(2, 8)C .(1, 0)和(-1, -4)D .(2, 8)和(-1, -4)【答案】C 【解析】依题意,令2()314f x x '=+=,解得1x =±(1)0,(1)4f f =-=-故0P 点的坐标为(1, 0)和(-1, -4),故选:C3.(2020·甘肃城关·兰州一中高二期中(文)) 设函数f (x )=24x -a ln x ,若f ′(2)=3,则实数a 的值为( ) A .4B .-4C .2D .-2 【答案】B【解析】f ′(x )=-,故f ′(2)=-=3,因此a =-4.4.(2020·唐山市第十一中学高二期末)设()ln f x x x =,若()3f a '=,则a =( ) A .eB .ln 2C .2eD .ln 22【答案】C 【解析】对()f x 求导得()ln +1f x x '=将a 带入有()2ln +13f a a a e '==⇒=. 5.(2020·陕西新城·西安中学高二期末(理))如图,()y f x =是可导函数,直线:2l y kx =+是曲线()y f x =在3x =处的切线,令()()g x xf x =,'()g x 是()g x 的导函数,则'(3)g =( ).A .-1B .0C .2D .4【答案】B 【解析】将点()3,1代入直线2y kx =+的方程得321k +=,得13k =-,所以,()133f k '==-, 由于点()3,1在函数()y f x =的图象上,则()31f =,对函数()()g x xf x =求导得()()()g x f x xf x ''=+, ()()()133331303g f f ⎛⎫''∴=+=+⨯-= ⎪⎝⎭,故选B .。
导数的概念及运算练习含答案

第1讲导数的概念及运算一、选择题1.设y=x2e x,则y′=() A.x2e x+2x B.2x e xC.(2x+x2)e x D.(x+x2)e x解析y′=2x e x+x2e x=(2x+x2)e x.答案 C2.已知函数f(x)的导函数为f′(x),且满足f(x)=2x·f′(1)+ln x,则f′(1)等于() A.-e B.-1C.1 D.e解析由f(x)=2xf′(1)+ln x,得f′(x)=2f′(1)+1 x,∴f′(1)=2f′(1)+1,则f′(1)=-1.答案 B3.曲线y=sin x+e x在点(0,1)处的切线方程是() A.x-3y+3=0 B.x-2y+2=0C.2x-y+1=0 D.3x-y+1=0解析y′=cos x+e x,故切线斜率为k=2,切线方程为y=2x+1,即2x-y +1=0.答案 C4.(2017·成都诊断)已知曲线y=ln x的切线过原点,则此切线的斜率为()A.e B.-e C.1e D.-1e解析y=ln x的定义域为(0,+∞),且y′=1x,设切点为(x0,ln x0),则y′|x=x0=1x0,切线方程为y-ln x0=1x0(x-x0),因为切线过点(0,0),所以-ln x0=-1,解得x0=e,故此切线的斜率为1 e.答案 C5.(2017·昆明诊断)设曲线y=1+cos xsin x在点⎝⎛⎭⎪⎫π2,1处的切线与直线x-ay+1=0平行,则实数a等于()A.-1 B.1 2C.-2 D.2解析∵y′=-1-cos xsin2x,∴=-1.由条件知1a=-1,∴a=-1.答案 A二、填空题6.若曲线y=ax2-ln x在点(1,a)处的切线平行于x轴,则a=________.解析因为y′=2ax-1x,所以y′|x=1=2a-1.因为曲线在点(1,a)处的切线平行于x轴,故其斜率为0,故2a-1=0,解得a=1 2.答案1 27.(2017·长沙一中月考)如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=________.解析 由图形可知:f (3)=1,f ′(3)=-13,∵g ′(x )=f (x )+xf ′(x ), ∴g ′(3)=f (3)+3f ′(3)=1-1=0. 答案 08.(2015·全国Ⅱ卷)已知曲线y =x +ln x 在点(1,1)处的切线与曲线y =ax 2+(a +2)x +1相切,则a =________.解析 由y =x +ln x ,得y ′=1+1x ,得曲线在点(1,1)处的切线的斜率为k =y ′|x =1=2,所以切线方程为y -1=2(x -1),即y =2x -1. 又该切线与y =ax 2+(a +2)x +1相切, 消去y ,得ax 2+ax +2=0, ∴a ≠0且Δ=a 2-8a =0,解得a =8. 答案 8 三、解答题9.已知点M 是曲线y =13x 3-2x 2+3x +1上任意一点,曲线在M 处的切线为l ,求:(1)斜率最小的切线方程; (2)切线l 的倾斜角α的取值范围. 解 (1)y ′=x 2-4x +3=(x -2)2-1≥-1, 所以当x =2时,y ′=-1,y =53, 所以斜率最小的切线过点⎝ ⎛⎭⎪⎫2,53,斜率k =-1,所以切线方程为x +y -113=0. (2)由(1)得k ≥-1,所以tan α≥-1,所以α∈⎣⎢⎡⎭⎪⎫0,π2∪⎣⎢⎡⎭⎪⎫3π4,π.10.已知曲线y =x 3+x -2在点P 0处的切线l 1平行于直线4x -y -1=0,且点P 0在第三象限. (1)求P 0的坐标;(2)若直线l ⊥l 1,且l 也过切点P 0,求直线l 的方程. 解 (1)由y =x 3+x -2,得y ′=3x 2+1, 由已知令3x 2+1=4,解之得x =±1. 当x =1时,y =0;当x =-1时,y =-4.又∵点P 0在第三象限,∴切点P 0的坐标为(-1,-4).(2)∵直线l ⊥l 1,l 1的斜率为4,∴直线l 的斜率为-14.∵l 过切点P 0,点P 0的坐标为(-1,-4),∴直线l 的方程为y +4=-14(x +1),即x +4y +17=0. 11.(2016·山东卷)若函数y =f (x )的图像上存在两点,使得函数的图像在这两点处的切线互相垂直,则称y =f (x )具有T 性质,下列函数中具有T 性质的是( )A .y =sin xB .y =ln xC .y =e xD .y =x 3解析 若y =f (x )的图像上存在两点(x 1,f (x 1)),(x 2,f (x 2)), 使得函数图像在这两点处的切线互相垂直,则f ′(x 1)·f ′(x 2)=-1.对于A :y ′=cos x ,若有cos x 1·cos x 2=-1,则当x 1=2k π,x 2=2k π+π(k ∈Z )时,结论成立;对于B :y ′=1x ,若有1x 1·1x 2=-1,即x 1x 2=-1,∵x 1>0,x 2>0,∴不存在x 1,x 2,使得x 1x 2=-1;对于C :y ′=e x ,若有e x 1·e x 2=-1,即e x 1+x 2=-1.显然不存在这样的x 1,x2;对于D:y′=3x2,若有3x21·3x22=-1,即9x21x22=-1,显然不存在这样的x1,x2.答案 A12.(2017·合肥模拟)点P是曲线x2-y-ln x=0上的任意一点,则点P到直线y =x-2的最小距离为()A.1 B.32 C.52 D. 2解析点P是曲线y=x2-ln x上任意一点,当过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小,直线y=x-2的斜率为1,令y=x2-ln x,得y′=2x-1x=1,解得x=1或x=-12(舍去),故曲线y=x2-ln x上和直线y=x-2平行的切线经过的切点坐标为(1,1),点(1,1)到直线y=x-2的距离等于2,∴点P到直线y=x-2的最小距离为 2.答案 D13.若函数f(x)=12x2-ax+ln x存在垂直于y轴的切线,则实数a的取值范围是________.解析∵f(x)=12x2-ax+ln x,∴f′(x)=x-a+1x(x>0).∵f(x)存在垂直于y轴的切线,∴f′(x)存在零点,即x+1x-a=0有解,∴a=x+1x≥2(当且仅当x=1时取等号).答案[2,+∞)14.已知函数f(x)=x-2x,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.解根据题意有f′(x)=1+2x2,g′(x)=-ax.曲线y=f(x)在x=1处的切线斜率为f′(1)=3,曲线y=g(x)在x=1处的切线斜率为g′(1)=-a,所以f′(1)=g′(1),即a=-3.曲线y=f(x)在x=1处的切线方程为y-f(1)=3(x-1).所以y+1=3(x-1),即切线方程为3x-y-4=0.曲线y=g(x)在x=1处的切线方程为y-g(1)=3(x-1),所以y+6=3(x-1),即切线方程为3x-y-9=0,所以,两条切线不是同一条直线.。
导数的运算法则随堂练习

1.2.2导数的运算法则导数的四则运算法则设是)(),(x g x f 可导的,则:(1)='±])()([x g x f .(2)='])()([x g x f .(3)='])()([x g x f . 求下列函数的导数(1)32log cos 3x x y x e π=+++ (2)n x y x e =(3))3)(2)(1(+++=x x x y (4)31sin x y x-=随堂练习1.已知f (x )=ax 3+9x 2+6x -7,若f ′(-1)=4,则a 的值等于( )A .193B .163C .103D .1332.设f (x )=sin x -cos x ,则f (x )在x =π4处的导数f ′(π4)=( ) A . 2 B .- 2 C .0 D .22 3.已知y =tan x ,x ∈⎝⎛⎭⎪⎫0,π2,当y ′=2时,x 等于( ) A .π3 B .23π C .π4 D .π64. 函数x x x y sin cos -=的导数是 ( )A. x x sinB.x x sin -C.x x cosD.x x cos -5.若函数f (x )=e x sin x ,则此函数图象在点(4,f (4))处的切线的倾斜角为( )A .π2B .0C .钝角D .锐角 6.曲线f (x )=x ln x 在点x =1处的切线方程为( )A .y =2x +2B .y =2x -2C .y =x -1D .y =x +1课后探究1.函数y =(x +1)2(x -1)在x =1处的导数等于2.若f (x )=x 2-2x -4ln x ,则f ′(x )>0的解集为_____ ___.3.已知函数f (x )=x ·2x ,当f ′(x )=0时,x =______ __.4.曲线C :f (x )=sin x +e x +2在x =0处的切线方程为_____ ___.5.曲线C :f (x )=sin xx在x =π处的切线方程为__ ______. 6.偶函数f (x )=ax 4+bx 3+cx 2+dx +e 的图象过点P (0,1),且在x =1处的切线方程为y =x -2,求y =f (x )的解析式.。
导数及导数的运算练习题

导数的几何意义与导数运算1.若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则000()()limh f x h f x h h →+-- 的值为( )A .'0()f x B .'02()f x C .'02()f x - D .0 2.(2008海南) 设()ln f x x x =,若0()2f x '=,则0x =( ) A2e B e C ln 22 D ln23.(2010·江西高考)若函数f (x )=ax 4+bx 2+c 满足f ′(1)=2,则f ′(-1)=( ) A .-1 B .-2 C .2 D .04.已知函数f (x ) = a x 2 +c ,且(1)f '=2 , 则a 的值为 ( )A.1B.2C.-1D. 05.过点(1,0)且与曲线11x y x +=-在点(3,2)处的切线平行的直线方程为( ) A .y =x -1 B .y =-x +1 C .y =11-x +22D .y =11-x -226.已知曲线()421128=y x ax a a =++-+在点,处切线的斜率为,则 ( )A .9B .6C .-9D .-67.(2010·辽宁高考)已知点P 在曲线y =4e x+1上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是 ( ) A .(0,π4)B .(π4,π2)C .(π2,3π4)D .[3π4,π)8.已知P,Q 为抛物线x 2=2y 上两点,点P,Q 的横坐标分别为4,-2,过P,Q 分别作抛物线的切线,两切线交于点A ,则点A 的纵坐标为( )(A) 1 (B) 3 (C) -4 (D) -8 9.函数21()2l n 2f x x x a x =--存在平行于x 轴的切线,则实数a 的取值范围是 。
10. 已知函数2()1xf x x=+,则'()f x ___________. 11.已知函数'2()(1)1xf x e f x =++,则'(2)f =12.(2010·江苏高考)函数y =x 2(x >0)的图象在点(a k ,a 2k )处的切线与x 轴的交点的横坐标为a k +1,其中k ∈N *.若a 1=16,则a 1+a 3+a 5的值是________.13. 如图,函数F (x )=f (x )+15x 2的图象在点P 处的切线方程是y =-x +8,则f (5)+f ′(5)=______. 14. 求下列函数的导数:2(1)1x y e x ax =---1(2)l n 1ay x a x x-=-+-(3) 32sin ().tan 3f x x x θθθ=+ (4)sin ()sin cos x f x x x =+15.求下列函数的导数:(1)y=(2x 2-1)(3x+1) (2)x x y sin 2=(3) 11x x e y e +=- (4) xe x y 2=(5)xx y 22+= (6))cos 1(sin x x y +=16.已知两曲线ax x y +=3和c bx x y ++=2都经过点P (1,2),且在点P 处有公切线,试求a,b,c 值。
