第07章耦合电感与变压器38638
《耦合电感和变压器》课件

变压器广泛应用于电力系统中,用于 调节电压、隔离电路以及实现远距离 输电等。
优缺点的比较
耦合电感
耦合电感的优点在于体积小、重量轻、结构简单,同时具有较好的频率特性, 适用于高频信号的处理。缺点在于其传递的功率较小,通常用于信号传输和变 换。
变压器
变压器的优点在于能够传递大功率的电能,实现电压的调节和隔离,同时具有 较好的绝缘性能和过载能力。缺点在于体积较大,结构复杂,且在高频应用时 可能会出现磁饱和等问题。
变压器的分类
根据用途不同,变压器可以分为电力 变压器、电源变压器、音频变压器、 脉冲变压器等。电力变压器主要用于 电力系统中的电压变换,而电源变压 器则用于电子设备和仪器的电源供应 。音频变压器和脉冲变压器则分别用 于音频信号和脉冲信号的处理和传输 。
VS
根据结构不同,变压器可以分为芯式 变压器和壳式变压器。芯式变压器的 绕组围绕铁芯缠绕,而壳式变压器的 绕组则围绕圆柱形铁芯外部缠绕。芯 式变压器具有较高的绝缘性能和机械 强度,而壳式变压器则具有较小的体 积和较高的功率密度。
耦合电感器在电路中的作用
能量传输与转换
耦合电感器在电路中主要起能量 传输和转换的作用,可以将电能 转换为磁场能,再传输到另一个
线圈中转换为电能。
阻抗变换
通过改变耦合电感器的匝数比,可 以实现阻抗的变换,用于匹配电路 中的阻抗。
信号分离与处理
在信号处理电路中,耦合电感器可 以用于分离不同频率的信号,或者 对信号进行滤波、陷波等处理。
01
02
03
电力传输
变压器用于升高或降低电 压,以实现电力的远距离 传输或适配不同设备的电 压需求。
家电设备
家用电器中的电源变压器 将家庭电压转换为设备内 部电路所需的电压。
耦合电感和理想变压器

本章重点
• 耦合电感中的磁耦合现象 • 互感和耦合电感的同名端 • 互感线圈中电压与电流的关系 • 互感电路的分析与计算 • 空心变压器、理想变压器的初步概念
8.1 耦合电感
8.1.1 基本概念
1
2
11
21
自感 磁通
i1
N1
N2
互 感
磁
当两个线圈相距较近时,各自线圈上的电流变化会通
2013.3农业部的调查
家庭农场初具规模
——截至2012年底,全国30个省、区、市(不含西藏)共有符 合本次统计调查条件的家庭农场87.7万个,经营耕地面积 达到1.76亿亩,占全国承包耕地面积的13.4%。平均每个 家庭农场有劳动力6.01人,其中家庭成员4.33人,长期雇 工1.68人。
家庭农场以种养业为主
家庭农场注册
——已被有关部门认定或注册的共有3.32万个,其中农业部 门认定1.79万个,工商部门注册1.53万个。
家庭工业概念和地位
概念
——主要指以家庭为基本生产单位,以家庭住宅或承租场 地为生产场所,以家庭成员为主要劳动力,生产资料归 家庭所有,劳动成果归家庭共同所有,并以家庭财产对 债务承担相应责任的一种工业生产组织形式。
农户与农村常住户
农户 ——农业户口、农村常住户 ——基本经营单位、农村经济社会发展基本细胞 农村常住户 ——长期(一年以上)居住在乡镇(不包括城关镇)行
政管理区域内的住户,以及长期居住在城关镇所 辖行政村范围内的农村住户。
种粮大户肖建军
思考题:肖建军在生产经营中面临的主要困难及解 决方案?
1.耕种面积1020亩,遍布双江口镇3个村,仅日常管理工 作雇工6人。
电路分析第七章-含有耦合电感的电路

* --
(a)
+
i1 +
M **
u1u12L1
i2
+
L2u21
-
u2
--
-+
(b)
解:图(a)中
u1
=
L1
di1 dt
+
u12
u12
=
−M
di2 dt
∴u1
=
L1
di1 dt
−M
di2 dt
u2
=
L2
di2 dt
+ u21
u21
=
−M
di1 dt
∴u2
=
L2
di2 dt
−M
di1 dt
图(b)中
u1
若u21
=
−M
di1 dt
线圈1 线圈2
i1 ∆1’
*1
2*’
u21+2∆
1端与2’端互为同名端 1’端与2端互为同名端
N1
Φ1
N2
Φ2
i1
i2
1‘ - u1+ 1 2‘- u2+ 2
图(a)
N1
Φ1
N2
Φ2
i1
i2
1‘ - u1+ 1 2‘+ u2 - 2
图(b)
M
*
*
L1
L2
1‘
1 2‘
2
图(a)的电路符号
图(b)
u1
=
L1
di1 dt
+
M
di2 dt
u2
=
L2
di2 dt
+
M
耦合电感与理想变压器

103
22030 2103 j314(1
4
2 1)
59.2
6.2mA
i 59.22cos(314t 6.2)mA
2 去耦等效法
该方法是先画出耦合电感电路的去耦等效电路。在正弦稳态 情况下,对所得的去耦等效电路可按一般交流电路来列方程。
下面讨论两个耦合电感的串联、并联和T型连接电路的去耦 等效电路。
1)耦合电感的串联及其去耦等效
去耦等效电路
①顺接连接
M
i * L1 * L2
u
i Leq u
U& ( jL1I& jMI&) ( jL2I& jMI&) j(L1 L2 2M )I&
同样,线圈2中的电流i2也产生自感磁通链Ψ22和互感磁通链
Ψ12。
22 L2i2 L2为线圈2的自感系数
12 M12i2 M12称为互感系数
可以证明:M12= M21= M。
当两个线圈都有电流时,每一线圈的磁链为自磁链与互磁
链的代数和: 1 11 12 L1i1 Mi2
2 22 21 L2i2 Mi1
Φ11
L1 N1
L2 N2
Φ21
11 N111
* i1
1
1' 2
u1
* i2 2'
u2
21 N2 21
线圈1中通入电流i1时,在线圈1中产生的磁通Φ11称为自 感磁通,Φ11与线圈1的N1匝交链,产生磁通链Ψ11称为自感磁 通链;Φ11中的一部分或全部(互感磁通)与线圈2交链,产 生磁通链Ψ21称为互感磁通链。两线圈间有磁的耦合。
u1
d 1
dt
L1
di 1 dt
电路分析基础~~第七章 耦合电感与理想变压器

21
i1 + u1
i2 + u2
1 (t ) 11 (t ) 12 (t ) 2 (t ) 22 (t ) 21 (t )
-
-
12
22
自感磁链与互感磁链的方向可能相同也可能相反,由线圈 电流方向、线圈绕向等因素决定。因此广义的讲,每一个线圈 的总磁链又可表示为
初级回路的自阻抗 次级回路的自阻抗
jωM +
I1 R1
R2
jωL2
I2
RL
US
jωL1
US I1 (M ) 2 Z11 Z 22
-
(b)
j M I I2 1 Z 22
(M ) 2 Z i Z11 Z 22
空芯变压器从电源端看进去的输入阻抗为
次级回路在初级回 路的反映阻抗
7-3 空芯变压器
变压器也是电路中常用的一种器件,其电路模型由耦 合电感构成。
空芯变压器:耦合电感中的两个线圈绕在非铁磁性材料的 芯子上,则构成空芯变压器 铁芯变压器:耦合电感中的两个线圈绕在铁芯上,则构成
铁芯变压器
空芯变压器和铁芯变压器的主要区别: 前者属松耦合,耦合系数K较小, 后者属紧耦合,耦合系数K接近于1。
( R1 jL1 ) I 1 jMI 2 U S jMI 1 ( R2 RL jL2 ) I 2 0
令 Z11 R1 jL1 Z 22 R2 RL jL2 则上式可变换为 Z11 I 1 jMI 2 U S jMI 1 Z 22 I 2 0 求解以上方程可得:
a
j2Ω b
1Ω
US 100 I1 4.38 38 A 4 (M ) 2 1 j3 Z11 1 j2 Z 22
耦合及变压

dψ dt d i1 dt d i1 dt
d i1 dt
1
u
1
=
1
= L1 =M
+M + L2
d i2 dt d i2 dt
d i2
2
1
i1
+
●
M
●
i2
+ – L2
2
u2 =
dψ dt
u1
1'
L1
u2
2'
2
–
式中: 自感电压: 式中: 自感电压:L
, L
dt
分别为线圈1 和线圈2 的自感电压; 分别为线圈 和线圈 的自感电压; 分别为线圈1 和线圈2 的互感电压。 分别为线圈 和线圈 的互感电压。
8
Φ a b
●
﹡
c d
﹡
●
2、同名端的判别 、
若知线圈的绕向,则同名端易判(根据右手螺旋法则)。若不知其绕向, 若知线圈的绕向,则同名端易判(根据右手螺旋法则)。若不知其绕向, )。若不知其绕向 则要用实验的方法进行测定。 则要用实验的方法进行测定。
⑴ 交流法
首先测出某两端是同一线圈并作标记; 首先测出某两端是同一线圈并作标记;再给任一 线圈加一较低且便于测量的电压; 线圈加一较低且便于测量的电压;将两线圈的任一端连 在一起( ),用电压表 V 在一起(如 2 和 3),用电压表 ~ 测1、4 端。 ), 、 V 读数为两电压U 之和, 若电压表 ~ 读数为两电压 12 和U34 之和, 为同名端;反之,若为两电压之差, 则 1 与 3 为同名端;反之,若为两电压之差, 为同名端。 则 1 与 4 为同名端。
电路与模拟电子技术:耦合电感与变压器

21
i1
+
N1
e11
u11
–
N2
e21
s1 漏磁通 11 N111 自感磁链
i1 11
21 互感磁通 21 N 221 互感磁链
自感磁通
21
N 221
M 21
线圈1对线圈2的互感系数,单位:H
i1
i1
电感的耦合和互感
同理
s 2
i2 22
dt
dt
dt
电感的耦合和互感
di1
u11 L1
dt
di2
u22 L2
dt
di1
u21 M 21
dt
di2
u12 M 12
dt
在正弦情况下,相量形式为:
U11 j LI1
U 21
U 21 j M 21 I1
U12 j M 12 I 2
U 22 j LI 2
I1
12
M 12
12
i2
漏磁通
互感磁通
N112
i2
22 N 222 自感磁链
12 N112 互感磁链
线圈2对线圈1的互感系数,单位:H
当线圈周围无铁磁物质(空心线圈)时,有 M12= M21= M。
互感系数 M 只与两个线圈的几何尺寸、匝数 、 相互位置和周
围的介质磁导率有关。
( R1 jωL1 )I 1 jωM I 2 U S
一次侧自阻抗Z11
•
•
jωM I 1 ( R2 jωL2 Z ) I 2 0
二次侧自阻抗Z22
j MI1
I2
电路分析基础耦合电感和理想变压器

电路分析基础耦合电感和理想变压器耦合电感(mutual inductance)是指两个或多个电感器件之间由于相互作用而产生的互感现象,其中一个电感器件的磁通变化会在另一个电感器件中感应出电动势。
理想变压器(ideal transformer)是一种特殊的耦合电感,其工作原理是利用磁感应定律,将输入电压和输出电压之间按一定的变比比例转换。
在电路分析中,耦合电感和理想变压器经常被用来探讨和解决一些特定的问题。
下面将分别介绍其基本原理和应用。
1.耦合电感:耦合电感的基本原理是根据电磁感应定律,当一个电感器件中通过的电流变化时,会在另一个电感器件中感应出电动势。
考虑两个简单的线圈,分别为主线圈和副线圈。
当主线圈中的电流变化时,根据电磁感应定律,在副线圈中也会感应出一个与主线圈中电流变化相关的电动势。
这种相互作用可以由一个耦合系数k表示,取值范围为0-1,表示两个线圈之间磁通的共享程度。
耦合电感可以用于共振电路、振荡电路等。
在共振电路中,当主线圈与副线圈之间有耦合时,可以通过调整耦合系数k来改变电路的共振频率,实现频率调谐的效果。
在振荡电路中,耦合电感可以提供正反馈,增强电路的振荡效果。
2.理想变压器:理想变压器是电路分析中常用的电气元件之一,其特点是无能量损耗、无电阻、无磁滞,能够以一定的变比将输入电压转换为输出电压。
理想变压器的基本结构由两个线圈绕制在共同的磁芯上组成。
理想变压器的工作原理是利用电磁感应定律和电压平衡原理。
当输入线圈(初级线圈)中通过的电流变化时,根据电磁感应定律,在输出线圈(次级线圈)中也会感应出一个与输入电流变化相关的电动势。
由于磁通守恒,输入线圈的磁通变化与输出线圈的磁通变化成一定的比例,从而实现输入电压和输出电压之间的变比转换。
理想变压器可以用于电压调整、功率传递等电路。
在电压调整电路中,通过改变输入线圈和输出线圈的匝数比例,可以实现对输入电压和输出电压之间的调整。
在功率传递电路中,根据变压器的功率平衡原理,输入功率和输出功率之间的关系可以用变压器变比关系表示。
西电第7章 耦合电感和理想变压器

电流。
Im
Usm (1 j2)( j j2)
2 j2
20
(1 j2) ( j j2)
7.2.2 耦合电感的T形等效
[例7.3] 求RL吸收的功率。
由分流公式得:
ILm
1
j j2 j2 j
j2
Im
2(135
)A
RL吸收的均功率:
PL
1 2
I
2 Lm
RL
1 2
22
1W
2W
方法二:戴维南定理法(课后练习)
L L1 L2 2M
第7章 7.2 耦合电感的去耦等 效
7.2.1 耦合电感的串并联等效
1. 耦合电感的串联等效
串联反接如图b,反接就是一对同名端相接,应用KVL:
(a)
u
u1
u2
L1
di( bM)di dt dt
L2
di dt
M
di dt
(L1
L2
2M )
di dt
L
di dt
L L1 L2 2M
2.耦合电感的等效电路 由于耦合电感中的互感反映了一个线圈对另一个线圈的耦
合关系,因此耦合线圈的互感电压可用受控源——电流控制 电压源CCVS等效模型来表示。 参考方向确定方法:
如果电流的参考方向由线圈的同名端流向另一端,那么由这 个电流在另一线圈内产生的互感电压的参考方向由该线圈的同 名端指向另一端。
空芯变压器常有的分析方法:直接列方程法、反映阻抗法、 戴维南等效电路法。
7.3 含空芯变压器的电路分析方法 1. 直接列方程法
如图7.14(a)所示等效电路如图7.14(b)所示,对两个回路列KVL
方程
jL1I1 jMI2 US
耦合电感和变压器电路分析

变压器具有变换电压、电流和阻抗的 功能,能够实现电能的安全传输和分 配。
变压器的物理结构
铁芯
作为磁路,传递磁通, 分为闭合磁路和开放磁
路。
绕组
作为电路,传递电能, 分为一次绕组和二次绕
组。
油箱
作为变压器的外壳,保 护内部结构和绝缘。
其他附件
如分接开关、冷却系统 等。
变压器的电气参数
额定电压
变压器正常工作时的输入和输 出电压值。
行能量传递。
02 03
耦合电感的电路模型
在电路分析中,耦合电感通常用电路模型表示,包括串联和并联两种形 式。串联耦合电感通过一个公共磁路连接,而并联耦合电感则通过各自 的磁路连接。
耦合电感的电压和电流关系
对于串联耦合电感,电压与磁通量成正比,电流与磁通量变化率成正比; 对于并联耦合电感,电流与磁通量成正比,电压与磁通量变化率成正比。
额定电流
变压器正常工作时的输入和输 出电流值。
额定容量
变压器正常工作时的最大输出 功率。
效率
变压器传输电能的有效程度, 通常以百分比表示。
03
耦合电感和变压器的工作 原理
耦合电感器的工作原理
磁耦合
耦合电感器由两个或多个线圈组 成,通过磁场相互耦合。当一个 线圈中的电流发生变化时,会在 另一个线圈中产生感应电动势。
互感现象
当一个线圈中的电流发生变化时, 会在另一个线圈中产生感应电动 势,这个电动势的大小与两个线 圈之间的互感系数和电流的变化
率成正比。
电压和电流关系
在耦合电感器中,电压和电流之 间存在一定的相位差,这取决于
线圈的匝数比和耦合系数。
变压器的工作原理
电压变换
变压器通过改变线圈匝数比,实现输入和输出电 压之间的变换。
第七章耦合电感与变压器答案01
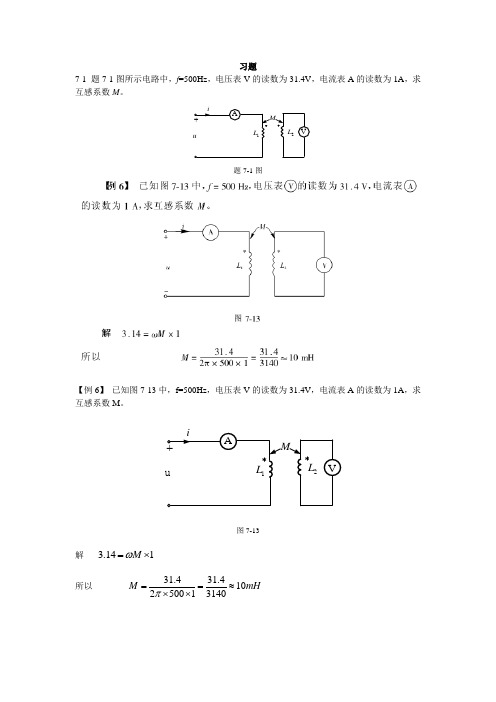
习题7-1 题7-1图所示电路中,f =500Hz ,电压表V 的读数为31.4V ,电流表A 的读数为1A ,求互感系数M 。
题7-1图【例6】 已知图7-13中,f=500Hz ,电压表V 的读数为31.4V ,电流表A 的读数为1A ,求互感系数M 。
图7-13解 3.141M ω=⨯ 所以 31.431.410250013140M mH π==≈⨯⨯7-2 电路如题7-2图 (a)、(b)所示,写出端口电压与电流的关系式。
12122(a)(b)题7-2图例 7-1 电路如图7-6 (a)、(b)所示,写出端口电压与电流的关系式。
M12i M122(a ) (b)图7-6 例7-1 图解 图7-6(a)所示电路,两线圈端口的电压与电流均为关联参考方向,故互感部分均为正;电流2i 从标有“·”的端子流入,因此数值为2d d i Mt的互感电压,其“+”极性端位于第一个线圈的同名端处,即标有“·”的端子上;同理,电流1i 感应到第二个线圈的互感电压1d d i Mt,其“+”极性端位于电流1i 流入端子的同名端处,所以有 1211d d d d i i u L M t t =+,2122d d d d i i u L M t t=+对于图7—6(b )所示电路,第一个线圈的电压与电流为关联参考方向,故其自感电压表达式前取“+”, 互感电压2d d i Mt的“+”极性端是在与电流2i 流入端的同名端处,即“·”端子处,故其互感电压表达式前取“—”;第二个线圈的电压与电流为非关联参考方向,故其互感电压表达式前取“—”,故互感电压1d d i Mt的“+”极性端是在与电流1i 流入端的同名端处,即没有标“·”的端子上,故互感电压表达式前取“+”。
于是1211d d d d i i u L M t t =-,2122d d d d i iu L M t t=-+ 若互感线圈是处在正弦交流稳态电路中,电压、电流的关系式可以用相量形式表示11122221j j j j U L I MI U L I MI w w w w üï=北ïýï=北ïþ(7—13) 自感电压、互感电压前取“+”还是取“—”,须根据电压、电流的参考方向以及两线圈的同名端关系确定。
电路第7章含有耦合电感的电与变压器精品文档

i 1 2 2 c o s ( 2 0 0 0 t 5 3 . 1 ) A u 2 8 2 c o s ( 2 0 0 0 t 3 6 . 9 ) V
开关S闭合时:
U 1 (R 1 jL 1 )I 1 jM I 2 (R 2jL 2)I2jM I1 = 0
dt
M
di1 dt
线圈1的自感电压 线圈2的互感电压
u11
e1
L1
d i1 dt
u 21 e2 M
d i1 dt
e 1 称为自感电动势 e 2 称为互感电动势
返回
电路分析基础
第7章 含有耦合电感的电路与变压器
同理:对于b)图有
e1
d12
dt
M
di2 dt
e2
返回
电路分析基础
第7章 含有耦合电感的电路与变压器
(2)反接 (同名端相连)
u
u1
u2
L1
di dt
M
di dt
L2
di dt
M
di dt
di (L1 L2 2M) dt
Ldi dt
相量式为 U U 1 U 2 j(L 1 L 2 2 M )I
返回
电路分析基础
返回
电路分析基础
第7章 含有耦合电感的电路与变压器
【例7.3】如图电路中,输入电压 u1102co2s0t0V 0,
R1 3,L 1 2 m ,L 2 3 H m , M H 2 m , R 2 H 8 。
i 试求开关S打开与闭合时的 1 和u 2 。
电路应用基础(姚建永)章 (7)

10
若k=0,说明两线圈无耦合;而k=1则为全耦合。k愈大, 说明互感磁通在自感磁通中占的比例愈大,两线圈的耦合则 愈紧密。
耦合系数的大小与两线圈的相对位置有关。如果两线圈 彼此靠近且互相平行,或紧密绕在一起,则k值有可能接近 于1;反之,如果它们相距很远,或者它们的轴线互相垂直, 如图7-1-3所示,则k值将很小,甚至可能为零。因此,通过 调整两线圈的相对位置,可以改变耦合系数的大小,当L1、 L2一定时,也就相应地改变了互感系数M的大小。
41
7.3.1 耦合电感的串联 耦合电感串联有两种接法,如果串联时把异名端相接,
19
1.同名端的定义 若彼此有互感的两线圈分别有电流流入,且两电流建立 的磁场互相加强,则两电流的流入端为两线圈的同名端(当 然,两电流的流出端也是同名端)。同名端以相同的记号 “·”或“*”标注。如果知道互感线圈的相对绕向,则很 容易根据定义确定它们的同名端。如图7-2-1所示,当电流i1、 i2分别从a端、a¢端流入互感线圈①、②时,根据右手定则可 判断,i1和i2建立的磁场是互相加强的,即端a和端a¢为线圈 ①和②的同名端。图中在a端和a¢端分别标注了“*”号。
在理想情况下,由电磁感应定律得知
u21
d 21
dt
d (M i1 ) dt
M
d i1 dt
(7-1-4)
14
与此类似,如果线圈②中有电流i2通过,则i2变化也要引起 它在线圈①中所建立的互感磁链Y12的变化,从而在线圈①中 感应出互感电压u12。当u12的参考方向与F12的参考方向关联 时,有
u12
d12
dt
d(Mi2 ) dt
M
d i2 dt
(7-1-5)
形式上式相(7似-,1-但4)电、感式元(7件-1的-5V)与CR是电同感一元个件元的件VC的R即电u压L 与L 电dditL流
§13-5___耦合电感与理想变压器的关系

我们介绍了耦合电感和理想变压器两种电路元件,其 电压电流关系如下所示,一个是双口动态元件,另一个是 电阻双口元件,它们都是从具有互感耦合的线圈抽象出的 理想电路元件,为什么要提出两种电路元件?它们之间的
关系如何?
di1 di 2 u1 L1 M dt dt di1 di 2 u2 M L2 dt dt
I 2
i1 ( t ) 2 2 cos(103 t 53.1 )A
i2 ( t ) 2 2 cos(103 t 3.69 )A
图13-21
根据最大功率传输定理,当负载为
Z L Z o (0.5 j1.8)
时可获得最大功率
2 U oc 5 W 2.5W 4 Ro 4 0.5
di1 di2 u1 di1 u1 L1 L1 L2 dt dt L1 dt 1 u1dt i1 L1
L2 di2 L1 dt
L2 L1 i2 0 i2 i1 ni1 L1 L2
u1 nu2 i2 ni1
以上讨论表明:用导线绕制的磁耦合线圈,在忽略导 线和磁心(或铁心)损耗的条件下,可以用一个耦合电感或 两个电感和一个变压器的组合作为它的电路模型。
图13-21
Zi (3 j4)
再计算出电流
(2 j1)V U oc
Zo (0.5 j1.8)
j1 2 36.9 A I 1 j1 1 j1
U 10 0 S I A 2 53 . 1 1 Zi 3 j4
(a)
(b)
k=1
N1 n N2 Lm L1 LS 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A、B为同名端,B、C为同名端,但A、C不一定 是同名端。
(2) 互感电压的符号有两重含义:同名端;参考方向
互感现象的利与弊: 利用——变压器:信号、功率传递 避免——干扰 克服:合理布置线圈相互位置减少互感作用。
7. 2 耦合电感电路的分析
Mddti
(L1 L2 2M)ddti L反串ddti
i + u –
L反串
L 反 串 L 1L 2 2M
互感的测量方法:
* 顺接一次,反接一次,就可以测出互感:
M L顺 L反 4
二、互感线圈的并联
•
I1
j M
•
I2
+
*
•
U1
j L1
+
*
j L2
•
U2
_
_
U 1jω L 1I 1jω M I 2 U 2jω M I 1jω L 2I 2
L 1— — 自 感 抗 ( ) M — — 互 感 抗 ( ) j L 1 — — 自 感 阻 抗 ( ) j M — — 互 感 阻 抗 ( )
第7章 耦合电感与变压器
7. 1 互感和互感电压 7. 2 耦合电感电路的分析 7. 3 空芯变压器电路分析 7. 4 理想变压器和全耦合变压器 7. 5 变压器的电路模型
7. 1 互感和互感电压
一、 互感和互感电压 11
21
N1 i1
+ u11 –
N2 + u21 –
当线圈1中通入电流i1时,在线圈1中产生磁通(magnetic flux),同时,有部分磁通穿过临近线圈2。
u 1 1d d Ψ t 1 1N 1d d Φ t11 u 2 1d d Ψ t2 1N 2d d Φ t21
u11:自感电压; u21:互感电压。 :磁链 (magnetic linkage)
当线圈周围无铁磁物质(空心线圈)时,有
u 11L 1d d it1
u21 M 21d d it1
12
d ef
L1
11 i1
def
M 21
21 i1
线圈1的自感系数 (self-inductance coefficient)
线圈1对线圈2的互感系数,单位:H (mutual inductance coefficient)
当i1与u11关联取向;u21与磁通符合右手螺旋法则时, 根据电磁感应定律和楞次定律:
i1 +
L1 u1 +
M d i2
d t_
i2
+
L2
+
M
u2
d i1
_ dt _
I1
+
j L1
U1
+
j _
M
I
2_
I2
+
j L2
+
U2
j _
M
I1
_
互感的时域等效模型
互感的等效相量模型
注:上图中将互感电压用受控电压源表示后,L1 与L2就
不再具有耦合关系。
注意:
(1) 一个线圈可以不只和一个线圈有磁耦合关系;
def
k
M
L1 L2
可以证明, 0 k1
全耦合(perfect coupling): K=1
紧耦合
K≈1
无耦合(孤立电感)
K=0
M L1L2 M m ax L1L2
(K 1, 即 全 耦 合 时 )
互感小于两元件自感的几何平均值。
二、互感线圈的同名端 具有互感的线圈两端的电压包含自感电压和互感电
压。表达式的符号与参考方向和线圈绕向有关。
互感的性质
u1
u11
u12
L1
di1 dt
Mdi2 dt
u2
u21
u22
M di1 dt
L2
di2 dt
①可以证明,M12=M21=M
②互感系数 M 只与两个线圈的几何尺寸、匝数 、 相互位置 和周围的介质磁导率有关。
耦合系数 (coupling coefficient)k:
k 表示两个线圈磁耦合的紧密程度。
22
N1
i2
N2
+ u12 – + u22 –
自 感 电 压 u22d dt22 N2d dt22L2d dit2
互 感 电 压 u12d dt12N1dd t12 M 12d dit2
(L2 i222) (M 12 i212)
可以证明:M12= M21= M。
当两个线圈同时通以电流时,每个线圈两端的电压均包 含自感电压和互感电压:
i1 M
*
+
L1
L2 *
_uM
uM
M
di1 dt
i1 M i2
i1 M i2
+* u_1 L1
*+ L2 _u2
+* u_1 L1
+ L2 _u2 *
时域形式:
u1
L1ddit1
Mdi2 dt
u1
L1ddit1
Mdi2 dt
u2
Mdi1 dt
L2
di2 dt
u2
Mdi1 dt
L2ddit2
在正弦交流电路中,其相量形式的方程为
另一线圈中互感电压的高电位端为其相应的同名端。
例.
1•*
2
3
1'
2'*
3' •
同名端的实验测定: R S1i *
1'
*2
+
V –
2'
如图电路,当开关S突然闭合时,i增加,
di0, dt
u2'2M d dti0
电压表正偏。
当两组线圈装在黑盒里,只引出四个端线组,要确定 其同名端,就可以利用上面的结论来加以判断。
对自感电压: 当u11, i 1关联取向 当u11, i1 非关联取向
u11
L1
di1 dt
u11L1
di1 dt
对互感电压,因产生该电压的的电流在另一线圈上, 因此,要确定其符号,就必须知道两个线圈的绕向。这在 电路分析
+ u11 –
0
N2
N3
*
•
+ u21 – + u31 –
u 21
M 21
di1 dt
u 31
M 31
d i1 dt
引入同名端可以解决这个问题。
同名端:当两个电流分别从两个线圈的对应端子流入 ,其所
产生的磁场相互加强时,则这两个对应端子称为同名端,
否则为异名端。
同名端表明了线圈的相互绕法关系。
同名端的另一种定义: 当随时间增大的时变电流从一线圈的一端流入时,则
一、互感线圈的串联
1. 顺串
i
i
+
+*
u
u1 –
L1 M
+*
–
u2 L2 –
+
u
L顺串
–
uL1
di dt
Mddti
L2
di dt
Mddti
(L1 L2 2M)ddti L顺串ddti
L 顺 串 L 1L 22M
2. 反串
i
+
u
–
+*
u1 L1
– +
M
u2 –
L2 *
uL1
di dt
Mddti
L2
di dt
当S突然闭合时: 电压表若正偏,则1、2为同名端 电压表若反偏,则1、2`为同名端
三、由同名端及u,i参考方向确定互感线圈的特性方程
互感电压的正负号判定规则:
当电流的流入端与该电流引起的互感电压的参考正极 端为同名端时,互感电压取正号,反之,取负号。
i1 M
* *+
L1
L2 _uM
uM
M
di1 dt
